A Novel High-Efficiency Variable Parameter Double Integration ZNN Model for Time-Varying Sylvester Equations
Abstract
1. Introduction
- A new variable-parameter double integration model (HEVPDIZNN) is proposed to solve time-varying Sylvester matrix equations. This model introduces a novel, simpler, and more efficient time-varying parameter function. Unlike previously used increasing parameter functions, this paper selects a monotonically decreasing function that gradually converges to a constant, improving the feasibility of the model and achieving efficient resource allocation.
- We provide theoretical proofs of the convergence and robustness of the HEVPDIZNN model under scenarios of no noise, constant noise, and linear noise.
- Comprehensive experiments are conducted to compare the proposed HEVPDIZNN model with other methods designed in this paper, as well as with existing ZNN models for solving time-varying Sylvester matrix equations. On one hand, the experiments validate that the method of combining monotonically decreasing time-varying parameters with double integration outperforms methods using monotonically increasing time-varying parameters with double integration, fixed-parameter double integration, and activation functions combined with double integration. Additionally, the experiments demonstrate the enhanced performance of the HEVPDIZNN model as the maximum and minimum design parameters increase. On the other hand, the experiments confirm that the HEVPDIZNN model achieves faster solution speed, lower average error, and smaller error variance compared to existing ZNN models under different initial values and noise conditions, including constant noise, linear noise, and quadratic noise.
2. Problem Description and Model Introduction
2.1. Time-Varying Sylvester Matrix Equation
2.2. The Design Process of the HEVPDIZNN Model
3. Theoretical Analyses
3.1. Convergence Analysis
3.2. Robustness Analysis
4. Experiments
4.1. Example A
4.1.1. Performance Comparison of DIZNN Models with Various Parameters
4.1.2. Comparison Between HEVPDIZNN and Activation Function-Based DIZNN Models
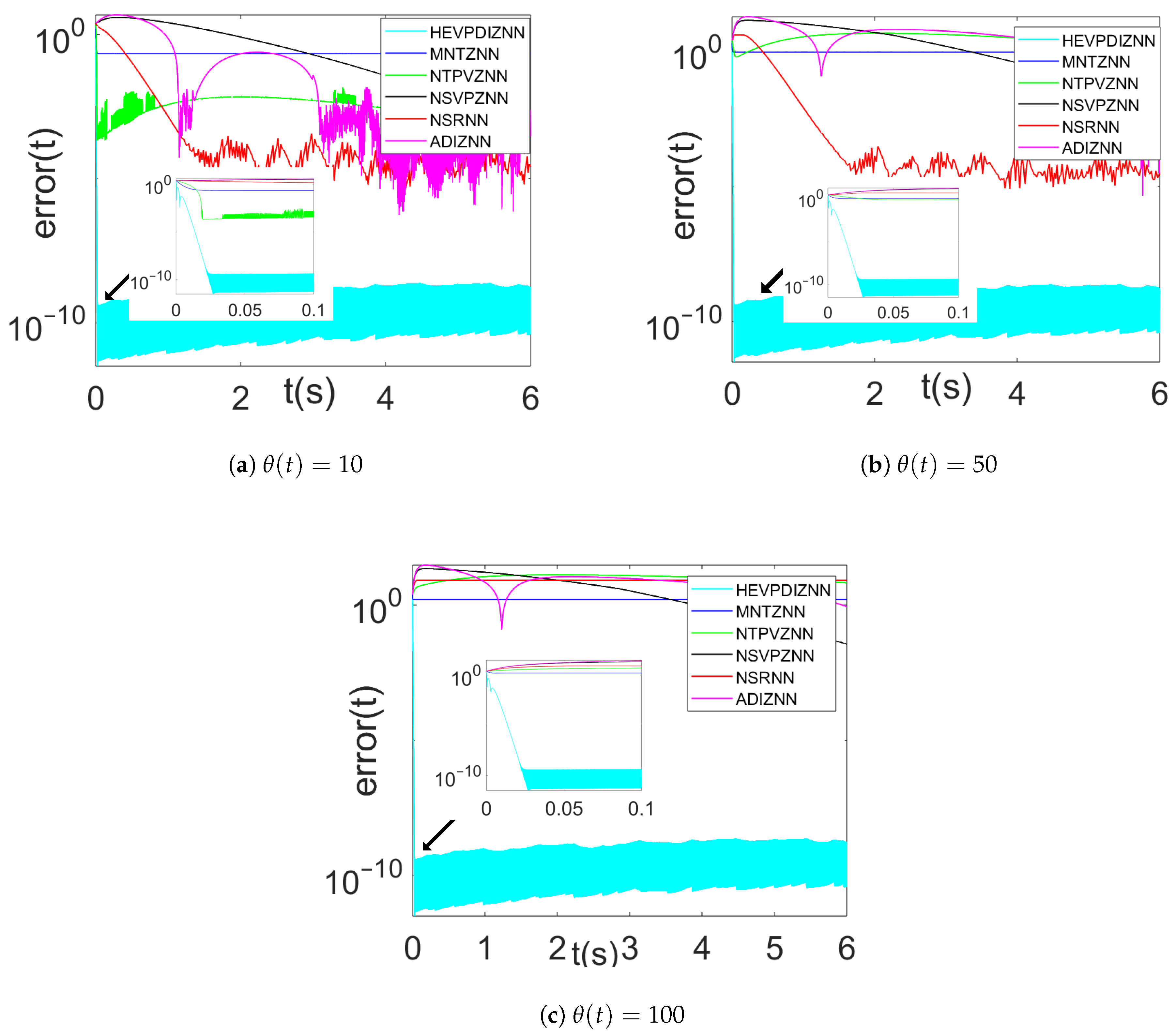
4.1.3. Comparison of Different Parameters of HEVPDIZNN Model
4.2. Example B
4.2.1. Comparison of Different Error Initial Values in Noiseless
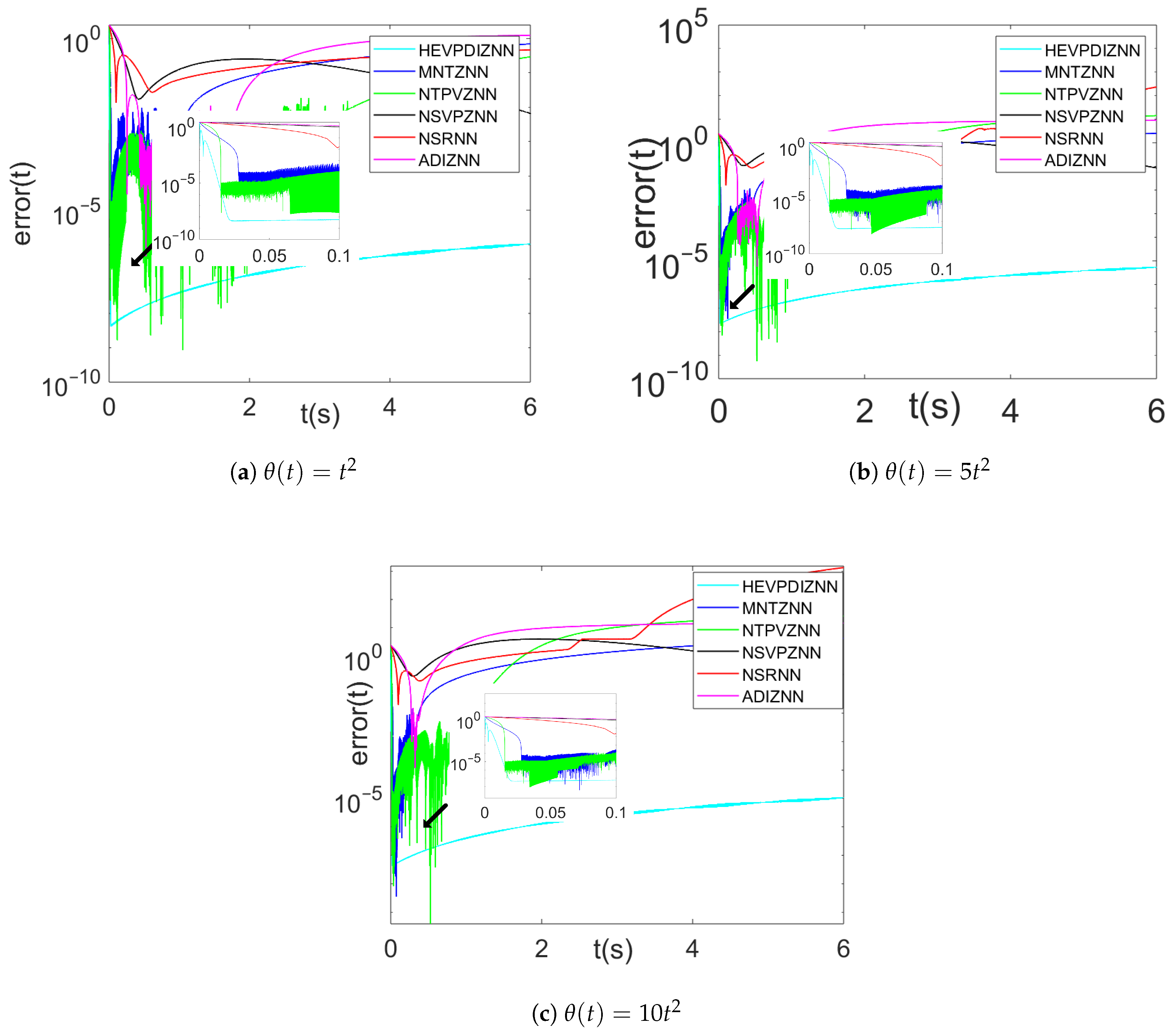
4.2.2. Comparison Under Different Noise Environments
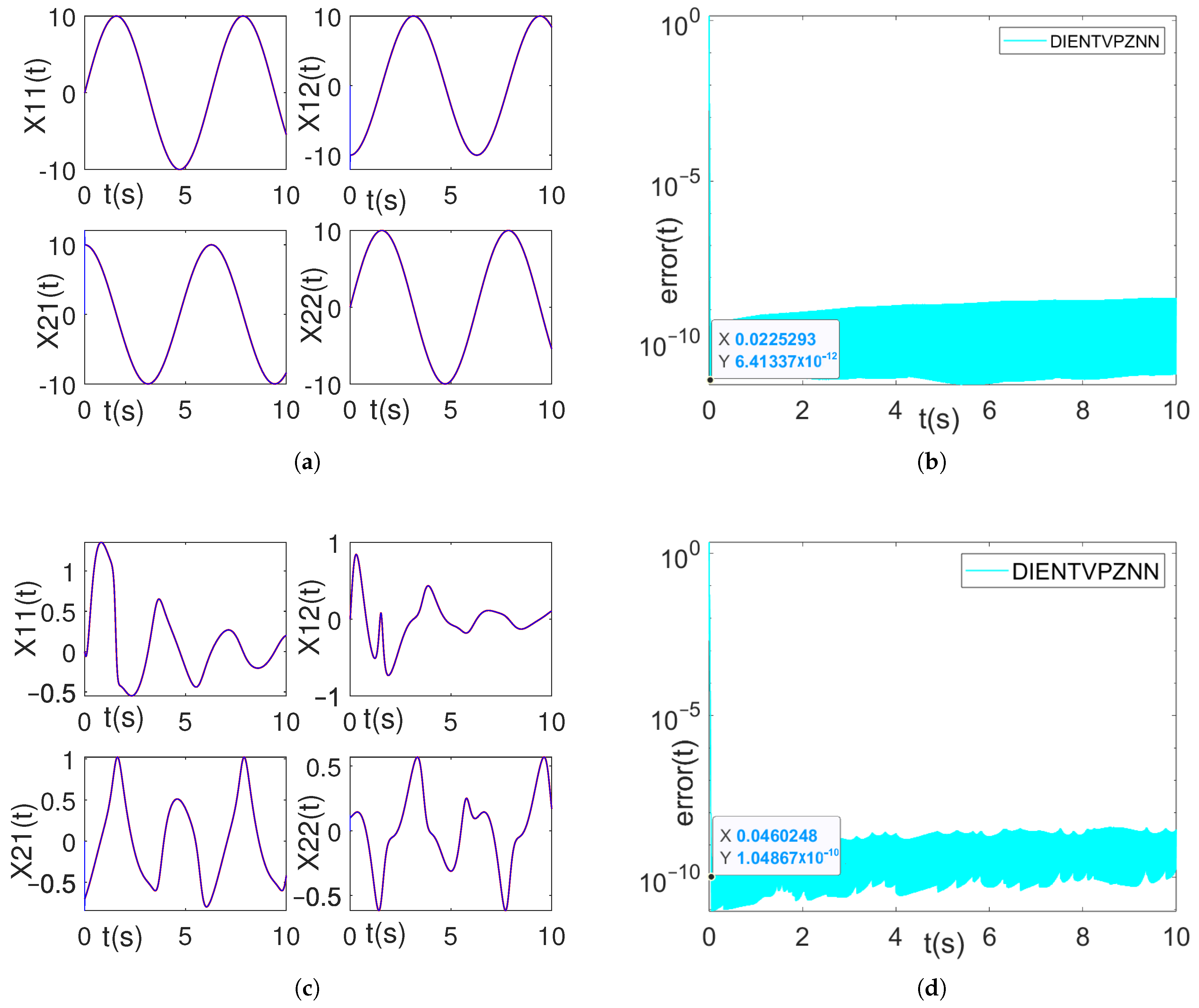
4.3. Example C
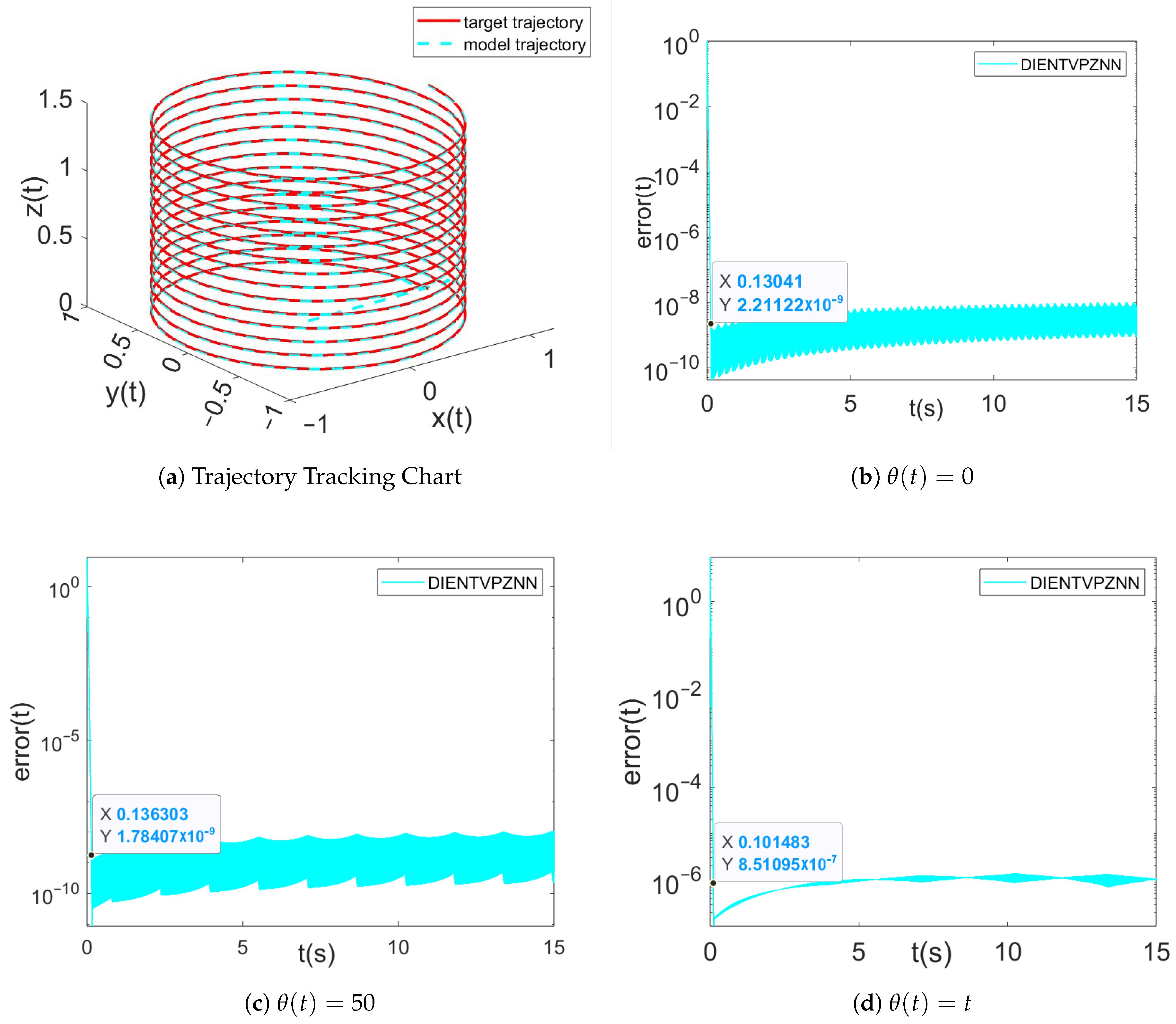
5. Applications in Target Tracking
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, D.Y.; Reichel, L. Krylov-subspace methods for the Sylvester equation. Linear Algebra Its Appl. 1992, 172, 283–313. [Google Scholar] [CrossRef]
- Darouach, M. Solution to Sylvester equation associated to linear descriptor systems. Syst. Control Lett. 2006, 55, 835–838. [Google Scholar] [CrossRef]
- Tan, Z. Fixed-time convergent gradient neural network for solving online Sylvester equation. Mathematics 2022, 10, 3090. [Google Scholar] [CrossRef]
- Fang, L.; He, N.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Extinction Profiles Fusion for Hyperspectral Images Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1803–1815. [Google Scholar] [CrossRef]
- Jin, L.; Yan, J.; Du, X.; Xiao, X.; Fu, D. RNN for solving time-variant generalized Sylvester equation with applications to robots and acoustic source localization. IEEE Trans. Ind. Inform. 2020, 16, 6359–6369. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Shepelev, I.I.; Sherkunov, V.V.; Simos, T.E.; Mourtas, S.D.; Katsikis, V.N. A novel quaternion linear matrix equation solver through zeroing neural networks with applications to acoustic source tracking. AIMS Math. 2023, 8, 25966–25989. [Google Scholar] [CrossRef]
- Xiao, L.; He, Y. A noise-suppression ZNN model with new variable parameter for dynamic Sylvester equation. IEEE Trans. Ind. Inform. 2021, 17, 7513–7522. [Google Scholar] [CrossRef]
- Zheng, B.; Han, Z.; Li, C.; Zhang, Z.; Yu, J.; Liu, P.X. A flexible-predefined-time convergence and noise-suppression ZNN for solving time-variant Sylvester equation and its application to robotic arm. Chaos Solitons Fractals 2024, 178, 114285. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, Y. Zeroing neural network with coefficient functions and adjustable parameters for solving time-variant Sylvester equation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 6757–6766. [Google Scholar] [CrossRef]
- Lee, D.; Thimmaraya, R.; Nataraj, C. Linear Time-varying Tracking Control With Application to Unmanned Aerial Vehicle. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010. [Google Scholar]
- Bartels, R.H.; Stewart, G.W. Algorithm 432 [C2]: Solution of the matrix equation AX + XB = C [F4]. Commun. ACM 1972, 15, 820–826. [Google Scholar] [CrossRef]
- Golub, G.; Nash, S.; Van Loan, C. A Hessenberg-Schur method for the problem AX + XB = C. IEEE Trans. Autom. Control 1979, 24, 909–913. [Google Scholar] [CrossRef]
- Li, S.; Ma, C. An improved gradient neural network for solving periodic Sylvester matrix equations. J. Frankl. Inst. 2023, 360, 4056–4070. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Wang, J. A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans. Neural Netw. 2002, 13, 1053–1063. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Qiu, L. A robust fast convergence zeroing neural network and its applications to dynamic Sylvester equation solving and robot trajectory tracking. J. Frankl. Inst. 2022, 359, 3183–3209. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Zhao, L.; Chen, L.; Tang, Z. A nonlinear zeroing neural network and its applications on time-varying linear matrix equations solving, electronic circuit currents computing and robotic manipulator trajectory tracking. Comput. Appl. Math. 2022, 41, 319. [Google Scholar] [CrossRef]
- He, Y.; Xiao, L.; Sun, F.; Wang, Y. A variable-parameter ZNN with predefined-time convergence for dynamic complex-valued Lyapunov equation and its application to AOA positioning. Appl. Soft Comput. 2022, 130, 109703. [Google Scholar] [CrossRef]
- Li, S.; Li, Y. Nonlinearly activated neural network for solving time-varying complex Sylvester equation. IEEE Trans. Cybern. 2013, 44, 1397–1407. [Google Scholar] [CrossRef]
- Xiao, L.; Yi, Q.; Zuo, Q.; He, Y. Improved finite-time zeroing neural networks for time-varying complex Sylvester equation solving. Math. Comput. Simul. 2020, 178, 246–258. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, Y.; Dai, J.; Li, J.; Li, W. New noise-tolerant ZNN models with predefined-time convergence for time-variant Sylvester equation solving. IEEE Trans. Syst. Man. Cybern. Syst. 2019, 51, 3629–3640. [Google Scholar] [CrossRef]
- Zhang, M.; Zheng, B. Accelerating noise-tolerant zeroing neural network with fixed-time convergence to solve the time-varying Sylvester equation. Automatica 2022, 135, 109998. [Google Scholar] [CrossRef]
- Han, C.; Zheng, B.; Xu, J. A modified noise-tolerant ZNN model for solving time-varying Sylvester equation with its application to robot manipulator. J. Frankl. Inst. 2023, 360, 8633–8650. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Weng, J.; Mao, Y.; Lu, W.; Xiao, L. A new varying-parameter recurrent neural-network for online solution of time-varying Sylvester equation. IEEE Trans. Cybern. 2018, 48, 3135–3148. [Google Scholar] [CrossRef] [PubMed]
- Gerontitis, D.; Behera, R.; Tzekis, P.; Stanimirović, P. A family of varying-parameter finite-time zeroing neural networks for solving time-varying Sylvester equation and its application. J. Comput. Appl. Math. 2022, 403, 113826. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Qiu, L.; Zhu, J.; Liu, H. A noise tolerant parameter-variable zeroing neural network and its applications. Math. Comput. Simul. 2023, 207, 482–498. [Google Scholar] [CrossRef]
- Lei, Y.; Luo, J.; Chen, T.; Ding, L.; Liao, B.; Xia, G.; Dai, Z. Nonlinearly activated IEZNN model for solving time-varying Sylvester equation. IEEE Access 2022, 10, 121520–121530. [Google Scholar] [CrossRef]
- Liao, B.; Han, L.; Cao, X.; Li, S.; Li, J. Double integral-enhanced Zeroing neural network with linear noise rejection for time-varying matrix inverse. CAAI Trans. Intell. Technol. 2024, 9, 197–210. [Google Scholar] [CrossRef]
- Han, L.; He, Y.; Liao, B.; Hua, C. An accelerated double-integral ZNN with resisting linear noise for dynamic Sylvester equation solving and its application to the control of the SFM chaotic system. Axioms 2023, 12, 287. [Google Scholar] [CrossRef]
- Mishra, P.K.; Saroha, G. A study on video surveillance system for object detection and tracking. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; pp. 221–226. [Google Scholar]
- Dai, J.; Li, Y.; Xiao, L.; Jia, L. Zeroing neural network for time-varying linear equations with application to dynamic positioning. IEEE Trans. Ind. Inform. 2021, 18, 1552–1561. [Google Scholar] [CrossRef]


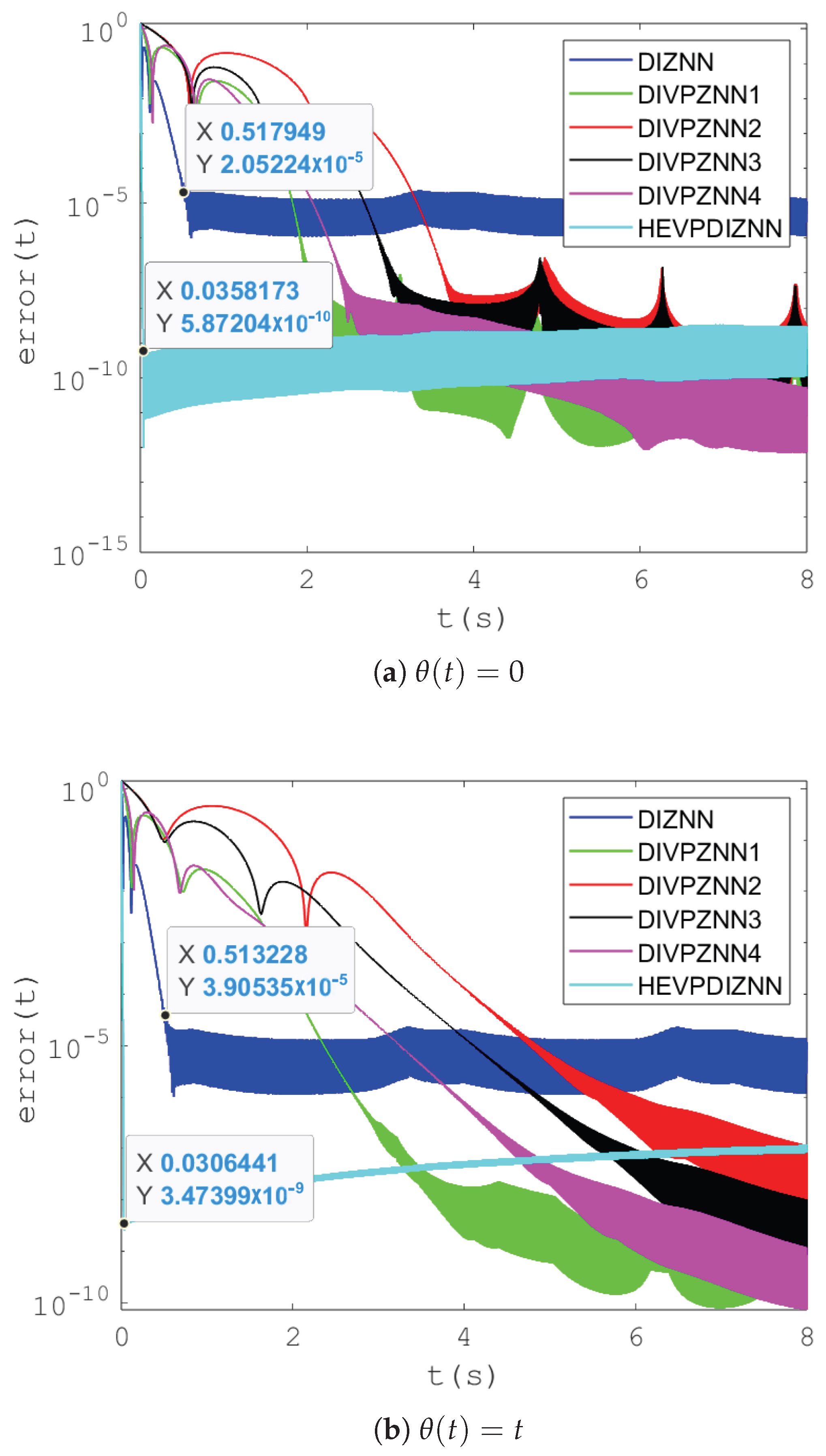
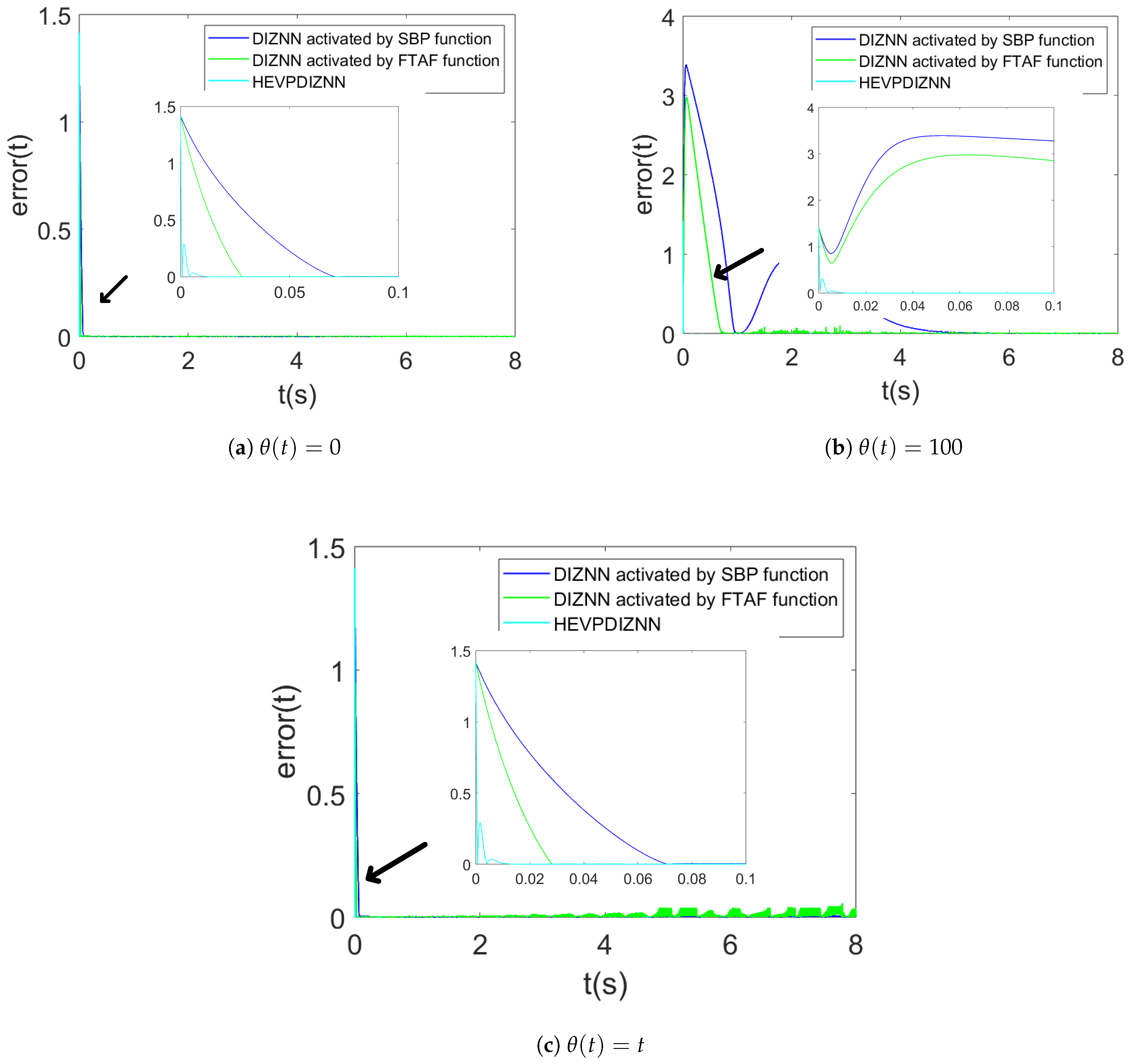


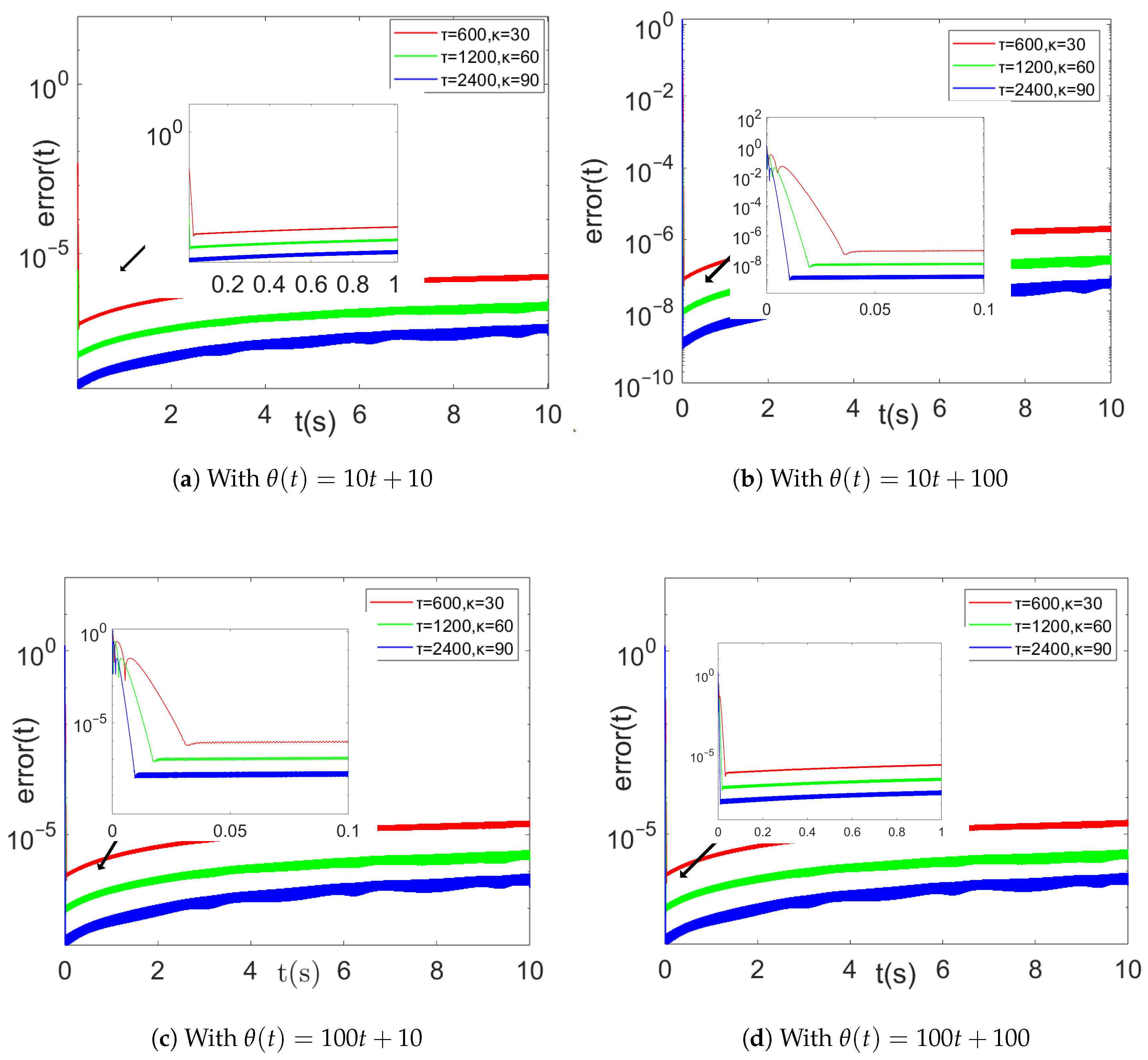
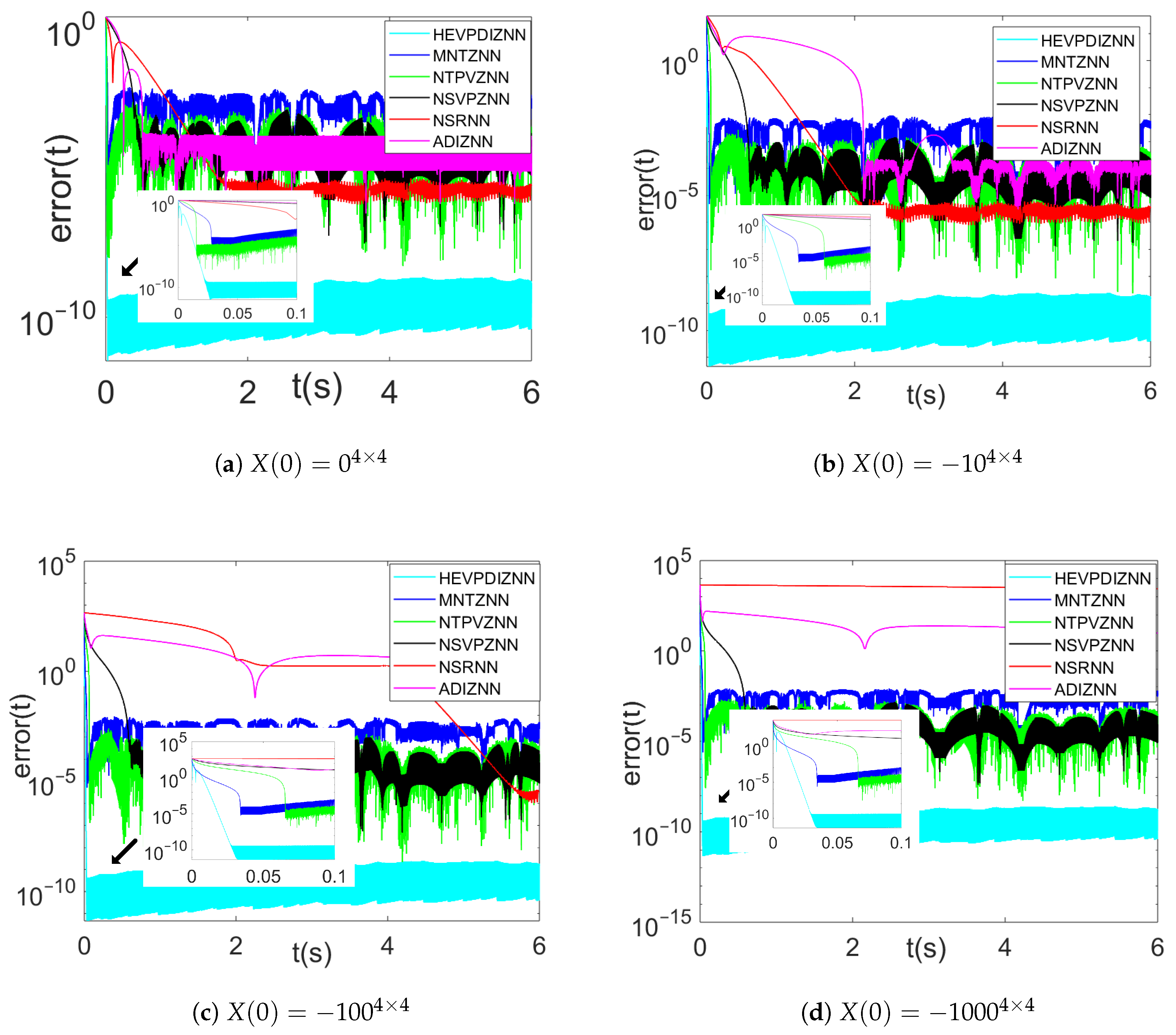

| Integral Time | 8 s | 12 s | 14 s | |
|---|---|---|---|---|
| Model | ||||
| DIZNN | 0.36 s | 0.58 s | 0.67 s | |
| DIVPZNN1 | 92.10 s | 781.96 s | 1250.82 s | |
| DIVPZNN2 | 4.55 s | 112.24 s | 829.76 s | |
| DIVPZNN3 | 4.94 s | 252.27 s | 1694.25 s | |
| DIVPZNN4 | 4.53 s | 1804.89 s | 11,817.15 s | |
| HEVPDIZNN | 9.54 s | 10.96 s | 10.43 s | |
| Model | Activation Function | Design Parameter | Parameter Settings |
|---|---|---|---|
| MNTZNN [22] | |||
| NTPVZNN [25] | |||
| NSVPZNN [7] | |||
| NSRNN [5] | |||
| ADIZNN [28] | |||
| HEVPDIZNN (this work) | NO |
| Noise | HEVPDIZNN | MNTZNN | NTPVZNN | NSVPZNN | NSRNN | ADIZNN |
|---|---|---|---|---|---|---|
| 0 | 7.86 | |||||
| 10 | 7.86 | |||||
| t | 1.83 | |||||
| 3.26 |
| Noise | HEVPDIZNN | MNTZNN | NTPVZNN | NSVPZNN | NSRNN | ADIZNN |
|---|---|---|---|---|---|---|
| 0 | ||||||
| 10 | ||||||
| t | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Huang, Y.; Xu, H. A Novel High-Efficiency Variable Parameter Double Integration ZNN Model for Time-Varying Sylvester Equations. Mathematics 2025, 13, 706. https://doi.org/10.3390/math13050706
Peng Z, Huang Y, Xu H. A Novel High-Efficiency Variable Parameter Double Integration ZNN Model for Time-Varying Sylvester Equations. Mathematics. 2025; 13(5):706. https://doi.org/10.3390/math13050706
Chicago/Turabian StylePeng, Zhe, Yun Huang, and Hongzhi Xu. 2025. "A Novel High-Efficiency Variable Parameter Double Integration ZNN Model for Time-Varying Sylvester Equations" Mathematics 13, no. 5: 706. https://doi.org/10.3390/math13050706
APA StylePeng, Z., Huang, Y., & Xu, H. (2025). A Novel High-Efficiency Variable Parameter Double Integration ZNN Model for Time-Varying Sylvester Equations. Mathematics, 13(5), 706. https://doi.org/10.3390/math13050706






