Travelling Waves in Neural Fields with Continuous and Discontinuous Neuronal Activation
Abstract
1. Introduction
2. Preliminary Work
3. Main Results
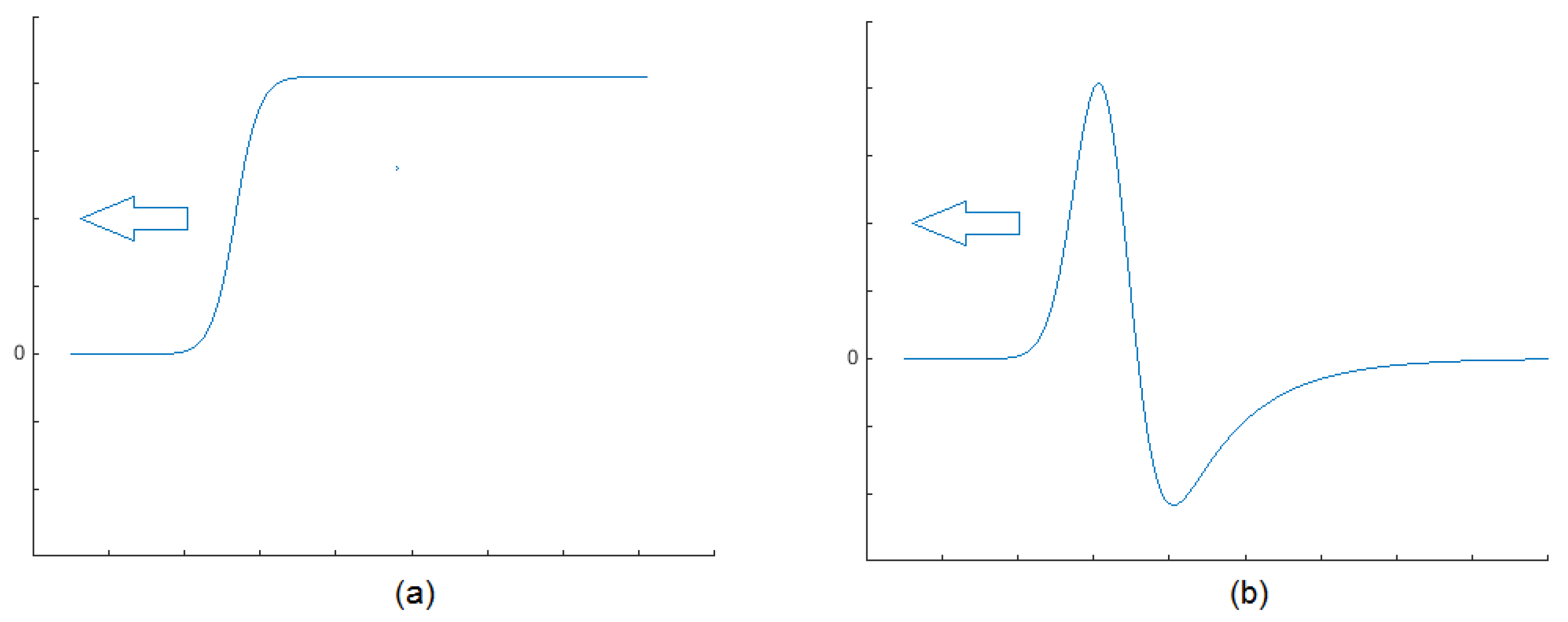
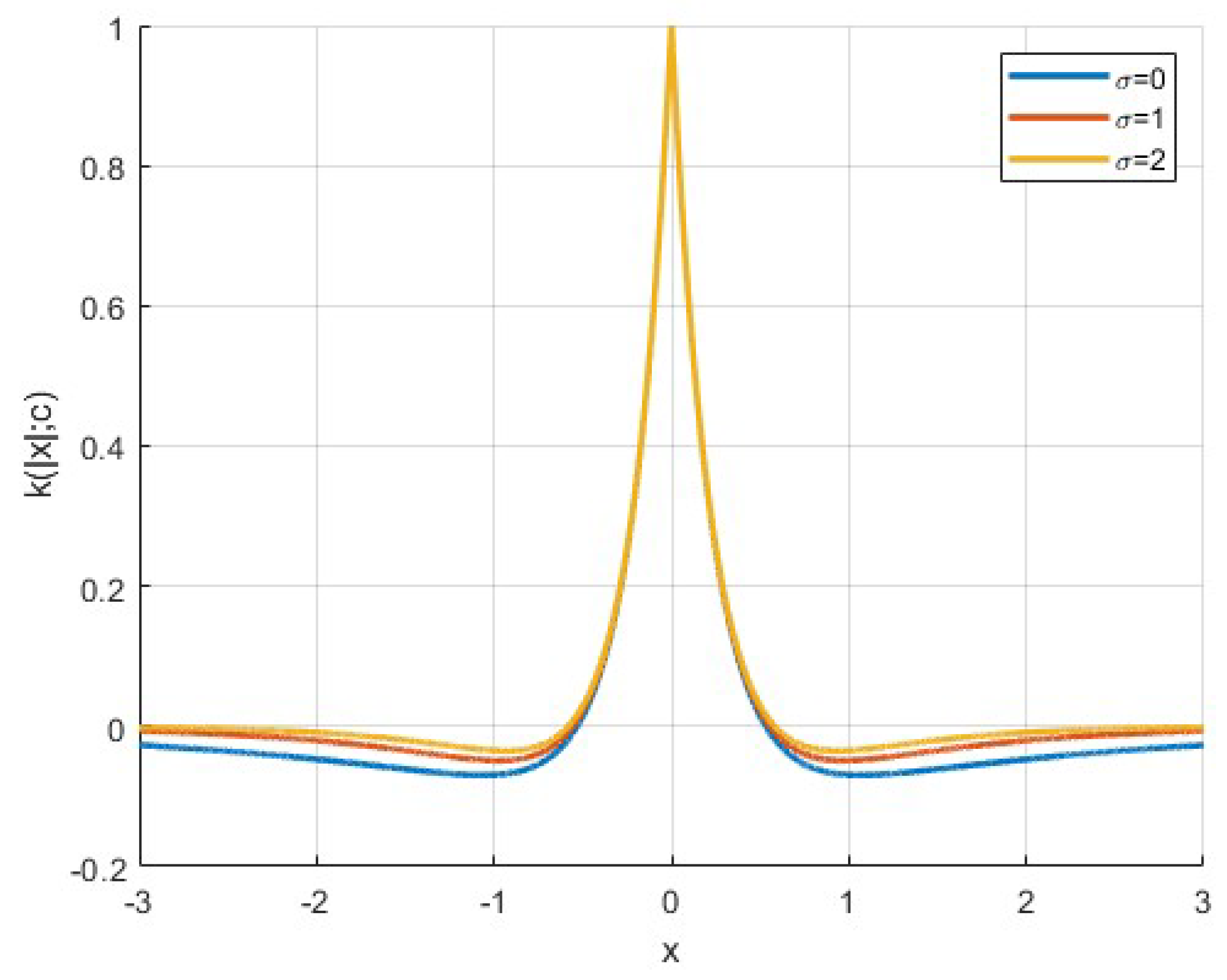
3.1. Problem Setting
- (i)
- uniformly on for ;
- (ii)
- For any , uniformly on for .
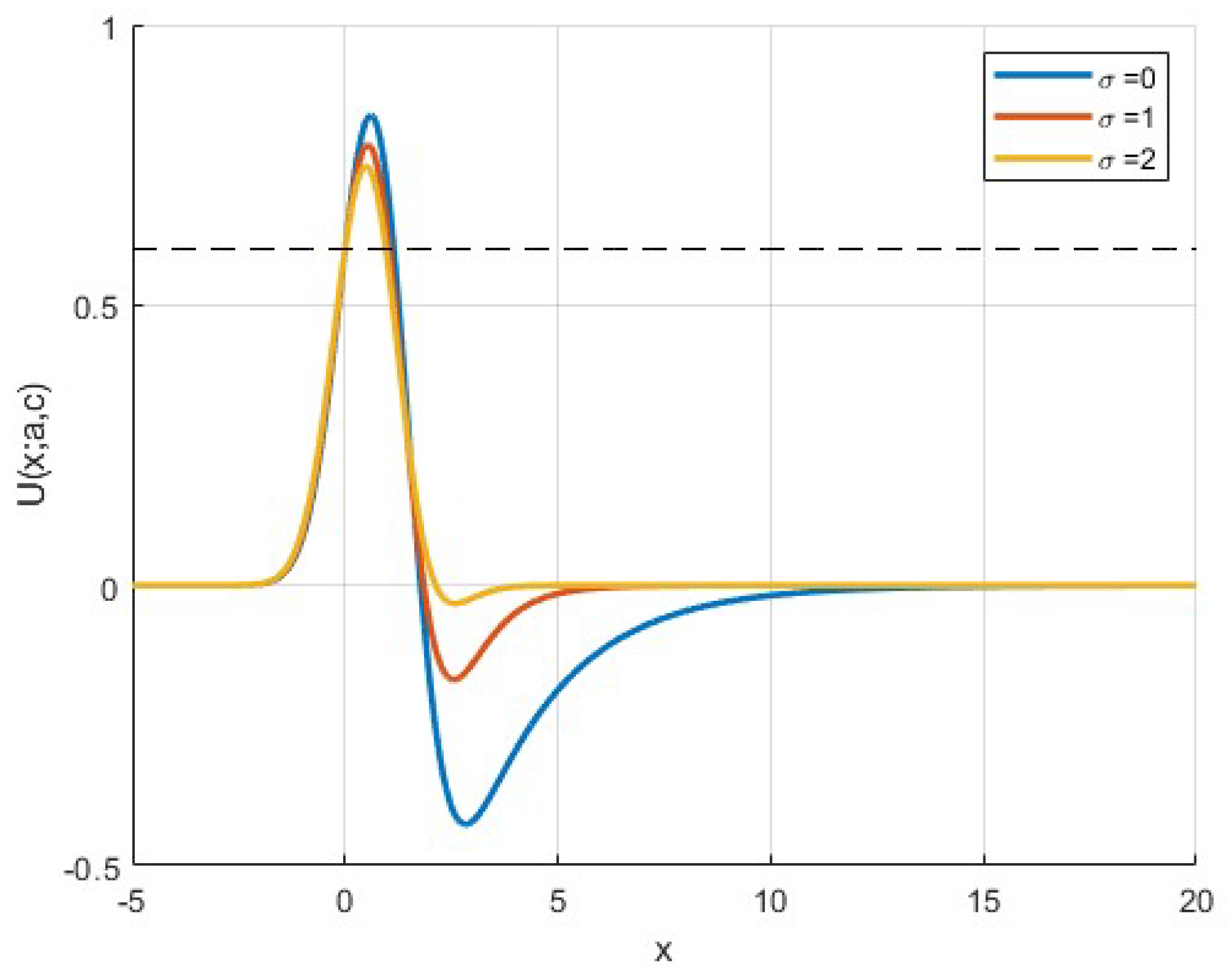
3.2. Existence and Continuous Dependence of Travelling Wave Profiles on Firing Rate Functions
- (i)
- is continuous on ;
- (ii)
- The operators are collectively compact.
3.3. Existence and Continuous Dependence of Travelling Waves on Firing Rate Functions
4. Conclusions and Further Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| e.g., | exempli gratia (for example) |
| EEG | electroencephalography |
| MEG | magnetoencephalography |
References
- Davis, Z.W.; Muller, L.; Trujillo, J.-M.; Sejnowski, T.; Reynolds, J. Spontaneous travelling cortical waves gate perception in awake behaving primates. Nature 2020, 587, 432–436. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Brincat, S.L.; Lundqvist, M.; Miller, E.K. Traveling waves in the prefrontal cortex during working memory. PLoS Comput. Biol. 2022, 18, e1009827. [Google Scholar] [CrossRef]
- Butler, K.; Cruz, L. Neuronal traveling waves form preferred pathways using synaptic plasticity. Comput. Neurosci. 2024; ahead-of-print. [Google Scholar] [CrossRef] [PubMed]
- Magosso, E.; Borra, D. The strength of anticipated distractors shapes EEG alpha and theta oscillations in a Working Memory task. NeuroImage 2024, 300, 120835. [Google Scholar] [CrossRef]
- Davis, Z.W.; Benigno, G.B.; Fletterman, C.; Desbordes, T.; Steward, C.; Sejnowski, T.J.; Reynolds, J.H.; Muller, L. Spontaneous traveling waves naturally emerge from horizontal fiber time delays and travel through locally asynchronous-irregular states. Nat. Commun. 2021, 12, 6057. [Google Scholar] [CrossRef] [PubMed]
- Koller, D.P.; Schirner, M.; Ritter, P. Human connectome topology directs cortical traveling waves and shapes frequency gradients. Nature Comm. 2024, 15, 3570. [Google Scholar] [CrossRef] [PubMed]
- Drukarch, B.; Wilhelmus, M.M.M. Thinking about the action potential: The nerve signal as a window to the physical principles guiding neuronal excitability. Front. Cell. Neurosci. 2023, 17, 1232020. [Google Scholar] [CrossRef] [PubMed]
- Rahmouni, L.; Merlini, A.; Pillain, A.; Andriulli, F.P. On the modeling of brain fibers in the EEG forward problem via a new family of wire integral equations. J. Comp. Phys. X 2020, 5, 100048. [Google Scholar] [CrossRef]
- Næss, S.; Halnes, G.; Hagen, E.; Hagler, D.J., Jr.; Dale, A.M.; Einevoll, G.T.; Ness, T.V. Biophysically detailed forward modeling of the neural origin of EEG and MEG signals. NeuroImage 2021, 225, 117467. [Google Scholar] [CrossRef] [PubMed]
- Byrne, À.; Ross, J.; Nicks, R.; Coombes, S. Mean-field models for EEG/MEG: From oscillations to waves. Brain Topogr. 2021, 15, 36–53. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Myers, J.; Mathur, R.; Shofty, B.; Metzger, B.A.; Bijanki, K.; Wu, C.; Jacobs, J.; Sheth, S.A. Spontaneous neuronal oscillations in the human insula are hierarchically organized traveling waves. eLife 2022, 11, e76702. [Google Scholar] [CrossRef]
- Wilson, H.R.; Cowan, J.D. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 1973, 13, 55–80. [Google Scholar] [CrossRef]
- Amari, S. Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 1977, 27, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Ermentrout, G.B.; McLeod, J. Existence and uniqueness of travelling waves for a neural network. Proc. Royal Soc. Edinb. Sect. A Mathem. 1993, 123, 461–478. [Google Scholar] [CrossRef]
- Klimesch, W.; Hanslmayr, S.; Sauseng, P.; Gruber, W.R.; Doppelmayr, M. P1 and traveling alpha waves: Evidence for evoked oscillations. J. Neurophys. 2007, 97, 1311–1318. [Google Scholar] [CrossRef] [PubMed]
- Pinto, D.J.; Ermentrout, G.B. Spatially structured activity in synaptically coupled neuronal networks: I. Traveling fronts and pulses. SIAM J. Appl. Math. 2001, 62, 206–225. [Google Scholar] [CrossRef]
- Laing, C.R.; Troy, W. Two-bump solutions of Amari-type models of neuronal pattern formation. Phys. D Nonlinear Phenom. 2023, 178, 190–218. [Google Scholar] [CrossRef]
- Owen, M.R.; Laing, C.R.; Coombes, S. Bumps and rings in a two-dimensional neural field: Splitting and rotational instabilities. New J. Phys. 2007, 9, 378. [Google Scholar] [CrossRef]
- Blomquist, P.; Wyller, J.; Einevoll, G.T. Localized activity patterns in two-population neuronal networks. Phys. D Nonlinear Phenom. 2005, 206, 180–212. [Google Scholar] [CrossRef]
- Naoumenko, D.; Gong, P. Complex dynamics of propagating waves in a two-dimensional neural field. Front. Comput. Neurosci. 2019, 13, 50. [Google Scholar] [CrossRef] [PubMed]
- Pinto, D.J.; Jackson, R.K.; Wayne, C.E. Existence and stability of traveling pulses in a continuous neuronal network. SIAM J. Appl. Dyn. Syst. 2005, 4, 954–984. [Google Scholar] [CrossRef]
- Coombes, S.; Owen, M.R. Evans functions for integral neural field equations with Heaviside firing rate function. SIAM J. Appl. Dyn. Syst. 2004, 3, 574–600. [Google Scholar] [CrossRef]
- Meijer, H.G.; Coombes, S. Numerical continuation of travelling waves and pulses in neural fields. BMC Neurosc. 2013, 14, P70. [Google Scholar] [CrossRef]
- Zhang, L. Existence, uniqueness, and exponential stability of traveling wave solutions of some integral differential equations arising from neuronal networks. Diff. Int. Eqs. 2003, 16, 513–536. [Google Scholar] [CrossRef]
- Folias, S.E. Nonlinear analysis of breathing pulses in a synaptically coupled neural network. SIAM J. Appl. Dyn. Syst. 2011, 10, 744–787. [Google Scholar] [CrossRef]
- Sandstede, B. Evans functions and nonlinear stability of traveling waves in neuronal network models. Int. J. Bifurc. Chaos. 2007, 17, 2693–2704. [Google Scholar] [CrossRef]
- Zhang, L. How Do Synaptic Coupling and Spatial Temporal Delay Influence Traveling Waves in Nonlinear Nonlocal Neuronal Networks? SIAM J. Appl. Dyn. Syst. 2007, 6, 597–644. [Google Scholar] [CrossRef]
- Bressloff, P.C.; Folias, S.E. Front bifurcations in an excitatory neural network. SIAM J. Appl. Math. 2004, 65, 131–151. [Google Scholar] [CrossRef]
- Kilpatrick, Z.P.; Folias, S.E.; Bressloff, P.C. Traveling pulses and wave propagation failure in inhomogeneous neural media. SIAM J. Appl. Dyn. Syst. 2008, 7, 161–185. [Google Scholar] [CrossRef]
- Nielsen, B.F.; Wyller, J.A. Ill-posed point neuron models. J. Math. Neurosc. 2016, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Burlakov, E. On inclusions arising in neural field modeling. Diff. Eqs. Dynam. Syst. 2021, 29, 765–787. [Google Scholar] [CrossRef]
- Potthast, R.; Graben, P.B. Existence and properties of solutions for neural field equations. Math. Methods Appl. Sci. 2010, 8, 935–949. [Google Scholar] [CrossRef]
- Burlakov, E.; Verkhlyutov, V.; Ushakov, V. A simple human brain model reproducing evoked MEG based on neural field theory. Stud. Comp. Intell. 2021, 1008, 109–116. [Google Scholar]
- Mawhin, J. Leray-Schauder degree: A half century of extensions and applications. Topol. Meth. Nonlinear Anal. 1999, 14, 195–228. [Google Scholar] [CrossRef]
- Katok, A.; Hasselblatt, B. Introduction to the Modern Theory of Dynamical Systems; Cambridge University Press: London, UK, 1995; 793p. [Google Scholar]
- Oleynik, A.; Ponosov, A.; Wyller, J. On the properties of nonlinear nonlocal operators arising in neural field models. J. Math. Anal. Appl. 2013, 398, 335–351. [Google Scholar] [CrossRef]
- Hutson, V.; Pym, J.S.; Cloud, M.J. Applications of Functional Analysis and Operator Theory; Elsevier: Amsterdam, The Netherlands, 2005; 432p. [Google Scholar]
- Granas, A. The Leray-Schuder index and the fixed point theory for arbitrary ANRs. Bull. Soc. Math. 1972, 100, 209–228. [Google Scholar]
- Coppel, W.A. Dichotomies in Stability Theory; Springer: New York, NY, USA, 1978; 97p. [Google Scholar]
- Dunford, N.; Schwartz, J.T. Linear Operators: I. General Theory; John Wiley & Sons: New York, NY, USA, 1958; 872p. [Google Scholar]
- Malkov, I.; Burlakov, E.; Verkhlyutov, V.; Ushakov, V. A model of travelling waves in the neural medium with directional variability of inhibitory effects. Stud. Comp. Intell. 2025, 1179, 244–253. [Google Scholar]
- Kolodina, K.; Kostrykin, V.; Oleynik, A. Existence and stability of periodic solutions in a neural field equation. Russ. Univ. Rep. Math. 2021, 26, 271–295. [Google Scholar] [CrossRef]
- Ponosov, A.; Oleynik, A.; Kostrykin, V.; Sobolev, A. Spatially localized solutions of the Hammerstein equation with sigmoid type of nonlinearity. J. Diff. Eqs. 2016, 261, 5844–5874. [Google Scholar]
- Bressloff, P.C.; Carroll, S.R. Laminar neural field model of laterally propagating waves of orientation selectivity. PLoS Comput. Biol. 2015, 11, e1004545. [Google Scholar] [CrossRef] [PubMed]
- Burlakov, E.O.; Verkhlyutov, V.M.; Malkov, I.N. On well-posedness of a mathematical model of evoked activity in the primary visual cortex. Russ. Univ. Rep. Math. 2024, 29, 43–50. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burlakov, E.; Oleynik, A.; Ponosov, A. Travelling Waves in Neural Fields with Continuous and Discontinuous Neuronal Activation. Mathematics 2025, 13, 701. https://doi.org/10.3390/math13050701
Burlakov E, Oleynik A, Ponosov A. Travelling Waves in Neural Fields with Continuous and Discontinuous Neuronal Activation. Mathematics. 2025; 13(5):701. https://doi.org/10.3390/math13050701
Chicago/Turabian StyleBurlakov, Evgenii, Anna Oleynik, and Arcady Ponosov. 2025. "Travelling Waves in Neural Fields with Continuous and Discontinuous Neuronal Activation" Mathematics 13, no. 5: 701. https://doi.org/10.3390/math13050701
APA StyleBurlakov, E., Oleynik, A., & Ponosov, A. (2025). Travelling Waves in Neural Fields with Continuous and Discontinuous Neuronal Activation. Mathematics, 13(5), 701. https://doi.org/10.3390/math13050701





