Multilayer Neurolearning of Measurement-Information-Poor Hydraulic Robotic Manipulators with Disturbance Compensation
Abstract
1. Introduction
- Smooth and non-smooth modeling uncertainties can be compensated.
- Matched and mismatched time-varying disturbances can be compensated.
- The proposed controller does not depend on the angular velocity measurements of the joints and is free of “explosion of complexity”.
- The proposed controller has the advantages of low noise sensitivity and can resist to input saturation.
2. Problem Formulation
3. Multilayer Neurocontroller with Disturbance Compensation
3.1. Multilayer Neuroadaptive Approximation
3.2. Observer Design
3.3. Controller Design
3.4. Theoretical Results
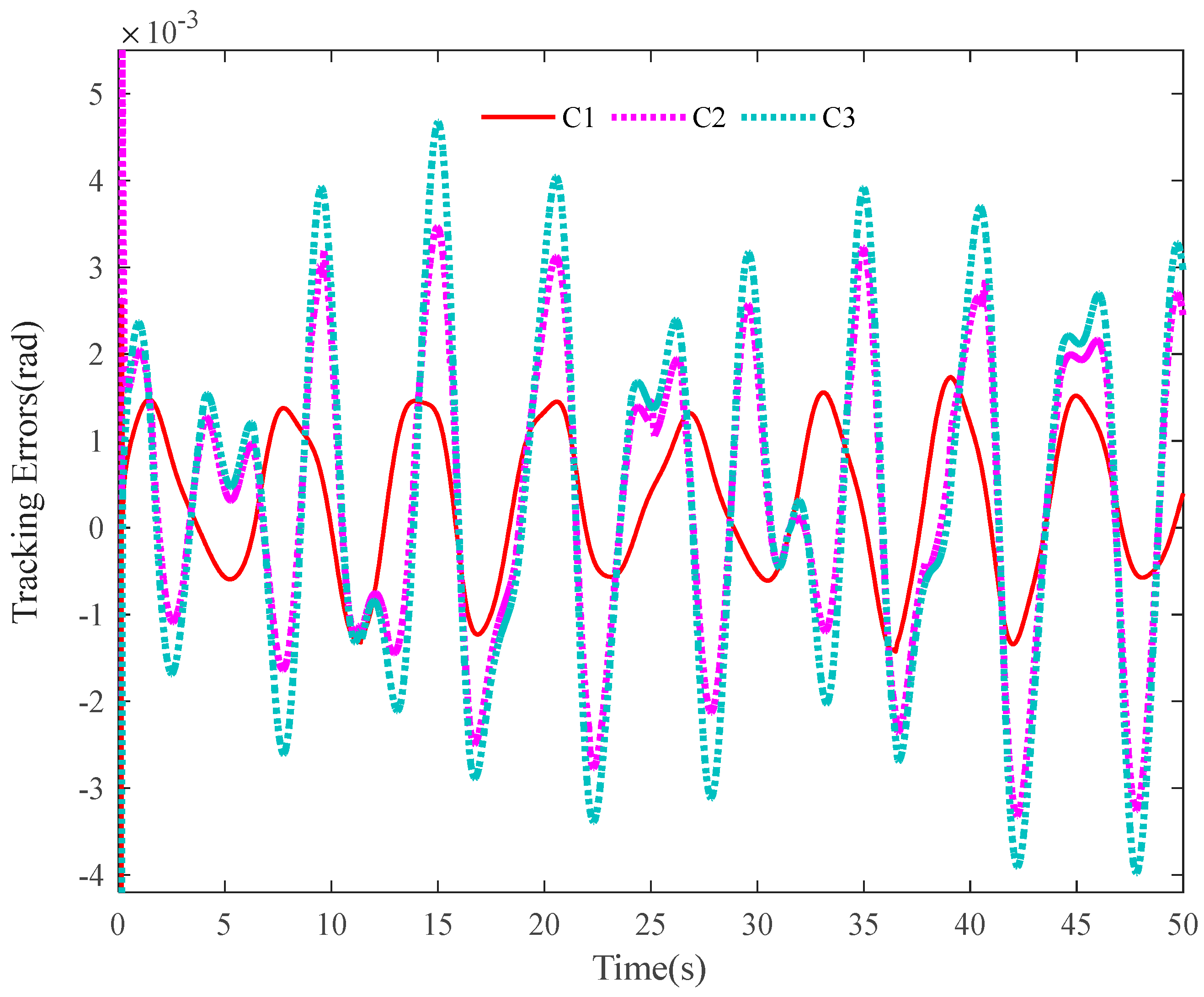
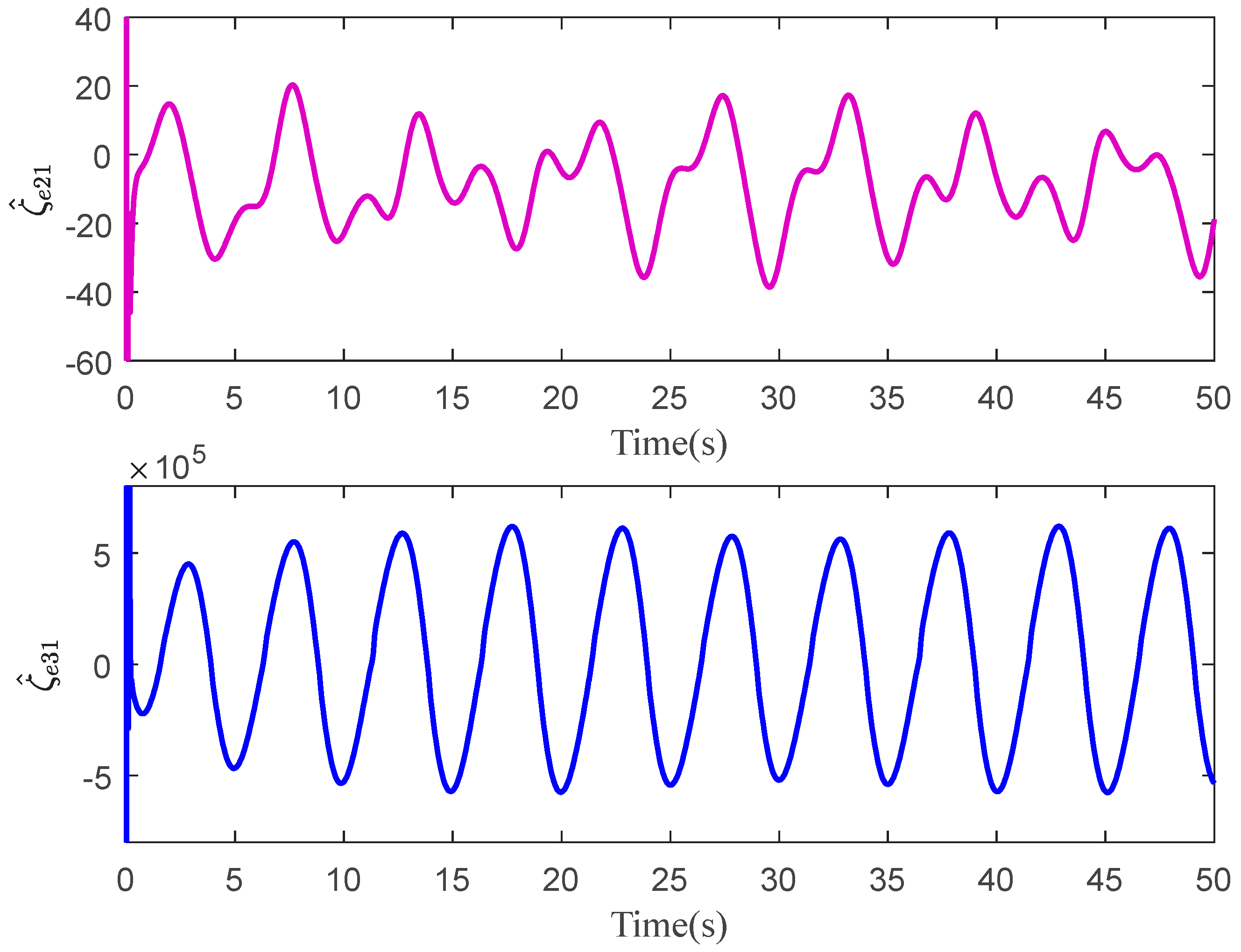
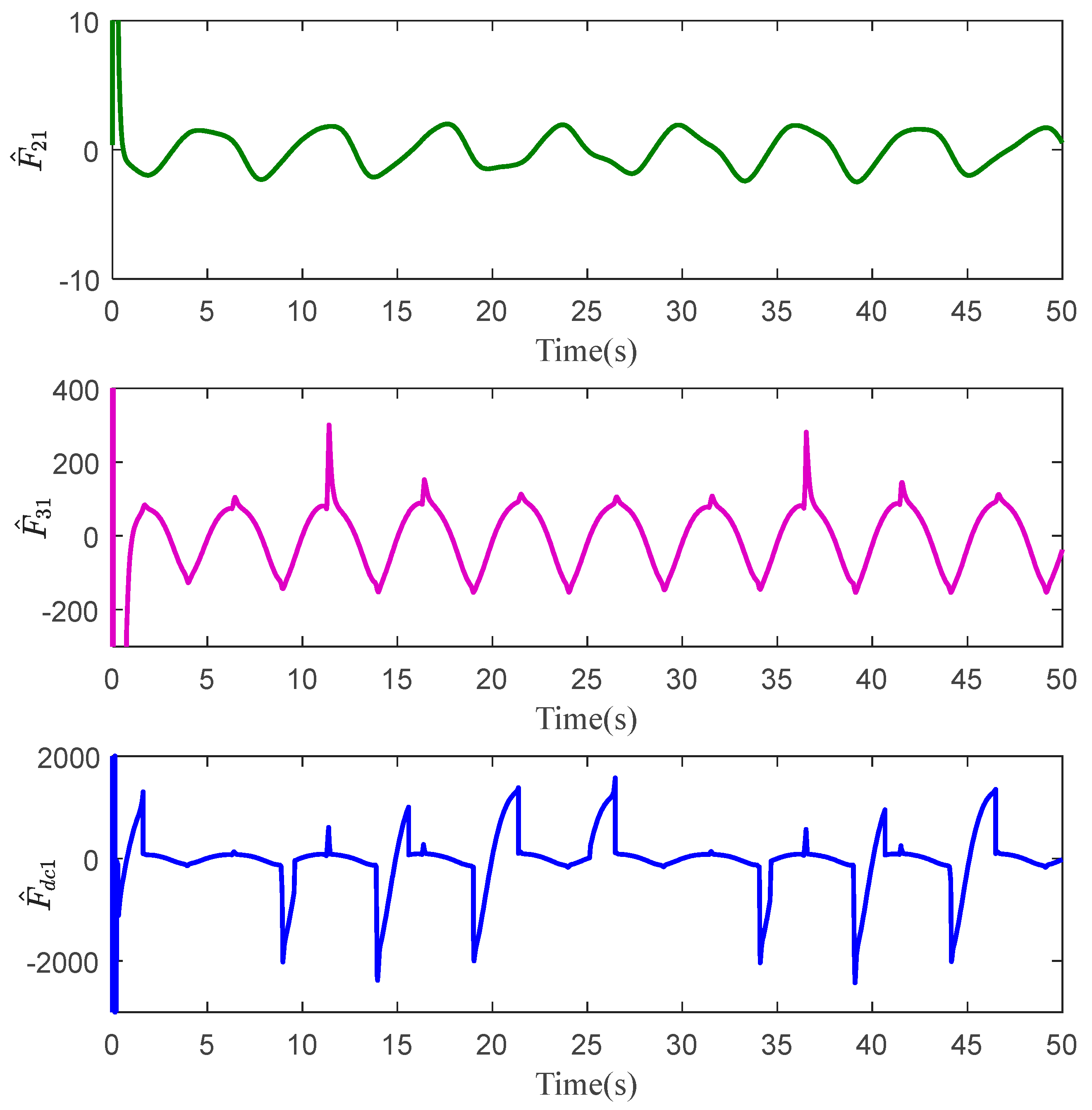
4. Comparative Verification
4.1. A 2-DOF Hydraulic Manipulator
4.2. Comparative Results
- (1)
- (2)
- C2: It is same as C1 but without disturbance compensation. Notably, k3 = diag{350, 350}.
- (3)
- C3: It is the backstepping based feedback controller.
| The gains of the controller | k1 = diag{80, 500}, k2 = diag{200, 500}, k3 = diag{300, 300}, ke = diag{5, 5} |
| The bandwidths of the observers | ωo1 = diag{350, 350}, ωo2 = diag{500, 500} |
| The activation functions of the MLNN | = tanh(), = tanh(), = |
| The gains of the MLNN adaptive laws | ϒW2 = [1 × 102I11, 1 × 102I11]T, ϒV2 = [1 × 104I5, 1 × 104I5]T, ϒW3 = [8 × 101I14, 8 × 101I14]T, ϒV3 = [1 × 104I7, 1 × 104I7]T, ϒdc = [1 × 103I14, 5 × 102I14]T, γW2 = [1 × 10−1I11, 1 × 10−1I11]T, γV2 = [1 × 10−1I5, 1 × 10−1I5]T, γW3 = [1 × 10−1I14, 1 × 10−1I14]T, γV3 = [1 × 10−1I7, 1 × 10−1I7]T, γdc = [1 × 10−1I14, 1 × 10−1I14]T |
| The gains of the filters | ωc1 = diag{3 × 103, 3 × 103}, ωc2 = diag{3.2 × 103, 3.2 × 103} |
| Other parameters | e0 = [1 × 10−1, 1 × 10−1]T, = [10, 10]T, = [–10, –10]T |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Guo, Q.; Wang, Q.; Zuo, Z.; Zhang, Y.; Jiang, D.; Shi, Y. Parametric adaptive control of electro-hydraulic system driving two-DOF robotic arm. In Proceedings of the IEEE 56th Annual Conference on Decision and Control, Melbourne, VIC, Australia, 12–15 December 2017; pp. 3283–3288. [Google Scholar]
- Yang, G. State filtered disturbance rejection control. Nonlinear Dyn. 2024, 1–17. [Google Scholar] [CrossRef]
- Xia, Y.; Nie, Y.; Chen, Z.; Lyu, L.; Hu, P. Motion control of a hydraulic manipulator with adaptive nonlinear model compensation and comparative experiments. Machines 2022, 10, 214. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Z.; Yao, B. Precision cascade force control of multi-DOF hydraulic leg exoskeleton. IEEE Access 2018, 6, 8574–8583. [Google Scholar] [CrossRef]
- Bu, F.; Yao, B. Nonlinear model based coordinated adaptive robust control of electro-hydraulic robotic manipulators: Methods and comparative studies. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 11–16 November 2001; pp. 651–659. [Google Scholar]
- Zhou, S.; Shen, C.; Xia, Y.; Chen, Z.; Zhu, S. Adaptive robust control design for underwater multi-DoF hydraulic manipulator. Ocean Eng. 2022, 248, 110822. [Google Scholar] [CrossRef]
- Petrović, G.R.; Mattila, J. Mathematical modelling and virtual decomposition control of heavy-duty parallel–serial hydraulic manipulators. Mech. Mach. Theory 2022, 170, 104680. [Google Scholar] [CrossRef]
- Koivumäki, J.; Mattila, J. Stability-guaranteed force-sensorless contact force/motion control of heavy-duty hydraulic manipulators. IEEE Trans. Rob. 2015, 31, 918–935. [Google Scholar] [CrossRef]
- Rigatos, G.; Zervos, N.; Abbaszadeh, M.; Pomares, J.; Wira, P. Non-linear optimal control for multi-DOF electro-hydraulic robotic manipulators. IET Cyber-Syst. Robot. 2020, 2, 96–106. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J.; Dong, Z. Neuroadaptive learning algorithm for constrained nonlinear systems with disturbance rejection. Int. J. Robust Nonlinear Control 2022, 32, 6127–6147. [Google Scholar] [CrossRef]
- Dao, H.V.; Ahn, K.K. Extended sliding mode observer-based admittance control for hydraulic robots. IEEE Rob. Autom. Lett. 2022, 7, 3992–3999. [Google Scholar] [CrossRef]
- Shen, M.; Wang, X.; Park, J.H.; Yi, Y.; Che, W.W. Extended disturbance-observer-based data-driven control of networked nonlinear systems with event-triggered output. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3129–3140. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, G. Dual extended state observer-based adaptive dynamic surface control for a hydraulic manipulator with actuator dynamics. Mech. Mach. Theory 2022, 169, 104647. [Google Scholar] [CrossRef]
- Dinh, T.X.; Thien, T.D.; Anh, T.H.V.; Ahn, K.K. Disturbance observer based finite time trajectory tracking control for a 3 DOF hydraulic manipulator including actuator dynamics. IEEE Access 2018, 6, 36798–36809. [Google Scholar] [CrossRef]
- Dao, H.V.; Tran, D.T.; Ahn, K.K. Active fault tolerant control system design for hydraulic manipulator with internal leakage faults based on disturbance observer and online adaptive identification. IEEE Access 2021, 9, 23850–23862. [Google Scholar] [CrossRef]
- Tran, D.T.; Truong, H.V.A.; Ahn, K.K. Adaptive backstepping sliding mode control based RBFNN for a hydraulic manipulator including actuator dynamics. Appl. Sci. 2019, 9, 1265. [Google Scholar] [CrossRef]
- Yang, G. Multilayer neuroadaptive constraint-handling control architecture for a family of nonlinear systems with uncertainty compensation. Inf. Sci. 2025, 690, 121517. [Google Scholar] [CrossRef]
- Selmic, R.R.; Lewis, F.L. Neural-network approximation of piecewise continuous functions: Application to friction compensation. IEEE Trans. Neural Netw. 2002, 13, 745–751. [Google Scholar] [CrossRef] [PubMed]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- He, W.; Dong, Y.; Sun, C. Adaptive neural impedance control of a robotic manipulator with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 334–344. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2399–2405. [Google Scholar]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef] [PubMed]
- Yang, G. Asymptotic tracking with novel integral robust schemes for mismatched uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2023, 33, 1988–2002. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]







| Parameter | Value (Unit) | Parameter | Value (Unit) |
|---|---|---|---|
| Jm1 | 5.2 (kg) | L10 | 0.2 (m) |
| Jm2 | 6.2 (kg) | L11 | 0.2 (m) |
| JI1 | 2.25 (kg•m2) | L12 | 0.2 (m) |
| JI2 | 1.25 (kg•m2) | Ps | 50 (bar) |
| JL | 15.2 (kg) | Pr | 0 (bar) |
| Sc1 | 0.2 (m) | βef | 1.26 × 109 (Pa) |
| Sc2 | 0.15 (m) | Aa11 | 1 × 10−3 (m2) |
| S1 | 0.5 (m) | Ab11 | 5 × 10−4 (m2) |
| S2 | 0.2 (m) | Aa22 | 1.22 × 10−4 (m3/rad) |
| Ctl11, Ctl22 | 2.8 × 10−12 (m3/s/Pa) | Ab22 | 1.22 × 10−4 (m3/rad) |
| Cd11ωd11Kg11 | 3.2 × 10−8 (m3/s/V/) | Cd22ωd22Kg22 | 2.2 × 10−8 (m3/s/V/) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Shi, Z. Multilayer Neurolearning of Measurement-Information-Poor Hydraulic Robotic Manipulators with Disturbance Compensation. Mathematics 2025, 13, 683. https://doi.org/10.3390/math13040683
Yang G, Shi Z. Multilayer Neurolearning of Measurement-Information-Poor Hydraulic Robotic Manipulators with Disturbance Compensation. Mathematics. 2025; 13(4):683. https://doi.org/10.3390/math13040683
Chicago/Turabian StyleYang, Guichao, and Zhiying Shi. 2025. "Multilayer Neurolearning of Measurement-Information-Poor Hydraulic Robotic Manipulators with Disturbance Compensation" Mathematics 13, no. 4: 683. https://doi.org/10.3390/math13040683
APA StyleYang, G., & Shi, Z. (2025). Multilayer Neurolearning of Measurement-Information-Poor Hydraulic Robotic Manipulators with Disturbance Compensation. Mathematics, 13(4), 683. https://doi.org/10.3390/math13040683







