Abstract
Granule description is a fundamental problem in granular computing. However, how to describe indefinable granules is still an open, interesting, and important problem. The main objective of this paper is to give a preliminary solution to this problem. Before proceeding, the framework of approximate description is introduced. That is, any indefinable granule is characterized by an ordered pair of formulas, which form an interval set, where the first formula is the -prior approximate optimal description and the second formula is the -prior approximate optimal description. More concretely, given an indefinable granule, by exploring the description of its lower approximate granule, its -prior approximate optimal description is obtained. Likewise, by consulting the description of its upper approximate granule, its -prior approximate optimal description can also be derived. Following this idea, the descriptions of indefinable granules are investigated. Firstly, ∧-approximate descriptions of indefinable granules are investigated based on the classical concept lattice, and -approximate descriptions of indefinable granules are given via object pictorial diagrams. And then, it is revealed from some examples that the classical concept lattice is no longer effective and negative attributes must be taken into consideration. Therefore, a three-way concept lattice is adopted instead of the classical concept lattice to study -approximate descriptions and -approximate descriptions of indefinable granules. Finally, some discussions are presented to show the differences and similarities between our study and existing ones.
Keywords:
rough sets; granular computing; granule description; formal concept analysis; three-way concept lattice MSC:
68P01
1. Introduction
Granular computing (GrC) is a discipline that specializes in the theoretical, methodological, technical, and tool approaches to problem-solving and information processing of information granules and their structures in datasets [1,2,3]. Any methodologies, theories and tools that treat complex information entities in different levels of granules fall into the scope of granular computing [1,2,3,4,5]. The concept of granular computing has been widely used in many research fields, such as cognitive science and cognitive informatics [6].
Although different systems may have different external differences, information granules can be identified based on their essential similarities, which may include functional or physical adjacency, coherency, and the like [7,8]. Once information granules are obtained, they can be combined and used to construct more complicated hierarchical structures. Moreover, by shifting from one level to another level, we can obtain important clues to solve many complicated problems [9,10].
No matter what we want to do with the information granules, the first step is to characterize the research object. Furthermore, if we want to communicate with other granules and intelligent machines, we still have to find a concise way to explicitly depict these granules. Then, descriptions of granules deserve our great concern [11]. Studies of granule description can not only help achieve a profound understanding of the discussed question, but also shed light on some unsolved psychological problems. Generally speaking, any research which tries to find a good description of the subset of the problem space falls within the scope of granule description. In a narrow sense, granule description is aimed at finding a logical formula that best describes a given granule.
There are two crucial issues in granule description. The first step is to select a scheme that best fits the objective of the problem under consideration. For example, if we want to investigate the features shared by different granules, we have to choose common attribute analysis. At this time, we will derive a series of formal concepts [12]. However, if we want to know which features are possessed by a granule but are not possessed by other granules, we must resort to necessary attribute analysis. At this time, we will derive a collection of object-oriented concepts [13]. Therefore, it is not surprising that a granule is definable via common attribute analysis but it may become indefinable via necessary attribute analysis, and vice versa. The other issue is the selection of basic definable granules which can be used to approximate more complicated indefinable granules. For example, in knowledge representation, basic granules are used as the building blocks by which more complex granules can be characterized via logic connections [11,14,15,16]. In cognitive learning processes, basic granules, known as granular concepts, are always the starting point from which complicated concepts can be derived by incorporating new information [17].
Two strategies are frequently used in the descriptions of granules and related studies. One is the set approximation from rough set theory (RST), presented by Pawlak [18]; the other is the extension-intension view highlighted in formal concept analysis (FCA) [19]. Some scholars have explained that RST and FCA are essentially related to each other and are two effective methods of granular computing [20,21,22,23]. Essentially, these two theories have the same opinion with respect to granule description. That is, they first select a scheme to obtain a collection of basic granules, and then adopt approximations to characterize other granules. However, there are differences between them. Compared to RST, FCA establishes a partial order between granules and gives each granule a unique label to explicitly show the corresponding intension. Generally speaking, RST is good at describing a target set based on similar objects, while FCA is skilled at providing the description of a granule by using a set of attributes. So, which one is better greatly depends on our requirements.
After several years of rapid development, RST has become a useful tool for uncertain data management [24]. In the study of granule description in RST, indefinable granules are actually the ones that contain uncertain parts. In other words, there exist granules that cannot be described by basic knowledge. Then, an alternative approach is provided to solve this problem by using a pair of lower and upper approximations. Furthermore, the precision of this model is measured by the fraction of the lower approximation to the upper approximation. Motivated by the requirements of multi-source information fusion, multigranulation rough sets have become a hot research field in RST [25]. After all kinds of generalizations, many new types of multigranulation rough sets were presented to fit different types of information systems, such as incomplete, neighborhood, covering, and fuzzy information systems [26,27].
RST can be integrated with FCA to improve the ability of granule representation. For example, by combining concept approximation of RST with the concept-building strategies of FCA, AFS-concept [14], property-oriented concepts [21], and the object-oriented concept lattice [13] have been presented to meet different requirements. Moreover, basic terms of granular computing can be directly applied in these generalized concept lattices to define important notions, such as granular concept and granular rule [28]. The basic ideas of granular computing can also be combined with optimization algorithms to make decisions [29]. Moreover, some studies have shown that negative attributes are of equal importance as positive ones in characterizing a target granule [30]. In these studies, only positive attributes were used to describe a given granule while negative ones were ignored.
Three-way concept analysis (3WCA), a combination of three-way decisions [31,32] and FCA, proposed by Qi et al. [33], has become a hot topic [17,34,35,36,37]. In fact, 3WCA not only develops FCA but also provides a way to understand problems from both positive and negative perspectives. Three-way concept lattices can be built based on formal concept lattices [38], and they can enable us to describe granules from a more broad and profound perspective.
Until now, granule description has involved a few preliminary explorations. By combining the merits of RST and FCA, Yao [16] interpreted the notions of RS-definable concepts and the Boolean algebra of RS-definable concepts. An interesting conclusion was obtained in Yao [16]. That is, RS-definable concepts can serve as the basic knowledge to approximate RS-indefinable concepts. Necessary attribute analysis was proposed, and RS-definable concepts are identical to object-oriented concepts as reported in our previous work [39]. Thus, describing indefinable granules becomes a more interesting and appealing problem.
To this end, this paper focus on the descriptions of indefinable granules. The main contribution of this paper is as follows: Given an indefinable granule, we first find two definable granules to approximate this indefinable granule. That is, one granule serves as its lower approximate granule and the other serves as its upper approximate granule. Then, we use the description of its lower approximate granule as its -prior approximate optimal description and use the description of its upper approximate granule as its -prior approximate optimal description. Finally, we characterize this indefinable granule by an ordered pair of formulas, which actually form an interval set, where the first formula is the -prior approximate optimal description and the second formula is the -prior approximate optimal description.
Following this idea, the description of indefinable granules is investigated. The remainder of the paper is organized as follows: In Section 2, we review some basic notions, such as formal concept analysis, three-way concept analysis, and Pawlak’s rough set. In Section 3, we discuss the fundamentals of approximate descriptions. In Section 4, we propose approximate description methods of granules-based FCA. Concretely, we first investigate ∧-approximate descriptions based on a concept lattice. Next, we continue studying -approximate descriptions of granules based on an object pictorial diagram. In Section 5, we present -approximate descriptions and -approximate descriptions of granules based on 3WCA, respectively. In Section 6, we present a case study and experimental analysis. Finally, some discussions are given in Section 7.
2. Preliminaries
In this section, we review some basic notions to make our paper self-contained.
2.1. Basic Notions in FCA
Let G be a domain. Then, all possible granules form a power set of G, denoted as . However, at best, only a small proportion of the granules can be studied in a certain theory. This is also true for FCA. As one of the rapidly developing research areas of granular computing, FCA concerns the granules that fulfill some rigid constraints.
As is well known, FCA starts with a formal context, which is usually represented as a triple , where G is a set of objects, M is a set of attributes, and specifies the relation between G and M.
A formal concept is a pair [12], where , , , and . Moreover, X and A are called the extent and the intent of the concept , respectively. In addition, we use and to denote the extent and the intent of the concept , respectively.
Let and be two formal concepts. Then, the partial order is defined by:
Furthermore, if there does not exist another concept such that , we call a lower neighbor of , or an upper neighbor of , denoted by .
Then, the concept lattice of K, denoted as , is constituted by all the formal concepts together with the partial order .
2.2. Basic Notions in 3WCA
Let M be an attribute set and be the Cartesian product of and . Then, we introduce a partial order ≤ in :
Moreover, we define . The intersection ∩ and the union ∪ in are, respectively, defined as:
For a formal context , let and , where . Then, a three-way formal concept is a pair [33], where and . In this case, X and are called the extent and intent of , respectively. In addition, we use and to denote the extent and the intent of the three-way concept , respectively.
Let and be two three-way formal concepts. Then, the partial order is defined by:
Furthermore, if there does not exist another three-way formal concept such that , we call a lower neighbor of , or an upper neighbor of , denoted by .
Similarly, the three-way concept lattice of K, denoted as , is constituted by all the three-way formal concepts together with the partial order .
2.3. Basic Notions in RST
Let be an information system, be a target set, and , where the finite nonempty set U is the universe, the finite nonempty set is the attributes, and R specifies the relations between the universe and the attributes.
Then, we can describe any target set X in two steps:
(i) Based on the following equivalence relation
we partition the universe U into equivalence classes .
(ii) We approximate the target set X by a pair , where
Furthermore, the accuracy of this approximate description is where denotes the cardinality of a set.
According to Pawlak’s rough set [18], definable granules have the following properties:
(i) Both ∅ and U are definable granules;
(ii) If X and Y are definable granules, then is a definable granule;
(iii) If X and Y are definable granules, then is a definable granule;
(iv) If X is a definable granule, then is also a definable granule.
In this paper, the ideas of upper and lower approximations will be incorporated into the descriptions of indefinable granules. Furthermore, logic connectives ∧, ∨, and ¬ will be used to establish description formulas, and they correspond to ∩, ∪, and − in the set-theoretic formulation method of RST.
3. Approximate Description Based on Logic Language
In this section, we present the fundamentals of granule description and investigate the descriptive abilities of description languages.
3.1. Fundamentals of Granule Description
Logic language, originating from the decision logic language, is a very important language used in knowledge discovery [40].
In this paper, atomic formulas are denoted by lowercase letters, such as a, b, and c. When a set of atomic formulas is considered, more complicated formulas can be obtained by recursively using logic connectives, such as ¬, ∧, ∨, →, and ↔.
Moreover, we give a language a name based on the logic connectives we use. For example, if only logic connectives ∧ and ¬ are used in a language, we call this language a -language.
Furthermore, it should be pointed out that the discussion on the descriptions of granules will be confined to a certain predefined language.
Let G be a nonempty set of individuals and K be a knowledge base with respect to G. If an individual satisfies a formula , then we denote this case as .
Definition 1
([41]). The meaning of a formula φ is the set of individuals which satisfy the formula φ, i.e.,
According to Definition 1, it is easy to obtain the following Proposition 1.
Proposition 1
([41]). Let φ and ψ be two formulas. Then, the following properties hold:
(i) ;
(ii) ;
(iii) ;
(iv) ;
(v) .
Definition 2
([39]). Let X be a granule and φ be a formula. The recall and precision indices of φ with respect to X are defined by:
Note that if there is no confusion, we use and instead of and for the sake of convenience.
Definition 3.
Let X be a granule, φ be a formula, and . If , we say that x necessarily belongs to X, denoted by ; if , we say that x possibly belongs to X, denoted by .
Definition 4.
Let X be a granule and Φ be the set of all formulas of a language. If both and have the biggest values among all the formulas in Φ, then we call φ the optimal description of the granule X.
For a given granule, there may not be a formula that has the biggest values and simultaneously. So, Definition 4 is only theoretically sound. Thus, we have to find an approximate optimal description in a feasible manner. The following definition actually gives two kinds of approximate optimal descriptions, which take recall and precision into consideration in order.
Definition 5.
Let X be a granule and Φ be the set of all formulas of a language. If and has the biggest value among all the formulas in Φ, then we call φ the α-prior approximate optimal description of X, and denote it as . Correspondingly, if and has the biggest value among all the formulas in Φ, then we call φ the β-prior approximate optimal description of X, and denote it as .
By using Definition 3, we have the following propositions:
(i) if , then ;
(ii) if , then .
Proposition 2.
Let X be a granule. Then, .
Theorem 1.
Let X be a granule and Φ be the set of all formulas of a language. The α-prior approximate optimal description of X is:
where .
Theorem 2.
Let X be a granule and Φ be the set of all formulas of a language. The β-prior approximate optimal description of X is:
where .
Definition 6.
Let X be a granule. We call the approximate description of X. And the approximate description accuracy is defined by:
Definition 7
([41]). Let be the power set of U. Given a pair of sets with ,
is called a closed interval set.
Let X be a granule with its approximate description . Based on Proposition 2, it is easy to see that forms a closed interval set.
Definition 8.
Let X be a granule with its approximate description . If , we say that the granule X is definable; otherwise, we say that the granule X is indefinable.
Note that if X is definable, we use the denotation instead of .
Proposition 3.
Let X be a granule. The following properties are equivalent to each other:
(i) ;
(ii) ;
(iii) There exists a formula φ such that ;
(iv) There exists a formula φ such that and .
Proposition 4.
Let X, and be granules. The following properties hold:
(i) ;
(ii) ;
(iii) ;
(iv) ;
(v) , where ∖, ⊓ and ⊔ are the interval-set complement, intersection, and union given in [42]. That is, for two interval sets and ,
Definition 9.
Let X be an indefinable granule. is called a lower approximate granule of X if is definable and there does not exist another definable granule such that . Correspondingly, is called an upper approximate granule of X if is definable and there does not exist another definable granule such that .
Proposition 5.
Let X be an indefinable granule, be its lower approximate granule and be its upper approximate granule. Then, is its β-prior approximate optimal description and is its α-prior approximate optimal description.
Definition 10.
Let X be a granule. The recall and precision indices of the approximate optimal description of X are defined as:
Proposition 6.
Let X, and be granules. Then, the following properties hold:
(i) ;
(ii) ;
(iii) ;
(iv) .
It is necessary to point out that the following properties do not hold:
(i) ;
(ii) ;
(iii) ;
(iv) .
Actually, Definition 9 and Proposition 5 manifest our main idea about the approximate description of indefinable granules. That is, given an indefinable granule, we first find two definable granules to serve as its lower and upper approximate granules. And then, we use the descriptions of these two approximate granules to construct the approximate description of this indefinable granule.
3.2. Descriptive Abilities of Description Languages
The fact that some concepts seem to be difficult, complicated, and incoherent, while others are psychologically easy and simple to be understood has widely been accepted by cognitive scientists. Some experiments have demonstrated that two factors strongly affect the difficulty of describing a concept. One factor is the length of the descriptive formulas for the concepts, and the other factor is the logic connectives used in the descriptive formula. Generally speaking, the shorter the descriptive formula is, the less difficult the concept seems to be. Moreover, disjunctive (‘Or’) concepts are hard to learn compared with conjunctive (‘And’) concepts. These finding may partly explain the phenomenon why the descriptive logics used in existing studies mainly rely on conjunctive formulas, such as the ones in the traditional FCA and rough set theory. Only a few studies have used disjunctive formulas, such as those in monotone concepts [14,43], multigranulation rough sets [44], and negative association rules [30].
Note that indefinable granules are defined in Definition 8. In fact, the discussions about whether a granule is definable only make sense under a predefined logic language. On most occasions, if we resort to a more powerful logic language, some indefinable granules will become definable.
Definition 11
([39]). Let X be a granule. If only the logic connective ∧ is enough in the description of X, we say that it is a ∧-definable granule; if the logic connectives ∧ and ¬ are enough in the description of X, we say that it is a -definable granule; if the logic connectives ∧ and ∨ are enough in the description of X, we say that it is a -definable granule.
It is obvious that all the ∧-definable granules are both -definable and -definable.
Definition 12.
Let X be a granule. If the logic connectives ∧, ∨, and ¬ are enough in the description of X, we say that it is a -definable granule. Moreover, if a granule is -indefinable, we say it is absolutely indefinable.
Remark 1.
Whether a granule is definable or not depends on the description logic language we use and the perspective from which we look at the problem.
Example 1.

Consider the formal context shown in Table 1, where and .

Table 1.
A formal context .
It is easy to observe that is a ∧-indefinable granule. Moreover, we can show that both and are ∧-definable granules. However, if we take the logic connective ¬ into consideration, then the granule will also become -definable, and has a description .
Take a different perspective and consider the complement formal context shown in Table 2 (see Table 1). In this formal context, turns out to be a ∧-definable granule. Meanwhile, both and turn out to be ∧-indefinable granules. But if the connective ¬ is adopted in the descriptive language, both and are -definable granules.

Table 2.
The complement formal context of the one shown in Table 1.
It is well known that ∧-definable granules play an important role in FCA and concept learning, while -definable granules have an intimate relationship with 3WCA and three-way decisions [37,45,46]. So, we will investigate ∧, -indefinable granules and , -indefinable granules based on FCA and 3WCA in the subsequent discussions.
In what follows, we discuss the relations between -indefinable granules and -definable granules, and those between -definable granules and -indefinable granules.
Remark 2.
Some -indefinable granules can be -definable.
Example 2.

Consider the formal context shown in Table 3, where and .

Table 3.
A formal context .
Note that we cannot find a formula containing the connectives ∧ and ¬ only to crisply describe . So, is -indefinable. On the other hand, since , we conclude that is -definable.
Remark 3.
Some -indefinable granules can be -definable.
Example 3.
Continued with Example 2. Note that we cannot find a formula containing the connectives ∧ and ∨ only to describe . So, is -indefinable. On the other hand, since , we conclude that is -definable.
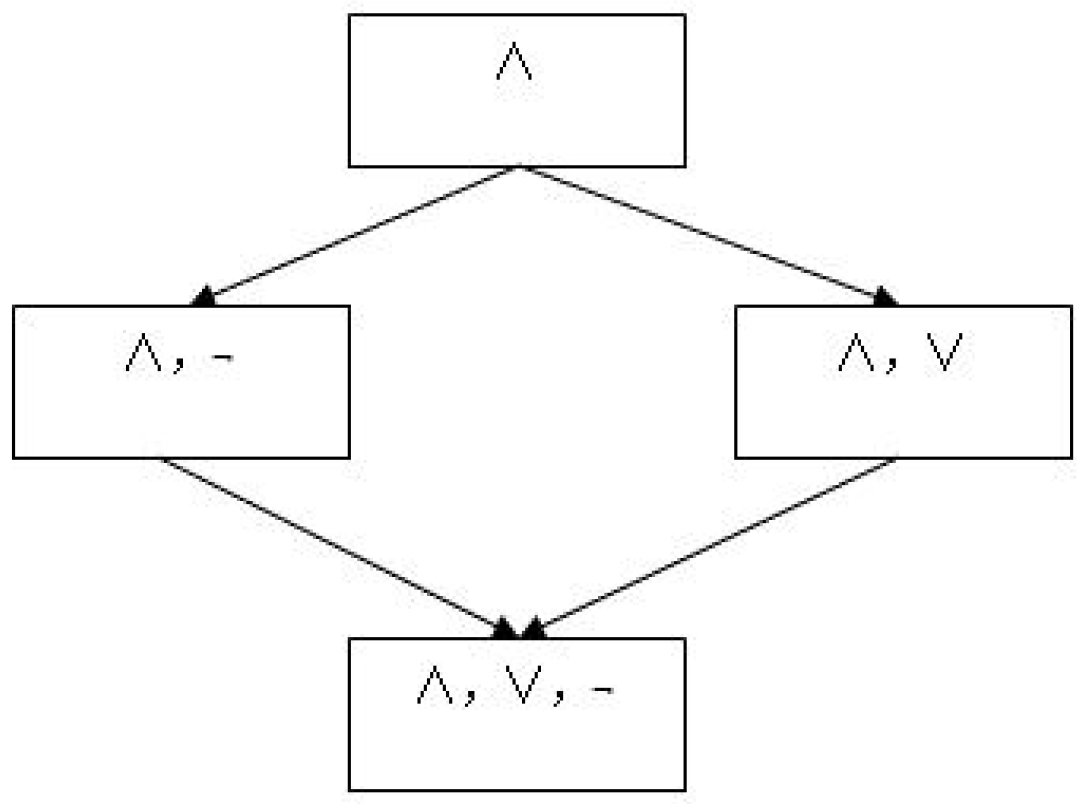
Furthermore, it is obvious that all the and -definable granules are also -definable granules. To sum up, the descriptive abilities of ∧, , and -languages can be shown by Figure 1 in which the arrows from top to bottom represent stronger descriptive abilities.
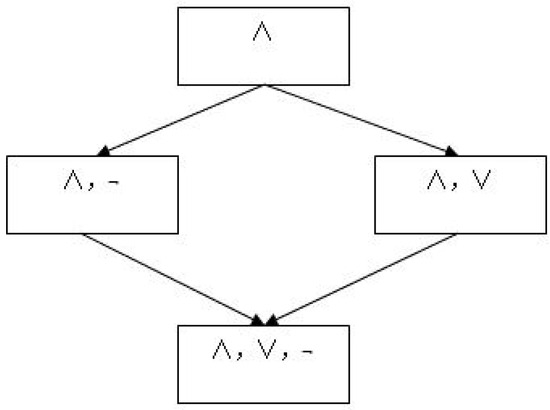
Figure 1.
Descriptive ability comparison of four types of logic languages.
It should be pointed out that the more powerful the language we use, the higher the description accuracy we will obtain and the more complicated the formula that should be used. Then, it is natural that we will usually make a tradeoff between the accuracy and the description complexity to cater to different applications. And this may be a satisfying explanation for the necessity of discussing approximate descriptions by using different logic languages.
4. Approximate Description Methods for Indefinable Granules Based on FCA
In this section, we will give some strategies on the approximate descriptions of indefinable granules based on FCA.
4.1. ∧-Approximate Descriptions of Indefinable Granules Based on the Concept Lattice
In this subsection, we explore the ∧-approximate descriptions of indefinable granules based on the concept lattice. Let be a formal context and . If X is an extent of a formal concept of K, then we call X a basic granule.
Lemma 1.
Let be a formal context and be a granule. If there exists a concept of , then X is ∧-definable.
Proof.
Since there exists a concept with an extent equal to X, it is trivial to show that , where . Hence, X is ∧-definable. □
Definition 13.
Let be a formal context and be a granule. If there exist two concepts and such that , we say that X is approximately ∧-definable.
Theorem 3.
All granules are approximately ∧-definable.
Proof.
Let be a formal context and be a granule. On the one hand, if there exists a concept of with its extent equal to X, then X is ∧-definable based on Lemma 1. On the other hand, if there does not exist a concept with its extent equal to X, there must be two concepts and with their extents . As the granules G and are ∧-definable, it follows that X is approximately ∧-definable. To sum up, this theorem is at hand. □
Definition 14.
Let be a formal context and be a granule. is called the upper ∧-approximate concept of X if and there does not exist such that .
Correspondingly, is called the lower ∧-approximate concept of X, if and there does not exist such that .
It should be pointed out that both the upper and lower ∧-approximate concepts of X may not be unique. According to Definitions 2 and 14, there exists an upper ∧-approximate concept of X such that and reaches the biggest value. Similarly, there exists a lower ∧-approximate concept of X such that and reaches the biggest value. Actually, is the upper ∧-approximate granule of X and is the lower ∧-approximate granule of X. Then, based on Definitions 5 and 6, we can use the upper and lower ∧-approximate concepts of X to construct the -prior approximate optimal description, -prior approximate optimal description, and ∧-approximate description of X. The detailed procedure is shown in Algorithm 1.
| Algorithm 1 Computing the ∧-approximate description of a granule. |
|
Note that the minimal generator of a concept is often a more concise way to describe a granule than the intent of the concept [39]. So, Algorithm 1 adopts such a technique as usual.
Let N be the number of concepts contained in . The time complexity of Algorithm 1 depends on the cost of finding the upper and lower ∧-approximate concepts and the calculation of minimal generators. On the one hand, the number of concepts that need to be visited is less than N when finding the upper and lower ∧-approximate concepts. On the other hand, when calculating the minimal generator of a given concept, the number of visited concepts is also less than N. So, the time complexity of Algorithm 1 is .
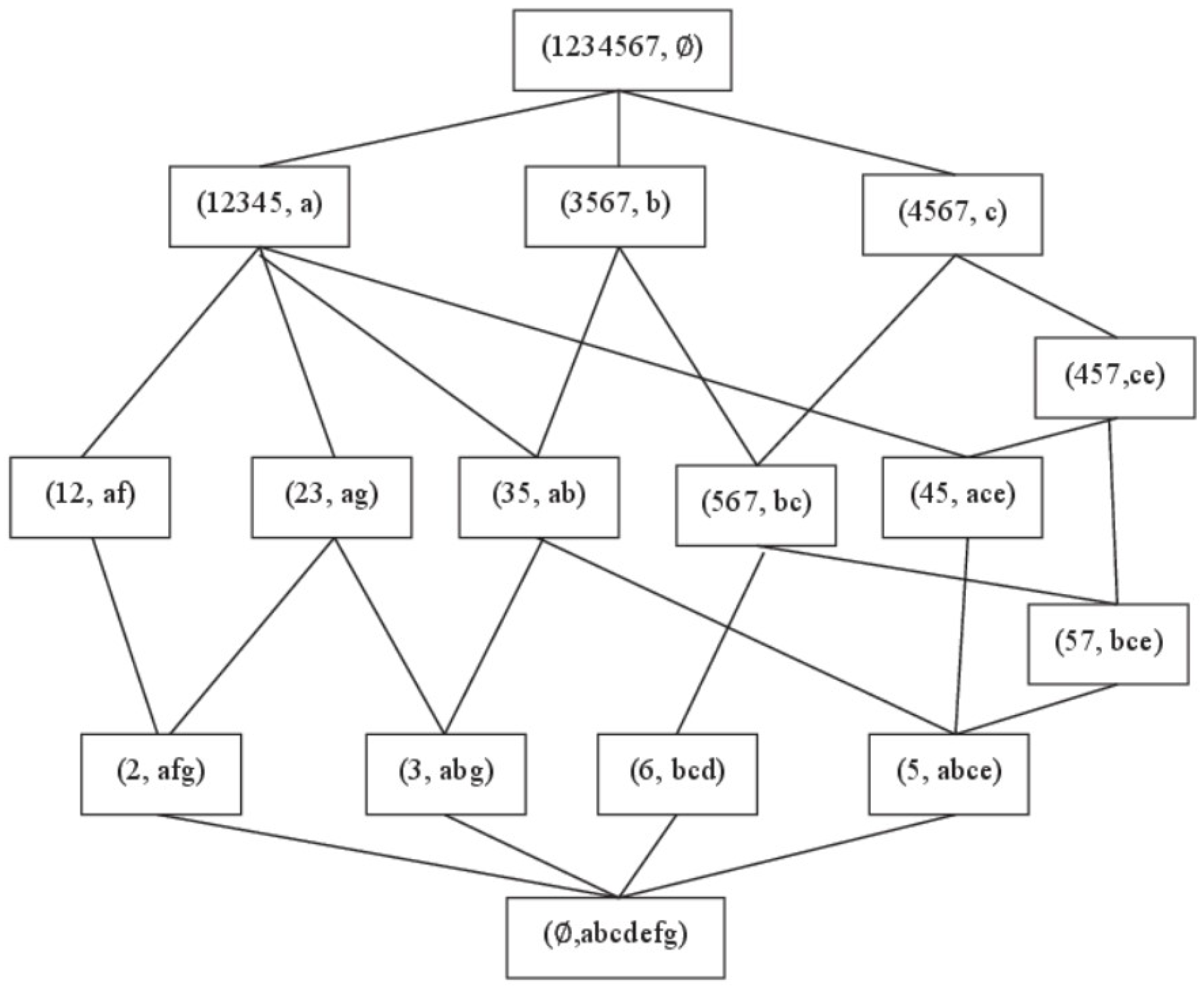
Example 4.
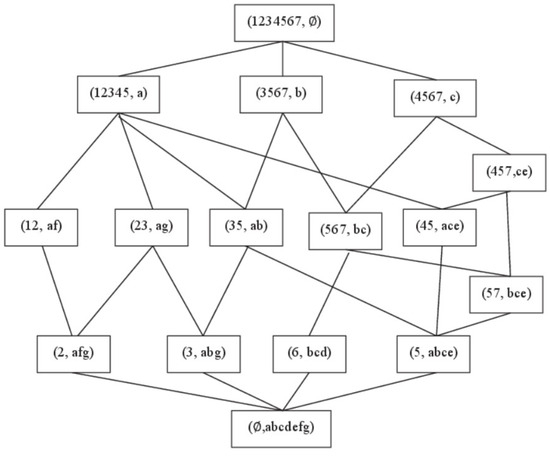
The formal context is presented in Table 3. The corresponding concept lattice is sketched in Figure 2. For convenience, curly braces and commas are omitted in the representations of concepts.

Figure 2.
Concept lattice of the formal context in Table 3.
Let be a granule. we have
with
Actually, the final results are not unique. We also have
with
As another instance, let . We have , and thus is definable.
In what follows, we give some counterexamples for the second part of Proposition 6. It is observed that , , and , which verify that is not valid. It can be easily verified through counterexamples in a similar way that the other three sentences do not hold.
4.2. -Approximate Descriptions of Indefinable Granules Based on the Object Pictorial Diagram
In this subsection, we present a method for -approximate descriptions of indefinable granules based on the object pictorial diagram.
Definition 15
([15]). Let be a formal context and . For any , if or , we say that and are comparable, denoted by or . is called the object pictorial diagram of K, and is called a labeled object class on G.
Furthermore, for each , the down-set of x, denoted by , is defined as:
Correspondingly, the up-set of x, denoted by , is defined as:
Definition 16.
Let be a formal context. For any , a pair of operators are defined, respectively, as:
Definition 17
([39]). Let be a formal context and . If any two elements of X are comparable, we say that X is a list.
Definition 18
([39]). Let be a formal context and be a list. If , we say that X is a down-set complete list. Correspondingly, if , we say that X is an up-set complete list. Moreover, if X is both down-set complete and up-set complete, we say that X is a complete list.
Furthermore, if , where each is a down-set complete list, we say that X is a down-set complete set. Correspondingly, if , where each is an up-set complete list, we say that X is an up-set complete set. Moreover, if X is both down-set complete and up-set complete, we say that X is a complete set.
Proposition 7.
Let X be a granule. If X is an up-set complete list, then X is -definable.
Proof.
Suppose and . Then, it is trivial to show and , which means that is a concept. Hence, based on Lemma 1, X is ∧-definable. □
Corollary 1.
Let X be a granule. Then, both and are -definable.
Proof.
According to the definition of , we can suppose that , where is an up-set complete list. Moreover, according to Proposition 8, we can suppose that the description of is , where is a formula only containing the connective ∧. Then, we have . Hence, is -definable.
Moreover, is -definable can be proved in a similar way. □
Corollary 2.
Let X be a granule. If or , then X is -definable.
Corollary 3.
Let X be a granule. is the upper -approximate granule of X and is the lower -approximate granule of X.
Definition 19.
Let be a formal context and be a granule. If there exist two -definable granules and such that , we say that X is approximately -definable.
Theorem 4.
All granules are approximately -definable.
Proof.
Let be a formal context and be a granule. First, we can always derive and . Moreover, Corollary 1 states that both and are -definable. Then, it follows that X is approximately ∧-definable. □
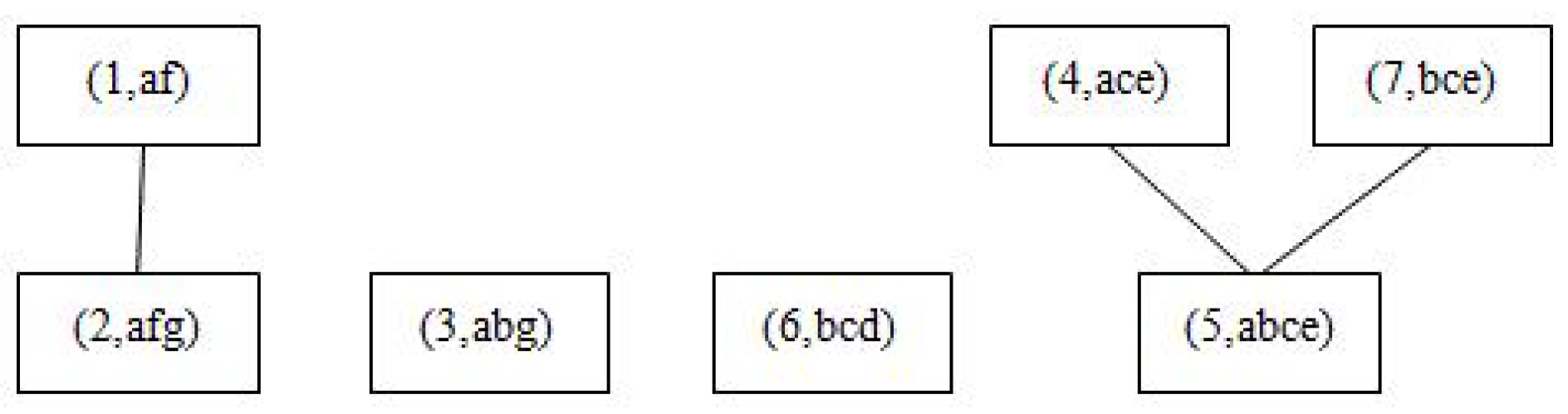
Example 5.
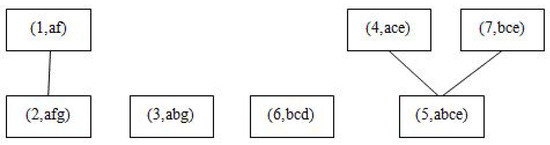
Consider the formal context in Table 3. The corresponding object pictorial diagram is shown in Figure 3.

Figure 3.
of the formal context in Table 3.
Let be a granule. We have
Furthermore, if we resort to ∧-approximate description, we have
From a mathematical viewpoint, -definable granules can be obtained by computing the span of the set of basic granules. Formally, let be a family of sets, the span of is defined as .
In Algorithm 2, we propose a method for the descriptions of –definable granules.
| Algorithm 2 Computing the -description of a granule. |
|
Based on the above discussions, there exists an upper -approximate granule of X such that and reaches the biggest value. Similarly, there exists a lower -approximate granule of X such that and reaches the biggest value. Then, based on Definitions 5 and 6, we can use the upper and lower -approximate granules of X to construct the -prior approximate optimal description, -prior approximate optimal description, and -approximate description of X. The detailed procedure is shown in Algorithm 3.
The time complexity of Algorithm 3 mainly relies on Algorithm 2, which is used to compute the approximate descriptions of two granules. In Algorithm 2, Steps 3 and 4 compute the description of a -definable granule by connecting the descriptions of its sub-granules via the logic connective ∨. As the information we use is limited to the lists embedded in the object pictorial diagram , the number of concepts we visited is bounded by N. So, the time complexity of Algorithm 3 is .
| Algorithm 3 Computing the -approximate description of a granule. |
|
5. Approximate Description Methods for Indefinable Granules Based on 3WCA
In this section, we investigate the -approximate and -approximate descriptions of indefinable granules. Before proceeding, we show that FCA is no longer valid in dealing with this problem. Therefore, we resort to 3WCA and propose approaches regarding this problem.
5.1. The Defects of -Approximate Descriptions Based on FCA
Following the discussions in the previous section, we analyze the defects of -approximate descriptions based on FCA.
Proposition 8.
Let be a formal context and be a granule. If for any object , we have , then X is -indefinable.
Proof.
According to the assumption, if there exists an object and , then there is no attribute to distinguish y from X. Hence, we obtain the conclusion. □
Proposition 9.
Down-set complete sets can be -definable or -indefinable.
We use the following example to confirm our statement in Proposition 9.
Example 6.
Consider the formal context in Table 3. Let . Then, , , . By Proposition 8, it can be concluded that is (∧, ¬)-indefinable.
Next, we discuss two down-set complete sets and . Since , we conclude that is -definable. Note that we cannot find a formula containing the connectives ∧ and ¬ only to describe . So, is -indefinable.
Proposition 10.
Up-set complete sets can be -definable or -indefinable.
We use the following example to confirm our statement in Proposition 10.
Example 7.
Consider the formal context in Table 3. Discuss two up-set complete sets and .
Since , we conclude that is -definable. Note that we cannot find a formula containing the connectives ∧ and ¬ only to describe . So, is -indefinable.
Following the above discussions, we can obtain the following two propositions immediately.
Proposition 11.
Let X be a granule. Then, both and can be -definable or -indefinable.
Proposition 12.
Let X be a granule, and Then, both and can be -definable or -indefinable.
In summary, we know that both and cannot serve as the upper -approximate granule, and both and cannot act as the lower -approximate granule. Then, we conclude that FCA is not an effective tool for the -approximate descriptions of granules.
5.2. -Approximate Descriptions of Indefinable Granules Based on the Three-Way Concept Lattice
In this section, we present a method for -approximate descriptions of indefinable granules based on the three-way concept lattice. Let be a formal context and . If X is an extent of a three-way concept of K, then we call X a basic granule in the settings of three-way concept analysis.
In order to obtain simpler descriptions of granules, we first extend the notion of a minimal generator from a formal concept [39,47] to a three-way concept.
Definition 20.
Let be a formal context and . If there are a subset E of A and a subset F of B such that and for any , , then we call a minimal generator of . Furthermore, if , we call an intent reduct of .
Proposition 13.
Let be a formal context and . Then, both and are three-way concepts.
Proof.
Let and . On the one hand, we have . On the other hand, as , and , we can obtain . Then, is a three-way concept. Moreover, the rest of the proposition can be proved likewise. □
According to Proposition 13, we can define two types of attribute-induced three-way concepts.
Definition 21.
Let be a formal context. If a three-way concept can be rewritten as or , then this concept is referred to as an attribute-induced three-way concept. Moreover, we say that is a type-I attribute-induced three-way concept and is a type-II attribute-induced three-way concept.
Theorem 5
([38]). Let and be two three-way concepts of a formal context . Then, the infimum and supremum are given by:
Theorem 6.
Let be a formal context and be the three-way concept lattice of K. If a three-way concept of has only one upper neighbor, then it is an attribute-induced three-way concept.
Proof.
As has only one upper neighbor, it follows that is a lower bound irreducible element. In other words, , which implies that . Let . Then, according to Theorem 5, we have . Therefore, we have , which means or . If , then there must exist an attribute and such that can be rewritten as . If , then there must exist an attribute and such that can be rewritten as . To sum up, is an attribute-induced three-way concept. □
Theorem 7.
Let be a formal context and a three-way concept of has at least two upper neighbors , where I is an index set and . If , then is an attribute-induced three-way concept.
Proof.
Since , there exists or . If there is , then this concept can be rewritten as . If there is , then this concept can be rewritten as . To sum up, the required conclusion is at hand. □
Theorem 8.
Let be a formal context and be the three-way concept lattice of K. is a minimal generator of , and is a minimal generator of .
Proof.
According to the notions of an attribute-induced three-way concept and minimal generator of a three-way concept, the proof can be completed easily. □
Definition 22.
Let be a pair of two attribute sets. The simplification function carried on is defined as:
Definition 23.
Let be a pair of two attribute sets. The simplification function carried on the first element and second element of are, respectively, defined as:
Definition 24.
Let and be two pairs of attribute sets. The simplification-union function carried on and is defined as:
Lemma 2.
Let be a pair of two attribute sets and . Then, the following properties hold:
(i) , ;
(ii) .
Proof.
(i) Without loss of generality, we assume that there exist two attributes and with . Then, , so a simple manipulation leads to the equation . Moreover, can be proved likewise.
(ii) It follows immediately from Definition 24. □
Lemma 3.
In a three-way concept lattice, if a concept is not an attribute-induced three-way concept, then this concept has at least two upper neighbors.
Proof.
It follows immediately from Theorem 6. □
Lemma 4.
In a three-way concept lattice, if a concept is not an attribute-induced three-way concept, then one of its intent reducts is the union of any two upper neighbors’ minimal generators.
Proof.
Assume that is not an attribute-induced three-way concept. Lemma 3 indicates that has at least two upper neighbors and we denote them by , where I is an index set. Moreover, we denote the minimal generator of by . Furthermore, . In addition, we take and into consideration, and then we have . Thence, the proof is completed. □
Theorem 9.
In a three-way concept lattice, if a concept is not an attribute-induced three-way concept, then one of its minimal generators is the simplification union of any two upper neighbors’ minimal generators.
Proof.
This theorem follows immediately from Lemmas 2–4. □
To sum up, according to Theorems 6 and 7, we can identify attribute-induced three-way concepts. Based on Theorems 8 and 9, we can obtain the minimal generators of each three-way concept. Algorithm 4 computes minimal generators of each three-way concept of a given three-way concept lattice.
| Algorithm 4 Computing the minimal generator of each three-way concept. |
|
Let N be the number of concepts of . In Algorithm 4, it is obvious that each three-way concept is visited just once, so the time complexity of this algorithm is .
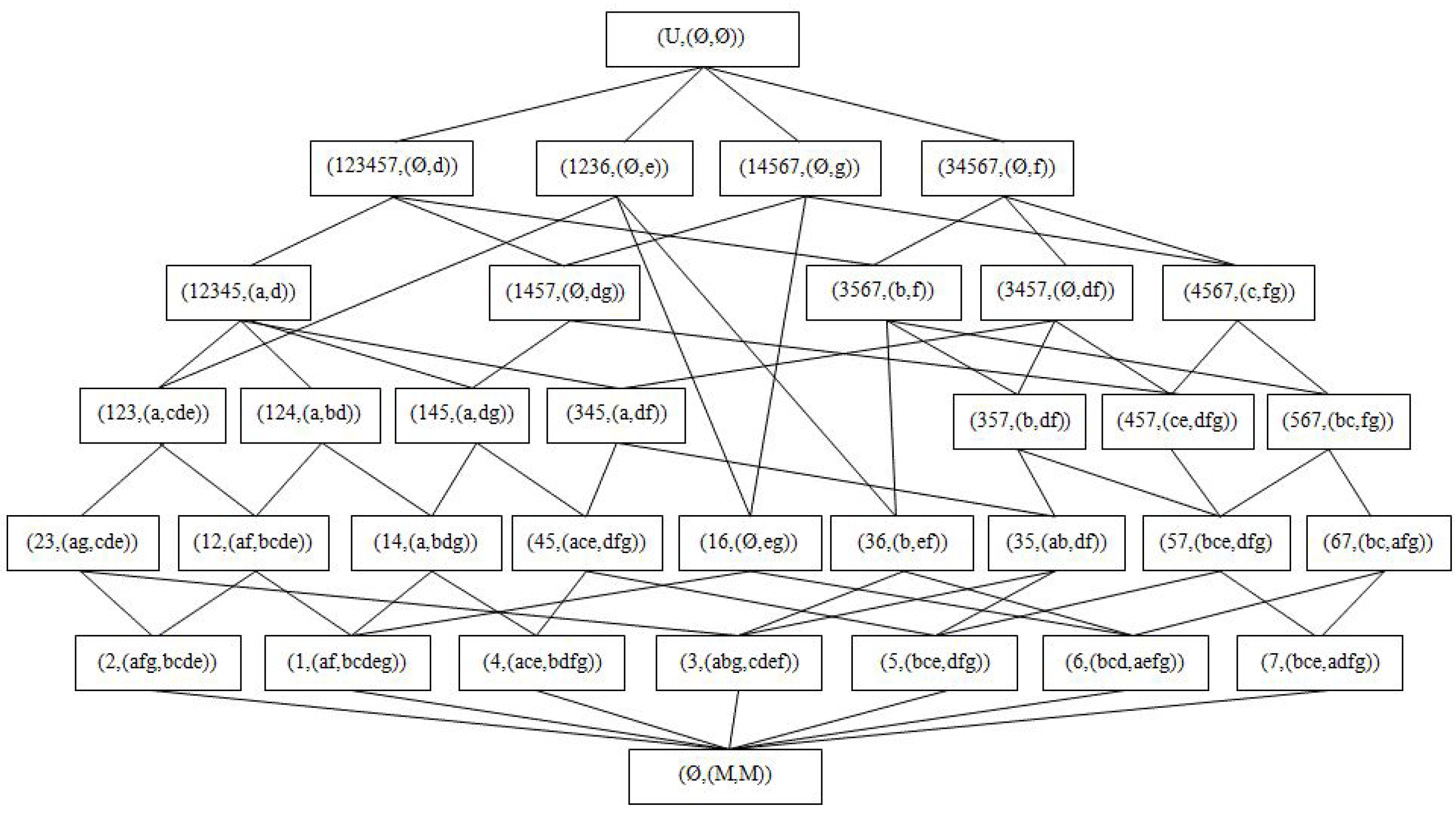
Example 8.
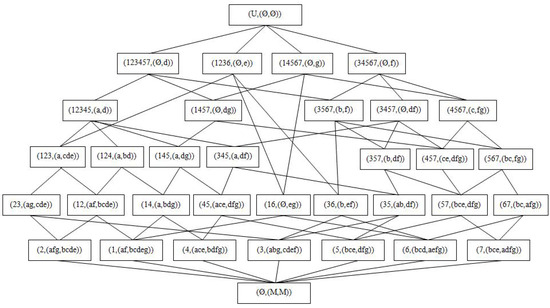

Consider the formal context in Table 3. The three-way concept lattice is shown in Figure 4. Actually, each three-way concept corresponds to a -definable granule. By using Algorithm 4, we obtain the minimal generators of all three-way concepts except and . Then, we obtain their descriptions shown in Table 4.

Figure 4.
Three-way concept lattice of the formal context in Table 3.

Table 4.
Descriptions of -definable granules.
Definition 25.
Let be a formal context and be a granule. If there exist two three-way concepts and such that , we say that X is approximately -definable.
Theorem 10.
All granules are approximately -definable.
Proof.
This theorem can be proved similarly to that of Theorem 3. □
Definition 26.
Let be a formal context and be a granule. is called the upper -approximate three-way concept of X if and there does not exist such that . Correspondingly, is called the lower -approximate three-way concept of X if and there does not exist such that .
Similar to the case in Algorithm 1, here both the upper and lower -approximate three-way concepts of X may not be unique. According to Definitions 2 and 26, there exists an upper -approximate three-way concept of X such that
and reaches the biggest value. Similarly, there exists a lower -approximate three-way concept of X such that
and reaches the biggest value. Actually, is the upper -approximate granule of X and is the lower -approximate granule of X. Then, based on Definitions 5 and 6, we can use the upper and lower -approximate three-way concepts of X to construct the -prior approximate optimal description, the -prior approximate optimal description, and the -approximate description of X. The detailed procedure is shown in Algorithm 5.
| Algorithm 5 Computing the -approximate description of a granule. |
|
Note that the minimal generator of a concept is often more concise to describe a granule than the intent of the concept [39]. So, Algorithm 5 adopts such a technique as usual.
The time complexity of Algorithm 5 depends on the cost of finding the upper and lower approximate three-way concepts and the calculation of minimal generators. Apparently, in order to find the upper and lower -approximate three-way concepts, the number of visited concepts is less than N. Moreover, when computing minimal generators, the number of visited concepts is still less than N. So, the time complexity of Algorithm 5 is .
Example 9.
Consider the formal context in Table 3. Let . It is easy to check that X is a -indefinable granule.
Then, by using Algorithm 5, we can compute its -approximate description in three steps:
(i) we obtain the upper -approximate three-way concept of X and the result is ;
(ii) we obtain the lower -approximate thee-way concept of X and the result is or ;
(iii) we derive the approximate description of X and the result is or or with .
5.3. -Approximate Descriptions of Indefinable Granules Based on a Three-Way Concept Lattice
In this section, we propose a method for -approximate descriptions of indefinable granules based on a three-way concept lattice.
Proposition 14.
Let be a formal context and be a granule. If there exist and such that , then X is -indefinable; otherwise, X is -definable.
Proof.
If there exist and such that , then we cannot distinguish x from y by using both positive and negative attributes. By the definition of an -indefinable granule, it follows that X is -indefinable. Otherwise, we always have a description . Hence, X is -definable. □
Definition 27.
Let be a formal context. For any , a pair of operators are defined, respectively, as:
Based on Proposition 14 and Definition 27, we immediately obtain the following Corollaries 4, 5, and 6.
Corollary 4.
Let X be a granule. Then, both and are -definable.
Corollary 5.
Let X be a granule. If or , then X is -definable.
Corollary 6.
Let X be a granule. is the lower -approximate granule of X and is the upper -approximate granule of X.
Definition 28.
Let be a formal context and be a granule. If there exist two -definable granules and such that , we say that X is approximately -definable.
Theorem 11.
All granules are approximately -definable.
Proof.
Let be a formal context and be a granule. First, we can always derive and . Moreover, Corollary 4 states that both and are -definable. Then, it follows that X is approximately -definable. □
For a given -definable granule X, we have . However, it needs time to obtain the simplest form of by performing logical operations. To solve this problem, we resort to a three-way concept lattice.
By using Algorithm 6, we can calculate the descriptions of -definable granules.
| Algorithm 6 Computing the description of a -definable granule. |
|
Example 10.
Consider the formal context in Table 3. Let . By using Algorithm 6, we obtain the description of X by combining the -descriptions of the granules , and . That is, .
Similar to the case in Algorithm 3, there exists an upper -approximate granule of X such that and reaches the biggest value. Similarly, there exists a lower -approximate granule of X such that and reaches the biggest value. Then, based on Definitions 5 and 6, we can use the upper and lower -approximate granules of X to construct the -prior approximate optimal description, the -prior approximate optimal description, and the -approximate description of X. The detailed procedure is shown in Algorithm 7. In addition, the time complexity of Algorithm 7 is .
| Algorithm 7 Computing the -approximate description of a granule. |
|
Example 11.
Consider the formal context in Table 3. Let . If we add a new object 8 with the same description as that of object 3 into X, then X changes to be a -indefinable granule. According to Algorithm 7, we obtain the upper and lower -approximate granules and , respectively. And then, we have the -approximate description
with
6. A Case Study and Experimental Analysis
Example 12.

In a science and education film called “Biology and Water” in Hungary, there are eight species of organisms, namely, grasshoppers (1), fish (2), frogs (3), dogs (4), aquatic plants (5), reeds (6), beans (7), and corn (8). At the same time, this movie emphasizes nine biological attributes, namely, a (requiring water), b (living in water), c (living on land), d (having chlorophyll), e (dicotyledonous), f (having a single cotyledon), g (being able to move), h (having limbs), and i (breastfeeding). The formal context of these organisms is shown in Table 5 [12].

Table 5.
Formal context “Biology and Water”.
By using FCA, we can obtain the concept lattice , which has 19 formal concepts. In other words, there are 19 basic granules (∧-definable granules) in the settings of classical formal concept analysis, and these basic granules are described with ∧-based language. For instance, is an extent of , and thus is a basic and ∧-definable granule with a description , which means that they need water, live in water, and have the ability to move. Based on ∧-definable granules, we can obtain -definable granules.
Based on three-way concept analysis, we can derive the three-way concept lattice , which has 44 three-way concepts. Therefore, we can obtain 44 basic granules (-definable granules) in the settings of three-way concept analysis, and describe these basic granules with -based language. For instance, is an extent of , and thus is a basic and -definable granule with a description , which means that they live on land, and are not dicotyledonous and breastfeeding. Based on -definable granules, we can obtain -definable granules.
By comparing the FCA and three-way concept analysis-based method, the latter can derive more basic granules, and thus can improve the description accuracy. In what follows, we test this based on experiments by randomly generated formal contexts.
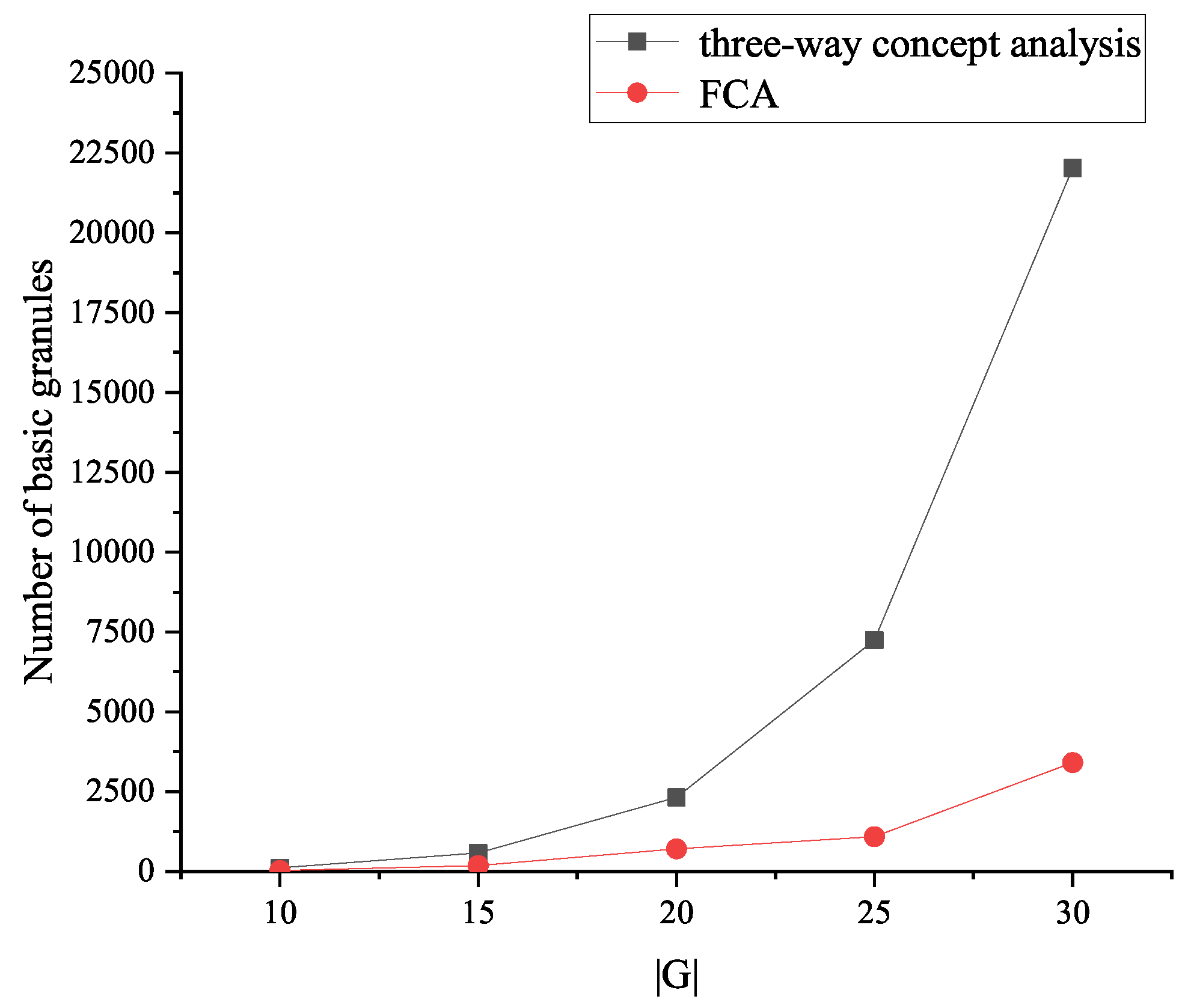
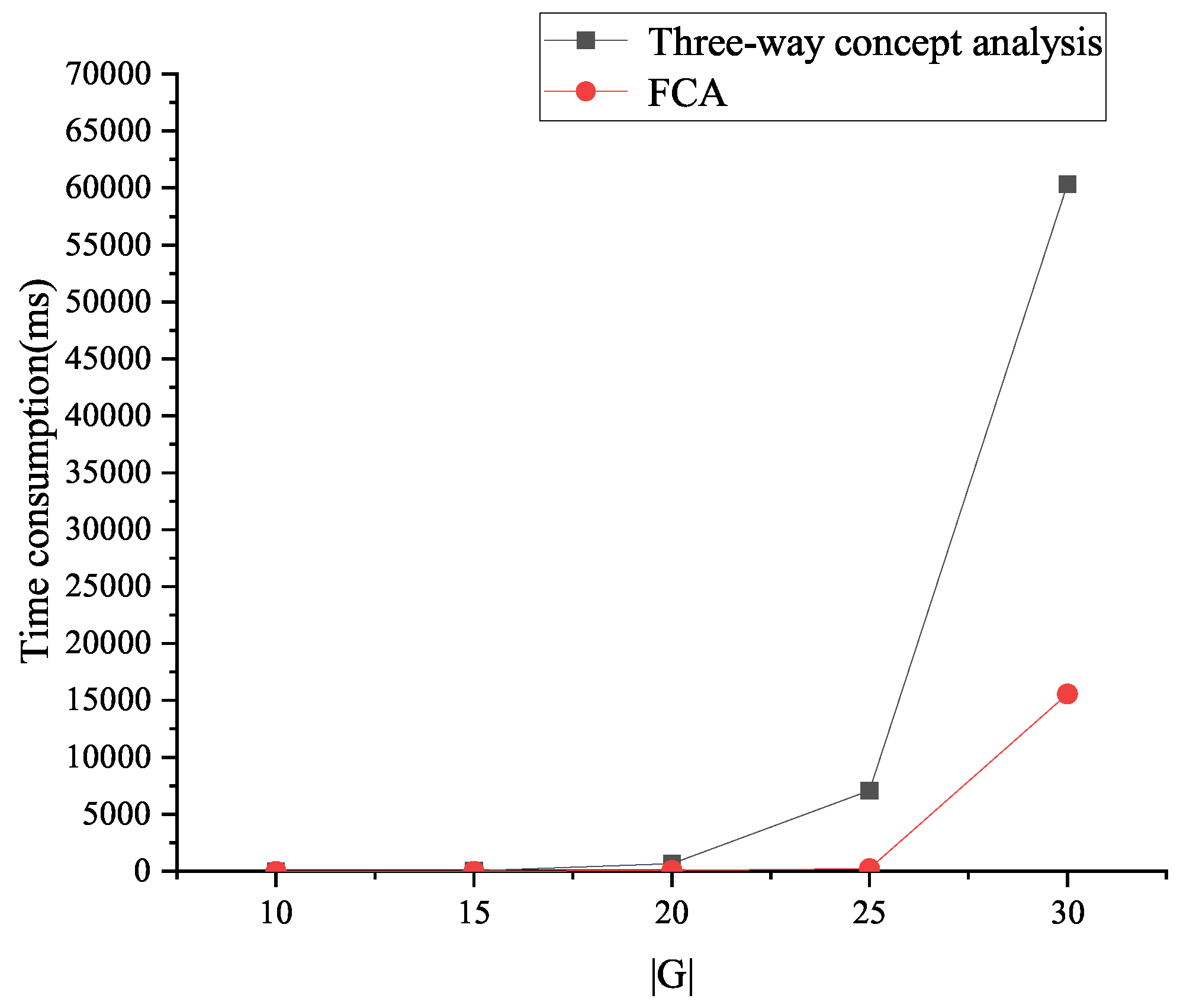
In the experiments, the number of basic granules and the time consumptions to acquire them are investigated. It should be pointed out that the time consumption contains the process of building the concept lattices. The formal contexts are generated by fixing the fill ratio and while changing and . The experimental results in terms of the number of concepts and time consumptions are shown in Figure 5 and Figure 6, which reveals that the three-way concept analysis-based method can derive more basic granules, and the FCA-based method needs less time consumption.
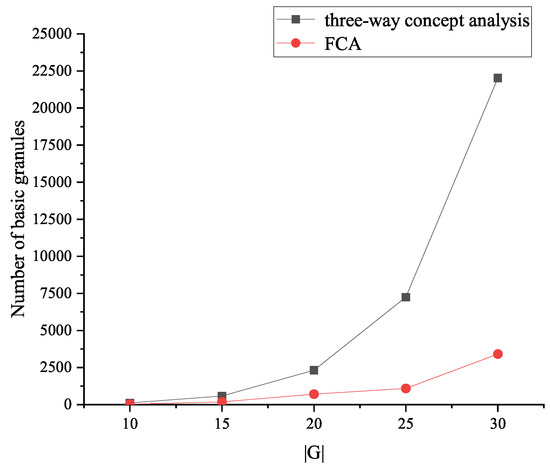
Figure 5.
Experimental results on the number of basic granules.
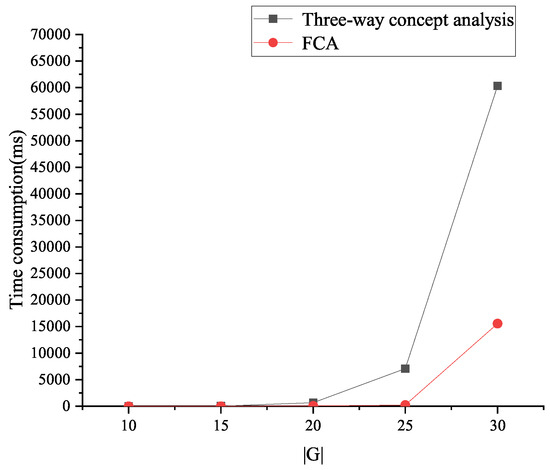
Figure 6.
Experimental results on time consumption.
7. Conclusions
In this section, we draw some conclusions to show the main contributions of our paper and give an outlook for further study.
(i) A brief summary of our study
In this study, the approximate description of granules has been investigated. More specifically, approximate description logic has been introduced and we have approximated indefinable granules by using a couple of descriptions of two definable granules, that is the -prior optimal approximate description and the -prior optimal approximate description. By using this idea throughout our study, at first, we explored the ∧-approximate descriptions of granules based on FCA, and then we presented the -approximate descriptions of granules by using object pictorial diagrams. After that, some necessary discussions were presented to show the ineffectiveness of FCA until negative attributes are taken into consideration. Therefore, we have resorted to 3WCA instead of FCA to characterize granules both in positive and negative perspectives. Concretely, we presented -approximate descriptions and -approximate descriptions of granules based on a three-way concept lattice, respectively.
(ii) The differences and similarities between our study and existing ones
Formal concept analysis and rough set analysis are two related theories used in granular computing. By incorporating these two theories, Yao proposed rough-set concept analysis in which -definable concepts were studied [16]. In some sense, according to the mathematical logic used in rough-set concept analysis, rough-set definable concepts are actually attribute concepts under the framework of the object-oriented concept lattice. So, given a rough-set definable granule, the description of the granule can be obtained by consulting the intent of its corresponding object-oriented concept.
More precisely, let X be a rough-set definable granule. Then, the description of X is
where .
However, in our studies, common attribute analysis is used. That is, if X is a ∧-definable granule, then the description of X is
where .
Moreover, in our studies, a more flexible logic has been adopted which contains the connectives ∧, ∨, and ¬. The existing studies, including Yao’s work [16], have provided a granule description for basic granules. Putting it simply, if a granule X is an extent of a formal concept, then X is a basic granule. A basic granule X can be described by connecting the attribute contained in , i.e., , where . Then, it is clear that only the connective ∧ is adopted to construct a formula to describe a granule. But in this study, we consider using the connectives ∧, ∨, and ¬ to build more powerful descriptions.
In addition, in [39], we gave the descriptions of ∧-definable granules based on FCA, and presented the problem of describing indefinable granules. In this paper, we have systematically investigated the approximate descriptions of four important types of indefinable granules, i.e., ∧-indefinable granules, -indefinable granules, -indefinable granules, and -indefinable granules. So, this study can not only be regarded as a continuation of our previous research, but also brings us a more deep understanding of indefinable granules.
(iii) An outlook for further study
Note that the aim of this paper is to give an approximate description method for the granules of complete data. But in most circumstances, we have to deal with the granules of incomplete data. So, how to approximately describe the granules of incomplete data is a challenging and important issue. In addition, granule description can serve as the basic mathematical model for a variety of applications. As an instance, in conflict analysis, the allied, conflict, and neutral cliques are actually granules with different features [48]. Approximate description of these cliques is necessary on many occasions, especially in vague and uncertain settings. More efforts are needed for these problems.
Author Contributions
Conceptualization, H.W. and H.Z.; methodology, H.Z.; software, H.Z.; validation, Y.L.; formal analysis, H.Z.; investigation, H.W.; resources, H.Z.; data curation, H.Z.; writing—original draft preparation, H.W. and H.Z.; writing—review and editing, H.W. and H.Z.; visualization, H.Z.; supervision, Y.L.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Fujian Province under Grant No. 2024J01793.
Data Availability Statement
Data are contained within the article. The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Belohlavek, R.; Baets, B.D.; Konecny, J. Granularity of attributes in formal concept analysis. Inf. Sci. 2014, 260, 149–170. [Google Scholar] [CrossRef]
- Hu, H.; Pang, L.; Tian, D.P. Perception granular computing in visual haze-free task. Expert Syst. Appl. 2014, 41, 2729–2741. [Google Scholar] [CrossRef]
- Salehi, S.; Selamata, A.; Fujita, H. Systematic mapping study on granular computing. Knowl.-Based Syst. 2015, 80, 78–97. [Google Scholar] [CrossRef]
- Lu, W.; Pedrycz, W.; Liu, X.D.; Yang, J.H.; Li, P. The modeling of time series based on information granules. Expert Syst. Appl. 2014, 41, 3799–3808. [Google Scholar] [CrossRef]
- Yao, J.T.; Vasilakos, A.V.; Pedrycz, W. Granular computing: Perspectives and challenges. IEEE Trans. Cybern. 2013, 43, 1977–1989. [Google Scholar] [CrossRef]
- Wang, Y.X.; Wang, Y. Cognitive informatics models of the brain. IEEE Trans. Syst. Man Cybern. Part-Appl. Rev. 2006, 36, 203–207. [Google Scholar] [CrossRef]
- Novak, V. Intensional theory of granular computing. Soft Comput. 2004, 8, 281–290. [Google Scholar] [CrossRef]
- Zadeh, L.A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 19, 111–127. [Google Scholar] [CrossRef]
- George, P.; Mandi, M. A neural-fuzzy modelling framework based on granular computing: Concepts and applications. Fuzzy Sets Syst. 2010, 161, 2808–2830. [Google Scholar]
- Skowron, A.; Stepaniuk, J.; Swiniarski, R. Modeling rough granular computing based on approximation spaces. Inf. Sci. 2012, 184, 20–43. [Google Scholar] [CrossRef]
- Davis, R.; Shrobe, H.; Szolovits, P. What is a knowledge representation? AI Mag. 2002, 14, 17–33. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer: Berlin, Germany, 1999. [Google Scholar]
- Medina, J. Relating attribute reduction in formal, object-oriented and property-oriented concept lattices. Comput. Math. Appl. 2012, 64, 1992–2002. [Google Scholar] [CrossRef]
- Wang, L.D.; Liu, X.D. Concept analysis via rough set and AFS algebra. Inf. Sci. 2008, 178, 4125–4137. [Google Scholar] [CrossRef]
- Wei, L.; Wan, Q. Granular transformation and irreducible element judgment theory based on pictorial diagrams. IEEE Trans. Cybern. 2016, 46, 380–387. [Google Scholar] [CrossRef]
- Yao, Y.Y. Rough-set analysis: Interpreting RS-definable concepts based on ideas from formal concept analysis. Inf. Sci. 2016, 346–347, 442–462. [Google Scholar] [CrossRef]
- Shivhare, R.; Cherukuri, A.K. Three-way conceptual approach for cognitive memory functionalities. Int. J. Mach. Learn. Cybern. 2017, 8, 21–34. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Oosthuizen, G.D. Rough sets and concept lattices. In Fuzzy Sets and Knowledge Discovery. Workshops in Computing; Ziarko, W., Ed.; Springer: London, UK, 1994; pp. 24–31. [Google Scholar]
- Dias, S.M.; Vieira, N.J. A methodology for analysis of concept lattice reduction. Inf. Sci. 2017, 396, 202–217. [Google Scholar] [CrossRef]
- Düntsch, I.; Gediga, G. Modal-style operators in qualitative data analysis. In Proceedings of the 2002 IEEE International Conference on Data Mining, Washington, DC, USA, 9–12 December 2002; pp. 155–162. [Google Scholar]
- Shao, M.W.; Leung, Y. Relations between granular reduct and dominance reduct in formal contexts. Knowl.-Based Syst. 2014, 65, 1–11. [Google Scholar] [CrossRef]
- Wei, L.; Qi, J.J. Relation between concept lattice reduction and rough set reduction. Knowl.-Based Syst. 2010, 23, 934–938. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way decisions with probabilistic rough sets. Inf. Sci. 2010, 180, 341–353. [Google Scholar] [CrossRef]
- Wu, W.Z.; Leung, Y. Theory and applications of granular labelled partitions in multi-scale decision tables. Inf. Sci. 2011, 181, 3878–3897. [Google Scholar] [CrossRef]
- Huang, C.C.; Li, J.H.; Mei, C.L.; Wu, W.Z. Three-way concept learning based on cognitive operators: An information fusion viewpoint. Int. J. Approx. Reason. 2017, 83, 218–242. [Google Scholar] [CrossRef]
- She, Y.H.; He, X.L. On the structure of the multigranulation rough set model. Knowl.-Based Syst. 2012, 36, 81–92. [Google Scholar] [CrossRef]
- Li, J.; Mei, C.; Cherukuri, A.K.; Zhang, X. On rule acquisition in decision formal contexts. Int. J. Mach. Learn. Cybern. 2013, 4, 721–731. [Google Scholar] [CrossRef]
- Pedrycz, W. Allocation of information granularity in optimization and decision-making models: Towards building the foundations of Granular Computing. Eur. J. Oper. Res. 2014, 232, 137–145. [Google Scholar] [CrossRef]
- Wu, X.D.; Zhang, C.Q.; Zhang, S.C. Efficient mining of both positive and negative nssociation rules. Acm Trans. Inf. Syst. 2004, 22, 381–405. [Google Scholar] [CrossRef]
- Lang, G.M.; Miao, D.Q.; Cai, M.J. Three-way decision approaches to conflict analysis using decision-theoretic rough set theory. Inf. Sci. 2017, 406–407, 185–207. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Xia, D.Y.; Wang, G.Y. Three-way decision model with two types of classification errors. Inf. Sci. 2017, 420, 431–453. [Google Scholar] [CrossRef]
- Qi, J.J.; Wei, L.; Yao, Y.Y. Three-way formal concept analysis. In Rough Sets and Knowledge Technology, RSKT 2014; Miao, D., Pedrycz, W., Ezak, D., Peters, G., Hu, Q., Wang, R., Eds.; LNCS; Springer: Cham, Switzerlands, 2014; Volume 8818, pp. 732–741. [Google Scholar]
- Li, M.Z.; Wang, G.Y. Approximate concept construction with three-way decisions and attribute reduction in incomplete contexts. Knowl.-Based Syst. 2016, 91, 165–178. [Google Scholar] [CrossRef]
- Qian, T.; Wei, L.; Qi, J. Constructing three-way concept lattices based on apposition and subposition of formal contexts. Knowl.-Based Syst. 2017, 166, 39–48. [Google Scholar] [CrossRef]
- Singh, P.K. Medical diagnoses using three-way fuzzy concept lattice and their Euclidean distance. Comput. Appl. Math. 2018, 37, 3283–3306. [Google Scholar] [CrossRef]
- Yao, Y.Y. Interval sets and three-way concept analysis in incomplete contexts. Int. J. Mach. Learn. Cybern. 2017, 8, 3–20. [Google Scholar] [CrossRef]
- Qi, J.J.; Qian, T.; Wei, L. The connections between three-way and classical concept lattices. Knowl.-Based Syst. 2016, 91, 143–151. [Google Scholar] [CrossRef]
- Zhi, H.L.; Li, J. Granule description based on formal concept analysis. Knowl.-Based Syst. 2016, 104, 62–73. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Zhou, B. A logic language of granular computing. In Proceedings of the 6th IEEE International Conference on Cognitive Informatics, Lake Tahoe, CA, USA, 6–8 August 2007; pp. 178–185. [Google Scholar]
- Yao, Y.Y.; Liu, Q. A generalized decision logic in interval-set-valued information tables. In New Directions in Rough Sets, Data Mining, and Granular-Soft Computing; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1711, pp. 285–293. [Google Scholar]
- Yao, Y.Y. Interval-set algebra for qualitative knowledge representation. In Proceedings of the 5th International Conference on Computing and Information, Sudbury, ON, Canada, 9–10 March 1993; pp. 370–374. [Google Scholar]
- Deoguna, J.S.; Saquer, J. Monotone concepts for formal concept analysis. Discret. Appl. Math. 2004, 144, 70–78. [Google Scholar] [CrossRef]
- Qian, Y.H.; Li, S.Y.; Liang, J.Y.; Shi, Z.Z.; Wang, F. Pessimistic rogh set based decisions: A multigranulation fusion strategy. Inf. Sci. 2014, 264, 196–210. [Google Scholar] [CrossRef]
- Liu, D.; Liang, D.C.; Wang, C.C. A novel three-way decision model based on incomplete information system. Knowl.-Based Syst. 2016, 91, 32–45. [Google Scholar] [CrossRef]
- Peters, J.F.; Ramanna, S. Proximal three-way decisions: Theory and applications in social networks. Knowl.-Based Syst. 2016, 91, 4–15. [Google Scholar] [CrossRef]
- Kuznetsov, S.O. On stability of a formal concept. Ann. Math. Artif. Intell. 2005, 49, 101–105. [Google Scholar] [CrossRef]
- Zhi, H.L.; Li, J.H.; Li, Y.N. Multi-level conflict analysis based on fuzzy formal contexts. IEEE Trans. Fuzzy Syst. 2022, 30, 5128–5142. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).