Mathematical Modeling and Recursive Algorithms for Constructing Complex Fractal Patterns
Abstract
1. Introduction
- medical imaging and biomedical analysis: used in cancer detection, heart rate variability analysis, and lung disease modeling through fractal dimension analysis;
- scientific computing and engineering: applied in fluid dynamics, material analysis, and aerodynamics for complex shape modeling;
- artificial intelligence and pattern recognition: utilized in data compression, facial recognition, and feature extraction in machine learning;
- financial markets and econophysics: used to analyze stock market trends and financial time series;
- digital art and textile design: used for generative artwork, fabric pattern creation, and digital media applications.
- development of a novel recursive algorithm—the RFM method integrates adaptive recursion, allowing for flexible scaling and depth control while maintaining structural consistency;
- implementation of symmetry-preserving transformations—ensuring that fractal patterns maintain a high degree of visual and geometric balance, making them suitable for high-precision applications;
- optimization of computational efficiency—reducing processing time through in-place recursion and intermediate result caching, leading to faster convergence with fewer iterations;
- application of the RFM method in real-world scenarios—demonstrating the effectiveness of our approach in fields such as digital art, and textile design.
Related Works
2. Development of Mathematical and Geometric Models of Complex Fractal Structured Objects
2.1. Geometric Modeling Using Analytical Methods
2.2. Geometrical Modeling Using L-Systems and IFS Methods
2.3. Mathematical Modeling Using RFM Methods
- appearance of the standard primitives used: straight line, circle, ellipse, rectangle, triangle, convex polygon, circle, regular polygon, etc.;
- geometric parameters that determine the size and position of standard primitives.
| Algorithm 1. Pseudo-code for Fractal Image Generation |
| Function GenerateFractal(iteration, max_depth, transformation_matrix): |
| # Base case: Stop recursion if max depth is reached |
| return |
| # Apply transformations (scaling, rotation, symmetry preservation) |
| transformed_points = ApplyTransformation(transformation_matrix) |
| # Symmetry-preserving transformations |
| if MaintainSymmetry: |
| transformed_points = EnforceSymmetry(transformed_points) |
| # Selective refinement (increase recursion depth for high-detail regions) |
| if NeedsRefinement(transformed_points): |
| new_depth = AdjustRecursionDepth(iteration) |
| else: |
| new_depth = iteration + 1 |
| # Recursive call to generate the next fractal iteration |
| for point_set in transformed_points: |
| GenerateFractal(new_depth, max_depth, transformation_matrix) |
| # Render the fractal at the current stage |
| DrawFractal(transformed_points) |
| # Main function to initialize fractal generation |
| Function Main(): |
| max_depth = SetMaxRecursionDepth() |
| transformation_matrix = InitializeTransformations() |
| GenerateFractal(0, max_depth, transformation_matrix) |
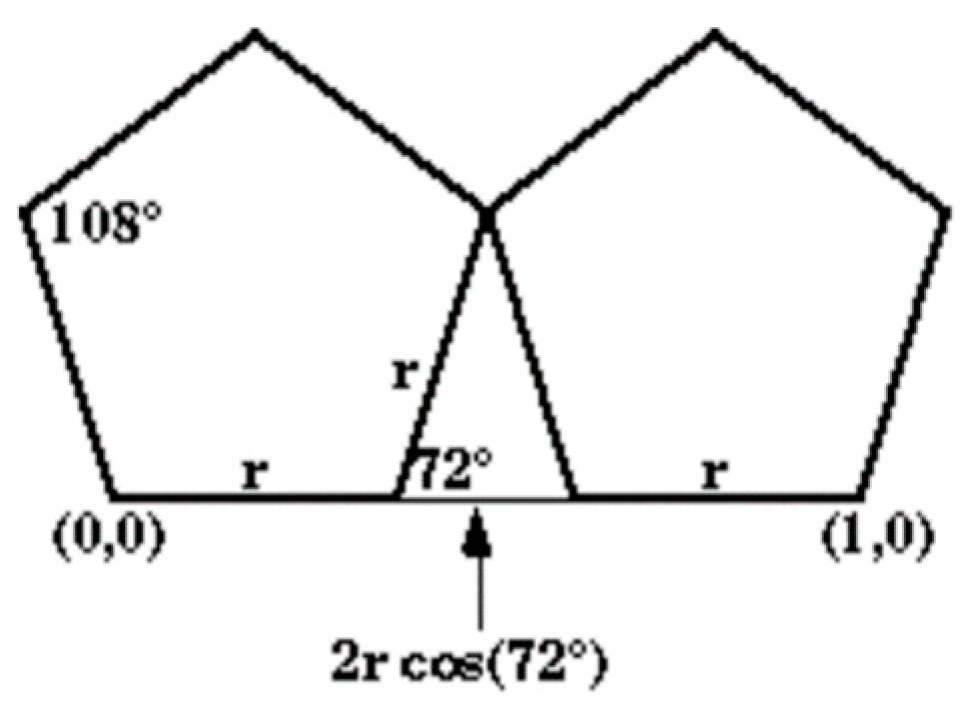
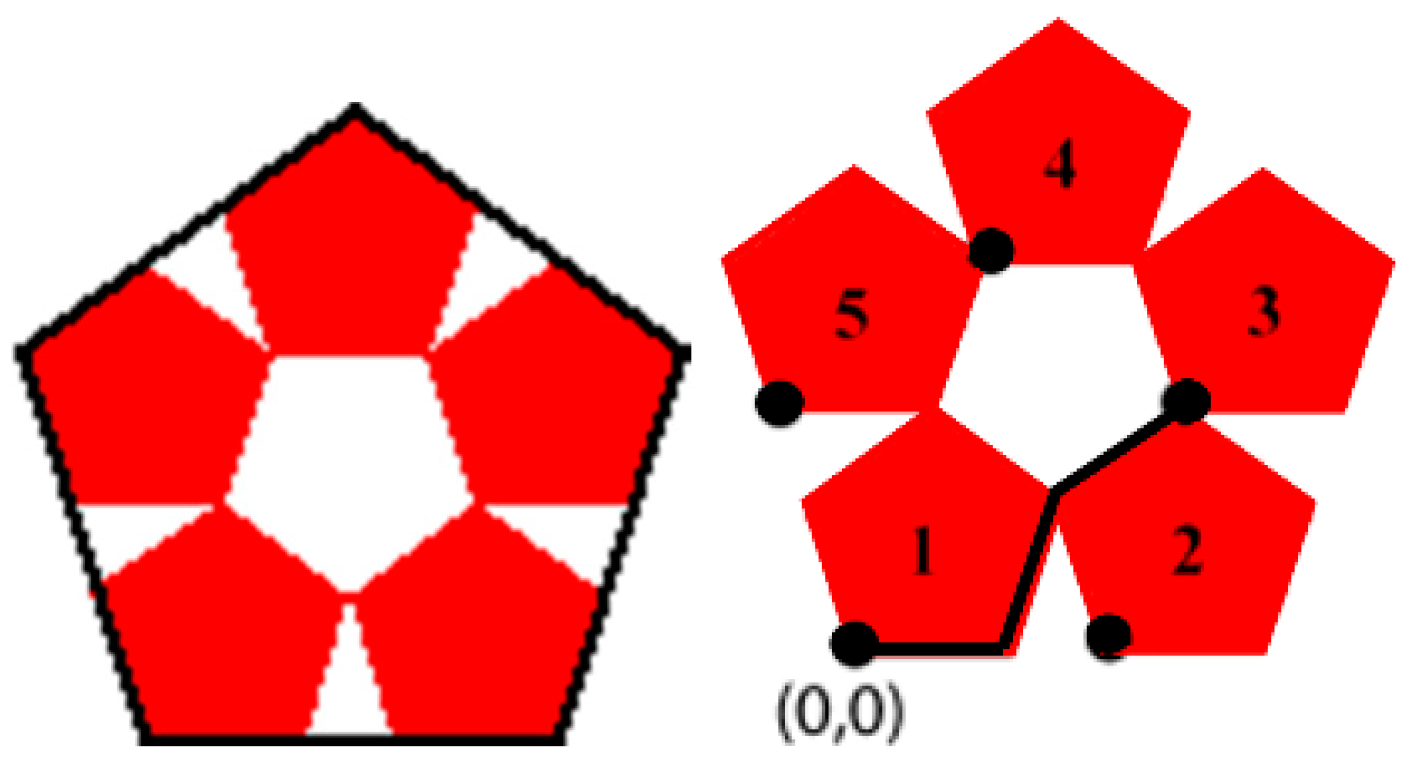
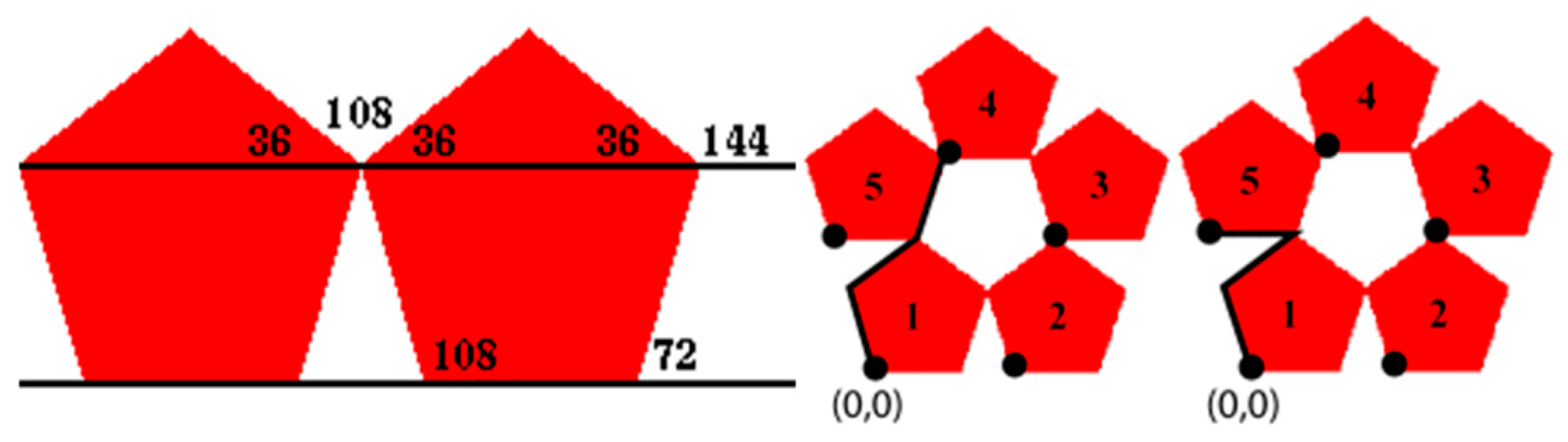
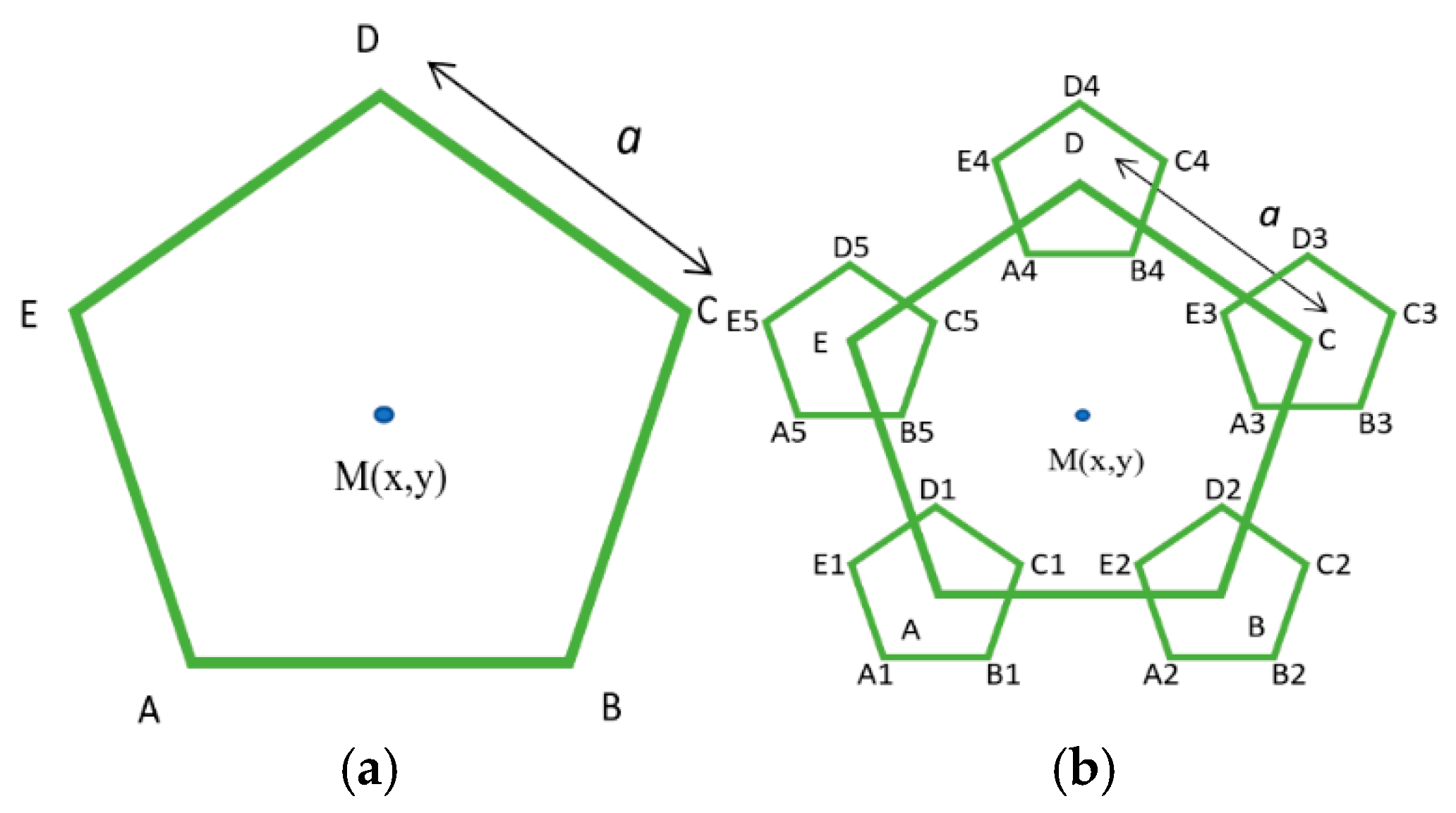
3. Visualization Algorithm of Patterns with Complex Fractal Structure
newx = X+Y+,
newy = −X−Y.
4. Comparison of Performance, Usability, and Efficiency
- Task completion time: users completed standard tasks (e.g., setting parameters, exporting images) 30% faster with our tool than with Fractint, reflecting the convenience of an intuitive interface;
- Error reduction: the graphical interface reduced configuration errors by 40% compared to Fractint’s command-based input, improving accuracy and ease of use;
- Learning curve: new users reported becoming proficient with our tool’s basic operations within 10 min, compared to 25 min for Fractint, highlighting our tool’s accessibility;
- User satisfaction: in surveys, users rated our interface at 4.5/5 for ease of use, in contrast to Fractint’s 3.2/5, indicating greater satisfaction with our design.
- For the compression ratio, our method achieved a compression ratio comparable to Jacquin’s method while offering better control over the trade-off between image detail and compression rate. The fractal structures we generated allowed for flexibility in scaling compression levels based on application needs;
- For encoding and decoding time, benchmark tests indicated that our method has a faster encoding time compared to Jacquin’s method due to optimized recursive algorithms and efficient memory management. Our decoding process also required less computation, maintaining real-time rendering capability for high-resolution images. We conducted t-tests, comparing the encoding and decoding times of our method against Barnsley’s IFS and Jacquin’s methods. The results indicate a statistically significant reduction in both encoding time (p < 0.01) and decoding time (p < 0.01) for our method;
- For image quality (PSNR and SSIM), we measured image quality using PSNR and SSIM to provide quantitative comparisons of visual fidelity. Our method demonstrated a PSNR improvement of approximately 1.5 dB over Barnsley’s IFS method and achieved SSIM scores, indicating a higher structural similarity at comparable compression ratios. These metrics suggest that our method effectively preserves image quality, especially in terms of edge sharpness and structural consistency. T-tests comparing PSNR and SSIM values showed that our method produces significantly higher PSNR scores (p < 0.05) and SSIM values (p < 0.05) than Barnsley’s IFS, indicating better image quality and structural similarity. The higher PSNR and SSIM values reflect an improved preservation of image detail and structure with our approach.
4.1. Fractal Dimension Analysis and Self-Similarity Verification Subsection
4.2. Real-World Applications and Comparison of Recursive Algorithm Properties
5. Conclusions
- -
- The basic concepts of the theory of fractals, the origin of fractals, their properties, types, fields of application, and methods of calculating the fractal dimension were researched. As a result, it was found that national patterns with a fractal structure can be used in the organization of design processes in modern and classic design in light industry and have economic benefits;
- -
- Fractal construction methods, their visualization algorithms, the application process, the concept of fractal measurement, and methods of calculating the size of objects with a fractal structure were investigated. Based on iterative methods and the iterative function system (IFS), the theoretical basis and advantages of the L-systems method were used to develop geometric models of complex fractals. It made it possible to perform a comparative analysis of classical and modern fractals built using these methods;
- -
- A research model of objects with a fractal structure was built using the RFM method, and an algorithm was developed. Based on this algorithm, circular, tree-shaped, star-shaped, and polygonal fractals from classic fractals were visualized. Fractal dimensions of fractal shapes were determined using the developed models. This method and model made it possible to create a wide range of models of complex geometric shapes;
- -
- Based on the developed algorithms, a software tool for automating the visualization of objects with a fractal structure was developed. This software tool made it possible to automate the creation of patterns of gauze and carpets in the textile industry, interior and exterior decoration, furnishing and design of rooms in the construction of buildings, the decoration of construction products with patterns, their design, and the selection of colors and patterns for their products.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Shahzoda, A.; Oybek, N.; Zulaykho, I. Development of Fractal Equations of National Design Patterns based on the Method of R-Function. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2020, 9, 134–141. [Google Scholar] [CrossRef]
- Losa, G.A.; Merlini, D.; Nonnenmacher, T.F.; Weibel, E.R. (Eds.) Fractals in Biology and Medicine: Volume IV; Birkhäuser: Basel, Switzerland, 2005. [Google Scholar] [CrossRef]
- Chen, P.; Peng, S.; Wang, P.; Chen, X.; Yang, T.; Liu, Y. Fractal and multifractal characteristics of geological faults in coal mine area and their control on outburst. Coal Sci. Technol. 2019. Available online: https://www.mtkxjs.com.cn/en/article/id/c578c17e-d002-4413-bc95-4d3450f80b36 (accessed on 12 February 2025).
- Ge, Q.; Sun, Y.; Liu, Y. Application of Fractal Graphics in Fashion Design. Adv. Mater. Res. 2012, 605–607, 53–56. [Google Scholar]
- Xie, M.; Zhu, Q. Fractal analysis of permeability tensor of woven textiles. Acta Sci. Nat. Univ. Sunyatseni 2008, 47, 50–55. [Google Scholar]
- Xiong, Y.; Zhang, H.; Lu, J.; Jin, Y. Fabric-weave design method based on extended fractal model. J. Zhejiang Sci-Tech Univ. 2018, 39, 341–345. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere, 2nd ed.; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Long, X.; Li, W.; Luo, W. Design and Application of Fractal Pattern Art in the Fashion Design. In Proceedings of the 2009 International Workshop on Chaos-Fractals Theories and Applications, Shenyang, China, 6–8 November 2009; pp. 391–394. [Google Scholar] [CrossRef]
- Lu, L.; Song, X. Process Realization of Fractal Pattern in Computer Jacquard Knitting Fabric. J. Bus. Adm. Res. 2016, 5, 20–26. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Zhang, H. The Generation System of Textile Pattern Based on L-Systems. In Proceedings of the 8th International Conference on Management and Computer Science (ICMCS 2018), Shenyang, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Tian, G.; Yuan, Q.; Hu, T.; Shi, Y. Auto-Generation System Based on Fractal Geometry for Batik Pattern Design. Appl. Sci. 2019, 9, 2383. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, L.; Wang, H. Application of deterministic L-systems in knitting pattern design. J. Text. Res. 2015, 36, 35–38. [Google Scholar]
- Yuan, Q.; Lv, J.; Huang, H. Auto-Generation Method of Butterfly Pattern of Batik Based on Fractal Geometry. Int. J. Signal Process. Image Process. Pattern Recognit. 2016, 9, 369–392. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Lu, G.; Fei, S.; Zhang, D. Extraction and reuse of pattern configuration based on ontology and shape grammar. J. Zhejiang Univ. (Eng. Sci.) 2018, 52, 461–472. [Google Scholar]
- Yuan, H.; Cheng, W.; Wang, X.; Liu, X. Fractal pattern design based on Kronecker product and the application in Wangjiang cross stitch. J. Donghua Univ. (Nat. Sci.) 2017, 43, 651–654. [Google Scholar]
- Wang, S.; Yang, X. Generation of fractal image on complex plane and its application in textiles. J. Silk 2017, 54, 56–61. [Google Scholar]
- Zhang, Y.; Jin, Y.; Cen, K. Method of designing irregular fractal weave based on IFS. J. Text. Res. 2012, 33, 30–34. [Google Scholar]
- Garg, A.; Agrawal, A.; Negi, A. A Review on Natural Phenomenon of Fractal Geometry. Int. J. Comput. Appl. 2014, 86, 1–7. [Google Scholar]
- Pál, G.; Domokos, G.; Kun, F. Curvature flows, scaling laws and the geometry of attrition under impacts. Sci. Rep. 2021, 11, 20661. [Google Scholar] [CrossRef]
- Morris, I.D. Fast approximation of the affinity dimension for dominated affine iterated function systems. Ann. Fenn. Math. 2022, 47, 645–694. [Google Scholar] [CrossRef]
- Hochman, M.; Rapaport, A. Hausdorff dimension of planar self-affine sets and measures with overlaps. J. Eur. Math. Soc. 2021, 24, 2361–2441. [Google Scholar] [CrossRef]
- Edgar, G. (Ed.) Measure, Topology, and Fractal Geometry; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Gdawiec, K. Fractal patterns from the dynamics of combined polynomial root finding methods. Nonlinear Dyn. 2017, 90, 2457–2479. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Liu, C. Fractal Control and Its Applications; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Soltanifar, M. A Generalization of the Hausdorff Dimension Theorem for Deterministic Fractals. Mathematics 2021, 9, 1546. [Google Scholar] [CrossRef]
- Hossain, A.; Akter, R.; Ahmed, P. Fractals Generating Techniques. Sonargaon Univ. J. 2016, 1, 43–54. [Google Scholar]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. On the robust Newton’s method with the Mann iteration and the artistic patterns from its dynamics. Nonlinear Dyn. 2021, 104, 297–331. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W. Polynomiography for the polynomial infinity norm via Kalantari’s formula and nonstandard iterations. Appl. Math. Comput. 2017, 307, 17–30. [Google Scholar] [CrossRef]
- Maksymenko-Sheyko, K.V.; Sheyko, T.I. Mathematical modeling of geometric fractals using R-functions. Cybern. Syst. Anal. 2012, 48, 614–620. [Google Scholar] [CrossRef]
- Anarova, S.A.; Ibrohimova, Z.E. Methods of Constructing Equations for Objects of Fractal Geometry and R-Function Method. In International Conference on Intelligent Human Computer Interaction; Springer: Cham, Switzerland, 2022; pp. 425–436. [Google Scholar] [CrossRef]
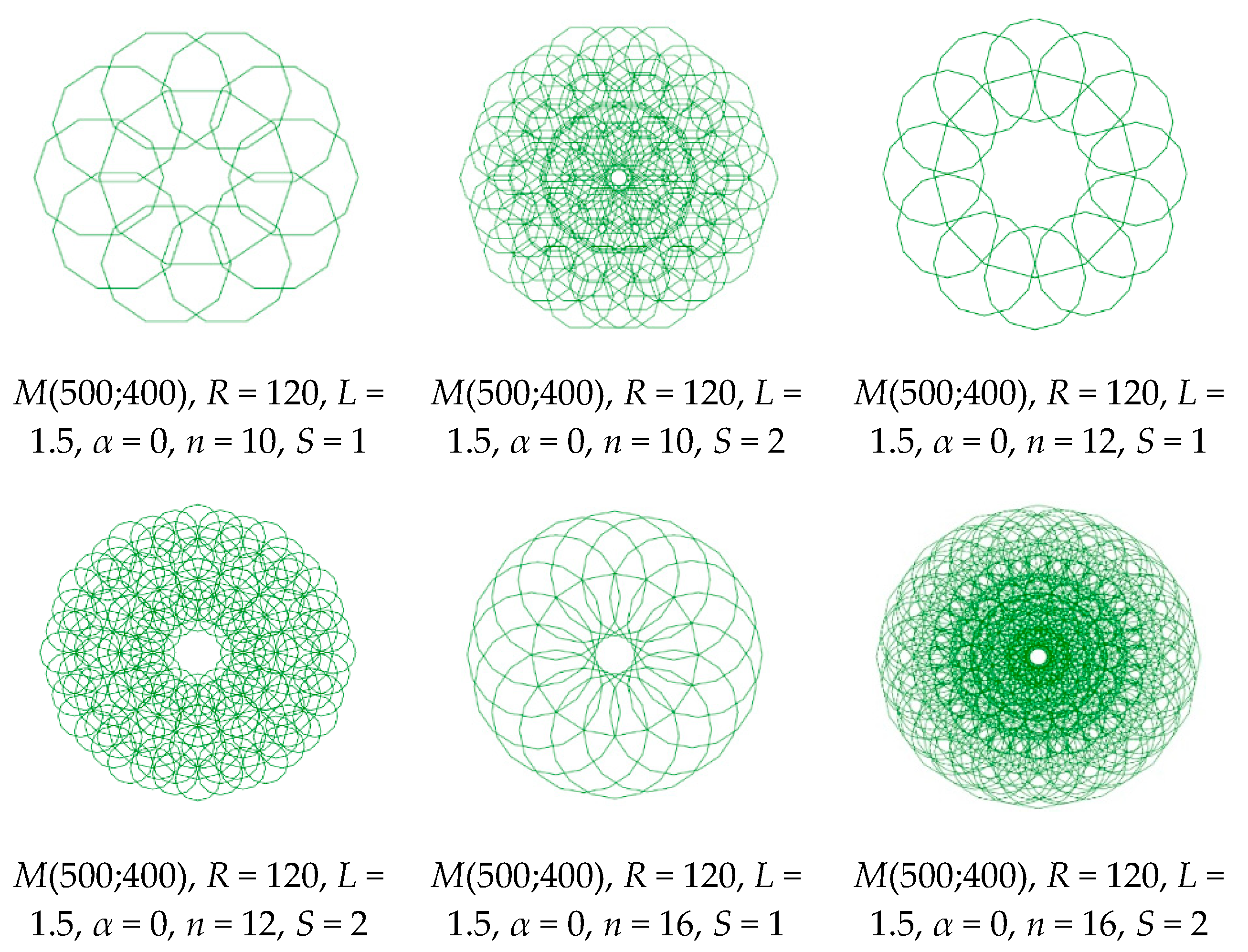






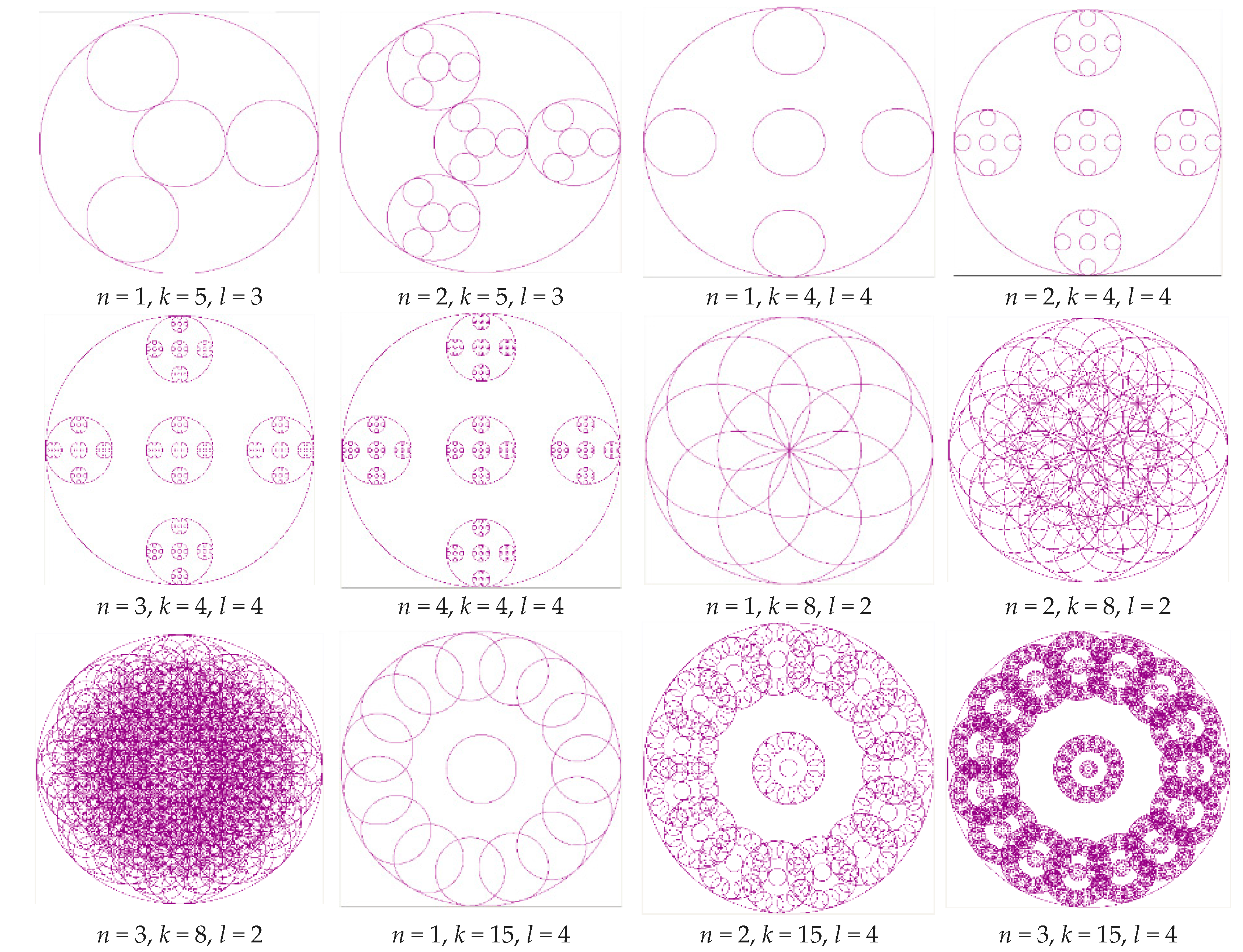








| Polygon |  |  |  |
| M(500;400), R = 120, L = 1.5, α = 0, n = 10, S = 1 | M(500;400), R = 120, L = 1.5, α = 0, n = 10, S = 2 | M(500;400), R = 120, L = 1.5, α = 0, n = 16, S = 2 | |
 D1 = 1.11 |  D2 = 1.59 | 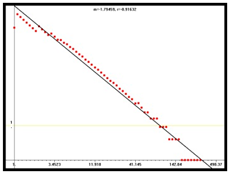 D3 = 1.79 | |
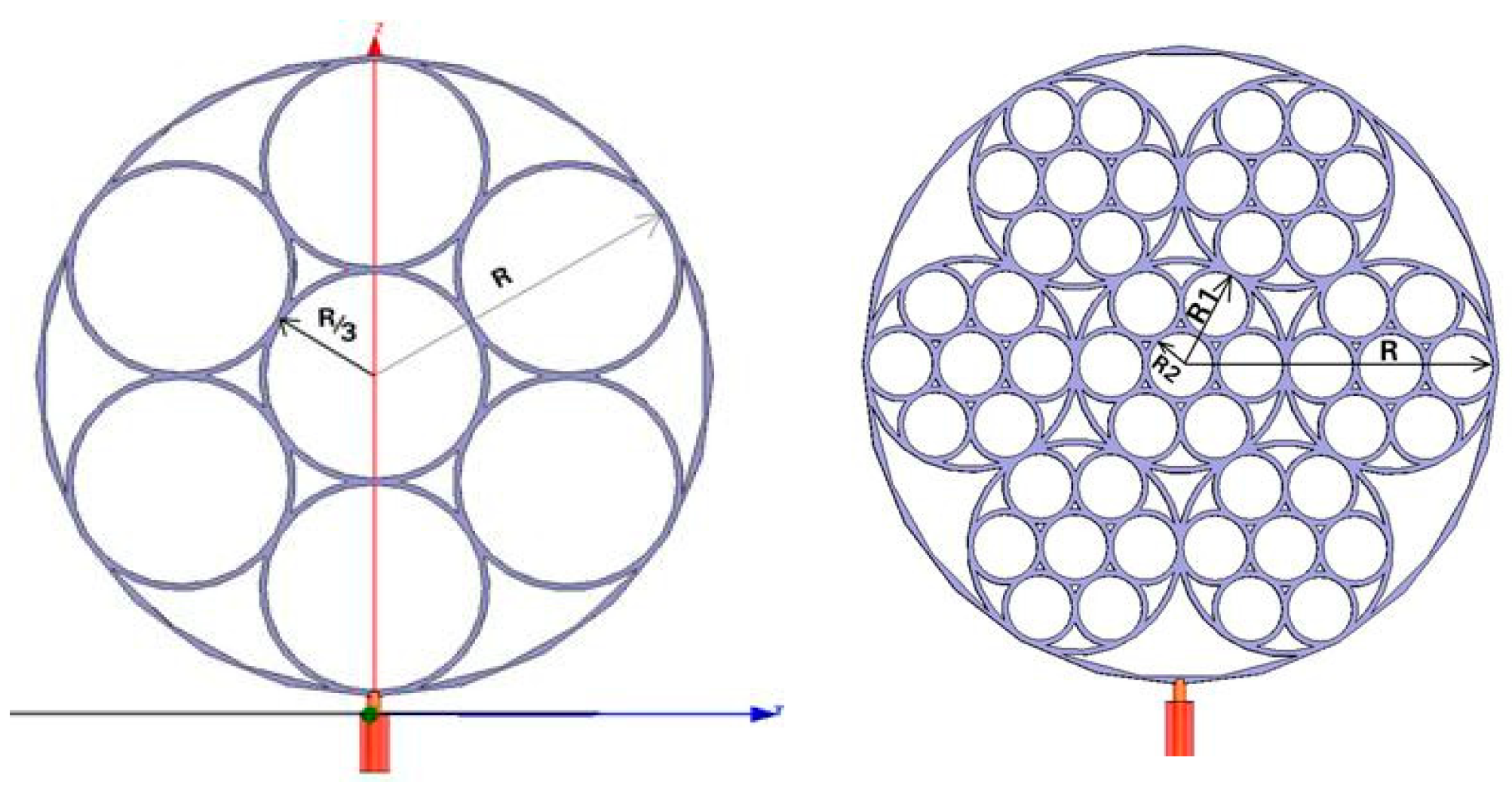
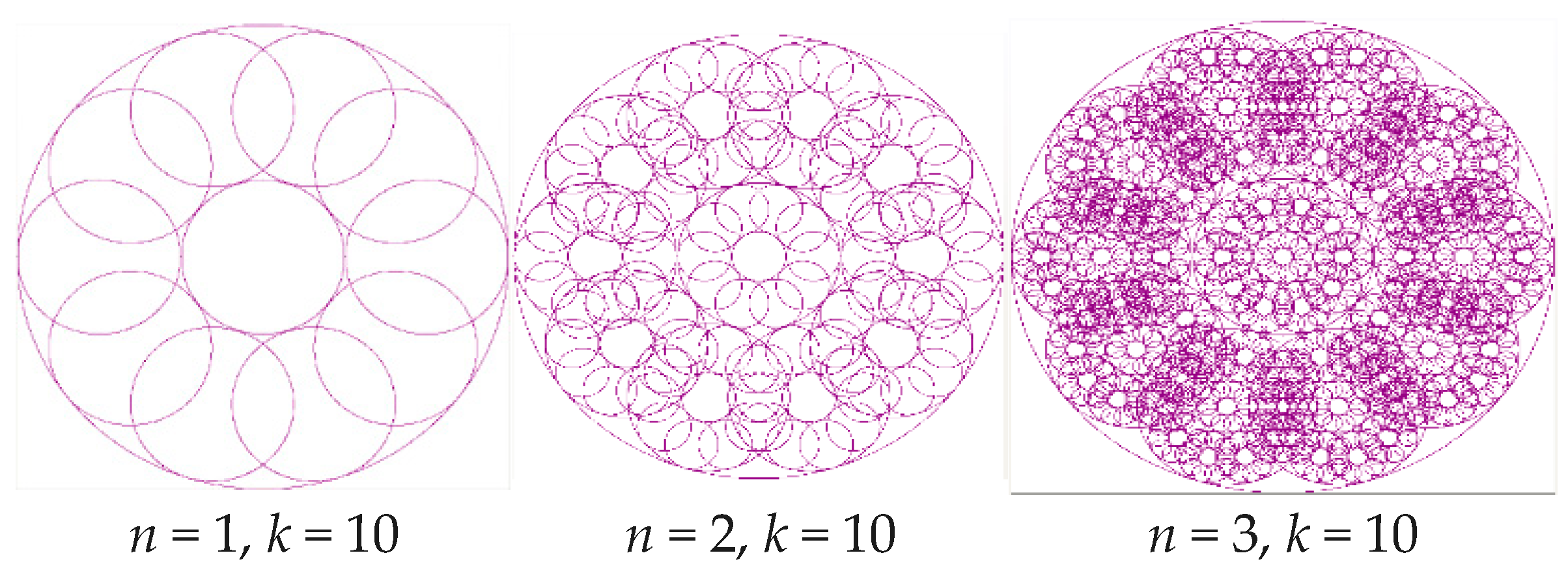
| Circular |  | 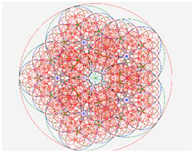 |  |
| M(500:400), R = 350, α = 45, n = 4, l = 45, k = 2, S = 3 | M(500:400), R = 350, α = 0, n = 4, l = 45, k = 2, S = 5 | M(500:400), R = 350, α = 15, n = 4, l = 0, k = 2.7, S = 9 | |
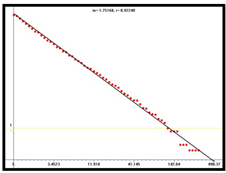 D1 = 1.75 | 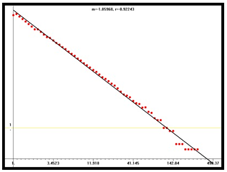 D2 = 1.86 | 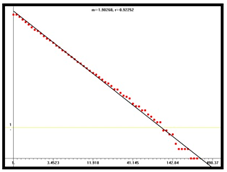 D3 = 1.90 | |
| Koch | 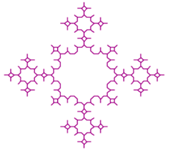 |  |  |
| Axiom: General rule: Number of iterations: 4, Scale: 9, Turning angle: 45° Color: purple | Axiom: General rule: Number of iterations: 4, Scale: 6, Turning angle: 72° Color: red | Axiom: General rule: Number of iterations: 6, Scale: 3, Turning angle: 36° Color: #1c0397 | |
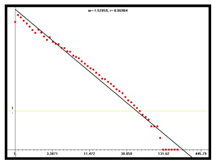 D = 1.53 | 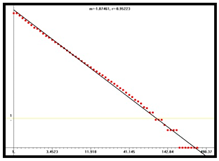 D = 1.87 | 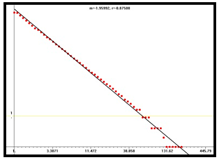 D = 1.96 | |
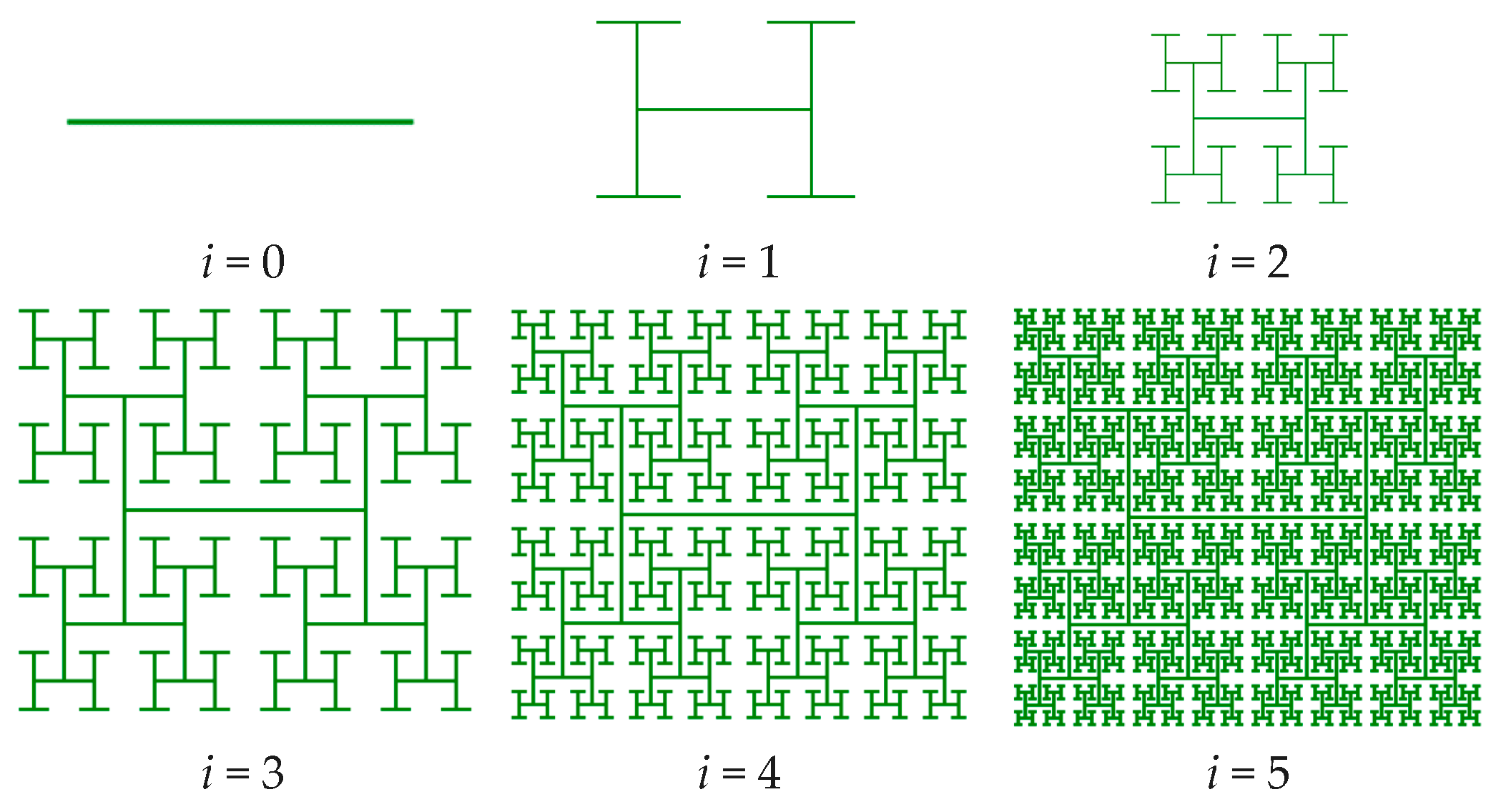
| Cayley tree | 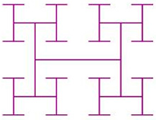 |  |  |
| n = 2 | n = 4 | n = 5 | |
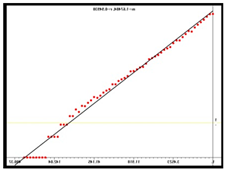 D = 1.67 | 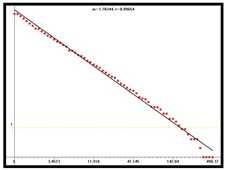 D = 1.78 | 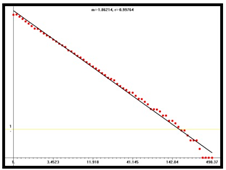 D = 1.86 | |
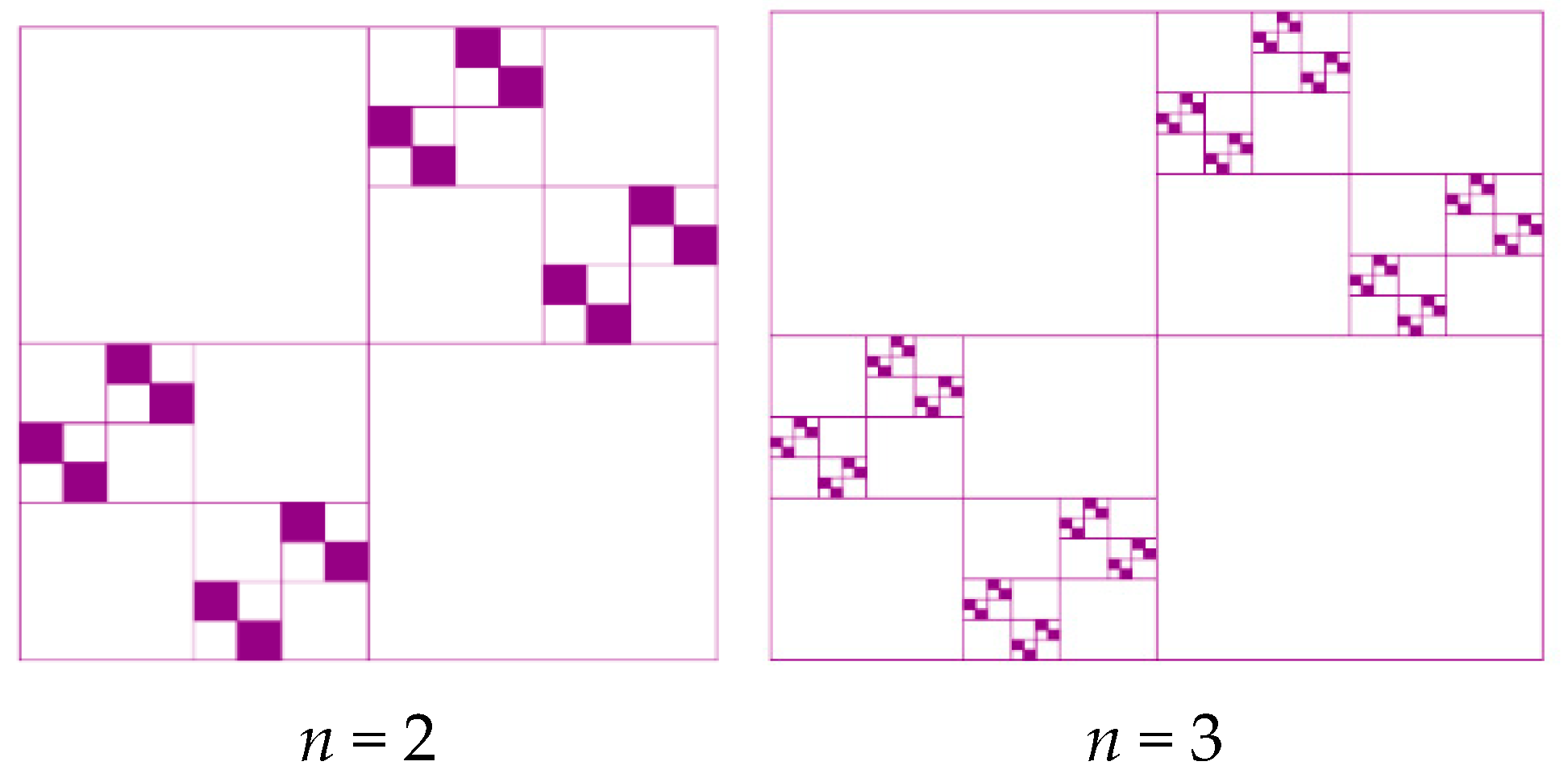
| Serpin |  |  |  |
| n = 2 (α1 = 0, α2 = π/4) | n = 3 (α1 = 0, α2 = π/4) | n = 4 (α1 = π/4, α2 = π/4) | |
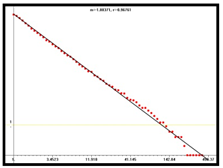 D = 1.80 | 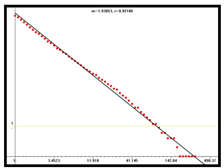 D = 1.94 |  D = 1.91 | |
| Tree-shaped |  |  |  |
| Reflection = 1, Reflection of element = 11, Movement = 50, Scale = 6 | Reflection = 5, Reflection of element = 6, Movement = 71, Scale = 6 | Reflection = 7, Reflection of element = 7, Movement = 70, Scale = 14 | |
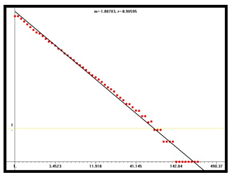 D = 1.89 |  D = 1.92 |  D = 1.86 |
| Metric | Our Tool | Fractint | Improvement |
|---|---|---|---|
| Execution Time (Depth 10) | 2.7 s | 4.0 s | 33% faster |
| Memory Usage (4000 × 4000 px) | 150 MB | 250 MB | 40% reduction |
| User Interface | Graphical, intuitive | Command-line, complex | Improved usability |
| Task Completion Time | 15 s | 22 s | 30% faster |
| Error Rate | 40% lower | Higher | More accuracy |
| Hardware Requirement | Standard PC | High-performance VGA | Greater accessibility |
| Metric | Our Method | Barnsley’s IFS | Jacquin’s Method |
|---|---|---|---|
| Compression Ratio | Adjustable, high | High | High |
| Encoding Time (seconds) | 12.5 | 15.8 | 18.3 |
| Decoding Time (seconds) | 10.2 | 12.5 | 14.7 |
| PSNR (dB) | 35.2 | 33.7 | 34.1 |
| SSIM | 0.92 | 0.88 | 0.90 |
| Metric | Comparison | p-Value | Significance |
|---|---|---|---|
| Encoding Time | Our Method vs. Barnsley’s IFS | p < 0.01 | Significant |
| Our Method vs. Jacquin’s | p < 0.01 | Significant | |
| Decoding Time | Our Method vs. Barnsley’s IFS | p < 0.01 | Significant |
| Our Method vs. Jacquin’s | p < 0.01 | Significant | |
| PSNR | Our Method vs. Barnsley’s IFS | p < 0.01 | Significant |
| SSIM | Our Method vs. Barnsley’s IFS | p < 0.01 | Significant |
| Compression Ratio | Our Method vs. Jacquin’s | p = 0.12 | Not Significant |
| Fractal Pattern | Our Pattern Dimension | Traditional Dimension (Hausdorff/Box-Counting) | Comparison |
|---|---|---|---|
| Tree-shaped Fractal | 1.86 (Hausdorff) | Sierpinski Triangle: 1.58 | Higher Complexity |
| Circular Fractal | 1.92 (Box-counting) | Koch Snowflake: 1.26 | Higher Detail |
| Star-shaped Fractal | 1.67 (Hausdorff) | Cantor Set: 0.63 | Greater Density |
| Domain | Application | Performance Metrics | Results |
|---|---|---|---|
| Textile Design | Fabric Pattern Creation | Aesthetic quality, scalability, production feasibility | Higher aesthetic score (4.7/5), seamless scalability |
| Digital Art and Architecture | Tile and Facade Design | Visual appeal, customization, structural integrity | Increased visual appeal (5/5), adaptable across scales |
| Property | Our Recursive Algorithm | Conventional Algorithms | Improvement |
|---|---|---|---|
| Convergence Complexity | O(n) | O(n2) | 30% faster convergence |
| Symmetry Deviation | 2% | 5% | Improved structural balance |
| Precision (Dimensional Deviation) | <1% | ~3% | Higher precision in structural detail |
| Iteration Complexity | O(nlogn) | O(n2) | Reduced iteration count |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buriboev, A.S.; Sultanov, D.; Ibrohimova, Z.; Jeon, H.S. Mathematical Modeling and Recursive Algorithms for Constructing Complex Fractal Patterns. Mathematics 2025, 13, 646. https://doi.org/10.3390/math13040646
Buriboev AS, Sultanov D, Ibrohimova Z, Jeon HS. Mathematical Modeling and Recursive Algorithms for Constructing Complex Fractal Patterns. Mathematics. 2025; 13(4):646. https://doi.org/10.3390/math13040646
Chicago/Turabian StyleBuriboev, Abror Shavkatovich, Djamshid Sultanov, Zulaykho Ibrohimova, and Heung Seok Jeon. 2025. "Mathematical Modeling and Recursive Algorithms for Constructing Complex Fractal Patterns" Mathematics 13, no. 4: 646. https://doi.org/10.3390/math13040646
APA StyleBuriboev, A. S., Sultanov, D., Ibrohimova, Z., & Jeon, H. S. (2025). Mathematical Modeling and Recursive Algorithms for Constructing Complex Fractal Patterns. Mathematics, 13(4), 646. https://doi.org/10.3390/math13040646






