Novel Approach for Robust Control of Axial Piston Pump
Abstract
1. Introduction
- The general novelty of this paper is that for the first time, a discrete time multivariable robust μ-controller for open-circuit axial piston pumps is designed. Moreover, it is implemented in a conventional digital device. In this way, the traditional hydro-mechanical controller is replaced with an electro-hydraulic proportional valve controlled by an industrial microcontroller.
- The design and implementation of a laboratory test bench enable the real-time control and rapid prototyping of μ-controllers. Moreover, this test bench provides the possibility of investigating relatively easily an axial piston pump control system with all types of digital controllers.
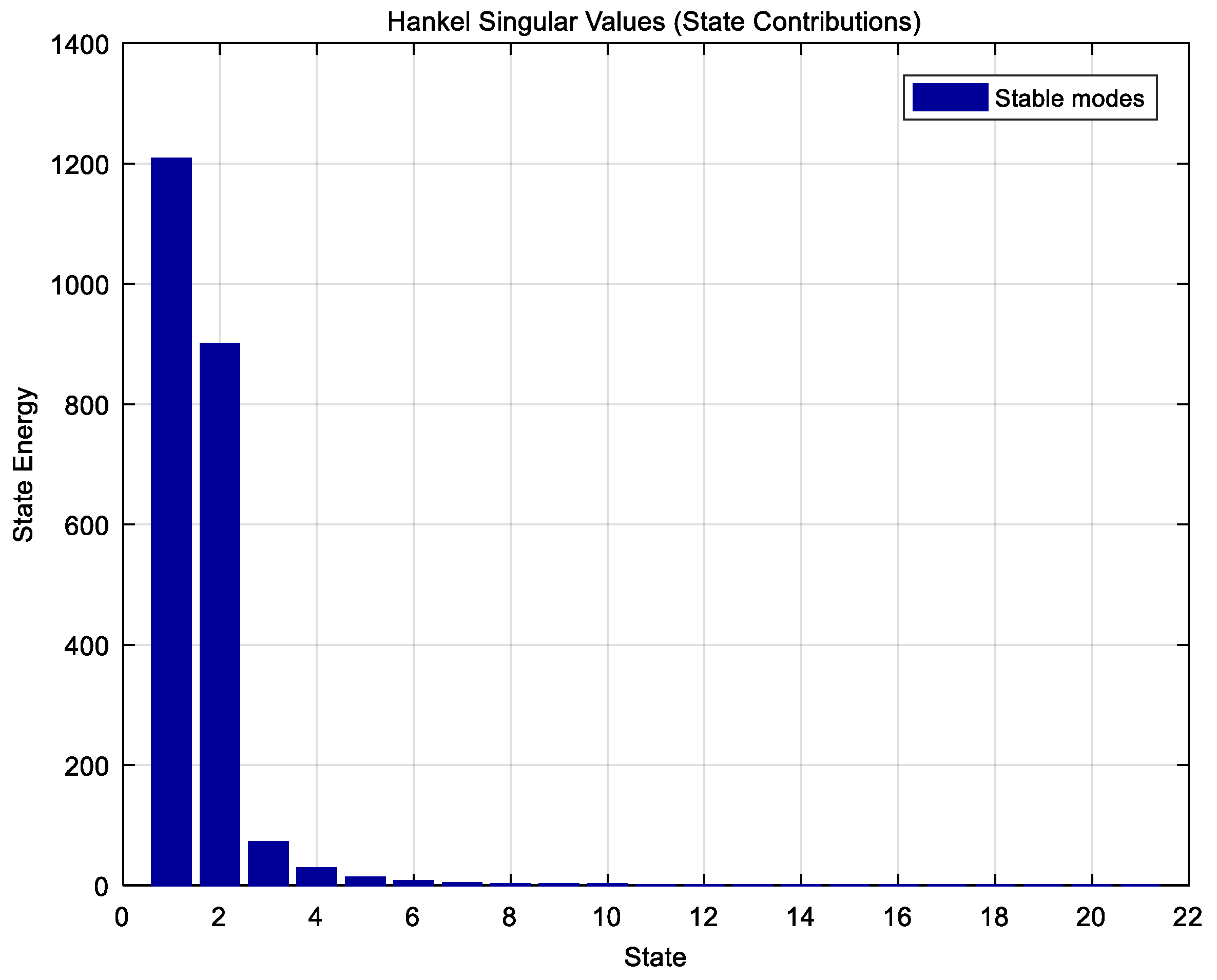
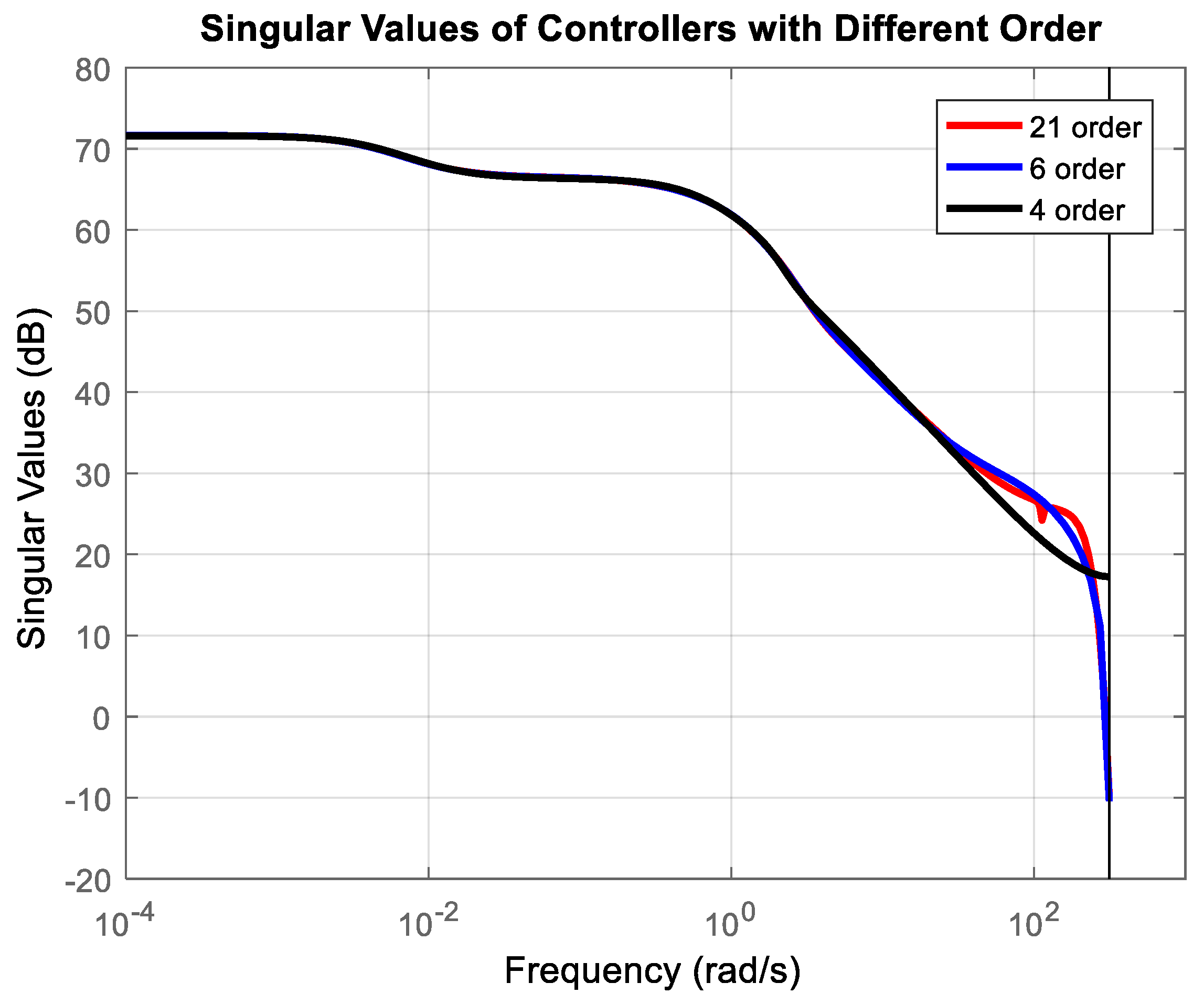
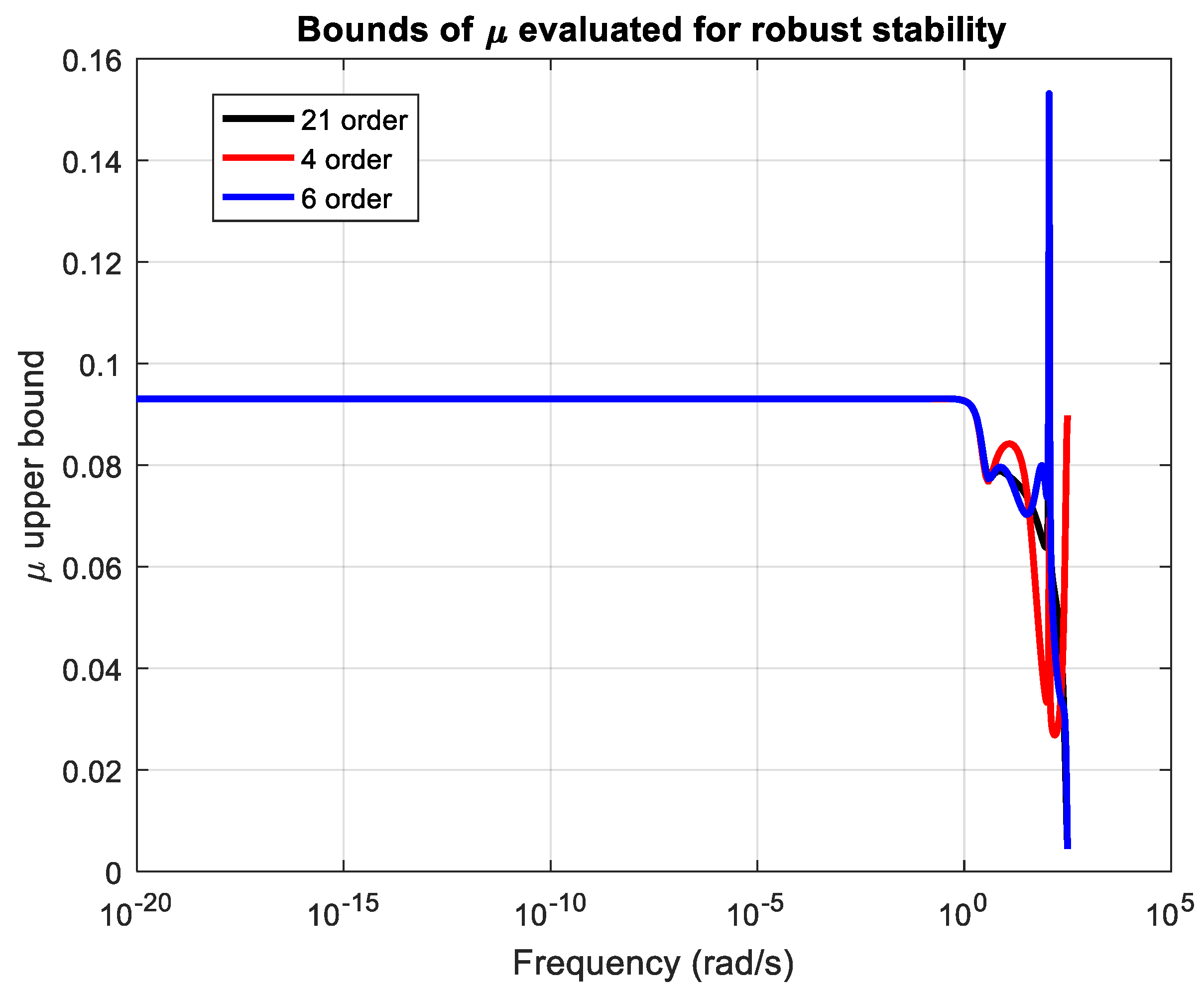
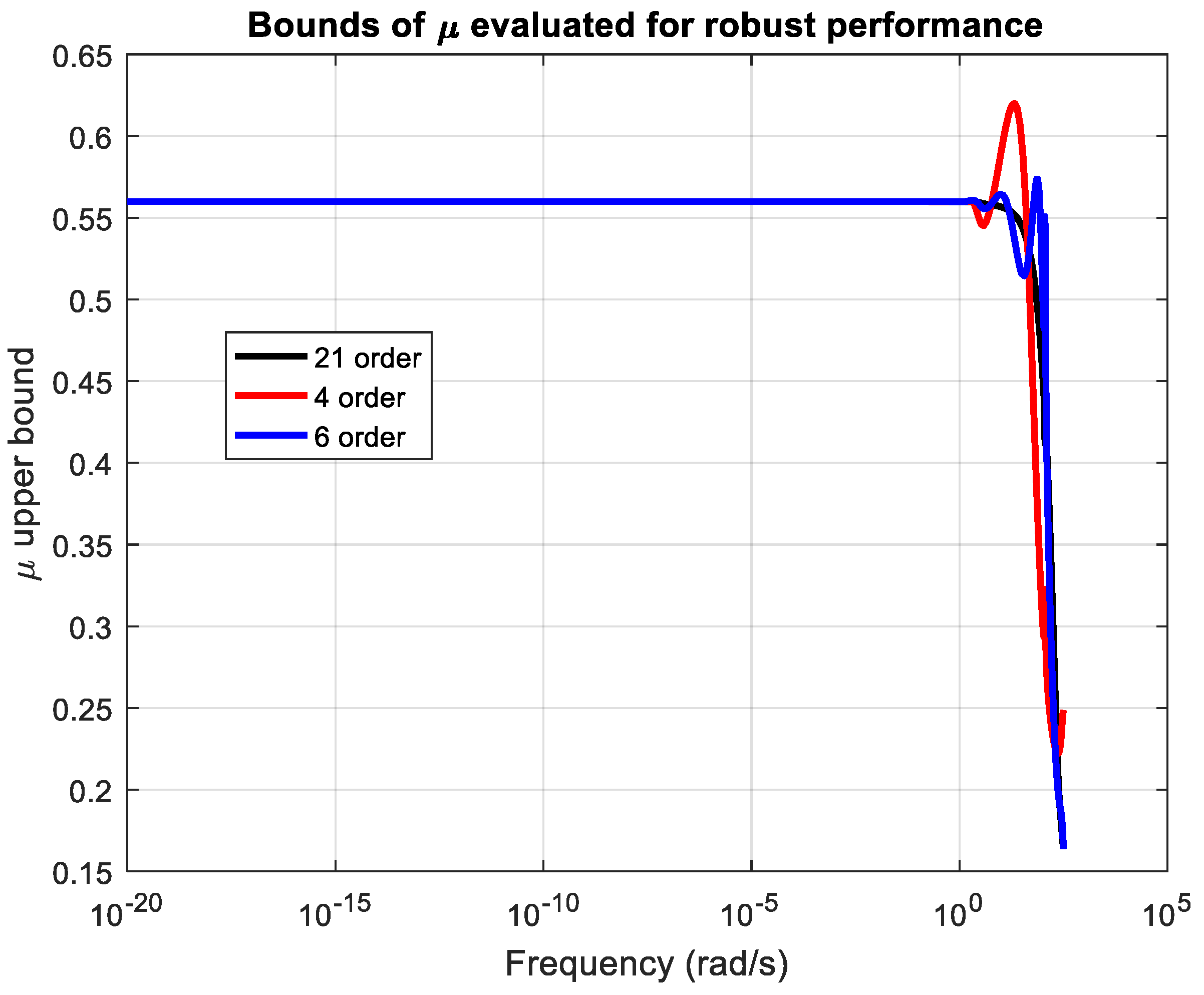
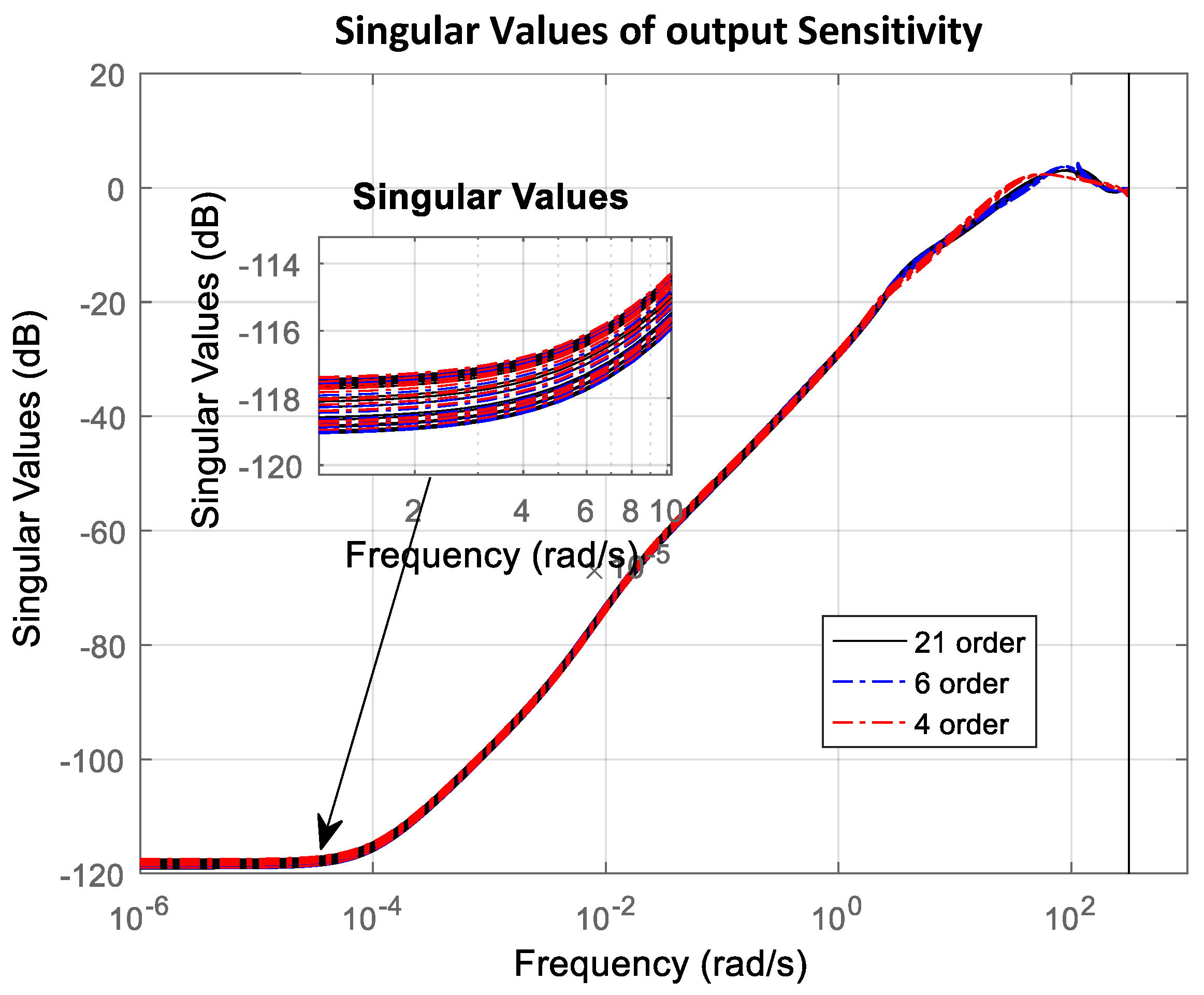
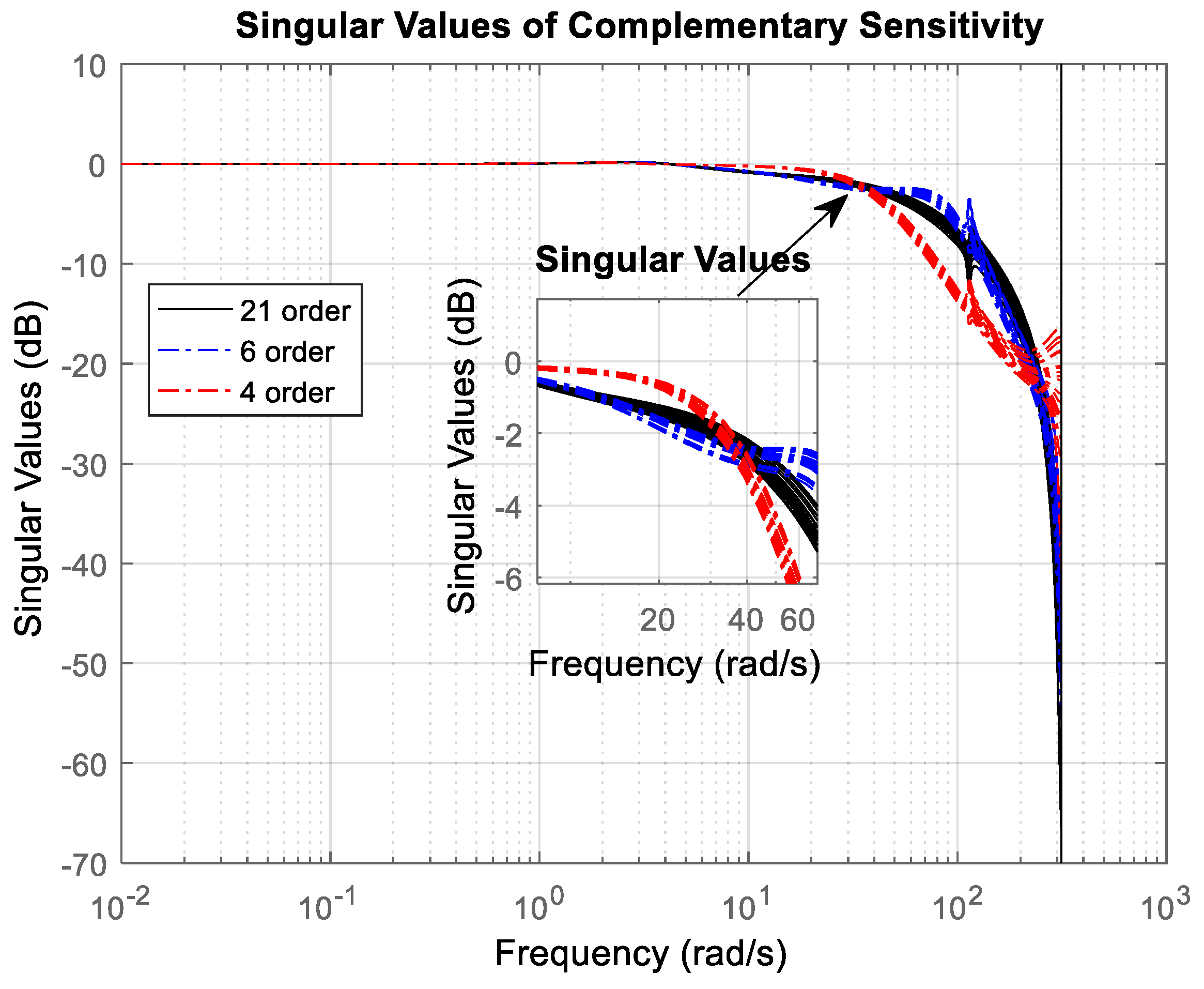
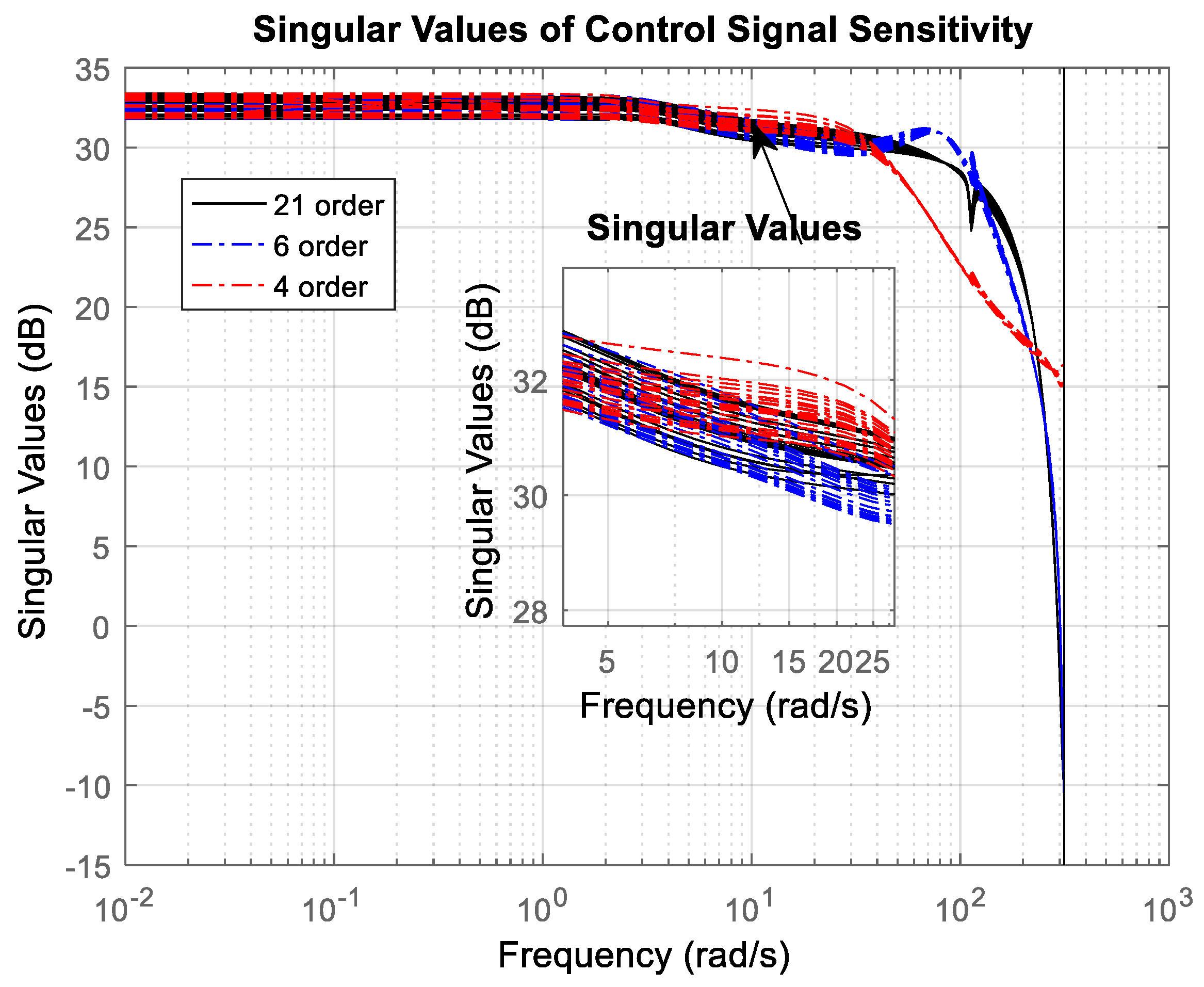
- The performance of robust stability and robust performance analysis of uncertain systems with designed full-order and reduced-order μ-controllers.
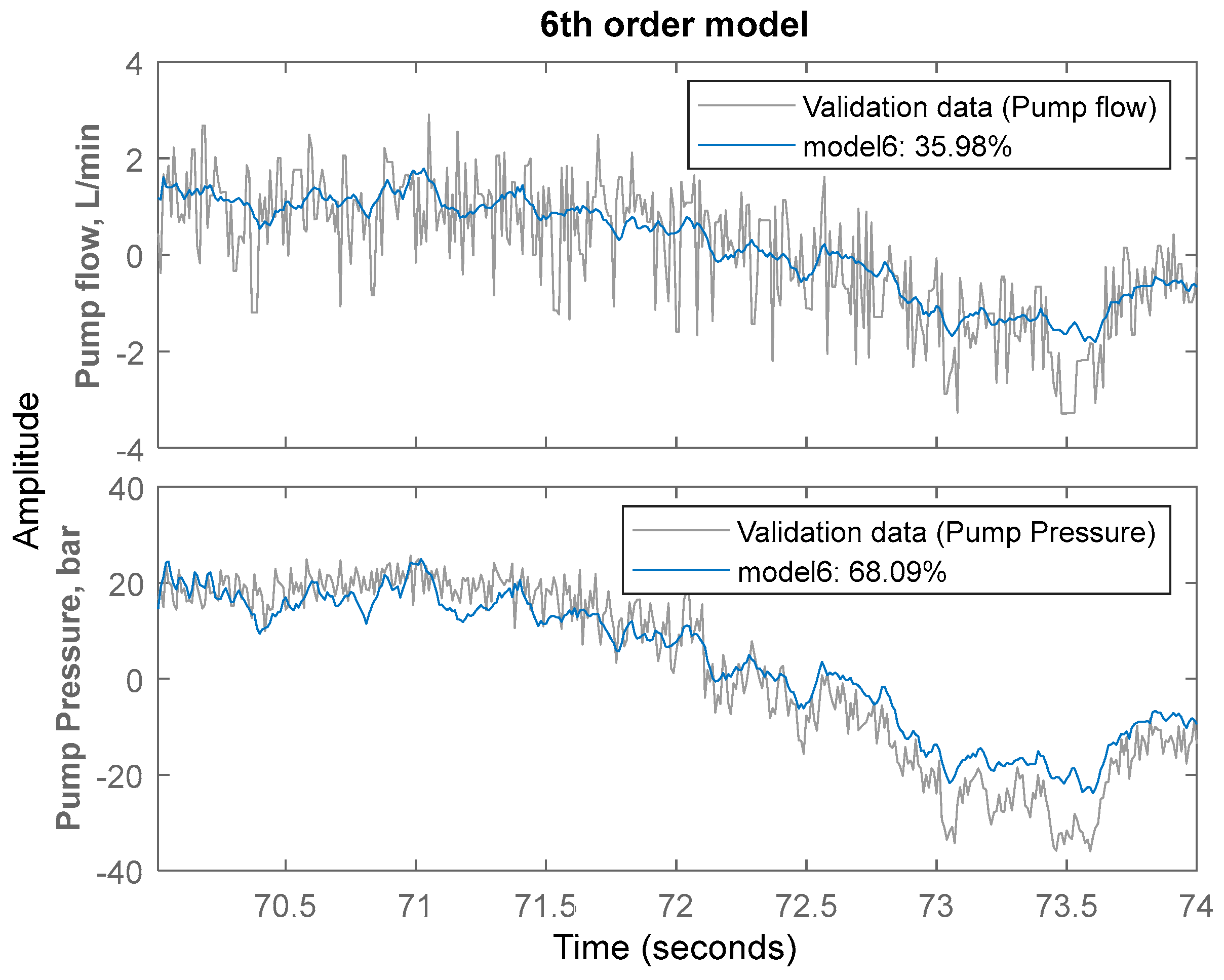
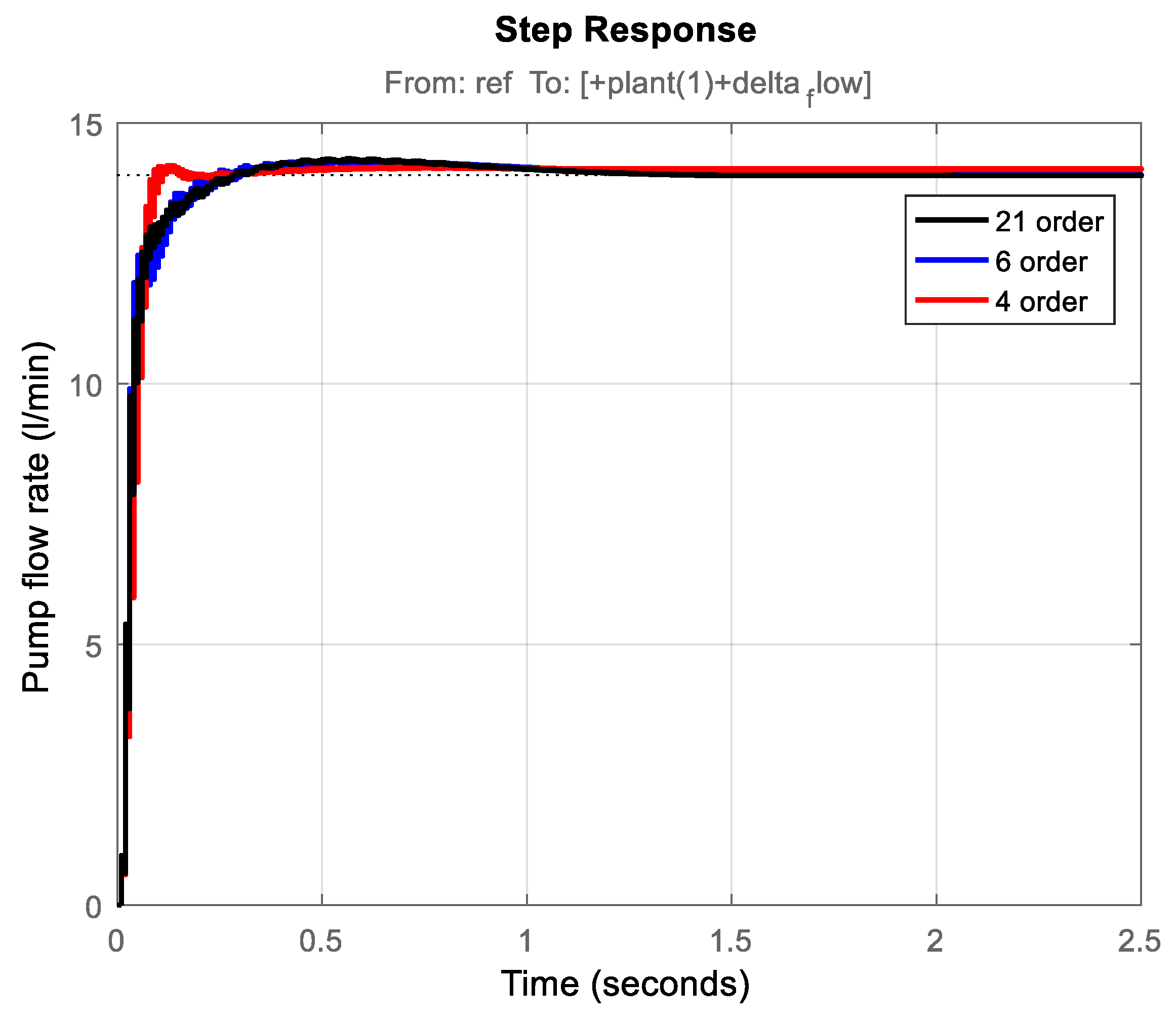
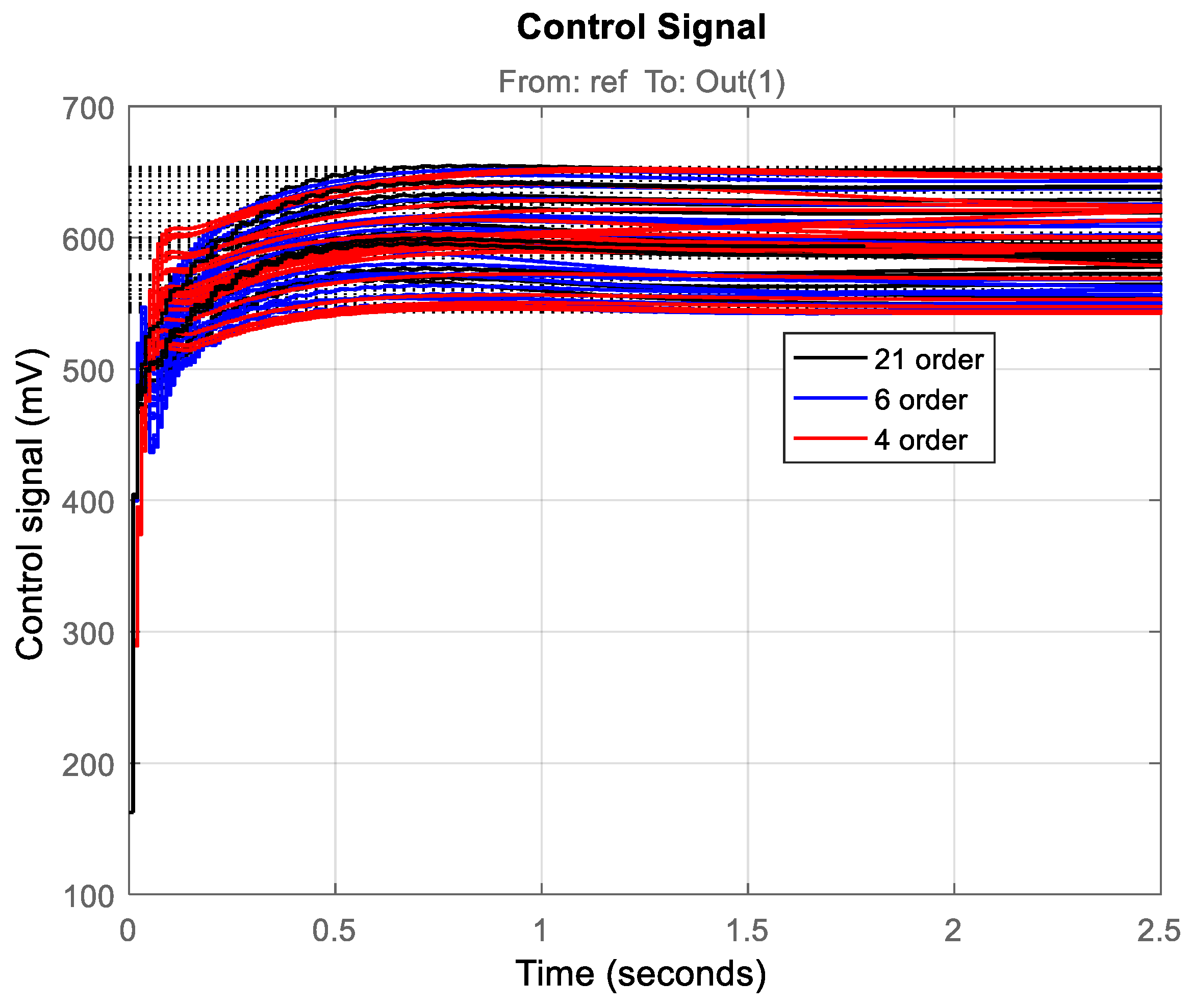
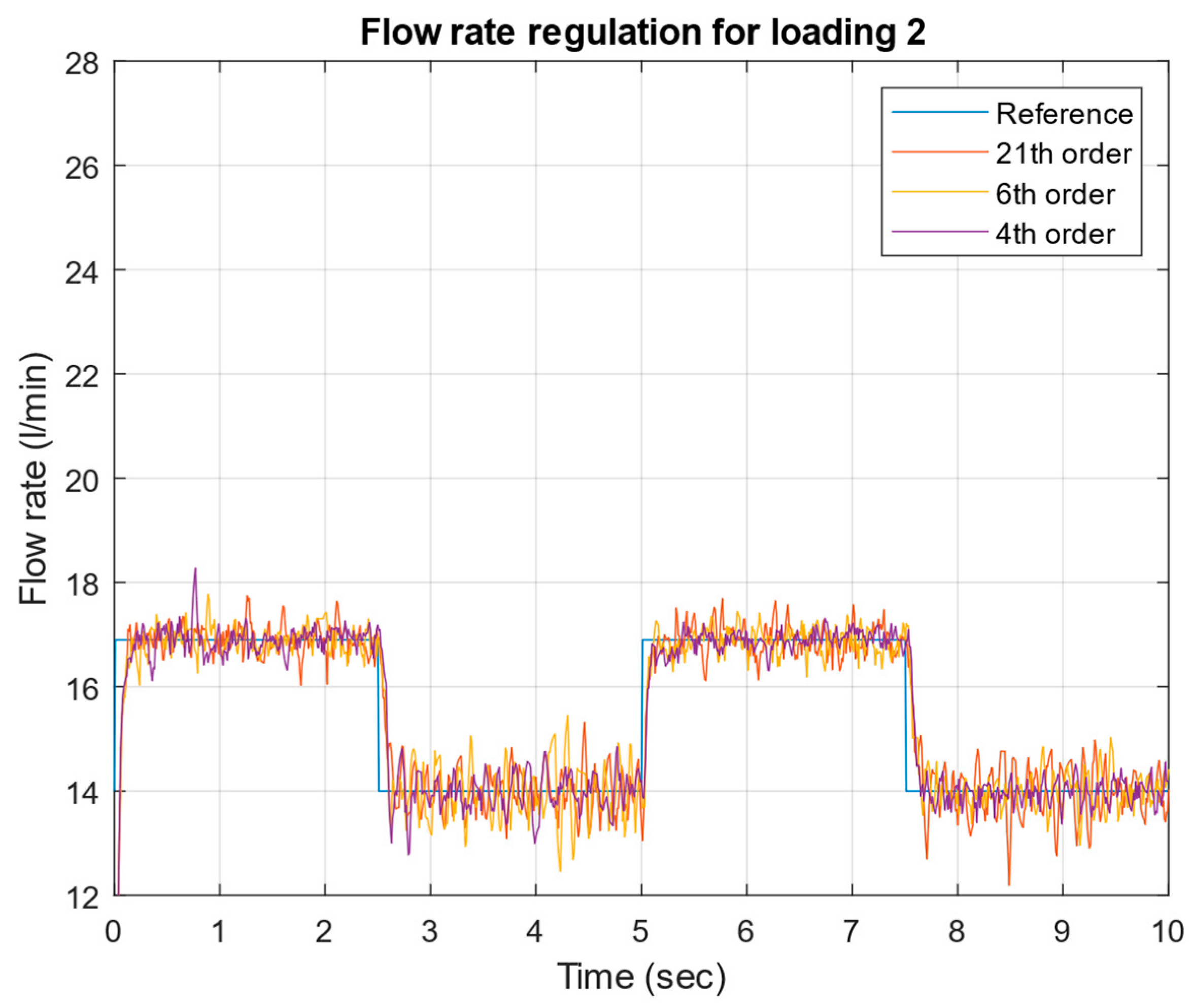
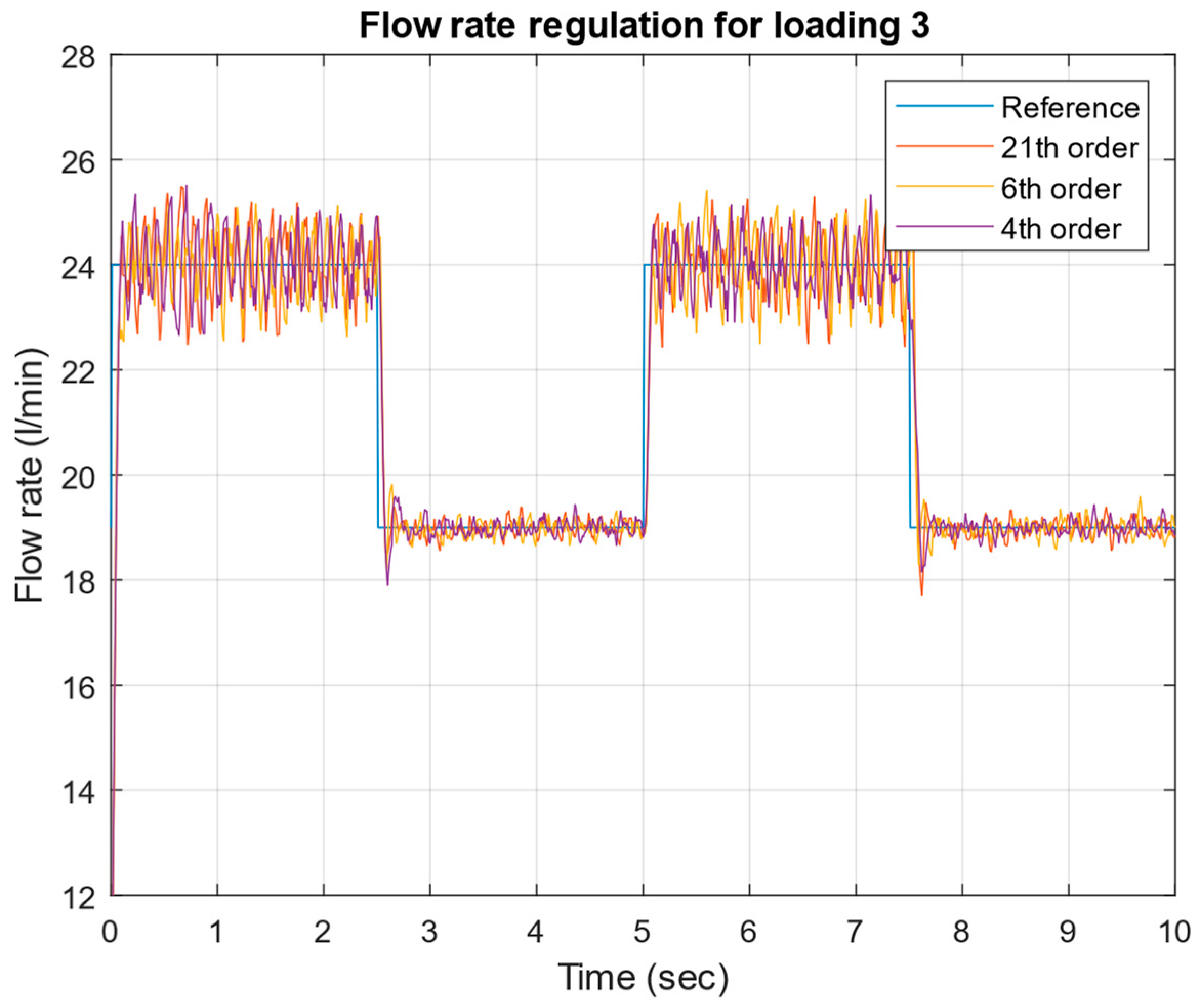
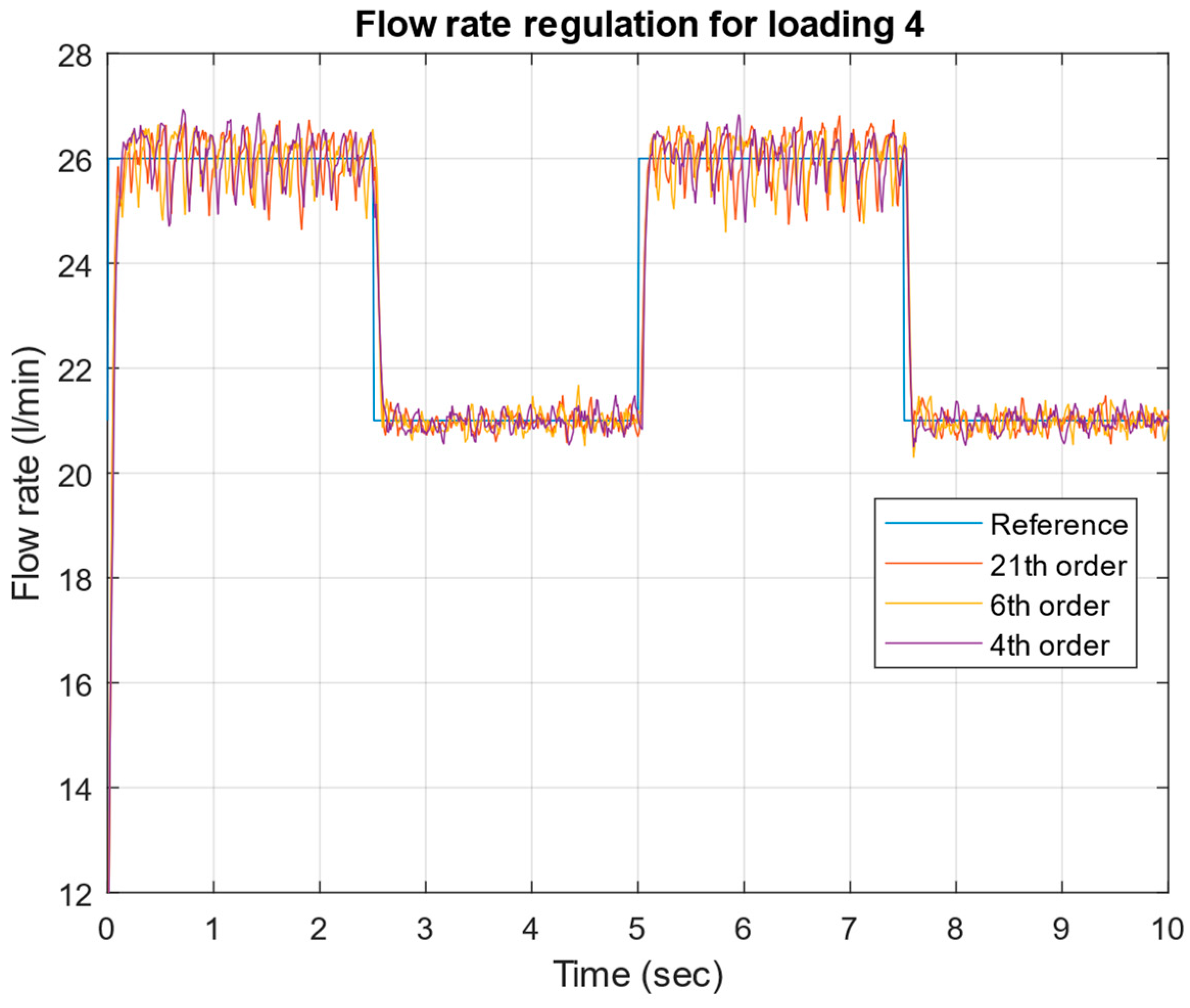
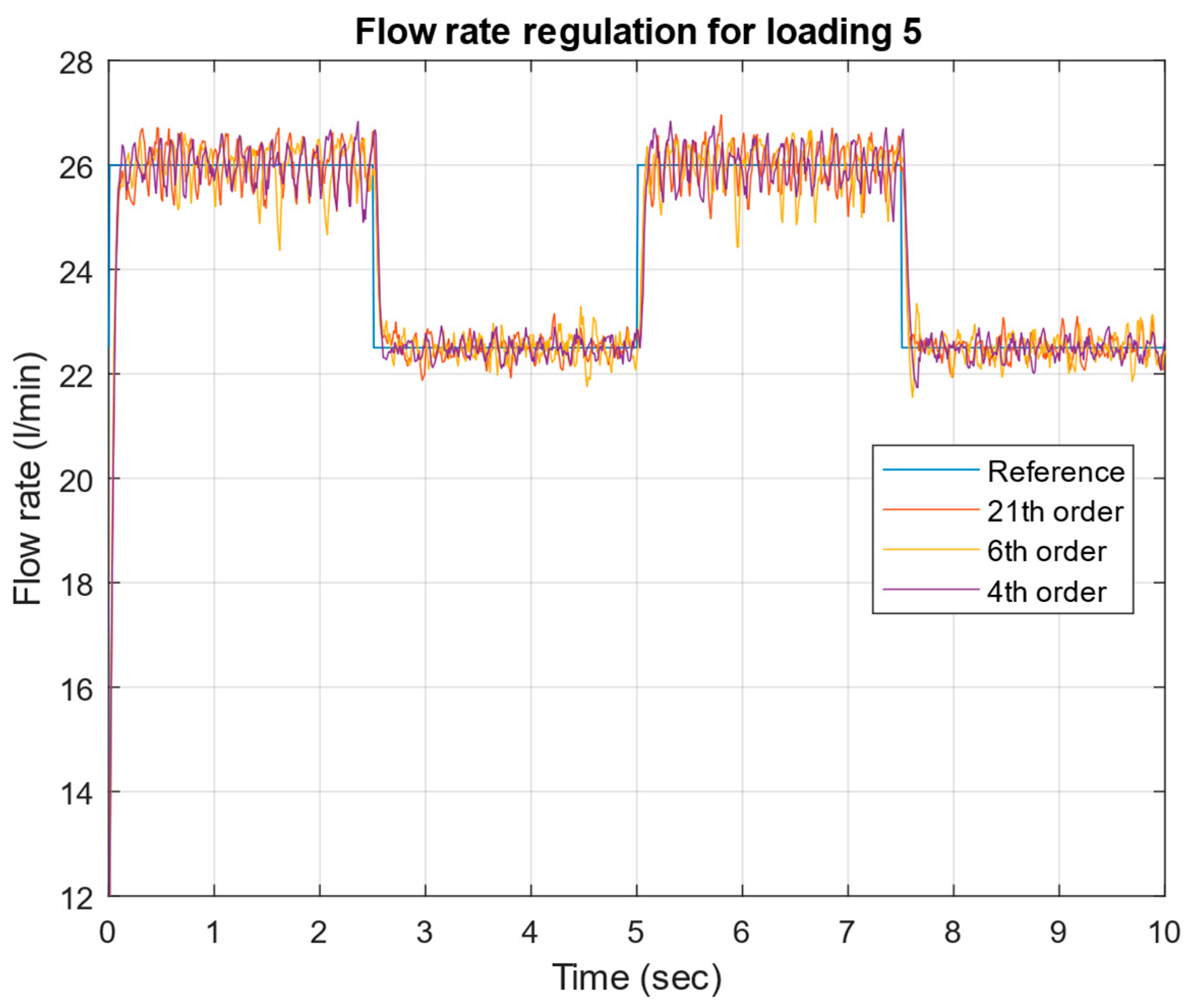
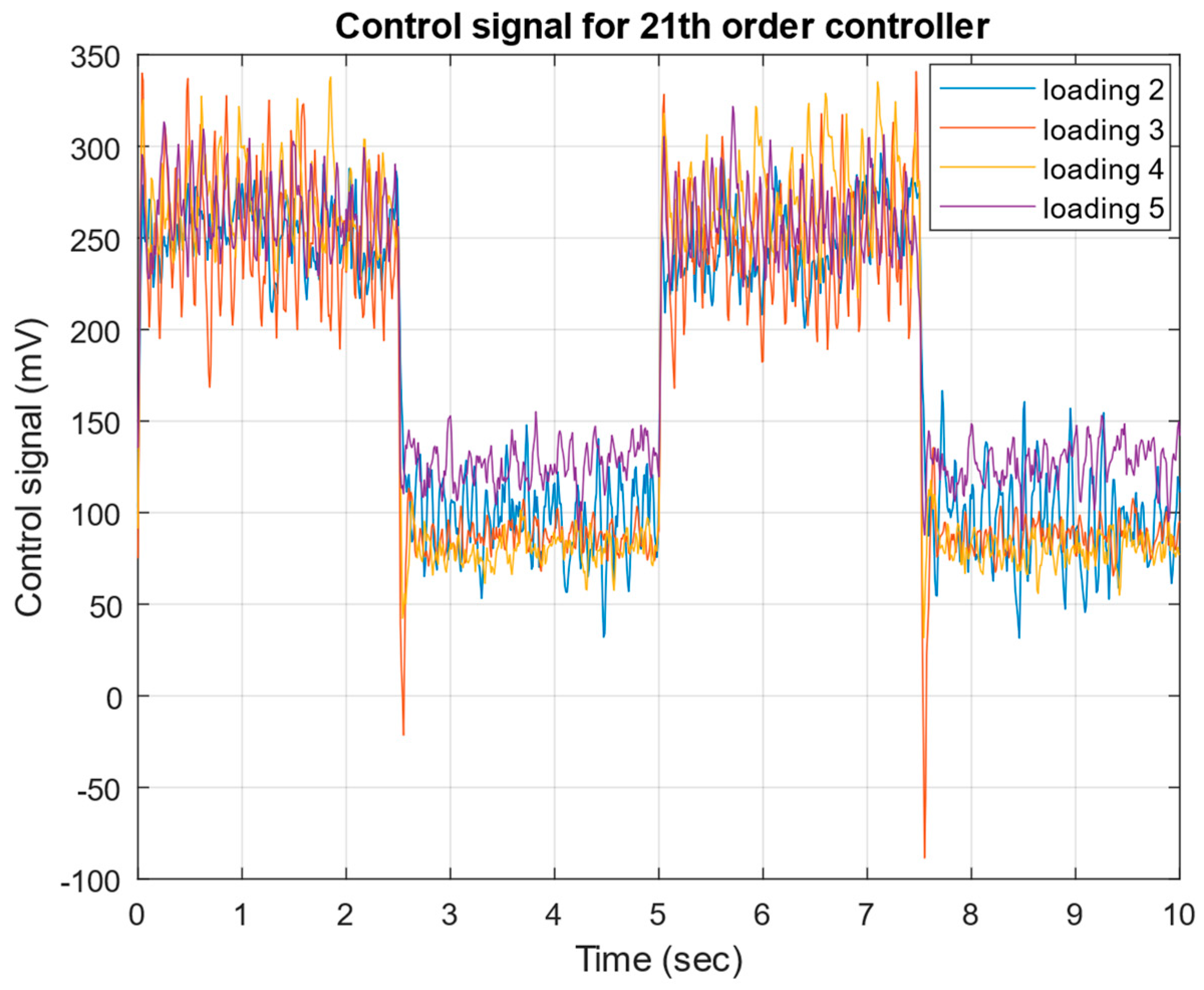
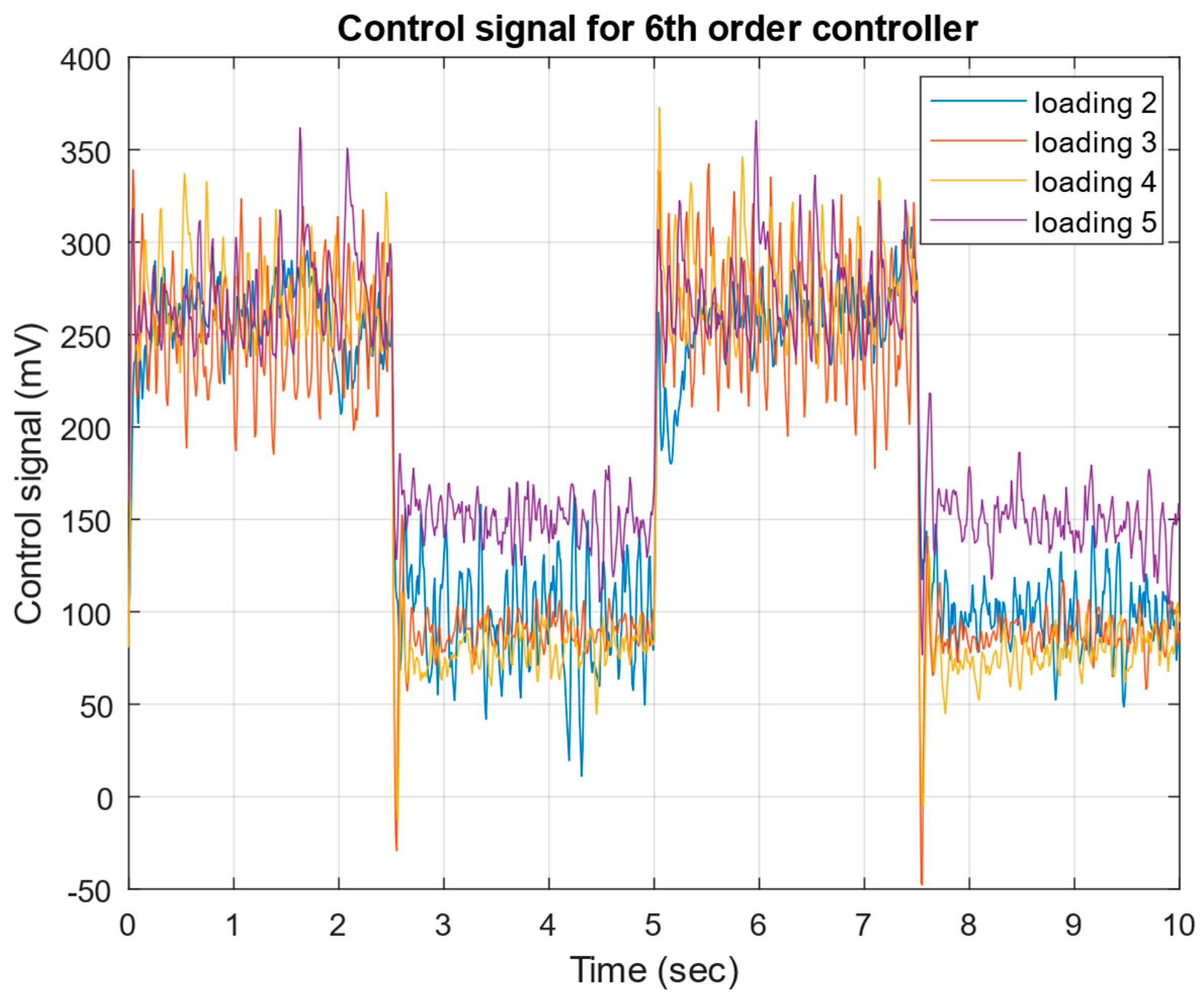
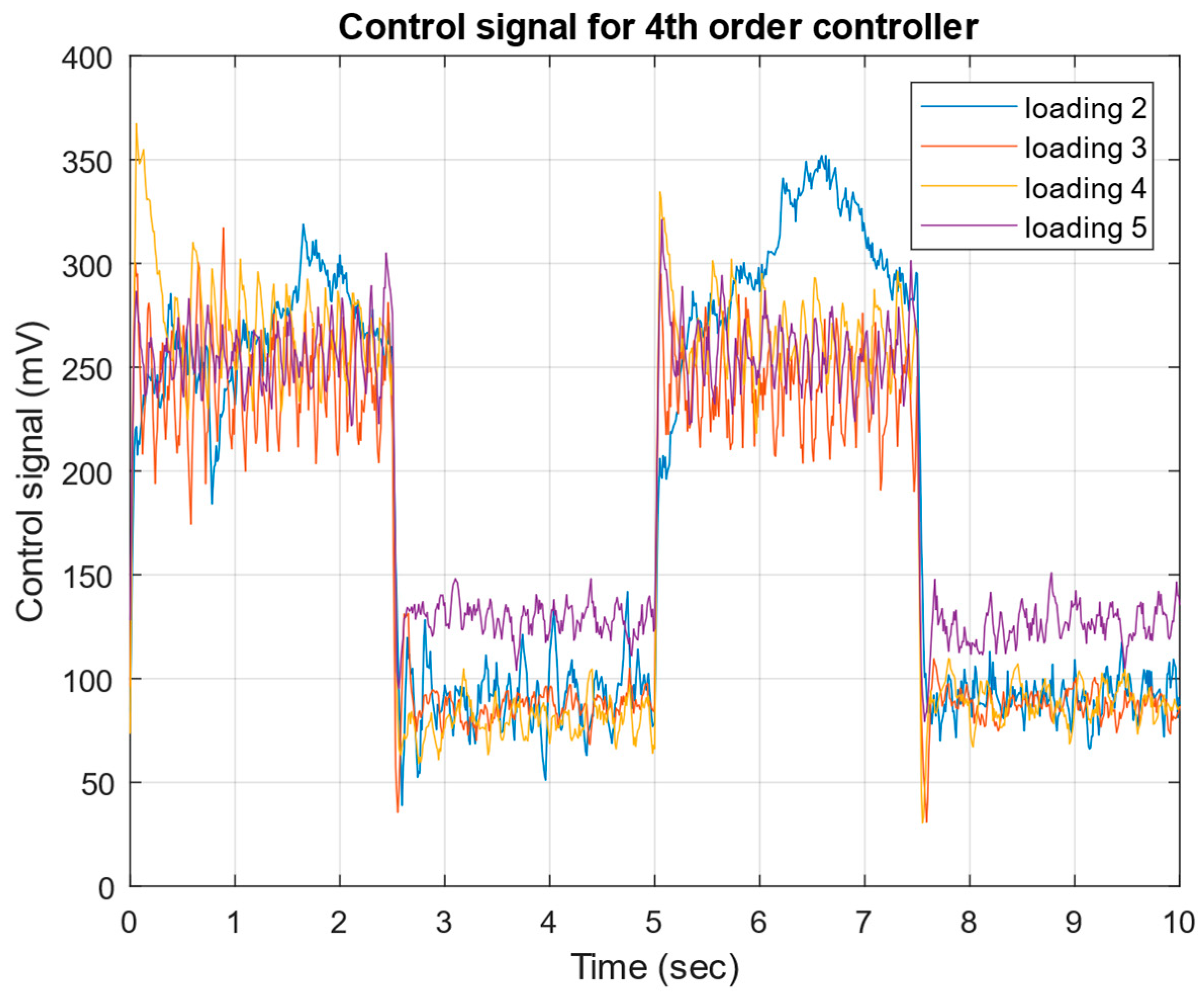
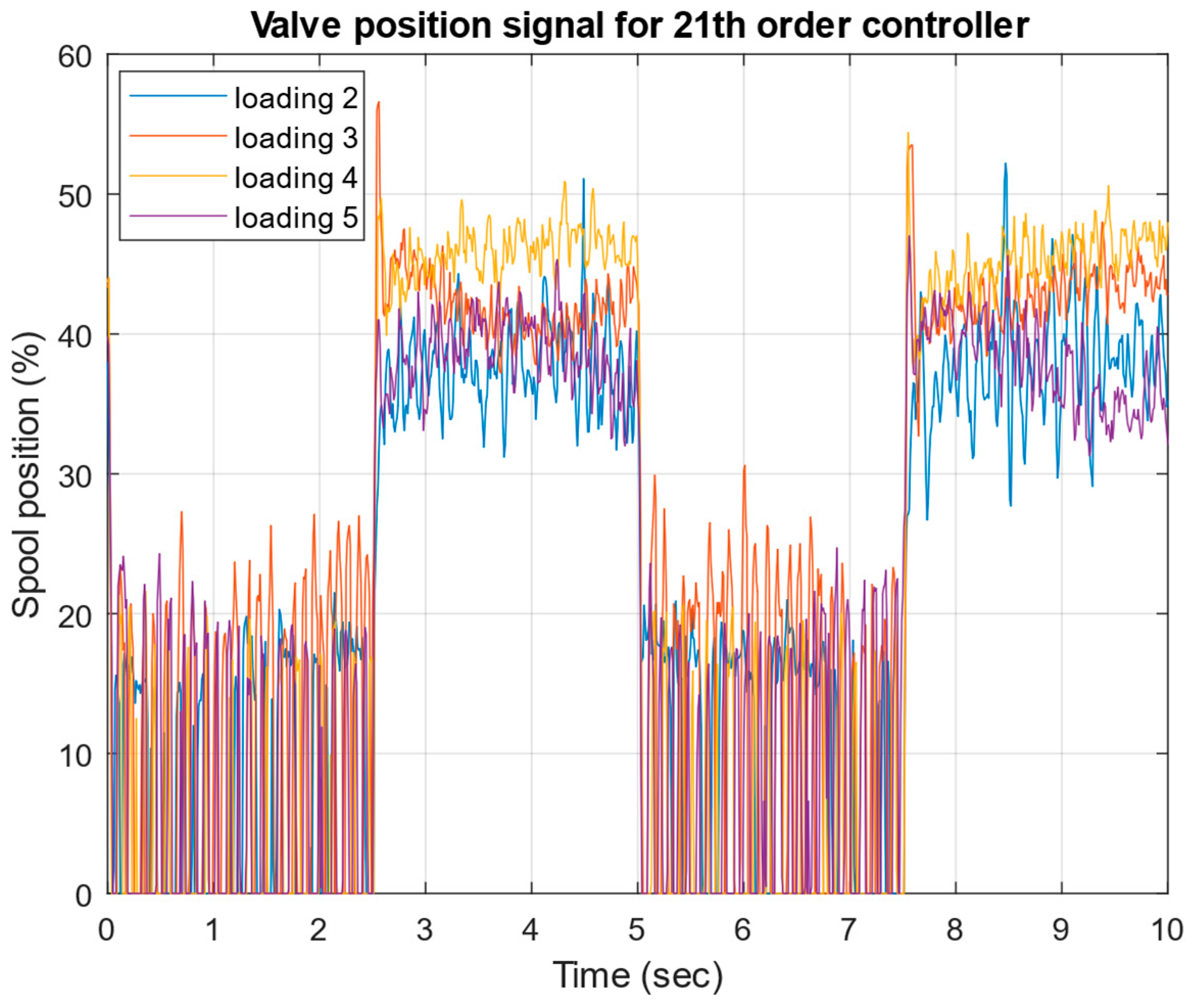
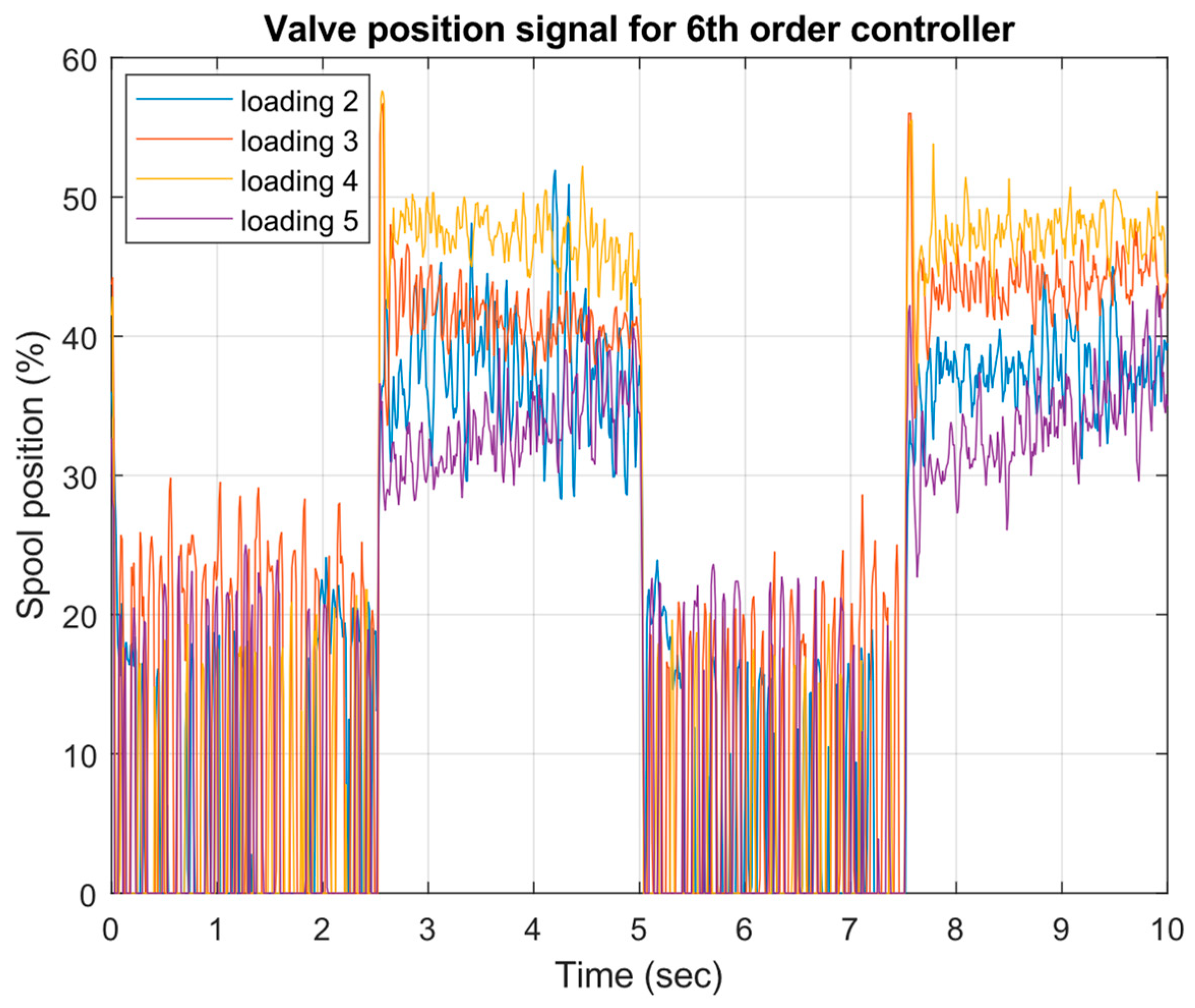
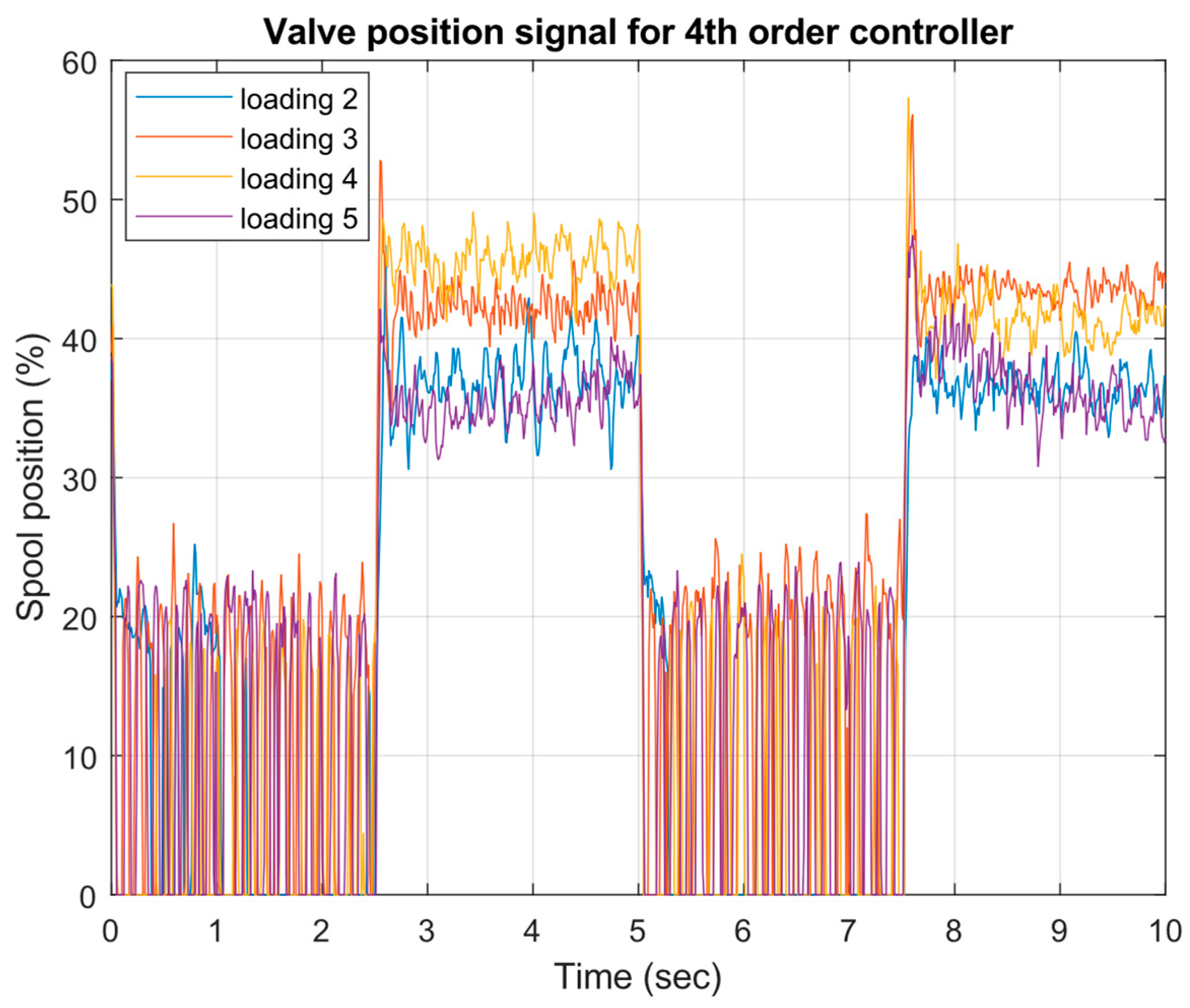
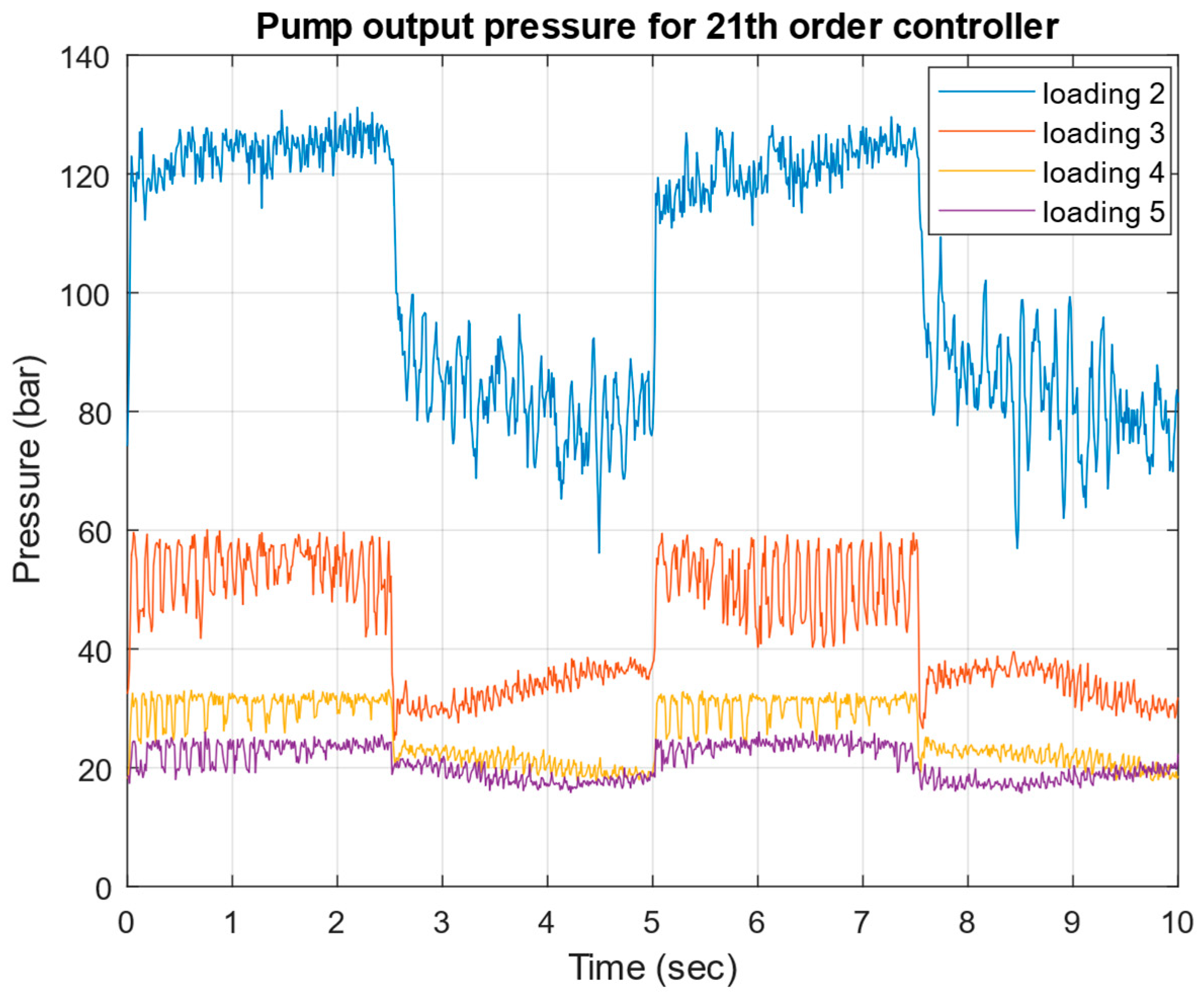
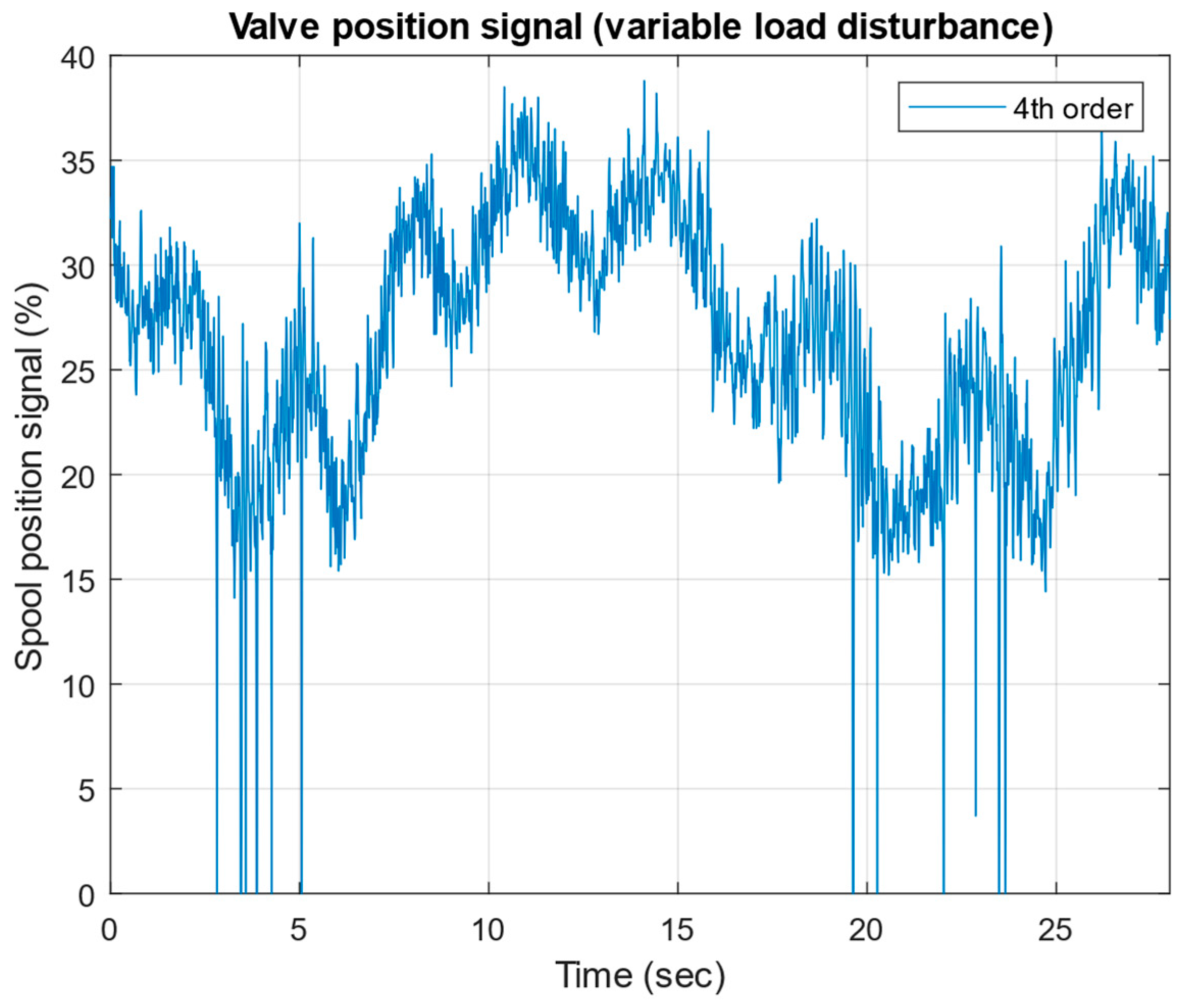
- Successful implementation and experimental validation of μ-controllers of different orders (21st, 6th, and 4th), demonstrating robust stability and robust performance across a wide range of operating conditions.
2. Plant Description and Modeling
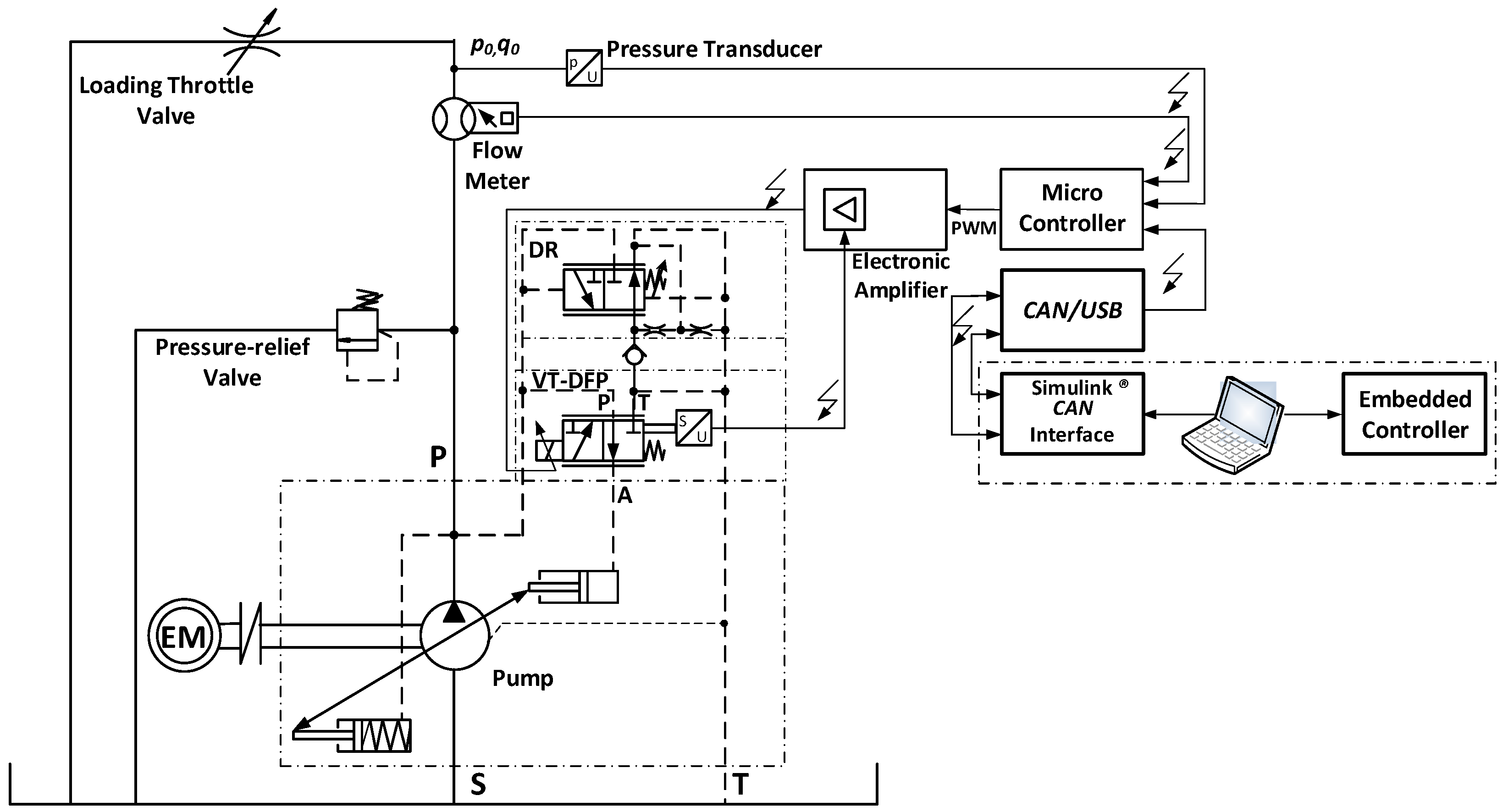
2.1. System for Rapid Prototyping of Control Algorithms
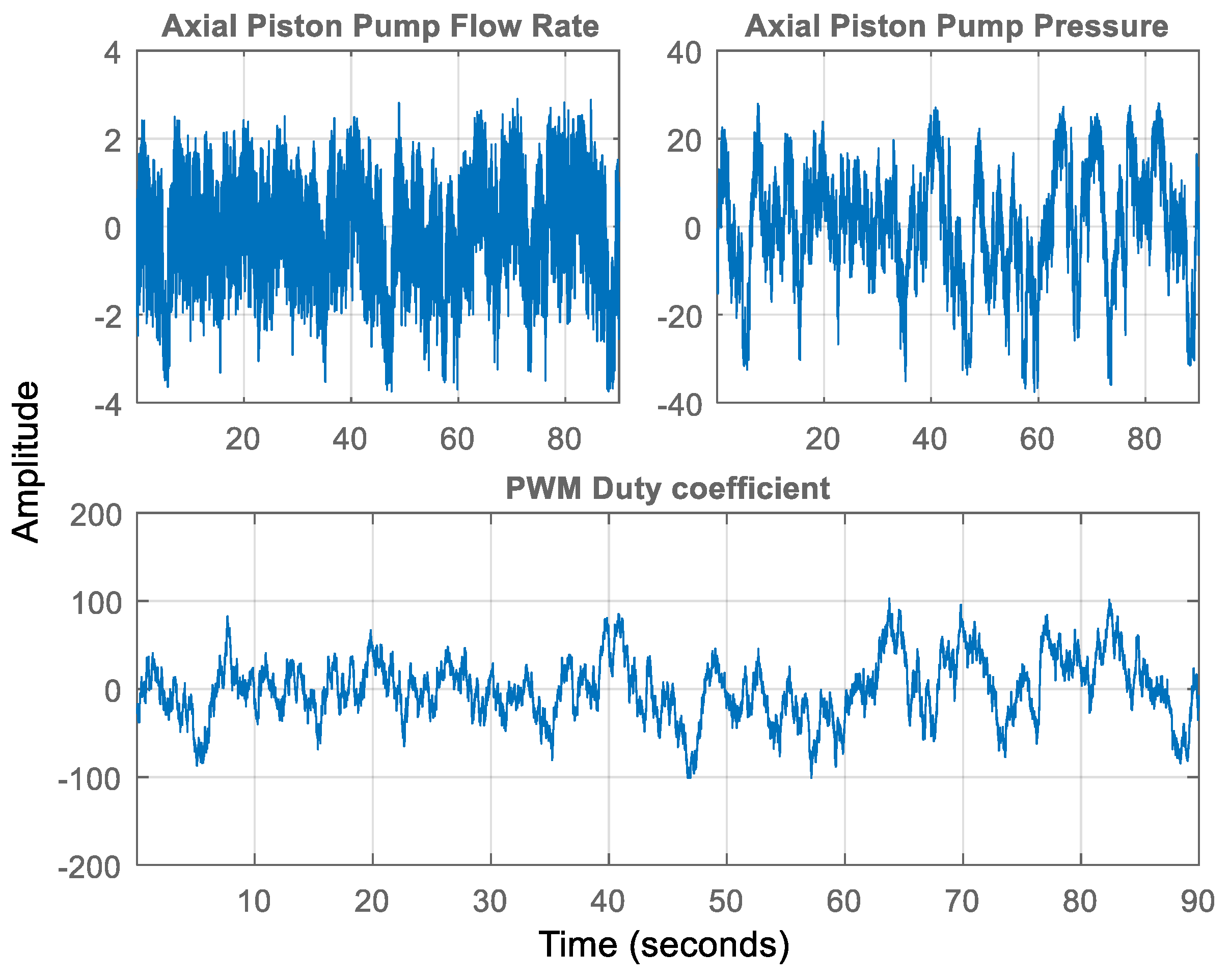
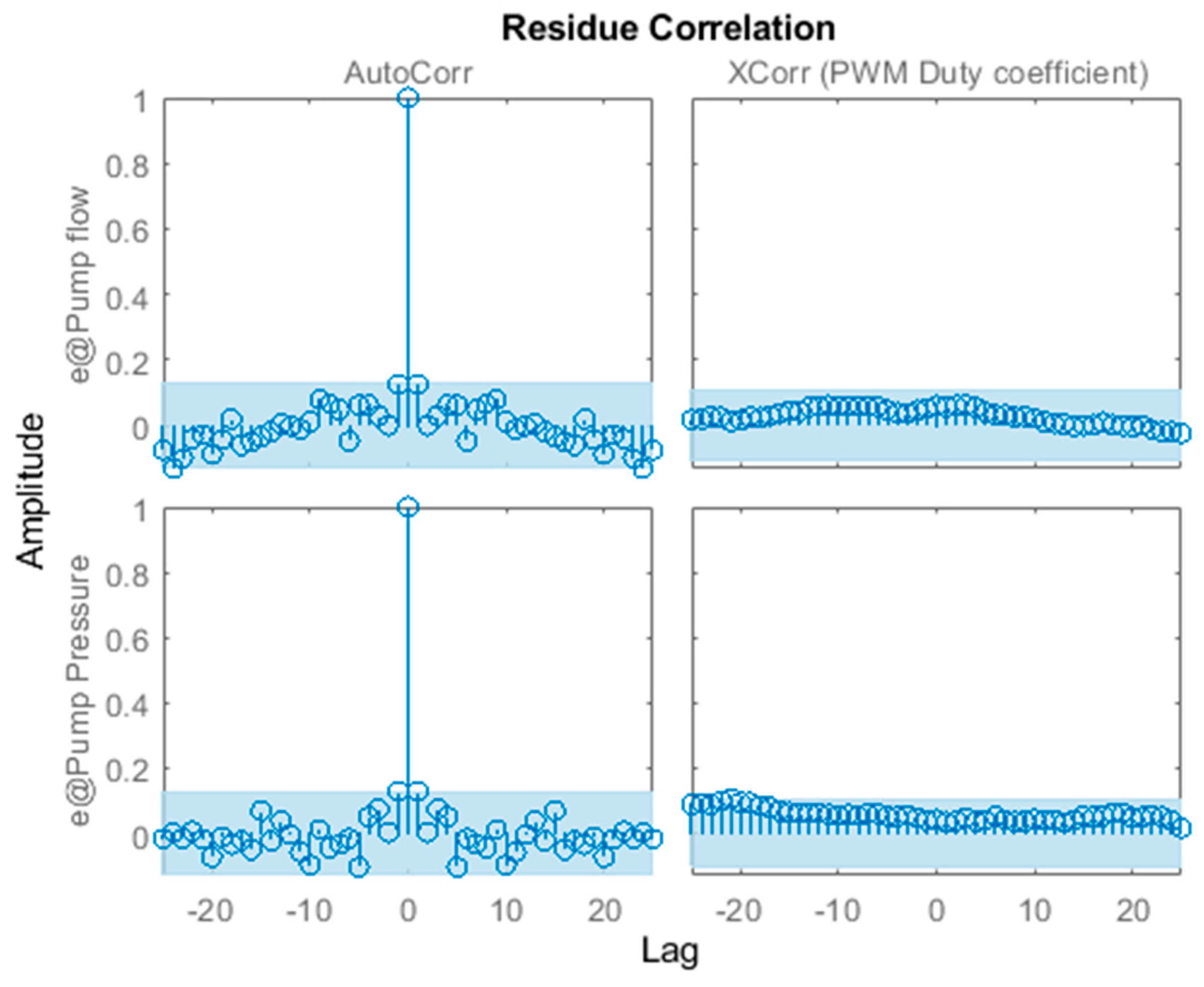
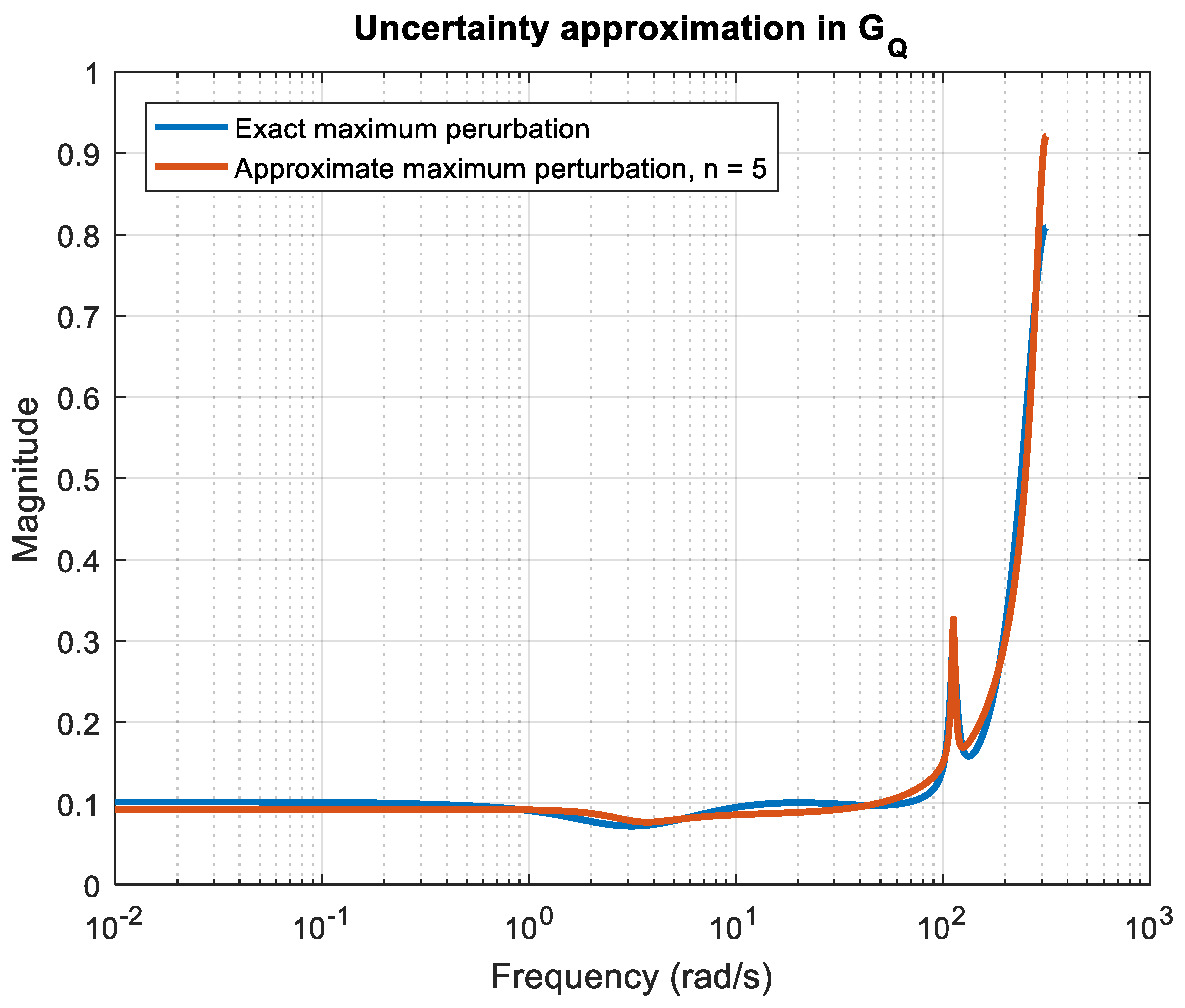
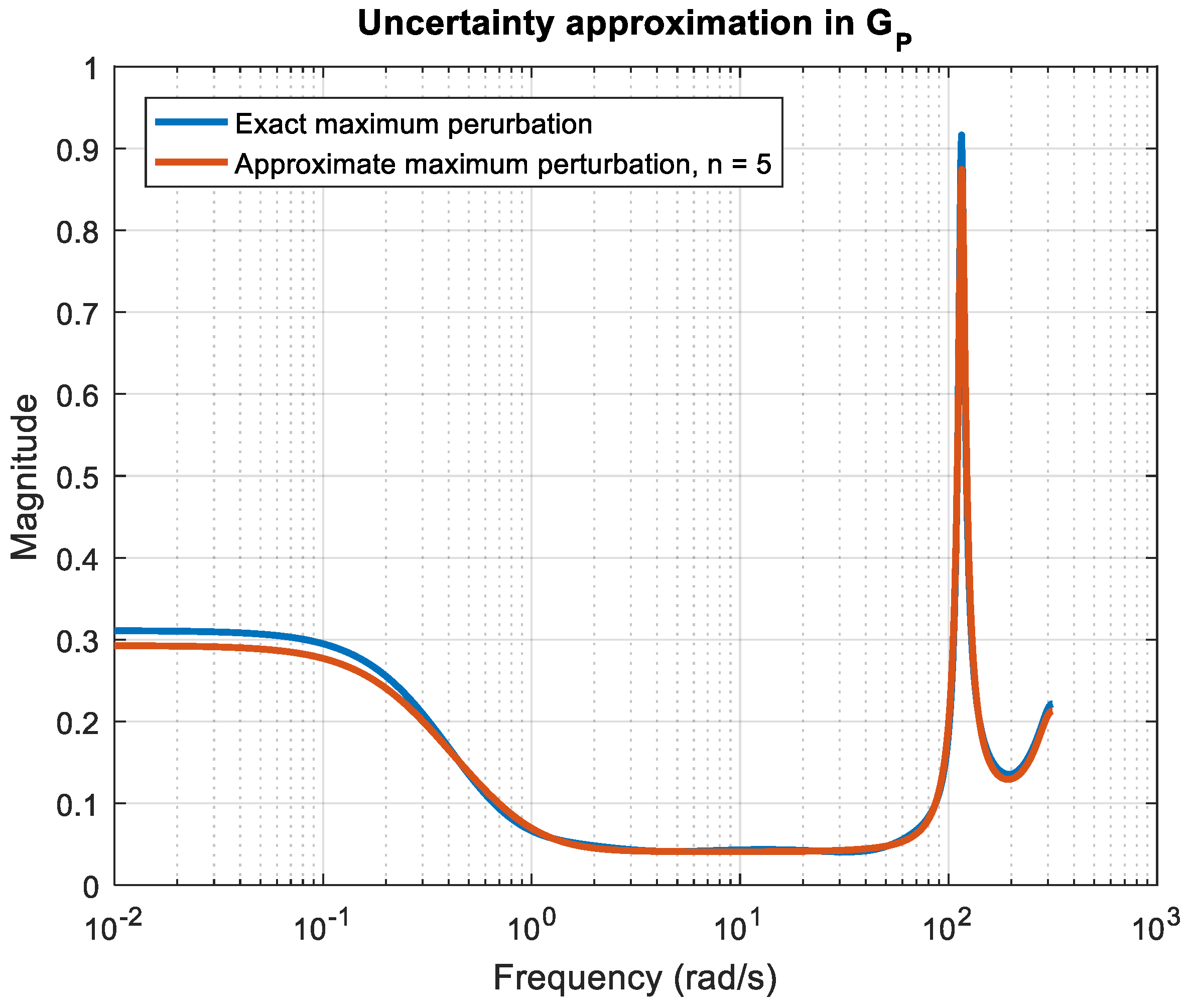
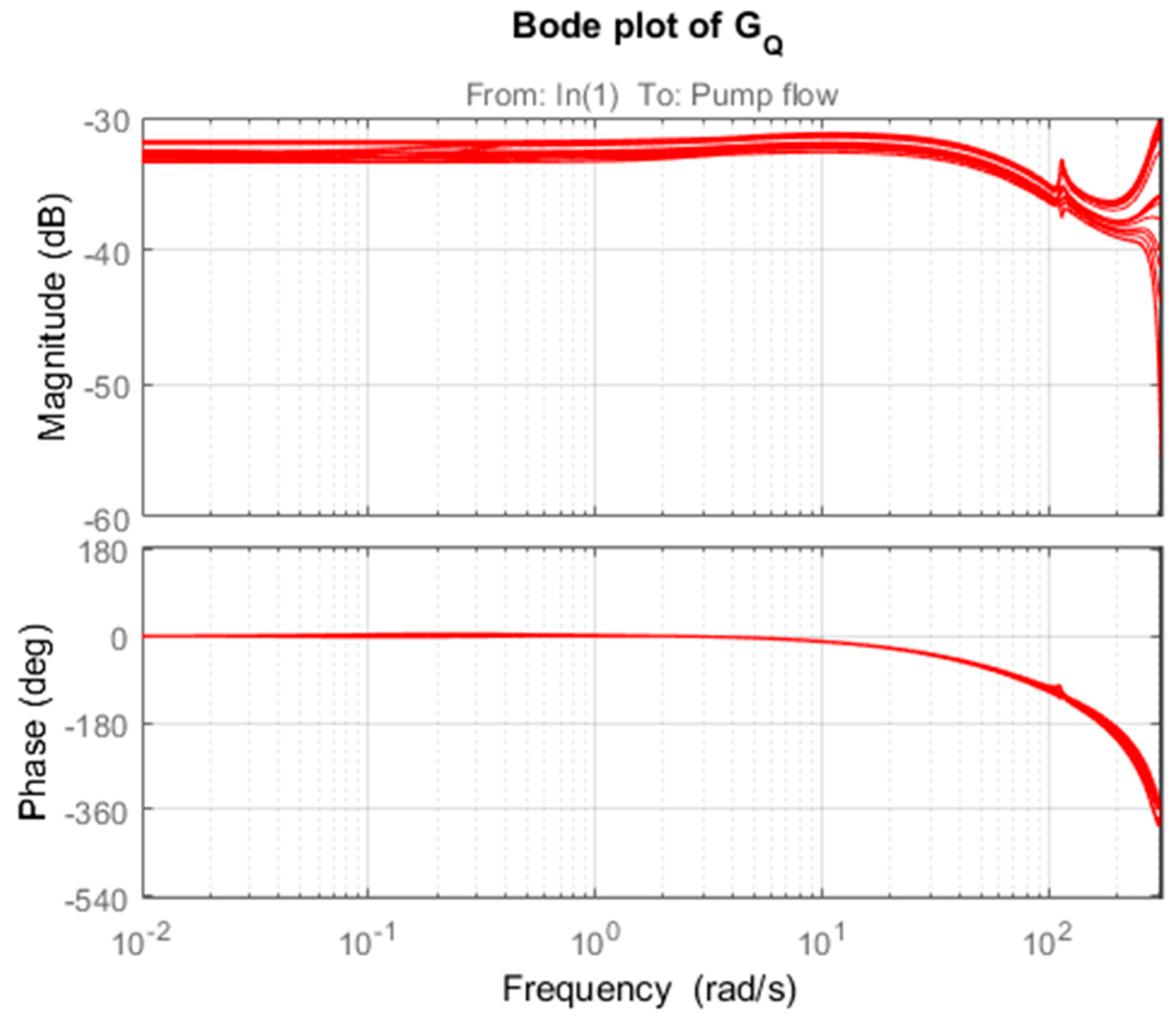
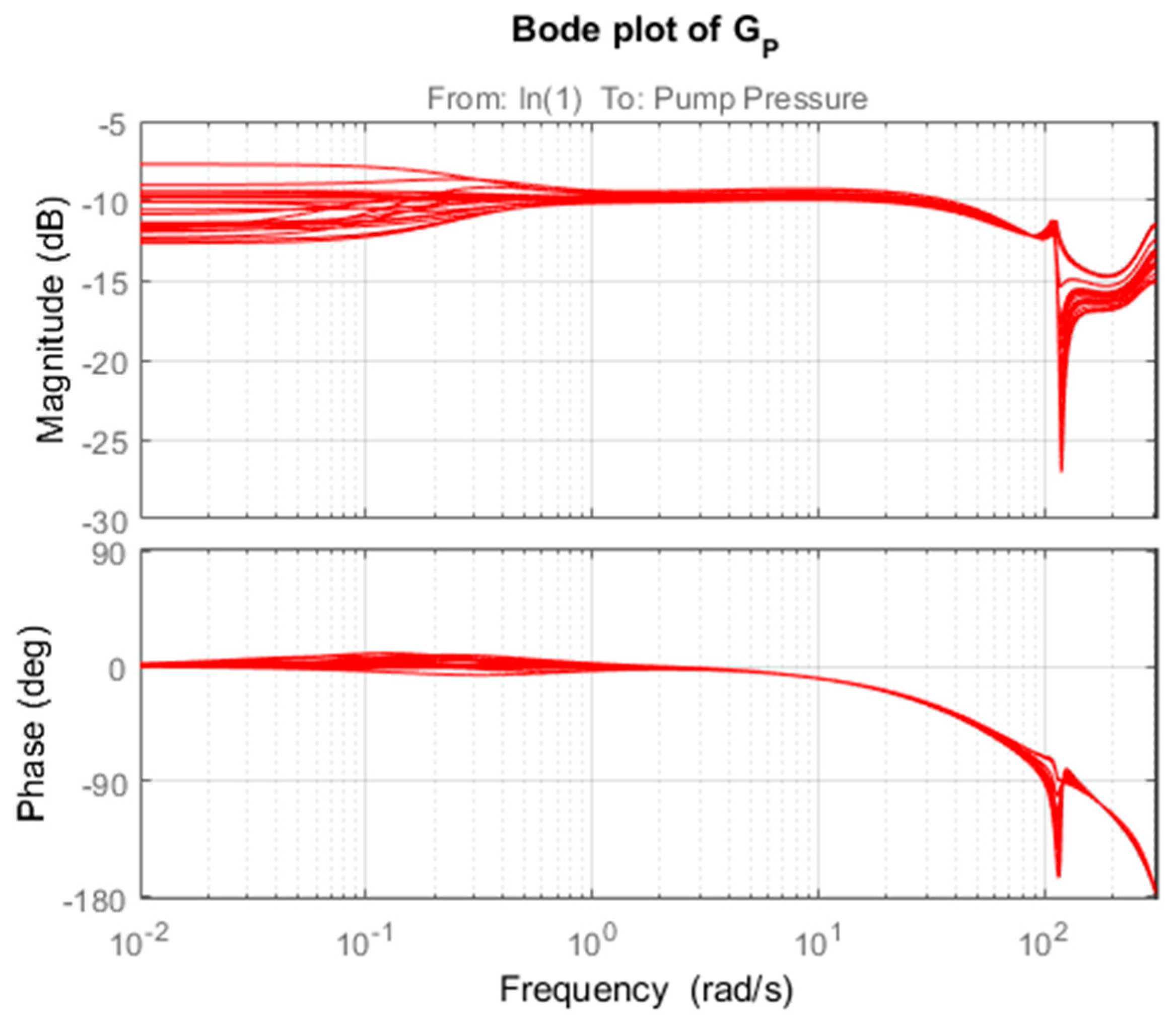
2.2. Identification Model with Multiplicative Uncertainty
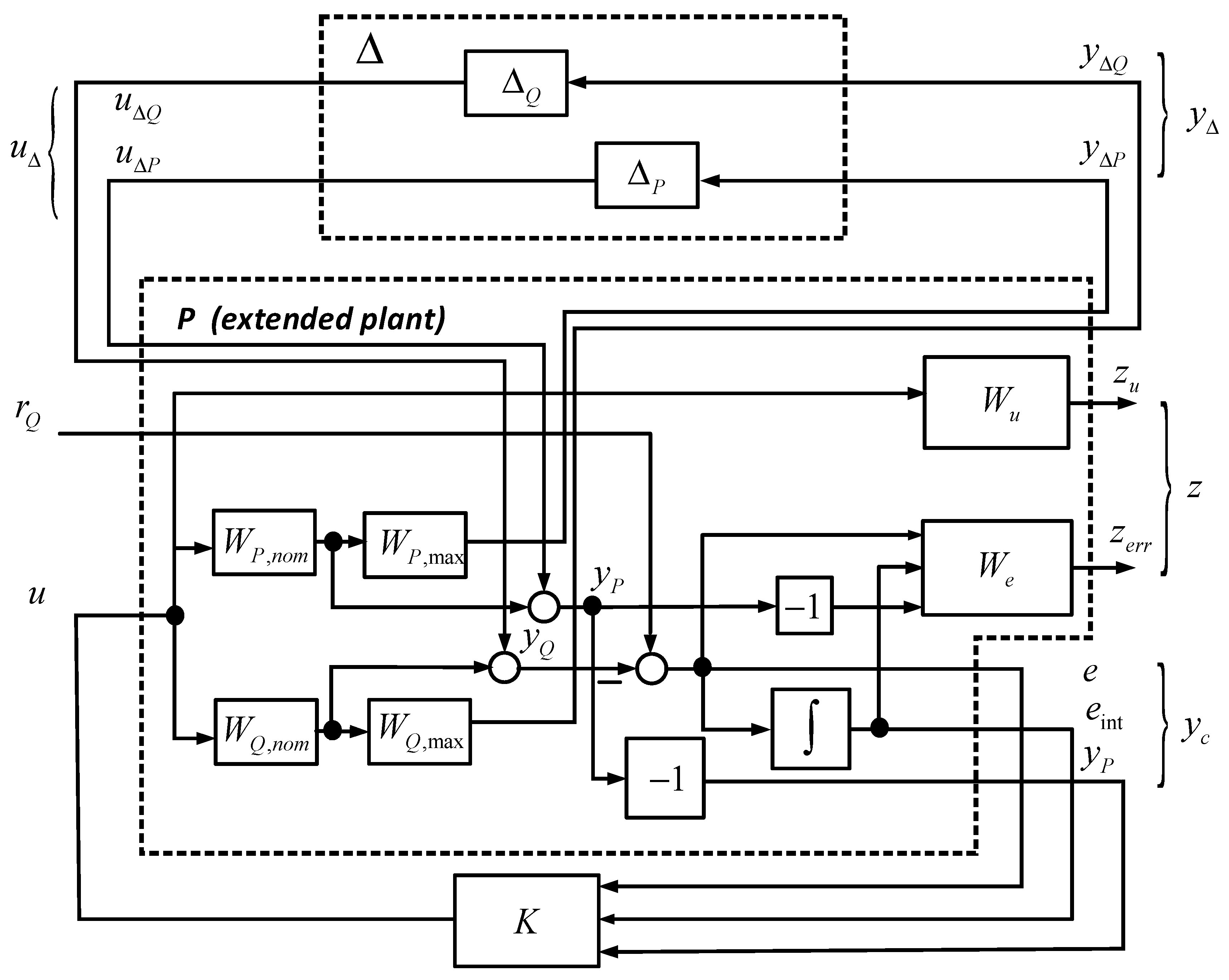
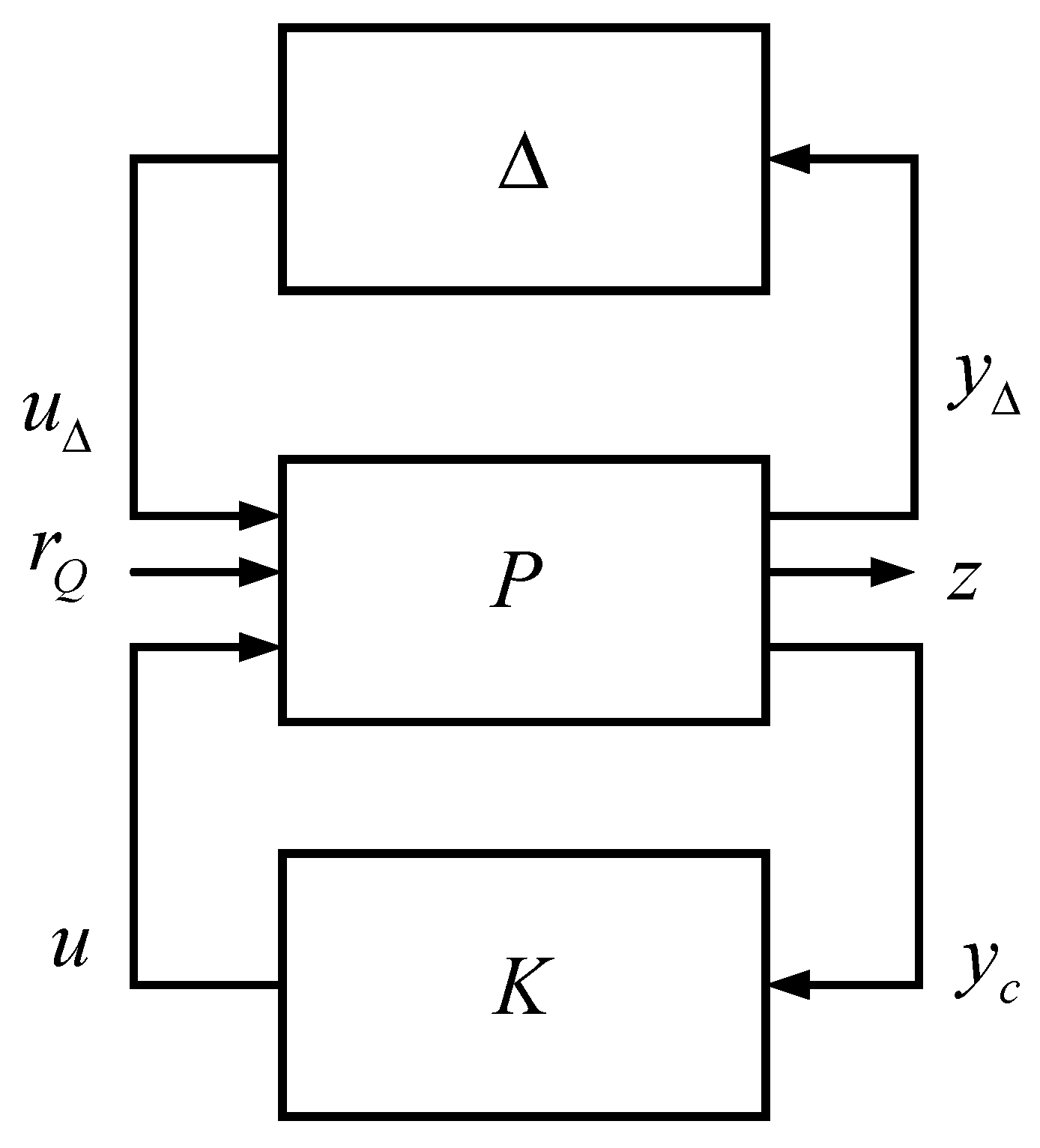
3. Robust Control Approach
3.1. μ-Control Design
- —inputs due to model uncertainty with respect to flow rate and pump pressure ;
- —external input (pump flow rate reference signal);
- —control input (control signal);
- —outputs due to model uncertainty with respect to flow rate and pump pressure ;
- —external performance outputs, , —performance output of the flow rate error, —performance output of the discrete time integral of the flow rate error,—performance output of the pump pressure, and —performance output of the control signal;
- —measured (controlled) outputs, where is the pump flow rate error and is the discrete time integral of the pump flow rate error.
- .
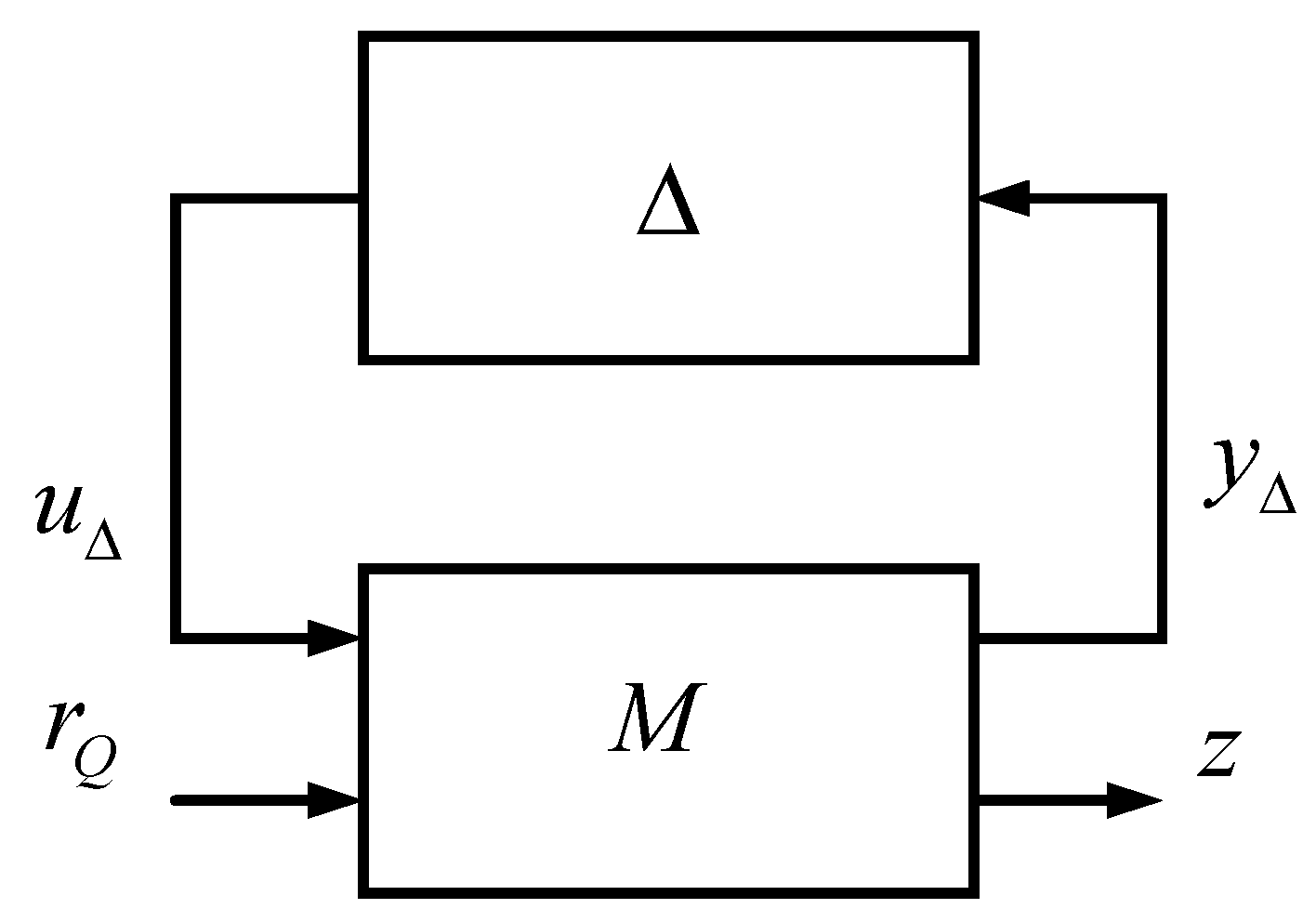
3.2. Robust Stability and Robust Performance Analysis
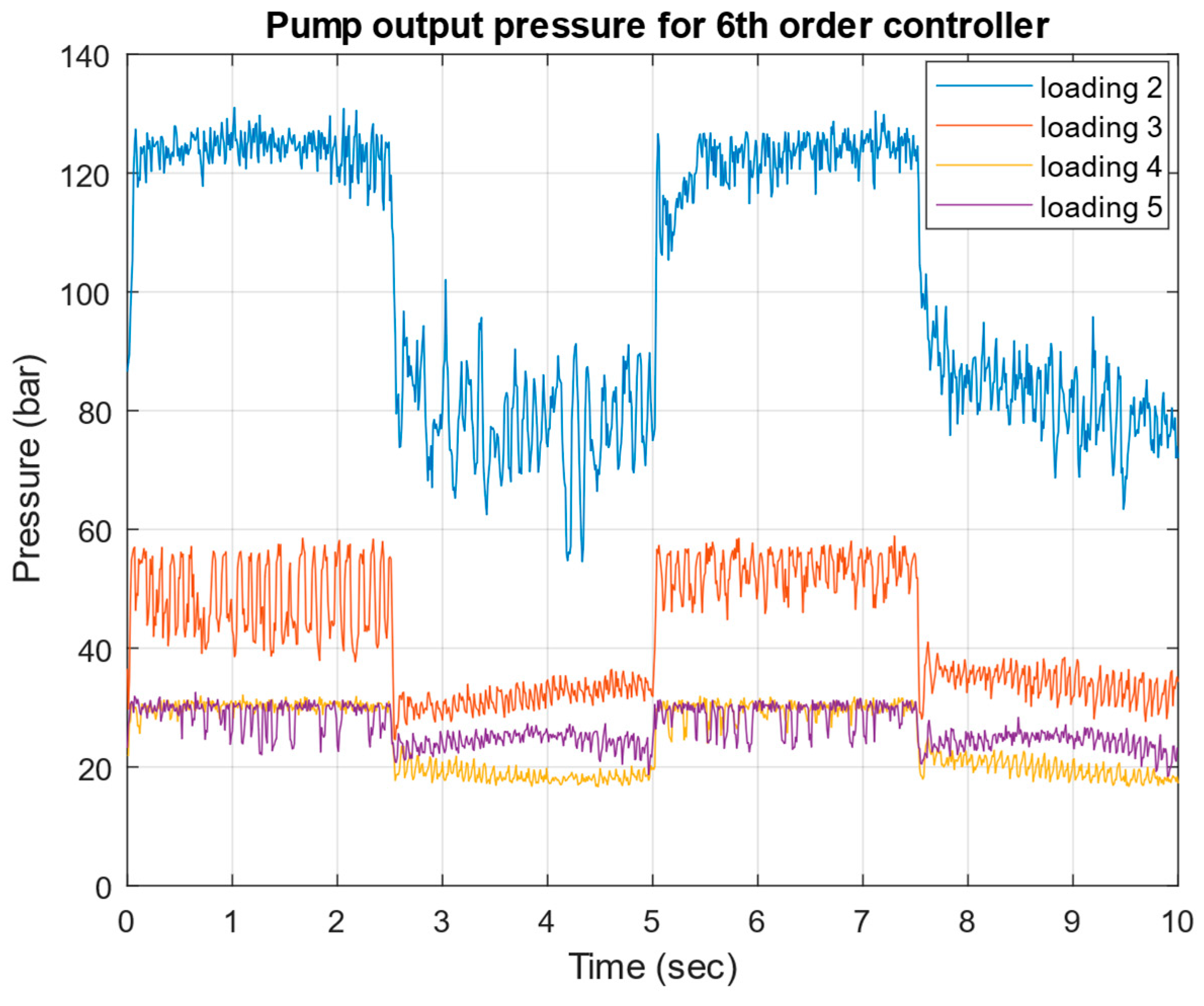
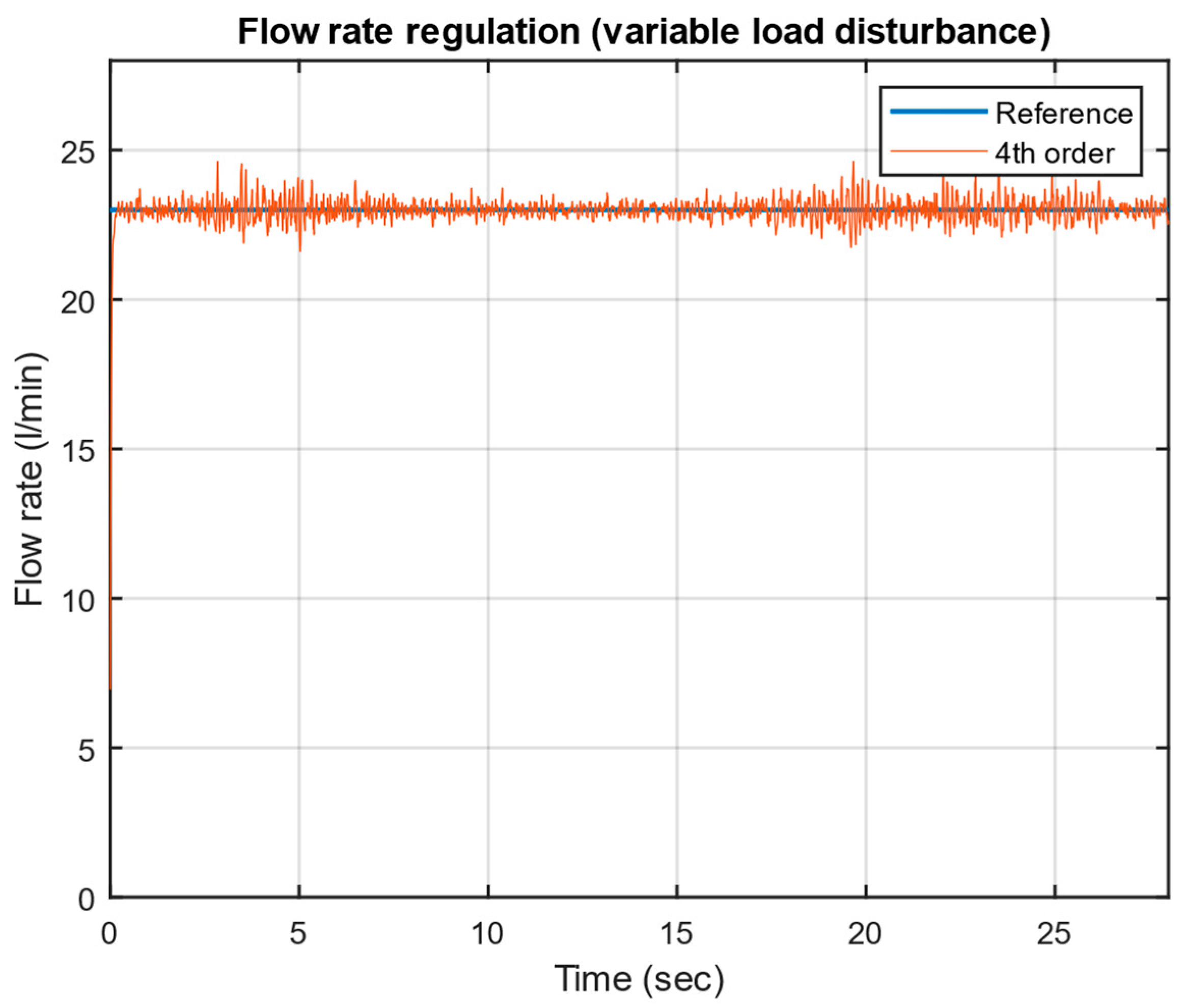
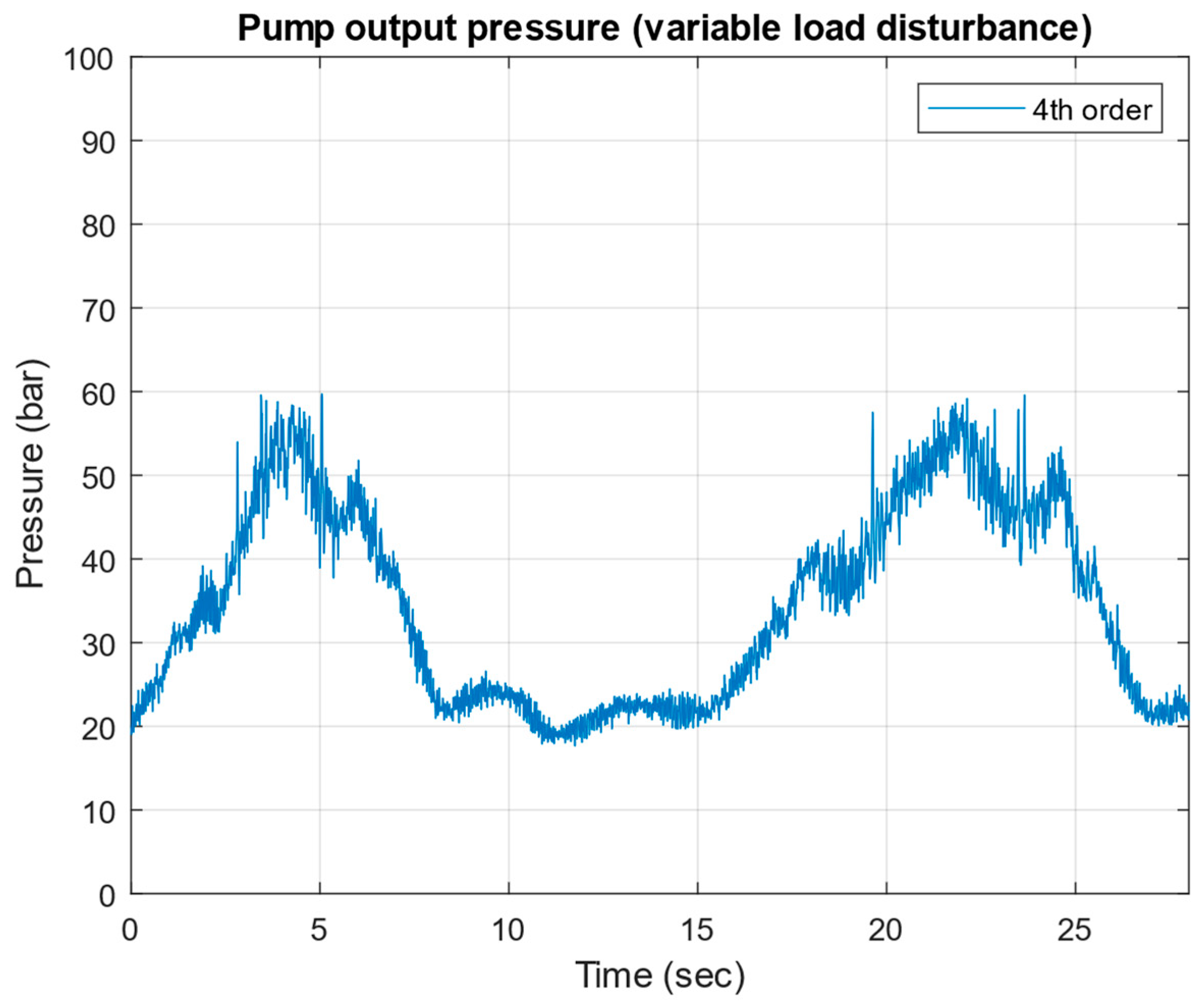
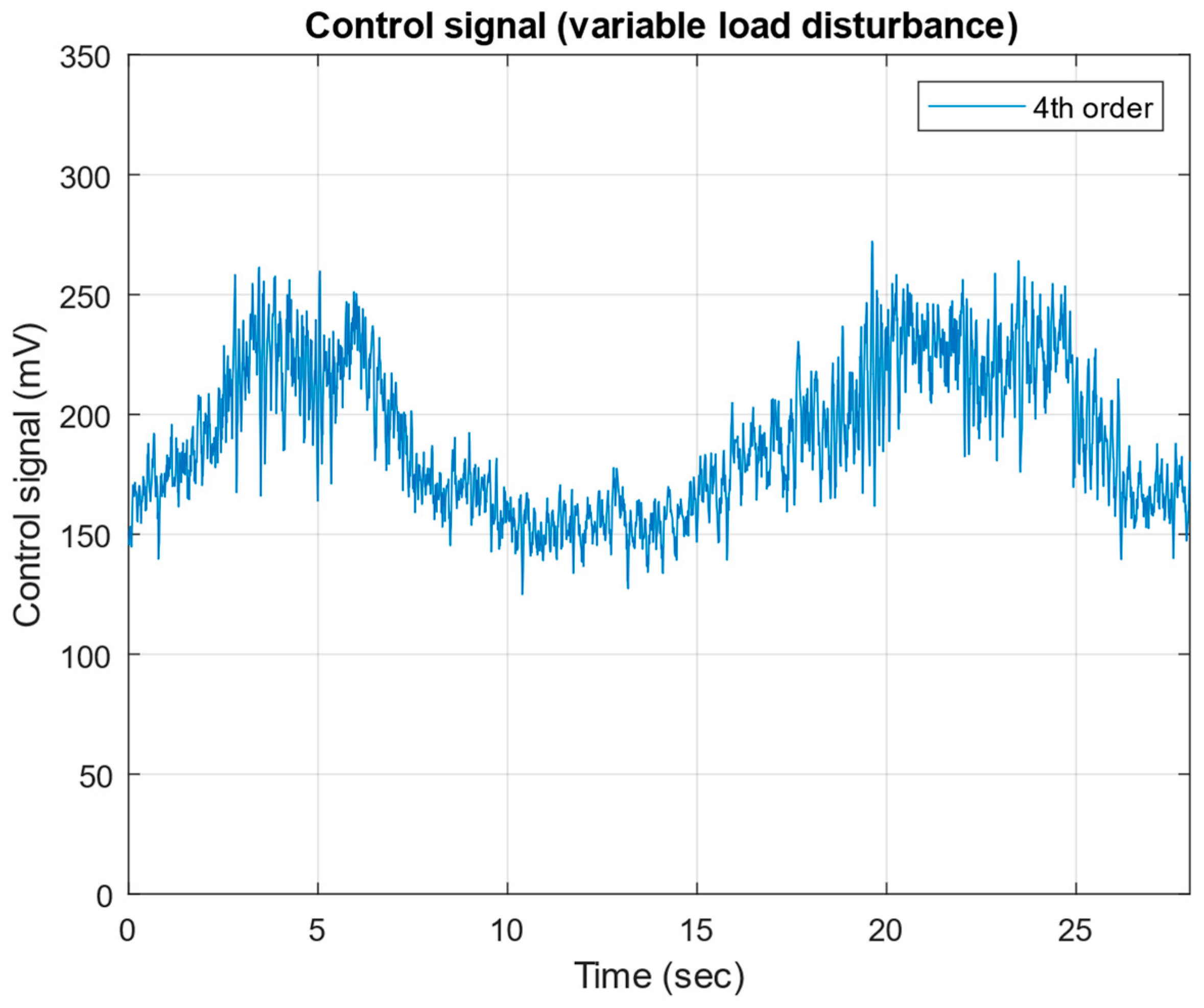
4. Experimental Test of the Robust μ-Controller
- Sensor Data Acquisition: The MC012-022 collects sensor signals from the pressure transducer, proportional spool valve LVDT, and gear flow meter and transmits them to the Simulink® model running on the host PC.
- Actuator Control: Upon receiving control signals generated by the Simulink® model, the MC012-022 processes these signals and converts them into the PWM output to drive the spool actuator.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Findeisen, D.; Helduser, S. Ölhydraulik; Springer: Berlin/Heidelber, Germany, 2015. [Google Scholar]
- Skarpetis, M.G. Automatic Control of Hydraulic Systems; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2023. [Google Scholar]
- Frankenfield, T. Using Industrial Hydraulics. In Rexroth Worldwide Hydraulics; Penton Publishing Inc.: New York, NY, USA, 1984. [Google Scholar]
- Tonyan, M. Electronically Controlled Proportional Valves; Marcel Dekker Inc.: New York, NY, USA, 1985. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing; Academia Books International: New Delhi, India, 2001. [Google Scholar]
- Manring, N. Fluid Power Pumps and Motors: Analysis, Design, and Control; McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Zhou, K.; Doyle, J. Robust and Optimal Control; Prentice Hall International: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Petkov, P.; Slavov, T.s.; Kralev, J. Design of Embedded Robust Control Systems Using MATLAB®/Simulink®; IET Control: London, UK, 2018. [Google Scholar]
- Helian, B.; Mustalahti, P.; Mattila, J.; Chen, Z.; Yao, B. Adaptive robust pressure control of variable displacement axial piston pumps with a modified reduced-order dynamic model. Mechatronics 2022, 87, 102879. [Google Scholar] [CrossRef]
- Feng, Y.; Jian, Z.; Li, J.; Tao, Z.; Wang, Y.; Xue, J. Advanced Control Systems for Axial Piston Pumps Enhancing Variable Mechanisms and Robust Piston Positioning. Appl. Sci. 2023, 13, 9658. [Google Scholar] [CrossRef]
- Busquets, E.; Ivantysynova, M.; Handroos, H. Discontinuous projection-based adaptive robust control for displacement-controlled actuators. J. Dyn. Syst. Meas. Control Trans. ASME 2015, 137, 8. [Google Scholar] [CrossRef]
- Haggag, S.A. Robust control and modelling of a heavy equipment variable displacement pump hydraulic system. Int. J. Heavy Veh. Syst. 2011, 18, 288–302. [Google Scholar] [CrossRef]
- Guo, K.; Wei, J. Adaptive robust control of variable displacement pumps. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Park, S.; Lee, J.; Kim, J. Robust control of the pressure in a control-cylinder with direct drive valve for the variable displacement axial piston pump. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2009, 223, 455–465. [Google Scholar] [CrossRef]
- Haack, S.; Meißelbach, A.; Bosch Rexroth, A.G. Industrial Hydraulics–Are we really on track concerning Industry 4.0? In Proceedings of the 11th International Fluid Power Conference, Aachen, Germany, 20–21 March 2018. [Google Scholar]
- Zhang, Q.; Kong, X.; Yu, B.; Ba, K.; Jin, Z.; Kang, Y. Review and Development Trend of Digital Hydraulic Technology. Appl. Sci. 2020, 10, 579. [Google Scholar] [CrossRef]
- Lu, W. Review of the Digital Hydraulics Technologies. Corso di laurea magistrale in Ingegneria Meccanica (Mechanical Engineering). Master’s Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Hershberger, T. Mobile Hydraulics: Challenges and Opportunities: Equipment electrification will lead to an integrated approach. Hydraul. Pneum. 2020, 73, 20–25. [Google Scholar]
- Belan, H.C.; Locateli, C.C.; Lantto, B.; Krus, P.; de Negri, V.J. Digital secondary control architecture for aircraft application. In Proceedings of the 7th Workshop on Digital Fluid Power, Linz, Austria, 26–27 February 2015. [Google Scholar]
- Kordak, R. Hydrostatic Drives with Control of the Secondary Unit. In The Hydraulic Trainer Vol.6; Mannesmann Rexroth GmbH: Lohr a. Main, Germany, 1996; Volume 6. [Google Scholar]
- Sun, Z.; Zeng, Q.; Wan, L.; Xiao, Y. Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance. Actuators 2023, 12, 260. [Google Scholar] [CrossRef]
- Khalil, M.K.B.; Yurkevich, V.D.; Svoboda, J.; Bhat, R.B. Implementation of single feedback control loop for constant power regulated swash plate axial piston pumps. Int. J. Fluid Power 2002, 3, 27–36. [Google Scholar] [CrossRef][Green Version]
- Mitov, A.; Kralev, J.; Slavov, T.S.; Angelov, I. Design of Embedded Control System for Open Circuit Axial Piston Pump. In Proceedings of the 2022 22nd International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 1–4 June 2022. [Google Scholar]
- Zeiger, G.; Akers, A. The Application of Linear Optimal Control Techniques to Axial Piston Pump Controller Design; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1989. [Google Scholar]
- Lin, S.; Akers, A. Optimal control theory applied to pressure-controlled axial piston pump design. J. Dyn. Syst. Meas. Control Trans. ASME 1990, 112, 475–481. [Google Scholar] [CrossRef]
- Berg, H.; Ivantysynova, M. Design and testing of a robust linear controller for secondary controlled hydraulic drive. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1999, 213, 375–385. [Google Scholar] [CrossRef]
- Zeiger, G.; Akers, A. Dynamic Analysis of an Axial Piston Pump Swashplate Control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1986, 200, 49–58. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Mitov, A.; Kralev, J.; Slavov, T.S. Identification of Variable Displacement Axial-Piston Pump with Proportional Valve Control. In Proceedings of the 14th International Scientific Conference on Aeronautics, Automotive, and Railway Engineering and Technologies, Sozopol, Bulgaria, 10–13 September 2022; Volume 3064. [Google Scholar]
- Bensaad, D.; Soualhi, A.; Guillet, F. A new leaky piston identification method in an axial piston pump based on the extended Kalman filter. Meas. J. Int. Meas. Confed. 2019, 148, 106921. [Google Scholar] [CrossRef]
- Koivumäki, J.; Mattila, J. Adaptive and nonlinear control of discharge pressure for variable displacement axial piston pumps. J. Dyn. Syst. Meas. Control Trans. ASME 2017, 139, 10. [Google Scholar] [CrossRef]
- Berg, H.; Ivantysynova, M. Robust closed loop speed and angular position control for variable displacement hydraulic motors supplied from a constant pressure mains system. Olhydraulik Und Pneum. 1999, 43, 405–410. [Google Scholar]
- Zhang, R.; Alleyne, A.; Prasetiawan, E. Modeling and H2/H∞ MIMO control of an earthmoving vehicle powertrain. J. Dyn. Syst. Meas. Control Trans. ASME 2002, 124, 625–636. [Google Scholar] [CrossRef]
- Lennevi, J.; Palmberg, J.-O. Application and implementation of LQ design method for the velocity control of hydrostatic transmissions. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1995, 209, 255–268. [Google Scholar] [CrossRef]
- Heybroek, K.; Larsson, J.; Palmberg, J.-O. Open Circuit Solution for Pump Controlled Actuators. In Proceedings of the 4th FPNI-PhD Symposium, Sarasota, FL, USA, 13–17 June 2006; pp. 27–40. [Google Scholar]
- Zhang, P.; Li, Y. Research on Control Methods for the Pressure Continuous Regulation Electrohydraulic Proportional Axial Piston Pump of an Aircraft Hydraulic System. Appl. Sci. 2019, 9, 1376. [Google Scholar] [CrossRef]
- Kemmetmüller, W.; Fuchshumer, F.; Kugi, A. Nonlinear pressure control of self-supplied variable displacement axial piston pumps. Control Eng. Pract. 2010, 18, 84–93. [Google Scholar] [CrossRef]
- Wei, J.; Guo, K.; Fang, J.; Tian, Q. Nonlinear supply pressure control for a variable displacement axial piston pump. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 614–624. [Google Scholar] [CrossRef]
- Mitov, A.; Slavov, T.; Kralev, J. Comparison of Advanced Multivariable Control Techniques for Axial-Piston Pump. Processes 2024, 12, 1797. [Google Scholar] [CrossRef]
- Rexroth Bosch Group. Pressure and Flow Control System; Technical Data Sheet, RE 30630; Rexroth Bosch Group: Lohr am Main, Germany, 2015. [Google Scholar]
- Rexroth Bosch Group. Proportional Directional Valves, Direct Operated, with Electrical Position Feedback as Pilot Control Valve for Control Systems SY(H)DFE; Technical Data Sheet, RE 29016; Rexroth Bosch Group: Lohr am Main, Germany, 2019. [Google Scholar]
- Mitov, A.; Slavov, T.; Kralev, J. Rapid Prototyping of H∞ Algorithm for Real-Time Displacement Volume Control of Axial Piston Pumps. Algorithms 2023, 16, 120. [Google Scholar] [CrossRef]
- Danfoss. Plus+1 Controllers MC012-020 and 022; Data Sheet, 11077167, Rev DA; Danfoss: Nordborg, Denmark, 2013. [Google Scholar]
- Ljung, L. System Identification Toolbox™ User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
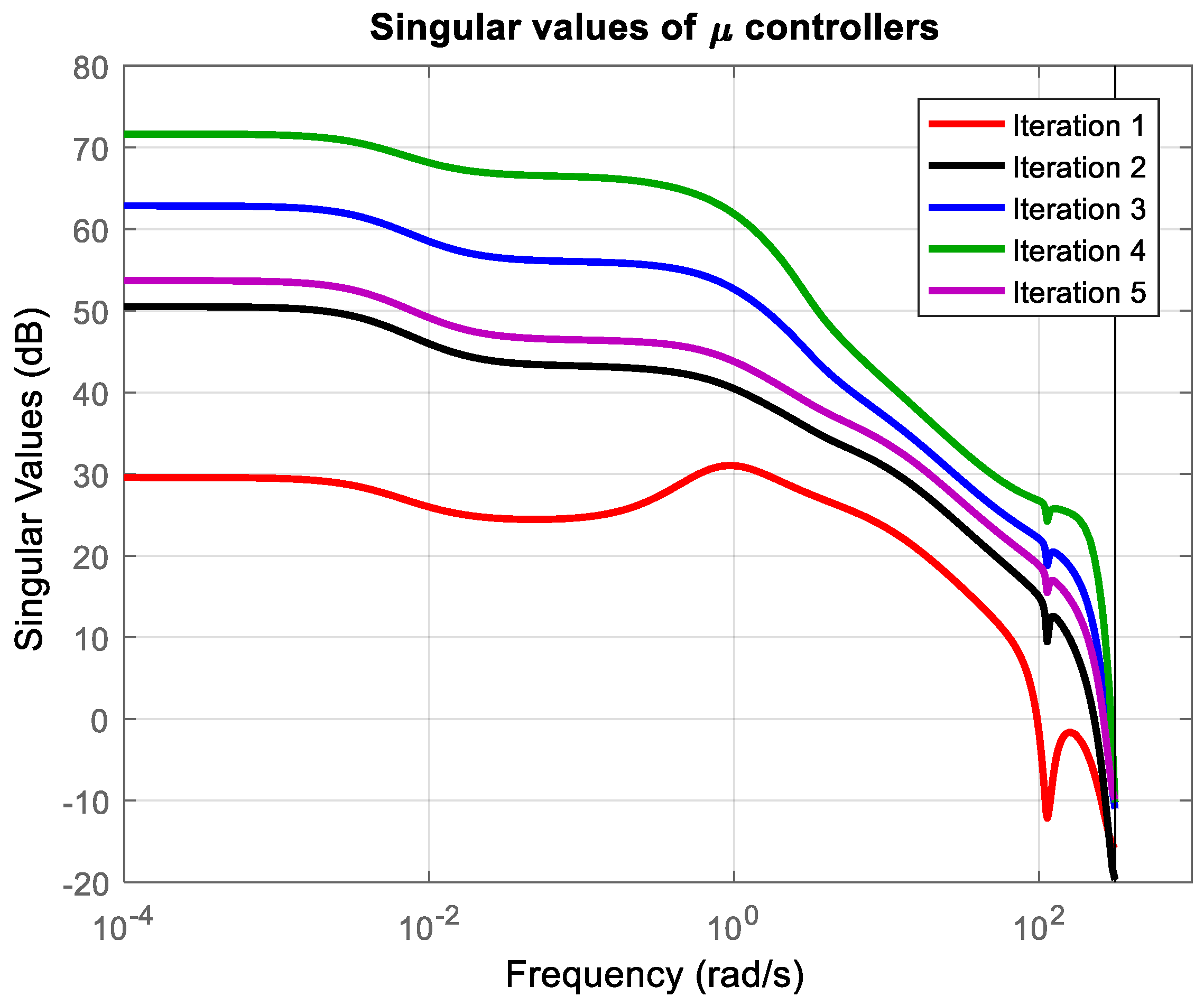


| Iteration | Achieved | Peak | D-Scale Order | Controller Order |
|---|---|---|---|---|
| 1 | 6.462 | 1.7510 | 0 | 19 |
| 2 | 0.646 | 0.5900 | 0 | 19 |
| 3 | 0.564 | 0.5632 | 2 | 21 |
| 4 | 0.565 | 0.5630 | 2 | 21 |
| 5 | 0.571 | 0.5710 | 2 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slavov, T.; Mitov, A.; Kralev, J. Novel Approach for Robust Control of Axial Piston Pump. Mathematics 2025, 13, 643. https://doi.org/10.3390/math13040643
Slavov T, Mitov A, Kralev J. Novel Approach for Robust Control of Axial Piston Pump. Mathematics. 2025; 13(4):643. https://doi.org/10.3390/math13040643
Chicago/Turabian StyleSlavov, Tsonyo, Alexander Mitov, and Jordan Kralev. 2025. "Novel Approach for Robust Control of Axial Piston Pump" Mathematics 13, no. 4: 643. https://doi.org/10.3390/math13040643
APA StyleSlavov, T., Mitov, A., & Kralev, J. (2025). Novel Approach for Robust Control of Axial Piston Pump. Mathematics, 13(4), 643. https://doi.org/10.3390/math13040643









