Abstract
On October 16th 1843, the prominent Irish mathematician Sir William Rowan Hamilton, in an inspired act of vandalism, carved his famous on the Brougham Bridge in Dublin, thus starting a major clash of ideas with the potential to change the course of history. Quaternions, as he called his invention, were quite useful in describing Newtonian mechanics, and as it turned out later—also quantum and relativistic phenomena, which were yet to be discovered in the next century. However, the scientific community did not embrace this new approach with enthusiasm: there was a battle to be fought and Hamilton failed to make a compelling case probably because he was standing alone at the time. Although Quaternions were soon to find useful applications in geometry and physics (with the works of Clifford, Cayley, Maxwell, Einstein, Pauli, and Dirac), the battle seemed lost a few decades after Hamilton’s death. But, a century later computer algorithms turned the tides, and nowadays we are witnessing a revived interest in the subject, prompted by technology.
MSC:
15A67; 46S05; 01A55
1. Introduction
For all we know, Quaternions were originally invented by Gauss in 1819, who did not consider them significant or interesting enough to publish his results. The concept was then rediscovered by Hamilton in 1843, who developed the rigorous theory and notation we use today. Both their derivations were based on an analogy with Cardano’s complex numbers dating back to the sixteenth century. Hamilton, in particular, came across the idea while attempting to develop a three-dimensional algebraic tool for rigid transformations of spatial objects but soon realized a fourth component was necessary as well. Quaternions, denoted with in honor of Sir Hamilton, constitute one of the four Hurwitz (normed division) algebras, essential in both mathematics and theoretical physics, and the first among them that is non-commutative (see [1] for more details). Similarly to and , and unlike Octonions , which are non-associative, they are also a Clifford (geometric) algebra, intrinsically linked to both rigid transformations in three-dimensional space and the Lorentz group in special relativity. Hamilton did not live long enough to see the amazing applications of his discovery but had a strong conviction that it would inevitably change the course of mathematics forever. And it did so, for a while, only to be forgotten for more than a century and then revived from the ashes of history in quite an unusual way.
The first major breakthrough came with Maxwell’s equations of electrodynamics, which he derived in [2] using Hamilton’s quaternion-based differential calculus. James Clerk Maxwell, considered by many the father of modern theoretical physics, advocated Hamilton’s approach, but his results were later rewritten by Heaviside and Gibbs (who strongly opposed it) in the so-called ’vector calculus’ formalism, commonly used today by physicists and engineers. In essence, it takes Quaternions out of the Quaternion algebra and analysis but keeps the consequences of the underlying structure, such as the dot and cross product, Hamilton’s gradient operator [3], along with the divergence and curl (see [4]). This allows for rewriting Maxwell’s theory (like in [5]) without the ’unnecessary burden’ of Quaternions, as they saw it at the time. Since Hamilton had passed away decades before that, there was no defendant strong enough to prevent the demolition of his work. Maxwell was after all a physicist, and Tait, who ‘took the torch’ from Hamilton (see [6]) and engaged in heated debates with Gibbs and Heaviside, could not turn the tides on his own: Quaternions were to be torn out of physics and nearly forgotten for about a century. Their fate is rather unfortunate, given the fact that soon after Maxwell found a rather convincing application in physics, Sophus Lie came up with the theory of differentiable groups and William Kingdon Clifford invented his famous geometric algebras [7], which generalize the quaternion construction to spaces of arbitrary dimension and metric signature. These two inventions certainly had a major impact on theoretical physics as the following years showed with Einstein’s relativity and Heisenberg’s quantum mechanics. In fact, both theories had many pillars, such as Lorentz, Poincaré and Hilbert in the former case, Planck, Schrödinger, Bohr and again Einstein, in the latter. But what they had in common was the extensive use of symmetries, i.e., Lie groups, and geometric algebras, in particular and . Even so, the scientific community was somewhat reluctant to go back to Quaternions and continued describing the world using vector calculus and matrices, which became the usual language of Lie groups and algebras, as well as the foundation of Heisenberg’s version of quantum mechanics, although Clifford’s perspective gives an advantage in many ways, e.g., conformal and metric groups appear most naturally from the corresponding geometric algebra, and the notion of spin makes its involvement inevitable. However, physicists still find a way to cheat, invoking the so-called ’Pauli matrices’ instead of Quaternions and Dirac’s ‘gamma matrices’ instead of Clifford’s space–time algebra . Students struggle with these clumsy artificial constructions, which substitute something quite natural and easy to implement, and that ultimately impedes their progress and deeper understanding. It is rather peculiar how physics in the past century relied significantly on Hamilton’s ideas, from the least action principle to the study of integrable systems, but for some reason neglected the extremely useful quaternion algebra and analysis, substituting them with their ‘crippled’ vector versions, which seem to mimic the shape while lacking the content.
Altman argues in his review [8] that the tragic fate of Quaternions might have been avoided if Hamilton, in all his brilliance, had not made a crucial error thinking that the action on vectors is given by simple multiplication, while it involves what people in the Clifford community call a ‘sandwich product’, or the adjoint representation, as we put it in group-theoretic terms. However, as pointed out by Pujol [9], the proper description follows soon after the invention, and is certainly in [3], along with the correct relation of the angles. There was no way for Hamilton to know about the existence of spinors or the topology of in advance as it took decades and the brilliance of Clifford, Cartan, and Weyl to come up with these ideas. But Rodrigues had already got there in 1840—three years before the discovery of Quaternions (which took place, weirdly enough, on Rodrigues’ birthday). Yet, Hamilton probably never read his paper, and few people did at the time. Rodrigues was not an academic; he was a wealthy banker, economist, and social activist of Jewish origin, who wrote only two papers in mathematics (including his PhD thesis): one on special functions and one on the rotation group. They both remained in history but hardly anyone in the scientific community knew his name back then. Unfortunately, Hamilton, who was not only smart but very influential, could not promote his invention convincingly enough, and after his death, critics like Gibbs, Heaviside, and Lord Kelvin prevailed, wiping it out of science for quite a long time. The Renaissance of Quaternions (and geometric algebras in general) came in the late twentieth century: first with the devoted works of Hestenes in theoretical physics, but then it was boosted by the necessity of optimization in computer graphics gaming engines and then spread to other areas, such as robotics and artificial intelligence. This paper is an attempt to follow the evolution of the core ideas in this subject not so much in chronological, but mostly in logical order. We begin with Rodrigues’ legacy, carried on in the next century by Fedorov and Mladenova in the physical context. Then, we briefly discuss Clifford’s geometric algebras as a natural generalization of Hamilton’s idea, as well as the associated differential calculus, leading to Maxwell’s equations and other valuable treasures along the away. Finally, we discuss the new school begun by Hestenes and in particular some applications in modern engineering.
2. Projectivity, Euler–Rodrigues’ Parameters and the Cayley Transform
Leonard Euler certainly made a significant contribution to the theory of rotations, among other things: their orthogonal property, the invariant axis theorem, the famous Euler angles used to this day in mechanics and engineering. When Olinde Rodrigues published in 1840 the first version of Quaternions available to the mathematical community (see [10]), he borrowed a lot from Euler: the ‘four squares formula’, the universal trigonometric substitution , as well as the famous Euler formula for complex numbers
which, combined with the invariant axis theorem and orthogonal decomposition, ultimately leads to the equally famous Rodrigue’s rotation formula
where yields the Lie algebra element via for any and is simply the parallel projector onto the unit vector along the rotation axis: . One may easily obtain a similar expression in higher dimensions and different signatures via the Plücker embedding, as long as the generator is associated with a single plane. But, Rodrigues made much more than that; he actually provided a faithful representation of the group via projective quaternions years before Hamilton came up with his i, j, k units and decades before the ‘invention’ of Lie groups. Now that we have the convenience of these notions, it is easy to analyze and finally appreciate Rodrigues’ contribution to the subject. He proposed a description based on the so-called ‘Euler–Rodrigues’ parameters’:
which we now interpret as a real (scalar) and imaginary (vector) part of a unit quaternion (the conjugation here is Hermitian, just like in the complex plane, i.e., ):
and showed explicitly the composition law for these quantities, i.e., the multiplication of quaternions. Moreover, interpreting them as homogeneous coordinates in projective space, equipped with this algebraic structure, we end up with a natural parametrization of the rotation group (we denote non-zero reals with , and similarly ):
by means of the so-called ‘Rodrigues’ vector’ [11,12], or ‘vector-parameter’ [13], given as
Using this representation, one easily rewrites Rodrigues’ formula via the Cayley transform
or in other words, exclusively in terms of rational functions. The latter is no big surprise, as we essentially performed Euler’s trigonometric substitution on the so-called ‘rotation vector’ . More importantly, however, we now have a convenient faithful representation of , which circumvents the redundant parameters in matrix descriptions, the computational complexity of commutators and exponential maps, the topological singularities of Euler angles (leading to the well-known ‘gimbal lock’ problem), and shortcuts the process
involving unnecessary normalization. Instead, it resorts to central projection compatible with quaternion multiplication (denoted as ∨ in the commutative diagram shown below):
and the composition yields the group multiplication in in the form
which is clearly associative, and agrees with the usual matrix representation, i.e.,
and provides the trivial and inverse elements respectively as
In particular, for symmetric rotations (or ‘half-turns’, as they are often called since in that case ), which correspond to the infinite plane in our model space , the group action (7) and composition (10) can be defined using L’Hôpital’s rule or some other regularization technique.
Rodrigues’ parametrization has many advantages, including computational efficiency and clarity of the expressions, which make it suitable for both analytic calculations and numerical applications in various mechanical problems (see [11,14,15] for concrete examples). One of its best and not yet fully explored features, however, is the room for generalization. In particular, a central extension of the scalar field leads to the so-called ‘dual numbers’:
which in turn yields the dual Quaternions and the dual sphere playing the role of a spin covering for the Galilean group in 3D space. Following the transfer principle, one may also describe the latter via straightforward projection, with the dual Rodrigues’ vector
where is referred to as the dual axis and is the dual angle (cf [16]). Dual Quaternions, as well as their projective version, appear quite useful in kinematics and robotics (in particular, for screws, twists, and wrenches), computer vision, etc. (see [16,17,18]).
As for kinematics, straightforward differentiation of the Cayley transform (7) yields
for the angular velocity defined in the body (resp. lab) frame as , , while in the reverse one easily derives the Riccati equations for the vector-parameter [14]:
3. Fedorov’s Parametrization of the Lorentz Group
Another generalization, however, plays a central role in mathematical physics, namely the complex extension which Fedorov uses in its projective version to parametrize the Lorentz group (see [13]). It is based on the well-known realization of the proper Lorentz group via complex orthogonal (or unimodular) transformations, namely
which allows for straightforward implementation of Rodrigues’ parametrization for . In particular, the main results (2) and (10) remain valid for the complex projective parameter . Note, however, that in this case, the isometry group is not isomorphic to the whole projective space, as the quadric needs to be excluded. The realization
is also present in [13], along with a study of different applications of this approach in elementary particle physics. From a relativistic perspective, the real part of yields the rotational component of the transformation, while the imaginary one is associated with the rapidity of a Lorentz boost. Similarly, in the context of electrodynamics they provide the magnetic and electric field, respectively. If those two are mutually orthogonal, or in other words, the imaginary part of vanishes, we end up with a pseudo-rotation in a plane given by the Plücker embedding; i.e., one of the so-called Wigner little groups is realized, in particular yields an isotropic mapping, which simplifies the calculations greatly.
Fedorov’s approach to special relativity is also quite efficient on the infinitesimal level (see for example [19]). One particular example is the description of the Thomas precession (note that the Einstein rule for summation of velocities is already in (10) without the necessity of invoking any additional artificial constructions, such as gyrogroups), for which it provides a very elegant framework, associated with geometric phases (cf. [20]). This particular application cannot be found in [13], but it is not hard to derive from there. Far more disappointing is that Fedorov does not mention Quaternions even once in his otherwise well-written book, nor does he reference Rodrigues, who came up with the whole machinery. Perhaps for political reasons (the year is 1979, during the Cold War), mostly Soviet authors are cited. And in return, his contribution was never properly acknowledged in the Western literature, which is a pity since it has a lot of potential to offer. On the one hand, it makes the analogy between rigid body kinematics and electrodynamics quite evident (see [21]), while on the other, it allows for quite natural generalizations once we realize the underlying algebraic structure. For example, the dimensional projective construction, which turns out to be quite useful for decompositions in hyperbolic geometry and quantum scattering, similar to the Euler decomposition in the Euclidean case (cf. [15,20]). It is also straightforward to consider six-dimensional Lie groups with direct product local structure, such as , , and since their Lie algebras can be split into direct sums as
and the famous twistor correspondence allows for realization in higher dimensions via the Plücker embedding [22]. However, neglecting the Hamiltonian, and for that matter, the Cliffordian nature of this projective construction, restricts one’s ability to invoke its full potential. This more general framework was certainly not available to Rodrigues but may have been used by Fedorov in order to reveal the deeper structure behind its apparent computational benefits. One could also explore further generalizations, beyond the trivial embedding, related, for instance, to the spin groups and , or their real forms, e.g., and (see [1,21]). In the next section, we focus on that general framework introduced by W.K. Clifford in 1878.
4. The Contribution of Grassmann and Clifford
As it often happens in mathematics, the resolution of a problem comes naturally when it is placed in the proper context. That is essentially what Clifford did with Quaternions in [7]. He saw the link between Hamilton’s 1843 invention and Grassmann’s exterior algebras [23] that came around a year after. Grassmann was a German schoolteacher, a polymath like Hamilton, but quite unfamiliar to the scientific community, like Rodrigues. His Ausdehnungslehre von 1844 [23] laid the foundations of linear algebra and tensor and differential calculus that we use today as the language of modern geometry and physics. Nevertheless, that immense contribution was appreciated about a quarter of a century later, so when Clifford wrote his pioneering work on geometric algebras, Grassmann had been famous for just a few years but had also recently passed away. Clifford’s perspective on Quaternions was quite different from Hamilton’s: he viewed the imaginary units i, j, and k as bivectors, rather than vectors (Figure 1), which is way more beneficial for the applications in geometry and physics. He uses Grassmann’s anti-commutative exterior product, which is already present in Quaternions (remember that ), but also the commutative inner product () intertwined in what we refer to as geometric multiplication
defined above for vectors expanded in the orthonormal basis , but easily extended to higher grade objects, and by linearity, to Clifford polynomials. Thus, we end up with an algebra that is not -graded (like that of Grassmann) but -graded. In particular, the subset of even elements constitutes a subalgebra, associated with orientation-preserving transformations of the underlying vector space, and unit quaternions appear naturally in this context as spin cover of the orthogonal group in 3D space, the same way that complex numbers (which arise as the even sub-algebra for ) are associated with plane rotations.
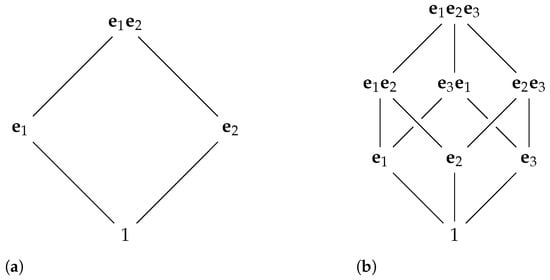
Figure 1.
Hamilton’s minimal lattice for (a) and Clifford’s Biquaternions containing as an even sub-algebra (b). Note that the pseudo-scalar in this case belongs to the center, so Rodrigues’ projective construction is well defined and simply yields the complex extension of the Euclidean rotation group.
In Clifford’s approach, one begins simply with an orthonormal basis in , rather than using mysterious imaginary units. Then, the geometric product is defined with
More generally, if are all different, is a k-vector in the geometric algebra , more precisely, a k-blade (k-vector monomial). Those constitute a basis in the -dimensional subspace of k-vectors usually denoted via grade projectors with . In particular, zero grade elements lie in the field of scalars (more generally, or any other field with characteristic not equal to 2 works as well), yields the vector space itself ; for , we have bi-vectors, which generate the group and, respectively, . Once established for the basis multi-vectors, Clifford multiplication extends to any element in the algebra via linearity and has the associative property, similar to Grassmann’s exterior product but unlike the ‘dot’ and ‘cross’ products derived from it. All geometric algebras have a lattice structure with scalars at the bottom and ascending grades, as depicted in Figure 1. The highest grade is also one-dimensional, spanned by the so-called ’pseudo-scalar’ , often denoted also as due to its obvious association with volumes. It plays an important role in associating k-vectors with -vectors (with ) via the linear mapping
known as Hodge duality in the context of differential calculus. However, like the multi-vector concept, it too came from Grassmann. Note also that by definition , and depending on the dimension and signature, the pseudo-scalar may belong to the center, i.e., commute with all other elements, thus acting as a complex or split-complex extension of the even sub-algebra . That is the case for example with Quaternions, defined as (we write instead of ), while the whole Clifford algebra of is isomorphic to : the algebra of complex matrices. It consists of real scalars, vectors (the so-called Pauli matrices ), bi-vectors (pure quaternions), and a pseudo-scalar, which behaves like the scalar imaginary unit . Thus, Clifford’s Biquaternions, which we use to describe electrodynamics and relativistic effects, are just a complex extension of , and unit norm restriction yields the well-known realization of . More generally, we have
which is quite convenient and reveals plenty of isomorphisms, such as . In order to study the structure of real Clifford algebras, one uses additional isomorphisms like
assuming of course that all dimensions above are non-negative. Yet, the key result here is
referred to as Bott periodicity, although this term originally appears in a different context. It allows for representing the whole classification in an table, known as the ‘Clifford chessboard’ (Table 1). It has apparent symmetries that have been thoroughly studied, and Quaternions play an essential role here as well, but this discussion goes beyond the scope of the present paper. Note, however, that geometric algebras over are much easier for classification since in this case all metric signatures are equivalent and the ’chessboard’ has only eight positions. We refer the reader to the classic literature (see [24]) for more details.

Table 1.
Structure of the geometric algebra for . Higher dimensions are derived using Bott periodicity. Here, denotes the algebra of matrices with coefficients in .
5. Maxwell, Dirac, and Weyl: Geometric Calculus in Modern Physics
Introducing covariant differentiation in a Clifford algebra, we obtain the notion of geometric calculus. Classical complex analysis provides a good example of this concept, but Hamilton developed its Quaternion version with the aid of his quite useful ’nabla’ operator
which was later stripped from its underlying algebraic structure by Heaviside and Gibbs, to be turned into what nowadays physicists and engineers know as gradient—the backbone of vector calculus. The well-known divergence and curl operators are then constructed artificially with the aid of the dot and cross product, respectively, as and , whereas in the Hamiltonian (or more generally, Cliffordian) framework, they appear naturally from
where is usually a vector field, but we can differentiate similarly various -valued functions acting on . Now, if is a (pseudo-)orthonormal basis in , we may consider the vector-valued linear differential operator (Einstein summation over repeated indices is assumed here and below for convenience, and ) acting on smooth mappings and define Clifford analyticity via the Cauchy–Riemann equation
Let us illustrate this with the classical example , where the pseudo-scalar plays the role of imaginary unit . Hence, and
yields the well-known Cauchy–Riemann equations in complex analysis. Similarly, if we take with playing the same role in the even sub-algebra (for both examples see Figure 1), it is not hard to see what analyticity looks like for Quaternion-valued functions of a vector argument , namely:
Since only the last term on the right is of grade three, we have , so there exists a vector potential such that , hence , which begins to resemble something familiar, but this is not how Maxwell’s equations are derived. The above formulation of ∇ takes place in the Pauli spin equation, where the vector basis in is given by the famous Pauli matrices or in the Dirac equation with the -matrices used as generators of the space–time algebra . Maxwell, on the other hand, allowed the differential operator to also have a scalar component, associated with a time derivative, i.e.,
and similarly would be its Clifford conjugate and the corresponding D’Alambert wave operator. Sometimes, D is called the Cauchy–Riemann–Fueter operator (or Weyl operator) and its kernel consists of analytic (also referred to as left-regular or left-monogenic) functions of , and t. Note that in the -complex plane
so it is another way to generalize the notion of holomorphic functions without embedding the algebra, working with the minimal representation only. This so-called ‘Fueter analyticity’ treats as rather than (like before) and works similarly on pure biquaternion-valued functions without the need to invoke . Let us denote
Then, yields (via grade projection) the equations of electrodynamics in vacuum as
Likewise, introducing external sources in the form , one obtains
which is the Maxwell’s system in a generic setting (with as physicists like to write). Note that the analogy with complex analysis does not end here: one also has Cauchy-type integral theorems for Quaternions [25], e.g., the Gauss law, with sources playing the role of residua. Let us consider a left-monogenic function with scalar and vector components. Then the condition is decomposed via grade projections to the system
which is easily satisfied if we choose to substitute and , in other words , and we end up with the wave equation for the potential . Hence, left-monogenic functions over (or ) naturally lead to the wave equation, just like holomorphic functions over invoke the Laplace equation. Note, however, that the above definition is not so useful if we are interested in spinors, in which case the Dirac operator needs to be applied instead. Also, as we have seen above, there are different but equivalent ways to define analyticity in . In particular, one may define it algebraically, demanding that infinitesimal transformations preserve the complex structure, which leads to a symmetry of the Jacobian, identical to the Cauchy–Riemann equations. As pointed out in [26], however, for Quaternions this condition is too restrictive and leaves us only with linear functions. For more details on Clifford analysis, we refer to [25,27,28].
To conclude this section, let us note that just like geometric algebras may be viewed as an extension to the Grassmann algebras, the Dirac operator defined above is a close analogue of the exterior derivative used in classical differential calculus and its applications. Thus, we may carry over our analysis from flat vector spaces to cotangent bundles of smooth manifolds. The geometric product of differential forms is not hard to define as both its inner and exterior components have already been provided by Grassmann. Indeed, if we chose a basis in the fiber of one-forms , such that for and (by contraction of indices), we easily extend the geometric product (20) to k–forms, namely if and , then . Similarly, the Dirac operator acts as a map from to , assuming where n is the dimension of the underlying manifold. In particular, for scalar functions (forms), it is identical to the exterior differential d, while on 1–forms one ends up with a divergence-like and a curl-like term. More generally, we have the decomposition known from Hodge–de Rham theory. This works also with tensor-valued forms and when the manifold is not flat, one introduces a connection for the parallel transport from one fiber to another in the usual manner following Cartan’s moving frame concept (cf. [29]). This is roughly the basis of Kähler’s differential calculus actively promoted by Vargas in recent decades [30,31]. Generalizing the covariant differential to Clifford bundles, as well as principal bundles, allows for algebraic treatment of the Yang–Mills models in analogy with Maxwell’s equations discussed above [32,33]. Clifford-Kähler and Quaternion calculi have also proven useful in quantum mechanics [34,35] and grand unification theories [36].
6. Hestenes and the Geometric Algebra Renaissance
One might ask why, after Clifford provided a unifying consistent framework for mathematical physics as early as 1878, the scientific community still refused to embrace that as a standard tool. Moreover, Clifford was not a marginal character at the time, like Grassmann or Rodrigues, but a well-recognized figure, although not as influential as Hamilton was in the previous decades. The trouble is he died the year after his big discovery was made, tragically in his prime at age 33, leaving no followers behind him to keep pushing for change like Tait did after Hamilton’s death. So, this mass movement had to wait another century until a new charismatic figure showed up gathering momentum. That figure was David Hestenes—an American mathematical physicist who devoted much of his life to the development and promotion of Clifford’s geometric algebras and was probably the first in that field who actually managed to establish a school of followers, starting with Lasenby, Doran, Gull, and many others joining over the years. But, what allowed Hestenes to succeed where Hamilton, Tait, and Clifford had failed? Apart from personal traits, devotion, and productivity, there were objective circumstances facilitating the resurrection of nineteenth-century mathematical concepts. From a physical perspective, that was the time of ‘grand unification’ attempts—the effort to replace the standard model with a theory that allows for general relativity and quantum mechanics to co-exist peacefully. One would expect the success of that endeavor to depend on some sort of universal low-level description of phenomena, or ‘unifying language’ as Lasenby puts it in [37]. Since Felix Klein’s Erlangen program, the group-theoretic approach has been the main candidate for that role, and dominant in mathematical physics. Apart from it, the least action principle modern physics relies on is certainly universal but not so much ‘low-level’, while, for instance, topology used in string theory seems to be as low-level as one may obtain, but probably not so universal. Geometric algebras are also ideal for compact simplified descriptions and quite easy to grasp, which is highly appreciated with the increasing complexity of physical models and the information overload in students’ heads nowadays. That was not the case at the dawn of the twentieth century when it took much more time for new ideas to propagate and there were already enough puzzling sensations in theoretical physics. On the other hand, much effort was directed at purging the theory from superstition and unnecessary artifacts (like the luminiferous aether), and unfortunately, Quaternions fell innocent victim to that purge.
Without underestimating any of these factors, however, we should admit that the greatest advantage Hestenes had over Hamilton and Clifford was modern technology. On the one hand, this provided him with the means of communication for his ideas to reach many people in a short amount of time, but most importantly, the technological development that demands the continual update and refinement of the mathematical description. When Hamilton invented Quaternions, electromagnetism (one of the major applications) was still unrevealed to the world. Similarly, Clifford did not live long enough to see the profound importance of his geometric algebras in mathematical physics in the twentieth century: Einstein’s special relativity, Heisenberg’s quantum mechanics, Yang–Mills’ gauge theories, etc. And to make things worse, physicists like Pauli and Dirac, who needed Clifford’s algebras, had to re-invent them as they did not know such a thing existed. Hestenes, on the other hand, had all this at his disposal and thus could see the big picture, comparing different models and mathematical tools supporting them. Moreover, his followers have plenty of interesting applications to work on, arising from contemporary engineering problems in diverse fields of science and technology. The rapid development of robotics, computer graphics and vision, 3D simulations, and even artificial intelligence, boosts the development of geometric algebras for purely practical reasons, as they prove to be an efficient tool in all these (and many more) applications. This includes good old Quaternions, especially their dual version introduced by Clifford, which are perfectly suited for the description of rigid body motion and multi-joint systems [38], but also new developments like the so-called Projective Geometric Algebra (PGA) and Conformal Geometric Algebra (CGA) that have quite impressive and useful features too (see [39,40,41,42]).
CGA of is simply the geometric algebra of the conformal group —for the engineering applications one is usually interested in with generators for and for the extra dimensions, with . Although the structure of this object is no different than what we already know from Table 1, its use in conformal setting is different: here we begin with a stereographic projection from , followed by projective embedding in . Interpreting the coefficients on the right as homogeneous coordinates, we can get rid of the denominator and rewrite the result as
where the two null vectors and (satisfying , ) are defined as
Note that in this manner, points in three-dimensional Euclidean space are mapped to the isotropic ‘light cone’ in , since . Then, spheres and planes (resp. lines and circles) can be obtained as intersections via the so-called ‘meet’ or, alternatively, as linear spans via the ‘join’; e.g., a circle is represented as the join of three points and if one of these points is at infinity, we end up with a straight line, connecting the other two . The ‘join’ given by the familiar wedge product can also be used for incidence relations: for example, a point A belongs to the plane if and only if . This makes CGA appropriate for projective geometry, but the Euclidean distance is also encoded in it, as we have .
The true power of CGA, however, comes from geometric transformations, and in particular the possibility to reflect with respect to both flat and spherical surfaces. It is of crucial importance in optics, robotics, and computer vision (see [42]), but certainly has its benefits in the description of non-Euclidean geometry in terms of Möbius groups. If one is interested only in the study of flats and rigid motion, however, it is simpler to use PGA, which is a subalgebra of CGA, deprived of conics [41]. PGA is essentially the extra dimension being spanned by the null vector , and it is convenient to use the Hodge duality in to represent points as 3-vectors, lines as 2-vectors and planes as 1-vectors. A point is introduced with its homogeneous coordinates in the basis of 3-vectors as
and the projection plane is ; i.e., the Cartesian coordinates are , while yields a ‘point at infinity’. Similarly, lines are given by means of their Plücker coordinates
with and denoting the so-called displacement and moment vector, respectively. Finally,
represents a plane in , and the incidence relation is now given as instead of the usual . Using the duality in , we represent Euclidean ‘flats’ as
and we can define the ‘meet’ and ‘join’ satisfying the famous De Morgan laws
where ∗ requires inversion outside of PGA (but within CGA) [40,41] since is ill defined due to the null vector . The former is useful in finding intersections of objects, e.g., for a line ℓ and a plane , we have for the point , while the latter generates linear spans of objects, e.g., yields the line connecting P and Q.
Note that since we use the dual representation of PGA, the ‘meet’ is now given by the progressive product, and the ‘join’ by the regressive one, contrary to what we had in CGA. Similarly, the ‘origin’ in CGA has become an infinite element in PGA, and any point with , e.g., the intersection of two parallel lines, is a point at infinity. It is fair to say, however, that both algebras have their direct and dual representations, but the latter is commonly used for practical reasons,; e.g., the intersection problem is rather straightforward, without invoking cumbersome linear systems. Once the basic construction is established, we can play with various algebraic operations and explore their geometric effect. For example, in this representation yields a line ℓ perpendicular to and incident with P. Similarly, returns the projection of P onto , and its reflection with respect to [40]. One may also use points or lines as reflectors, and in the latter setting the exponential map yields a rigid motion which corresponds to either a rotation (), translation (), or a screw displacement if ℓ is not a blade, i.e., . In this way, we cover the Galilean motions one may otherwise describe simply with dual Quaternions . PGA and CGA, however, can accomplish much more due to their projective nature: they work quite efficiently in many engineering applications and because of that have become increasingly popular in the recent decades (see [40,41,42]). This development is a product of the twenty-first century and an area of active current research. However, what Hestenes and his followers did based on Clifford, was inspired by Hamilton’s . Thus, the battle for Quaternions continues to this day.
7. Discussion
It is not clear what the future holds for geometric algebras and geometric calculus, but in about one and a half centuries (almost two since the invention of Quaternions) they have proven a quite useful, efficient, and powerful tool in the mathematical description of various problems arising in different branches of geometry, physics, and engineering. After many decades of undeserved neglect, Quaternions and their many generalizations were resurrected by the vast hunger for more accurate methods and faster algorithms imposed by the technological development of the twenty-first century. It is quite interesting to note that theoretical physics, which is the most natural context for Hamilton’s and Clifford’s algebras, did not embrace them at the times of its peak flourishing but does so more and more as it sinks into an existential crisis, struggling to find its ‘unified language’. Perhaps geometric algebras will play an important role in the resolution of this problem, as they do already in the slow but irreversible reunion of fundamental and applied science in our era.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
I would like to express my gratitude to Petko Nikolov, who first got me intrigued by the subject; Jose Vargas, who invited me into the community; and Rafal Ablamowicz, who showed me a deeper level of understanding beneath the user-friendly welcoming surface of geometric algebras.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PGA | Projective Geometric Algebra |
| CGA | Conformal Geometric Algebra |
References
- Dray, T.; Manogue, C. The Geometry of the Octonions; World Scientific: Singapore, 2015. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Macmillan and Co.: London, UK, 1873; Volume 1. [Google Scholar]
- Hamilton, W.R. Lectures on Quaternions; Hodges and Smith: Dublin, Ireland, 1853. [Google Scholar]
- Gibbs, J.W.; Wilson, E.B. Vector Analysis; Charles Scribner’s Sons: New York, NY, USA, 1901. [Google Scholar]
- Heaviside, O. Electromagnetic Theory; “The Electrician” Printing and Publishing Company Ltd.: London, UK, 1893. [Google Scholar]
- Tait, P.G. An Elementary Treatise on Quaternions; Cambridge University Press: London, UK, 1890. [Google Scholar]
- Clifford, W. Applications of Grassmann’s extensive algebra. Am. J. Math. 1878, 1, 350–358. [Google Scholar] [CrossRef]
- Altmann, S. Hamilton, Rodrigues, and the quaternion scandal. Math. Mag. 1989, 62, 291–308. [Google Scholar] [CrossRef]
- Pujol, J. Hamilton, Rodrigues, Gauss, Quaternions, and Rotations: A Historical Reassessment. Commun. Math. Anal. 2012, 13, 1–14. [Google Scholar]
- Rodrigues, O. Des lois géométriques qui regissent les déplacéments d’un systéme solide dans l’espace, et de la variation des coordonnées provenant de ces déplacéments considérés indépendamment des causes qui peuvent les produire. J. Math. Pures Appl. 1840, 5, 380–440. [Google Scholar]
- Piña, E. Rotations with Rodrigues’ Vector. Eur. J. Phys. 2011, 32, 1171–1178. [Google Scholar] [CrossRef]
- Bauchau, O.; Trainelli, L.; Bottaso, C. The Vectorial Parameterization of Rotation. Nonlinear Dyn. 2003, 32, 71–92. [Google Scholar] [CrossRef]
- Fedorov, F. The Lorentz Group; Nauka: Moscow, USSR, 1979. (In Russian) [Google Scholar]
- Mladenova, C. Approach to Description of a Rigid Body Motion. C. R. Acad. Sci. Bulg. 1985, 38, 1657–1660. [Google Scholar]
- Brezov, D.; Mladenova, C.; Mladenov, I. A Decoupled Solution to the Generalized Euler Decomposition Problem in R3 and R2,1. J. Geom. Symmetry Phys. 2014, 33, 47–78. [Google Scholar]
- Wittenburg, J. Kinematics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Farias, J.G.; De Pieri, E.; Martins, D. A Review on the Applications of Dual Quaternions. Machines 2024, 12, 402. [Google Scholar] [CrossRef]
- Valverde, A.; Tsiotras, P. Spacecraft Robot Kinematics Using Dual Quaternions. Robotics 2018, 7, 64. [Google Scholar] [CrossRef]
- Kuvshinov, V.; Tho, N. Local Vector Parameters of Groups, The Cartan Form and Applications to Gauge and Chiral Field Theory. Phys. Elem. Part. Nucl. 1994, 25, 603–648. [Google Scholar]
- Brezov, D.; Mladenova, C.; Mladenov, I. Wigner Rotation and Thomas Precession: Geometric Phases and Related Physical Theories. J. Korean Phys. Soc. 2015, 66, 1656–1663. [Google Scholar] [CrossRef]
- Brezov, D. On Complex Kinematics and Relativity. Adv. Appl. Clifford Algebr. 2022, 32, 38. [Google Scholar] [CrossRef]
- Brezov, D. Higher-Dimensional Representations of SL2 and its Real Forms via Plücker Embedding. Adv. Appl. Clifford Algebr. 2017, 27, 2375–2392. [Google Scholar] [CrossRef]
- Grassmann, H. Die lineale Ausdehnungslehre, ein neuer Zweig der Mathematik; (von 1844); Verlag von Otto Wigand: Leipzig, Germany, 1878. [Google Scholar]
- Lounesto, P. Clifford Algebras and Spinors; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Delanghe, R. Clifford Analysis: History and Perspective. Comput. Methods Funct. Theory 2001, 1, 107–153. [Google Scholar] [CrossRef]
- De Leo, S.; Rotelli, P.P. Quaternionic Analyticity. Appl. Math. Lett. 2003, 16, 1077–1081. [Google Scholar] [CrossRef]
- Jefferies, B. The Monogenic Functional Calculus. In Operator Theory; Alpay, D., Ed.; Springer: Basel, Switzerland, 2015. [Google Scholar]
- Hestenes, D.; Garret Sobczyk, G. Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Ivey, T.; Landsberg, J. Cartan for Begginers: Differential Geometry via Moving Frames and Exterior Differential Systems; American Mathematical Society: Providence, RI, USA, 2003. [Google Scholar]
- Vargas, J.G. Differential Geometry for Physicists and Mathematicians; World Scientific: Singapore, 2014. [Google Scholar]
- Vargas, J.G. The Foundations of Quantum Mechanics and the Evolution of the Cartan-Kähler Calculus. Found. Phys. 2008, 38, 610–647. [Google Scholar] [CrossRef]
- Shirokov, D. Covariantly Constant Solutions of the Yang–Mills Equations. Adv. Appl. Clifford Algebr. 2018, 28, 53. [Google Scholar] [CrossRef]
- Shirokov, D. On Solutions of the Yang-Mills Equations in the Algebra of h-Forms. J. Phys. Conf. Ser. 2021, 2099, 012015. [Google Scholar] [CrossRef]
- Danielewski, M.; Sapa, L. Foundations of the Quaternion Quantum Mechanics. Entropy 2020, 22, 1424. [Google Scholar] [CrossRef] [PubMed]
- Adler, S. Quaternionic Quantum Mechanics and Quantum Fields; Oxford University Press Inc.: New York, NY, USA, 1995. [Google Scholar]
- Castro, C. A Clifford algebra-based grand unification program of gravity and the Standard Model: A review study. Can. J. Phys. 2014, 92, 1501–1527. [Google Scholar] [CrossRef]
- Lasenby, A.N. Geometric Algebra as a Unifying Language for Physics and Engineering and Its Use in the Study of Gravity. Adv. Appl. Clifford Algebr. 2017, 27, 733–759. [Google Scholar] [CrossRef]
- Valverde, A.; Tsiotras, P. Dual Quaternion Framework for Modeling of Spacecraft-Mounted Multibody Robotic Systems. Front. Robot. AI 2018, 5, 128. [Google Scholar] [CrossRef]
- Hitzer, E. Introduction to Clifford’s Geometric Algebra. SICE J. Control. Meas. Syst. Integr. 2011, 4, 001–011. [Google Scholar]
- Dorst, L.; De Keninck, S. A Guided Tour to the Plane-Based Geometric Algebra PGA. 2022. Available online: https://bivector.net/PGA4CS.html (accessed on 12 February 2025).
- Hrdina, J.; Návrat, A.; Vašik, P.; Dorst, L. Projective Geometric Algebra as a Subalgebra of Conformal Geometric algebra. Adv. Appl. Clifford Algebr. 2021, 31, 18. [Google Scholar] [CrossRef]
- Bayro-Corrochano, E. Geometric Computing: For Wavelet Transforms, Robot Vision, Learning, Control and Action; Springer: London, UK, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).