On the Asymptotic Normality of the Method of Moments Estimators for the Birnbaum–Saunders Distribution with a New Parametrization

Abstract

This study investigates the asymptotic properties of method-of-moments estimators for the Birnbaum–Saunders distribution under a newly proposed parametrization. Theoretical derivations establish the asymptotic normality of these estimators, supported by explicit expressions for the mean vector and variance–covariance matrix. Simulation studies validate these results across various sample sizes and parameter values. A practical application is demonstrated through modeling cumulative rainfall data from northeastern Thailand, highlighting the distribution’s suitability for extreme weather prediction.

1. Introduction

The two-parameter Birnbaum–Saunders distribution, introduced by Birnbaum and Saunders [1], was originally developed as a model for failure times resulting from fatigue under cyclic load. Over time, this distribution has found widespread application in reliability theory, particularly in modeling the lifetimes of objects where failure results from the propagation of fatigue cracks. In recent years, climate change has emerged as a pressing concern, especially in tropical and humid regions, where severe flooding due to continuous rainfall during the rainy season has become increasingly common. To address this issue, we propose fitting the total rainfall data from consecutive rainy days by the Birnbaum–Saunders distribution. This approach aims to improve the predictions of rainfall events that could lead to flooding in agricultural areas. For a comprehensive discussion of the statistical theory, methodology, and other applications of the Birnbaum–Saunders distribution, we recommend the book by V. Leiva [2]. In this research paper, we present the theoretical framework, validate its accuracy using simulation data, and apply it to real rainfall data from northeastern Thailand.

A continuous random variable X has a Birnbaum–Saunders distribution if X has the following cumulative distribution function:

$$F_X(x;\alpha ,\beta )=1-\Phi \left[{\displaystyle \frac{1}{\alpha }}\left(\sqrt{{\displaystyle \frac{\beta }{x}}}-\sqrt{{\displaystyle \frac{x}{\beta }}}\right)\right],x>0,$$

where $\Phi (·)$ is the cumulative distribution function of the standard normal distribution. The density function of the Birnbaum–Saunders distribution is

$$f_X(x;\alpha ,\beta )={\displaystyle \frac{\sqrt{x/\beta }+\sqrt{\beta /x}}{2\sqrt{2\pi }\alpha x}}exp\left\{-{\displaystyle \frac{{(\sqrt{x/\beta }-\sqrt{\beta /x})}^2}{2{\alpha }^2}}\right\}.$$

The parameters $\alpha >0$ and $\beta >0$ are the shape and scale parameters, respectively. The density function is a mixture (with equal weights) of the Inverse Gaussian and the Length Biased Inverse Gaussian density functions. We call it the classical parametrization; it was introduced in Birnbaum and Saunders [1].

In Ahmed et al. [3], a new parametrization of the Birnbaum–Saunders distribution was proposed. A continuous random variable X has a Birnbaum–Saunders distribution, denoted $X\sim \mathrm{BirSau}(\lambda ,\mu )$ if X has the cumulative distribution function as

$$F_X(x;\mu ,\lambda )=1-\Phi \left({\displaystyle \frac{\lambda }{\sqrt{x}}}-\mu \sqrt{x}\right),x>0,$$

where $\lambda >0$ and $\mu >0$ are the parameters. The density function of the Birnbaum–Saunders distribution after the re-parametrization is as follows:

$$f_X(x;\mu ,\lambda )={\displaystyle \frac{1}{2\sqrt{2\pi }}}\left({\displaystyle \frac{\lambda }{x\sqrt{x}}}+{\displaystyle \frac{\mu }{\sqrt{x}}}\right)exp\left\{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\lambda }{\sqrt{x}}}-\mu \sqrt{x}\right)}^2\right\},x>0.$$

A new parametrization of the Birnbaum–Saunders distribution is closely related to its applications in engineering and reliability: consider a metallic sample, which has the form of a rectangular plate of thickness h and is fixed on two sides; suppose there is a cyclic loading, which results in the development of a crack. The Birnbaum–Saunders distribution models the time at which the crack achieves the critical value h. Importantly, the new re-parametrization fits the physics of studying phenomena since the proposed parameters $\lambda$ and $\mu$ correspond to the thickness h of the sample and cyclic loading on the plate, respectively; see Ahmed et al. [3].

At the same time, the classical parametrization with $\alpha$ and $\beta$ is more suitable for investigating pure statistical properties of the Birnbaum–Saunders distribution due to their direct interpretation as the shape and scale parameters. Because of wide applications of the Birnbaum–Saunders distribution in engineering and reliability, we believe that a deeper understanding of its physical interpretation is more important. Therefore, this article focuses on using the new parametrization for a more meaningful representation. Moreover, as it is established in Ahmed et al. [3], the interrelations between the classical parameters $\alpha ,\beta$ and new parameters $\lambda$ and $\mu$ are as follows:

$$\begin{array}{ccc}\lambda & ={\displaystyle \frac{\sqrt{\beta }}{\alpha }},\mu & ={\displaystyle \frac{1}{\alpha \sqrt{\beta }}},\\ \alpha & ={\displaystyle \frac{1}{\sqrt{\mu \lambda }}},\beta & ={\displaystyle \frac{\lambda }{\mu }}.\end{array}$$

(1)

We note that the relationship between classical and new parameters is highly non-linear, which makes it impossible to convert the inference process from the classical parametrization to the new one. This is the main reason why we develop estimation methods in terms of the new parameters $\lambda$ and $\mu$. Another reason for us to consider the new parametrization is in the elegant beauty of the formulae. As an example, we present the following proposition (note that for the classical parametrization, this formula is much more complicated).

Proposition 1. 

If random variable $X\sim \mathrm{BirSau}(\lambda ,\mu )$, then its reciprocal ${\displaystyle \frac{1}{X}}\sim \mathrm{BirSau}(\mu ,\lambda )$.

Proof. 

The cumulative distribution function of the reciprocal for $x>0$ is

$$\begin{array}{cc}\hfill F_{1/X}\left(x\right)& =\mathbb{P}\left({\displaystyle \frac{1}{X}}\le x\right)=\mathbb{P}\left(X\ge {\displaystyle \frac{1}{x}}\right)=1-\left(1-\Phi \left({\displaystyle \frac{\lambda }{\sqrt{\frac{1}{x}}}}-\mu \sqrt{{\displaystyle \frac{1}{x}}}\right)\right)\hfill \\ \hfill & =\Phi \left({\displaystyle \frac{\lambda }{\sqrt{\frac{1}{x}}}}-\mu \sqrt{{\displaystyle \frac{1}{x}}}\right)=1-\Phi \left({\displaystyle \frac{\mu }{\sqrt{x}}}-\lambda \sqrt{x}\right).\hfill \end{array}$$

The last expression is the cumulative distribution function of the $\mathrm{BirSau}(\mu ,\lambda )$ distribution. □

The maximum likelihood estimators of the classical and new parameters of the Birnbaum–Saunders distribution cannot be derived in closed form; see Section 2 in Ahmed et al. [3]. Because of that, we focus on the method of moments estimators. We focus on analyzing the probability distribution of the estimators obtained through the method of moments in the case of large samples. By applying the delta method, we aim to show that as the sample size increases, both moment-method estimators converge to a bivariate normal distribution. Furthermore, we derive the formula for the mean vector and the variance–covariance matrix of these estimators.

The method-of-moments estimators for the classical parametrization are derived and investigated in refs. [4,5]. As we mentioned above, due to the highly non-linear nature of the relationship between classical and new parameters, it is impossible to convert the inference process from the classical parametrization to the new one. At the same time, the new parametrization has remarkable advantages that we show throughout the manuscript.

We also note an interesting article, Zhang, Chen, and Yang [6], where the parameters of the Birnbaum–Saunders distribution are estimated using simple random sampling and ranked set sampling is considered.

2. Method of Moments Estimation for the Parameters of Birnbaum–Saunders Distribution

The method-of-moments estimators for the parameters $\lambda$ and $\mu$ of the Birnbaum–Saunders distribution were introduced by Ahmed et al. [3]. However, their derivations were not provided, and asymptotic variances were incorrectly calculated. To address these issues, we derive the estimators and their properties. As a starting point, it is essential to understand the mean of the Birnbaum–Saunders distribution. For completeness, we also present the variance, even though it is not directly required for deriving the method-of-moment estimators.

Proposition 2. 

If random variable $X\sim \mathrm{BirSau}(\lambda ,\mu )$; then, its mean and variance are

$$\mathbb{E}\left(X\right)={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}} \mathrm{and}\mathrm{Var}\left(X\right)={\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}}.$$

Proof. 

The proposition can be proven by a direct evaluation of the mean and variance using the density function, but it is simpler to use the formulae for the mean and variance of the Birnbaum–Saunders distribution with the classical parametrization derived in [1]. That is, if a random variable X has the Birnbaum–Saunders distribution with the classical parameters $\alpha$ and $\beta$, then

$$\mathbb{E}\left(X\right)=\beta \left(1+{\displaystyle \frac{1}{2}}{\alpha }^2\right) \mathrm{and}\mathrm{Var}\left(X\right)={\left(\alpha \beta \right)}^2\left(1+{\displaystyle \frac{5}{4}}{\alpha }^2\right).$$

Taking into consideration the relation between the classical and new parameters in Equation (1), we obtain

$$\begin{array}{cc}\hfill \mathbb{E}\left(X\right)& ={\displaystyle \frac{\lambda }{\mu }}\left(1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{1}{\sqrt{\mu \lambda }}}\right)}^2\right)={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}},\hfill \\ \hfill \mathrm{Var}\left(X\right)& ={\left({\displaystyle \frac{1}{\sqrt{\mu \lambda }}}\times {\displaystyle \frac{\lambda }{\mu }}\right)}^2\left(1+{\displaystyle \frac{5}{4}}{\left({\displaystyle \frac{1}{\sqrt{\mu \lambda }}}\right)}^2\right)={\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}},\hfill \end{array}$$

compared with Equation (6) in Ahmed et al. [3]. □

Let $X_1,X_2,\dots ,X_n$ be a sample of size n from the $\mathrm{BirSau}(\lambda ,\mu )$ distribution. The classical method of moments consists of equating a sample and theoretical moments of distribution. In our case, it is simpler not to consider the first and second moments but to consider the first and reciprocal moments, namely, to consider two sample moments:

$$\overline{X}=T_1={\displaystyle \frac{1}{n}}\sum _{k=1}^n{X}_k \mathrm{and}{T}_2={\displaystyle \frac{1}{n}}\sum _{j=1}^n{\displaystyle \frac{1}{X_j}}.$$

The statistic $T_2$ can be considered as a sample mean of the reciprocals, so we can also denote it by $\overline{X^{-1}}$.

Proposition 3. 

The method-of-moment estimators of the $\mathrm{BirSau}(\lambda ,\mu )$ distribution is

$$\widehat{\lambda }={\displaystyle \frac{1}{\sqrt{2}}}{(T_2-T_2^{1/2}{T}_1^{-1/2})}^{-1/2} \mathrm{and} \widehat{\mu }={\displaystyle \frac{1}{\sqrt{2}}}{(T_1-T_1^{1/2}{T}_2^{-1/2})}^{-1/2},$$

where $T_1={\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{X}_k \mathrm{and} T_2={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{\displaystyle \frac{1}{X_j}}$.

Proof. 

Note that by Propositions 1 and 2,

$$\mathbb{E}\left({\displaystyle \frac{1}{X}}\right)={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}.$$

(2)

The method-of-moments equations can be written as

$$\begin{array}{cc}\hfill \mathbb{E}\left(X\right)& =T_1\hfill \\ \hfill \mathbb{E}\left({\displaystyle \frac{1}{X}}\right)& =T_2,\hfill \end{array}$$

Or by Propositions 2 and (2) as

$$\begin{array}{cc}\hfill {\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}& =T_1\hfill \\ \hfill {\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}& =T_2.\hfill \end{array}$$

To solve this system of equations for $\lambda$ and $\mu$, we divide the first equation by the second one to obtain

$${\displaystyle \frac{{\lambda }^2}{{\mu }^2}}={\displaystyle \frac{T_1}{T_2}} \mathrm{o}\mathrm{r} \lambda =\sqrt{{\displaystyle \frac{T_1}{T_2}}}\mu .$$

Substituting the last expression for $\lambda$ into the first expression, we have

$${\displaystyle \frac{2\sqrt{\frac{T_1}{T_2}}{\mu }^2+1}{2{\mu }^2}}=T_1 \mathrm{o}\mathrm{r} {\mu }^2\left(T_1-\sqrt{{\displaystyle \frac{T_1}{T_2}}}\right)={\displaystyle \frac{1}{2}}.$$

Solving for $\mu$:

$$\widehat{\mu }=\sqrt{{\displaystyle \frac{\sqrt{T_2}}{2(T_1\sqrt{T_2}-\sqrt{T_1})}}}={\displaystyle \frac{1}{\sqrt{2}}}{(T_1-T_1^{1/2}{T}_2^{-1/2})}^{-1/2}.$$

Knowing that $\lambda =\sqrt{{\displaystyle \frac{T_1}{T_2}}}\mu$, we obtain

$$\widehat{\lambda }=\sqrt{{\displaystyle \frac{T_1}{T_2}}}{\displaystyle \frac{1}{\sqrt{2}}}{(T_1-T_1^{1/2}{T}_2^{-1/2})}^{-1/2}={\displaystyle \frac{1}{\sqrt{2}}}{(T_2-T_2^{1/2}{T}_1^{-1/2})}^{-1/2}.$$

□

Remark 1. 

Note that Ahmed at al. [3] presents the method of moments estimators as

$$\widehat{\lambda }=\sqrt{{\displaystyle \frac{\sqrt{T_1}}{2T(\sqrt{T}-1)}}} \mathrm{and}\widehat{\mu }=\sqrt{{\displaystyle \frac{\sqrt{T}}{2T_1(\sqrt{T}-1)}}},$$

where $T=T_1{T}_2$. Simple algebra shows that these formulae and formulae from Proposition 3 are the same. We would like to use the formulae presented in Proposition 3 to facilitate differentiation. It also shows the advantage of the new parametrization; the formulae for $\widehat{\lambda }$ and $\widehat{\mu }$ are beautifully symmetric with respect to $T_1$ and $T_2$. The method-of-moments estimators for the classical parametrization with α and β do not have such symmetry.

3. On the Joint Asymptotic Normality of the Method of Moments Estimators of the Parameters of the Birnbaum–Saunders Distribution

Somehow, the joint asymptotic normality of $\widehat{\lambda }$ and $\widehat{\mu }$ is not discussed in Ahemd et al. [3], not looking at a wrong attempt to calculate the asymptotic variances (mean squared errors) of these estimators.

The classical textbooks that mention the delta method are [7,8]. In order to apply the delta method, we note that the basic statistics are $T_1={\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{X}_k$ and $T_2={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{\displaystyle \frac{1}{X_j}}$. Our first step is to establish the joint asymptotic normality of the basis statistics.

Proposition 4. 

Statistics $T_1$ and $T_2$ are jointly asymptotically normal with mean $\left(\begin{array}{c}{\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\\ {\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\end{array}\right)$ and the covariance matrix

$$\tilde{\Sigma }={\displaystyle \frac{1}{4}}\left(\begin{array}{cc}{\displaystyle \frac{4\lambda \mu +5}{{\mu }^4}}& -{\displaystyle \frac{4\lambda \mu +1}{{\lambda }^2{\mu }^2}}\\ -{\displaystyle \frac{4\lambda \mu +1}{{\lambda }^2{\mu }^2}}& {\displaystyle \frac{4\lambda \mu +5}{{\lambda }^4}}\end{array}\right);$$

That is, the distribution of the random vector $\sqrt{n}\left(\begin{array}{c}{T}_1-{\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\\ T_2-{\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\end{array}\right)$ converges in distribution as $n\to \infty$ to the bivariate normal distribution

$$N\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\tilde{\Sigma }\right).$$

Proof. 

Let $V_i=X_i$ and $W_i={\displaystyle \frac{1}{X_i}}$; then, $T_1=\overline{V}$ and $T_2=\overline{W}$. From Proposition 2, we know that

$$\mathbb{E}\left(V_i\right)={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}} \mathrm{and}\mathrm{Var}\left(V_i\right)={\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}},$$

and by Propositions 1 and 2 (see also (2)),

$$\mathbb{E}\left(W_i\right)={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}} \mathrm{and}\mathrm{Var}\left(W_i\right)={\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}}.$$

We also need the covariance:

$$\mathrm{Cov}(V_i,W_i)=\mathbb{E}\left(V_i{W}_i\right)-\mathbb{E}\left(V_i\right)\mathbb{E}\left(W_i\right)=1-{\displaystyle \frac{{(2\lambda \mu +1)}^2}{4{\lambda }^2{\mu }^2}}=-{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}},$$

where we use the fact that $\mathbb{E}\left(V_i{W}_i\right)=\mathbb{E}\left(X_i{\displaystyle \frac{1}{X_i}}\right)=\mathbb{E}\left(1\right)=1$.

Returning to statistics $T_1$ and $T_2$, we can summarize these findings as follows:

$$\begin{array}{ccc}\hfill & \mathbb{E}\left(T_1\right)={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}},\hfill & \hfill \mathbb{E}\left(T_2\right)={\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}},\\ \hfill & \mathrm{Var}\left(T_1\right)={\displaystyle \frac{1}{n}}{\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}},\hfill & \hfill \mathrm{Var}\left(T_1\right)={\displaystyle \frac{1}{n}}{\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}},\\ \hfill & \mathrm{Cov}(T_1,T_2)=-{\displaystyle \frac{1}{n}}{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}},\hfill \end{array}$$

or, in matrix form:

$$\mathbb{E}\left(\begin{array}{c}{T}_1\\ T_2\end{array}\right)=\left(\begin{array}{c}{\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\\ {\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}}\end{array}\right),\mathrm{Cov}\left(\begin{array}{c}{T}_1\\ T_2\end{array}\right)={\displaystyle \frac{1}{n}}\left(\begin{array}{cc}{\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}}& -{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}}\\ -{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}}& {\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}}\end{array}\right).$$

By the Bivariate Central Limit Theorem (see [8], Theorem 5.2.1), the distribution of the random vector is represented by the following.

$$\sqrt{n}\left(\begin{array}{c}{T}_1-{\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\\ T_2-{\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\end{array}\right)$$

converges in distribution as $n\to \infty$ to the bivariate normal distribution:

$$N\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\displaystyle \frac{4\lambda \mu +5}{4{\mu }^4}}& -{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}}\\ -{\displaystyle \frac{4\lambda \mu +1}{4{\lambda }^2{\mu }^2}}& {\displaystyle \frac{4\lambda \mu +5}{4{\lambda }^4}}\end{array}\right)\right).$$

□

Our next step is to apply the famous delta method. By Proposition 3, $\widehat{\lambda }={\displaystyle \frac{1}{\sqrt{2}}}{(T_2-T_2^{1/2}{T}_1^{-1/2})}^{-1/2}$ and $\widehat{\mu }={\displaystyle \frac{1}{\sqrt{2}}}{(T_1-T_1^{1/2}{T}_2^{-1/2})}^{-1/2}$; hence, we introduce two functions of two variables:

$$\begin{array}{cc}\hfill g_1(t_1,t_2)& ={\displaystyle \frac{1}{\sqrt{2}}}{(t_2-t_2^{1/2}{t}_1^{-1/2})}^{-1/2},\hfill \\ \hfill g_2(t_1,t_2)& ={\displaystyle \frac{1}{\sqrt{2}}}{(t_1-t_1^{1/2}{t}_2^{-1/2})}^{-1/2}.\hfill \end{array}$$

Then, our estimators can be expressed in terms of statistics $T_1$ and $T_2$ as $\widehat{\lambda }=g_1(T_1,T_2)$ and $\widehat{\mu }=g_2(T_1,T_2)$.

Partial derivatives of the functions are

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial g_1(t_1,t_2)}{\partial t_1}}& =-{\displaystyle \frac{1}{4\sqrt{2}}}{(t_2-t_2^{1/2}{t}_1^{-1/2})}^{-3/2}{t}_2^{1/2}{t}_1^{-3/2},\hfill \\ \hfill {\displaystyle \frac{\partial g_1(t_1,t_2)}{\partial t_2}}& =-{\displaystyle \frac{1}{2\sqrt{2}}}{(t_2-t_2^{1/2}{t}_1^{-1/2})}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{t}_2^{-1/2}{t}_1^{-1/2}\right),\hfill \\ \hfill {\displaystyle \frac{\partial g_2(t_1,t_2)}{\partial t_1}}& =-{\displaystyle \frac{1}{2\sqrt{2}}}{(t_1-t_1^{1/2}{t}_2^{-1/2})}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{t}_1^{-1/2}{t}_2^{-1/2}\right),\hfill \\ \hfill {\displaystyle \frac{\partial g_2(t_1,t_2)}{\partial t_2}}& =-{\displaystyle \frac{1}{4\sqrt{2}}}{(t_1-t_1^{1/2}{t}_2^{-1/2})}^{-3/2}{t}_1^{1/2}{t}_2^{-3/2}.\hfill \end{array}$$

We need to evaluate the functions and partial derivatives at the points $t_1=e_1=\mathbb{E}\left(T_1\right)={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}$ and $t_2=e_2=\mathbb{E}\left(T_2\right)={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}$. The following evaluations helps us:

$$\begin{array}{cc}\hfill e_2-e_2^{1/2}{e}_1^{-1/2}& ={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}-{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{-1/2}\hfill \\ \hfill & ={\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}-{\displaystyle \frac{\mu }{\lambda }}={\displaystyle \frac{1}{2{\lambda }^2}},\hfill \\ \hfill e_1-e_1^{1/2}{e}_2^{-1/2}& ={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}-{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{-1/2}\hfill \\ \hfill & ={\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}-{\displaystyle \frac{\lambda }{\mu }}={\displaystyle \frac{1}{2{\mu }^2}}.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill g_1(e_1,e_2)& ={\displaystyle \frac{1}{\sqrt{2}}}{(e_2-e_2^{1/2}{e}_1^{-1/2})}^{-1/2}={\displaystyle \frac{1}{\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\lambda }^2}}\right)}^{-1/2}=\lambda ,\hfill \\ \hfill g_2(e_1,e_2)& ={\displaystyle \frac{1}{\sqrt{2}}}{(e_1-e_1^{1/2}{e}_2^{-1/2})}^{-1/2}={\displaystyle \frac{1}{\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\mu }^2}}\right)}^{-1/2}=\mu ,\hfill \\ \hfill {\displaystyle \frac{\partial g_1(e_1,e_2)}{\partial t_1}}& =-{\displaystyle \frac{1}{4\sqrt{2}}}{(e_2-e_2^{1/2}{e}_1^{-1/2})}^{-3/2}{e}_2^{1/2}{e}_1^{-3/2}\hfill \\ \hfill & =-{\displaystyle \frac{1}{4\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\lambda }^2}}\right)}^{-3/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{-3/2}=-{\displaystyle \frac{{\lambda }^2{\mu }^3}{2\lambda \mu +1}},\hfill \\ \hfill {\displaystyle \frac{\partial g_1(e_1,e_2)}{\partial t_2}}& =-{\displaystyle \frac{1}{2\sqrt{2}}}{(e_2-e_2^{1/2}{e}_1^{-1/2})}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{e}_2^{-1/2}{e}_1^{-1/2}\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\lambda }^2}}\right)}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{-1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{-1/2}\right)\hfill \\ \hfill & =-{\lambda }^3\left(1-{\displaystyle \frac{\lambda \mu }{2\lambda \mu +1}}\right)=-{\lambda }^3{\displaystyle \frac{\lambda \mu +1}{2\lambda \mu +1}},\hfill \\ \hfill {\displaystyle \frac{\partial g_2(e_1,e_2)}{\partial t_1}}& =-{\displaystyle \frac{1}{2\sqrt{2}}}{(e_1-e_1^{1/2}{e}_2^{-1/2})}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{e}_1^{-1/2}{e}_2^{-1/2}\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\mu }^2}}\right)}^{-3/2}\left(1-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{-1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{-1/2}\right)\hfill \\ \hfill & =-{\mu }^3\left(1-{\displaystyle \frac{\lambda \mu }{2\lambda \mu +1}}\right)=-{\mu }^3{\displaystyle \frac{\lambda \mu +1}{2\lambda \mu +1}},\hfill \\ \hfill {\displaystyle \frac{\partial g_2(e_1,e_2)}{\partial t_2}}& =-{\displaystyle \frac{1}{4\sqrt{2}}}{(e_1-e_1^{1/2}{e}_2^{-1/2})}^{-3/2}{e}_1^{1/2}{e}_2^{-3/2}\hfill \end{array}$$

$$=-{\displaystyle \frac{1}{4\sqrt{2}}}{\left({\displaystyle \frac{1}{2{\mu }^2}}\right)}^{-3/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\mu }^2}}\right)}^{1/2}{\left({\displaystyle \frac{2\lambda \mu +1}{2{\lambda }^2}}\right)}^{-3/2}=-{\displaystyle \frac{{\lambda }^3{\mu }^2}{2\lambda \mu +1}}.$$

The Jacobian matrix takes the form

$$J=\left(\begin{array}{cc}-{\displaystyle \frac{{\lambda }^2{\mu }^3}{2\lambda \mu +1}}& -{\lambda }^3{\displaystyle \frac{\lambda \mu +1}{2\lambda \mu +1}}\\ -{\mu }^3{\displaystyle \frac{\lambda \mu +1}{2\lambda \mu +1}}& -{\displaystyle \frac{{\lambda }^3{\mu }^2}{2\lambda \mu +1}}\end{array}\right)=-{\displaystyle \frac{1}{2\lambda \mu +1}}\left(\begin{array}{cc}{\lambda }^2{\mu }^3& {\lambda }^3(\lambda \mu +1)\\ {\mu }^3(\lambda \mu +1)& {\lambda }^3{\mu }^2\end{array}\right).$$

The resulting asymptotic covariance matrix of $\widehat{\lambda }$ and $\widehat{\mu }$ is

$$\begin{array}{cc}\hfill & \Sigma =J\tilde{\Sigma }{J}^{\prime }={\displaystyle \frac{1}{4{(2\lambda \mu +1)}^2}}\hfill \\ \hfill & \times \left(\begin{array}{cc}{\lambda }^2{\mu }^3& {\lambda }^3(\lambda \mu +1)\\ {\mu }^3(\lambda \mu +1)& {\lambda }^3{\mu }^2\end{array}\right)\left(\begin{array}{cc}{\displaystyle \frac{4\lambda \mu +5}{{\mu }^4}}& -{\displaystyle \frac{4\lambda \mu +1}{{\lambda }^2{\mu }^2}}\\ -{\displaystyle \frac{4\lambda \mu +1}{{\lambda }^2{\mu }^2}}& {\displaystyle \frac{4\lambda \mu +5}{{\lambda }^4}}\end{array}\right)\left(\begin{array}{cc}{\lambda }^2{\mu }^3& {\mu }^3(\lambda \mu +1)\\ {\lambda }^3(\lambda \mu +1)& {\lambda }^3{\mu }^2\end{array}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{4{(1+2\lambda \mu )}^2}}\left(\begin{array}{cc}{\lambda }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)& \lambda \mu (-1+4\lambda \mu +8{\lambda }^2{\mu }^2)\\ \lambda \mu (-1+4\lambda \mu +8{\lambda }^2{\mu }^2)& {\mu }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)\end{array}\right).\hfill \end{array}$$

The following theorem collects our findings.

Theorem 1. 

The method-of-moments estimators $\widehat{\lambda }$ and $\widehat{\mu }$ and asymptotically normal with mean vector $\left(\begin{array}{c}\lambda \\ \mu \end{array}\right)$ and covariance matrix

$$\Sigma ={\displaystyle \frac{1}{4{(1+2\lambda \mu )}^2}}\left(\begin{array}{cc}{\lambda }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)& \lambda \mu (-1+4\lambda \mu +8{\lambda }^2{\mu }^2)\\ \lambda \mu (-1+4\lambda \mu +8{\lambda }^2{\mu }^2)& {\mu }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)\end{array}\right);$$

that is,

$$\sqrt{n}\left(\begin{array}{c}\widehat{\lambda }-\lambda \\ \widehat{\mu }-\mu \end{array}\right)⟶N\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\Sigma \right)$$

as $n\to \infty$ in distribution.

In particular, we obtain

• The estimator $\widehat{\lambda }$ is asymptotically normal with mean $\lambda$ (asymptotically unbiased) and variance ${\displaystyle \frac{{\lambda }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)}{4{(2\lambda \mu +1)}^2}}$. This is an asymptotic result; it implies that

  $$\mathrm{Var}\left(\widehat{\lambda }\right)={\displaystyle \frac{{\lambda }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)}{4{(2\lambda \mu +1)}^{2}n}}+O\left(n^{-2}\right).$$
• The estimator $\widehat{\mu }$ is asymptotically normal with mean $\mu$ (asymptotically unbiased) and variance ${\displaystyle \frac{{\mu }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)}{4{(2\lambda \mu +1)}^2}}$. This is an asymptotic result; it implies that

  $$\mathrm{Var}\left(\widehat{\mu }\right)={\displaystyle \frac{{\mu }^2(5+12\lambda \mu +8{\lambda }^2{\mu }^2)}{4{(2\lambda \mu +1)}^{2}n}}+O\left(n^{-2}\right).$$
• The covariance of the method of moments estimators $\widehat{\lambda }$ and $\widehat{\mu }$ is

  $$\mathrm{Cov}(\widehat{\lambda },\widehat{\mu })={\displaystyle \frac{\lambda \mu (-1+4\lambda \mu +8{\lambda }^2{\mu }^2)}{4{(2\lambda \mu +1)}^{2}n}}+O\left(n^{-2}\right).$$

4. Simulation Study

First, we outline the procedure of obtaining a Birnbaum–Saunders random variate.

Assume that a random variable Y has the standard normal distribution $N(0,1)$, and consider the equation

$${\displaystyle \frac{\lambda }{\sqrt{X}}}=Y+\mu \sqrt{X}.$$

Solving this equation for a positive X, some straightforward but slightly tedious algebra shows that

$$X={\left({\displaystyle \frac{-Y+\sqrt{Y^2+4\lambda \mu }}{2\mu }}\right)}^2.$$

It is possible to prove that the random variable X has the Birnbaum–Saunders distribution with parameters $\mu$ and $\lambda$; see Ahmed et al. [3], Section 5.2.

Therefore, the following is the procedure to obtain n random numbers that follow the Birnbaum–Saunders distribution with parameters $\lambda$ and $\mu$:

• Algorithm 1. Step 0. Fix $n,\mu >0$ and $\lambda >0$.

Step 1. Generate n standard normal random numbers $y_1,\dots ,y_n$.

Step 2. For each $j=1,\dots ,n$ calculate $x_j={\left({\displaystyle \frac{-y_j+\sqrt{y_j^2+4\lambda \mu }}{2\mu }}\right)}^2$. Then $x_1,\dots ,x_n$ are random numbers that follow the Birnbaum–Saunders distribution with parameters $\lambda$ and $\mu$.

Now we start the simulation procedure. We consider the number of simulations $N=\mathrm{10,000}$.

• Algorithm 2. Step i. Simulate N samples of size n of random numbers that follow the Birnbaum–Saunders distribution with parameters $\lambda$ and $\mu$ by Algorithm 1.

Step ii. For each sample $i=1,\dots ,N$, calculate the method of moments estimates ${\widehat{\lambda }}_i$ and ${\widehat{\mu }}_i$ from Proposition 3.

Step iii. Calculate the sample means (bias) and sample variances for N values of ${\widehat{\lambda }}_i$ and ${\widehat{\mu }}_i, i=1,\dots ,N$.

4.1. Scope

The following values of parameters and sample sizes are considered in: $n=10, 30, 50, 100, 200, 500; \lambda =0.5, 1, 5, 10$, and $\mu =0.5, 1, 5, 10$. This gives $6\times 4\times 4=96$ scenarios.

4.2. Comparing the Simulation and Theoretical Results

The following tables provide a detailed comparison of simulation results and theoretical outcomes for various sample sizes and parameter values. Specifically, we analyze the mean, variance, and covariance of the estimators $\widehat{\lambda }$ and $\widehat{\mu }$. These estimates are evaluated across a range of sample sizes, from small to large, and for different combinations of the true values of $\lambda$ and $\mu$. The results are categorized into three sample sizes: small ($n=10,30$), moderate ($n=50,100$), and large ($n=200,500$).

For small sample sizes, the simulation results often deviate more from the theoretical results because the estimators are less stable with fewer data points. Theoretical results typically provide a more stable estimate of the lower variance, while simulation results exhibit more variation, especially for smaller sample sizes. As the parameters $\lambda$ and $\mu$ increase, the variance increases substantially in the simulation. This suggests that larger values of the parameters lead to more variability in the estimator’s performance, especially when the sample size is small. The covariance values also tend to differ between the simulation and the theoretical results, especially for larger values of $\mu$, indicating that the simulation tends to introduce more variability or correlation.

For moderate sample sizes, the simulation results are closer to the theoretical values, but some deviations still remain. The variance and covariance are larger in the simulation but are still closer to the theoretical values than for small samples. This reflects the fact that increasing the sample size reduces the variability in the estimates and aligns them better with theoretical predictions.

For large sample sizes, we observe that the simulation results converge closely to the theoretical values. For example, when $n=200$, $\lambda$ = 0.5, and $\mu$ = 0.5, the simulation estimate for $\widehat{\lambda }$ is 0.5016, which is extremely close to the true value of 0.5, and the variance is very small (0.0005), which aligns very well with the theoretical variance (0.0005). This demonstrates the precision of the estimators as the sample size increases. The covariance between $\widehat{\lambda }$ and $\widehat{\mu }$ also decreases, and for large samples, it gets closer to the theoretical value of 0.0001, which is negligible, indicating very little relationship between the two estimators as the sample size grows. Overall, the simulation results continue to be close to the theoretical predictions, with the means and variances aligning more closely as the sample size grows.

Based on the results from Table 1, Table 2 and Table 3, we can conclude that across all sample sizes, the mean estimates $mean(\widehat{\lambda })$ and $mean\left(\widehat{\mu }\right)$ approach their respective true values ($\lambda$,$\mu$) as n increases. This demonstrates the asymptotic unbiasedness of the estimators. Additionally, the theoretical variances and covariances closely align with the simulated values as n grows, highlighting the reliability of the joint estimation process and further validating the robustness of the theoretical findings. The impact of parameters $\lambda$ and $\mu$ is more pronounced for small sample sizes. Larger values of these parameters lead to greater deviation in the simulation results, but the effects diminish as sample size increases.

Table 1. The simulation and theoretical results for small sample sizes.

n	$\mathit{\lambda }$	$\mathit{\mu }$	Simulation Result					Theoretical Result
			$\mathit{mean}(\widehat{\mathit{\lambda }})$	$\mathit{mean}(\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$
10	0.5	0.5	0.6058	0.6053	0.0576	0.0590	0.0063	0.0236	0.0236	0.0014
10	0.5	1	0.5960	1.1951	0.0429	0.1757	0.0250	0.0203	0.0813	0.0094
10	0.5	5	0.5815	5.8192	0.0289	2.8181	0.2101	0.0148	1.4757	0.1024
10	0.5	10	0.5805	11.6205	0.0269	10.8728	0.4825	0.0137	5.4752	0.2262
10	1	0.5	1.1878	0.5954	0.1669	0.0428	0.0264	0.0813	0.0203	0.0094
10	1	1	1.1778	1.1707	0.1337	0.1327	0.0746	0.0694	0.0694	0.0306
10	1	5	1.1595	5.8011	0.1048	2.5920	0.4663	0.0548	1.3688	0.2262
10	1	10	1.1576	11.5777	0.1025	10.2823	0.9136	0.0524	5.2438	0.4756
10	5	0.5	5.7873	0.5821	2.7430	0.0280	0.2300	1.4757	0.0148	0.1024
10	5	1	5.8103	1.1606	2.6498	0.1037	0.4630	1.3688	0.0548	0.2262
10	5	5	5.8025	5.8011	2.5626	2.5756	2.6054	1.2748	1.2748	1.2252
10	5	10	5.7804	11.5464	2.4573	9.7477	4.8360	1.2624	5.0498	2.4751
10	10	0.5	11.5864	0.5779	10.4475	0.0258	0.4549	5.4752	0.0137	0.2262
10	10	1	11.5590	1.1558	10.1876	0.1014	0.9656	5.2438	0.0524	0.4756
10	10	5	11.5118	5.7584	9.7821	2.4553	4.9364	5.0498	1.2624	2.4751
10	10	10	11.5277	11.5258	9.8778	9.9101	9.9482	5.0249	5.0249	4.9751
30	0.5	0.5	0.5303	0.5302	0.0103	0.0101	0.0008	0.0079	0.0079	0.0005
30	0.5	1	0.5275	1.0538	0.0086	0.0345	0.0045	0.0068	0.0271	0.0031
30	0.5	5	0.5234	5.2413	0.0059	0.5825	0.0432	0.0049	0.4919	0.0341
30	0.5	10	0.5233	10.4598	0.0056	2.2367	0.0903	0.0046	1.8251	0.0754
30	1	0.5	1.0552	0.5248	0.0344	0.0083	0.0042	0.0271	0.0068	0.0031
30	1	1	1.0541	1.0521	0.0295	0.0294	0.0136	0.0231	0.0231	0.0102
30	1	5	1.0456	5.2327	0.0224	0.5526	0.0964	0.0183	0.4563	0.0754
30	1	10	1.0448	10.4456	0.0211	2.0734	0.1973	0.0175	1.7479	0.1585
30	5	0.5	5.2448	0.5245	0.6098	0.0060	0.0420	0.4919	0.0049	0.0341
30	5	1	5.2429	1.0476	0.5827	0.0238	0.0934	0.4563	0.0183	0.0754
30	5	5	5.2192	5.2167	0.5199	0.5261	0.5042	0.4249	0.4249	0.4084
30	5	10	5.2093	10.4164	0.4925	1.9749	1.0392	0.4208	1.6833	0.8250
30	10	0.5	10.4333	0.5223	2.1690	0.0055	0.0889	1.8251	0.0046	0.0754
30	10	1	10.4290	1.0431	2.1484	0.0214	0.1911	1.7479	0.0175	0.1585
30	10	5	10.4637	5.2302	2.1203	0.5264	1.0212	1.6833	0.4208	0.8250
30	10	10	10.4623	10.4624	2.0842	2.0807	2.0807	1.6750	1.6750	1.6584

Table 2. The simulation and theoretical results for moderate sample sizes.

n	$\mathit{\lambda }$	$\mathit{\mu }$	Simulation Result					Theoretical Result
			$\mathit{mean}(\widehat{\mathit{\lambda }})$	$\mathit{mean}(\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$
50	0.5	0.5	0.5177	0.5183	0.0055	0.0057	0.0002	0.0047	0.0047	0.0003
50	0.5	1	0.5146	1.0325	0.0046	0.0186	0.0023	0.0041	0.0163	0.0019
50	0.5	5	0.5143	5.1367	0.0033	0.3291	0.0230	0.003	0.2951	0.0205
50	0.5	10	0.5137	10.2578	0.0031	1.2049	0.0500	0.0027	1.095	0.0452
50	1	0.5	1.0348	0.5158	0.0191	0.0046	0.0023	0.0163	0.0041	0.0019
50	1	1	1.0294	1.0305	0.0157	0.0161	0.0068	0.0139	0.0139	0.0061
50	1	5	1.0257	5.1319	0.012	0.2996	0.0520	0.011	0.2738	0.0452
50	1	10	1.0272	10.2731	0.0118	1.197	0.1100	0.0105	1.0488	0.0951
50	5	0.5	5.1385	0.5136	0.3344	0.0034	0.0229	0.2951	0.003	0.0205
50	5	1	5.1359	1.0261	0.2992	0.0124	0.0516	0.2738	0.011	0.0452
50	5	5	5.1398	5.1381	0.289	0.2886	0.2707	0.255	0.255	0.2450
50	5	10	5.1296	10.2574	0.2866	1.1452	0.5580	0.2525	1.0100	0.4950
50	10	0.5	10.2679	0.5134	1.207	0.0031	0.0530	1.095	0.0027	0.0452
50	10	1	10.2506	1.0252	1.179	0.0118	0.1089	1.0488	0.0105	0.0951
50	10	5	10.2621	5.1311	1.1119	0.2772	0.5506	1.01	0.2525	0.4950
50	10	10	10.2627	10.2612	1.1212	1.1184	1.1087	1.005	1.005	0.9950
100	0.5	0.5	0.5081	0.5086	0.0026	0.0026	0.0002	0.0024	0.0024	0.0001
100	0.5	1	0.5084	1.0162	0.0022	0.0085	0.0011	0.002	0.0081	0.0009
100	0.5	5	0.5075	5.0737	0.0016	0.1591	0.0109	0.0015	0.1476	0.0102
100	0.5	10	0.5068	10.1391	0.0015	0.5934	0.0242	0.0014	0.5475	0.0226
100	1	0.5	1.0151	0.5078	0.0086	0.0022	0.0011	0.0081	0.002	0.0009
100	1	1	1.0136	1.0136	0.0075	0.0073	0.0033	0.0069	0.0069	0.0031
100	1	5	1.0132	5.0704	0.0058	0.1464	0.0247	0.0055	0.1369	0.0226
100	1	10	1.0137	10.1363	0.0056	0.5499	0.0510	0.0052	0.5244	0.0476
100	5	0.5	5.0661	0.5064	0.1556	0.0016	0.0108	0.1476	0.0015	0.0102
100	5	1	5.0681	1.0127	0.1477	0.0059	0.0237	0.1369	0.0055	0.0226
100	5	5	5.0627	5.0622	0.1356	0.1358	0.1309	0.1275	0.1275	0.1225
100	5	10	5.0661	10.1301	0.1344	0.5377	0.2619	0.1262	0.505	0.2475
100	10	0.5	10.138	0.5066	0.581	0.0014	0.0244	0.5475	0.0014	0.0226
100	10	1	10.1329	1.013	0.5487	0.0054	0.0507	0.5244	0.0052	0.0476
100	10	5	10.12	5.0606	0.5347	0.1339	0.2657	0.505	0.1262	0.2475
100	10	10	10.1176	10.1178	0.5205	0.5237	0.5217	0.5025	0.5025	0.4975

Table 3. The simulation and theoretical results for large sample sizes.

n	$\mathit{\lambda }$	$\mathit{\mu }$	Simulation Result					Theoretical Result
			$\mathit{mean}(\widehat{\mathit{\lambda }})$	$\mathit{mean}(\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$	$\mathit{Var}(\widehat{\mathit{\lambda }})$	$\mathit{Var}(\widehat{\mathit{\mu }})$	$\mathit{Covar}(\widehat{\mathit{\lambda }},\widehat{\mathit{\mu }})$
200	0.5	0.5	0.5016	0.5016	0.0005	0.0005	0.0001	0.0005	0.0005	0.0001
200	0.5	1	0.5017	1.0036	0.0004	0.0016	0.0005	0.0004	0.0016	0.0005
200	0.5	5	0.5014	5.0132	0.0003	0.0295	0.0054	0.0003	0.0295	0.0051
200	0.5	10	0.5013	10.0281	0.0003	0.1121	0.0121	0.0003	0.1095	0.0113
200	1	0.5	1.0039	0.5017	0.0017	0.0004	0.0005	0.0016	0.0004	0.0005
200	1	1	1.0028	1.0029	0.0014	0.0014	0.0016	0.0014	0.0014	0.0015
200	1	5	1.0028	5.0154	0.0011	0.0284	0.0118	0.0011	0.0274	0.0113
200	1	10	1.0024	10.0265	0.0011	0.1083	0.0245	0.001	0.1049	0.0238
200	5	0.5	5.0149	0.5013	0.0299	0.0003	0.0054	0.0295	0.0003	0.0051
200	5	1	5.0133	1.0031	0.0271	0.0011	0.0115	0.0274	0.0011	0.0113
200	5	5	5.0119	5.0123	0.0261	0.0262	0.0642	0.0255	0.0255	0.0613
200	5	10	5.0152	10.0296	0.0264	0.1052	0.1277	0.0252	0.101	0.1238
200	10	0.5	10.0263	0.5014	0.1116	0.0003	0.0118	0.1095	0.0003	0.0113
200	10	1	10.0239	1.0023	0.1065	0.0011	0.0240	0.1049	0.001	0.0238
200	10	5	10.0219	5.011	0.1025	0.0257	0.1328	0.101	0.0252	0.1238
200	10	10	10.0297	10.0297	0.102	0.1018	0.2502	0.1005	0.1005	0.2488
500	0.5	0.5	0.5008	0.5007	0.0002	0.0002	0.0000	0.0002	0.0002	0.0000
500	0.5	1	0.5006	1.0016	0.0002	0.0008	0.0002	0.0002	0.0008	0.0002
500	0.5	5	0.5007	5.0057	0.0001	0.0147	0.0021	0.0001	0.0148	0.0020
500	0.5	10	0.5006	10.0107	0.0001	0.0543	0.0045	0.0001	0.0548	0.0045
500	1	0.5	1.0016	0.5008	0.0008	0.0002	0.0002	0.0008	0.0002	0.0002
500	1	1	1.0017	1.0013	0.0007	0.0007	0.0006	0.0007	0.0007	0.0006
500	1	5	1.0016	5.0074	0.0006	0.0137	0.0045	0.0005	0.0137	0.0045
500	1	10	1.0018	10.0171	0.0005	0.0521	0.0095	0.0005	0.0524	0.0095
500	5	0.5	5.0061	0.5006	0.0147	0.0002	0.0021	0.0148	0.0001	0.0020
500	5	1	5.0079	1.0015	0.0138	0.0006	0.0046	0.0137	0.0005	0.0045
500	5	5	5.0061	5.0065	0.0127	0.0128	0.0251	0.0127	0.0127	0.0245
500	5	10	5.0072	10.0148	0.0125	0.05	0.0497	0.0126	0.0505	0.0495
500	10	0.5	10.0137	0.5006	0.0544	0.0001	0.0046	0.0548	0.0001	0.0045
500	10	1	10.0138	1.0015	0.052	0.0005	0.0097	0.0524	0.0005	0.0095
500	10	5	10.0101	5.0053	0.0512	0.0128	0.0509	0.0505	0.0126	0.0495
500	10	10	10.0137	10.0137	0.0517	0.0518	0.0994	0.0502	0.0502	0.0995

5. Real-Life Example

There are several datasets available for the Birnbaum–Saunders distribution in [2,9], any of which can be utilized. In this study, we demonstrate the applicability of the Birnbaum–Saunders distribution to model the total rainfall amounts over consecutive rainy days. Specifically, we collect rainfall data from 31 meteorological stations in the northeastern region of Thailand, spanning from January 1984 to September 2024. Our analysis focuses on cumulative rainfalls on periods ranging from 2 to 7 consecutive days. This range is chosen because a single day of rainfall is unlikely to impact flooding, while extending the period beyond 7 days results in a small sample size.

We began characterizing the data by creating box plots and density plots for each station for each rainfall period from consecutive rainy days. It can be seen that most stations will have total rainfall with a tail that is long on the right or skewed to the right as in Figure 1.

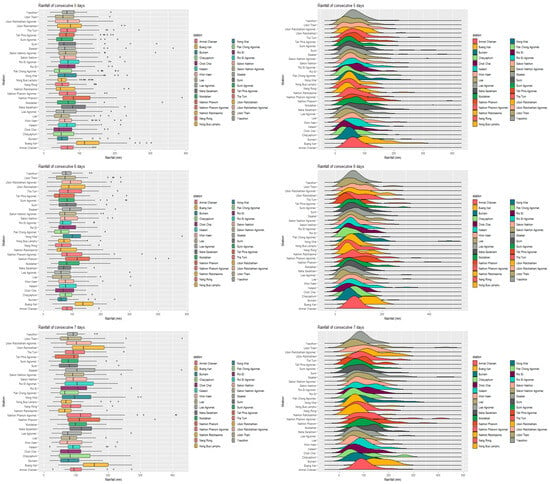
Figure 1. Box plot and density plot showing the distribution of data for all 31 stations.

Next, the suitability of the data for the Birnbaum–Saunders distribution was assessed using the Kolmogorov–Smirnov test. The parameters of the distribution function were estimated using the method of moments. The results of the analysis are presented in the form of a map, showing the locations of all 31 stations as in the Figure 2.

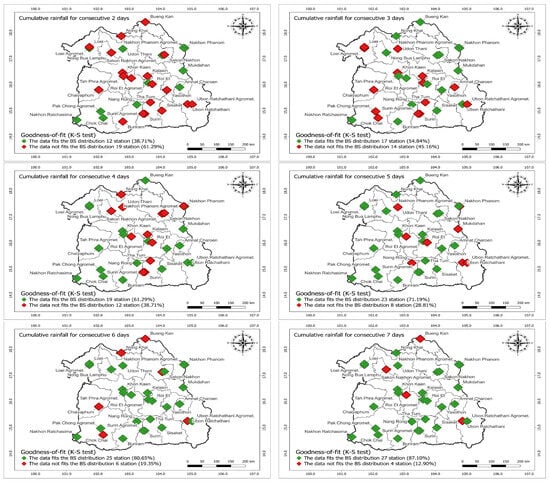
Figure 2. Goodness-of-fit analysis from the Kolmogorov–Smirnov test ($\alpha =0.05$).

Figure 2 presents the results of the Kolmogorov–Smirnov test for goodness-of-fit, applied at a significance level of $\alpha =0.05$. Each subfigure represents a specific dataset from each station, visually showing how well the observed data fit the expected distribution. The results indicate that many stations have cumulative rainfall data for consecutive rainy days that align well with the Birnbaum–Saunders distribution. Green symbols denote stations where the total rainfall follows the Birnbaum–Saunders distribution, while red symbols indicate stations where the total rainfall does not fit the Birnbaum–Saunders distribution, as determined by the Kolmogorov–Smirnov test and parameter estimation using the method of moments. Notably, as the number of consecutive rainy days increases, the proportion of stations with cumulative rainfall data that fit the Birnbaum–Saunders distribution tends to increase as well.

Next, we apply the theory established in Theorem 1, drawing conclusions from our findings. Specifically, we demonstrate that the parameter estimation of the Birnbaum–Saunders distribution using the method of moments follows a Bivariate Normal distribution for large sample sizes. This distribution is then used to calculate confidence intervals for parameter estimates. We construct the simultaneous confidence region (CR) for the vector of $\lambda$ and $\mu$ using Hotelling’s $T^2$. The confidence region is based on the fact that for large-enough samples, Hotelling’s $T^2$ statistic is related to a scaled version of the F-distribution.

We selected some stations whose total rainfall follows the Birnbaum–Saunders distribution; see Table 4. The resulting range of estimations will be employed to forecast the return level and predict the total rainfall on consecutive rainy days in the future.

Table 4. $95\%$ Confidence intervals for parameters of the Birnbaum–Saunders distribution.

Data	ID	Station	n	$\widehat{\mathit{\mu }}$	L-limit ($\mathit{\mu }$)	U-limit ($\mathit{\mu }$)	$\widehat{\mathit{\lambda }}$	L-limit ($\mathit{\lambda }$)	U-limit ($\mathit{\lambda }$)
CONS-2	48350	Loei Agromet	402	2.428	2.266	2.590	5.106	4.871	5.341
	48354	Udon Thani	358	2.290	2.123	2.456	10.202	9.851	10.553
	48357	Nakhon Phanom	332	2.568	2.386	2.751	13.061	12.649	13.473
	48391	Amnat Charoen	372	6.548	6.273	6.822	15.236	14.817	15.655
	48431	Nakhon Ratchasima	439	2.240	2.091	2.388	8.583	8.292	8.874
CONS-3	48352	Nong Khai	207	0.185	0.117	0.253	4.742	4.398	5.085
	48357	Nakhon Phanom	188	0.179	0.109	0.250	4.468	4.116	4.821
	48383	Mukdahan	204	0.189	0.120	0.257	4.862	4.512	5.212
	48407	Ubon Ratchathani	217	0.181	0.115	0.246	5.044	4.699	5.390
	48431	Nakhon Ratchasima	223	0.189	0.123	0.256	4.061	3.752	4.370
CONS-4	48350	Loei Agromet	136	0.187	0.103	0.270	6.109	5.632	6.587
	48357	Nakhon Phanom	99	0.164	0.072	0.255	7.859	7.225	8.494
	48383	Mukdahan	113	0.209	0.114	0.303	9.313	8.680	9.946
	48407	Ubon Ratchathani	117	0.192	0.102	0.282	7.942	7.362	8.522
	48431	Nakhon Ratchasima	114	0.178	0.088	0.268	5.814	5.301	6.327
CONS-5	48350	Loei Agromet	93	0.183	0.084	0.282	9.183	8.484	9.883
	48358	Nakhon Phanom Agromet	76	0.240	0.117	0.363	14.662	13.704	15.620
	48363	Bueng Kan	83	0.214	0.105	0.323	25.197	24.010	26.385
	48391	Amnat Charoen	88	0.284	0.161	0.406	17.781	16.812	18.749
	48431	Nakhon Ratchasima	69	0.181	0.065	0.296	8.264	7.483	9.045
CONS-6	48350	Loei Agromet	66	0.188	0.069	0.307	10.674	9.776	11.571
	48357	Nakhon Phanom	55	0.146	0.031	0.261	15.322	14.141	16.503
	48383	Mukdahan	51	0.191	0.055	0.327	15.111	13.900	16.322
	48408	Ubon Ratchathani Agromet	48	0.161	0.030	0.291	13.300	12.114	14.486
	48431	Nakhon Ratchasima	41	0.195	0.040	0.350	13.647	12.346	14.948
CONS-7	48350	Loei Agromet	27	0.207	0.005	0.408	16.264	14.475	18.053
	48357	Nakhon Phanom	34	0.153	0.000	0.307	16.036	14.466	17.606
	48383	Mukdahan	33	0.248	0.054	0.442	24.038	22.127	25.949
	48408	Ubon Ratchathani Agromet	35	0.177	0.016	0.339	16.448	14.893	18.004
	48431	Nakhon Ratchasima	23	0.228	-0.006	0.461	13.549	11.748	15.350

6. Return Level of Birnbaum–Saunders Distribution

The return level is a statistical concept used primarily in extreme value theory to describe the magnitude of a certain event, the cumulative rainfall in consecutive rainy days, which is expected to occur once over a specified time period, based on historical data or a modeled distribution. The return level is used to interpret rainfall.

The return level for a return period T is calculated as the quantile corresponding to the $1/T$-th left percentile of the distribution; that is, the solution of the equation $F_X\left(z\right)={\displaystyle \frac{1}{T}}$ for z, where $F(·)$ is the distribution function. For the Birnbaum–Saunders distribution, this equation can be written as

$$1-\Phi \left({\displaystyle \frac{\lambda }{\sqrt{z}}}-\mu \sqrt{z}\right)={\displaystyle \frac{1}{T}}.$$

Some straightforward but slightly tedious algebra shows that the return level for the return period T for the Birnbaum–Saunders distribution is

$${\widehat{z}}_T={\displaystyle \frac{\lambda }{4\mu }}{\left(\sqrt{{\displaystyle \frac{\mu }{\lambda }}}{\Phi }^{-1}\left(1-{\displaystyle \frac{1}{T}}\right)+\sqrt{{\left(\sqrt{{\displaystyle \frac{\mu }{\lambda }}}{\Phi }^{-1}\left(1-{\displaystyle \frac{1}{T}}\right)\right)}^2+4}\right)}^2,$$

where ${\Phi }^{-1}(·)$ is the quantile function of the standard normal distribution.

Table 5 provides estimated return levels for cumulative rainfall over various return periods (2, 10, 20, 50, and 100 years) in multiple datasets labeled as consecutive rainy days (CONS-2 through CONS-7), each associated with specific station IDs. For each dataset, the table lists the cumulative rainfall amounts (in millimeters) for the given return periods, along with their corresponding uncertainty intervals in parentheses. For example, for the CONS-2 dataset at station ID 48350, the estimated rainfall for a 2-year return period is 9.4 mm, with a confidence interval $95\%$ of (7.6, 11.1) mm. The data show a clear trend to increase the amounts of rainfall with longer return periods, suggesting that more extreme rainfall events tend to be more intense and less frequent. The return level for a T-year return period refers to the amount of rainfall expected to be exceeded once every T years. We present the estimated rainfall values and their corresponding intervals (in parentheses) for return periods of 2, 10, 20, 50, and 100 years. These values are critical for the design of infrastructure, such as flood defenses and reservoirs, to account for extreme rainfall events.

Table 5. Estimated return levels for cumulative rainfall at various return periods.

Data	ID	2 Years	10 Years	20 Years	50 Years	100 Years
CONS-2	48350	9.4 (7.6, 11.1)	41.7 (40.0, 43.5)	58.6 (56.8, 60.3)	82.1 (80.4, 83.8)	100.5 (98.8, 102.3)
	48354	10.1 (7.7, 12.5)	51.1 (48.6, 53.5)	73.0 (70.5, 75.4)	103.7 (101.3, 106.1)	127.8 (125.4, 130.2)
	48357	12.9 (9.6, 16.1)	66.4 (63.2, 69.6)	95.1 (91.9, 98.3)	135.4 (132.1, 138.6)	167 (163.8, 170.2)
	48391	21.0 (19.4, 22.7)	50.3 (48.6, 52.0)	63.1 (61.4, 64.8)	80.3 (78.6, 82.0)	93.5 (91.8, 95.1)
	48431	9.6 (7.6, 11.6)	48.7 (46.8, 50.7)	69.6 (67.6, 71.6)	98.9 (96.9, 100.9)	121.9 (119.9, 123.9)
CONS-3	48352	25.1 (20.5, 29.7)	90.1 (85.5, 94.7)	122.3 (117.7, 126.9)	166.9 (162.3, 171.4)	201.6 (197.0, 206.2)
	48357	24.4 (19.2, 29.6)	92.4 (87.2, 97.6)	126.5 (121.3, 131.7)	173.9 (168.7, 179.1)	210.8 (205.6, 216.1)
	48383	25.6 (20.4, 30.7)	89.7 (84.6, 94.9)	121.3 (116.1, 126.5)	164.9 (159.8, 170.1)	198.9 (193.8, 204.1)
	48407	27.6 (22.4, 32.7)	97.1 (91.9, 102.2)	131.3 (126.1, 136.5)	178.7 (173.5, 183.8)	215.6 (210.4, 220.7)
	48431	21.0 (16.8, 25.1)	81.3 (77.2, 85.5)	111.8 (107.6, 116.0)	154.2 (150.0, 158.4)	187.3 (183.1, 191.5)
CONS-4	48350	32.4 (25.9, 39.0)	101.1 (94.5, 107.6)	133.8 (127.2, 140.3)	178.7 (172.1, 185.2)	213.5 (207.0, 220.1)
	48357	47.8 (37.2, 58.3)	140.3 (129.8, 150.9)	183.7 (173.1, 194.2)	242.9 (232.3, 253.5)	288.8 (278.2, 299.3)
	48383	44.5 (38.2, 50.8)	108.3 (101.9, 114.6)	136.4 (130.0, 142.7)	174.1 (167.8, 180.4)	203.1 (196.7, 209.4)
	48407	41.2 (33.8, 48.7)	111.7 (104.3, 119.1)	143.9 (136.4, 151.3)	187.5 (180.1, 195.0)	221.2 (213.8, 228.7)
	48431	32.2 (25.1, 39.3)	105.7 (98.6, 112.7)	141.2 (134.1, 148.3)	190.1 (183.0, 197.2)	228.1 (221, 235.2)
CONS-5	48350	49.9 (41.4, 58.4)	129.2 (120.7, 137.8)	165 (156.5, 173.5)	213.2 (204.7, 221.7)	250.4 (241.9, 258.9)
	48358	61.0 (53.3, 68.8)	119.3 (111.6, 127.1)	142.9 (135.2, 150.7)	173.8 (166, 181.6)	197.0 (189.3, 204.8)
	48363	117.8 (105.8, 129.8)	203.2 (191.2, 215.2)	235.9 (223.9, 247.8)	277.8 (265.8, 289.8)	308.9 (297, 320.9)
	48391	62.7 (56.7, 68.7)	110.1 (104.1, 116.2)	128.4 (122.4, 134.5)	152.0 (146.0, 158.0)	169.5 (163.5, 175.6)
	48431	45.5 (34.9, 56.0)	124.3 (113.8, 134.9)	160.4 (149.9, 171.0)	209.5 (199.0, 220.1)	247.4 (236.8, 258)
CONS-6	48350	56.6 (45.4, 67.9)	136.1 (124.9, 147.3)	170.9 (159.7, 182.1)	217.7 (206.5, 228.9)	253.5 (242.3, 264.7)
	48357	104.8 (83.4, 126.2)	241.0 (219.6, 262.5)	299.8 (278.4, 321.2)	378.3 (356.9, 399.7)	438.3 (416.8, 459.7)
	48383	79.1 (64.5, 93.7)	165.4 (150.8, 180.0)	201.2 (186.6, 215.8)	248.6 (234.0, 263.2)	284.5 (269.9, 299.1)
	48408	82.3 (66.3, 98.2)	192.5 (176.5, 208.4)	240.3 (224.4, 256.2)	304.4 (288.4, 320.3)	353.3 (337.4, 369.2)
	48431	70.0 (54.6, 85.4)	150.7 (135.2, 166.1)	184.6 (169.2, 200.1)	229.6 (214.2, 245)	263.8 (248.3, 279.2)
CONS-7	48350	78.7 (59.1, 98.2)	156.1 (136.6, 175.6)	187.6 (168.1, 207.1)	228.9 (209.4, 248.4)	260.1 (240.6, 279.6)
	48357	104.4 (80.5, 128.3)	231.4 (207.5, 255.3)	285.5 (261.6, 309.4)	357.4 (333.5, 381.3)	412.1 (388.2, 436.0)
	48383	96.8 (83.3, 110.3)	162.6 (149.1, 176.1)	187.5 (174.0, 201.0)	219.3 (205.8, 232.8)	242.8 (229.3, 256.3)
	48408	92.6 (74.6, 110.5)	192.8 (174.9, 210.7)	234.4 (216.5, 252.3)	289.3 (271.4, 307.3)	331.0 (313.0, 348.9)
	48431	59.4 (43.8, 74.9)	121.3 (105.7, 136.8)	146.8 (131.2, 162.3)	180.3 (164.8, 195.9)	205.7 (190.2, 221.3)

7. Discussion

Our theoretical results in Theorem 1 differ significantly from those of Ahmed et al. [3], particularly regarding the mean square errors (MSEs) of the estimators $\widehat{\lambda }$ and $\widehat{\mu }$. Ahmed et al. [3] provide the following expressions for MSE, as presented in Equations 3 and 4:

$$\mathrm{MSE}\left(\widehat{\lambda }\right)={\displaystyle \frac{(\lambda \mu +5/4)({\lambda }^2{(\lambda \mu +1)}^2+{\lambda }^4{\mu }^2)}{n{(2\lambda \mu +1)}^2}}-{\displaystyle \frac{2{\lambda }^3\mu (\lambda \mu +1/4)(\lambda \mu +1)}{n{(2\lambda \mu +1)}^2}}+O\left(n^{-2}\right),$$

(3)

$$\mathrm{MSE}\left(\widehat{\mu }\right)={\displaystyle \frac{(\lambda \mu +5/4)({\mu }^2{(\lambda \mu +1)}^2+{\lambda }^2{\mu }^4)}{n{(2\lambda \mu +1)}^2}}-{\displaystyle \frac{2\lambda {\mu }^3(\lambda \mu +1/4)(\lambda \mu +1)}{n{(2\lambda \mu +1)}^2}}+O\left(n^{-2}\right).$$

(4)

Our result found that because the estimators are asymptotically unbiased, the mean square error is asymptotically equal to the variance. The expressions for the variances presented in our theorem are different from those presented in Ahmed et al. [3]. We expect that there is a mistake in the derivations in Ahmed et al. [3] because our simulation results support the formulae of Theorem 1. Because the calculations are not presented by Ahmed et al. [3], we do not know where the error lies. We also note that in Ahmed et al. [3], the joint asymptotic normality is not established and the covariance of the estimators is not derived. The statement of our Theorem 1 is stronger than the statement of the theorem in Ahmed et al. [3], Section 3.

This research not only contributes to the theoretical result on distributional properties, but also emphasizes its practical relevance by modeling cumulative rainfall data. We do this to show that the BS distribution is not only applied to modeling the lifetimes of objects where failure results from the propagation of fatigue cracks, but it can be applied to forecasting and mitigating flooding impacts in agriculture-dependent regions such as the northeastern area of Thailand.

8. Conclusions

This study rigorously explores the asymptotic normality of method-of-moments estimators for the Birnbaum–Saunders distribution under a new parametrization. We derive explicit formulas for the estimators, their mean vector, and the variance–covariance matrix. Through theoretical derivations supported by simulation studies, we demonstrate that the estimators converge to a bivariate normal distribution as the sample size increases, validating their consistency and efficiency.

The application of these results to rainfall data in northeastern Thailand showcases the practical utility of the Birnbaum–Saunders distribution to model extreme weather events. Using the new parametrization, the analysis provides information on rainfall trends, with implications for flood prediction and agricultural planning. These findings provide a valuable tool for forecasting and risk assessment in hydrological and environmental studies.