Finite-Time and Fixed-Time Synchronization of Memristor-Based Cohen–Grossberg Neural Networks via a Unified Control Strategy
Abstract
1. Introduction
2. Preliminaries
3. Finite-Time Synchronization
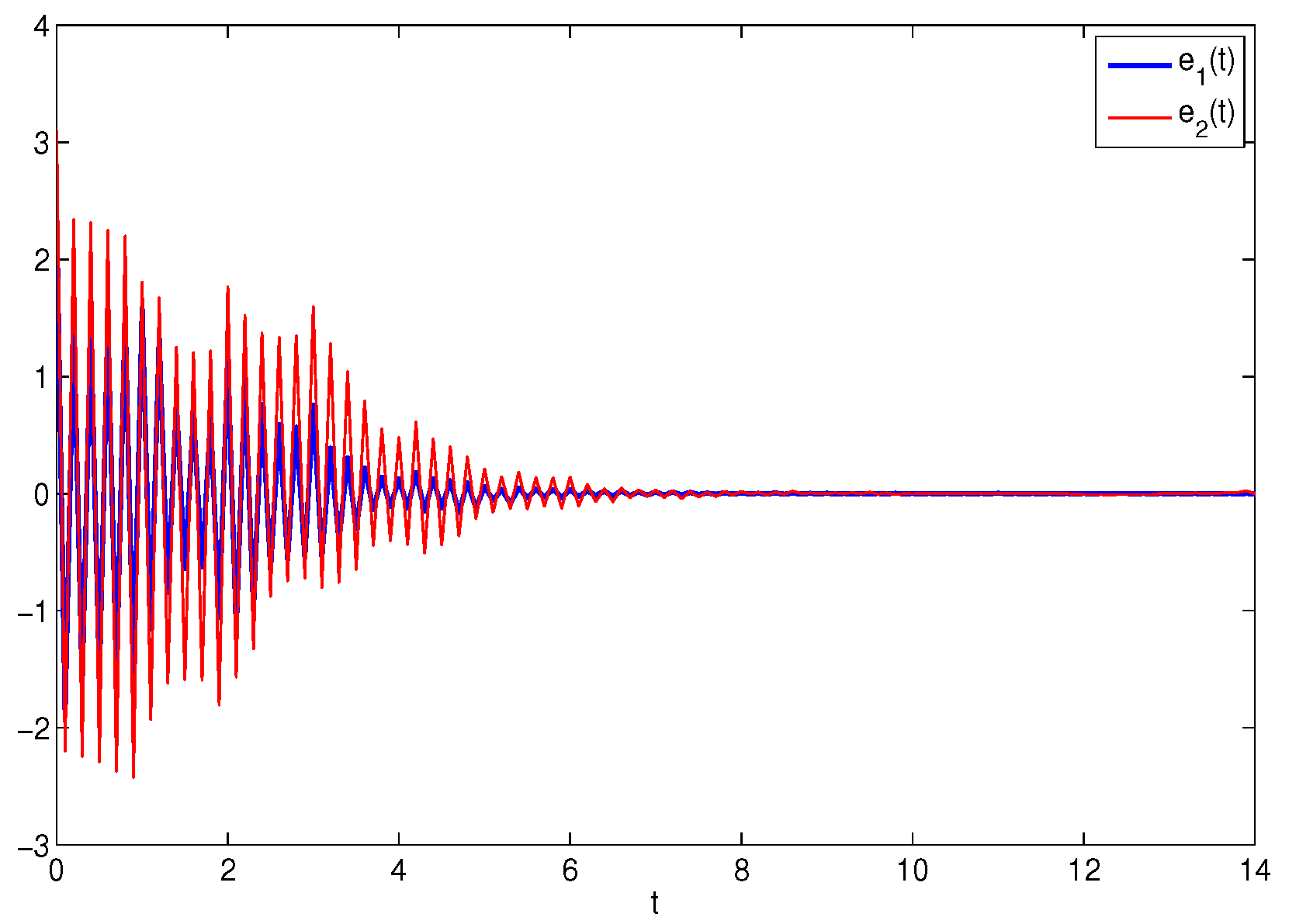
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuits Syst. 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.; Snider, G.; Stewart, D.; Williams, R. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, S.; Fang, X.; Wang, W. Adaptive anti-synchronization of memristor-based complex-valued neural networks with time delays. Phys. Stat. Mech. Its Appl. 2019, 535, 122427. [Google Scholar] [CrossRef]
- Li, H.; Fang, J.; Li, X.; Huang, T. Exponential synchronization of multiple impulsive discrete-time memristor-based neural networks with stochastic perturbations and time-varying delays. Neurocomputing 2020, 392, 86–97. [Google Scholar] [CrossRef]
- He, J.; Pei, L. Function matrix projection synchronization for the multi-time delayed fractional order memristor-based neural networks with parameter uncertainty. Appl. Math. Comput. 2023, 454, 128110. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y. Mean square exponential stability for stochastic memristor-based neural networks with leakage delay. Chaos Soliton. Fract. 2021, 146, 110811. [Google Scholar] [CrossRef]
- Ren, F.; Jiang, M.; Xu, H.; Fang, X. New finite-time synchronization of memristive Cohen-Grossberg neural network with reaction-diffusion term based on time-varying delay. Neural Comput. Appl. 2021, 33, 4315–4328. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H. Pinning synchronization of fractional memristor-based neural networks with neutral delays and reaction-diffusion terms. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107039. [Google Scholar] [CrossRef]
- Sarra, Z.; Bouziane, M.; Bouddou, R.; Benbouhenni, H.; Mekhilef, S.; Elbarbary, Z.M.S. Intelligent control of hybrid energy storage system using NARX-RBF neural network techniques for microgrid energy management. Energy Rep. 2024, 12, 5445–5461. [Google Scholar] [CrossRef]
- Zaidi, S.; Meliani, B.; Bouddou, R.; Belhadj, S.M.; Bouchikhi, N. Comparative study of different types of DC/DC converters for PV systems using RBF neural network-based MPPT algorithm. J. Renew. Energy 2024, 1, 13–31. [Google Scholar] [CrossRef]
- Adiche, S.; Larbi, M.; Toumi, D.; Bouddou, R.; Bajaj, M.; Bouchikhi, N.; Belabbes, A.; Zaitsev, I. Advanced control strategy for AC microgrids: A hybrid ANN-based adaptive PI controller with droop control and virtual impedance technique. Sci. Rep. 2024, 14, 31057. [Google Scholar] [CrossRef] [PubMed]
- Ji, G.; Hu, C.; Yu, J.; Jiang, H. Finite-time and fixed-time synchronization of discontinuous complex networks: A unified control framework design. J. Franklin Inst. 2018, 355, 4665–4685. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Lu, J.; Lou, J. Finite-time synchronization of complex networks with partial communication channels failure. Inf. Sci. 2023, 634, 539–549. [Google Scholar] [CrossRef]
- Jin, X.; Jiang, J.; Chi, J.; Wu, X. Adaptive finite-time pinned and regulation synchronization of disturbed complex networks. Commun. Nonlinear Sci. Numer. Simul. 2023, 124, 107319. [Google Scholar] [CrossRef]
- Wang, L.; Tan, X.; Wang, Q.; Hu, J. Multiple finite-time synchronization and settling-time estimation of delayed competitive neural networks. Neurocomputing 2023, 124, 107319. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Aouiti, C.; Assali, E.; Foutayeni, Y. Finite-time and fixed-time synchronization of inertial Cohen-Grossberg-Type neural networks with time varying delays. Neural Process. Lett. 2019, 50, 2407–2436. [Google Scholar] [CrossRef]
- Pu, H.; Li, F. Finite-/fixed-time synchronization for Cohen-Grossberg neural networks with discontinuous or continuous activations via periodically switching control. Cogn. Neurodyn. 2022, 16, 195–213. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J.; Alsaedi, A. Fixedtime sSynchronization of Memristive Cohen-Grossberg neural networks with impulsive effects. Int. J. Control, Autom. Syst. 2018, 16, 2214–2224. [Google Scholar] [CrossRef]
- Kong, F.; Zhu, Q.; Liang, F. Robust fixed-time synchronization of discontinuous Cohen-Grossberg neural networks with mixed time delays. Nonlinear Anal. Model. 2019, 24, 603–625. [Google Scholar] [CrossRef]
- Hui, M.; Wei, C.; Zhang, J.; Iu, H.H.; Luo, N.; Yao, R. Finite-time synchronization of Memristor-based fractional order Cohen-Grossberg neural networks. IEEE Access 2020, 8, 2214–2224. [Google Scholar] [CrossRef]
- Pershin, Y.; Ventra, M. On the validity of memristor modeling in the neural network literature. Neural Netw. 2020, 121, 52–56. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, S.; Mei, J.; Shen, Y. Finite-time synchronization control of a class of memristor-based recurrent neural networks. Neural Netw. 2015, 63, 133–140. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.; Jiang, M.; Wang, B.; Long, B. Finite-time parameter identification and adaptive synchronization between two chaotic neural networks. J. Frankl. Inst. 2013, 350, 1617–1633. [Google Scholar] [CrossRef]
- Zhu, Q.; Cao, J. Adaptive synchronization of chaotic Cohen-Grossberg neural networks with mixed time delays. Nonlinear Dyn. 2010, 61, 517. [Google Scholar] [CrossRef]
- Gan, Q. Adaptive synchronization of Cohen-Grossberg neural networks with unknown parameters and mixed time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3040–3049. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J.; Alsaedi, A. Finite-time and fixed-time synchronization analysis of inertial memristive neural networks with time-varying delays. Cogn. Neurodyn. 2018, 12, 121–134. [Google Scholar] [CrossRef]
- Cao, J.; Li, R. Fixed-time synchronization of delayed memristor-based recurrent neural networks. Inf. Sci. 2017, 60, 032201. [Google Scholar] [CrossRef]
- Yang, C.; Huang, L.; Cai, Z. Fixed-time synchronization of coupled memristor-based neural networks with time-varying delays. Neural Netw. 2019, 116, 101–109. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Lu, B.; Wang, J.; Jiang, H.; Hu, C. Finite-Time and Fixed-Time Synchronization of Memristor-Based Cohen–Grossberg Neural Networks via a Unified Control Strategy. Mathematics 2025, 13, 630. https://doi.org/10.3390/math13040630
Liu M, Lu B, Wang J, Jiang H, Hu C. Finite-Time and Fixed-Time Synchronization of Memristor-Based Cohen–Grossberg Neural Networks via a Unified Control Strategy. Mathematics. 2025; 13(4):630. https://doi.org/10.3390/math13040630
Chicago/Turabian StyleLiu, Mei, Binglong Lu, Jinling Wang, Haijun Jiang, and Cheng Hu. 2025. "Finite-Time and Fixed-Time Synchronization of Memristor-Based Cohen–Grossberg Neural Networks via a Unified Control Strategy" Mathematics 13, no. 4: 630. https://doi.org/10.3390/math13040630
APA StyleLiu, M., Lu, B., Wang, J., Jiang, H., & Hu, C. (2025). Finite-Time and Fixed-Time Synchronization of Memristor-Based Cohen–Grossberg Neural Networks via a Unified Control Strategy. Mathematics, 13(4), 630. https://doi.org/10.3390/math13040630






