Stochastic Zeroth-Order Multi-Gradient Algorithm for Multi-Objective Optimization
Abstract
1. Introduction
- This paper introduces a new gradient-free MOO algorithm called stochastic zeroth-order multi-gradient descent algorithm (SZMG), which applies the zeroth-order optimization method to multi-objective optimization problems.
- The convergence rate of is established for the SZMG algorithm under non-convex settings and mild assumptions, where d is the dimensionality of the model parameters and T is the number of iterations.
- Numerical experiments demonstrate the effectiveness of the SZMG algorithm.
2. Related Work
2.1. Gradient-Based Deterministic MOO
2.2. Gradient-Based Stochastic MOO
2.3. Gradient-Free MOO
3. Preliminaries
3.1. Problem Setup
3.2. Multi-Gradient Descent Algorithm
| Algorithm 1 Multi-gradient descent algorithm (MGDA) |
3.3. Zeroth-Order Optimization
4. Stochastic Zeroth-Order Multi-Gradient Algorithm
| Algorithm 2 Stochastic zeroth-order multi-gradient algorithm (SZMG) |
5. Convergence Analysis
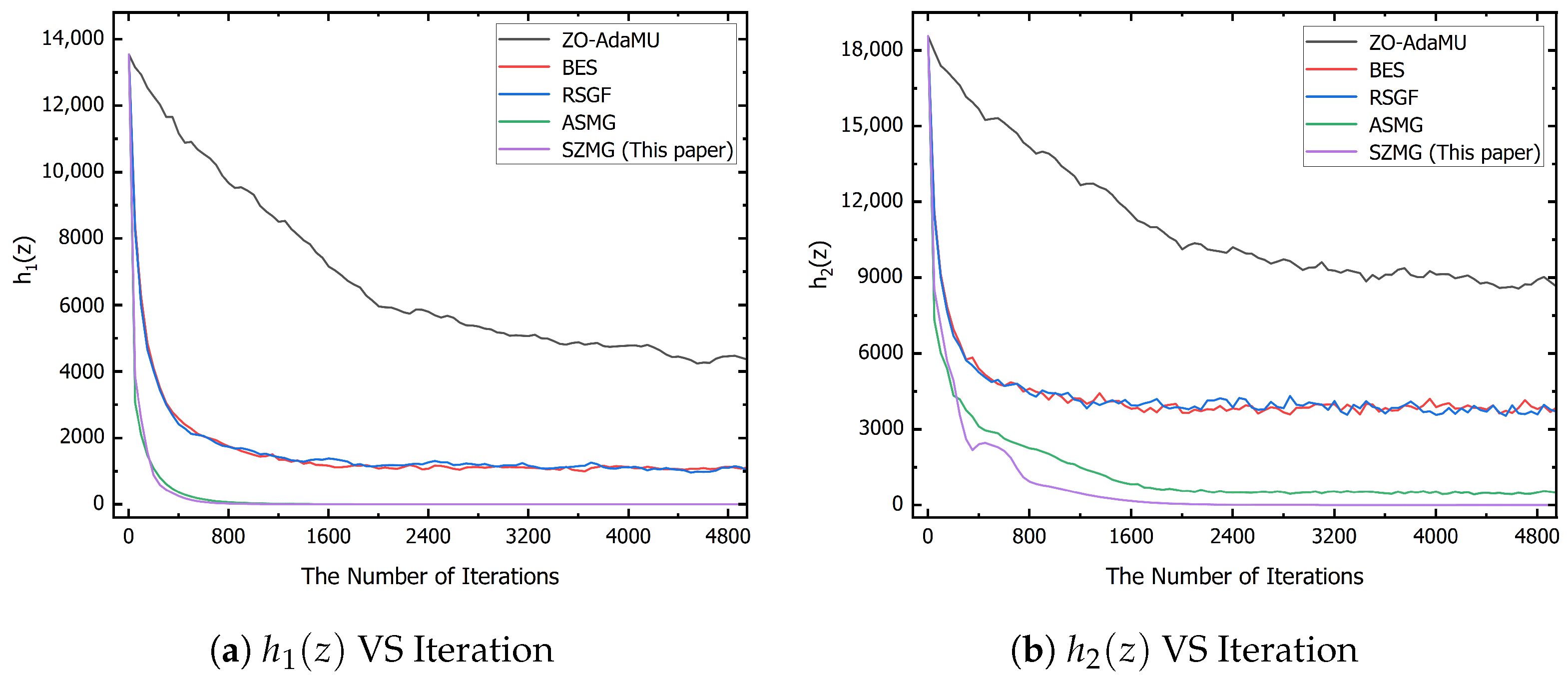
6. Experiments
6.1. Toy Example
6.2. Separable and Non-Separable Functions
6.2.1. Runtime
6.2.2. Scalability
6.2.3. Sensitiveness to Batch Size
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Extra Lemmas
Appendix B. Proof of the Results in Section 5
References
- Lu, W.; Zhou, Y.; Wan, G.; Hou, S.; Song, S. L3-Net: Towards Learning Based LiDAR Localization for Autonomous Driving. In Proceedings of the 31th IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Fernandes, P.; Ghorbani, B.; Garcia, X.; Freitag, M.; Firat, O. Scaling Laws for Multilingual Neural Machine Translation. In Proceedings of the 40th International Conference on Machine Learning, ICML, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Satija, H.; Thomas, P.S.; Pineau, J.; Laroche, R. Multi-Objective SPIBB: Seldonian Offline Policy Improvement with Safety Constraints in Finite MDPs. In Proceedings of the 35th Advances in Neural Information Processing Systems, NeurIPS, Virtual, 6–14 December 2021. [Google Scholar]
- Zhang, L.; Liu, X.; Mahmood, K.; Ding, C.; Guan, H. Dynamic Gradient Balancing for Enhanced Adversarial Attacks on Multi-Task Models. CoRR 2023. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling Multiple Objectives With Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; dos Santos Coelho, L. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Saha, S.; Maulik, U.; Deb, K. A Simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA. IEEE Trans. Evol. Comput. 2008, 12, 269–283. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, Q.; Pan, Y.; Xiang, Y.; Lin, Y.; Wu, X.; Liu, C.; Song, X. ZO-AdaMU Optimizer: Adapting Perturbation by the Momentum and Uncertainty in Zeroth-Order Optimization. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, AAAI, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar] [CrossRef]
- Gao, K.; Sener, O. Generalizing Gaussian Smoothing for Random Search. In Proceedings of the 39th International Conference on Machine Learning, ICML, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Ghadimi, S.; Lan, G. Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming. SIAM J. Optim. 2013, 23, 2341–2368. [Google Scholar] [CrossRef]
- Ye, F.; Lyu, Y.; Wang, X.; Zhang, Y.; Tsang, I.W. Adaptive Stochastic Gradient Algorithm for Black-box Multi-Objective Learning. In Proceedings of the 12th International Conference on Learning Representations, ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Zerbinati, A.; Desideri, J.A.; Duvigneau, R. Comparison Between MGDA and PAES for Multi-Objective Optimization; Research Report RR-7667; INRIA: Le Chesnay-Rocquencourt, France, 2011. [Google Scholar]
- Gass, S.; Saaty, T. The computational algorithm for the parametric objective function. Nav. Res. Logist. 1955, 2, 39–45. [Google Scholar] [CrossRef]
- Haimes, Y. On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Trans. Syst. Man Cybern. Syst. 1971, SMC-1, 296–297. [Google Scholar] [CrossRef]
- Chen, Z.; Ngiam, J.; Huang, Y.; Luong, T.; Kretzschmar, H.; Chai, Y.; Anguelov, D. Just Pick a Sign: Optimizing Deep Multitask Models with Gradient Sign Dropout. In Proceedings of the 34th Advances in Neural Information Processing Systems, NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Désidéri, J.A. Multiple-gradient descent algorithm (MGDA) for multiobjective optimization. C. R. Math. 2012, 350, 313–318. [Google Scholar] [CrossRef]
- Lin, X.; Zhen, H.; Li, Z.; Zhang, Q.; Kwong, S. Pareto Multi-Task Learning. In Proceedings of the 33th Advances in Neural Information Processing Systems, NeurIPS, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Mahapatra, D.; Rajan, V. Multi-Task Learning with User Preferences: Gradient Descent with Controlled Ascent in Pareto Optimization. In Proceedings of the 37th International Conference on Machine Learning, ICML, Virtual Event, 13–18 July 2020. [Google Scholar]
- Mercier, Q.; Poirion, F.; Désidéri, J. A stochastic multiple gradient descent algorithm. Eur. J. Oper. Res. 2018, 271, 808–817. [Google Scholar] [CrossRef]
- Liu, S.; Vicente, L.N. The stochastic multi-gradient algorithm for multi-objective optimization and its application to supervised machine learning. Ann. Oper. Res. 2024, 339, 1119–1148. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, W.; Jiang, J.; Zhong, W.; Gu, J.; Zhu, W. On the Convergence of Stochastic Multi-Objective Gradient Manipulation and Beyond. In Proceedings of the 36th Advances in Neural Information Processing Systems, NeurIPS, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Xiao, P.; Ban, H.; Ji, K. Direction-oriented Multi-objective Learning: Simple and Provable Stochastic Algorithms. In Proceedings of the 37the Advances in Neural Information Processing Systems, NeurIPS, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Chen, R.; Li, Y.; Chai, T. Multi-Objective Derivative-Free Optimization Based on Hessian-Aware Gaussian Smoothing Method. In Proceedings of the 18th IEEE International Conference on Control & Automation, ICCA, Reykjavík, Iceland, 18–21 June 2024. [Google Scholar] [CrossRef]
- Tammer, C.; Winkler, K. A new scalarization approach and applications in multicriteria d.c. optimization. J. Nonlinear Convex Anal. 2003, 4, 365–380. [Google Scholar]
- Fliege, J.; Svaiter, B.F. Steepest descent methods for multicriteria optimization. Math. Methods Oper. Res. 2000, 51, 479–494. [Google Scholar] [CrossRef]
- Bonnel, H.; Iusem, A.N.; Svaiter, B.F. Proximal Methods in Vector Optimization. SIAM J. Optim. 2005, 15, 953–970. [Google Scholar] [CrossRef]
- Fliege, J.; Drummond, L.M.G.; Svaiter, B.F. Newton’s Method for Multiobjective Optimization. SIAM J. Optim. 2009, 20, 602–626. [Google Scholar] [CrossRef]
- Carrizo, G.A.; Lotito, P.A.; Maciel, M.C. Trust region globalization strategy for the nonconvex unconstrained multiobjective optimization problem. Math. Program. 2016, 159, 339–369. [Google Scholar] [CrossRef]
- Pérez, L.R.L.; da Fonseca Prudente, L. Nonlinear Conjugate Gradient Methods for Vector Optimization. SIAM J. Optim. 2018, 28, 2690–2720. [Google Scholar] [CrossRef]
- Liu, L.; Li, Y.; Kuang, Z.; Xue, J.; Chen, Y.; Yang, W.; Liao, Q.; Zhang, W. Towards Impartial Multi-task Learning. In Proceedings of the 9th International Conference on Learning Representations, ICLR, Virtual Event, 3–7 May 2021. [Google Scholar]
- Fernando, H.D.; Shen, H.; Liu, M.; Chaudhury, S.; Murugesan, K.; Chen, T. Mitigating Gradient Bias in Multi-objective Learning: A Provably Convergent Approach. In Proceedings of the 11th International Conference on Learning Representations, ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Chen, L.; Fernando, H.D.; Ying, Y.; Chen, T. Three-Way Trade-Off in Multi-Objective Learning: Optimization, Generalization and Conflict-Avoidance. J. Mach. Learn. Res. 2024, 25, 193:1–193:53. [Google Scholar]
- Fernando, H.D.; Chen, L.; Lu, S.; Chen, P.; Liu, M.; Chaudhury, S.; Murugesan, K.; Liu, G.; Wang, M.; Chen, T. Variance Reduction Can Improve Trade-Off in Multi-Objective Learning. In Proceedings of the 49th IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP, Seoul, Republic of Korea, 14–19 April 2024. [Google Scholar] [CrossRef]
- Laumanns, M.; Ocenasek, J. Bayesian Optimization Algorithms for Multi-objective Optimization. In Proceedings of the 7th Parallel Problem Solving from Nature, PPSN, Granada, Spain, 7–11 September 2002. [Google Scholar] [CrossRef]
- Belakaria, S.; Deshwal, A.; Jayakodi, N.K.; Doppa, J.R. Uncertainty-Aware Search Framework for Multi-Objective Bayesian Optimization. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, AAAI, New York, NY, USA, 7–12 February 2020. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Fliege, J.; Vaz, A.I.F.; Vicente, L.N. Complexity of gradient descent for multiobjective optimization. Optim. Methods Softw. 2019, 34, 949–959. [Google Scholar] [CrossRef]
- Liu, S.; Chen, P.; Kailkhura, B.; Zhang, G.; III, A.O.H.; Varshney, P.K. A Primer on Zeroth-Order Optimization in Signal Processing and Machine Learning: Principals, Recent Advances, and Applications. IEEE Signal Process. Mag. 2020, 37, 43–54. [Google Scholar] [CrossRef]
- Berahas, A.S.; Cao, L.; Choromanski, K.; Scheinberg, K. A Theoretical and Empirical Comparison of Gradient Approximations in Derivative-Free Optimization. Found. Comput. Math. 2022, 22, 507–560. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Ghadimi, S. Zeroth-Order Nonconvex Stochastic Optimization: Handling Constraints, High Dimensionality, and Saddle Points. Found. Comput. Math. 2022, 22, 35–76. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Xu, K.; Li, X.; Lin, X.; Hong, M.; Cox, D.D. ZO-AdaMM: Zeroth-Order Adaptive Momentum Method for Black-Box Optimization. In Proceedings of the 33th Advances in Neural Information Processing Systems, NeurIPS, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization Methods for Large-Scale Machine Learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Williams, P.N.; Li, K. Black-Box Sparse Adversarial Attack via Multi-Objective Optimisation CVPR Proceedings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2023, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Papernot, N.; McDaniel, P.D.; Goodfellow, I.J.; Jha, S.; Celik, Z.B.; Swami, A. Practical Black-Box Attacks against Machine Learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, AsiaCCS 2017, Abu Dhabi, United Arab Emirates, 2–6 April 2017. [Google Scholar]
- Nesterov, Y.E.; Spokoiny, V.G. Random Gradient-Free Minimization of Convex Functions. Found. Comput. Math. 2017, 17, 527–566. [Google Scholar] [CrossRef]
- Shamir, O.; Zhang, T. Stochastic Gradient Descent for Non-smooth Optimization: Convergence Results and Optimal Averaging Schemes. In Proceedings of the 30th International Conference on Machine Learning, ICML, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]












| Algorithms | Time Complexity | Space Complex |
|---|---|---|
| ZO-AdaMU [10] | ||
| BES [11] | ||
| RSGF [12] | ||
| ASMG [13] | ||
| SZMG (This paper) |
| Notation | Introduction |
|---|---|
| z | Decision variable |
| w | Data random variable independence of z |
| u | A random vector following the Gaussian distribution |
| Smoothness parameter | |
| d | The dimension of parameter z |
| M | Total number of functions |
| The i-th objective function | |
| The smoothed version of function | |
| Gradient of the i-th objective function | |
| Gradient of the function | |
| Stochastic gradient of the function | |
| A matrix containing as columns | |
| A matrix containing as columns | |
| A matrix containing as columns | |
| Learning rates | |
| A constant greater than 0 |
| K | |||||||
|---|---|---|---|---|---|---|---|
| ZO-AdaMU | 0.00001 | 8 | 8 | 0.002 | - | - | - |
| BES | 0.00001 | 8 | 8 | 0.002 | - | - | - |
| RSGF | 0.00001 | 8 | 8 | 0.002 | - | - | - |
| ASMG | - | 8 | 8 | 0.01 | - | - | |
| MGDA | - | - | full | 0.002 | - | - | - |
| SZMG | 0.00001 | 8 | 8 | 0.002 | 1 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wu, Q.; Zhang, M.; Wang, L.; Ge, Y.; Wang, G. Stochastic Zeroth-Order Multi-Gradient Algorithm for Multi-Objective Optimization. Mathematics 2025, 13, 627. https://doi.org/10.3390/math13040627
Li Z, Wu Q, Zhang M, Wang L, Ge Y, Wang G. Stochastic Zeroth-Order Multi-Gradient Algorithm for Multi-Objective Optimization. Mathematics. 2025; 13(4):627. https://doi.org/10.3390/math13040627
Chicago/Turabian StyleLi, Zhihao, Qingtao Wu, Moli Zhang, Lin Wang, Youming Ge, and Guoyong Wang. 2025. "Stochastic Zeroth-Order Multi-Gradient Algorithm for Multi-Objective Optimization" Mathematics 13, no. 4: 627. https://doi.org/10.3390/math13040627
APA StyleLi, Z., Wu, Q., Zhang, M., Wang, L., Ge, Y., & Wang, G. (2025). Stochastic Zeroth-Order Multi-Gradient Algorithm for Multi-Objective Optimization. Mathematics, 13(4), 627. https://doi.org/10.3390/math13040627






