The Constraint Function Response Shifting Scalar-Based Optimization Method for the Reliability-Based Dynamic Optimization Problem
Abstract
:1. Introduction
2. Related Work
2.1. Dynamic Optimization Problem and Direct Transcription Method
2.2. Reliability-Based Design Optimization and the SORA Method
3. The Constraint Function Response Shift Scalar-Based RB-DOP Optimization Method
3.1. Reliability-Based Dynamic Optimization Problem
3.2. The Constraint Function Response Shift Scalar
3.3. The CFRSS-Based RB-DOP Optimization Method
3.3.1. Formulate an Equivalent Deterministic DOP
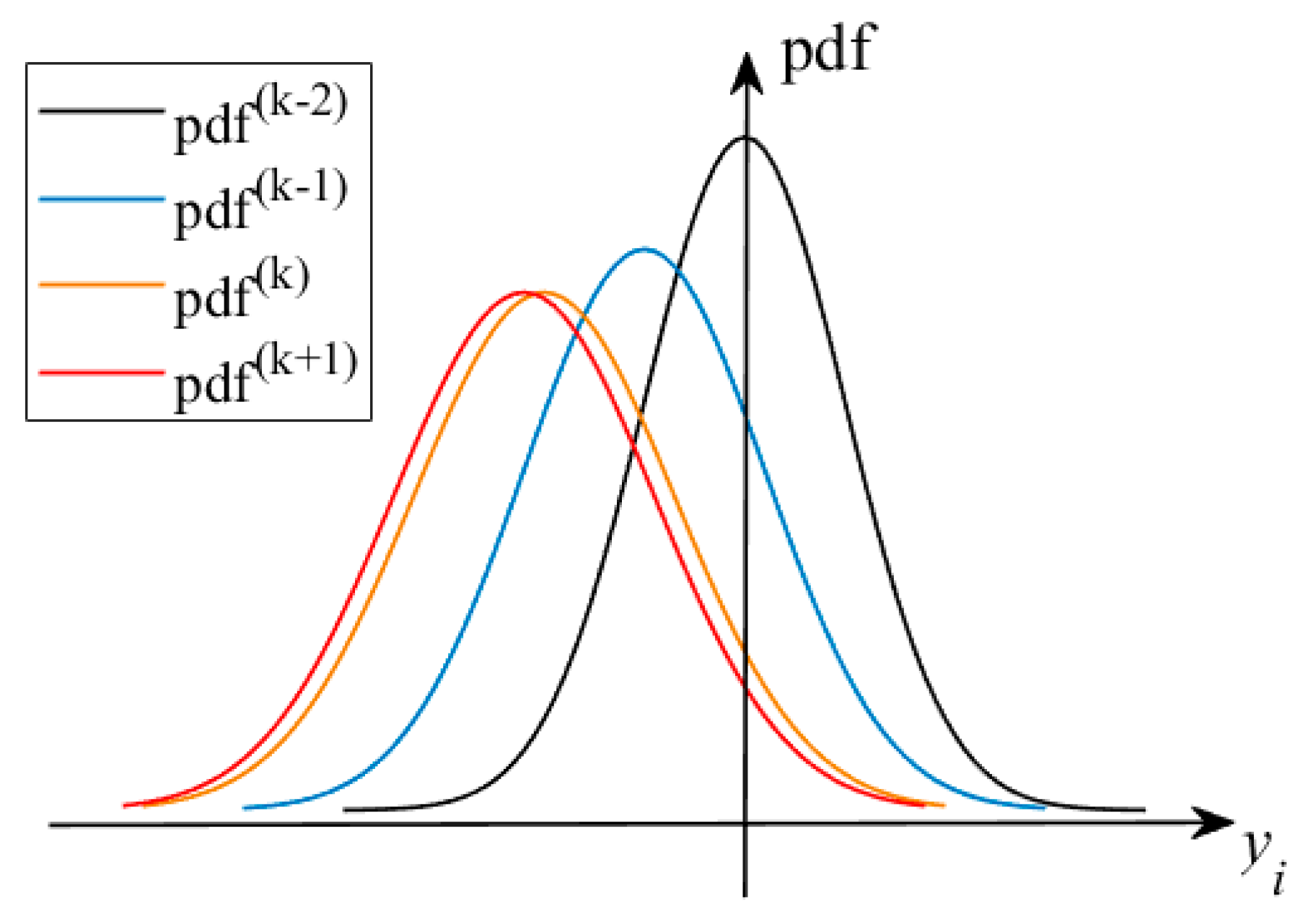
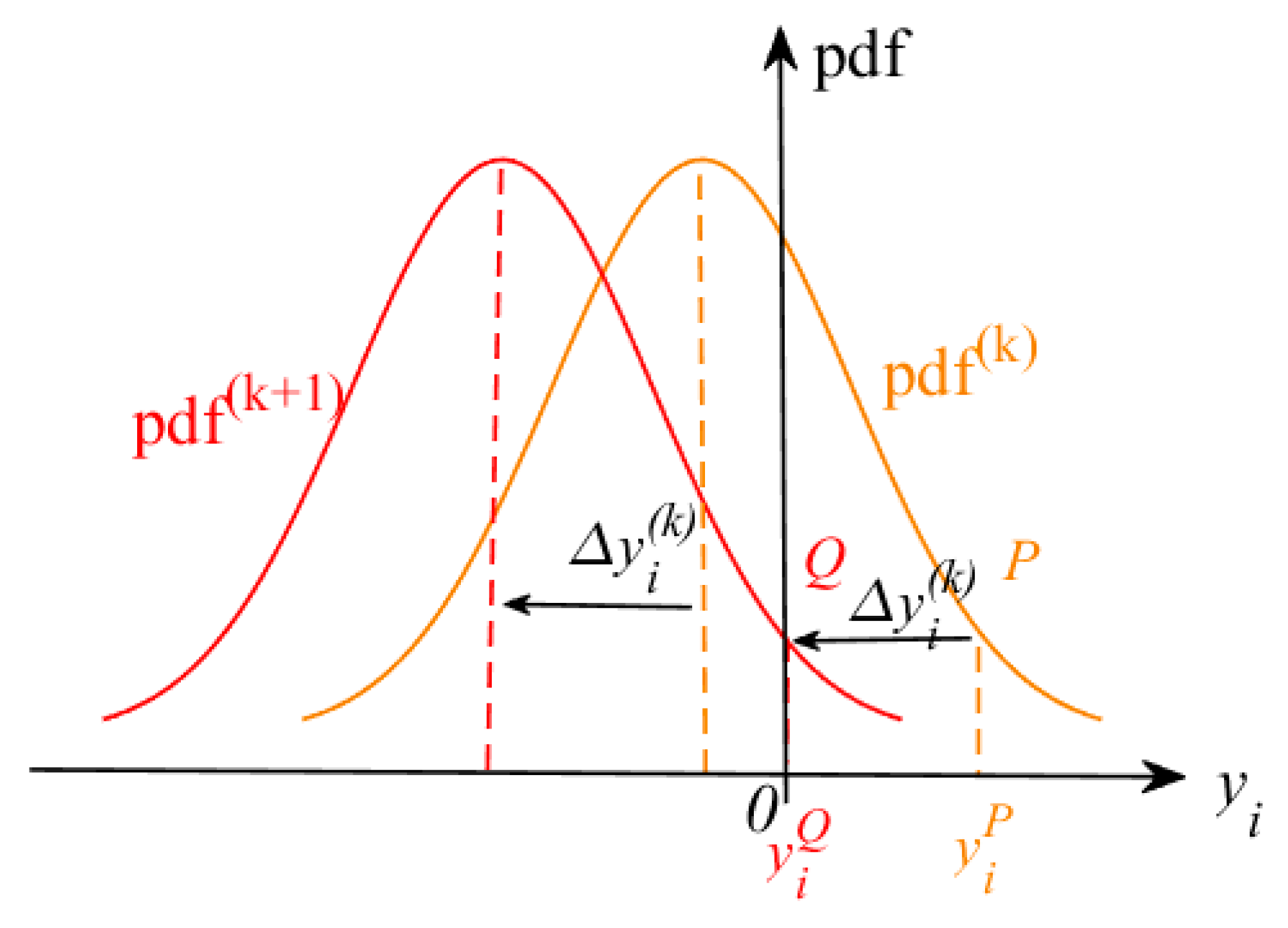
3.3.2. Search for the Constraint Function Response Shift Scalar
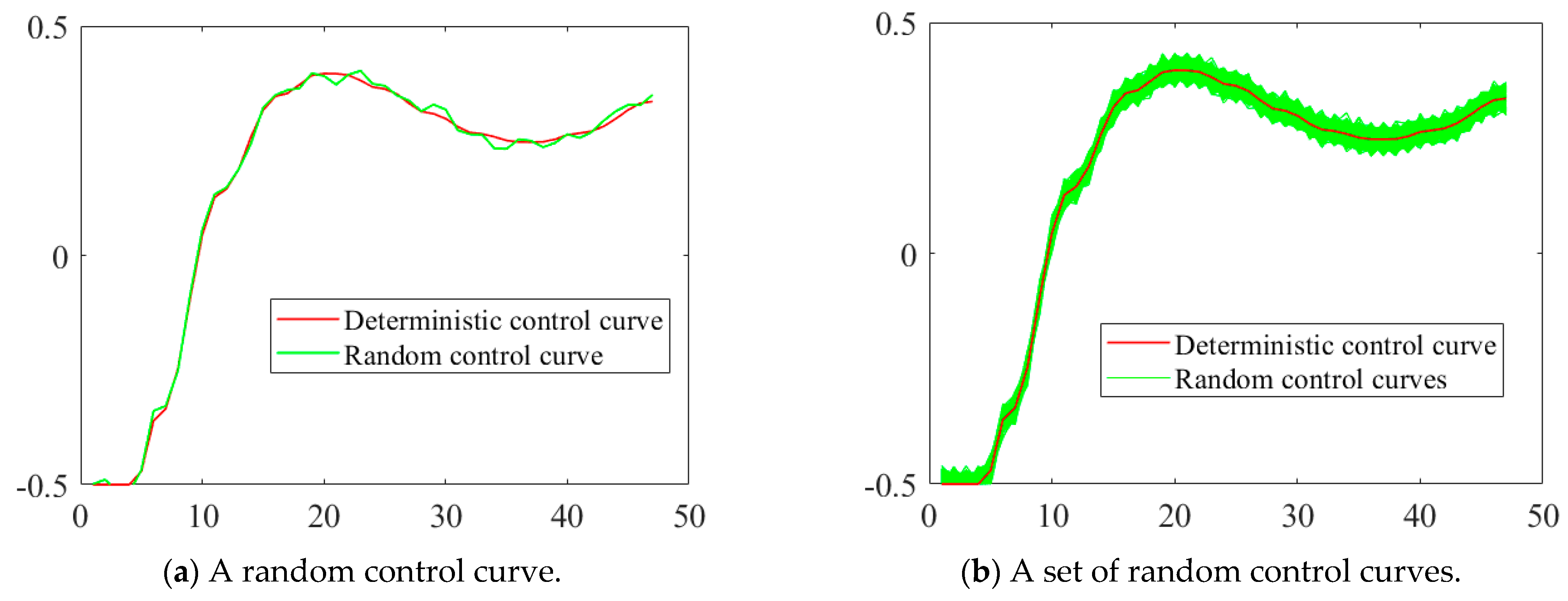
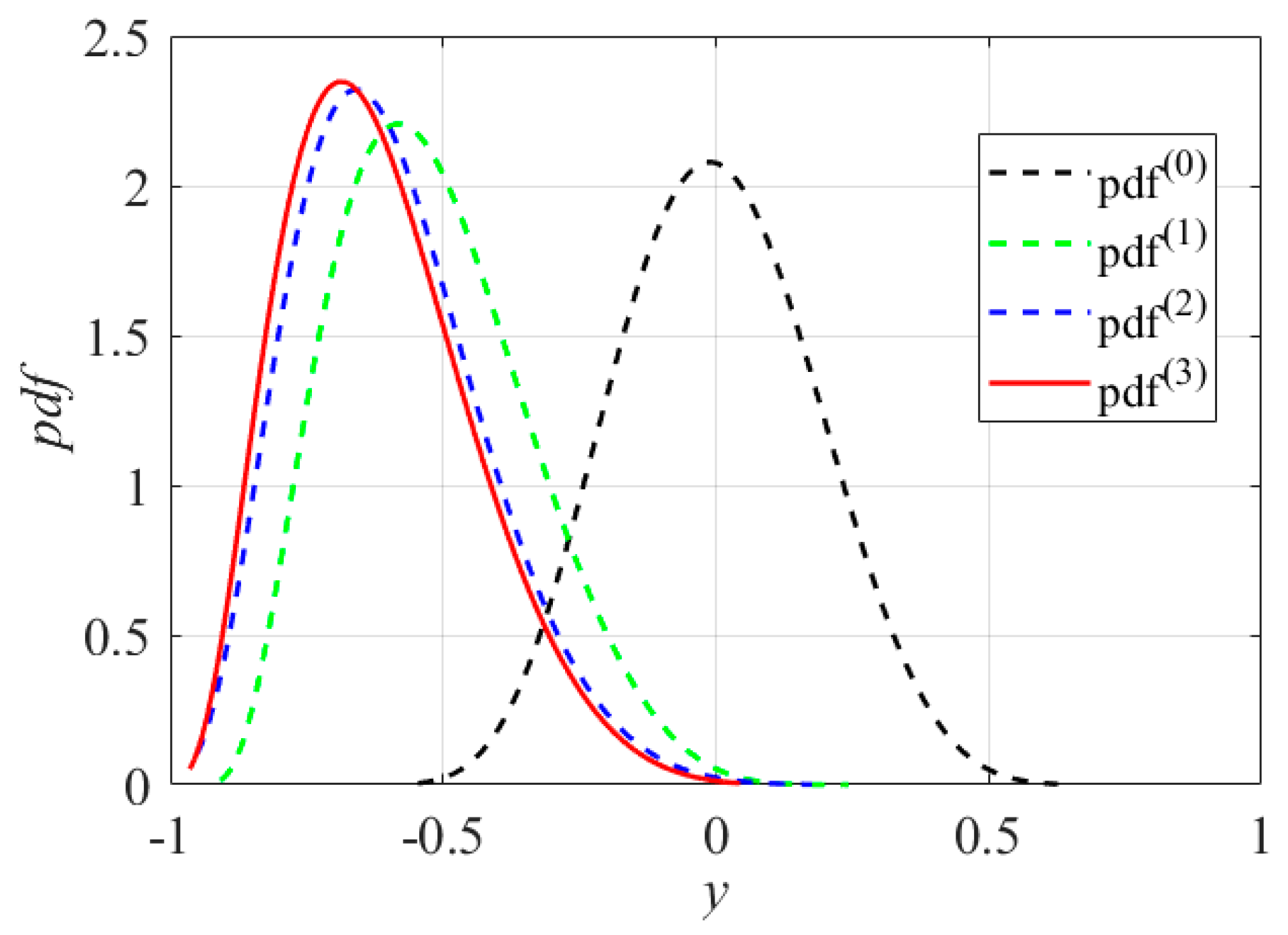
3.3.3. Fit the PDF of the Constraint Function Response
- If the constraint function, , does not contain state variables , then
- If the constraint function, , contains state variables , the state trajectory sample set of is first calculated based on the state equations and using the Runge–Kutta algorithm, then
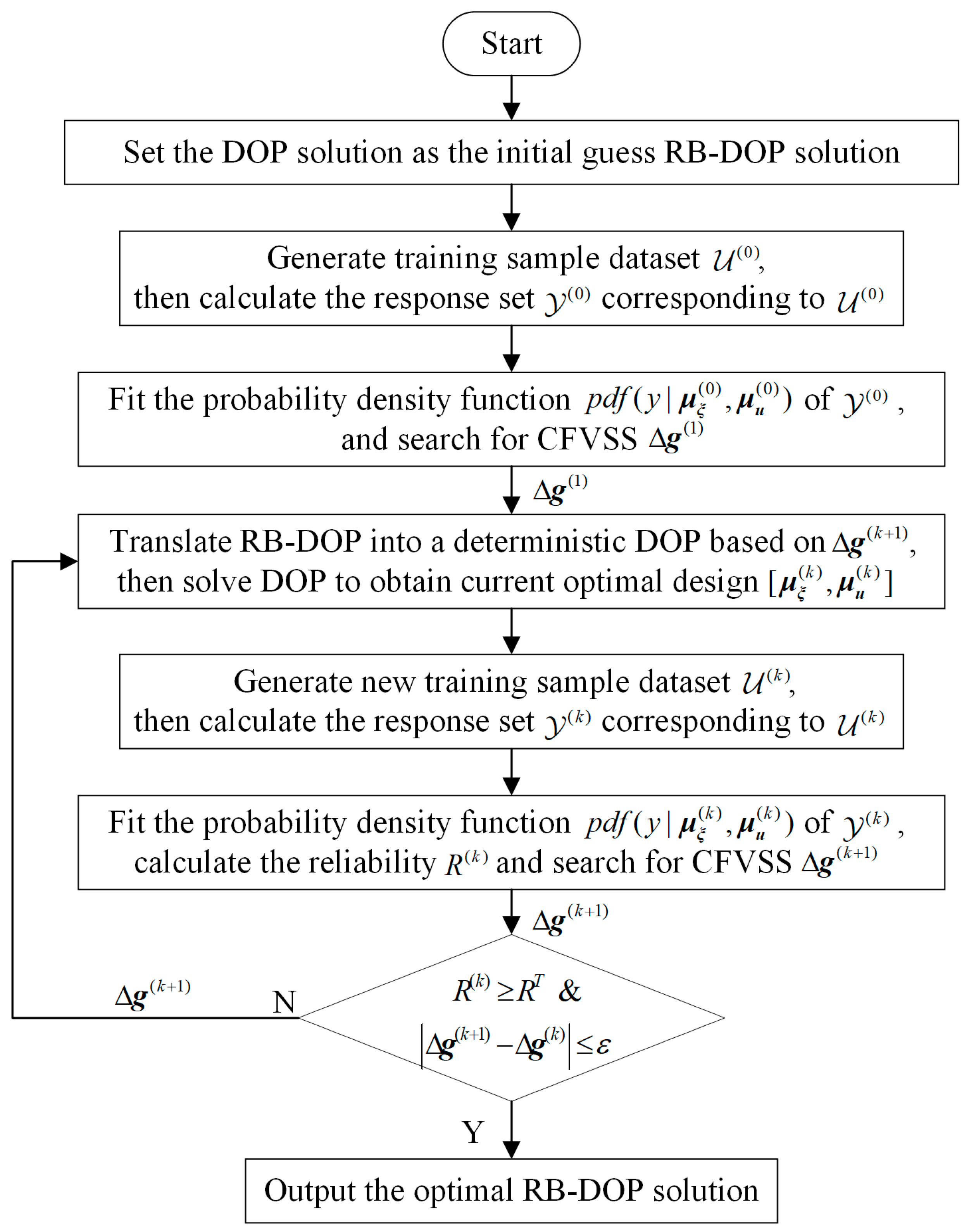
3.4. The Implementation Process of the CFRSS-Based RB-DOP Optimization Method
4. Test Examples
4.1. Numerical Example 1
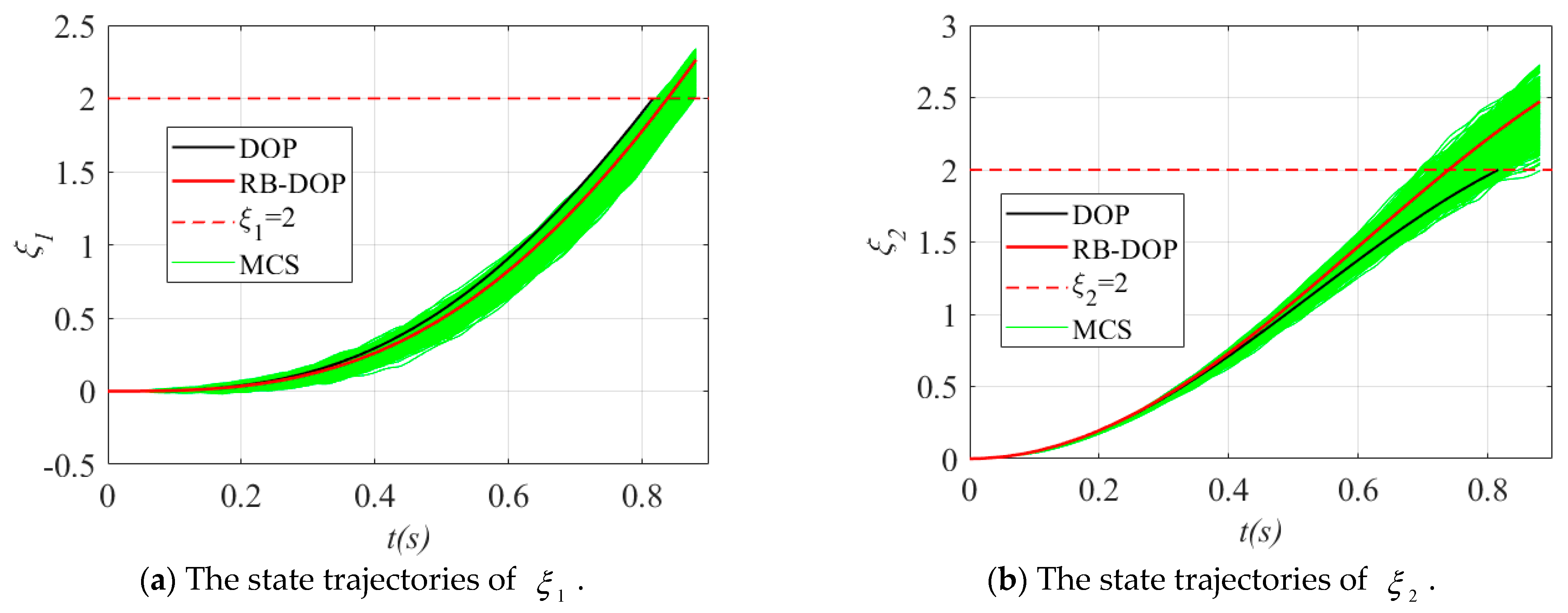
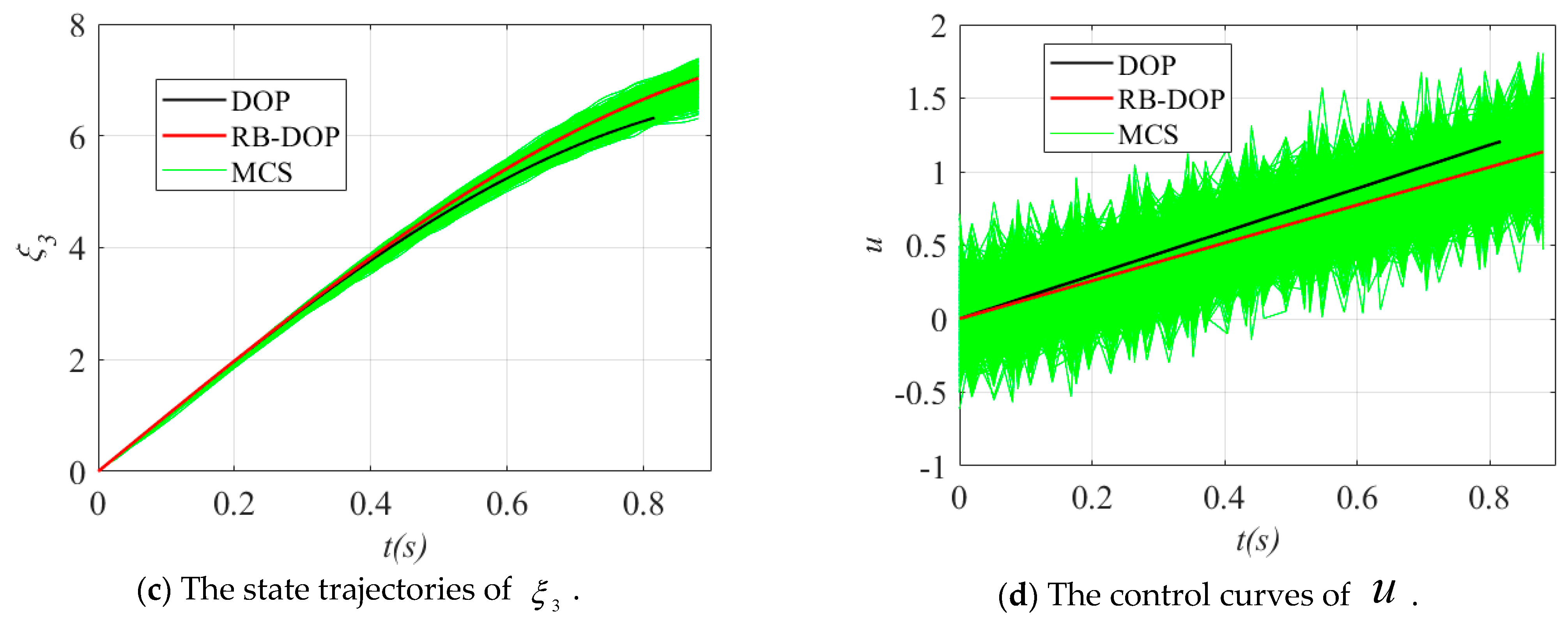
4.2. Numerical Example 2
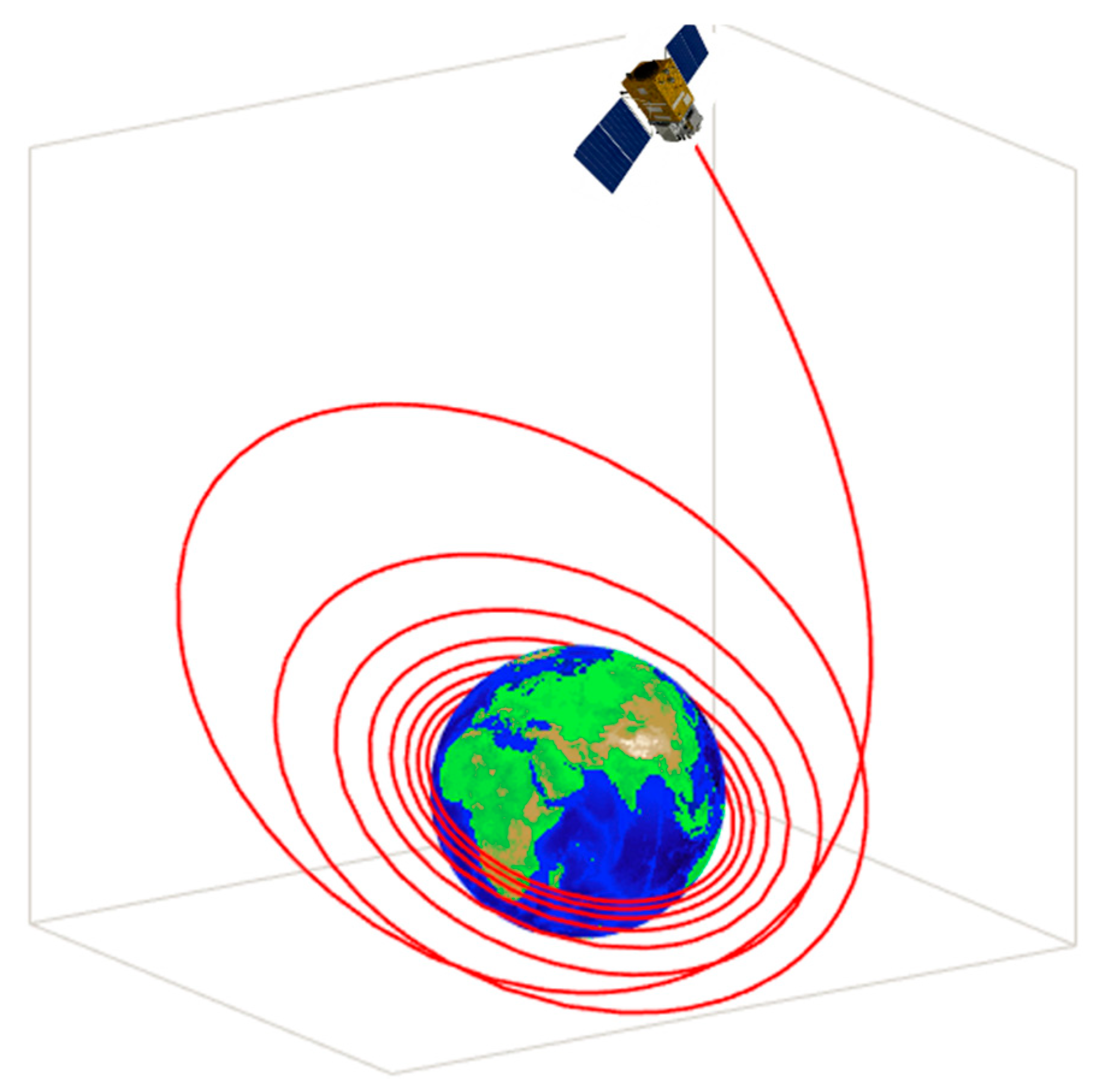
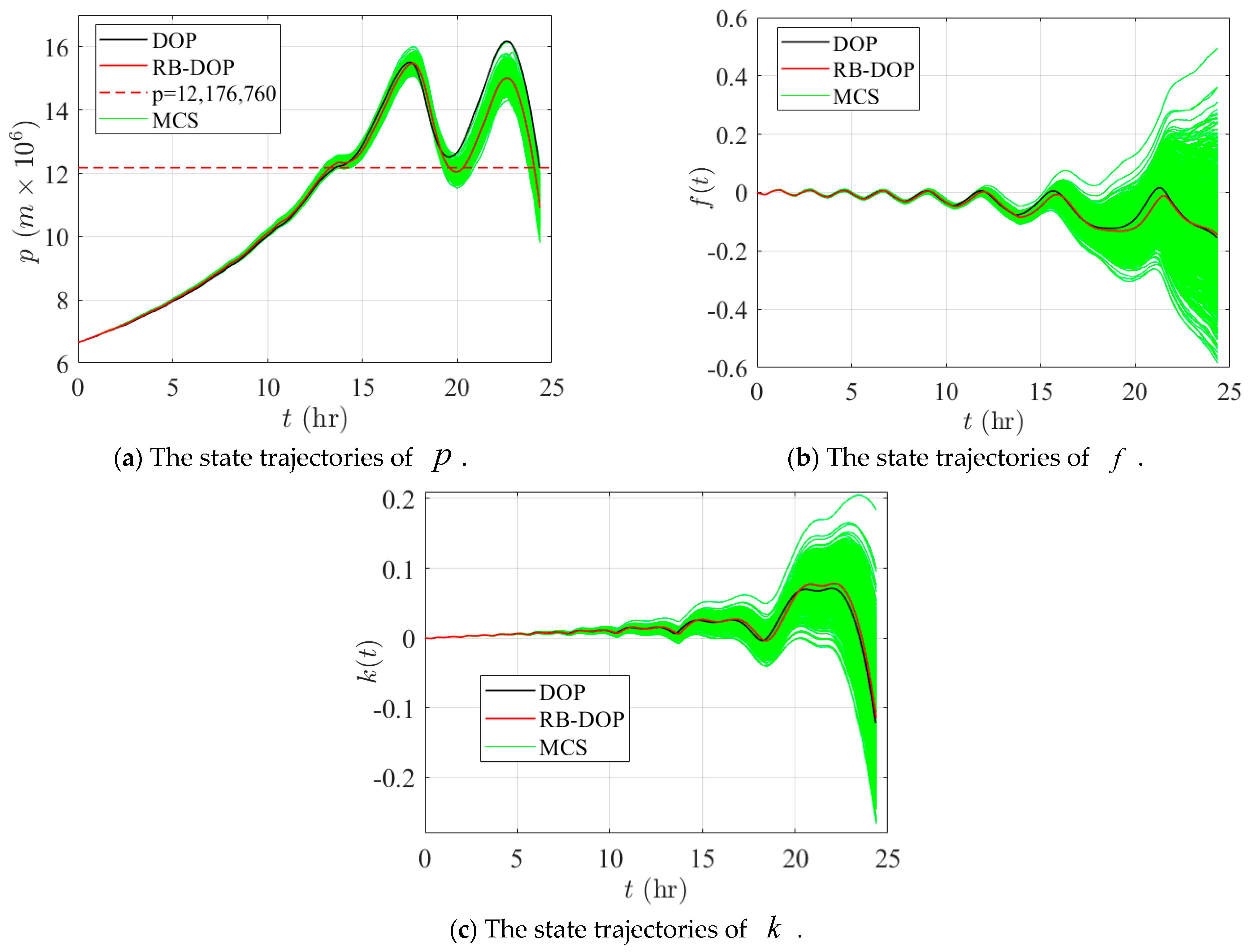
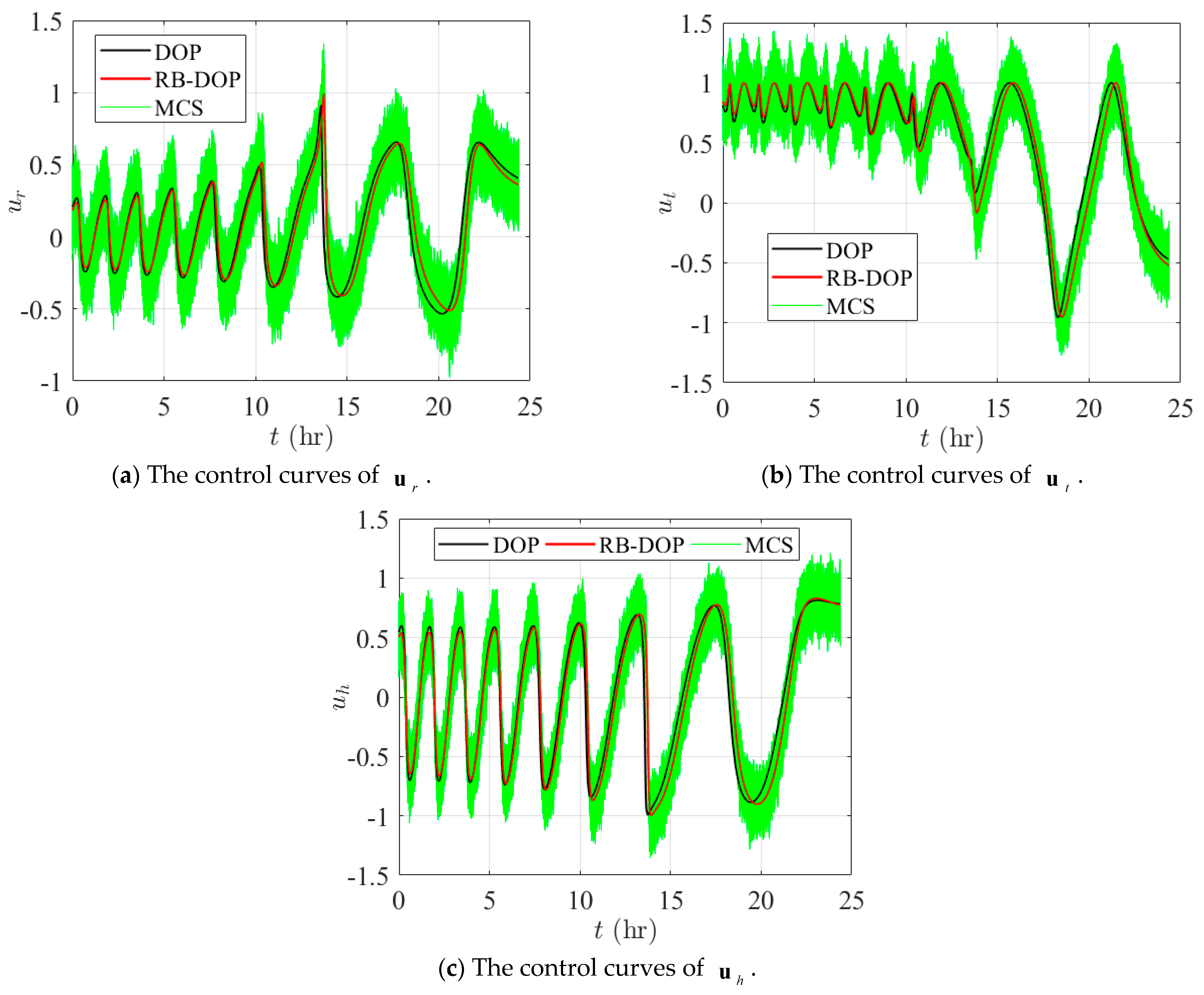
4.3. An RB-DOP in Low-Thrust Orbit Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Mean state variables | Constraint function response shift scalar of | ||
| Mean control variables | Reduced form of | ||
| Objective function of the DOP and RB-DOP | Shift vector component of state and control design variables in the kth iteration | ||
| Objective function of the RBDO | Discrete matrices of | ||
| The ith inequality constraint function | Response value of the constraint | ||
| Discrete state matrix | The PDF of | ||
| Discrete control matrix | The PDF of for design variables | ||
| Random design variables | The PDF of for design variables in the kth iteration | ||
| Mean values of | Constraint function response at point | ||
| Actual reliability of | Target reliability of | ||
| Standard normal cumulative distribution function | Constraint function response shift distance | ||
| Target reliability index of | Integral term of the PDF moves | ||
| Shift vector in the kth iteration | Inverse function of | ||
| The minimum performance target point in the original space | Control sample set | ||
| Standard normal variables converted from | The normal distribution with mean values and standard deviation | ||
| Mean values of | State trajectory sample set | ||
| Mean values of | Constraint function response set | ||
| The ith probability constraint enforced on the design variables at the time node | Error tolerance |
Appendix A
Johnson Distribution
References
- Allison, J.T.; Guo, T.; Han, Z. Co-design of an active suspension using simultaneous dynamic optimization. J. Mech. Des. 2014, 136, 081003. [Google Scholar] [CrossRef]
- Qiao, P.; Liu, X.; Zhang, Q.; Xu, B. An optimal control algorithm toward unknown constrained nonlinear systems based on the sequential sampling and updating of surrogate model. ISA Trans. 2024, 153, 117–132. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Y.; Qiao, P.; Lu, L.; Xia, Z. A right-hand side function surrogate model-based method for the black-box dynamic optimization problem. J. Mech. Des. 2023, 145, 091701. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.; Gamdrelidze, R.; Mishchenko, E. Mathematical Theory of Optimal Processes, 1st ed.; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Liu, P.; Li, G.; Liu, X.; Xiao, L.; Wang, Y.; Yang, C.; Gui, W. A novel non-uniform control vector parameterization approach with time grid refinement for flight level tracking optimal control problems. ISA Trans. 2018, 73, 66–78. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Xu, H. Multiple-interval pseudospectral approximation for nonlinear optimal control problems with time-varying delays. Appl. Math. Model. 2019, 68, 137–151. [Google Scholar] [CrossRef]
- Delkhosh, M.; Cheraghian, H. An efficient hybrid method to solve nonlinear differential equations in applied sciences. Comput. Appl. Math. 2022, 41, 322. [Google Scholar] [CrossRef]
- Pirastehzad, A.; Yazdanpanah, M.J. A Successive Pseudospectral-Based Approximation of the Solution of Regulator Equations. IEEE Trans. Autom. Control 2022, 67, 1760–1775. [Google Scholar] [CrossRef]
- Song, Y.; Pan, B.; Fan, Q.; Xu, B. A computationally efficient sequential convex programming using Chebyshev collocation method. Aerosp. Sci. Technol. 2023, 141, 108584. [Google Scholar] [CrossRef]
- Deshmukh, A.P.; Allison, J.T. Multidisciplinary dynamic optimization of horizontal axis wind turbine design. Struct. Multidiscip. Optim. 2016, 53, 15–27. [Google Scholar] [CrossRef]
- Herber, D.R.; Allison, J.T. Nested and simultaneous solution strategies for general combined plant and control design problems. J. Mech. Des. 2019, 141, 011402. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Y.; Qiao, P. A Dendrite Net based decoupled framework for the reliability-based control co-design problem. Qual. Reliab. Eng. Int. 2024, 40, 925–947. [Google Scholar] [CrossRef]
- Biegler, L.T.; Zavala, V.M. Large-scale nonlinear programming using IPOPT: An integrating framework for enterprise-wide dynamic optimization. Comput. Chem. Eng. 2009, 33, 575–582. [Google Scholar] [CrossRef]
- Serrancolí, G.; Pàmies-Vilà, R. Analysis of the influence of coordinate and dynamic formulations on solving biomechanical optimal control problems. Mech. Mach. Theory 2019, 142, 103578. [Google Scholar] [CrossRef]
- Schueller, G.I.; Jensen, H.A. Computational methods in optimization considering uncertainties—An overview. Comput. Methods Appl. Mech. Eng. 2008, 198, 2–13. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, Z.; Zhou, H. A novel experimental data-driven exponential convex model for reliability assessment with uncertain-but-bounded parameters. Appl. Math. Model. 2020, 77, 773–787. [Google Scholar] [CrossRef]
- Bey, O.; Chemachema, M. Finite-time event-triggered output-feedback adaptive decentralized echo-state network fault-tolerant control for interconnected pure-feedback nonlinear systems with input saturation and external disturbances: A fuzzy control-error approach. Inf. Sci. 2024, 669, 120557. [Google Scholar] [CrossRef]
- Bounemeur, A.; Chemachema, M. Finite-time output-feedback fault tolerant adaptive fuzzy control framework for a class of MIMO saturated nonlinear systems. Int. J. Syst. Sci. 2024, 56, 733–752. [Google Scholar] [CrossRef]
- Meng, Z.; Yildiz, B.S.; Li, G.; Zhong, C.T.; Mirjalili, S.; Yildiz, A.R. Application of state-of-the-art multiobjective metaheuristic algorithms in reliability-based design optimization: A comparative study. Struct. Multidiscip. Optim. 2023, 66, 191. [Google Scholar] [CrossRef]
- Shirgir, S.; Shamsaddinlou, A.; Zare, R.N.; Zehtabiyan, S.; Bonab, M.H. An efficient double-loop reliability-based optimization with metaheuristic algorithms to design soil nail walls under uncertain condition. Reliab. Eng. Syst. Saf. 2023, 232, 109077. [Google Scholar] [CrossRef]
- Ma, Y.-Z.; Jin, X.-X.; Wu, X.-L.; Xu, C.; Li, H.-S.; Zhao, Z.-Z. Reliability-based design optimization using adaptive Kriging-A single-loop strategy and a double-loop one. Reliab. Eng. Syst. Saf. 2023, 237, 109386. [Google Scholar] [CrossRef]
- Kohtz, S.; Zhao, J.; Renteria, A.; Lalwani, A.; Xu, Y.; Zhang, X.; Haran, K.S.; Senesky, D.; Wang, P. Optimal sensor placement for permanent magnet synchronous motor condition monitoring using a digital twin-assisted fault diagnosis approach. Reliab. Eng. Syst. Saf. 2024, 242, 109714. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, L.; Xiao, M.; Lee, S.; Eshghi, A.T. An active learning Kriging-assisted method for reliability-based design optimization under distributional probability-box model. Struct. Multidiscip. Optim. 2020, 62, 2341–2356. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, J.; Gao, L. A system active learning Kriging method for system reliability-based design optimization with a multiple response model. Reliab. Eng. Syst. Saf. 2020, 199, 106935. [Google Scholar] [CrossRef]
- Meng, Z.; Guo, L.; Wang, X. A general fidelity transformation framework for reliability-based design optimization with arbitrary precision. Struct. Multidiscip. Optim. 2022, 65, 14. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Fu, J. A novel projection outline based active learning method and its combination with Kriging metamodel for hybrid reliability analysis with random and interval variables. Comput. Methods Appl. Mech. Eng. 2018, 341, 32–52. [Google Scholar] [CrossRef]
- Zhu, X.; Lu, Z.; Yun, W. An efficient method for estimating failure probability of the structure with multiple implicit failure domains by combining Meta-IS with IS-AK. Reliab. Eng. Syst. Saf. 2020, 193, 106644. [Google Scholar] [CrossRef]
- Jiang, C.; Qiu, H.; Gao, L.; Wang, D.; Yang, Z.; Chen, L. EEK-SYS: System reliability analysis through estimation error-guided adaptive Kriging approximation of multiple limit state surfaces. Reliab. Eng. Syst. Saf. 2020, 198, 106906. [Google Scholar] [CrossRef]
- Nikolaidis, E.; Burdisso, R. Reliability based optimization: A safety index approach. Comput. Struct. 1988, 28, 781–788. [Google Scholar] [CrossRef]
- Fang, Y.; He, C.; Su, Y.; Feng, K.; He, Z. Supplement to the reliability index approach and its application to tunnel reliability problems. Comput. Geotech. 2023, 163, 105767. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.K.; Park, Y.H. A new study on reliability-based design optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef]
- Du, X.P.; Chen, W. Sequential optimization and reliability assessment method for efficient probabilistic design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef]
- Li, G.; Yang, H.; Zhao, G. A new efficient decoupled reliability-based design optimization method with quantiles. Struct. Multidiscip. Optim. 2020, 61, 635–647. [Google Scholar] [CrossRef]
- Liu, W.-S.; Cheung, S.H. Reliability based design optimization with approximate failure probability function in partitioned design space. Reliab. Eng. Syst. Saf. 2017, 167, 602–611. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L. A new local update-based method for reliability-based design optimization. Eng. Comput. 2021, 37, 3591–3603. [Google Scholar] [CrossRef]
- Rocchetta, R.; Crespo, L.G. A scenario optimization approach to reliability-based and risk-based design: Soft-constrained modulation of failure probability bounds. Reliab. Eng. Syst. Saf. 2021, 216, 107900. [Google Scholar] [CrossRef]
- Jiang, X.; Lu, Z. A novel quantile-based sequential optimization and reliability assessment method for safety life analysis. Reliab. Eng. Syst. Saf. 2024, 243, 109810. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, W.; Jiang, C. A PDF-based performance shift approach for reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2021, 374, 113610. [Google Scholar] [CrossRef]
- Allison, J.T.; Herber, D.R. Multidisciplinary design optimization of dynamic engineering systems. AIAA J. 2014, 52, 691–710. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Zhang, Q.; Wu, Y.; Lu, L.; Qiao, P. A single-loop framework for the reliability-based control co-design problem in the dynamic system. Machines 2023, 11, 262. [Google Scholar] [CrossRef]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef]
- Debrota, D.J.; Roberts, S.D.; Swain, J.J.; Dittus, R.S.; Wilson, J.R.; Venkatraman, S. Input modeling with the Johnson System of distributions. In Proceedings of the 1988 Winter Simulation Conference Proceedings, San Diego, CA, USA, 12–14 December 1988; pp. 165–179. [Google Scholar]



| Δg | R | J | |
|---|---|---|---|
| Initial iteration | \ | 50.67% | 1.9699 |
| First iteration | 0.5196 | 99.51% | 2.1114 |
| Second iteration | 0.6024 | 99.80% | 2.1614 |
| Third iteration | 0.6171 | 99.91% | 2.1712 |
| Fourth iteration | 0.6172 | \ | \ |
| Δg1 | Δg2 | R1 | R2 | J | |
|---|---|---|---|---|---|
| Initial iteration | 0 | 0 | 5.37% | 28.35% | 0.8165 |
| First iteration | 0.2075 | 0.4044 | 98.80% | 99.73% | 0.8691 |
| Second iteration | 0.2570 | 0.4621 | 99.87% | 99.89% | 0.8790 |
| Third iteration | 0.2633 | 0.4727 | 99.89% | 99.90% | 0.8804 |
| Fourth iteration | 0.2645 | 0.4727 | 99.90% | 99.90% | 0.8806 |
| Fifth iteration | 0.2645 | 0.4727 | \ | \ | \ |
| Δg1 | Δg2 | R1 | R2 | J | |
|---|---|---|---|---|---|
| Initial iteration | 0 | 0 | 47.42% | 100.00% | 0.09630 |
| First iteration | 4,306,504.6 | 0 | 99.92% | 100.00% | 0.09571 |
| Second iteration | 4,172,686.4 | 0 | 99.91% | 100.00% | 0.09573 |
| Third iteration | 4,164,885.3 | 0 | 99.90% | 100.00% | 0.09575 |
| Fourth iteration | 4,168,412.6 | 0 | \ | \ | \ |
| p(tf)/m | J/kg | R1 | R2 | |
|---|---|---|---|---|
| DOP | 12,176,760 | 0.09630 | 47.42% | 100% |
| RB-DOP | 10,907,302.9 | 0.09575 | 99.90% | 100% |
| Change | ↓ 10.42% | ↓ 0.57% | ↑ 52.48% | = |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, P.; Zhang, Q.; Wu, Y. The Constraint Function Response Shifting Scalar-Based Optimization Method for the Reliability-Based Dynamic Optimization Problem. Mathematics 2025, 13, 567. https://doi.org/10.3390/math13040567
Qiao P, Zhang Q, Wu Y. The Constraint Function Response Shifting Scalar-Based Optimization Method for the Reliability-Based Dynamic Optimization Problem. Mathematics. 2025; 13(4):567. https://doi.org/10.3390/math13040567
Chicago/Turabian StyleQiao, Ping, Qi Zhang, and Yizhong Wu. 2025. "The Constraint Function Response Shifting Scalar-Based Optimization Method for the Reliability-Based Dynamic Optimization Problem" Mathematics 13, no. 4: 567. https://doi.org/10.3390/math13040567
APA StyleQiao, P., Zhang, Q., & Wu, Y. (2025). The Constraint Function Response Shifting Scalar-Based Optimization Method for the Reliability-Based Dynamic Optimization Problem. Mathematics, 13(4), 567. https://doi.org/10.3390/math13040567





