Abstract
In this paper, a classical layer-resolving finite difference scheme is formulated to solve a system of two singularly perturbed time-dependent initial value problems with discontinuity occurring at in the source terms and Robin initial conditions. The delay term occurs in the spatial variable, and the leading term of the spatial derivative of each equation is multiplied by a distinct small positive perturbation parameter, inducing layer behaviors in the solution domain. Due to the presence of perturbation parameters, discontinuous source terms, and delay terms, initial and interior layers occur in the solution domain. In order to capture the abrupt change that occurs due to the behavior of these layers, the solution is further decomposed into smooth and singular components. Layer functions are also formulated in accordance with layer behavior. Analytical results and bounds of the solution and its components are derived. The formulation of a finite difference scheme involves discretization of temporal and spatial axes by uniform and piecewise uniform meshes, respectively. The formulated scheme achieves first-order convergence in both time and space. At last, to bolster the numerical scheme, example problems are computed to prove the efficacy and accuracy of our scheme.
Keywords:
finite difference scheme; singularly perturbed problems; discontinuous source terms; spatial delay; Robin initial conditions; interior layers MSC:
35L03; 65M06; 65M12; 65M15; 65M22; 65M50
1. Introduction
Solving singular perturbation problems (SPPs) is very tedious due to the presence of layer phenomena in the solution domain. They have a wide range of applications in the field of applied mathematics and engineering due to their complex boundary layer phenomena. Their application is prevalent in areas such as aerodynamics to examine boundary layer behavior; in fluid mechanics to model flow transitions and turbulence; in elasticity to study material deformation under stress; and also in the fields of optimal control theory, chemical processes, biological modeling, population dynamics, and ecology [1,2,3,4,5,6,7,8,9], demonstrating their wide-ranging relevance. Singularly perturbed delay differential equations (SPDDEs) have a wide range of applications in diverse fields [10,11,12,13,14].
The presence of discontinuity in the source term further complicates solving SPPs as the solution tends to behave unevenly or non-smoothly at the discontinuity point. This leads to the formation of an interior layer at the region in the domain where the discontinuity occurs. To tackle such difficulties in estimating the solution of SPPs, classical numerical schemes, such as fitted mesh methods [15], are modified by employing highly refined meshes (i.e., Shishkin mesh or Bakhvalov mesh) to provide numerical approximations by preserving the monotonicity of the original problem. Many specialized techniques have been introduced by researchers across the globe in order to overcome difficulties arising in solving SPPs.
Abagero et al. [16] employed a fitted nonstandard numerical method to solve SPPs with Robin-type boundary conditions and discontinuous source terms. Sahoo & Gupta [17] employed a first-order upwind scheme on a Shishkin mesh to solve convection–diffusion SPPs with discontinuous convective and source terms. They further employed the Richardson extrapolation scheme to enhance the order of convergence. Singh et al. [18] devised spline-based numerical techniques, such as the Crank–Nicolson scheme and trigonometric B-spline basis function, to solve two-parameter SPPs with discontinuity in the convection coefficient and source term. The Richardson extrapolation scheme was implemented by the authors to enhance the accuracy in the spatial direction. Chawla et al. [19] employed a backward difference scheme on Shishkin and Bakhvalov meshes to solve first-order singularly perturbed differential equations (SPDEs) with discontinuous source terms. Cen et al. [20] developed a quadratic B-spline collocation method on a Shishkin-type mesh to solve a semilinear reaction–diffusion SPP with a discontinuous source term. Soundararajan et al. [21] employed the backward Euler Method for time discretization and the streamline-diffusion Finite Element Method (FEM) on a Shishkin mesh to solve 1D parabolic SPPs with a discontinuous source term. Ajay Singh Rathore & Vembu Shanthi [22] proposed an exponentially fitted mesh method to solve a singularly perturbed Fredholm integro-differential equation with a discontinuous source term.
In [23], Ismail & Elmekkawy utilized the Restrictive Padé Approximation to solve a singularly perturbed first-order hyperbolic Partial Differential Equation, where a small perturbation is multiplied by the term containing the time derivative. The present paper differs from [23] in the treatment of the numerical analysis as well as in the problem formulation. The problems considered in this article involve solving a system of two singularly perturbed time-dependent initial value problems. These problems contain distinct perturbation parameters that multiply the spatial term involving the highest-order derivative. Additionally, they contain a spatial delay, and a discontinuity occurs at in the source terms. Initial and interior layers occur in the solution domain due to the presence of perturbation parameters, discontinuous source terms, and delay terms. This divergent problem structure and the complex behavior of the solution necessitate developing a classical layer-resolving finite difference scheme (FDS) [24] using a highly refined Shishkin mesh. This method is able to precisely capture the layer behavior of solutions and achieves first-order convergence in both time and space. Numerical illustrations confirm the effectiveness of the proposed method and clearly exhibit its first-order convergence. The subsequent section outlines the organizing framework of the paper. The notation and terminology are discussed in Section 2. Section 3 outlines the problem statement. The solution components and layer functions are discussed in Section 4. In Section 5, the bounds on the solution and its components are derived. Discrete solution components and error estimates are discussed in Section 6. A numerical scheme is constructed for example problems in Section 7.
2. Notation and Terminology
This section defines the key notation and terminology used throughout the paper to ensure clarity and consistency.
- singular perturbation parameter
- independent variables
- solution of the continuous problem (1)
- smooth component of the solution
- singular component of the solution
- solution of the discrete problem (29)
- discrete smooth component of the solution
- discrete singular component of the solution
- continuous barrier function
- discrete barrier function
- backward difference operators
- forward difference operators
- is the point at which discontinuity occurs in the domain
The jump at is denoted by a function where
For any n-vector , the norm
For any scalar-valued function is a closed set in ,
For any vector-valued function y,
For any function , the vector discrete maximum norm defined on the Shishkin mesh
Domain defined for continuous case
Domain defined for discrete case
Temporal domain
: , :
Spatial domain
: , : .
The presence of discontinuity in domain necessitates the consideration of two different cases. In Case 1, the discontinuity occurs in the interval , and, in Case 2, the discontinuity occurs in the interval .
Case 1: Here, , , and
Case 2: Here, and ,
3. The Problem Statement
In this section, we consider the following system of two singularly perturbed time-dependent initial value problems with spatial delay and discontinuity source terms.
with Robin initial conditions in space variable and Dirichlet initial condition in time variable
For all ,,, with , , and . The functions are assumed to be in , and can operate on functions in the domain .
Furthermore, for all , the components of and , respectively, satisfy the following conditions:
and, for any positive number ,
The function is discontinuous at due to a finite jump. So, the solution does not possess a continuous first-order derivative at .
Case 1:
Problem (1) can be reformulated as
where .
For problems (6) and (7), the solution components and exhibit an initial layer at and interior layers at , , and , each of width . Furthermore, the solution component exhibits additional layers of width at , , , and .
Case 2:
Problem (1) can be reformulated as
For problems (8) and (9), the solution components and exhibit an initial layer at and interior layers at and , each of width . Furthermore, the solution component exhibits additional layers of width at , , and .
The existence of the solution of problem (1) is discussed in the following theorem by adopting similar procedure to that in [24].
Proof.
The proof is by construction.
Case 1: Let be the particular solutions of
Consider the function
where , and are solutions of
and , where are any particular vector constants. can be derived in the following way so as to have .
The product between vectors is the Schur product of vectors.
Case 2: Let be the particular solutions of
Consider the function
where , and are solutions of
and , where are any particular vector constants. can be determined as follows to ensure that .
A similar approach confirms the existence of a solution for . When exists and is continuous at as is both well defined and continuous at this point. The proof of the theorem is complete. □
Uniqueness and Stability Analysis
- Continuous case
Lemma 1.
Proof.
For , let us consider . If , there is nothing to prove. Let us assume that . Suppose and then
which contradicts our assumption, and, for which also contradicts our assumption. Therefore, . Also, and .
Thus, for , it follows that
which contradicts our assumption.
For , it follows that
which contradicts our assumption. If , then and there exists a neighborhood such that for all . If for any point , and then . If for all , it can be noted that is an increasing function in ; as a consequence, cannot attain its minimum at , which contradicts our assumption. This implies that and for all , and then . The proof of the lemma is complete. □
Proof.
Consider the barrier functions
where
If , then
and
Lemma 1 implies that on . Then,
The proof of the lemma is complete. □
4. Solution Components and Layer Functions
The continuous solution of (1) is decomposed into .
represents the solution of the following equation.
Case 1:
Case 2:
represents the solution of the following equation.
Case 1:
Case 2:
with ,
Functions , known as layer functions, are introduced and associated with the solution as follows
where
5. Solution Bounds
Theorem 2.
Let conditions (4) (5) hold for and . Let represent the solution of problems (1), (2), and (3). Then, for each , there exists a constant C such that, for all
for Case 1 and for all
Proof.
The bounds on the solutions are derived by employing steps and techniques analogous to those of Lemma 3.1 in [25]. □
The succeeding lemmas deal with finding bounds on and their derivatives.
Lemma 3.
Proof.
The bounds on the and its derivatives are derived by employing steps and techniques analogous to those of Lemma 5.1 in [26]. □
Lemma 4.
Case 1:
For all and
Case 2:
For all and
Proof.
The bounds on the and its derivatives are derived by employing steps and techniques analogous to those of Lemma 5.2 in [26]. □
5.1. Sharper Estimates
Definition 1.
For each , for Case 1 and for Case 2, the unique point in is defined by
Definition 2.
For all such that , there exist points that are uniquely defined and satisfy the inequalities presented below for Case 1 and Case 2.
Case 1:
Case 2:
Lemma 5.
for which the following estimates hold for each .
Case 1:
For all and
Case 2:
For all and
Proof.
The required estimates are derived by employing steps and techniques analogous to those of Lemma 10.3 in [26]. □
5.2. Domain Discretization
Temporal domain is meticulously discretized into a uniform mesh composed of M mesh intervals on . Now, to capture the intricate layer behavior of the solutions, the spatial domain is discretized into a piecewise-uniform Shishkin mesh composed of N mesh intervals.
For Case 1, the interval is partitioned into 12 sub-intervals, outlined as follows
The transition parameters are defined as
The sub-intervals and are discretized using a uniform mesh consisting of mesh points. A uniform mesh consisting of mesh points is deployed on each of the sub-intervals , and .
For Case 2, the interval is partitioned into 9 distinct sub-intervals, outlined as follows
The transition parameters are defined as
The sub-intervals and are discretized using a uniform mesh consisting of mesh points. A uniform mesh consisting of mesh points is deployed on each of the sub-intervals , and
Also, , , .
For problems (1)–(3), a classical layer-resolving finite difference scheme is developed using the aforementioned discretization.
The problem represented in (29) is reformulated for Case 1 and Case 2 as follows:
Case 1:
Case 2:
where
for
Lemma 6.
Proof.
For , let and consider the case where the lemma does not hold. Then, From the stipulated hypotheses, it is simple to establish that , and
If , then
which is a contradiction. For , which leads to a contradiction.
Case 1: For
which contradicts our assumption. For it follows that
which contradicts our assumption.
Case 2: For
which contradicts our assumption. For it follows that
which contradicts our assumption.
If for Case 1, then
Also,
so
Then, which contradicts our assumption.
If for Case 2, then
Also,
so
Then, which contradicts our assumption. This implies that The proof of the lemma is complete. □
Lemma 7.
for , and, for Case 2,
for
Proof.
Define barrier functions
It is evident that on and also on on , and, for , it follows that
Hence, from the result of Lemma 6, it follows that on for Case 1. By applying analogous procedure used in Case 1, the required result on for Case 2 is obtained. The proof of the lemma is complete. □
6. Discrete Solution Components and Error Estimates
The discrete solution of (29) is decomposed into , where and are discrete smooth and discrete singular components, respectively.
The problems represented in (35) and (36) are reformulated for Case 1 and Case 2 as follows:
Case 1:
Case 2:
The error at each point is provided by . For in Case 1 and in Case 2, the local truncation errors can be expressed as follows:
Theorem 3.
Proof.
The proof of the theorem is complete. □
Theorem 4.
Proof.
The procedure outlined in Theorem 10.5 of [26] is employed in this theorem as it leads to a similar result. □
From the above results, it is concluded that, for Case 1, or or , and, for Case 2, or ,
Now, at the point or or for Case 1 and or for Case 2, it follows that
Theorem 5.
Proof.
For Case 1, consider the two mesh functions
and, for Case 2,
where C is suitably chosen as sufficiently large constant. Hence, for Case 1, or or , and, for Case 2, or
and, for Case 1, or or , and, for Case 2, or
For Case 1, or or , and, for Case 2, or
Thus, for sufficiently large N,
The proof of the theorem is complete. □
7. Numerical Illustrations
To elucidate the proposed numerical scheme, numerical examples are introduced in this section to address two distinct cases resulting from the presence of discontinuous source term in the domain.
The following are some of the notations present in this section:
- : maximum point-wise two-mesh differences;
- : —uniform maximum point-wise two-mesh differences;
- : —uniform order of local convergence;
- : —uniform order of convergence;
- : —uniform error constant.
M and N are the numbers of mesh points in temporal and spatial domains, respectively. Two-mesh algorithm [27] is applied to compute along with .
The —uniform maximum point-wise two-mesh differences value is obtained as follows:
The —uniform order of convergence is obtained as follows:
The —uniform error constant is obtained as follows:
Example 1.
Consider the following system of two singularly perturbed time-dependent delay initial value problems,
where
Case 1: presents in the interval
Case 2: presents in the interval
and, with Robin initial conditions in space and Dirichlet initial conditions in time
The perturbation parameters are expressed in terms of as and , with taking different values as outlined in Table 1, Table 2, Table 3 and Table 4. The values and are calculated using the procedure outlined above, and the results are presented in Table 1 for Case 1 and Table 3 for Case 2. The values and are obtained from Table 1 for Case 1 and the values and are obtained from Table 3 for Case 2. From both tables, it is evident that, as N increases, the values of increase, whereas the values of decrease. The computation times in seconds for obtaining the maximum point-wise errors for Case 1 are presented in Table 2, while those for Case 2 are provided in Table 4. Figure 1 represents the solutions of Case 1 of Example 1 for , and . The solutions and exhibit rapid transitions in the initial and interior regions of the domain due to the influence of perturbation parameters, discontinuous source terms, and delay terms. The solution components and form initial layers at near boundary region of the domain, while the interior layers emerge at due to the delay terms, as well as at and as a result of discontinuities in the source terms. Figure 2 represents the solutions of Case 2 of Example 1 for , and . The solution components and form initial layers at near boundary region of the domain, while interior layers emerge at due to the delay terms, and at as a result of discontinuities in the source terms.

Table 1.
For Case 1 (Example 1), values of and generated for .

Table 2.
Computation time in seconds for obtaining maximum point-wise errors of Example 1 (Case 1).

Table 3.
For Case 2 (Example 1), values of and generated for .

Table 4.
Computation time in seconds for obtaining maximum point-wise errors of Example 1 (Case 2).
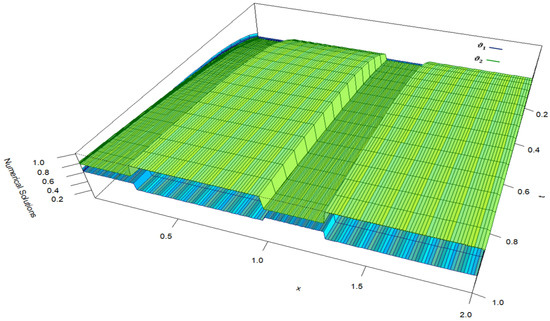
Figure 1.
Visualization of numerical solutions of Case 1 (Example 1), illustrating initial layers at , interior layers at due to the delay terms, as well as at and due to discontinuities.
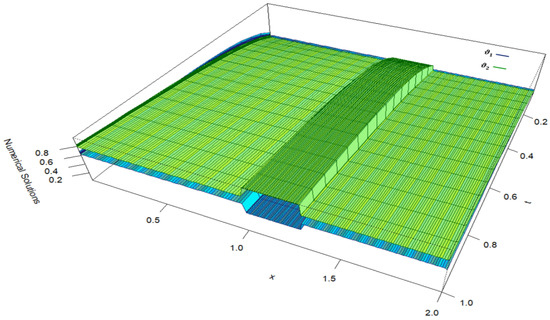
Figure 2.
Visualization of numerical solutions of Case 2 (Example 1), illustrating initial layers at , interior layers at due to the delay terms, and at due to discontinuities.
Example 2.
Consider the following system of two singularly perturbed time-dependent delay initial value problems,
where
Case 1: presents in the interval
Case 2: presents in the interval
and, with Robin initial conditions in space and Dirichlet initial conditions in time,
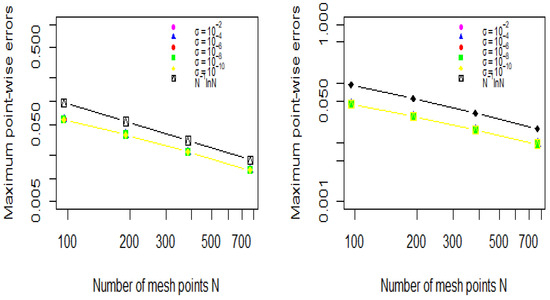
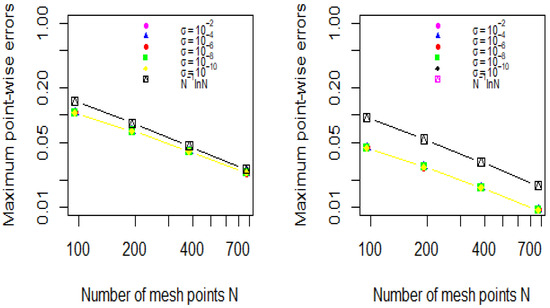
The perturbation parameters are expressed in terms of as and , with taking different values as outlined in Table 5, Table 6, Table 7 and Table 8. The values and are calculated using the procedure outlined above, and the results are presented in Table 5 for Case 1 and Table 7 for Case 2. The values and are obtained from Table 5 for Case 1 and the values and are obtained from Table 7 for Case 2. From both tables, it is evident that, as N increases, the values of increase, whereas the values of decrease. The computation times in seconds for obtaining the maximum point-wise errors for Case 1 are presented in Table 6, while those for Case 2 are provided in Table 8. Figure 3 represents the solutions of Case 1 of Example 2 for , and . The solutions and exhibit rapid transitions in the initial and interior regions of the domain due to the influence of perturbation parameters, discontinuous source terms, and delay terms. The solution components and form initial layers at near the boundary region of the domain, while the interior layers emerge at due to the delay terms, as well as at and as a result of discontinuities in the source terms. Figure 4 represents the solutions of Case 2 of Example 2 for , and . The solution components and form initial layers at near the boundary region of the domain, while the interior layers emerge at due to the delay terms, and at as a result of discontinuities in the source terms. Figure 5 and Figure 6 present log-log plots of the maximum point-wise errors for Example 1 (Case 1 and Case 2) from Table 1 and Table 3, and for Example 2 (Case 1 and Case 2) from Table 5 and Table 7, respectively.

Table 5.
For Case 1 (Example 2), values of and generated for .

Table 6.
Computation time in seconds for obtaining maximum point-wise errors of Example 2 (Case 1).

Table 7.
For Case 2 (Example 2), values of and generated for .

Table 8.
Computation time in seconds for obtaining maximum point-wise errors of Example 2 (Case 2).
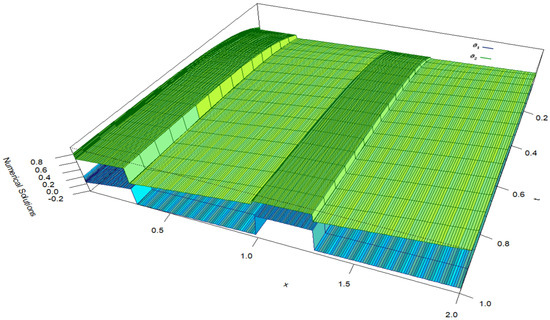
Figure 3.
Visualization of numerical solutions of Case 1 (Example 2), illustrating initial layers at , interior layers at due to the delay terms, as well as at and due to discontinuities.
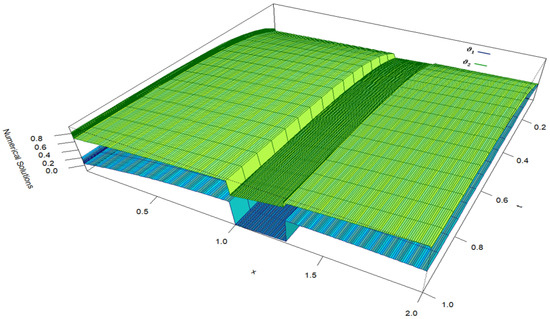
Figure 4.
Visualization of numerical solutions of Case 2 (Example 2), illustrating initial layers at , interior layers at due to the delay terms, and at due to discontinuities.
8. Conclusions
In this article, a classical layer-resolving numerical scheme was constructed for solving a system of two singularly perturbed time-dependent delay initial value problems with source terms that exhibit a jump at a specific point due to discontinuity and Robin initial conditions. This scheme incorporates a specially crafted piecewise uniform mesh to capture the layer behavior of the solutions in the initial and interior regions of the solution domain owing to the existence of delay and discontinuous source terms. The numerical experiments validated the computational outcomes, demonstrating strong concordance with the theoretical analysis. Additionally, the proposed method achieved first-order convergence. Moreover, the results clearly demonstrate that, as the number of mesh points increases, the order of convergence improves, while the error constant decreases. This demonstrates the robustness and efficiency of the proposed scheme. The results indicate that the proposed method remains stable and accurate across varying perturbation parameters, making it an efficient tool to solve complex equations. Future research will focus on extending the work to semilinear and nonlinear problems, with an emphasis on developing novel numerical methods to enhance computational efficiency.
Author Contributions
Conceptualization, J.P.M. and R.B.K.; methodology, R.B.K. and J.P.M.; software, J.P.M. and R.B.K.; validation, J.P.M., G.E.C., and S.L.P.; formal analysis, R.B.K. and J.P.M.; investigation, R.B.K., J.P.M., and G.E.C.; resources, J.P.M. and R.B.K.; data curation, R.B.K. and J.P.M.; writing—original draft preparation, R.B.K. and J.P.M.; writing—review and editing, R.B.K., J.P.M., G.E.C., and S.L.P.; visualization, R.B.K.; supervision, G.E.C. and J.P.M.; project administration, J.P.M. and G.E.C.; funding acquisition, G.E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SPPs | Singularly Perturbed Problems |
| SPDEs | Singularly Perturbed Differential Equations |
| SPDDEs | Singularly Perturbed Delay Differential Equations |
| FEM | Finite Element Method |
| FDS | Finite Difference Scheme |
References
- Shakti, D.; Mohapatra, J. Numerical simulation and convergence analysis for a system of nonlinear singularly perturbed differential equations arising in population dynamics. J. Differ. Equations Appl. 2018, 24, 1185–1196. [Google Scholar] [CrossRef]
- Siddarth, A.; Valasek, J. Global Tracking Control Structures for Nonlinear Singularly Perturbed Aircraft Systems. In Advances in Aerospace Guidance, Navigation and Control; Holzapfel, F., Theil, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 235–246. [Google Scholar] [CrossRef]
- Cai, X.; Lin, Y.; Liu, L.; Lin, C. Control design of a continuous model and its application in highway traffic flow. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2575–2579. [Google Scholar] [CrossRef]
- Naidu, D.S.; Rajagopalan, P.K. Application of Vasileva’s singular perturbation method to a problem in ecology. Int. J. Syst. Sci. 1979, 10, 761–773. [Google Scholar] [CrossRef]
- Richardson, W.; Volk, L.; Lau, K.H.; Lin, S.H.; Eyring, H. Application of the singular perturbation method to reaction kinetics. Proc. Natl. Acad. Sci. USA 1973, 70, 1588–1592. [Google Scholar] [CrossRef][Green Version]
- Garg, M.; Swarup, A.; Kanth, A.S.V.R. Application of singular perturbation theory in modeling and control of flexible robot arm. Int. J. Adv. Technol. Eng. Explor. 2016, 3, 176–181. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Alamri, S.Z.; Ellahi, R.; Abdelsalam, S.I. Intra-uterine particle–fluid motion through a compliant asymmetric tapered channel with heat transfer. J. Therm. Anal. Calorim. 2020, 144, 2259–2267. [Google Scholar] [CrossRef]
- Glizer, V. Asymptotic Analysis and Solution of a Finite-Horizon H ∞ Control Problem for Singularly-Perturbed Linear Systems with Small State Delay. J. Optim. Theory Appl. 2003, 117, 295–325. [Google Scholar] [CrossRef]
- Saksena, V.; O’Reilly, J.; Kokotovic, P. Singular perturbations and time-scale methods in control theory: Survey 1976–1983. Automatica 1984, 20, 273–293. [Google Scholar] [CrossRef]
- Govindarao, L.; Mohapatra, J.; Das, A. A fourth-order numerical scheme for singularly perturbed delay parabolic problem arising in population dynamics. J. Appl. Math. Comput. 2020, 63, 171–195. [Google Scholar] [CrossRef]
- Daba, I.T.; Duressa, G.F. Extended cubic B–spline collocation method for singularly perturbed parabolic differential–difference equation arising in computational neuroscience. Int. J. Numer. Methods Biomed. Eng. 2020, 37, e3418. [Google Scholar] [CrossRef]
- Nagarajan, S.; Miller, J.J.H.; Sigamani, V. Robust numerical solutions of two singularly perturbed problems in mathematical biology. Biomath Commun. 2014, 1. [Google Scholar] [CrossRef][Green Version]
- Longtin, A.; Milton, J.G. Complex oscillations in the human pupil light reflex with “mixed” and delayed feedback. Math. Biosci. 1988, 90, 183–199. [Google Scholar] [CrossRef]
- Lange, C.G.; Miura, R.M. Singular Perturbation Analysis of Boundary Value Problems for Differential-Difference Equations. V. Small Shifts with Layer Behavior. SIAM J. Appl. Math. 1994, 54, 249–272. [Google Scholar] [CrossRef]
- Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems; World Scientific Publishing Co. Pte Ltd.: Singapore, 2012. [Google Scholar] [CrossRef]
- Abagero, B.; Duressa, G.; Debela, H. Singularly perturbed Robin-type boundary value problems with discontinuous source term in geophysical fluid dynamics. Iran. J. Numer. Anal. Optim. 2021, 11, 351–364. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Gupta, V. Higher-order robust numerical computation for singularly perturbed problems involving discontinuous convective and source terms. Math. Methods Appl. Sci. 2022, 45, 4876–4898. [Google Scholar] [CrossRef]
- Singh, S.; Choudhary, R.; Kumar, D. An efficient numerical technique for two-parameter singularly perturbed problems having discontinuity in convection coefficient and source term. Comput. Appl. Math. 2023, 42, 62. [Google Scholar] [CrossRef]
- Chawla, S.; Urmil; Singh, J. A parameter-robust convergence scheme for a coupled system of singularly perturbed first-order differential equations with discontinuous source term. Int. J. Appl. Comput. Math. 2021, 7, 118. [Google Scholar] [CrossRef]
- Cen, Z.; Huang, J.; Xu, A. A quadratic B-spline collocation method for a singularly perturbed semilinear reaction–diffusion problem with discontinuous source term. Mediterr. J. Math. 2023, 20, 269. [Google Scholar] [CrossRef]
- Soundararajan, R.; Subburayan, V.; Wong, P.J.Y. Streamline diffusion finite element method for singularly perturbed 1D-parabolic convection-diffusion differential equations with line discontinuous source. Mathematics 2023, 11, 2034. [Google Scholar] [CrossRef]
- Rathore, A.S.; Shanthi, V. A numerical solution of singularly perturbed Fredholm integro-differential equation with discontinuous source term. J. Comput. Appl. Math. 2024, 446, 115858. [Google Scholar] [CrossRef]
- Ismail, H.; Elmekkawy, A. Restrictive Pade’Approximation for Solving Singularly Perturbed Initial Boundary Value Problem for Hyperbolic Partial Differential Equation. In Proceedings of the International Conference on Aerospace Sciences and Aviation Technology, 9 (ASAT CONFERENCE), Cairo, Egypt, 8–10 May 2001; pp. 1–9. [Google Scholar] [CrossRef]
- Shivaranjani, N.; Miller, J.J.H.; Sigamani, V. A Parameter Uniform Numerical Method for an Initial Value Problem for a System of Singularly Perturbed Delay Differential Equations with Discontinuous Source Terms. In Differential Equations and Numerical Analysis. Springer Proceedings in Mathematics & Statistics; Sigamani, V., Miller, J., Narasimhan, R., Mathiazhagan, P., Victor, F., Eds.; Springer: New Delhi, India, 2016; Volume 172, pp. 135–150. [Google Scholar] [CrossRef]
- Selvaraj, D.; Mathiyazhagan, J.P. A parameter-uniform convergence for a system of two singularly perturbed initial value problems with different perturbation parameters and Robin initial conditions. Malaya J. Mat. 2021, 9, 498–505. [Google Scholar] [CrossRef]
- Bharathi, K.R.; Chatzarakis, G.E.; Panetsos, S.L.; Paramasivam, M.J. Robust Layer Resolving Scheme for a System of Two Singularly Perturbed Time-Dependent Delay Initial Value Problems with Robin Initial Conditions. Aust. J. Math. Anal. Appl. 2025, accepted for publication.
- Farrell, P.; Hegarty, A.; Miller, J.M.; O’Riordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).