Convergence Analysis for Differentially Private Federated Averaging in Heterogeneous Settings ^†

Abstract

Federated learning (FL) has emerged as a prominent approach for distributed machine learning, enabling collaborative model training while preserving data privacy. However, the presence of non-i.i.d. data and the need for robust privacy protection introduce significant challenges in theoretically analyzing the performance of FL algorithms. In this paper, we present novel theoretical analysis on typical differentially private federated averaging (DP-FedAvg) by judiciously considering the impact of non-i.i.d. data on convergence and privacy guarantees. Our contributions are threefold: (i) We introduce a theoretical framework for analyzing the convergence of DP-FedAvg algorithm by considering different client sampling and data sampling strategies, privacy amplification and non-i.i.d. data. (ii) We explore the privacy–utility tradeoff and demonstrate how client strategies interact with differential privacy to affect learning performance. (iii) We provide extensive experimental validation using real-world datasets to verify our theoretical findings.

1. Introduction

With the rapid growth of the Internet of Things (IoT) in recent years, the number of intelligent devices has surged globally. Many of these devices are equipped with various sensors and increasingly powerful hardware, enabling them to collect and process data at unprecedented scales [1,2,3]. However, this growth has been accompanied by rising concerns about data privacy. Federated learning (FL) has emerged as a key solution in this context, which enables collaborative machine learning (ML) by allowing a parameter server (PS) to coordinate the training of a global model across distributed clients, thus eliminating the need to centralize sensitive data [4,5]. However, FL systems may involve millions of clients, and clients collect their own data based on their local environments and usage patterns; the size and distribution of local datasets vary significantly across clients [6]. This variation leads to data heterogeneity, as data generated by different clients are typically non-independent and identically distributed (non-i.i.d.) [7]. Data heterogeneity is also reflected in the diverse dynamics exhibited by different devices and their communication network.

Federated Averaging (FedAvg), proposed by [5], is one of the most popular FL algorithms. In FedAvg, a small subset of clients is randomly selected to perform local model updates at each communication round, which are then aggregated by the PS to update the global model. Due to its simplicity and effectiveness, FedAvg serves as the foundation for most subsequent FL algorithms. Despite its widespread adoption, the convergence behavior of FedAvg under data heterogeneity remains poorly understood. Theoretical results, such as those in [8,9], suggest that data heterogeneity significantly impacts FedAvg, requiring many more communication rounds to converge as client gradients diverge. These findings are consistent with observations on synthetic or artificially partitioned datasets [10,11]. However, in many real-world FL tasks, FedAvg often performs remarkably well [5], contrary to these theoretical predictions. Furthermore, advanced methods designed to address data heterogeneity, such as SCAFFOLD [12], demonstrate significant advantages on synthetic heterogeneous datasets but exhibit similar performance to FedAvg on realistic datasets. This inconsistency between theory and real-world performance raises questions about the practical relevance of data heterogeneity and the adequacy of existing theoretical models for real-world FL systems.

On the other hand, FedAvg still faces significant challenges, particularly in ensuring robust privacy protections. Data privacy in FL is inherently at risk during the exchange of model parameters between clients and the PS, as adversaries may attempt to infer sensitive information from these exchanges [13]. Differential privacy (DP) has emerged as a key tool to address this risk by introducing calibrated noise into the learning process [14], offering mathematically rigorous privacy guarantees. However, the added DP noise can negatively affect model accuracy and algorithm convergence, requiring a careful balance between privacy and utility [15,16].

Currently, there are numerous works focused on analyzing the impact of data heterogeneity in FedAvg [17,18]. However, to the best of our knowledge, none of the existing works have provided a complete theoretical analysis on FedAvg for handling data heterogeneity together with the consideration of client and data sampling strategies as well as privacy amplification analysis, hence motivating us to develop an advanced theoretical framework for a DP-based FedAvg algorithm (DP-FedAvg) over non-i.i.d. data.

1.1. Related Work

This section provides a focused review of the literature to contextualize our work within the broader scope of FL research:

• FL in the presence of data heterogeneity: A substantial body of research has tackled the challenges posed by non-i.i.d. data in FL. Studies such as [6,19] indicate that the convergence rate of FL models in non-i.i.d. settings is significantly lower than in i.i.d. scenarios. These works also provide theoretical analyses suggesting that effective client selection schemes can improve convergence rates in non-i.i.d. scenarios. Many existing FL frameworks [5,11,20] rely on random client selection strategies [19]. Additionally, some works [21,22] consider device heterogeneity by taking into account factors like wireless channel capacity and computational power. However, a unified theoretical analysis that examines both non-i.i.d. data effects and client sampling strategies in a single framework remains unexplored.
• FL with privacy considerations: Privacy protection has become a critical focus in the FL system. The works [23,24] have explored DP as a robust mechanism to protect data privacy in FL, demonstrating its effectiveness in achieving privacy guarantees without incurring excessive computational overhead. Numerous privacy protection techniques based on DP algorithm in FL have been investigated, including DP-SGD [25], DP-FedAvg [1,26] and the DP-based primal-dual method (DP-PDM) [27], where additive noise is applied to local gradients/models. Notably, the impact of this additive noise on learning performance can be quantified through convergence analysis, and total privacy loss can be readily tracked during the training process. However, few of these studies consider privacy amplification techniques [28,29] to reduce the adverse effect of DP noise, which could potentially improve the privacy–utility tradeoff.

To the best of our knowledge, none of the existing works have fully explored the interplay between DP noise and non-i.i.d. data on the convergence of the DP-FedAvg algorithm. Although various attempts have been made to integrate DP into FL algorithms, such as DP-SGD [1,26], DP-Prox [30] and DP-SCAFFOLD [31], the privacy–utility tradeoffs achieved by these methods remain suboptimal in non-i.i.d. settings, especially, they did not include the privacy amplification analyses. This poor privacy–utility tradeoff can be attributed to both data heterogeneity and the added DP noise, as existing FL works do not comprehensively integrate DP noise, privacy amplification, data heterogeneity, client selection and data sampling strategies within one work. This work addresses these gaps, providing robust privacy protections through DP while offering strong theoretical guarantees.

1.2. Contributions

The main contributions are summarized as follows:

• Theoretical framework: We propose a novel theoretical framework to analyze the convergence of DP-FedAvg under various client sampling strategies, with a particular focus on the impact of privacy protection and non-i.i.d. data. This framework enables us to quantify how client sampling methods and data heterogeneity influence the algorithm’s convergence rate and privacy guarantees.
• Privacy–utility tradeoff: We explore the tradeoff between privacy protection and learning performance, taking into account the effects of privacy amplification. Our theoretical results demonstrate how various system parameters influence this tradeoff and highlights that the privacy protection level and gradient clipping play a crucial role in determining the privacy–utility tradeoff in practical FL systems.
• Empirical validation: We empirically validate our theoretical findings through extensive experiments on real-world datasets, demonstrating the behavior of DP-FedAvg under non-i.i.d. data conditions.

Synopsis: For ease of the ensuing presentation, all the mathematical notations used are listed in

Table 1. Notations.

Notation	Definition
$\parallel ·\parallel$	Euclidean norm.
$\langle \mathit{x},\mathit{y}\rangle ={\mathit{x}}^{\top }\mathit{y}$	The inner product operator.
$ϵ$, $\delta$	The DP parameter.
$▵$	The ${\ell }_2$-norm sensitivity.
N	The total number of clients.
T	The total number of iterations.
Q	The number of local SGD updates.
$\left|\mathcal{D}\right|$	The size of set $\mathcal{D}$.
${\mathit{w}}^{\top }$	Transpose of vector $\mathit{w}$.
${\mathit{w}}_t$	The global model at t-th iteration.
${\mathit{w}}_t^k$	The local model for k-th client at t-th iteration.
$F_k\left(\mathit{w}\right)$	The objective function for the client k.
$\nabla F_k\left({\mathit{w}}_t^k,{\mathcal{B}}_t^k\right)$	The mini-batch gradient using the data ${\mathcal{B}}_t^k$ at client k.
$\Gamma$	The degree of non-i.i.d. data.
$\mathcal{G}$	The gradient clipping level.
n, $n_k$	The number of data samples for all client and the client k.
b	The size of mini-batch data.
d	The dimension of model parameters.
${\varphi }_k$	The variance of stochastic gradients for the k-th client.
L	L-smooth parameter.
$\mu$	$\mu$-strong convex parameter.
$\mathbb{E}[·]$, $\mathbb{P}[·]$	The statistical expectation and the probability function, respectively.

. Section 2 introduces the preliminaries of FL, DP and the existing DP-FedAvg algorithm. Section 3 provides the convergence analysis and privacy analysis for the DP-FedAvg algorithm. Experimental results are presented in Section 4, and Section 5 concludes the paper.

2. Preliminaries

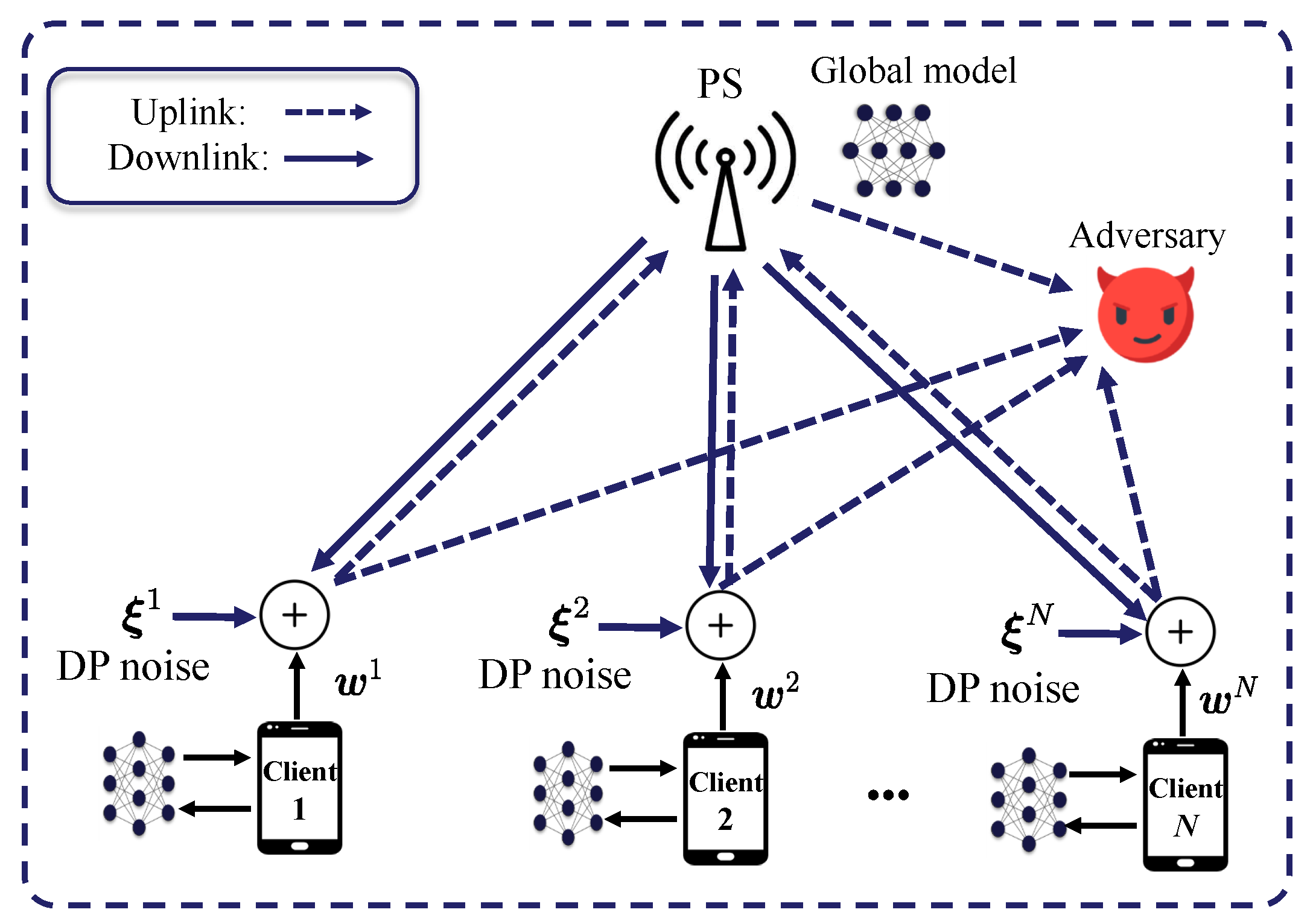
2.1. Federated Learning

We consider a vanilla FL system that consists of one parameter server (PS) and N clients in which each client has its local dataset ${\mathcal{D}}_k:=\left\{\left({\mathit{x}}_{k,j},{\mathit{y}}_{k,j}\right),\forall k\in \left[N\right],j\in \left[n_k\right]\right\}$, where $n_k$ and $n={\sum }_{k=1}^N{n}_k$ denote the number of k-th client’s training samples and its number of training samples, respectively. ${\mathit{x}}_{k,j}$ denotes the training data sample and ${\mathit{y}}_{k,j}$ is the corresponding label, while $\left[N\right]$ denotes the set $\{1,2,\cdots ,N\}$. The FL algorithm is to solve the following distributed optimization problem:

$$\begin{array}{c}\hfill \underset{\mathit{w}}{min}\left\{F\left(\mathit{w}\right)\triangleq \sum _{k=1}^N{p}_k{F}_k\left(\mathit{w}\right)\right\}\end{array}$$

(1)

where $\mathit{w}$ is the global model and $p_k=n_k/n$ is the weight of the k-th client and ${\sum }_{k=1}^N{p}_k=1$; the $F_k$ is the local objective function for client k, which is defined by

$$\begin{array}{c}\hfill F_k\left(\mathit{w}\right)={\displaystyle \frac{1}{n_k}}\sum _{j=1}^{n_k}\mathit{\ell }\left(\mathit{w};{\mathit{x}}_{k,j},{\mathit{y}}_{k,j}\right),\end{array}$$

(2)

where $\mathit{\ell }(·)$ is a user-specified loss function. Problem (1) can be solved using the well-known FedAvg algorithm [5]. Specifically, FedAvg involves T communication rounds, and each round contains the following steps:

1.

First, at the beginning of round $t\in \{0,\cdots ,T-1\}$, the PS selects a subset of clients ${\mathcal{S}}_t\subseteq \left[N\right]$ to participate and sends them the latest global model ${\mathit{w}}_t$.

2.

Each client $i\in {\mathcal{S}}_t$ initializes its local model ${\mathit{w}}_{t+1}^k$ to be the global model ${\mathit{w}}_t$ and then performs Q iterations of stochastic gradient descent (SGD) on its local dataset.

$$\begin{array}{cc}\hfill {\mathit{w}}_{t+1}^k=& {\mathit{w}}_t,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathit{w}}_{t+j}^k=& {\mathit{w}}_{t+j-1}^k-{\eta }_{t+j-1}\left(\nabla F_k\left({\mathit{w}}_{t+j-1}^k,{\mathcal{B}}_{t+j-1}^k\right)\right),j\in \left[Q\right],k\in {\mathcal{S}}_t,\hfill \end{array}$$

(4)

where ${\eta }_{t+j-1}$ represents the learning rate, and ${\mathcal{B}}_{t+j-1}^k\subseteq {\mathcal{D}}^k$ is the mini-batch data with $|{\mathcal{B}}_{t+j-1}^k|=b$; $\nabla F_k\left({\mathit{w}}_{t+j-1}^k,{\mathcal{B}}_{t+j-1}^k\right)$ denotes the stochastic gradient.

3.

Each client $i\in {\mathcal{S}}_t$ uploads the final local model update ${\mathit{w}}_{t+Q}^k$ to the PS.

4.

The PS aggregates the local model updates from all participating clients and improves the global model as

$$\begin{array}{cc}\hfill {\mathit{w}}_{t+Q}& =\sum _{k\in {\mathcal{S}}_t}{p}_k{\mathit{w}}_{t+Q}^k.\hfill \end{array}$$

(5)

The same procedure repeats for the next round until the algorithm converges.

2.2. Differential Privacy

Although FedAvg avoids the direct information leakage by keeping the data locally, the intermediate updates exchanged during the collaboration process such as ${\mathit{w}}_{t+Q}^k$ and ${\mathit{w}}_{t+Q}$ could still leak private information about the local data as demonstrated in recent advanced attacks such as model inversion attacks and membership attacks [32]. Figure 1 depicts the FL system model under attacks from an adversary. The adversary in this context can be either an “honest-but-curious” aggregation PS or clients within the system. The aggregation PS is assumed to honestly follow the designed training protocol but may be curious about clients’ private data and attempt to infer it from the shared messages. To provide strong privacy protection for local data, we adopt $(ϵ,\delta )$-DP, which is defined as follows.

Definition 1

($(ϵ,\delta )$-DP [14]). A randomized mechanism $\mathcal{M}$ satisfies $(ϵ,\delta )$-DP if for any two adjacent datasets $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$ differing in only one record, and for any subsets of outputs $S\subseteq range\left(\mathcal{M}\right)$,

$$\begin{array}{c}\hfill \mathbb{P}\left[\mathcal{M}\left(\mathcal{D}\right)\in S\right]\le exp\left(ϵ\right)·\mathbb{P}\left[\mathcal{M}\left({\mathcal{D}}^{\prime }\right)\in S\right]+\delta ,\end{array}$$

(6)

where $ϵ>0$ accounts for privacy protection level, and $\delta \ge 0$ is the probability threshold to break $(ϵ,0)$-DP.

For a query function $g:\mathcal{X}\to \mathbb{R}$, the $(ϵ,\delta )$-DP mechanism can be implemented by adding artificial Gaussian noise to function g as follows [14]:

$$\begin{array}{c}\hfill \mathcal{M}\left(\mathcal{D}\right)\triangleq g\left(\mathcal{D}\right)+\mathcal{N}\left(0,{\Delta }^2·{\sigma }^2\right),\end{array}$$

(7)

where $\Delta$ is the sensitivity of function g, defined by   

$$\begin{array}{c}\hfill \Delta =\underset{\mathcal{D},{\mathcal{D}}^{\prime }}{max}\parallel g\left(\mathcal{D}\right)-g\left({\mathcal{D}}^{\prime }\right)\parallel ,\end{array}$$

(8)

in which $\mathcal{D},{\mathcal{D}}^{\prime }\subseteq \mathcal{X}$ are neighboring datasets. ${\sigma }^2$ denotes the minimal required “noise scale” for achieving $(ϵ,\delta )$-DP given by the following lemma in [14].

Lemma 1.

Suppose that the query function g accesses the dataset $\mathcal{D}$ via randomized mechanism $\mathcal{M}$. Then, $\mathcal{M}$ satisfies $(ϵ,\delta )$-DP if

$$\begin{array}{c}\hfill {\sigma }^2\ge {\displaystyle \frac{2{\Delta }^{2}ln(1.25/\delta )}{{ϵ}^2}}.\end{array}$$

(9)

Definition 2

(Privacy loss [14]). Suppose that a randomized mechanism $\mathcal{M}$ satisfies $(ϵ,\delta )$-DP. Let $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$ be two neighboring datasets and $\mathit{o}$ be a possible output of $\mathcal{M}\left(\mathcal{D}\right)$ and $\mathcal{M}\left({\mathcal{D}}^{\prime }\right)$. The privacy loss is defined by

$$\begin{array}{c}\hfill c\left(\mathit{o}\right)=ln\left({\displaystyle \frac{\mathbb{P}\left[\mathcal{M}\left(\mathcal{D}\right)=\mathit{o}\right]}{\mathbb{P}\left[\mathcal{M}\left({\mathcal{D}}^{\prime }\right)=\mathit{o}\right]}}\right).\end{array}$$

(10)

It has been known that, running on a randomly generated subset of a dataset, the DP mechanism can yield stronger privacy protection than running on the entire dataset. This fact implies that the DP noise required for achieving a predefined DP level can be reduced when partial data are randomly selected at each local update. For the ease of later analysis, we restate the privacy amplification theorem as follows [7].

Theorem 1.

Suppose that a mechanism $\mathcal{M}$ is $(ϵ,\delta )$-DP over a given dataset $\mathcal{D}$ with size $\left|\mathcal{D}\right|=n$. Consider the subsampling mechanism that outputs a random sample uniformly over all subsets ${\mathcal{D}}_s\subseteq \mathcal{D}$ with size $|{\mathcal{D}}_s|=b$. Then, when $ϵ\le 1$, executing $\mathcal{M}$ mechanism on the subset ${\mathcal{D}}_s$ guarantees $({ϵ}^{\prime },{\delta }^{\prime })$-DP, where ${ϵ}^{\prime }$ and ${\delta }^{\prime }$ are given by

$$\begin{array}{cc}\hfill {ϵ}^{\prime }=& min\left(2qϵ,ϵ\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\delta }^{\prime }=& q\delta ,\hfill \end{array}$$

(12)

where $q=b/n$ is the data sampling ratio when data are sampled without replacement.

According to Theorem 1, the privacy would be amplified when $q\le 1/2$. Note that the privacy amplification is pervasively adopted in the existing literature on FL [1,7,23] since only a small portion of data are currently being used in local SGD.

2.3. The Typical DP-FedAvg Algorithm

In this subsection, we present the typical DP-FedAvg, which is summarized in Algorithm 1. The main steps follow the FedAvg framework outlined in Section 2.1. The key distinctions between DP-FedAvg and FedAvg are twofold: $\left(i\right)$ Gaussian noise is added to local gradients to ensure robust privacy protection and $\left(ii\right)$ gradient clipping is applied to the locally updated model. Specifically, to protect the privacy of the local model ${\mathit{w}}_t^k$, we apply DP by adding Gaussian noise ${\mathit{\xi }}_{t+1}^k\sim \mathcal{N}(0,{\left({\sigma }_{t+1}^k\right)}^2{\mathbf{I}}_d)$ to the local gradient as follows:

$$\begin{array}{c}\hfill {\mathit{w}}_{t+1}^k={\mathit{w}}_t^k-{\eta }_t\left({\tilde{\mathit{g}}}_t^k+{\mathit{\xi }}_{t+1}^k\right),\end{array}$$

(13)

where ${\tilde{\mathit{g}}}_t^k$ is the clipped local gradient, defined by

$$\begin{array}{c}\hfill {\tilde{\mathit{g}}}_t^k={\mathit{g}}_t^k/max\left(1,{\displaystyle \frac{\parallel {\mathit{g}}_t^k\parallel }{\mathcal{G}}}\right),\end{array}$$

(14)

in which ${\mathit{g}}_t^k$ is the local stochastic gradient, given as follows:

$$\begin{array}{c}\hfill {\mathit{g}}_t^k=\nabla F_k\left({\mathit{w}}_t^k,{\mathcal{B}}_t^k\right).\end{array}$$

(15)

It is important to note that determining the ${\ell }_2$-sensitivity requires bounded local gradients. Therefore, gradient clipping is applied to the locally updated model. Specifically, if $\parallel {\mathit{g}}_{t+1}^k\parallel \ge \mathcal{G}$, the gradient is scaled down to have a norm of $\mathcal{G}$; otherwise, it remains unchanged. Gradient clipping is a standard operation in SGD with DP, particularly for determining sensitivity in FL systems.

Algorithm 1 Proposed DP-FedAvg algorithm

1: $\mathbf{Input}:$ Initial values of ${\mathit{w}}_0^1,\cdots ,{\mathit{w}}_0^N$ at the clients, and initial value of ${\mathit{w}}_0$ at the server. 2: for$t=0,1,\dots ,T-1$do 3:    $\mathbf{Client}\mathbf{side}:$ 4:    for $k\in {\mathcal{S}}_t$ in parallel do 5:      Calculate local gradients: ${\mathit{g}}_t^k$ via (15). 6:      Perform gradient clipping: ${\tilde{\mathit{g}}}_t^k$ via (14). 7:      if $t+1\ne zQ,z=1,2,\dots$ then 8:         Update ${\mathit{w}}_{t+1}^k={\mathit{w}}_t^k-{\eta }_t{\mathit{g}}_t^k$ 9:      else if$t+1=zQ,z=1,2,\dots$ then 10:       Update ${\mathit{w}}_{t+1}^k$ via (13). 11:     end if 12:     $\mathbf{Server}\mathbf{side}:$ 13:     Update ${\mathit{w}}_{t+1}={\sum }_{k=1}^K{p}_k{\mathit{w}}_{t+1}^k$. 14:     Update the subset of clients ${\mathcal{S}}_{t+1}\subseteq \left[N\right]$ through uniformly sampling, and broadcast ${\mathbf{x}}_0^t$ to all clients. 15:    end for 16: end for

3. Theoretical Analysis for DP-FedAvg

In this section, we give the formal privacy guarantee and rigorous convergence analysis of DP-FedAvg. Before stating our results, we make the following assumptions.

3.1. Assumptions

Assumption 1.

$F_1$, $F_2$,…, $F_N$ are all L-smooth: for all $\mathit{w}$ and $\mathit{v}$, $F_k\left(\mathit{v}\right)\le F_k\left(\mathit{w}\right)+{(\mathit{v}-\mathit{w})}^{\top }\nabla F_k\left(\mathit{w}\right)+{\displaystyle \frac{L}{2}}{\parallel \mathit{v}-\mathit{w}\parallel }^2,\forall k\in \left[N\right]$.

Assumption 2.

$F_1$, $F_2$,…, $F_N$ are all μ-strong convex: for all $\mathit{w}$ and $\mathit{v}$, $F_k\left(\mathit{v}\right)\ge F_k\left(\mathit{w}\right)+{(\mathit{v}-\mathit{w})}^{\top }\nabla F_k\left(\mathit{w}\right)+{\displaystyle \frac{\mu }{2}}{\parallel \mathit{v}-\mathit{w}\parallel }^2,\forall k\in \left[N\right]$.

Assumption 3.

Denote ${\mathcal{B}}_t^k$ as the mini-batch data from the dataset in client k with size $|{\mathcal{B}}_t^k|=b$; then, the variance of stochastic gradients in each client is bounded, that is, $\mathbb{E}\left[\parallel \nabla F_k({\mathit{w}}_t^k,{\mathcal{B}}_t^k)-\nabla F_k\left({\mathit{w}}_t^k\right){\parallel }^2\right]\le {\varphi }_k^2/b,\forall k\in \left[N\right]$.

Assumption 4.

The local gradient is bounded, i.e., $\parallel \nabla F_k({\mathit{w}}_t^k,{\mathcal{B}}_t^k)\parallel \le \mathcal{G}$.

$\mathbf{Quantifying}\mathbf{the}\mathbf{degree}\mathbf{of}\mathbf{non}-\mathbf{i}.\mathbf{i}.\mathbf{d}.\mathbf{data}$. Inspired by [6], we quantify data heterogeneity through the degree of non-i.i.d. data, defined as

$$\begin{array}{c}\hfill \Gamma =F^{🟉}-\sum _{k=1}^K{p}_k{F}_k^{🟉},\end{array}$$

(16)

where $F^{🟉}$ and $F_k^{🟉}$ represent the minimum values of F and $F_k$, respectively. A larger value of $\Gamma$ indicates a higher degree of data heterogeneity. Specifically, when the data are i.i.d., $\Gamma$ approaches zero.

3.2. Privacy Analysis

We firstly estimate the sensitivity on client perspective. The ${\ell }_2$-norm sensitivity for each local uploaded model is given in following Lemma.

Lemma 2.

Supposed that the Assumptions 1–4 hold and $mod(t+1,Q)=0$. The ${\ell }_2$-norm sensitivity is given by

$$\begin{array}{c}\hfill {▵}_{t+1}=\underset{{\mathcal{D}}_k,{\mathcal{D}}_k^{\prime }}{max}\parallel {\mathit{w}}_{t+1,{\mathcal{D}}_k}^k-{\mathit{w}}_{t+1,{\mathcal{D}}_k^{\prime }}^k\parallel =4Q\mathcal{G}{\eta }_{t+1},\end{array}$$

(17)

where ${\mathit{w}}_{t+1,{\mathcal{D}}_k}^k$ and ${\mathit{w}}_{t+1,{\mathcal{D}}_k^{\prime }}^k$ denote the local model parameters updated from two neighboring datasets ${\mathcal{D}}_k$ and ${\mathcal{D}}_k^{\prime }$, respectively.

Proof. 

See Appendix A. □

Lemma 3.

According to the privacy amplification theorem in Theorem 1, the required privacy protection level to guarantee $(ϵ,\delta )$-DP is given by

$$\begin{array}{cc}\hfill {ϵ}^{\prime }=& {\displaystyle \frac{ϵ}{2q}},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\delta }^{\prime }=& {\displaystyle \frac{\delta }{q}},\hfill \end{array}$$

(19)

where q is the data sampling ratio.

By Lemma 2 and Lemma 3, the total DP noise scale for t-th iteration is

$$\begin{array}{c}\hfill {\sigma }_t^2=\sum _{k=1}^K{p}_k{\left({\sigma }_t^k\right)}^2={\displaystyle \frac{128{\eta }_t^2{Q}^4{b}^2{\mathcal{G}}^2}{n{ϵ}^2}}\sum _{k=1}^K{\displaystyle \frac{log(1.25Qb/n_k\delta )}{n_k}}.\end{array}$$

(20)

One can observe from (20) that the increasing Q promptly increases the noise scale, which is consistent the result in Lemma 2. According to (20), the DP noise scale is primarily determined by the privacy protection level $ϵ$, the gradient clipping threshold $\mathcal{G}$ and other algorithm-specific parameters, such as Q, b and ${\eta }_t$. Thus, in practical FL systems, achieving a balance between privacy protection and learning performance relies on effectively controlling the key parameters $ϵ$ and $\mathcal{G}$.

Then, the accumulated noise over the entire training process with total $T/Q$ communication rounds can be obtained by

$$\begin{array}{c}\hfill {\sigma }_{total}^2=\sum _{t=1}^{T/Q}\sum _{k=1}^K{p}_k{\left({\sigma }_t^k\right)}^2={\displaystyle \frac{128T{Q}^3{b}^2{\mathcal{G}}^2}{n{ϵ}^2}}\sum _{t=1}^{T/Q}{\eta }_t^2\sum _{k=1}^K{\displaystyle \frac{log(1.25Qb/n_k\delta )}{n_k}}.\end{array}$$

(21)

By considering privacy amplification, the total privacy loss after T communication rounds has been explored in [27]. For the sake of clarity and ease of later analysis, we restate it here as follows.

Theorem 2.

Suppose that any client $i,\forall i\in \left[N\right]$ in Algorithm 1 is uniformly sampled with probability $p_i$ and each communication round guarantees $(ϵ,\delta )$-DP. The total privacy loss for client i after T communication rounds satisfies

$$\begin{array}{c}\hfill {\overline{ϵ}}_i=c_0{q}_iϵ\sqrt{{\displaystyle \frac{p_{i}T}{1-q_i}}},\forall i\in \left[N\right],\end{array}$$

(22)

where $c_0>0$ is a constant and $q_i$ is given by

$$\begin{array}{c}\hfill q_i=\left\{\begin{array}{cc}{\displaystyle \frac{Qb}{|{\mathcal{D}}_i|}},\hfill & datasamplingWOR,\hfill \\ 1-{(1-{\displaystyle \frac{1}{|{\mathcal{D}}_i|}})}^{Qb},\hfill & datasamplingWR,\hfill \end{array}\right.\end{array}$$

(23)

where WOR and WR denote data sampling without and with replacement, respectively.

Remark 1.

By Theorem 2, the total privacy loss is significantly impacted by data sampling strategies. Specifically, the total privacy loss for data sampling with replacement is smaller than that for data sampling without replacement due to $1-(1-1/|{\mathcal{D}}_i{\left|\right)}^{Qb}\le Qb/|{\mathcal{D}}_i|$.

3.3. Convergence Analysis for DP-FedAvg

In this section, we analyze the convergence performance of the DP-FedAvg algorithm. Let T denote the total number of iterations and ${\mathit{w}}^{🟉}$ the optimal solution of $F\left(\mathit{w}\right)$. The convergence performance is measured by $\mathbb{E}\left[F\left({\mathit{w}}_T\right)-F\left({\mathit{w}}^{🟉}\right)\right]$, where the expectation is taken over the algorithm’s randomness. This metric represents the gap between the achieved objective value and the optimal objective value after T iterations. Notably, when $\mathbb{E}\left[F\left({\mathit{w}}_T\right)-F\left({\mathit{w}}^{🟉}\right)\right]=0$, the algorithm converges to the optimal solution.

Theorem 3.

For the full-participation case, assume that Assumption 1, Assumption 2 and Assumption 3 hold. Let $\kappa =L/\mu$, $\alpha =max\{8\kappa ,Q\}$, and the learning rate ${\eta }_t=2/\left(\mu (\alpha +t)\right)$. Then, the following inequality holds:

$$\begin{array}{c}\hfill \mathbb{E}\left[F\left({\overline{\mathit{w}}}_t\right)-F^{🟉}\right]\le {\displaystyle \frac{2\kappa }{t+\alpha }}\left({\displaystyle \frac{A+B}{\mu }}+2L{\parallel {\mathit{w}}_0-{\mathit{w}}^{🟉}\parallel }^2\right),\end{array}$$

(24)

where

$$\begin{array}{cc}\hfill & A=\sum _{k=1}^K{p}_k^2{\varphi }_k^2/b+8{(Q-1)}^2{\mathcal{G}}^2+6L\Gamma ,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & B={\displaystyle \frac{8d{Q}^4{b}^2{\mathcal{G}}^2}{n{L}^2{ϵ}^2}}log\left(n\right)log(1.{25}^2{Q}^2{b}^2/n{\delta }^2)\left(2{(Q-1)}^2+1\right).\hfill \end{array}$$

(26)

Proof. 

See Appendix B. □

Remark 2.

In Theorem 3, since $\parallel {\mathit{w}}_0-{\mathit{w}}^{🟉}{\parallel }^2\le {\displaystyle \frac{1}{{\mu }^2}}{\left(\nabla F\left(\mathit{w}\right)-\nabla F\left({\mathit{w}}^{🟉}\right)\right)}^2\le {\displaystyle \frac{4{\mathcal{G}}^2}{{\mu }^2}}$, the dominating term in (24) is $\mathcal{O}\left({\displaystyle \frac{A+B}{\mu T}}\right)$. Therefore, the DP-FedAvg algorithm achieves a convergence rate in the order of

$$\begin{array}{c}\hfill \mathcal{O}\left({\displaystyle \frac{{\sum }_{k=1}^K{p}_k^2{\varphi }_k^2/b+Q^2{\mathcal{G}}^2+L\Gamma }{\mu T}}+{\displaystyle \frac{d{Q}^4{b}^2{\mathcal{G}}^{2}log\left(n\right)log(Q^2{b}^2/n{\delta }^2)}{\mu Tn{L}^2{ϵ}^2}}\right).\end{array}$$

(27)

Therefore, an increase in Q can significantly increase the noise scale, thereby deteriorating the convergence performance.

Next, we present the convergence analysis by considering client sampling. Inspired by [6], we make the following assumption.

Assumption 5.

Assume the total number of clients is N and the size of the selected client set is $|{\mathcal{S}}_t|=K$. If we uniformly sample the participating clients with replacement with sampling probabilities $p_1,\cdots ,p_N$, then the aggregation step on the server side performs ${\mathit{w}}_t={\displaystyle \frac{1}{K}}{\sum }_{k\in {\mathcal{S}}_t}{\mathit{w}}_t^k$. Otherwise, if we uniformly sample the participated clients without replacement from $\left[N\right]$, then the aggregation step on the PS performs ${\mathit{w}}_t={\displaystyle \frac{N}{K}}{\sum }_{k\in {\mathcal{S}}_t}{p}_k{\mathit{w}}_t^k$.

Theorem 4.

Suppose that Assumptions 1, 2, 3 and 5 hold. Let κ, α, ${\eta }_t$, A and B be defined in Theorem 3. Then, the following inequality holds:

$$\begin{array}{c}\hfill \mathbb{E}\left[F\left({\overline{\mathit{w}}}_t\right)-F^{🟉}\right]\le {\displaystyle \frac{2\kappa }{t+\alpha }}\left({\displaystyle \frac{A+B+H}{\mu }}+2L{\parallel {\mathit{w}}_0-{\mathit{w}}^{🟉}\parallel }^2\right),\end{array}$$

(28)

if sampling the clients with replacement:

$$\begin{array}{c}\hfill H={\displaystyle \frac{4}{K}}{Q}^2{\mathcal{G}}^2,\end{array}$$

(29)

and if sampling the clients without replacement:

$$\begin{array}{c}\hfill H={\displaystyle \frac{N-K}{N-1}}{\displaystyle \frac{4}{K}}{Q}^2{\mathcal{G}}^2.\end{array}$$

(30)

Proof. 

See Appendix D. □

Theorem 4 provides an upper bound of the average total local SGDs over t iterations. A smaller value indicates a higher convergence rate and a lower cost function value in (28). Based on Theorems 3 and 4, we have following remarks.

Remark 3. 

(The impact of Q on communication efficiency) By denoting $T_{\epsilon }$ as the number of required iterations for DP-FedAvg to achieve an ε accuracy. Based on the result in (27), the number of required communication rounds $T_{\epsilon }/Q$ is

$$\begin{array}{c}\hfill {\displaystyle \frac{T_{\epsilon }}{Q}}\propto \mathcal{O}\left({\displaystyle \frac{d{b}^2{\mathcal{G}}^{2}log\left(n\right)log(Q^2{b}^2/n{\delta }^2)}{\mu Tn{L}^2{ϵ}^2}}{Q}^3+{\mathcal{G}}^{2}Q+{\displaystyle \frac{{\sum }_{k=1}^K{p}_k^2{\varphi }_k^2/b+L\Gamma }{Q}}\right).\end{array}$$

(31)

From (31), we observe that the communication round $T_{\epsilon }/Q$ is the function of Q, and $T_{\epsilon }/Q$ first decreases and then increases, i.e., there exists an optimal Q such that the communication cost is optimal. Furthermore, if Q is too large, the ${\mathit{w}}_k$ will promptly achieve local optimal, making FedAvg behave like one-shot average [33]. However, the one-shot averaging does not perform well in the non-i.i.d. data case as demonstrated in [6].

Remark 4. 

(The impact of Q on learning performance) The DP noise scale increases significantly with larger values of Q, which inevitably degrades learning performance. However, a larger Q can also reduce the number of communication rounds, as stated in Remark 3. Therefore, there exists an optimal value of Q that balances learning performance and communication efficiency.

Remark 5. 

(The impact of gradient clipping bound level $\mathcal{G}$) The convergence performance is influenced by gradient clipping level $\mathcal{G}$. However, limiting the gradient norm has the following shortcomings: $\left(i\right)$ Gradient clipping destroys the unbiasedness of the gradient estimate. $\left(ii\right)$ If $\mathcal{G}$ is too small, the average of the clipped gradients may point in a direction significantly different from the true gradient, potentially leading to poor convergence. $\left(iii\right)$ If $\mathcal{G}$ is too large, the gradients will carry more DP noise, as $\mathcal{G}$ determines the sensitivity.

4. Numerical Experiments

4.1. Experimental Setting

In this section, we evaluate the performance of DP-FedAvg under a non-i.i.d. data setting. Denote the $\ell (\mathit{w};{\mathbf{x}}_i)$ as the prediction model with parameter $\mathit{w}=(\mathbf{W},\mathbf{b})$, then the form for logistic regression and softmax regression are $\ell (\mathit{w};{\mathbf{x}}_i,{\mathbf{y}}_i)=\mathrm{logisitc}(\mathbf{W}\mathbf{x}+\mathbf{b})$ and $\ell (\mathit{w};{\mathbf{x}}_i,{\mathbf{y}}_i)=\mathrm{softmax}(\mathbf{W}\mathbf{x}+\mathbf{b})$, respectively. The loss function for both problems is given by

$$\begin{array}{c}\hfill F_k\left(\mathit{w}\right)={\displaystyle \frac{1}{n_k}}\sum _{j=1}^{n_k}\mathrm{CrossEntropy}(\ell \left(\mathit{w};{\mathbf{x}}_j),{\mathbf{y}}_j\right).\end{array}$$

(32)

Note that this is a convex and smooth problem. The testing accuracy (learning accuracy over the testing data) is evaluated as the learning performance in the experiments.

Datasets: Two benchmark datasets, Adult [34] and MNIST [35], were considered for performance evaluation. The MNIST dataset consists of 60,000 training samples and 10,000 testing samples, while the Adult dataset consists of 32,561 training samples and 16,281 testing samples. To simulate the FL system, we distributed all training samples across $N=100$ clients in a non-i.i.d. manner, ensuring that each client possessed partial labels for the data:

• For the MNIST dataset, following the heterogeneous data partition method in [6], each client was allocated data samples of only four different labels with $|{\mathcal{D}}_i|=600$. This led to a high degree of non-i.i.d. datasets among clients.
• For the Adult dataset, following [1], all the training samples were uniformly distributed among a total $N=100$ clients such that each client only contained data from one class with $|{\mathcal{D}}_i|=325$.

$\mathbf{Parameter}\mathbf{setting}:$ For all experiments, we maintained the following parameter settings: $K=10$, $b=10$ and $\delta ={10}^{-5}$. The choice of the learning rate ${\eta }^t$ depended on the dataset under consideration.

For the MNIST dataset, the local learning rate was set to ${\eta }^t=0.04/\sqrt{1+t}$, while for the Adult dataset, ${\eta }^t=0.01/\sqrt{1+t}$. Following the rule of gradient clipping in [25], we selected the value of $\mathcal{G}$ by taking the median of the norms of the unclipped gradients over the training process.

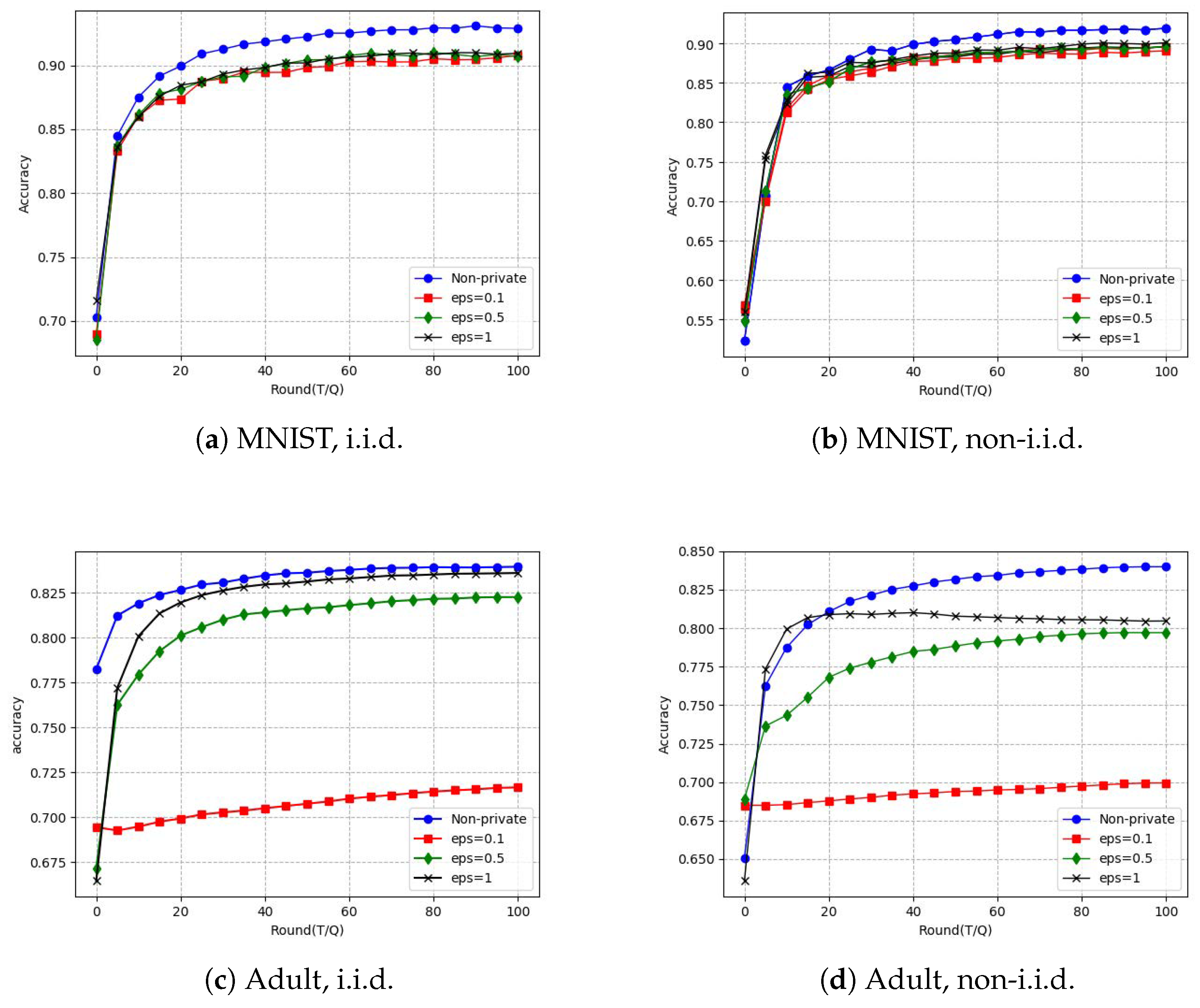
4.2. Impact of the Privacy Protection Level $ϵ$

To validate the learning performance at various privacy protection levels, the parameters were set as $K=10$, $Q=5$ and $\delta ={10}^{-5}$, and the testing accuracy was computed with respect to communication rounds ($T/Q$). We compared the accuracy with various values of $ϵ$ under both i.i.d. and non-i.i.d. scenarios. As illustrated in Figure 2, both the MNIST and Adult datasets provided strong privacy protection without a significant decrease in testing accuracy. Moreover, we find that MNIST has a higher tolerance to DP noise than the Adult dataset. Specifically, the difference in testing accuracy between the non-private and private models for both i.i.d. and non-i.i.d. datasets is much smaller than the corresponding drop in accuracy for the Adult dataset. The reason for the MNIST dataset’s robustness to DP noise compared with the Adult dataset may have been due to the following reasons:

• Impact of non-i.i.d. data: The presence of non-i.i.d. data across clients in FL amplifies the impact of DP noise. The Adult dataset, which contains categorical and numerical features, is more sensitive to such heterogeneity. Conversely, the MNIST dataset, consisting of grayscale images of handwritten digits with simpler patterns, is inherently more resilient to non-i.i.d. data settings.
• Inherent data structure: The MNIST dataset benefits from the spatial coherence of pixel intensities, where patterns such as the shapes of digits remain discernible when DP noise is introduced. This property of image data enables models to identify meaningful features despite perturbations. On the other hand, the Adult dataset, being tabular with categorical and numerical features, lacks such spatial structure. DP noise in tabular data can obscure critical relationships between features and labels, making it harder for the FL model to extract meaningful patterns under noisy conditions.

Figure 2. The testing accuracy versus communication rounds of the DP-FedAvg algorithm on various privacy protection levels under Adult and MNIST datasets.

Figure 2. The testing accuracy versus communication rounds of the DP-FedAvg algorithm on various privacy protection levels under Adult and MNIST datasets.

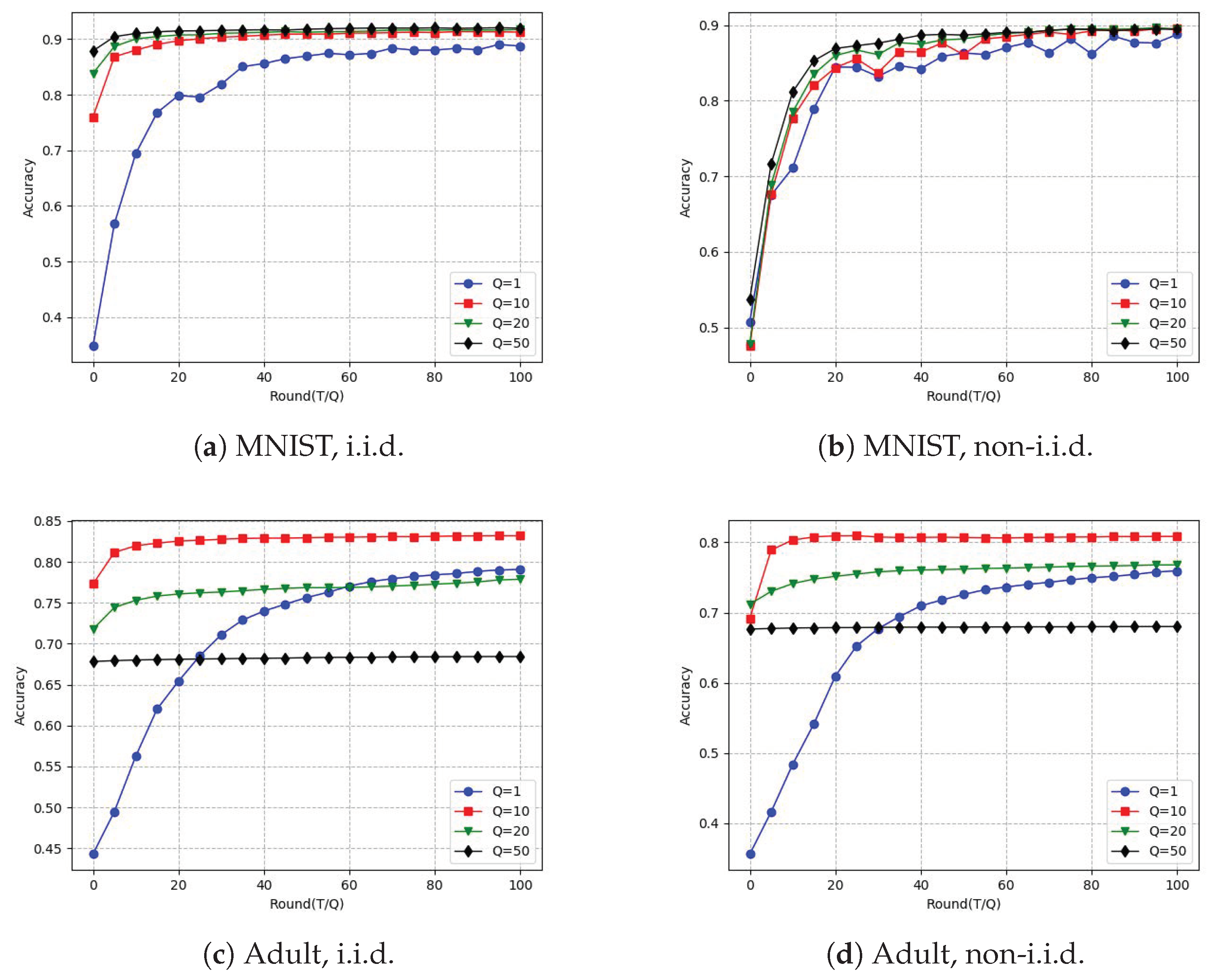
4.3. Impact of Local Epoch Length Q

In this experiment, we compared the learning performance under the parameter settings $ϵ=0.5$, $K=10$ and $\delta ={10}^{-5}$ for various values of Q. As shown in Figure 3, we observed that both excessively large and excessively small values of Q reduced the convergence rate on the Adult dataset. However, for the MNIST dataset, a large Q had a negligible effect on convergence. This may have been due to two reasons: $\left(i\right)$ The optimal value of Q for MNIST is significantly larger than for the Adult dataset, and $\left(ii\right)$ MNIST exhibits a higher tolerance to noise compared to the Adult dataset. Although a large Q alleviates the communication burden, it substantially increases the noise scale, thereby degrading learning performance as discussed in Remark 4. Additionally, our simulation results indicate that the optimal value of Q is sensitive to both the parameter settings and the training dataset. Furthermore, for both datasets, the convergence performance on i.i.d. data is better than on non-i.i.d. data under the same parameter settings.

5. Conclusions and Future Works

In this paper, we conducted a thorough theoretical analysis of DP-FedAvg under different client and data sampling strategies, with a particular focus on the impact of non-i.i.d. data on the convergence and privacy protection of FL algorithms. Our work fills a significant gap in the literature by providing a unified framework that integrates data heterogeneity with DP. Through our analysis, we demonstrated that the DP-FedAvg algorithm maintains robustness toward data heterogeneity and DP noise, achieving a sublinear convergence rate for convex FL problems. Additionally, our convergence and privacy analyses offer valuable insight and perspectives into how various system parameters in the FL framework influence learning performance, which can be used as guidelines for the practical FL algorithm design. Our theoretical findings are supported by extensive numerical experiments on real-world datasets, which are consistent with our theoretical findings.

While our theoretical analysis provides useful insights for DP-FedAvg under the data heterogeneity scenario, several promising directions remain for future research. First, our work is based on the typical star network framework, consisting of one server and multiple clients. A promising direction would be to explore hierarchical FL systems, where multiple servers collaborate to train a global model. This framework could involve more clients and larger datasets, potentially improving learning performance. Second, another promising avenue for future work involves examining the tradeoffs between privacy, utility and computational overhead when implementing advanced methods in resource-constrained FL systems, such as those in mobile edge computing environments. Finally, while the DP mechanism offers strong privacy guarantees, more sophisticated approaches could be employed to further enhance privacy protection. Techniques such as homomorphic encryption could be integrated to strengthen the security of DP-FedAvg. Addressing these challenges and exploring innovative theoretical analyses will be an exciting and valuable direction for future research.