Abstract
This work presents a mathematical framework based on uncertain numbers to address the inherent uncertainty in nonlinear systems, a challenge that traditional mathematical frameworks often struggle to fully capture. By establishing five axioms, a formal system of uncertain numbers is developed and embedded within set theory, providing a comprehensive characterization of uncertainty. This framework allows phenomena such as infinity and singularities to be treated as uncertain numbers, offering a mathematically rigorous analytical approach. Subsequently, an algebraic structure for uncertain numbers is constructed, defining fundamental operations such as addition, subtraction, multiplication, and division. The framework is compatible with existing mathematical paradigms, including complex numbers, fuzzy numbers, and probability theory, thereby forming a unified theoretical structure for quantifying and analyzing uncertainty. This advancement not only provides new avenues for research in mathematics and physics but also holds significant practical value, particularly in improving numerical methods to address singularity problems and optimizing nonconvex optimization algorithms. Additionally, the anti-integral-saturation technique, widely applied in control science, is rigorously derived within this framework. These applications highlight the utility and reliability of the uncertain number framework in both theoretical and practical domains.
Keywords:
uncertain numbers; uncertain logic; nonlinear systems; nonlinearity; uncertainty; infinity; singularities; fuzzy; probability MSC:
03A10; 03B60; 32S15; 35A21; 68T37; 90C70; 93C10
1. Introduction
Traditional mathematical frameworks predominantly address problems characterized by determinism and linearity, operating under the assumption that all input data are known with certainty and can be precisely predicted. This enables the system’s behavior to be described and computed using well-defined mathematical formulations. However, with the continued advancement of scientific and engineering disciplines, an increasing number of real-world challenges involve systems that are nonlinear, fuzzy, or inherently uncertain, domains where conventional mathematical tools exhibit significant limitations. This is especially evident in the nonlinear dynamics and high levels of uncertainty and complexity inherent in game-theoretic models [1], as well as in the constraints posed by nonlinear partial differential equations when applied to highly nonlinear and uncertain systems [2].
In actuality, nonlinearity and uncertainty are closely related. Losacco et al. [3] demonstrated that uncertainty is inevitable in nonlinear systems and expands with the growth of nonlinearity. Meng et al. [4] tackled the fixed-time stability of nonlinear systems with parametric uncertainty using adaptive control strategies, proving that uncertainty in nonlinear systems requires special treatment to ensure stability. Li et al. [5] applied an LSTM model and Monte Carlo dropout method to address uncertainty in the stress–strain relationship of frozen soil, showing that considering uncertainty significantly improves prediction accuracy in nonlinear systems. Therefore, in nonlinear systems, uncertainty is inevitable and expands with the increase in nonlinearity.
To better understand how uncertainty manifests in nonlinear systems, let us examine the example of a simple quadratic equation, where the relationship between the roots and the coefficients illustrates how changes in system parameters can affect the solutions. Consider the quadratic equation , where a, b, and c are constants, with , and is the variable. The solutions to this equation can be expressed through factorization as , where and represent the roots of the equation, which can be real or complex. These roots, and , reflect different possible outcomes of the equation. The existence of multiple solutions indicates the inherent uncertainty in the process described by the equation. This multisolution nature suggests that while several scenarios are mathematically possible, only one can be realized in practice, reflecting the uncertainty of the system. This is reflected in the many studies on dynamical systems [6,7].
Probability theory and stochastic processes are core methods for addressing uncertainty. In constructing a probability space , represents the sample space, and is a -algebra consisting of subsets of the sample space. The structure of the -algebra depends on the specific definition of the sample space, and it requires the sample space to be fixed [8]. However, Axtell et al. [9] highlighted the complexity of financial markets through agent-based models (ABMs), demonstrating that the dynamic behavior of market participants and external factors render traditional static models, such as the Capital Asset Pricing Model (CAPM) [10] and random walk model [11], less effective in predicting market performance during extreme volatility. Unlike static systems, financial markets are dynamically evolving, with both market states and participant behaviors continuously changing in response to information flows. Consequently, the sample space is not fixed, and traditional probability theory and stochastic processes fall short in addressing uncertainties in dynamic environments, such as extreme weather events [12] or financial crises [13].
Fuzzy mathematics is a method for dealing with uncertainty. It describes uncertainty by associating elements with membership degrees in fuzzy sets and uses fuzzy operations and reasoning to manipulate these membership degrees, thereby modeling uncertainty. The core concept is the membership function , which represents the degree of membership of element x in fuzzy set A, reflecting the extent to which x belongs to set A. Fuzzy operations (such as union, intersection, and complement) are based on standard set operations but are adjusted to account for the membership degrees of elements [14]. Although fuzzy mathematics has been widely applied in many fields, it still faces significant limitations. In reality, uncertainty is often multidimensional and interwoven, with different types of uncertainty exhibiting distinct mathematical properties. For example, in machine learning, both fuzziness and randomness coexist [15]; while in multicriteria decision analysis, environmental uncertainty requires additional considerations [16]; risk analysis needs to address the interplay between model uncertainty and epistemic uncertainty [17]. These interwoven uncertainties increase the complexity of reasoning and decision making, and in extreme cases, fuzzy mathematics proves insufficient in handling multiple uncertainties simultaneously.
Several approaches, in addition to stochastic and fuzzy mathematics, address uncertainty in complex systems. Bayesian methods [18] update prior probabilities to infer posteriors, making them suitable for dynamic systems, though computationally intensive and reliant on prior accuracy. Evidence theory [19] aggregates evidence from diverse sources but struggles with consistency in conflicts and depends on high-quality inputs. Grey system theory [20] is effective for limited data, though predictive accuracy drops with more data. Rough set theory [21] handles incomplete data but may struggle with complexity. Interval mathematics [22] uses intervals for uncertain quantities, though results can be overly conservative. Possibility theory [23] employs distributions for ambiguous problems but lacks event likelihood measures. Monte Carlo methods [24] apply simulations to solve multidimensional problems but can be expensive and inefficient for large datasets. Evidence reasoning [25] integrates heterogeneous data but struggles with inconsistent evidence. These limitations emphasize the need for an intuitive framework combining methods to address dynamic uncertainties and improve predictions and decision-making.
Uncertainty theory has gained significant attention recently. Ferson et al. [26] proposed a method that represents uncertain input variables as interval boundaries, incorporating both upper and lower probability limits. Levin et al. [27] introduced uncertainty factors by blending fuzzy mathematics and stochastic processes to model system randomness and ambiguity. Hall [28] introduced “uncertain numbers”, a concept aiming to unify a quantity’s value with its uncertainty, and defined the basic operations for these numbers. However, these approaches still require further development in specific mathematical or physical contexts, particularly in algebraic geometry and singularity problems in general relativity. The computation and error propagation of uncertain numbers rely on particular models and rules [29], which may fail in the presence of mathematical singularities [30], potentially leading to errors or halting the computation.
The singularity problem [31] in quantum gravity has been a widely discussed issue. Capellmann’s research [32] suggests that spacetime at the quantum scale is not a continuous, smooth manifold, but is composed of discrete quantum structures governed by quantum fluctuations. In this view, spacetime coordinates (position and time) are quantized and exhibit uncertain discrete characteristics, potentially preventing the formation of singularities by altering the assumption of spacetime continuity. Gonçalves et al. [33] explored the connection between singularity formation and the conservation of the stress–energy tensor within gravity theory. This theory modifies Einstein’s field equations by combining the Ricci scalar R and the trace T of the stress–energy tensor, adjusting the conservation relationship between matter and energy to suppress singularity formation. This adjustment can be seen as a form of uncertainty correction that influences both spacetime and quantum fluctuations. Capozziello et al. [34] proposed a method to smooth spacetime by introducing quantum correction terms, which prevent infinite curvature under extreme conditions and maintain the finiteness of the metric. These terms are crucial at high energy densities or small scales, effectively avoiding gravitational singularities and providing new directions for quantum gravity research. If the intuitive uncertain framework can effectively describe singularities, traditional gravity theory is expected to be improved, and it may potentially drive the development of the quantum gravity field.
Singularity and uncertainty problems have long been challenging issues in the fields of partial differential equations (PDEs) and algebraic geometry. Guo et al. [35] addressed the existence, uniqueness, and regularity of solutions to fully nonlinear PDEs on non-Kähler manifolds by introducing estimates and comparison methods for Monge–Ampère equations. Building upon this, the introduction of intuitive uncertainty is expected to capture solution errors and volatility, thus enhancing the stability of numerical computations, especially in high-dimensional settings with singularities. Kebekus et al. [36] studied the geometric uncertainties caused by singularities, proposing conditions for extending holomorphic forms from regular submanifolds to singular spaces. Incorporating uncertainty expressions can provide a more precise understanding over this extension problem, offering new insights into geometric analysis. Bringmann et al. [37] applied random tensor theory to study the invariance of Gibbs measures under the three-dimensional cubic wave equation, proving the existence of local time solutions and addressing measure singularities. If the intuitive uncertain framework can effectively describe singularities, it is expected to offer perspectives on the random fluctuations of solutions, opening up directions for future research.
In mathematical logic, the novel mathematical framework must address concepts such as “infiniteness” and “speciality” by constructing limits or boundary conditions. This would contribute to a deeper understanding of the existence of mathematical objects, particularly within the context of intuitionism [38]. Such a framework could characterize limiting behaviors based on intuitionistic principles and employ symbolic rules [39] to formalize limits, offering insights into the challenges of formalism. Additionally, it must be consistent with Gödel’s incompleteness theorem [40], ensuring that the system remains both consistent and complete in limiting cases, thus providing perspectives on the inconsistencies encountered by logicism.
This study aims to develop an intuitive, unified mathematical framework that captures the inherent uncertainty in nonlinear systems and singularities while remaining consistent with established paradigms like intuitionism, formalism, and logicism. To achieve this, five fundamental axioms are introduced, which, to the best of my knowledge, have not been previously identified and are believed to reflect key properties of the real world. These axioms form the foundation of the proposed framework, including the Axiom of Uncertainty (Axiom 1), the Axiom of Order (Axiom 2), the Axiom of Alignment (Axiom 3), the Axiom of Dynamics of Truth Value (Axiom 4), and the Axiom of Truth Values Condition (Axiom 5). These axioms collectively form the foundation of an uncertainty logic system, addressing the mathematical and logical challenges of uncertainty while providing a solid philosophical and logical basis for future research.
Based on the axiom system (Axioms 1–5), this study rigorously derives the definition of uncertain numbers (Definitions 7 and 8) through relevant theories in modern mathematics, which represents the core contribution of this research. To avoid potential logical paradoxes, this study employs recursive logic to construct uncertain numbers, thereby ensuring the precision of the definitions and the internal consistency of the system. Based on these definitions, and to comply with the Axiom of Alignment (Axiom 3), the definition of the trailing numbers of uncertain numbers (Definition 10) is proposed by referencing the method of defining decimals, along with the establishment of corresponding alignment rules (Theorem 7). Furthermore, the operational rules for addition and multiplication (Definition 11) are clearly defined, ensuring that the arithmetic operations on uncertain numbers are both effective and consistent, strictly following the axiom system (Axioms 1–5), and compatible with traditional mathematical frameworks.
In addition, this study employs methods from real analysis (Theorem 10), surreal analysis (Theorem 11), and hyperreal analysis (Theorem 12) to rigorously explore the existence of large uncertain numbers within the framework of uncertain numbers. This study demonstrates that, under the conditions defined for uncertain numbers, any element of a large uncertain number is at least greater than or equal to any real number, and provides a precise formal definition of this concept (Definition 12). Furthermore, this study introduces the concept of small uncertain numbers (Definition 13) and proves their density (Theorem 13) and boundedness (Theorem 14). Additionally, the stability of the real numbers is examined (Theorem 15), laying the theoretical foundation for subsequent discussions on singularities.
By invoking the Axiom of Uncertainty (Axiom 1), 0 is conceptualized as an uncertain number with dual characteristics, denoted as (Definition 15). Building on the stability of real numbers (Theorem 15), the reciprocal relationship between and large uncertain numbers is explored (Theorem 17). Additionally, the absorbing properties of uncertain numbers are examined (Definition 16 and Theorems 18 and 19), with a more detailed elucidation of their algebraic operational rules (Definition 18). Furthermore, it is asserted that the processes of absorption and release are intrinsic properties of the absorbing elements and , which do not exist as independent real numbers, as they fail to satisfy the determinacy requirement of real numbers. These results provide a solid theoretical foundation for the algebraic structure of uncertain numbers (Theorem 22).
Finally, a quantitative analysis of uncertain numbers is conducted by integrating probability theory (Definitions 19–21), fuzzy mathematics (Theorem 24), and the complex number system (Theorem 5) into a unified framework. This system provides a coherent theoretical approach to address uncertainty in nonlinear domains. As practical applications, the uncertainty conservation equation in theoretical physics is derived (Theorem 23), offering a solution to Newton’s method singularity problem (Equation (1)) and the “local confusion” issue in gradient descent (Equation (2)). Additionally, the anti-windup technique in control science is rigorously derived based on this framework (Equation (5)). These applications demonstrate the utility and reliability of uncertain number theory framework.
2. Uncertain Logics
The multiple solutions of nonlinear equations [41,42] are one of their intrinsic characteristics, reflecting the diversity and uncertainty of solutions in complex systems [43,44]. To better elucidate this feature, we can divide the timeline into two stages: “history” and “future”. This division helps us to understand the different properties and perspectives of solutions to nonlinear equations. We refer to the time before the critical point as history and the time after it as the future. From the critical point perspective, the solution to a nonlinear equation typically appears as a unique solution or a specific solution selected under certain conditions, as we can only experience one solution as the trajectory, rather than simultaneously experiencing multiple solutions. However, from the critical point looking forward, the solution set of the nonlinear equation manifests as a set of possible solutions, embodying uncertainty and diversity. At this juncture, each solution in the set corresponds to a potential state or outcome of the system.
For example, consider the decision problem of “What to have for dinner?” This can be likened to the process of solving a nonlinear equation, where each potential dinner option represents a possible solution. Suppose, at a certain moment in the past, the individual always chose steak (denoted as ) for dinner. From the critical point looking at the past, i.e., from the present perspective reflecting on the past, this choice appears to be a determined decision. However, when the situation changes, and from the critical point looking at the future, the range of dinner options expands. It could be chicken (denoted as ), steak (denoted as ), or even fish (denoted as ). At this point, the decision for the future yields a solution set , where each element represents a different choice, and the decision-making process for the future is filled with uncertainty.
In logic, when a proposition involves multiple possible instances or options, uncertainty is introduced. To handle this uncertainty, set theory provides a method of quantification [45]. Specifically, the proposition “Dinner is steak” can be represented by a set containing all possible types of steak. For example, the proposition “Dinner is steak” can be expressed as , where x represents the specific type of steak chosen for dinner. The truth value of the proposition depends on whether there exists a particular type of steak within the set.
From a broader perspective, propositions in reality are often relative and conditional. Each proposition’s subject has multiple characteristics, such as size, color, shape, and function, which can convey different meanings depending on the context. As a result, the intension and extension of a proposition change continuously within specific situations [46]. Additionally, the inherent ambiguity and polysemy of language can result in different interpretations of the same proposition depending on the context [47]. The subjectivity [48], knowledge background [49], and experiences [50] of the observer also shape their understanding and judgment of a proposition, influencing its accuracy and validity. We are often unable to obtain complete information about an object, introducing uncertainty into propositions. In summary, we can find fundamental axiom in uncertain systems.
Axiom 1
(Uncertainty). For any proposition P, there exists a set of all possible sub-propositions such that the proposition P can be expressed as
where each is a possible sub-proposition, and the set of propositions has a disjunctive structure. The uncertainty of P is manifested in its composition from multiple possible sub-propositions.
From an omniscient perspective, the proposition P is fully determined and certain. However, the uncertainty arises from our limited access to the full structure of P. The proposition P is, in fact, a composition of potentially infinite or complex sub-propositions, , each representing a possible aspect of truth or reality. In this view, the uncertainty we experience is a reflection of our inability to perceive the entire set of possible sub-propositions that make up P, leaving us with an incomplete understanding of its truth.
Uncertain logic can be defined from a human perspective as a logical system capable of handling variations in propositional truth values under incomplete knowledge and uncertain information. In other words, it is a system that accommodates uncertainty by allowing truth values to fluctuate rather than be fixed. In such a system, the truth of a proposition is binary (true or false), but exists within a spectrum of possibilities, which can dynamically change based on the acquisition of new information or the discovery of previously unknown sub-propositions. This flexibility is crucial, as it acknowledges that our understanding of truth is often constrained by the limits of our information and perception. Uncertain logic aims to provide a framework for reasoning under conditions where knowledge is partial, incomplete, or ambiguous, allowing for more nuanced and flexible conclusions than traditional classical logic.
To distinguish between known and uncertain propositions, a set of standard rules can be applied [51]. Known propositions refer to variables that can be precisely identified and measured, with outcomes that are predictable, such as established physical constants or verified historical data. In contrast, according to Axiom 1, any proposition can be expressed in an uncertain form, and the formulation of an uncertain proposition may incorporate the structure of a certain proposition. For instance, based on Axiom 1, when reflecting on past events at a critical moment, any given proposition can be represented as , where is a specific sub-proposition. It is evident that each sub-proposition in a certain proposition is essentially identical, and, thus, they can be expressed in various ways through repetition. However, to avoid conflicts with the fundamental principles of set theory, particularly the axiom of the uniqueness of sets, which asserts that every element in a set must be unique, the formulation of sub-propositions must follow a specific order. This ensures that each sub-proposition is assigned an ordinal, and the entire proposition takes the form of a set with a binary algebraic structure composed of sub-propositions and ordinals, thereby maintaining compliance with the uniqueness axiom. Consequently, this leads to the derivation of an important axiom.
Axiom 2
(Order). A proposition may contain repeated sub-propositions with the same essence, but these sub-propositions are ordered. Specifically, for any proposition, a sub-proposition is denoted by , where represents the essence of the sub-proposition and i is its ordinal index. The formal structure of the axiom is as follows:
- 1.
- Repeatability: It is allowed that for , meaning that the essence of sub-propositions may be identical, but they are distinguished by their indices.
- 2.
- Ordering: for , i.e., the pairs are distinct because they are differentiated by their unique indices.
Thus, while the essence of the sub-propositions may be identical, each implies distinctness due to its unique index i.
In addition, the sub-propositions within an uncertain proposition are also subject to uncertainty. For example, if a sub-proposition is uncertain, then, according to Axiom 1, the proposition reflects this uncertainty at multiple levels. In this framework, the formulation of Axiom 1 effectively captures the multilevel nature of uncertainty. More specifically, when information about a given factor is complete and can be accurately predicted using established theories or data models, that factor is considered “known” [52]. In contrast, when information is incomplete or influenced by randomness, ambiguity, or other interacting variables, it is characterized as exhibiting multilevel uncertainty. The term “multilevel uncertainty” refers to the presence of uncertainty across various hierarchical layers, where each level may involve different interacting factors. These uncertainties are not isolated; they can influence one another, with changes at one level potentially triggering cascading effects at other levels. Moreover, uncertainty in certain sub-propositions can propagate through these layers, amplifying or altering the uncertainty in other propositions, thus reinforcing the multilevel uncertainty that pervades the entire structure. Due to the significant differences in the multilevel uncertainty structures of various propositions, we can propose a third axiom to address these challenges.
Axiom 3
(Alignment). For any finite proposition, countably infinite proposition, or uncountably infinite proposition P, there exists a transformation by which P can be converted into an equivalent uncountably infinite proposition. This transformation reflects the Alignment of Propositions.
Axiom 3 addresses the relationship between omniscience and limited cognition in uncertain logic. From the perspective of omniscience, the proposition P is fully determined. In fact, P is composed of multiple potential sub-propositions , each representing a specific aspect of truth or reality. According to uncertain logic, due to the human inability to fully perceive the state of all sub-propositions, there exists a certain partiality from the perspective of limited cognition, which makes it difficult to fundamentally resolve extreme uncertainty. Axiom 3 states that these sub-proposition sets can essentially be equated to an infinite set, thus providing a more flexible framework for handling extreme uncertainty events than sample spaces and fuzzy sets. This means that even when a sudden state occurs in the future, the possibility of such a state already existed in the initial process, but might not be recorded in the fuzzy set or sample space, and its truth value was zero in normal conditions.
More importantly, the objects and phenomena in the real world are inherently dynamic, continuously evolving as they are influenced by changes in time, environment, and various other factors. As emphasized by modern science [53] and philosophy [54], change is a fundamental characteristic of the universe. This realization forces both philosophers and scientists to reconsider traditional models of knowledge, urging us to develop more flexible frameworks that account for the fluidity of reality rather than attempting to freeze it in fixed, deterministic terms. While static observations provide useful insights at a given moment, they fail to capture the underlying processes of change that define the nature of reality. As Heraclitus [55] once asserted, “Everything flows”; the universe is in a state of perpetual flux. The notion of stasis and fixation is merely a misinterpretation of the nature of change. Any static observation is merely a snapshot of a particular moment and cannot fully reflect the ongoing process of transformation. As a result, the validity of propositions may evolve over time or under changing conditions. A defining characteristic of these logical frameworks is that such dynamic changes are driven by external or internal factor , such as time [56], actions [57], or transitions between possible worlds [58]. These factors can significantly alter the truth value of propositions at different temporal stages or under varying conditions. The fourth axiom in uncertain systems can, thus, be derived.
Axiom 4
(Dynamics of Truth Value). Let P be a proposition, and let denote the truth value of P under the influence factor γ. The truth value of P changes with γ is
where represents the truth value set, and denotes the set or domain of the influencing factor γ.
According to Axiom 4, an uncertain proposition P is dynamically evolving. As information changes, the sub-propositions (where ) that were originally uncertain may gradually transform into known propositions, i.e., their truth values may be determined. Mechanisms such as information gain, factor exclusion, and the reduction in ambiguity contribute to adjusting the uncertain proposition, thereby reducing uncertainty in the decision-making process. For instance, with the introduction of new meteorological data, the accuracy of weather forecasting improves [59], and factors that were initially highly uncertain may become more determined and known. It can be observed that, on one hand, as the factor varies, the number of sub-propositions of a finite uncertain proposition changes accordingly. Under certain conditions where , the change in conditions may introduce an additional sub-proposition. On the other hand, although the proposition follows binary logic [60], the truth values of its sub-propositions dynamically change with the influence of factor . Therefore, we need to construct a dynamic function to describe the evolving nature of these sub-propositions.
Definition 1
(Dynamic function of sub-proposition). Let denote the set or domain of influencing factors, P be a proposition, and be the real interval. If there exists a mapping , such that for each sub-proposition , the mapping is defined by , then φ is called a dynamic function. The mapping φ represents the extent to which the influence factor γ affects the proposition P.
According to Definition 1, as the influence factor varies continuously, the dynamic function will yield a unique value within the interval . Suppose that at a certain point, has transitioned to a state . At this stage, each sub-proposition within the proposition P will assume a specific value . As the proposition P encompasses all possible sub-propositions , the truth of P will hold if and only if there exists at least one sub-proposition such that . This is because the truth of P depends on the state of all sub-propositions it contains, where the degree of influence of each sub-proposition is governed by the dynamic function .
As the influence factor changes, the dynamic function assigns a specific level of influence, denoted , to each sub-proposition, with ranging from 0 to 1. If, for a particular sub-proposition , , this indicates that the condition for that sub-proposition is fully satisfied under the current value of . Consequently, the proposition P will hold true only if at least one sub-proposition has . Conversely, if all sub-propositions have , then proposition P will not hold. For instance, consider proposition P as “It will rain today”, where the sub-propositions are the following: “It will rain if humidity exceeds 80% today”, “It will rain if air pressure falls below 1000hPa today”, and “It will rain if cloud cover exceeds 70% today”. If, at some point, the influence factor results in the humidity sub-proposition having , this means that the humidity condition is fully satisfied under the current value of . Therefore, we can derive the fifth axiom within the framework of uncertain logics.
Axiom 5
(Truth Value Condition). Let be a proposition composed of a set of sub-propositions . When the influence factor , the truth value , is determined as follows:
- 1.
- If , such that , then .
- 2.
- If , such that , then .
The uncertainty of P is represented by the set of possible sub-propositions , where the truth of P implies that at least one of these sub-propositions must be true under the influence factor .
Axiom 5 establishes the standard for determining truth values in uncertainty logic, aligning with classical propositional logic while also establishing close connections with fuzzy logic [61], Bayesian logic [62], and quantum logic [63] in the sub-propositional set (Axiom 1). Fuzzy sets represent degrees of membership ranging from 0 to 1, allowing truth values to vary continuously rather than being limited to the binary states of “true” or “false”. In Bayesian logic, probability quantifies the likelihood of events occurring within a sample space. Quantum logic, on the other hand, describes the relationships and reasoning processes between quantum states through probability amplitudes and the uncertainty principle. Fuzzy logic, Bayesian logic, and quantum logic each capture uncertainty in the face of incomplete information, from different perspectives and using their respective frameworks.
In uncertain logic, the membership function in fuzzy logic and the probabilities in Bayesian logic correspond to the values for sub-propositions. The interpretation of depends on the specific context of uncertainty. For example, if represents the degree of membership in a fuzzy set, uncertainty logic aligns with fuzzy logic. If represents the probability of an event, uncertainty logic aligns with Bayesian logic. If corresponds to the probability amplitude of a quantum state, uncertainty logic can be interpreted as quantum logic. Thus, serves as an abstract quantity whose meaning depends on the uncertainty framework in use, allowing uncertainty logic to integrate and unify various logical systems, each suited to different contexts and applications.
Axioms 1–5 provide an axiomatic system for addressing “infinity” and “specificity”, particularly from an intuitionistic perspective. Axiom 1 decomposes a proposition into multiple sub-propositions, reflecting the inherent uncertainty of the proposition and exploring how it approaches a limit, thus contributing to the understanding of the existence of mathematical objects. Axiom 2 introduces the concept of ordering sub-propositions, highlighting the intuitionistic emphasis on the reasoning process itself, rather than solely on the final truth value. Axiom 3 allows for the transformation of propositions into uncountable forms, providing a tool for addressing limits and boundary conditions. The dynamic change of truth values discussed in Axioms 4 and 5 indicates that the truth value of a proposition may vary with changing conditions, a feature that both relates to the limitations of Gödel’s incompleteness theorems [40] and offers a perspective for reflecting on challenges within formalism and logicism.
In addition, Wittgenstein [64] suggests that “The limits of my language mean the limits of my world” highlights the intimate relationship between language and our cognitive experience of the world. He further elaborates that “The meaning of a word is its use in the language”, a viewpoint that suggests meaning is neither intrinsic nor immutable, but is instead shaped through its practical application within specific contexts, exhibiting significant uncertainty. The axiomatic system developed in this work extends and applies this central idea to mathematical structures. Following this, the proposed axiomatic system will be employed to formulate uncertain numbers.
3. Formulation of Uncertain Numbers
Traditional mathematical methods typically rely on a classical logical framework, where propositions adhere to binary logic [65]. However, within the framework of uncertainty logic, while propositions themselves still follow classical binary logic (Axiom 4), the collection of sub-propositions involved forms a complex system (Definition 1) that incorporates features from various nonclassical logics, such as fuzzy logic, Bayesian logic, and quantum logic. This logical system offers the possibility of extending traditional mathematical methods and holds the potential to introduce entirely noval mathematical concepts. From a so-called “God’s-eye view”, it aims to construct a new kind of “uncertain number” that characterizes the most fundamental uncertainties, thereby describing the core structure of uncertain algebra. In accordance with Axiom 1, this system must be systematically constructed and analyzed from the perspective of set theory.
Zermelo–Fraenkel set theory with the Axiom of Choice (ZFC) [66] is the standard axiomatic framework for modern set theory, comprising both the Zermelo–Fraenkel (ZF) axioms and the Axiom of Choice. The ZF axioms provide the foundational structure for set operations, while the Axiom of Choice serves as a crucial tool in addressing selection problems, particularly in the context of infinite sets. The introduction of the Axiom of Choice does not lead to paradoxes or inconsistencies within the system, and the ZFC framework has been shown to be consistent. Although the Axiom of Choice may give rise to some counterintuitive results, such as the Banach–Tarski paradox [67], these phenomena do not indicate contradictions within the system. Rather, they illustrate the nonintuitive consequences of the Axiom of Choice in certain constructions. The Axiom of Choice simplifies many mathematical derivations and resolves existence issues that would be problematic in its absence.
According to Axiom 2, as the theory of uncertain logic necessitates inherent repeatability and orderliness, this implies that from a mathematical construction perspective, the first step should be to construct a multiset [68] to ensure its intrinsic repeatability. Then, to satisfy the orderliness requirement of Axiom 2, a specific order must be assigned to the elements within the multiset.
Definition 2
(Multiset [68]). Let S be a set and let be a mapping, where is the set of nonnegative integers including 0. Define M as a multiset constructed as follows:
- 1.
- For each element , if , then x is included in M with multiplicity .
- 2.
- for some , then x is not included in M.
Here, S is referred to as the underlying set of the multiset M, and the function ψ is called the multiplicity function, which assigns the multiplicity of each element x in M.
Multiplicity (Definition 2) is used to accurately record the frequency of each element in the multiset S. To organize the multiset into a structure suitable for rigorous analysis, and in accordance with the requirements of Axiom 2, each element must be assigned an ordinal index. This process should begin with a thorough examination of the well-ordering [69], which establishes the theoretical basis for the properties of these ordinal indices.
Definition 3
(Fully and Well-ordered [69]). Let Z be a set and “⩽” be a binary relation on Z. If the pair satisfies the following conditions hold for and :
- 1.
- Reflexivity: .
- 2.
- Antisymmetric: if and , then .
- 3.
- Transitivity: if and , then .
- 4.
- Totality: or . Then Z is a fully ordered set.
- 5.
- Well-ordering: and , , if , then .
Then, the fully ordered set Z is a well-ordered set. The binary relation “⩽” is called a well-ordering on Z, and the pair is said to be well-ordered.
After defining a well-ordering on a set (Definition 3), it naturally corresponds to a unique ordinal that precisely reflects its underlying structure, thereby formally introducing the concept of ordinal numbers [70].
Definition 4
(Ordinal [70]). Given a well-ordered set , there exists a unique ordinal α isomorphic to it, such that there is an order-isomorphism satisfying the following:
- 1.
- Bijectivity: f is a bijection, such that ;
- 2.
- Orderliness: f preserves the order, .
Thus, is considered the order type of and is class of ordinals, if , , then is the class initial segment of class .
In the indexing scheme, ordinal numbers (Definition 4) are used to systematically assign indices to elements within well-ordered sets (Definition 3), where every nonempty subset has a least element. This approach is crucial for our indexing system, as ordinals enable a unique and orderly organization of elements. The well-ordering theorem [71] plays a fundamental role in this foundational concept.
Theorem 1
(Well-Ordering Theorem [71]). Every set can be well-ordered. This means that for any set S, there exists a binary relation ⩽ such that the ordered pair is a well-ordered set. In a well-ordered set, every nonempty subset has a least element under the ordering ⩽. (Proof omitted)
The Well-Ordering Theorem (Theorem 1) and the Axiom of Choice [66] are logically equivalent. In fact, the Well-Ordering Theorem is a special case of the Axiom of Choice, asserting that every set (whether finite, countable, or uncountable) can be well-ordered. Whether in number theory, topology, analysis, or the more abstract field of set theory, the Well-Ordering Theorem provides powerful support and can be regarded as a core concept in the foundations of mathematics.
Building upon ordinals, Theorem 1 ensures any set can be well-ordered, denoting by an ordinal with the same cardinality as our set. Applying this theorem, there exists , allowing for a well-defined indexing system, avoiding Russell’s paradox [72]. For multisets, where elements may repeat, an indexing system must reflect this, maintaining order and unique indices. The existence of , assured by the well-ordering theorem, enables consistent indexing for such structures.
Theorem 2
(Existence of an Indexing System). Every multiset S admits a well-ordering indexing system I.
Proof.
Consider two cases: the countable case and the uncountable case.
- Countable case: Suppose S is countable. The elements of S can be listed with repetition according to their multiplicities. Specifically, for each element , we list x as many times as its multiplicity , thereby forming a sequence that enumerates the elements of S, respecting multiplicities. This enumeration induces a bijection that preserves the multiplicities of elements.As is well-ordered under its standard order, we can transfer this well-ordering to S by defining a relation on S as follows . This defines a well-ordering on S. The indexing system I is then defined by assigning to each element the least natural number such that . Explicitly, we define . It gives a well-ordering indexing system for S.
- Uncountable case: Suppose S is uncountable. By the Axiom of Choice (AC), every set, including S, can be well-ordered. Therefore, there exists an ordinal of the same cardinality as S, and a bijection . The ordinal has the same cardinality as S, and the bijection g establishes a well-ordering of S, where the order of S is inherited from the well-ordering of . Specifically, for any , we define the relation by . This induces a well-ordering on S. The indexing system I is then defined by assigning to each element the ordinal . This is a well-ordering indexing system for S.
In both cases, the indexing system I is a well-ordering of the multiset S, as required. □
In the proof of Theorem 2, we extend bijectivity from sets to multisets, and recognizing that the well-ordering of a multiset S provided by Theorem 2 is not unique due to the potential isomorphism of different well-orderings. Applying Theorem 2 directly to multisets is inappropriate as it forces a single order across them, which is unsuitable. For clarity in subsequent discussions, we refine the concept of sequential isomorphism [73].
Definition 5
(Order isomorphism [73]). Let A and B be two ordered sets. Exists mapping satisfies the following:
- 1.
- Bijection: f is a bijection from A to B.
- 2.
- Order-preserving: , .
- 3.
- Order-reflecting: .
Then mapping is called an order isomorphism, denoted as .
In order to illuminate the fundamental principles outlined in Theorem 2, we begin by examining the order structure of the multiset S under a well-defined ordering. Let us introduce the notation ⩽ to represent a well-ordering relation on the set of natural numbers , or, more generally, on an ordinal . This ordering induces a corresponding well-ordering, denoted , on the multiset S. By invoking the concept of an order isomorphism, we define a mapping I from S to or , which establishes a bijective correspondence between the elements of S and the ordered set or . This mapping preserves and reflects the order relations inherent in both sets. Consequently, we claim that S is order-isomorphic (Definition 5) to or , i.e., or .
To further analyze this structure, we construct ordered pairs , where is an element of the multiset and is its image under the mapping I. The purpose of this construction is to explore the well-orderedness of the collection of these pairs. Specifically, we seek to determine whether the set of ordered pairs, when endowed with a suitably defined ordering relation , satisfies the rigorous criteria of well-ordering. This investigation is essential, as it ensures that each element is paired with a unique index , thereby establishing a clear, unambiguous ordering among the elements of S. By confirming the well-ordered nature of the set of ordered pairs, we further substantiate the order-preserving properties of the indexing set I, which are central to the structured construction of the indexed pair set Z.
Definition 6
(Indexing set of multiset). Let S be a multiset, and I is a well-ordered set, and “⩽” is the order relation on I. Construct a set Z composed of ordered pairs , “” is the order relation on Z, such that , the set I have
- 1.
- Uniqueness: each is uniquely paired with each occurrence of , denoted .
- 2.
- Order preservation: , we have if and only if .
This structure allows us to refer to I as the indexing set that, together with S, systematically constructs the indexed pair set Z.
Definition 6 establishes a connection between a multiset S and a well-ordered set I, enabling the construction of a new set Z consisting of ordered pairs , where and . This definition captures the concept of indexing the multiset S by the well-ordered set I, providing a structured framework for organizing Z. More precisely, Definition 6 introduces I as the indexing set for S and defines two essential properties. First, uniqueness ensures that each element is uniquely paired with each occurrence of an element , thereby allowing I to function as a set of indices that accounts for the multiplicities of the elements in S. Second, order preservation defines the order relation on Z in such a way that for any two ordered pairs and , we have if and only if in I. This ensures that the ordering of Z mirrors the order of the indexing set I, while preserving the multiplicity structure of S. With this definition in place, we now state the following theorem, which formalizes the relationship between S and I and asserts the existence of a bijection between them.
Theorem 3
(Bijection). Let S be an arbitrary multiset, where each element x has multiplicity , and let I be a well-ordered set such that the cardinality of I is equal to the sum of multiplicities of all elements in S, i.e., . Then, there exists a bijection such that for each element , the cardinality of the preimage set is equal to the multiplicity of . Furthermore, one can define an order relation on such that and , we have if and only if in I.
Proof.
We aim to show that there exists a bijection such that for each , the size of the preimage is exactly , and that a well-ordering can be defined on the product .
- Countable case: Assume that S is a countable multiset. Specifically, let , where each element appears exactly times in S, and I is a well-ordered set with cardinality . The goal is to construct a bijection such that for each , the preimage contains exactly elements.Let be a well-ordered set, where is the total cardinality of S. To construct the desired bijection, we can assign the first elements of I to , the next elements of I to , and so on. In other words, for each , we assign the consecutive elements from I to . This ensures that each is mapped to exactly elements in I, and the mapping is a bijection.Next, we define the order on as follows: for any , we say that . As I is well-ordered, the relation is a well-order on Z.To verify this, let be a nonempty subset. The least element of W can be found by first identifying the smallest in W, based on the well-ordering of I. Once the least is identified, we then choose the least among the elements of W with . As I is well-ordered and S is finite at each fixed i, the least element of W always exists. Therefore, Z is well-ordered.Thus, in the countable case, we have constructed a bijection , and we have shown that is well-ordered under the relation .
- Uncountable case: Assume that S is an uncountable multiset. In this case, we, again, have a well-ordered set I such thatWe aim to construct a bijection and to define a well-order on . By the Axiom of Choice, we can well-order the multiset S, say , where is an uncountable cardinal and denotes the multiplicity of .We then recursively assign elements from I to the elements of S based on their multiplicities. Specifically, for each , we assign distinct elements from I to , ensuring that the total number of elements in I used matches the sum of the multiplicities. As I is well-ordered, this process can be completed, and a bijection is constructed.Next, we define the order on as follows: for any , . As I is well-ordered, this relation defines a well-order on Z.To verify the well-ordering of Z, consider a nonempty subset . Its least element is identified by first selecting the least in W (in the well-order of I), and then selecting the least among the elements of W with . As I is well-ordered and S is finite at each fixed i, the least element of W always exists, ensuring that Z is well-ordered.Thus, in the uncountable case, we have constructed a bijection , and we have shown that is well-ordered under the relation .
In both the countable and uncountable cases, we have constructed a bijection , and we have shown that is well-ordered under the relation . This completes the proof. □
The construction of the multiset S extends beyond the mere aggregation of its individual elements; it serves as a reflective counterpart to the well-ordered set I. By introducing the intermediary set Z, which pairs each element of S with a unique index from I, we establish a mapping that preserves the well-ordering of I within a new relational framework. Specifically, for each composite element in the Cartesian product , the pair not only respects the sequential order of I but also accurately reflects the multiplicities assigned to the elements of S.
This construction is directly informed by Theorem 3, which guarantees the existence of a bijection between I and S, ensuring that each element of S is indexed by a unique element from I according to its multiplicity. As a result, the set Z, formed by ordered pairs , serves as a well-defined structure that mirrors the order of I and maintains the multiplicity of elements in S. The well-ordered nature of Z is further formalized in the following theorem, which builds upon the structure established in Theorem 3.
In conclusion, this construction offers a rigorous method for associating the elements of the multiset S with a well-ordered set I, preserving both order and multiplicity.
Theorem 4
(Indexed pair set is well-ordered). Let S be a multiset, and let there exist a well-ordered set I that can be injectively mapped onto the elements of S such that each instance of an element in S, even if it appears multiple times, is assigned a unique index . Define a set Z such that for each element , there is a unique corresponding index , forming an ordered pair . The set Z is composed of these ordered pairs, and an order relation “” on Z is defined such that , we have if and only if . Then, the set Z is a well-ordered set.
Proof.
Utilizing Definition 3, we construct the pairs , and for and , leverage the well-ordering property of I to
- Reflexivity: holds, confirming the reflexivity of Z.
- Antisymmetric: if and both hold, then by the definition of our order relation on Z, we must have and . As I is well-ordered and antisymmetric, follows. Consequently, for the pairs and to be equal in the context of the multiset S, x and y must be the same instance of the multiset element. Thus implies both , satisfying antisymmetry.
- Transitivity: if and , then holds. , and . Therefore, if and , then , which confirms transitivity for Z.
- Totality: or , we can obtain or holds, which establishes the totality for the set Z.
- Well-ordering: consider any nonempty subset . Construct as follows: . As is nonempty, is also nonempty, and I is well-ordered set, there exists a least element . By the well-ordering of I, we have that . This implies that for , we can find , and . Therefore, is the least element of . Given the arbitrary nature of , it follows that every nonempty subset of Z has a least element. Hence, Z is well-ordered.
By Definition 3, Z is a well-ordered set. □
Based on Axiom 2, we can conclude that the essence of sub-propositions is the core focus of our attention, while ordinals serve merely as a tool to prevent the duplication of elements within a set. However, in the previous discussion, the order of the set Z was entirely determined by the ordinal sequence (see Theorems 3 and 4). This indicates that Z fails to adequately capture the essence of sub-propositions. Therefore, we introduce the symbol to replace Z, and in this new construction, the ordering method is modified to better reflect the inherent characteristics of indeterminacy. It is important to note that, whether in Z or , there is no substantial change in the ordered pairs, and thus Theorems 3 and 4) remain unaffected. In summary, we arrive at the most fundamental definition of this research.
To obtain a more precise definition, we first introduce the concept of an “uncertain number”. This uncertain number is composed entirely of complex numbers, with its elements free from any form of uncertainty. In simple terms, there is no multi-layered uncertainty involved.
Definition 7
(0-order Uncertain Numbers). Let be a nonempty multiset such that for every element , it holds that , where denotes the set of all complex numbers, constructed by all real and hyperreal numbers . Let be an index set and be a bijective mapping that assigns a unique index to each element . Define as the set of all ordered pairs , where and . The set is defined as the 0-order uncertain number, encompassing all such pairs. All 0-order uncertain numbers constitute the set of all 0-order uncertain numbers, denoted as .
Suppose we directly treat 0-order uncertain numbers as the definition of uncertain numbers, and construct a new set , defined similarly to the set in Russell’s paradox, . Specifically, the set contains all ordered pairs that satisfy the following condition: , where is some element, and is the index corresponding to , such that , i.e., the index is not an element of itself. This construction aims to describe indices that do not intersect with themselves. To clarify this construction, observe that functions as an “index” or “label” for the elements of the uncertain number . It is intended to represent specific mathematical entities. Under this definition, cannot be an element of itself. If we assume , that is, suppose is an element of itself, then by definition, we must have , meaning cannot be an element of itself, which leads to a contradiction. In other words, assuming that is an element of itself results in a logical contradiction.
On the other hand, if we assume , i.e., suppose is not an element of itself, then by definition, must be an element of itself, i.e., , which contradicts the assumption that . Thus, we encounter the classic Russell’s paradox [72], which suggests that the set of uncertain numbers could potentially contain itself as an element. From this derivation of the paradox, we can conclude that uncertain numbers are not singular but, rather, have a hierarchical structure. This implies that when defining uncertain numbers, we must introduce the concept of “rank” or “level” in order to handle uncertainty in a layered manner, thus avoiding logical contradictions.
Definition 8
(n-Order Uncertain Numbers). Let be a nonempty multiset such that for every element , it holds that , where denotes the set of -order uncertain number. Let be an index set for . A bijective function assigns a unique index to each . Define as n-order uncertain numbers.
All n-order uncertain numbers constitute a set of all n-order uncertain numbers, denoted as . A set of all uncertain number is defined as
where the multiset , , and are named by basis, index, element and ele-index of n-order uncertain number , respectively.
Definitions 7 and 8 together establish a rigorous formulation of uncertain numbers. These definitions, along with Axiom 2, highlight the primary importance of sequence order while eliminating the need to explicitly express the ordinal positions of elements. Uncertain numbers are represented solely by their values in the form , where the sequence order determines their uniqueness, and the values themselves carry no intrinsic significance beyond their positions. For example, two 0-order uncertain numbers, and , are distinct because their left-to-right (or top-to-bottom) orders differ, even though they contain the same set of values. This distinction underscores the fundamental role of sequence order in the interpretation of uncertain numbers, where each specific arrangement corresponds to a unique representation. In essence, uncertain numbers are characterized by the precise arrangement of their elements, which defines their mathematical identity. As a result, the value of an uncertain number is inherently tied to its sequence, making the order of its elements critical to its meaning and application.
4. Fundamental Operations of Uncertain Numbers
Definitions 7 and 8 provide a precise formulation of uncertain numbers. Now, it is necessary to establish the corresponding operational rules for uncertain numbers, including addition, subtraction, multiplication, and division. According to Axioms 4 and 5, the truth values of propositions are governed by classical bivalent logic. Therefore, the operations on propositions as a whole should also adhere to the traditional rules of arithmetic. In this framework, the operations on uncertain numbers will be conducted directly on their representative values, i.e., by performing addition, subtraction, multiplication, and division on the corresponding components, without considering boundary effects or intervals. This approach ensures that the arithmetic of uncertain numbers remains consistent with classical mathematical operations, thus maintaining a strong connection between uncertain number theory and traditional mathematics.
To define operations on uncertain numbers, it is essential first to classify them based on the nature of their uncertainty. This classification provides the foundation for establishing precise and appropriate arithmetic rules for various types of uncertain numbers. The classification will follow the principles outlined in Definitions 7 and 8, ensuring a methodological approach rooted in rigorous mathematical formalism. By categorizing uncertain numbers, a foundation is established for deductive reasoning and hypothesis formulation.
Definition 9
(Classification of Uncertain Numbers). Let be an uncertain number. The classification of Π is determined by the following conditions:
- 1.
- A 0-order uncertain number, denoted as , is classified as a certain number and is represented as , if and only if the equality holds universally. The set of all certain numbers is denoted by .
- 2.
- Π is classified as an absolute uncertain number, if and , where is the set of all uncertain number and is the set of all certain numbers.
The nature of the uncertainty is further characterized based on the structure of the uncertain number basis S:
- 1.
- If S forms a countable multiset, then Π is a countable absolute uncertain number.
- 2.
- If S does not form a countable multiset, then Π is an uncountable absolute uncertain number.
According to Definition 9, numbers can be classified based on the nature of their possible values. For example, is a certain number, equivalent to , while is a countable absolute uncertain number, representing a countably infinite set of even numbers. Similarly, is an uncountable absolute uncertain number, as it includes all real numbers between 0 and 1, an uncountably infinite set. is also a countable absolute uncertain number, and is an uncountable absolute uncertain number, encompassing all positive real numbers. These classifications distinguish between certain and uncertain numbers, further divided into countable and uncountable sets, forming a fundamental framework for understanding their relationships.
In traditional mathematics, the complex number field is one of the most foundational and expansive number fields. According to Axiom 1, every uncertain proposition inherently contains certain propositions. Thus, the complex number field can be viewed as a subset of the set of uncertain numbers. Based on Definition 7, it follows that any complex number can be represented as a multiset of singleton elements , where . This multiset may further consist of an indeterminate collection of pairs , with . This observation leads to the formulation of a theorem.
Theorem 5
(Complex Number Fields). Let denote the set of complex numbers, the set of 0-order uncertain numbers, and the set of all uncertain numbers. Then, the following inclusion holds: , and the set of complex numbers as uncertain numbers, , is an element of , i.e., .
Proof.
Let be an arbitrary complex number. By Definition 7, we define the singleton set . We index this set with the natural number 1, forming the pair . This constructs a 0-order uncertain number, denoted as .
As is the set of all 0-order uncertain numbers, it follows that . Furthermore, by Definition 8, the inclusion extends to the broader set of uncertain numbers, giving us .
Next, we consider the set of all complex numbers, denoted by . We define . According to Definition 7, the set can be treated as a 0-order uncertain number. In order to represent this more formally, we invoke the ordinal , where is the cardinality of the countably infinite set of natural numbers.
The ordinal serves as an indexing set, where each complex number is uniquely associated with a specific ordinal within this well-ordered set. This results in a construction of the 0-order uncertain number , where are complex numbers. By Definition 8, it follows that .
Thus, the inclusion holds, and we have shown that . □
The newly established theorem facilitates the representation of all conventional numbers within an uncertain number system, that is , embedding them into a comprehensive mathematical schema. Given a nonempty multiset S, the corresponding uncertain number is derivable by applying the indexing scheme as delineated in Definitions 7 and 8.
Theorem 6
(Judgement). For any order of uncertain number , it is necessary and sufficient that the foundational multiset , from which is recursively constructed, is a nonempty multiset of complex numbers, i.e., and .
Proof.
By induction, separately establishing the necessity and the sufficiency of the given condition.
- Necessity: Proof by mathematical induction.Base case : for a 0-order uncertain number , it is explicitly constructed from . By Definition 7, , and . This establishes the necessity for the base case.Inductive step: Assume the necessity holds for an -order uncertain number, i.e., its construction is based on a foundational multiset of complex numbers that is nonempty. For an n-order uncertain number , constructed from by Definition 8, where each is an element of , the inductive hypothesis implies that all such ultimately trace back to an that is a nonempty multiset of complex numbers. Hence, the necessity condition is satisfied for all orders n.
- Sufficiency: Proof by mathematical induction.Base case : Given a nonempty multiset , constructed from complex numbers, one can construct a 0-order uncertain number by Definition 7, satisfying the base case of sufficiency.Inductive step: Assuming the sufficiency for constructing a -order uncertain number, we need to demonstrate that it holds for order n. By Definition 8, given the ability to construct from , we form as a collection of -order uncertain numbers. Utilizing these, can be constructed, thereby proving sufficiency for all orders n.
In conclusion, the condition that the foundational multiset is a nonempty multiset constructed from complex numbers is both necessary and sufficient for the constitution of uncertain numbers of any order. □
Based on Definitions 7 and 8, the structure of uncertainty numbers exhibits considerable complexity. According to Axiom 3, any uncertainty number can be transformed into a set with an uncountable basis. Therefore, compared to uncountable sets, the structure of finite and countably infinite uncertainty numbers contains a substantial amount of “gaps” to some extent. For example, consider the uncertainty number . Relative to the uncountable uncertainty number formed by the entire set of real numbers, there are significant gaps between these numbers. To formalize these gaps, we can introduce a filling mechanism, such as using trailing zeros, to meet the requirements of Axiom 3.
Definition 10
(0-Trailing number). Define as the maximal index in a countable absolute uncertain number Π, beyond which all subsequent elements must be 0, termed as 0-trailing numbers. The inclusion of these trailing zeros does not alter Π. Formally, this property allows for Π to be equivalently expressed as irrespective of the number of trailing zeros appended.
Definition 10 establishes a robust foundational framework for the alignment of any two zero-order uncertain numbers. This initial construct is pivotal as it provides the necessary theoretical underpinnings for extending the alignment process to uncertain numbers of higher orders. The framework systematically demonstrates that it is not only feasible but also methodologically sound to achieve congruence between uncertain numbers, aligning them in terms of both their maximum indices and respective orders. This congruence ensures that any comparative or computational operations performed on these uncertain numbers adhere to a consistent and rigorous mathematical structure, thus preserving the integrity and reliability of subsequent analyses and applications. Through this rigorous alignment, the framework ensures the preservation of accuracy and reliability in subsequent analyses and applications.
Theorem 7
(Alignment). For any two uncertain numbers , there exists a process to align their order and maximum index. This procedure shall henceforth be referred to as the Alignment process, denote as .
Proof.
Consider and with and . The alignment involves two key steps:
- Order alignment: Without loss of generality, assuming that , we increment the order of to n by iteratively constructing from by Definition 7 and 8, ensuring that elements of are in , until reaching and, thus, making an n-order uncertain number. Define iteratively for . This yields transforming into in terms of order.
- Max index alignment: Let and be maximal indexes of and , respectively. Without loss of generality, assume that .
- (1).
- If is a certain number, extend by appending for by Definition 9.
- (2).
- If is an absolute uncertain number, extend by appending for . This operation aligns with , utilizing the property of Definition 10.
Hence, and are aligned in both order and maximal index. □
Here, the process of aligning uncertain numbers is demonstrated through three examples. First, consider the alignment of a finite uncertain number with a countably infinite uncertain number. Let be a finite uncertain number containing two elements, and be a countably infinite uncertain number representing all natural numbers. Since is a finite uncertain number and is a countably infinite uncertain number, we need to extend the index set of to a countably infinite uncertain number of the same size as . For example, we can extend to , thus aligning the index sets of the two uncertain numbers.
Next is the alignment of a countably infinite uncertain number with an uncountably infinite uncertain number. Let be an uncountably infinite uncertain number representing all real numbers in the interval , and let be a countably infinite uncertain number representing all even numbers. Since is an uncountable uncertain number and is countable, in order to align their cardinalities, we can extend by adding a set of all zeros to make it have the same uncountable cardinality as . This results in the extended uncertain number , achieving the alignment.
Finally, consider the alignment of a finite uncertain number with an uncountably infinite uncertain number. Let be a finite uncertain number containing two elements, and let be an uncountably infinite uncertain number representing all real numbers in the interval . When aligning these two uncertain numbers, since is finite and is uncountable, we need to extend so that its cardinality aligns with that of . This can be done by extending to , ensuring the alignment.
In discussing the alignment of different types of indeterminate numbers, we primarily focus on three categories: finite, countably infinite, and uncountably infinite indeterminate numbers. Specifically, alignment can be achieved through the following methods. For aligning countably infinite and finite indeterminate numbers, this can be done by extending the index set of finite indeterminate numbers—i.e., by adding zero elements—to match the countably infinite indeterminate numbers. For the alignment between finite or countably infinite indeterminate numbers and uncountably infinite indeterminate numbers, this can be accomplished by extending the finite or countably infinite indeterminate numbers into an uncountably infinite set, i.e., by adding uncountably infinite zero elements, thus achieving alignment. In this way, different types of indeterminate numbers can be compared and operated within the same cardinal framework. The core of these methods lies in the appropriate extension operations, allowing different categories of indeterminate numbers to be effectively compared and manipulated within a unified mathematical structure.
Once the alignment issue is resolved, we are in a position to define both addition and multiplication within the framework of uncertain numbers.
Definition 11
(Addition and Multiplication). Let represent two uncertain numbers with index sets and , respectively, such that and . Prior to operations, alignment is meticulously conducted on both entities to standardize the maximum index and order, resulting in aligned representations with index sets and , respectively.
- 1.
- Addition “+”: The operation defines the addition of two uncertain numbers, aligning their indices for element-wise summation.
- 2.
- Multiplication “×”: The operation specifies the multiplication of two uncertain numbers, ensuring index congruence for element-wise product.
Here, denotes an element of for each , and represents an element of for each .
As demonstrated in Axioms 4 and 5, the truth values of propositions follow classical logic. Therefore, uncertain numbers must comply with conventional mathematical laws. This framework (Definition 11) ensures that the extended operations remain consistent with established mathematical principles, thereby extending traditional arithmetic to accommodate a broader mathematical context.
Consider the following examples of addition and multiplication operations on uncertain numbers. Let and , where the index sets and are already aligned. The addition operation yields , while the multiplication operation gives . In a second example, consider with index set , and with . After alignment, we obtain and , resulting in the addition and the multiplication . These examples illustrate how addition and multiplication operations are performed element-wise on uncertain numbers after aligning their index sets.
When dealing with operations involving finite sets, countably infinite sets, and uncountably infinite sets, the situation is relatively complex, requiring the use of cardinal arithmetic rules from set theory [74]. Let represent an uncountably infinite set (with cardinality ), and let represent a countably infinite set (with cardinality ). To align the cardinalities for certain operations, we construct a multiset composed entirely of zeros, with cardinality matching that of the real numbers, . This multiset of zeros can be denoted as and appended to . According to cardinal arithmetic, the union of a set with cardinality and a set with cardinality results in a set with cardinality . Thus, the aligned set can be expressed as . This aligned set now has the same cardinality as , i.e., . We can then define operations using cardinal arithmetic. The sum set , representing the set of all elements obtained by adding each element of to each element of (Definition 11). Similarly, the product set , representing the set of all elements obtained by multiplying each element of with each element of (Definition 11).
Theorem 8
(Closure Properties). Let denote the set of uncertain numbers. Then is closed under addition and multiplication. That is, , it holds that and .
Proof.
By Definition 11 of the operations “+” and “×” within , we consider the following two cases:
- Additive closure: The operation is defined such that it preserves the uncertain nature of the elements in . As includes all elements that are uncertain by Theorem 6, the sum must also be an element of , confirming that is closed under addition.
- Multiplicative closure: Similarly, the product will also preserve the uncertain characteristic of . Consequently, by Theorem 6, the product must be an element of , verifying that is closed under multiplication.
Therefore, exhibits closure under both addition and multiplication. □
Theorem 8 states that is closed under addition and multiplication, ensuring that mathematical operations do not eliminate the uncertainty in uncertainty modeling. It guarantees that the result of operations on uncertain numbers remains within the set of uncertain numbers. This property provides a foundation for further research in areas such as uncertainty algebra, fuzzy logic, and related fields.
5. Infinity from the Perspective of Uncertain Numbers
In traditional mathematics and physics, the concepts of division by zero [75] and singularities [76] are closely related, especially in the analysis of function limits and the study of extreme physical phenomena [77]. In classical mathematics, division by zero (e.g., ) is typically undefined [78], but through the concept of limits, we can investigate the behavior of functions as their denominators approach zero. For example, consider the function . As x approaches zero, tends to either positive or negative infinity, indicating the presence of a singularity at .
In complex analysis [79], a singularity refers to a point at which a function exhibits irregular or singular behavior in its vicinity. The division by zero issue is an example of such irregular behavior. Division by zero problems are typically associated with functions tending toward infinity or exhibiting indeterminate forms, which reflect the singularity of the function at that point. Therefore, the issue of division by zero can essentially be viewed as a singularity problem, revealing the anomalous behavior of a function in the process of taking limits.
Specifically, in the case of division by zero, , itself lacks a defined numerical value, but it can be interpreted through the indeterminacy inherent in the limit process. This indeterminacy can be decomposed into multiple potential sub-propositions, with each describing a specific behavior pattern. For example, for the function , as , may either tend toward positive infinity or negative infinity, reflecting the uncertainty [80] in the behavior of the function near .
In physics, singularities often appear in theoretical models under extreme conditions, such as the center of a black hole in general relativity or the spacetime singularity at the very beginning of the Big Bang. In these regions, physical quantities tend to infinity, and current physical theories cannot fully describe the phenomena. At these physical singularities, extreme uncertainty and the failure of existing theories often occur, which is similar to the indeterminacy encountered in division by zero problems. This similarity suggests that the “multiple possible sub-propositions” (Axiom 1) structure in uncertain number (Definitions 7 and 8) aligns closely with the limiting behavior found at physical singularities.
Therefore, the study of division by zero and singularities in mathematics and physics can be further deepened through the perspective of uncertain numbers. This concept holds promise as a new tool for analyzing and understanding the uncertainty and anomalous behavior that emerge in limiting processes or extreme conditions.
Theorem 9
(Divergent). Let be a 0-order uncertain number with the property that , such that . Additionally, for each , such that . If a sequence is constructed such that and for any given , there exists an such that , then .
Proof.
Given with the stated properties, consider a sequence , where each . By the definition of with . Define the set such that where . This is feasible because with and , indicating contains elements arbitrarily larger than or equal to any given real number M.
To demonstrate , consider any arbitrary . By the construction of such that . Thus, , such an N can be found, satisfying the criterion for divergence to infinity. Hence, it is proved that . □
Building upon the established Theorem 9, which characterizes divergence for a sequence within the real numbers , we extend our discourse to encompass broader number systems.
Theorem 10
(Real Analysis). Let be a divergent sequence in such that as , , and let be a dense set in . Then , there exists an such that .
Proof.
Given that is divergent with as , for any real number M, we can consider . There exists such that . Choose to ensure that . Using the density of , for any open interval around , there must exist at least one point in due to the density property. Specifically, , consider the interval . Let , which is positive as . By the density of , there exists some such that . Using the reverse triangle inequality, we have . Therefore, , there exists an such that , thus completing the proof. □
Theorem 11
(Surreal Analysis). Let denote the class of all infinite surreal numbers. For every real number , there exists such that .
Proof.
Consider an arbitrary real number . We proceed by constructing an infinite surreal number such that , considering the sign of M.
- : Define , where . According to the construction rules for surreal numbers, is greater than any element of . Therefore, is an infinite surreal number satisfying .
- : Define , where . By the construction rules for surreal numbers, is less than any element of . Therefore, is an infinite surreal number satisfying .
In both cases, we have explicitly constructed an infinite surreal number , which may be either or , such that . As M was arbitrarily chosen from the real numbers, this construction can be applied universally, thereby proving the theorem. □
Theorem 12
(Hyperreal Analysis). Let denote the set of all infinite hyperreal numbers. For every real number , there exists such that .
Proof.
Consider the set of real numbers and let M be an arbitrary real number. We wish to show that there exists an infinite hyperreal number such that . The hyperreal numbers extend the real numbers to include infinitesimals and infinite quantities. An infinite hyperreal is one that is greater than any standard real number. We use the construction of the hyperreals via ultrapowers, which involves taking the power set of the natural numbers, modulo an ultrafilter.
Let be a nonprincipal ultrafilter on and consider the ultrapower , which contains equivalence classes of sequences of real numbers. A hyperreal number represented by a sequence is infinite if and only if for every real number M, there exists such that . To construct such an infinite hyperreal, consider the sequence . This sequence is mapped to an equivalence class . For every real number M, there certainly is an such that . Thus, the equivalence class is greater than any M for sufficiently large n, which implies that is an infinite hyperreal number. Therefore, , the infinite hyperreal number satisfies , and hence . This concludes the proof. □
The condition is crucial for the conception of “infinity” in the real numbers (Theorem 10), superreal numbers (Theorem 11), and hyperreal numbers (Theorem 12). Based on this, we introduce the notation in Definition 7 to precisely define “infinitesimals” and “infinite” within the context of uncertain numbers. The central idea of this framework is that encompasses the infinite spectrum of numbers, excluding only real numbers smaller than M. For any , the condition guarantees that includes elements at least as large as , extending to potentially infinite magnitudes.
Definition 12
(Large Uncertain Number). Let Ω be a 0-order uncertain number consisting of all elements such that for every real number , the inequality is satisfied. For any two elements , if , then there exists another infinite number such that . The 0-order uncertain number Ω is referred to as a large uncertain number, LUN.
The concept of LUN is closely related to the idea of infinity. According to Definition 12, an LUN is defined as an uncertain number whose elements have magnitudes far greater than any real number. In this sense, LUNs can be considered as “infinitely large” because their magnitudes can grow without bound. Specifically, for any real number , every element of the LUN satisfies , meaning that no matter how large M is, the elements of the LUN are always larger than M. Thus, the LUN defines an unbounded range that not only tends toward infinity but also encompasses infinitely many larger numbers. This property establishes a close relationship between LUNs and infinity.
In Definition 12, is defined as an unbounded numerical entity, encompassing the concept of infinity across various systems, including the reals (Theorem 10), surreals (Theorem 11), and hyperreals (Theorem 12). This provides a foundation for defining its dual, the minimal uncertain number.
Definition 13
(Small Uncertain Number). Let ϵ be a 0-order uncertain number consisting of all elements such that for . The 0-order uncertain number ϵ is referred to as a small uncertain number, SUN.
In contrast, the concept of an SUN is related to the idea of infinitesimal. This is because the reciprocal of a very large quantity, such as an LUN, results in an exceedingly small quantity. According to Definition 13, an SUN is the reciprocal of an LUN; therefore, specifically, if an LUN exists, then the reciprocal belongs to an SUN . As LUNs are infinitely large, their reciprocals become exceedingly small, making SUNs “infinitesimal” numbers that are smaller than any real number.This infinitesimal property of SUNs is what makes them conceptually distinct from standard real numbers. Considering the density and boundedness of LUNs, it can be proved that SUNs are also dense (Theorem 13) and bounded (Theorem 14).
Theorem 13
(Dense of SUN). The small uncertain number ϵ is dense in itself.
Proof.
Let be any two distinct elements such that . By Definition 12, there exist elements such that and . As , it follows that . Because is dense in itself, there exists an element such that . Taking the reciprocals, we obtain . Let , then by the Definition 13, and we have . This proves that between any two elements of an SUN, there exists another element in , which shows that an SUN is dense in itself. □
Theorem 14
(Boundness of SUN). Let a small uncertain number ϵ, then satisfies .
Proof.
Take , by Definition 13, there corresponds an such that . By the properties of , for any real , holds. As is positive and greater than any positive real number, it follows that . By choosing , we find that , which demonstrates the boundedness of SUNs relative to real numbers. □
Considering the density of the real number system and the conclusion of Theorem 14, we find that SUNs cannot be defined within the real number range. To address this issue, we adopt the hyperreal number system from nonstandard analysis [81]. This system extends the framework of real numbers by introducing infinitesimals and infinite quantities, allowing us to effectively define and analyze SUNs within the hyperreal number system, thus overcoming the limitations of the real number system.
Theorem 15
(Stability of Real Numbers). Given any real number and a small uncertain number ϵ as defined in Definition 13, it holds that .
Proof.
By Definition 9, we construct a certain number . We consider the following cases based on the value of :
- Case 1: If , then clearly . This trivially satisfies the theorem as the standard part of a remains unchanged.
- Case 2: If , is infinitesimal (i.e., is infinitely close to 0 but not equal to it). In this case, , the numbers and are infinitesimally close to a, meaning that their differences from a are infinitesimal. According to nonstandard analysis, if the difference between two hyperreal numbers x and y is infinitesimal, then their standard parts are equal: . Therefore, , the standard part of both and is equal to a, so .
Thus, we have established that , proving the theorem. □
Theorem 16
(Bijection between SUN and LUN). Let Ω be an LUN and ϵ be an SUN. There exists a bijective mapping such that , with .
Proof.
We prove the bijection by demonstrating that f is injective and surjective.
- Injectivity: Let and assume that . By definition of f, which maps each to its multiplicative inverse in , we have that and . Therefore, if , it implies that . Multiplying both sides by yields , proving injectivity.
- Surjectivity: We need to show , such that . Given , by Definition 13, with . f is defined as for . Thus, for the chosen , we have , demonstrating the existence of for every , and proving surjectivity.
As f is both injective and surjective, it is bijective. □
According to Theorem 15 on the stability of real numbers, SUNs cannot be contained within the standard real number system . This theorem states that for any real number and any SUN , we have , meaning that adding or subtracting an SUN does not change the value of a real number. Considering Theorem 16, which establishes a bijection between LUNs and SUNs, we infer a one-to-one correspondence between them, defining it as the hierarchy change between the number lines (Figure 1).
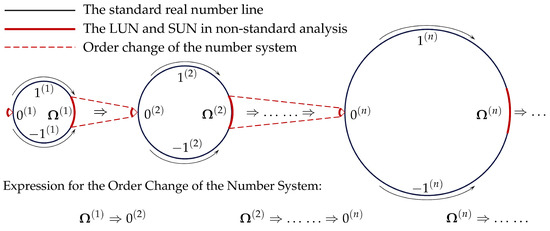
Figure 1.
Real certain number axis. The black axis represents the conventional real number axis, while the red axis depicts a certain number axis derived from the hyperreal number system, an extension of the traditional real numbers.
Definition 14
(Order Change of the number system). Owing to the intrinsic bijection between the LUN and the SUN, wherein the LUN is mapped to replace the zero, we propose it as the order change of the number system. An uncertain number belonging to the p-th order system is represented as , and the order change of the number system is designated as . Unless specifically marked as “” and “”, it is assumed by default that p is consistent.
Figure 1 visualizes the transition between number systems, showing how the hyperreal system maps the concept of to the 0 of the next order system. This process highlights the fundamental role of scale changes in problem-solving and subtly reveals the essence of calculus, particularly in the context of limits and continuity.
6. Singularities from the Perspective of Uncertain Numbers
Singularities and division by zero are closely intertwined in mathematics [82], as a singularity typically refers to points or regions where a function or expression exhibits abnormal behavior or becomes undefined. Division by zero is a prime example of such a singularity. When division by zero occurs, the result often becomes indeterminate or tends to infinity, thereby creating a singularity. In mathematical analysis, division by zero is often the starting point for discussions of singularities, particularly in the contexts of limits, continuity, and differentiation. More broadly, division by zero is not simply an algebraic error; it also involves the understanding and treatment of infinitesimals, the behavior of limits, and how to manage these “uncertainties” or “indeterminacies” in mathematical modeling. As such, division by zero is a critical aspect of studying singularities, and resolving division by 0 is often an essential step in addressing singular.
Generally speaking, the number 0 possesses two key properties. It is both the starting point of counting, i.e., the additive identity, and the absorbing element in multiplication [83]. In the application of 0, different characteristics emerge depending on the context of the operation, which can be interpreted as a form of “or” relationship. Specifically, 0 implicitly carries distinct properties in various mathematical operations. According to Axiom 1, we may treat 0 as an expression of uncertainty in a proposition.
Definition 15
(Categorization of Zero in Uncertain Logic). 0 is categorized into two distinct types according to uncertain logic, :
- 1.
- Identity element, , signifies the addition identity element of 0.
- 2.
- Absorptive element, , denotes the absorption of 0.
In accordance with order change in Definition 14, , it logically follows that the entity also possesses the described property.
Definition 15 can be interpreted as an application of uncertain logic, as expressed in Axiom 1. From this, a computational framework for 0 follows, as detailed in Theorem 17. The concepts of absorption and distributive processes are introduced in Definition 16 and Theorem 18.
Standard components are of considerable practical significance in applied disciplines, owing to their proven reliability, seamless compatibility, and extensive support infrastructure. In contrast, while non-standard components may offer theoretical advantages, their deployment in real-world applications is often accompanied by inherent risks. Consequently, this discussion will focus exclusively on standard components, with the exception of LUN and SUN.
Theorem 17
(Inverse of 0). In the set of uncertain numbers , the following relationship exists:
where and are identity element and LUN.
Proof.
According to Definition 13, we have . We examine the relationship by Definition 11, aiming to show that represents a large uncertain number. We define M as the multiplicative inverse of any positive real number r, thus , where . Given , for the reciprocal of each , by Definition 11, we obtain . As , and considering , it follows that . Thus, , according to Definition 12. Furthermore, by Theorem 15, considering , it implies that . □
Definition 16
(Absorption and Distributive Processes). In an algebraic structure , if there exists an element such that , and the conditions and are satisfied, then the operation ⊗ is said to have the absorption process with an absorbing element a. To distinguish this from the relation, we use the symbol “⊢” to denote the absorption process, and the resultant element after absorption is referred to as an absorbed element, denoted with a hat. Thus, the above conditions can be expressed as and . Otherwise, the operation can be formally characterized as a distributive process, denoted symbolically by “⊣”.
Theorem 18
(Distributive Process). For the absorbing element , there exists an equivalent relation universally.
Proof.
Construct an uncertain number within an algebraic structure . Given is an absorbing element, the conditions and are satisfied. There exists a equivalent relation by Definition 16. In accordance with Definition 11, when an uncertain number is subjected to either addition or multiplication with another uncertain number, the result invariably remains an uncertain number. Hence, the retains its generality. □
Upon formalizing Definition 16, we ascertain that 0 qualifies as an absorptive element, succinctly expressible through the relation . According to Theorem 18, the nature of an absorption element is explicitly determined by the outcome of either releasing “⊣” or absorbing “⊢”. Therefore, whenever an absorption or distributive process occurs, the absorber a is marked as “”. If , then , where , because , and , where . In this context, absorption and distributive processes (Definition 16) are considered intrinsic properties.
Theorem 19
(Absorbing Element ). An LUN Ω is characterized as an absorbing element.
Proof.
For the operation, ⊗ represents either addition or multiplication by Theorem 11.
- Case 1: Operation by a certain number, a. Let a be an arbitrary real number. Consider the operation , which, by Definition 11, produces the set . By Definition 12, the property of , , there exists an such that . For an arbitrary i and assuming , it follows that , satisfying the definition of . Thus, the resulting uncertain number , proving the absorptive nature with respect to a certain number a.
- Case 2: Operation by uncertain numbers . Consider the multiplication operation . Given the definition of , for any real number M, there exists a corresponding such that . Consequently, for each product , where represents the respective elements from the set , it holds that , which also satisfies the definition of . Hence, the product set , demonstrating the absorptive nature when multiplied by an uncertain number set.
Through the formal proof presented above, we have demonstrated that both a real number and a set of uncertain numbers, when multiplied by , result in a set whose elements still adhere to the defining characteristics of , i.e., their absolute values exceed that of any given real number. □
Remark 1
(Absorbing Elements of Uncertain Numbers). Within the uncertain number set , the algebraic structures pertaining to the operations of addition and multiplication are characterized by their distinct absorbing elements, denoted by and , respectively.
- 1.
- Addition absorbing element: , and , where , .
- 2.
- Multiplication absorbing elements:
- (a)
- , and , where , .
- (b)
- , and , where , .
Multiplication between absorbing elements “” and “”:where 0 and Ω represent all types of 0 and LUNs, include and , and . Here, a represents an uncertain number containing a certain number, and , , , represent absolute uncertain numbers.
Let us conduct a thought experiment: Imagine a person standing in an open area in a city. To this person, the city appears to be infinitely large. As the person gradually ascends, the boundaries of city begin to reveal themselves in a fractal-like structure. As the height increases further, the fractal boundary of the city transitions from a jagged, discrete shape to a smoother contour. Beyond a certain point, as the height continues to rise, the boundary of city evolves into a continuous function. Finally, as the height increases even more, the city’s extent contracts into a single point, entering the realm of the infinitesimally small.
Throughout this process, as the city’s size transitions from infinite to infinitesimal, the external boundary and shape of city undergo significant changes, yet at each stage, the state of city still represents a form of existence. This thought experiment illustrates why the concepts of infinity and infinitesimal can transform into an uncertain state. The reason lies in the fact that and 0 absorb intrinsic uncertainties (Remark 1). These uncertainties can, in turn, be quantified and represented through the framework illustrated in Figure 1.
In summary, the behaviors of uncertain numbers , , , and differentiate when considering zero versus LUNs, highlighting a dependency on type.
Remark 2.
The absorption elements and exhibit a clear uncertainty, without interfering with the axiomatic system of traditional mathematics for certain numbers.
Definition 17
(Identity Elements). In uncertain number set , let us establish the following elements, which are critical to its algebraic structure:
- 1.
- is identified as the additive identity, satisfying .
- 2.
- 1 serves as the multiplicative identity, ensuring that .
- 3.
- is additive inverse, satisfies , where is the additive identity.
- 4.
- is multiplicative inverse, satisfies , where 1 is the multiplicative identity.
- 5.
- i is the imaginary unit, satisfies .
These elements are integral to the structure of the uncertain number set and facilitate the exploration of its intrinsic algebraic properties.
In examining structured sets as delineated under Definition 10, the computation of inverse elements uncovers subtle complexities. Contrary to preliminary postulations, the uncertain number , when augmented to , does not correspond to . Instead, it aligns with a set typified by the LUN as defined in Definition 12, symbolized by . Hence, we represent the augmented sequence as . Here, is designated as the tailing number, which is distinct from itself.
Remark 3

(0-Inverse). In uncertain number set , let us establish the following elements, which are critical to its algebraic structure, in Table 1:

Table 1.
Additive and multiplicative structures of the elements 0 and .
Here, , and . In conclusion, we need to map the absorbing element “” back to the identity element “”, and then use the above formula to calculate.
From Table 1, it is evident that the framework of uncertain numbers introduces a novel perspective that diverges from the traditional axiom in mathematics, which asserts that the product of zero and any number is always zero. In the context of uncertain numbers, however, the product of zero with any number leads to the formation of a new class of entities, which we refer to as uncertain numbers. This is a significant departure from the conventional interpretation. Nevertheless, it is crucial to emphasize that this innovation does not contradict the principles of classical mathematics. Specifically, within the domain of certain numbers—i.e., the classical framework—it remains valid that the product of zero and any certain number is zero. This relationship is still consistent within the uncertain number framework, as demonstrated by the following expression: for any certain number , we have . Thus, while the concept of uncertain numbers opens new possibilities, it preserves the foundational truths of classical arithmetic within the context of certain numbers.
7. Algebraic Properties of Uncertain Numbers
Addition and multiplication were already defined in Definition 11. The identity elements are defined in Definition 17. Now, we define division and subtraction.
Definition 18
(Subtraction and Division). Let be two uncertain numbers with index sets and , respectively, such that and . Alignment is executed to standardize their maximum index and order, yielding with and .
- 1.
- Subtraction “−”: , defining the subtraction of two uncertain numbers after alignment in Theorem 7.
- 2.
- Division “÷”: , defining the division of two uncertain numbers post alignment in Theorem 7.
Here, denotes an element of for each , and an element of for each .
The next step is to establish that the set of uncertain numbers forms a field. This proof is divided into three parts: First, we prove the set of 0-order uncertain numbers (Theorem 20). Second, we demonstrate the set of n-order uncertain numbers (Theorem 21).
Theorem 20
(Field of ). The set of uncertain numbers forms a field .
Proof.
For any elements , where , and . In aligned representations with index sets , , and , respectively, let , ensuring that .
- Closure: By Definition 11, the sum and the product . By Theorem 6, both and are elements of , affirming the closure property.
- Associativity: For , with . The associativities of addition and multiplication are demonstrated through by Theorem 11, and , respectively, as substantiated by Theorem 11.
- Identity: The elements 0 and 1 act as the additive and multiplicative identities in , respectively, as established by Theorem 17.
- Inverse: For every , there exists an additive inverse , and a multiplicative inverse , ensuring that , and , as delineated by Theorem 17.
- Commutativity: The operations and are commutative, evidenced by their symmetry in operation as indicated by Theorem 11.
- Distributivity: For , the distributive law is validated through , confirming the distributive property over addition.
Therefore, is the field structure, where is the underlying set of the field. □
Theorem 21
(Field of ). The set of uncertain numbers forms a field .
Proof.
Grounded in the principles articulated in Theorem 20, a rigorous proof is established via the method of mathematical induction. Assume that forms a field for some arbitrary . We then show that also forms a field, thereby completing the inductive step. For any elements , where , and . In aligned representations with index sets , and , respectively. Let , ensuring that .
- Closure: By Theorem 11, consider that and forms a field, the sum and the product . By Theorem 6, both and are elements of , affirming the closure property for addition and multiplication.
- Associativity: For , with and forms a field. The associativities of addition and multiplication are demonstrated through by Theorem 11, and , respectively, as substantiated by Theorem 11.
- Identity: The elements 0 and 1 act as the additive and multiplicative identities in , respectively, as established by Theorem 17.
- Inverse: For every , there exists an additive inverse , and a multiplicative inverse , ensuring that , and , as delineated by Theorem 17.
- Commutativity: Consider and forms a field, the operations and are commutative, evidenced by their symmetry in operation as indicated by Theorem 11.
- Distributivity: Consider and forms a field, for , the distributive law is validated through , confirming the distributive property over addition.
Therefore, is the field structure, where is the underlying set of the field . □
Finally, we combine all the above information to prove that the set of uncertain numbers forms a field.
Theorem 22
(Field of P). The set of uncertain numbers forms a field .
Proof.
Based on Definition 7, we are able to adjust any two uncertain numbers of differing orders to a common order, by Theorems 20 and 21, thereby establishing that constitutes a field . □
Theorem 22 defines the set of uncertain numbers as a field, suggesting that they may possess fundamental algebraic properties such as closure under addition, subtraction, multiplication, anddivision. This structure could facilitate operations involving uncertainty, enabling more consistent treatment of uncertain quantities and expanding applications in solving equations, conducting algebraic operations, andanalyzing systems with imprecision or variability. Additionally, it may open new avenues for applying techniques from field theory and algebraic geometry, contributing to more sophisticated modeling of uncertainty in fields like physics, economics, andengineering. The formal recognition of uncertain numbers as a field could also inspire new mathematical tools and frameworks, enhancing our ability to tackle problems in stochastic processes, decision theory, and data science.
8. The Quantification of Uncertainty in Uncertain Numbers
The essence of an uncertainty number is a set that encapsulates all possible outcomes of a numeral event (Definition 7 and 8). In practice, however, due to limitations in cognition, environment, and conditions, it is often not possible to enumerate “all” possibilities. As a result, the maximal index of an uncertainty number (Definition 10) typically changes with variations in influencing factors. Assuming that the maximal index remains constant, the uncertainty number can be regarded as a sample space, within which probability measures and probability density functions can be defined for its sub-propositions (Axiom 1).
Definition 19
(Probability Space for Uncertain Number). Let Π denote an uncertain number. A probability space for an uncertain number is defined by a triple , where Π is a sample space representing the uncertain number, is a σ-algebra on Π, is a probability measure. The probability space must satisfy the following axioms:
- 1.
- , that is the total probability of all outcomes is 1;
- 2.
- , that is the probability of the empty set is 0;
- 3.
- Countable additivity: For any countable collection of disjoint sets such that , we have
Definition 20
(Random Variable for Uncertain Number). Let be a probability space for uncertain numbers. A random variable X on this probability space is a measurable function such that for every Borel set , the pre-image . In other words, X is a measurable function with respect to the σ-algebra . If , we say that X is a random variable on the probability space .
Definition 21
(Probability Density Function). Let be a probability space for an uncertain number, and let be a random variable on this probability space. Then, X has a probability density function, if X is a continuous random variable and there exists a measurable function such that for every Borel set , the following condition holds:
In this case, is called the probability density function of the random variable X.
Definitions 19–21 are commonly found in probability theory [8,84], primarily expressed by replacing the sample space with uncertain number. I do not discuss these definitions in detail. As each sub-proposition corresponds to a dynamic function (Definition 1), functionals can be constructed for each sub-proposition or element to describe the dynamic process of its probability density as it changes with influence factor .
Definition 22
(Dynamic Extension for Path Spaces). Let be a random variable, where is a space of possible paths, and each path , represents a potential trajectory by influence factor γ. Here, define the probability density functional as the probability density of the path and its γ-derivative at influence factor γ. To ensure proper normalization, we introduce a normalization factor defined by
The probability measure of a subset is then given by
In Definition 22, we presented a detailed construction of the probability measure on the path space and its normalization factor. Next, in Theorem 23, we further explore how to determine the most probable evolutionary trajectory of the path through variational analysis of the probability density function, thus deriving the dynamic equation that reveals the most likely dynamic path of the system under the influence of an external factor.
Theorem 23
(Dynamic Equation). Let be the probability density function of the path and its derivative under the influence factor γ, and let be the normalization factor. The probability measure functional is defined as
where is the integration region in the path space, and γ is the influence factor. In order for the functional to attain an extremum at the path , the path must satisfy the following variational equation:
Proof.
Consider the path variation induced by a small change :
where is an arbitrary variation function. We compute the variation of the functional , defined as
Substituting the variations into the functional expression, we obtain
For small , we perform a Taylor expansion of , obtaining
We substitute this approximation into the variation formula, yielding
For the functional to attain an extremum at , the variation must be zero for all . Therefore, we have
For the term involving , we apply integration by parts. Consider the following integral; we obtain
Combining the two integrals, we obtain
As is arbitrary, this implies that the expression inside the parentheses must be zero. Thus, we obtain the following equation:
For the functional to attain an extremum, the joint probability density of the path and velocity and the normalization factor must satisfy the evolution equation. □
From a physics perspective, the main goal of Theorem 23 is to describe the most probable path of a system under dynamic conditions. The probability density of the system’s path, , and its derivative, , is influenced by an external factor, . The probability measure functional is defined over the space of paths, and by solving the associated variational equation, we can determine how the system’s dynamics are most likely to unfold under the influence of . This approach can be likened to finding the most probable path in the path integral method [85], which in statistical physics describes the system’s equilibrium or steady state. However, here, equilibrium is characterized by the extremum of the probability density, rather than by stable trajectories as in classical mechanics. Specifically, the system’s path must satisfy a variational equation to ensure that the probability measure functional attains an extremum, thus describing the most probable dynamic trajectory.
Additionally, similar to Noether’s theorem [86], Theorem 23 also reveals an important conservation law in physics: When the influencing factors satisfy translational symmetry (such as time), the probability density in the path space will remain conserved. This conclusion has actually been verified through various physical phenomena, such as the evolution of the density matrix in quantum statistical mechanics [87], and the Liouville equation in classical mechanics [88].
According to Axiom 5, the truth value of a proposition depends on the truth values of its sub-propositions. While the truth value of a proposition follows classical binary logic, the truth values of its sub-propositions are influenced by the parameter . When uncertainty quantification from probability theory is applied, probability corresponds to a specific value of , which represents a particular future condition (i.e., ). When , it indicates that a sub-proposition will certainly be true in the future, and thus the proposition will also be true when . Conversely, if there is uncertainty about the sub-proposition when , the proposition must be false. For example, consider observing the outcome of a dice game from a future perspective. We know that at some point, a number between 1 and 6 will certainly appear, so the proposition “a number appears on the die” will be true. However, if the specific number is still uncertain at that moment, the proposition “a number appears on the die” must be false, as the precise outcome has not yet been determined.
In addition to probability theory, fuzzy mathematics [89,90] is another widely used approach for uncertainty quantification. Fuzzy mathematics characterizes the degree of membership of an element within a set through the use of a membership function. This framework gives rise to the concepts of fuzzy sets (Definition 23) and fuzzy numbers (Definition 24). Next, the relationship between fuzzy numbers and uncertain numbers will be discussed.
Definition 23
(Fuzzy Set [89]). A fuzzy set F in a universe of discourse X is defined as a set of ordered pairs:
where is the membership function of F. The function represents the degree of membership of x in the fuzzy set F, with indicating no membership and indicating full membership.
Definition 24
(Fuzzy Number [90]). A fuzzy number F is a convex, normalized fuzzy set F on the real number line such that:
- 1.
- There exists a real number where (normalization condition).
- 2.
- is a piecewise continuous function.
- 3.
- F is convex, i.e.,
The set of all fuzzy numbers is denoted by , which is a collection of fuzzy numbers on .
Theorem 24
(Relationship of Fuzzy Number and Uncertain Numbers). The set of fuzzy numbers is a subset of the set of uncertain numbers , i.e.,
Proof.
Let be a fuzzy number, where is a real interval, and is the membership function, with for some . By Definition 24, is normalized, piecewise continuous, and convex. As , every is also an element of , i.e., .
Next, construct a multiset , where each , and define a bijection between the index set I and the elements of X. The membership function assigns a degree of membership to each . By Definition 7, each can be interpreted as a 0-order uncertain number, represented as the ordered pair . Therefore, f is an element of the set of uncertain numbers. Thus, . □
Basic on Theorem 24, the set of all fuzzy numbers is a subset of the set of all uncertain numbers. From this perspective, there is a close relationship between uncertain numbers and fuzzy numbers. According to Axiom 5, the truth value of a proposition depends on the truth values of its sub-propositions. While the truth value of a proposition follows classical binary logic, the truth value of its sub-propositions is influenced by the parameter . In fuzzy mathematics, when uncertainty is quantified, the membership degree corresponds to a specific value, which represents a particular deterministic state (i.e., ). When , it indicates that the sub-proposition definitively belongs to the set, and, thus, the proposition is also true when . On the other hand, if all possible sub-propositions still exhibit fuzziness when , the proposition must be false.
For example, consider the room temperature, which may range from 20 to 25 degrees Celsius. If the most accurate temperature measurement is 22.3 degrees, which lies within this range, then the proposition “The room temperature may be between 20 and 25 degrees” is true. However, if the most accurate temperature measurement is 25.5 degrees, even though there is some fuzzy membership within the range of 20 to 25 degrees, as the membership degree is not equal to 1, the proposition “The room temperature may be between 20 and 25 degrees” should be considered false.
In addition, the uncertain numbers defined in Definitions 7 and 8, by accommodating different orders of uncertainty, are well suited for addressing complex uncertain events. For example, they can model systems involving stochasticity, fuzziness, cognitive uncertainty, and various other forms of environmental uncertainty. An uncertain number can be represented as shown in Figure 2, which illustrates the intricate nature of uncertain numbers by categorizing uncertainty into four main components: environmental uncertainty (blue box), stochasticity (green box), cognitive uncertainty (orange box), and fuzziness (red box). This framework effectively captures the diverse sources and dimensions of uncertainty present in uncertain numbers.
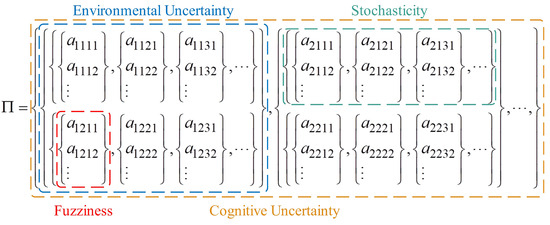
Figure 2.
Complex expression of 4-order uncertain number.
9. Applications of Uncertain Numbers
Nonlinear problems often exhibit significant uncertainty [91], particularly when simulating mechanical and physical phenomena, where such uncertainty is especially pronounced [92]. For instance, in fluid mechanics, simulating complex phenomena like boundary layer separation [93] and flow transition [94] presents considerable challenges. Although many advanced numerical methods exist to address these nonlinear issues, the presence of uncertainty typically exacerbates the computational complexity of discretization and matrix-solving techniques, affecting their convergence. Specifically, boundary element methods, due to their inherent linear mathematical structure [95], cannot be directly applied to solving nonlinear problems [96]. In optimization problems [97], when faced with multiple local minima, algorithms are prone to becoming trapped in local optima, and even global optimization methods such as simulated annealing may fail due to inappropriate parameter selection. Frequency domain analysis [98] and spectral methods usually assume the problem to be linear; however, for strongly nonlinear problems or higher-order nonlinear terms, they tend to fail and require complex corrections [99]. Monte Carlo methods encounter the so-called “curse of dimensionality” [100], while Lagrange interpolation can lead to the “Runge phenomenon” [101], resulting in unstable interpolation outcomes.
Uncertain numbers (Definitions 7 and 8), due to their ability to directly model uncertain features (Axiom 1), hold significant potential in solving nonlinear problems. In fact, it has been rigorously proven that the complex number system belongs to the class of uncertain numbers. Furthermore, probabilistic methods (Theorem 23) and fuzzy mathematics (Theorem 24) can also be incorporated into the framework of uncertain numbers. As these applications have already been extensively studied, they will not be discussed further here. The following sections will present a few simple examples to demonstrate how uncertain numbers can address problems that traditional mathematical methods have been unable to explain or express.
9.1. Singularities in Newton’s Method
Newton’s method [102] is a widely used iterative algorithm in numerical analysis for solving nonlinear equations. The basic idea is to approximate the root of the equation by using linearization at each step. The update formula is given by
Although the method is efficient in many cases, it faces several issues related to singularities. One major problem arises when the derivative at any point during the iteration. In such cases, the update formula becomes undefined due to division by zero. Even if the derivative is not exactly zero but very small, the update step can become excessively large, leading to instability and potential divergence. This situation can cause the method to fail or converge very slowly, forming a singularity in the process. Consider the function , with its derivative given by . If the initial point is chosen as , the derivative is close to zero. As Newton’s method involves the derivative in its iterative formula, when the derivative approaches zero, the iteration process may experience convergence difficulties or numerical errors, leading to the occurrence of a singularity near this point, which can affect the stability and accuracy of the solution.
Now, the problem is addressed within the framework of uncertain numbers. Under this framework, the problem takes the following form:
Based on Theorem 17, which states that , that is
From Theorem 19, Remark 1, or Remark 3, which state that and , we obtain
Considering Definition 16 and Theorem 18, absorption and distributive processes are regarded as Intrinsic Properties. Thus,
Now, we use the order change of the number system in Definition 14, which corresponds to viewing it on a larger scale.
Consider Theorem 15, which states that .
At this point, has successfully been transformed into an uncertain number, which can be represented as
This expression indicates that is an uncertain value fluctuating around , with its fluctuation range controlled by . By dynamically adjusting , the instability issues that may arise near singularities in Newton’s method can be effectively mitigated. Before each iteration, it is necessary to check whether the derivative is close to a singularity. If it is, the singularity is transformed into an uncertain value using the aforementioned method, ensuring that the algorithm can continue its search for the roots of the equation. Ultimately, the program not only stably finds the root of the equation but also successfully solves all four roots under the influence of uncertainty.
Figure 3 illustrates the performance of Newton’s method in solving equation roots under the framework of uncertain numbers. The figure consists of four sub-plots, each depicting the iteration process starting from different initial points that are refracted from singularities, showing the variation of function values and corresponding iteration paths. Specifically, the blue curve represents the graph of the target function , the red points indicate the inherent roots of the equation, and the blue points represent the results of the iterations. The horizontal axis represents the number of iterations, while the vertical axis shows both the iteration values x and the corresponding function values . The light yellow line represents the iteration path. The four sub-plots show the iteration processes and results starting from four uncertain initial points, all of which are refracted from the original singularity.
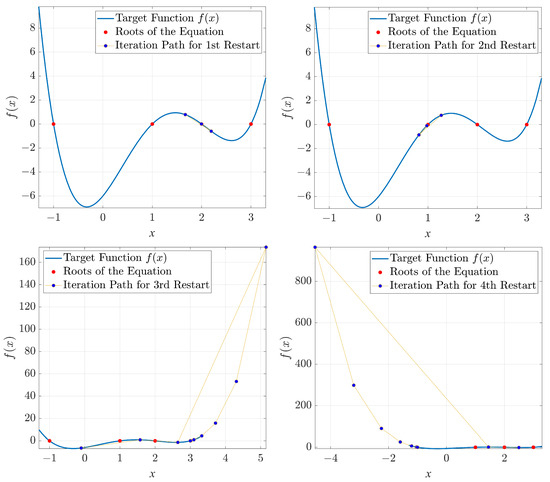
Figure 3.
To solve for the roots of the equation starting from a singularity, the process involves four uncertain restart points.
In traditional mathematical frameworks, each input value x corresponds to a unique function value . This strict one-to-one correspondence can lead to division-by-zero errors in numerical calculations, particularly when using Newton’s method to solve for the roots of an equation. The convergence of Newton’s method relies on the nonzero nature of the derivative at each step. However, when the algorithm encounters a derivative close to zero, numerical methods may exhibit instability, even leading to division-by-zero errors.
In contrast, under the uncertain number framework, as shown in Equation (1), the input value x can fluctuate within a small range, thereby breaking the strict one-to-one correspondence between each input and its corresponding output. This uncertainty framework associates the input with a range of possible output values, effectively avoiding division-by-zero issues caused by small fluctuations. By dynamically adjusting the fluctuation range, the algorithm can more flexibly explore all possible roots of the equation, overcoming the limitations imposed by division-by-zero errors in the traditional mathematical framework.
Therefore, after adopting the uncertain number framework, even when encountering singularities during the iteration process of Newton’s method, the algorithm remains stable and successfully identifies all possible roots of the equation. This improvement significantly enhances the stability and convergence of the numerical algorithm in complex situations, thereby increasing the robustness of the solving process.
9.2. The “Local Optimum” Problem in Gradient Descent Methods
In the gradient descent method, the “local optimum” problem [103] refers to the situation where the algorithm may become stuck in a local minimum or local maximum, failing to converge to the global optimum (Figure 4A).
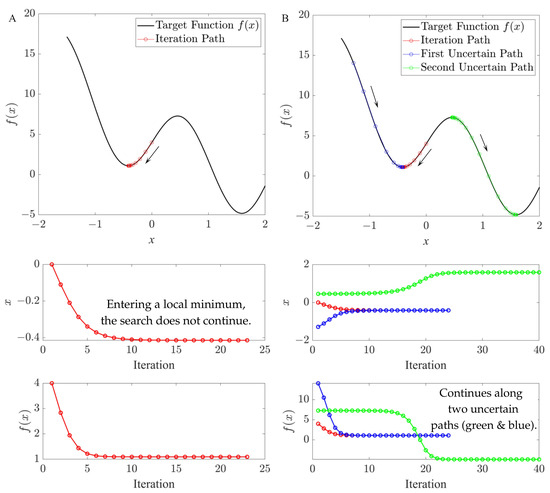
Figure 4.
“Local optimum” of . (A) illustrates the local optimum problem. (B) demonstrates a solution using the framework of uncertain numbers, which continues along two uncertain paths.
To simplify the explanation, a one-dimensional case is chosen to visually demonstrate this process. Let the objective function be , where is the parameter (see Figure 4A). The upper part of Figure 4A shows the curve of the function and the gradient descent trajectory (represented by red circles) starting from an initial point. The lower part displays the values of x and at different iteration steps. From Figure 4A, it can be observed that the algorithm starts from an initial point , and, after several iterations, gradually stabilizes and ultimately converges to a local minimum. In this case, the gradient descent method is trapped in a local minimum and cannot further optimize, demonstrating the algorithm’s tendency to converge to local optima. The emergence of such issues mainly stems from the update rules of the gradient descent method in the one-dimensional case:
where is the learning rate, is the gradient at , and is the unit vector in the x-direction. The gradient points in the direction of the steepest descent, and the algorithm updates the parameters along this direction to iteratively approach the minimum. However, when the objective function has multiple local minima or maxima, gradient descent may become stuck at a local optimum , rather than the global optimum. For a local optimum , the following conditions hold:
This means that is a local minimum, but not necessarily the global minimum. This issue is particularly pronounced in high-dimensional and complex optimization problems, such as the nonconvex objective functions commonly encountered in deep learning.
In the framework of uncertain numbers, the problem of “local optimality” can be formulated as follows:
Based on Theorem 15, a certain number can be uncertainized, i.e., , that is
According to Equation (2), by running gradient descent from two uncertain perturbed starting points ( and ), the algorithm explores potential solutions in nearby regions and avoids becoming stuck in a local optimum. The uncertainty factor is gradually adjusted, ensuring that the algorithm continues to explore and refine its search for the global optimum, i.e., .
The calculation results are shown in Figure 4B. The upper half of Figure 4B illustrates the curve of the function alongside the gradient descent trajectories originating from different initial points. Upon encountering a “local optimum” point, the trajectories are modified according to Equation (2), with distinct colors representing different initial points and their corresponding paths. Specifically, blue and green denote different restarting positions. The lower half of Figure 4B presents two plots showing the variation of multiple x values and their corresponding values at different iteration steps. Additionally, Figure 4B demonstrates the effect of perturbing the initial points by introducing an uncertainty factor , followed by multiple searches in different regions. This strategy is designed to prevent the algorithm from converging to local optima and to increase the likelihood of finding the global optimum. As shown in Figure 4B, the trajectories from different initial points converge to different points after varying numbers of iterations, with some trajectories successfully finding better solutions.
In the traditional mathematical framework, numerical values are typically treated as fixed constants. As a result, conventional gradient descent methods begin at an initial point and often terminate upon reaching a local minimum, with no theoretical foundation for reselecting the initial point and no guarantee of finding the global optimum. However, within the framework of uncertain numbers, this situation undergoes a significant transformation. By introducing an uncertain parameter (as shown in Figure 4B), even when the algorithm becomes trapped in a local optimum, it can reinitialize the starting point through Equation (2), allowing the initial point to fluctuate within a certain range. This fluctuation simulates the distribution of multiple initial points within the neighborhood, effectively preventing the algorithm from becoming stuck in a local optimum and facilitating a more thorough exploration of the global optimum. This framework cleverly transitions from traditional deterministic mathematics to uncertainty-based models, overcoming the limitations of the conventional approach and making optimization algorithms more flexible and efficient when dealing with complex functions. Specifically, Figure 4B illustrates the gradient descent trajectories from different initial points, providing a clear explanation of how uncertainty theory helps the gradient descent algorithm escape the trap of local minima and converge to a better solution. This approach highlights the distinctiveness and practicality of the uncertain numbers theory framework in addressing problems within the computer science.
9.3. The Issue of Integrator Windup in Control Systems
Integrator windup [104] is a common issue in control systems, especially those utilizing proportional–integral–derivative (PID) controllers. It occurs when the integral term accumulates significant error during periods when the actuator is saturated and cannot respond to the control signal. This accumulation can cause the controller to overreact once the actuator is no longer saturated, potentially resulting in large overshoots and system instability. The standard PID controller formula is given by
where denotes the control output, representing the action applied to the system; represents the error, defined as the difference between the setpoint and the actual value; refers to the proportional gain; corresponds to the integral gain; and indicates the derivative gain.
To illustrate the impact of integral windup, a PID control system can be designed to simulate the ascent of an object. The object begins at an initial height of , with a target height of and a mass of , subject to the gravitational acceleration . The parameters of the PID controller are set as follows: proportional gain , integral gain , and derivative gain . According to Equation (3), the control system computes the required thrust based on the error between the current height and the target height to regulate the object’s ascent. As the error persists, the integral term accumulates over time, leading to an increase in the control signal, which eventually results in the occurrence of integral windup.
Specifically, Figure 5A demonstrates the dynamic variations in altitude, velocity, and thrust of a system operating without control saturation. The altitude exhibits substantial fluctuations across a wide range, with an evident tendency to oscillate, indicating the potential onset of instability within the system. Likewise, the velocity profile reveals pronounced oscillatory behavior, marked by significant variations, which further supports the hypothesis of an unstable system. The thrust, characterized by intense oscillations of considerable amplitude, experiences frequent and abrupt alternations between peaks and troughs. These pronounced fluctuations in the thrust signal underscore the severe instability in the control input. Such oscillatory dynamics can be primarily attributed to the unbounded accumulation of the integral term, wherein the lack of control saturation exacerbates the phenomenon of “integral windup”. This effect ultimately induces considerable instability, significantly degrading the system’s performance.
Figure 5.
Effect of integrator windup on system dynamic response in PID control. (A) shows the variations in altitude, velocity, and thrust when integrator windup occurs, while (B) illustrates the system response under an uncertain framework without integrator windup. Each row represents the changes in altitude (first row), velocity (second row), and thrust (third row) over a 30-second period.
To address the problem, the theoretical framework of uncertain numbers is employed. Firstly, Equation (3) can be rewritten in its algebraic form as
where , , and represent the distinct approaches to error handling, corresponding to the proportional, integral, and derivative components, respectively, of the control law.
In the context of PID control, when the control signal reaches its maximum value , the integral term reaches its maximum limit . If the control signal continues to increase at this point, according to Definition 12, assuming that the boundary of the effective array is , the integral term will satisfy the following condition:
where represents an LUN (Definition 12), whose inherent strong uncertainty implies that the system is about to enter a state of severe instability and lead to the occurrence of integral windup.
First, the integral term of the controller can be expressed in terms of the integral of the error :
and its Laplace transform is given by
where is the Laplace transform of the error . From the above equation, the relationship between the error and the integral term can be obtained as follows:
.
Then, this relationship indicates that there is a direct proportionality between the error and the integral term . In order to design an optimal controller, the objective is to minimize the system error, thereby optimizing the performance criterion (such as integral error). According to Definition 12, the LUN possesses boundedness, and its minimum value is M, which corresponds to . Therefore, based on Axiom 1, it can be concluded that in the LUN, there exists an exclusive OR (XOR) relationship between M and the other elements in an LUN. Thus, by considering the minimization and optimization of system errors, the final result can be obtained:
Equation (5) indicates that when the control signal reaches or exceeds the maximum value , the integral term is constrained by its maximum value , which may lead the system into a state of strong instability.
In Figure 5B, the variations in altitude, velocity, and thrust after applying control saturation (i.e., setting a maximum control signal ) are shown. Initially, the altitude experiences a significant transitional process, after which it gradually stabilizes, and the amplitude of oscillations decreases. The velocity fluctuates greatly at first but soon stabilizes, with the oscillation amplitude significantly reduced compared to Figure 5A, indicating that the system’s stability has improved. The thrust variation trend is consistent with that of altitude and velocity, initially exhibiting a peak fluctuation before rapidly decreasing and eventually stabilizing. Comparative analysis shows that the introduction of control saturation effectively suppresses the infinite growth of the integral term, successfully avoiding the “integral windup” phenomenon, thereby stabilizing the system in the end.
In fact, this method refers to the anti-windup technique [105], which has been widely applied in various PID control engineering fields as an effective anti-integral strategy. However, to date, it has not been rigorously proven through traditional mathematical frameworks. The primary reason for this is that the core idea of the anti-windup technique introduces a nonlinear correction (saturation) by limiting the integral part to prevent excessive accumulation. This correction inherently complicates the system’s dynamic behavior, and theoretically, the stability and performance analysis of systems with such saturated nonlinear controllers often cannot be rigorously proven using classical linear control theory.
In PID control, the integral term possesses an accumulation characteristic, akin to a system with infinite memory. Without the anti-windup technique, the state of the integral term might continuously grow, leading the system into an uncontrollable and unstable “infinite” region, thereby increasing the complexity of the system’s nonlinear response. The anti-windup technique mitigates this issue by limiting the growth, but this limiting mechanism largely relies on engineering experience and practice rather than strict theoretical derivation.
The work presented here can be seen as providing a rigorous mathematical proof for the anti-windup technique within the framework of uncertain numbers theory. Rigorous mathematical proof is crucial in control theory. It not only profoundly reveals the underlying mechanisms of controller behavior and provides theoretical support for the design of new control strategies but also aids in understanding the role, stability boundaries, and integration of anti-windup techniques with other control strategies. For specific systems or under certain assumptions, rigorous proof can enhance the theoretical rigor and depth.
From another perspective, by performing a rigorous analysis within the framework of uncertain numbers theory, we arrive at conclusions that align with those already widely accepted and applied in engineering practice. This subtle coincidence actually highlights the potential practical value of uncertain systems theory in control science.
10. Discussion
This work establishes an intuitive and unified mathematical framework based on uncertain numbers (Definitions 7 and 8) by proposing five axioms (Axioms 1–5). It organically integrates probability theory (Definitions 19–21), fuzzy numbers (Theorem 24), and complex number systems (Theorem 5) to address the inherent uncertainty in nonlinear systems, while also creating a bridge between traditional mathematical frameworks and uncertain systems.
From a theoretical perspective, it is worth mentioning that Axiom 5 plays a central role by linking the truth value of a proposition to the continuously varying truth values of its constituent sub-propositions. This relationship allows uncertain numbers to be interpreted not only as an extension of traditional mathematical frameworks but also as a novel tool for analyzing uncertainty. Additionally, this integration presents a potential solution to the theoretical challenges arising from the absence of a formal axiomatic system in fuzzy mathematics (Definitions 23 and 24).
Furthermore, the definitions (Definitions 12 and 13) and the analysis (Section 5 and Section 6) of LUNs and SUNs, based on Axiom 1, apply uncertain logic to resolve difficulties related to singularity expressions. These developments lay a robust mathematical foundation for addressing scale-dependent issues (such as singularities and infinities), as well as uncertainty-related problems (e.g., the multisolvability of nonlinear equations). The development of uncertain mathematical analysis based on uncertain numbers, particularly in the context of solving the Navier–Stokes equations [106], Einstein’s field equations [107], and Yang–Mills equations [108], represents a key direction in the ongoing theoretical advancements.
From a practical perspective, based on Axioms 1–5, the truth value of a proposition can be determined through the combination of multiple sub-propositions, each of which is associated with a different “possibility”. This framework reveals that values approaching singularities or zeros can be viewed as uncertain numbers, similar to SUNs (Definition 13), and infinity can be regarded as LUNs (Definition 12).
As discussed in Section 9.1, singularity problems (such as cases where the derivative equals zero, i.e., ) often cause traditional numerical methods to fail due to division by zero errors or numerical instability. By modeling as an uncertain number (see Definitions 7 and 8), this approach successfully avoids division by zero errors and ensures the continuity of the iterative process. The effectiveness of this method is attributed to the absorption and release mechanisms described in Definition 16 and Theorem 18, which further highlight the practicality and reliability of the uncertain numbers theory framework in addressing division by zero issues.
Moreover, as mentioned in Section 9.2, to solve the local minimum problem in gradient descent algorithms, the method expands the search space significantly by converting zero values into uncertain numbers (see Theorem 15), effectively preventing the algorithm from becoming stuck at local optima. This improvement enhances the global search capability of gradient descent, making it particularly suitable for nonconvex optimization problems and high-dimensional scenarios. The resolution of the local minimum issue further underscores the unique advantage of the uncertain numbers theory framework in combining traditional mathematical models with uncertainty systems, while also demonstrating its broad application potential in computer science.
Finally, as explored in Section 9.3, the uncertain number theory framework also provides rigorous mathematical derivations for the anti-integrator wind-up technique, fully demonstrating the reliability and practicality of this framework in addressing the integrator wind-up issue in PID control systems. While the anti-integrator wind-up technique has been widely adopted in engineering practice, its theoretical foundation has previously been relatively weak. Through the analysis of uncertain numbers, this framework not only validates the effectiveness of this technique but also highlights the potential application value of uncertain numbers theory in control systems, emphasizing its scientific significance and practical utility as a tool for solving complex control problems.
In the framework of uncertain numbers theory, its practicality and reliability in solving problems in fields such as physics and engineering are clearly evident. Particularly in addressing nonlinear problems, uncertain numbers demonstrate unique advantages and hold significant application potential. However, challenges remain in practical applications. Although existing research has shown that uncertain numbers possess alignment properties (see Axiom 3 and Theorem 16), the related uncertainties regarding singularities have not been fully understood in actual computations. This results in the need to dynamically adjust the range and associated parameters of uncertain numbers during each iteration, potentially introducing additional computational overhead. Therefore, accurately and effectively estimating or measuring the uncertainties induced by singularities, while the problem is not fully resolved, has become a critical research direction that requires immediate attention. Furthermore, the introduction of uncertain numbers (see Definitions 7 and 8) inevitably leads to a significant increase in computational cost. Therefore, achieving a balance between precision and stability in numerical computations remains a major challenge that must be overcome when applying uncertain numbers to practical problems.
This set of code addresses the singularity issue in the initial stages of Newton’s method, the local optimum problem in the gradient descent method, and the integrator windup issue in control systems by incorporating Uncertainty Theory. Each code introduces uncertainty factors into traditional methods to enhance stability and convergence, making them more adaptable to real-world challenges involving uncertainty. Specific applications are shown in Table 2.

Table 2.
Specific applications.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13030496/s1, Code S1: Code for handling singularities at the start of Newton’s method. Description: This code aims to address the singularity problem that may occur in the initial stages of the Newton’s method. In Newton’s method, when the Jacobian matrix (used for optimization or root-finding) is singular or nearly singular, it often leads to instability or failure to converge. This code identifies this issue. Code S2: Solution code for singularities in Newton’s method within the Uncertain Numbers Theory framework. Description: This code addresses the singularity problem in Newton’s method within the framework of Uncertainty Theory. Uncertainty Theory deals with uncertainties, approximations, or imprecisions in numerical methods, especially when handling singularity problems. By introducing uncertainty factors related to singularity, the code provides an innovative solution to enhance the stability and convergence of Newton’s method. Code S3: Code for solving the local optimum problem using the gradient descent method. Description: This script uses the gradient descent method to solve local optimization problems. The gradient descent method gradually minimizes the objective function by moving in the direction of the steepest descent. In practical applications, the function might get trapped in local minima or maxima, leading to local optimum issues. This script identifies this problem. Code S4: Code for solving the local optimum problem using the gradient descent method within the Uncertain Numbers Theory framework. Description: This script uses the gradient descent method to solve local optimization problems within the framework of Uncertainty Theory. In this framework, the gradient descent method considers zero-point uncertainties in numerical calculations. By incorporating uncertainty elements or addressing data imprecision during the optimization process, this approach can better handle real-world challenges. Code S5: Code addressing the integrator windup issue in control systems. Description: This script reveals the "integrator windup" problem in control systems. Integrator windup refers to the excessive control action that may occur when a control system, particularly a PID controller, accumulates too much error in a saturated or constrained state, potentially leading to system instability. This code identifies the integrator windup problem. Code S6: Code for solving the integrator windup issue in control systems within the Uncertain Numbers Theory framework. Description: This code addresses the integrator windup problem in control systems within the framework of Uncertainty Theory. The solution discovered is a form of anti-windup technique, which has been widely applied in engineering but has not been fully mathematically proven. Nonetheless, this method demonstrates the potential of the Uncertainty Theory framework due to its practical effectiveness in engineering applications.
Funding
This research did not receive any funding. All research and publication expenses were borne by the author.
Data Availability Statement
The data that support the findings of this study are available within this article.
Acknowledgments
Before submission, the author did not recommend any reviewers, which undoubtedly increased the workload of the editorial team. The author is deeply grateful for the support of the editors and the invaluable feedback provided by the reviewers. Special thanks also go to all the colleagues who read and supported this research before its publication, as well as the many friends who shared insightful suggestions, either through email or in person. Lastly, the author would like to express heartfelt appreciation to everyone who has taken the time to read this article. Your attention and support have been vital in helping me overcome challenges and successfully complete this work. I also wish you continued success in all your future endeavors!
Conflicts of Interest
The author declares no conflicts of interest.
References
- Meskine, H.; Abdelouahab, M.S.; Lozi, R. Nonlinear dynamic and chaos in a remanufacturing duopoly game with heterogeneous players and nonlinear inverse demand functions. J. Differ. Equ. Appl. 2023, 29, 1503–1515. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Nonlinear dynamics of the generalized unstable nonlinear Schrödinger equation: A graphical perspective. Opt. Quantum Electron. 2023, 55, 628. [Google Scholar] [CrossRef]
- Losacco, M.; Fossà, A.; Armellin, R. Low-order automatic domain splitting approach for nonlinear uncertainty mapping. J. Guid. Control Dyn. 2024, 47, 2. [Google Scholar] [CrossRef]
- Meng, Q.; Ma, Q.; Shi, Y. Adaptive fixed-time stabilization for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 6929–6936. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Liu, Y. A data-driven method to model stress-strain behaviour of frozen soil considering uncertainty. Cold Reg. Sci. Technol. 2023, 213, 103906. [Google Scholar] [CrossRef]
- Li, J.; Ding, J.; Chai, T.; Lewis, F.L.; Jagannathan, S. Adaptive interleaved reinforcement learning: Robust stability of affine nonlinear systems with unknown uncertainty. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 270–280. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Bai, W.; Zhao, X.; Liu, P.X. Finite-time-prescribed performance-based adaptive fuzzy control for strict-feedback nonlinear systems with dynamic uncertainty and actuator faults. IEEE Trans. Cybern. 2022, 52, 6959–6971. [Google Scholar] [CrossRef] [PubMed]
- Laha, R.G.; Rohatgi, V.K. Probability Theory; Courier Dover Publications: Mineola, NY, USA, 2020. [Google Scholar]
- Axtell, R.L.; Farmer, J.D. Agent-based modeling in economics and finance: Past, present, and future. J. Econ. Lit. 2022, 1, 1–101. [Google Scholar]
- Dessaint, O.; Olivier, J.; Otto, C.A.; Thesmar, D. CAPM-based company (mis)valuations. Rev. Financ. Stud. 2021, 34, 1–66. [Google Scholar] [CrossRef]
- Carletti, T.; Battiston, F.; Cencetti, G.; Fanelli, D. Random walks on hypergraphs. Phys. Rev. E 2020, 101, 022308. [Google Scholar] [CrossRef]
- Weilnhammer, V.; Schmid, J.; Mittermeier, I.; Schreiber, F.; Jiang, L.; Pastuhovic, V.; Herr, C.; Heinze, S. Extreme weather events in Europe and their health consequences—A systematic review. Int. J. Hyg. Environ. Health 2021, 233, 113688. [Google Scholar] [CrossRef] [PubMed]
- Eriotis, N.; Vasiliou, D. Economic and social views of neoliberalism in Greece: Insights from the financial crisis and recovery. In Proceedings of the International Conference on Science, Innovations and Global Solutions, Berlin, Germany, 18–20 September 2024; Challoumis, C., Eriotis, N., Vasiliou, D., Eds.; pp. 241–245. [Google Scholar]
- Hájek, P. Metamathematics of Fuzzy Logic; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Modibbo, U.M.; Hassan, M.; Ahmed, A.; Ali, I. Multi-criteria decision analysis for pharmaceutical supplier selection problem using fuzzy TOPSIS. Manag. Decis. 2022, 60, 806–836. [Google Scholar] [CrossRef]
- Bakhtavar, E.; Valipour, M.; Yousefi, S.; Sadiq, R.; Hewage, K. Fuzzy cognitive maps in systems risk analysis: A comprehensive review. Complex Intell. Syst. 2021, 7, 621–637. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Gu, K.; Li, M. Artificial neural network (ANN)—Bayesian probability framework (BPF) based method of dynamic force reconstruction under multi-source uncertainties. Knowl.-Based Syst. 2022, 237, 107796. [Google Scholar] [CrossRef]
- Deng, Y. Uncertainty measure in evidence theory. Sci. China Inf. Sci. 2020, 63, 210201. [Google Scholar] [CrossRef]
- Javed, S.A.; Mahmoudi, A.; Liu, S. Grey absolute decision analysis (GADA) method for multiple criteria group decision-making under uncertainty. Int. J. Fuzzy Syst. 2020, 22, 1073–1090. [Google Scholar] [CrossRef]
- Zhang, P.; Li, T.; Wang, G.; Luo, C.; Chen, H.; Zhang, J.; Wang, D.; Yu, Z. Multi-source information fusion based on rough set theory: A review. Inf. Fusion 2021, 68, 85–117. [Google Scholar] [CrossRef]
- Kulpa, Z.; Pownuk, A.; Skalna, I. Analysis of linear mechanical structures with uncertainties by means of interval methods. Comput. Assist. Methods Eng. Sci. 2023, 5, 443–477. [Google Scholar]
- Dubois, D.; Prade, H. Possibility theory. In Granular, Fuzzy, and Soft Computing; Lin, T.Y., Liau, C.J., Kacprzyk, J., Eds.; Encyclopedia of Complexity and Systems Science Series; Springer: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Zhang, J. Modern Monte Carlo methods for efficient uncertainty quantification and propagation: A survey. Wiley Interdiscip. Rev. Comput. Stat. 2021, 13, e1539. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, D.; Bai, Y.; Chang, L.; Li, J. Evidence reasoning rule-based classifier with uncertainty quantification. Inf. Sci. 2020, 516, 192–204. [Google Scholar] [CrossRef]
- Ferson, S.; Hajagos, J.G. Arithmetic with uncertain numbers: Rigorous and (often) best possible answers. Reliab. Eng. Syst. Saf. 2004, 85, 135–152. [Google Scholar] [CrossRef]
- Levin, D.; Ozdenoren, E. Auctions with uncertain numbers of bidders. J. Econ. Theory 2004, 118, 229–251. [Google Scholar] [CrossRef]
- Hall, B.D. Computing uncertainty with uncertain numbers. Metrologia 2006, 43, L56. [Google Scholar] [CrossRef]
- Manousakis, I.; Goiri, Í.; Bianchini, R.; Rigo, S.; Nguyen, T.D. Uncertainty propagation in data processing systems. In Proceedings of the ACM Symposium on Cloud Computing (SoCC ’18); Association for Computing Machinery: New York, NY, USA, 2018; pp. 95–106. [Google Scholar] [CrossRef]
- Ye, W.; Gao, Y.; Liu, J. Singular points of polarizations in the momentum space of photonic crystal slabs. Phys. Rev. Lett. 2020, 124, 153904. [Google Scholar] [CrossRef] [PubMed]
- Lange-Hegermann, M.; Robertz, D.; Seiler, W.M.; Seiß, M. Singularities of algebraic differential equations. Adv. Appl. Math. 2021, 131, 102266. [Google Scholar] [CrossRef]
- Capellmann, H. Space-Time in Quantum Theory. Found. Phys. 2021, 51, 44. [Google Scholar] [CrossRef]
- Gonçalves, T.B.; Rosa, J.L.; Lobo, F.S.N. Cosmological sudden singularities in f(R, T) gravity. Eur. Phys. J. C 2022, 82, 418. [Google Scholar] [CrossRef]
- Capozziello, S.; De Bianchi, S.; Battista, E. Avoiding singularities in Lorentzian-Euclidean black holes: The role of atemporality. Phys. Rev. D 2024, 109, 104060. [Google Scholar] [CrossRef]
- Guo, B.; Phong, D. On L∞ estimates for fully non-linear partial differential equations. Ann. Math. 2024, 200, 365–398. [Google Scholar] [CrossRef]
- Kebekus, S.; Schnell, C. Extending holomorphic forms from the regular locus of a complex space to a resolution of singularities. J. Amer. Math. Soc. 2021, 34, 315–368. [Google Scholar] [CrossRef]
- Bringmann, B.; Deng, Y.; Nahmod, A.R.; Yue, H. Invariant Gibbs measures for the three-dimensional cubic nonlinear wave equation. Invent. Math. 2024, 236, 1133–1411. [Google Scholar] [CrossRef]
- Posy, C.J. Mathematical Intuitionism; Elements in the Philosophy of Mathematics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Luckow, K.; Kersten, R.; Pǎsǎreanu, C. Symbolic Complexity Analysis Using Context-Preserving Histories. IEEE Int. Conf. Softw. Test. Verif. Valid. (ICST) 2017, 2017, 58–68. [Google Scholar] [CrossRef]
- Kennedy, J. Gödel’s Incompleteness Theorems; Elements in Philosophy and Logic; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Lü, X.; Chen, S.J. Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dyn. 2021, 103, 947–977. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ilhan, O.A.; Abdulazeez, S.T.; Manafian, J.; Mohammed, S.A.; Osman, M.S. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys. 2021, 21, 103769. [Google Scholar] [CrossRef]
- Chang, L.; Song, X.; Zhang, L. Uncertainty-oriented reliability and risk-based output control for complex systems with compatibility considerations. Inf. Sci. 2022, 606, 512–530. [Google Scholar] [CrossRef]
- Huang, S.; Duan, R.; He, J.; Feng, T.; Zeng, Y. Fault Diagnosis Strategy for Complex Systems Based on Multi-Source Heterogeneous Information Under Epistemic Uncertainty. IEEE Access 2020, 8, 50921–50933. [Google Scholar] [CrossRef]
- Sullivan, T.J. Introduction to Uncertainty Quantification; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Braun, D. Chapter 1: Extension, Intension, Character, and Beyond. In Routledge Companion to Philosophy of Language; Routledge: London, UK, 2012; p. 9. ISBN 9780203206966. [Google Scholar]
- Carston, R. Polysemy: Pragmatics and Sense Conventions. Mind Lang. 2020, 36, 108–133. [Google Scholar] [CrossRef]
- Wang, W.; He, L.; Wu, Y.J.; Goh, M. Signaling Persuasion in Crowdfunding Entrepreneurial Narratives: The Subjectivity vs Objectivity Debate. Comput. Hum. Behav. 2021, 114, 106576. [Google Scholar] [CrossRef]
- Zalata, A.M.; Ntim, C.G.; Alsohagy, M.H.; Malagila, J. Gender Diversity and Earnings Management: The Case of Female Directors with Financial Background. Rev. Quant. Financ. Account. 2022, 58, 101–136. [Google Scholar] [CrossRef]
- Narayan, A.J.; Lieberman, A.F.; Masten, A.S. Intergenerational Transmission and Prevention of Adverse Childhood Experiences (ACEs). Clin. Psychol. Rev. 2021, 85, 101997. [Google Scholar] [CrossRef]
- Peterson, M. An Introduction to Decision Theory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Taujanskaitē, K.; Kuizinaitē, J. Development of FinTech business in Lithuania: Driving factors and future scenarios. Bus. Manag. Econ. Eng. 2022, 20, 96–118. [Google Scholar] [CrossRef]
- Budrikis, Z. Collective Motion Strategies of Sheep. Nat. Rev. Phys. 2023, 5, 82. [Google Scholar] [CrossRef]
- Zwart, H. Dialectical Materialism. In Continental Philosophy of Technoscience; Philosophy of Engineering and Technology; Springer: Cham, Switzerland, 2022; Volume 38, pp. 67–109. [Google Scholar] [CrossRef]
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. “Panta Rhei—everything flows”: Change in hydrology and society—The IAHS scientific decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Rescher, N.; Urquhart, A. Temporal Logic; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Punčochář, V.; Sedlár, I. Inquisitive Propositional Dynamic Logic. J. Log. Lang. Inf. 2021, 30, 91–116. [Google Scholar] [CrossRef]
- Faller, M.T. A possible worlds semantics for Cuzco Quechua evidentials. In Evidentials and Modals; Brill: Leiden, The Netherlands, 2020; pp. 41–68. [Google Scholar]
- Fathi, M.; Haghi Kashani, M.; Jameii, S.M.; Mahdipour, E. Big data analytics in weather forecasting: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 1247–1275. [Google Scholar] [CrossRef]
- Lee, C.; Lee, C.; Lee, S.; Choi, J.; Yoo, H.; Im, S.G. A reconfigurable binary/ternary logic conversion-in-memory based on drain-aligned floating-gate heterojunction transistors. Nat. Commun. 2023, 14, 3757. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy Logic. In Granular, Fuzzy, and Soft Computing; Encyclopedia of Complexity and Systems Science Series; Lin, T.Y., Liau, C.J., Kacprzyk, J., Eds.; Springer: New York, NY, USA, 2009; pp. 19–49. [Google Scholar] [CrossRef]
- Howson, C. The Logic of Bayesian Probability. In Foundations of Bayesianism; Applied Logic Series; Corfield, D., Williamson, J., Eds.; Springer: Dordrecht, The Netherlands, 2001; Volume 24, pp. 137–159. [Google Scholar] [CrossRef]
- Psaroudaki, C.; Panagopoulos, C. Skyrmion qubits: A new class of quantum logic elements based on nanoscale magnetization. Phys. Rev. Lett. 2021, 127, 067201. [Google Scholar] [CrossRef]
- Wittgenstein, L. Philosophical Investigations; John Wiley & Sons: Oxford, UK, 2009. [Google Scholar]
- Adamowicz, Z.; Zbierski, P. Logic of Mathematics: A Modern Course of Classical Logic; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rathjen, M. Power Kripke–Platek set theory and the axiom of choice. J. Log. Comput. 2020, 30, 447–457. [Google Scholar] [CrossRef]
- Liu, X. Paradox. In Mathematics in Programming; Springer: Singapore, 2024; pp. 273–302. [Google Scholar] [CrossRef]
- Blizard, W.D. Multiset theory. Notre Dame J. Form. Log. 1989, 30, 36–66. [Google Scholar] [CrossRef]
- Rado, R. Partial well-ordering of sets of vectors. Mathematika 1954, 1, 89–95. [Google Scholar] [CrossRef]
- Kleene, S.C. On notation for ordinal numbers. J. Symb. Log. 1938, 3, 150–155. [Google Scholar] [CrossRef]
- Kanamori, A. The mathematical import of Zermelo’s well-ordering theorem. Bull. Symb. Log. 1997, 3, 281–311. [Google Scholar] [CrossRef][Green Version]
- Kneale, W.C. Russell’s paradox and some others. Br. J. Philos. Sci. 1971, 22, 321–338. [Google Scholar] [CrossRef]
- Šemrl, P. Order isomorphisms of operator intervals. Integral Equations Oper. Theory 2017, 89, 1–42. [Google Scholar] [CrossRef]
- Hausdorff, F. Set Theory; American Mathematical Soc.: Providence, RI, USA, 2021. [Google Scholar]
- Michiwaki, H.; Saitoh, S.; Yamada, M. Reality of the division by zero z/0 = 0. Int. J. Appl. Phys. Math 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Némethi, A. Normal Surface Singularities; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Ni, J.; Huang, C.; Zhou, L.-M.; Gu, M.; Song, Q.; Kivshar, Y.; Qiu, C.-W. Multidimensional phase singularities in nanophotonics. Science 2021, 374, eabj0039. [Google Scholar] [CrossRef]
- Mwangi, W.P. Definite Probabilities from Division of Zero by Itself Perspective. Asian J. Probab. Stat. 2020, 6, 1–26. [Google Scholar] [CrossRef]
- Needham, T. Visual Complex Analysis; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Liu, Y.; Carranza, E.J.M. Uncertainty Analysis of Geochemical Anomaly by Combining Sequential Indicator Co-simulation and Local Singularity Analysis. Nat. Resour. Res. 2022, 31, 1889–1908. [Google Scholar] [CrossRef]
- Khalili Golmankhaneh, A.; Welch, K.; Serpa, C.; Jørgensen, P.E. Non-standard analysis for fractal calculus. J. Anal. 2023, 31, 1895–1916. [Google Scholar] [CrossRef]
- Chelnokov, Y.N. Quaternion methods and regular models of celestial mechanics and space flight mechanics: Local regularization of the singularities of the equations of the perturbed spatial restricted three-body problem generated by gravitational forces. Mech. Solids 2023, 58, 1458–1482. [Google Scholar] [CrossRef]
- Farzalipour, F.; Ghiasvand, P. Absorbing prime multiplication modules over a pullback ring. J. Algebr. Syst. 2024, 11, 33–51. [Google Scholar]
- Kao, E.P. An Introduction to Stochastic Processes; Courier Dover Publications: Mineola, NY, USA, 2019. [Google Scholar]
- Khandekar, D.C.; Bhagwat, D.K.S.L.K.; Lawande, S.V.; Bhagwat, K.V. Path-Integral Methods and Their Applications; Allied Publishers: Mumbai, India, 2002. [Google Scholar]
- Halder, A.K.; Paliathanasis, A.; Leach, P.G.L. Noether’s Theorem and Symmetry. Symmetry 2018, 10, 744. [Google Scholar] [CrossRef]
- Fano, U. Description of states in quantum mechanics by density matrix and operator techniques. Rev. Mod. Phys. 1957, 29, 74. [Google Scholar] [CrossRef]
- Kubo, R. Stochastic Liouville equations. J. Math. Phys. 1963, 4, 174–183. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy numbers: An overview. Readings in Fuzzy Sets for Intelligent Systems; Elsevier: Amsterdam, The Netherlands, 1993; pp. 112–148. [Google Scholar] [CrossRef]
- Yue, P.; Xiao, J.; Xu, K.; Li, M.; Jiang, F.; Lu, Y.; Peng, D. Mathematical model and analysis method for flowfield separation and transition. Phys. Fluids 2021, 33, 044116. [Google Scholar] [CrossRef]
- Yue, P.; Zhang, J.; Wei, S. Mathematical model for excited state fluid dynamics. J. Phys. Conf. Ser. 2023, 2650, 012031. [Google Scholar] [CrossRef]
- Yue, P.; Zhang, J.; Peng, D.; Wei, S. Mathematical principle analysis of separation point prediction. J. Phys. Conf. Ser. 2021, 2101, 012018. [Google Scholar] [CrossRef]
- Yue, P.; Zhang, J.; Peng, D.; Wei, S. Mathematical principle analysis of transition point prediction. In Applied Mathematics, Modeling and Computer Simulation; IOS Press: Amsterdam, The Netherlands, 2022; pp. 72–80. [Google Scholar] [CrossRef]
- Lu, Y.; Yue, P.; Wei, S. Extension of calculus operations in Cartesian tensor analysis. Mathematics 2020, 8, 561. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, S.; Yue, P.; Li, G. Surface pressure calculation method of multi-field coupling mechanism under the action of flow field. Symmetry 2023, 15, 1064. [Google Scholar] [CrossRef]
- Gambella, C.; Ghaddar, B.; Naoum-Sawaya, J. Optimization problems for machine learning: A survey. Eur. J. Oper. Res. 2021, 290, 807–828. [Google Scholar] [CrossRef]
- Fu, C.; Li, Q.; Shen, M.; Xu, K. Realtime robust malicious traffic detection via frequency domain analysis. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 15–19 November 2021; ACM: New York, NY, USA, 2021; pp. 3431–3446. [Google Scholar]
- Xu, K.; Yue, P.; Liu, Q.; Liu, C.; Lu, Y.; Zhang, J. Numerical implementation of boundary element method for determining aerodynamic characteristics around airfoil system by viscous media. AIP Adv. 2020, 10, 055126. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Glynn, P.W. How to deal with the curse of dimensionality of likelihood ratios in Monte Carlo simulation. Stoch. Model. 2009, 25, 547–568. [Google Scholar] [CrossRef]
- Fornberg, B.; Zuev, J. The Runge phenomenon and spatially variable shape parameters in RBF interpolation. Comput. Math. Appl. 2007, 54, 379–398. [Google Scholar] [CrossRef]
- Polyak, B.T. Newton’s method and its use in optimization. Eur. J. Oper. Res. 2007, 181, 1086–1096. [Google Scholar] [CrossRef]
- Paquete, L.; Chiarandini, M.; Stützle, T. Pareto Local Optimum Sets in the Biobjective Traveling Salesman Problem: An Experimental Study. In Metaheuristics for Multiobjective Optimisation; Lecture Notes in Economics and Mathematical Systems; Gandibleux, X., Sevaux, M., Sörensen, K., T’kindt, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 535, pp. 177–199. [Google Scholar] [CrossRef]
- Hodel, A.S.; Hall, C.E. Variable-structure PID control to prevent integrator windup. IEEE Trans. Ind. Electron. 2001, 48, 442–451. [Google Scholar] [CrossRef]
- Sarsembayev, B.; Suleimenov, K.; Do, T.D. High Order Disturbance Observer Based PI-PI Control System With Tracking Anti-Windup Technique for Improvement of Transient Performance of PMSM. IEEE Access 2021, 9, 66323–66334. [Google Scholar] [CrossRef]
- Łukaszewicz, G.; Kalita, P. Navier–Stokes Equations: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ablowitz, M.J.; Chakravarty, S.; Halburd, R.G. Integrable systems and reductions of the self-dual Yang–Mills equations. J. Math. Phys. 2003, 44, 3147–3173. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).