The Irreducibility and Monodromy of Some Families of Linear Series with Imposed Ramifications

Abstract

Suppose that the adjusted Brill–Noether number is zero; we prove that there exists a family of twice-marked smooth projective curves such that the family of linear series with two imposed ramification conditions is irreducible. Moreover, under certain conditions, we show that the monodromy group contains the alternating group. In the case $r=1$, the monodromy group is the full symmetric group.

1. Introduction

Let C be a smooth projective curve of genus g over $\mathbb{C}$; then, all the linear series of degree d and rank r on C form a projective moduli space $G_d^r\left(C\right)$, which is known as the Brill–Noether locus. The classical Brill–Noether theorem [1] states that, if C is a general projective curve and the Brill–Noether number

$$\rho (g,r,d)=g-(r+1)(g-d+r)\ge 0,$$

then $G_d^r\left(C\right)$ is a smooth variety of dimension exactly $\rho (g,r,d)$ [2]. Moreover, if $\rho (g,r,d)>0$, the variety $G_d^r\left(C\right)$ is also irreducible.

Eisenbud and Harris [3] considered the analogy of such irreducibility when $\rho (g,r,d)=0$. If $\rho (g,r,d)=0$, then the variety $G_d^r\left(C\right)$ is reducible and precisely consists of

$$N(g,r,d)=g!\prod _{i=0}^r{\displaystyle \frac{i!}{(g-d+r+i)!}}$$

reduced points. However, if we consider a family of curves $\mathcal{C}\to B$, the corresponding family of linear series $G_d^r(\mathcal{C}/B)$ may be irreducible. Eisenbud and Harris proved the following theorem:

Theorem 1 

([3], Theorem 1). There exists a family of smooth projective curves $\mathcal{C}/B$ such that $G_d^r(\mathcal{C}/B)$ is irreducible.

In this paper, we generalize this theorem to the case of linear series with imposed ramification conditions at two generic points. Let $\alpha ,\beta$ be two ramification sequences. Given a smooth projective curve C and two distinct points $p,q$ on C, all the linear series of degree d and rank r on C with ramification sequence at least $\alpha$ at p and at least $\beta$ at q also form a projective moduli space $G_d^r(C,(p,\alpha ),(q,\beta ))$ [4]. Eisenbud and Harris [4] proved that if C is a general projective curve, then $G_d^r(C,(p,\alpha ),(q,\beta ))$ has dimension exactly

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|,$$

which is often called the adjusted Brill–Noether number.

Now we consider the case of $\rho (g,r,d,\alpha ,\beta )=0$. In this case, $G_d^r(C,(p,\alpha ),(q,\beta ))$ consists of precisely $N(g,r,d,\alpha ,\beta )$ reduced points. We will prove the following theorem:

Theorem 2 

(Theorem 8). Let $\alpha ,\beta$ be two ramification sequences, and suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0.$$

Then there exists a family of twice-marked smooth projective curves $(\mathcal{C}/B,p,q)$ such that the corresponding $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ is irreducible.

Moreover, we can demonstrate that, in some cases, the monodromy group of the family given in the proof of Theorem 2 is at least the alternating group. This result also generalizes Edidin’s theorem ([5], Theorem 2).

Theorem 3 

(Theorem 11, Proposition 5). Given two ramification sequences $\alpha ,\beta$. Suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0.$$

Let $N=N(g,r,d,\alpha ,\beta )$. If $\alpha ,\beta$ satisfy the conditions of Lemma 3, then the monodromy group of $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ in Theorem 2 is either the alternating group $A_N$ or the symmetric group $S_N$. Moreover, if $r=1$, then the monodromy group is $S_N$.

Brill–Noether loci with fixed ramification have been studied in some studies in the literature, such as [6,7,8].

1.1. Notational Conventions

We mention some conventions that will be used throughout this paper.

(1)

The numbers $g,r,d$ will always be non-negative and satisfy $g-d+r\ge 0$.

(2)

The symbols $a={\left(a_i\right)}_i$, $b={\left(b_i\right)}_i$ will refer to vanishing sequences of a linear series. The numbers $a_i$ and $b_i$ will be in increasing order. The symbols $\alpha ={\left({\alpha }_i\right)}_i$, $\beta ={\left({\beta }_i\right)}_i$ will refer to the corresponding ramification sequences of a linear series, defined by ${\alpha }_i=a_{r-i}-(r-i)$, ${\beta }_i=b_{r-i}-(r-i)$. The numbers ${\alpha }_i$ and ${\beta }_i$ will be in non-increasing order.

1.2. Structure of This Paper

In Section 2, we provide the necessary background on limit linear series. Section 3 explores the combinatorics of limit linear series and monodromy actions on a certain reducible curve. In Section 4, we prove the irreducibility result and establish some technical combinatorial lemmas. Finally, in Section 5, we prove our main results about monodromy groups.

2. Preliminaries

Let C be a smooth projective curve over $\mathbb{C}$.

Definition 1. 

A linear series on a curve C of degree d and rank r is a pair $(\mathcal{L},V)$, where $\mathcal{L}$ is a line bundle of degree d on C, and V is an $(r+1)$-dimensional subspace of ${\mathrm{H}}^0(C,\mathcal{L})$.

A linear series of degree d and rank r is historically denoted as ${\mathfrak{g}}_d^r$.

For any linear series, we can define its vanishing sequence and ramification sequence at each point.

Definition 2. 

Let $L=(\mathcal{L},V)$ be a ${\mathfrak{g}}_d^r$ on a curve C. For any $p\in C$, the vanishing sequence of $(\mathcal{L},V)$ at p is the increasing sequence of orders of sections in V at the point p:

$$0\le a_0\left(p\right)<a_1\left(p\right)<\cdots <a_r\left(p\right)\le d$$

and the corresponding ramification sequence is the non-increasing sequence

$$d-r\ge {\alpha }_0\left(p\right)=a_r\left(p\right)-r\ge {\alpha }_1\left(p\right)=a_{r-1}\left(p\right)-(r-1)\ge \cdots \ge {\alpha }_r\left(p\right)=a_0\left(p\right)-0\ge 0,$$

where ${\alpha }_i\left(p\right)=a_{r-i}\left(p\right)-(r-i)$.

If ${\alpha }_i\left(p\right)=0$ for all $0\le i\le r$, then p is called a non-ramification point; otherwise, it is a ramification point.

Some studies in the literature define the ramification sequence as a non-decreasing sequence, i.e., ${\alpha }_i\left(p\right)=a_i\left(p\right)-i$. Here, to match with Schubert indices later on, we define it as a non-increasing sequence. We say a linear series has ramification at least $\alpha$ at p if its ramification sequence at p is greater than or equal to $\alpha$ term by term.

The following theorem is a generalization of the Brill–Noether theorem, proved by Eisenbud and Harris.

Theorem 4 

([4], Theorem 4.5). Given $g,r,d,n$ and ramification sequences ${\alpha }^j$ for each $j=1,\cdots ,n$, let

$$\rho =g-(r+1)(g-d+r)-\sum _{j=1}^n\left|{\alpha }^j\right|.$$

Then, for all smooth projective curves C of genus g, and distinct marked points $p_1,\cdots ,p_n\in C$, there is a projective moduli space $G_d^r(C,(p_1,{\alpha }^1),\cdots ,(p_n,{\alpha }^n))$ of ${\mathfrak{g}}_d^r$’s on C with ramification at least ${\alpha }^j$ at each $p_j$, and it has every component of dimension at least ρ if it is non-empty. On a general curve C of genus g, the space of ${\mathfrak{g}}_d^r$’s has dimension exactly ρ, and, in particular, is empty if $\rho <0$.

2.1. Limit Linear Series

The original proofs of the Brill–Noether theorem [1], along with many other results, relied on analyzing linear series on smooth curves and studying their degeneration to singular curves. Later, Eisenbud and Harris [4] developed the theory of limit linear series, which describes how linear series specialized as smooth curves degenerate into curves of compact type. This theory, known for its ability to characterize the behavior of linear series under degenerations, has become a powerful tool in algebraic geometry.

A (possibly) reducible curve C is of compact type if its Jacobian is compact, or equivalently, if its irreducible components are smooth and meet transversely at a time and its dual graph obtained by considering the components as vertices and intersection relationships as edges is a tree.

Definition 3. 

Let C be a curve of compact type. For each irreducible component Y of C, let $L_Y=({\mathcal{L}}_Y,V_Y)$ be a ${\mathfrak{g}}_d^r$ on Y. If the collection

$$L=\{L_Y=({\mathcal{L}}_Y,V_Y):Y\mathit{is}\mathit{an}\mathit{irreducible}\mathit{component}\mathit{of}C\}$$

satisfies, for any two irreducible components Y and Z of C with $p=Y\cap Z$, and for any $j=0,\cdots ,r$, we have

$$a_j^{L_Y}\left(p\right)+a_{r-j}^{L_Z}\left(p\right)\ge d,$$

then L is called a crude limit linear series of degree d and rank r on C. If all these inequalities are equalities, then L is called a refined limit linear series, or, simply, a limit linear series, on C.

If L is a crude limit linear series but not refined, we call L a strictly crude limit linear series.

Eisenbud and Harris constructed a scheme parameterizing linear series and limit linear series for any smoothing family [4], and concluded the following:

Theorem 5 

([4], Theorem 3.3). Let $\mathcal{C}/B,p_1,\cdots ,p_n$ be an (n-pointed genus-g curve) smoothing family and ${\alpha }^1,\cdots ,{\alpha }^n$ be ramification sequences. Let

$$\rho =g-(r+1)(g-d+r)-\sum _{j=1}^n\left|{\alpha }^j\right|.$$

Then, there is a quasiprojective scheme $G=G_d^r(\mathcal{C}/B,(p_1,{\alpha }^1),\cdots ,(p_n,{\alpha }^n))$ parameterizing linear series on smooth fibers of $\mathcal{C}$, and limit linear series on singular fibers of $\mathcal{C}$, both of degree d and dimension r, and having ramification at least ${\alpha }^j$ at each $p_j$ for $j=1,\cdots ,n$. The dimension of any component of G is at least $\rho +dim\left(B\right)$.

If either

$$\sum _{j=1}^n\left|{\alpha }^j\right|=(r+1)d+\left({\displaystyle \genfrac{}{}{0pt}{}{r+1}{2}}\right)(2g-2),$$

or no reducible fibers $C_0$ of $\mathcal{C}$ have strictly crude ${\mathfrak{g}}_d^r$’s with the prescribed ramifications, then G is proper over B.

It is also worth noting that Osserman developed a functorial construction for limit linear series and provided a systematic framework to generalize the classical theory of limit linear series to all nodal curves (see [9,10]).

2.2. Linear Series on ${\mathbb{P}}^1$ and Schubert Cycles

It is well known that linear series of degree d and rank r on $Y={\mathbb{P}}^1$ correspond to $(r+1)$-dimensional subspaces of ${\mathrm{H}}^0(Y,{\mathcal{O}}_Y\left(d\right))$. Let $\mathrm{Gr}(r,d)$ be the Grassmannian parameterizing all $(r+1)$-dimensional subspaces of ${\mathrm{H}}^0(Y,{\mathcal{O}}_Y\left(d\right))$, or equivalently, all r-dimensional subspaces of ${\mathbb{P}}^d$.

Ramification sequences of linear series on $Y={\mathbb{P}}^1$ are closely connected to Schubert indices. For any point $q\in Y$, we define subspaces $f^i\left(q\right)$

$$f^i\left(q\right)=\{\sigma \in {\mathrm{H}}^0(Y,\mathcal{O}\left(d\right)):\mathrm{ord}q\left(\sigma \right)\ge d-i\}.$$

These subspaces form a complete flag in ${\mathrm{H}}^0(Y,\mathcal{O}\left(d\right))$. For a Schubert index $\alpha =({\alpha }_0,\cdots ,{\alpha }_r)$ satisfying

$$d-r\ge {\alpha }_0\ge \cdots \ge {\alpha }_r\ge 0,$$

we define the associated Schubert cycle in the Grassmannian as

$${\sigma }_{\alpha }\left(q\right)=\{V\in \mathrm{Gr}(r,d):\dim (V\cap f^{(d-r+i-{\alpha }_i)}\left(q\right))>i\},$$

which is a subvariety of codimension $\left|\alpha \right|={\sum }_i{\alpha }_i$. The relationship between ramification sequences and Schubert varieties can be expressed as follows:

Proposition 1. 

If $({\mathcal{O}}_Y\left(d\right),V)$ is a linear series on $Y={\mathbb{P}}^1$, then its ramification sequence at point q is greater than or equal to $({\alpha }_0,\cdots ,{\alpha }_r)$ term by term if and only if $V\in {\sigma }_{{\alpha }_0,\cdots ,{\alpha }_r}\left(q\right)$.

Proof. 

The proof is straightforward. Suppose the vanishing sequence of $({\mathcal{O}}_Y\left(d\right),V)$ at q is $(b_0,\cdots ,b_r)$ and the corresponding ramification sequence is $({\beta }_0,\cdots ,{\beta }_r)$. On the other hand, let $(a_0,\cdots ,a_r)$ be the corresponding vanishing sequence of $({\alpha }_0,\cdots ,{\alpha }_r)$. Then we have

$$\begin{array}{cc}\hfill V\in {\sigma }_{{\alpha }_0,\cdots ,{\alpha }_r}\left(q\right)& \iff \mathrm{for}\mathrm{any}i,\dim (V\cap f^{d-r+i-(a_{r-i}-(r-i))})>i,\hfill \\ \hfill & \iff \mathrm{for}\mathrm{any}i,\dim (V\cap f^{d-a_{r-i}})>i,\hfill \\ \hfill & \iff \mathrm{for}\mathrm{any}i,\dim \{\sigma \in V:{\mathrm{ord}}_q\left(\sigma \right)\ge a_{r-i}\}\ge i+1,\hfill \\ \hfill & \iff \mathrm{for}\mathrm{any}i,\mathrm{codim}\{\sigma \in V:{\mathrm{ord}}_q\left(\sigma \right)\ge a_{r-i}\}\le r-i,\hfill \\ \hfill & \iff \mathrm{for}\mathrm{any}i,b_{r-i}\ge a_{r-i},\hfill \\ \hfill & \iff \mathrm{for}\mathrm{any}i,{\beta }_i\ge {\alpha }_i.\hfill \end{array}$$

□

Let $q_1,\cdots ,q_k$ denote distinct points of ${\mathbb{P}}^1$ and ${\alpha }^{\left(1\right)},\cdots ,{\alpha }^{\left(k\right)}$ represent ramification sequences associated with these points. An important fact that we will frequently use, which can be found in [11], is that the intersection ${\bigcap }_{i=1}^k{\sigma }_{{\alpha }^{\left(i\right)}}\left(q_i\right)$ has the expected codimension ${\sum }_{i=1}^k\left|{\alpha }^{\left(i\right)}\right|$.

3. Limit Linear Series with Two Imposed Ramifications

As in [3], we prove our results by degenerating smooth curves into reducible nodal curves, leveraging the combinatorial representations of limit linear series on such curves. A commonly used degeneration method involves chains of elliptic and rational curves. Specifically, we examine a twice-marked reducible nodal curve $C_{\infty }$, which is the same as the one discussed in [3], as illustrated in Figure 1.

Figure 1. Curve $C_{\infty }$.

Here, $Y_1,\cdots ,Y_{g+1}$ are rational curves isomorphic to ${\mathbb{P}}^1$, $E_1,\cdots ,E_g$ are elliptic curves attached to $Y_1,\cdots ,Y_g$, and $p_1=p$, $p_{g+2}=q$ are the marked points. To ensure the stability of $C_{\infty }$, we may label an additional point on $Y_{g+1}$, although for simplicity of notation, we temporarily omit it. Later, we will provide a detailed description of all limit linear series on $C_{\infty }$ with ramification sequences at least $\alpha$ at $p_1$ and at least $\beta$ at $p_{g+2}$.

To investigate the monodromy action on the limit linear series of the curve $C_{\infty }$, we can examine some one-parameter families where each curve also takes the form of chains of elliptic and rational curves. For any $1\le i\le g$, we consider the one-parameter family $C_{i,p}$, where as p approaches infinity, the stable limit of $C_{i,p}$ is $C_{\infty }$. The curve $C_{i,p}$ is depicted in Figure 2.

Figure 2. Curve $C_{i,p}$.

The curve $C_{i,p}$ differs from $C_{\infty }$ in that it excludes the rational curve $Y_{i+1}$ and instead attaches the elliptic curve $E_{i+1}$ to $Y_i$. In terms of coordinates on $Y_i$, the intersection points of $Y_{i-1},E_i,E_{i+1}$, and $Y_{i+1}$ with $Y_i$ are $0,1,p$, and ∞, respectively, where $p\ne 0,1,\infty$. As p tends to infinity, the stable limit of the curves $C_{i,p}$ results in the blow-up of the curve at $p=\infty$, precisely adding another rational curve ${\mathbb{P}}^1$, which is exactly the curve $C_{\infty }$.

3.1. Combinatorial Representation of Limit Linear Series on $C_{\infty }$ and $C_{i,p}$

Next, we study the combinatorial representation of limit linear series with ramification conditions at the given two points on the curves $C_{i,p}$ and $C_{\infty }$. We will utilize some results from [3], and for convenience, we include relevant propositions here. The curves $C_{i,p}$ and $C_{\infty }$ primarily have only two distinct local types, denoted as D and $D^{\prime }$, as shown in Figure 3.

Figure 3. Curves D and $D^{\prime }$.

Let L be a limit ${\mathfrak{g}}_d^r$ on the curve D. Then, L consists of linear series on the two irreducible components of D: $L_Y=({\mathcal{O}}_Y\left(d\right),V_Y)$ and $L_E=({\mathcal{L}}_E,V_E)$. We denote the vanishing sequence of $L_Y$ at $p_1$ as $a^{\left(1\right)}$ and at $p_2$ as $b^{\left(1\right)}$, corresponding to ramification sequences ${\alpha }^{\left(1\right)}$ and ${\beta }^{\left(1\right)}$, respectively. Furthermore, let ${\alpha }^{\left(2\right)}={\left({\beta }^{\left(1\right)}\right)}^{\vee }$ denote the dual ramification sequence of ${\beta }^{\left(1\right)}$, where for any $0\le i\le r$,

$${\alpha }_i^{\left(2\right)}=d-r-{\beta }_{r-i}^{\left(1\right)}.$$

For the curve $D^{\prime }$, we use the same notation. Then, the limit linear series on D and $D^{\prime }$ can be characterized as follows:

Lemma 1 

([3], Corollary 1.2). We have:

1.  

On the curve D, it holds that $|{\alpha }^{\left(2\right)}| \ge |{\alpha }^{\left(1\right)}| + r$. If equality holds, then ${\mathcal{L}}_E={\mathcal{O}}_E\left(dp\right)$, $V_E$ is the image of ${\mathrm{H}}^0\left({\mathcal{L}}_E(-(r+1)p)\right)$ in ${\mathrm{H}}^0\left({\mathcal{L}}_E\right)$, and there exists a unique i such that

$$b_{r-i}^{\left(1\right)}=d-a_i^{\left(1\right)},$$

and for any $j\ne i$,

$$b_{r-j}^{\left(1\right)}=d-a_j^{\left(1\right)}-1.$$

Conversely, given vanishing sequences $a^{\left(1\right)}$ and $b^{\left(1\right)}$ satisfying these conditions, there exists a unique limit ${\mathfrak{g}}_d^r$ on D such that the vanishing sequences at $p_1$ and $p_2$ are, respectively, $a^{\left(1\right)}$ and $b^{\left(1\right)}$.

2.  

On the curve $D^{\prime }$, it holds that $|{\alpha }^{\left(2\right)}| \ge |{\alpha }^{\left(1\right)}| + 2r$. If the equality holds, then the linear series $({\mathcal{L}}_E,V_E)$ and $({\mathcal{L}}_{E^{\prime }},V_{E^{\prime }})$ of the elliptic curve parts are determined in the same way as D.

Given vanishing sequences $a^{\left(1\right)}$ and $b^{\left(1\right)}$ such that the corresponding ramification sequences satisfy $|{\alpha }^{\left(2\right)}| = |{\alpha }^{\left(1\right)}| + 2r$, there is at most one limit ${\mathfrak{g}}_d^r$ on $D^{\prime }$ with these sequences except in the following case, where there are either 1 or 2 such series. There exist integers $i<j$ such that the following are true:

(1)  

If $i>0$, then $a_{i-1}^{\left(1\right)}<a_i^{\left(1\right)}-1$;

(2)  

$a_{j-1}^{\left(1\right)}<a_j^{\left(1\right)}-1$;

(3)  

$b_{r-i}^{\left(1\right)}=d-a_i^{\left(1\right)}-1$;

(4)  

$b_{r-j}^{\left(1\right)}=d-a_j^{\left(1\right)}-1$;

(5)  

For any $k\ne i,j$, $b_{r-k}^{\left(1\right)}=d-a_k^{\left(1\right)}-2$.

Using this lemma, we can fully characterize limit linear series on $C_{i,p}$ and $C_{\infty }$ with the imposed ramification conditions $\alpha$ and $\beta$ at $p_1$ and $p_{g+2}$, respectively. Let L be such a limit ${\mathfrak{g}}_d^r$ on $C_{\infty }$, then the restriction of L on each part remains a limit ${\mathfrak{g}}_d^r$. Suppose the vanishing sequence and the ramification sequence of $({\mathcal{L}}_{Y_i},V_{Y_i})$ at $p_i$ are $a^{\left(i\right)}=(a_0^{\left(i\right)},\cdots ,a_r^{\left(i\right)})$ and ${\alpha }^{\left(i\right)}=(a_r^{\left(i\right)}-r,\cdots ,a_0^{\left(i\right)}-0)$, respectively. According to Lemma 1, for any $1\le i\le g$, we have

$$|{\alpha }^{(i+1)}| \ge |{\alpha }^{\left(i\right)}| + r,$$

which leads to

$$|{\alpha }^{(g+1)}| \ge |{\alpha }^{\left(1\right)}| + rg\ge |\alpha |+rg.$$

(1)

On the other hand, to ensure the intersection ${\sigma }_{{\alpha }^{(g+1)}}·{\sigma }_{\beta }$ is nonempty, it is required that

$$|{\alpha }^{(g+1)}| + |\beta |\le \dim G(r,d)=(r+1)(d-r).$$

While at the beginning we assume

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0,$$

so that

$$\begin{array}{cc}\hfill |{\alpha }^{(g+1)}| + |\beta |& \le (r+1)(d-r)\hfill \\ \hfill & =rg+\left|\alpha \right|+\left|\beta \right|.\hfill \end{array}$$

(2)

By combining inequalities (1) and (2), we deduce that all the equalities must hold. Thus, ${\alpha }^{\left(1\right)}=\alpha$ and for any $1\le i\le g$, $|{\alpha }^{(i+1)}| = |{\alpha }^{\left(i\right)}| + r$.

For the curve $C_{i,p}$, we use the same notation. For any $1\le j\le g$ and $j\ne i,i+1$, we have

$$|{\alpha }^{(j+1)}| \ge |{\alpha }^{\left(j\right)}| + r,$$

and

$$|{\alpha }^{(i+2)}| \ge |{\alpha }^{\left(i\right)}| + 2r.$$

Consequently,

$$|{\alpha }^{(g+1)}| \ge |{\alpha }^{\left(1\right)}| + (r-2)g+2g\ge |\alpha |+rg.$$

Similarly, in this case, the inequality (2) also holds, confirming that these inequalities are all equalities. Therefore, ${\alpha }^{\left(1\right)}=\alpha$ and for any $1\le j\le g$ where $j\ne i,i+1$, it must be that $|{\alpha }^{(j+1)}| = |{\alpha }^{\left(j\right)}| + r$ and $|{\alpha }^{(i+2)}| = |{\alpha }^{\left(i\right)}| + 2r$.

In summary, a limit linear series satisfying ramification at least $\alpha$ at $p_1$ and at least $\beta$ at $p_2$ L on the curve $C=C_{\infty }$ corresponds to a chain of Schubert cycles:

$$\Delta \left(L\right)=({\sigma }_{{\alpha }^{\left(1\right)}}={\sigma }_{\alpha },\cdots ,{\sigma }_{{\alpha }^{(g+1)}}={\sigma }_{\beta }^{\vee })$$

(3)

where ${\sigma }_{\beta }^{\vee }$ is the Poincaré dual of ${\sigma }_{\beta }$. This correspondence is indeed one-to-one, which we formulate as the following theorem:

Theorem 6. 

Suppose $\alpha ,\beta$ are two ramification sequences and

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0.$$

Let Σ be the set of sequences of $g+1$ Schubert cycles in $\mathrm{Gr}(r,d)$:

$$s_1={\sigma }_{\alpha },\cdots ,s_{g+1}={\sigma }_{\beta }^{\vee }$$

such that for any $1\le i<g+1$:

$$s_i·{\sigma }_{1,\cdots ,1,0}·s_{i+1}^{\vee }\ne 0.$$

Then, the limit linear series ${\mathfrak{g}}_d^r$ on the curve $C_{\infty }$ satisfying the ramification sequences at $p_1$, $p_{g+2}$ being at least α, β, respectively, correspond bijectively to Σ, where the limit linear series L corresponds to $\Delta \left(L\right)$ as given in Equation (3).

Proof. 

As discussed above, the limit linear series L corresponds to a chain of Schubert cycles $\Delta \left(L\right)$. For any $1\le i\le g$, let the restriction of L on the rational curve $Y_i$ be $L_i$. The ramification sequences of $L_i$ at $p_i,p_{i+1}$ and its intersection with $E_i$ are ${\alpha }^{\left(i\right)},{\left({\alpha }^{(i+1)}\right)}^{\vee },(1,\cdots ,1,0)$, respectively, where ${\left({\alpha }^{(i+1)}\right)}^{\vee }$ is the Schubert index of ${\left({\sigma }_{{\alpha }^{(i+1)}}\right)}^{\vee }$. The existence of such $L_i$ implies

$${\sigma }_{{\alpha }^{\left(i\right)}}·{\sigma }_{1,\cdots ,1,0}·{\left({\sigma }_{{\alpha }^{(i+1)}}\right)}^{\vee }\ne 0,$$

hence, the sequence

$${\sigma }_{{\alpha }^{\left(1\right)}}={\sigma }_{\alpha },\cdots ,{\sigma }_{{\alpha }^{(g+1)}}={\sigma }_{\beta }^{\vee }$$

belongs to Σ.

Conversely, given a sequence in Σ:

$$s_1={\sigma }_{\alpha },\cdots ,s_{g+1}={\sigma }_{\beta }^{\vee }$$

such that for any $1\le i<g+1$,

$$s_i·{\sigma }_{1,\cdots ,1,0}·s_{i+1}^{\vee }\ne 0,$$

then by Lemma 1 (1), there exists a unique limit linear series L on $C_{\infty }$ such that its ramification sequences at points $p_1$, $p_2$ are $s_1$, $s_2$, respectively. □

Combinatorics in Schubert calculus is often represented by Young tableaux. Here, we can also transform such sequences of Schubert cycles into Young tableaux, making it easier to handle the combinatorics. This approach is particularly useful for studying monodromy actions. Bercov and Proctor [12] were the first to use Young tableaux to parameterize limit linear series. Now, we restate Theorem 6 using Young tableaux.

Given ramification sequences $\alpha$ and $\beta$, we construct a (skew) Young diagram $\sigma =\sigma (g,r,d,\alpha ,\beta )$ as shown in Figure 4. We place the sequence $\alpha$ from bottom to top on the left side of an $(r+1)\times (g-d+r)$ rectangle, while the sequence $\beta$ from top to bottom on the right side. The reversal of $\beta$ is due to the fact that the last term in the sequence of Schubert cycles as above is the Poincaré dual of ${\sigma }_{\beta }$. The assumption $\rho (g,r,d,\alpha ,\beta )=0$ implies that the entire Young diagram consists of g boxes.

Figure 4. Young diagram corresponding to limit linear series on $C_{\infty }$.

We have the following theorems.

Theorem 7. 

Let α and β be two ramification sequences, and suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0.$$

Then, the limit linear series ${\mathfrak{g}}_d^r$ on the curve $C_{\infty }$ with ramification sequences at $p_1$ and $p_{g+2}$ at least α and β correspond bijectively to the Young tableaux of the Young diagram $\sigma (g,r,d,\alpha ,\beta )$.

Proof. 

By Theorem 6, limit linear series on $C_{\infty }$ correspond bijectively to sequences in Σ. Let $({\sigma }_{{\alpha }^{\left(0\right)}}={\sigma }_{\alpha },\cdots ,{\sigma }_{{\alpha }^{(g+1)}}={\sigma }_{\beta }^{\vee })$ be a sequence in Σ. We now construct the corresponding Young tableau inductively.

Suppose $k\ge 1$ and the integers $1,2,\cdots ,k-1$ have already been filled in the Young diagram $\sigma (g,r,d,\alpha ,\beta )$. According to Lemma 1, there exists a unique $0\le j\le r$ such that ${\alpha }_j^{\left(k\right)}={\alpha }_j^{(k+1)}$. To proceed, we fill k into the first available empty box from the left in the $(r-j+1)$-th row. The existence of this empty box is guaranteed by the definition of Σ.

We now demonstrate that the resulting tableau is a Young tableau, meaning it increases from left to right and from top to bottom. Firstly, each row is increasing from left to right due to our construction. Suppose that there exists a column where adjacent boxes in rows j and $j+1$ are filled with integers k and $k^{\prime }$, respectively, and $k>k^{\prime }$. When placing $k^{\prime }$, the box directly above it must still be empty. This implies ${\alpha }_{j+1}^{\left(k^{\prime }\right)}<{\alpha }_j^{\left(k^{\prime }\right)}$, contradicting the non-increasing property of ramification sequences. Therefore, the constructed tableau is indeed a Young tableau.

Conversely, a Young tableau can be used to construct the original sequence in a similar manner. Thus, limit linear series on the curve $C_{\infty }$ with ramification sequences at $p_1$ and $p_{g+2}$ at least $\alpha$ and $\beta$ correspond bijectively to the Young tableaux of the Young diagram $\sigma$. □

Example 1. 

Consider a curve C of genus 7 and a ${\mathfrak{g}}_6^1$ on C, denoted as L. Let $\alpha =(1,0),\beta =(2,0)$ be ramification sequences. In this case, we have

$$\rho (g,r,d,\alpha ,\beta )=7-(1+1)\ast (7-6+1)-1-2=0.$$

Assume that L is represented as the sequence

$${\sigma }_{{\alpha }^{\left(1\right)}}={\sigma }_{1,0},{\sigma }_{{\alpha }^{\left(2\right)}}={\sigma }_{2,0},{\sigma }_{{\alpha }^{\left(3\right)}}={\sigma }_{2,1},{\sigma }_{{\alpha }^{\left(4\right)}}={\sigma }_{3,1},{\sigma }_{{\alpha }^{\left(5\right)}}={\sigma }_{3,2},$$

$${\sigma }_{{\alpha }^{\left(6\right)}}={\sigma }_{3,3},{\sigma }_{{\alpha }^{\left(7\right)}}={\sigma }_{4,3},{\sigma }_{{\alpha }^{\left(8\right)}}={\sigma }_{5,3}={\left({\sigma }_{2,0}\right)}^{\vee }$$

Given that ${\alpha }^{\left(1\right)}$ and ${\alpha }^{\left(2\right)}$ are identical exactly at index $j=1$: ${\alpha }_1^{\left(1\right)}={\alpha }_1^{\left(2\right)}$, we place 1 into the first empty box from the left in the $r-j+1=1$-th row. Similarly, since ${\alpha }^{\left(2\right)}$ and ${\alpha }^{\left(3\right)}$ are identical exactly at index $j=0$: ${\alpha }_0^{\left(2\right)}={\alpha }_0^{\left(3\right)}$, we place 2 into the first empty box from the left in the $r-j+1=2$-th row. This process continues until all $g=7$ entries are filled, resulting in the corresponding Young tableau shown below (Figure 5):

Figure 5. Young tableaux of L.

Conversely, starting from such a Young tableau, we can reconstruct the original sequence of Schubert cycles in the same manner.

3.2. Combinatorial Representation of Certain Monodromy Actions

Next, we investigate the monodromy group action induced by the one-parameter family $C_{i,p}$ on the limit linear series of the curve $C_{\infty }$ with imposed ramification conditions. To proceed, we need the following lemma:

Lemma 2 

([3], Theorem 1.3). Let $a,b$ be two vanishing sequences, such that there exist $0\le i<j\le r$ such that

(1)  

if $i>0$, $a_{i-1}^{\left(1\right)}<a_i^{\left(1\right)}-1;$

(2)  

$a_{j-1}^{\left(1\right)}<a_{j-1}^{\left(1\right)};$

(3)  

$b_{r-i}^{\left(1\right)}=d-a_{i-1}^{\left(1\right)};$

(4)  

$b_{r-j}^{\left(1\right)}=d-a_{j-1}^{\left(1\right)};$

(5)  

$\mathit{For}\mathit{any}k\ne i,j,\mathit{we}\mathit{have}{b}_{r-k}^{\left(1\right)}=d-a_k^{\left(1\right)}-2$.

Then, on ${\mathbb{P}}^1$, all vanishing sequences at 0 are at least a, at ∞ are at least b, and at 1 and another point $p\ne 0,1,\infty$ are cusps, and the moduli space of linear series ${\mathfrak{g}}_d^r$ is an irreducible rational curve G. The map from each linear series to the corresponding point p gives a map $G\to {\mathbb{P}}^1$ which is a double cover, branching at two points on ${\mathbb{P}}^1\setminus \{0,1,\infty \}$, and these two branching points are determined by $a_j-a_i$. Conversely, any branching point also determines the value of $a_j-a_i$.

We denote the subgroup of the monodromy group generated by the one-parameter families $C_{i,p}$ as the EH group. Using Lemmas 1 and 2, we can determine how the EH group acts on the Young tableaux.

The distance between two boxes in a Young diagram is defined as the sum of their horizontal and vertical distances. Specifically, the distance between adjacent boxes is 1. Following Edidin’s arguments in [5] Proposition 1, we establish that:

Proposition 2. 

The EH group is generated by elements $\{{\pi }_{t,a}:t,a\in \mathbb{Z},1\le t<g,a>0\}$. The action ${\pi }_{t,a}$ exchanges the entries t with $t+1$ in all Young tableaux of shape σ, where t and $t+1$ are in different rows and columns and have a distance of a.

Proof. 

Let $L_1$ and $L_2$ be limit linear series on $C_{\infty }$ and correspond to sequences

$$\Delta \left(L_1\right):{\sigma }_{{\alpha }^{\left(1\right)}}={\sigma }_{\alpha },\cdots ,{\sigma }_{{\alpha }^{(t-1)}},{\sigma }_{{\alpha }^{\left(t\right)}},{\sigma }_{{\alpha }^{(t+1)}},\cdots ,:{\sigma }_{{\alpha }^{(g+1)}}={\sigma }_{\beta }^{\vee }$$

$$\Delta \left(L_2\right):{\sigma }_{{\beta }^{\left(1\right)}}={\sigma }_{\alpha },\cdots ,{\sigma }_{{\beta }^{(t-1)}},{\sigma }_{{\beta }^{\left(t\right)}},{\sigma }_{{\beta }^{(t+1)}},\cdots ,:{\sigma }_{{\beta }^{(g+1)}}={\sigma }_{\beta }^{\vee }$$

We translate the conditions on vanishing sequences on the limit ${\mathfrak{g}}_d^r$ on the curve $D^{\prime }$ in Lemma 1 into conditions on the ramification sequences ${\alpha }^{\left(1\right)}$ and ${\alpha }^{\left(2\right)}$. There exist $0\le i<j\le r$ such that the following hold:

(1)

if $i>0$, ${\alpha }_{i-1}^{\left(1\right)}<{\alpha }_i^{\left(1\right)};$

(2)

${\alpha }_{j-1}^{\left(1\right)}<{\alpha }_j^{\left(1\right)};$

(3)

${\alpha }_i^{\left(2\right)}={\alpha }_i^{\left(1\right)}+1;$

(4)

${\alpha }_j^{\left(2\right)}={\alpha }_j^{\left(1\right)}+1;$

(5)

$\mathrm{for}\mathrm{any}k\ne i,j,{\alpha }_i^{\left(2\right)}={\alpha }_i^{\left(1\right)}+2.$

Therefore, some family $C_{t,p}$ exchanges $L_1$ with $L_2$ only if there exist $1\le t<g$ and $0\le i<j\le r$ such that for any $k\ne i,j$, we have ${\alpha }_k^{(t+1)}={\beta }_k^{(t+1)}$, and

$${\alpha }^{\left(1\right)}={\beta }^{\left(1\right)},\cdots ,{\alpha }^{\left(t\right)}={\beta }^{\left(t\right)},{\alpha }^{(t+2)}={\beta }^{(t+2)},\cdots ,{\alpha }^{(g+1)}={\beta }^{(g+1)}.$$

This is because ${\alpha }^{\left(t\right)},{\alpha }^{(t+2)}$ correspond to vanishing sequences $a^{\left(t\right)},a^{(t+2)}$, which satisfy the conditions in Lemma 2. Thus, there exists a monodromy action exchanging the restriction of $L_1$ and $L_2$ on the union of $Y_t$ and $Y_{t+1}$ in $C_{\infty }$, leaving the other parts of the limit linear series unchanged, thereby exchanging the limit linear series $L_1$ with $L_2$ on $C_{\infty }$. Let $a=a_j^{(t-1)}-a_i^{(t-1)}$. From Lemma 2, we know that the branching points are determined by a, indicating that the number of all possible branching points is finite. Hence, there exists a monodromy action that exchanges the limit linear series with $a_j^{(t-1)}-a_i^{(t-1)}=a$. This action, denoted by ${\pi }_{t,a}$, is the product of all such transpositions and is determined only by t and a.

Let S and T be the Young tableaux representation of $L_1$ and $L_2$, respectively. According to Theorem 6, each step in the chain of Schubert cycles for the limit linear series involves keeping one of the Schubert indices unchanged and incrementing the rest by 1, while maintaining the monotonicity of the indices. Since $L_1$ and $L_2$ are exactly the same except for ${\sigma }_{{\alpha }^{t+1}}$, the only difference between $L_1$ and $L_2$ is the order in which the fixed indices are chosen in the steps:

$${\sigma }_{{\alpha }^t}\supset {\sigma }_{{\alpha }^{t+1}}\supset {\sigma }_{{\alpha }^{t+2}}$$

and

$${\sigma }_{{\beta }^t}\supset {\sigma }_{{\beta }^{t+1}}\supset {\sigma }_{{\beta }^{t+2}}.$$

Therefore, when represented using Young tableaux, the difference between S and T is that t and $t+1$ are exchanged.

Since S and T are both Young tableaux, they satisfy the monotonicity of rows and columns, meaning t and $t+1$ cannot be in the same row or column in either S or T. Moreover, according to the construction of the Young tableau, the horizontal distance between t and $t+1$ in S is exactly ${\alpha }_j^{\left(t\right)}-{\alpha }_i^{\left(t\right)}$, and the vertical distance between t and $t+1$ in S is exactly $j-i$. Given that

$$a=a_j^{\left(t\right)}-a_i^{\left(t\right)}={\alpha }_j^{\left(t\right)}-{\alpha }_i^{\left(t\right)}+(j-i),$$

we conclude that the distance between t and $t+1$ in the Young tableaux S and T is exactly a.

Therefore, the monodromy action ${\pi }_{t,a}$ on the Young tableaux representation of the limit linear series is to exchange t with $t+1$ in all Young tableaux where t and $t+1$ are located in different rows and columns and have a distance of a. □

Example 2. 

Let L be the limit linear series in Example 1. The Young tableau representation T of L is shown on the left in Figure 6.

(1)  

The action ${\pi }_{3,2}$ exchanges 3 with 4 whenever 3 and 4 are at a distance of 2. Thus, ${\pi }_{3,2}$ transforms the tableau T of L into the tableau shown on the right below.

(2)  

The action of ${\pi }_{3,3}$ leaves T unchanged since 3 and 4 are not at a distance of 3 in T.

(3)  

For any $k\ge 1$, the action of ${\pi }_{4,k}$ will fix T because 4 and 5 are in the same row in T.

Figure 6. The action of ${\pi }_{3,2}$.

4. Doubly Transitivity of the Monodromy Action

Let $YT(g,r,d,\alpha ,\beta )$ be the collection of all Young tableaux of shape $\sigma$; then, we have

Proposition 3. 

The action of the EH group on $YT(g,r,d,\alpha ,\beta )$ is transitive.

Proof. 

Assign a lexicographic order to the set $YT(g,r,d,\alpha ,\beta )$: column-wise from left to right and top to bottom within each column. In other words, the smallest Young tableau S is the one where $1,2,\cdots ,g$ are sequentially filled into each column from left to right, and within each column from top to bottom. We only need to prove that any Young tableau can be moved to S by an EH group element. In fact, we only need to prove that for any Young tableau $T\ne S$, there exists an EH group element that moves it to a Young tableau $T^{\prime }$ that is smaller than T in the lexicographic order. Since this process will eventually stop after a finite number of steps, the final tableau must be S.

Given a Young tableau $T\ne S$, let M be the first integer different from S in the lexicographic order. Then $M-1$ must not be to the left or above M in T, because the left and upper sides of M in T are the same as those in S and M is the first integer different from S. Additionally, according to the definition of Young tableaux, the integers below and to the right of M are larger than M, so M and $M-1$ are in different rows and columns. Let a be their distance, then the monodromy action ${\pi }_{M-1,a}$ in the EH group moves T to $T^{\prime }$, which is smaller than T in the lexicographic order. □

Theorem 8. 

Let $\alpha ,\beta$ be two ramification sequences and suppose that

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0.$$

Then, there exists a family of twice-marked smooth projective curves $(\mathcal{C}/B,p,q)$ such that the corresponding $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ is irreducible.

Actually, it can be seen from the proof that this theorem is true for any sufficiently small irreducible family of twice-marked smooth curves, whose stable limits contain all curves of the form in Figure 7.

Figure 7. Reducible curve.

Proof. 

Let $(\mathcal{C}/B,p,q)$ be an irreducible family of twice-marked smooth curves and its stable limit contains all stable curves of the form in Figure 7. Then the stable curve obtained by letting $p_i$ approach $p_{i+1}$ will add another rational curve ${\mathbb{P}}^1$. Repeatedly performing this operation will eventually result in the curves $C_{i,p}$ and $C_{\infty }$. Therefore, the stable limit of this family include all $C_{i,p}$ and $C_{\infty }$.

Shrink B if necessary so that the family $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ is smooth. To prove that $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ is irreducible, it suffices to show that the monodromy action on the fiber is transitive.

According to [4], the family $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))$ can be extended to its stable limit (at least along one-parameter families). Harris [13] proved that the monodromy group is birational invariant, so it is enough to show that the action on the fiber of $C_{\infty }$ is transitive. Now by Proposition 3, the group action induced by the one-parameter families $C_{i,p}$ on the fiber of $C_{\infty }$ has already been transitive, so we are done. □

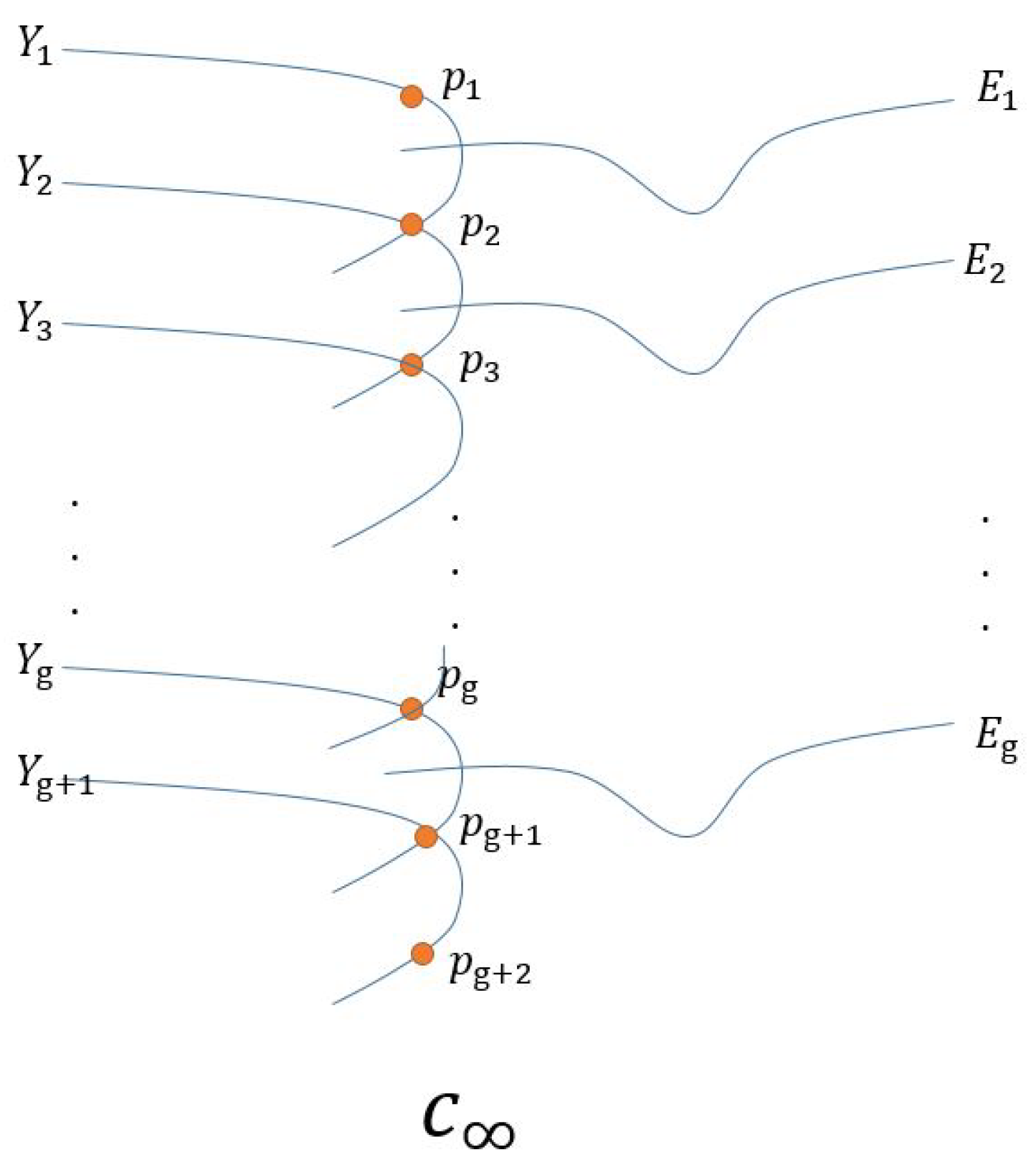
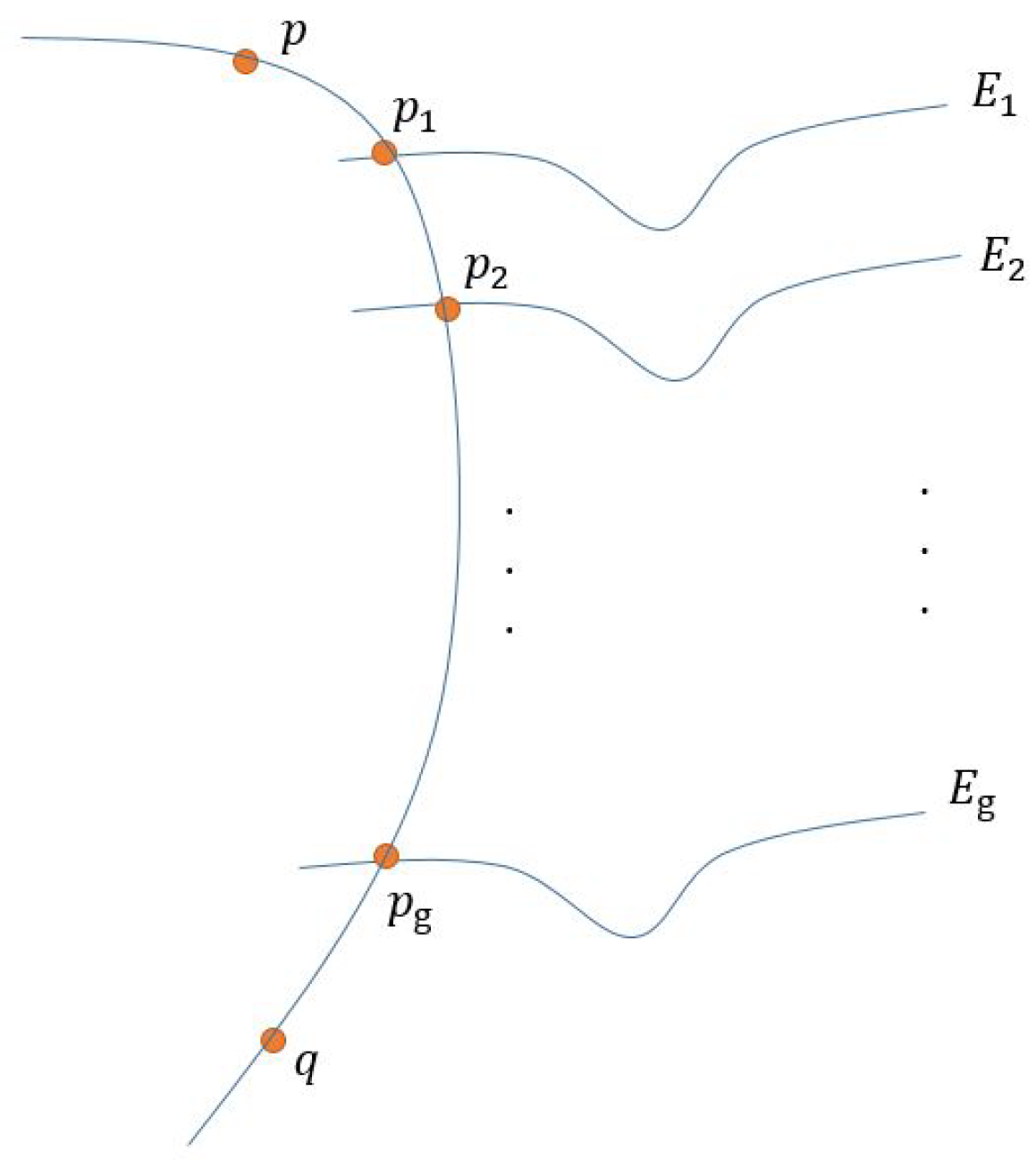
More generally, under certain conditions, we can prove that the action of the EH group on $YT(g,r,d,\alpha ,\beta )$ is doubly transitive.

Definition 4. 

Let G be a group acting on a set S. The action of G on S is doubly transitive if for any $x,y,w,z\in S$ with $x\ne y$ and $z\ne w$, there exists a group element $g\in G$ such that $g·x=y$ and $g·z=w$.

Lemma 3. 

If the given ramification sequences $\alpha ,\beta$ satisfy the following conditions:

(1)  

$max\{{\alpha }_0-{\alpha }_r,1\}<{min}_{0\le j<r}\{{\alpha }_{r-j-1}+{\beta }_j\}+g-d$;

(2)  

${\sum }_{i=0}^r({\alpha }_i-{\alpha }_r)<{\alpha }_r+g-d+r+{\beta }_r$;

(3)  

For any $0\le i<r$, ${\alpha }_{r-i}+{\beta }_i-1<{min}_{i\le j<r}\{{\alpha }_{r-i-j-1}+{\beta }_j\}$;

(4)  

For any $0<i<r$, ${\alpha }_{r-i}+{\beta }_i={\alpha }_{r-1}+{\beta }_1\ge {\alpha }_r+{\beta }_0$.

Then, the action of the EH group on $YT(g,r,d,\alpha ,\beta )$ is doubly transitive.

Proof. 

Similar to the proof of Proposition 3, we assign a lexicographic order to the set $YT(g,r,d,\alpha ,\beta )$: column-wise from left to right and top to bottom in each column. Let S be the smallest tableau in this order. Let Z be the Young tableau obtained by filling the boxes row-wise from top to bottom and from left to right in each row. By using induction on the size of the Young diagram, we can see that Z is the largest tableau in the lexicographic order.

To establish the doubly transitivity of the EH group action, it is sufficient to prove that any Young tableau can be transformed into S by an EH group element while preserving the Young tableau Z. Actually, it is enough to prove that for any Young tableau $T\ne S$, there exists an EH group element $\pi$ that moves T to a tableau $T^{\prime }$ smaller in the lexicographic order, with $\pi$ fixing the tableau Z. Since this process is finite, it will eventually stop, with the final tableau being S, while the tableau Z remains unchanged.

Given a Young tableau $T\ne S$, let $M+1$ be the first integer in the lexicographic order that differs from S. Let $T_{i,j}$ represent the integer in the box located at the i-th (starting from 1) row from top to bottom and the j-th (starting from 1) column from left to right in tableau T. The integer M cannot appear to the left of or above the box containing $M+1$, because at these positions, T and S are identical, and $M+1$ is the first different integer. Therefore, M can only lie above and to the right of $M+1$. Let $M+1=T_{a,b}$, $M=T_{c,d}$. We denote their distance as

$$L=(a-c)+(d-b).$$

We aim to exchange M with $M+1$ in T, while keeping Z fixed, so that T becomes a Young tableau with a smaller lexicographic order. If M and $M+1$ are in the same row in Z, then the group action ${\pi }_{M,L}$ is sufficient to achieve this. Therefore, we only need to consider the case where M and $M+1$ are not in the same row. Let us assume M is at the end of the i-th row and $M+1$ is at the beginning of the $(i+1)$-th row in Z. If the distance between M and $M+1$ in Z is not equal to L, i.e.,

$${\beta }_{i-1}+{\alpha }_{r-i}+g-d+r\ne L,$$

then the group action ${\pi }_{M,L}$ can exchange M with $M+1$ in T while fixing Z. Therefore, in the following proof, we always assume

$${\beta }_{i-1}+{\alpha }_{r-i}+g-d+r=L.$$

Now we consider the position of $M-1$ and let $M-1=T_{e,f}$. Then the possible positions of $M-1$ are as follows:

(1)

$c<e<a,b<f<d$;

(2)

$e<c, f>d$;

(3)

$f\le b$;

(4)

$f=d$;

(5)

$e=c$.

This is illustrated in Figure 8.

Figure 8. Possible positions of $M-1$.

Case 1: If $c<e<a,b<f<d$, we can use the group action ${\pi }_{M-1,(e-c)+(d-f)}$ to exchange M with $M-1$. Since $M-1$ is in the same row as M in Z, ${\pi }_{M-1,(e-c)+(d-f)}$ fixes Z. Then, we apply the group action ${\pi }_{M,(a-e)+(f-b)}$ to exchange M with $M+1$ in T. Given that

$$(a-e)+(f-b)<(a-c)+(d-b)=L,$$

the action ${\pi }_{M,(a-e)+(f-b)}$ fixes Z. Thus, the composition of these two group actions exchange M with $M+1$ in T while keeping Z unchanged.

Case 2: If $e<c, f>d$, the proof follows a similar approach to that in Case 1. First we use the group action ${\pi }_{M-1,(c-e)+(f-d)}$ to exchange M with $M-1$ while maintaining Z. Subsequently, we apply the group action ${\pi }_{M,(a-e)+(f-b)}$ to exchange M with $M+1$ in T. Since

$$(a-e)+(f-b)>(a-c)+(d-b)=L,$$

the action ${\pi }_{M,(a-e)+(f-b)}$ fixes Z. Therefore, the composition of these two group actions achieves the goal.

Case 3: If $f=b$, meaning $M-1$ and $M+1$ are in the same column, then $M-1$ must be directly above $M+1$. If not, M would also have to be positioned between $M-1$ and $M+1$, contradicting our assumption. In this case, M must be positioned in one of the upper-left corners of the columns to the right of the column containing $M+1$. This is because the smallest integer in these columns is M. Additionally, according to Assumption (1), we have

$$\begin{array}{cc}\hfill L& =(a-c)+(d-b)\hfill \\ \hfill & \le {\alpha }_0-{\alpha }_r+r\hfill \\ \hfill & <{\beta }_{i-1}+{\alpha }_{r-i}+g-d+r\hfill \\ \hfill & =L,\hfill \end{array}$$

which is a contradiction. Therefore, this case cannot occur.

If $f<b$, indicating that $M-1$ is in one of the columns to the left of $M+1$, then M must be in the first box of the column it belongs to. As in the previous case, M must be in one of the upper-left corners of the columns to the right of the one containing $M+1$. Thus, by using a similar argument, we arrive at a contradiction in this case as well.

Case 4: If $f=d$, i.e., $M-1$ is above M, then it must be adjacent to M; otherwise, there would be no integer between $M-1$ and M to fill in. In this case, we can first exchange M with $M+1$ in T using ${\pi }_{M,L}$. Note that this exchange also affects M and $M+1$ in Z. Next, we exchange $M-1$ and M in ${\pi }_{M,L}\left(T\right)$ using ${\pi }_{M-1,L+1}$. Since $M-1$ and M in ${\pi }_{M,L}\left(Z\right)$ are separated by a distance of $L-1<L+1$, they remain unchanged in ${\pi }_{M,L}\left(Z\right)$. Finally, we exchange M with $M+1$ in ${\pi }_{M-1,L+1}\left({\pi }_{M,L}\left(Z\right)\right)$ using ${\pi }_{M,L}$, resulting in

$${\pi }_{M,L}\left({\pi }_{M-1,L+1}\left({\pi }_{M,L}\left(Z\right)\right)\right)=Z,$$

while $M+1$ and M in ${\pi }_{M-1,L+1}\left({\pi }_{M,L}\left(T\right)\right)$ are in the same column and thus remain unchanged. Therefore, ${\pi }_{M,L}\circ {\pi }_{M-1,L+1}\circ {\pi }_{M,L}$ fixes Z and reduces $M+1$ to $M-1$ in T, hence

$${\pi }_{M,L}\circ {\pi }_{M-1,L+1}\circ {\pi }_{M,L}\left(T\right)<T.$$

This process does not require the conditions.

Case 5: If $M-1$ is in the same row as M, then $M-1$ must be adjacent to M. Note that we have already addressed Case 3, so we assume $f\ne b$. In this case, we consider the position of $M-2$. If $M-2$ is also in the same row and adjacent to $M-1$, we continue this process with $M-3$, and so on, until we find $M-k$ such that $M-k,M-(k-1),\cdots ,$ $M-1,$ M are consecutive in the same row, but $M-(k+1)$ is not. Let $M-k=T_{c,g}$. Since $a>c$, it must be that $g\ge b$.

Subcase 5.1: If $g=b$, meaning that $M-k$ is in the same column as $M+1$, then $M-k$ must be adjacent to $M+1$, as the integers $M-(k-1),\cdots ,M$ are not in this column. Therefore, $a=c+1$, which means $M+1$ and M are in adjacent rows. Additionally, since $M+1$ is the first integer in the Young tableau T that differs from S, there are no integers lying above $M-k,\cdots ,M$. Hence, the condition (1) implies that M must be in the first row. According to Condition (3)

$$\begin{array}{c}\hfill {\alpha }_r+{\beta }_0-1<L,\end{array}$$

in the second row, there must be exactly ${\alpha }_{r-1}-{\alpha }_r$ boxes to the left of $M+1$ boxes. Condition (2) implies that

$$\begin{array}{c}\hfill M<{\alpha }_r+{\alpha }_{r-1}+2\ast (g-d+r)+{\beta }_0+{\beta }_1,\end{array}$$

hence M can only be at the end of the first row in Z. This means that the first row of T is $1,\cdots ,M$, namely, the first row of T is exactly the same as the first row of Z.

We proceed by using induction on the number of rows $r+1$ to prove that, when the first row of T is the same as that of Z, T can be moved to a lexicographically smaller tableau $T^{\prime }$ through an EH group action. If $r=1$, then the Young diagram has only two rows. The first row of T is identical to that of Z, so there is only one way to fill the second row, which implies T is the same as Z. However, this contradicts the assumption that $T\ne Z$. Therefore, this case cannot occur when $r=1$.

If $r=s>1$, by the induction hypothesis, for Young diagrams with s rows satisfying the conditions, the action of the EH group on all of its Young tableaux is doubly transitive. Let $\tilde{\sigma }$ be the sub-Young diagram of $\sigma (g,r,d,\alpha ,\beta )$ obtained by removing the first row. Similarly, let $\tilde{T}$ and $\tilde{Z}$ be the Young tableaux obtained by removing the first row from T and Z, respectively. Then the $\tilde{\sigma }$ has s rows and $\tilde{T}$, $\tilde{Z}$ are Young tableaux of $\tilde{\sigma }$ satisfying the conditions.

We can identify actions ${\pi }_{t,a}$ on the set of Young tableaux of $\tilde{\sigma }$ with actions ${\pi }_{t+M,a}$ on the tableaux of $\sigma$ that have the same first row as Z, since actions ${\pi }_{t+M,a}$ do not change the integers $1,\cdots ,M$ in the first row. If $\tilde{T}$ is not the lexicographically smallest Young tableau of diagram $\tilde{\sigma }$, then by the induction hypothesis, there exists an EH group action ${\pi }_{t,a}$ such that ${\pi }_{t,a}\left(\tilde{T}\right)<\tilde{T}$ in the lexicographic order and consequently, ${\pi }_{t+M,a}\left(T\right)<T$. If $\tilde{T}$ is the lexicographically smallest Young tableau of $\tilde{\sigma }$, then since $s>1$, $M+2$ must be in the same column as $M+1$ and directly below $M+1$. Now, we first exchange M with $M+1$ in T using ${\pi }_{M,L}$, which simultaneously changes Z. Next, we apply ${\pi }_{M+1,L+1}$ to exchange $M+1$ and $M+2$ in ${\pi }_{M,L}\left(T\right)$. Since the distance between $M+2$ and $M+1$ in ${\pi }_{M,L}\left(Z\right)$ is $M-1<M+1$, no changes occur in ${\pi }_{M,L}\left(Z\right)$. Finally, we exchange M with $M+1$ in ${\pi }_{M+1,L+1}\left({\pi }_{M,L}\left(Z\right)\right)$ using ${\pi }_{M,L}$, resulting in

$${\pi }_{M,L}\left({\pi }_{M+1,L+1}\left({\pi }_{M,L}\left(Z\right)\right)\right)=Z.$$

Because $M+1$ and M in ${\pi }_{M+1,L+1}\left({\pi }_{M,L}\left(T\right)\right)$ are in the same column, they remain unchanged. Thus, ${\pi }_{M,L}\circ {\pi }_{M+1,L+1}\circ {\pi }_{M,L}$ fixes Z and reduces $M+1$ to M in T, hence

$${\pi }_{M,L}\circ {\pi }_{M+1,L+1}\circ {\pi }_{M,L}\left(T\right)<T.$$

Therefore, the claim is proved according to the induction hypothesis. Also note that this induction depends on proving other cases of the lemma, but other cases do not need induction, thus avoiding circular reasoning.

Subcase 5.2: If $g>b$, that is $M-k$ and $M+1$ are in different columns, then we consider the position of $M-(k+1)$.

Subcase 5.2.1: If $M-(k+1)=0$, then $M-k=1,\cdots ,M=k+1$, hence there is no integer above M. If M is not in the first row, then by Assumption (1),

$$\begin{array}{cc}\hfill L=(a-c)+(d-b)& \le {\alpha }_0-{\alpha }_r+r\hfill \\ \hfill & <{\alpha }_{r-i+1}+g-d+r+{\beta }_{i-1}\hfill \\ \hfill & =L,\hfill \end{array}$$

which is a contradiction. Therefore, $1,\cdots ,k+1=M$ is the first row of T. This means that the first row of T is exactly the same as the first row of Z. We have already addressed such a case in Case 5.1, so we are done.

Subcase 5.2.2: If $M-(k+1)\ge 1$, Let $M-(k+1)=T_{u,v}$. Similarly, the possible positions for $M-(k+1)$ are as follows:

(1)

$c<u<a,b<v<g;$

(2)

$u<c,v>d;$

(3)

$v=d;$

(4)

$v=b$.

We can sequentially exchange adjacent pairs of $M-(k+1),M-k,\cdots ,M-1$ to move $M-1$ to the original position of $M-(k+1)$ in T. This reduces to Cases 1, 2, or 3, which have been proved earlier. Thus, through a composition of several group actions, we can exchange M with $M+1$ in the tableau T to obtain a Young tableau with a smaller lexicographic order. However, we need to check that Z remains unchanged after these actions.

If $i=1$, i.e., M is at the end of the first row in Z, then since $M-(k+1)>0$, the numbers $M-(k+1)$, $M-k,\cdots ,M-1$ are also in the first row in Z. Hence, the actions leave Z unchanged. If $1<i<r$, the length of the i-th row is at least as long as the row containing M in T. Consequently, $M-(k+1)$, $M-k,\cdots ,M$ all lie in the same row of Z, keeping Z unchanged. Since M and $M+1$ are in different rows, it follows that $i\ne r$. Therefore, we have completed the proof of Case 5.

Combining all the cases above, we are done. □

Example 3. 

(1)  

If $r=1$, then the Young diagram $\sigma (g,r,d,\alpha ,\beta )$ consists of 2 rows. In this case, all the conditions in Lemma 3 become vacuous. Therefore, for any ramification sequences $\alpha ,\beta$, the EH group is doubly transitive.

(2)  

If $\alpha =\beta =(0,0,\cdots ,0)$, which corresponds to the unramified case, then the conditions of Lemma 3 simplify to $r+1<g-d+r$, so this lemma serves as a generalization of Edidin’s theorem from [5].

(3)  

This lemma also leads to several interesting cases. For instance, if $\alpha =\beta =(1,\cdots ,1,0)$, which are known as cusps, then the conditions of Lemma 3 simplify to $r<g-d+r$, so the EH group acts doubly transitively in this case (Figure 9).

Figure 9. Example (3).

(4)  

If $\alpha =({\alpha }_0,{\alpha }_1,{\alpha }_2=0)$, $\beta =(0,0,0)$, then the conditions of Lemma 3 simplify to the following:

(1)  

$max\{{\alpha }_0-{\alpha }_1,1\}<{\alpha }_1+g-d$;

(2)  

${\alpha }_0+{\alpha }_1<g-d+2$.

For instance, when $(g,r,d)=(16,2,14)$ and $\alpha =(3,1,0)$, the EH group acts doubly transitively. (Figure 10)

Figure 10. Example (4).

Remark 1. 

Section 3 of [5] addressed the unramified case, but the proof has some gaps: case (4a) in [5] does not consider when $T\in Y(m,n)$ is the smallest element, and case (3) does not consider when $M-c$ is above M. Here, we provide a complete proof and simplify the arguments for case (5) in [5].

Using the doubly transitivity of the EH group action, we can establish that the EH group is actually a very large subgroup. Under certain conditions, it is either the alternating group or the full symmetric group. To begin, let us revisit a classical theorem in group theory.

Theorem 9 

(Bochert). Let G be a doubly transitive subgroup of the symmetric group $S_n$. If there exists an element $g\ne 1$ in G such that the number of elements moved by g is fewer than ${\displaystyle \frac{n}{3}}-2{\displaystyle \frac{\sqrt{n}}{3}}$, then G is either the symmetric group $S_n$ or the alternating group $A_n$.

This theorem tells us that we need to find a nontrivial element that moves only a sufficiently small number of elements.

Lemma 4. 

If $r\ge 2$ and ${\alpha }_r+{\beta }_r+g-d+r>r+1$, then there is an element of the EH group that moves at most one-quarter of the Young tableaux.

Proof.  

Let s be the length of the first column of $\sigma$ and $t={\alpha }_r+{\beta }_0+g-d+r$ be the length of the first row. Additionally, let $L={\alpha }_0+{\beta }_0+g-d+2r-1$ be the distance from the lower-left corner to the upper-right corner of the Young diagram $\sigma =\sigma (g,r,d,\alpha ,\beta )$.

If the ramification sequence $\alpha$ satisfies

$${\alpha }_0={\alpha }_1=\cdots ={\alpha }_r,$$

we consider the EH group element ${\pi }_{s+t-2,L}$. Let A be the set of all Young tableaux moved by ${\pi }_{s+t-2,L}$, i.e., those not fixed by ${\pi }_{s+t-2,L}$. Let T be a Young tableau in A. Since L is the farthest distance between two boxes in $\sigma$ and

$${\alpha }_r+{\beta }_r+g-d+r>r+1,$$

L can only be the distance between the lower-left corner $T_{s-1,0}$ and the upper-right corner $T_{0,t-1}$ of $\sigma$. Thus, the integers in the lower-left box or the upper-right box must be $s+t-2,$$s+t-1$. Since the total number of boxes in the first column and row is $s+t-1$ and the integers filled in the boxes except the lower-left and upper-right boxes must be less than $s+t-2$, the numbers filled in the first row and column are exactly $1,2,\cdots ,s+t-1$. Now, consider $s+t$ and $s+t+1$. Since $s+t$ is the smallest integer after removing the first row and first column, we have $T_{1,1}=s+t$. Similarly, $s+t+1$ is the second smallest integer after removing the first row and first column, so either $T_{1,2}=s+t+1$ or $T_{2,1}=s+t+1$.

We construct three Young tableaux $T_1,T_2,T_3$ from T. The tableau $T_1$ is obtained by exchanging $s+t-1$ with $s+t$, $T_2$ by exchanging $s+t-2$ with $s+t$, and $T_3$ by first exchanging $s+t-1$ with $s+t$, and then $s+t-2$ with $s+t+1$. Due to the special positions of $s+t$ and $s+t+1$, the resulting tableaux are still Young tableaux. Since each of $T_1,T_2,T_3$ has at least one of $s+t-1$ and $s+t-2$ not in the lower-left corner or the upper-right corner, they will all be fixed by ${\pi }_{s+t-2,L}$.

For any $S\in A$ with $S\ne T$, we can similarly construct the corresponding three tableaux $S_1,S_2,S_3$. Next, we show that $S_1,S_2,S_3$ and $T_1,T_2,T_3$ are distinct Young tableaux. By construction, $S_1$ is different from $S_2$ and $S_3$. Moreover, since the lower-left corner and the upper-right corner of $S_1$ are $s+t,s+t-2$, and those of $T_2,T_3$ are $s+t,s+t-1$ and $s+t,s+t+2$, respectively, $S_1$ is different from $T_2,T_3$. The tableaux $S_1$ and $T_1$ are obtained by the actions ${\pi }_{s+t-1,a}$ and ${\pi }_{s+t-1,a^{\prime }}$ on T and S, respectively. If $a\ne a^{\prime }$, then the distances between $s+t-1$ and $s+t$ in $T_1$ and $S_1$ are different, so $T_1\ne S_1$. If $a=a^{\prime }$, then ${\pi }_{s+t-1,a}={\pi }_{s+t-1,a^{\prime }}$. Since $T\ne S$, we have

$$S_1={\pi }_{s+t-1,a^{\prime }}\left(S\right)\ne {\pi }_{s+t-1,a}\left(T\right)=T_1.$$

Therefore, $S_1$ is different from $S_2,S_3,T_1,T_2,T_3$. Similarly, by symmetry, $S_2$ is distinct from $S_1,S_3,T_1,T_2,T_3$ and $S_3$ is distinct from $S_1,S_2,T_1,T_2$ as well. $S_3$ and $T_3$ are obtained from $S_1$ and $T_1$, respectively, by exchanging $s+t-2$ with $s+t+1$. If the positions of $s+t-2,s+t+1$ $S_3$ and $T_3$ are different, then $S_3\ne T_3$. If the positions of $s+t-2,s+t+1$ in $S_3$ and $T_3$ are the same, then the positions of $s+t-2$ and $s+t+1$ would be completely identical, contradicting the distinctness of $S_1$ and $T_1$. Hence, $S_3$ and $T_3$ must be distinct. Therefore, $S_1,S_2,S_3,T_1,T_2,T_3$ are mutually distinct Young tableaux.

By constructing $T_1$ for each T in A, we obtain a new set $A_1$ of Young tableaux. Similarly, sets $A_2,A_3$ can be obtained. As argued earlier, the sets $A,A_1,A_2,A_3$ have equal cardinality and are pairwise disjoint. Therefore, the number of Young tableaux moved by ${\pi }_{s+t-2,L}$ is at most one-quarter of the total number of Young tableaux.

If the ramification sequence $\alpha$ does not satisfy

$${\alpha }_0={\alpha }_1=\cdots ={\alpha }_r,$$

we then consider the EH group element ${\pi }_{s+t-1,L}$. The proof follows a similar approach to the previous case. Let A be the set of all Young tableaux moved by ${\pi }_{s+t-1,L}$. For any $T\in A$, the lower-left corner and the upper-right corner of T are $s+t-1$ and $s+t$. We denote the Young diagram obtained from removing the first row and first column of $\sigma$ as $\tilde{\sigma }$. If $\tilde{\sigma }$ has only one upper-left corner, it must be in the first row of $\tilde{\sigma }$. Given that the smallest integer in $\tilde{\sigma }$ is $s+t+1$, the upper-left corner of $\tilde{\sigma }$ must be $s+t+1$, and $s+t+2$ must be adjacent to $s+t+1$ either to the right or below. Since the upper-left corner is in the first row of $\tilde{\sigma }$, $s+t+2$ cannot be in the same row as $s+t-1$ or $s+t$.

For T, we construct $T_1,T_2,T_3$ as follows: $T_1$ is obtained from T by exchanging $s+t-1$ with $s+t+1$, $T_2$ by exchanging $s+t$ with $s+t+1$, and $T_3$ by first exchanging $s+t$ with $s+t+1$ and then $s+t-1$ with $s+t+2$. The resulting tableaux are still Young tableaux. By arguments analogous to those used previously, $S_1,S_2,S_3$ and $T_1,T_2,T_3$ are pairwise distinct Young tableaux. Therefore, similarly, we can conclude that the number of Young tableaux moved by ${\pi }_{s+t-1,L}$ is at most one-quarter of all Young tableaux.

If $\tilde{\sigma }$ has more than one upper-left corner, we choose any two of them, denoted as $T_{i,j}$ and $T_{p,q}$. For any $T\in A$, we construct corresponding tableaux $T_1,T_2,T_3$ as follows: $T_1$ is obtained from exchanging $T_{s-1,0}$ with $T_{i,j}$, $T_2$ by exchanging $T_{s-1,0}$ with $T_{p,q}$, and $T_3$ by exchanging $T_{0,t-1}$ with $T_{i,j}$. Since both $T_{i,j}$ and $T_{p,q}$ are upper-left corners, the resulting tableaux remain Young tableaux after these exchanges. Moreover, the tableaux $T_1,T_2,T_3$ are fixed by the EH group element ${\pi }_{s+t-1,L}$. Finally, using similar reasoning, we conclude that the number of Young tableaux moved by ${\pi }_{s+t-1,L}$ is at most one-quarter of all Young tableaux. □

Theorem 10. 

Given two ramification sequences $\alpha ,\beta$. Suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0$$

and $r\ge 2$, ${\alpha }_r+{\beta }_r+g-d+r>r+1$. Let $N=N(g,r,d,\alpha ,\beta )$ denote the number of Young tableaux of the Young diagram $\sigma =\sigma (g,r,d,\alpha ,\beta )$. If $\alpha ,\beta$ satisfy the conditions of Lemma 3, then the EH group is either the alternating group $A_N$ or the symmetric group $S_N$.

Proof.  

If the ramification sequences $\alpha ,\beta$ satisfy the conditions of Lemma 3, then the action of the EH group on the set of all Young tableaux $YT(g,r,d,\alpha ,\beta )$ is doubly transitive. Next, we demonstrate that the EH group also satisfies the condition of Bochert’s theorem.

The Young diagram $\sigma$ contains a maximal rectangle-shaped sub-Young diagram $\tau$ of size $(r+1)\times ({\alpha }_r+{\beta }_r+g-d+r)$. Its left and right sides are also sub-skew Young diagrams, which we denote by ${\sigma }_1$ and ${\sigma }_2$, respectively. Since $r\ge 2$, $\sigma$ has at least three rows. Furthermore,

$${\alpha }_r+{\beta }_r+g-d+r>r+1,$$

ensuring that the size of the rectangle-shaped Young diagram $\tau$ is at least $3\times 4$. Let m be the number of boxes in ${\sigma }_1$ and n be the number of boxes in ${\sigma }_2$. We can fill $1,2,\cdots ,m$ lexicographically into ${\sigma }_1$ and $g-n+1,\cdots ,g$ into ${\sigma }_2$. By filling $m+1,\cdots ,g-n$ into the middle rectangle $\tau$ such that $\tau$ forms a Young tableau, this filling yields a Young tableau of the entire Young diagram $\sigma$. Conversely, if $m+1,\cdots ,g-n$ are filled in such a way that $\sigma$ forms a Young tableau, then $\tau$ becomes a Young tableau as well. Hence, the number of Young tableaux of the (skew) Young diagram $\sigma$ is at least the number of Young tableaux of the shape $(r+1)\times ({\alpha }_r+{\beta }_r+g-d+r)$. On the other hand, by considering placing a $3\times 4$ subrectangle at the upper-left of $\tau$, we have

$$N(g,r,d,\alpha ,\beta )\ge N(r+1,{\alpha }_r+{\beta }_r+g-d+r)\ge N(3,4).$$

For Young diagrams, the hook-length formula calculates the number of all Young tableaux. Specifically, for a rectangle-shaped diagram of size $s\times t$, according to the hook-length formula, the number of all Young tableaux is

$$N(s,t)=\left(st\right)!\prod _{i=0}^{s-1}{\displaystyle \frac{i!}{(t+i)!}}.$$

Thus, we have

$$N=N(g,r,d,\alpha ,\beta )\ge N(3,4)=\left(12\right)!\prod _{i=0}^2{\displaystyle \frac{i!}{(4+i)!}}=231.$$

This implies

$$({\displaystyle \frac{N}{3}}-2{\displaystyle \frac{\sqrt{N}}{3}}){\displaystyle \frac{1}{N}}={\displaystyle \frac{1}{3}}-{\displaystyle \frac{2}{3\sqrt{N}}}>{\displaystyle \frac{1}{4}},$$

Therefore, to apply Bochert’s theorem, we only need to identify a nontrivial element in the EH group that moves at most one-quarter of the Young tableaux. Lemma 4 constructs such an element, establishing that the EH group is at least the alternating group. Since the EH group is a subgroup of the monodromy group, it follows that the monodromy group is also at least the alternating group; hence, we are done. □

5. Monodromy Groups of Families of Linear Series with Imposed Ramifications

In this section, we utilize the lemmas proved earlier to establish the main results.

Theorem 11. 

Given two ramification sequences $\alpha ,\beta$. Suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0$$

and $r\ge 2$, ${\alpha }_r+{\beta }_r+g-d+r>r+1$. Let $N=N(g,r,d,\alpha ,\beta )$ denote the number of Young tableaux of the Young diagram $\sigma =\sigma (g,r,d,\alpha ,\beta )$. If α, β satisfy the conditions of Lemma 3, then the monodromy group of $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))\to B$ in Theorem 8 is either the alternating group $A_N$ or the symmetric group $S_N$.

Proof. 

By the proof of Theorem 8, the monodromy group of $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))\to B$ is the same as the monodromy group of the fiber of the stable limit $C_{\infty }$, and the EH group induced by the one-parameter families $C_{i,p}$ is a subgroup of the monodromy group. Since $\alpha ,\beta$ satisfy the conditions of Theorem 10, the EH group is either the alternating group or the symmetric group. Consequently, the monodromy group is either the alternating group $A_N$ or the symmetric group $S_N$. □

For $r=2$, we can determine the EH group in some cases.

Proposition 4. 

Assume $\rho (g,r,d,\alpha ,\beta )=0$. If ${\alpha }_0={\alpha }_1={\alpha }_2$, ${\beta }_0={\beta }_1={\beta }_2$, and ${\alpha }_0+{\beta }_0+g-d+r=2^i$ for some integer $i>1$, then the monodromy group of $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))\to B$ in Theorem 8 is the symmetric group.

Proof. 

The given $\alpha$ and $\beta$ satisfy the conditions of Lemma 3; hence, by Theorem 11, the monodromy group is at least the alternating group. To show that it is indeed the full symmetric group, it suffices to find an odd permutation in it. Let $L={\alpha }_0+{\beta }_0+g-d+r$. We prove that the EH group action $\pi ={\pi }_{2+L-1,2+L}$ exchanging $2+L-1$ with $2+L$ is odd when $L=2^i$ for some integer i. We consider the number n of pairs of Young tableaux exchanged by this action. Given that the set of integers in the first row and the first column is determined, there are $L-1$ choices for the first row and column. After removing the first row and the first column, the resulting diagram is a $2\times (L-1)$ rectangle. The number of Young tableaux of this diagram is the Catalan number $C_{L-1}$. A result about the oddity of Catalan numbers (see [14]) states that $C_{L-1}$ is odd if and only if $L-1=2^i-1$ for some integer i. Therefore, when $L=2^i$ for some i, the number $n=(L-1)\ast C_{L-1}$ is odd. This implies that $\pi$ is an odd permutation, so that the monodromy group is the full symmetric group. □

When $r=1$, we can prove a stronger result: the monodromy group is indeed the full symmetric group for any $\alpha$ and $\beta$.

Lemma 5. 

If $r=1$, then the EH group is the full symmetric group.

Proof. 

Let $\sigma$ be the Young diagram associated to the ramification sequences $\alpha ,\beta$. We consider the EH group element ${\pi }_{s+t-2,L}$ or ${\pi }_{s+t-1,L}$ constructed in the proof of Lemma 4, where s is the length of the first column of $\sigma$, t is the length of the first row of $\sigma$, and L denotes the distance from the lower-left corner to the upper-right corner of $\sigma$.

If the first row and the first column share common boxes, we take $\pi ={\pi }_{s+t-2,L}$. Let T be a Young tableau of $\sigma$ and be moved by $\pi$; then, the integer in the lower-left corner of T is either $s+t-2$ or $s+t-1$ and $T_{0,0}$ must be 1. Hence, integers in the boxes except for the last one in the first row and the first column are uniquely determined. Since $r=1$, $\sigma$ has only two rows. Therefore, integers greater than $s+t-1$ can only be arranged sequentially in the remaining boxes of the second row. Thus, the integers in the boxes in T, except for the lower-left corner and the upper-right corner, are uniquely determined. Therefore, the action of $\pi$ on all Young tableaux is just a transposition, moving only T and $\pi \left(T\right)$.

If the first row and the first column do not share common boxes, we take $\pi ={\pi }_{s+t-1,L}$. Let T be a Young tableau of $\sigma$ moved by $\pi$. Similarly, except for the lower-left corner and the upper-right corner, the integers in the boxes of T are uniquely determined. Hence, the action of $\pi$ on all Young tableaux is also a transposition.

Given that $\alpha ,\beta$ satisfy the conditions of Lemma 3, according to Lemmas 3, we know that the EH group is doubly transitive. Let $\pi =(T,T^{\prime })$ be a transposition where $T,T^{\prime }\in YT(g,r,d,\alpha ,\beta )$. For any pair of distinct Young tableaux $S,S^{\prime }$, the doubly transitivity of the EH group ensures there exists an EH group element g such that

$$g\left(T\right)=S,g\left(T^{\prime }\right)=S^{\prime }.$$

Consider the group element $g\circ \pi \circ g^{-1}$. Then,

$$g\circ \pi \circ g^{-1}\left(S\right)=g\circ \pi \left(T\right)=S^{\prime },g\circ \pi \circ g^{-1}\left(S^{\prime }\right)=g\circ \pi \left(T^{\prime }\right)=S.$$

For any $U\ne S,S^{\prime }$, we have

$$g\circ \pi \circ g^{-1}\left(U\right)=g\circ \pi \left(g^{-1}\left(U\right)\right)=g\left(g^{-1}\left(U\right)\right)=U,$$

showing that $g\circ \pi \circ g^{-1}$ is the transposition $(S,S^{\prime })$. Therefore, the EH group includes all transpositions. It follows that the EH group is the full symmetric group. □

Thus, we obtain

Proposition 5. 

Given two ramification sequences $\alpha ,\beta$. Suppose

$$\rho (g,r,d,\alpha ,\beta )=g-(r+1)(g-d+r)-\left|\alpha \right|-\left|\beta \right|=0$$

and let $N=N(g,r,d,\alpha ,\beta )$. If $r=1$, then the monodromy group of the family of linear series $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))\to B$ in Theorem 8 is the symmetric group $S_N$.

Proof. 

Similar to the proof of Theorem 11, the monodromy group of the family of linear series $G_d^r(\mathcal{C}/B,(p,\alpha ),(q,\beta ))\to B$ contains the EH group. Given that the EH group is the full symmetric group, it follows that the monodromy group is $S_N$. □