Numerical Solution of a Sixth-Order Anharmonic Oscillator for Triaxial Deformed Nuclei
Abstract
1. Introduction
2. Hamiltonian Model
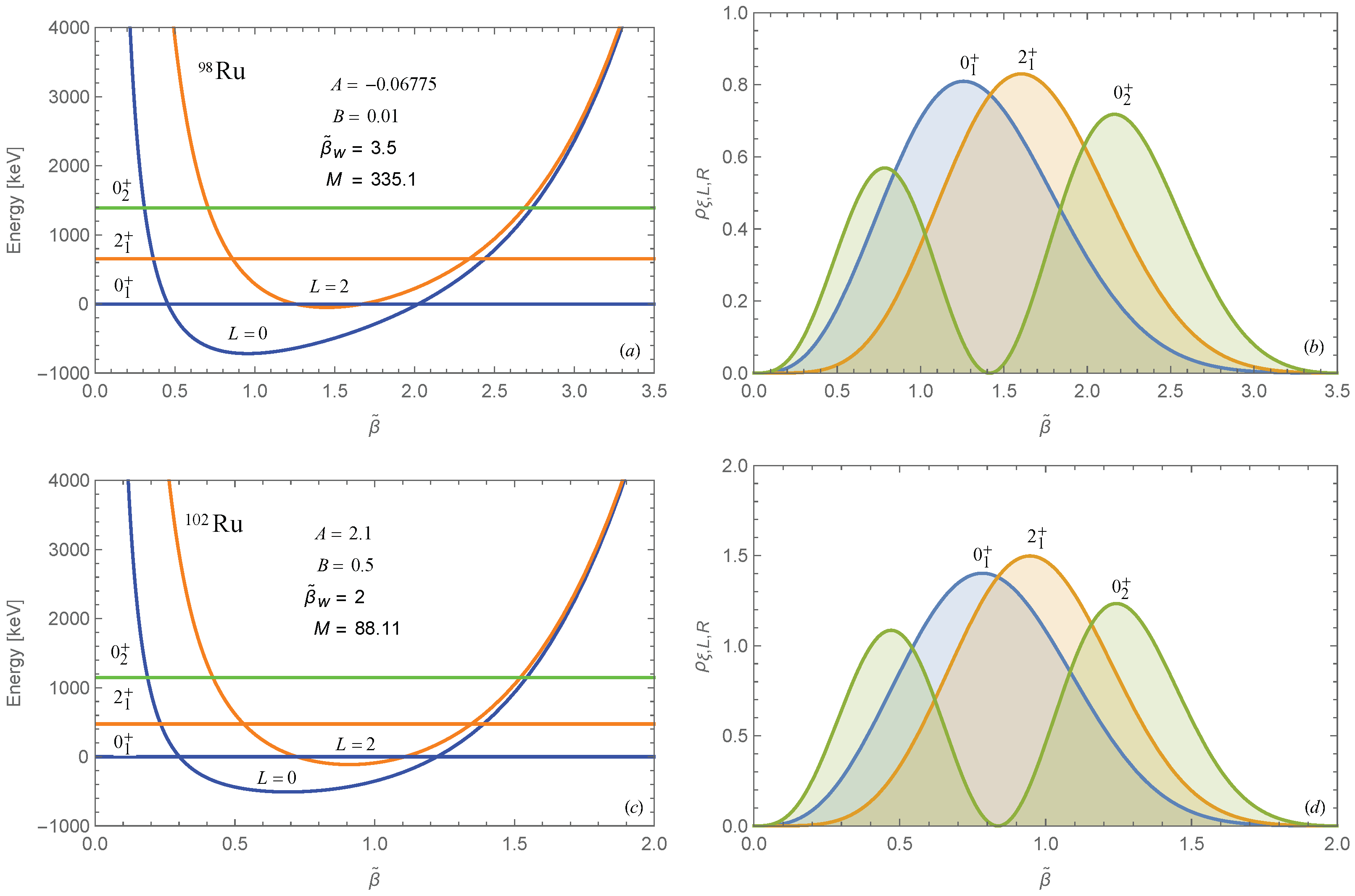
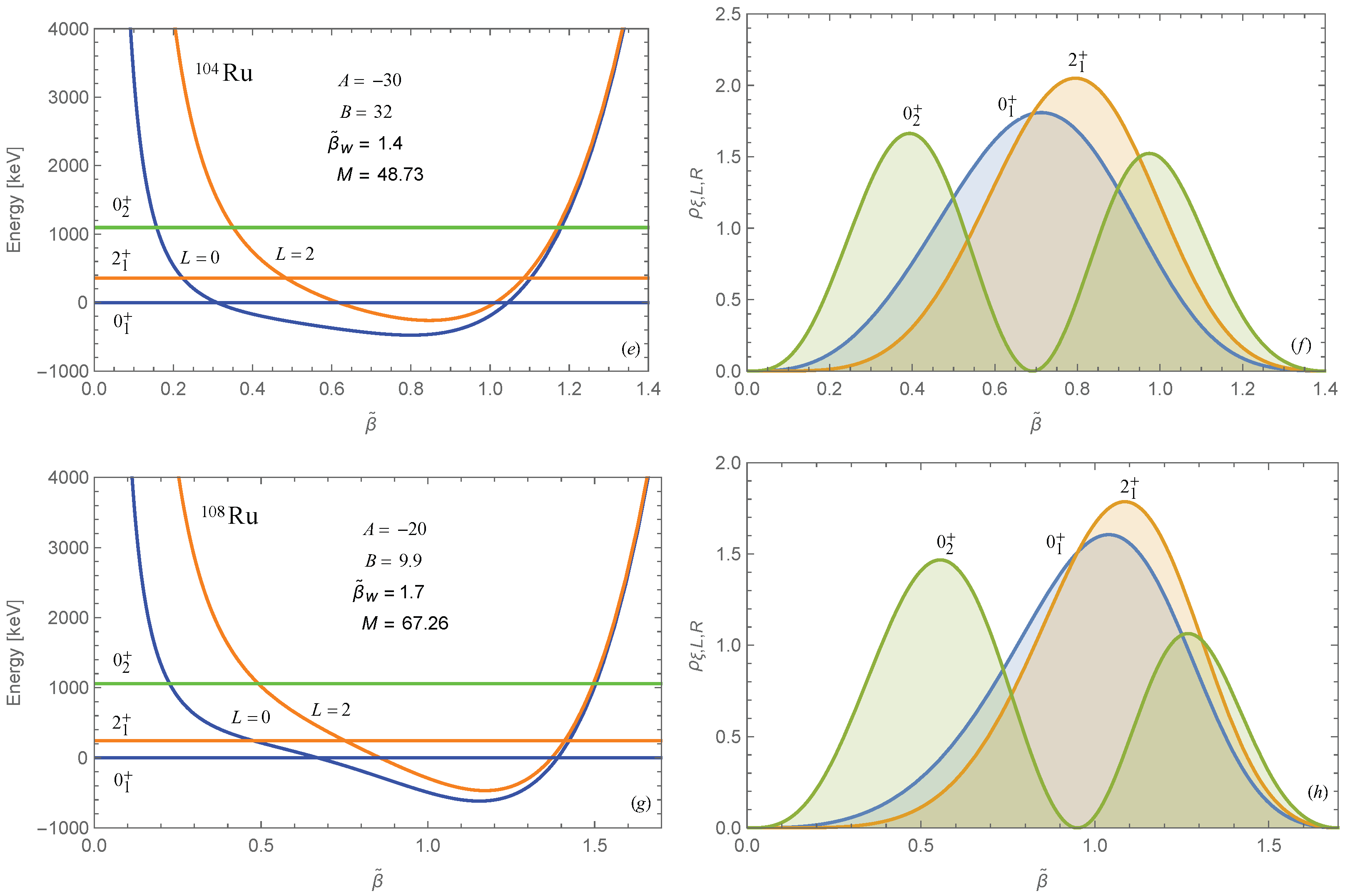
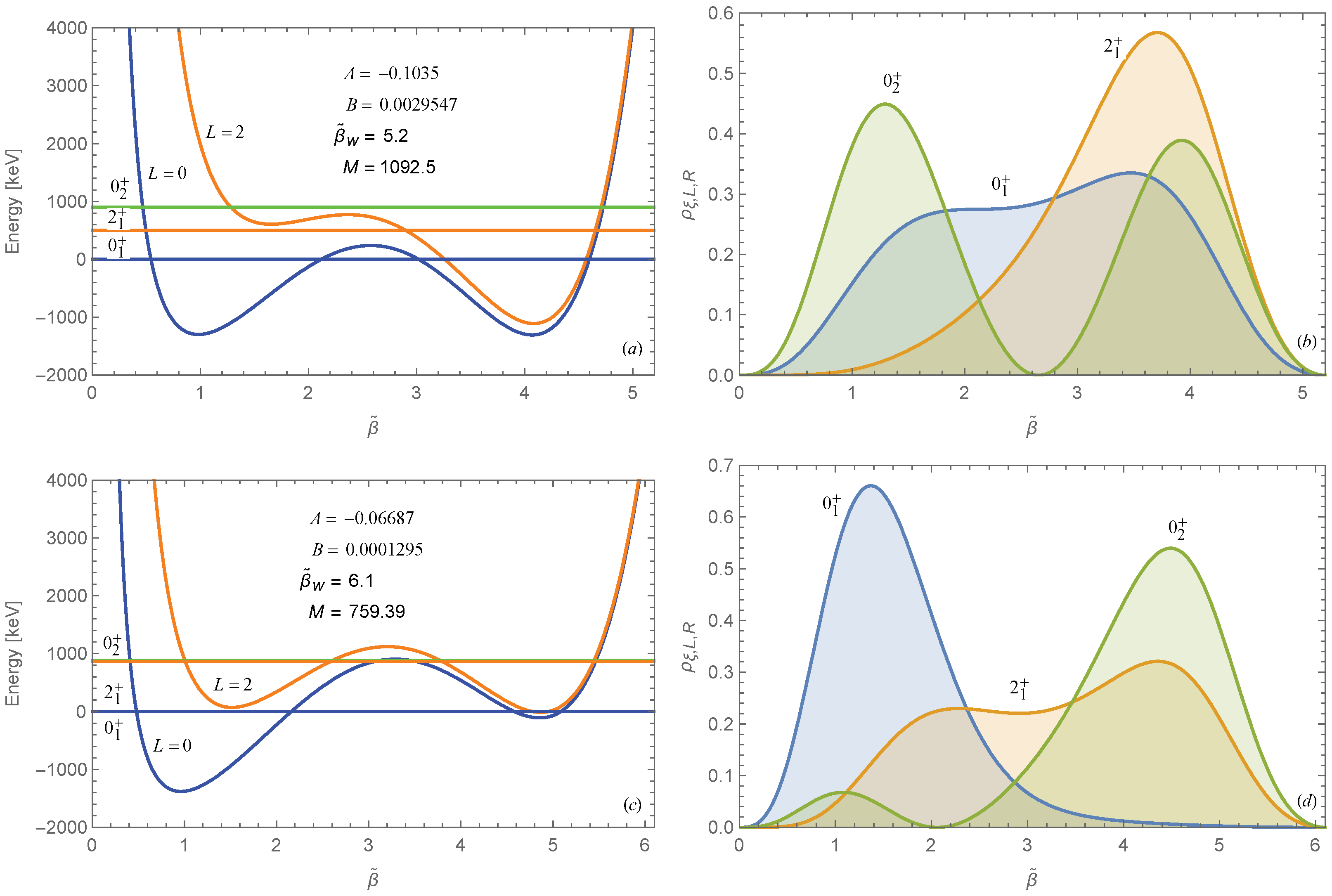
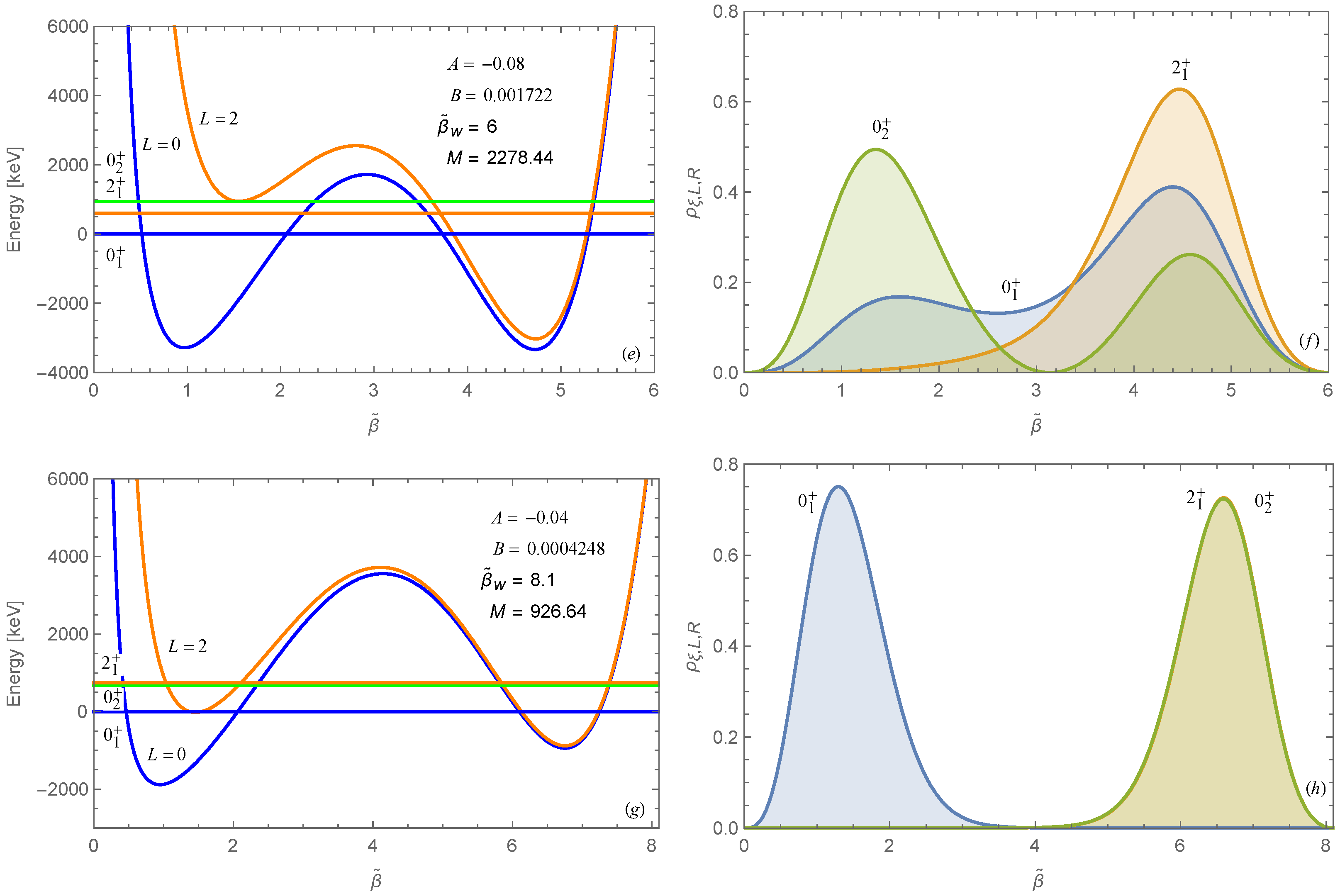
3. Numerical Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bohr, A.; Mottelson, B.R. Nuclear Structure, Vol. II: Nuclear Deformation; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1998. [Google Scholar]
- Iachello, F. Dynamic symmetries at the critical point. Phys. Rev. Lett. 2000, 85, 3580. [Google Scholar] [CrossRef]
- Iachello, F. Analytic description of critical point nuclei in a spherical-axially deformed shape phase transition. Phys. Rev. Lett. 2001, 87, 052502. [Google Scholar] [CrossRef]
- Bohr, A. The coupling of nuclear surface oscillations to the motion of individual nucleons. Dan. Mat. Fys. Medd. 1952, 26, 14. [Google Scholar]
- Wilets, L.; Jean, M. Surface oscillations in even-even nuclei. Phys. Rev. 1956, 102, 788. [Google Scholar] [CrossRef]
- Bès, D.R. The γ-independent part of the wave functions representing γ-unstable surface vibrations. Nucl. Phys. 1959, 10, 373–385. [Google Scholar] [CrossRef]
- Davydov, A.S. Collective excitations corresponding to quadrupole nuclear surface vibrations. Nucl. Phys. 1961, 24, 682–694. [Google Scholar] [CrossRef]
- Ginocchio, J.N.; Kirson, N.W. Relationship between the Bohr Collective Hamiltonian and the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1744. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; Scholten, O.; Iachello, F. Classical limit of the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1747. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Collective nuclear states as representations of a SU(6) group. Phys. Rev. Lett. 1975, 35, 1069. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states I. The vibrational limit. Ann. Phys. 1976, 99, 253–317. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states IV. The O(6) limiy. Ann. Phys. 1979, 123, 468–492. [Google Scholar] [CrossRef]
- Iachello, F. Phase transitions in angle variables. Phys. Rev. Lett. 2003, 91, 132502. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A. Z(5): Critical point symmetry for the prolate to oblate nuclear shape phase transition. Phys. Lett. B 2004, 588, 172–179. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. γ-rigid solution of the Bohr Hamiltonian for γ=30∘ compared to the E(5) critical point symmetry. Phys. Lett. B 2005, 621, 102–108. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. X(3): An exactly separable γ-rigid version of the X(5) critical point symmetry. Phys. Lett. B 2006, 632, 238–242. [Google Scholar] [CrossRef]
- Fortunato, L.; Vitturi, A. Analytically solvable potentials for γ-unstable nuclei. J. Phys. G Nucl. Part. Phys. 2003, 29, 1341. [Google Scholar] [CrossRef]
- Elliott, J.P.; Evans, J.A.; Park, P. A soluble γ-unstable Hamiltonian. Phys. Lett. B 1986, 169, 309–312. [Google Scholar] [CrossRef]
- Budaca, R. Quartic oscillator potential in the γ-rigid regime of the collective geometrical model. Eur. Phys. J. A 2014, 50, 87. [Google Scholar] [CrossRef]
- Lévai, G.; Arias, J.M. The sextic oscillator as a γ-independent potential. Phys. Rev. C 2004, 69, 014304. [Google Scholar] [CrossRef]
- Fortunato, L. Solutions of the Bohr Hamiltonian, a compendium. Eur. Phys. J. A 2005, 26, 1–30. [Google Scholar] [CrossRef]
- Buganu, P.; Fortunato, L. Recent approaches to quadrupole collectivity: Models, solutions and applications based on the Bohr hamiltonian. J. Phys. G Nucl. Part. Phys. 2016, 43, 093003. [Google Scholar] [CrossRef]
- Fortunato, L. Quantum phase transitions in algebraic and collective models of nuclear structure. Prog. Part. Nucl. Phys. 2021, 121, 103891. [Google Scholar] [CrossRef]
- Lévai, G.; Arias, J.M. Search for critical-point nuclei in terms of the sextic osciilator. Phys. Rev. C 2010, 81, 044304. [Google Scholar] [CrossRef]
- Raduta, A.A.; Buganu, P. Description of the isotope chain 180-196Pt within several solvable approaches. Phys. Rev. C 2013, 88, 064328. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. Sextic potential for γ-rigid prolate nuclei. J. Phys. G Nucl. Part. Phys. 2015, 42, 105106. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. Analytical solution for the Davydov-Chaban Hamiltonian with a sextic potential for γ=30∘. Phys. Rev. C 2015, 91, 014306. [Google Scholar] [CrossRef]
- Budaca, R.; Buganu, P.; Chabab, M.; Lahbas, L.; Oulne, M. Extended study on a quasi-exact solution of the Bohr Hamiltonian. Ann. Phys. 2016, 375, 65–90. [Google Scholar] [CrossRef]
- Lahbas, A.; Buganu, P.; Budaca, R. Quasi-exact description of the γ-unstable shape phase transition. Mod. Phys. Lett. A 2020, 35, 2050085. [Google Scholar] [CrossRef]
- Ushveridze, A.G. Quasi-Exactly Solvable Models in Quantum Mechanics; IOP: London, UK, 1994. [Google Scholar]
- Raduta, A.A.; Buganu, P. Toward a new description of triaxial nuclei. Phys. Rev. C 2011, 83, 034313. [Google Scholar] [CrossRef]
- Buganu, P.; Raduta, A.A.; Faessler, A. New features of the triaxial nuclei described with a coherent state model. J. Phys. G Nucl. Part. Phys. 2012, 39, 025103. [Google Scholar] [CrossRef]
- Raduta, A.A.; Buganu, P. Application of the sextic oscillator with a centrifugal barrier and the spheroidal equation for some X(5) candidate nuclei. J. Phys. G Nucl. Part. Phys. 2013, 40, 025108. [Google Scholar] [CrossRef]
- Buganu, P.; Raduta, A.A. Energy spectra, E2 transition probabilities and shape deformations for the even-even isotopes 180-196Pt. Rom. J. Phys. 2015, 60, 161–178. [Google Scholar]
- El Batoul, A.; Oulne, M.; Tagdamte, I. Collective states of even-even nuclei in γ-rigid quadrupole Hamiltonian with minimal length unde the sexit potential. J. Phys. G Nucl. Part. Phys. 2021, 48, 085106. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Waroquier, M.; Wood, J.L.; Meyer, R.A. Coexistence in odd-mass nuclei. Phys. Rep. 1983, 102, 291–393. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; van Duppen, P. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101–201. [Google Scholar]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1655. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K. A focus on shape coexistence in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 020402. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Mertzimekis, T.J.; Karakatsanis, K.E.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. The islands of shape coexistence within the Elliott and the proxy-SU(3) Models. Eur. Phys. J. A 2021, 57, 84. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Peroulis, S.K.; Karakatsanis, K.E.; Mertzimekis, T.J.; Minkov, N. Islands of shape coexistence: Theoretical predictions and experimental evidence. Symmetry 2023, 15, 29. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Mertzimekis, T.J.; Minkov, N. Signatures for shape coexistence and shape/phase transitions in even-even nuclei. J. Phys. G Nucl. Part. Phys. 2023, 50, 075105. [Google Scholar] [CrossRef]
- Wang, T. A collective description of the unusually low ratio B4/2 = B(E2;41+→21+)/B(E2;21+→01+). Europhys. Lett. 2020, 129, 52001. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.-W.; Karlsson, D.; Pan, F.; Draayer, J.P. A theoretical interpretation of the anomalous reduced E2 transition probabilities along the yrast line of neutron-deficient nuclei. Phys. Lett. B 2022, 834, 137442. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Coexistence, mixing and fluctuation of nuclear shapes. Europhys. Lett. 2018, 123, 42001. [Google Scholar] [CrossRef]
- Budaca, R.; Buganu, P.; Budaca, A.I. Bohr model description of the critical point for the first order shape phase transition. Phys. Lett. B 2018, 776, 26–31. [Google Scholar] [CrossRef]
- Taşeli, H.; Zafer, A. Bessel basis with applications: N-dimensional isotropic polynomial oscillators. Int. J. Quant. Chem. 1997, 63, 935. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. A unified description of the shape phase transition, shape coexistence and mixing phenomena in nuclei. EPJ Web Conf. 2024. submitted. [Google Scholar]
- Budaca, R.; Buganu, P.; Budaca, A.I. Geometrical model description of shape coexistence in Se isotopes. Nucl. Phys. A 2019, 990, 137–148. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I.; Buganu, P. Application of the Bohr Hamiltonian with a double-well sextic potential to collective states in Mo isotopes. J. Phys. G Nucl. Part. Phys. 2019, 46, 125102. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R.; Budaca, A.I. Shapes coexistence in the frame of the Bohr model. Nucl. Theory 2019, 38, 68–73. [Google Scholar]
- Ait Ben Mennana, A.; Benjedi, R.; Budaca, R.; Buganu, P.; El Bassem, Y.; Lahbas, A.; Oulne, M. Mixing of the coexisting shapes in the ground state of 74Ge and 74Kr. Phys. Scr. 2021, 96, 125306. [Google Scholar] [CrossRef]
- Ait Ben Mennana, A.; Benjedi, R.; Budaca, R.; Buganu, P.; El Bassem, Y.; Lahbas, A.; Oulne, M. Shape and structure for the low-lying states of the 80Ge nucleus. Phys. Rev. C 2022, 105, 034347. [Google Scholar] [CrossRef]
- Benjedi, R.; Budaca, R.; Buganu, P.; El Bassem, Y.; Lahbas, A.; Oulne, M. Shapes and structure for the lowest states of the 42,44Ca isotopes. Phys. Scr. 2024, 99, 055307. [Google Scholar] [CrossRef]
- Davydov, A.S.; Chaban, A.A. Rotation-vibration interaction in non-axial even nuclei. Nucl. Phys. 1960, 20, 499–508. [Google Scholar] [CrossRef]
- Meyer-Ter-Vehn, J. Collective model description of transitional odd-A nuclei: (I). The triaxial-rotor-plus-particle model. Nucl. Phys. A 1975, 249, 111–140. [Google Scholar] [CrossRef]
- Wood, J.L.; Zganjar, E.F.; De Coster, C.; Heyde, K. Electric monopol transitions from low energy excitations in nuclei. Nucl. Phys. A 1999, 651, 323–368. [Google Scholar] [CrossRef]
- Davydov, A.S.; Rostovsky, V.S. Electric monopole transitions in non-spherical nuclei. Nucl. Phys. 1964, 60, 529–543. [Google Scholar] [CrossRef]
- Baglin, C.M. Nuclear Data Sheets for A = 192. Nucl. Data Sheets 2012, 113, 1871–2111. [Google Scholar] [CrossRef]
- Singh, B. Nuclear Data Sheets for A = 194. Nucl. Data Sheets 2006, 107, 1531–1746. [Google Scholar] [CrossRef]
- Huang, X. Nuclear Data Sheets for A = 196. Nucl. Data Sheets 2007, 108, 1093–1286. [Google Scholar]
| 192Pt | 194Pt | 196Pt | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | QE I | QE II | NS | Exp. | QE I | QE II | NS | Exp. | QE I | QE II | NS | |
| R1,4,4 | 2.479 | 2.439 | 2.412 | 2.278 | 2.470 | 2.415 | 2.414 | 2.317 | 2.465 | 2.513 | 2.418 | 2.231 |
| R1,6,6 | 4.314 | 3.787 | 3.821 | 3.797 | 4.298 | 3.835 | 3.869 | 3.916 | 4.290 | 3.709 | 3.691 | 3.664 |
| R1,8,8 | 6.377 | 5.773 | 5.780 | 5.531 | 6.392 | 5.880 | 5.879 | 5.772 | 6.333 | 5.579 | 5.511 | 5.279 |
| R1,10,10 | 8.624 | 7.350 | 7.453 | 7.461 | 8.672 | 7.573 | 7.629 | 7.873 | 8.558 | 6.914 | 6.970 | 7.060 |
| R1,2,0 | 1.935 | 1.653 | 1.660 | 1.796 | 1.894 | 1.661 | 1.669 | 1.817 | 1.936 | 1.646 | 1.637 | 1.770 |
| R1,3,2 | 2.910 | 2.303 | 2.330 | 2.509 | 2.809 | 2.332 | 2.355 | 2.558 | 2.852 | 2.249 | 2.264 | 2.450 |
| R1,4,2 | 3.795 | 4.229 | 4.218 | 4.198 | 3.743 | 4.268 | 4.267 | 4.343 | 3.636 | 4.179 | 4.090 | 4.040 |
| R1,5,4 | 4.682 | 4.342 | 4.360 | 4.395 | 4.563 | 4.402 | 4.422 | 4.553 | 4.526 | 4.243 | 4.197 | 4.223 |
| R1,6,4 | 5.905 | 6.358 | 6.440 | 6.604 | 5.644 | 6.041 | 6.069 | 6.271 | ||||
| R1,7,6 | 6.677 | 6.065 | 6.171 | 6.428 | ||||||||
| R1,8,6 | 8.186 | 9.163 | 9.221 | 9.100 | 7.730 | 8.564 | 8.573 | 8.563 | ||||
| R2,0,0 | 3.776 | 3.397 | 3.510 | 3.317 | 3.858 | 3.706 | 3.727 | 3.615 | 3.192 | 2.954 | 3.031 | 3.002 |
| R2,2,2 | 4.547 | 4.995 | 5.134 | 5.146 | 4.603 | 5.409 | 5.407 | 5.643 | 3.828 | 4.308 | 4.476 | 4.697 |
| rms | 0.614 | 0.601 | 0.605 | 0.543 | 0.525 | 0.525 | 0.682 | 0.686 | 0.714 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buganu, P.; Benjedi, R.; Oulne, M. Numerical Solution of a Sixth-Order Anharmonic Oscillator for Triaxial Deformed Nuclei. Mathematics 2025, 13, 460. https://doi.org/10.3390/math13030460
Buganu P, Benjedi R, Oulne M. Numerical Solution of a Sixth-Order Anharmonic Oscillator for Triaxial Deformed Nuclei. Mathematics. 2025; 13(3):460. https://doi.org/10.3390/math13030460
Chicago/Turabian StyleBuganu, Petricǎ, Radi Benjedi, and Mustapha Oulne. 2025. "Numerical Solution of a Sixth-Order Anharmonic Oscillator for Triaxial Deformed Nuclei" Mathematics 13, no. 3: 460. https://doi.org/10.3390/math13030460
APA StyleBuganu, P., Benjedi, R., & Oulne, M. (2025). Numerical Solution of a Sixth-Order Anharmonic Oscillator for Triaxial Deformed Nuclei. Mathematics, 13(3), 460. https://doi.org/10.3390/math13030460






