A Two-Stage Adaptive Differential Evolution Algorithm with Accompanying Populations

Abstract

Stochastic simulations are often used to determine the crossover rates and step size of evolutionary algorithms to avoid the tuning process, but they cannot fully utilize information from the evolutionary process. A two-stage adaptive differential evolution algorithm (APDE) is proposed in this article based on an accompanying population, and it has unique mutation strategies and adaptive parameters that conform to the search characteristics. The global exploration capability can be enhanced by the accompanying population to achieve a balance between global exploration and local search. This algorithm has proven to be convergent with a probability of 1 using the theory of Markov chains. In numerical experiments, the APDE is statistically compared with nine comparison algorithms using the CEC2005 and CEC2017 standard set of test functions, and the results show that the APDE is statistically superior to the comparison methods.

1. Introduction

Among many evolutionary optimization methods, differential evolution (DE) is a heuristic stochastic search algorithm based on population differences. For its simple structure, easy implementation, fast convergence, and robustness, DE is widely used in various fields such as data mining [1], pattern recognition [2], digital filter design [3], artificial neural networks [4], and electromagnetism [5]. However, the performance of DE depends seriously on the control parameters and mutation strategies. Inappropriate parameters or mutation strategies will reduce the convergence performance of the algorithm or fall into the local optimum. Therefore, many scholars have conducted research on the update strategy and algorithmic structure of DE algorithms in recent years. Current improvements in DE can mainly be categorized as follows: multi-population [6], multi-evolutionary model [7], parameter adaptive [8,9], strategy and search space adaptive [10,11,12,13], variant strategy updating [14,15,16,17], online algorithmic configurations [18], parameter free [19], etc.

Incorporating multi-population or multi-evolution modules into the algorithm can improve the global search capability and convergence rate of the evolutionary algorithm. For example, DSPPDE [6] employs the idea of isolated evolution and information exchanging in parallel DE algorithms via serial program structure; MEDE [7] realizes multi-strategy cooperation based on the fact that each evolution strategy of DE has common peculiarities but different characteristics; MCDE [8] uses a population structure with multi-populations so that covariance learning can establish a proper rotational coordinate system for the crossover operation, and it uses adaptive control parameters to balance the ability of population surveys and convergence; BMEA-DE [9] divides the population into three sub-populations based on fitness, which uses separate variation strategies and control parameters for different populations.

On the other hand, the parameters are critical to the accuracy of DE and its convergence rate. For example, if the mutation rate of CR is too small, it will reduce the ability of the algorithm in the global search and eventually fall into the local optimum; if the mutation rate of CR is too large, it is computationally consuming, resulting in a decrease in the speed of convergence of the algorithm. Therefore, many scholars have introduced adaptive operators to adjust parameters based on certain information. For example, ADE [10] introduces an adaptive mutation operator according to the comparison between each individual’s fitness and the best one’s fitness, and it adds a competition operation with a random new population to improve the global search capability. ISADE [11] incorporates space-adaptive ideas into DE to realize the automatic search for the suitable space and improve the convergence rate and accuracy. IDE [12] generates the initial population with a reverse learning strategy and selects individuals via the Metropolis criterion of simulated annealing algorithms. APSDE [13] optimizes the mutation strategy and control parameters through the accompanying population, in which individuals are composed of suboptimal solutions.

The mutation operator of DE has high randomness and is mainly composed of only one evolutionary direction. This kind of operator makes DE prone to problems such as premature phenomena and slow convergence speeds. Moreover, DE cannot realize both a global search of space and local optimization operations at the same time. As a result, many scholars have conducted many studies on the update strategy of DE. SSDE [14] employs an opposition-based learning method to enhance global convergence performance when producing the initial population. GSDE [15] optimizes the exploitation ability with Gaussian random walk and local search performances with simplified crossovers and mutations based on individuals’ performance. SEFDE [16] achieves the feedback adjustment of mutation strategies via the stage of the individual, which can be self-adaptively determined by designing the state judgment factor. Consequently, the algorithm can obtain a trade-off between exploration and exploitation. HHSDE [17] introduces a new mutation operation to improve the efficiency of mutations within the new harmony generation mechanics of the harmony algorithm (HS).

In addition, some algorithmic configuration methods have been developed in recent years. For example, OAC [18] selects a trial strategy for vector generation via the multi-armed bandit algorithm, in which kernel density estimation is employed to tune the control parameters during the searching process.

In summary, most of the studies on the improvements in DE are focused on the strategies of mutation operators and control parameters, often disregarding the algorithm’s distinctive search characteristics across various stages.

In general, evolutionary algorithms are generally divided into two stages. The main task of the first stage of the algorithm is to explore the target region globally. Meanwhile, in the second stage, the focus shifts to narrowing down the search region to the neighborhood of the better-performing particles, aiming at finding the locally optimal solutions in the region and avoiding premature convergence. Thus, in this paper, a novel two-stage algorithm is proposed. This algorithm has two kinds of populations and constructs new mutation patterns with adaptive direction vector weight factors and crossover factors. As a result, it is able to achieve fast convergence and avoid the local optimum.

2. A Two-Stage Adaptive Differential Evolution Algorithm (APDE) with Accompanying Populations

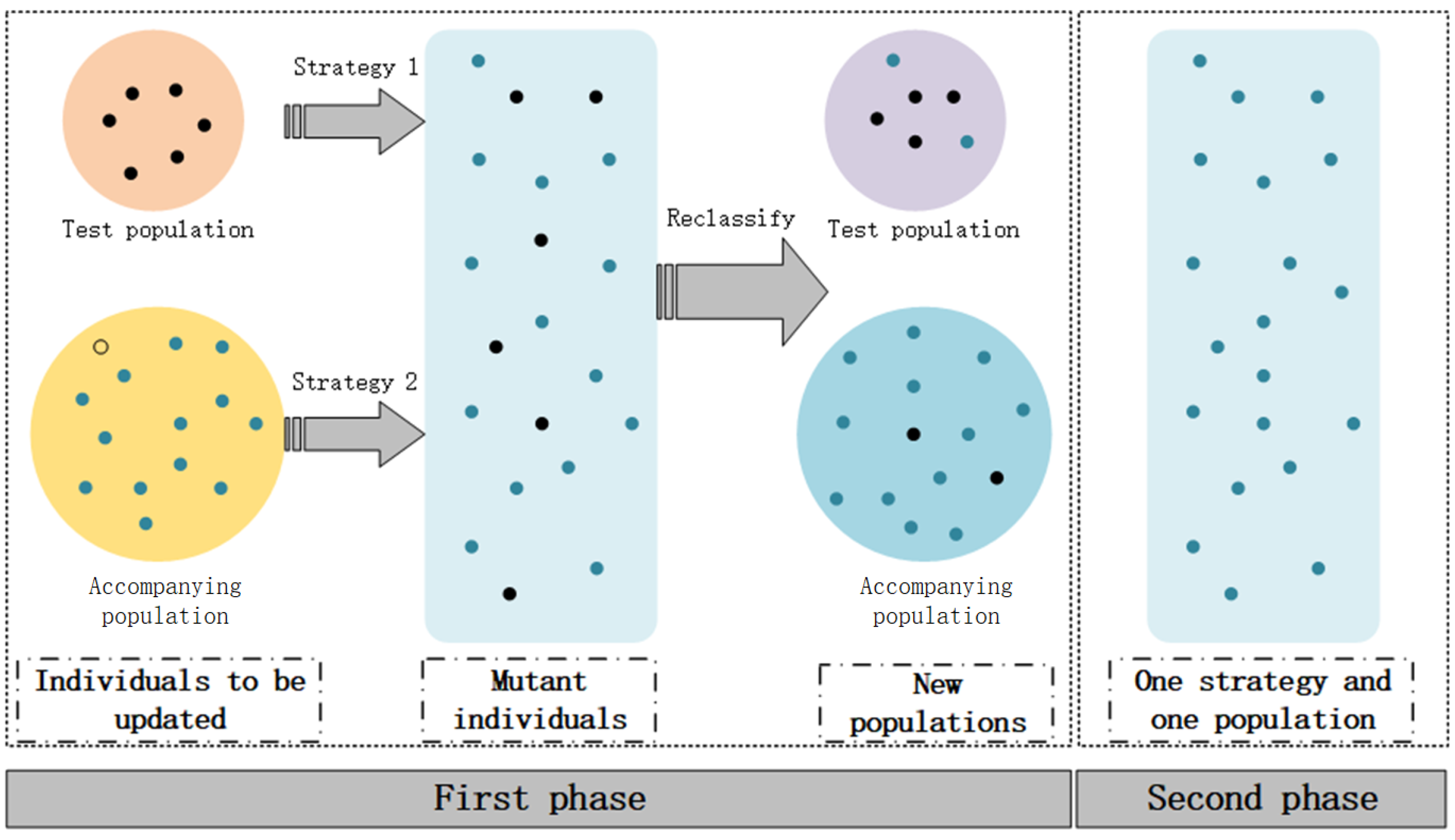
In this section, a two-stage adaptive differential evolutionary algorithm with accompanying populations is proposed. In this algorithm, we use different mutation strategies for the test and accompanying populations in order to maximize the mutation efficiency.

The updated individuals will be reclassified according to their fitness value, which ensures evolutionary diversity and achieves information exchange between populations. In addition, APDE divides the algorithm into two stages according to the search characteristics of the evolutionary algorithm. Therefore, the algorithm can quickly converge in the early stage and escapes local optimum efficiently in the later stage by enhancing its stochastic mutability. This operation can help improve computing efficiency and maintain convergence speeds. Figure 1 depicts the specific operation of each stage in APDE.

2.1. Initialization

APDE uses the Good Point Set Method [20] to generate the initial population. Then, the initial individuals are evenly distributed in the search space to overcome blindness and randomness and improve population diversity. The initialization formulas are as follows:

$$r_j=2cos\left(\left(2\pi \times j\right)/\phantom{\left(2\pi \times j\right)\left(2D+3\right)}\left(2D+3\right)\right),$$

(1)

$$x_{ij}\left(0\right)=x_{ij}^L+mod\left(r_j\times i,1\right)\times \left(x_{ij}^U-x_{ij}^L\right).$$

(2)

Here, $j\in \left\{1,2,\cdots ,D\right\}$, $i\in \left\{1,2,\cdots ,N\right\}$. $x_{ij}^L$ and $x_{ij}^U$ are the upper and lower bounds of the range of values taken by the jth component $x_{ij}$ of the individual.

2.2. Population Segmentation

The population of APDE is divided into 2 classes. One is the test population, for which its main function is to explore the optimal solution based on the information of the optimal individuals. The other one is the accompanying population, which has lower fitness values and is randomly distributed throughout the entire search space. Its primary function is to explore uncharted regions and augment population diversity. After multiple trials, APDE uses a empirical 3:7 ratio to divide the population, and the individuals are reordered according to the fitness value at the end of each iteration. The segmentation operation can be specifically expressed as follows:

$$\left[\begin{array}{cc}f& I\end{array}\right]=sort\left(\left[\begin{array}{cccc}f\left(x_1\right)& f\left(x_2\right)& \cdots & f\left(x_{NP}\right)\end{array}\right]\right),$$

(3)

$$c_i=\left\{\begin{array}{c}0,iff\left(x_i\left(g\right)\right)\le f_{0.3NP},\hfill \\ 1,otherwise.\hfill \end{array}\right.$$

(4)

where $c_i$ is the population classification information for the ith individual. Here, 0 indicates the test population, and 1 indicates the accompanying population.

2.3. Improved Mutation Operator

In 2022, Civicioglu [19] proposed an elitist mutation operator in the Bernstein–Levy differential evolution(BDE) algorithm, which uses three vectors to generate mutation directions. The generation process of this mutation operator is partially elitist. This structure enhances the algorithm’s local search capability and improves the algorithm’s ability to generate effective mutation patterns. The first two direction vectors $d{v}_1$ and $d{v}_2$ are generated by obtaining the difference in the two different individuals selected at random. The generation method is as follows:

$$\left\{\begin{array}{c}d{v}_1=x_{i1}-x_{i=1:N}\left|i1=permute\left(\left[1:N\right]\right),\right.\hfill \\ d{v}_2=x_{i2}-x_{i=1:N}\left|i2=permute\left(\left[1:N\right]\right),\right.\hfill \\ i1\ne i2,andi1,i2\ne \left[1:N\right].\hfill \end{array}\right.$$

(5)

where $permute\left(\left[1:N\right]\right)$ denotes the vector replacement function.

$d{v}_3$ is generated via the location information about the current optimal solution. The information can be used directly or after numerical perturbation within the limits of the relevant search space.

(1) When current optimal solution $BestP$ is used directly,

$$d{v_3}_i=BestP-x_i.$$

(6)

(2) When current optimal solution $BestP$ is used after applying a numerical perturbing progress,

$$r_0=BestP+k_1^3\left(x_i^U-BestP\right),$$

(7)

$$r=r+k_2^3\left(x_i^L-r_0\right),$$

(8)

$$d{v}_{3i}=r-x_i.$$

(9)

$k_1$ and $k_2$ are random numbers obeying a uniform distribution in $\left[0,1\right]$.

BDE selects these two generation methods with a probability of 50%. However, this strategy is too dependent on randomness and does not match the search characteristics of the algorithm. As a result, it slows down the convergence of the algorithm in the early stage and squanders computational resources. Obviously, the generation in (1) is more conducive for the algorithm for quickly approaching the current optimal solution, while the generation in (2) is more suitable for enhancing the global search capability of the algorithm. Therefore, the algorithm in this paper innovates the mutation strategy as follows.

$$d{v}_{3i}=\left\{\begin{array}{c}BestP-x_i,if{c}_i=1,\hfill \\ r-x_i,otherwise.\hfill \end{array}\right.$$

(10)

To synthesize the three direction vectors in the test population, an adaptive weight factor is proposed in this paper according to the iterative process of the algorithm:

$$w_1=w_2=rand\left(N,1\right),$$

(11)

$$\begin{array}{c}{w}_3=w_1+\left(ones\left(N,1\right)-w_1\right)\times 0.6\times sin\left({\displaystyle \frac{\pi }{2}}\times \left(1-{\displaystyle \frac{epk}{epoch}}\right)\right).\hfill \end{array}$$

(12)

where $w_1$, $w_2$, and $w_3$ are the combined weight factors of $d{v}_1$, $d{v}_2$, and $d{v}_3$; $epk$ is the current iteration number; $epoch$ is the maximum number of iterations. It is easy to know from the above equations that $d{v}_1$ and $d{v}_2$ are generated in the same way, so they have the same weights. In order to fully utilize the leadership of the current optimal solution, the weight of $d{v}_3$ should be higher than $w_1$ and $w_2$ and increase with the number of iterations. As a result, $d{v}_3$ is a direction vector with elite strategies.

For the accompanying population, its combined direction vector consists of the difference between direction vectors $d{v}_2$ and $d{v}_3$. This structure enables the accompanying population to have a stronger exploration ability.

In summary, the combined direction vector $dv$ is defined as follows:

$$dv\left(i,:\right)=\left\{\begin{array}{c}F\left(i,:\right)\otimes \left(w_1\otimes d{v}_1\left(i,:\right)+w_2\otimes d{v}_2\left(i,:\right)\right.\hfill \\ \left.+w_3\otimes d{v}_3\left(i,:\right)\right),ifc\left(i\right)=0,\hfill \\ \\ d{v}_1\left(i,:\right)+F\left(i,:\right)\otimes \left(d{v}_3\left(i,:\right)-\right.\hfill \\ \left.d{v}_2\left(i,:\right)\right),otherwise.\hfill \end{array}\right.$$

(13)

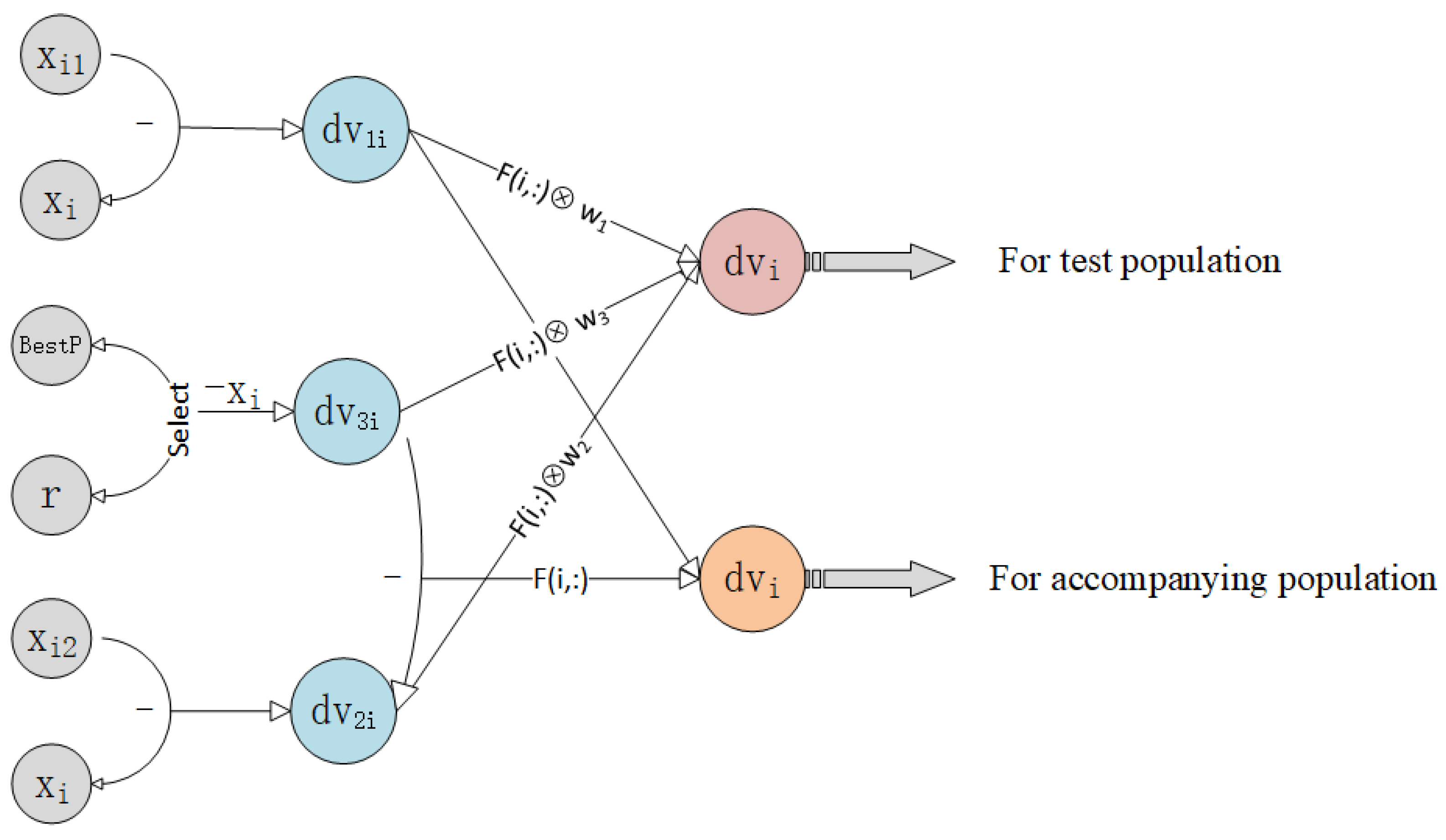
where ⊗ denotes the Hadamard product. $F(i,:)$ is the value of the evolutionary step size of the ith individual. The step size is generated by the Levy distribution, which has more powerful exploratory capabilities. Figure 2 exemplifies the specific way in which the mutation operates.

2.4. Crossover and Selection

The crossover rate plays a critical role in the global searching ability and convergence speed of DE, which are conflicting. Thus, the key is to find a suitable crossover rate to balance the convergence rate and the global searching ability. The adaptive exponential distribution is employed to generate crossover rates rather than the traditional constant value in APDEs, which enables the algorithm to efficiently escape the local optimum in later stages.

$$CR=0.3+0.6\times \left(1-e^{-{\displaystyle \frac{5epk}{epoch}}}\right).$$

(14)

The crossover process is controlled by the mapping matrix from BDE, in which the permutation operation is employed to embed the crossover rate CR into the searching directions of each individual. This embedding map is initialized as an $N\times D$ zero matrix. At each BDE iteration step, the numerical values of the map elements are updated via the following Equation (15):

$$map\left(i,h\left(1:[CR\times D]\right)\right)=1,$$

(15)

$$\tilde{x}=x+map\otimes dv.$$

(16)

where $h=permuted\left(1:D\right)$, and $\tilde{x}$ is an offspring generation after crossover and mutation. When the value of $\tilde{x}$ is outside the search region, it will be adapted by a random number within the search region.

Finally, we can update the populations as follows.

$$x_i\left(g+1\right)=\left\{\begin{array}{c}{\tilde{x}}_i\left(g\right),iff\left({\tilde{x}}_i\right)<f\left(x_i\right),\hfill \\ x_i\left(g\right),otherwise.\hfill \end{array}\right.$$

(17)

2.5. Two-Stage Evolutionary Strategy

As is known to all, it is challenging for evolutionary algorithms to avoid falling into a local optimum without reducing the algorithm’s convergence rate. Indeed, it is to balance the randomness and optimization of the search within the algorithmic process. Thus, we focus on solving the problem with different search goals in the early and later stages of the algorithm.

A multi-population strategy can enhance the algorithm’s search ability and population diversity, enabling rapid convergence in the early stages and emphasizing selecting random mutation strategies in the later stage.

In the two stages of the proposed algorithm, we use half of the maximum iteration as the dividing point, and we implement different mutation operator selection strategies. In the first stage, APDE formulates different mutation strategies with various populations, thus achieving effective information exchange between populations. In the second stage, the quality of individuals in the test and accompanying populations increases, and the efficiency of multi-population strategy decreases. As a result, the test and accompanying populations are merged in this stage, and the mutation strategies are selected with equal probability. This operation increases the algorithmic randomness to enhance the search capability of the algorithm in the later stages. The pseudo-code of the APDE is as shown in Algorithm 1.

Algorithm 1 APDE Algorithm.

1: $//$ Initialization; 2: $r_j=2cos\left(\right(2$$\pi$$j)/(2D+3\left)\right)$; 3: $x_{ij}\left(0\right)=x_{ij}^L+mod(i{r}_j,1)\times (x_{ij}^U-x_{ij}^L)$; 4: $BestX=minf\left(x_i\right)|i\in$1:NP; 5: for  $Iteration=1toMaxCycle$  do 6:     $//$ Population Segmentation; 7:     $\left[fI\right]=sort\left([f\left(x_1\right)f\left(x_2\right)\cdots f\left(x_{NP}\right)]\right)$; 8:     if $f\left(x_i\left(g\right)\right)\le f_{0.3NP}$ then 9:         $c_i=0$ 10:     else 11:         $c_i=1$ 12:     end if 13:     $//$ Generation of Random Direction Vectors; 14:     $d{v}_1=x_{i1}-x_{i=1:NP}|i1=permute\left([i:N]\right)$ 15:     $d{v}_2=x_{i2}-x_{i=1:NP}|i2=permute\left([i:N]\right)|i1\ne i2,andi1,i2\ne [1:N]$; 16:     $//$ Generation of Evolutionary Step Size Value; 17:     for $i=1$ to $NP$ do 18:         $F_{(i,1)}=1/(\beta ·\varphi )|\varphi \sim \Gamma (\alpha =0.50,\beta /2|\sim U$$1:16$); 19:         $F_{(1:NP,1:D)}={\left({\left(F_{(1:NP,1)}\right)}^T\right)}_{(1:NP,1)}·O_{(1,1:D)}$ 20:     end for 21:     $//$ First Phase; 22:     if $Iteration\le 1/2MaxCycle$ then 23:         if $c_i=0$ then 24:            $d{v}_{3i}=BestX-x_i$; 25:            $dv(i,:)=F_{(i,:)}\otimes (w_1\otimes d{v}_1(i,:)+w_2\otimes d{v}_2(i,:)+w_3\otimes d{v}_3(i,:))$; 26:         else 27:            $d{v}_{3i}=r-x_i$; 28:            $dv(i,:)=d{v}_1(1,:)+F(i,:)\otimes (d{v}_3(i,:)-d{v}_2(i,:))$; 29:         end if 30:     end if 31:     $//$ Second Phase; 32:     if $Iteration>1/2MaxCycle$ then 33:         if $a<b\left|\right(a,b)\sim U(0,1)$ then 34:            $d{v}_{3i}=BestX-x_i$; 35:         else 36:            $d{v}_{3i}=r-x_i$; 37:         end if 38:         if $a<b\left|\right(a,b)\sim U(0,1)$ then 39:            $dv(i,:)=F_{(i,:)}\otimes (w_1\otimes d{v}_1(i,:)+w_2\otimes d{v}_2(i,:)+w_3\otimes d{v}_3(i,:))$; 40:         else 41:            $dv(i,:)=d{v}_1(1,:)+F(i,:)\otimes (d{v}_3(i,:)-d{v}_2(i,:))$; 42:         end if 43:     end if 44:     $//$ Crossing and Selection; 45:     $map(i=1:N,j=1:D)=0$; 46:     $CR=0.3+0.6\times (1-e^{-{\displaystyle \frac{5epk}{epoch}}})$; 47:     for $i=1$ to $NP$ do 48:         $map(i,h(1:[CR\times D]\left)\right)=1$; 49:     end for 50:     $//$ Generation of Trial Pattern Vectors; 51:     $\tilde{x}=x+map\otimes dv$; 52:     $//$ Boundary Control Mechanism; 53:     for $i=1$ to $NP$ do 54:         for $j=1$ to D do 55:            if ${\tilde{x}}_{ij}<lo{w}_{j}or{\tilde{x}}_{ij}>u{p}_j$ then 56:                ${\tilde{x}}_{ij}=lo{w}_j+\delta ·(u{p}_j-lo{w}_j)|\delta \sim U(0,1)$; 57:            end if 58:         end for 59:     end for 60:     $//$ Update; 61:     for $i=1$ to $NP$ do 62:         if $f\left({\tilde{x}}_i\right)<f\left(x_i\right)$ then 63:            $[x_i,f\left(x_i\right)]=[{\tilde{x}}_i,f\left({\tilde{x}}_i\right)]$; 64:         end if 65:     end for 66:     $f\left(x_{\gamma }\right)=minf\left(x_i\right)|i\in \left\{1:NP\right\}$; 67:     $[BestX,BestObjval]=[f\left(x_{\gamma }\right),x_{\gamma }]$. 68: end for

3. Convergence Analysis of APDE

In this section, the convergence of APDE is analyzed using the tool of Markov chains [21]. It is shown that the presented algorithm converges to the global optimum in probability.

Definition 1. 

Let a random sequence $\left\{X_n;n\ge 0\right\}$ consist of random variables taking values on a discrete set; the totality of the discrete values is denoted as $H_L=\left\{j\right\}$. $H_L$ is called the state space. If for $\forall n\ge 1$, $i_k\in H_L\left(k\le n+1\right)$, there is

$$\begin{array}{c}P\left\{X_{n+1}=i_{n+1}\left|X_n=i_n,\cdots ,X_0=i_0\right.\right\}\hfill \\ =P\left\{X_{n+1}=i_{n+1}\left|X_n=i_n\right.\right\}.\hfill \end{array}$$

(18)

Then, $\left\{X_n;n\ge 0\right\}$ is called a Markov Chain [21].

The state space $H_L$ of the random sequence $\left\{X_n;n\ge 0\right\}$ can either be finite or infinite states as needed, and for the differential evolution class of algorithms, we consider $H_L$ to be finite.

Definition 2. 

Let m and n be positive integers. If the Markov Chain is in state i at time m, the probability of transferring to state j after n steps is $P_{ij}\left(m,m+n\right)=P\left\{X_{m+n}=j\left|X_m=i\right.\right\}$. If the corresponding transfer probabilities are independent of time m, that is, $P_{ij}\left(m,m+n\right)={P_{ij}}^{\left(n\right)}$, the Markov chain $\left\{X_n;n\ge 0\right\}$ is said to be time-homogeneous [21].

Lemma 1. 

When the crossover rate $CR$ is fixed, the population sequence $\left\{X_n;n\ge 0\right\}$ of APDE is a finite time-homogeneous Markov Chain.

Proof. 

Let the length of individuals be M, the population size be N, and the dimension of the state space be v; then, the size of the state space is $v^{NM}$. As the individuals in APDE take real values and the state space of the population sequence is a finite set under finite precision conditions, the sequence of populations is finite. Also, the mutation, crossover, and selection operators of the population sequence in APDE are independent with time t when the crossover rate is a constant. The next state $X_{t+1}$ is solely dependent on the current state $X_t$. Therefore, the sequence of populations is time-homogeneous. As a result, $\left\{X_n;n\ge 0\right\}$ is a finite time-homogenous Markov Chain. □

Let $X_t=\left\{x_1\left(t\right),x_2\left(t\right),\cdots ,x_N\left(t\right)\right\}$ be a population sequence during the tth iteration. $x_i\left(t\right)$ is an individual in $X_t$, and f is the fitness function on $X_t$. Let

$$\stackrel{*}{f}=min\left\{f\left(x\right),x\in X_t\right\}$$

(19)

be the global optimal fitness value; then, we have the following definition.

Definition 3. 

Let $f_t=min\left\{f\left(x_i\left(t\right)\right),i=1,2,\cdots ,N\right\}$ be a sequence of random variables. The variables in the sequence denote the best fitness of the population in the state at time t. An algorithm is said to be convergent if and only if

$$\underset{t\to \infty }{lim}P\left\{f_t=\stackrel{*}{f}\right\}=1.$$

(20)

This definition indicates that algorithm convergence means that the probability of containing the global optimal solution in the population is almost 1, as the algorithm iterates through a sufficient number of generations.

Theorem 1. 

When the number of iterations of the algorithm is large enough, the APDE algorithm converges to the optima of the problem with a probability of 1.

Proof. 

Let $p_i\left(t\right)$ be the probability that population $X_t$ is in state $s_i$, $p_{ij}\left(t\right)$ be the probability that population $X_t$ moves from state $s_i$ to state $s_j$, S be the state collection, I be a set consisting of optimal states, and $CR$ be a constant value. Note that $p_t={\displaystyle \sum _{i\notin I}}{p}_i\left(t\right)$; by the nature of Markov chains, we have

$$\begin{array}{c}{p}_{t+1}={\displaystyle \sum _{s_i\in S}}{\displaystyle \sum _{j\notin I}}{p}_i\left(t\right)p_{ij}\left(t\right)={\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\notin I}}{p}_i\left(t\right)p_{ij}\left(t\right)+\hfill \\ {\displaystyle \sum _{i\notin I}}{\displaystyle \sum _{j\notin I}}{p}_i\left(t\right)p_{ij}\left(t\right).\hfill \end{array}$$

(21)

Moreover,

$$\sum _{i\notin I}\sum _{j\in I}{p}_i\left(t\right)p_{ij}\left(t\right)+\sum _{i\notin I}\sum _{j\notin I}{p}_i\left(t\right)p_{ij}\left(t\right)=\sum _{i\notin I}{p}_i\left(t\right)=p_t.$$

(22)

It is equal to

$$\sum _{i\notin I}\sum _{j\notin I}{p}_i\left(t\right)p_{ij}\left(t\right)=p_t-\sum _{i\notin I}\sum _{j\in I}{p}_i\left(t\right)p_{ij}\left(t\right).$$

(23)

So, there is

$$\begin{array}{c}0\le p_{t+1}={\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\notin I}}{p}_i\left(t\right)p_{ij}\left(t\right)+p_t-{\displaystyle \sum _{i\notin I}}{\displaystyle \sum _{j\in I}}{p}_i\left(t\right)p_{ij}\left(t\right)\hfill \\ \le {\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\notin I}}{p}_i\left(t\right)p_{ij}\left(t\right)+p_t.\hfill \end{array}$$

(24)

After crossover and mutation, an individual will not be selected when its fitness value is worse than the current optimal solution, and there is

$$\sum _{i\in I}\sum _{j\notin I}{p}_i\left(t\right)p_{ij}\left(t\right)=0.$$

(25)

Then,

$$0\le p_{t+1}\le p_t.$$

(26)

So,

$$\underset{t\to \infty }{lim}{p}_t=0.$$

(27)

This is because

$$\underset{t\to \infty }{lim}P\left\{f_t=\stackrel{*}{f}\right\}=1-\sum _{i\notin I}{p}_i\left(t\right)=1-\underset{t\to \infty }{lim}{p}_t=1.$$

(28)

We have

$$\underset{t\to \infty }{lim}P\left\{f_t=\stackrel{*}{f}\right\}=1.$$

(29)

□

In APDE, $CR$ is adaptive in the range of $(0.3,0.9)$. The probability $p_{ij}\left(t\right)$ is determined primarily by the probability of state transfers resulting from the mutation process. It is calculated as follows:

$$p_{(v,s_i)\to s_j}\left(t\right)=\prod _{n=1}^{N}K\left(n\right),$$

(30)

$$\begin{array}{c}K\left(n\right)=(1-CR)\times Sel\left(map\right(i,n)=0)+\hfill \\ CR\times Sel\left(map\right(i,n)=1),\hfill \end{array}$$

(31)

$$Sel\left(x\right)=\left\{\begin{array}{ccc}\hfill 1& ,\hfill & \hfill xistrue,\\ \hfill 0& ,\hfill & \hfill xisfalse.\end{array}\right.$$

(32)

Here, $map(i,n)$ denotes the mutation locus generated for the nth dimension of the ith individual. N denotes the dimension of the optimization problem.

From the previous proof, we can conclude that the probability of the optimal solution being included in the global optimum converges to 1 when $K\left(n\right)$ takes a lower bound of 0.1 or an upper bound of 0.9. Additionally, we have

$$\begin{array}{c}\underset{t\to \infty }{lim}{P}_{ij}\left(t\right|K\left(n\right)=0.1)\le \underset{t\to \infty }{lim}{P}_{ij}\left(t\right|CR\in (0.3,0.9))\hfill \\ \le \underset{t\to \infty }{lim}{P}_{ij}\left(t\right|K\left(n\right)=0.9).\hfill \end{array}$$

(33)

It can be shown that when $CR$ is taken adaptively in $(0.3,0.9)$, the conclusion can still be reached using the Squeeze Theorem [22].

In summary, APDE can find the optimal solution with a probability of 1 under the condition that the number of iterations is sufficiently large.

4. Numerical Experiment

In this paper, we employ the test functions in CEC2005 and CEC2017 to verify the performance of APDE, the specific information of which is listed in Appendix A and Appendix B. The algorithm of this paper is compared to six DE-type variants and three other types of intelligent optimization algorithms. Each algorithm is set to run 30 times independently, with the maximum number of function evaluations set at $1000\times D$. The values of the dimension D are given in

Table A1. Uni-modal benchmark functions.

Functions	Dimensions	Range	${\mathit{f}}_{\mathit{min}}$
$F_1={\sum }_{i=1}^n{x}_i^2$	30	$\left[-100,100\right]$	0
$F_2={\sum }_{i=0}^n\left|x_i\right|+{\prod }_{i=0}^n\left|x_i\right|$	30	$\left[-10,10\right]$	0
$F_3={\sum }_{i=1}^d{\left({\sum }_{j=1}^i{x}_j\right)}^2$	30	$\left[-100,100\right]$	0
$F_4=max\left\{\left|x_i\right|,1⩽i⩽n\right\}$	30	$\left[-100,100\right]$	0
$F_5={\sum }_{i=1}^{n-1}\left[100\left(x_i^2-x_{i+1}\right)+{\left(1-x_i\right)}^2\right]$	30	$\left[-30,30\right]$	0
$F_6={\sum }_{i=1}^n{\left(\left[x_i+0.5\right]\right)}^2$	30	$\left[-100,100\right]$	0
$F_7={\sum }_{i=0}^{n}i{x}_i^4+rand\left[0,\left.1\right)\right.$	30	$\left[-128,128\right]$	0
$F_8={\sum }_{i=1}^n\left(-x_{i}sin\left(\sqrt{\left|x_i\right|}\right)\right)$	30	$\left[-500,500\right]$	$-12,569.5$
$F_9={\sum }_{i=1}^n\left[x_i^2-10cos\left(2\pi x_i\right)+10\right]$	30	$\left[-5.12,5.12\right]$	0
$F_{10}=-20exp\left(-0.2\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{x}_i^2}\right)-exp\left({\displaystyle \frac{1}{n}}{\sum }_{i=1}^{n}cos\left(2\pi x_i\right)\right)+20+e$	30	$\left[-32,32\right]$	0
$F_{11}=1+{\displaystyle \frac{1}{4000}}{\sum }_{i=1}^n{x}_i^2-{\prod }_{i=1}^{n}cos\left({\displaystyle \frac{x_i}{\sqrt{i}}}\right)$	30	$\left[-600,600\right]$	0
$\begin{array}{c}{F}_{12}={\displaystyle \frac{\pi }{n}}\left\{10sin\left(\pi y_1\right)\right\}+{\sum }_{i=1}^{n-1}{\left(y_i-1\right)}^2\left[1+10{sin}^2\left(\pi y_{i+1}\right)\right.\\ +\left.{\sum }_{i=1}^{n}u\left(x_i,10,100,4\right)\right]\end{array}$	30	$\left[-50,50\right]$	0
where $y_i=1+{\displaystyle \frac{x_i+1}{4}},u\left(x_i,a,k,m\right)\left\{\begin{array}{c}K{\left(x_i-a\right)}^m{x}_i>a\hfill \\ 0-a⩽x_i⩾a\hfill \\ K{\left(-x_i-a\right)}^m-a⩽x_i\hfill \end{array}\right.$
$\begin{array}{c}\begin{array}{c}\hfill F_{13}=0.1\left\{{sin}^2\left(3\pi x_1\right)+{\sum }_{i=1}^n{\left(x_i-1\right)}^2\left[1+{sin}^2\left(3\pi x_{i+1}\right)\right]\right.\\ \hfill +\left.{\left(x_n-1\right)}^2\left[1+{sin}^2\left(3\pi x_n\right)\right]\right\}+{\sum }_{i=1}^{n}u\left(x_i,5,100,4\right)\end{array}\end{array}$	30	$\left[-50,50\right]$	0
$F_{14}={\left({\displaystyle \frac{1}{500}}+{\sum }_{j=1}^{25}{\displaystyle \frac{1}{j+{\sum }_{i=1}^2{\left(x_i-a_{i,j}\right)}^6}}\right)}^{-1}$	2	$\left[-65,65\right]$	1
$F_{15}={\sum }_{i=1}^{11}{\left[a_i-{\displaystyle \frac{x_1\left(b_i^2+b_i{x}_2\right)}{b_i^2+b_i{x}_3+x_4}}\right]}^2$	4	$\left[-5,5\right]$	$0.003075$
$F_{16}=4x_1^2-2.1x_1^4+{\displaystyle \frac{1}{3}}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4$	2	$\left[-5,5\right]$	$-1.0316285$
$F_{17}={\left(x_2-{\displaystyle \frac{5.1}{4{\pi }^2}}{x}_1^2+{\displaystyle \frac{5}{\pi }}{x}_1-6\right)}^2+10\left(1-{\displaystyle \frac{1}{8\pi }}\right)cos{x}_1+10$	2	$\left[-5,5\right]$	$0.398$
$\begin{array}{c}{F}_{18}=\left[1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1+3x_1^2-14x_2+6x_1{x}_2+3x_2^2\right)\right]\\ \times \left[30+{\left(2x_1-3x_2\right)}^2\left(18-32x_1+12x_1^2+48x_2-36x_1{x}_2+27x_2^2\right)\right]\end{array}$	2	$\left[-2,2\right]$	3
$F_{19}=-{\sum }_{i=1}^4{c}_{i}exp\left(-{\sum }_{j=1}^3{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)$	3	$\left[0,1\right]$	$-3.8628$
$F_{20}=-{\sum }_{i=1}^4{c}_{i}exp\left(-{\sum }_{j=1}^6{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)$	6	$\left[0,1\right]$	$-0.32$
$F_{21}=-{\sum }_{i=1}^5{\left[\left(X-a_i\right){\left(X-a_i\right)}^{\mathrm{T}}+c_i\right]}^{-1}$	4	$\left[0,1\right]$	$-10.1532$
$F_{22}=-{\sum }_{i=1}^7{\left[\left(X-a_i\right){\left(X-a_i\right)}^{\mathrm{T}}+c_i\right]}^{-1}$	4	$\left[0,1\right]$	$-10.4028$
$F_{23}=-{\sum }_{i=1}^{10}{\left[\left(X-a_i\right){\left(X-a_i\right)}^{\mathrm{T}}+c_i\right]}^{-1}$	4	$\left[0,1\right]$	$-10.5363$

and

Table A2. CEC2017 standard test functions.

	No.	Functions	${\mathit{F}}_{\mathit{i}}^{*}={\mathit{F}}_{\mathit{i}}\left({\mathit{x}}^{*}\right)$
Unimodal Functions	1	Shifted and Rotated Bent Cigar Function	100
	3	Shifted and Rotated Zakharov Function	300
	4	Shifted and Rotated Rosenbrock Function	400
	5	Shifted and Rotated Rastrigin Function	500
	6	Shifted and Rotated Expanded Scaffer F6 Function	600
Simple Multimodal Functions	7	Shifted and Rotated Lunacek Bi-Rastrigin Function	700
	8	Shifted and Rotated Non-Continuous Rastrigin Function	800
	9	Shifted and Rotated Levy Function	900
	10	Shifted and Rotated Schwefel Function	1000
Hybrid Functions	11	Hybrid Function 1	1100
	12	Hybrid Function 2	1200
	13	Hybrid Function 3	1300
	14	Hybrid Function 4	1400
	15	Hybrid Function 5	1500
	16	Hybrid Function 6	1600
	17	Hybrid Function 6	1700
	18	Hybrid Function 6	1800
	19	Hybrid Function 6	1000
	20	Hybrid Function 6	2000
Composition Functions	21	Composition Function 1	2100
	22	Composition Function 2	2200
	23	Composition Function 3	2300
	24	Composition Function 4	2400
	25	Composition Function 5	2500
	26	Composition Function 6	2600
	27	Composition Function 7	2700
	28	Composition Function 8	2800
	29	Composition Function 9	2900
	30	Composition Function 10	3000
D = 30; Search Range: ${[-100,100]}^D$

in Appendix A. Finally, we used the Wilcoxon signed-rank test to assess the significant difference between APDE and the competition algorithms.

4.1. Comparative Analysis with APDE and DE-Type Algorithms

In this section, CoDE [23], DE [24], BDE, JADE [25], NSDE [26], and SaDE [27] are selected as comparisons to verify the performance of APDE. In

Table 1. Initial values of the related parameters used in DE-type algorithms.

	Algorithm	Initial Values of the Related Parameters
1	CoDE	$N=30$,$F=\left[1.01.00.8\right]$, and $CR=\left[0.10.90.2\right]$
2	BDE	$N=30$
3	JADE	$N=30$,$F=0.5$,$CR=0.5$, and $p_0=0.1$
4	SADE	$CR\sim (0.5,0.1)$,$F\sim (0.4,0.003333)$, and $iku{n}_i=0.25(i=1,2,3,4)$
5	DE	$N=30$, $F=0.6$, and $CR=0.8$

, the initial values of their internal parameters are listed, and the experimental results are shown in

Table 2. Experimental results of DE-type algorithms with respect to CEC2005.

		APDE	CoDE	DE	BDE	JADE	NSDE	SaDE
F1	Mean	$2.0111\times {10}^{-5}$	$5.9860\times {10}^{-1}$	$3.4653\times {10}^{-5}$	$6.6900\times {10}^{-2}$	$1.8312\times {10}^{-29}$	$5.2000\times {10}^{-2}$	$1.4692\times {10}^{-22}$
	Std	$2.4701\times {10}^{-5}$	$1.7170\times {10}^{-1}$	$5.7341\times {10}^{-5}$	$4.5200\times {10}^{-2}$	$8.0982\times {10}^{-29}$	$2.6350\times {10}^{-1}$	$8.0112\times {10}^{-22}$
F2	Mean	$1.3000\times {10}^{-3}$	$1.3970\times {10}^{-1}$	$4.9000\times {10}^{-3}$	$7.5400\times {10}^{-2}$	$1.7680\times {10}^{-16}$	$7.4564\times {10}^{-4}$	$4.9802\times {10}^{-13}$
	Std	$8.7158\times {10}^{-4}$	$3.5500\times {10}^{-2}$	$2.3000\times {10}^{-3}$	$2.3500\times {10}^{-2}$	$2.3758\times {10}^{-16}$	$1.7000\times {10}^{-3}$	$1.3189\times {10}^{-12}$
F3	Mean	$1.4930\times {10}^{-1}$	$2.0261\times {10}^4$	$5.9992\times {10}^3$	$5.207021\times {10}^2$	5.9828	$1.974929\times {10}^2$	$5.905769\times {10}^2$
	Std	$1.5820\times {10}^{-1}$	$2.6561\times {10}^3$	$1.9340\times {10}^3$	$2.841297\times {10}^2$	3.6729	$9.50277\times {10}^1$	$5.814403\times {10}^2$
F4	Mean	$1.2400\times {10}^{-2}$	$3.75102\times {10}^1$	8.5599	2.2086	$9.7000\times {10}^{-3}$	$3.9982\times {10}^1$	2.3680
	Std	$1.3200\times {10}^{-2}$	3.0228	4.8623	$7.25500\times {10}^{-1}$	$8.3000\times {10}^{-3}$	6.1335	1.5353
F5	Mean	$4.4316\times {10}^{-4}$	$4.453352\times {10}^2$	$3.41989\times {10}^1$	$7.08419\times {10}^1$	$1.34262\times {10}^1$	$2.043849\times {10}^2$	$3.27313\times {10}^1$
	Std	$4.8201\times {10}^{-4}$	$9.62976\times {10}^1$	$2.15395\times {10}^1$	$4.66516\times {10}^1$	$1.23849\times {10}^1$	$1.551284\times {10}^2$	$2.41183\times {10}^1$
F6	Mean	$1.9954\times {10}^{-5}$	$6.0020\times {10}^{-1}$	$4.8356\times {10}^{-5}$	$6.9100\times {10}^{-2}$	$1.6210\times {10}^{-29}$	$1.1180\times {10}^{-1}$	$8.8471\times {10}^{-25}$
	Std	$3.1580\times {10}^{-5}$	$2.2910\times {10}^{-1}$	$3.2976\times {10}^{-5}$	$4.4700\times {10}^{-2}$	$4.8882\times {10}^{-29}$	$4.5750\times {10}^{-2}$	$2.5111\times {10}^{-24}$
F7	Mean	$2.0000\times {10}^{-3}$	$8.0680\times {10}^{-1}$	$3.1200\times {10}^{-2}$	$3.5700\times {10}^{-2}$	$7.1716\times {10}^{-2}$	$2.1490\times {10}^{-1}$	$1.1200\times {10}^{-2}$
	Std	$9.7877\times {10}^{-4}$	$2.1410\times {10}^{-1}$	$8.4000\times {10}^{-3}$	$1.3300\times {10}^{-2}$	$3.4930\times {10}^{-2}$	$1.0650\times {10}^{-1}$	$4.4850\times {10}^{-3}$
F8	Mean	$-1.2569\times {10}^4$	$-1.2359\times {10}^4$	$-6.4519\times {10}^3$	$-1.2519\times {10}^4$	$-9.88444\times {10}^3$	$-9.2891\times {10}^3$	$-1.0362\times {10}^4$
	Std	$4.5000\times {10}^{-3}$	$1.508268\times {10}^2$	$5.33804\times {10}^2$	$6.10444\times {10}^1$	$3.037302\times {10}^2$	$6.812488\times {10}^2$	$1.4838\times {10}^3$
F9	Mean	$2.5615\times {10}^{-5}$	$1.4697\times {10}^1$	$1.927408\times {10}^2$	$2.39388\times {10}^1$	$1.86455\times {10}^1$	$3.97028\times {10}^1$	$1.050872\times {10}^2$
	Std	$3.3880\times {10}^{-5}$	2.5241	$1.41917\times {10}^1$	3.3626	2.6113	$1.04575\times {10}^1$	$1.43169\times {10}^1$
F10	Mean	$9.4246\times {10}^{-4}$	$1.70904\times {10}^1$	6.3566	$8.1100\times {10}^{-2}$	$1.3910\times {10}^{-1}$	$1.41083\times {10}^1$	$1.3340\times {10}^{-13}$
	Std	$7.5380\times {10}^{-4}$	5.8214	9.1827	$1.9400\times {10}^{-2}$	$3.6308\times {10}^{-1}$	5.9864	$1.6936\times {10}^{-13}$
F11	Mean	$5.5418\times {10}^{-4}$	$7.5300\times {10}^{-1}$	$3.3000\times {10}^{-3}$	$2.1770\times {10}^{-1}$	$4.9899\times {10}^{-3}$	$1.4640\times {10}^{-1}$	$2.5457\times {10}^{-3}$
	Std	$2.6000\times {10}^{-3}$	$1.0630\times {10}^{-1}$	$9.2000\times {10}^{-3}$	$9.6300\times {10}^{-2}$	$1.2366\times {10}^{-2}$	$4.0030\times {10}^{-1}$	$4.9465\times {10}^{-3}$
F12	Mean	$1.4094\times {10}^{-7}$	$2.2710\times {10}^{-1}$	$4.7075\times {10}^{-5}$	$5.8715\times {10}^{-4}$	$1.3866\times {10}^{-2}$	1.2814	$3.4556\times {10}^{-3}$
	Std	$3.8140\times {10}^{-7}$	$1.1530\times {10}^{-1}$	$8.1738\times {10}^{-5}$	$5.4181\times {10}^{-4}$	$4.4994\times {10}^{-2}$	2.4849	$1.8927\times {10}^{-2}$
F13	Mean	$2.1444\times {10}^{-6}$	$6.8000\times {10}^{-2}$	$7.0836\times {10}^{-6}$	$4.5000\times {10}^{-3}$	$1.0987\times {10}^{-3}$	$6.9840\times {10}^{-1}$	$1.1990\times {10}^{-1}$
	Std	$1.1358\times {10}^{-6}$	$2.4500\times {10}^{-2}$	$3.2267\times {10}^{-6}$	$3.0000\times {10}^{-3}$	$3.3526\times {10}^{-3}$	2.4797	$6.5680\times {10}^{-1}$
F14	Mean	$9.9800\times {10}^{-1}$	$9.9800\times {10}^{-1}$	1.0974	$9.9800\times {10}^{-1}$	$9.9800\times {10}^{-1}$	1.3279	1.0643
	Std	0	0	$3.0330\times {10}^{-1}$	0	0	$9.8170\times {10}^{-1}$	$2.5220\times {10}^{-1}$
F15	Mean	$3.0749\times {10}^{-4}$	$1\times {10}^{-3}$	$1.7\times {10}^{-3}$	$3.075\times {10}^{-4}$	$3.685\times {10}^{-4}$	$1.4\times {10}^{-3}$	$3\times {10}^{-3}$
	Std	$1.9206\times {10}^{-19}$	$5.0063\times {10}^{-4}$	$5.1\times {10}^{-3}$	$1.5907\times {10}^{-8}$	$2.3232\times {10}^{-4}$	$3.6\times {10}^{-3}$	$6.9\times {10}^{-3}$
F16	Mean	$-1.0316$	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	Std	$6.3208\times {10}^{-16}$	$6.7752\times {10}^{-16}$	$6.7752\times {10}^{-16}$	$6.3532\times {10}^{-16}$	$6.7752\times {10}^{-16}$	$6.7752\times {10}^{-16}$	$6.7752\times {10}^{-16}$
F17	Mean	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$
	Std	0	0	0	0	0	0	0
F18	Mean	3	3	3	3	3	3	3
	Std	$4.7536\times {10}^{-15}$	$1.3550\times {10}^{-15}$	$1.9375\times {10}^{-15}$	$4.0803\times {10}^{-15}$	$1.9946\times {10}^{-15}$	$1.1865\times {10}^{-15}$	$2.1615\times {10}^{-15}$
F19	Mean	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628
	Std	$2.5973\times {10}^{-15}$	$2.7101\times {10}^{-15}$	$7.3446\times {10}^{-15}$	$7.1201\times {10}^{-15}$	$2.7101\times {10}^{-15}$	$2.7101\times {10}^{-15}$	$2.7101\times {10}^{-15}$
F20	Mean	−3.2625	−3.2269	−3.219	−3.322	−3.2943	−3.2388	−3.2665
	Std	$6.0500\times {10}^{-2}$	$4.8400\times {10}^{-2}$	$4.1100\times {10}^{-2}$	$1.4729\times {10}^{-15}$	$5.1146\times {10}^{-2}$	$5.54\times {10}^{-2}$	$6.03\times {10}^{-2}$
F21	Mean	$-1.01532\times {10}^1$	$-1.01532\times {10}^1$	−9.9833	$-1.01532\times {10}^1$	−9.3972	−9.475	−9.485
	Std	$3.3404\times {10}^{-15}$	$6.9584\times {10}^{-15}$	$9.308\times {10}^{-1}$	$5.627\times {10}^{-15}$	2.0002	1.7587	2.0722
F22	Mean	$-1.04029\times {10}^1$	$-1.04029\times {10}^1$	$-1.04029\times {10}^1$	$-1.04029\times {10}^1$	$-1.01803\times {10}^1$	−9.1173	$-1.02258\times {10}^1$
	Std	$1.0881\times {10}^{-16}$	$1.2342\times {10}^{-15}$	$1.1427\times {10}^{-15}$	$3.2986\times {10}^{-16}$	1.2193	2.3819	$9.704\times {10}^{-1}$
F23	Mean	$-1.05364\times {10}^1$	$-1.05364\times {10}^1$	$-1.05364\times {10}^1$	$-1.05364\times {10}^1$	$-1.05364\times {10}^1$	−8.4124	$-1.03577\times {10}^1$
	Std	$1.4752\times {10}^{-15}$	$1.8067\times {10}^{-15}$	$3.2643\times {10}^{-15}$	$2.7202\times {10}^{-15}$	$1.8067\times {10}^{-15}$	3.0976	$9.787\times {10}^{-1}$

and

Table 3. Experimental results of DE-type algorithms with respect to CEC2017.

		APDE	CoDE	DE	BDE	JADE	NSDE	SaDE
F1	Mean	3140	$8.3196\times {10}^6$	$1.5296\times {10}^4$	$5.4656\times {10}^5$	100.1182	120,980	113.433
	Std	2371.8	$1.9186\times {10}^6$	$1.4744\times {10}^4$	$2.7159\times {10}^5$	0.18915	595,290	24.0785
F3	Mean	50,653	$1.4192\times {10}^5$	$1.4044\times {10}^5$	$4.2345\times {10}^4$	35402	39,225	96,478
	Std	11,710	$1.9977\times {10}^4$	$2.1116\times {10}^4$	$1.3805\times {10}^4$	16,724	12,526	22,086
F4	Mean	496.3799	$5.204201\times {10}^2$	$4.882713\times {10}^2$	$5.135177\times {10}^2$	443.0121	508.0222	493.96
	Std	23.9316	$1.32951\times {10}^1$	1.1872	$1.6671\times {10}^1$	34.1803	35.8647	12.9516
F5	Mean	549.3403	$6.639587\times {10}^2$	$7.160121\times {10}^2$	$6.226352\times {10}^2$	553.2752	584.1904	680.6822
	Std	27.9434	$1.13691\times {10}^1$	$1.26556\times {10}^1$	$1.44561\times {10}^1$	13.117	26.4174	12.5815
F6	Mean	600.5493	$6.028136\times {10}^2$	$6.001868\times {10}^2$	$6.008292\times {10}^2$	600.2091	606.629	600.0182
	Std	0.3261	$4.337\times {10}^{-1}$	$1.057\times {10}^{-1}$	$2.988\times {10}^{-1}$	0.29412	5.2815	0.0996
F7	Mean	801.3148	$9.23662\times {10}^2$	$9.550189\times {10}^2$	$8.763957\times {10}^2$	782.657	854.0382	915.6208
	Std	47.8577	$1.68969\times {10}^1$	$1.17354\times {10}^1$	$1.57737\times {10}^1$	9.3993	34.1609	13.6573
F8	Mean	837.7225	$9.74909\times {10}^2$	$1.0221\times {10}^3$	$9.243664\times {10}^2$	847.5331	874.735	975.4408
	Std	9.9356	$1.42838\times {10}^1$	$1.03089\times {10}^1$	$1.00326\times {10}^1$	9.0904	23.0084	14.229
F9	Mean	967.2169	$4.0333\times {10}^3$	$9.010213\times {10}^2$	$1.0038\times {10}^3$	904.7297	1447.7	900.3961
	Std	82.7747	$7.788275\times {10}^2$	$7.331\times {10}^{-1}$	$9.09459\times {10}^1$	8.6947	429.1811	0.5461
F10	Mean	7794.9	$6.14\times {10}^3$	$8.469\times {10}^3$	$5.3364\times {10}^3$	4614.6	4553.8	7865.7
	Std	1085.7	$3.341728\times {10}^2$	$3.581\times {10}^2$	$3.330016\times {10}^2$	742.8817	875.5873	659.3392
F11	Mean	1177.7	$1.2997\times {10}^3$	$1.2381\times {10}^3$	$1.2466\times {10}^3$	1205.7	1224.8	1219.5
	Std	37.373	$1.71649\times {10}^1$	$2.1279\times {10}^1$	$3.34554\times {10}^1$	36.045756	47.2925	29.6147
F12	Mean	123,480	$2.668\times {10}^7$	$2.3824\times {10}^6$	$1.276\times {10}^6$	32,856	479,990	596,300
	Std	155,350	$6.2779\times {10}^6$	$3.436\times {10}^6$	$9.0697\times {10}^5$	26,573	811,250	1.1177
F13	Mean	2519	$1.3822\times {10}^4$	$1.3419\times {10}^4$	$1.7272\times {10}^4$	3193.1	24,408	39,356
	Std	946.358	$4.3167\times {10}^3$	$1.1755\times {10}^4$	$1.3849\times {10}^4$	3417.6	21,207	26,625
F14	Mean	3313.3	$1.5042\times {10}^3$	$1.4963\times {10}^3$	$3.1815\times {10}^3$	7251.9	2274.1	2336.6
	Std	2501.5	$1.02349\times {10}^1$	9.3189	$1.981\times {10}^3$	15,289	1549.4	1583.7
F15	Mean	3489.3	$1.8207\times {10}^3$	$1.6517\times {10}^3$	$7.1935\times {10}^3$	1993.2	7235.4	2368.5
	Std	2859.3	$4.02862\times {10}^1$	$3.87281\times {10}^1$	$5.4051\times {10}^3$	1080.3	10,222	550.5201
F16	Mean	2326.9	$2.7748\times {10}^3$	$3.3051\times {10}^3$	$2.6774\times {10}^3$	2387.1	2448.7	2866.5
	Std	298.5276	$1.576967\times {10}^2$	$1.67845\times {10}^2$	$2.371197\times {10}^2$	180.9872	276.2654	201.866
F17	Mean	1825.1	$2.0855\times {10}^3$	$2.2338\times {10}^3$	$2.0229\times {10}^3$	1866.9	2009.8	2061.9
	Std	100.5111	$1.103453\times {10}^2$	$2.317953\times {10}^2$	$1.279731\times {10}^2$	82.6965	204.75	95.2961
F18	Mean	88,453	$1.7984\times {10}^5$	$4.5786\times {10}^4$	$9.2897\times {10}^4$	65,553	58,304	562,850
	Std	57,972	$9.6414\times {10}^4$	$2.6365\times {10}^4$	$6.1834\times {10}^4$	104,790	41,686	459,140
F19	Mean	3835.5	$2.198\times {10}^3$	$1.958\times {10}^3$	$8.1099\times {10}^3$	2583.1	6798.2	2958.9
	Std	2509.9	$1.206883\times {10}^2$	$1.29483\times {10}^1$	$7.5543\times {10}^3$	2262.6	6656.4	2186.6
F20	Mean	2214.6	$2.3514\times {10}^3$	$2.396\times {10}^3$	$2.3442\times {10}^3$	2287.3	2414.9	2369
	Std	140.867	$1.794837\times {10}^2$	$2.467335\times {10}^2$	$1.238921\times {10}^2$	77.3064	148.0423	123.7216
F21	Mean	2339.8	$2.4676\times {10}^3$	$2.5102\times {10}^3$	$2.4217\times {10}^3$	2350.4	2368.5	2470.5
	Std	13.3063	$1.34699\times {10}^1$	$1.27128\times {10}^1$	$1.60098\times {10}^1$	10.2615	14.994	16.1366
F22	Mean	2661.1	$6.8675\times {10}^3$	$8.2854\times {10}^3$	$2.3038\times {10}^3$	2543.3	4502.1	4974.6
	Std	1387	$1.6838\times {10}^3$	$3.0569\times {10}^3$	$2.4445\times {10}^3$	927.7152	1890.3	3433.5
F23	Mean	2702.3	$2.8077\times {10}^3$	$2.8574\times {10}^3$	$2.7709\times {10}^3$	2707.4	2737.1	2829.4
	Std	14.2395	$1.26972\times {10}^1$	$1.48102\times {10}^1$	$1.35514\times {10}^1$	13.6504	33.2872	21.7018
F24	Mean	2863.4	$3.0085\times {10}^3$	$3.0263\times {10}^3$	$2.9508\times {10}^3$	2873	2921.7	3009.8
	Std	11.0091	$1.76891\times {10}^1$	$1.18241\times {10}^1$	$3.02613\times {10}^1$	15.2932	40.4895	15.1783
F25	Mean	2894.5	$2.92840\times {10}^3$	$2.8872\times {10}^3$	$2.8976\times {10}^3$	2887.6	2901.1	2889.5
	Std	10.3697	$1.2405\times {10}^1$	$1.249\times {10}^{-1}$	$1.03817\times {10}^1$	1.5547	21.3929	4.8153
F26	Mean	4174.7	$5.3037\times {10}^3$	$5.7368\times {10}^3$	$4.6578\times {10}^3$	4335.2	4768	5356.7
	Std	303.6389	$1.411554\times {10}^2$	$9.43115\times {10}^1$	$7.712681\times {10}^2$	163.635526	325	146.235
F27	Mean	3231.6	$3.217\times {10}^3$	$3.2062\times {10}^3$	$3.2431\times {10}^3$	3226.1	3233.5	3213.2
	Std	12.6571	4.7566	9.429	6.9698	13.1675	19.7762	10.2316
F28	Mean	3233.5	$3.3681\times {10}^3$	$3.2355\times {10}^3$	$3.2463\times {10}^3$	3166.5	3253.9	3233.6
	Std	23.2686	$1.951512\times {10}^2$	$4.56795\times {10}^1$	$2.54496\times {10}^1$	56.5691	49.5677	20.2092
F29	Mean	3645.7	$3.7776\times {10}^3$	$4.0828\times {10}^3$	$3.6926\times {10}^3$	3704	3738.6	3928.4
	Std	133.8336	$1.295276\times {10}^2$	$2.46855\times {10}^2$	$9.95814\times {10}^1$	69.367131	227.148	186.4757
F30	Mean	14,192	$3.3062\times {10}^4$	$1.8645\times {10}^4$	$3.3147\times {10}^4$	10,845	10,447	25,852
	Std	5799	$1.0354\times {10}^4$	$8.4415\times {10}^3$	$2.7317\times {10}^4$	6453.8	3501.8	16,160

. The results show that APDE achieves optimal values with respect to 16 test functions in CEC2005 and 13 test functions in CEC2017. Although APDE fails to achieve the best results in the remaining test functions, it still performs well in several comparative algorithms. Among the 16 multi-peak test functions of CEC2005, APDE fails to find the optimal solution in only three test functions. This indicates that APDE has a strong ability to jump out of the local optimum and still maintains good optimization performance with respect to multi-extreme problems.

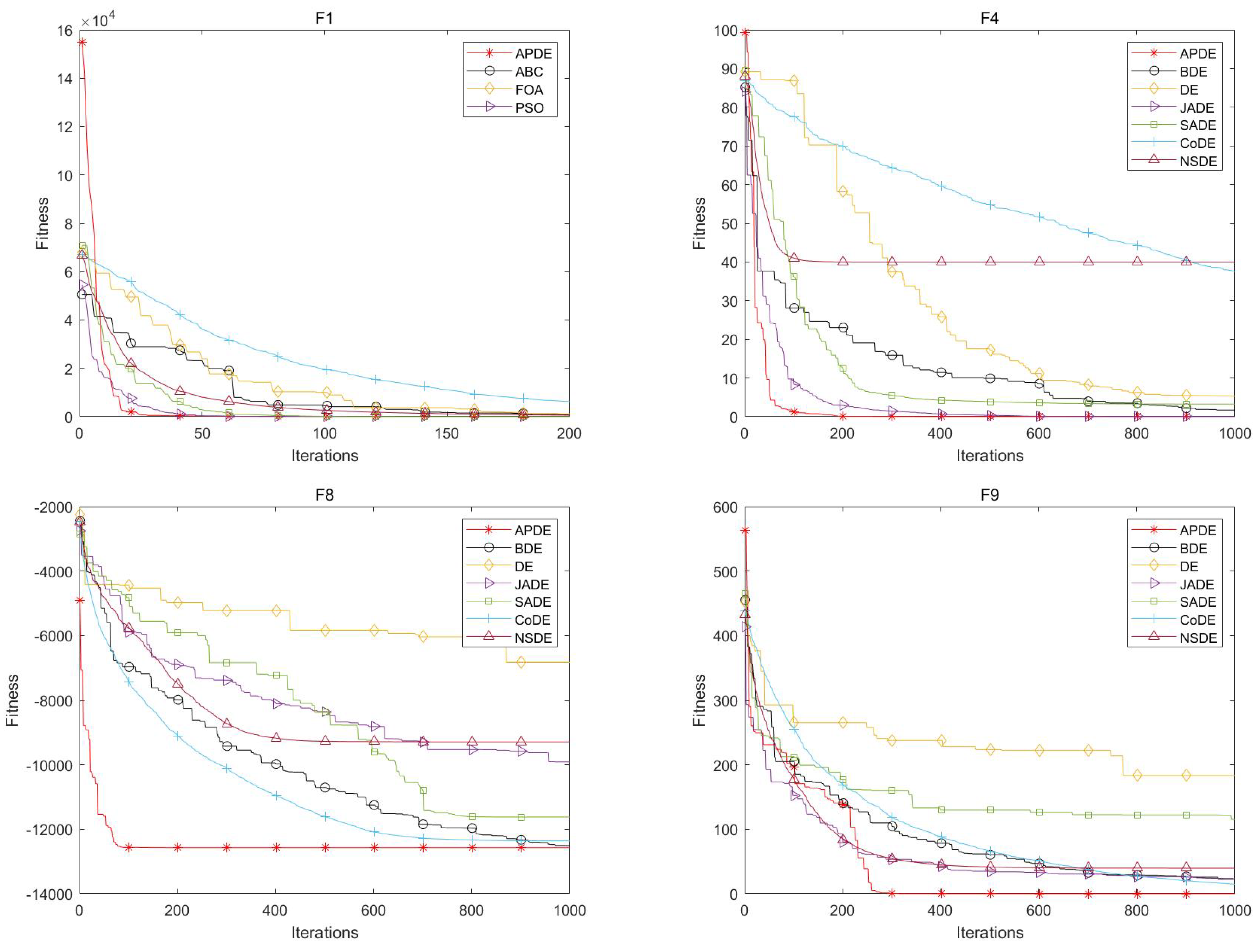
The convergence curves of the six comparison algorithms with respect to test functions F1, F4, F8, and F9 in CEC2005 are illustrated in Figure 3. The horizontal coordinate is the number of iterations, and the vertical coordinate is the adaptation value. From these figures, it can be seen that the convergence curve of APDE is significantly faster than that of the comparison algorithms, especially with respect to F8. For problem F8, APDE is able to converge to the optimal solution more quickly, while the other comparative algorithms all appear to fall into the phenomenon of the local optimum, resulting in slow convergence or being unable to converge to the optimal solution.

Figure 4 shows the convergence curves of the six comparison algorithms on test functions F5, F8, F20, and F26 in CEC2017. It can be seen that the convergence curve of APDE is faster than the comparison algorithms and has an extremely strong global search capability. Taking F20 as an example, we find that APDE appears to fall into the local optimum at about 100 iterations, and the convergence speed slows down significantly but soon jumps out of the local optimum and rapidly approaches the optimal solution. In contrast, other algorithms converge much slower after falling into a local optimum and fail to jump out of that search region.

4.2. Comparative Analysis with APDE and Non-DE Algorithms

In this section, three algorithms, FOA [28], PSO [29], and ABC [30], are selected for comparison to verify the performance of APDE. The initial values of the internal parameters of the comparison method are given in

Table 4. Initial values of the related parameters used by non-DE algorithms.

	Algorithm	Initial Values of the Related Parameters
1	FOA	$R=1$, and $N=30$
2	PSO	$N=30$, $ws=0.9$, and $we=0.4$
3	ABC	$N=30$

. The experimental results in

Table 5. Experimental results of APDE and non-DE algorithms on CEC2005.

		APDE	FOA	PSO	ABC
F1	Mean	$2.7671\times {10}^{-5}$	$3.4789\times {10}^{-4}$	5.8619	$6.47356\times {10}^1$
	Std	$3.6728\times {10}^{-5}$	$7.2446\times {10}^{-6}$	3.2605	$3.30347\times {10}^1$
F2	Mean	$2.2\times {10}^{-3}$	$1.344\times {10}^{-1}$	8.5755	5.2943
	Std	$2.1\times {10}^{-3}$	$1.1\times {10}^{-3}$	2.5337	1.5917
F3	Mean	$1.493\times {10}^{-1}$	0.1	$3.809795\times {10}^2$	$6.794023\times {10}^2$
	Std	$1.582\times {10}^{-1}$	$2\times {10}^{-3}$	$1.634104\times {10}^2$	$1.794454\times {10}^2$
F4	Mean	$1.24\times {10}^{-2}$	$6.2\times {10}^{-3}$	5.6896	9.2921
	Std	$1.32\times {10}^{-2}$	$2.4324\times {10}^{-4}$	1.6489	2.6104
F5	Mean	$4.4316\times {10}^{-4}$	$2.72574\times {10}^1$	$5.282974\times {10}^2$	$1.4153\times {10}^3$
	Std	$4.8201\times {10}^{-5}$	$1.798\times {10}^{-1}$	$3.730906\times {10}^2$	$8.773188\times {10}^2$
F6	Mean	$1.9954\times {10}^{-5}$	7.6012	5.4966	$5.80605\times {10}^1$
	Std	$3.158\times {10}^{-5}$	$1.3\times {10}^{-3}$	2.5967	$2.87079\times {10}^1$
F7	Mean	$2\times {10}^{-3}$	$7.5\times {10}^{-3}$	$2.29\times {10}^{-1}$	$1.51\times {10}^{-2}$
	Std	$9.7877\times {10}^{-4}$	$2.7\times {10}^{-3}$	$1.232\times {10}^{-1}$	$6.3\times {10}^{-3}$
F8	Mean	$-1.2569\times {10}^4$	$-1.221234\times {10}^2$	$-2.8008\times {10}^3$	$-9.7418\times {10}^3$
	Std	$4.5\times {10}^{-3}$	$9.05318\times {10}^1$	$4.774341\times {10}^2$	$1.4094\times {10}^3$
F9	Mean	$2.5615\times {10}^{-5}$	$1.2132\times {10}^1$	$7.28722\times {10}^1$	$5.35102\times {10}^1$
	Std	$3.388\times {10}^{-5}$	4.0147	$1.25021\times {10}^1$	$1.50707\times {10}^1$
F10	Mean	$9.4246\times {10}^{-4}$	$1.76\times {10}^{-2}$	6.1122	5.6689
	Std	$7.538\times {10}^{-4}$	$1.6755\times {10}^{-4}$	1.0414	$9.457\times {10}^{-1}$
F11	Mean	$5.5418\times {10}^{-4}$	$3.4162\times {10}^{-6}$	$1.3268\times {10}^1$	1.5883
	Std	$2.6\times {10}^{-3}$	$2.2187\times {10}^{-7}$	5.2127	$3.157\times {10}^{-1}$
F12	Mean	$1.4094\times {10}^{-7}$	1.6861	5.9645	$1.13509\times {10}^1$
	Std	$3.814\times {10}^{-7}$	$1.8933\times {10}^{-4}$	2.8066	4.0749
F13	Mean	$2.1444\times {10}^{-6}$	2.8738	$2.45472\times {10}^1$	8.559
	Std	$1.1358\times {10}^{-6}$	$6.77\times {10}^{-2}$	$1.02842\times {10}^1$	3.8716
F14	Mean	$9.98\times {10}^{-1}$	$1.26705\times {10}^1$	1.5581	$9.98\times {10}^{-1}$
	Std	0	$2.5973\times {10}^{-15}$	1.3639	0
F15	Mean	$3.0749\times {10}^{-4}$	$3.1044\times {10}^{-4}$	$1.1\times {10}^{-3}$	$1.1\times {10}^{-3}$
	Std	$1.9206\times {10}^{-19}$	$2.8809\times {10}^{-6}$	$3.7\times {10}^{-3}$	$3.4709\times {10}^{-4}$
F16	Mean	−1.0316	$-9.904\times {10}^{-1}$	−1.0316	−1.0316
	Std	$6.3208\times {10}^{-16}$	$1.9\times {10}^{-3}$	$6.7752\times {10}^{-16}$	0
F17	Mean	$3.979\times {10}^{-1}$	1.3679	$3.979\times {10}^{-1}$	$3.979\times {10}^{-1}$
	Std	0	1.7189	0	0
F18	Mean	3	$4.637548\times {10}^2$	3	3
	Std	$4.7536\times {10}^{-15}$	$2.327856\times {10}^2$	$8.4903\times {10}^{-16}$	$1.2176\times {10}^{-15}$
F19	Mean	−3.8628	−3.8614	−3.8617	−3.8628
	Std	$2.5973\times {10}^{-15}$	$1.1\times {10}^{-3}$	$2.7\times {10}^{-3}$	$2.7101\times {10}^{-15}$
F20	Mean	−3.2625	−3.2731	−3.1106	−3.3061
	Std	$6.05\times {10}^{-2}$	$6.04\times {10}^{-2}$	$1.741\times {10}^{-1}$	$4.12\times {10}^{-2}$
F21	Mean	$-1.01532\times {10}^1$	−4.8652	−7.0755	−6.7295
	Std	$3.3404\times {10}^{-15}$	$9.76\times {10}^{-2}$	3.6272	2.412
F22	Mean	$-1.04029\times {10}^1$	−4.9067	−7.5511	−7.2148
	Std	$1.0881\times {10}^{-16}$	$8.09\times {10}^{-2}$	3.6222	2.6192
F23	Mean	$-1.05364\times {10}^1$	−4.918	−6.9553	−7.8598
	Std	$1.4752\times {10}^{-15}$	$1.01\times {10}^{-1}$	3.9217	2.7264

and

Table 6. Experimental results of APDE and non-DE algorithms on CEC2017.

		APDE	FOA	PSO	ABC
F1	Mean	2729.5	$7.6172\times {10}^{10}$	$1.6858\times {10}^8$	$2.5996\times {10}^9$
	Std	2165	$5.575\times {10}^9$	$1.9251\times {10}^8$	$8.7395\times {10}^8$
F3	Mean	57,005	$3.1394\times {10}^5$	$1.619\times {10}^4$	$4.378\times {10}^4$
	Std	10,801	$9.7971\times {10}^5$	$7.0253\times {10}^3$	$9.0639\times {10}^3$
F4	Mean	505.7209	$2.734\times {10}^4$	$5.670727\times {10}^2$	$9.637917\times {10}^2$
	Std	21.8697	$3.7648\times {10}^3$	$4.47303\times {10}^1$	$1.487912\times {10}^2$
F5	Mean	552.7471	$1.0771\times {10}^3$	$7.226343\times {10}^2$	$7.405149\times {10}^2$
	Std	28.5613	$2.7584\times {10}^1$	$4.15171\times {10}^1$	$3.9513\times {10}^1$
F6	Mean	600.5737	$7.374679\times {10}^2$	$6.579862\times {10}^2$	$6.597004\times {10}^2$
	Std	0.3657	3.6679	7.997	7.94
F7	Mean	801.4768	$1.6074\times {10}^3$	$1.169\times {10}^3$	$1.1579\times {10}^3$
	Std	49.5881	$2.5624\times {10}^1$	$6.98711\times {10}^1$	$8.95354\times {10}^1$
F8	Mean	838.5942	$1.2721\times {10}^3$	$9.582994\times {10}^2$	$9.880909\times {10}^2$
	Std	15.6357	$2.7983\times {10}^1$	$2.87134\times {10}^1$	$2.62331\times {10}^1$
F9	Mean	978.0673	$2.4794\times {10}^4$	$6.1283\times {10}^3$	$4.6741\times {10}^3$
	Std	63.4706	$2.9842\times {10}^3$	$2.8367\times {10}^3$	$8.580764\times {10}^2$
F10	Mean	8128.5	$1.0705\times {10}^4$4	$7.6199\times {10}^3$	$6.5063\times {10}^3$
	Std	332.5984	$2.726\times {10}^2$	$1.2668\times {10}^3$	$9.590753\times {10}^2$
F11	Mean	1186.1	$2.3779\times {10}^7$	$1.3065\times {10}^3$	$1.6442\times {10}^3$
	Std	35.6117	$9.1104\times {10}^7$	$4.9848\times {10}^1$	$1.701857\times {10}^2$
F12	Mean	186,230	$2.6497\times {10}^{10}$	$1.7366\times {10}^7$	$2.3806\times {10}^8$
	Std	175,930	$1.538\times {10}^9$	$1.7629\times {10}^7$	$1.8372\times {10}^8$
F13	Mean	2620.3	$3.8269\times {10}^{10}$	$5.5492\times {10}^4$	$1.3492\times {10}^7$
	Std	934.8219	$1.8839\times {10}^9$	$2.1185\times {10}^4$	$5.1156\times {10}^7$
F14	Mean	3318.5	$3.3829\times {10}^8$	$5.6594\times {10}^3$	$1.0177\times {10}^4$
	Std	2825.7	$1.4838\times {10}^7$	$7.8943\times {10}^3$	$9.7779\times {10}^3$
F15	Mean	3649.6	$2.0954\times {10}^9$	$1.0978\times {10}^4$	$8.6969\times {10}^4$
	Std	2398.1	$1.9261\times {10}^9$	$1.23\times {10}^4$	$7.5067\times {10}^4$
F16	Mean	2343.1	$2.4409\times {10}^4$	$3.205\times {10}^3$	$3.619\times {10}^3$
	Std	293.1592	$1.0266\times {10}^3$	$4.301665\times {10}^2$	$5.440168\times {10}^2$
F17	Mean	1862.6	$1.6042\times {10}^5$	$2.54\times {10}^3$	$2.6673\times {10}^3$
	Std	140.6238	$5.4233\times {10}^4$	$2.750784\times {10}^2$	$2.905801\times {10}^2$
F18	Mean	114,850	$2.7169\times {10}^8$	$1.1528\times {10}^5$	$1.9465\times {10}^5$
	Std	112,900	$1.9373\times {10}^8$	$8.8694\times {10}^4$	$1.9488\times {10}^5$
F19	Mean	4294.4	$3.8767\times {10}^9$	$2.2328\times {10}^4$	$1.4227\times {10}^6$
	Std	2941.8	$1.2126\times {10}^9$	$3.7165\times {10}^4$	$1.1775\times {10}^6$
F20	Mean	2257.2	$4.0039\times {10}^3$	$2.9327\times {10}^3$	$2.6397\times {10}^3$
	Std	154.4296	$2.406754\times {10}^2$	$2.512879\times {10}^2$	$1.902986\times {10}^2$
F21	Mean	2339.3	$3.1295\times {10}^3$	$2.5419\times {10}^3$	$2.5409\times {10}^3$
	Std	12.7166	$7.43221\times {10}^1$	$4.7216\times {10}^1$	$5.16423\times {10}^1$
F22	Mean	2780.5	$1.2535\times {10}^4$	$8.2113\times {10}^3$	$4.802\times {10}^3$
	Std	1744	$3.405273\times {10}^2$	$2.6454\times {10}^3$	$1.9759\times {10}^3$
F23	Mean	2703.1	$7.455\times {10}^3$	$3.381\times {10}^3$	$3.1637\times {10}^3$
	Std	11.5086	$3.75245\times {10}^2$	$1.618321\times {10}^2$	$1.227726\times {10}^2$
F24	Mean	2862	$5.064\times {10}^3$	$3.5219\times {10}^3$	$3.3313\times {10}^3$
	Std	14.8097	$8.7008\times {10}^1$	$1.145412\times {10}^2$	$1.611433\times {10}^2$
F25	Mean	2895.5	$7.8666\times {10}^3$	$2.9708\times {10}^3$	$3.1424\times {10}^3$
	Std	10.8019	$7.263779\times {10}^2$	$2.8147\times {10}^1$	$1.02589\times {10}^2$
F26	Mean	4179.2	$1.4981\times {10}^4$	$7.8871\times {10}^3$	$7.3541\times {10}^3$
	Std	290.9716	$1.0514\times {10}^3$	$1.9508\times {10}^3$	$1.1313\times {10}^3$
F27	Mean	3230.2	$9.9802\times {10}^3$	$4.3406\times {10}^3$	$3.5674\times {10}^3$
	Std	10.6208	$4.872097\times {10}^2$	$3.5174\times {10}^2$	$1.982072\times {10}^2$
F28	Mean	3240.1	$9.3889\times {10}^3$	$3.3532\times {10}^3$	$3.5575\times {10}^3$
	Std	22.1760	$6.178348\times {10}^2$	$6.43858\times {10}^1$	$1.308719\times {10}^2$
F29	Mean	3649.4	$1.4735\times {10}^5$	$4.9034\times {10}^3$	$5.3525\times {10}^3$
	Std	114.5539	$3.6258\times {10}^4$	$4.992055\times {10}^2$	$8.169842\times {10}^2$
F30	Mean	14,693	$8.3891\times {10}^9$	$7.8374\times {10}^5$	$1.6123\times {10}^7$
	Std	6737	$7.8877\times {10}^8$	$9.49\times {10}^5$	$2.0258\times {10}^7$

show that APDE achieved optimal values for 17 test functions in CEC2005 and 27 test functions in CEC2017. Although APDE failed to achieve the best results on the remaining eight functions, it still ranked second or found the optimal value among several comparative algorithms.

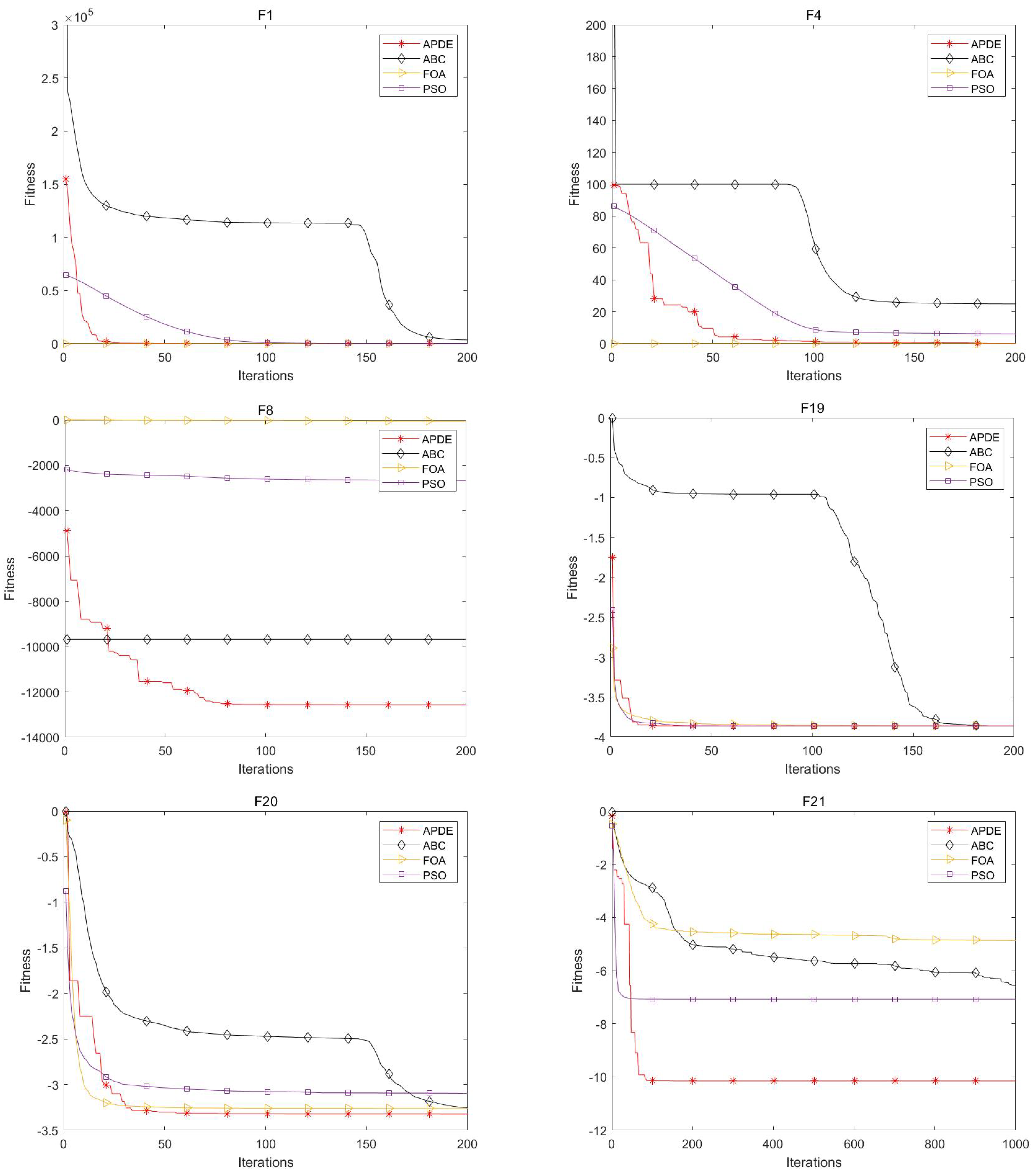
In Figure 5, the convergence curves of the three comparison algorithms with respect to test functions F1, F4, F8, F19, F20, and F21 in CEC2005 are presented. It can be seen from the figure that APDE can not only converge more quickly but also finds better solutions compared to other algorithms. On F1 and F4, the APDE converges second only to the FOA, which is due to the fact that the initial fitness value of the FOA is more close to the optimal solution 0. With respect to F8, F19, F20, and F21, the optimal value of the test function is negative, and the FOA has no initial solution advantage. At this point, APDE achieves the fastest convergence rate, as well as the smallest fitness value, through its powerful global exploration capability.

In Figure 6, the convergence curves of the three comparison algorithms on test functions F1, F5, F9, F22, F24, and F28 with respect to CEC2017 are presented. APDE has a unique two-stage structure and a mutation strategy that is more conducive to global search. Then, APDE is able to jump out of the current search region after briefly falling into a local optimum, which enhances the vitality of the algorithm. As can be seen in Figure 6, APDE has the fastest convergence rate, as well as the optimal fitness value, especially for F22. After APDE and PSO fall into a local optimum at the same node, PSO slowly stops updating the optimal solution, whereas APDE obtains a secondary search capability by jumping out of the current search region.

4.3. Wilcoxon Signed-Rank Test

To further analyze the performance of APDE, the Wilcoxon signed rank test is employed in this paper to compare the experimental results of CEC2005 and CEC2017 provided by APDE and other algorithms in a two-by-two manner. The Wilcoxon signed-rank test adds the ranks of the absolute values of the difference between the observed values and the center of the null hypothesis according to different signs as its test statistic. It suits paired comparisons without needing the differences between pairs of data to be normally distributed. From

Table A3. Wilcoxon signed-rank test results for CEC2005.

Fnc	CoDE				DE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	51	414	$9.83\times {10}^{-8}$	+
F2	0	465	$3.02\times {10}^{-11}$	+	35	430	$7.74\times {10}^{-6}$	+
F3	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F4	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F5	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F6	0	465	$3.02\times {10}^{-11}$	+	85	380	0.002	+
F7	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F10	0	465	$3.02\times {10}^{-11}$	+	13	452	$1.1\times {10}^{-8}$	+
F11	0	465	$3.02\times {10}^{-11}$	+	177	288	0.0392	+
F12	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F13	0	465	$3.02\times {10}^{-11}$	+	28	437	$1.03\times {10}^{-6}$	+
F14	0	0	0	=	0	1	0.3337	−
F15	0	465	$2.49\times {10}^{-7}$	+	0	36	0.0028	+
F16	0	0	0	=	0	0	0	=
F17	0	0	0	=	0	0	0	=
F18	0	465	0.0055	+	0	0	0.0055	+
F19	0	0	0	=	0	0	0	=
F20	192	273	0.3166	−	156	222	0.2145	−
F21	0	0	0	=	0	0	0	=
F22	0	0	0	=	0	0	0	=
F23	0	0	0	=	0	0	0	=
+				15				15
=				7				6
−				1				2
Fnc	BDE				JADE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	465	0	$3.02\times {10}^{-11}$	+
F2	0	465	$3.02\times {10}^{-11}$	+	465	0	$3.02\times {10}^{-11}$	+
F3	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F4	0	465	$3.02\times {10}^{-11}$	+	347	118	0.0232	+
F5	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F6	0	465	$3.02\times {10}^{-11}$	+	465	0	$3.02\times {10}^{-11}$	+
F7	0	465	$3.34\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F10	0	465	$3.02\times {10}^{-11}$	+	300	165	$4.65\times {10}^{-5}$4	+
F11	0	465	$3.02\times {10}^{-11}$	+	183	282	0.1079	−
F12	0	465	$3.02\times {10}^{-11}$	+	235	230	0.007	+
F13	0	465	$3.02\times {10}^{-11}$	+	325	140	$9.51\times {10}^{-6}$	+
F14	0	0	0	=	0	0	0	=
F15	0	153	$1.21\times {10}^{-12}$	+	0	3	0.1607	−
F16	0	0	0	=	0	0	0	=
F17	0	0	0	=	0	0	0	=
F18	0	0	0.0055	+	0	0	0.0055	+
F19	0	0	0	=	0	0	0	=
F20	465	0	$1.21\times {10}^{-12}$	+	390	45	$2.73\times {10}^{-9}$	+
F21	0	0	0	=	0	10	0.0419	+
F22	0	0	0	=	0	10	0.0419	+
F23	0	0	0	=	0	3	0.1608	−
+				16				16
=				7				4
−				0				3
Fnc	NSDE				SaDE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$5.07\times {10}^{-10}$	+	465	0	$3.02\times {10}^{-11}$	+
F2	409	56	$3.81\times {10}^{-7}$	+	465	0	$3.02\times {10}^{-11}$	+
F3	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F4	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F5	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F6	12	453	$5.46\times {10}^{-9}$	+	465	0	$3.02\times {10}^{-11}$	+
F7	0	465	$3.02\times {10}^{-11}$	+	0	465	$6.07\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F10	0	465	$3.02\times {10}^{-11}$	+	435	30	$5.54\times {10}^{-10}$	+
F11	11	454	$4.18\times {10}^{-9}$	+	264	201	0.0035	+
F12	0	465	$3.02\times {10}^{-11}$	+	435	30	$5.57\times {10}^{-10}$	+
F13	0	465	$3.02\times {10}^{-11}$	+	378	87	$1.07\times {10}^{-7}$	+
F14	0	465	0.0215	+	0	0	0	=
F15	0	465	$6.36\times {10}^{-5}$	+	0	3	0.1608	−
F16	0	0	0	=	0	0	0	=
F17	0	0	0	=	0	0	0	=
F18	0	465	0.0055	+	0	0	0.0055	+
F19	0	0	0	=	0	0	0	=
F20	233	232	0.0858	−	375	90	$3.75\times {10}^{-6}$	+
F21	351	114	0.0419	+	0	10	0.0419	+
F22	276	189	0.0055	+	0	3	0.1607	−
F23	210	255	0.000658	+	0	0	0	=
+				19				16
=				3				5
−				1				2
Fnc	FOA				PSO
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F2	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F3	229	236	0.379	−	0	465	$3.02\times {10}^{-11}$	+
F4	411	54	0.000399	+	0	465	$3.02\times {10}^{-11}$	+
F5	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F6	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F7	13	452	$1.55\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F10	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F11	461	4	$8.48\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F12	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F13	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F14	0	465	$3.02\times {10}^{-11}$	+	0	465	0.0056	+
F15	0	465	$1.21\times {10}^{-12}$	+	0	465	0.0216	+
F16	0	465	$1.21\times {10}^{-12}$	+	0	0	0	=
F17	0	465	$1.21\times {10}^{-12}$	+	0	0	0	=
F18	0	465	$7.57\times {10}^{-12}$	+	0	465	0.0055	+
F19	0	465	$1.21\times {10}^{-12}$	+	351	114	0.0418	+
F20	280	185	0.2905	−	44	421	0.000156	+
F21	0	465	$1.21\times {10}^{-12}$	+	153	312	$6.13\times {10}^{-5}$	+
F22	0	465	$1.21\times {10}^{-12}$	+	171	294	0.000144	+
F23	0	465	$1.21\times {10}^{-12}$	+	136	329	$2.9\times {10}^{-5}$	+
+				21				21
=				0				2
−				2				0
Fnc	ABC
	R+		R−		p-Value		Sig.
F1	0		465		$3.02\times {10}^{-11}$		+
F2	0		465		$3.02\times {10}^{-11}$		+
F3	0		465		$3.02\times {10}^{-11}$		+
F4	0		465		$3.02\times {10}^{-11}$		+
F5	0		465		$3.02\times {10}^{-11}$		+
F6	0		465		$3.02\times {10}^{-11}$		+
F7	0		465		$6.7\times {10}^{-11}$		+
F8	1		464		$5.57\times {10}^{-10}$		+
F9	0		465		$3.02\times {10}^{-11}$		+
F10	0		465		$3.02\times {10}^{-11}$		+
F11	0		465		$3.02\times {10}^{-11}$		+
F12	0		465		$3.02\times {10}^{-11}$		+
F13	0		465		$3.02\times {10}^{-11}$		+
F14	0		0		0		=
F15	0		465		$8.99\times {10}^{-11}$		+
F16	0		465		1		−
F17	0		465		1		−
F18	0		465		0.0055		+
F19	0		0		0		=
F20	392		73		$6.04\times {10}^{-7}$		+
F21	45		420		$2.1\times {10}^{-8}$		+
F22	66		399		$8.78\times {10}^{-8}$		+
F23	105		360		$4.27\times {10}^{-6}$		+
+							19
=							2
−							2

and

Table A4. Wilcoxon signed-rank test results for CEC2017.

Fnc	CoDE				DE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	26	439	$2.88\times {10}^{-6}$	+
F3	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F4	27	438	$6.77\times {10}^{-5}$	+	361	104	0.0798	−
F5	0	465	$4.98\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F6	0	465	$3.02\times {10}^{-11}$	+	457	8	$8.1\times {10}^{-10}$	+
F7	2	463	$4.2\times {10}^{-10}$	+	0	465	$3.02\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	465	0	$3.02\times {10}^{-11}$	+
F10	432	33	$9.26\times {10}^{-9}$	+	70	395	$5.27\times {10}^{-5}$	+
F11	0	465	$3.02\times {10}^{-11}$	+	6	459	$5.09\times {10}^{-8}$	+
F12	0	465	$3.02\times {10}^{-11}$	+	6	459	$8.1\times {10}^{-10}$	+
F13	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.82\times {10}^{-10}$	+
F14	461	4	$8.48\times {10}^{-9}$	+	462	3	$7.77\times {10}^{-9}$	+
F15	398	67	0.0037	+	465	0	$1.61\times {10}^{-10}$	+
F16	24	441	$8.35\times {10}^{-8}$	+	0	465	$3.02\times {10}^{-11}$	+
F17	7	458	$2.67\times {10}^{-9}$	+	7	458	$3.2\times {10}^{-9}$	+
F18	46	419	$5.46\times {10}^{-6}$	+	379	86	0.000422	+
F19	393	72	0.0083	+	462	3	$7.38\times {10}^{-10}$	+
F20	95	370	0.002	+	97	368	0.0028	+
F21	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F22	9	456	$1.07\times {10}^{-9}$	+	8	457	$7.6\times {10}^{-7}$	+
F23	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F24	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F25	4	461	$5.07\times {10}^{-10}$	+	415	50	$2.2\times {10}^{-7}$	+
F26	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F27	441	24	$1.11\times {10}^{-6}$	+	456	9	$2.23\times {10}^{-9}$	+
F28	0	465	$3.02\times {10}^{-11}$	+	258	207	0.4204	−
F29	84	381	0.000189	+	8	457	$3.65\times {10}^{-8}$	+
F30	11	454	$7.38\times {10}^{-10}$	+	88	377	0.0076	+
+				29				27
=				0				0
−				0				2
Fnc	BDE				JADE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	465	0	$3.02\times {10}^{-11}$	+
F3	344	121	0.0138	+	383	82	0.000446	+
F4	116	349	0.000104	+	464	1	$2.83\times {10}^{-8}$	+
F5	3	462	$34.18\times {10}^{-9}$	+	132	333	0.0076	+
F6	69	396	$2.6\times {10}^{-5}$	+	422	43	$2.49\times {10}^{-6}$	+
F7	17	448	$2.32\times {10}^{-6}$	+	290	175	0.5692	−
F8	0	465	$3.02\times {10}^{-11}$	+	51	414	0.000399	+
F9	129	336	0.0014	+	465	0	$1.96\times {10}^{-10}$	+
F10	460	5	$8.48\times {10}^{-9}$	+	462	3	$5\times {10}^{-9}$	+
F11	4	461	$2.83\times {10}^{-8}$	+	106	359	0.007	+
F12	5	460	$1.21\times {10}^{-10}$	+	437	28	$3.81\times {10}^{-7}$	+
F13	0	465	$6.72\times {10}^{-10}$	+	240	225	0.3953	−
F14	221	244	0.6952	−	287	178	0.000239	+
F15	49	416	0.000168	+	379	86	$1.19\times {10}^{-6}$	+
F16	35	430	$1.75\times {10}^{-5}$	+	199	266	0.2226	−
F17	22	443	$8.35\times {10}^{-8}$	+	139	326	0.0076	+
F18	221	244	0.7618	−	333	132	0.00077	+
F19	76	389	0.000952	+	399	66	$1.25\times {10}^{-7}$	+
F20	83	382	0.000399	+	100	365	0.0037	+
F21	0	465	$3.02\times {10}^{-11}$	+	72	393	0.0013	+
F22	289	176	0.7731	−	408	57	$9.58\times {10}^{-9}$	+
F23	0	465	$3.02\times {10}^{-11}$	+	166	299	0.1858	−
F24	0	465	$3.34\times {10}^{-11}$	+	107	358	0.0095	+
F25	163	302	0.0224	+	366	99	0.0012	+
F26	129	336	$7.74\times {10}^{-6}$	+	98	367	0.0176	+
F27	79	386	0.000168	+	301	164	0.1023	−
F28	142	323	0.0378	+	442	23	$1.39\times {10}^{-6}$	+
F29	151	314	0.0281	+	119	346	0.0024	+
F30	40	425	$3.75\times {10}^{-6}$	+	364	101	0.000471	+
+				26				24
=				0				0
−				3				5
Fnc	NSDE				SaDE
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	60	405	0.000158	+	465	0	$3.02\times {10}^{-11}$	+
F3	405	60	0.00077	+	0	465	$1.61\times {10}^{-10}$	+
F4	190	275	0.3632	−	279	186	0.4825	−
F5	50	415	$7.09\times {10}^{-8}$	+	0	465	$3.34\times {10}^{-11}$	+
F6	0	465	$3.34\times {10}^{-11}$	+	465	0	$1.78\times {10}^{-10}$	+
F7	35	430	$5.86\times {10}^{-6}$	+	0	465	$9.76\times {10}^{-10}$	+
F8	9	456	$2.67\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	15	450	$2.67\times {10}^{-9}$	+	465	0	$2.84\times {10}^{-11}$	+
F10	462	3	$1.17\times {10}^{-9}$	+	230	235	0.5793	−
F11	55	410	0.000133	+	61	404	$4.35\times {10}^{-5}$	+
F12	25	440	$3.37\times {10}^{-5}$	+	79	386	0.000253	+
F13	7	458	$4.18\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F14	340	125	0.0327	+	333	132	0.0364	+
F15	154	311	0.1809	−	278	187	0.7172	−
F16	151	314	0.1224	−	6	459	$7.12\times {10}^{-9}$	+
F17	47	418	$2.13\times {10}^{-5}$	+	5	460	$5.46\times {10}^{-9}$	+
F18	357	108	0.0127	+	16	449	$1.47\times {10}^{-7}$	+
F19	148	317	0.0378	+	316	149	0.1055	−
F20	37	428	$6.28\times {10}^{-6}$	+	47	418	$5.27\times {10}^{-5}$	+
F21	9	456	$1.56\times {10}^{-8}$	+	0	465	$3.02\times {10}^{-11}$	+
F22	92	373	0.0635	−	178	287	0.3478	−
F23	34	431	0.000129	+	0	465	$3.02\times {10}^{-11}$	+
F24	0	465	$1.17\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F25	178	287	0.2009	−	328	137	0.1023	−
F26	6	459	$2.92\times {10}^{-9}$	+	0	465	$3.02\times {10}^{-11}$	+
F27	207	258	0.865	−	443	22	$5.19\times {10}^{-7}$	+
F28	145	320	0.0635	−	228	237	0.8418	−
F29	141	324	0.0519	−	27	438	$2.57\times {10}^{-7}$	+
F30	374	91	0.0038	+	67	398	0.000225	+
+				21				22
=				0				0
−				8				7
Fnc	FOA				PSO
	R+	R−	p-Value	Sig.	R+	R−	p-Value	Sig.
F1	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F3	0	465	$3.02\times {10}^{-11}$	+	1	464	$6.07\times {10}^{-11}$	+
F4	0	465	$3.02\times {10}^{-11}$	+	0	465	$8.15\times {10}^{-11}$	+
F5	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.34\times {10}^{-11}$	+
F6	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F7	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F8	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F9	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F10	0	465	$3.02\times {10}^{-11}$	+	272	193	0.3255	−
F11	0	465	$3.02\times {10}^{-11}$	+	1	464	$2.37\times {10}^{-10}$	+
F12	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F13	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F14	0	465	$3.02\times {10}^{-11}$	+	136	329	0.0877	−
F15	0	465	$3.02\times {10}^{-11}$	+	60	405	$3.09\times {10}^{-6}$	+
F16	0	465	$3.02\times {10}^{-11}$	+	3	462	$8.89\times {10}^{-10}$	+
F17	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.69\times {10}^{-11}$	+
F18	0	465	$3.02\times {10}^{-11}$	+	175	290	0.1413	−
F19	0	465	$3.02\times {10}^{-11}$	+	63	402	0.000239	+
F20	0	465	$3.02\times {10}^{-11}$	+	0	465	$4.08\times {10}^{-11}$	+
F21	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F22	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.82\times {10}^{-10}$	+
F23	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F24	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F25	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F26	0	465	$3.02\times {10}^{-11}$	+	10	455	$8.2\times {10}^{-7}$	+
F27	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F28	0	465	$3.02\times {10}^{-11}$	+	0	465	$5.49\times {10}^{-11}$	+
F29	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
F30	0	465	$3.02\times {10}^{-11}$	+	0	465	$3.02\times {10}^{-11}$	+
+				29				26
=				0				0
−				3				0
Fnc	ABC
	R+		R−		p-Value		Sig.
F1	0		465		$3.02\times {10}^{-11}$		+
F3	340		125		0.0138		+
F4	0		465		$3.02\times {10}^{-11}$		+
F5	0		465		$3.02\times {10}^{-11}$		+
F6	0		465		$3.02\times {10}^{-11}$		+
F7	0		465		$6.7\times {10}^{-11}$		+
F8	1		464		$5.57\times {10}^{-10}$		+
F9	0		465		$3.02\times {10}^{-11}$		+
F10	414		51		$4.11\times {10}^{-7}$		+
F11	0		465		$3.02\times {10}^{-11}$		+
F12	0		465		$3.02\times {10}^{-11}$		+
F13	0		465		$3.02\times {10}^{-11}$		+
F14	37		428		$5.86\times {10}^{-6}$		+
F15	0		465		$6.07\times {10}^{-11}$		+
F16	0		465		$3.69\times {10}^{-11}$		+
F17	0		465		$3.69\times {10}^{-11}$		+
F18	78		387		0.00077		+
F19	0		465		$3.69\times {10}^{-11}$		+
F20	4		461		$2.61\times {10}^{-10}$		+
F21	0		465		$3.02\times {10}^{-11}$		+
F22	45		420		$2.92\times {10}^{-9}$		+
F23	0		465		$3.69\times {10}^{-11}$		+
F24	0		465		$3.69\times {10}^{-11}$		+
F25	0		465		$3.69\times {10}^{-11}$		+
F26	0		465		$3.69\times {10}^{-11}$		+
F27	0		465		$3.69\times {10}^{-11}$		+
F28	0		465		$3.69\times {10}^{-11}$		+
F29	0		465		$3.69\times {10}^{-11}$		+
F30	0		465		$3.69\times {10}^{-11}$		+
+							29
=							0
−							0

in the Appendix B, we give the results of the significance comparisons based on the Wilcoxon signed rank test with $p-level=0.5$. The comparison results are represented as (+, =, -) in the last row of Table A3 and Table A4. Here, (+) indicates that APDE is statistically superior to the comparison algorithms on current benchmark functions. (=) indicates that APDE is statistically neck-to-neck relative to the effect of the correlation comparison algorithm. (-) indicates that APDE does not perform better than the competition algorithms with respect to the current benchmark function.

The Wilcoxon signed-rank test results on the CEC2005 test set can be expressed as follows: CoDE (15,7,1), DE (15,6,2), BDE (16,7,0), JADE (16,4,3), NSDE (19,3,1), SaDE (16,5,2), FOA (21,0,2), PSO (21,2,0), and ABC (19,2,2). APDE outperforms the comparison algorithm in solving 158 of the 207 standardized test functions of CEC2005, and it performs statistically neck-to-neck relative to the comparison algorithm with respect to 36 functions.

The results on CEC2017 are: CoDE (29,0,0), DE (27,0,2), BDE (26,0,3), JADE (24,0,5), NSDE (21,0,8), SaDE (22,0,7), FOA (29,0,0), PSO (26,0,3), ABC (29,0,0). Here APDE outperforms the comparison algorithm in solving 233 of the 261 standardized test functions, and performs statistically worse than the comparison algorithm on only 28 functions.

4.4. Computational Complexity Analysis

The time complexity of APDE and the other comparison algorithms in this paper is $O(1000\times D\times N)$. Therefore, to deeply analyze the computational complexity of APDE,

Table 7. The execution times of various algorithms on the F18 benchmark.

	Alg.	APDE	CoDE	BDE	JADE	NSDE	SADE	DE	FOA	PSO	ABC
D
10		17.70 s	66.84 s	22.93 s	77.84 s	329.44 s	23.00 s	78.90 s	15.64 s	2.31 s	6.46 s
30		19.79 s	141.29 s	35.32 s	55.96 s	328.55 s	33.87 s	90.16 s	21.80 s	1.85 s	20.26 s
50		23.25 s	269.50 s	55.61 s	141.23 s	347.53 s	35.11 s	87.36 s	25.64 s	3.20 s	42.62 s

provides the execution times of each algorithm running 20,000 times on CEC2017’s F18. The table indicates that the computational speed of APDE is surpassed by only PSO among the 10 algorithms evaluated, a circumstance that may be attributed to the simplistic architecture of PSO. Nevertheless, the employment of PSO necessitates a considerable investment of latent time dedicated to the fine-tuning of parameters. It can be observed from Figure 7 that APDE exhibits stability across problems of varying dimensions, with its runtime not significantly altering with an increase in dimensionality. This further validates the advantage of APDE in addressing high-dimensional problems.

5. Conclusions

Traditional DE-type algorithms are all parametric, which often need a lengthy process of parameter tuning, especially in solving different models to guarantee accuracy. Additionally, few of the current algorithms have been designed to take into account the characteristics of the iterative process. These may lead to an inadequate equilibrium between the efficiency and accuracy of the algorithm.

This paper proposes a two-stage adaptive differential evolutionary algorithm with accompanying populations, which develops different mutation strategies based on the search characteristics of each stage in the algorithm. APDE divides the search process into two phases by analyzing the search features, giving the calculation of adaptive weight factors and crossover factors with new distributional characteristics and balancing local searches and global exploration through population classification. Therefore, APDE can both converge quickly in the early stage and avoid falling into local optima in the later search stage.