The Finite Coarse Shape Paths

Abstract

In this paper, we introduce the notions of finite coarse shape path and finite coarse shape path connectedness of a topological space. We prove that the solenoid ${\Sigma }_{\left(p_n\right)}$, which is known to be coarse shape path connected but not shape path connected, is not finite coarse shape path connected either. Furthermore, we show that every finite coarse shape path induces an isomorphism between finite coarse shape groups of the topological space at different base points, with some interesting and useful properties. We also show that finite coarse shape groups of the same space, in general, depend on the choice of a base point. Hence, the pointed finite coarse shape type of $\left(X,x\right)$, in general, depends on the choice of the point x. Finally, we prove that if X is a finite coarse shape path connected paracompact locally compact space, then the pointed finite coarse shape type of $\left(X,x\right)$ does not depend on the choice of the point x.

1. Introduction

A new classification of topological spaces based on the finite coarse shape theory was introduced in [1]. Although this theory is abstract and makes sense for any pair $\left(C,D\right)$ consisting of the category C and its full and dense subcategory D, the most important case is if $C=HTop$ ($C=HTo{p}_{🟉}$) (homotopy class of all (pointed) topological spaces) and $D=HPol$ ($D=HPo{l}_{🟉}$) (class of (pointed) topological spaces that have the homotopy type of some (pointed) polyhedron) because it yields the (pointed) topological finite coarse shape category $S{h}^{⊛}(S{h}_{🟉}^{⊛}$). So far, many interesting invariants of the finite coarse shape theory have been investigated. The most important of them are the (relative) finite coarse shape groups of (bi)pointed topological spaces.

In this paper, we introduce the notion of the finite coarse shape path between two points x and $x^{\prime }$ in a topological space X. The space X is said to be finite coarse shape path connected if for every pair of points in X there exists a finite coarse shape path in X between these points, and we show that being finite coarse shape path connected is a topological property (Corollary 1). We also investigate an interesting example of the solenoid ${\Sigma }_{\left(p_n\right)}$, which is known to be coarse shape path connected but not shape path connected and prove that there are infinitely many finite coarse shape path components in ${\Sigma }_{\left(p_n\right)}$.

Furthermore, by Theorem 1, we show that, for every $k\in \mathbb{N}$, every finite coarse shape path ${\mathrm{\Omega }}^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ induces a group isomorphism (for $k=0$ a basepoint preserving bijection) from ${\check{\pi }}_k^{⊛}\left(X,x_0\right)$ to ${\check{\pi }}_k^{⊛}\left(X,x_1\right)$ with some interesting and useful properties (Proposition 2). Example 2 shows that finite coarse shape groups of the same space, in general, depend on the choice of a base point. Hence, since these groups are finite coarse shape invariant, the pointed finite coarse shape type of $\left(X,x\right)$, in general, depends on the choice of point x. However, there is a large class of topological spaces for which this is not true. We prove that if X is a finite coarse shape path-connected paracompact locally compact space, the pointed finite coarse shape type of $\left(X,x\right)$ does not depend on the choice of the point x (Theorem 2).

2. Preliminaries

Let us now recall the basics of the finite coarse shape theory. A finite ∗-morphism (i.e., ⊛-morphism) between inverse systems $\mathbf{X}=\left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ and $\mathbf{Y}=\left(Y_{\mu },q_{\mu {\mu }^{\prime }},M\right)$ in a category C is a pair $\left(f,f_{\mu }^m\right)$ which consists of a function $f:M\to \mathrm{\Lambda }$ (called an index function) and, for every $\mu \in M$, of a sequence of morphisms $f_{\mu }^m:X_{f\left(\mu \right)}\to Y_{\mu }$, $m\in \mathbb{N}$, in C such that

$\left(1\right)$

for every pair $\mu ,{\mu }^{\prime }\in M$, $\mu \le {\mu }^{\prime }$, there exist $\lambda \in \mathrm{\Lambda }$, $\lambda \ge f\left(\mu \right),f\left({\mu }^{\prime }\right)$, and $m_{\mu {\mu }^{\prime }}\in \mathbb{N}$ such that, for every $m\ge m_{\mu {\mu }^{\prime }}$,

$$f_{\mu }^m{p}_{f\left(\mu \right)\lambda }=q_{\mu {\mu }^{\prime }}{f}_{{\mu }^{\prime }}^m{p}_{f\left({\mu }^{\prime }\right)\lambda }$$

$\left(2\right)$

for every $\mu \in M$

$$\mathrm{card}\left\{f_{\mu }^m:m\in \mathbb{N}\right\}<{\aleph }_0.$$

Under the composition of ⊛-morphisms $\left(f,f_{\mu }^m\right):\mathbf{X}\to \mathbf{Y}$ and $\left(g,g_{\nu }^m\right):\mathbf{Y}\to \mathbf{Z}=\left(Z_{\nu },r_{\nu {\nu }^{\prime }},N\right)$ we understand a ⊛-morphism $\left(h,h_{\nu }^m\right):\mathbf{X}\to \mathbf{Z}$ such that

$$h=fg\mathrm{and}{h}_{\nu }^m=g_{\nu }^m{f}_{g\left(\nu \right)}^m,\mathrm{for}\mathrm{all}m\in \mathbb{N},\nu \in N.$$

Given a category C, a category $in{v}^{⊛}$-C is defined having all inverse systems in C as objects and, for any pair of objects $\mathbf{X}$ and $\mathbf{Y}$, having all ⊛-morphisms between $\mathbf{X}$ and $\mathbf{Y}$ as morphisms with the composition mentioned above as the categorial composition.

A ⊛-morphism $\left(f,f_{\mu }^m\right):\mathbf{X}\to \mathbf{Y}$ is said to be equivalent to a ⊛-morphism $\left(f^{\prime },f_{\mu }^{\prime m}\right):\mathbf{X}\to \mathbf{Y}$, denoted by $\left(f,f_{\mu }^m\right)\sim \left(f^{\prime },f_{\mu }^{\prime m}\right)$, if every $\mu \in M$ admits $\lambda \in \mathrm{\Lambda }$, $\lambda \ge f\left(\mu \right),f^{\prime }\left(\mu \right)$, and $m_{\mu }\in M$ such that, for every $m\ge m_{\mu }$,

$$f_{\mu }^m{p}_{f\left(\mu \right)\lambda }=f_{\mu }^{\prime m}{p}_{f^{\prime }\left(\mu \right)\lambda }.$$

The relation ∼ is an equivalence relation on each set of ⊛-morphisms between two inverse systems in C. The equivalence class $\left[\left(f,f_{\mu }^m\right)\right]$ of $\left(f,f_{\mu }^m\right):\mathbf{X}\to \mathbf{Y}$ will be denoted by ${\mathbf{f}}^{⊛}$.

By $pr{o}^{⊛}$-C we denote a category whose class of objects consists of all inverse systems in C and whose morphisms are all equivalence classes ${\mathbf{f}}^{⊛}$. The categorical composition in $pr{o}^{⊛}$-C is defined by the representatives, i.e.,

$${\mathbf{g}}^{⊛}\circ {\mathbf{f}}^{⊛}={\mathbf{h}}^{⊛}=\left[\left(h,h_{\nu }^m\right)\right],$$

where $\left(h,h_{\nu }^m\right)=\left(fg,g_{\nu }^m{f}_{g\left(\nu \right)}^m\right)$.

A faithful functor ${\mathbf{J}}_C^{⊛}:pro$-$C\to pr{o}^{⊛}$-C is defined using the joining which associates with each morphism $\mathbf{f}=\left[\left(f,f_{\mu }\right)\right]:\mathbf{X}\to \mathbf{Y}$ of $pro$-C the $pr{o}^{⊛}$-C morphism ${\mathbf{f}}^{⊛}=\left[\left(f,f_{\mu }^m\right)\right]:\mathbf{X}\to \mathbf{Y}$ such that $f_{\mu }^m=f_{\mu }$, for all $\mu \in M$, $m\in \mathbb{N}$, while keeping inverse systems in C fixed. Thus, $pro$-C can be regarded as a subcategory of $pr{o}^{⊛}$-C.

Analogously, a faithful functor ${\mathbf{J}}_C^{\ast }:pr{o}^{⊛}$-$C\to pr{o}^{\ast }$-C is defined using the joining which associates with each morphism ${\mathbf{f}}^{⊛}=\left[\left(f,f_{\mu }^m\right)\right]:\mathbf{X}\to \mathbf{Y}$ of $pr{o}^{⊛}$-C the same morphism as morphism ${\mathbf{f}}^{\ast }=\left[\left(f,f_{\mu }^m\right)\right]:\mathbf{X}\to \mathbf{Y}$ of $pr{o}^{\ast }$-C, while keeping inverse systems in C fixed. Thus, $pr{o}^{⊛}$-C is a subcategory of $pr{o}^{\ast }$-C.

Let C be any category and let $D\subseteq C$ be full and dense subcategory of C. Let $\mathbf{p}:\left(X\right)\to \mathbf{X}$ and ${\mathbf{p}}^{\prime }:\left(X\right)\to {\mathbf{X}}^{\prime }$ be two D-expansions of the object $X\in Ob\left(C\right)$ and let $\mathbf{q}:\left(Y\right)\to \mathbf{Y}$ and ${\mathbf{q}}^{\prime }:\left(Y\right)\to {\mathbf{Y}}^{\prime }$ be two D-expansions of the object $Y\in Ob\left(C\right)$. For a morphism ${\mathbf{f}}^{⊛}:\mathbf{X}\to \mathbf{Y}$ we say that it is equivalent to a morphism ${\mathbf{f}}^{\prime ⊛}:{\mathbf{X}}^{\prime }\to {\mathbf{Y}}^{\prime }$ in $pr{o}^{⊛}$-D, denoted by ${\mathbf{f}}^{⊛}\sim {\mathbf{f}}^{\prime ⊛}$, if

$${\mathbf{J}}_D^{⊛}\left(\mathbf{j}\right)\circ {\mathbf{f}}^{⊛}={\mathbf{f}}^{\prime ⊛}\circ {\mathbf{J}}_D^{⊛}\left(\mathbf{i}\right),$$

where $\mathbf{i}:\mathbf{X}\to {\mathbf{X}}^{\prime }$ and $\mathbf{j}:\mathbf{Y}\to {\mathbf{Y}}^{\prime }$ are isomorphisms of different expansions of X and Y, respectively. Note that ∼ is an equivalence relation such that ${\mathbf{f}}^{⊛}\sim {\mathbf{f}}^{\prime ⊛}$ and ${\mathbf{g}}^{⊛}\sim {\mathbf{g}}^{\prime ⊛}$ imply ${\mathbf{g}}^{⊛}{\mathbf{f}}^{⊛}\sim {\mathbf{g}}^{\prime ⊛}{\mathbf{f}}^{\prime ⊛}$ when compositions ${\mathbf{g}}^{⊛}{\mathbf{f}}^{⊛}$ and ${\mathbf{g}}^{\prime ⊛}{\mathbf{f}}^{\prime ⊛}$ make sense. The equivalence class of a morphism ${\mathbf{f}}^{⊛}$ is denoted by $〈{\mathbf{f}}^{⊛}〉$.

Using the relation ∼ of $pr{o}^{⊛}$-D with each pair $\left(C,D\right)$ (where D is full and dense in C), we associate a category $S{h}_{\left(C,D\right)}^{⊛}$ such that

−

$Ob\left(S{h}_{\left(C,D\right)}^{⊛}\right)=Ob\left(C\right)$;

−

For every pair $X,Y$ of objects in $S{h}_{\left(C,D\right)}^{⊛}$, the set $S{h}_{\left(C,D\right)}^{⊛}\left(X,Y\right)$ consists of classes $〈{\mathbf{f}}^{⊛}〉$ of all $pr{o}^{⊛}$-D-morphisms ${\mathbf{f}}^{⊛}:\mathbf{X}\to \mathbf{Y}$, where $\mathbf{p}:X\to \mathbf{X}$ and $\mathbf{q}:Y\to \mathbf{Y}$ are arbitrary D-expansions of X and Y, respectively;

−

The composition of classes $〈{\mathbf{f}}^{⊛}〉:X\to Y$ and $〈{\mathbf{g}}^{⊛}〉:Y\to Z$ is defined by

$$〈{\mathbf{g}}^{⊛}〉\circ 〈{\mathbf{f}}^{⊛}〉:=〈{\mathbf{g}}^{⊛}\circ {\mathbf{f}}^{⊛}〉:X\to Z.$$

Category $S{h}_{\left(C,D\right)}^{⊛}$ is called the abstract finite coarse shape category of a pair $\left(C,D\right)$, while morphisms $〈{\mathbf{f}}^{⊛}〉:X\to Y$ in $S{h}_{\left(C,D\right)}^{⊛}$ are called finite coarse shape morphisms and denoted by $F^{⊛}:X\to Y$. A finite coarse shape morphisms $F^{⊛}:X\to Y$ can be described using a diagram

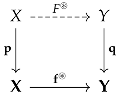It is important to emphasize that set $S{h}_{\left(C,D\right)}^{⊛}\left(X,Y\right)$ is bijectively correspondent with a set $pr{o}^{⊛}$-$D\left(\mathbf{X},\mathbf{Y}\right)$ for any D-expansions $\mathbf{X}$ and $\mathbf{Y}$ of objects X and Y, respectively.

Isomorphic objects X and Y in category $S{h}_{\left(C,D\right)}^{⊛}$ are said to have the same finite coarse shape type. This is denoted by $s{h}^{⊛}\left(X\right)=s{h}^{⊛}\left(Y\right)$.

Mentioned functors ${\mathbf{J}}_C^{⊛}:pro$-$C\to pr{o}^{⊛}$-C and ${\mathbf{J}}_C^{\ast }:pr{o}^{⊛}$-$C\to pr{o}^{\ast }$-C induce faithful functors $J_{\left(C,D\right)}^{⊛}:S{h}_{\left(C,D\right)}\to S{h}_{\left(C,D\right)}^{⊛}$ and $J_{\left(C,D\right)}^{\ast }:S{h}_{\left(C,D\right)}^{⊛}\to S{h}_{\left(C,D\right)}^{\ast }$, respectively, by putting

−

$J_{\left(C,D\right)}^{⊛}\left(X\right)=J_{\left(C,D\right)}^{\ast }\left(X\right)=X,\mathrm{for}\mathrm{every}\mathrm{object}X\in C,$

−

$J_{\left(C,D\right)}^{⊛}\left(F\right)=F^{⊛}=〈{\mathbf{J}}_D^{⊛}\left(\mathbf{f}\right)〉,\mathrm{for}\mathrm{every}\mathrm{shape}\mathrm{morphism}F=〈\mathbf{f}〉,$

−

$J_{\left(C,D\right)}^{\ast }\left(F^{⊛}\right)=F^{\ast }=〈{\mathbf{J}}_D^{\ast }\left({\mathbf{f}}^{⊛}\right)〉,\mathrm{for}\mathrm{every}\mathrm{finite}\mathrm{coarse}\mathrm{shape}\mathrm{morphism}{F}^{⊛}=〈{\mathbf{f}}^{⊛}〉.$

Hence, abstract shape category $S{h}_{\left(C,D\right)}$ can be considered as a subcategory of the abstract finite coarse shape category $S{h}_{\left(C,D\right)}^{⊛}$, and $S{h}_{\left(C,D\right)}^{⊛}$ is a subcategory of the abstract coarse shape category $S{h}_{\left(C,D\right)}^{\ast }$.

The composition of functors $S_{\left(C,D\right)}:C\to S{h}_{\left(C,D\right)}$ (shape functor) and $J_{\left(C,D\right)}^{⊛}$ is called the abstract finite coarse shape functor, denoted by $S_{\left(C,D\right)}^{⊛}:C\to S{h}_{\left(C,D\right)}^{⊛}$.

Throughout this paper, observed categories C and D will be $C=HTop$ ($C=HTo{p}_{\ast }$, $C=HTo{p}_{\ast \ast }$) and $D=HPol$ ($D=HPo{l}_{\ast }$, $D=HPo{l}_{\ast \ast }$). In other words, we will deal with the ((bi)pointed) topological finite coarse shape category, briefly denoted by $S{h}^{⊛}$ ($S{h}_{\ast }^{⊛}$, $S{h}_{\ast \ast }^{⊛}$).

Recall that the objects of $HTo{p}_{\ast }$ are all the pointed topological spaces $\left(X,x_0\right)$, $x_0\in X$, and morphisms are all the homotopy classes $\left[f\right]$ of mappings of pointed spaces $f:\left(X,x_0\right)\to \left(Y,y_0\right)$, i.e., homotopy classes of functions $f:X\to Y$ satisfying $f\left(x_0\right)=y_0$. Analogously, objects of $HTo{p}_{\ast \ast }$ are all the bipointed topological spaces $\left(X,x_0,x_1\right)$, $x_0,x_1\in X$, and morphisms are all the homotopy classes $\left[f\right]$ of mappings of bipointed spaces $f:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$, i.e., homotopy classes of functions $f:X\to Y$ satisfying $f\left(x_0\right)=y_0$ and $f\left(x_1\right)=y_1$. We will usually denote an H-map $\left[f\right]$ by omitting the brackets unless we need to especially highlight some mapping f and the corresponding homotopy class $\left[f\right]$. When the object class is reduced to all (bi)pointed topological spaces with the homotopy type of some (bi)pointed polyhedron, we obtain a full subcategory $HPo{l}_{\ast }\subseteq HTo{p}_{\ast }$ ($HPo{l}_{\ast \ast }\subseteq HTo{p}_{\ast \ast }$).

By Theorems 1.4.2 and 1.4.7 of [2], every topological space X admits an $HPol$-expansion

$$\mathbf{p}:X\to \left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right),$$

while every pointed topological space $\left(X,x_0\right)$ admits an $HPo{l}_{\ast }$-expansion

$$\mathbf{q}:\left(X,x_0\right)\to \left(\left(X_{\mu },x_{0\mu }\right),q_{\mu {\mu }^{\prime }},M\right).$$

Moreover, by Lemma 2.3 of [3], given polyhedral resolution $\left[\left(p_{\lambda }\right)\right]:X\to \left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ of X, for every $x_0,x_1\in X$ morphisms $\left[\left(p_{\lambda }\right)\right]:\left(X,x_0\right)\to \left(\left(X_{\lambda },x_{\lambda }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ and $\left[\left(p_{\lambda }\right)\right]:\left(X,x_0,x_1\right)\to \left(\left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ of $pro$-$To{p}_{\ast }$ and $pro$-$To{p}_{\ast \ast }$, respectively, are also resolutions (of $\left(X,x_0\right)$ and $\left(X,x_0,x_1\right)$, respectively). Hence, by applying the homotopy functor H to these resolutions, one obtains corresponding polyhedral expansions $\mathbf{p}:\left(X,x_0\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}}\right)$ and $\mathbf{p}:\left(X,x_0,x_1\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\right)$, which are both determined by the $HPol$-expansion $\mathbf{p}=\left[\left(p_{\lambda }\right)\right]:X\to \mathbf{X}=\left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ of X. This is why each finite coarse shape morphism $F^{⊛}:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$ (morphism of $S{h}_{\ast \ast }^{⊛}$) can be regarded as a morphism of $S{h}_{\ast }^{⊛}$ between the corresponding pointed spaces (from $\left(X,x_0\right)$ to $\left(Y,y_0\right)$ or from $\left(X,x_1\right)$ to $\left(Y,y_1\right)$).

For each $k\in {\mathbb{N}}_0$ and every pointed topological space $\left(X,x_0\right)$ the k-th finite coarse shape group${\check{\pi }}_k^{⊛}\left(X,x_0\right)$ is defined in the following way: for each $k\in \mathbb{N}$, ${\check{\pi }}_k^{⊛}\left(X,x_0\right)$ is a group (if $k\ge 2$ it is moreover an abelian group) having $S{h}_{🟉}^{⊛}\left(\left({\mathbb{S}}^k,s_0\right),\left(X,x_0\right)\right)$ as underlying set with a group operation defined by the formula

$$A^{⊛}+B^{⊛}=〈{\mathbf{a}}^{⊛}〉+〈{\mathbf{b}}^{⊛}〉=〈{\mathbf{a}}^{⊛}+{\mathbf{b}}^{⊛}〉=〈\left[\left(a_{\lambda }^n\right)\right]+\left[\left(b_{\lambda }^n\right)\right]〉=〈\left[\left(a_{\lambda }^n+b_{\lambda }^n\right)\right]〉.$$

(1)

Here, the finite coarse shape morphisms $A^{⊛}$ and $B^{⊛}$ are represented by $pr{o}^{⊛}$-$HPo{l}_{🟉}$ morphisms ${\mathbf{a}}^{⊛}=\left[\left(a_{\lambda }^n\right)\right]$ and ${\mathbf{b}}^{⊛}=\left[\left(b_{\lambda }^n\right)\right]:\left({\mathbb{S}}^k,s_0\right)\to \left(\left(X_{\lambda },x_{\lambda }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$, respectively, where

$$\mathbf{p}:\left(X,x_0\right)\to \left(\left(X_{\lambda },x_{\lambda }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$$

is an $HPo{l}_{🟉}$-expansion of $\left(X,x_0\right)$. Note that $a_{\lambda }^n+b_{\lambda }^n$ denotes the sum in the corresponding k-th homotopy group ${\pi }_k\left(X_{\lambda },x_{\lambda }\right)$. In the case when $k=0$, ${\check{\pi }}_0^{⊛}\left(X,x_0\right)$ is a pointed set of all finite coarse shape morphisms between $\left({\mathbb{S}}^0,s_0\right)$ and $\left(X,x_0\right)$, i.e., the set $S{h}_{🟉}^{⊛}\left(\left({\mathbb{S}}^0,s_0\right),\left(X,x_0\right)\right)$.

For every $k\in {\mathbb{N}}_0$ and for every finite coarse shape morphism $F^{⊛}:\left(X,x_0\right)\to \left(Y,y_0\right)$, a homomorphism of finite coarse shape groups (for $k=0$ a base point preserving function)

$${\check{\pi }}_k^{⊛}\left(F^{⊛}\right):{\check{\pi }}_k^{⊛}\left(X,x_0\right)\to {\check{\pi }}_k^{⊛}\left(Y,y_0\right)$$

is defined by the rule

$${\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\left(A^{⊛}\right)=F^{⊛}\circ A^{⊛},$$

for any finite coarse shape morphism $A^{⊛}\in {\check{\pi }}_k^{⊛}\left(X,x_0\right)$. For every $k\in \mathbb{N}$, this induces a functor ${\check{\pi }}_k^{⊛}:S{h}_{🟉}^{⊛}\to Grp$ (for $k=0$${\check{\pi }}_0^{⊛}:S{h}_{🟉}^{⊛}\to Se{t}_{🟉}$) associating with every pointed topological space $\left(X,x_0\right)$ the k-th finite coarse shape group ${\check{\pi }}_k^{⊛}\left(X,x_0\right)$. The functor ${\check{\pi }}_k^{⊛}:S{h}_{🟉}^{⊛}\to Grp$ is called the k-th finite coarse shape group functor (see [4] for details).

Finally, to facilitate readers’ access, let us state some basic facts about solenoids. Marked with ${\Sigma }_{\left(p_n\right)}$, where ${\left(p_n\right)}_n$ is a sequence in $\mathbb{N}$, solenoid is the inverse limit of the inverse sequence $(X_n,p_{nn+1})$, where $X_n=S^1=\left\{z\in \mathbb{C}\mid \left|z\right|=1\right\}$ and $p_{nn+1}\left(z\right)=z^{p_n}$, for every $n\in \mathbb{N}$. In [5], A. van Heemert proved that solenoids are indecomposable continua; hence, they are partitioned into disjoint composants. Krasinkiewicz and Minc proved in [6] that solenoids are not weakly joinable between any two points belonging to different composants. Afterwards, Š. Ungar proved in [7] that joinability and shape path connectedness coincide on the class of all metrizable continua; therefore, solenoids are not shape path connected. Nevertheless, according to [3], Example 3.4, they are coarse shape path connected.

3. The Finite Coarse Shape Path Connectedness

Definition 1.

Let X be a topological space, and let $x_0,x_1\in X$. A finite coarse shape path in X from $x_0$ to $x_1$ is a bipointed finite coarse shape morphism ${\mathrm{\Omega }}^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$. Space X is said to be finite coarse shape path connected if for every pair $x_0,x_1\in X$ there exists a finite coarse shape path in X from $x_0$ to $x_1$.

Let $\mathbf{p}=\left[\left(p_{\lambda }\right)\right]:X\to \mathbf{X}=\left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ be a $HPol$-expansion of the space X and let $x_0,x_1,x_2\in X$ such that there exist finite coarse shape paths ${\mathrm{\Omega }}_0^{⊛}=〈\left[\left({\omega }_{\lambda }^m\right)\right]〉$ and ${\mathrm{\Omega }}_1^{⊛}=〈\left[\left({\omega }_{\lambda }^{\prime m}\right)\right]〉$ in X from $x_0$ to $x_1$ and from $x_1$ to $x_2$, respectively. Note that

$$\left({\omega }_{\lambda }^m\right):\left(I,0,1\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\right)=\left(\left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$$

and

$$\left({\omega }_{\lambda }^{\prime m}\right):\left(I,0,1\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}}\right)=\left(\left(X_{\lambda },x_{\lambda }^{\prime },x_{\lambda }^{\prime \prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$$

are $in{v}^{⊛}$-$HPol$ morphisms such that, for all $\lambda \in \mathrm{\Lambda }$ and $m\in \mathbb{N}$, components ${\omega }_{\lambda }^m$ and ${\omega }_{\lambda }^{\prime m}$ are homotopy classes of ordinary paths in $X_{\lambda }$ from $x_{\lambda }$ to $x_{\lambda }^{\prime }$ and from $x_{\lambda }^{\prime }$ to $x_{\lambda }^{\prime \prime }$, respectively. Now, the product ${\mathrm{\Omega }}_0^{⊛}·{\mathrm{\Omega }}_1^{⊛}$ is defined as a finite coarse shape path ${\mathrm{\Omega }}^{⊛}=〈\left[\left({\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}\right)\right]〉:\left(I,0,1\right)\to \left(X,x_0,x_2\right)$, where ${\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}$ denotes the homotopy class of the product of ordinary paths ${\omega }_{\lambda }^m$ and ${\omega }_{\lambda }^{\prime m}$.

Furthermore, a trivial finite coarse shape path $E^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_0\right)$ is a bipointed finite coarse shape morphism represented by $in{v}^{⊛}$-$HPol$ morphism which consists of the trivial loops in $X_{\lambda }$ for all $\lambda \in \mathrm{\Lambda }$ and $m\in \mathbb{N}$. Finally, an inverse of a finite coarse shape path ${\mathrm{\Omega }}^{⊛}=〈\left[\left({\omega }_{\lambda }^m\right)\right]〉:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ is a finite coarse shape path ${\left({\mathrm{\Omega }}^{⊛}\right)}^{-1}:\left(I,0,1\right)\to \left(X,x_1,x_0\right)$ represented by an $in{v}^{⊛}$-$HPol$ morphism $\left({\left({\omega }_{\lambda }^m\right)}^{-1}\right)$, where ${\left({\omega }_{\lambda }^m\right)}^{-1}$ denotes an inverse path of a path ${\omega }_{\lambda }^m$, for all $\lambda \in \mathrm{\Lambda }$ and $m\in \mathbb{N}$.

Remark 1.

The composite of a finite coarse shape path and an appropriate bipointed finite coarse shape morphism is a finite coarse shape path. More precisely, if there exists a finite coarse shape path ${\mathrm{\Omega }}^{⊛}$ in X from $x_0$ to $x_1$, then, for every bipointed finite coarse shape morphism $F^{⊛}:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$, the composite $F^{⊛}\circ {\mathrm{\Omega }}^{⊛}$ is a finite coarse shape path in Y from $y_0$ to $y_1$.

According to the previous remark, it is straightforward to prove the following proposition:

Proposition 1.

Let X and Y be topological spaces such that for every pair $y_0,y_1\in Y$ there exists a pair $x_0,x_1\in X$ and a finite coarse shape morphism $F^{⊛}:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$. If X is finite coarse shape path connected, then so is Y.

An important consequence of the Proposition 1 is that the finite coarse shape path connectedness is a topological property.

Corollary 1.

Let $f:X\to Y$ be a continuous surjection between topological spaces. If X is finite coarse shape path connected, then so is Y.

According to [3], Example 3.4, solenoids are coarse shape path connected but not shape path connected. In the next example, we show that they are not finite coarse shape path connected either.

Example 1.

As stated in the preliminaries, the common definition of the solenoid ${\Sigma }_{\left(p_n\right)}$, where ${\left(p_n\right)}_n$ is a sequence in $\mathbb{N}$, is as the inverse limit of the inverse sequence of circles $S^1$ and bonding maps $p_{nn+1}:S^1\to S^1$, given by $p_{nn+1}\left(z\right)=z^{p_n}$, for every $n\in \mathbb{N}$. Nevertheless, it can be obtained as the inverse limit of an inclusive inverse system of solid tori.

Let $T_0=S^1\times D$ be a solid torus and, for each $n\in \mathbb{N}$, let $T_{n+1}$ be a solid torus that is wrapped longitudinally $p_n$ times inside the solid torus $T_n$ without folding. In this manner, we get the sequence

$$T_1\supset T_2\supset \cdots \supset T_n\supset \cdots$$

and the intersection ${\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n$ is homeomorphic to the solenoid ${\Sigma }_{\left(p_n\right)}$.

Moreover, ${\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n=\underleftarrow{lim}(T_n,i_{nn+1})$, where $i_{nn+1}:T_{n+1}\hookrightarrow T_n$, $n\in \mathbb{N}$, is the inclusion. Indeed, for $\mathbf{i}=\left[\left(i_n\right)\right]:{\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n\to (T_n,i_{nn+1})$, where $i_n:{\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n\hookrightarrow T_n$ is the inclusion, and for any morphism $\mathbf{f}=\left[\left(f_n\right)\right]:X\to (T_n,i_{nn+1})$ in pro-Top we have $f_m\left(x\right)=i_{mn}\left(f_n\left(x\right)\right)=f_n\left(x\right)$, for every $x\in X$ and every $m,n\in \mathbb{N}$, $m\le n$. Therefore, for every $x\in X$ and for every $n\in \mathbb{N}$, $f_1\left(x\right)=f_n\left(x\right)$ and, consequently, $f_1\left(x\right)\in {\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n$. Now, $f:X\to {\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n$ defined by $f\left(x\right)=f_1\left(x\right)$ for $x\in X$ satisfies $\mathbf{i}\circ \left(f\right)=\mathbf{f}$, and it is unique since $i_n$ is injective for every $n\in \mathbb{N}$.

Recall that, by [5], solenoids are indecomposable continua. By [8], indecomposable continua have $2^{{\aleph }_0}$ composants, and in solenoids they coincide with the path components.

Let $x,y\in {\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n$ be arbitrary elements in two distinct path components. It is obvious that

$$i_n\left(x\right)=x,i_n\left(y\right)=y,\forall n\in \mathbb{N}.$$

Let us now assume that there is a finite coarse shape path from x to y,

$$\omega =〈\left[\left({\omega }_n^m\right)\right]〉:I\to \bigcap _{n\in \mathbb{N}}{T}_n,$$

$$\omega \left(0\right)=x,\omega \left(1\right)=y,$$

where

$${\omega }_n^m:I\to T_n,\forall n\in \mathbb{N},\forall m\in \mathbb{N},$$

such that

$$\mathrm{card}\left\{{\omega }_n^m\mid m\in \mathbb{N}\right\}<{\aleph }_0,\forall n\in \mathbb{N}.$$

Since $\left[\left({\omega }_n^m\right)\right]$ is a morphism in $pr{o}^{⊛}$-$HPol$, we have that for every $n\in \mathbb{N}$ there exists $m_n\in \mathbb{N}$ such that for every $m\ge m_n$,

$${\omega }_1^m=i_{1n}\circ {\omega }_n^m={\omega }_n^m$$

(as homotopy clases). Also, since $\mathrm{card}\left\{{\omega }_1^m\mid m\in \mathbb{N}\right\}<{\aleph }_0$, there is a stationary subsequence ${\left({\omega }_1^{m_k}\right)}_k$ of ${\left({\omega }_1^m\right)}_m$. Let ${\omega }_1^{m_k}={\omega }_1^{m_0}$ for some $m_0\in \mathbb{N}$, for every $k\in \mathbb{N}$. Then, for every $n\in \mathbb{N}$ there exists $m\ge m_n$ and $k\in \mathbb{N}$ such that ${\omega }_1^{m_0}={\omega }_1^{m_k}={\omega }_n^m$, meaning that homotopy class ${\omega }_1^{m_0}$ contains a path between x and y in $T_n$ for every n and, consequently, a path between x and y in ${\displaystyle \bigcap _{n\in \mathbb{N}}}{T}_n$, which is a contradiction with the asumption that x and y are not in the same path component.

Let us recall that an inverse system $\mathbf{X}$ is n-movable, $n\in \mathbb{N}$, provided every $\lambda \in \mathrm{\Lambda }$ admits a ${\lambda }^{\prime }\ge \lambda$ such that for every ${\lambda }^{″}\ge \lambda$, every polyhedron P with $dimP\le n$ and every map $h:P\to X_{{\lambda }^{\prime }}$, there exists a map $r:P\to X_{{\lambda }^{″}}$ such that

$$p_{\lambda {\lambda }^{″}}r\simeq p_{\lambda {\lambda }^{\prime }}h.$$

Now, a topological space X is said to be n-movable provided it admits an $HPol$-expansion $\mathbf{p}:X\to \mathbf{X}$ such that the inverse system $\mathbf{X}=\left(X_{\lambda },p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ is n-movable. Furthermore, for an n-movable topological space, every $HPol$-expansion (i.e., an associated inverse system) is n-movable.

Also recall that, for every metrizable continuum X, the following statements are equivalent (Ch. VII. of [9], ref. [6] and II. 8. of [2]):

$\left(i\right)$

There exists a point $x_0\in X$ such that the pointed space $\left(X,x_0\right)$ is 1-movable.

$\left(ii\right)$

For every point $x\in X$ the pointed space $\left(X,x\right)$ is 1-movable.

$\left(iii\right)$

X is shape path connected.

Therefore, by Corollary 3.9 of [3], the following holds:

Corollary 2.

On the class of all pointed 1-movable metrizable compacta, the shape path connectedness, finite coarse shape path connectedness, coarse shape path connectedness and connectedness are equivalent properties.

4. Isomorphisms Induced by Finite Coarse Shape Paths

Let $x_0$ and $x_1$ be arbitrary points in X and let ${\mathrm{\Omega }}^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ be a finite coarse shape path in X from $x_0$ to $x_1$. Then, there exists a $pr{o}^{⊛}$-$HPo{l}_{\ast \ast }$ morphism $\left[\left({\omega }_{\lambda }^m\right)\right]:\left(I,0,1\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\right)$ such that ${\mathrm{\Omega }}^{⊛}=〈\left[\left({\omega }_{\lambda }^m\right)\right]〉$, where $\mathbf{p}=\left(p_{\lambda }\right):\left(I,0,1\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\right)=\left(\left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ is an $HPo{l}_{\ast \ast }$-expansion of a bipointed space $\left(X,x_0,x_1\right)$ and, for all $\lambda \in \mathrm{\Lambda }$ and $m\in \mathbb{N}$, ${\omega }_{\lambda }^m:\left(I,0,1\right)\to \left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right)$ is a homotopy class of a path in $X_{\lambda }$ from $x_{\lambda }$ to $x_{\lambda }^{\prime }$.

Let us, for every $k\in {\mathbb{N}}_0$ and an arbitrary $A^{⊛}=〈\left[\left(a_{\lambda }^m\right)\right]〉\in {\check{\pi }}_k^{⊛}\left(X,x_0\right)$, define a joining $i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right):\left(S^k,s_0\right)\to \left(X,x_1\right)$ by the rule

$$i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right)=〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)\right]〉,$$

(2)

where $i_{{\omega }_{\lambda }^m}:{\pi }_k\left(X,x_0\right)\to {\pi }_k\left(X,x_1\right)$ is an induced homomorphism (for $k=0$ a base point preserving function) induced by ${\omega }_{\lambda }^m$.

To show that $i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right)\in {\check{\pi }}_k^{⊛}\left(X,x_1\right)$, it sufficies to show that $\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)$ is an $in{v}^{⊛}$-$HPo{l}_{\ast }$ morphism. Since

$$\left({\omega }_{\lambda }^m\right):\left(I,0,1\right)\to \left(\left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$$

and

$$\left(a_{\lambda }^m\right):\left(S^k,s_0\right)\to \left(\left(X_{\lambda },x_{\lambda }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$$

are $in{v}^{⊛}$-$HPo{l}_{\ast }$ morphisms, for every pair $\lambda \le {\lambda }^{\prime }$ there exists $m_0\in \mathbb{N}$ such that ${\omega }_{\lambda }^m=p_{\lambda {\lambda }^{\prime }}\circ {\omega }_{{\lambda }^{\prime }}^m$ and $a_{\lambda }^m=p_{\lambda {\lambda }^{\prime }}\circ a_{{\lambda }^{\prime }}^m$, for every $m\ge m_0$. Thus,

$$p_{\lambda {\lambda }^{\prime }}\circ i_{{\omega }_{{\lambda }^{\prime }}^m}\left(a_{{\lambda }^{\prime }}^m\right)={\pi }_k\left(p_{\lambda {\lambda }^{\prime }}\right)\left(i_{{\omega }_{{\lambda }^{\prime }}^m}\left(a_{{\lambda }^{\prime }}^m\right)\right)=i_{p_{\lambda {\lambda }^{\prime }}\circ {\omega }_{{\lambda }^{\prime }}^m}\left({\pi }_k\left(p_{\lambda {\lambda }^{\prime }}\right)\left(a_{{\lambda }^{\prime }}^m\right)\right)=i_{{\omega }_{\lambda }^m}\left(p_{\lambda {\lambda }^{\prime }}\circ a_{{\lambda }^{\prime }}^m\right)=i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)$$

holds for every $m\ge m_0$. Finally, since for every $\lambda \in \mathrm{\Lambda }$ inequalities $card\left\{{\omega }_{\lambda }^m:m\in \mathbb{N}\right\}<{\aleph }_0$ and $card\left\{a_{\lambda }^m:m\in \mathbb{N}\right\}<{\aleph }_0$ hold, we infer that $card\left\{i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right):m\in \mathbb{N}\right\}<{\aleph }_0$. This proves that $\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)$ is an $in{v}^{⊛}$-$HPo{l}_{\ast }$ morphism, i.e., $i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right)$ is a finite coarse shape morphism.

Theorem 1.

Let ${\mathrm{\Omega }}^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ be a finite coarse shape path in X from $x_0$ to $x_1$. For every $k\in \mathbb{N}$, the ${\mathrm{\Omega }}^{⊛}$ induces a group isomorphism (for $k=0$ a base point preserving bijection) $i_{{\mathrm{\Omega }}^{⊛}}:{\check{\pi }}_k^{⊛}\left(X,x_0\right)\to {\check{\pi }}_k^{⊛}\left(X,x_1\right)$ given by the rule (2). Moreover, $i_{{\left({\mathrm{\Omega }}^{⊛}\right)}^{-1}}=i_{{\mathrm{\Omega }}^{⊛}}^{-1}$.

Proof. 

We will first show that $i_{{\mathrm{\Omega }}^{⊛}}$ is a homomorphism for every $k\ge 1$. Let $A^{⊛},B^{⊛}\in {\check{\pi }}_k^{⊛}\left(X,x_0\right)$ be finite coarse shape morphisms represented by $pr{o}^{⊛}$-$HPo{l}_{\ast }$ morphisms $\left[\left(a_{\lambda }^m\right)\right]$ and $\left[\left(b_{\lambda }^m\right)\right]$, respectively. Since (see [4])

$$A^{⊛}+B^{⊛}=〈\left[\left(a_{\lambda }^m\right)\right]〉+〈\left[\left(b_{\lambda }^m\right)\right]〉=〈\left[\left(a_{\lambda }^m+b_{\lambda }^m\right)\right]〉,$$

where $a_{\lambda }^m+b_{\lambda }^m$ is the sum in the corresponding k-th homotopy group ${\pi }_k\left(X_{\lambda },x_{\lambda }\right)$, it follows that

$$i_{\mathrm{\Omega }}^{⊛}\left(A^{⊛}+B^{⊛}\right)=〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m+b_{\lambda }^m\right)\right)\right]〉=〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)+i_{{\omega }_{\lambda }^m}\left(b_{\lambda }^m\right)\right)\right]〉=$$

$$=〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)\right]〉+〈\left[\left(i_{{\omega }_{\lambda }^m}\left(b_{\lambda }^m\right)\right)\right]〉=i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right)+i_{{\mathrm{\Omega }}^{⊛}}\left(B^{⊛}\right).$$

It is well known (from homotopy group theory) that for every path ${\omega }_{\lambda }^m:\left(I,0,1\right)\to \left(X,x_{\lambda },x_{{\lambda }^{\prime }}\right)$, the induced homomorphism $i_{{\omega }_{\lambda }^m}$ is an isomorphism (for $k=0$ a base point preserving bijection), and it holds that ${\left(i_{{\omega }_{\lambda }^m}\right)}^{-1}=i_{{\left({\omega }_{\lambda }^m\right)}^{-1}}$. Thus,

$$i_{{\mathrm{\Omega }}^{⊛}}^{-1}:=i_{{\left({\mathrm{\Omega }}^{⊛}\right)}^{-1}}:{\check{\pi }}_k^{⊛}\left(X,x_1\right)\to {\check{\pi }}_k^{⊛}\left(X,x_0\right)$$

is the inverse of $i_{{\mathrm{\Omega }}^{⊛}}$. This proves that $i_{{\mathrm{\Omega }}^{⊛}}$ is a group isomorphism for every $k\in \mathbb{N}$ (a base point preserving bijection for $k=0$). □

Proposition 2.

A group isomorphism $i_{{\mathrm{\Omega }}^{⊛}}:{\check{\pi }}_k^{⊛}\left(X,x_0\right)\to {\check{\pi }}_k^{⊛}\left(X,x_1\right)$ has the following properties:

$\left(i\right)$

${\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\circ i_{{\mathrm{\Omega }}^{⊛}}=i_{F^{⊛}\circ {\mathrm{\Omega }}^{⊛}}\circ {\check{\pi }}_k^{⊛}\left(F^{⊛}\right):{\check{\pi }}_k^{⊛}\left(X,x_0\right)\to {\check{\pi }}_k^{⊛}\left(Y,y_1\right)$, for every finite coarse shape morphism $F^{⊛}:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$.

$\left(ii\right)$

$i_{{\mathrm{\Omega }}_1^{⊛}}\circ i_{{\mathrm{\Omega }}_0^{⊛}}=i_{{\mathrm{\Omega }}_0^{⊛}·{\mathrm{\Omega }}_1^{⊛}}$, for all finite coarse shape paths ${\mathrm{\Omega }}_0^{⊛}$ and ${\mathrm{\Omega }}_1^{⊛}$ in X from $x_0$ to $x_1$ and from $x_1$ to $x_2$, respectively.

$\left(iii\right)$

$i_{O^{⊛}}=1_{{\check{\pi }}_k^{⊛}\left(X,x_0\right)}$, where $O^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_0\right)$ is the trivial finite coarse shape path at $x_0$.

Proof. 

Each finite coarse shape morphism $F^{⊛}:\left(X,x_0,x_1\right)\to \left(Y,y_0,y_1\right)$ of $S{h}_{\ast \ast }^{⊛}$, represented by a $pr{o}^{⊛}$-$HPo{l}_{\ast \ast }$ morphism $\left[\left(f,f_{\mu }^m\right)\right]:\left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\right)\to \left(\mathbf{Y},{\mathbf{y}}_{\mathbf{0}},{\mathbf{y}}_{\mathbf{1}}\right)=\left(\left(Y_{\mu },y_{\mu },y_{\mu }^{\prime }\right),q_{\mu {\mu }^{\prime }},M\right)$, can be regarded as both $F^{⊛}:\left(X,x_0\right)\to \left(Y,y_0\right)$ and $F^{⊛}:\left(X,x_1\right)\to \left(Y,y_1\right)$ of $S{h}_{\ast }^{⊛}$ (we will denote all of these morphisms with the same label $F^{⊛}$, taking care of the context in which they are used). The finite coarse shape group functor ${\check{\pi }}_k^{⊛}$ (see [4]) associates each of them with corresponding homomorphism (for $k=0$ with corresponding base point preserving function) ${\check{\pi }}_k^{⊛}\left(F^{⊛}\right):{\check{\pi }}_k^{⊛}\left(X,x_0\right)\to {\check{\pi }}_k^{⊛}\left(Y,y_0\right)$ and ${\check{\pi }}_k^{⊛}\left(F^{⊛}\right):{\check{\pi }}_k^{⊛}\left(X,x_1\right)\to {\check{\pi }}_k^{⊛}\left(Y,y_1\right)$, respectively. Now, take an arbitrary $A^{⊛}=〈\left[\left(a_{\lambda }^m\right)\right]〉\in {\check{\pi }}_k^{⊛}\left(X,x_0\right)$. It holds that

$$\left({\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\circ i_{{\mathrm{\Omega }}^{⊛}}\right)\left(A^{⊛}\right)={\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\left(i_{{\mathrm{\Omega }}^{⊛}}\left(A^{⊛}\right)\right)=〈\left[\left(f,f_{\mu }^m\right)\right]〉\circ 〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)\right]〉=$$

$$=〈\left[f_{\mu }^m\circ i_{{\omega }_{f\left(\mu \right)}^m}\left(a_{f\left(\mu \right)}^m\right)\right]〉=〈\left[\left(i_{f_{\mu }^m\circ {\omega }_{f\left(\mu \right)}^m}\left(f_{\mu }^m\circ a_{f\left(\mu \right)}^m\right)\right)\right]〉=$$

$$=i_{F^{⊛}\circ {\mathrm{\Omega }}^{⊛}}\left(F^{⊛}\circ A^{⊛}\right)=i_{F^{⊛}\circ {\mathrm{\Omega }}^{⊛}}\left({\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\left(A^{⊛}\right)\right)=\left(i_{F^{⊛}\circ {\mathrm{\Omega }}^{⊛}}\circ {\check{\pi }}_k^{⊛}\left(F^{⊛}\right)\right)\left(A^{⊛}\right)$$

and $\left(i\right)$ is proved.

Let ${\mathrm{\Omega }}_0^{⊛}=〈\left[\left({\omega }_{\lambda }^m\right)\right]〉$ and ${\mathrm{\Omega }}_1^{⊛}=〈\left[\left({\omega }_{\lambda }^{\prime m}\right)\right]〉$ be finite coarse shape paths in X from $x_0$ to $x_1$ and from $x_1$ to $x_2$, respectively, and take an arbitrary $A^{⊛}=〈\left[\left(a_{\lambda }^m\right)\right]〉\in {\check{\pi }}_k^{⊛}\left(X,x_0\right)$. Now

$$i_{{\mathrm{\Omega }}_0^{⊛}·{\mathrm{\Omega }}_1^{⊛}}\left(A^{⊛}\right)=〈\left[\left(i_{{\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}}\left(a_{\lambda }^m\right)\right)\right]〉=〈\left[\left({\left({\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}\right)}^{-1}·a_{\lambda }^m·{\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}\right)\right]〉=$$

$$=〈\left[\left({\left({\omega }_{\lambda }^{\prime m}\right)}^{-1}·{\left({\omega }_{\lambda }^m\right)}^{-1}·a_{\lambda }^m·{\omega }_{\lambda }^m·{\omega }_{\lambda }^{\prime m}\right)\right]〉=〈\left[\left(i_{{\omega }_{\lambda }^{\prime m}}\left({\left({\omega }_{\lambda }^m\right)}^{-1}·a_{\lambda }^m·{\omega }_{\lambda }^m\right)\right)\right]〉=$$

$$=〈\left[\left(i_{{\omega }_{\lambda }^{\prime m}}\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)\right)\right]〉=i_{{\mathrm{\Omega }}_1^{⊛}}\left(〈\left[\left(i_{{\omega }_{\lambda }^m}\left(a_{\lambda }^m\right)\right)\right]〉\right)=$$

$$=i_{{\mathrm{\Omega }}_1^{⊛}}\left(i_{{\mathrm{\Omega }}_0}^{⊛}\left(A^{⊛}\right)\right)=\left(i_{{\mathrm{\Omega }}_1^{⊛}}\circ i_{{\mathrm{\Omega }}_0^{⊛}}\right)\left(A^{⊛}\right)$$

shows that (ii) holds true.

Finally, from $\left(ii\right)$ and Theorem 1, for every trivial finite coarse shape path ${\mathrm{\Omega }}^{⊛}$ at $x_0$ we infer that

$$i_{O^{⊛}}=i_{{\mathrm{\Omega }}^{⊛}{\left({\mathrm{\Omega }}^{⊛}\right)}^{-1}}=i_{{\left({\mathrm{\Omega }}^{⊛}\right)}^{-1}}\circ i_{{\mathrm{\Omega }}^{⊛}}=i_{{\mathrm{\Omega }}^{⊛}}^{-1}\circ i_{{\mathrm{\Omega }}^{⊛}}=1_{{\check{\pi }}_k^{⊛}\left(X,x_0\right)}$$

holds. □

In [2], Example II.3.4, the authors constructed a metric continuum in which the change of base point affects the pointed shape. In [3], Theorem 2.5 states that, for the same continuum, there exists a pair of base points for which the pointed shape differs and the pointed coarse shape is the same. In the following example, we show that the change of base point also affects the pointed finite coarse shape.

Example 2.

Let X be the wedge ${\Sigma }_2\vee S^1$ of the dyadic solenoid and 1-sphere with the identifying point *. The sphere $(S^1,\ast )$ is a retract of $(X,\ast )$, and the inclusion $(S^1,\ast )\hookrightarrow (X,\ast )$ induces a monomorphism on ${\check{\pi }}_1^{⊛}(X,\ast )$ so ${\check{\pi }}_1^{⊛}(X,\ast )\cong {{\displaystyle \prod _{n\in \mathbb{N}}}}^f\mathbb{Z}/{\displaystyle \underset{n\in \mathbb{N}}{⨁}}\mathbb{Z}$.

We want to show that the finite coarse shape group of X depends on the choice of base point.

Let $P=S^1\vee S^1$ with the identifying point *, let $z\in S^1$, $z\ne \ast$ and let ${\omega }_1$, ${\omega }_2$ and ${\omega }_3$ be paths in P as shown in the following figure.

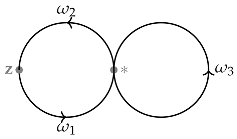The fundamental group ${\pi }_1(P,z)$ is isomorphic to the free group $\mathbb{Z}\ast \mathbb{Z}$ on generators $u=\left[{\omega }_1{\omega }_3{\omega }_1^{-1}\right]$ and $v=\left[{\omega }_1{\omega }_2\right]$.

As in [2], Example II.3.4, we define mapings $f,g:(P,z)\to (P,z)$, f taking the paths ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ to ${\omega }_1$, ${\omega }_2{\omega }_1{\omega }_2$, ${\omega }_3$, respectively and g taking the paths ${\omega }_1,{\omega }_2,{\omega }_3$ to ${\omega }_1{\omega }_2{\omega }_1$, ${\omega }_2$, ${\omega }_3$, respectively.

Now we have

$${\pi }_1\left(f\right)\left(u\right)=u,{\pi }_1\left(f\right)\left(v\right)=v^2,$$

$${\pi }_1\left(g\right)\left(u\right)=vu{v}^{-1},{\pi }_1\left(g\right)\left(v\right)=v^2.$$

The dyadic solenoid $({\Sigma }_2,\ast )$ is the inverse limit of the sequence

$$(S^1,\ast )\stackrel{h}{\leftarrow }(S^1,\ast )\stackrel{h}{\leftarrow }(S^1,\ast )\stackrel{h}{\leftarrow }(S^1,\ast )\stackrel{h}{\leftarrow }\cdots$$

where $h:S^1\to S^1$ is the map that uniformly wraps the domain circle twice around the codomain circle, and one can see that the inverse limit of the sequence

$$(P,z)\stackrel{f}{\leftarrow }(P,z)\stackrel{g}{\leftarrow }(P,z)\stackrel{f}{\leftarrow }(P,z)\stackrel{g}{\leftarrow }\cdots$$

is homeomorphic to $(X,x)$ for some $x\in X$. Therefore, ${\check{\pi }}_1^{⊛}(X,x)$ is isomorphic to the inverse limit of the sequence

$$G\stackrel{{\check{\pi }}_1^{⊛}\left(f\right)}{\leftarrow }G\stackrel{{\check{\pi }}_1^{⊛}\left(g\right)}{\leftarrow }G\stackrel{{\check{\pi }}_1^{⊛}\left(f\right)}{\leftarrow }G\stackrel{{\check{\pi }}_1^{⊛}\left(g\right)}{\leftarrow }\cdots ,$$

where $G={{\displaystyle \prod _{n\in \mathbb{N}}}}^f\mathbb{Z}\ast \mathbb{Z}/{\displaystyle \underset{n\in \mathbb{N}}{⨁}}\mathbb{Z}\ast \mathbb{Z}$.

We want to show that this inverse limit is trivial.

Let us assume the opposite, i.e., there is an element

$$0\ne x=(x_i,i\in \mathbb{N})\in {\check{\pi }}_1^{⊛}(X,x)\le {\displaystyle \prod _{p\in \mathbb{N}}}\left({{\displaystyle \prod _{n\in \mathbb{N}}}}^f\mathbb{Z}\ast \mathbb{Z}/{\displaystyle \underset{n\in \mathbb{N}}{⨁}}\mathbb{Z}\ast \mathbb{Z}\right).$$

Here, for each $i\in \mathbb{N}$, the i-th coordinate $x_i$ of x is actually a sequence ${\left(x_i^m\right)}_m$ of words in letters u and v such that

$$\mathrm{card}\left\{x_i^m\mid m\in \mathbb{N}\right\}<{\aleph }_0.$$

Also, for every pair $i,i^{\prime }\in \mathbb{N}$, $i\le i^{\prime }$, there exists $m_{i{i}^{\prime }}\in \mathbb{N}$ such that

$$x_i^m=p_{i{i}^{\prime }}{x}_{i^{\prime }}^m,\mathrm{for}\mathrm{every}m\ge m_{i{i}^{\prime }},$$

where $p_{i{i}^{\prime }}$ is the bonding morphism.

Since $x\ne 0$, there exists $i_0\in \mathbb{N}$ such that $0\ne x_{i_0}\in {{\displaystyle \prod _{n\in \mathbb{N}}}}^f\mathbb{Z}\ast \mathbb{Z}/{\displaystyle \underset{n\in \mathbb{N}}{⨁}}\mathbb{Z}\ast \mathbb{Z}$. Furthermore, there exists a subsequence ${\left(x_{i_o}^{m_k}\right)}_k$ of ${\left(x_{i_o}^m\right)}_m$ such that $x_{i_o}^{m_k}\ne 0$ for every $k\in \mathbb{N}$.

Without loss of generality, we can assume that $i_0$ is an odd integer.

Now, for $h={\pi }_1\left(f\right){\pi }_1\left(g\right)$ we have that for every $l\in \mathbb{N}$ and $i=i_0+2l$ there exists $m_{i_{0}i}\in \mathbb{N}$ such that $x_{i_0}^m=h^l{x}_i^m$, $\forall m\ge m_{i_{0}i}$. Consequently, there is $k_i\in \mathbb{N}$ such that

$$0\ne x_{i_0}^{m_{k_i}}=h^l{x}_i^{m_{k_i}}.$$

Let us, for every non-zero word $y\in \mathbb{Z}\ast \mathbb{Z}$, define the integer $\rho \left(y\right)$ as the maximal absolute value of the exponents of v appearing in the word y. It is obvious that $\rho \left(y\right)=\rho \left(y^{-1}\right)$. Also, let

$$\rho \left(x_{i_0}\right)=max\left\{\rho \left(x_{i_0}^{m_k}\right)\mid k\in \mathbb{N}\right\}.$$

It exists since

$$\mathrm{card}\left\{x_{i_0}^{m_k}\mid k\in \mathbb{N}\right\}\le \mathrm{card}\left\{x_{i_0}^m\mid m\in \mathbb{N}\right\}<{\aleph }_0.$$

Now we can analyze $\rho \left(h\left(x_i^{m_{k_i}}\right)\right)$ for various forms of the word $x_i^{m_{k_i}}$.

1. 

If $\rho \left(x_i^{m_{k_i}}\right)=0$ then $x_i^{m_{k_i}}=u^n$, $n\ne 0$ and

$$h\left(u^n\right)={\pi }_1\left(f\right)\left({\pi }_1\left(g\right)\left(u^n\right)\right)={\pi }_1\left(f\right)\left(v{u}^n{v}^{-1}\right)=v^2{u}^n{v}^{-2}⟹\rho \left(h\left(x_i^{m_{k_i}}\right)\right)=2.$$

2. 

If $\rho \left(x_i^{m_{k_i}}\right)\ne 0$ we can assume that $x_i^{m_{k_i}}=\cdots u^m{v}^r{u}^n\cdots$ where $r=\rho \left(x_i^{m_{k_i}}\right)\ge 1$. Then

(a) 

$m=n=0⟹x_i^{m_{k_i}}=v^r$ and

$$h\left(v^r\right)={\pi }_1\left(f\right)\left({\pi }_1\left(g\right)\left(v^r\right)\right)={\pi }_1\left(f\right)\left(v^{2r}\right)=v^{4r}⟹\rho \left(h\left(x_i^{m_{k_i}}\right)\right)=4r;$$

(b) 

$m=0,n\ne 0⟹x_i^{m_{k_i}}=v^r{u}^n\cdots$ and

$$h(v^r{u}^n\cdots )={\pi }_1\left(f\right)(v^{2r}v{u}^n{v}^{-1}\cdots )=v^{4r+2}{u}^n{v}^{-2}\cdots ⟹\rho \left(h\left(x_i^{m_{k_i}}\right)\right)\ge 4r+2;$$

(c) 

$m\ne 0,n=0⟹x_i^{m_{k_i}}=\cdots u^m{v}^r$ and

$$h(\cdots u^m{v}^r)={\pi }_1\left(f\right)(\cdots v{u}^m{v}^{-1}{v}^{2r})=\cdots v^2{u}^m{v}^{4r-2}⟹\rho \left(h\left(x_i^{m_{k_i}}\right)\right)\ge 4r-2;$$

(d) 

$m,n\ne 0⟹x_i^{m_{k_i}}=\cdots u^m{v}^r{u}^n\cdots$ and

$$h(\cdots u^m{v}^r{u}^n\cdots )={\pi }_1\left(f\right)(\cdots v{u}^m{v}^{-1}{v}^{2r}v{u}^n{v}^{-1}\cdots )=\cdots v^2{u}^m{v}^{4r}{u}^n{v}^{-2}\cdots$$

$$⟹\rho \left(h\left(x_i^{m_{k_i}}\right)\right)\ge 4r.$$

We can see that

$$\rho \left(h\left(x_i^{m_{k_i}}\right)\right)\ge max\left\{2,4\rho \left(x_i^{m_{k_i}}\right)-2\right\}.$$

Consequently,

$$\rho \left(h^l\left(x_i^{m_{k_i}}\right)\right)\ge 4^{l-1}\left(\rho \left(h\left(x_i^{m_{k_i}}\right)\right)-{\displaystyle \frac{2}{3}}\right)+{\displaystyle \frac{2}{3}}\ge 4^{l-1}.$$

Therefore, if we take sufficiently large l, we can achieve

$$4^{l-1}>\rho \left(x_{i_0}\right)$$

which is a contradiction.

The previous example shows that finite coarse shape groups of the same space, in general, depend on the choice of a base point. Hence, since those groups are finite coarse shape invariant (see [4]), the pointed finite coarse shape type of $\left(X,x\right)$, in general, depends on the choice of point x. However, there is a large class of topological spaces for which this is not true—we prove that if X is a finite coarse shape path connected paracompact locally compact space, then the pointed finite coarse shape type of $\left(X,x\right)$ does not depend on the choice of point x.

Theorem 2.

Let X be a topological space admitting a metrizable polyhedral resolution, and let $x_0,x_1\in X$. If there exists a finite coarse shape path in X from $x_0$ to $x_1$, then $\left(X,x_0\right)$ and $\left(X,x_1\right)$ have the same pointed finite coarse shape type, i.e., $\left(X,x_0\right)$ and $\left(X,x_1\right)$ are isomorphic in $S{h}_{\ast }^{⊛}$.

Proof. 

Let $\left[\left(p_{\lambda }\right)\right]:\left(X,x_0,x_1\right)\to \left(\left(X_{\lambda },x_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$, $\left[\left(p_{\lambda }\right)\right]:\left(X,x_0\right)\to \left(\left(X_{\lambda },x_{\lambda }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ and $\left[\left(p_{\lambda }\right)\right]:\left(X,x_1\right)\to \left(\left(X_{\lambda },x_{\lambda }^{\prime }\right),p_{\lambda {\lambda }^{\prime }},\mathrm{\Lambda }\right)$ be $pr{o}^{⊛}$-$Hpo{l}_{\ast \ast }$ ($pr{o}^{⊛}$-$Hpo{l}_{\ast }$) expansions of $\left(X,x_0,x_1\right)$, $\left(X,x_0\right)$ and $\left(X,x_1\right)$, respectively. Let ${\mathrm{\Omega }}^{⊛}=〈\left[\left({\omega }_{\lambda }^m\right)\right]〉:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ be a finite coarse shape path in X from $x_0$ to $x_1$. In the analogous way as in the proof of Theorem II.8.9 of [2] an isomorphism ${\mathbf{f}}^{⊛}:\left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}}\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{1}}\right)$ of $pr{o}^{⊛}$-$HPo{l}_{\ast }$ and its inverse ${\mathbf{g}}^{⊛}:\left(\mathbf{X},{\mathbf{x}}_{\mathbf{1}}\right)\to \left(\mathbf{X},{\mathbf{x}}_{\mathbf{0}}\right)$ are constructed. Isomorphisms ${\mathbf{f}}^{⊛}$ and ${\mathbf{g}}^{⊛}$ determine the pointed finite coarse shape (iso)morphisms $F^{⊛}=〈{\mathbf{f}}^{⊛}〉:\left(X,x_0\right)\to \left(X,x_1\right)$ and $G^{⊛}=〈{\mathbf{g}}^{⊛}〉:\left(X,x_1\right)\to \left(X,x_0\right)$, respectively. Thus, $s{h}^{⊛}\left(X,x_0\right)=s{h}^{⊛}\left(X,x_1\right)$. □

Example 3.

In the solenoid ${\Sigma }_{\left(p_n\right)}$, for every two points $x_0,x_1\in {\Sigma }_{\left(p_n\right)}$ belonging to the same composant, there is a finite coarse shape path from $x_0$ to $x_1$. Then, by Theorem 2, $\left({\Sigma }_{\left(p_n\right)},x_0\right)$ and $\left({\Sigma }_{\left(p_n\right)},x_1\right)$ are isomorphic in $S{h}_{\ast }^{⊛}$.

Theorem 2 is obviously valid for all compact metric spaces. Moreover, by [10], all paracompact locally compact spaces admit a metrizable polyhedral resolution. That fact yields the following corollary:

Corollary 3.

Let X be a finite coarse shape path connected paracompact locally compact space. Then, the pointed finite coarse shape type of $\left(X,x_0\right)$ does not depend on the choice of point $x_0$.

Remark 2.

It would be interesting and useful to find, if it exists, an example of a space that is finite coarse shape path connected, but not shape path connected. However, that example must be rather exotic since it does not, by Corollary 2, belong to the class of pointed 1-movable metrizable compacta.

5. Conclusions

The finite coarse shape theory was introduced recently in [1]. This new theory categorically classifies topological spaces in such a way that the shape category $Sh$ can be regarded as a proper subcategory of the finite coarse shape category $S{h}^{⊛}$, while $S{h}^{⊛}$ is a proper subcategory of the coarse shape category $S{h}^{\ast }$.

In this paper, the authors define notions of finite coarse shape path and finite coarse shape path connectedness and prove that being finite coarse shape path connected is a topological property. We also investigate an interesting example of the solenoid ${\Sigma }_{\left(p_n\right)}$ and prove that there are infinitely many finite coarse shape path components in ${\Sigma }_{\left(p_n\right)}$.

Furthermore, we show that, for every $k\in \mathbb{N}$, every finite coarse shape path ${\mathrm{\Omega }}^{⊛}:\left(I,0,1\right)\to \left(X,x_0,x_1\right)$ induces a group isomorphism (for $k=0$ a base point preserving bijection) from ${\check{\pi }}_k^{⊛}\left(X,x_0\right)$ to ${\check{\pi }}_k^{⊛}\left(X,x_1\right)$ with some nice properties. By virtue of the Example 2, it is shown that finite coarse shape groups of the same space, in general, depend on the choice of a base point. Hence, since those groups are finite coarse shape invariant, the pointed finite coarse shape type of $\left(X,x\right)$, in general, depends on the choice of point x. Still, we prove that if X is a finite coarse shape path-connected paracompact locally compact space, then the pointed finite coarse shape type of $\left(X,x\right)$ does not depend on the choice of point x.