Dragon Intermittency at the Transition to Synchronization in Coupled Rulkov Neurons

Abstract

We investigate the synchronization dynamics of two non-identical, mutually coupled Rulkov neurons, emphasizing the effects of coupling strength and parameter mismatch on the system’s behavior. At low coupling strengths, the system exhibits multistability, characterized by the coexistence of three distinct 3-cycles. As the coupling strength is increased, the system becomes monostable with a single 3-cycle remaining as the sole attractor. A further increase in the coupling strength leads to chaos, which we identify as arising through a novel type of intermittency. This intermittency is characterized by alternating dynamics between two low-dimensional invariant subspaces: one corresponding to synchronization and the other to asynchronous behavior. We show that the system’s phase-space trajectory spends variable durations near one subspace before being repelled into the other, revealing non-trivial statistical properties near the onset of intermittency. Specifically, we find two key power-law scalings: (i) the mean duration of the synchronization interval scales with the coupling parameter, exhibiting a critical exponent of $-0.5$ near the onset of intermittency, and (ii) the probability distribution of synchronization interval durations follows a power law with an exponent of $-1.7$ for short synchronization intervals. Intriguingly, for each fixed coupling strength and parameter mismatch, there exists a most probable super-long synchronization interval, which decreases as either parameter is increased. We term this phenomenon “dragon intermittency” due to the distinctive dragon-like shape of the probability distribution of synchronization interval durations.

1. Introduction

Chaotic synchronization is a fundamental phenomenon in dynamical systems that governs the collective behavior of interacting nonlinear oscillators [1,2]. It covers a wide range of natural and engineered processes, from biological rhythms to advanced communication systems. Among the various facets of this phenomenon, transitions from asynchronous to synchronous dynamics in coupled systems are of particular importance [3,4,5,6,7]. These transitions often reveal rich and complex dynamical behaviors, including intermittent states when the system dynamics switches between order and chaos. The intermittency route to chaos is an important research topic in nonlinear dynamics, describing how systems transition to chaotic behavior as control parameters cross critical thresholds. Characterized by the alternation between nearly regular “laminar” phases and irregular “turbulent” bursts, this transition is a hallmark of many nonlinear systems. The turbulent bursts typically exhibit durations weakly dependent on the control parameter, whereas the mean duration of laminar phases decreases as the system progresses further into chaos, eventually vanishing altogether. Traditionally, such transitions are governed by singular bifurcation mechanisms that delineate the onset of chaos.

Classical forms of intermittency, as categorized by Pomeau and Manneville [8,9], provide a theoretical foundation for these transitions. Type-I intermittency emerges from saddle–node bifurcations, type-II intermittency from Hopf bifurcations, and type-III intermittency from inverse period-doubling bifurcations. Other types, such as crisis-induced intermittency, occur due to the collision of a chaotic attractor with a periodic orbit or its basin boundary [10], while multistate intermittency is induced by noise in a system with coexisting attractors [11,12]. Each type exhibits distinct scaling laws near the critical point, offering insight into the universal features of chaotic systems. For example, on–off intermittency—a common phenomenon near synchronization boundaries—displays a mean laminar phase duration that scales with the control parameter as $-1$ and a probability density of laminar durations that scales as $-3/2$ [13,14].

In coupled chaotic systems, intermittency plays a pivotal role in the transitions between asynchronous and synchronous states. Over the last two decades, extensive research has been dedicated to uncovering intermittent behaviors near synchronization regimes [15,16,17]. These studies highlight the sensitivity of intermittency to various factors, including the type of synchronization, parameter mismatches, noise, and coupling mechanisms. Near synchronization boundaries, systems frequently exhibit phenomena such as type-I intermittency [9,18,19], eyelet intermittency [20,21], or ring intermittency [22,23]. Eyelet intermittency typically occurs near the boundary separating synchronization and type-I intermittency, while ring intermittency arises in systems with significant parameter mismatches, leading to detuning of fundamental frequencies.

Initially, it was believed that coupled chaotic oscillators primarily transitioned to synchronization through mechanisms like on–off intermittency [24] or jump intermittency [25]. Jump intermittency, characterized by its irregular dynamics and intricate statistical properties, is particularly prominent near generalized synchronization. However, ongoing investigations continue to uncover new intermittency mechanisms in both continuous and discrete-time systems, reflecting the diverse pathways by which coupled chaotic systems approach synchronization. This rich tapestry of intermittency behaviors underscores the complexity of transitions in nonlinear systems and highlights the need for further exploration to unravel the underlying principles.

In this paper, we focus on the dynamics of two mutually coupled, non-identical Rulkov neurons, investigating the emergence of a novel type of intermittency during transitions to chaos. The Rulkov map, a discrete-time nonlinear model, is widely recognized for its ability to reproduce spiking and bursting dynamics observed in biological neurons with remarkable computational simplicity [26]. This makes the Rulkov model particularly suitable for exploring complex neural behaviors, including synchronization, chaos, and multistability, under varying coupling strengths and parameter mismatches. Recent studies have demonstrated that coupled Rulkov neurons exhibit intricate dynamics, such as multistability, periodicity, and chaotic transitions, depending on the control parameters [12,27]. It should be noted that multistability has also been observed in other coupled neural systems [2,11,28].

Here, we extend this understanding by uncovering a unique intermittency phenomenon that arises when the coupled neurons attempt to synchronize but are disrupted by desynchronizing dynamics due to parameter mismatches. Unlike classical forms of intermittency, this new type—termed dragon intermittency—is distinguished by specific scaling behaviors and a probability density function with a unique “dragon-like” shape. We identify two critical power-law scalings near the onset of intermittency: (i) the mean duration of synchronization intervals scales with a control parameter with a critical exponent of $-0.5$, and (ii) the probability distribution of synchronization intervals scales with an exponent of $-1.7$ for short intervals. Interestingly, we also observe the existence of a most probable super-long laminar phase duration for each fixed coupling strength and parameter mismatch, which diminishes as the parameters are further increased.

The discovery of dragon intermittency broadens the landscape of known intermittency types in coupled dynamical systems and reveals new pathways for the interplay between synchronization and chaos in discrete-time neural models. These findings contribute to a deeper understanding of the mechanisms underlying synchronization transitions in systems with parameter mismatches, offering potential implications for both theoretical studies and practical applications, such as neural network modeling, brain dynamics, and coupled oscillator systems in physics and biology.

The remainder of this paper is organized as follows. Section 2 introduces the mathematical model of coupled Rulkov neurons and provides an overview of the numerical methods employed. Section 3 explores the observed dynamics in detail, including the coexistence of attractors and the structure of their basins of attraction. In Section 4, we present the key results, focusing on the scaling laws and statistical properties associated with dragon intermittency. Finally, Section 5 summarizes the main conclusions and suggests promising directions for future research.

2. Model of Coupled Rulkov Neurons

Consider a system of two non-identical neurons mutually coupled by electrical synapses:

$$\begin{array}{c}{x}_{t+1}=f({\gamma }_1,x_t)+\sigma (y_t-x_t),y_{t+1}=f({\gamma }_2,y_t)+\sigma (x_t-y_t),\hfill \end{array}$$

(1)

where $\sigma$ represents the coupling strength, and f is a nonlinear Rulkov function given by [26]

$$f(\gamma ,v)={\displaystyle \frac{\alpha }{1+v^2}}+\gamma$$

with parameter $\gamma ={\gamma }_1,{\gamma }_2$, variable $v=x,y$, and constant $\alpha =4.1$. In system (1), one of the map parameters slightly differs, such that ${\gamma }_2={\gamma }_1+\Delta$, where $\Delta$ denotes parameter mismatch or detuning.

The dynamics of system (1) are determined by the control parameter $\gamma$, as illustrated in the bifurcation diagram in Figure 1. In the subsequent analysis, we fix ${\gamma }_1=-1.75$, a value for which the isolated map $x_{t+1}=f({\gamma }_1,x_t)$ exhibits a stable 3-cycle. This specific choice of the control parameter is motivated by the seminal paper by Li and Yorke [29], where at $\gamma =-1.75$ the system resides in the period-3 window. This choice ensures that both neurons operate within the parameter range of 3-cycles. In addition, in this study we consider a small mismatch in the range $0\le \Delta \le 0.002$, ensuring that the isolated neuron is in a 3-cycle oscillatory mode.

The dynamics of the coupled system (1) are strongly influenced by the coupling parameter $\sigma$. This dependence is illustrated in Figure 2 through bifurcation diagrams, where $\sigma$ is used as the control parameter. The diagrams compare the system’s behavior in two scenarios: one with no mismatch ($\Delta =0$) and the other with slight detuning ($\Delta =0.002$). In these diagrams, the x coordinates of various attractors, found by randomly varying initial conditions, are represented in red ($\mathcal{R}$), green ($\mathcal{G}$), and blue ($\mathcal{B}$).

In the case of an isolated one-dimensional subsystem, the phase space is one-dimensional and hosts a single attractor corresponding to a 3-cycle, as shown in Figure 1. However, in the coupled system, even when the coupling strength is zero ($\sigma =0$), the phase space becomes two-dimensional, representing two uncoupled one-dimensional subsystems. This configuration results in the coexistence of three distinct 3-cycles within the two-dimensional phase space, each corresponding to a unique synchronization mode. This multirhythmicity is clearly seen in the bifurcation diagram in Figure 2 by the $\mathcal{R}$, $\mathcal{G}$, and $\mathcal{B}$ branches.

The insets in Figure 2 provide a detailed view of these cycles, emphasizing the intricate and diverse dynamics introduced by coupling. These findings highlight the profound impact of coupling and detuning on the system’s behavior, revealing complex synchronization patterns and transitions.

At a critical value of $\sigma$, the multirhythmicity vanishes, leaving the 3-cycle $\mathcal{R}$ as the sole attractor. As $\sigma$ increases further, system (1) transitions from the regular 3-cycle to a chaotic regime through a crisis bifurcation at ${\sigma }_{*}$. For $\Delta =0$, chaos emerges at ${\sigma }_{*}=0.0711516$ (Figure 2a), while for $\Delta =0.002$, it appears at ${\sigma }_{*}=0.019011$ (Figure 2b). Notably, this $\sigma$ threshold is significantly lower in the presence of mismatch ($\Delta =0.002$) compared to the case without mismatch ($\Delta =0$).

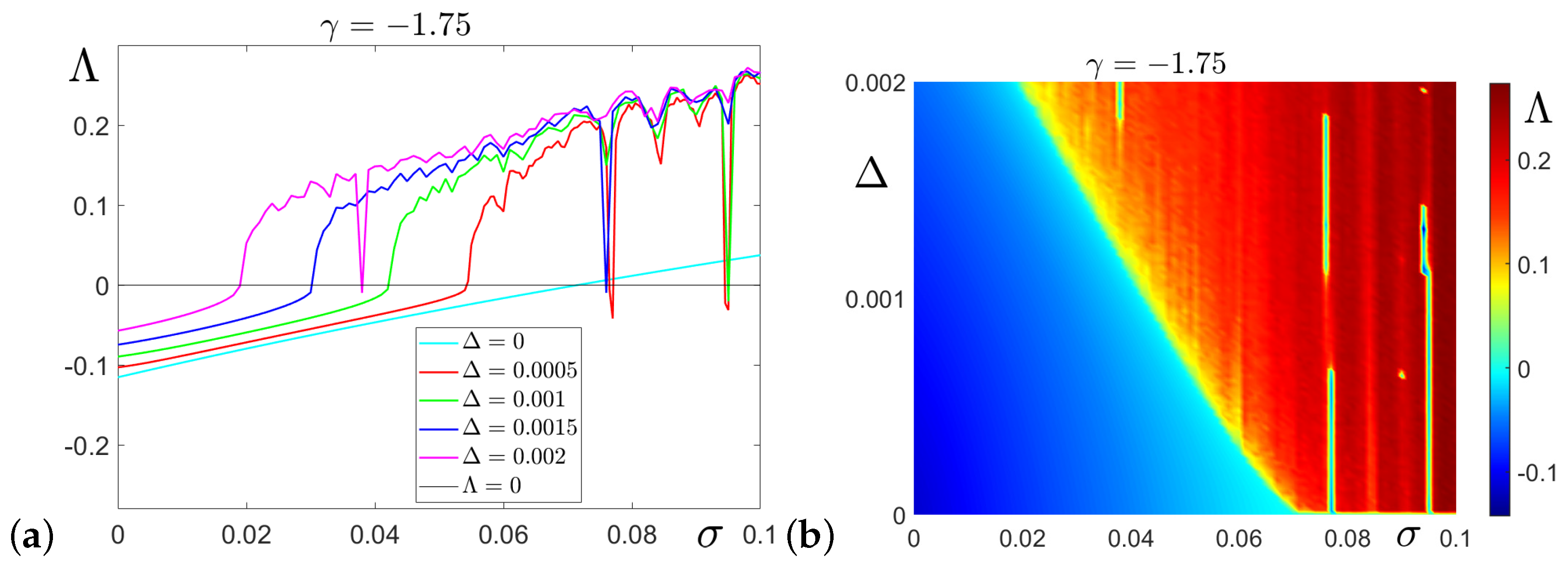
The results of our detailed parametric analysis of the order-to-chaos transition are presented in Figure 3, where the largest Lyapunov exponents $\Lambda$ are plotted as functions of $\sigma$ and $\Delta$. Positive values of $\Lambda$ indicate chaotic behavior. As shown in Figure 3a, the crisis bifurcation point ${\sigma }_{*}$ decreases as the mismatch $\Delta$ is increased. In the two-parameter space, the crisis bifurcation line appears approximately linear, as depicted in Figure 3b. These findings underscore the sensitivity of the system’s dynamics to parameter mismatches and provide valuable insights into the mechanisms driving the transition to chaos.

3. Basins of Attraction

We examine the arrangement of regular and chaotic attractors, as well as the geometry of their basins of attraction, in the phase plane. Representative examples are presented in Figure 4 and Figure 5, corresponding to $\Delta =0$ and $\Delta =0.002$, respectively.

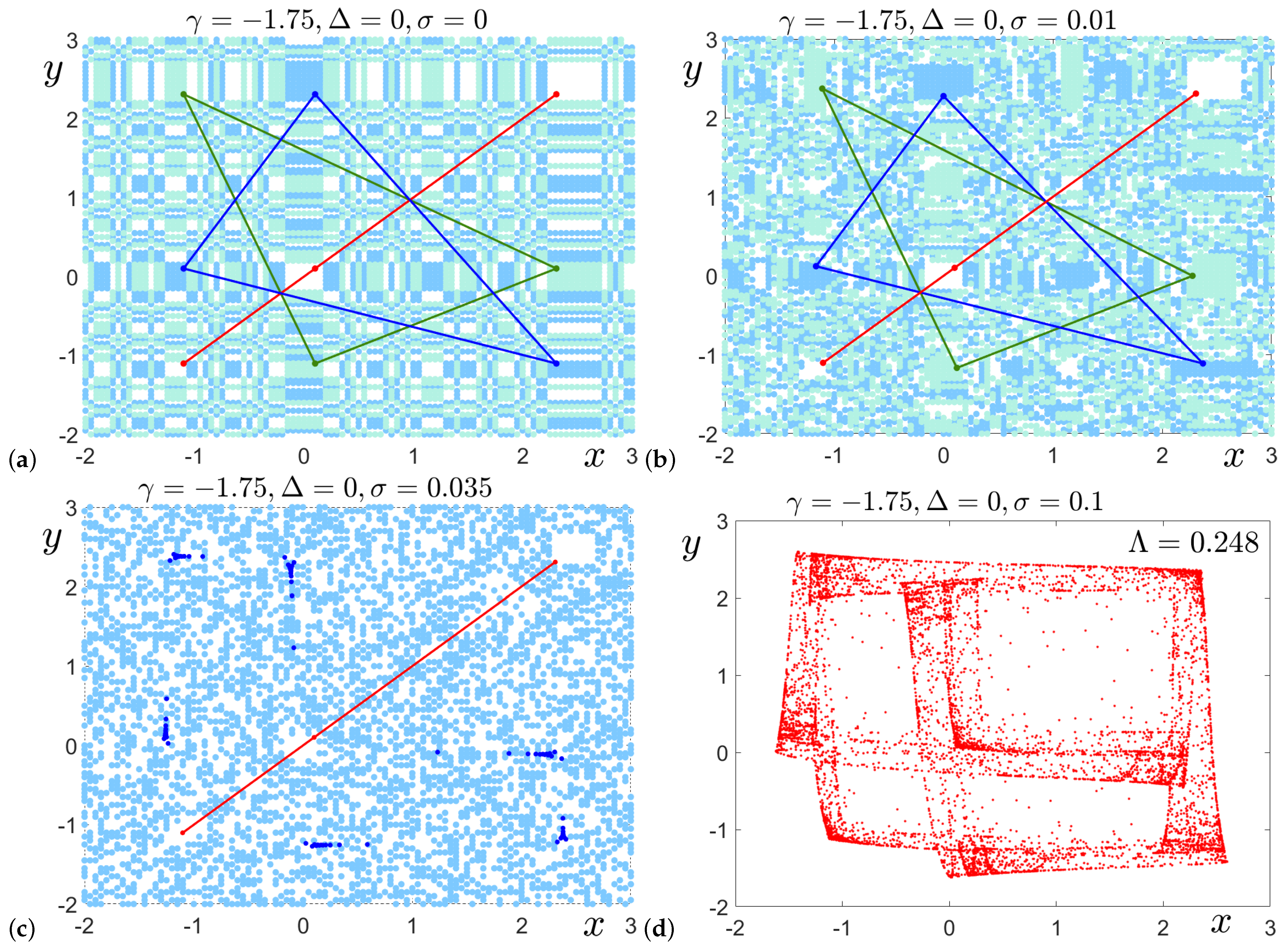
System (1) with zero coupling ($\sigma =0$) and no mismatch ($\Delta =0$) exhibits three stable, coexisting 3-cycles ($\mathcal{R}$, $\mathcal{G}$, and $\mathcal{B}$), as shown in Figure 4a. The basins of attraction for these cycles form a “parquet” of rectangles: white for $\mathcal{R}$, light green for $\mathcal{G}$, and light blue for $\mathcal{B}$. When the coupling strength is slightly increased to $\sigma =0.01$ (Figure 4b), the attractors remain the same, but their basin structures change qualitatively, transitioning to fractal boundaries.

As $\sigma$ increases further, the stable cycles $\mathcal{G}$ and $\mathcal{B}$ vanish, and the system becomes nearly monostable with the $\mathcal{R}$ attractor dominating, as seen in the bifurcation diagram in Figure 2a. However, narrow $\sigma$ intervals still exist where the stable $\mathcal{R}$ 3-cycle coexists with other attractors. For example, at $\sigma =0.035$ (Figure 4c), the $\mathcal{R}$ 3-cycle coexists with a 74-cycle, the basin of which is shown in light blue.

When $\sigma$ exceeds the crisis point ${\sigma }_{*}=0.0711516$, the stability of the $\mathcal{R}$ cycle is lost, and the system transitions to chaos. The chaotic attractor for $\sigma =0.1$ and $\Delta =0$ is shown in Figure 4d, with a largest Lyapunov exponent of $\Lambda =0.248$.

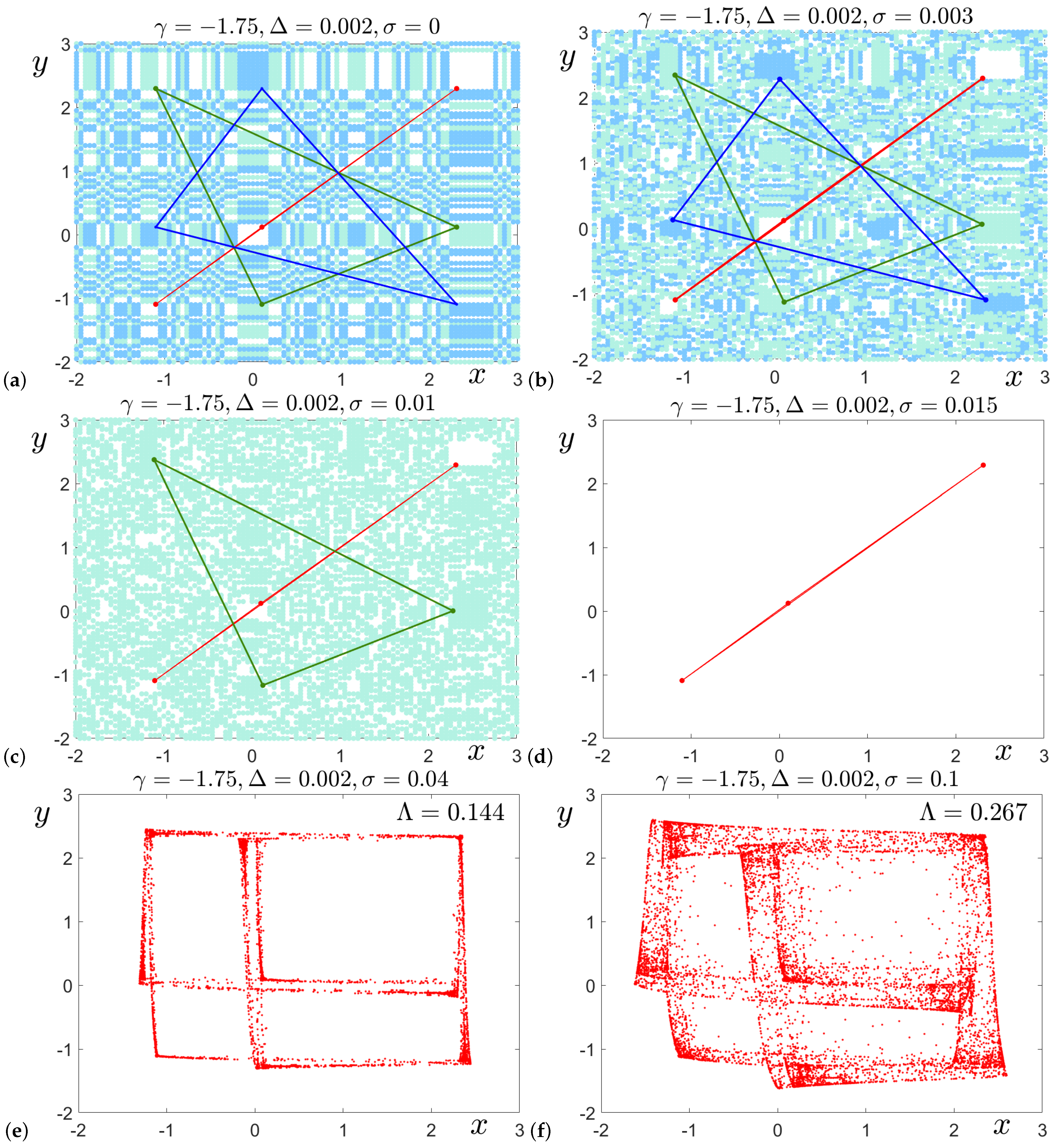
Next, we consider the effects of increasing the mismatch to $\Delta =0.002$ (Figure 5). Similar to the case with $\Delta =0$, distinct basin boundaries are observed at zero coupling ($\sigma =0$) (Figure 5a), and the basins exhibit fractal structures as the coupling strength increases (Figure 5b). However, unlike the case with $\Delta =0$, when $\Delta =0.002$, a further increase in $\sigma$ results in the annihilation of only the $\mathcal{B}$ cycle. This leaves the system bistable with two coexisting 3-cycles ($\mathcal{R}$ and $\mathcal{G}$), as shown in Figure 5c for $\sigma =0.01$. As $\sigma$ is increased further, the system becomes monostable with only the $\mathcal{R}$ 3-cycle for $\sigma =0.015$ (Figure 5c), and eventually chaotic for $\sigma >0.02$. Examples of chaotic attractors with Lyapunov exponents of $\Lambda =0.144$ (Figure 5e) and $\Lambda =0.267$ (Figure 5f) are shown for $\sigma =0.04$ and $\sigma =0.1$, respectively. As illustrated, the chaotic attractor becomes increasingly blurred as the coupling strength is raised.

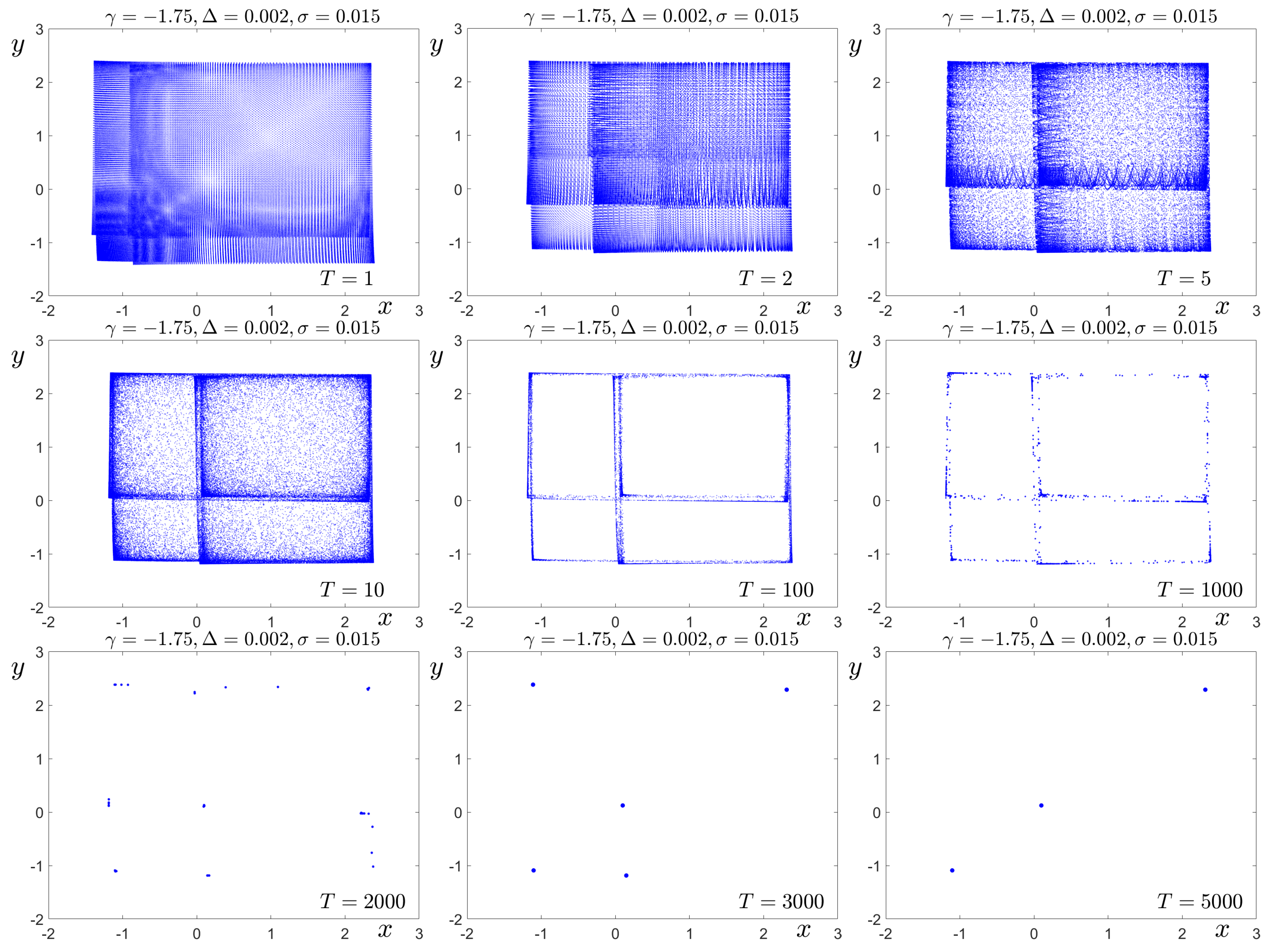
Let us draw your attention to Figure 5d, which illustrates the case of monostability. Although the attractor appears simple, it embodies a complexity not immediately apparent in this figure. While system (1) is monostable and all initial conditions eventually converge to the same 3-cycle, $\mathcal{R}$, the convergence process itself reveals an important characteristic: the system reaches the stable solution through chaotic transient behavior. This transient behavior is further illustrated in Figure 6, where an ensemble of solutions is shown, starting from the nodes of a uniform grid in the region $[-2,3]\times [-2,3]$. As seen in the figure, for a sufficiently long transient period, the state distribution of this ensemble is metastable and resembles the chaotic attractor shown in Figure 5e. It takes several thousand iterations for the ensemble to begin localizing near the points of the stable 3-cycle, $\mathcal{R}$. This phenomenon, known as transient chaos [30], highlights the intricate dynamics underlying the system’s apparent simplicity.

4. Synchronization and Intermittency

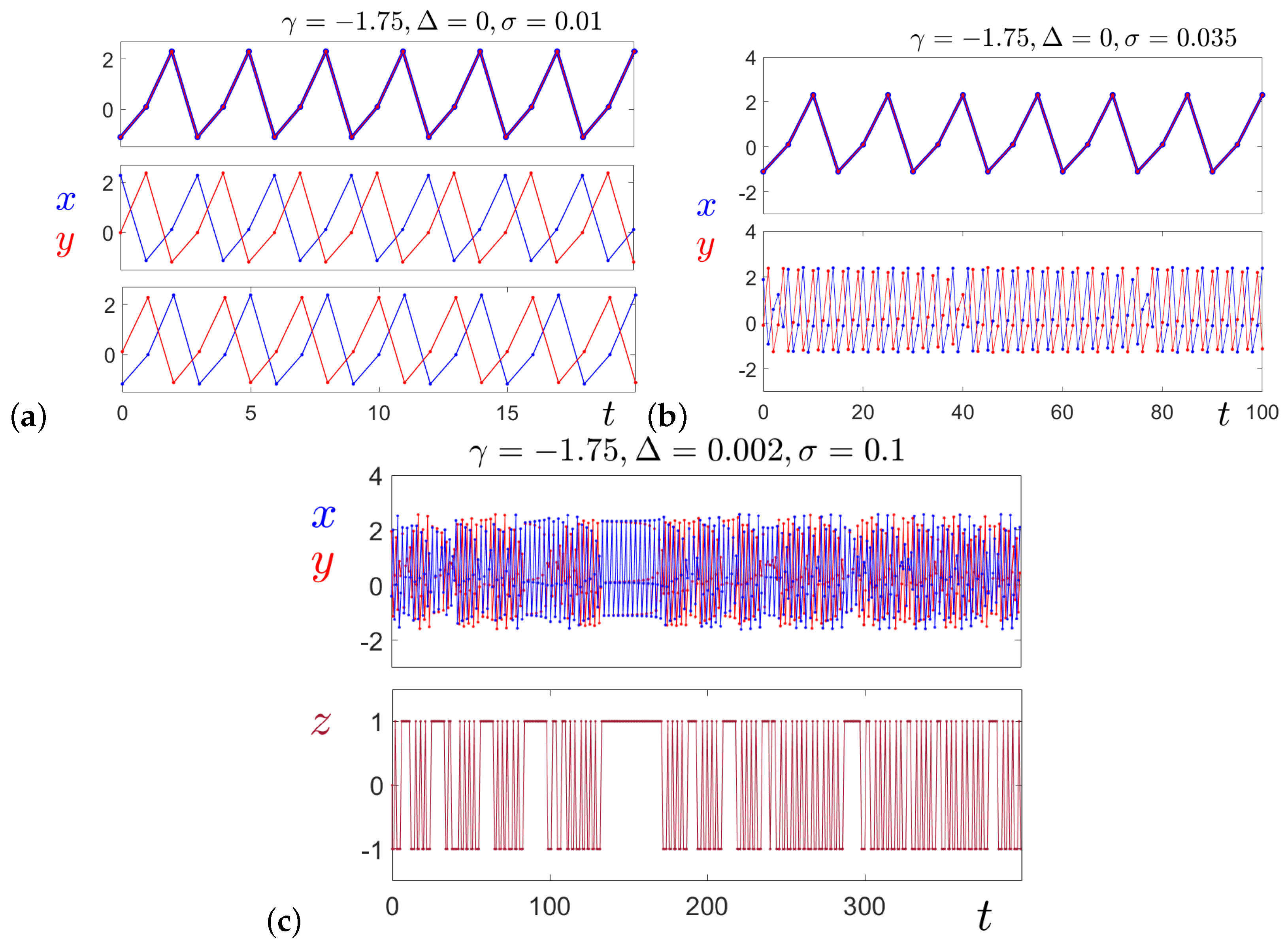
We now turn our attention to how the changes in the oscillatory activity of system (1) influence synchronization dynamics. The synchronization of identical neurons ($\Delta =0$) for various values of $\sigma$ is illustrated in Figure 7 through time series. For weak coupling ($\sigma =0.01$), we observe three distinct synchronization patterns, as shown in Figure 7a. These include complete synchronization (top panel), which occurs for initial conditions within the basin of the 3-cycle $\mathcal{R}$, as well as two forms of lag synchronization: one for solutions starting in the basins of $\mathcal{G}$ (middle panel) and another for solutions starting in the basins of $\mathcal{B}$ (bottom panel), both of which exhibit a one-step lag in synchronization.

Figure 7b displays two types of synchronization for $\sigma =0.035$: complete synchronization for the 3-cycle $\mathcal{R}$ (top panel) and lag synchronization for solutions starting in the basin of attraction of the 74-cycle (bottom panel). In the latter case, the synchronous dynamics are disrupted by phase slips in the x coordinate, which alternately lead it one step ahead and one step behind the y coordinate.

As $\sigma$ exceeds the critical value ${\sigma }_{*}=0.0711516$, system (1) becomes monostable with the 3-cycle $\mathcal{R}$ as the sole attractor. In this regime, the system reaches complete synchronization regardless of the initial conditions.

Synchronization in the chaotic regime is illustrated in Figure 7c for $\sigma =0.1$. Here, alternating time intervals of in-phase synchronization and complex mixed oscillations are observed. To identify the in-phase synchronization intervals, we introduce a synchronization indicator variable z defined as:

$$z_t=\mathrm{sgn}\left((x_{t+1}-x_t)(y_{t+1}-y_t)\right).$$

The value z serves as a simple and convenient indicator for identifying synchronization states: $z=1$ corresponds to in-phase synchronization, while $z=-1$ means asynchronous behavior. This measure has been previously introduced and successfully utilized in [31,32].

The time series of the synchronization indicator z is shown in the bottom panel of Figure 7c. It is evident that long intervals of in-phase synchronization ($z=1$) are interrupted by alternating periods of mixed synchronous and asynchronous behaviors. One can see that even with identical neurons, increasing the coupling strength induces intermittent synchronization.

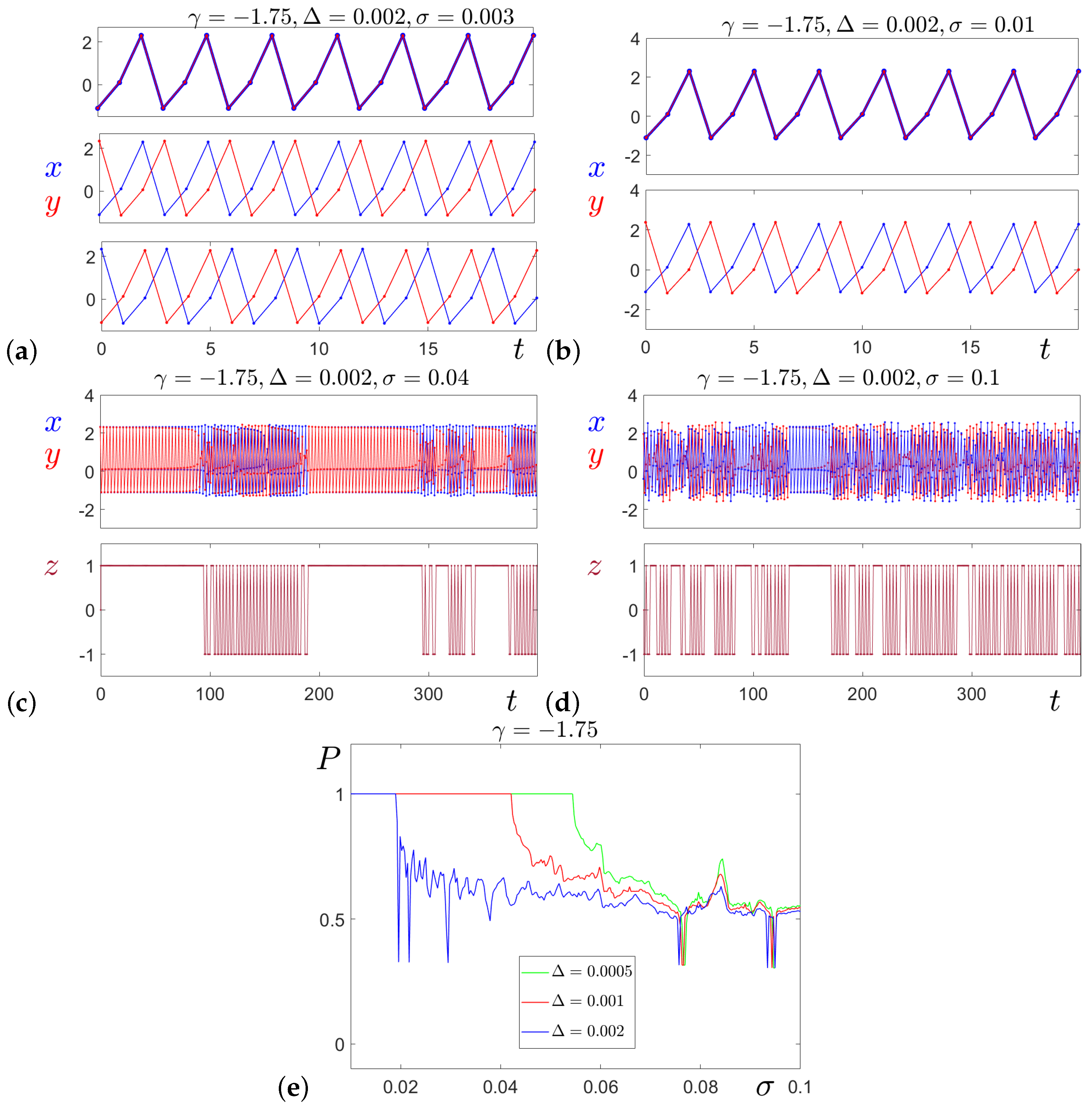
Now, let us explore the synchronization scenarios for the case of non-identical neurons with a mismatch of $\Delta =0.002$. The time series illustrating different synchronization regimes are presented in Figure 8 for various values of $\sigma$.

Figure 8a illustrates three variants of synchronization in the trirhythmic system (1) with $\sigma =0.003$, where the dynamics exhibit the coexistence of three 3-cycles ($\mathcal{R}$, $\mathcal{G}$, and $\mathcal{B}$). The basins of attraction of these cycles are shown in Figure 5b. For stronger coupling ($\sigma =0.01$), as shown in Figure 8b, the system transitions to a birhythmic state, where only two 3-cycles ($\mathcal{R}$ and $\mathcal{G}$) coexist, with their basins of attraction shown in Figure 5c.

At larger coupling strengths, intermittent synchronization emerges. Figure 8c and Figure 8d display examples of this behavior, where time intervals of in-phase synchronization ($z=1$) are interrupted by periods of mixed complex oscillations for $\sigma =0.04$ and $\sigma =0.1$, respectively. Notably, for $\sigma =0.04$, the time intervals of co-directed behavior ($\tau$) are longer than those for $\sigma =0.1$. The duration $\tau$ of these intervals is random. To compute $\tau$ numerically, we determine the number of successive time steps during which $z=1$. This approach ensures that $\tau$ reflects the length of each continuous synchronization interval.

Due to the unpredictable nature of $\tau$ in the chaotic regime, we focus on studying the probability P that the system remains in a state of co-directed oscillations ($z=1$). Figure 8e shows how this probability P depends on the coupling strength $\sigma$ for three different mismatch values $\Delta$. The smaller the mismatch $\Delta$, the wider the range of $\sigma$ values for which co-directed behavior ($z=1$) is observed with $P=1$. As $\sigma$ is increased, the probability P decreases. However, it is important to note that for nearly all values of $\sigma$, the probability remains greater than 0.5, indicating that in the complex chaotic regime, the time intervals of in-phase synchronization prevail over asynchronous behavior.

Let us now examine the statistical properties of the intermittency observed. First, we will analyze how the mean values $\langle \tau \rangle$ of the synchronous intervals $\tau$ vary with the parameter $\sigma$ near the crisis bifurcation point ${\sigma }_{*}$, which marks the onset of intermittency. To identify this bifurcation, Figure 9a,b present the largest Lyapunov exponents $\Lambda$ as a function of $\sigma$ for $\Delta =0.001$ and $\Delta =0.002$, respectively. The bifurcation points ${\sigma }_{*}$ are indicated by vertical dashed lines.

Let d denote a small deviation in the coupling parameter $\sigma$ from the crisis bifurcation point ${\sigma }_{*}$, such that $\sigma ={\sigma }_{*}+d$. Our analysis reveals that the mean duration of synchronization intervals follows a power law:

$$\langle \tau \rangle \sim d^{-0.5}.$$

In Figure 9c,d, this scaling relation is depicted by red lines for $\Delta =0.001$ and $\Delta =0.002$, respectively. The values of $\langle \tau \rangle$ obtained numerically are marked with asterisks.

Another key characteristic of intermittency is the probability distribution of time intervals $\tau$ exhibiting co-directed behavior ($z=1$). Figure 10a,b display the time series of variables $x,y$, and synchronization indicator z for two values of deviation ($d={10}^{-4}$ and $d={10}^{-3}$) from the onset of intermittency. As shown, the time intervals of synchronous behavior become shorter and occur more frequently as d is increased.

The probability density functions $p\left(\tau \right)$ of these intervals are presented in Figure 11 for two different values of $\Delta$ and d. For small values of $\tau$, the asymptotic behavior follows a power law

$$p\left(\tau \right)\sim {\tau }^{-1.7},$$

which is highlighted in green.

As $\tau$ is increased, an interesting feature emerges in the probability density function $p\left(\tau \right)$. Narrow peaks with high probability become clearly visible, highlighting the most frequently observed time intervals with co-directed behavior. Notably, during these intervals, the system tends to remain near the states of the unstable 3-cycle.

5. Conclusions

In this paper, we investigated the complex dynamics of two non-identical neurons coupled through electrical synapses within a discrete dynamical framework based on the Rulkov model. Our study uncovered a rich dynamic of joint behaviors and transitions, illustrating how coupling strength and parameter mismatches govern the stability, synchronization, and complexity of the system.

We found that for small coupling strengths and parameter mismatches, the system exhibits the coexistence of three distinct 3-cycles. This trirhythmicity diminishes as coupling strength or mismatch parameters are increased, ultimately driving the system through a transition to chaos. This transition underscores the system’s sensitivity to both intrinsic (parameter mismatches) and extrinsic (coupling) control variables, highlighting the interplay between heterogeneity and connectivity in shaping the system dynamics.

In the chaotic regime, we identified a novel type of intermittency characterized by the statistical properties of synchronization intervals during co-directional neuron activity. Two key scaling laws emerged: (i) a power-law scaling of $\langle \tau \rangle \sim d^{-0.5}$ for the mean duration of synchronous phases near the crisis bifurcation, reflecting the system’s critical sensitivity near the transition to chaos, and (ii) a power-law scaling of $p\left(\tau \right)\sim {\tau }^{-1.7}$, for the probability density of synchronous interval durations, revealing the statistical structure of intermittency for short intervals.

The intermittent behavior identified in our study represents a transition between synchronous and asynchronous states, characterized by alternating synchronized and desynchronized dynamics. This interplay underscores the intricate relationship between these regimes. The observed intermittency emerges near a crisis bifurcation but fundamentally differs from classical crisis-induced intermittency [10], as it is governed by unique scaling laws. Remarkably, the probability distribution function of synchronization interval durations exhibits a “dragon-like” shape—an unprecedented feature in the scientific literature, to the best of our knowledge. This finding highlights the exceptional coherence properties within the intermittency dynamics. Notably, longer synchronization intervals display significant coherence, setting this system apart. The distinctive “dragon-like” tail further emphasizes the irregularity and unpredictability inherent in the chaotic dynamics. This unique signature inspired the nomenclature for this type of intermittency and establishes it as a novel phenomenon in the study of coupled systems.

The scaling laws and dynamical patterns revealed in this work enhance our understanding of the fundamental mechanisms in coupled non-identical chaotic maps. Their robustness across parameter ranges suggests that these findings may generalize to other coupled chaotic systems, including neuronal networks and biological systems with similar coupling dynamics. Future research could extend these insights by investigating the role of more complex network topologies and interactions, assessing the biological relevance of these dynamics in real neural systems, and exploring the effects of noise, time delays, or alternative coupling forms on synchronization and intermittency. Establishing a robust mathematical justification for the dynamical behavior observed in this study would be highly relevant and valuable. However, a comprehensive theoretical framework capable of rigorously proving these behaviors is currently lacking. This remains an open avenue for future research and theoretical exploration. By delving deeper into these universal scaling behaviors and the intricate interplay of synchronization and chaos, this study contributes to the broader understanding of coupled dynamical systems, with implications for both theoretical and applied contexts.