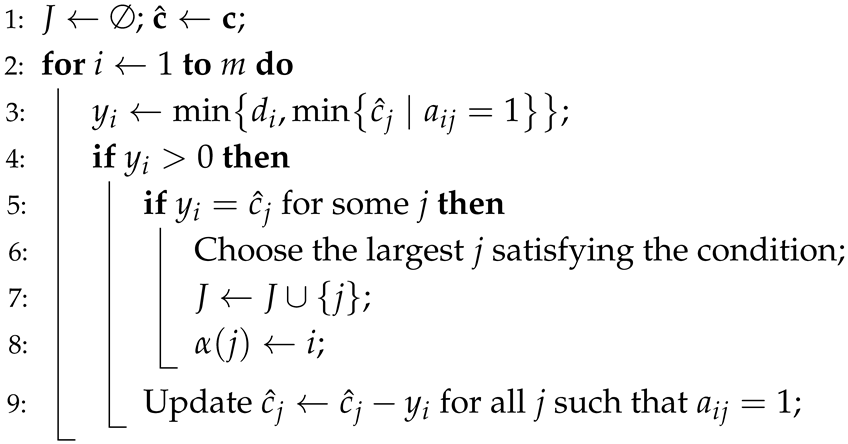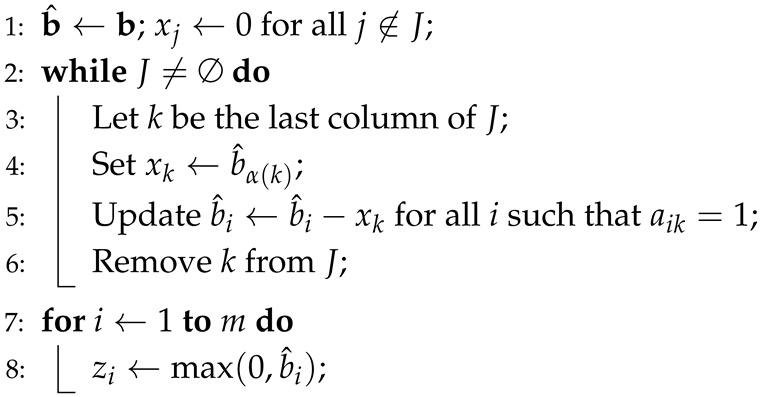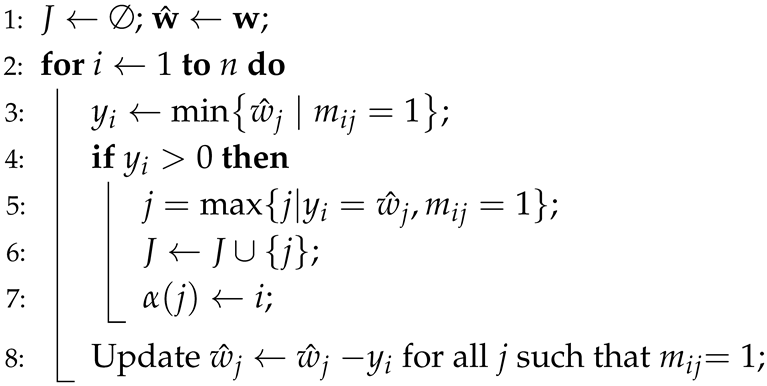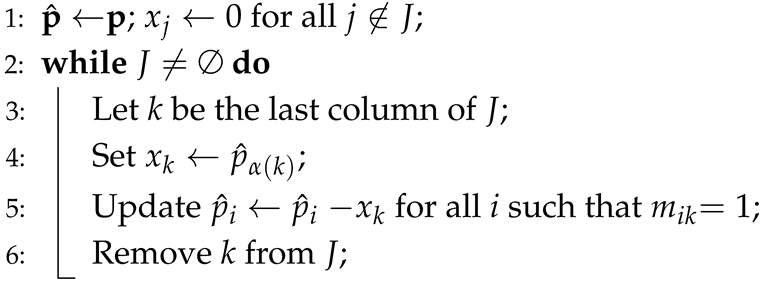Exploring Dominating Functions and Their Complexity in Subclasses of Weighted Chordal Graphs and Bipartite Graphs

Abstract

Domination problems are fundamental problems in graph theory with diverse applications in optimization, network design, and computational complexity. This paper investigates $\left\{k\right\}$-domination, k-tuple domination, and their total domination variants in weighted strongly chordal graphs and chordal bipartite graphs. Specifically, the $\left\{k\right\}$-domination problem in weighted strongly chordal graphs and the total $\left\{k\right\}$-domination problem in weighted chordal bipartite graphs are shown to be solvable in $\mathcal{O}(n+m)$ time. For weighted proper interval graphs and convex bipartite graphs, we solve the k-tuple domination and total k-tuple domination problems in $\mathcal{O}(n^{2.371552}{log}^2\left(n\right)log(n/\delta ))$, where $\delta$ is the desired accuracy. Furthermore, for weighted unit interval graphs, the k-tuple domination problem achieves a significant complexity improvement, reduced from $\mathcal{O}\left(n^{k+2}\right)$ to $\mathcal{O}(n^{2.371552}{log}^2\left(n\right)log(n/\delta ))$. These results are achieved through a combination of linear and integer programming techniques, complemented by totally balanced matrices, totally unimodular matrices, and graph-specific matrix representations such as neighborhood and closed neighborhood matrices.

1. Introduction

Domination is a fundamental concept in graph theory and is widely regarded as a critical graph optimization problem. Over the years, it has attracted significant attention due to its diverse applications in network design, resource optimization, social network analysis, and computational complexity. Its importance was first notably recognized in 1990, when a special issue of Discrete Mathematics was dedicated entirely to this topic [1]. By 1998, more than 1200 papers had been published on domination and its variants, which led to the release of two seminal books on the subject [2,3]. Since then, the field has experienced rapid growth, with over 5000 papers exploring various types of domination in graphs. Three additional books [4,5,6] have been published in recent years to capture the latest advancements in domination theory. Among these variants, total domination has gained particular prominence and has become a well-researched problem, as outlined in [7].

1.1. Current Research Directions

An active area of current research focuses on $\left\{k\right\}$-domination and total $\left\{k\right\}$-domination. Domination and total domination are special cases when $k=1$. Extensive studies on these problems have revealed insights into computational complexity and solution techniques [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. For instance, $\left\{k\right\}$-domination is polynomial-time solvable for strongly chordal graphs, but remains NP-complete for chordal bipartite graphs [8]. Similarly, total $\left\{k\right\}$-domination is solvable in polynomial time for chordal bipartite graphs [9] but NP-complete for bipartite planar graphs [10]. From an approximation perspective, both problems can be approximated within a factor of $lnn$ in polynomial time, where n is the number of vertices in the graph [11].

Beyond $\left\{k\right\}$-domination, the k-tuple domination and total k-tuple domination problems have also garnered attention. While polynomial-time solutions exist for specific graph families, such as trees, strongly chordal graphs, interval graphs, $P_4$-lite graphs, and web graphs [27,28,29,30,31], the problems remain NP-complete for others, such as chordal and planar graphs [12,28]. The k-tuple total domination problem can be solved in $\mathcal{O}\left(n^{3k}\right)$ time for weighed proper interval graphs [32]. Furthermore, for $k<4$, the running time of $\mathcal{O}\left(n^{3k}\right)$ can be improved to be $\mathcal{O}\left(n^{2k+4}\right)$. For weighted unit interval graphs, the k-tuple and total k-tuple domination problems can be solved in $\mathcal{O}\left(n^{k+2}\right)$ and $\mathcal{O}\left(n^{k+3}\right)$ time [33], respectively. The dichotomy between tractable and intractable cases has also been a focus of study in [34,35,36,37,38,39,40,41]. It is worth noting that Roman domination is closely related to $\left\{k\right\}$-domination and k-tuple domination. Several research papers have been conducted on variations of this problem in weighted graphs, such as the (independent) $(a,b)$-Roman domination problem for weighted chordal and strongly chordal graphs [42], and double Roman domination for trees and general graphs [43].

1.2. Research Gap and Motivation

Despite significant advancements, most studies on (total) $\left\{k\right\}$-domination and (total) k-tuple domination have primarily focused on unweighted graphs. In contrast, much less attention has been given to these problems in weighted graphs, even though weighted graphs are widely used in real-world systems to model varying costs, capacities, or priorities. This gap underscores a key motivation for our research: exploring these domination problems in weighted graphs offers significant opportunities for both theoretical advancements and practical applications.

For instance, similar to the discussion in [43], these domination problems are highly relevant to practical resource allocation, where costs or resource availability may vary by location. Unlike standard unweighted domination problems, which assume uniform costs across all vertices, our study emphasizes minimizing actual costs rather than merely the number of resources. This approach better reflects real-world scenarios where the expenses of providing services or resources can differ significantly due to factors such as geographic disparities or operational constraints.

To address this motivation and bridge the identified gap, we focus on the $\left\{k\right\}$-domination and total $\left\{k\right\}$-tuple domination problems for weighted strongly chordal graphs and chordal bipartite graphs. We also investigate k-tuple domination and total k-tuple domination for weighted proper interval graphs and weighted convex bipartite graphs.

1.3. Scope of Study

Strongly chordal graphs and chordal bipartite graphs are well-studied classes that include several important subclasses, such as trees, proper interval graphs, convex bipartite graphs, and bipartite permutation graphs [44]. These classes are characterized by specific vertex ordering constraints, which facilitate various computational operations. Employing these properties, we aim to develop efficient algorithms for solving domination problems on weighted graphs.

Most existing research on domination in weighted graphs assigns weights to vertices, with each vertex’s weight representing attributes, like importance, cost, or influence, that directly impact domination parameters. Following this convention, this paper focuses exclusively on vertex-weighted graphs, and the term “weighted graph” refers specifically to this context.

1.4. Contributions

This paper presents the following contributions.

1.

{k}-Domination for Weighted Strongly Chordal Graphs (Section 3): We demonstrate that the $\left\{k\right\}$-domination problem in weighted strongly chordal graphs can be solved in $\mathcal{O}(n+m)$ time, where n and m denote the number of vertices and edges, respectively. This result is achieved by refining Hoffman et al.’s method [45] and leveraging properties of adjacency lists and totally balanced matrices.

2.

Total {k}-Domination for Weighted Chordal Bipartite Graphs (Section 4): Building on structural similarities between chordal bipartite graphs and strongly chordal graphs, we extend the refined framework to solve the total $\left\{k\right\}$-domination problem in $\mathcal{O}(n+m)$ time for weighted chordal bipartite graphs.

3.

k-Tuple Domination for Weighted Proper Interval Graphs (Section 5): Using linear and integer linear programming techniques, we solve the k-tuple domination problem for weighted proper interval graphs in $\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right)$ time, where $\delta$ is the desired accuracy. Since a graph is a proper interval graph if and only if it is a unit interval graph [44], we reduce the complexity from $\mathcal{O}\left(n^{k+2}\right)$ [33] to $\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log({\displaystyle \frac{n}{\delta }})\right).$

4.

Total k-Tuple Domination for Weighted Convex Bipartite Graphs (Section 5): We achieve the same time complexity bound, $\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log({\displaystyle \frac{n}{\delta }})\right)$, for solving the total k-tuple domination problem in weighted convex bipartite graphs.

This study is purely theoretical and includes formal proofs of correctness and efficiency, enriching the understanding of domination problems in these graph classes.

Except for Section 1, Section 3, Section 4, and Section 5, the remainder of the paper is organized as follows:

• Section 2: Preliminaries
  This section provides a foundation of essential concepts and definitions that underpin our research. We introduce and explore fundamental properties of strongly chordal graphs, chordal bipartite graphs, proper interval graphs, and convex bipartite graphs. To set the stage for our linear programming approach, we formally define (total) $\left\{k\right\}$-domination and (total) k-tuple domination. Additionally, we review matrix-theoretic tools, specifically adjacency matrices, totally balanced matrices, greedy matrices, and totally unimodular matrices, which play a critical role in our modeling framework.
• Section 6: Conclusions
  The paper concludes by summarizing our findings, discussing the theoretical implications of our results, and proposing directions for future research that extends these domination techniques to other classes of weighted graphs.

2. Preliminaries

This paper integrates critical insights from multiple fields, including graph classes, linear algebra, graph theory, algorithms, and linear programming, each contributing indispensable tools and perspectives that enhance both the formulation and depth of our analysis. This section presents the fundamental concepts most pertinent to understanding the study’s objectives and methodology. For definitions, notations, additional concepts, or more comprehensive details not covered in this section, standard textbooks and monographs—such as Introduction to Algorithms [46], Theory of Linear and Integer Programming [47], Graph Theory [48], Introduction to Linear Algebra [49], and  Graph Classes: A Survey [44]—are recommended as supplementary resources.

2.1. Graphs and Their Representations

Each graph $G=(V,E)$ in this paper is finite, undirected, and contains no multiple edges or self-loops, where V is the vertex set and E is the edge set of G. If the vertex and edge sets are not explicitly specified, they are denoted by $V\left(G\right)$ and $E\left(G\right)$, respectively.

Two vertices u and v in a graph G are adjacent if they are connected with an edge, i.e., $(u,v)\in E\left(G\right)$, and are also called neighbors. The degree of a vertex v in G, denoted by $de{g}_G\left(v\right)$, is the number of neighbors of v. For any vertex $v\in V\left(G\right)$, the neighborhood of v in G, denoted by $N_G\left(v\right)$, is the set of neighbors of v, so that $|N_G\left(v\right)|=de{g}_G\left(v\right)$. A vertex u is a closed neighbor of v if either $u\in N_G\left(v\right)$ or $u=v$. The closed neighborhood of v, denoted by $N_G\left[v\right]$, is the set of closed neighbors of v.

Let $G=(V,E)$ and $G^{\prime }=(V^{\prime },E^{\prime })$ be two graphs. If $V^{\prime }\subseteq V$ and $E^{\prime }\subseteq E$, then $G^{\prime }$ is a subgraph of G. If $G^{\prime }$ is a subgraph of G, and $G^{\prime }$ contains all the edges $(u,v)\in E$ with $u,v\in V^{\prime }$, then $G^{\prime }$ is an induced subgraph; we say that $G^{\prime }$ is induced by $V^{\prime }$ and written as $G\left[V^{\prime }\right]$.

Graphs in this paper are represented using adjacency lists. The adjacency-list representation of a graph $G=(V,E)$ consists of an array of $\left|V\right|$ lists. Each vertex $v\in V$ is associated with a list of all neighbors of v. Figure 1 provides an example of the adjacency-list representation for a graph G with four vertices and four edges.

This representation is efficient in terms of memory usage. The amount of memory required to store a graph in this representation is $\mathcal{O}(n+m)$, where n and m represent the number of vertices and edges, respectively. Adjacency lists support efficient operations such as

• Neighbor Access: Accessing all (closed) neighbors of a vertex v takes $\mathcal{O}\left(deg\right(v)+1)$ time, as they are directly stored in a list. With each vertex maintaining its own neighbor list, this structure enables quick access to both neighbors and closed neighbors.
• Traversal: Traversing all vertices and edges in the graph takes $\mathcal{O}(n+m)$ time. This efficiency is particularly advantageous in algorithms like Depth-First Search (DFS) and Breadth-First Search (BFS).

2.2. {k}-Domination and Total {k}-Domination in Weighted Graphs

A dominating set D of a graph $G=(V,E)$ is a subset of V such that $|N_G\left[v\right]\cap D|\ge 1$ for every $v\in V$, while a total dominating set D is a subset of V such that $|N_G\left(v\right)\cap D|\ge 1$ for every $v\in V$. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality of a dominating set of G. The total domination number of G, denoted by ${\gamma }_t\left(G\right)$, is the minimum cardinality of a total dominating set of G. The domination problem is to find a dominating set of G with the minimum cardinality, and the total domination problem is to find a total dominating set of G with the minimum cardinality.

Domination and total domination can be expressed in terms of functions. Let $f:V\to \{0,1\}$ be a labeling function of a graph $G=(V,E)$. The function f is a dominating (respectively, total dominating) function of G if ${\sum }_{v\in N_G\left[v\right]}f\left(v\right)\ge 1$ (respectively, ${\sum }_{v\in N_G\left(v\right)}f\left(v\right)\ge 1$) for every $v\in V$. The labeling weight of f is defined as ${\sum }_{v\in V}f\left(v\right)$.

Clearly, the domination number $\gamma \left(G\right)$ is the minimum labeling weight of a dominating function, i.e., 

$$\gamma \left(G\right)=min\{\sum _{v\in V}f\left(v\right)\mid f \mathrm{is} \mathrm{a} \mathrm{dominating} \mathrm{function} \mathrm{of} G\}.$$

Similarly, the total domination number ${\gamma }_t\left(G\right)$ is the minimum labeling weight of a total dominating function, i.e., 

$${\gamma }_t\left(G\right)=min\left\{\sum _{v\in V}f\left(v\right)\mid f \mathrm{is} \mathrm{a} \mathrm{total} \mathrm{dominating} \mathrm{function} \mathrm{of} G\right\}.$$

Definition 1. 

Let k be a fixed positive integer, and let $f:V\to \{0,1,\dots ,k\}$ be a labeling function of a graph $G=(V,E)$. The function f is a $\left\{k\right\}$-dominating (respectively, total $\left\{k\right\}$-dominating) function of G if ${\sum }_{v\in N_G\left[v\right]}f\left(v\right)\ge k$ (respectively, ${\sum }_{v\in N_G\left(v\right)}f\left(v\right)\ge k$) for every $v\in V$. The labeling weight of f is defined as ${\sum }_{v\in V}f\left(v\right)$. The $\left\{k\right\}$-domination problem is to find a $\left\{k\right\}$-dominating function of G with the minimum labeling weight, while the total $\left\{k\right\}$-domination problem is to find a total $\left\{k\right\}$-dominating function of G with the minimum labeling weight.

By Definition 1, domination and total domination correspond to $\left\{1\right\}$-domination and total $\left\{1\right\}$-domination, respectively.

We now introduce the concepts of $\left\{k\right\}$-domination and total $\left\{k\right\}$-domination for weighted graphs. As mentioned earlier in the introduction, this paper focuses exclusively on vertex-weighted graphs.

Definition 2. 

Let $w:V\to \mathbb{R}$ be a function that assigns a weight $w\left(v\right)$ to each vertex v of a graph $G=(V,E)$. We refer to w as a vertex-weight function, and $(G,w)$ as a weighted graph.

Definition 3. 

The labeling weight of a $\left\{k\right\}$-dominating function or a total $\left\{k\right\}$-dominating function f of a weighted graph $(G,w)$ is defined as ${\sum }_{v\in V\left(G\right)}f\left(v\right)·w\left(v\right)$. The $\left\{k\right\}$-domination problem for a weighted graph $(G,w)$ is to find a $\left\{k\right\}$-dominating function of G with the minimum labeling weight, while the total $\left\{k\right\}$-domination problem is to find a total $\left\{k\right\}$-dominating function with the minimum labeling weight.

An unweighted graph H can be treated as a specific case of a weighted graph, where every vertex $v\in V\left(H\right)$ has a weight $w\left(v\right)=1$. The primary difference in defining the $\left\{k\right\}$-domination problem for unweighted and weighted graphs lies in the calculation of the labeling weight.

• In unweighted graphs, the labeling weight of a $\left\{k\right\}$-dominating function is simply the sum of the function values assigned to each vertex, i.e., ${\sum }_{v\in V}f\left(v\right)$, where each vertex has an implicit weight of 1.
• In weighted graphs, each vertex is assigned a specific weight through a vertex-weight function $w\left(v\right)$. The labeling weight is then calculated as ${\sum }_{v\in V}f\left(v\right)·w\left(v\right)$, meaning that the contribution of each vertex to the total weight depends on both the value of the labeling function $f\left(v\right)$ and the vertex’s weight $w\left(v\right)$.

This distinction also applies to the definitions of total $\left\{k\right\}$-domination on unweighted and weighted graphs. Therefore, the introduction of vertex weights in weighted graphs alters how the overall labeling weight is determined in both the $\left\{k\right\}$-domination and total $\left\{k\right\}$-domination problems.

2.3. k-Tuple Domination and Total k-Tuple Domination in Weighted Graphs

Let k be a fixed positive integer, and let $f:V\to \{0,1\}$ be a labeling function for a graph $G=(V,E)$. The function f is a k-tuple dominating function of G if ${\sum }_{v\in N_G\left[v\right]}f\left(v\right)\ge k$ for every $v\in V$. Similarly, f is a total k-tuple dominating function if ${\sum }_{v\in N_G\left(v\right)}f\left(v\right)\ge k$ for every $v\in V$. The labeling weight of f is defined as ${\sum }_{v\in V}f\left(v\right)$.

The k-tuple domination problem aims to find a k-tuple dominating function of G with the minimum labeling weight. Similarly, the total k-tuple domination problem seeks a total k-tuple dominating function with the minimum labeling weight.

Domination and total domination correspond to 1-tuple domination and total 1-tuple domination, respectively.

The labeling weight of a k-tuple dominating function or a total k-tuple dominating function f of a weighted graph $(G,w)$ is defined as ${\sum }_{v\in V\left(G\right)}f\left(v\right)·w\left(v\right)$. The k-tuple domination problem for a weighted graph $(G,w)$ is to find a k-tuple dominating function with the minimum labeling weight. Similarly, the total k-tuple domination problem is to find a total k-tuple dominating function with the minimum labeling weight.

2.4. Strongly Chordal Graphs and Chordal Bipartite Graphs

A chord in a cycle of a graph is an edge that connects two non-consecutive vertices in the cycle. A chordal graph is a graph in which every cycle with four or more vertices has a chord. A perfect elimination ordering of a graph $G=(V,E)$ is an ordering $v_1,v_2,\dots ,v_n$ of the vertices such that for any indices $i<j<k$, if $(v_i,v_j)\in E$ and $(v_i,v_k)\in E$, then $(v_j,v_k)\in E$. Rose [50] proved that a graph is chordal if and only if it admits a perfect elimination ordering. A strong elimination ordering $v_1,v_2,\dots ,v_n$ of a graph $G=(V,E)$ is a perfect elimination ordering such that for each $i<j$ and $k<\mathsf{\ell }$, if $(v_i,v_{\mathsf{\ell }})\in E$, $(v_i,v_k)\in E$, and $(v_k,v_j)$, then $(v_{\mathsf{\ell }},v_j)\in E$. Farber [51] proved that a graph is a strongly chordal graph if and only if it admits a strong elimination ordering.

A bipartite graph is a graph $G=(X,Y,E)$ in which the vertex set $V\left(G\right)$ can be partitioned into two disjoint sets X and Y such that every edge in the graph connects a vertex in X to a vertex in Y, and no edge connects two vertices within the same set. In other words, there are no edges between vertices within X or within Y. Therefore, a bipartite graph does not have a cycle of an odd number of vertices. A chordal bipartite graph is a bipartite graph in which every cycle of more than four vertices contains a chord.

Let $G=(V,E)$ be a graph, and let $v_1,v_2,\dots ,v_n$ be an ordering of V. Let $G_i$ be a subgraph of G induced by $\{v_i,v_{i+1},\dots ,v_n\}$. A weak elimination ordering of G is an ordering $v_1,v_2,\dots ,v_n$ such that for any indices $i<j<k$, if $v_j,v_k\in N_{G_i}\left(v_i\right)$, then $N_{G_i}\left(v_j\right)\subseteq N_{G_i}\left(v_k\right)$. Uehara [52] showed that a graph is chordal bipartite if and only if it admits a weak elimination ordering.

2.5. Proper Interval Graphs and Convex Bipartite Graphs

A graph $G=(V,E)$ is an interval graph if there exists an interval model on the real line such that each closed interval $I_v=[a_v,b_v]$ in the interval model corresponds to a vertex $v\in V$, and  two vertices $u,v\in V$ are adjacent in G if and only if their corresponding intervals overlap, that is:

$$I_u\cap I_v\ne \varnothing .$$

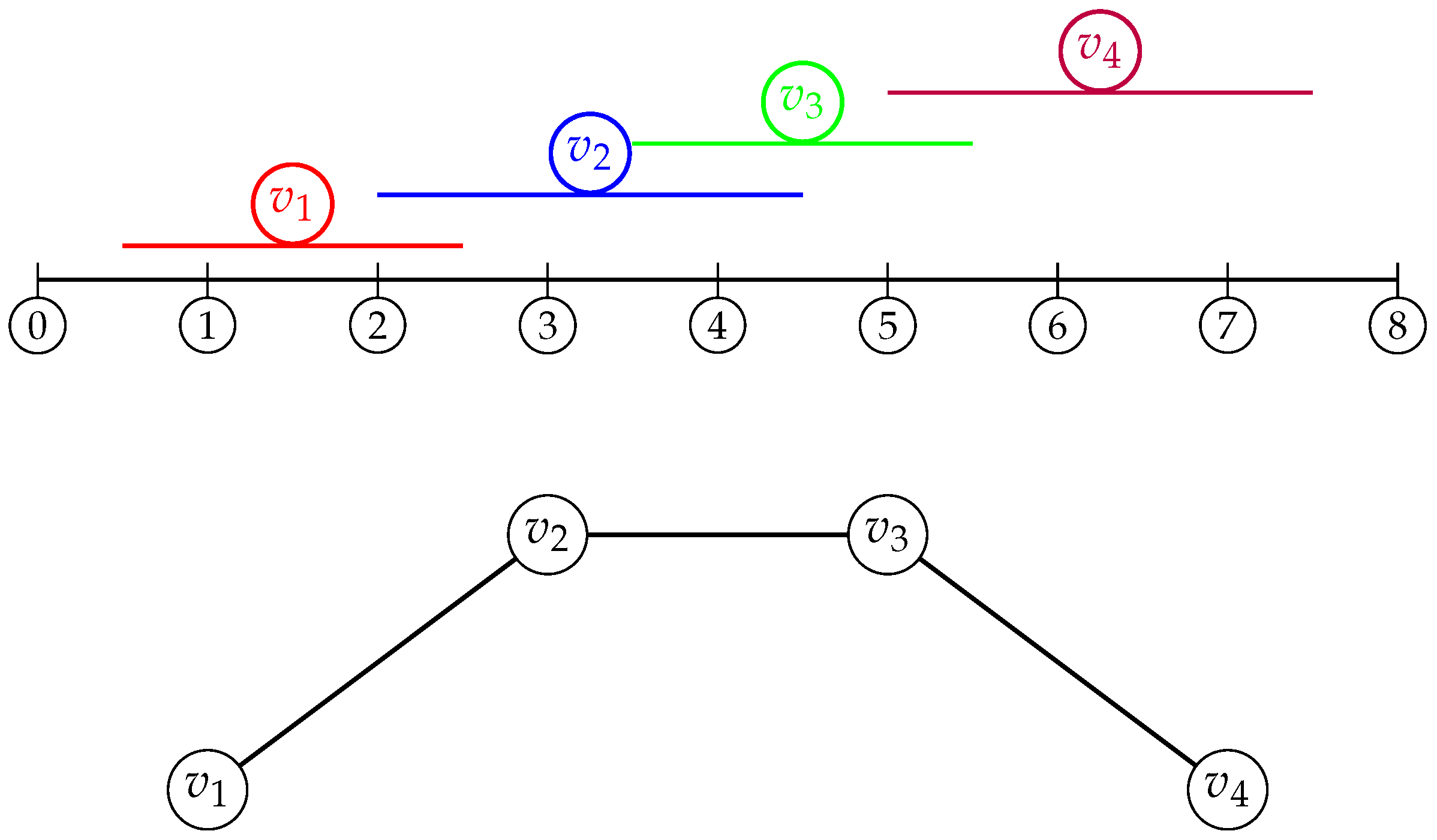
Figure 2 illustrates an interval graph $G=(V,E)$, which is constructed from an interval model on the real line.

An interval graph is called a proper interval graph if there exists an interval model for this interval graph such that for every pair of intervals $[a_u,b_u]$ and $[a_v,b_v]$ in the model, neither interval is strictly contained within the other, i.e., it is not true that $a_u\le a_v$ and $b_v\le b_u$. A unit interval graph is a special type of interval graph where all the intervals associated with the vertices have the same length. In fact, G is a unit interval graph if and only if G is a proper interval graph [53]; they are the same class of graph.

Let $B=(X,Y,E)$ be a bipartite graph. An ordering P of X in B has the adjacency property if for each vertex $y\in Y$, $N_B\left(y\right)$ consists of vertices that are consecutive in the ordering P of X. A bipartite graph $B=(X,Y,E)$ is a convex bipartite graph if there is an ordering of X or Y satisfying the adjacency property.

2.6. Totally Balanced, Totally Unimodular, and Greedy Matrices

A matrix $\mathbf{M}$ is called a $(0,1)$-matrix if every entry in $\mathbf{M}$ is either 1 or 0. In a matrix of numbers, the sum of all entries in a row is called the row sum, while the sum of all entries in a column is called the column sum. A $(0,1)$-matrix is totally balanced if it does not contain as a submatrix the incidence matrix of any cycle of length at least three. Equivalently, a $(0,1)$-matrix is totally balanced it does not contain any square submatrix satisfying all the following “forbidden conditions” [45]:

1.

All row sums are equal to 2.

2.

All column sums are equal to 2.

3.

All columns are distinct.

Here is an example of a matrix that is not totally balanced:

$$\mathbf{A}=\left(\begin{array}{ccccc}1& 0& 1& 0& 0\\ 0& 1& 1& 0& 1\\ 1& 1& 0& 1& 0\\ 0& 1& 0& 1& 1\\ 1& 0& 1& 1& 0\end{array}\right).$$

A $(0,1)$-matrix is greedy if it does not contain any of the following forbidden submatrices:

$$\left(\begin{array}{cc}1& 1\\ 0& 1\\ 1& 0\end{array}\right)\mathrm{and}\left(\begin{array}{cc}1& 1\\ 1& 0\\ 0& 1\end{array}\right).$$

A greedy matrix is in standard greedy form [45] if it does not contain the following $\Gamma$-matrix as a submatrix:

$$\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right).$$

Let $det\left(\mathbf{M}\right)$ denote the determinant of a matrix $\mathbf{M}$. The matrix M is totally unimodular if $det\left({\mathbf{M}}^{\prime }\right)\in \{-1,0,1\}$ for every square submatrix ${\mathbf{M}}^{\prime }$ of $\mathbf{M}$.

A matrix has the consecutive ones property if its rows can be permuted in such a way that, in every column, all the 1s appear consecutively. This property is particularly relevant in applications involving binary matrices and is a useful tool for analyzing matrix structures.

The following theorem reveals a connection between the consecutive ones property and total unimodularity.

Theorem 1 

([47]). If a $(0,1)$-matrix has the consecutive ones property for columns, then it is totally unimodular.

2.7. Linear and Integer Linear Programming

Consider the following two optimization problems:

$$min\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}\mathrm{and}max\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\le \mathbf{b}\}.$$

A solution to an optimization problem is a column vector $\mathbf{x}={(x_1,x_2,\dots ,x_n)}^T$, often called a point because each solution corresponds to a specific set of values for the variables, which can be represented as a single point in geometric space. In other words, each feasible solution is associated with a unique location in this space. A solution that satisfies all constraints is known as a feasible solution, whereas a solution that fails to satisfy at least one constraint is an infeasible solution. The set of points that satisfy all the constraints is referred to as the feasible region. In linear programming, the feasible region is called a polyhedron, as it is the intersection of linear constraints. A polyhedron is often denoted by P, such as $P=\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}$, representing the set of all points $\mathbf{x}$ that meet the specified constraints.

In an optimization problem, a constraint is called active at a given solution point if the solution causes the constraint to hold as an equality, effectively “binding” the solution at the boundary defined by the constraint. An extreme point of a polyhedron occurs where several of the constraints in the problem are active, often as many as the dimension of the space.

The fundamental theorem of linear programming ([54]) states that if a linear program has an optimal solution, at least one optimal solution will be located at an extreme point of the polyhedron. This result is foundational because it allows optimization algorithms like the simplex method to focus on the extreme points of the feasible region, significantly reducing the computational effort required to find an optimal solution. If every extreme point of a polyhedron consists of integer values for all variables, then the polyhedron is said to be integral. Theorem 2 establishes that linear programs satisfy strong duality.

Theorem 2 

([46]).

$$min\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}=max\{{\mathbf{b}}^T\mathbf{y}\mid \mathbf{y}\ge 0,{\mathbf{A}}^T\mathbf{y}\le \mathbf{c}\}.$$

An integer linear program is an optimization model similar to a linear program, but includes an additional constraint that requires all decision variables to be integers. This distinction substantially impacts both the complexity and solution methods for these problems. While linear programs can be solved in polynomial time [55], integer linear programs are NP-complete [56], making them more computationally challenging.

Integer linear programs satisfy weak duality but do not always satisfy strong duality, meaning the optimal values of an integer linear program and its dual may differ.

To solve integer linear programs, advanced methods such as branch-and-bound, branch-and-cut, and cutting planes are often employed. These methods frequently use linear relaxations, which remove the integer constraints to produce a continuous solution. In certain cases, the optimal objective value of an integer linear program matches that of its linear relaxation, as illustrated by Theorem 3.

Theorem 3 

([57]). If $\mathbf{A}$, $\mathbf{b}$, and $\mathbf{c}$ all have integer entries, with at least one of $\mathbf{b}$ or $\mathbf{c}$ as a constant vector, and $\mathbf{A}$ is totally balanced, then the optimal objective values of the integer program

$$max\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{A}\mathbf{x}\le \mathbf{b},\mathbf{x}\in \mathbb{Z}\mathit{and}\mathbf{x}\ge 0\}$$

and its linear relaxation are the same.

3. {k}-Domination in Weighted Strongly Chordal Graphs

In this section, we demonstrate that the $\left\{k\right\}$-domination problem in weighted strongly chordal graphs with n vertices and m edges can be solved in $\mathcal{O}(n+m)$ time. The solution follows a four-step framework, as outlined below:

(1)

Modeling (Section 3.1): The $\left\{k\right\}$-domination problem is formulated as an integer linear programming task using matrix representations, particularly adjacency matrices. This formulation establishes the theoretical foundation for the algorithmic approaches described in subsequent sections. We aim to solve the integer linear program by its relaxation.

(2)

Primal and Dual Algorithms by Hoffman et al. (Section 3.2): We introduce the primal and dual algorithms proposed by Hoffman et al. [45], which solve the linear program:

$$min\{{\mathbf{c}}^T\mathbf{x}+{\mathbf{d}}^T\mathbf{z}\mid \mathbf{A}\mathbf{x}+\mathbf{z}\ge \mathbf{b},\mathbf{x}\ge 0,\mathbf{z}\ge 0\}.$$

These algorithms provide a robust framework for solving linear programming problems, forming the basis for adapting solutions to the $\left\{k\right\}$-domination problem.

(3)

Refined Algorithms for Weighted Strongly Chordal Graphs (Section 3.3): Building on Hoffman et al.’s [45] algorithms, this section introduces refinements tailored to the structural properties of weighted strongly chordal graphs. These refinements reduce the computational complexity to $\mathcal{O}\left(n^2\right)$, representing an intermediate step toward the final optimized solution.

(4)

Optimized Algorithms with Enhanced Data Structures (Section 3.4): By integrating advanced data structures, this section further reduces the overall time complexity from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}(n+m)$. This optimization capitalizes on the sparsity and adjacency structure of strongly chordal graphs, achieving linear-time performance relative to the graph’s size.

3.1. Modeling

We start by presenting Lemma 1 to concentrate exclusively on non-negative vertex weights ($w\left(v\right)\in {\mathbb{R}}_{\ge 0}$). This simplification allows us to assume that all weighted graphs have non-negative vertex weights.

Lemma 1. 

Let w be a vertex-weight function of a graph $G=(V,E)$, and let ${\gamma }_k(G,w)$ represent the the minimum labeling weight of a $\left\{k\right\}$-dominating function for $(G,w)$. Define $S=\{v\mid v\in V,w(v)<0\}$ and let $w^{\prime }$ be a vertex-weight function such that $w^{\prime }\left(v\right)=max\{w\left(v\right),0\}$ for each $v\in V$. Then, ${\gamma }_k(G,w)={\gamma }_k(G,w^{\prime })+k{\sum }_{v\in S}w\left(v\right)$.

Proof. 

Let f be a $\left\{k\right\}$-dominating function for $(G,w)$ with minimum weight, so ${\gamma }_k(G,w)={\sum }_{v\in V}w\left(v\right)f\left(v\right)$. Define a function $f^{\prime }$ such that $f^{\prime }\left(v\right)=k$ for $v\in S$ and $f^{\prime }\left(v\right)=f\left(v\right)$ for $v\in V\setminus S$. Since $f^{\prime }$ is also a $\left\{k\right\}$-dominating function of G and $w^{\prime }\left(v\right)=0$ for $v\in S$, we obtain

$$\begin{array}{cc}\hfill {\gamma }_k(G,w^{\prime })& \le \sum _{v\in V}{w}^{\prime }\left(v\right)f^{\prime }\left(v\right)=\sum _{v\in V\setminus S}w\left(v\right)f\left(v\right)\hfill \\ \hfill & =\sum _{v\in V}w\left(v\right)f\left(v\right)-\sum _{v\in S}w\left(v\right)f\left(v\right)\hfill \\ \hfill & \le {\gamma }_k(G,w)-k\sum _{v\in S}w\left(v\right).\hfill \end{array}$$

Conversely, let h be a $\left\{k\right\}$-dominating function for $(G,w^{\prime })$ with the minimum labeling weight, so

$${\gamma }_k(G,w^{\prime })=\sum _{v\in V}{w}^{\prime }\left(v\right)h\left(v\right)=\sum _{v\in V\setminus S}{w}^{\prime }\left(v\right)h\left(v\right).$$

Define f such that $f\left(v\right)=k$ for $v\in S$ and $f\left(v\right)=h\left(v\right)$ for $v\in V\setminus S$. Clearly, f is a $\left\{k\right\}$-dominating function of G, and $w^{\prime }\left(v\right)=0$ for $v\in S$. We have

$$\begin{array}{cc}\hfill {\gamma }_k(G,w)& \le \sum _{v\in V}w\left(v\right)f\left(v\right)=\sum _{v\in V\setminus S}w\left(v\right)f\left(v\right)+k\sum _{v\in S}w\left(v\right)\hfill \\ \hfill & =\sum _{v\in V\setminus S}{w}^{\prime }\left(v\right)h\left(v\right)+k\sum _{v\in S}w\left(v\right)\hfill \\ \hfill & ={\gamma }_k(G,w^{\prime })+k\sum _{v\in S}w\left(v\right).\hfill \end{array}$$

This completes the proof.    □

Let $(G,w)$ be a weighted graph with $V\left(G\right)=\{v_1,v_2.\dots ,v_n\}$. We associate a variable $x_j$ with each $v_j\in V\left(G\right)$ and require that $x_j\in \{0,1,\dots ,k\}$ for $j=1,2,\dots ,n$. Let $w_j=w\left(v_j\right)$ for $1\le i\le n$. The $\left\{k\right\}$-domination problem for the weighted graph $(G,w)$ is formulated as the following integer linear program ${\mathcal{IP}}_k(G,w)$:

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{j=1}^n{w}_j{x}_j\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \sum _{v_j\in N_G\left[v_i\right]}{x}_j\ge k\mathrm{for}i=1,2,\dots ,n\hfill \\ \hfill & x_j\in \{0,1,\dots ,k\}\mathrm{for}j=1,2,\dots ,n.\hfill \end{array}$$

We formulate the integer linear program $I{P}_k(G,w)$ from ${\mathcal{IP}}_k(G,w)$ as follows:

$$\begin{array}{c}\hfill I{P}_k(G,w):\\ \hfill \mathrm{minimize}& \sum _{j=1}^n{w}_j{x}_j\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \sum _{v_j\in N_G\left[v_i\right]}{x}_j\ge k\mathrm{for}i=1,2,\dots ,n\hfill \\ \hfill & x_j\ge 0\mathrm{and}{x}_j\in \mathbb{Z}\mathrm{for}i=1,2,\dots ,n.\hfill \end{array}$$

Lemma 2. 

Let ${\mathbf{x}}^{\ast }=(x_1^{\ast },x_2^{\ast },\dots ,x_n^{\ast })$ be an optimal solution to $I{P}_k(G,w)$. Then, $0\le x_j^{\ast }\le k$ for all $j=1,2,\dots ,n$.

Proof. 

By the constraints of $I{P}_k(G,w)$, we know that $x_j\ge 0$ for $j=1,2,\dots ,n$. Since $x^{\ast }$ is an optimal solution to $I{P}_k(G,w)$, ${\sum }_{j=1}^n{w}_j{x}_j^{\ast }$ is minimized. Assume that there exists an $x_i^{\ast }$ in ${\mathbf{x}}^{\ast }$ such that $x_i^{\ast }>k$. For any constraint involving $x_i^{\ast }$, the constraint remains satisfied if $x_i^{\ast }$ is replaced with k, by Lemma 1. Consequently, the resulting objective value is less than ${\sum }_{j=1}^n{w}_j{x}_j^{\ast }$, leading to a contradiction. Therefore, the lemma holds.    □

By Lemma 2, it is clear that an optimal solution $x^{\ast }$ to $I{P}_k(G,w)$ if and only if it is also an optimal solution to ${\mathcal{IP}}_k(G,w)$. Thus, we can solve the $\left\{k\right\}$-domination problem for the weighed graph $(G,w)$ by solving the integer linear program $I{P}_k(G,w)$.

In graph theory, the neighborhood matrix and the closed neighborhood matrix are two distinct representations of the adjacency relationships in a graph H with vertices $V\left(H\right)=\{v_1,v_2,\dots ,v_n\}$.

• The neighborhood matrix of G is a matrix $\mathbf{N}=\left(n_{ij}\right)\in {\mathbb{R}}^{n\times n}$ such that $n_{ij}=1$ if $v_j\in N_H\left(v_i\right)$; otherwise, $n_{ij}=0$.
• The closed neighborhood matrix of G is a matrix $\mathbf{M}=\left(m_{ij}\right)\in {\mathbb{R}}^{n\times n}$ such that $m_{ij}=1$ if $v_j\in N_H\left[v_i\right]$; otherwise, $m_{ij}=0$.

Let $\mathbf{M}=\left(m_{ij}\right)\in {\mathbb{R}}^{n\times n}$ be the closed neighborhood matrix of the weighted graph G with $\mathbf{w}=\left(w_j\right)\in {\mathbb{R}}_{\ge 0}^n$, $\mathbf{x}=\left(x_j\right)\in {\mathbb{R}}^n$, and $\mathbf{p}=\left(p_i\right)\in {\mathbb{R}}^n$, where $p_i=k$ for $1\le i\le n$.

We present the linear program $L{P}_k(G,w)$ and its dual $L{P}_k^d(G,w)$ using the closed neighborhood matrix $\mathbf{M}$.

$$\begin{array}{ccc}\hfill \mathrm{Primal}({LP}_k(G,w)):& \hfill & \hfill \mathrm{Dual}({LP}_k^d(G,w)):\\ \hfill \mathrm{minimize}& {\mathbf{w}}^T\mathbf{x}\hfill & \hfill \mathrm{maximize}& {\mathbf{p}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{M}\mathbf{x}\ge \mathbf{p}\hfill & \hfill \mathrm{subject}\mathrm{to}& {\mathbf{M}}^T\mathbf{y}\le \mathbf{w}\hfill \\ \hfill & \mathbf{x}\ge 0.\hfill & \hfill & \mathbf{y}\ge 0.\hfill \end{array}$$

Let $I{P}_{\mathrm{opt}}$ and ${LP}_{\mathrm{opt}}$ denote the optimal objective values of an integer linear program $IP$ and its linear relaxation $LP$, respectively. The polyhedron for $IP$ is a subset of the polyhedron for $LP$, since $IP$ includes the additional constraint that variables must be integers. Therefore, the optimal value of $LP$, minimized over a larger polyhedron, cannot be greater than the optimal value of $IP$. Hence, ${LP}_{\mathrm{opt}}\le {IP}_{\mathrm{opt}}$.

In subsequent sections, we aim to demonstrate that for weighted strongly chordal graphs, the optimal value of $I{P}_k(G,w)$ is equal to the optimal value of its linear relaxation $L{P}_k(G,w)$. This allows us to solve this integer linear program by obtaining an integral solution directly from its linear relaxation.

3.2. Primal and Dual Algorithms by Hoffman et al.’s [45]

Let $\mathbf{A}=\left(a_{ij}\right)\in {\mathbb{R}}^{m\times n}$ be a greedy matrix in standard form, with vectors $\mathbf{x}=\left(x_j\right)\in {\mathbb{R}}^n$, $\mathbf{y}=\left(y_i\right)\in {\mathbb{R}}^m$, and $\mathbf{z}=\left(z_i\right)\in {\mathbb{R}}^m$ as variables. Let $\mathbf{c}=\left(c_j\right)\in {\mathbb{R}}^n$, $\mathbf{b}=\left(b_i\right)\in {\mathbb{R}}^m$, and $\mathbf{d}=\left(d_i\right)\in {\mathbb{R}}^m$ be constant vectors with $\mathbf{c}\ge 0$, $\mathbf{d}\ge 0$, and  $b_1\ge b_2\ge \cdots \ge b_m\ge 0$. The primal linear program P is defined as:

$$\begin{array}{cc}\hfill \mathrm{minimize}& {\mathbf{c}}^T\mathbf{x}+{\mathbf{d}}^T\mathbf{z}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{A}\mathbf{x}+\mathbf{z}\ge \mathbf{b}\hfill \\ \hfill & \mathbf{x}\ge 0,\mathbf{z}\ge 0.\hfill \end{array}$$

The dual program D is formulated as:

$$\begin{array}{cc}\hfill \mathrm{maximize}& {\mathbf{b}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& {\mathbf{A}}^T\mathbf{y}\le \mathbf{c}\hfill \\ \hfill & \mathbf{y}\ge 0,\mathbf{y}\le \mathbf{d}.\hfill \end{array}$$

Hoffman et al. [45] introduced two greedy algorithms to solve P and its dual D in polynomial time, and constructed an integer optimal solution for P. These algorithms are presented in Algorithms 1 and 2.

Algorithm 1 provides an integer optimal solution for D. The dual program D contains n constraints and m decision variables $y_1,y_2,\dots ,y_m$. A constraint j is defined as tight if

$$\sum _{i=1}^m{a}_{ij}{y}_i=c_j.$$

Let $J=\{j\mid j\mathrm{is}\mathrm{tight}\}$ and $\alpha \left(j\right)=max\{i\mid a_{ij}=1,y_i>0,{\sum }_{i=1}^m{a}_{ij}{y}_i=c_j\}$. Algorithm 1 determines each variable $y_i$ in increasing order of i and takes the largest feasible value. It also computes J and $\alpha \left(j\right)$ for use in Algorithm 2.

Algorithm 1: Dual Solution for Program D with Greedy Matrices

Algorithm 2 computes the primal solution corresponding to the dual solution by iteratively adjusting $x_j$ values.

Algorithm 2: Primal Solution for Program P Corresponding to Dual Solution

Theorem 4 

([45]). The dual program D is solved by Algorithm 1 for all $\mathbf{c}\ge 0,\mathbf{d}\ge 0$, and $b_1\ge b_2\ge \cdots \ge b_m\ge 0$ if and only if A is greedy in standard greedy form. Further, Algorithm 2 constructs an integer optimal solution to the primal problem P. Both algorithms run in $\mathcal{O}\left(mn\right)$ time.

3.3. Refined Algorithms for Weighted Strongly Chordal Graphs

We present Lemma 3 as a fundamental observation linking greedy matrices in standard greedy form to the closed neighborhood matrices of strongly chordal graphs with strong elimination orderings.

Lemma 3. 

If the vertices of a strongly chordal graph G are ordered by its strong elimination ordering, then the closed neighborhood matrix of G is a greedy matrix in standard greedy form.

Proof. 

We start by proving the following claim.

Claim 1. 

A greedy matrix in standard greedy form is precisely a totally balanced matrix that contains no submatrix identical to the Γ-matrix.

Let $S_1$ represent the set of all greedy matrices in standard greedy form, and let $S_2$ represent the set of all totally balanced matrices that exclude any submatrix identical to the $\Gamma$-matrix. To prove the claim, we will show that $S_1=S_2$.

According to Hoffman et al. [45], every greedy matrix is totally balanced. This establishes that $S_1\subseteq S_2$.

By definition, a greedy matrix is a $(0,1)$-matrix that does not contain either of the following forbidden submatrices:

$$F_1=\left(\begin{array}{cc}1& 1\\ 0& 1\\ 1& 0\end{array}\right)\mathrm{and}{F}_2=\left(\begin{array}{cc}1& 1\\ 1& 0\\ 0& 1\end{array}\right).$$

It is clear that a totally balanced matrix that excludes any submatrix identical to the $\Gamma$-matrix must also exclude $F_1$ and $F_2$ as submatrices. Therefore, any matrix in $S_2$ must also be in $S_1$, giving us $S_2\subseteq S_1$.

Since we have both $S_1\subseteq S_2$ and $S_2\subseteq S_1$, it follows that $S_1=S_2$. This completes the proof of the claim.

Farber [51] showed that if the vertices of a strongly chordal graph G are ordered by its strong elimination ordering, then the closed neighborhood matrix of G is totally balanced and excludes any submatrix identical to the $\Gamma$-matrix.

Thus, the lemma holds.    □

For clarity and ease of reference, we present the formulations of P, D, $L{P}_k(G,w)$, and ${LP}_k^d(G,w)$ together below.

$$\begin{array}{ccc}\hfill \mathrm{Primal}(P):& \hfill & \hfill \mathrm{Dual}(D):\\ \hfill \mathrm{minimize}& {\mathbf{c}}^T\mathbf{x}+{\mathbf{d}}^T\mathbf{z}\hfill & \hfill \mathrm{maximize}& {\mathbf{b}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject} \mathrm{to}& \mathbf{A}\mathbf{x}+\mathbf{z}\ge \mathbf{b}\hfill & \hfill \mathrm{subject}\mathrm{to}& {\mathbf{A}}^T\mathbf{y}\le \mathbf{c}\hfill \\ \hfill & \mathbf{x}\ge 0,\mathbf{z}\ge 0.\hfill & \hfill & \mathbf{y}\ge 0,\mathbf{y}\le \mathbf{d}.\hfill \\ \hfill \mathrm{Primal}({LP}_k(G,w)):& \hfill & \hfill \mathrm{Dual}({LP}_k^d(G,w)):\\ \hfill \mathrm{minimize}& {\mathbf{w}}^T\mathbf{x}\hfill & \hfill \mathrm{maximize}& {\mathbf{p}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{M}\mathbf{x}\ge \mathbf{p}\hfill & \hfill \mathrm{subject}\mathrm{to}& {\mathbf{M}}^T\mathbf{y}\le \mathbf{w}\hfill \\ \hfill & \mathbf{x}\ge 0.\hfill & \hfill & \mathbf{y}\ge 0.\hfill \end{array}$$

Theorem 5. 

For weighted strongly chordal graphs $(G,w)$ with n vertices arranged by strong elimination ordering, the $\left\{k\right\}$-domination problem can be solved in $\mathcal{O}\left(n^2\right)$ time.

Proof. 

Lemma 3 allows us to observe that for a weighted strongly chordal graph $(G,w)$ with n vertices arranged in strong elimination ordering, the closed neighborhood matrix $\mathbf{M}$ of G is a greedy matrix in standard greedy form. Additionally, in the linear program ${LP}_k(G,w)$, we have $\mathbf{w}\ge 0$, and the vector $\mathbf{p}$ is constant with entries equal to k. Consequently, the programs ${LP}_k(G,w)$ and its dual ${LP}_k^d(G,w)$ for the weighted strongly chordal graph $(G,w)$ are specific instances of the programs P and D, where $\mathbf{z}=0$ and the vector $\mathbf{d}$ is absent.

This connection enables us to modify and simplify Hoffman et al.’s [45] original algorithms, Algorithms 1 and 2, to yield Algorithms 3 and 4. We present Algorithms 3 and 4 below with the necessary line-by-line transformations.

To modify and simplify Algorithm 1 into Algorithm 3, the following line-by-line adjustments were made:

1.

Line 1: Replace $\widehat{\mathbf{c}}$ with $\widehat{\mathbf{w}}$ and $\mathbf{c}$ with $\mathbf{w}$.

2.

Line 2: Adjust the loop range from m to n.

3.

Line 3: Simplify the min calculation from $min\{d_i,min\{{\widehat{c}}_j\mid a_{ij}=1\}\}$ to $min\{{\widehat{w}}_j\mid m_{ij}=1\}$.

4.

Lines 5 and 6: Replace the original lines with the simplified expression $j=max\{j\mid y_i=$${\widehat{w}}_j,m_{ij}=1\}$. Note that in the simplified algorithm, $d_i$ is unnecessary in Line 3. Therefore, if $y_i>0$, then $y_i$ from $min\{{\widehat{w}}_j\mid m_{ij}=1\}$ must equal ${\widehat{w}}_j$ for some j. Thus, the largest j is chosen such that $y_i={\widehat{w}}_j$ can be expressed equivalently as $j=max\{j\mid y_i={\widehat{w}}_j,m_{ij}=1\}$.

5.

Line 9: Substitute each ${\widehat{c}}_j$ with ${\widehat{w}}_j$ and $a_{ij}$ with $m_{ij}$ in the update statement.

Algorithm 3: Simplified Algorithm for ${LP}_k^d(G,w)$

To modify and simplify Algorithm 2 into Algorithm 4, we made the following adjustments (highlighted:

1.

Line 1: Change $\widehat{\mathbf{b}}$ to $\widehat{\mathbf{p}}$. Replace $\mathbf{b}$ with $\mathbf{p}$.

2.

Line 4: Adjust ${\widehat{b}}_{\alpha \left(k\right)}$ to ${\widehat{p}}_{\alpha \left(k\right)}$.

3.

Line 5: Replace ${\widehat{b}}_i$ with ${\widehat{p}}_i$. Replace $a_{ik}$ with $m_{ik}$.

4.

Remove Lines 7 and 8, since they are unnecessary in the simplified algorithm for ${LP}_k(G,w)$.

Algorithm 4: Simplified Algorithm for ${LP}_k(G,w)$ with totally balanced matrices

By Theorem 4, the linear program ${LP}_k(G,w)$ and its dual ${LP}_k^d(,w)$ are solvable in $\mathcal{O}\left(n^2\right)$ time for weighted strongly chordal graphs G with vertices in strong elimination ordering, and Algorithms 3 and 4 can provide integer optimal solutions for ${LP}_k(G,w)$ and ${LP}_k^d(G,w)$. Thus, the $\left\{k\right\}$-domination problem for weighted strongly chordal graphs can be solved in $\mathcal{O}\left(n^2\right)$ time. □

3.4. Optimized Algorithms with Enhanced Data Structures

In the previous section, we established that the linear program ${LP}_k(G,w)$ and its dual are special cases of the problems tackled by Hoffman et al.’s [45] algorithms. This enables us to apply their method directly to solve these programs in $\mathcal{O}\left(n^2\right)$ time. Hoffman et al.’s [45] algorithms are robustly constructed around the relationships between totally balanced matrices, greedy matrices, and linear programs, using the strengths of matrix structures and concepts from linear and integer programming. In contrast, the closed neighborhood matrices $\mathbf{M}$ in ${LP}_k(G,w)$ are closely tied to graph adjacency structures.

The adjacency-list representation, as discussed in Section 2.1, plays a crucial role in enhancing the efficiency of Algorithms 3 and 4. By incorporating optimized data structures for critical steps in these algorithms, we improve the overall time complexity from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}(n+m)$, where n represents the number of vertices, and m represents the number of edges in a graph. Since the maximum number of edges in a graph is $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)=\mathcal{O}\left(n^2\right)$, this improvement makes the algorithms particularly effective for sparse strongly chordal graphs when $m\ll n^2$. Theorem 6 demonstrates how to obtain the desired time complexity.

Theorem 6. 

For weighted strongly chordal graphs $(G,w)$ with n vertices arranged by strong elimination ordering, the $\left\{k\right\}$-domination problem can be solved in $\mathcal{O}(n+m)$ time, where m is the number of edges in G.

Proof. 

We begin with demonstrating how each line of Algorithm 3 relates to the adjacency list and other optimized data structures and the running time of each line based on the adjacency list representation and the number of vertices (n) and edges (m):

1.

Line 1: This line initializes the set J to keep track of selected indices j and makes a copy of the vector $\mathbf{w}$ as $\widehat{\mathbf{w}}$. This step does not directly involve the adjacency list, as it is a basic initialization of variables. We implement J as an array with n entries and initialize the array with each entry set to zero. This array structure allows us to store specific information about each element efficiently, and each entry can be accessed, updated, or retrieved in $\mathcal{O}\left(1\right)$ time. The initialization step takes $\mathcal{O}\left(n\right)$ time.

2.

Line 2: This loop iterates over each index i, where n corresponds to the number of constraints equal to the number of vertices. It executes n times in total. For each iteration, it processes Lines 3–8.

(a)

Line 3: For each i, the algorithm assigns $y_i$ the minimum value among the entries ${\widehat{w}}_j$ for all j such that $m_{ij}=1$. Clearly, $m_{ij}=1$ means $v_j\in N_G\left[v_i\right]$. Using the adjacency list, the algorithm can directly access all neighbors of $v_i$, including $v_i$ itself, in $\mathcal{O}(de{g}_G\left(v_i\right)+1)$ time.

(b)

Line 4: This line checks whether the calculated $y_i$ value is greater than 0. It can be completed in $\mathcal{O}\left(1\right)$ time.

(c)

Lines 5–7: This block finds the largest j for i such that $y_i={\widehat{w}}_j$ and $m_{ij}=1$.

The adjacency list helps here by providing access to each index j of $v_j\in N_G\left[v_i\right]$, allowing the algorithm to identify all possible values of j where $y_i={\widehat{w}}_j$. Once the appropriate j is found, J and $\alpha \left(j\right)$ are updated. Since J is an array, the operation $J\cup \left\{j\right\}$ is translated to setting $J\left[j\right]=1$. Conversely, J does not contain some k if $J\left[k\right]=0$. We also implement the operation $\alpha \left(j\right)\leftarrow i$ by an array. The operation $\alpha \left(j\right)\leftarrow i$ is translated to setting $\alpha \left[j\right]=i$.

Hence, the steps take $\mathcal{O}(de{g}_G\left(v_i\right)+1)$ time.

(d)

Line 8: This line updates ${\widehat{w}}_j$ for each index j of vertices $v_j\in N_G\left[v_i\right]$, subtracting $y_i$ from ${\widehat{w}}_j$. Using the adjacency list, the algorithm can efficiently locate each j where $m_{ij}=1$ and apply the update only to those specific j values for vertices $v_j\in N_G\left[v_i\right]$.

The overall time complexity depends on the sum of all neighbor operations across vertices, yielding

$$\mathcal{O}\left(n+\sum _{i=1}^n(de{g}_G\left(v_i\right)+1)\right)=\mathcal{O}(n+m),$$

where n is the number of vertices and m is the number of edges.

We next demonstrate how each line of Algorithm 4 relates to the adjacency list and other optimized data structures and the running time of each line based on the adjacency list representation and the number of vertices (n) and edges (m):

1.

Line 1: This line initializes $\widehat{\mathbf{p}}$ as a copy of $\mathbf{p}$ and sets $x_j=0$ for all $j\notin J$.

To set $x_j=0$ for all $j\notin J$, we implement a stack $\widehat{J}$ and set it to be empty. Then, we visit each entry $J\left[j\right]$ for $1\le j\le n$, set $x_j=0$ if $J\left[j\right]=0$, and push j into the stack $\widehat{J}$ if $J\left[j\right]\ne 0$. After visiting all entries of J, we delete J and rename $\widehat{J}$ with J. All operations can be completed in $\mathcal{O}\left(n\right)$ time. Since $\mathbf{p}$ also has n entries, copying $\mathbf{p}$ takes $\mathcal{O}\left(n\right)$ time.

2.

Line 2 (While Loop): The loop runs until J is empty, so the number of iterations depends on the number of elements in J. Clearly, it executes at most n times. Each iteration involves Lines 3–6, so we analyze each of these lines within the context of a single iteration.

(a)

Line 3: Select the last column k from J. In other words, we have to select the largest index k of J with $J\left[k\right]=1$. Since we have implemented a stack, pushing each index j with $J\left[j\right]=1$ into the stack from smallest one to the largest one, deleting J, and renaming the stack with J. Therefore, selecting the last column of J is equivalent to popping an element from J. Hence, it takes $\mathcal{O}\left(1\right)$ time.

(b)

Line 4: Set $x_k$ based on ${\widehat{p}}_{\alpha \left(k\right)}$. Retrieving the value from $\alpha \left(k\right)$ and assigning $x_k$ takes $\mathcal{O}\left(1\right)$ time.

(c)

Line 5: Update ${\widehat{p}}_i$ for all i such that $m_{ik}=1$. Since $m_{ik}=1$, this operation iterates over each index i of vertices $v_i\in N_G\left[v_k\right]$. Using the adjacency list, this step takes $\mathcal{O}(\mathrm{deg}\left(v_k\right)+1)$ for each iteration.

(d)

Line 6: Remove k from J. J is implemented as a stack. Removing the last element takes $\mathcal{O}\left(1\right)$ time.

The overall time complexity of the algorithm is:

$$\mathcal{O}\left(n+\sum _{k\in J}(de{g}_G\left(v_k\right)+4)\right)=\mathcal{O}(n+m),$$

where n is the number of vertices and m is the number of edges in the graph. This linear time complexity makes the algorithm efficient for sparse graphs.

Following the discussion above, Algorithms 3 and 4 both run in $\mathcal{O}(n+m)$ time. Consequently, the theorem holds. □

4. Total {k}-Domination in Weighted Chordal Bipartite Graphs

The total $\left\{k\right\}$-domination problem in weighted chordal bipartite graphs can be efficiently solved by the structural properties of these graphs. Specifically, we demonstrate how the neighborhood matrix of a chordal bipartite graph ordered by its weak elimination ordering forms a greedy matrix in standard greedy form. The following lemma establishes the foundational connection between weak elimination orderings and greedy matrices.

Lemma 4. 

If the vertices of a chordal bipartite graph are ordered by its weak elimination ordering, then the neighborhood matrix of the graph is a greedy matrix in standard greedy form.

Proof. 

Let G be a chordal bipartite graph with the vertices ordered by its weak elimination ordering $v_1,v_2,\dots ,v_n$, and let $\mathbf{N}=\left(n_{ij}\right)\in {\mathbb{R}}^{n\times n}$ be the neighborhood matrix of G. Since the neighborhood matrix of a chordal bipartite graph is totally balanced [51], $\mathbf{N}$ is totally balanced. We now check if $\mathbf{N}$ contains the $\Gamma$-matrix as a submatrix:

$$\Gamma =\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right).$$

Assume that $\mathbf{N}$ contains the $\Gamma$-matrix as a submatrix, shown below with entries chosen by rows $i,j$ and columns $k,\mathsf{\ell }$, where $i<j$ and $k<\mathsf{\ell }$:

$$\begin{array}{cccc}& k& \mathsf{\ell }& \\ inei& 1& 1& \\ j& 1& 0& \hfill .\end{array}$$

Since $\mathbf{N}$ is a neighborhood matrix, each $a_{ii}$ is 0 for $1\le i\le j$. It imples that $i\ne k$, $i\ne \mathsf{\ell }$, and $j\ne k$. Furthermore, as bipartite graphs contain only cycles with even number of vertices, if $j=\mathsf{\ell }$, then $v_i,v_j$, and $v_k$ would form a cycle of odd number of vertices, which is impossible. Thus, $j\ne \mathsf{\ell }$.

Consider three cases:

• Case 1: $i<k$. Then, $v_i,v_j,v_k$, and $v_{\mathsf{\ell }}$ are all vertices of $G_i$. Since $v_i$ is adjacent to both $v_k$ and $v_{\mathsf{\ell }}$, the neighborhood relationship $N_{G_i}\left(v_k\right)\subseteq N_{G_i}\left(v_{\mathsf{\ell }}\right)$ must hold. As $v_j\in N_{G_i}\left(v_k\right)$, it follows that $v_j\in N_{G_i}\left(v_{\mathsf{\ell }}\right)$. However, this implies that $v_j$ is adjacent to $v_{\mathsf{\ell }}$, which contradicts the assumption that $v_j$ and $v_{\mathsf{\ell }}$ are not adjacent.
• Case 2: $k<i<\mathsf{\ell }$. In this case, $v_i,v_j,v_k$, and $v_{\mathsf{\ell }}$ are all vertices of $G_k$. Since $v_i$ is adjacent to both $v_k$ and $v_{\mathsf{\ell }}$, the neighborhood relationship $N_{G_k}\left(v_i\right)\subseteq N_{G_k}\left(v_{\mathsf{\ell }}\right)$ must hold. Consequently, $v_j\in N_{G_k}\left(v_i\right)$ implies $v_j\in N_{G_k}\left(v_{\mathsf{\ell }}\right)$. However, this contradicts the assumption that $v_j$ and $v_{\mathsf{\ell }}$ are not adjacent.
• Case 3: $\mathsf{\ell }<i$. Here, $v_i,v_j,v_k$, and $v_{\mathsf{\ell }}$ are again vertices of $G_k$. By reasoning similar to Case 2, the adjacency of $v_i$ to both $v_k$ and $v_{\mathsf{\ell }}$ implies $N_{G_k}\left(v_i\right)\subseteq N_{G_k}\left(v_{\mathsf{\ell }}\right)$. Since $v_j\in N_{G_k}\left(v_i\right)$, we deduce that $v_j\in N_{G_k}\left(v_{\mathsf{\ell }}\right)$, which means $v_j$ and $v_{\mathsf{\ell }}$ are adjacent. This contradicts the assumption that $v_j$ and $v_{\mathsf{\ell }}$ are not adjacent.

These cases confirm that $\mathbf{N}$ is totally balanced and excludes the $\Gamma$-matrix as a submatrix. By Claim 1, we conclude that the neighborhood matrix of a chordal bipartite graph ordered by its weak elimination ordering is a greedy matrix in standard greedy form. □

The following lemma is similar to Lemma 1. It allows us to concentrate exclusively on non-negative vertex weights (${\mathbb{R}}_{\ge 0}$).

Lemma 5. 

Let w be a vertex-weight function of a graph $G=(V,E)$, and let ${\gamma }_{tk}(G,w)$ represent the the minimum labeling weight of a total $\left\{k\right\}$-dominating function for $(G,w)$. Define $S=\{v\mid v\in V,w(v)<0\}$ and let $w^{\prime }$ be a vertex-weight function such that $w^{\prime }\left(v\right)=max\{w\left(v\right),0\}$ for each $v\in V$. Then, ${\gamma }_{tk}(G,w)={\gamma }_{tk}(G,w^{\prime })+k{\sum }_{v\in S}w\left(v\right)$.

Proof. 

This lemma can be proved by the arguments similar to those for proving Lemma 1. □

Let G be a chordal bipartite graph with the vertices arranged in weak elimination ordering with $\mathbf{N}=\left(n_{ij}\right)\in {\mathbb{R}}^{n\times n}$ as its neighborhood matrix. Let $\mathbf{w}=\left(w_j\right)\in {\mathbb{R}}_{\ge 0}^n$, $\mathbf{x}=\left(x_j\right)\in {\mathbb{R}}^n$, and $\mathbf{p}=\left(p_i\right)\in {\mathbb{R}}^n$, where $p_i=k$ for $1\le i\le n$.

The total $\left\{k\right\}$-domination problem for weighted chordal bipartite graphs can be formulated as the following integer linear program $I{P}_{tk}(G,w)$:

$$\begin{array}{c}\hfill I{P}_{tk}(G,w):\\ \hfill \mathrm{minimize}& {\mathbf{w}}^T\mathbf{x}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{Nx}\ge \mathbf{p}\hfill \\ \hfill & \mathbf{x}\ge 0,\mathbf{x}\in \mathbb{Z}.\hfill \end{array}$$

Let $L{P}_{tk}(G,w)$ be the linear relaxation of $I{P}_{tk}(G,w)$, and let $L{P}_{tk}^d(G,w)$ be the dual program of $L{P}_{tk}(G,w)$. We present the formulations of P, D, $L{P}_{tk}(G,w)$, and $L{P}_{tk}^d(G,w)$ together below:

$$\begin{array}{ccc}\hfill \mathrm{Primal}(P):& \hfill & \hfill \mathrm{Dual}(D):\\ \hfill \mathrm{minimize}& {\mathbf{c}}^T\mathbf{x}+{\mathbf{d}}^T\mathbf{z}\hfill & \hfill \mathrm{maximize}& {\mathbf{b}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{A}\mathbf{x}+\mathbf{z}\ge \mathbf{b}\hfill & \hfill \mathrm{subject}\mathrm{to}& {\mathbf{A}}^T\mathbf{y}\le \mathbf{c}\hfill \\ \hfill & \mathbf{x}\ge 0,\mathbf{z}\ge 0.\hfill & \hfill & \mathbf{y}\ge 0,\mathbf{y}\le \mathbf{d}.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{Primal}({LP}_{tk}(G,w)):& \hfill & \hfill \mathrm{Dual}(L{P}_{tk}^d(G,w)):\\ \hfill \mathrm{minimize}& {\mathbf{w}}^T\mathbf{x}\hfill & \hfill \mathrm{maximize}& {\mathbf{p}}^T\mathbf{y}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{N}\mathbf{x}\ge \mathbf{p}\hfill & \hfill \mathrm{subject}\mathrm{to}& {\mathbf{N}}^T\mathbf{y}\le \mathbf{w}\hfill \\ \hfill & \mathbf{x}\ge 0.\hfill & \hfill & \mathbf{y}\ge 0.\hfill \end{array}$$

Theorem 7. 

For weighted chordal bipartite graphs $(G,w)$ with n vertices arranged by its weak elimination ordering, the total $\left\{k\right\}$-domination problem can be solved in $\mathcal{O}(n+m)$ time, where m is the number of edges in G.

Proof. 

The proof proceeds in three steps:

1.

Neighborhood Matrix Properties: By Lemma 4, we have established that for a weighted chordal bipartite graph $(G,w)$ with n vertices arranged by its weak elimination ordering, the neighborhood matrix $\mathbf{N}$ of G is a greedy matrix in standard greedy form. This property ensures that the constraints of the total $\left\{k\right\}$-domination problem are well-structured for efficient computation.

2.

Connection to Linear Programs: The primal and dual linear programs, $L{P}_{tk}(G,w)$ and $L{P}_{tk}^d(G,w)$, for the weighted chordal bipartite graphs are specific instances of the linear programs P and D, where $\mathbf{z}=0$ and the vector $\mathbf{d}$ is absent. These simplifications reduce the computational overhead associated with solving the general cases.

3.

Efficient Computation: Using arguments similar to those in the proofs of Theorems 5 and 6, we use the greedy matrix property of $\mathbf{N}$ and advanced primal-dual algorithms to solve the relaxed problem efficiently. Optimized data structures ensure that each step in the algorithm operates in linear time relative to the size of the graph.

Combining these observations, the total $\left\{k\right\}$-domination problem for weighted chordal bipartite graphs $(G,w)$ can be solved in $\mathcal{O}(n+m)$ time. □

5. Total k-Tuple Domination and k-Tuple Domination

The k-tuple domination and total k-tuple domination problems are fundamental in graph theory, with applications in optimization and network analysis. In this section, we investigate these problems for weighted proper interval graphs and weighted convex bipartite graphs. Utilizing structural properties of these graph classes, we formulate integer linear programs with totally unimodular constraint matrices, enabling efficient solutions via linear relaxations.

5.1. Integer Linear Programs with Totally Unimodular Matrices

Totally unimodular matrices allow integer solutions to be obtained directly from linear relaxations, making them crucial in solving the k-tuple and total k-tuple domination problems efficiently. This section presents our results about totally unimodular matrices and their applications.

5.1.1. Problem Formulations

Let $(G,w)$ be a weighed graph with n vertices and m edges. The k-tuple domination problem for $(G,w)$ is formulated as an integer linear program $I{P}_{\times k}(G,w)$:

$$\mathrm{minimize}{\mathbf{w}}^T\mathbf{x},\mathrm{subject}\mathrm{to}\mathbf{M}\mathbf{x}\ge \mathbf{p},\mathbf{x}\in {\{0,1\}}^n,$$

where $\mathbf{M}$ is the closed neighborhood matrix of G, $\mathbf{w}$ is the weight vector, and $\mathbf{p}$ is a k-vector. Its linear relaxation $L{P}_{\times k}(G,w))$ is

$$\mathrm{minimize}{\mathbf{w}}^T\mathbf{x},\mathrm{subject}\mathrm{to}\mathbf{M}\mathbf{x}\ge \mathbf{p},0\le \mathbf{x}\le 1.$$

To incorporate the constraint $\mathbf{x}\le 1$ into the standard inequality framework, we express it equivalently as:

$$\mathbf{x}\le 1⟺-\mathbf{x}\ge -1.$$

This transformation allows us to maintain a unified form for all constraints. Using this approach, the linear program $L{P}_{\times k}(G,w)$ can be rewritten as:

$$\mathrm{minimize}{\mathbf{w}}^T\mathbf{x},\mathrm{subject}\mathrm{to}{\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime },\mathbf{x}\ge 0,$$

where ${\mathbf{M}}^{\prime }=\left(\begin{array}{c}\mathbf{M}\\ -\mathbf{I}\end{array}\right)$, ${\mathbf{p}}^{\prime }=\left(\begin{array}{c}\mathbf{p}\\ -\mathbf{q}\end{array}\right)$, $\mathbf{I}$ is the identity matrix, and $\mathbf{q}$ is a 1-vector.

Similarly, the total k-tuple domination problem is formulated as an integer linear program $I{P}_{\times tk}(G,w)$:

$$\mathrm{minimize}{\mathbf{w}}^T\mathbf{x},\mathrm{subject}\mathrm{to}\mathbf{N}\mathbf{x}\ge \mathbf{p},\mathbf{x}\in {\{0,1\}}^n,$$

where $\mathbf{N}$ is the neighborhood matrix. Its linear relaxation $L{P}_{\times tk}(G,w))$ can be formulated as:

$$\mathrm{minimize}{\mathbf{w}}^T\mathbf{x},\mathrm{subject}\mathrm{to}{\mathbf{N}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime },\mathbf{x}\ge 0,$$

where ${\mathbf{N}}^{\prime }=\left(\begin{array}{c}\mathbf{N}\\ -\mathbf{I}\end{array}\right)$, ${\mathbf{p}}^{\prime }=\left(\begin{array}{c}\mathbf{p}\\ -\mathbf{q}\end{array}\right)$, $\mathbf{I}$ is the identity matrix, and $\mathbf{q}$ is a 1-vector.

5.1.2. Fundamental Lemmas on Totally Unimodular Matrices

In this section, we present our fundamental lemmas on totally unimodular matrices.

Lemma 6. 

Let $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ be a totally unimodular matrix, and let $\mathbf{I}\in {\mathbb{R}}^{n\times n}$ be the identity matrix. Then, the matrix

$$\mathbf{B}=\left(\begin{array}{c}\mathbf{A}\\ -\mathbf{I}\end{array}\right)$$

is also totally unimodular.

Proof. 

It is clear that the matrix $-\mathbf{I}$ is totally unimodular, as each determinant of any square submatrix of $-\mathbf{I}$ evaluates to $-1,0,$ or 1, satisfying the definition of total unimodularity. Let ${\mathbf{B}}^{\prime }=\left(b_{ij}^{\prime }\right)\in {\mathbb{R}}^{p\times p}$ be any square submatrix of $\mathbf{B}$.

First, if the rows of ${\mathbf{B}}^{\prime }$ are formed exclusively from either $\mathbf{A}$ or $-\mathbf{I}$, then ${\mathbf{B}}^{\prime }$ is totally unimodular because $\mathbf{A}$ and $-\mathbf{I}$ satisfy the definition of total unimodularity by ensuring that every determinant of their square submatrices is in $\{-1,0,1\}$.

Next, consider the case where the rows of ${\mathbf{B}}^{\prime }$ are formed from both $\mathbf{A}$ and $-\mathbf{I}$. We compute $det\left({\mathbf{B}}^{\prime }\right)$ using the Laplace expansion along a row i formed from $-\mathbf{I}$. By the definition of Laplace expansion:

$$det\left({\mathbf{B}}^{\prime }\right)=\sum _{j=1}^p{b}_{ij}^{\prime }{(-1)}^{i+j}det\left({\mathbf{B}}_{ij}^{\prime }\right),$$

where ${\mathbf{B}}_{ij}^{\prime }$ is the $(p-1)\times (p-1)$ square submatrix obtained by removing the i-th row and j-th column from ${\mathbf{B}}^{\prime }$.

Since row i comes from $-\mathbf{I}$, it has at most one nonzero entry, which is $-1$. This means that:

$$det\left({\mathbf{B}}^{\prime }\right)=0\mathrm{or}det\left({\mathbf{B}}^{\prime }\right)={(-1)}^{s}det\left({\mathbf{B}}_{ij}^{\prime }\right),$$

where s is a non-negative integer determined by the row and column indices of the nonzero entry.

If ${\mathbf{B}}_{ij}^{\prime }$ still contains rows from $-\mathbf{I}$, we recursively apply the Laplace expansion and remove rows and columns associated with $-\mathbf{I}$. Each step multiplies the determinant by ${(-1)}^s$, with $s\in \{0,1\}$. Eventually, the process reduces ${\mathbf{B}}^{\prime }$ to a square submatrix of $\mathbf{A}$.

Since $\mathbf{A}$ satisfies the definition of total unimodularity, every determinant of its square submatrices is in $\{-1,0,1\}$. Therefore, $det\left({\mathbf{B}}^{\prime }\right)\in \{-1,0,1\}$ as well.

Thus, $\mathbf{B}$ is totally unimodular. □

Lemma 7. 

Let $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ be a totally unimodular matrix, and let $\mathbf{I}\in {\mathbb{R}}^{m\times m}$ be the identity matrix. Then, the matrix

$$\left(\begin{array}{cc}\mathbf{A}& -\mathbf{I}\end{array}\right)$$

is also totally unimodular.

Proof. 

By Lemma 6, we know that the matrix

$$\mathbf{B}=\left(\begin{array}{c}\mathbf{A}\\ -\mathbf{I}\end{array}\right)$$

is totally unimodular. Take the transpose of $\mathbf{B}$ to obtain $\left(\begin{array}{cc}\mathbf{A}& -\mathbf{I}\end{array}\right)$. The determinant of each square submatrix remains unchanged by transposing, so $\det \left(\mathbf{M}\right)=\det \left({\mathbf{M}}^T\right)$ for each square submatrix $\mathbf{M}$ of $\left(\begin{array}{cc}\mathbf{A}& -\mathbf{I}\end{array}\right)$. Consequently, $\left(\begin{array}{cc}\mathbf{A}& -\mathbf{I}\end{array}\right)$ is a totally unimodular matrix. □

Theorem 8 

([47]). Let $\mathbf{A}$ be an integral matrix. Then, $\mathbf{A}$ is totally unimodular if and only if for each integral vector $\mathbf{b}$, the polyhedron

$$\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\le \mathbf{b}\}$$

is integral.

Lemma 8. 

Let $\mathbf{A}$ be an integral matrix. Then, $\mathbf{A}$ is totally unimodular if and only if for each integral vector $\mathbf{b}$, the polyhedron

$$\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}$$

is integral.

Proof. 

Assume that $\mathbf{A}$ contains r rows. By the properties of determinants under scalar multiplication ([49]), for each square submatrix ${\mathbf{A}}^{\prime }$ of $\mathbf{A}$, we have

$$det(-{\mathbf{A}}^{\prime })={(-1)}^r·det\left({\mathbf{A}}^{\prime }\right).$$

If $\mathbf{A}$ is totally unimodular, then $det(-{\mathbf{A}}^{\prime })\in \{-1,0,1\}$, which implies that $-\mathbf{A}$ is totally unimodular. Let $\mathbf{s}$ be an integer vector. Clearly,

$$\mathbf{s}\in \{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\mathbf{s}\in \{\mathbf{x}\mid \mathbf{x}\ge 0,-\mathbf{A}\mathbf{x}\le -\mathbf{b}\}.$$

By Theorem 8, the polyhedron $\{\mathbf{x}\mid \mathbf{x}\ge 0,-\mathbf{A}\mathbf{x}\le -\mathbf{b}\}$ is integral. Therefore, $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}$ is also integral.

Conversely, if $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}$ is integral, then so is $\{\mathbf{x}\mid \mathbf{x}\ge 0,-\mathbf{A}\mathbf{x}\le -\mathbf{b}\}$. By Theorem 8, $-\mathbf{A}$ is totally unimodular. Following the same reasoning as above, $-(-\mathbf{A})=\mathbf{A}$ is therefore also totally unimodular.

Thus, the lemma holds. □

Lemma 9. 

Let $\mathbf{A}$ be a totally unimodular matrix. For each integral vector $\mathbf{b}$, the polyhedron

$$\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}=\mathbf{b}\}$$

is integral.

Proof. 

It is clear that the polyhedron $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}=\mathbf{b}\}$ is equivalent to the following:

$$\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b},\mathbf{A}\mathbf{x}\le \mathbf{b}\}=\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}\cap \{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\le \mathbf{b}\}.$$

Following Theorem 8 and Lemma 8, the polyhedra $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\ge \mathbf{b}\}$ and $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}\le \mathbf{b}\}$ are integral. Therefore, $\{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}=\mathbf{b}\}$ is integral. □

5.2. k-Tuple Domination in Weighted Proper Interval Graphs

We have formulated the k-tuple domination problem for weighted graphs $(G,w)$ as the integer linear program $I{P}_{\times k}(G,w)$. For weighted proper interval graphs, solving $I{P}_{\times k}(G,w)$ is equivalent to directly solving the k-tuple domination problem.

The following lemma establishes a critical connection between the closed neighborhood matrices of weighted proper interval graphs and totally unimodular matrices. This connection enables $I{P}_{\times k}(G,w)$ to be solved efficiently by addressing its linear relaxation $L{P}_{\times k}(G,w)$.

Lemma 10. 

The closed neighborhood matrix of a weighted proper interval graph is totally unimodular.

Proof. 

The lemma follows from two established results:

• A graph is a proper interval graph if and only if its closed neighborhood matrix has the consecutive ones property for columns [44].
• If a $(0,1)$-matrix has the consecutive ones property for columns, then it is totally unimodular [47].

□

Theorem 9. 

The k-tuple domination problem for weighted proper interval graphs $(G,w)$ can be solved in the running time of

$$\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right),$$

where n is the number of vertices, and δ is the desired accuracy within the range $(0,1].$

Proof. 

Following Lemmas 6, 8, and 10, we know that the closed neighborhood matrix $\mathbf{M}$ of G and the constraint matrix ${\mathbf{M}}^{\prime }$ in ${LP}_{\times k}(G,w)$ are totally unimodular, and the polyhedron of ${LP}_{\times k}(G,w)$ is integer. Therefore, the optimal objective values of ${LP}_{\times k}(G,w)$ and ${IP}_{\times k}(G,w)$ are equal. Thus, solving ${\mathrm{IP}}_{\times tk}(G,w)$ is equivalent to finding an integral solution to ${\mathrm{LP}}_{\times tk}(G,w)$. This implies that the total k-tuple domination problem for weighted convex bipartite graphs can be solved by computing an integral solution to ${\mathrm{LP}}_{\times tk}(G,w)$.

Recently, van den Brand [58] derandomized the algorithm of Cohen et al. [59] to achieve that linear programs of the form $min\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}=\mathbf{b}\}$ with no redundant constraints can be solved in the running time

$$\mathcal{O}\left((n^{\omega }+n^{2.5-\alpha /2+o\left(1\right)}+n^{2+1/6+o\left(1\right)}){log}^2\left(n\right)log(n/\delta )\right),$$

where n is the number of decision variables, $\omega$ is the exponent of matrix multiplication, $\alpha$ is the dual exponent of matrix multiplication, and $\delta$ is the desired accuracy within the range $(0,1]$. Williams et al. [60] established $\omega \le 2.371552$ and $\alpha \ge 0.321334$. This yields a simplified complexity of $\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right)$.

The linear program ${LP}_{\times k}(G,w)$ is $min\{{\mathbf{w}}^T\mathbf{x}\mid \mathbf{x}\ge 0,{\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }\}$. To solve $L{P}_{\times k}(G,w)$ by van den Brand’s algorithm, we transform $L{P}_{\times k}(G,w)$ into the form $min\{{\mathbf{c}}^T\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{A}\mathbf{x}=\mathbf{b}\}$ using slack variables. The transformation steps are as follows:

1.

Introduce Slack Variables.

Convert the inequality ${\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }$ into an equality by introducing slack variables. Rewrite it as:

$${\mathbf{M}}^{\prime }\mathbf{x}={\mathbf{p}}^{\prime }+\mathbf{s},$$

where $\mathbf{s}\ge 0$ is a vector of slack variables. This ensures each constraint in the original inequality has a corresponding non-negative slack variable.

2.

Rewrite as Equalities.

Rearrange the equality above as:

$${\mathbf{M}}^{\prime }\mathbf{x}-\mathbf{s}={\mathbf{p}}^{\prime }.$$

Define a new vector $\tilde{\mathbf{x}}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{s}\end{array}\right)$, so we can express the constraints in matrix form as:

$$\left(\begin{array}{cc}{\mathbf{M}}^{\prime }& -\mathbf{I}\end{array}\right)\tilde{\mathbf{x}}={\mathbf{p}}^{\prime }.$$

3.

Extend the Objective Function.

Since the original objective function is ${\mathbf{w}}^T\mathbf{x}$, extend it to include the slack variables by setting:

$$\mathbf{c}=\left(\begin{array}{c}\mathbf{w}\\ \mathbf{j}\end{array}\right),$$

where $\mathbf{j}$ is a zero vector. This ensures that the slack variables $\mathbf{s}$ do not affect the objective function.

Thus, the transformed linear program becomes:

$$min\{{\mathbf{c}}^T\tilde{\mathbf{x}}\mid \tilde{\mathbf{x}}\ge 0,\mathbf{A}\tilde{\mathbf{x}}=\mathbf{b}\},$$

where $\mathbf{A}=\left(\begin{array}{cc}{\mathbf{M}}^{\prime }& -\mathbf{I}\end{array}\right)$, $\mathbf{b}={\mathbf{p}}^{\prime }$, $\tilde{\mathbf{x}}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{s}\end{array}\right)$, and $\mathbf{c}=\left(\begin{array}{c}\mathbf{w}\\ \mathbf{j}\end{array}\right)$.

We verify the correctness and analyze the time complexity of this transformation by confirming that the feasible sets of $\mathbf{x}$ and objective functions of the original and transformed problems are equivalent. The steps are as follows:

1.

Converting Inequalities to Equalities via Slack Variables

In $L{P}_{\times k}(G,w)$, the inequality ${\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }$ restricts $\mathbf{x}$ so that each entry of ${\mathbf{M}}^{\prime }\mathbf{x}$ is at least the corresponding entry of ${\mathbf{p}}^{\prime }$. To convert this inequality into an equality, we introduce a vector of slack variables $\mathbf{s}\ge 0$, rewriting it as:

$${\mathbf{M}}^{\prime }\mathbf{x}={\mathbf{p}}^{\prime }+\mathbf{s}.$$

This ensures that ${\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }$ holds if and only if there exists a non-negative vector $\mathbf{s}$ such that ${\mathbf{M}}^{\prime }\mathbf{x}={\mathbf{p}}^{\prime }+\mathbf{s}$. Since ${\mathbf{M}}^{\prime }$ has $2n$ rows and n columns, the vector $\mathbf{s}$ consists of $2n$ entries. Setting up the slack variables takes $\mathcal{O}\left(n\right)$ time.

2.

Reformulating Constraints with Augmented Matrices

We define $\tilde{\mathbf{x}}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{s}\end{array}\right)$ and rewrite the equality as:

$$\mathbf{A}\tilde{\mathbf{x}}=\mathbf{b},$$

where $\mathbf{A}=\left(\begin{array}{cc}{\mathbf{M}}^{\prime }& -\mathbf{I}\end{array}\right)$ and $\mathbf{b}={\mathbf{p}}^{\prime }$. This matrix formulation ensures that each slack variable $s_i$ directly accounts for the surplus required to satisfy each inequality. Constructing $\mathbf{A}$ requires combining ${\mathbf{M}}^{\prime }$ with $-\mathbf{I}$, and constructing $\tilde{\mathbf{x}}$ requires combining $\mathbf{x}$ with $\mathbf{s}$.

The matrix $\mathbf{A}$ has $2n$ rows and $3n$ columns. The vector $\tilde{\mathbf{x}}$ has $3n$ rows and one column, resulting in an augmented matrix, which takes $\mathcal{O}\left(n^2\right)$ time. Hence, the step can be done in $\mathcal{O}\left(n^2\right)$ time.

3.

Ensuring Equivalence of Feasible Sets of $\mathbf{x}$

In the original linear program, the feasible region is defined by all $\mathbf{x}\ge 0$ such that ${\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }$. In the transformed linear program, the feasible region is defined by all non-negative vectors $\tilde{\mathbf{x}}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{s}\end{array}\right)\ge 0$ that satisfy $\mathbf{A}\tilde{\mathbf{x}}=\mathbf{b}$. Clearly,

$$\mathbf{x}\in \{\mathbf{x}\mid \mathbf{x}\ge 0,{\mathbf{M}}^{\prime }\mathbf{x}\ge {\mathbf{p}}^{\prime }\}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\mathbf{x}\in \{\mathbf{x}\mid \mathbf{x}\ge 0,\mathbf{s}\ge 0,{\mathbf{M}}^{\prime }\mathbf{x}={\mathbf{p}}^{\prime }+\mathbf{s}\}.$$

This establishes that the transformation preserves the feasible region.

4.

Ensuring Equivalence of Objective Functions

The original objective function ${\mathbf{w}}^T\mathbf{x}$ depends only on $\mathbf{x}$, so in the transformed program, we extend it by defining $\mathbf{c}=\left(\begin{array}{c}\mathbf{w}\\ \mathbf{j}\end{array}\right)$, where $\mathbf{j}$ is a zero vector. This construction prevents the slack variables $\mathbf{s}$ from influencing the objective function, so that the objective ${\mathbf{c}}^T\tilde{\mathbf{x}}={\mathbf{w}}^T\mathbf{x}$ in the transformed program is identical to the original objective. Extending the objective vector takes $\mathcal{O}\left(n\right)$ time.

Having verified that the transformation preserves both the feasible region and the objective function, we conclude that the transformation is correct with the time complexity of $\mathcal{O}\left(n^2\right)$.

Since ${\mathbf{M}}^{\prime }$ is totally unimodular, Lemmas 7 and 9 imply that $\mathbf{A}=\left(\begin{array}{cc}{\mathbf{M}}^{\prime }& -\mathbf{I}\end{array}\right)$ is totally unimodular, and the polyhedron of the transformed linear program is integer.

Despite the transformed linear program containing $3n$ variables, it can still be solved in $\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right)$ time. Consequently, the linear relaxation $L{P}_{\times k}(G,w)$ runs in time of:

$$\mathcal{O}\left(n^2+n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right)=\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log(n/\delta )\right).$$

□

5.3. Total k-Tuple Domination in Weighted Convex Bipartite Graphs

In this subsection, we explore the total k-tuple domination problem in weighted convex bipartite graphs. In Section 5.1.1, we formulated the total k-tuple domination problem for weighted graphs $(G,w)$ as the integer linear program $I{P}_{\times tk}(G,w)$. For weighted convex bipartite graphs $(G,w)$, solving $I{P}_{\times tk}(G,w)$ is equivalent to directly solving the total k-tuple domination problem.

To establish a connection between the neighborhood matrices of weighted convex bipartite graphs and totally unimodular matrices (as discussed in Section 5.1 and Section 5.2), we begin by examining the neighborhood matrix of a convex bipartite graph.

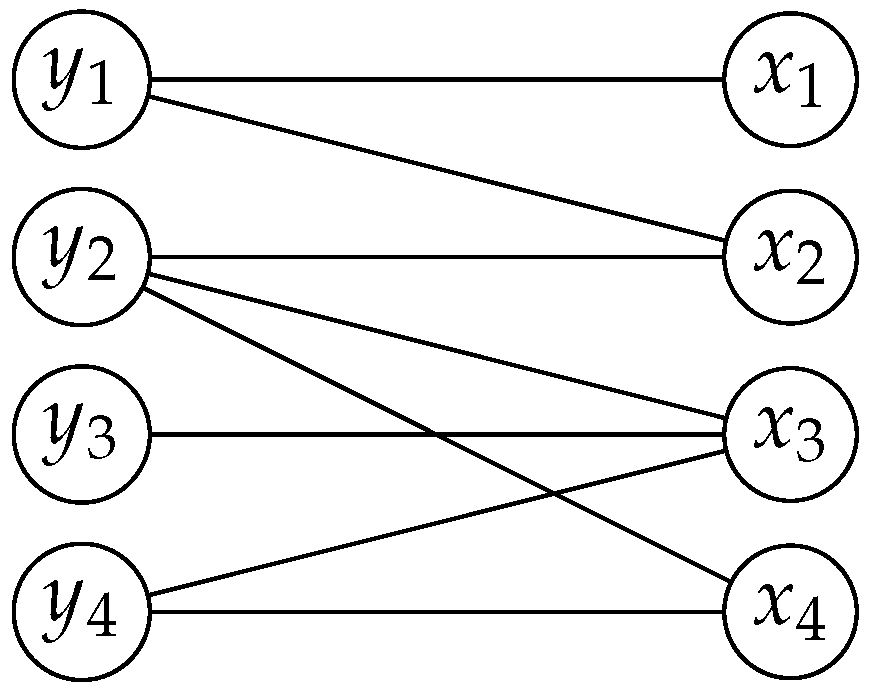
Figure 3 illustrates a convex bipartite graph $G=(X,Y,E)$, where $X=\{x_1,x_2,x_3,x_4\}$ and $Y=\{y_1,y_2,y_3,y_4\}$.

The neighborhood matrix $\mathbf{N}$ of G is shown below:

$$\begin{array}{ccccccccc}& x_1& x_2& x_3& x_4& y_1& y_2& y_3& y_4\\ ine{x}_1& 0& 0& 0& 0& 1& 0& 0& 0\\ x_2& 0& 0& 0& 0& 1& 1& 0& 0\\ x_3& 0& 0& 0& 0& 0& 1& 1& 1\\ x_4& 0& 0& 0& 0& 0& 1& 0& 1\\ ine{y}_1& 1& 1& 0& 0& 0& 0& 0& 0\\ y_2& 0& 1& 1& 1& 0& 0& 0& 0\\ y_3& 0& 0& 1& 0& 0& 0& 0& 0\\ y_4& 0& 0& 1& 1& 0& 0& 0& 0\end{array}=\left(\begin{array}{cc}{\mathbf{A}}_1& {\mathbf{A}}_2\\ {\mathbf{A}}_3& {\mathbf{A}}_4\end{array}\right)$$

The matrix $\mathbf{N}$ is partitioned into four blocks: ${\mathbf{A}}_1$, ${\mathbf{A}}_2$, ${\mathbf{A}}_3$, and ${\mathbf{A}}_4$. Since G is bipartite, no two vertices in X or Y are adjacent. Therefore, ${\mathbf{A}}_1$ and ${\mathbf{A}}_4$ are zero-matrices. Moreover, the adjacency property ensures that every column of ${\mathbf{A}}_2$ has consecutive ones. Then, ${\mathbf{A}}_2$ has the consecutive ones property for columns. The block ${\mathbf{A}}_3$ is the transpose of ${\mathbf{A}}_2$ because of the symmetry of a neighborhood matrix of a graph.

Lemma 11. 

Let $\mathbf{M}$ be a square matrix partitioned as

$$\mathbf{M}=\left(\begin{array}{cc}\mathbf{Q}& \mathbf{P}\\ \mathbf{S}& \mathbf{R}\end{array}\right),$$

where $\mathbf{Q}$ is a zero-matrix, and $\mathbf{P}$ and $\mathbf{S}$ are square matrices with $det\left(\mathbf{P}\right),det\left(\mathbf{S}\right)\in \{-1,0,1\}$. Then,

$$det\left(\mathbf{M}\right)\in \{-1,0,1\}.$$

Proof. 

By a factorization involving the Schur complement [61], we have

$$det\left(\begin{array}{cc}\mathbf{P}& \mathbf{Q}\\ \mathbf{R}& \mathbf{S}\end{array}\right)=det\left(\mathbf{P}\right)det\left(\mathbf{S}\right),$$

where $\mathbf{P}$ and $\mathbf{S}$ contribute independently to the determinant. Since $det\left(\mathbf{P}\right),det\left(\mathbf{S}\right)\in \{-1,0,1\}$, it follows that

$$det\left(\begin{array}{cc}\mathbf{P}& \mathbf{Q}\\ \mathbf{R}& \mathbf{S}\end{array}\right)\in \{-1,0,1\}.$$

Next, let

$${\mathbf{M}}^{\prime }=\left(\begin{array}{cc}\mathbf{P}& \mathbf{Q}\\ \mathbf{R}& \mathbf{S}\end{array}\right).$$

To transform ${\mathbf{M}}^{\prime }$ into $\mathbf{M}$, we perform column exchanges. Each column exchange introduces a sign change in the determinant. Therefore, we have

$$det\left(\mathbf{M}\right)={(-1)}^{s}det\left({\mathbf{M}}^{\prime }\right),$$

where s is the number of column exchanges.

Since $det\left({\mathbf{M}}^{\prime }\right)\in \{-1,0,1\}$, and sign changes do not affect the magnitude of the determinant, we conclude

$$det\left(\mathbf{M}\right)\in \{-1,0,1\}.$$

□

Theorem 10. 

Let $G=(X,Y,E)$ be a convex bipartite graph, where the ordering of X satisfies the adjacency property. Then, the neighborhood matrix $\mathbf{N}$ of G is totally unimodular.

Proof. 

Let $X=\{1,2,\dots ,r\}$ and $Y=\{r+1,r+2,\dots ,n\}$. The neighborhood matrix $\mathbf{N}$ of G, an $n\times n$ matrix, can be partitioned as

$$\mathbf{N}=\left(\begin{array}{cc}{\mathbf{N}}_1& {\mathbf{N}}_2\\ {\mathbf{N}}_3& {\mathbf{N}}_4\end{array}\right),$$

where ${\mathbf{N}}_1=\mathbf{N}(1:r,1:r),{\mathbf{N}}_2=\mathbf{N}(1:r,r+1:n),{\mathbf{N}}_3=\mathbf{N}(r+1:n,1:r),{\mathbf{N}}_4=\mathbf{N}(r+1:n,r+1:n).$ Since G is bipartite, ${\mathbf{N}}_1$ and ${\mathbf{N}}_4$ are zero-matrices.

The adjacency property of G ensures that ${\mathbf{N}}_2$ satisfies the consecutive ones property for columns. By Theorem 1, ${\mathbf{N}}_2$ is totally unimodular. Since ${\mathbf{N}}_3={\mathbf{N}}_2^T$ and the transpose of a totally unimodular matrix is also totally unimodular, ${\mathbf{N}}_3$ is totally unimodular.

To verify that $\mathbf{N}$ is totally unimodular, we show that every square submatrix ${\mathbf{N}}^{\prime }$ of $\mathbf{N}$ satisfies $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$. Assume that ${\mathbf{N}}^{\prime }$ is composed of p rows and p columns, where $1\le p\le n$. We consider three cases based on the structure of ${\mathbf{N}}^{\prime }$.

• Case 1: ${\mathbf{N}}^{\prime }$ is a submatrix of a single block.

If ${\mathbf{N}}^{\prime }$ is a submatrix of ${\mathbf{N}}_1$ or ${\mathbf{N}}_4$, it is a zero-matrix, so $det\left({\mathbf{N}}^{\prime }\right)=0$. If ${\mathbf{N}}^{\prime }$ is a submatrix of ${\mathbf{N}}_2$ or ${\mathbf{N}}_3$, the total unimodularity of ${\mathbf{N}}_2$ and ${\mathbf{N}}_3$ ensures $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$.

• Case 2: ${\mathbf{N}}^{\prime }$ includes rows and columns from exactly two blocks.

The rows and columns of ${\mathbf{N}}^{\prime }$ are from two blocks, ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$, ${\mathbf{N}}_2$ and ${\mathbf{N}}_4$, ${\mathbf{N}}_3$ and ${\mathbf{N}}_4$, or ${\mathbf{N}}_1$ and ${\mathbf{N}}_3$. Since ${\mathbf{N}}_1$ and ${\mathbf{N}}_4$ are zero-matrices, at least one row or column of ${\mathbf{N}}^{\prime }$ is entirely zero, implying $det\left({\mathbf{N}}^{\prime }\right)=0$.

• Case 3: ${\mathbf{N}}^{\prime }$ includes rows and columns from all four blocks.

We partition ${\mathbf{N}}^{\prime }$ as

$${\mathbf{N}}^{\prime }=\left(\begin{array}{cc}{\mathbf{N}}_1^{\prime }& {\mathbf{N}}_2^{\prime }\\ {\mathbf{N}}_3^{\prime }& {\mathbf{N}}_4^{\prime }\end{array}\right),$$

where ${\mathbf{N}}_1^{\prime }={\mathbf{N}}^{\prime }(1:s,1:t),{\mathbf{N}}_2^{\prime }={\mathbf{N}}^{\prime }(1:s,t+1:p),{\mathbf{N}}_3^{\prime }={\mathbf{N}}^{\prime }(s+1:p,1:t),{\mathbf{N}}_4^{\prime }={\mathbf{N}}^{\prime }(s+1:p,t+1:p).$

In this case, ${\mathbf{N}}_i^{\prime }$ is a submatrix of ${\mathbf{N}}_i$ for $1\le i\le 4$. Since ${\mathbf{N}}_1^{\prime }$ and ${\mathbf{N}}_4^{\prime }$ are submatrices of zero-matrices, they are zero-matrices themselves. This reduces ${\mathbf{N}}^{\prime }$ to a dependency on ${\mathbf{N}}_2^{\prime }$ and ${\mathbf{N}}_3^{\prime }$. We analyze based on the dimensions of the submatrices.

• Case 3.1: $p-t<s$.

In this case, $p-s<t$. We partition ${\mathbf{N}}^{\prime }$ as

$${\mathbf{N}}^{\prime }=\left(\begin{array}{cc}{\mathbf{N}}_1^{″}& {\mathbf{N}}_2^{″}\\ {\mathbf{N}}_3^{″}& {\mathbf{N}}_4^{″}\end{array}\right),$$

where ${\mathbf{N}}_1^{″}={\mathbf{N}}^{\prime }(1:s,1:p-s),{\mathbf{N}}_2^{″}={\mathbf{N}}^{\prime }(1:s,p-s+1:p),{\mathbf{N}}_3^{″}={\mathbf{N}}^{\prime }(s+1:p,1:p-s),{\mathbf{N}}_4^{″}={\mathbf{N}}^{\prime }(s+1:p,p-s+1:p).$

Here, ${\mathbf{N}}_1^{″}$ is a zero-matrix, and both ${\mathbf{N}}_2^{″}$ and ${\mathbf{N}}_3^{″}$ are square matrices. Notably, ${\mathbf{N}}_2^{″}$ contains a column of zeros because $p-s<t$. We have $det\left({\mathbf{N}}_2^{″}\right)=0$. Since ${\mathbf{N}}_3^{″}$ is a submatrix of ${\mathbf{N}}_3$, it preserves totally unimodularity, and thus $det\left({\mathbf{N}}_3^{″}\right)\in \{-1,0,1\}$. By Lemma 11, $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$.

• Case 3.2: $p-t>s$.

In this case, $p-s>t$. We partition ${\mathbf{N}}^{\prime }$ as

$${\mathbf{N}}^{\prime }=\left(\begin{array}{cc}{\mathbf{N}}_1^{″}& {\mathbf{N}}_2^{″}\\ {\mathbf{N}}_3^{″}& {\mathbf{N}}_4^{″}\end{array}\right),$$

where ${\mathbf{N}}_1^{″}={\mathbf{N}}^{\prime }(1:p-t,1:t),{\mathbf{N}}_2^{″}={\mathbf{N}}^{\prime }(1:p-t,t+1:p),{\mathbf{N}}_3^{″}={\mathbf{N}}^{\prime }(p-t+1:p,1:t),{\mathbf{N}}_4^{″}={\mathbf{N}}^{\prime }(p-t+1:p,t+1:p).$

Here, ${\mathbf{N}}_1^{″}$ is a zero-matrix, and both ${\mathbf{N}}_2^{″}$ and ${\mathbf{N}}_3^{″}$ are square matrices. Notably, ${\mathbf{N}}_2^{″}$ contains a row of zeros because $p-t>s$. We have $det\left({\mathbf{N}}_2^{″}\right)=0$. Since ${\mathbf{N}}_3^{″}$ is a submatrix of ${\mathbf{N}}_3$, it preserves totally unimodularity, and thus $det\left({\mathbf{N}}_3^{″}\right)\in \{-1,0,1\}$. By Lemma 11, $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$.

• Case 3.3: $p-t=s$.

In this case, $p-s=t$. We partition ${\mathbf{N}}^{\prime }$ as

$${\mathbf{N}}^{\prime }=\left(\begin{array}{cc}{\mathbf{N}}_1^{″}& {\mathbf{N}}_2^{″}\\ {\mathbf{N}}_3^{″}& {\mathbf{N}}_4^{″}\end{array}\right),$$

where ${\mathbf{N}}_1^{″}={\mathbf{N}}^{\prime }(1:s,1:t),{\mathbf{N}}_2^{″}={\mathbf{N}}^{\prime }(1:s,t+1:p),{\mathbf{N}}_3^{″}={\mathbf{N}}^{\prime }(s+1:p,1:t),{\mathbf{N}}_4^{″}={\mathbf{N}}^{\prime }(s+1:p,t+1:p).$

Here, ${\mathbf{N}}_1^{″}$ is a zero-matrix, and both ${\mathbf{N}}_2^{″}$ and ${\mathbf{N}}_3^{″}$ are square matrices. Since ${\mathbf{N}}_2^{″}$ and ${\mathbf{N}}_3^{″}$ are submatrices of totally unimodular matrices, their determinants satisfy $det\left({\mathbf{N}}_2^{″}\right)\in \{-1,0,1\}$ and $det\left({\mathbf{N}}_3^{″}\right)\in \{-1,0,1\}$. By Lemma 11, $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$.

In all subcases, $det\left({\mathbf{N}}^{\prime }\right)\in \{-1,0,1\}$. Therefore, the neighborhood matrix $\mathbf{N}$ of the convex bipartite graph G is totally unimodular. □

Theorem 11. 

The total k-tuple domination problem for weighted convex bipartite graphs $(G,w)$ can be solved in the running time of

$$\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log\left({\displaystyle \frac{n}{\delta }}\right)\right),$$

where n is the number of vertices in G, and δ is the desired accuracy within the range $(0,1]$.

Proof. 

By Lemma 6, Lemma 8, and Theorem 10, the neighborhood matrix $\mathbf{N}$ of G and the constraint matrix ${\mathbf{N}}^{\prime }$ in ${\mathrm{LP}}_{\times tk}(G,w)$ are totally unimodular. Consequently, the polyhedron associated with ${\mathrm{LP}}_{\times tk}(G,w)$ is integer, meaning that the optimal objective values of ${\mathrm{LP}}_{\times tk}(G,w)$ and ${\mathrm{IP}}_{\times tk}(G,w)$ are equal.

Thus, solving ${\mathrm{IP}}_{\times tk}(G,w)$ is equivalent to finding an integral solution to ${\mathrm{LP}}_{\times tk}(G,w)$. This implies that the total k-tuple domination problem for weighted convex bipartite graphs can be solved by computing an integral solution to ${\mathrm{LP}}_{\times tk}(G,w)$.

Following arguments analogous to those used in the proof of Theorem 9, we conclude that the total k-tuple domination problem can be solved in the running time of

$$\mathcal{O}\left(n^{2.371552}{log}^2\left(n\right)log\left({\displaystyle \frac{n}{\delta }}\right)\right).$$

□

6. Conclusions and Future Directions

This paper investigates the complexity of and algorithmic solutions for $\left\{k\right\}$-domination, k-tuple domination, and their total domination variants in weighted subclasses of chordal graphs and bipartite graphs. The primary contributions of this work are as follows:

1.

Developing efficient $\mathcal{O}(n+m)$ time algorithms for $\left\{k\right\}$-domination in weighted strongly chordal graphs and total $\left\{k\right\}$-domination in weighted chordal bipartite graphs.

2.

Establishing the running time of $\mathcal{O}(n^{2.371552}{log}^2\left(n\right)log(n/\delta ))$ for k-tuple and total k-tuple domination in weighted proper interval graphs and convex bipartite graphs. This result improves the running time for the k-tuple domination problem in unit proper interval graphs.

3.

Extending theoretical models to vertex-weighted graph settings, bridging gaps in the existing research on weighted graph domination.

4.

Leveraging linear and integer programming techniques, supported by totally balanced and totally unimodular matrices, to provide formal proofs of correctness and efficiency for the proposed algorithms.

These results advance both the theoretical understanding and computational efficiency of domination problems in weighted graph classes.

Future work can extend these domination techniques to other weighted graph classes, including real-world network applications and dynamic graph settings. Additionally, integrating these approaches with advanced optimization techniques, such as parallel computation and distributed systems, may yield even more efficient and scalable algorithms.