Abstract
The global adoption of hybrid renewable energy systems (HRESs) is accelerating as a strategic response to escalating energy demands and the imperative to mitigate greenhouse gas emissions. Despite the development of various technological tools, such as pre-feasibility analysis, sizing, and simulation tools, challenges persist due to their limited flexibility in modifying system architectures and their typically long computation times, which hinder their practical efficiency. This study introduces a novel hybrid method that integrates the Branch and Bound (BB) heuristic search algorithm with the k-Nearest Neighbors (kNN) algorithm to drastically reduce the simulation time of microgrid models in Simulink. Validation considering four distinct case studies reveals that our method can decrease the simulation time by up to 94.68% while maintaining an acceptable accuracy. Specifically, simulation times in certain cases were reduced from approximately 21,780 and 118,580 s to 1442.7969 and 6306.0625 s, respectively. This significant reduction facilitates the rapid evaluation and selection of optimal HRES configurations, enhancing the efficiency of both editable and non-editable systems. Through streamlining the simulation process, this approach not only accelerates the design and analysis phases but also supports the broader adoption and deployment of HRESs, which is critical for achieving a sustainable future. This advancement offers a robust and efficient methodology for optimizing simulation times, thereby addressing a key bottleneck in the development and implementation of hybrid renewable energy solutions.
MSC:
37M05
1. Introduction
The growing demand for energy, combined with the growing concern about environmental pollution and greenhouse gas production, is contributing to the increased use of renewable energy sources, including solar, wind, biomass, hydraulic, and geothermal sources. Although these sources are diverse, each has a unique energy supply issue. This uniqueness is mainly due to the energy source, the load demand to be met, and the implementation conditions. Moreover, the renewable sources that can be used in an area may not meet the projected energy demands and/or are subject to significant fluctuations. Therefore, renewable sources are often combined with generators for compensatory energy production and storage systems for energy storage to ensure the continuity of energy availability. These combinations are deemed hybrid renewable energy systems (HRESs).
Several technologies and approaches have been proposed to ease the problematic decision-making process related to choosing the right system. These are grouped into four subcategories [1] with complementary objectives. Pre-feasibility analysis tools help engineers in their initial analysis of the suitability of a renewable energy system. Sizing tools help to find the best values for various parameters, such as the number of solar photovoltaic panels to be used to meet energy demand. These tools consider energy demand as an objective and deal with the problem by searching for values that optimize different objective functions. There are also simulation and open architecture tools. Simulation tools, as the name suggests, are based on user-provided specifications, such as the size of the system to implement. The simulation tool then provides the user with a detailed analysis of the system’s behavior, which is supplied as an input to the simulation model. The last category is open-architecture tools, which are the opposite of the other types (particularly simulation tools, which are primarily black boxes that do not allow for structural modifications). As indicated in their name, such tools offer an open possibility to make modifications thanks to their R&D-oriented components.
The key problem of sizing a hybrid renewable energy system is related to the fact that renewable energy sources cannot consistently produce energy at all times of the day and year, which makes it essential to combine renewables with alternative energy sources. It is also important to find the best size for each source, considering factors such as investment costs and the available installation surface area. Even with a combination of different energy sources, in many cases, it is necessary to add a generator to the system (e.g., to supply energy to medical facilities, which need to be kept powered at all times). Considering when the generator will have to use fossil fuel, depending on the available investment cost, it is important to determine the correct generator size to limit this consumption as much as possible to reduce greenhouse gas emissions. In addition, given the variability of renewable energy production sources, it is necessary to attach external systems.
Adopting a hybrid renewable energy system requires carrying out three essential steps.
Step 1: Scenario generation—This step consists of defining different potentially feasible configurations of these systems, taking into account various factors such as the renewable energy sources available (solar, wind, biomass), the different energy demand profiles that the system must meet, and, above all, environmental and economic constraints (e.g., the location and total cost of the system must be taken into account) [2]. The literature abounds with methods, such as genetic algorithms (GAs) and probabilistic methods (Monte Carlo), which enable the definition of realistic data sets and scenarios based on temporal correlations and uncertainties [3]. Considering that renewable sources alone do not guarantee system resilience, the generation process can integrate not only storage sources (batteries) but also external production sources (generators) [4,5].
Step 2: Simulation of previously generated configurations—Simulation tools and software, such as HOMER/HOMER Pro (version 3.11.6561.20287) [1,2,6], are available to evaluate the performance of these configurations [7,8]. A large body of research has used optimization algorithms, such as particle swarm optimization (PSO) [9,10] and simulated annealing, with the aim of optimizing implementation costs and the proportion of renewable energy [11,12].
Step 3: Feasibility analysis—This final stage is crucial in determining which of the many final systems will be adopted. It consists of evaluating systems in terms of their technical, economic, environmental, and social aspects. In this stage, energy costs, net present value, CO2 emissions, job creation rates, and many other factors are evaluated to determine the optimal configuration [13,14,15]. Implementing these different steps, though necessary, requires significant costs in terms of both time and resources. These processes can take several tens of hours [16,17], depending on the different characteristics considered.
Simulation time is a significant research issue across multiple fields. The problem has attracted the attention of many researchers in various fields, including the energy field [17,18,19,20,21] and in the field of image characterization and reconstruction [22].
Table 1 summarizes the key contributions of previous work on hybrid renewable energy systems. Martinez-Turegano et al. (2019) [21] have addressed the problem of extended simulation time for wind farms through developing admittance models with the aim of reducing the mathematical complexity and maintaining acceptable accuracy in performance. This approach has proven very useful in the context of large-scale networks, such as offshore wind farms. In light of this work, Banihashemi et al. (2022) [19] proposed the use of the auto-encoder approach due to its ability to reduce the size of system parameters. In particular, the use of auto-encoders enables the extraction of the essential characteristics of energy systems, considerably reducing simulation times. This approach has many advantages when researchers have sufficient and representative data at their disposal. Regarding the work by Tounsi (2022) [17], the approach consisted of replacing modules which were deemed to be complex in the simulation model. Although this approach may address the issues of complexity and simulation time, it remains domain-specific. Finally, in a similar vein to the work of Banihashemi et al. and Tounsi, Mange and Skowronska (2023) [20] have proposed the use of machine learning (ML) models. The aim of their research was to replace the entire simulation model with predictive models. This reduces processing time while guaranteeing uncertainty management. In this approach, the ML models need to be trained on high-quality data sets and their reliability assessed based on robust model validation.

Table 1.
Summary of methodologies and applications.
Although these approaches have been effective in their application frameworks, there are a number of limitations. First, reliable data are required to construct machine learning models. In addition, simulations relating to sizing hybrid renewable energy systems remains a problem relative to each situation. This relativity is an essential problem, as load demands are not the same for two different consumers and energy production sources can differ considerably. When considering the use of a simulation model for hybrid renewable energy systems, such as HOMER (Hybrid Optimization Model for Renewable Energy) [1,23], it is not possible to develop a replacement component for an entity or for the entire model. In many cases, a researcher only has simulation rights for simulating the candidate systems they want to install. Next, the researcher must select an analysis methodology to adopt for the simulation data after running a simulation. The completion of the simulation(s) can be a very long process [16,24].
Various studies have also addressed multi-processor execution techniques [25,26]. A key concern regarding multi-processor execution is that it requires a machine with a multi-core processor and high processing speed [25]. Although many methods have been discussed in the literature, these methods can only be applied in well-defined study cases. Their application in our study is limited by (i) the non-availability of historical data to best represent all zones and (ii) the impossibility of having modification access to the model, in order to plan the feature extraction study or the replacement of a part of the model by a new optimized model block. Therefore, this study proposes a new methodology for reducing the simulation waiting time through applying a hybrid method based on machine learning and a heuristic search with no historical data or modification of the initial model. With the aim of simplifying the evaluation process for hybrid energy systems, the proposed hybrid methodology combines the k-Nearest Neighbors and Branch and Bound methods. This approach reduces the waiting time for simulation and feasibility analysis tools.
The main contributions of this work revolve around the following three points:
- Innovative hybrid kNN and Branch and Bound (BB)—the integration of kNN with BB optimization establishes a robust framework for the selection process of energy systems;
- Targeted exploration optimization—the application of BB enables a solution to the problem to be found through analyzing nodes and branches. This approach avoids the exploration of unnecessary branches based on the results obtained in the previous steps;
- Dynamic definition of sets of hybrid renewable energy systems—the kNN approach defines sets of feasible systems sharing common characteristics, such as similar neighboring systems. This approach allows for a preliminary classification of systems, which speeds up the search process.
The remainder of this article is structured as follows. Section 2 presents the methodology, beginning with our three-phase model, and describes how the two algorithms (kNN and BB) help to achieve the objective of the study. The results and comparison with traditional methods are presented in Section 3. The article ends with concluding remarks and recommendations for future work in Section 4.
2. Solution Approach
This section outlines the study’s toolset and comprehensive methodology, describing the approach adopted to address the research objectives.
2.1. Stepwise
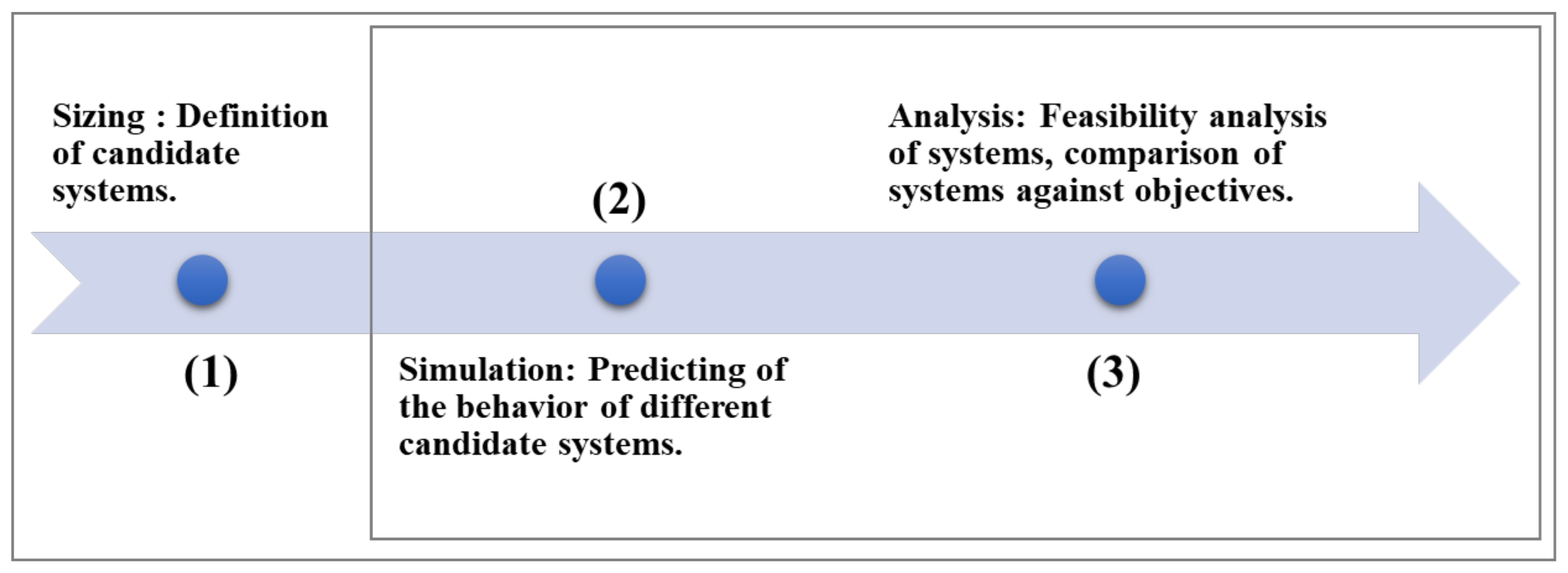
The tool used in our research is a three-part model, as described in Section 2 and illustrated in Figure 1. This tool is both a sizing model [1,6] and a simulation model; that is, it is a model to predict the behavior of a system extracted from the sizing phase, as well as a feasibility analysis tool [27].
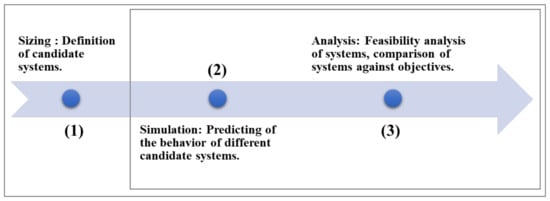
Figure 1.
Key steps of proposed hybrid renewable energy system (HRES) methodology.
A set of feasible systems (phase 1) is proposed based on the defined specifications, including the available installation area, technologies, and existential quantification constraints. These eligible systems are then evaluated one after the other by the tool’s core, which consists of a simulation model (phase 2). This simulation model is a multiple-input, multiple-output (MIMO) black-box model, as it does not present any details of its simulation process. When such a model is used in this context, it is important to remember that we will not have any editing rights, only the right to simulate our system.
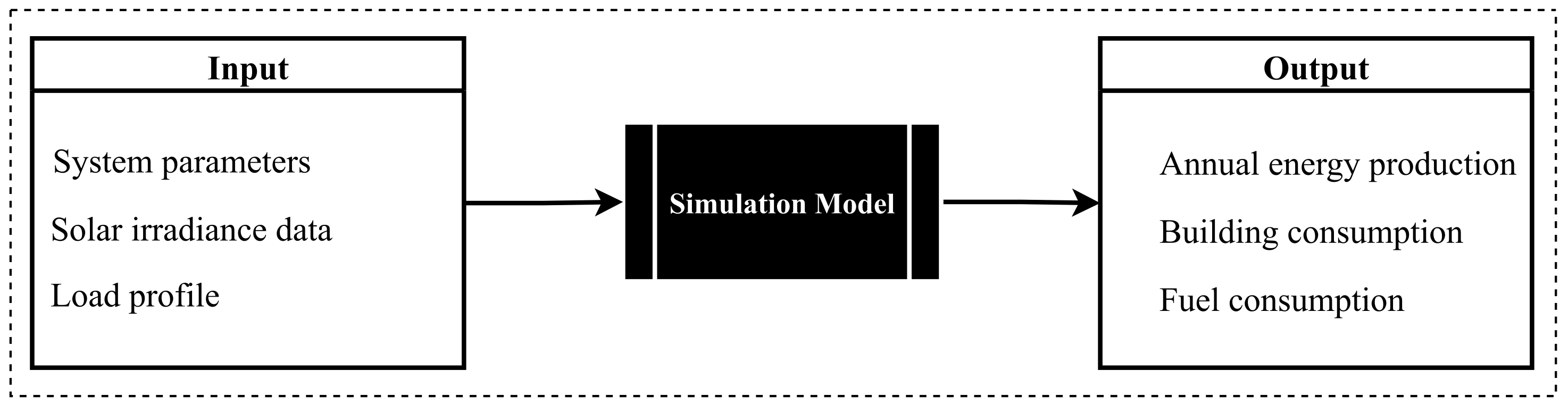
This simulation model, as shown in Figure 2, requires several inputs, which are listed below.
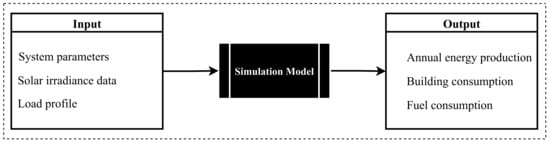
Figure 2.
Energy management process.
- Parameters that define the system to be simulated;
- An energy demand profile;
- Energy pricing;
- Historical solar irradiance data for one year (if evaluating energy production from solar power).
From these inputs, a one-year simulation is run and the outputs listed below are provided.
- Annual energy production;
- Total annual energy consumption;
- Fuel consumption.
Once all these simulations of the system have been completed, we move on to phase 3, in which all simulated systems are evaluated using a decision support method to determine the best system to implement based on pre-defined criteria [4,9,28], such as the items listed below.
- Investment costs;
- System reliability;
- The capital recovery period;
- The greenhouse gas emission rate.
The most expensive phases of this modeling tool are phases 2 and 3, comprising the simulation and feasibility analysis [8]. The search for the best system corresponds to finding as defined by Equation (1):
where g is the fitness function for the feasibility analysis; Y is the set of simulation results of feasible candidate systems produced by the simulation model, defined by the Equation (2); and y is the simulation result for a feasible candidate system.
where A is the simulation model definition matrix and x is the coordinate vector defining the characteristics of the system to be studied.
2.2. Methodology
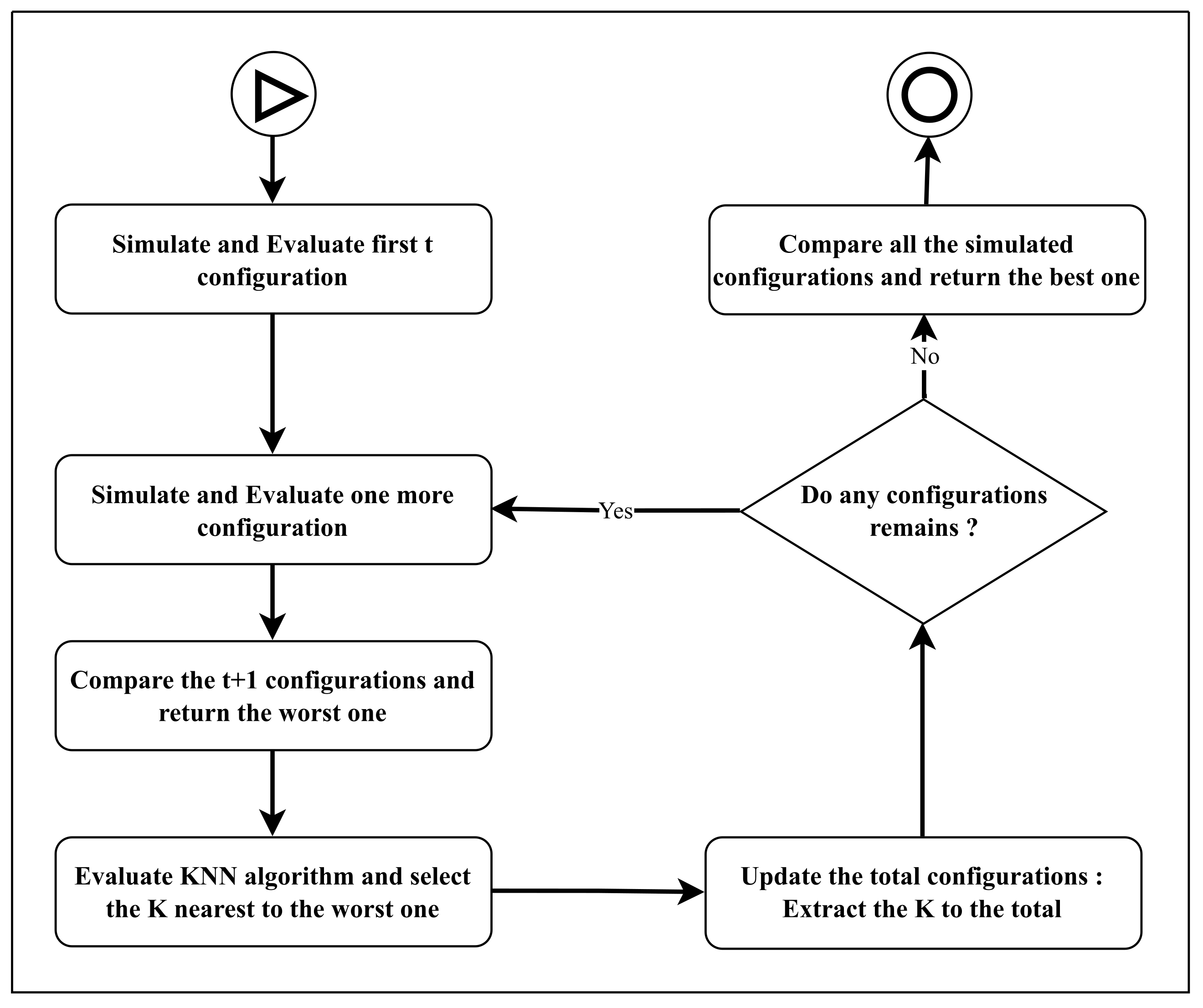
Given the considerable time that such a modeling tool may require, our proposed solution to reduce the waiting time applies to phases 2 and 3 shown in Figure 1. The proposed methodology uses a hybrid method based on the Branch and Bound optimization algorithm (BB) and the k-Nearest Neighbors (kNN) machine learning technique to minimize the simulation and analysis time of the candidate systems. This hybrid methodology takes advantage of the strengths of each of these methods. Applying the Branch and Bound method, we use the conclusions drawn from an initial evaluation of one of the candidate systems to dispense with the evaluation of other candidate systems and reduce the computation time. This process is called the branch pruning of candidate solutions. Given the tool we are studying in this research (i.e., a simulation model), we use the kNN algorithm to select candidate systems belonging to a defined set based on the distance criterion. These sets, defined by the kNN algorithm, represent the branches that will be pruned by the Branch and Bound method. The execution of this methodology requires the definition of a few parameters, as shown in Table 2. Figure 3 presents the sequence of this methodology.

Table 2.
Parameters to be defined in the proposed methodology.
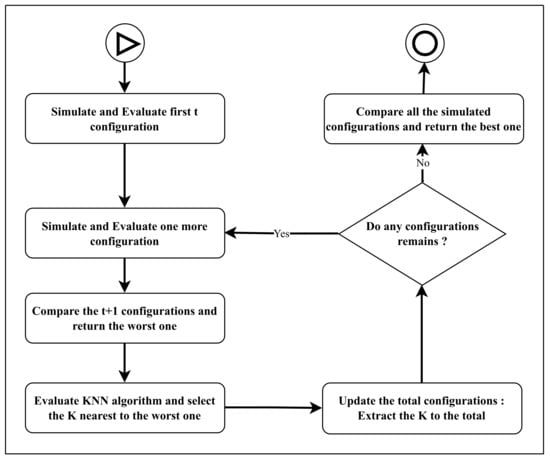
Figure 3.
Process of the proposed methodology.
The proposed methodology is described in detail in the following paragraphs.
First, we define the amount of time (in seconds) that we want to spend for the duration of the simulation or the maximum number of systems to be simulated in the search for the best system. Once the duration has been defined, the algorithm defines the number of configurations evaluated, as shown in Equation (3):
where represents the minimum number of systems to be simulated and is the average simulation time of a system, considering the characteristics of the used hardware. The total number of systems to be simulated during parameter initialization must not exceed :
Next, the process defines several t values for the best-ordered systems to be presented at the end of the process, highlighting the best one to emerge. At the end of this definition, the algorithm evaluates the first t systems utilizing the chosen search strategy. The process utilizes two search strategies: the random search process and the specific subset search process. The random process determines those systems that are simulated randomly, while the subset search process determines those systems with similar traits that are simulated at the same time. For example, systems that use energy storage devices (ESSs) without generators are systems to be analyzed together, and systems with ESSs and with generators will be analyzed together. Then, once the first t systems have been defined, the algorithm simulates another system. With each simulation, the total number of simulated systems is compared. The system with the worst result is passed to the filtering program by the kNN, which returns the branch containing the K systems likely to have the same results such that they can be eliminated. Finally, the algorithm updates the set of candidate systems that have not yet been simulated by eliminating the returned K systems. This process is continuous until no systems are left in the creation stage; that is, the kNN algorithm will have simulated or eliminated all systems. Thus, instead of a user defining the time predicted to be spent waiting for the simulation to finish, the number of systems to be evaluated can be defined, that is, systems. This number must be greater than or equal to and comply with the condition given in Equation (5). Thus, the number of neighboring systems K that will be eliminated by applying the kNN algorithm is defined by Equation (5).
where defines the total number of systems for a given project. This means that the number of systems to prune, K, is specific to each project and the best system is to be determined according to pre-defined constraints. The Branch and Bound method works by defining the branches that do not need to be explored in the search for the best system. Applying the kNN method enables us to eliminate a branch that represents a set of systems with a high probability of encountering the same results as a system which was previously judged to be irrelevant. To verify the results of our methodology, simulation tests with and without the proposed hybrid BB and kNN methodology were carried out for different projects implementing renewable energy hybrid systems.
2.2.1. Branch and Bound Algorithm
The Branch and Bound algorithm is an enumeration-based optimization approach [29]. This method subdivides the main problem into smaller sub-problems, each defining easily controllable search areas. The search is performed in a branch-by-branch manner, and those underlying branches that are not likely to provide better results for the cost function evaluation are pruned. In short, the Branch and Bound optimization algorithm reduces the search space for the best solution in the space of possible solutions that minimizes (or maximizes) a cost function f, as generally used in combinatorial problems (Equation (6)):
This optimization approach defines three essential components: the node, the node branching, and the generation process. The node represents the decision point for dividing a problem (or set) or subproblem (or subset) into subproblems (or search subsets) that are easier to solve. Branching and generating nodes generate all the child nodes that can be derived from a parent node. The Branch and Bound solution search consists of finding the possible set of solutions , which is a subset of X corresponding to a limit function such that the condition in Equation (7) is satisfied:
The major problem faced by this approach is defining the subset and the fitness function that best reduces the search space and computation time. Therefore, we apply the kNN machine learning algorithm to define the subset contained in the set of possible solutions.
2.2.2. k-Nearest Neighbors
The k-Nearest Neighbors (kNN) algorithm is a basic supervised machine learning method [30], which is mainly used for solving classification problems in various fields [31]. The process of the k-Nearest Neighbors (kNN) algorithm involves determining, for a given element or system, k systems with similar features (traits), where k represents an integer value that defines the number of systems with common features that should be considered when applying the algorithm. The kNN algorithm, derived from the Nearest-Neighbor approach [30] for unlabeled data processing problems, is implemented in three steps. First, the algorithm calculates the distances of the input data from the remainder of the available data set. Several distance functions can be applied, including the Euclidean distance (), Manhattan distance (), or the Hamming distance (). Once the various distances have been calculated, the algorithm selects the k systems with the smallest distances to the unlabeled input (the second step). Finally, the majority class among the k selected datasets is assigned to the unlabeled input. The major challenge in applying this algorithm is defining the optimal number of neighbors to be considered [30,32].
For the approach adopted in this study, the kNN algorithm selects the branch of systems to be eliminated, with a maximum of K systems to be eliminated simultaneously.
3. Results and Discussion
In this section, we explore the specific system under study by detailing its components and characteristics and defining the parameters used for modeling and evaluation. The simulation results are presented, and an analytical discussion is conducted to interpret the performance of the proposed methodology. This methodology was implemented using PyCharm, which leverages the Python programming language and its third-party libraries, including Numpy, Pandas, Scikit-Learn, and Scipy. This process facilitated comprehensive system analysis, data manipulation, and algorithm implementation for accurate simulations and robust evaluation.
3.1. Type of System Evaluated
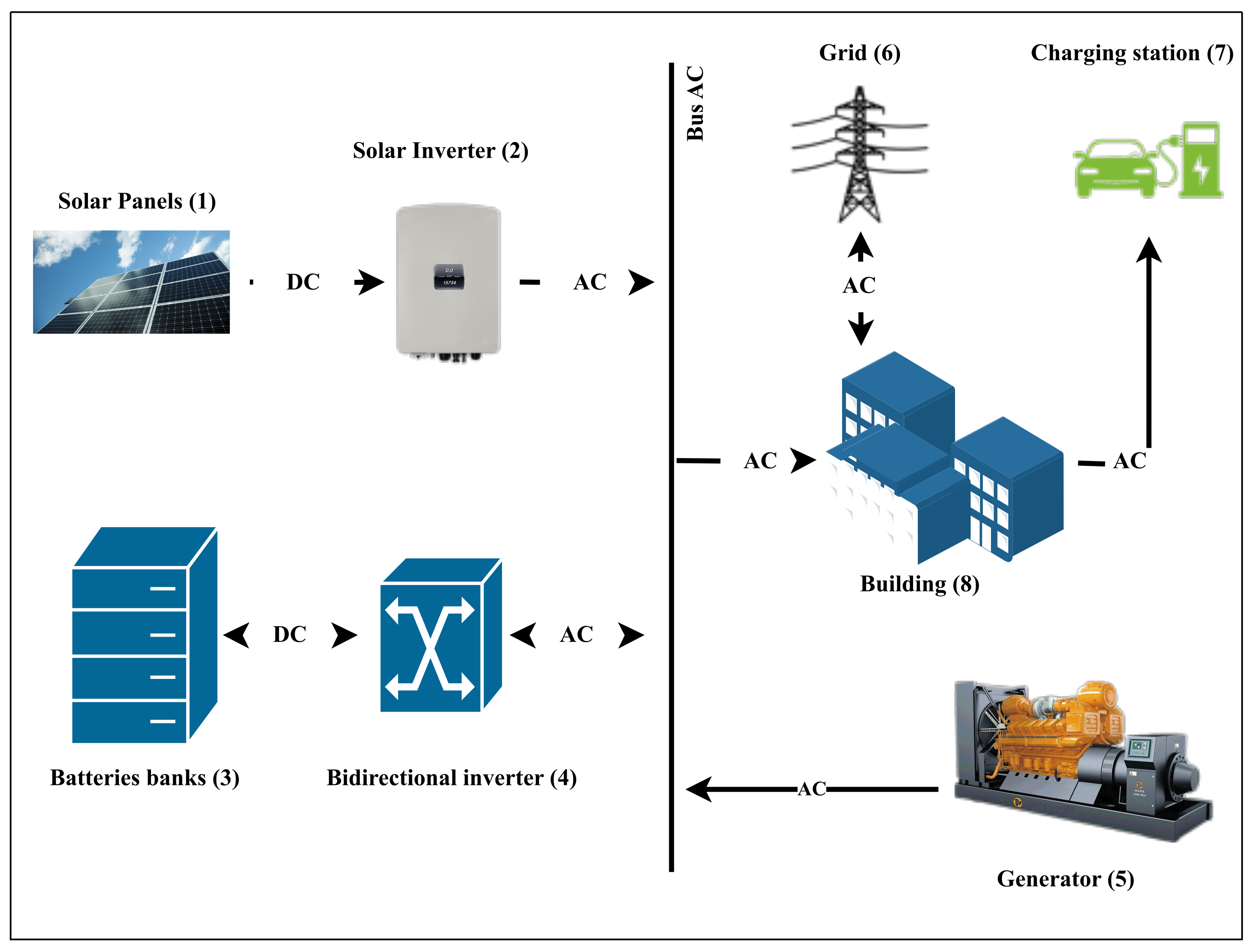
The proposed solution approach considers a series-connected hybrid renewable energy system (HRES) [33,34], as illustrated in Figure 4. One renewable energy generation source, solar, is used (1). The renewable source is supported by a generator (5) for provision of the energy difference between production and demand. In addition, a battery bank (3) is utilized to back up the surplus energy when the energy produced by the solar system exceeds the energy demand, which is the total amount of energy required to operate the loads (7 and 8). In addition, this study considers that, when the production surplus is very large and impossible to conserve, the consumer can inject it into the public grid (6).
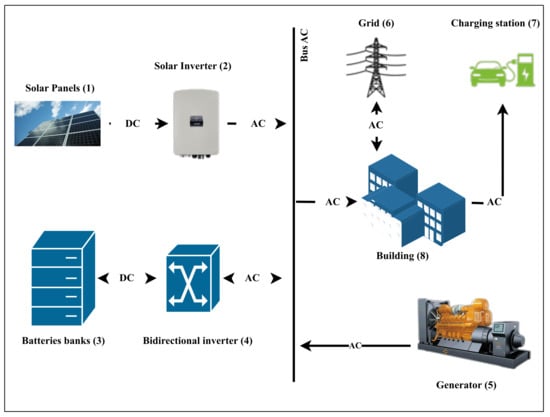
Figure 4.
Schematic of considered hybrid renewable energy system.
The solar inverter (2) in this system transfers electrical energy from the direct current (DC) produced by the solar panels to an alternating current (AC), which can be used directly by the loads. Meanwhile, the bidirectional converter (4) converts surplus energy from alternating current (AC) to direct current (DC), which is suitable for storage in batteries, to conserve it in battery banks in the event of overproduction or converts the energy stored in batteries from direct current (DC) to alternating current (AC) to supply loads in the event of underproduction.
Thousands of candidate systems were generated when this HRES was set up. In the following, we refer to these systems as configurations. A configuration denotes the assignment of specific values to the parameters of the hybrid renewable energy system [35]. These parameters include tilt, azimuth, solar panels, battery storage capacity, generator output, and the number of electric vehicle charging stations installed. Based on the above parameters, we define two configuration examples in Table 3 [10]. To validate our approach, different projects with different numbers of configurations were studied in order to compare the results of this methodology with the traditional approach, which consists of a complete simulation of all configurations before analysis for decision-making.

Table 3.
Example parameter value definitions.
3.2. Parameter Definition
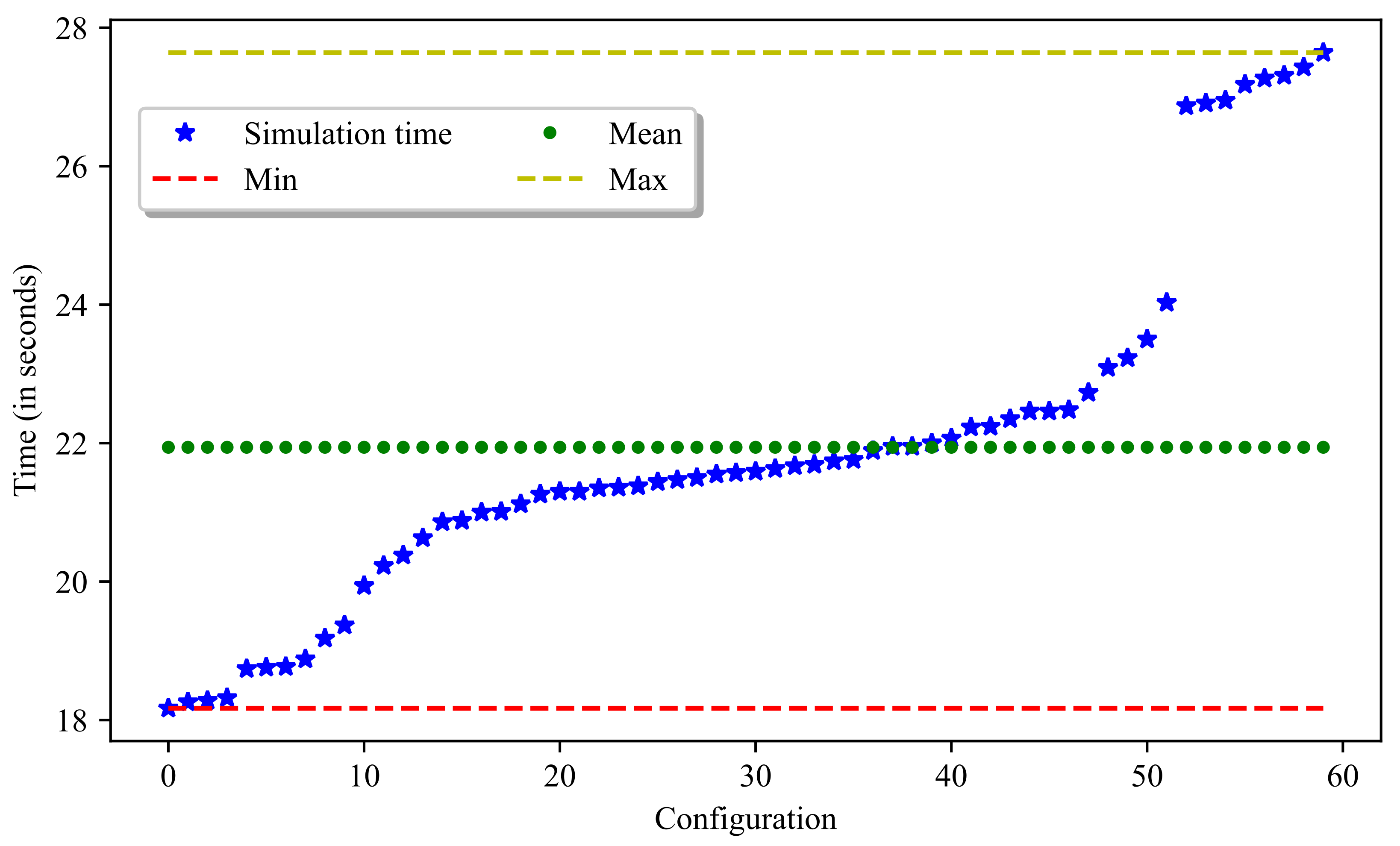
Considering the available computational power—that is, a computer with a 2.8 GHz Intel processor and 16 GB RAM—the first step was to define the average simulation time for a configuration. The time evaluation measure was CPU time. This measure represents the difference between the beginning and the end of the simulation process (i.e., the reception of parameters by the simulation model). For the simulation model considered in this study, the simulation time for 60 configurations was evaluated. The results of this evaluation are shown in Figure 5, with minimum and maximum simulation times of 18.17 and 27.64 s, respectively. This gives us an average time of 21.94 s over 60 configurations, which allowed us to consider an average time of 22 s for the remainder of the work. This means that, for a system whose candidate configuration generation generates 1000 configurations, the average simulation time required is 22,000 s (or 6 h, 6 min, and 40 s). Thus, this study considered the basic parameter definitions listed in Table 4, including the three simulation waiting times of 1 h, 1 h 30 min, and 2 h. The total number of best configurations t that we present at the end of the process is 10.
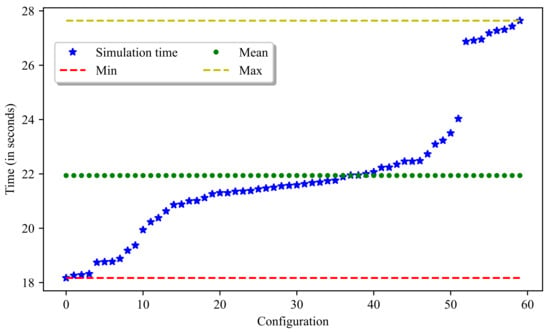
Figure 5.
Simulation times for different numbers of configurations.

Table 4.
Parameter initialization.
In addition, the maximum number of configurations to be simulated was limited to configurations. This limitation strikes a balance between computational constraints and performance, ensuring efficient simulation without compromising the quality of the results. Instead of defining the time we wish to spend searching for the best configuration, we define the minimum number of configurations to simulate as configurations. Finally, to validate the approach, different projects with different numbers of configurations to be evaluated, varying between 330 and 5930 (representing small- to large-scale projects), were evaluated to compare the final solution obtained with the proposed approach with that from the traditional approach. The different projects considered and the number of configurations are shown in Table 5.

Table 5.
Case study projects and their numbers of configurations.
Table 5 presents the four test cases and five parameters evaluated. Considering the different variations in the number of configurations (from 330 to 5930) and the simulation waiting time (from 3600 to 7200 s), the number of configurations to be simulated and the number of configurations to be pruned after the simulation of an additional configuration were determined. In the second step, this research provides in Table 6 the number of configurations needed to simulate and then calculate the number K of configurations to prune. Notably, the number K is specific to each project.

Table 6.
Parameters considered in this study.
3.3. Simulation Results and Discussion
3.3.1. Proposed BB and kNN Results
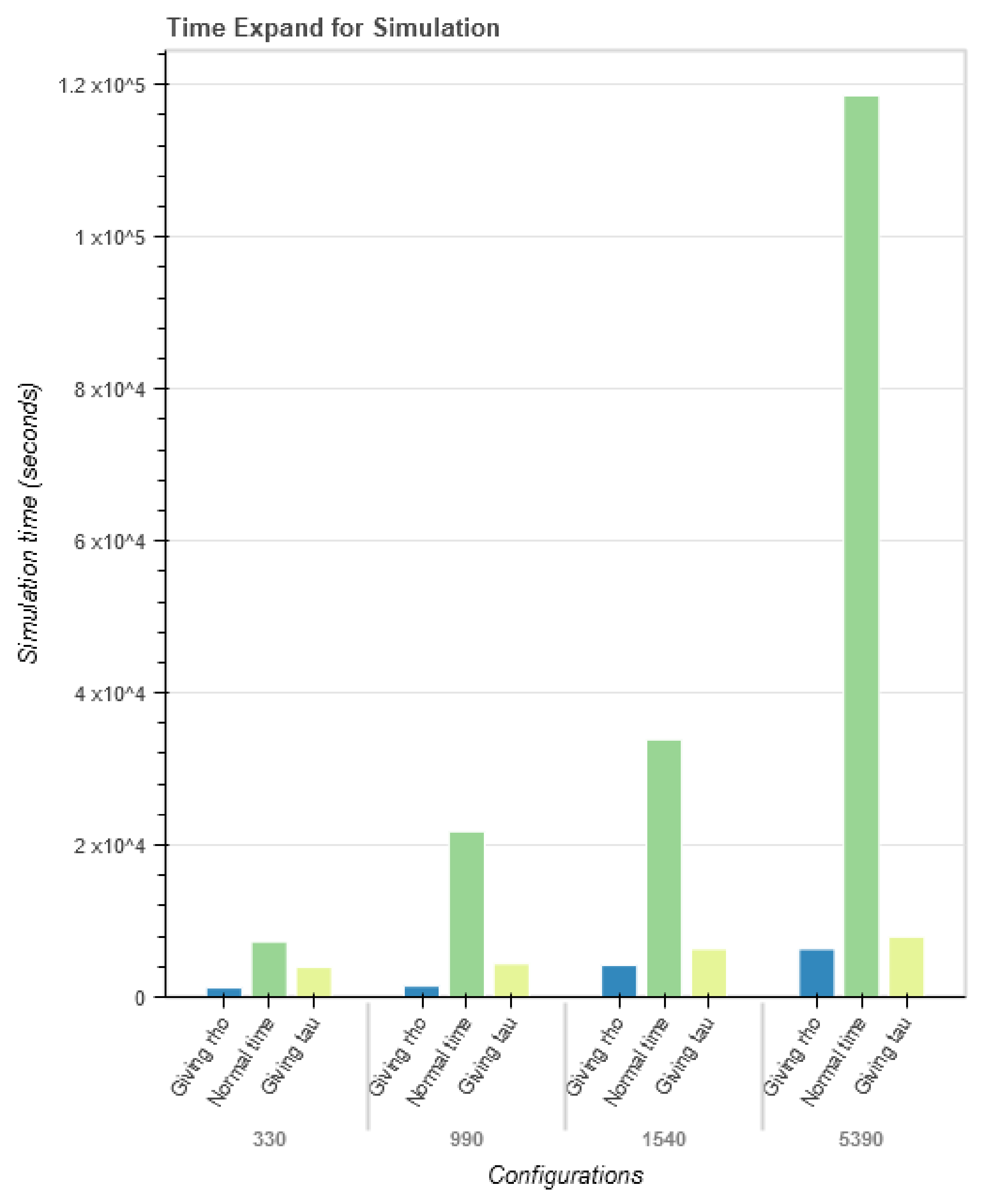
The results of this methodology are presented in Table 7, which shows the simulation time results; these are also visually represented in Figure 6. Both show two projects, each with four different numbers of configurations, defined as and . In this case, the results show almost identical simulation times for projects with 330 and 990 configurations when using our proposed BB and kNN approach. It should be noted that the approach implements a machine learning algorithm—the kNN algorithm—which also incurs a computational time cost. From this result, the conclusion was that, even though the proposed approach incorporates an algorithm that requires computations for each pass, the computation time decreases as the simulation process progresses and the final simulation time remained relatively short, compared to the traditional simulation approach. Applying this methodology allows the best configurations to be obtained without running all of the configurations through the simulation process, thereby considerably reducing the time required to select the best configuration.

Table 7.
Simulation time results.
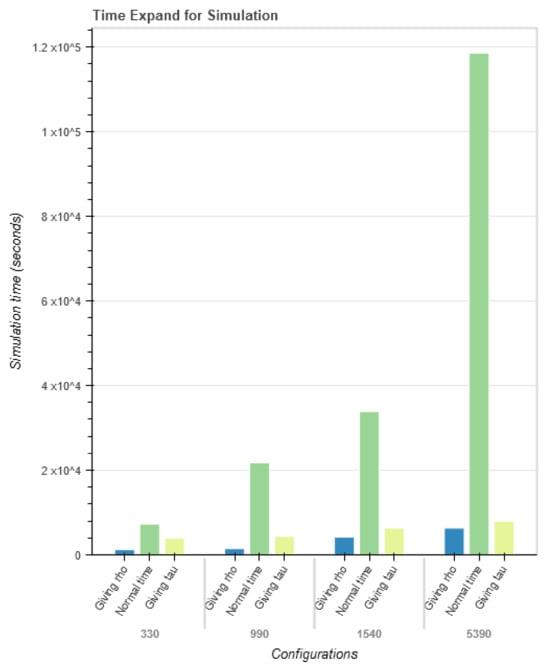
Figure 6.
Simulations time by method and number of configurations.
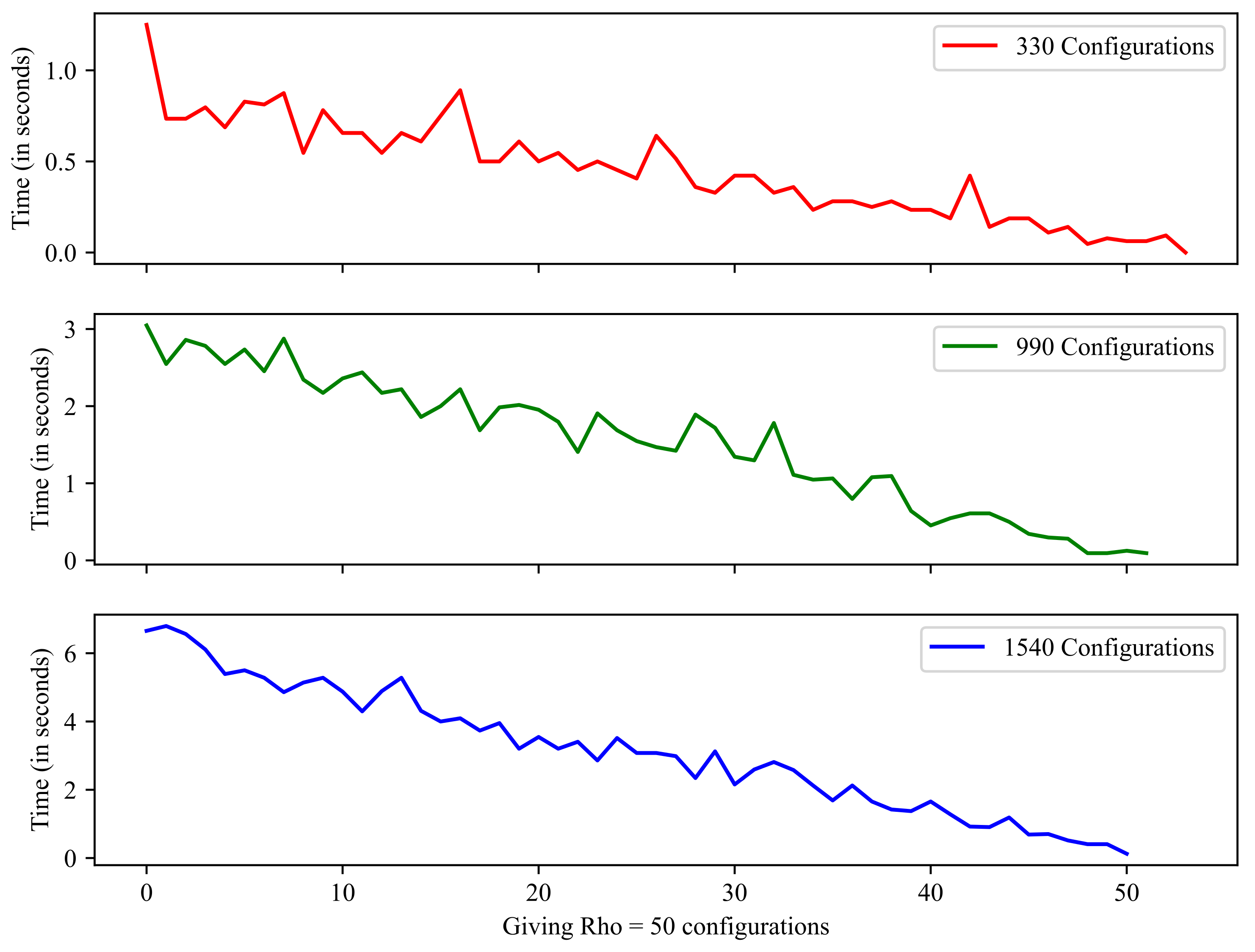
The computation time of the kNN algorithm was evaluated for three types of project—namely, with 330, 990, and 1540 configurations—considering the values and configurations. Figure 7 shows the evolution of the CPU execution time of the kNN algorithm for these three projects. As shown in Figure 7, the calculation time decreased over time as each time the algorithm is run, and the number of configurations that must be run is reduced by .
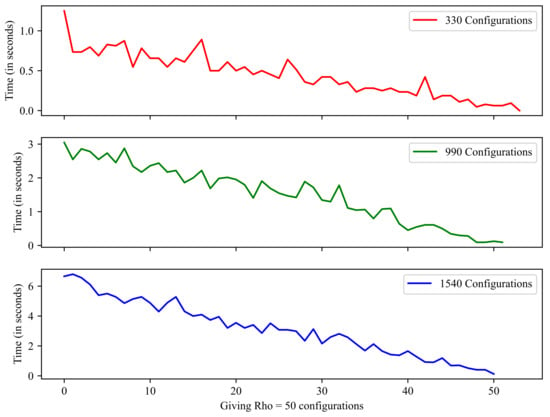
Figure 7.
kNN processing time depending on the number of configurations.
As can be seen from the results in Table 7, considering the two projects with 330 and 990 configurations, which would require 7260 s and 21,780 s, respectively, with the traditional approach and an average simulation time of 22 s, the results showed very similar search times for the best configuration. For a value of , the times obtained with the proposed approach were 1214.4219 and 1442.7969 s, respectively, for these two projects. With a value of s, the simulation obtained times of 3931.0156 and 4380.7812 s, respectively, for the same two projects.
3.3.2. Comparing the Proposed BB and kNN Approach with the Traditional Process
Applying the proposed hybrid Branch and Bound and kNN method considerably reduced the time needed to find the best configuration. Depending on the method chosen—that is, the definition of waiting time or the number of minimum configurations to be simulated—the percentage time reduction increases with the size of the project. Table 7 shows that the minimum and maximum reduction rates when the waiting time was set to s were 45.85% and 93.30%, respectively. The minimum and maximum rates were 83.27% and 94.68% for the number of configurations .
The proposed methodology was applied by random selection on the first two projects and by specific area selection on the last two projects. Comparing the best configuration score obtained with the proposed approach with that of the traditional method yielded the score accuracies listed in Table 8. The accuracy was measured by comparing the overlap of configurations selected by the proposed and traditional methods. The evaluation shows that the number of simulated configurations impacts the accuracy of the result when compared to the traditional method; namely, the greater the time reduction, the lower the precision. However, it is important to note that the very worst loss obtained was 16.73%, which is very important regarding the research time incurred. When applied to the simulation of hybrid renewable energy system configurations, this approach means that the best configuration can always be achieved while reducing the required time. In addition, the hybrid Branch and Bound and kNN method is versatile and can be adapted to other systems, such as those including fuel cells, with minor modifications to the simulation parameters.

Table 8.
Percentage time reduction using the proposed BB and kNN method.
4. Conclusions
The effective deployment of hybrid renewable energy systems hinges on the identification of a well-defined optimal system configuration. This process typically involves extensive and resource-intensive simulations due to the vast number of potential configurations. Our study presented a hybrid methodology that combines the Branch and Bound (BB) heuristic with the k-Nearest Neighbors (KNN) algorithm to significantly reduce the computational time required for selecting the best HRES configuration. Through implementing a continuous pruning process, our approach efficiently narrows down the configuration space, retaining only those sets with similar characteristics. When applied to four case studies, the proposed method demonstrated a substantial decrease in simulation time—up to 94.68%—while preserving acceptable accuracy. For instance, simulation times were reduced from 21,780 and 118,580 s to 1442.7969 and 6306.0625 s in two projects with differing energy demand profiles. This efficiency gain not only accelerates the selection process but also enhances the feasibility of using simulation tools in real-world scenarios where time and resources are constrained. In conclusion, the integration of the BB and kNN algorithms provides a robust framework for optimizing simulation times in HRES design, offering a significant improvement over traditional methods. Future research could extend this methodology to other domains requiring rapid simulation and optimization, as well as explore the dynamic adaptation of the kNN algorithm to better handle evolving configuration parameters. This advancement paves the way for more efficient and scalable approaches in the design and deployment of hybrid renewable energy systems, ultimately contributing to a more sustainable energy landscape.
Author Contributions
Conceptualization, I.L., T.W., N.M. and L.-A.D.; methodology, I.L., T.W., N.M. and L.-A.D.; software, I.L. and N.M.; validation, I.L., T.W., N.M. and L.-A.D.; formal analysis, I.L., T.W., N.M. and L.-A.D.; investigation, I.L.; resources, I.L., T.W. and L.-A.D.; data curation, I.L.; writing—original draft preparation, I.L.; writing—review and editing, T.W., N.M. and L.-A.D.; visualization, I.L.; supervision, T.W. and L.-A.D.; project administration, T.W. and L.-A.D.; funding acquisition, T.W. and L.-A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Natural Sciences and Engineering Research Council of Canada and by Innovee Québec.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kavadias, K.A.; Triantafyllou, P. Hybrid Renewable Energy Systems’ Optimisation. A Review and Extended Comparison of the Most-Used Software Tools. Energies 2021, 14, 8268. [Google Scholar] [CrossRef]
- Alluraiah, N.C.; Vijayapriya, P. Optimization, Design, and Feasibility Analysis of a Grid-Integrated Hybrid AC/DC Microgrid System for Rural Electrification. IEEE Access 2023, 11, 67013–67029. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Cao, Y.; Ma, R.; Wang, Y.; Li, C.; Liu, R.; Zou, S. Renewable Scenario Generation Based on the Hybrid Genetic Algorithm with Variable Chromosome Length. Energies 2023, 16, 3180. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Samu, R.; Taylan, O.; Fahrioglu, M. Sizing renewable energy systems with energy storage systems in microgrids for maximum cost-efficient utilization of renewable energy resources. Sustain. Cities Soc. 2020, 55, 102059. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, J.; Liu, Y.; Yao, L.; Wang, Y.; Wang, C.; Pei, S.; Zhou, J. Short-term optimal operation of wind-solar-hydro hybrid system considering uncertainties. Energy Convers. Manag. 2020, 205, 112405. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Bahgaat, N.K. Estimation of renewable energy systems for mobile network based on real measurements using HOMER software in Egypt. Sci. Rep. 2023, 13, 16713. [Google Scholar] [CrossRef]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-objective optimal design of stand-alone hybrid energy system using entropy weight method based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef]
- Mansouri Kouhestani, F.; Byrne, J.; Johnson, D.; Spencer, L.; Brown, B.; Hazendonk, P.; Scott, J. Multi-criteria PSO-based optimal design of grid-connected hybrid renewable energy systems. Int. J. Green Energy 2020, 17, 617–631. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. PSO-based smart grid application for sizing and optimization of hybrid renewable energy systems. PLoS ONE 2016, 11, e0159702. [Google Scholar] [CrossRef]
- Javed, M.S.; Ma, T.; Jurasz, J.; Mikulik, J. A hybrid method for scenario-based techno-economic-environmental analysis of off-grid renewable energy systems. Renew. Sustain. Energy Rev. 2021, 139, 110725. [Google Scholar] [CrossRef]
- Rtemi, L.A.; El-Osta, W.; Attaiep, A. Hybrid System Modeling for Renewable Energy Sources. Sol. Energy Sustain. Dev. J. 2023, 12. [Google Scholar] [CrossRef]
- Awan, A.B.; Zubair, M.; Sidhu, G.A.S.; Bhatti, A.R.; Abo-Khalil, A.G. Performance analysis of various hybrid renewable energy systems using battery, hydrogen, and pumped hydro-based storage units. Int. J. Energy Res. 2018, 43, 6296–6321. [Google Scholar] [CrossRef]
- Elkadeem, M.R.; Kotb, K.M.; Elmaadawy, K.; Ullah, Z.; Elmolla, E.; Liu, B.; Wang, S.; Dán, A.; Sharshir, S.W. Feasibility analysis and optimization of an energy-water-heat nexus supplied by an autonomous hybrid renewable power generation system: An empirical study on airport facilities. Desalination 2021, 504, 114952. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Tooryan, F.; Dargahi, V.; Jin, S. A cost-efficient sizing of grid-tied hybrid renewable energy system with different types of demands. Sustain. Cities Soc. 2021, 73, 103080. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Reliability/cost-based multi-objective Pareto optimal design of stand-alone wind/PV/FC generation microgrid system. Energy 2016, 115, 1022–1041. [Google Scholar] [CrossRef]
- Tounsi, S. Model of wind energy system with reduced simulation time validated by classical equivalent model developed under Simulink. Wind Eng. 2022, 46, 1011–1033. [Google Scholar] [CrossRef]
- Aranguren, C. Reducing Simulation Time in a Huff-And-Puff Gas Injection Project in Complex Shale Reservoirs: Sequence-Based Proxy Multi-Porosity Reservoir Simulator. In Proceedings of the SPE Canadian Energy Technology Conference and Exhibition, Calgary, AB, Canada, 15–16 March 2023. [Google Scholar]
- Banihashemi, F.; Weber, M.; Lang, W. Model order reduction of building energy simulation models using a convolutional neural network autoencoder. Build. Environ. 2022, 207, 108498. [Google Scholar] [CrossRef]
- Mange, J.; Skowronska, A.G. Autonomy and mobility simulation time reduction through machine learning while considering uncertainty and reliability prediction. Opt. Eng. 2023, 62, 031214. [Google Scholar] [CrossRef]
- Martínez-Turégano, J.; Añó-Villalba, S.; Bernal-Perez, S.; Blasco-Gimenez, R. Aggregation of Type-4 Large Wind Farms Based on Admittance Model Order Reduction. Energies 2019, 12, 1730. [Google Scholar] [CrossRef]
- Dou, Z.; Qian, J.; Li, Y.; Lin, R.; Wang, J.; Cheng, P.; Xu, Z. Reducing molecular simulation time for AFM images based on super-resolution methods. Beilstein J. Nanotechnol. 2021, 12, 775–785. [Google Scholar] [CrossRef] [PubMed]
- Saxena, V.; Kumar, N.; Manna, S.; Rajput, S.K.; Agarwal, K.L.; Diwania, S.; Gupta, V. Modelling, solution and application of optimization techniques in HRES: From conventional to artificial intelligence. Appl. Energy 2025, 380, 125047. [Google Scholar] [CrossRef]
- Sousa Junior, W.T.d.; Montevechi, J.A.B.; Miranda, R.d.C.; Oliveira, M.L.M.d.; Campos, A.T. Shop floor simulation optimization using machine learning to improve parallel metaheuristics. Expert Syst. Appl. 2020, 150, 113272. [Google Scholar] [CrossRef]
- Sampat, C.; Baranwal, Y.; Ramachandran, R. Accelerating multi-dimensional population balance model simulations via a highly scalable framework using GPUs. Comput. Chem. Eng. 2020, 140, 106935. [Google Scholar] [CrossRef]
- Zhaoqian, Z.; Edahiro, M. Model-based Parallelization for Simulink Models on Multicore CPUs and GPUs. In Proceedings of the 2019 International SoC Design Conference (ISOCC), Jeju, Republic of Korea, 6–9 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 103–104. [Google Scholar] [CrossRef]
- Khan, M.Y.; Ali, M.; Qaisar, S.; Naeem, M.; Chrysostomou, C.; Iqbal, M. Placement Optimization for Renewable Energy Sources: Ontology, Tools, and Wake Models. IEEE Access 2020, 8, 72781–72800. [Google Scholar] [CrossRef]
- Tabak, A.; Özkaymak, M.; Güneser, M.T.; Erkol, H.O. Optimization and evaluation of hybrid PV/WT/BM system in different initial costs and LPSP conditions. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 123–131. [Google Scholar] [CrossRef]
- Watanabe, A.; Tamura, R.; Takano, Y.; Miyashiro, R. Branch-and-bound algorithm for optimal sparse canonical correlation analysis. Expert Syst. Appl. 2023, 217, 119530. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient kNN classification with different numbers of nearest neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef] [PubMed]
- Mladenova, T.; Valova, I. Classification with K-Nearest Neighbors Algorithm: Comparative Analysis between the Manual and Automatic Methods for K-Selection. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 396–404. [Google Scholar] [CrossRef]
- Kumar, V.; Sahu, M. Evaluation of nine machine learning regression algorithms for calibration of low-cost PM2. 5 sensor. J. Aerosol Sci. 2021, 157, 105809. [Google Scholar] [CrossRef]
- Gourbi, A.; Bousmaha, I.; Brahami, M.; Tilmatine, A. Numerical Study of a Hybrid Photovoltaic Power Supply System. J. Power Technol. 2016, 96, 137–144. [Google Scholar]
- Jacob, E.; Farzaneh, H. Dynamic modeling and experimental validation of a standalone hybrid microgrid system in Fukuoka, Japan. Energy Convers. Manag. 2022, 274, 116462. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Shamma’a, A.A. Optimal configuration for isolated hybrid renewable energy systems. J. Renew. Sustain. Energy 2016, 8, 045502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).