AGTM Optimization Technique for Multi-Model Fractional-Order Controls of Spherical Tanks
Abstract
1. Introduction
2. Experimental Modelization
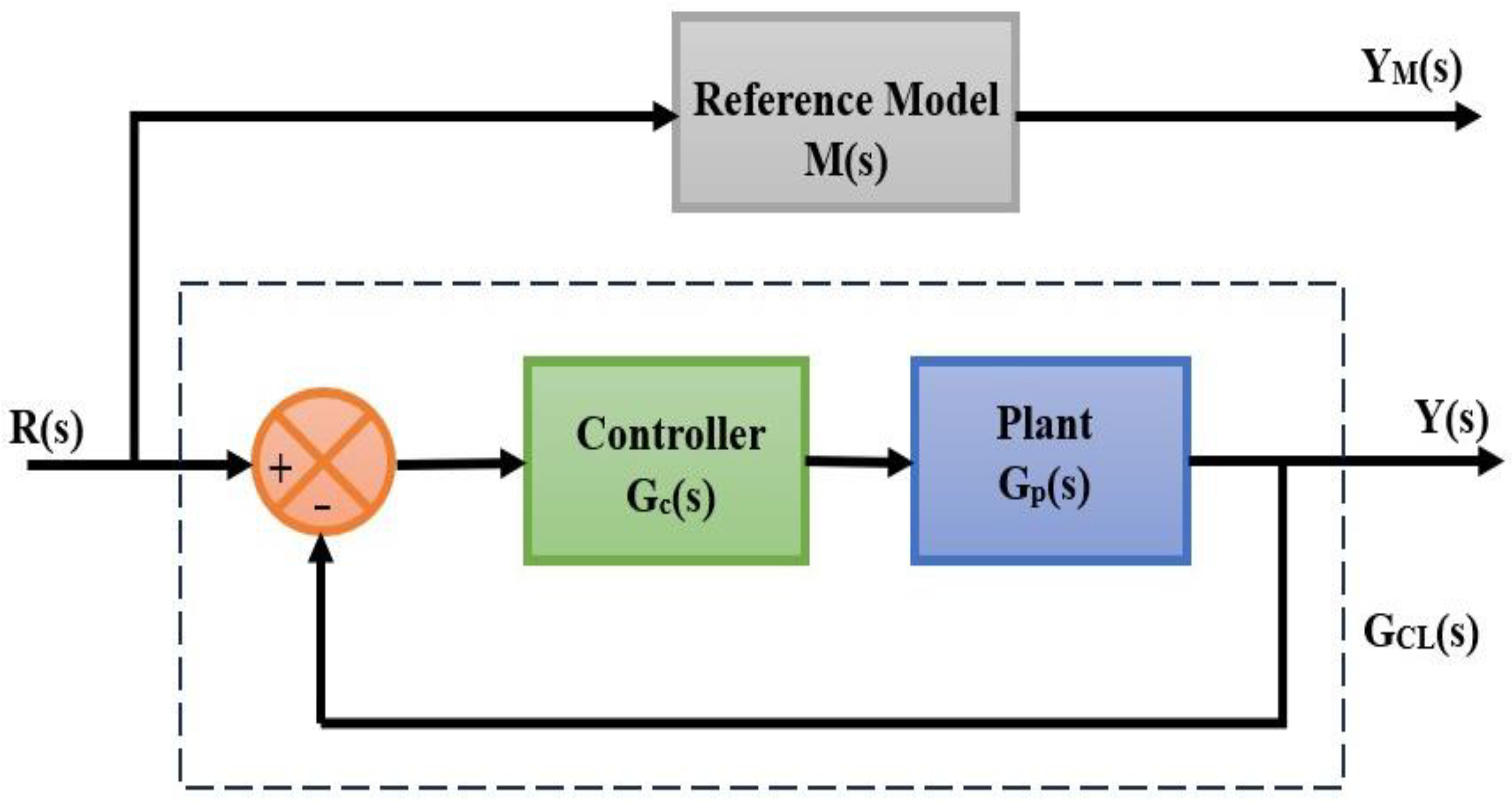
3. Multi-Model Control Design
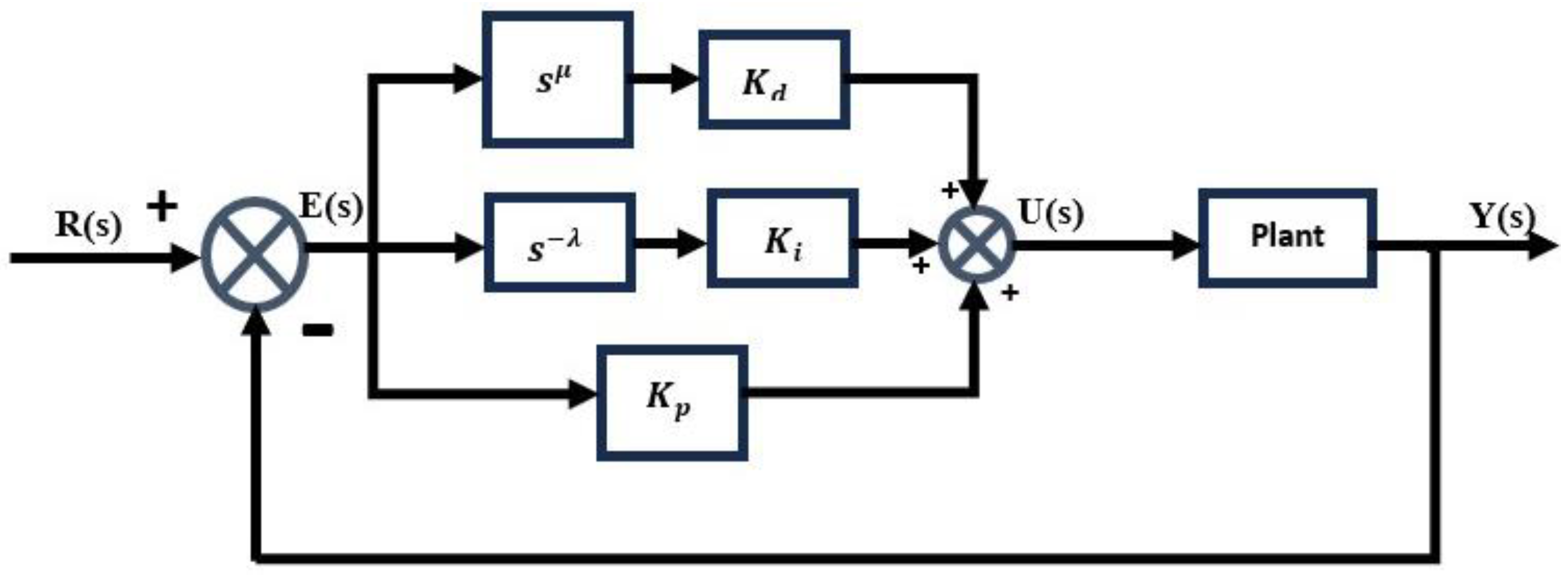
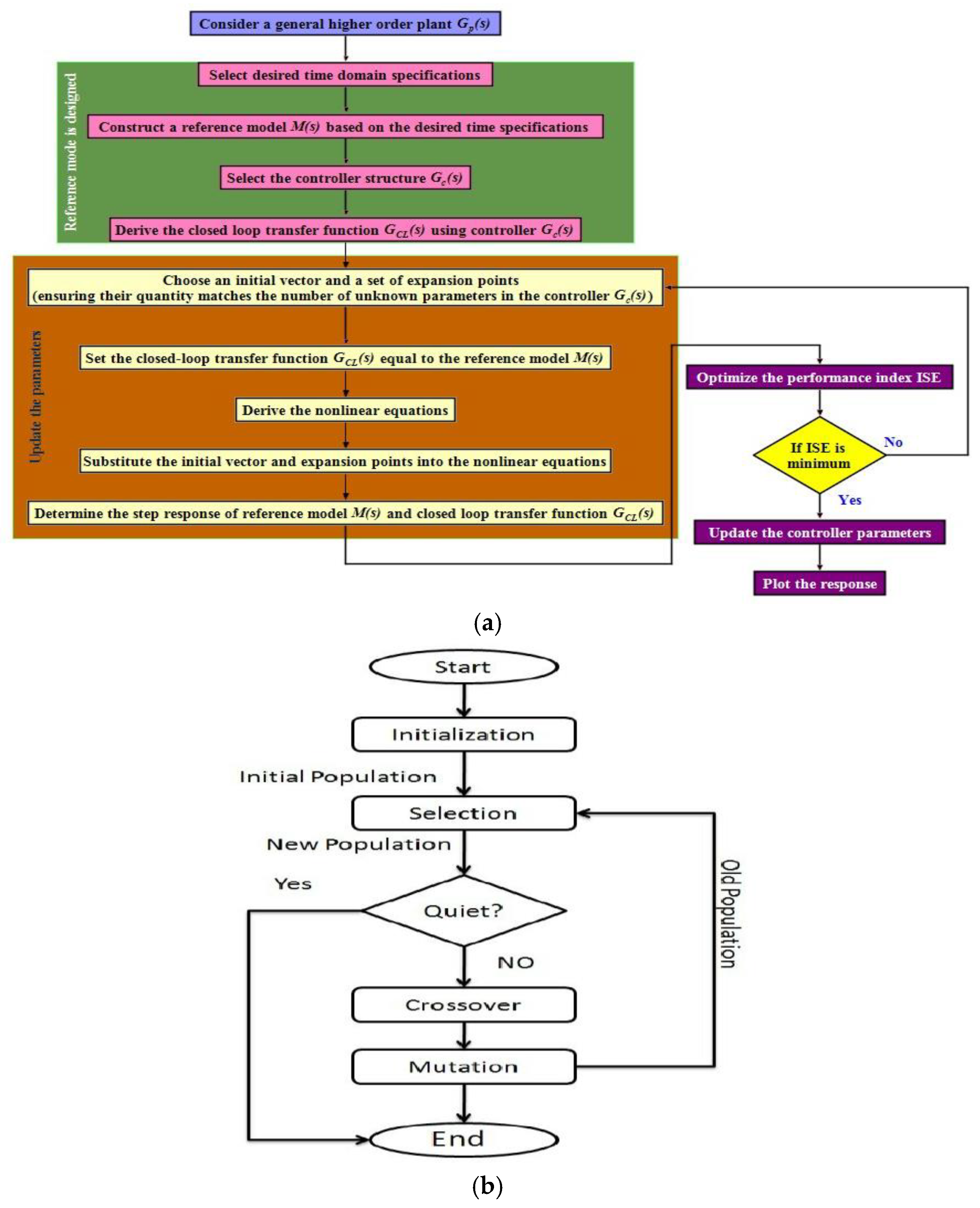
4. Approximate Generalized Time Moments (AGTM) Optimization Technique
5. Simulation and Experimental Results
5.1. Simulation Results
5.2. Comparative Experimental Results
5.2.1. Setpoint Variations
5.2.2. Load Variations
5.3. Single-Model vs. Multi-Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakravarthi, M.K.; Venkatesan, N. Experimental Validation of a Multi-Model PI Controller for a Non-Linear Hybrid System in LabVIEW. TELKOMNIKA 2015, 13, 547–555. [Google Scholar] [CrossRef]
- Zeigler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Zhuang, M.; Atherton, D.P. Automatic tuning of optimum PID controllers. Proc. IEEE 1993, 140, 216–224. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering. Begell House 2004, 32. [Google Scholar] [CrossRef]
- Debnath, L. A brief historical introduction to fractional calculus. Int. J. Math. Educ. Sci. Technol. 2004, 35, 487–501. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Chen, Y.Q. Lecture Notes on Fractional Calculus Applications in Automatic Control and Robotics. In Proceedings of the 41st IEEE CDC2002 Tutorial Workshop, Las Vegas, NV, USA, 10–13 December 2002; pp. 1–310. [Google Scholar]
- Xue, D.; Chen, Y. A comparative introduction of four fractional order controllers. In Proceedings of the 4th IEEE World Congress on Intelligent Control and Automation (WCICA02), Shanghai, China, 10–14 June 2002; pp. 3228–3235. [Google Scholar] [CrossRef]
- Chen, Y. Ubiquitous fractional order controls. In Proceedings of the Second IFAC Symposium on Fractional Derivatives and Applications (IFAC FDA06, Plenary Paper), Porto, Portugal, 19–21 July 2006; pp. 19–21. [Google Scholar] [CrossRef]
- Xue, D.; Zhao, C.; Chen, Y. Fractional order PID control of a DC-motor with an elastic shaft: A case study. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 3182–3187. [Google Scholar] [CrossRef]
- Manabe, S. The non-integer integral and its application to control systems. Jpn. Inst. Electr. Eng. J. 1960, 80, 589–597. [Google Scholar] [CrossRef]
- Oustaloup, A. Linear feedback control systems of fractional order between 1 and 2. In Proceedings of the IEEE Symposium on Circuit and Systems, Chicago, IL, USA, 27–29 April 1981. [Google Scholar]
- Axtell, M.; Bise, M.E. Fractional calculus applications in control systems. In Proceedings of the IEEE 1990 National Aerospace and Electronics Conference, New York, NY, USA, 21–25 May 1990; pp. 563–566. [Google Scholar] [CrossRef]
- José, A. Tenreiro Machado Analysis and design of fractional-order digital control systems. J. Syst. Anal. Model. Simul. 1997, 27, 107–122. [Google Scholar]
- José, A. Tenreiro Machado Special Issue on Fractional Calculus and Applications. Nonlinear Dyn. 2002, 29, 1–385. [Google Scholar]
- Ortigueira, M.D.; Machado, J.A.T. Special Issue on Fractional Signal Processing and Applications. Signal Process. 2003, 83, 2285–2480. [Google Scholar] [CrossRef]
- Ashwini, A.; Sriram, S.R.; Joel Livin, A. Quadruple spherical tank systems with automatic level control applications using fuzzy deep neural sliding mode FOPID controller. J. Eng. Res. 2023. [Google Scholar] [CrossRef]
- Jegatheesha, A.; Agees Kumar, C. Novel fuzzy fractional order PID controller for nonlinear interacting coupled spherical tank system for level process. Microprocess. Microsyst. 2020, 72, 102948. [Google Scholar] [CrossRef]
- Arivalahan, R.; Tamilarasan, P.; Kamalakannan, M. Liquid level control in two tanks spherical interacting system with fractional order proportional integral derivative controller using hybrid technique: A hybrid technique. Adv. Eng. Softw. 2023, 175, 103316. [Google Scholar] [CrossRef]
- Debnath, B.; Mija, S.J. Emotional Learning Based Controller for Quadruple Tank System—An Improved Stimuli Design for Multiple Set-Point Tracking. IEEE Trans. Ind. Electron. 2021, 68, 11296–11308. [Google Scholar] [CrossRef]
- Jáuregui, C.; Duarte, M.A.; Oróstica, R.; Travieso, J.C.; Beytía, O. Conical Tank Level Control with Fractional PID. IEEE Lat. Am. Trans. 2016, 14, 2598–2604. [Google Scholar] [CrossRef]
- Meng, X.; Yu, H.; Zhang, J.; Xu, T.; Wu, H.; Yan, K. Disturbance Observer-Based Feedback Linearization Control for a Quadruple-Tank Liquid Level System. ISA Trans. 2022, 122, 146–162. [Google Scholar] [CrossRef] [PubMed]
- Huo, M.; Luo, H.; Wang, X.; Yang, Z.; Kaynak, O. Real-Time Implementation of Plug-and-Play Process Monitoring and Control on an Experimental Three-Tank System. IEEE Trans. Ind. Inform. 2021, 17, 6448–6456. [Google Scholar] [CrossRef]
- Das, D.; Chakraborty, S.; Mehta, U.; Raja, L.G. Fractional Dual-Tilt Control Scheme for Integrating Time Delay Processes: Studied on a Two-Tank Level System. IEEE Access 2024, 12, 7479–7489. [Google Scholar] [CrossRef]
- Xu, T.; Yu, H.; Yu, J.; Meng, X. Adaptive Disturbance Attenuation Control of Two Tank Liquid Level System With Uncertain Parameters Based on Port-Controlled Hamiltonian. IEEE Access 2020, 8, 47384–47392. [Google Scholar] [CrossRef]
- Fu, Y.; Du, Q.; Zhou, X.J.; Fu, J.; Chai, T.Y. Dual-Rate Adaptive Decoupling Controller and Its Application to a Dual-Tank Water System. IEEE Trans. Control Syst. Technol. 2020, 28, 2515–2522. [Google Scholar] [CrossRef]
- Bhookya, J.; Kumar, V.M.; Ravi Kumar, J.; Seshagiri, R. A Implementation of PID controller for liquid level system using mGWO and integration of IoT application. J. Ind. Inf. Integr. 2022, 28, 100368. [Google Scholar] [CrossRef]
- Reddy, S.A.; Reddy, N.G. An adaptive fractional order controller design: A realization for liquid level regulation in liquid level plant. Meas. Sens. 2024, 31, 100977. [Google Scholar] [CrossRef]
- Wang, G.; Jia, Q.-S.; Qiao, J.; Bi, J.; Zhou, M. Deep Learning-Based Model Predictive Control for Continuous Stirred-Tank Reactor System. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3643–3652. [Google Scholar] [CrossRef]
- Matušů, R.; Şenol, B.; Pekař, L. Robust PI Control of Interval Plants With Gain and Phase Margin Specifications: Application to a Continuous Stirred Tank Reactor. IEEE Access 2020, 8, 145372–145380. [Google Scholar] [CrossRef]
- Alshammari, O.; Mahyuddin, M.N.; Jerbi, H. An Advanced PID Based Control Technique With Adaptive Parameter Scheduling for A Nonlinear CSTR Plant. IEEE Access 2019, 7, 158085–158094. [Google Scholar] [CrossRef]
- Chakravarthi, K.M.; Venkatesan, N. Design and Implementation of Adaptive Model Based Gain Scheduled Controller for a Real-Time Nonlinear System in LabVIEW. Res. J. Appl. Sci. Eng. Technol. 2015, 10, 188–196. [Google Scholar] [CrossRef]
- Joshi, S.M.; Tao, G.; Patre, P. Direct adaptive control using an adaptive reference model. Int. J. Control 2011, 84, 180196. [Google Scholar] [CrossRef]
- Bentayeb, A.; Maamri, N.; Trigeassou, J.-C. Design of PID controllers for delayed MIMO plants using the moments-based approach. J. Electr. Eng. 2006, 57, 318–328. [Google Scholar]
- Damodaran, S.; Kumar, T.S.; Sudheer, A.P. Design and implementation of GA tuned PID controller for desired interaction and trajectory tracking of a wheeled mobile robot. In Proceedings of the 2017 3rd International Conference on Advances in Robotics, New Delhi, India, 28 June–2 July 2017. [Google Scholar] [CrossRef]
- Yakoub, Z.; Chetoui, M.; Amairi, M.; Aoun, M. Model-based fractional order controller design. IFAC-Pap. 2017, 50, 1043110436. [Google Scholar] [CrossRef]
- Quinn, S.B.; Sanathanan, C.K. Model matching control for multivariable systems I. Stable plants. J. Frankl. Inst. 1990, 327, 699712. [Google Scholar] [CrossRef]
- Quinn, S.B.; Sanathanan, C.K. Model matching control for multivariable systems II. Unstable plants. J. Frankl. Inst. 1990, 327, 713729. [Google Scholar] [CrossRef]
- Szita, G.; Sanathanan, C.K. A model matching approach for designing decentralized MIMO controllers. J. Frankl. Inst. 2000, 337, 641660. [Google Scholar] [CrossRef]
- Szita, G.; Sanathanan, C.K. Model matching controller design for disturbance rejection. J. Frankl. Inst. 1996, 333, 747772. [Google Scholar] [CrossRef]
- Das, S.K.; Pota, H.R.; Petersen, I.R. Multivariable negative imaginary controller design for damping and cross-coupling reduction of nanopositioners: A reference model matching approach. IEEE/ASME Trans. Mechatron. 2015, 20, 31233134. [Google Scholar] [CrossRef]
- Mittal, S.K.; Chandra, D.; Dwivedi, B. The effects of time moments and Markov-parameters on reduced-order modeling. ARPN J. Eng. Appl. Sci. 2009, 4, 8–14. [Google Scholar]
- Dey, S.; Kumar, T.S.; Ashok, S.; Shome, S.K. Robust cascade control strategy for trajectory tracking to decouple disturbances using 3-degree-of-freedom inertial stabilized platform and its experimental validation. Trans. Inst. Meas. Control. 2023, 20, 01423312221150290. [Google Scholar] [CrossRef]
- Jayaram, S.; Venkatesan, N. Research on Fractional-Order Controllers for Liquid Level Control of Nonlinear System Using Optimization Technique. In Proceedings of the IEEE 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; pp. 403–408. [Google Scholar] [CrossRef]
- Pal, J. An algorithm method for the simplification of linear dynamic scalar systems. Int. J. Control 1986, 43, 257–269. [Google Scholar] [CrossRef]
- Beevi, F.P.; Kumar, T.S.; Jacob, J. Two degree of freedom controller design by AGTM/AGMP matching method for time delay systems. Procedia Technol. 2016, 25, 20–27. [Google Scholar] [CrossRef]
- Jayaram, S.; Venkatesan, N. Design and implementation of the fractional-order controllers for a real-time nonlinear process using the AGTM optimization technique. Sci. Rep. 2024, 14, 31714. [Google Scholar] [CrossRef]
- Sundaresan, K.R.; Krishnaswamy, P.R. Estimation of time delay time constant parameters in time, frequency, and Laplace domains. Can. J. Chem. Eng. 1978, 56, 257–262. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Y.; Guan, Y.; Li, W. Stability analysis of multi-point boundary conditions for fractional differential equation with non-instantaneous integral impulse. Math. Biosci. Eng. 2023, 20, 7020–7041. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Tang, J.; Shi, K.; Zhao, Y. Hybrid Impulsive Feedback Control for Drive–Response Synchronization of Fractional-Order Multi-Link Memristive Neural Networks with Multi-Delays. Fractal Fract. 2023, 7, 495. [Google Scholar] [CrossRef]
- Fan, H.; Rao, Y.; Shi, K.; Wen, H. Global Synchronization of Fractional-Order Multi-Delay Coupled Neural Networks with Multi-Link Complicated Structures via Hybrid Impulsive Control. Mathematics 2023, 11, 3051. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and Fractional-Order Controllers; Institute of Experimental Physics, Slovak Academy of Sciences: Kosice, Slovakia, 1994. [Google Scholar]
- Baker, G. A Essentials of Pade Approximation; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Kumar, T.S. Model Matching Controller Design Methods with Applications in Electrical Power Systems. Ph.D. Thesis, IIT Kharagpur, Kharagpur, India, 2009. [Google Scholar]
- Muthukumari, S.; Kanagalakshmi, S.; Kumar, T.S. Centralized model matching integer/fractional-order controller design for multivariable processes with real-time validation. Trans. Inst. Meas. Control 2023, 46, 1828–1841. [Google Scholar] [CrossRef]
- Damodaran, S.; Kumar, T.S.; Sudheer, A.P. Generalized method for rational approximation of SISO/MIMO fractional-order systems using squared magnitude function. Trans. Inst. Meas. Control 2023, 46, 207–222. [Google Scholar] [CrossRef]
- Muthukumari, S.; Kanagalakshmi, S.; Kumar, T.S. Development of a novel model matching decentralized controller design algorithm and its experimental validation through load frequency controller implementation in restructured power system using TMS320F28379D control CARD. ISA Trans. 2024, 148, 285–306. [Google Scholar] [CrossRef]
- Beevi, F.P.; Kumar, T.S.; Jacob, J.; Beevi, D.P. Novel two degree of freedom model matching controller for set-point tracking in MIMO systems. Comput. Electr. Eng. 2017, 61, 1–14. [Google Scholar] [CrossRef]
- Muhammed, S.; Mahesh, P.V.; Mathew, A.T.; Kumar, T.S. Model Approximation and Controller Synthesis for H∞ Robust Control of Multiple Time Delay Transfer Functions. Int. Rev. Autom. Control. (IREACO) 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Priyanka, K.K.D.; Santhosh Kiran, M.; Rajarao, G. A New Approach for Design of Model Matching Controllers for Time Delay Systems by Using GA Technique. Int. J. Eng. Res. Appl. 2015, 5, 89–99. [Google Scholar]
- Ganguli, S.; Kaur, G.; Sarkar, P. An approximate model matching technique for controller design of linear time-invariant systems using hybrid firefly-based algorithms. ISA Trans. 2022, 127, 437–448. [Google Scholar] [CrossRef]
- Norman, S. Nise Control Systems Engineering, 6th ed.; Wiley India Private Ltd.: New Delhi, India, 2018. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: A MATLAB toolbox for fractional-order system identification and control. Int. J. Microelectron. Comput. Sci. 2011, 2, 51–62. [Google Scholar]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Vu, T.N.L.; Lee, M. Analytical design of fractional-order proportional-integral controllers for time-delay processes. ISA Trans. 2013, 52, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; Roy, B.K. Fractional order PI control applied to level control in coupled two tank MIMO system with experimental validation. Control Eng. Pract. 2016, 48, 119–135. [Google Scholar] [CrossRef]
- Vinopraba, T.; Sivakumaran, N.; Narayanan, S.; Radhakrishnan, T.K. Design of internal model control based fractional order PID controller. J. Control Theory Appl. 2012, 10, 297–302. [Google Scholar] [CrossRef]
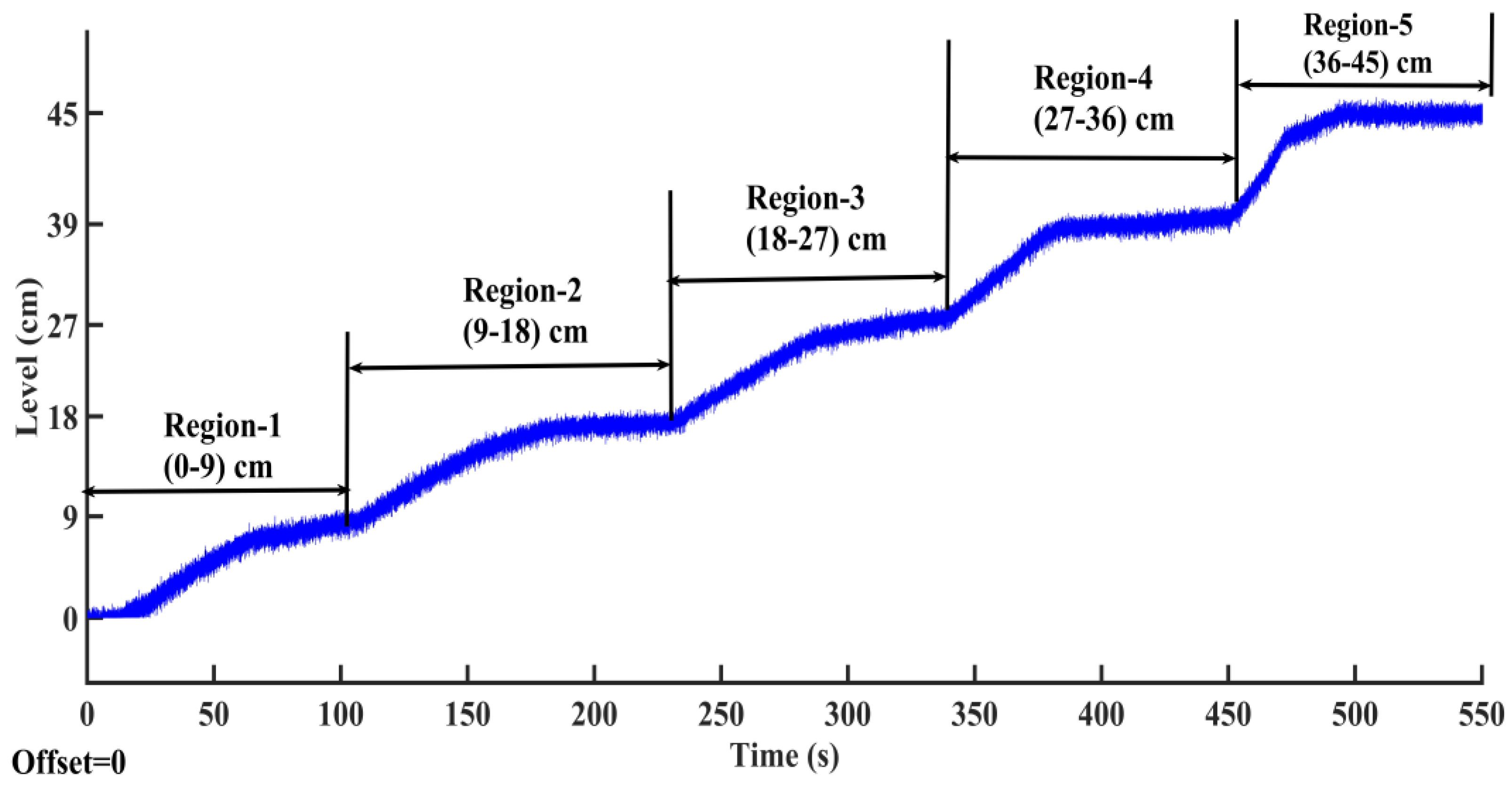
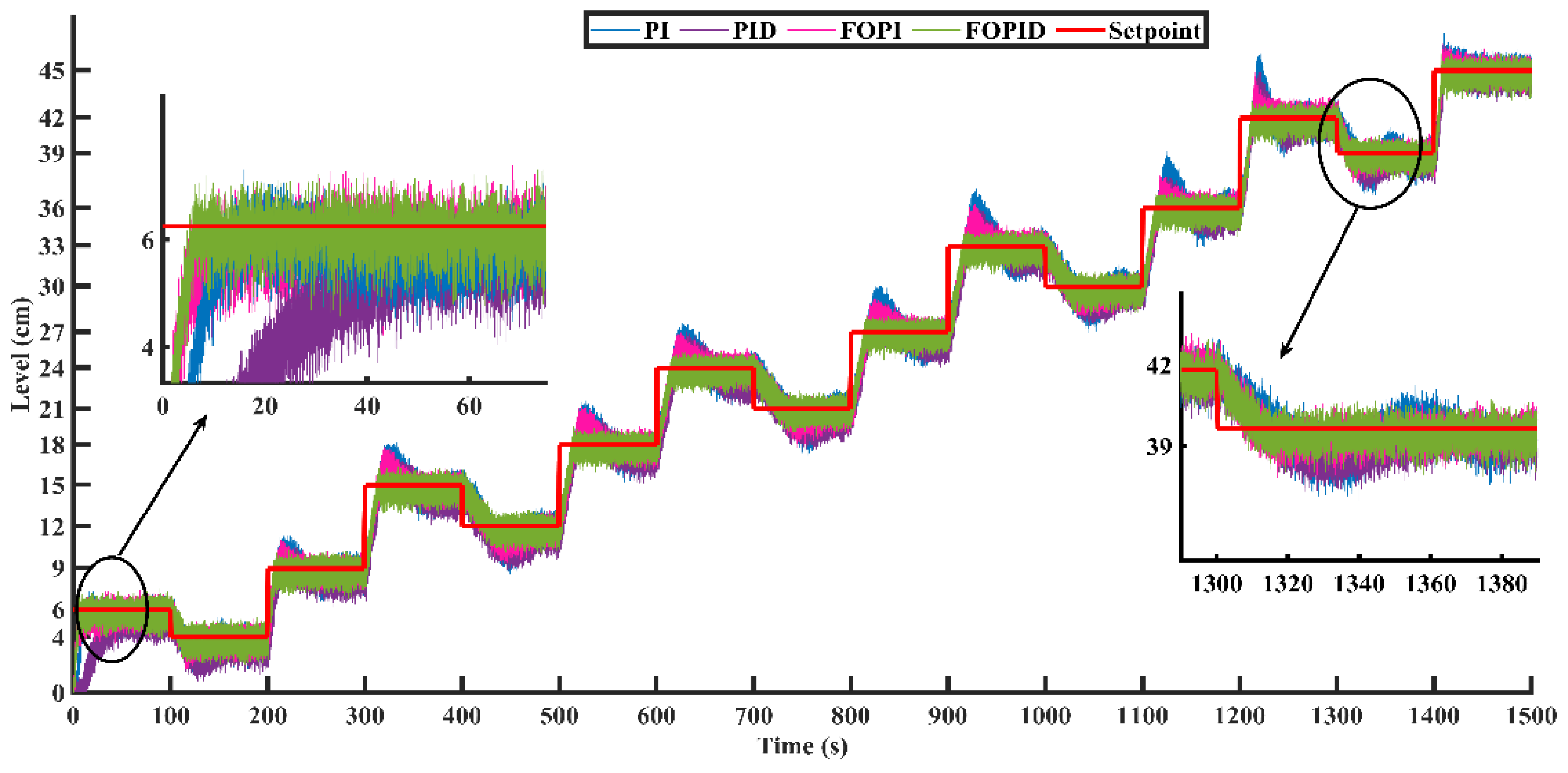
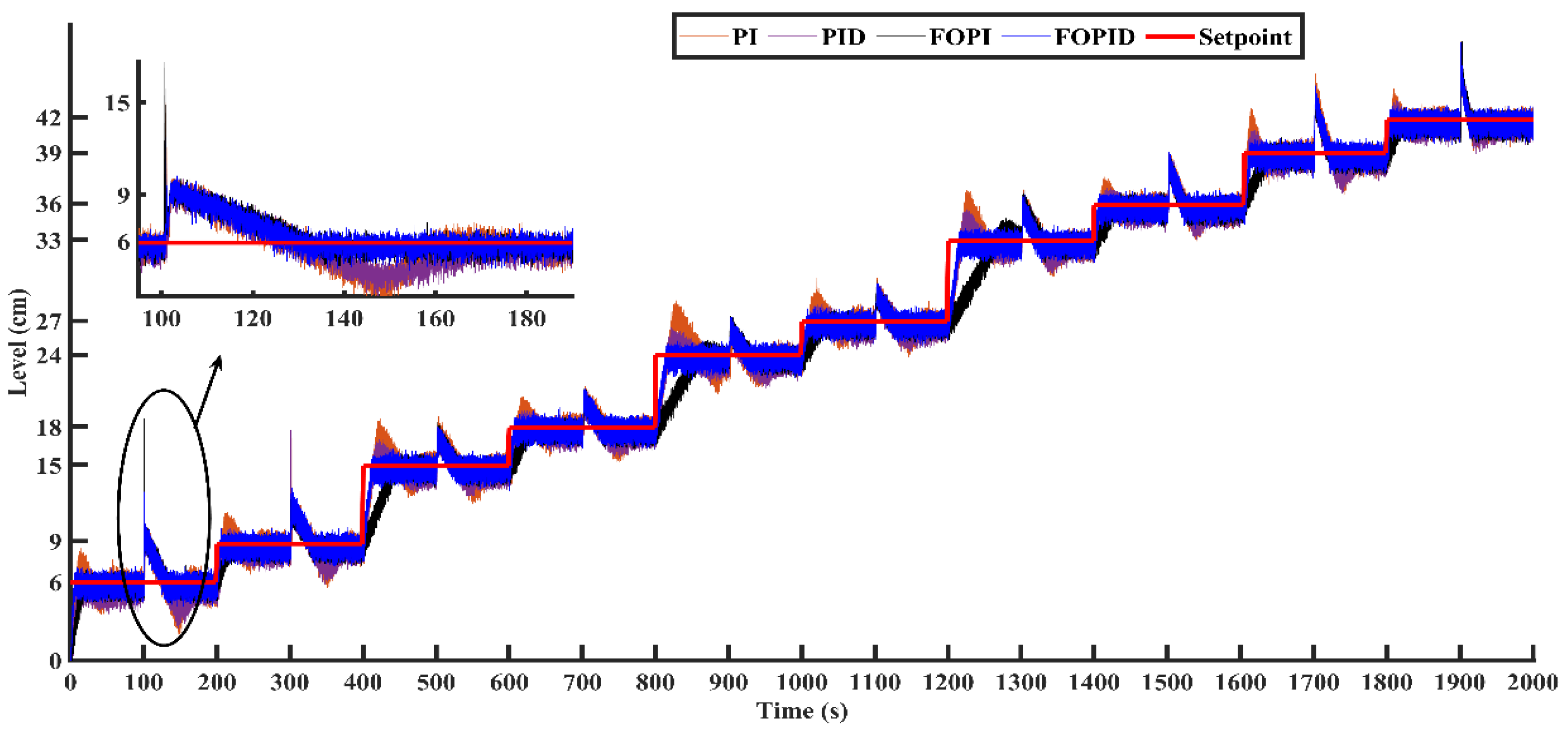
| Region of Operation (cm) | Regulated Inflow (lph) | Transfer Function |
|---|---|---|
| Region-1 (0–9) | 150 | |
| Region-2 (9–18) | 200 | |
| Region-3 (18–27) | 250 | |
| Region-4 (27–36) | 300 | |
| Region-5 (36–45) | 310 |
| Region (cm) | Type of Controller | Set of Expansion Points | Controller Parameters | ||||
|---|---|---|---|---|---|---|---|
| Region-1 (0–9) | PI | [0.7281, 0.0846] | 0.3593 | 0.1021 | - | - | - |
| PID | [0.0122, 0.0221, 0.0182] | 0.1512 | 0.0734 | 0.9803 | - | - | |
| FOPI | [0.04342, 0.0152, 0.1321] | 4.1539 | 3.6253 | - | 0.7371 | - | |
| FOPID | [0.0122, 0.0221, 0.0182, 0.03115, 0.032] | 6.9599 | 3.6319 | 5.6462 | 0.6982 | 0.3524 | |
| Region-2 (9–18) | PI | [0.001 0.002] | 0.4320 | 0.0143 | - | - | - |
| PID | [0.08 0.012 0.025] | 0.5630 | 0.0233 | 4.0126 | - | - | |
| FOPI | [0.04216 0.0331 0.0483] | 2.6541 | 0.6935 | - | 0.8085 | - | |
| FOPID | [1.04994, 1.3655, 3.08409, 1.04131, 1.03289] | 1.2945 | 0.6450 | 1.8051 | 0.7624 | 0.1023 | |
| Region-3 (18–27) | PI | [0.0004, 0.0023] | 0.2241 | 0.0062 | - | - | - |
| PID | [0.3187, 0.5868, 0.06945] | 0.0237 | 0.0044 | 0.0276 | - | - | |
| FOPI | [0.00026, 4.855, 0.0016] | 0.5625 | 0.1252 | - | 0.9390 | - | |
| FOPID | [0.0274, 0.557, 0.297, 0.781, 0.0074] | 3.1279 | 2.3109 | 2.6462 | 0.6582 | 0.5214 | |
| Region-4 (27–36) | PI | [0.0193, 0.0104] | 0.2230 | 0.0044 | - | - | - |
| PID | [0.08409, 0.04131, 0.03289] | 0.0775 | 0.0035 | 0.0352 | - | - | |
| FOPI | [0.7574, 0.3568, 0.9261] | 0.2245 | 0.7892 | - | 0.8510 | - | |
| FOPID | [0.08, 0.1, 0.2, 0.2, 0.25] | 1.9712 | 1.5312 | 1.9742 | 0.8275 | 0.7812 | |
| Region-5 (36–45) | PI | [0.00839, 0.00756] | 0.1450 | 0.0032 | - | - | - |
| PID | [0.0221, 0.012, 0.0115] | 0.0043 | 0.0031 | 0.0942 | - | - | |
| FOPI | [0.0281, 0.00246, 0.00246] | 1.7574 | 1.3568 | - | 0.9261 | - | |
| FOPID | [1.04994, 1.3655, 3.08409, 0.04131, 1.03289] | 4.7844 | 1.8653 | 1.4829 | 1.1985 | 1.0133 | |
| Region (cm) | Setpoint (cm) | Type of Controller | Time-Domain Properties | Performance Metrics | Stability | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rise Time (s) | Peak Time (s) | Settling Time (s) | Peak Overshoot (%) | Steady-State Error | ISE | IAE | ||||
| Region-1 (0–9) | (0,9) | PI | 15.2250 | 38 | 117.0728 | 28.2569 | 1.4433 × 10−15 | 11.3611 | 22.0504 | 1 |
| PID | 22.8295 | 49 | 120.1615 | 25.8438 | 2.8666 × 10−13 | 13.8422 | 27.3585 | 1 | ||
| FOPI | 3.0713 | 7 | 12.1355 | 10.1106 | 4.1198 × 10−4 | 0.6224 | 2.6593 | 1 | ||
| FOPID | 2.8492 | 8 | 8.5771 | 2.1080 | 6.2642 × 10−4 | 0.2948 | 2.3100 | 1 | ||
| Region-2 (9–18) | (9,18) | PI | 36.4510 | 99 | 192.4243 | 8.2164 | 2.1470 × 10−10 | 23.1790 | 35.7904 | 1 |
| PID | 24.2486 | 84 | 194.3785 | 24.9106 | 4.0283 × 10−10 | 16.7624 | 33.8065 | 1 | ||
| FOPI | 6.9656 | 15 | 25.5758 | 7.3268 | 8.3301 × 10−4 | 1.7879 | 5.9656 | 1 | ||
| FOPID | 7.8757 | 17 | 23.6653 | 3.4394 | 0.0016 | 1.7620 | 7.1373 | 1 | ||
| Region-3 (18–27) | (18,27) | PI | 83.2738 | 240 | 316.7094 | 8.1558 | 3.6866 × 10−6 | 107.6970 | 133.704 | 1 |
| PID | 157.8654 | 399 | 554.9373 | 7.0971 | 1.2123 × 10−4 | 147.6850 | 193.938 | 1 | ||
| FOPI | 17.1604 | 35 | 53.8693 | 7.9123 | 5.7551 × 10−4 | 5.8983 | 12.6740 | 1 | ||
| FOPID | 4.0299 | 9 | 13.5305 | 3.9177 | 0.0013 | 0.6152 | 4.2766 | 1 | ||
| Region-4 (27–36) | (27,36) | PI | 101.3722 | 328 | 587.3887 | 12.0177 | 2.9127 × 10−10 | 151.7279 | 191.251 | 1 |
| PID | 172.8368 | 462 | 654.9472 | 8.8564 | 3.1004 × 10−9 | 182.8178 | 237.990 | 1 | ||
| FOPI | 5.1907 | 12 | 30.8253 | 23.5460 | 3.9531 × 10−4 | 2.3821 | 6.3777 | 1 | ||
| FOPID | 4.0675 | 9 | 15.3859 | 9.4246 | 2.8060 × 10−4 | 0.7113 | 2.9099 | 1 | ||
| Region-5 (36–45) | (36,45) | PI | 152.0221 | 464 | 668.8141 | 11.5207 | 2.5697 × 10−8 | 206.0849 | 263.318 | 1 |
| PID | 183.6158 | 571 | 1234 | 24.8063 | 1.3221 × 10−4 | 255.7428 | 370.849 | 1 | ||
| FOPI | 2.8076 | 6 | 10.4536 | 8.3610 | 6.5749 × 10−5 | 0.5023 | 1.6582 | 1 | ||
| FOPID | 2.2441 | 6 | 10.3571 | 7.6123 | 1.6121 × 10−5 | 0.1857 | 1.0428 | 1 | ||
| Region (cm) | Type of Controller | Gain Margin (dB) | Phase Margin (Degrees) | Gain Cross-Over Frequency (wg) in rad/s | Phase Cross-Over Frequency (wp) in rad/s |
|---|---|---|---|---|---|
| Region-1 (0–9) | PI | 20.6006 | 66.0645 | 0.3771 | 0.1073 |
| PID | 22.3455 | 67.8368 | 2.6097 × 104 | 0.0809 | |
| FOPI | Inf | 116.3100 | NaN | 0.6013 | |
| FOPID | Inf | 161.3735 | NaN | 0.3369 | |
| Region-2 (9–18) | PI | 2.2476 | 49.2284 | 0.0563 | 0.0425 |
| PID | 1.7067 | 21.0020 | 0.0659 | 0.0574 | |
| FOPI | Inf | 135.4609 | NaN | 0.1988 | |
| FOPID | Inf | 151.6221 | NaN | 0.1360 | |
| Region-3 (18–27) | PI | 2.4005 | 69.6246 | 0.0237 | 0.0151 |
| PID | 6.0736 | 103.4978 | 0.0172 | 0.0073 | |
| FOPI | Inf | 128.2941 | NaN | 0.0840 | |
| FOPID | Inf | 150.2019 | NaN | 0.3079 | |
| Region-4 (27–36) | PI | 0.8638 | 19.2526 | 0.0169 | 0.0153 |
| PID | 4.5910 | 80.8244 | 0.0138 | 0.0076 | |
| FOPI | Inf | 64.9553 | NaN | 0.3668 | |
| FOPID | Inf | 130.3031 | NaN | 0.3814 | |
| Region-5 (36–45) | PI | 2.5467 | 49.8531 | 0.0123 | 0.0090 |
| PID | 1.0174 | 11.8328 | 0.0094 | 0.0088 | |
| FOPI | Inf | 118.8482 | NaN | 0.6637 | |
| FOPID | Inf | 145.7915 | NaN | 0.6011 |
| Region (cm) | Setpoint (cm) | Type of Controller | Time-Domain Specifications | Performance Metrics | |||||
|---|---|---|---|---|---|---|---|---|---|
| Rise Time (s) | Peak Time (s) | Settling Time (s) | Peak Overshoot (%) | Steady-State Error | ISE | IAE | |||
| Region-1 (0–9) | (0,6) | PI | 12.58 | 27.624 | 89.656 | 69.4762 | 0.0013 | 2.8981 | 7.2614 |
| PID | 10.968 | 34.136 | 67.132 | 87.5078 | 0.0614 | 1.4606 | 10.2694 | ||
| FOPI | 8.792 | 26.964 | 37.26 | 71.7135 | 0.0027 | 0.8538 | 6.396 | ||
| FOPID | 5.936 | 16.3 | 18.88 | 35.569 | 0.00427 | 0.5532 | 5.3738 | ||
| (6,4) | PI | 13.872 | 20.5 | 87.976 | 9.9372 | 0.0792 | 13.2023 | 29.781 | |
| PID | 52.74 | 59.08 | 73.852 | 42.474 | 0.1644 | 10.4265 | 23.8679 | ||
| FOPI | 7.5 | 10.864 | 18.248 | 51.1881 | 0.1374 | 5.1374 | 7.1025 | ||
| FOPID | 5.244 | 6.48 | 9.496 | 5.563 | 0.0792 | 1.4263 | 5.8915 | ||
| (4,9) | PI | 8.628 | 20.108 | 84.264 | 21.9847 | 0.0411 | 3.8301 | 8.7418 | |
| PID | 11.128 | 20.188 | 58.656 | 15.7091 | 0.0365 | 2.6299 | 10.7102 | ||
| FOPI | 7.176 | 13.628 | 32.856 | 27.2254 | 0.0385 | 1.2879 | 7.2072 | ||
| FOPID | 6.184 | 9.344 | 11.728 | 16.2429 | 0.0191 | 1.1934 | 6.165 | ||
| Region-2 (9–18) | (9,15) | PI | 25.684 | 48.964 | 95.584 | 35.5031 | 0.0193 | 2.5089 | 12.1807 |
| PID | 21.208 | 53.94 | 87.172 | 28.8356 | 0.0143 | 1.9451 | 11.7217 | ||
| FOPI | 24.844 | 60.152 | 71.28 | 36.3376 | 0.0518 | 1.8219 | 10.2102 | ||
| FOPID | 24.356 | 34.528 | 48.488 | 18.5042 | 0.0508 | 1.4764 | 8.131 | ||
| (15,12) | PI | 13.708 | 33.076 | 94.848 | 20.1115 | 0.0123 | 4.1397 | 14.0817 | |
| PID | 15 | 25.748 | 66.884 | 26.0982 | 0.1304 | 4.3335 | 13.5053 | ||
| FOPI | 13.308 | 19.76 | 52.188 | 20.1176 | 0.0275 | 3.2924 | 10.707 | ||
| FOPID | 12.26 | 14.132 | 22.548 | 10.4763 | 0.0354 | 2.8801 | 8.7004 | ||
| (12,18) | PI | 15.16 | 27.712 | 95.012 | 15.2460 | 0.0471 | 4.4652 | 14.79 | |
| PID | 16.776 | 24.24 | 75.924 | 26.6462 | 0.2307 | 4.2529 | 13.2605 | ||
| FOPI | 14.276 | 25.084 | 54.616 | 17.0127 | 0.0065 | 3.6017 | 11.4051 | ||
| FOPID | 13.224 | 14.696 | 21.884 | 10.7732 | 0.0637 | 2.9998 | 8.9307 | ||
| Region-3 (18–27) | (18,24) | PI | 26.048 | 55.276 | 83.808 | 20.265 | 0.0036 | 2.4715 | 12.3875 |
| PID | 25.644 | 50.748 | 91.796 | 18.973 | 0.0575 | 1.9961 | 12.0488 | ||
| FOPI | 27.34 | 53.268 | 68.284 | 20.9228 | 0.0230 | 1.8527 | 10.3609 | ||
| FOPID | 24.676 | 34.016 | 47.04 | 18.7202 | 0.0109 | 1.4070 | 8.0860 | ||
| (24,21) | PI | 15.968 | 24.44 | 94.156 | 18.6568 | 0.1061 | 4.2121 | 14.9116 | |
| PID | 16.064 | 31.132 | 82.348 | 19.8487 | 0.2031 | 4.8439 | 14.741 | ||
| FOPI | 15.24 | 25.696 | 57.468 | 9.0283 | 0.0589 | 3.2603 | 10.7845 | ||
| FOPID | 14.356 | 20.372 | 29.916 | 4.9598 | 0.0037 | 2.9983 | 9.1804 | ||
| (21,27) | PI | 16.572 | 27.648 | 94.84 | 14.7665 | 0.0405 | 4.5025 | 15.1836 | |
| PID | 17.984 | 25.988 | 76.612 | 10.7207 | 0.0503 | 4.3113 | 13.8317 | ||
| FOPI | 16.452 | 26.012 | 58.192 | 7.8619 | 0.0578 | 3.5814 | 11.1367 | ||
| FOPID | 13.72 | 16.664 | 22.152 | 7.2302 | 0.0714 | 2.9387 | 9.0866 | ||
| Region-4 (27–36) | (27,33) | PI | 22.42 | 44.64 | 93.43 | 15.4201 | 0.0413 | 2.2437 | 11.4821 |
| PID | 21.29 | 57.54 | 89.54 | 17.3188 | 0.1847 | 1.7767 | 11.2314 | ||
| FOPI | 22.34 | 51.47 | 62.16 | 13.3582 | 0.0015 | 1.5169 | 8.8585 | ||
| FOPID | 21.78 | 32.04 | 47.04 | 12.7893 | 0.0146 | 1.2779 | 7.6097 | ||
| (33,30) | PI | 17.26 | 28.516 | 93.948 | 11.9952 | 0.0337 | 5.9481 | 17.5668 | |
| PID | 19.808 | 29.68 | 95.884 | 10.2189 | 0.0636 | 6.3806 | 17.1467 | ||
| FOPI | 17.176 | 27.552 | 59.956 | 10.8369 | 0.0492 | 4.4213 | 12.6094 | ||
| FOPID | 15.24 | 18.192 | 28.456 | 4.2468 | 0.0038 | 3.9937 | 10.4214 | ||
| (30,36) | PI | 16.13 | 24.66 | 90.02 | 12.7905 | 0.0354 | 4.8821 | 15.1791 | |
| PID | 16.37 | 24.41 | 84.61 | 8.2671 | 0.0604 | 4.1698 | 13.4336 | ||
| FOPI | 15.64 | 21.41 | 47.22 | 7.0393 | 0.0029 | 3.3443 | 10.116 | ||
| FOPID | 12.74 | 15.72 | 21.8 | 6.2571 | 0.1120 | 2.9591 | 8.9719 | ||
| Region-5 (36–45) | (36,42) | PI | 15.24 | 55.6 | 98.91 | 9.5293 | 0.0128 | 1.2604 | 8.5979 |
| PID | 13.22 | 29.22 | 92.89 | 8.97 | 0.0542 | 1.2769 | 9.3684 | ||
| FOPI | 12.26 | 29.71 | 48.87 | 9.9604 | 0.0102 | 0.6426 | 5.3022 | ||
| FOPID | 10.48 | 14.61 | 27.4 | 5.1011 | 0.0279 | 0.4163 | 5.5633 | ||
| (42,39) | PI | 13.47 | 20.26 | 64.1 | 11.2987 | 0.0075 | 5.3179 | 14.3146 | |
| PID | 13.87 | 21.68 | 68.4 | 9.7821 | 0.0818 | 4.9721 | 13.858 | ||
| FOPI | 12.82 | 16.38 | 40.39 | 7.5828 | 0.0165 | 3.5310 | 9.9892 | ||
| FOPID | 11.61 | 13.03 | 20.29 | 1.3110 | 0.0915 | 2.6078 | 9.4409 | ||
| (39,45) | PI | 8.55 | 10.35 | 35.19 | 6.1638 | 0.0044 | 2.3505 | 8.0372 | |
| PID | 9.76 | 11.19 | 37.4 | 6.3963 | 0.1175 | 3.1196 | 8.9883 | ||
| FOPI | 8.55 | 9.54 | 32.8 | 4.1916 | 0.0101 | 2.1251 | 6.7832 | ||
| FOPID | 7.26 | 8.15 | 12.9 | 3.2933 | 0.0090 | 1.2854 | 7.6545 | ||
| Region (cm) | Setpoint (cm) | Performance Indices | Type of Controller | |||||
|---|---|---|---|---|---|---|---|---|
| PI | PID | FOPI | FOPID | SIMC-PI [1] | Skogestad’s-PI [33] | |||
| Region-1 (0–9) | (0,6) | ISE | 6.0818 | 6.6048 | 5.5092 | 3.2938 | 5134.143 | 5440.887 |
| IAE | 29.9915 | 27.3765 | 18.7046 | 13.8307 | 2567.652 | 2574.304 | ||
| (6,9) | ISE | 4.5151 | 3.6953 | 2.5484 | 2.0380 | 2231.789 | 2959.168 | |
| IAE | 25.9667 | 20.5177 | 14.3189 | 11.8835 | 1553.274 | 1942.761 | ||
| Region-2 (9–18) | (9,15) | ISE | 6.3387 | 5.9522 | 4.4630 | 3.4254 | The referred paper has not taken data for these setpoints (15 and 18) | |
| IAE | 26.9758 | 21.7785 | 20.9360 | 13.4707 | ||||
| (15,18) | ISE | 2.6733 | 2.2906 | 2.4002 | 1.3692 | |||
| IAE | 18.8121 | 16.1906 | 14.1190 | 10.3691 | ||||
| Region-3 (18–27) | (18,24) | ISE | 10.9168 | 9.6998 | 7.5124 | 3.4219 | 1414.623 | 965.0554 |
| IAE | 26.6642 | 20.9260 | 17.7185 | 13.6954 | 1098.509 | 998.3812 | ||
| (24,27) | ISE | 3.5213 | 2.5006 | 2.1199 | 1.2337 | 1121.784 | 1056.572 | |
| IAE | 18.5887 | 16.1540 | 13.4675 | 10.0067 | 1055.477 | 1082.533 | ||
| Region-4 (27–36) | (27,33) | ISE | 7.7351 | 6.2243 | 5.9101 | 4.5852 | The referred paper has not taken data for these setpoints (33 and 36) | |
| IAE | 26.0886 | 23.4025 | 16.7825 | 15.3406 | ||||
| (33,36) | ISE | 3.7570 | 2.8556 | 2.6484 | 1.6361 | |||
| IAE | 18.0486 | 17.6973 | 14.7455 | 10.9276 | ||||
| Region-5 (36–45) | (36,39) | ISE | 6.4573 | 5.2246 | 4.6697 | 3.1885 | 1056.572 | 2979.306 |
| IAE | 21.9127 | 20.5477 | 18.3970 | 13.4866 | 1082.533 | 1164.927 | ||
| (39,42) | ISE | 3.8711 | 2.4902 | 2.3031 | 1.5228 | 107.6896 | 50.12255 | |
| IAE | 18.0581 | 15.8220 | 13.3008 | 9.7016 | 217.542 | 150.8350 | ||
| Setpoint | Type of Controller | Time-Domain Specifications | Performance Metrics | |||||
|---|---|---|---|---|---|---|---|---|
| Rise Time (s) | Peak Time (s) | Settling Time (s) | Peak Overshoot (%) | Steady-State Error | ISE | IAE | ||
| (0–8) cm | SM FOPID | 7.348 | 12.744 | 28.06 | 20.4758 | 0.0269 | 2.8830 | 7.0800 |
| (8–16) cm | SM FOPID | 14.586 | 26.52 | 29.416 | 12.0933 | 0.0235 | 5.3262 | 10.3871 |
| (16–24) cm | SM FOPID | 17.872 | 23.284 | 28.98 | 5.5612 | 0.0005885 | 6.6258 | 12.1051 |
| (24–32) cm | SM FOPID | 17.628 | 32.548 | 39.388 | 4.6826 | 0.1451 | 6.8855 | 12.3215 |
| (32–40) cm | SM FOPID | 13.316 | 21.132 | 32.476 | 3.4150 | 0.0127 | 5.6649 | 10.4937 |
| (40–45) cm | SM FOPID | 4.9 | 7.804 | 27.456 | 3.0240 | 0.0005108 | 1.1101 | 5.4654 |
| Setpoint | Type of Controller | Performance Metrics | |
|---|---|---|---|
| ISE | IAE | ||
| (0–8) cm | SM FOPID | 5.6208 | 19.2696 |
| (8–16) cm | SM FOPID | 12.1502 | 37.3256 |
| (16–24) cm | SM FOPID | 20.0262 | 78.0615 |
| (24–32) cm | SM FOPID | 28.674 | 78.0615 |
| (32–40) cm | SM FOPID | 37.94 | 99.0582 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayaram, S.; Verrelli, C.M.; Venkatesan, N. AGTM Optimization Technique for Multi-Model Fractional-Order Controls of Spherical Tanks. Mathematics 2025, 13, 351. https://doi.org/10.3390/math13030351
Jayaram S, Verrelli CM, Venkatesan N. AGTM Optimization Technique for Multi-Model Fractional-Order Controls of Spherical Tanks. Mathematics. 2025; 13(3):351. https://doi.org/10.3390/math13030351
Chicago/Turabian StyleJayaram, Sabavath, Cristiano Maria Verrelli, and Nithya Venkatesan. 2025. "AGTM Optimization Technique for Multi-Model Fractional-Order Controls of Spherical Tanks" Mathematics 13, no. 3: 351. https://doi.org/10.3390/math13030351
APA StyleJayaram, S., Verrelli, C. M., & Venkatesan, N. (2025). AGTM Optimization Technique for Multi-Model Fractional-Order Controls of Spherical Tanks. Mathematics, 13(3), 351. https://doi.org/10.3390/math13030351








