Bifurcation Analysis and Soliton Behavior of New Combined Kairat-II-X Differential Equation Using Analytical Methods
Abstract
1. Introduction
2. The eMETFM for Combined Kairat-II-X Differential Equation
- First Case:
- Second Case:
- Third Case:
Three Types of Solutions Using eMETFM for the Combined Kairat-II-X Equation
- Solution 1:
- Solution 2:
- Solution 3:
- Solution 4:
- Solution 5:
3. New Modified -Expansion Method
- Product 1: With and , we get
- Product 2: With and , we get
- Product 3: With , , and we get
- Product 4: With , , and we get
- Product 5: With , , and we get
- Product 6: With and we get
- Product 7: With and we get
- Product 8: With , we get
- Product 9: With and , we get
- Product 10: With and , we get
- Product 11: With and , we get
Application of MTEM for the Combined Kairat-II-X Equation
- Merge I.Through Product 9, the exact cuspon solution is
- Merge III.Through Product 1, the exact periodic wave solution isso that .
- Merge IV.Through Product 9, the exact cuspon solution is
- Merge V.Through Product 5, the exact dark soliton solution isso that and .
- Merge VI.Through Product 1, the exact periodic wave solution isso that .
- Merge VII.Through Product 5, the exact combined dark soliton and singular solution isso that and .
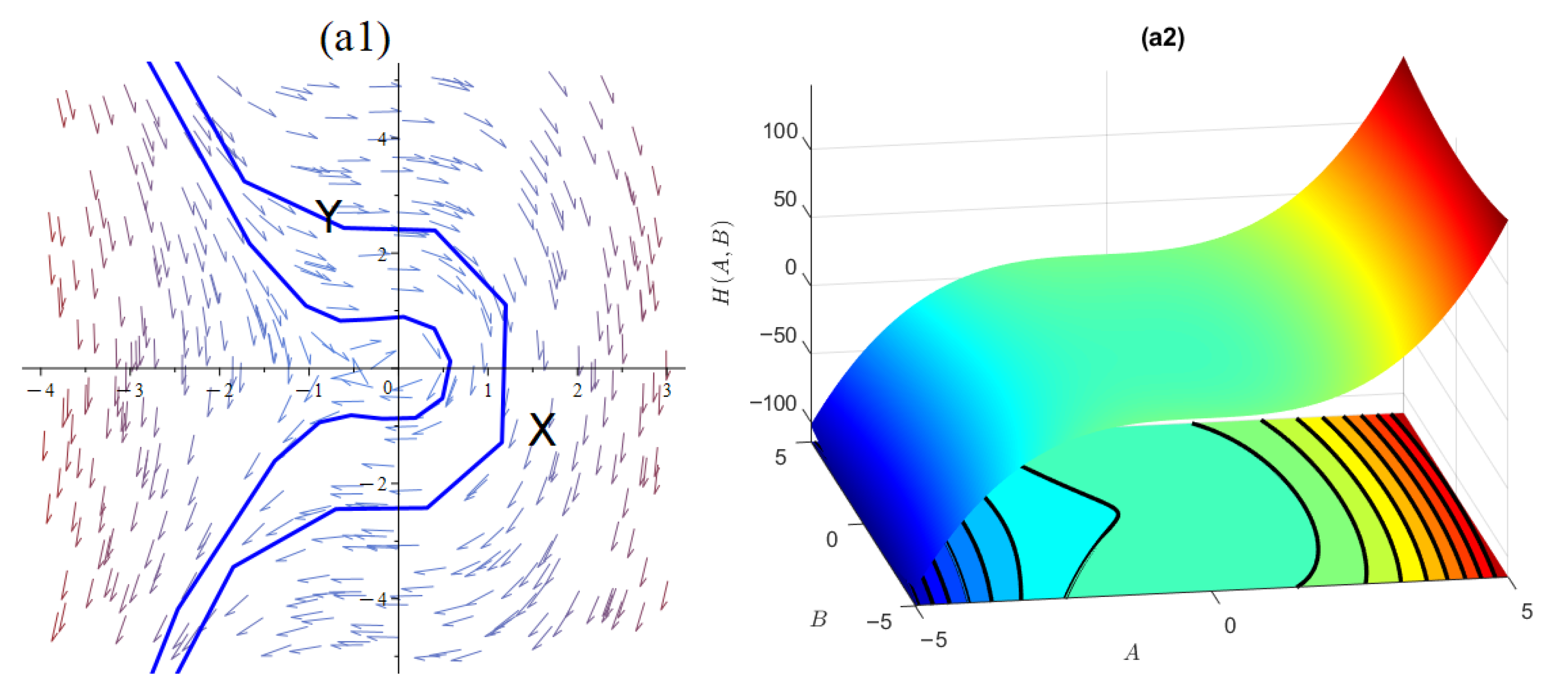
4. Bifurcation Analysis
- If the Jacobian is positive, the equilibrium point offers a center point.
- If the Jacobian is negative, the equilibrium point offers a saddle point.
- If the Jacobian is zero, the equilibrium point offers a cuspidal point. We have the following cases:
Sensitivity Analysis
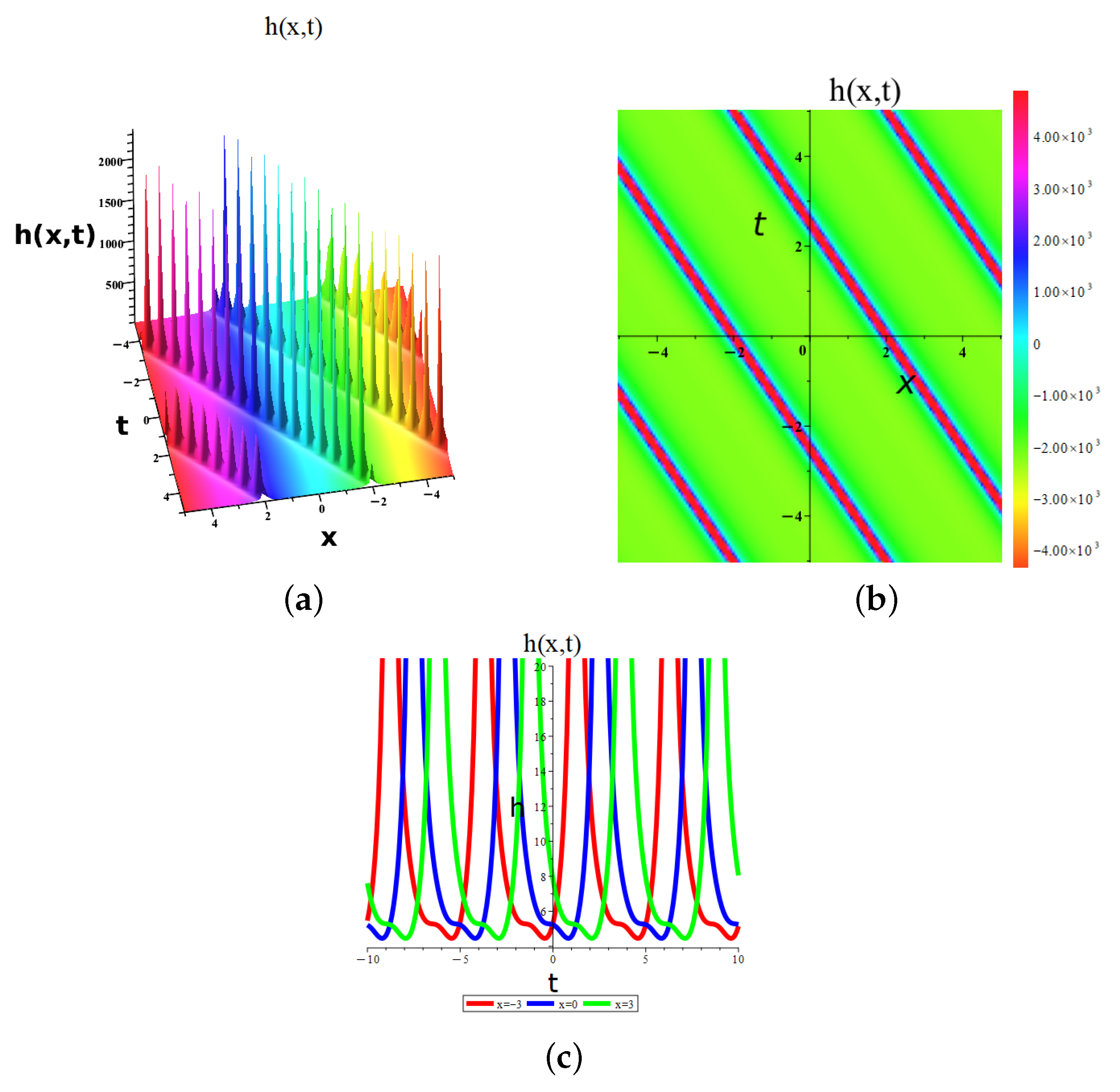
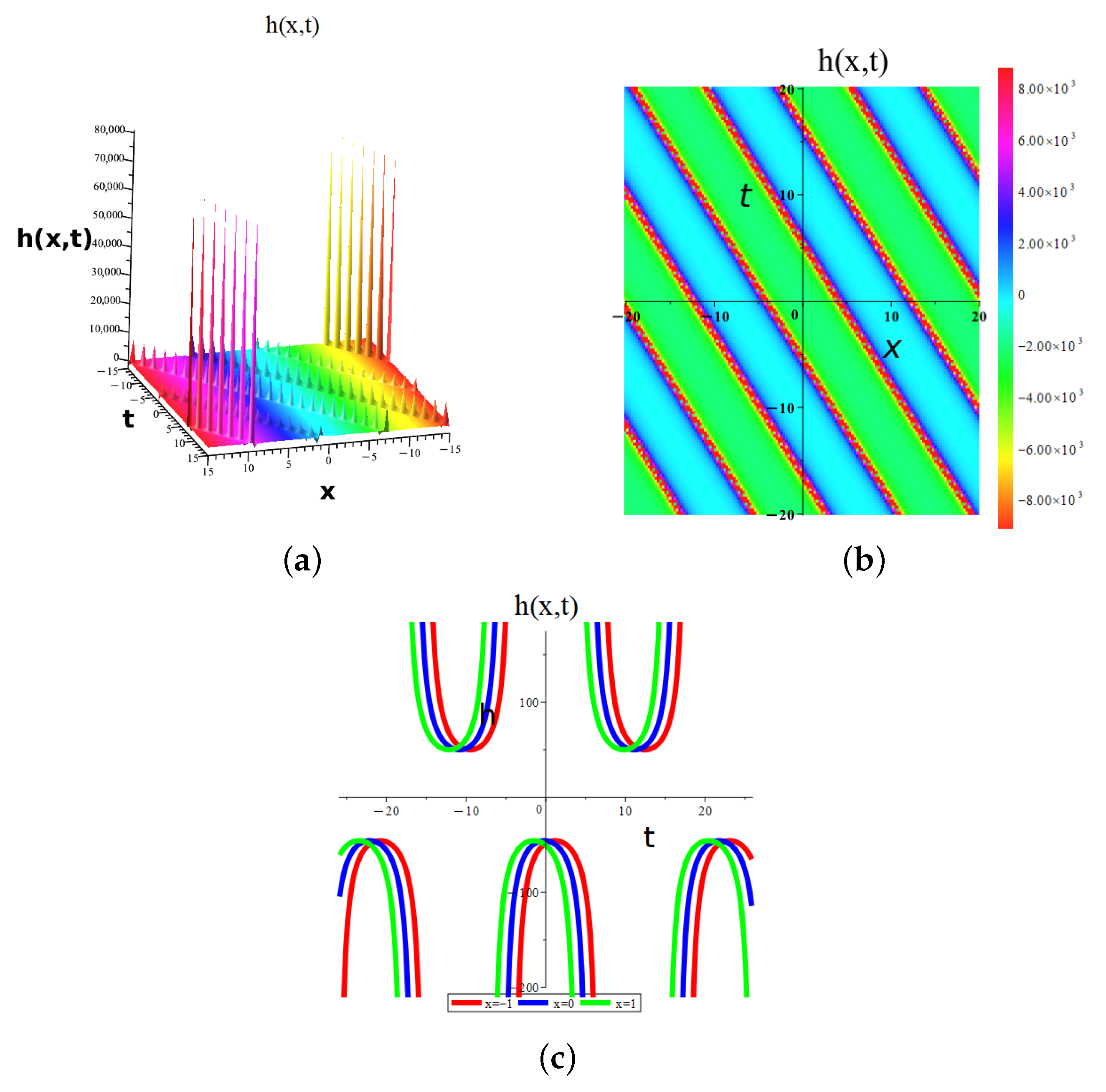
5. The Physical Interpretation of Solutions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Li, B. Semi-global stabilization of parabolic PDE-ODE systems with input saturation. Automatica 2025, 171, 111931. [Google Scholar] [CrossRef]
- Li, Y.; Rui, Z.; Hu, B. Monotone iterative and quasilinearization method for a nonlinear integral impulsive differential equation. Aims Math. 2025, 10, 21–37. [Google Scholar]
- Jin, J.; Zhao, L.; Chen, L.; Chen, W. A robust zeroing neural network and its applications to dynamic complex matrix equation solving and robotic manipulator trajectory tracking. Front. Neurorobot. 2022, 16, 1065256. [Google Scholar] [CrossRef] [PubMed]
- Chong, Z.; Wang, C.; Zhang, H.; Zhang, S. Sine-transform-based dual-memristor hyperchaotic map and analog circuit implementation. IEEE Trans. Instrum. Meas. 2025, 74, 1–14. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, J.; Meng, X.; Li, Z.; Wen, X.; Girard, P.; Yan, A. HALTRAV: Design of a high-performance and area-efficient latch With triple-node-upset recovery and algorithm-based Verifications. IEEE Trans. Comput.-Aided Des. Integr. Circuits And Syst. 2025, 44, 2367–2377. [Google Scholar]
- Lakestani, M.; Manafian, J. Analytical treatments of the space-time fractional coupled nonlinear Schrödinger equations. Opt. Quant. Elec. 2018, 50, 396. [Google Scholar]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. Int. J. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J. The solution of the variable coefficients fourth–order parabolic partial differential equations by homotopy perturbation method. Z. Naturforschung A 2009, 64a, 420–430. [Google Scholar]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Application of the Exp-function method for solving a partial differential equation arising in biology and population genetics. Int. Numer. Methods Heat Fluid Flow 2011, 21, 736–753. [Google Scholar] [CrossRef]
- Zhang, M.; Xie, X.; Manafian, J.; Ilhan, O.A.; Singh, G. Characteristics of the new multiple rogue wave solutions to the fractional generalized CBS-BK equation. J. Adv. Res. 2022, 38, 131–142. [Google Scholar]
- Liu, H.-Z. A modification to the first integral method and its applications. Appl. Math. Comput. 2022, 419, 126855. [Google Scholar] [CrossRef]
- Vakhnenko, V.O.; Parkes, E.J. The calculation of multi-soliton solutions of the vakhnenko equation by the inverse scattering method. Chaos Solitons Fractals 2002, 13, 1819–1826. [Google Scholar] [CrossRef]
- Moustafa, M.; Amin, A.M.; Laouini, G. New exact solutions for the nonlinear schrdinger’s equation with anti-cubic nonlinearity term via lie group method. Optik 2021, 248, 168205. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J. Study of the wave-breaking’s qualitative behavior of the Fornberg-Whitham equation via quasi-numeric approaches. Int. J. Num. Meth. Heat Fluid Flow 2012, 22, 537–553. [Google Scholar] [CrossRef]
- Oqielat, M.N.; Eriqat, T.; Ogilat, O.; El-Ajou, A.; Alhazmi, S.E.; Al-Omari, S. Laplace-residual power series method for solving time-fractional reaction-diffusion model. Fractal Fract. 2023, 7, 309. [Google Scholar] [CrossRef]
- Aghazadeh, A.; Mahmoudi, Y.; Saei, F.D. Legendre approximation method for computing eigenvalues of fourth order fractional Sturm-Liouville problem. Math. Comput. Simul. 2023, 206, 286–301. [Google Scholar] [CrossRef]
- Manafian, J.; Mohammadi-Ivatlo, B.; Abapour, M. Breather wave, periodic, and cross-kink solutions to the generalized Bogoyavlensky-Konopelchenko equation. Math. Meth. Appl. Sci. 2019, 43, 1753–1774. [Google Scholar] [CrossRef]
- Shen, X.; Manafian, J.; MJiang, M.; Ilhan, O.A.; Shafikk, S.S.; Zaidi, M. Abundant wave solutions for generalized Hietarinta equation with Hirota’s bilinear operator. Mod. Phys. Lett. B 2022, 36, 2250032. [Google Scholar] [CrossRef]
- Rao, X.; Manafian, J.; Mahmoud, K.H.; Hajar, A.; AB Mahdi, A.B.; Zaidi, M. The nonlinear vibration and dispersive wave systems with extended homoclinic breather wave solutions. Open Phys. 2022, 20, 795–821. [Google Scholar] [CrossRef]
- Pan, Y.; Manafian, J.; Zeynalli, S.M.; Al-Obaidi, R.; Sivaraman, R.; Kadi, A. N-Lump Solutions to a (3+1)-Dimensional Variable-Coefficient Generalized Nonlinear Wave Equation in a Liquid with Gas Bubbles. Qual. Theory Dyn. Syst. 2022, 21, 127. [Google Scholar] [CrossRef]
- Zou, Q.; Manafian, J.; Malmir, S.; Mahmoud, K.H.; Alsubaie, A.S.A.; Ewadh, N.A.; Alrekabi, I. Exact breather waves solutions in a spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions. Sci. Rep. 2024, 14, 31718. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Zhang, X.; Huang, Z.; Peng, L.; Lai, Y.; Aminakbari, N. Soliton and lump and travelling wave solutions of the (3+1) dimensional KPB like equation with analysis of chaotic behaviors. Sci. Rep. 2024, 14, 20966. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Lu, G.; Liu, Y.; Sun, W. Stabilizer testing and central limit theorem. Phys. Rev. A 2025, 111, 32421. [Google Scholar] [CrossRef]
- Gu, C. (Ed.) Soliton Theory and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Myrzakulova, Z.; Manukure, S.; Myrzakulov, R.; Nugmanova, G. Integrability, geometry and wave solutions of some Kairat equations. arXiv 2023, arXiv:2307.00027. [Google Scholar] [CrossRef]
- Faridi, W.A.; Wazwaz, A.M.; Mostafa, A.M.; Myrzakulov, R.; Umurzakhova, Z. The Lie point symmetry criteria and formation of exact analytical solutions for Kairat-II equation: Paul-Painleve approach. Chaos Solitons Fractals 2024, 182, 114745. [Google Scholar] [CrossRef]
- Awadalla, M.; Zafar, A.; Taishiyeva, A.; Raheel, M.; Myrzakulov, R.; Bekir, A. The analytical solutions to the M-fractional Kairat-II and Kairat-X equations. Front. Phys. 2023, 11, 1335423. [Google Scholar]
- Xiao, Y.; Barak, S.; Hleili, M.; Shah, K. Exploring the dynamical behaviourofoptical solitons in integrable kairat II and kairat-X equations. Phys. Scr. 2024, 99, 095261. [Google Scholar] [CrossRef]
- Aldwoah, K.; Mustafa, A.; Aljaaidi, T.; Mohamed, K.; Alsulami, A.; Hassan, M. Exploring the impact of Brownian motion on novel closed-form solutions of the extended Kairat-II equation. PLoS ONE 2025, 20, e0314849. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Alhejaili, W.; El-Tantawy, S. Study of a combined Kairat II-X equation: Painleve integrability, multiple kink, lump and other physical solutions. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 3715–3730. [Google Scholar] [CrossRef]
- Liang, Y.H.; Wang, K.J. Bifurcation analysis, chaotic phenomena, variational principle, Hamiltonian, solitary and periodic wave solutions of the fractional Benjamin Ono equation. Fractals 2025, 33, 2550016. [Google Scholar] [CrossRef]
- He, J.H.; Sun, C. A variational principle for a thin film equation. J. Math. Chem. 2019, 57, 2075–2081. [Google Scholar] [CrossRef]
- Fugarov, D.; Dengaev, A.; Drozdov, I.; Shishulin, V.; Ostrovskaya, A. Application of tan(ϕ/2)-expansion method for solving the fractional Biswas-Milovic equation for Kerr law nonlinearity. Comput. Methods Differ. Equ. 2025, 13, 1408–1424. [Google Scholar] [CrossRef]
- Khan, U.; Irshad, A.; Ahmed, N.; Mohyud-Din, S.T. Improved tan tan(ϕ(ξ)/2)-expansion method for (2+1)-dimensional KP-BBM wave equation. Opt. Quant. Elec. 2018, 50, 135. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Ismael, H.F.; Sulaiman, T.A.; Emadifar, H.; Ahmed, K.K. The New Combined Kairat-II-X Differential Equation: Diversity of Solitary Wave Structures via New Techniques. J. Nonlinear Math. Phys. 2025, 32, 55. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Ismael, H.F.; Sulaiman, T.A.; Emadifar, H.; Ahmed, K.K. Extended (3+1)-dimensional Kairat–II and Kairat–X equations: Painlevé integrability, multiple soliton solutions, lump solutions, and breather wave solutions. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 2177–2194. [Google Scholar]
- Rizvi, S.T.R.; Jlali, L.; Anjum, I.; Abad, H.; Solouma, E.; Seadawy, A.R. Nonlinear Stochastic Wave Behavior: Soliton Solutions and Energy Analysis of Kairat-II and Kairat-X Systems. Fractal Fract. 2025, 9, 728. [Google Scholar] [CrossRef]
- Mathanaranjan, T. Lie Symmetries, Soliton Solutions, Conservation Laws, and Stability Analysis of the Combined Kairat-II-X Equation. Math. Meth. Appl. Sci. 2025, 48, 16722–16729. [Google Scholar] [CrossRef]
- Mehanna, M.S.; Wazwaz, A.M. Tri-analytical approach to Kairat–II and Kairat–X equations. Rom. Rep. Phys. 2025, 77, 107. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, L.; Jin, J. A noise-tolerant fuzzy-type zeroing neural network for robust synchronization of chaotic systems. Concurr. Comput. Pract. Exp. 2024, 36, e8218. [Google Scholar] [CrossRef]
- Alam, N.; Ullah, M.S.; Manafian, J.; Mahmoud, K.H.; Alsubaie, A.S.A.; Ahmed, H.M.; Ahmed, K.K.; Khatib, S.A. Bifurcation analysis, chaotic behaviors, and explicit solutions for a fractional two-mode Nizhnik-Novikov-Veselov equation in mathematical physics. AIMS Math. 2025, 10, 4558–4578. [Google Scholar] [CrossRef]
- Tariq, K.U.; Manafian, J.; Malmir, S.; Tufail, R.N.; Ilhan, O.A.; Mahmoud, K.H. On the structure of the higher dimensional Date-Jimbo-Kashiwara-Miwa model emerging in water waves. Discov. Appl. Sci. 2025, 7, 576. [Google Scholar] [CrossRef]
- Ahmed, A.I.; Elbadri, M.; Al-Kuleab, N.; AlMutairi, D.M.; Taha, N.E.; Dafaalla, M.E. Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System. Mathematics 2025, 13, 3695. [Google Scholar] [CrossRef]
- Allogmany, R.; Alzahrani, S.S. Dynamic, Bifurcation, and Lyapunov Analysis of Fractional Rössler Chaos Using Two Numerical Methods. Mathematics 2025, 13, 3642. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, X.L.; Shi, F.; Li, G. Bifurcation and sensitivity analysis, chaotic behaviors, variational principle, Hamiltonian and diverse wave solutions of the new extended integrable Kadomtsev-Petviashvili equation. Phys. Let. A 2025, 534, 130246. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H. Mathematical model and the solution of the capillary vibration in a nanoscale deformable. Math. Methods Appl. Sci. 2025, 48, 8480–8486. [Google Scholar] [CrossRef]
- Nan, T.; Manafian, J.; Ilhan, O.A.; Malmir, S.; Fattah, A.A.; Mahmoud, K.H.; Ahmed, A.M.; Nasr, Y.M. Generalized trial equation scheme and enhance modified extended tanh function method with Nonparaxial pulse propagation to the cubic-quintic nonlinear Helmholtz equation. Qual. Theory Dyn. Syst. 2025, 24, 183. [Google Scholar] [CrossRef]
- Ozisik, M.; Bayram, M.; Secer, A.; Cinar, M. On the analytical soliton solutions of (1+1)-dimensional complex coupled nonlinear Higgs field model. Eur. Phys. J. Spec. Top. 2023, 10, 1140. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. Optical solitons with Biswas-Milovic equation for Kerr law nonlinearity. Eur. Phys. J. Plus 2015, 130, 61. [Google Scholar] [CrossRef]
- Gu, Y.; Manafian, J.; Malmir, S.; Eslami, B.; Ilhan, O.A. Lump, lump-trigonometric, breather waves, periodic wave and multi-waves solutions for a Konopelchenko-Dubrovsky equation arising in fluid dynamics. Int. J. Modern Phys. B 2023, 37, 2350141. [Google Scholar] [CrossRef]
- Wang, W.; Hasanirokh, K.; Manafian, J.; Abotaleb, M.; Yang, Y. Analytical approach for polar magnetooptics in multilayer spin-polarized light emitting diodes based on InAs quantum dots. Opt. Quantum Electron. 2022, 54, 137. [Google Scholar] [CrossRef]
- Ali, N.H.; Mohammed, S.A.; Manafian, J. New explicit soliton and other solutions of the Van der Waals model through the ESHGEEM and the IEEM. J. Modern Tech. Eng. 2023, 8, 5–18. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Bin Jebreen, H.; Nuray, R. Bifurcation Analysis and Soliton Behavior of New Combined Kairat-II-X Differential Equation Using Analytical Methods. Mathematics 2025, 13, 4025. https://doi.org/10.3390/math13244025
Zhang J, Bin Jebreen H, Nuray R. Bifurcation Analysis and Soliton Behavior of New Combined Kairat-II-X Differential Equation Using Analytical Methods. Mathematics. 2025; 13(24):4025. https://doi.org/10.3390/math13244025
Chicago/Turabian StyleZhang, Jun, Haifa Bin Jebreen, and Rzayeva Nuray. 2025. "Bifurcation Analysis and Soliton Behavior of New Combined Kairat-II-X Differential Equation Using Analytical Methods" Mathematics 13, no. 24: 4025. https://doi.org/10.3390/math13244025
APA StyleZhang, J., Bin Jebreen, H., & Nuray, R. (2025). Bifurcation Analysis and Soliton Behavior of New Combined Kairat-II-X Differential Equation Using Analytical Methods. Mathematics, 13(24), 4025. https://doi.org/10.3390/math13244025





