Robust Financial Fraud Detection via Causal Intervention and Multi-View Contrastive Learning on Dynamic Hypergraphs
Abstract
1. Introduction
- A causality-aware dynamic hypergraph framework that captures high-order group interactions in realistic financial graphs (review networks and contact networks), with hypergraphs constructed directly from observed structures and attributes in YelpChi, Amazon, and DGraph-Fin.
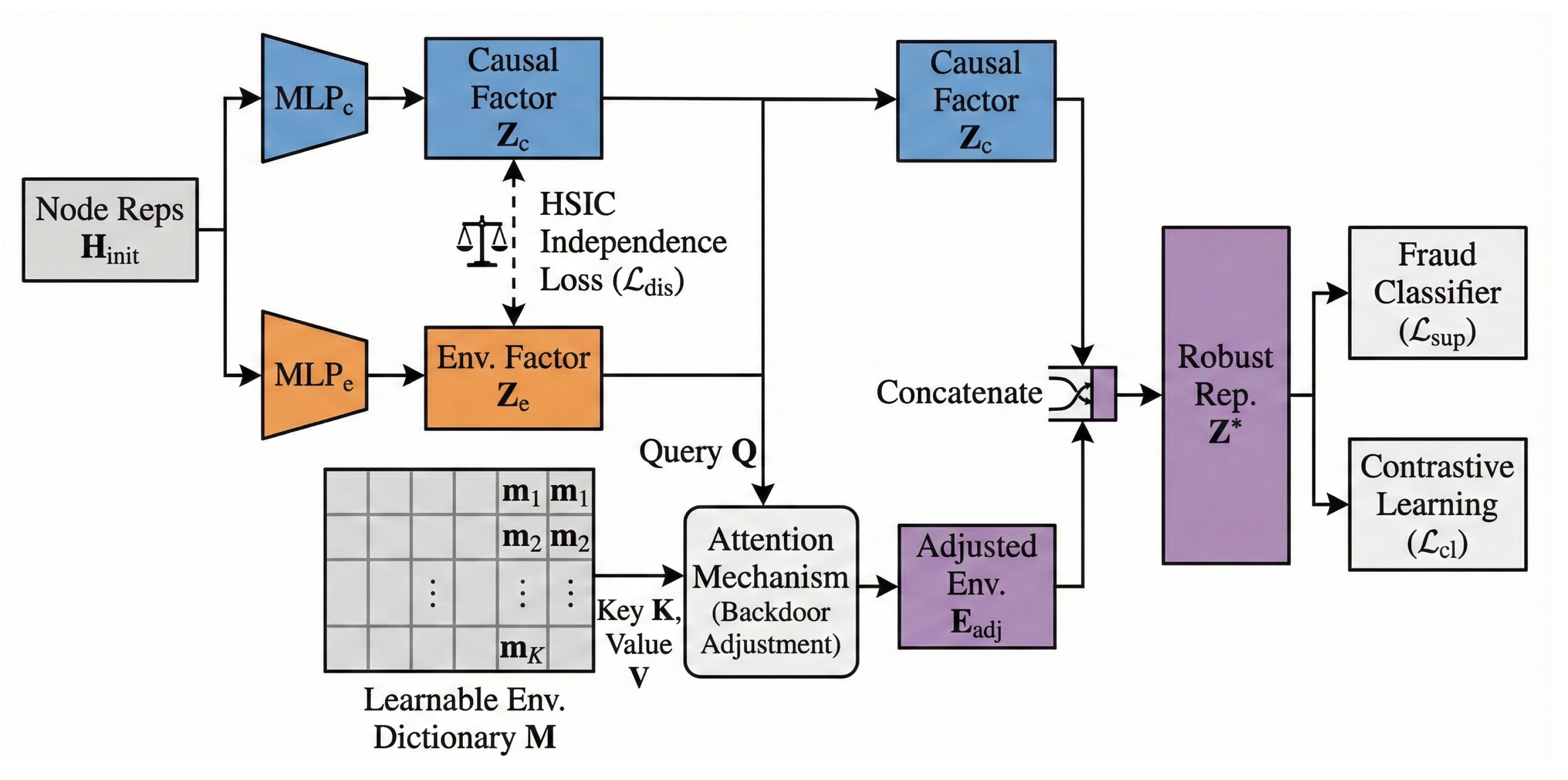
- A Causal Disentanglement Module that decomposes node representations into intrinsic causal and environment-related factors, enforces their independence via HSIC, and applies a dictionary-based backdoor adjustment mechanism to approximate the interventional distribution and suppress spurious environmental correlations.
- A multi-view hypergraph contrastive learning scheme that exploits unlabeled data under label scarcity, using edge dropping and feature masking together with an InfoNCE-style objective defined on disentangled representations.
- A theoretical characterization of the causal graph underlying Causal-DHG, explaining how HSIC-based disentanglement and dictionary-based backdoor adjustment approximate environment-marginalized prediction and analyze robustness and complexity under environment shifts.
- Extensive experiments on YelpChi, Amazon, and DGraph-Fin show consistent improvements over strong baselines such as CARE-GNN and PC-GNN (up to about four percentage points in AUC) and demonstrate that the causal module substantially mitigates performance degradation under feature perturbations and structural noise.
2. Related Work
2.1. Graph Neural Networks for Fraud Detection
2.2. Hypergraph Learning and Dynamic Modeling
2.3. Causal Inference on Graphs
3. Methodology: The Causal-DHG Framework
3.1. Dynamic Hypergraph Construction
- YelpChi (review nodes).(i) User-centric: For each user u, a hyperedge connects all reviews written by u. (ii) Product-centric: For each product p, a hyperedge connects all reviews of p in the window. (iii) Similarity-based: For each review, we connect it with its top-k structurally or textually similar neighbors (given by the released similarity edges) into a hyperedge.
- Amazon (user nodes). (i) Co-item: For each item p, users who reviewed p in a window form a hyperedge. (ii) Temporal co-activity: For each , users reviewing p within the same temporal bin form a hyperedge. (iii) Pattern-based: Users with similar rating or activity statistics (computed from released features) are grouped into hyperedges.
- DGraph-Fin (user nodes with contact edges ). (i) Shared-contact: For each contact user v and window t, a hyperedge connects all u such that occurs in t. (ii) Contact-pattern: For each contact type c and window t, users with at least one outgoing edge of type c in t form a hyperedge. (iii) Local structure: For each user, we build hyperedges over densely connected 1-hop ego neighborhoods to summarize tight contact circles.
3.2. Multi-Head Spatio-Temporal Hypergraph Attention
3.2.1. Spatial Hypergraph Attention
Node-to-Hyperedge Aggregation
Hyperedge-to-Node Aggregation
3.2.2. Temporal Aggregation
3.3. Causal Disentanglement and Backdoor Adjustment
3.3.1. Disentangled Representations
3.3.2. Dictionary-Based Backdoor Adjustment
3.4. Multi-View Contrastive Learning
3.4.1. Hypergraph Augmentations
- Hyperedge dropping. Each hyperedge is removed with probability , simulating missing or noisy group interactions.
- Feature masking. Each feature dimension is masked with probability , simulating incomplete or corrupted features (e.g., missing profile entries).
3.4.2. Contrastive Objective
3.5. Supervised Objective and Joint Training
4. Theoretical Analysis
4.1. Causal Formulation and Disentangled Representations
4.2. HSIC-Based Disentanglement
4.3. Dictionary-Based Backdoor Approximation and Robustness
4.4. Complexity Guarantees
5. Experimental Section
5.1. Experimental Setup
5.1.1. Datasets
YelpChi
Amazon
DGraph-Fin
5.1.2. Baselines
- GCN [23]: A standard spectral graph convolutional network.
- GAT [24]: A graph attention network.
- GraphSAGE [11]: A neighborhood sampling-based GNN.
- H-GNN [7]: A hypergraph neural network applied to static hypergraphs constructed from the same grouping strategy as our method but without temporal or causal modules.
- EvolveGCN [15]: Temporal GNN modeling evolving graphs.
- CARE-GNN [3]: A fraud-specialized GNN with camouflage-resistant neighbor selection.
- PC-GNN [6]: A GNN for imbalanced and camouflaged fraud detection with pick-and-choose sampling.
5.1.3. Evaluation Protocol
5.1.4. Implementation Details
5.2. Overall Performance
5.3. Robustness to Feature Perturbations
5.4. Ablation Study
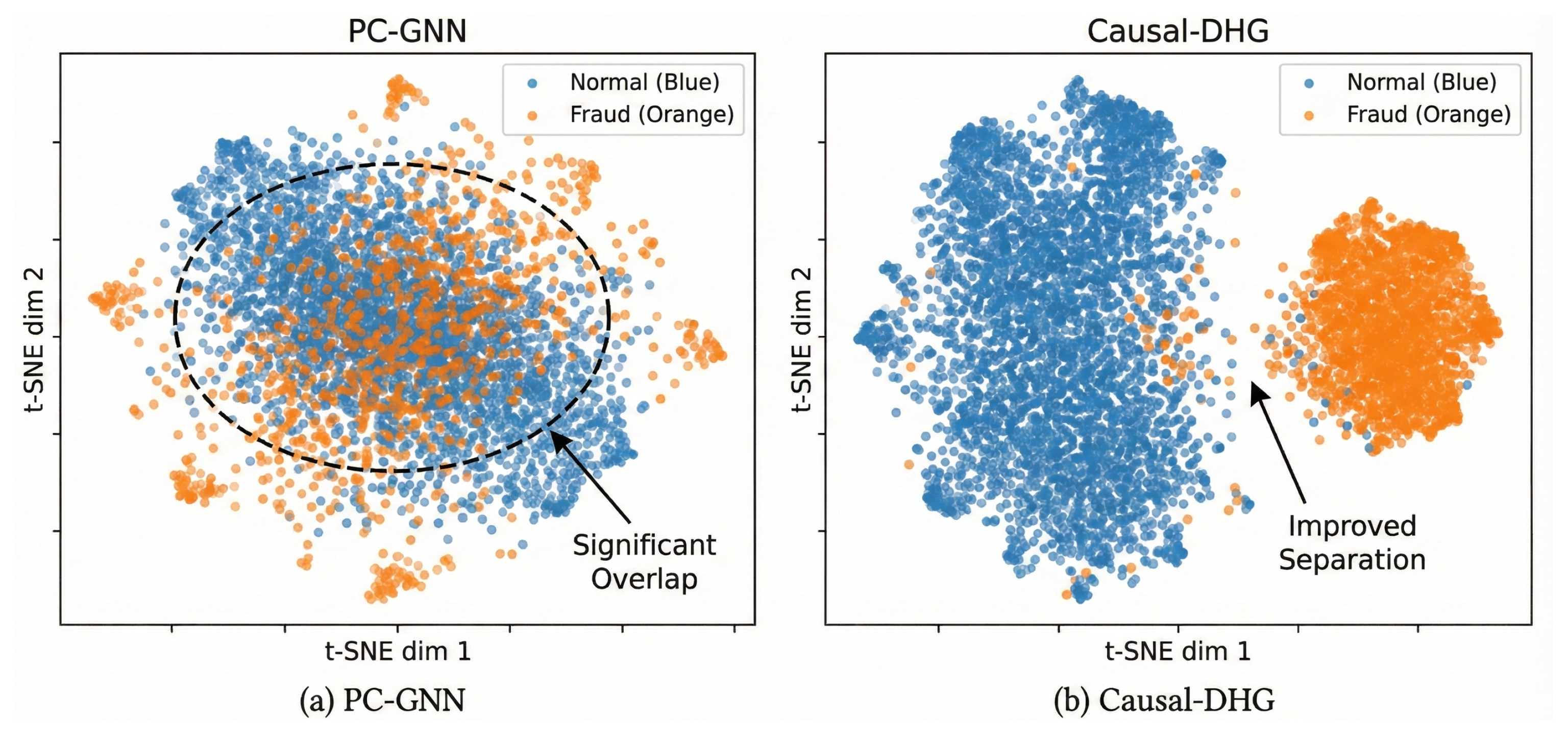
5.5. Representation Analysis
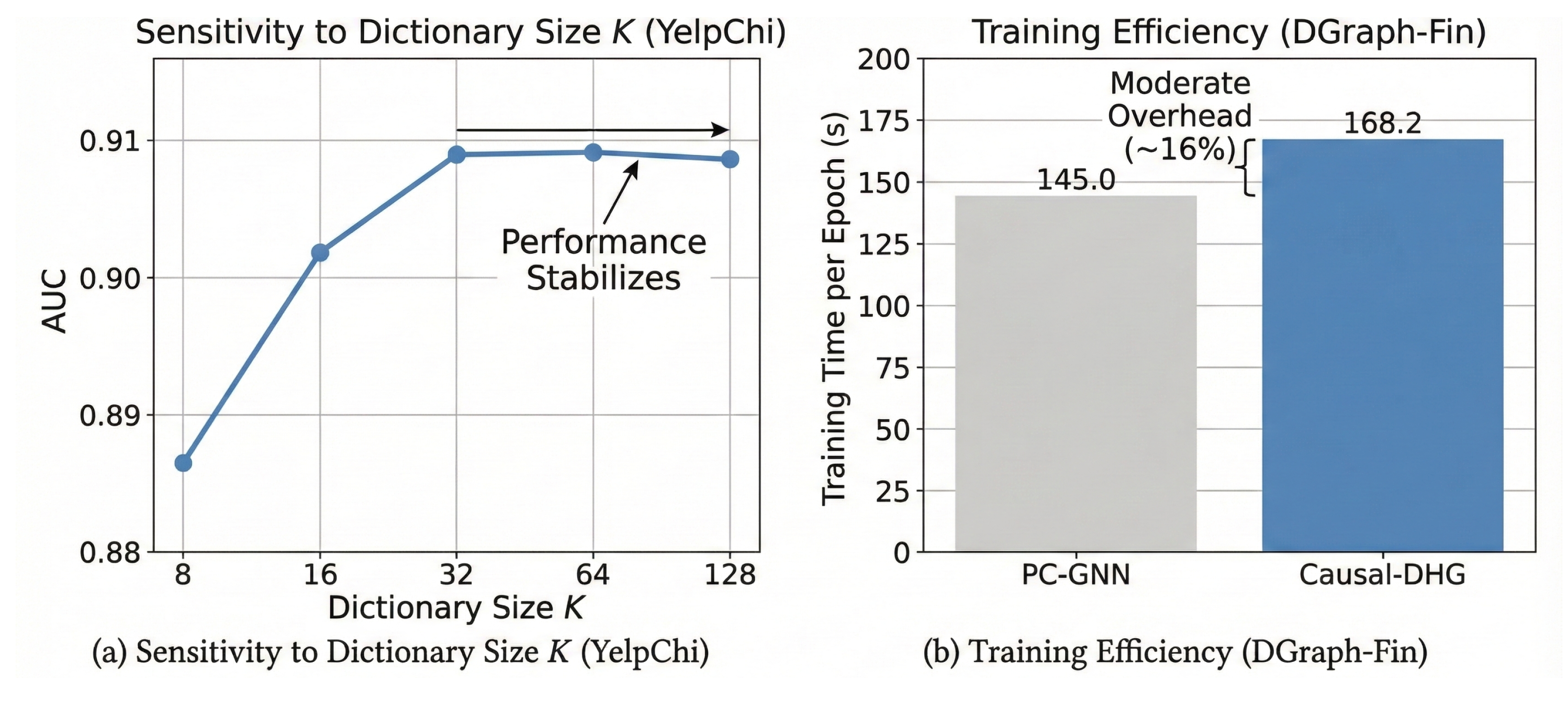
5.6. Hyperparameter Sensitivity and Efficiency
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Additional Experiments and Analyses
Appendix A.1. PR-AUC (Average Precision)
| Method | YelpChi | Amazon | DGraph-Fin |
|---|---|---|---|
| CARE-GNN | 0.7124 ± 0.011 | 0.7850 ± 0.009 | 0.2215 ± 0.013 |
| PC-GNN | 0.7560 ± 0.009 | 0.8120 ± 0.008 | 0.2450 ± 0.011 |
| Causal-DHG | 0.7950 ± 0.008 | 0.8410 ± 0.006 | 0.2940 ± 0.009 |
Appendix A.2. Sensitivity to Hyperedge Size (Top-ksim in Similarity Hyperedges)
| ksim | 5 | 10 | 15 | 20 | 30 |
| AUC | 0.8950 | 0.9020 | 0.9045 | 0.9035 | 0.9030 |
Appendix A.3. Sensitivity to the Number of Time Windows T (DGraph-Fin)
| T | 1 | 3 | 5 | 7 | 10 |
| AUC | 0.7610 | 0.7850 | 0.7920 | 0.7985 | 0.7820 |
Appendix A.4. Robustness to Structural Perturbations
| Method | |||
|---|---|---|---|
| PC-GNN | 0.8810 | 0.8540 | 0.8210 |
| Causal-DHG | 0.9045 | 0.8950 | 0.8820 |
References
- The Nilson Report. Card Fraud Losses Dip to $28.58 Billion in 2020; The Nilson Report: Santa Barbara, CA, USA, 2020. [Google Scholar]
- Xu, D.; Ruan, C.; Korpeoglu, E.; Kumar, S.; Achan, K. Inductive representation learning on temporal graphs. arXiv 2020, arXiv:2002.07962. [Google Scholar] [CrossRef]
- Dou, Y.; Liu, Z.; Sun, L.; Deng, Y.; Peng, H.; Yu, P.S. Enhancing graph neural network-based fraud detectors against camouflaged fraudsters. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual Event, 19–23 October 2020; pp. 315–324. [Google Scholar] [CrossRef]
- Wang, D.; Lin, J.; Cui, P.; Jia, Q.; Wang, Z.; Fang, Y.; Yu, Q.; Zhou, J.; Yang, S.; Qi, Y. A semi-supervised graph attentive network for financial fraud detection. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; IEEE: New York, NY, USA, 2019; pp. 598–607. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, C.; Li, L.; Zhou, J.; Li, X.; Song, L.; Qi, Y. Geniepath: Graph neural networks with adaptive receptive paths. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4424–4431. [Google Scholar] [CrossRef]
- Liu, Y.; Ao, X.; Qin, Z.; Chi, J.; Feng, J.; Yang, H.; He, Q. Pick and choose: A GNN-based imbalanced learning approach for fraud detection. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 12–23 April 2021; pp. 3168–3177. [Google Scholar] [CrossRef]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3558–3565. [Google Scholar] [CrossRef]
- Bengio, Y.; Deleu, T.; Rahaman, N.; Ke, R.; Lachapelle, S.; Bilaniuk, O.; Goyal, A.; Pal, C. A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar] [CrossRef]
- Pearl, J. Causality, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Wu, Q.; Zhang, H.; Yan, J.; Wipf, D. Handling distribution shifts on graphs: An invariance perspective. arXiv 2022, arXiv:2202.02466. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, J.; Zhang, J.; Leung, M.F. Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection. Mathematics 2025, 13, 2343. [Google Scholar] [CrossRef]
- Bretto, A. Hypergraph Theory: An Introduction; Springer: Cham, Switzerland, 2013; Volume 1, pp. 209–216. [Google Scholar]
- Jiang, J.; Wei, Y.; Feng, Y.; Cao, J.; Gao, Y. Dynamic hypergraph neural networks. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 2635–2641. [Google Scholar] [CrossRef]
- Pareja, A.; Domeniconi, G.; Chen, J.; Ma, T.; Suzumura, T.; Kanezashi, H.; Kaler, T.; Schardl, T.; Leiserson, C. Evolvegcn: Evolving graph convolutional networks for dynamic graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5363–5370. [Google Scholar] [CrossRef]
- Rossi, E.; Chamberlain, B.; Frasca, F.; Eynard, D.; Monti, F.; Bronstein, M. Temporal graph networks for deep learning on dynamic graphs. arXiv 2020, arXiv:2006.10637. [Google Scholar] [CrossRef]
- Xia, X.; Yin, H.; Yu, J.; Wang, Q.; Cui, L.; Zhang, X. Self-supervised hypergraph convolutional networks for session-based recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 4503–4511. [Google Scholar] [CrossRef]
- Schölkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward causal representation learning. Proc. IEEE 2021, 109, 612–634. [Google Scholar] [CrossRef]
- Kuang, K.; Xiong, R.; Cui, P.; Athey, S.; Li, B. Stable Prediction with Model Misspecification and Agnostic Distribution Shift. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar] [CrossRef]
- Gretton, A.; Bousquet, O.; Smola, A.; Schölkopf, B. Measuring Statistical Dependence with Hilbert-Schmidt Norms. In Proceedings of the Algorithmic Learning Theory (ALT), Singapore, 8–11 October 2005. [Google Scholar] [CrossRef]
- Bae, I.; Jeon, H.G. Disentangled multi-relational graph convolutional network for pedestrian trajectory prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 911–919. [Google Scholar] [CrossRef]
- Yang, D.; Zha, D.; Kurokawa, R.; Zhao, T.; Wang, H.; Zou, N. Factorizable Graph Convolutional Networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Virtual Event, 6–12 December 2020. [Google Scholar] [CrossRef]
- Kipf, T. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10-48550. [Google Scholar] [CrossRef]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar] [CrossRef]


| Dataset | Nodes | Edges | Node Feature Dim | Fraud Ratio |
|---|---|---|---|---|
| YelpChi | 45,954 (reviews) | 3,846,979 | 32 | 14.5% |
| Amazon | 11,944 (users) | 4,398,392 | 25 | 6.8% |
| DGraph-Fin | 3,700,550 (users) | 4,300,999 | 17 | 1.04% |
| Method | YelpChi | Amazon | DGraph-Fin | |||
|---|---|---|---|---|---|---|
| AUC | F1-Macro | AUC | F1-Macro | AUC | F1-Macro | |
| GCN | ||||||
| GAT | ||||||
| GraphSAGE | ||||||
| H-GNN | ||||||
| EvolveGCN | ||||||
| CARE-GNN | ||||||
| PC-GNN | ||||||
| Causal-DHG | ||||||
| Method | ||||
|---|---|---|---|---|
| PC-GNN | 0.8810 | 0.8450 | 0.7920 | 0.7150 |
| Causal-DHG | 0.9045 | 0.8911 | 0.8750 | 0.8520 |
| Variant | AUC | F1-Macro |
|---|---|---|
| Causal-DHG (full) | 0.9045 | 0.7820 |
| w/o Causal Module | 0.8720 | 0.7310 |
| w/o Hypergraph (pairwise only) | 0.8850 | 0.7540 |
| w/o Contrastive Learning | 0.8910 | 0.7620 |
| Method | Train Time/Epoch (s) | Inference Time (ms) |
|---|---|---|
| GraphSAGE | 15.2 | 45 |
| CARE-GNN | 128.5 | 210 |
| PC-GNN | 145.0 | 235 |
| Causal-DHG | 168.2 | 260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X. Robust Financial Fraud Detection via Causal Intervention and Multi-View Contrastive Learning on Dynamic Hypergraphs. Mathematics 2025, 13, 4018. https://doi.org/10.3390/math13244018
Luo X. Robust Financial Fraud Detection via Causal Intervention and Multi-View Contrastive Learning on Dynamic Hypergraphs. Mathematics. 2025; 13(24):4018. https://doi.org/10.3390/math13244018
Chicago/Turabian StyleLuo, Xiong. 2025. "Robust Financial Fraud Detection via Causal Intervention and Multi-View Contrastive Learning on Dynamic Hypergraphs" Mathematics 13, no. 24: 4018. https://doi.org/10.3390/math13244018
APA StyleLuo, X. (2025). Robust Financial Fraud Detection via Causal Intervention and Multi-View Contrastive Learning on Dynamic Hypergraphs. Mathematics, 13(24), 4018. https://doi.org/10.3390/math13244018






