Analysis of Cascading Conflict Risks of Autonomous Vehicles in Heterogeneous Traffic Flows

Abstract

As autonomous vehicles proliferate in mixed traffic streams, heterogeneous flows comprising vehicles with diverse driving strategies introduce significant complexity to cascading conflict propagation, while conventional conflict risk assessment methods based on homogeneous assumptions fail to capture the intricate risk transmission mechanisms embedded in high-dimensional trajectory data. To address the challenge, this study establishes a systematic data analytics framework. Firstly, a conflict risk quantification model is proposed by integrating safety field theory considering heterogeneity traffic flow, achieving precise quantification of microscopic interaction risks through vehicle risk coefficients that characterize differential risk sensitivity across distinct driving strategies. Secondly, a cascading conflict identification algorithm is designed to extract cascading propagation chains from trajectory data. Thirdly, a method to analyze cascading conflict risk propagation is developed using CatBoost (v1.2.8), coupled with SHapley Additive ExPlanations interpretability analysis to systematically reveal the propagation mechanisms underlying cascading conflicts. Empirical findings indicate that primary conflict intensity and longitudinal relative speed are the dominant predictive features for secondary conflicts; moreover, local traffic heterogeneity entropy exerts a significant moderating effect—quantitative analysis reveals that higher heterogeneity increases the likelihood of secondary conflicts under identical primary risk conditions. Comprehensive validation using SUMO microscopic simulation demonstrates that the proposed data analytics pipeline effectively identifies and accurately predicts and analyzes secondary conflicts across diverse traffic scenarios. This framework provides interpretable foundations for intelligent conflict-risk identification systems, propagation-mechanism analysis, and proactive safety interventions in heterogeneous traffic environments, offering significant implications for real-time traffic monitoring and intelligent transportation system design.

1. Introduction

During the development and popularization of autonomous vehicles, heterogeneous traffic flows composed of human-driven vehicles and autonomous vehicles with different driving strategies coexist in traffic scenarios. Compared with homogeneous traffic flows, the penetration rate and driving strategies of autonomous vehicles in heterogeneous traffic environments exert complex influences on cascading conflict risk propagation: at different penetration levels, the interaction patterns between autonomous vehicles and human-driven vehicles undergo fundamental changes—at low penetration rates, a small number of autonomous vehicles may intensify traffic flow disturbances due to behavioral differences, while at high penetration rates, they may reduce systemic risks through coordinated and consistent behavioral patterns; different autonomous driving strategies exhibit significant variations in risk perception, reaction speed, and collision avoidance behaviors, thereby leading to more complex risk propagation. Traditional risk assessment methods based on homogeneous traffic flow assumptions are inadequate for accurately identifying cascading risk propagation. Establishing methods that reflect risk propagation patterns among vehicles in heterogeneous traffic flows and revealing the influence of different factors on risk propagation are critical issues that urgently need to be addressed to improve the safety of mixed traffic flows.

2. Related Work

Autonomous vehicles can be classified into multiple types according to different driving styles. Some studies categorize them analogously to human driving styles into conservative, normal, and aggressive types [1]: conservative autonomous vehicles typically exhibit low-speed driving, maintain larger following distances, and tend to avoid risks; aggressive types prioritize efficient passage and are willing to assume higher risks to reduce delays; normal autonomous vehicles fall between these two extremes, with behavioral patterns approximating the average level of human drivers. Other studies approach from the overall decision-making logic of autonomous vehicles interacting with other traffic participants in mixed traffic environments, classifying autonomous driving strategies into four categories: defensive, competitive, negotiative, and cooperative. Defensive strategies assume that surrounding vehicles may exhibit irrational behaviors, prioritizing risk avoidance through conservative car-following and yielding principles; competitive strategies assume rational behavior from other vehicles and enhance individual passage efficiency through deep learning or reinforcement learning, but are prone to increased congestion or collision risks due to overconfidence; negotiative strategies allocate right-of-way through continuous negotiation via implicit communication, improving efficiency while ensuring safety; cooperative strategies rely on explicit communication and centralized/distributed scheduling to achieve globally or locally optimal fleet coordination [2].

Most studies on traffic conflict techniques have focused on pairwise interactions between two road users, emphasizing vehicle–vehicle conflict definitions [3,4,5], the construction of conflict measures/indices [6,7,8,9], the assessment of conflict severity [10,11], and conflict evaluation and prediction [12,13]. The characteristics of different risk assessment methods are shown in

Table 1. Characteristics of different risk assessment methods.

Method	Key Challenge Addressed	Limitations
Time-based indicator method [11,14]	Efficient in simple scenarios; mainly applied to SAE Level 1–2 automated driving	Difficult to account for multiple influencing factors simultaneously.
Potential field-based method [7,15]	Capable of simultaneously considering multiple factors within a unified framework.	Most models assume homogeneous vehicle behavior and do not explicitly account for differences in risk sensitivity arising from varying driving styles.

.

In recent years, research has increasingly considered multi-participant settings. Zhong et al. [14] matched conflicts across different vehicle pairs and developed a rule-based chain extraction algorithm to investigate latent characteristics of cascading conflicts. Samerei et al. [4], using five years of crash, traffic, and cross-section data from 11 suburban freeways in Iran, introduced a hybrid pipeline—Latent Class Clustering (LCC)—Random-Parameters Binary Logit (RPBLM)—interpretable machine learning—to handle unobserved heterogeneity, estimate random effects, and interpret factor interactions. Samerei et al. [16] developed a hybrid framework that combines latent class clustering, random-parameter binary logit models and interpretable machine learning to analyze how two-vehicle freeway crashes escalate into chain-reaction crashes and to identify key traffic, geometric and environmental factors and their critical thresholds that govern this transition. Building on a detailed incident database from Hampton Roads, Virginia, Zhang et al. [17] classified events into three categories—independent incidents, one primary–one secondary, and one primary with ≥2 secondary incidents—and employed an ordered regression model to analyze determinants and spatiotemporal identification boundaries of secondary incidents.

The summary of the characteristics of some of the research mentioned above on vehicle conflicts and their differences from this study are shown in

Table 2. Summary of research status.

Study	Research Focus	Traffic Flow Type	Type of Conflicts (Two-Vehicle/Multi-Vehicle)	Risk Quantification
Zhong et al. (2024) [14]	Cascading conflict chain extraction and evolution patterns.	Homogeneous	Multi-vehicle	TTC/MTTC-
Samerei & Aghabayk (2024) [16]	Transition from two-vehicle crashes to chain-reaction crashes.	Homogeneous	Multi-vehicle	Incident-level binary label (CRC vs. non-CRC)
Zhang & Khattak (2010) [17]	Multiple secondary incidents and event adversity on freeways.	Homogeneous	Multiple secondary incidents	-
Qi & Zheng (2025) [11]	Improved IDM-based vehicle conflict risk identification using ITTC in a calibrated VISSIM environment.	Homogeneous	Two-vehicle	Inverse TTC
The present study	Cascading conflict risk propagation in heterogeneous traffic.	Heterogeneous	Multi-vehicle	Safety potential field

.

In summary, existing research still has the following shortcomings in vehicle conflict risk analysis:

• Most current traffic conflict studies are based on homogeneous traffic flow assumptions or assume that autonomous vehicles share identical driving behaviors and characteristic parameters, neglecting the heterogeneous interaction features among vehicles with different driving styles. This limits the applicability of risk assessment models under mixed traffic conditions and results in insufficient adaptability to mixed traffic environments.
• In terms of conflict identification, existing research mainly focuses on two-vehicle conflict processes, lacking systematic modeling of multi-vehicle spatiotemporal correlations and cascading conflict propagation paths. This makes it difficult to reveal the diffusion mechanism of conflict risks in heterogeneous traffic flows.
• Although some studies have explored cascading conflict phenomena, there is still a lack of data-driven in-depth analysis on the core question of “under what conditions prior conflicts can trigger secondary conflicts”. Key mechanisms, such as how different characteristics synergistically interact, have yet to be systematically explained, making it difficult to uncover the propagation mechanisms of conflict risks in mixed traffic flows and limiting the formulation of traffic safety prevention and control strategies.

To address the aforementioned issues, this study systematically analyzes the propagation characteristics of chain-reaction conflict risks in heterogeneous traffic flows based on the logic of “risk quantification-association identification-mechanism exploration”.

• Extend the safety potential field theory to heterogeneous traffic flow environments and introducing a vehicle risk coefficient to capture differences in risk sensitivity across autonomous driving strategies. This mathematical framework captures differential risk sensitivity across autonomous driving strategies through parameterized models, enabling fine-grained risk quantification at the micro-interaction level from high-dimensional trajectory data.
• Design a data-driven graph search algorithm that transcends traditional two-vehicle conflict analysis limitations. By defining rigorous spatiotemporal proximity and vehicle association criteria through computational geometry and network analysis, the algorithm efficiently extracts cascading conflict propagation paths and quantifies impact ranges from large-scale trajectory datasets.
• At the level of chain-reaction conflict risk propagation identification and mechanism analysis, the study follows the logic of “association identification-mechanism analysis,” establishing a propagation mechanism exploration framework based on CatBoost and SHapley Additive ExPlanations (SHAP) interpretability analysis to deeply examine the propagation mechanisms of chain-reaction conflict risks in heterogeneous traffic flows.

The paper is structured as follows: Section 1 introduces the background, research motivation, and problem statement; Section 2 reviews the related work; Section 3 validates the effectiveness of the conflict identification method using real-world NGSIM trajectory data; Section 4 analyzes the propagation patterns of cascading conflicts under different autonomous driving strategies through SUMO simulation experiments and identifies key influencing factors; and Section 5 summarizes the paper and outlines future research directions.

3. Methodology

3.1. Quantification of Vehicle Conflict Risk Based on the Risk Field

The key to ensuring autonomous driving safety lies in conducting comprehensive and reasonable risk assessments to identify potential hazards and inform decision-making. Therefore, risk assessment has become a critical component in guaranteeing the safe operation of autonomous vehicles [18]. In this study, conflict risk is distinguished from conventional time-to-collision (TTC) and collision-risk notions used in previous research [5,19]. TTC is a purely kinematic indicator that measures the remaining time until two vehicles geometrically collide under the assumption of constant relative motion, and is therefore not a probabilistic risk measure. Collision risk metrics typically assess the probability or severity of an actual collision based on the host vehicle’s current state, TTC-like surrogate parameters, and the capabilities of perception, prediction, and control modules. Building on the traffic-conflict paradigm, the present study defines conflict risk as a safety-potential-field value that characterizes the intensity of unsafe interactions between vehicles. This indicator can be non-zero even when no physical collision is imminent, and it explicitly incorporates vehicle heterogeneity and local traffic-flow heterogeneity. As a result, the proposed conflict-risk measure focuses on pre-crash interaction hazards and cascading propagation among multiple vehicles, rather than on the probability of a single collision event. The safety potential field theory can comprehensively characterize the driving safety tendency of vehicles by integrating multiple factors within the field’s range of influence. It negates the single-dimensional evaluation model of “high speed equals danger” and couples various parameters to describe the current driving safety of vehicles through safety potential field levels, demonstrating strong robustness. The field strength calculation formula [15] is

$${|E}_v|=\lambda {\displaystyle \frac{{\mathrm{e}}^{{-\beta }_{1}a\cos \theta }}{\left|d_{ij}^{\prime }\right|}}$$

(1)

$$\left|d_{ij}^{\prime }\right|=\sqrt{{\left[(x^{\prime }-x_0){\displaystyle \frac{\tau }{{\mathrm{e}}^{\sigma v}}}\right]}^2+{\left[(y^{\prime }-y_0)\tau \right]}^2}$$

(2)

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)& \mathrm{s}\mathrm{i}\mathrm{n}\left(\phi \right)\\ -\mathrm{s}\mathrm{i}\mathrm{n}\left(\phi \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

(3)

where ${|E}_v|$ represents the magnitude of the field strength generated by the vehicle at a certain point, $d_{ij}^{\prime }$ is the corrected distance, $\phi$ is the steering angle of the field-source vehicle, $(x,y)$ denotes the original coordinates, $(x^{\prime },y^{\prime })$ represents the corresponding deflection values after considering the steering angle of the vehicle relative to the original coordinates, $\theta$ is the angle between the spatial coordinates of the vehicle’s centroid $\left(x_0,y_0\right)$ and a surrounding point relative to the direction of the field-source vehicle’s velocity, $a$ is the acceleration of the field-source vehicle, $v$ is the velocity of the field-source vehicle, $\sigma$ is the speed-related coefficient to be determined, and $\lambda , {\beta }_1, \tau$ are undetermined parameters.

Figure 1a–d illustrate the spatial distribution characteristics of the vehicle safety potential field under different motion states based on the preceding vehicle’s acceleration and lane-changing process (the horizontal axis X in the figures represents the longitudinal distance on the road, the vertical axis Y represents the lateral position on the road, and the red circle marked represents the vehicle’s center of mass). It can be observed that the field strength magnitude is closely related to the vehicle’s motion state. When a lane-changing vehicle accelerates, a distinct high-field-strength elliptical region forms ahead of it. The field strength ahead of an accelerating vehicle is significantly higher than that of a vehicle moving at a constant speed. Additionally, the interaction between vehicles manifests as a superposition effect in the field strength distribution, with dense vehicle regions forming continuous high-risk zones.

The potential driving risks of autonomous vehicles can be preliminarily assessed using safety potential fields. Meanwhile, the current driving risk of a vehicle is also related to factors such as its own motion state and attributes. To further quantify the conflict risk between different types of autonomous vehicles and other vehicles, referring to existing research [15,18], the conflict risk CR imposed on vehicle i by vehicle i − 1 is obtained as

$${|CR}_{i-1,i}|=\left|E_v^{i-1}\right|\cdot q{\cdot \zeta }_i={\zeta }_i\lambda {\displaystyle \frac{{\mathrm{e}}^{\alpha v_{i-1}-{\beta }_1{a}_{i-1}+{\beta }_2\cdot v_i}}{\Delta x\tau }}$$

(4)

$${\zeta }_i={({\mathrm{e}}^{{\displaystyle \frac{{\epsilon }_1{t}_r}{{{\epsilon }_{2}b}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}})}^{-\xi }$$

(5)

where ${\zeta }_i$ denotes the vehicle risk coefficient, representing the sensitivity of different vehicle types to potential conflict risks. A smaller ${\zeta }_i$ indicates better vehicle performance and a lower probability of encountering conflicts under identical environmental conditions. For instance, high-level autonomous vehicles, equipped with advanced sensing and decision-making algorithms, can identify and respond to potential conflicts more rapidly and accurately. Thus, their risk coefficients are lower than those of low-level autonomous vehicles. The value of the risk coefficient can be adjusted according to vehicle-specific characteristics such as reaction time and maximum deceleration capability. $t_r$ denotes the vehicle reaction time (s); $b_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum available deceleration ($\mathrm{m}\cdot {\mathrm{s}}^{-2}$), and ${\epsilon }_1$, ${\epsilon }_2$, and $\xi$ are parameters to be calibrated.

3.2. Identification of Cascading Conflict Risk

Cascading conflicts refer to the phenomenon in which the evasive actions taken by a following vehicle after an initial conflict subsequently affect nearby vehicles [13].

When a pair of vehicles is involved in a conflict, surrounding vehicles often initiate avoidance maneuvers that alter their dynamic states, which can influence adjacent vehicles in the same or neighboring lanes. This chain reaction may generate new traffic conflicts, forming a regional cascading effect.

In non-free mixed traffic environments, cascading conflicts tend to occur more frequently and exhibit greater complexity. On one hand, vehicles of different types vary in their risk perception capabilities, reaction times, and avoidance strategies. Once an initial conflict is triggered, these heterogeneous responses may become uncoordinated, forcing subsequent vehicles to take abrupt avoidance actions and thereby increasing the likelihood of secondary conflicts. On the other hand, the diversity of motion states and driving strategies within a region enhances traffic flow uncertainty, causing conflicts to re-emerge even after an initial disturbance has been mitigated.

The reaction process of a cascading conflict can be illustrated using the trajectory sequence of vehicles and speed curves in a same-lane car-following scenario, as shown in Figure 2a,b. At a given time, Vehicle 1 decelerates and conflicts with Vehicle 2, prompting Vehicle 2 to perform an evasive maneuver (deceleration). Consequently, Vehicle 3, stimulated by Vehicle 2’s deceleration, also initiates avoidance behavior at a subsequent moment, and the same applies to Vehicle 4. After Vehicle 2 decelerates, its conflict with Vehicle 1 is resolved, but a new conflict emerges between Vehicles 2 and 3; similarly, when Vehicle 3 slows down, its conflict with Vehicle 2 subsides while creating a potential conflict risk for Vehicle 4. This chain of reactions constitutes the cascading conflict effect. Lateral cascading conflicts across adjacent lanes follow a similar mechanism, with their influence extending to a broader spatial scope within the traffic stream.

Considering the sudden and short-term characteristics of accident risk, the overall driving risk can be decomposed into a steady phase and a local mutation phase, as illustrated in Figure 3. This temporal segmentation enables the identification of vehicles that first exhibit a pronounced risk peak exceeding the predefined threshold $C{R}_{\mathrm{thr}}$. The collection of such vehicles is used to determine the spatial and temporal origins of emerging conflicts within the traffic stream.

Step 1: Heterogeneous dynamic conflict detection. Define a single conflict between vehicles $v_i$ and $v_j$ as $c_{ij}$ if there exists a time interval $[t_s,t_e]$ such that the conflict–risk signal exceeds the threshold.

$$C{R}_{ij}\left(t\right)>C{R}_{\mathrm{t}\mathrm{h}\mathrm{r}},\forall t\in [t_s, t_e]$$

(6)

where $[t_s,t_e]$ is the conflict duration. For a surrounding vehicle $k$, the influence window induced by $c_{ij}$ is obtained as

$$[t_s, t_e+t_r^k]$$

(7)

where $t_r^k$ denotes the reaction time of vehicle $k$. Vehicles $v_i$ and $v_j$ are the two participants involved in $c_{ij}$.

Step 2: Associated-conflict identification. Within a given horizon, enumerate all conflicted pairs and form the initial conflict set $C_0$. Select the earliest detected conflict $c_{mn}$. Based on spatio-temporal proximity, check whether any other conflict $c_{pq}$ involving vehicles $v_p$ and $v_q$ occurs within the influence window of $c_{mn}$. If so, declare $c_{mn}$ and $c_{pq}$ cascading and add them to the cascading set $X$. For two adjacent conflicts $c_a$ and $c_b$, any common vehicle serves as a bridging vehicle linking $c_a$ and $c_b$. Accordingly, $c_a$ and $c_b$ satisfy:

(a)

Spatio-temporal overlap

$$[t_s^{\left(a\right)}, t_e^{\left(a\right)}+t_r^{*}] \cap [t_s^{\left(b\right)}, t_e^{\left(b\right)}]\ne \mathrm{\varnothing }$$

(8)

where $t_r^{\mathrm{*}}$ is the reaction time of the relevant bridging vehicle;

(b)

Vehicle relatedness

$$\left\{\mathrm{participants} \mathrm{of} c_a\right\} \cap \left\{\mathrm{participants} \mathrm{of} c_b\right\}\ne \mathrm{\varnothing }$$

(9)

Step 3: Breadth-first graph search. Starting from $C_0$, perform a breadth-first graph search over the conflict graph: if there exists any conflict whose relation to any element in $X$ satisfies Step 2, include it in $X$. Continue until no new associated conflicts $c_p$ can be found. The resulting set defines the preliminary cascading-conflict propagation network.

Step 4: Branch consolidation across chains. If during matching, a previously detected conflict has already been included in another cascading set $X_n$, also append the current conflict to $X_n$. This captures the fact that one conflict may trigger multiple downstream branches that progressively expand the conflict network over time.

Step 5: Spatial merging. Merge preliminarily identified conflicts according to a spatial-neighborhood criterion to avoid duplication and to improve the accuracy and robustness of subsequent analyses.

3.3. Mechanism Analysis of Cascading Conflict Risk Propagation

A deep understanding of the factors that cause primary conflict risks to trigger secondary conflict risks is crucial for developing effective risk prevention and control strategies. Traditional studies have primarily focused on the temporal characteristics of secondary conflicts, while overlooking a more fundamental question—under what conditions do upstream conflict risks propagate and induce secondary risks in heterogeneous traffic flows? To investigate the triggering mechanism of secondary conflicts, we formulated the problem as a binary classification task within a supervised learning framework. This section employs the CatBoost model to analyze the influence of different factors on the propagation of conflict risk and to reveal their respective contribution mechanisms.

To investigate the triggering mechanism of secondary conflict risk in heterogeneous traffic flows, the problem is formulated as a binary classification task within a supervised learning framework. Specifically, based on the system state at the occurrence of a primary conflict—such as vehicle speed, acceleration, and relative position—the presence or absence of secondary conflict risk within a predefined time window is used to define the label function as follows:

$$y=\left\{\begin{array}{ll}1,\hfill & t\in [t_0,t_0+T]\hfill \\ 0,\hfill & \mathrm{other}\hfill \end{array}\right.$$

(10)

where T denotes the predefined observation window (set to 5 s based on prior analytical results). Positive samples are directly extracted from the identified cascading conflicts: for each cascading conflict chain, all conflicts except the initial one are treated as positive instances. Negative samples are defined as cases in which the propagation conditions are satisfied but no secondary conflict occurs. To obtain such samples, all individual conflict sets are first identified as follows:

$$C_{\sin \mathrm{gle}}=C_{\mathrm{all}}\setminus {\displaystyle \underset{k}{\cup }{C}_k}$$

(11)

where $C_{\mathrm{a}\mathrm{l}\mathrm{l}}$ denotes the set of all detected conflicts, $C_k$ is the set of conflicts in the $k$-th cascading conflict chain, and $C_{\sin \mathrm{gle}}$ concludes all conflicts that do not belong to any cascading conflict chain.

For each individual conflict, a negative sample is defined if the following conditions are satisfied: there exists a following vehicle $k$ such that $d_{ik}\left(t\right)>d_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ and no conflict occurs within the observation window $[t_s, t_s+T]$, where $d_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ represents the critical car-following distance.

To balance the number of positive and negative samples, the Synthetic Minority Over-sampling Technique (SMOTE) is applied. In the feature space, a synthetic sample $x_{\mathrm{n}\mathrm{e}\mathrm{w}}$ generated between two positive samples $x_i$ and $x_j$ is defined as

$$X_{syn}=X_i+\mu \cdot (X_j-X_i)$$

(12)

where $\mu$ is a random interpolation coefficient uniformly distributed in $[0,1]$.

Feature engineering is essential for capturing the intrinsic characteristics of heterogeneous traffic flows. In this study, conflicts that directly trigger secondary conflicts are defined as primary conflicts. To investigate the factors contributing to secondary conflicts across different time intervals—from the occurrence of a primary conflict to the formation of a secondary one—a multi-level temporal feature framework is established. This framework extracts three categories of temporal features for each pair of secondary conflict and its corresponding primary conflict, including individual motion features, interactional features, and environmental contextual features. The detailed feature extraction scheme is summarized in

Table 3. Feature description.

Feature Category	Feature Name	Symbol	Description	Unit/Range
Individual Features	Speed	v	Vehicle Speed	m/s
	Acceleration	a	Vehicle Acceleration	m/s2
	Vehicle Type	d	Driving Strategy	{0, 1, 2}
	Acceleration/Deceleration State	A	Acceleration/Deceleration State	{0, 1}
Interaction Features	Relative Speed	$v_{rel}=v_j-v_i$	Relative Speed	m/s
	Relative Acceleration	$a_{rel}=a_j-a_i$	Relative Acceleration	m/s2
	Type Matching	T	Vehicle Type Matching	{0, 1}
Environmental Characteristics	Heterogeneity Entropy	$H$	Local Traffic Flow Heterogeneity	s
	Primary Conflict Risk	CR	Primary Conflict Risk Value	-

.

For the local heterogeneity entropy (H) mentioned in Table 3, the calculation method is given by the following equation:

$$H=-\sum _{k=0}^2{p}_k\mathrm{l}\mathrm{o}\mathrm{g}{ p}_k$$

(13)

where $p_k=n_k/N$ denotes the local proportion of each vehicle type, N represents the total number of vehicles within the study area, $n_k$ represents the number of a certain type of vehicle within the study area.

4. Results

4.1. Validation of Cascading Conflict Identification Method

4.1.1. Validation of the Single Conflict Identification Model

Considering that the NGSIM dataset provides critical benchmark data of high-fidelity human driving trajectories in densely interactive traffic scenarios, which are essential for establishing foundational models of cascading conflicts, this study selects the NGSIM dataset as the basis for methodological validation.

The single-conflict identification model is validated using the NGSIM dataset, which provides high-resolution vehicle trajectory data collected by overhead cameras. Based on this dataset, the safety potential field model is applied to calculate the conflict risk ($CR$) between each vehicle and its surrounding vehicles (particularly the preceding vehicle) throughout the driving process. It is assumed that the same pair of vehicles can experience at most one conflict within a given time interval $\Delta t$. When the conflict risk $CR$ exerted by a specific vehicle on another exceeds a predefined threshold, the two vehicles are considered to be in a conflict relationship.

The actual vehicle operation states extracted from the empirical data are used as quantitative indicators to calibrate and refine the influence range of the safety potential field model. A genetic algorithm (GA) is employed to optimize the model parameters $\alpha$, ${\beta }_1$, and ${\beta }_2$. The optimization process minimizes the discrepancy between the modeled field-intensity range and the headway-time distribution observed in the empirical dataset. The Root Mean Square Error (RMSE) is adopted as the evaluation metric for parameter calibration and model validation. In addition, the values of other parameters such as $\lambda$ and $\tau$ are determined with reference to previous studies [18,20]. The final calibrated parameter values of the safety potential field model are summarized in

Table 4. Parameter values.

Parameter	Value	Parameter	Value
$\lambda$	0.061	$\tau$	2.717
${\beta }_1$	0.312	$\xi$	1.212
${\beta }_2$	0.117	${\epsilon }_1$	0.924
$\sigma$	0.031	${\epsilon }_2$	2.513

.

The effectiveness of the safety potential field model in identifying vehicle conflicts is validated using empirical driving data. During driving, when a vehicle perceives a potential conflict risk, it typically changes its motion state—such as initiating sustained braking—to reduce speed. This process reflects the vehicle’s perception and response to risk, and the model’s validity can thus be examined by evaluating the consistency between the conflict risk value and the change in vehicle speed. Figure 4 illustrates the variation in conflict risk value and vehicle speed over time during a typical conflict process. The horizontal axis represents time (s), the left vertical axis denotes the instantaneous conflict risk value CR calculated based on the safety potential field model, and the right vertical axis indicates the vehicle speed v (km/h). The blue solid line depicts the conflict risk curve, while the red dashed line represents the vehicle speed curve. During the period of t ≈ 0∼0.5 s, the vehicle maintains a high speed with continuous acceleration, and the conflict risk gradually increases alongside changes in its motion state, reflecting the accumulation of potential risk. When the conflict risk peaks around t ≈ 0.6 s, the vehicle initiates continuous braking, leading to a noticeable decline in speed and a rapid attenuation of the corresponding conflict risk, which then drops to a lower level. Subsequently, both the vehicle speed and risk value stabilize, with only minor fluctuations occurring around t ≈ 3.5∼4.5 s, corresponding to a brief resurgence and subsequent reduction in risk. Overall, the changes in the conflict risk curve exhibit a strong temporal correlation with vehicle speed adjustments: the risk rises first, triggering deceleration, which in turn reduces the risk level. This demonstrates that the safety potential field model effectively captures the evolution of conflict risk under varying vehicle motion states, thereby validating its effectiveness for conflict identification.

4.1.2. Validation of Cascading Conflict Risk Identification

The proposed cascading conflict identification algorithm is applied to the processed NGSIM trajectory dataset, through which multiple cascading conflict events are successfully identified. Figure 5 illustrates the evolution process of a typical cascading conflict chain. In this case, vehicle 67 initiates the initial conflict and is therefore regarded as the primary vehicle. Subsequently, two additional vehicles (vehicle 73 and vehicle 77) successively engage in two secondary conflicts, forming a complete cascading conflict sequence. The corresponding variations in vehicle speed during the conflict process are shown in Figure 5.

Figure 5a,b illustrate that vehicle 67, due to its own state change (deceleration), initiated an initial conflict with the following vehicle 73 at time $t_1$ (represented by a red conflict linkage). As shown in Figure 5c,d, after perceiving the conflict risk with vehicle 67, vehicle 73 adopted an evasive maneuver (deceleration), and the resulting change in its motion state subsequently triggered a new conflict with vehicle 77 at time $t_2$($t_2>t_1$). Vehicle 77 then perceived the propagated risk and responded with a similar evasive action. Within this conflict network, vehicle 67 serves as the primary vehicle, initiating the initial risk; vehicle 73 acts as the bridging vehicle, functioning both as the receiver of the first conflict (with 67) and the initiator of the subsequent one (with 77). The network thus involves three vehicles (67, 73, and 77) and two associated conflicts (67–73 and 73–77), forming a typical cascading conflict propagation sequence of “vehicle 67 → vehicle 73 → vehicle 77.”

Figure 6 presents the speed variation curves of the three vehicles, providing behavioral evidence that supports the conflict identification results. After perceiving the conflict risk, both vehicle 73 and vehicle 77 exhibited clear deceleration behavior (a noticeable drop in their speed curves), which aligns with theoretical expectations that drivers tend to perform braking maneuvers when confronted with elevated risk. The onset of deceleration for vehicle 73 closely follows the initial deceleration event of vehicle 67, while that of vehicle 77 lags behind vehicle 73, indicating a temporal correlation that clearly reflects the risk propagation process from vehicle 67 to 73 and then to 77. After deceleration, the speeds of all involved vehicles gradually stabilized, suggesting that the evasive actions effectively mitigated the conflict risk and prevented potential collisions. This finding validates the algorithm’s ability to accurately capture risk propagation dynamics in real-world traffic data.

4.2. Experimental Analysis of Cascading Conflict Risk Propagation

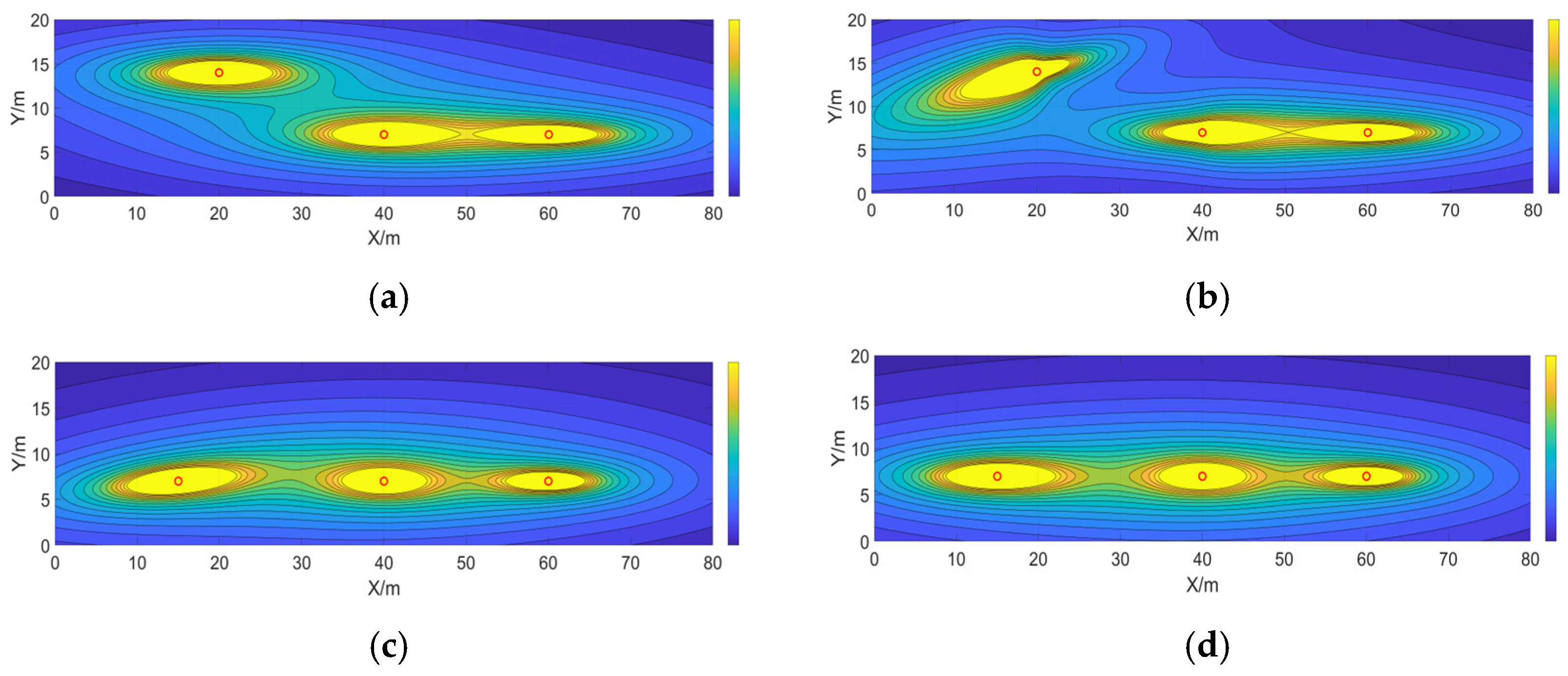
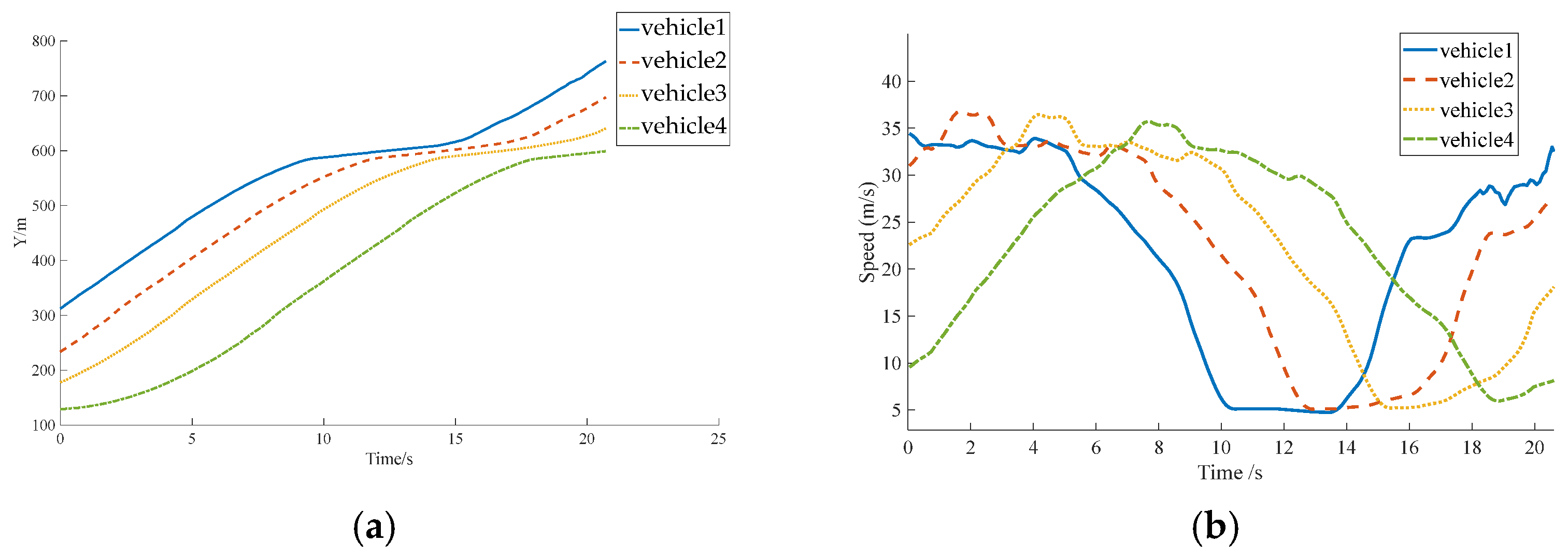
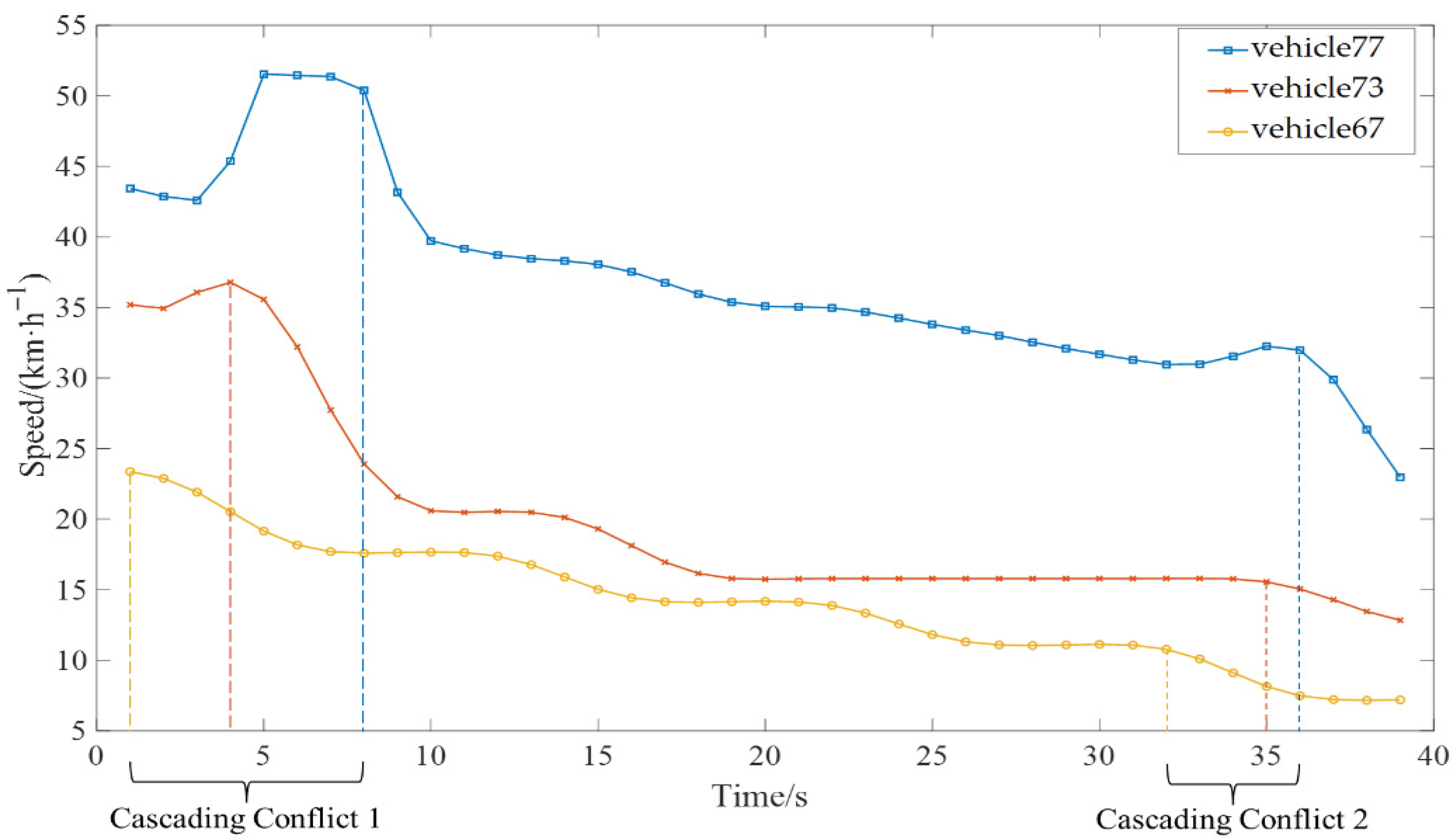
To further analyze the influence of autonomous vehicle control strategies and market penetration rates on the propagation of cascading conflict risk, a series of simulation experiments were conducted using typical microscopic traffic scenarios designed in SUMO.

4.2.1. SUMO Simulation Experiment

The SUMO microscopic traffic simulation platform was employed, in which different configurations of the Intelligent Driver Model (IDM) [20] were used to represent the heterogeneous driving behaviors of autonomous vehicles. To eliminate the effects of traffic signals, non-motorized vehicles, and pedestrians, and to focus exclusively on vehicle decision-making and driving behavior, the simulation scenario was configured as a three-lane urban expressway with a total length of 800 m, where an emergency stop event was set at the 750 m mark. All vehicles were modeled as standard passenger cars, with their acceleration and speed distributions constrained by scenario settings.

The simulation of vehicle dynamics in a microscopic traffic flow requires considering both longitudinal car-following and lateral lane-changing behaviors. To accurately model the driving characteristics of heterogeneous traffic, the Stefan Krauss model [21] was adopted as the longitudinal car-following model for human-driven vehicles (HDVs), while different parameter configurations of the IDM were used to represent various autonomous driving styles. The specific parameter settings are summarized in

Table 5. Parameter settings of car-following models.

Car-Following Model	Conservative	Normal	Aggressive
Vehicle length (m)	5	5	5
Maximum acceleration (m/s2)	1.5	2.6	3.6
Deceleration (m/s2)	3	4	5
Emergency braking deceleration (m/s2)	7.5	8	9
Safety distance (m)	3	2.5	1

.

Lateral lane-changing behavior was explicitly modeled to capture the interaction between heterogeneous vehicles. The lane-changing model uses SUMO’s built-in model [22]. Different lane-changing styles were represented by tuning the parameters lcCooperative and lcStrategic. The specific parameter settings for conservative, normal, and aggressive lane-changing models are summarized in

Table 6. Parameter settings of lane-changing models.

Lane-Changing Model	Conservative	Normal	Aggressive
lcCooperative	1	0.7	0.3
lcStrategic	0.5	0.5	0.5

.

4.2.2. Result Analysis

(1)

Computational Complexity Analysis

To evaluate the practical applicability of the proposed framework for real-time intelligent transportation systems, this study analyzes the computational complexity of each component and compares it with existing approaches.

(a)

Cascading Conflict Identification Complexity

The graph search-based cascading conflict identification algorithm processes conflicts incrementally without pre-constructing the complete conflict graph. The theoretical worst-case complexity is as follows:

$$\mathcal{O}(\mid C_0{\mid }^2)$$

(14)

where $\mid C_0\mid$ is the number of initially detected conflicts.

Practical complexity with spatiotemporal pruning is as

$$\mathcal{O}(\mid C_0\mid \cdot k_{\mathrm{avg}})$$

(15)

where $k_{\mathrm{avg} }$ is the average number of candidate-associated conflicts within the influence window of each conflict. Due to strict spatiotemporal constraints (Equations (8) and (9)), $k_{\mathrm{avg}}\ll \mid C_0\mid$.

Table 7. Time complexity comparison of identification methods.

Method	Time Complexity	Space Complexity	Scalability
Rule-based Matching	$\mathcal{O}(\parallel C_0{\parallel }^2)$	$\mathcal{O}(\parallel C_0\parallel )$	Requires exhaustive pairwise checks
Complete Graph + DFS	$\mathcal{O}(\parallel C_0{\parallel }^2)+\mathcal{O}(\parallel V\parallel +\parallel E\parallel )$	$\mathcal{O}(\parallel C_0{\parallel }^2)$	Quadratic space overhead
Proposed Algorithm	$\mathcal{O}(\parallel C_0\parallel \cdot k_{\mathrm{avg}})$	$\mathcal{O}(\parallel C_0\parallel )$	Incremental search

summarizes the time complexity, space complexity, and scalability of the proposed method alongside two existing identification approaches.

Statistical analysis of NGSIM data reveals $k_{\mathrm{avg}}=5.4$ across 1287 detected conflicts. For a typical highway segment monitoring $\mid C_0\mid =100$ conflicts over 5 min: Rule-based method: ${100}^2=\mathrm{10,000}$ comparisons; Our method: $100\times 5.4=540$ comparisons.

(b)

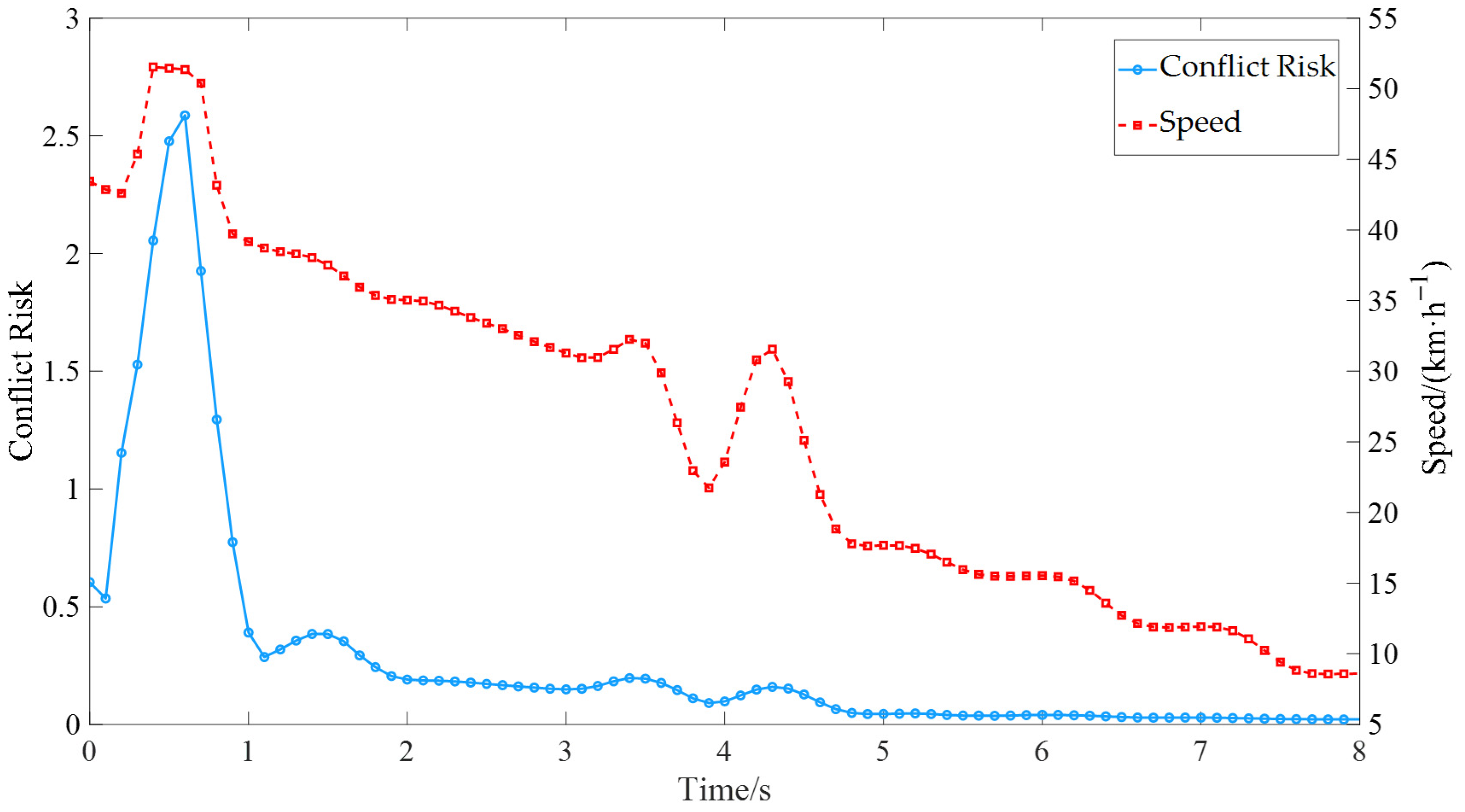
Mechanism Analysis of Cascading Conflict Risk Propagation

As shown in

Table 8. Comparison of computational complexity of different models.

Model	Training Time	SHAP Time	AUC
Logistic Regression	2.3 s	Instant	0.9753
Random Forest	15.7 s	50 ms	0.9861
XGBoost	8.4 s	30 ms	0.9812
CatBoost	6.2 s	20 ms	0.9885

, the four baseline models exhibit varying performance trade-offs between prediction accuracy and computational complexity. Logistic regression, as a linear model, has the lowest model capacity and shortest training time, but its AUC value (0.9753) is significantly inferior to tree-based ensemble methods. Random Forest and XGBoost substantially improve AUC by introducing nonlinear decision boundaries, but this comes at the cost of increased training and inference time due to the use of hundreds of trees. CatBoost achieves the highest AUC (0.9885) while maintaining moderate model size and competitive training time. Its per-sample inference latency meets real-time requirements. Additionally, CatBoost requires the shortest SHAP computation time (20 ms per sample among ensemble models), indicating an optimal balance between model complexity, efficiency, and interpretability.

(2)

Model Prediction Performance

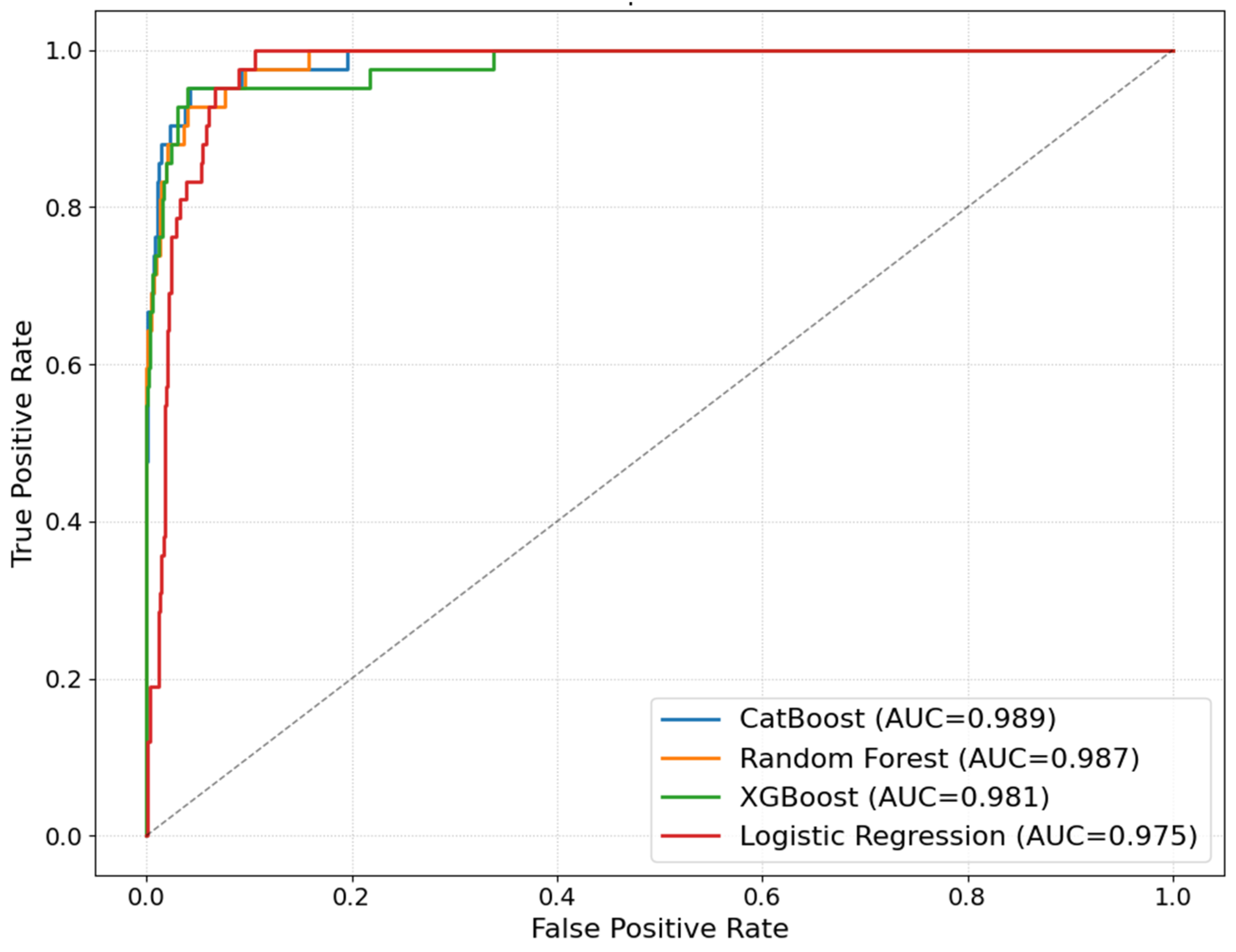
The ROC curves of the four classification models are shown in Figure 7. The horizontal axis denotes the false positive rate (FPR), and the vertical axis denotes the true positive rate (TPR), while the dashed diagonal line corresponds to a random classifier with AUC = 0.5. The blue, orange, green and red curves represent the CatBoost, Random Forest, XGBoost and logistic regression models, respectively, and the legend reports their AUC values (0.989, 0.987, 0.981 and 0.975). All four curves lie well above the random baseline, indicating strong discriminative power in distinguishing between secondary-conflict and non-secondary-conflict samples. Moreover, the CatBoost curve consistently dominates the others over most FPR ranges and achieves the highest AUC, followed by the two tree-based ensemble models, while logistic regression shows the lowest AUC among the four. This suggests that the nonlinear tree-ensemble models, especially CatBoost, better capture the complex interactions encoded in the constructed feature system and are therefore more suitable as the primary model for subsequent mechanism analysis.

(3)

Feature Importance Analysis

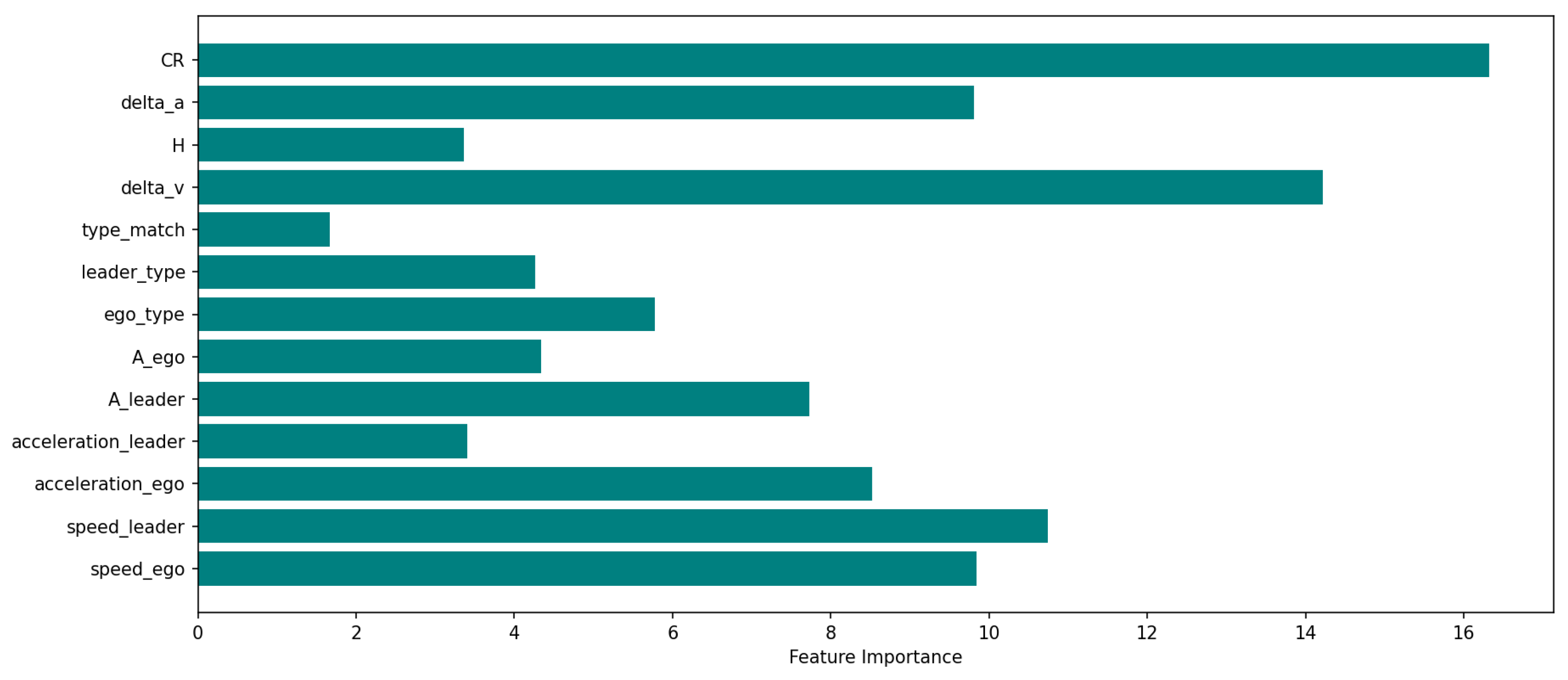
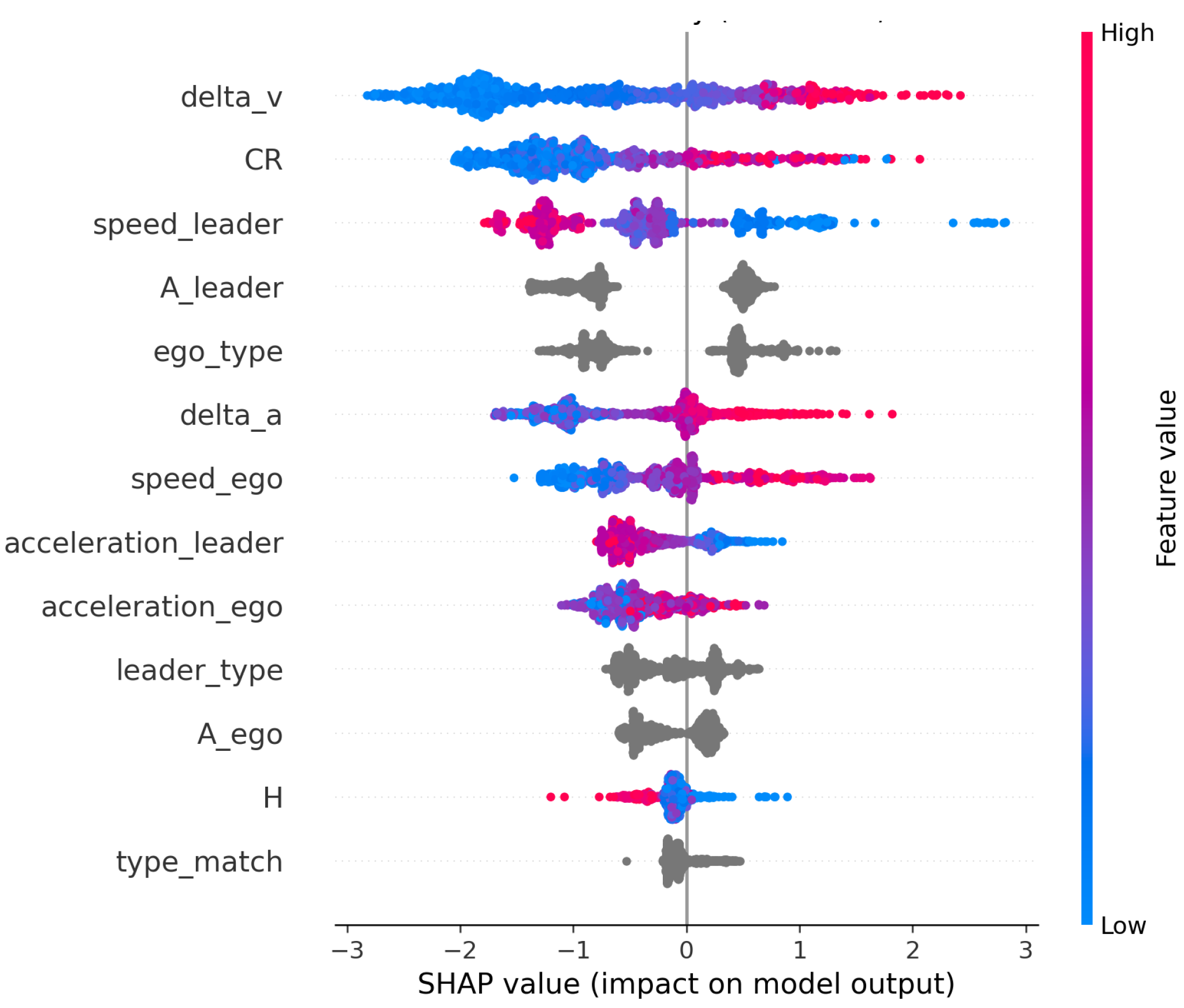
The feature importance ranking (Figure 8) indicates that dynamic interaction features between vehicles play a central role in driving the model’s predictions. Among them, the primary conflict intensity and the relative speed difference between vehicles exhibit the highest importance. The SHAP summary plot (Figure 9) further reveals that larger values of speed difference and conflict intensity substantially increase the likelihood of secondary conflict occurrence. The meanings and units of each parameter are shown in

Table 9. Parameter descriptions and units.

Parameters	Meaning	Unit
CR	Conflict Risk	-
delta_a	Relative Acceleration	m/s2
H	Heterogeneity Entropy	-
type_match	Vehicle Type Consistency	{0, 1}
leader_type	Type of leader vehicle	{0, 1, 2}
ego_type	Type of ego vehicle	{0, 1, 2}
A_ego	Acceleration/Deceleration State of ego vehicle	{0, 1}
A_leader	Acceleration/Deceleration State of leader vehicle	{0, 1}
acceleration_leader	Acceleration of leader vehicle	m/s2
acceleration_ego	Acceleration of ego vehicle	m/s2
speed_leader	Speed of leader vehicle	m/s
speed_ego	Speed of ego vehicle	m/s

.

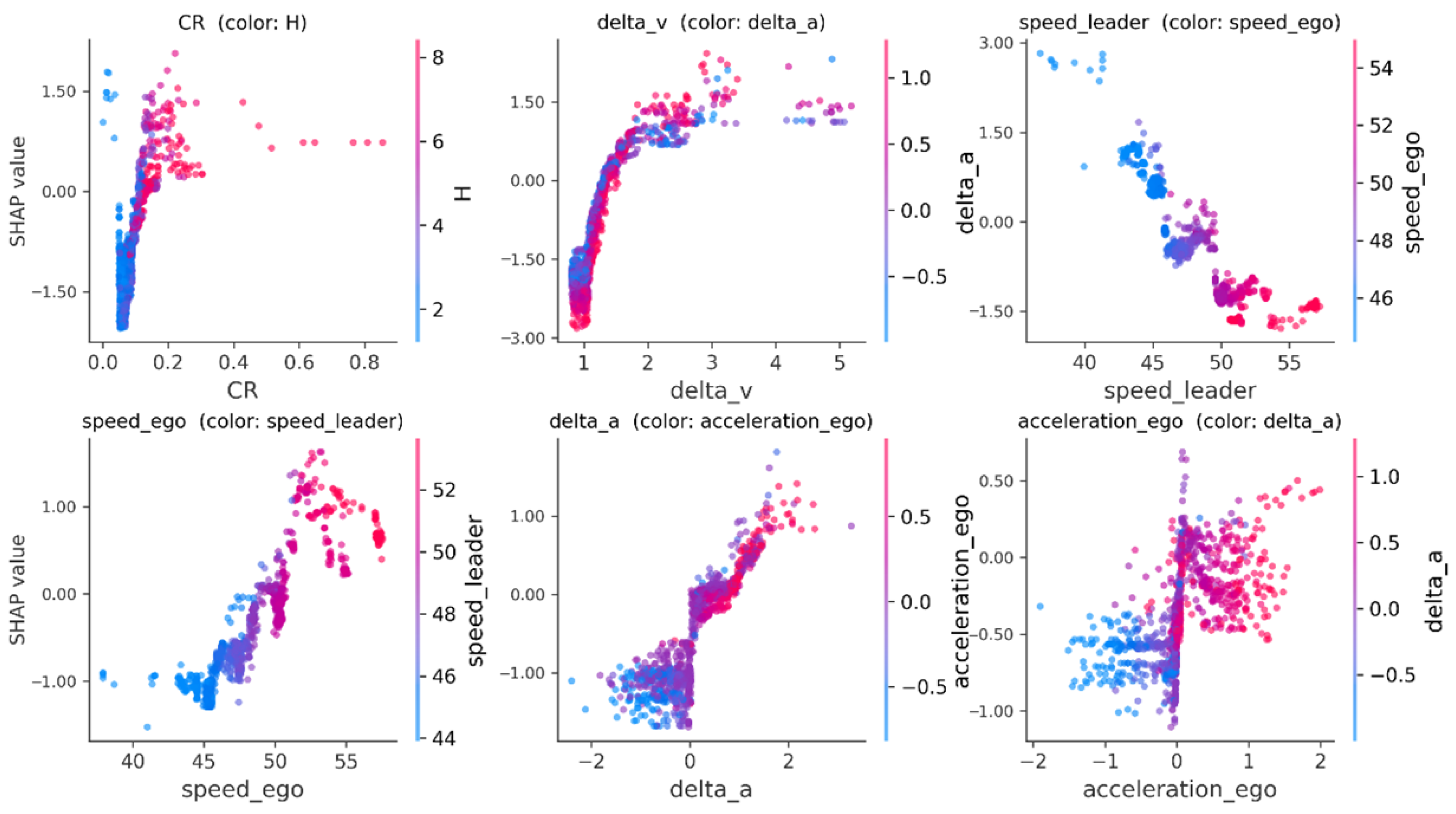
As can be seen from Figure 9 and Figure 10, cascading conflict risk exhibits a monotonically increasing contribution to cascading conflict risks, with a plateau emerging in the medium-to-high range. When CR increases from a low value to approximately 0.2–0.3, the SHAP value rapidly turns positive, after which the growth slope decreases. This indicates that the transition from low-to-medium risk to medium-to-high risk occurs within this interval, followed by a saturation phase with diminishing marginal returns. The color coding reveals that higher local heterogeneity entropy (H) corresponds to larger SHAP values at the same preceding risk level—i.e., greater heterogeneity in traffic flow makes it easier for the same “preceding risk” to propagate backward and trigger secondary conflicts. This suggests that interactions between different types of vehicles amplify the conflict propagation effect.

Relative speed shows a monotonically increasing trend with SHAP values, indicating that a larger speed difference between the leading and following vehicles leads to a higher risk of secondary conflict propagation. In the transition zone around Δv ≈ 1–3 m/s, the SHAP value rises sharply and crosses the zero axis (p < 0.01), meaning that even slight relative closing significantly increases risk. As the relative speed increases further, the contribution tends to saturate. The analysis also reveals its interaction with relative acceleration: at the same relative speed, a larger relative acceleration results in a higher SHAP value, indicating that the combination of “speed difference + acceleration difference” has a superlinear amplifying effect on risk. This provides a basis for joint constraints in control strategies: not only should instantaneous speed differences be suppressed, but also sudden changes in “relative acceleration” must be restricted.

The speed of the leading vehicle shows a significant negative correlation with risk contribution: the slower the leading vehicle, the higher the SHAP value. When the leading vehicle’s speed is around 40–45 km/h, the curve approaches a risk “tipping point,” beyond which risk increases sharply as speed decreases further. The color coding indicates that this negative correlation is stronger when the ego vehicle’s speed is higher (darker color), meaning that the combination of “fast ego vehicle + slow leading vehicle” is the most dangerous.

The main effect of the ego vehicle’s speed complements finding (3): the faster the ego vehicle, the higher the risk. A threshold feature appears around 50 km/h, where the SHAP value transitions from negative to positive, after which the contribution increases approximately linearly. The coloring shows that when the leading vehicle is slower, the same ego vehicle speed yields a larger SHAP value, reaffirming the critical role of speed mismatch in cascading conflict propagation.

The main effect of relative acceleration is approximately monotonically increasing with a steep slope, indicating that differences in acceleration alter the risk state more significantly than speed differences. The most pronounced jump in SHAP values occurs when relative acceleration transitions from negative to positive (i.e., changing from relative separation to relative closing). The coloring reveals that when the ego vehicle’s longitudinal acceleration is positive (accelerating), the same relative acceleration contributes more to risk, suggesting that “active acceleration by the ego vehicle during closing” is a key factor in amplifying risk.

The contribution of the ego vehicle’s acceleration generally increases with acceleration, showing asymmetry near 0 m/s²: mild braking corresponds to a limited decrease in SHAP value, whereas mild acceleration already significantly elevates risk. The coloring results indicate that when the relative acceleration is larger (indicating a stronger closing trend), the same ego acceleration leads to a higher marginal risk, reflecting the coupled amplification between individual actions and relative motion states.

Overall, dynamic interaction features account for 64.3% of the mean absolute SHAP contribution to secondary conflict risk. The rank correlation coefficients of feature importance exceed 0.9 across different random seeds and sampling ratios, demonstrating that the analytical results are stable and reliable.

5. Conclusions

This study proposed a data-driven analytical framework for big data in intelligent transportation systems, aiming to uncover the cascading conflict risk propagation mechanisms from high-dimensional trajectory data of heterogeneous traffic flow environments Key findings are summarized as follows.

• A conflict risk quantification method for heterogeneous traffic flows based on safety potential field theory was proposed. By characterizing the risk sensitivity of vehicles with different driving strategies, the method quantified differences in risk perception thresholds and reaction times among vehicles, thereby overcoming the limitation of traditional approaches that treat all autonomous vehicles as homogeneous entities and providing a reference for the development of adaptive control strategies for autonomous driving.
• A graph search-based cascading conflict identification algorithm was designed. By defining spatiotemporal proximity and vehicle correlation criteria for conflicts, the algorithm transcended the limitations of traditional two-vehicle conflict analysis and accurately identified conflict propagation chains, bridging vehicles, and conflict impact ranges. Analysis of real trajectory data successfully detected multiple typical cascading conflict incidents, thereby verifying the algorithm’s effectiveness in capturing “chain-reaction” propagation patterns in complex traffic scenarios.
• A propagation mechanism exploration framework was established using CatBoost and SHAP interpretability analysis. By constructing a multi-level feature system encompassing individual motion characteristics, interaction relationships, and environmental context features, the framework systematically addressed the core question of under what conditions preceding conflicts trigger secondary conflicts. This study found that the intensity of preceding conflict risk and longitudinal relative speed were key factors in the formation of secondary conflicts. Local traffic-flow heterogeneity significantly amplified and modulated risk propagation, with a clear superlinear coupling effect between speed difference and relative acceleration. Different vehicle-type combinations corresponded to differentiated risk thresholds. These findings not only revealed the propagation mechanisms of conflict risk in mixed traffic flows from a theoretical perspective but also provided a quantitative basis for formulating refined safety management measures, such as categorized speed limits, car-following constraints, and optimization of autonomous driving strategies.

The study offered theoretical foundations and methodological support for cascading conflict risk identification, propagation mechanism exploration, and traffic safety prevention in heterogeneous traffic flow environments. Its findings provide scientific references for traffic safety management, autonomous driving strategy optimization, and intelligent transportation system design under mixed traffic conditions.

Future research could expand in the following directions:

• Investigating cascading conflict propagation characteristics in more complex traffic scenarios (e.g., weaving zones, intersections, ramp merging areas) to broaden the method’s applicability. The proposed framework provided a generalizable foundation, though scenario-specific feature engineering and parameter recalibration would be necessary;
• Integrating real-time traffic data with edge computing technologies to develop real-time cascading conflict warning and proactive intervention systems based on mechanism models;
• Exploring collaborative optimization methods for diverse autonomous driving strategies to enhance overall operational efficiency of mixed traffic flows while ensuring safety.