Secure Dynamic Event-Triggered Cluster Synchronization Control of Complex Dynamical Networks Under Random Deception Attacks

Abstract

This paper is concerned with the secure and resource-efficient cluster synchronization problem of a class of complex dynamical networks (CDNs) under random deception attacks. Each node in the CDNs is modeled by a nonlinear dynamical system with multiple time-varying delays and nonlinear couplings. The central aim is to make each cluster of nodes converge to the same reference trajectory that is distinct for each cluster regardless of the adverse effects of random deception attacks while ensuring communication efficiency for each node. Toward this aim, a distributed dynamic event-triggered mechanism is first proposed such that each node can make its own decisions to transmit or not its data of interest over the communication channel. Second, by suitably modeling the random deception attacks, secure and event-based cluster synchronization controllers are constructed, which incorporate both the effects of random deception attacks and intermittent data arrivals. Then, sufficient conditions ensuring the secure cluster synchronization of the delayed CDNs under randomly occurring deception attacks are established by constructing some appropriate Lyapunov functionals. Furthermore, tractable design criteria on the existence of desired cluster synchronization controllers are derived. Finally, an illustrative example is presented to validate the effectiveness of the main theoretical results.

1. Introduction

Complex dynamical networks (CDNs) have attracted extensive research attention in recent years due to their widespread applications in fields such as power systems, water and gas distribution systems, and transportation systems. Typically, a CDN is composed of a large number of nodes (or agents and subsystems) that interact with each other across both physical and cyber layers in such a way as to achieve some cooperative dynamical behaviors. Not surprisingly, there have been many fruitful results available on dynamical behavior analysis for CDNs, including state estimation [1], synchronization [2,3], and finite-/fixed-time control [4,5].

Synchronization, as one of the most important collective dynamical behaviors for dynamical systems, has been investigated for decades [6,7,8]. To analyze synchronization performance and further design synchronization controllers, several methods have been reported, such as the master stability function method [9], the matrix measure analysis method [10], and the Lyapunov function method [11]. It is noteworthy that a large portion of existing results on synchronization of CDNs focus on complete synchronization; namely, all nodes in the CDNs share the common dynamical behavior when the time approaches infinity. However, cluster synchronization finds broader applications than complete synchronization in both nature and practical applications [12], such as during neuron discharging in the brain, multi-objective search and rescue, and military surveillance and tracking. Under a cluster synchronization setting, nodes are first split into different groups which are called clusters. Then nodes are driven to keep synchronized with their peers in the same cluster but not with those in different clusters. In the presence of multiple external reference sources, the nodes in the same cluster are then regulated to synchronize with each reference source. Up till now, a great deal of effort has been devoted to cluster synchronization of CDNs [13,14,15,16,17]. For example, the prescribed-time cluster synchronization issue for complex networks is studied in [14]. In [15], a pinning control strategy is presented to synchronization a class of linearly coupled CDNs into different clusters. In [16], the finite/prescribed-time cluster synchronization problem is studied for a class of CDNs with asynchronous switching. In [17], the problem of cluster synchronization is extended to deal with parameter mismatches and time-varying delays in CDNs under impulsive control. Nevertheless, it should be pointed out that the above cluster synchronization methods are based on two ideal assumptions that (1) the data transmissions/exchanges on each node are continual at every continuous time t and (2) the network environment, providing a two-way communication medium for the CDNs, is safe in a sense that all data transmissions/exchanges between sender nodes and receiver nodes are secure without any interruption or corruption.

Due to the openness and insufficient protection of most communication networks, CDNs are actually vulnerable to malicious attacks, such as denial-of service (DoS) attacks [18,19] and deception attacks [20,21]. Apparently, such malicious attacks may degrade the desired synchronization performance of CDNs or even destabilize the closed-loop CDNs. This thus calls for secure synchronization controllers against the adversarial effects of malicious attacks on CDNs. So far, several effective secure control methods have been developed in the literature of cyber-physical systems, e.g., [22,23,24,25,26]. Among the various attacks, deception attacks generally violate the integrity of transmitted data by injecting arbitrary and falsified information [27,28,29]. For example, in [27], for a class of linearly coupled complex networks under deception attacks and disturbance estimator, the synchronization issue is solved.

Apart from the security issue of CDNs aforementioned, another significant issue of synchronization control of CDNs is to preserve resource efficiency. This is because the synchronization control objective relies on the information transmission or exchange among the interacting nodes, while such an information sharing process inevitably occupies and consumes excessive resources. Event-triggered transmission mechanisms have yet shown their benefits in reducing unnecessary data transmissions and further controller updates. More specifically, compared with a conventional time-triggered mechanism where data transmissions are invoked typically at periodic times, the decisions of ‘whether or not each node’s data should be transmitted’ are determined by some well-defined events when an event-triggered mechanism is employed. Thus, event-triggered mechanisms can effectively reduce the frequency of data transmissions and further the communication resource occupancy. Naturally, the problem of event-triggered synchronization control for CDNs has been widely explored in the last decade [30,31,32,33,34,35,36]. Nevertheless, it is mentioned that the above event-triggered synchronization methods all fall into the category of static triggering, wherein the triggering conditions are based on only system available information. Recently, another strategy of dynamic triggering is proposed in [37] and has been greatly developed in the past several years. A key feature of such dynamic triggering is that some auxiliary or internal dynamic variable is introduced into the triggering conditions such that the triggering intervals can be generally prolonged. In other words, dynamic triggering can often leads to more resource efficiency than its static counterpart. Applying dynamic triggering to synchronization control problems of CDNs has also attracted great interest, see, e.g., [38,39,40]. To our knowledge, there have been relatively few results available on cluster synchronization of CDNs while taking into account both dynamic event-triggered mechanism and security countermeasure against deceptive attacks, which gives rise to the second motivation of this study.

In this paper, we investigate the secure cluster synchronization problem for a class of CDNs under random deception attacks. The main contributions of this paper are listed as follows. (1) A general CDN model is formulated by taking into account both nonlinear model dynamics, multiple time-varying delays, nonlinear and delayed couplings. Unlike the linear coupled CDNs [14], the CDN model researched in this paper can simulate actual nonlinear systems more accurately. (2) A unified secure cluster synchronization control framework is established to simultaneously address nonlinear dynamics, multiple time-varying delays, and random deceptive attacks. Most existing secure control works focus on denial-of-service (DoS) attacks or single-type synchronization (e.g., complete synchronization) [6,7,8], while this paper addresses cluster synchronization with deceptive attacks and provides explicit attack tolerance bounds, which fills the gap in heterogeneous state synchronization under data tampering. (3) Tractable stability analysis and control design criteria are derived such that the resulting closed-loop CDN achieve secure cluster synchronization while maintaining efficient resource occupancy over the communication channels. A special case of secure static event-triggered cluster synchronization control design is also presented. The controller design integrates attack compensation terms to counteract the adverse effects of data tampering, and sufficient conditions for synchronization are derived via Lyapunov-Krasovskii functionals with some integral inequalities, which are less conservative than existing delay-independent criteria [16].

The rest of this paper is organized as follows: Section 2 shows the model description. Section 3 gives the main results. In Section 4, a numerical example is presented, and concluding remarks are given in Section 5.

2. Preliminaries and Problem Formulation

2.1. Notation

Denote $\mathcal{N}$ and ${\mathcal{N}}^{+}$ as the set of natural numbers and non-negative integers, respectively. $R^n$ and $R^{n\times m}$ stands for the set of n-dimensional real space and $n\times m$ dimensional real spaces, respectively. Denote ${\mathcal{I}}_n\in R^{n\times n}$ as identity matrix, $n\in {\mathcal{N}}^{+}$. $\mathcal{B}>0$ ($\mathcal{B}<0$) means that the matrix $\mathcal{B}$ is a positive (negative) definite matrix. The superscript ‘T’ indicates matrix transposition and ‘⊗’ is the Kronecker product. Matrices are all with appropriate dimensions without special description.

The interconnection topology among nodes is modeled by a digraph $\mathcal{G}(\mathcal{V},\mathcal{E},A)$ of order $N\in {\mathcal{N}}^{+}$ with a set of nodes $\mathcal{V}=\{1,2,\cdots ,N\}$, a set of edges $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$, and weighted adjacency matrix $A={\left(a_{ij}\right)}_{N\times N}\in R^{N\times N}$, where $a_{ij}$ is the weight of the directed edge $(j,i)$ satisfying $a_{ij}\ne 0$ if $(j,i)\in \mathcal{E}$ and $a_{ij}=0$ otherwise. Moreover, it is assumed that $a_{ii}=0$, $i\in \mathcal{V}$ to avoid self-loops.

Let $\mathcal{M}=1,2,\cdots ,\overline{m}$ be a cluster set with $\overline{m}\ge 1$ and $\{{\mathcal{P}}_1,\cdots ,{\mathcal{P}}_{\overline{m}}\}$ be a partition of the initial node set $\mathcal{V}$ such that $\mathcal{V}={\cup }_{l=1}^{\overline{m}}{\mathcal{P}}_l$, and ${\mathcal{P}}_l\cap {\mathcal{P}}_k=\varnothing$ for $l\ne k$, $l,k\in \mathcal{M}$. Denote by ${\mathcal{P}}_1=\{l_0+1,\cdots ,l_1\}$, ⋯, ${\mathcal{P}}_k=\{l_{k-1}+1,\cdots ,l_k\}$, ⋯, ${\mathcal{P}}_{\overline{m}}=\{l_{\overline{m}-1}+1,\cdots ,l_{\overline{m}}\}$, $l_0=0$, $l_{\overline{m}}=N$. Denote the total number of the nodes in the kth cluster by $n_k=\lceil {\mathcal{P}}_k\rfloor$, $k\in \mathcal{M}$, where $\lceil ·\rfloor$ represents the cardinality of the set. Other key notations can be found in the

Table 1. Summary of Key Notations in the Paper.

Notation	Type	Definition
N	Positive integer	Total number of nodes in CDNs.
$\overline{m}$	Positive integer	Total number of clusters with $M=\{1,2,\cdots ,\overline{m}\}$.
$P_k$	Set	Index set of nodes belonging to the k-th cluster.
$n_k$	Positive integer	Number of nodes in the k-th cluster.
${\tau }_M$	Non-negative real number	Maximum delay in the CDNs.
$\alpha \left(t\right)$	Bernoulli random variable	Stochastic variable modeling random deception attacks.
$\overline{\alpha }$	Real number	Probability of deception attacks occurring.
$h(·)$	Continuous function	Deceptive signal injected by attackers into the communication channel.
H	$n\times n$ positive definite matrix	Bounding matrix for the deceptive signal $h(·)$.
${\overline{e}}_i\left(t\right)$	n-dimensional real vector	Actual error signal received by the controller (after possible attack modification).
$t_q^i$	Non-negative real number	q-th event-triggering time of the i-th node.
${\eta }_i\left(t\right)$	Non-negative real number	Auxiliary dynamic variable for the event-triggered mechanism.
${\pi }_i$, ${\theta }_i$, ${\zeta }_i$, ${\varrho }_i$	Positive real numbers	Tuning parameters for the dynamic event-triggered mechanism.
${\mathsf{\Psi }}_i$	$n\times n$ positive definite matrix	Weighting matrix in the event-triggered condition.
$K_i$	$n\times n$ real matrix	Controller gain matrix for the i-th node.
${\mathsf{\Gamma }}_{1k}$, ${\mathsf{\Gamma }}_{2k}$	$n\times n$ real matrices	Bounding matrices for the nonlinear function $f_k(·)$.
${\delta }_1$, ${\delta }_2$	Positive real numbers	Lipschitz constants for the coupling functions $g_1(·)$ and $g_2(·)$.
Q, $R_1$, $R_2$, $R_3$, $R_4$, $M_1$, $M_2$	Block-diagonal positive definite matrices	Weighting matrices introduced in the Lyapunov function for stability analysis.
$\mathsf{\Xi }$	Real matrix	Auxiliary variable for controller gain design.

.

2.2. Modeling of CDNs

Consider a class of CDNs consisting of N interacting nodes, in which the dynamics of the ith node, $\forall i\in \mathcal{V}$, are described by the following coupling state-space equation

$$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& {\breve{W}}_{1i}{\breve{f}}_i\left(x_i\left(t\right)\right)+{\breve{W}}_{2i}{\breve{f}}_i\left(x_i(t-{\tau }_1\left(t\right))\right)+\sum _{j=1}^N{a}_{ij}{\mathsf{\Lambda }}_1{g}_1\left(x_j\left(t\right)\right)\hfill \\ \hfill & +\sum _{j=1}^N{b}_{ij}{\mathsf{\Lambda }}_2{g}_2\left(x_j(t-{\tau }_2\left(t\right))\right)+u_i\left(t\right),\hfill \end{array}$$

(1)

where $x_i\left(t\right)={(x_{i1}\left(t\right),\cdots ,x_{in}\left(t\right))}^T\in R^n$ is the state vector of the ith node; ${\breve{W}}_{1i},{\breve{W}}_{2i}\in R^{n\times n}$ are the connection weight matrices; ${\breve{f}}_i\left(x_i\left(t\right)\right)=({\breve{f}}_i\left(x_{i1}\left(t\right)\right),\cdots$, ${\breve{f}}_i\left(x_{in}\left(t\right)\right){)}^T$, ${\breve{f}}_i\left(x_i(t-{\tau }_1\left(t\right))\right)={({\breve{f}}_i\left(x_{i1}(t-{\tau }_1\left(t\right))\right),\cdots ,{\breve{f}}_i\left(x_{in}(t-{\tau }_1\left(t\right))\right))}^T$ are continuous non-delayed and delayed nonlinear functions, $0\le {\tau }_1\left(t\right)\le {\tau }_1$, $0\le {\dot{\tau }}_1\left(t\right)\le {\overline{\tau }}_1<1$; $A={\left(a_{ij}\right)}_{N\times N}\in R^{N\times N}$ is the non-delayed output-coupling weight matrix with $a_{ii}=-{\displaystyle \sum _{j=1,j\ne i}^N}{a}_{ij}$, $a_{ii}\le 0$, $i\in \mathcal{V}$; ${\displaystyle \sum _{j\in {\mathcal{P}}_k}}{a}_{ij}=0$, $i\in {\mathcal{P}}_k$, $k\in \mathcal{M}$; $B={\left(b_{ij}\right)}_{N\times N}\in R^{N\times N}$ stands for the delayed output-coupling weight matrix with $b_{ii}=-{\displaystyle \sum _{j=1,j\ne i}^N}{b}_{ij}$, $b_{ii}\le 0$, $i\in \mathcal{V}$; ${\displaystyle \sum _{j\in {\mathcal{P}}_k}}{b}_{ij}=0$, $i\in {\mathcal{P}}_k$, $k\in \mathcal{M}$; ${\mathsf{\Lambda }}_1=\mathrm{diag}\{{\lambda }_{11},\cdots ,{\lambda }_{1n}\}>0$, ${\mathsf{\Lambda }}_2=\mathrm{diag}\{{\lambda }_{21},\cdots ,{\lambda }_{2n}\}>0$, represent the non-delayed inner-coupling matrix and delay inner-coupling matrix, respectively; $g_1\left(x_j\left(t\right)\right)={(g_{11}\left(x_{j1}\left(t\right)\right),\cdots ,g_{1n}\left(x_{jn}\left(t\right)\right))}^T$ means the nonlinearly non-delayed coupling vector function and $g_2\left(x_j(t-{\tau }_2\left(t\right))\right)={(g_{21}\left(x_{j1}(t-{\tau }_2\left(t\right))\right),\cdots ,g_{2n}\left(x_{jn}(t-{\tau }_2\left(t\right))\right))}^T$ means the nonlinearly delayed coupling vector function, where $j=1,\cdots ,N$, $0\le {\tau }_2\left(t\right)\le {\tau }_2$, $0\le {\dot{\tau }}_2\left(t\right)\le {\overline{\tau }}_2<1$; and $u_i\left(t\right)$=$(u_{i1}\left(t\right)$, ⋯, $u_{in}{\left(t\right))}^T$$\in R^n$ is the control input of the ith node. Besides, the initial state of system (1) is defined as $x_i\left(r\right)={\xi }_i\left(r\right)$, $r\in [-{\tau }_M,0]$, ${\tau }_M=max\{{\tau }_1,{\tau }_2\}$, $i\in \mathcal{V}$.

Our objective is to synchronize the CDN (1) of N nodes with $\overline{m}$ desired heterogeneous states, which can be $\overline{m}$ different reference trajectories, $\overline{m}$ equilibrium points, $\overline{m}$ periodic orbits or $\overline{m}$ chaotic attractors, event in the presence of deception attacks. For this purpose, we denote such $\overline{m}$ desired heterogeneous states by $s_k\left(t\right)\in R^n$, $k\in \mathcal{M}$, which are defined in accordance with the following equation:

$${\dot{s}}_k\left(t\right)=W_{1k}{f}_k\left(s_k\left(t\right)\right)+W_{2k}{f}_k\left(s_k(t-{\tau }_1\left(t\right))\right),$$

(2)

where $W_{1k}={\breve{W}}_{1i}$, $W_{2k}={\breve{W}}_{2i}$, $f_k(·)={\breve{f}}_i(·)$, $i\in {\mathcal{P}}_k=\{l_{k-1}+1,\cdots ,l_k\}$, $i\in \mathcal{V}$, $k\in \mathcal{M}$. The initial state of system (2) is defined as $s_k\left(r\right)={\widehat{\xi }}_k\left(r\right)$, $r\in [-{\tau }_1,0]$.

Combining the CDN in (1) and the heterogeneous states in (2), the objective is to design a suitable cluster synchronization controller $u_i\left(t\right)$ for each node i belonging to the cluster ${\mathcal{P}}_k$ such that $x_i\left(t\right)\to s_k\left(t\right)$ for any $i\in {\mathcal{P}}_k$ and $k\in \mathcal{M}$. Then, it is clear that

$$\begin{array}{c}\hfill \mathcal{S}\left(t\right)=\stackrel{n_1}{\overbrace{(s_1\left(t\right),\cdots ,s_1\left(t\right)}},\cdots ,\stackrel{n_{\overline{m}}}{\overbrace{s_{\overline{m}}\left(t\right),\cdots ,s_{\overline{m}}\left(t\right))}}\end{array}$$

denotes the desired cluster synchronization pattern under the proposed synchronization controller.

Furthermore, the nonlinear functions satisfy the following mild assumption.

Assumption 1 

([1]). There exist real constant matrices ${\mathsf{\Gamma }}_{1k}$ and ${\mathsf{\Gamma }}_{2k}$ with ${\mathsf{\Gamma }}_{2k}-{\mathsf{\Gamma }}_{1k}\ge 0$, $k\in \mathcal{M}$, such that for any w, $v\in R^n$, the following inequality holds

$$\begin{array}{cc}\hfill & {(f_k\left(w\right)-f_k\left(v\right)-{\mathsf{\Gamma }}_{1k}(w-v))}^T(f_k\left(w\right)-f_k\left(v\right)-{\mathsf{\Gamma }}_{2k}(w-v))\le 0.\hfill \end{array}$$

(3)

Remark 1. 

For the nonlinear function $f_k(·)$ which describes the internal dynamics of nodes in cluster k, the difference between its values at two arbitrary states w and v can be ‘sandwiched’ between two linear functions. In other words, $f_k(·)$ does not grow faster than a linear rate—this prevents unbounded nonlinearity from destabilizing the network. For example, let $f_k\left(x\right)=tanh\left(x\right)$, we can choose ${\mathsf{\Gamma }}_{1k}=0$ and ${\mathsf{\Gamma }}_{2k}=I_n$. For any w and v, ${(tanh\left(w\right)-tanh\left(v\right))}^T(tanh\left(w\right)-tanh\left(v\right)-I_m(w-v))\le 0$.

Assumption 2. 

There exist scalars ${\delta }_1$, ${\delta }_2>0$ such that for any $w,v\in R^{n\times n}$, the following inequalities hold

$$\begin{array}{c}\hfill {(g_1\left(w\right)-g_1\left(v\right))}^T(g_1\left(w\right)-g_1\left(v\right))\le {\delta }_1{(w-v)}^T(w-v),\\ \hfill {(g_2\left(w\right)-g_2\left(v\right))}^T(g_2\left(w\right)-g_2\left(v\right))\le {\delta }_2{(w-v)}^T(w-v).\end{array}$$

Remark 2. 

For the coupling nonlinear functions $g_1(·)$ and $g_2(·)$ which describe interactions between nodes, the ‘size’ (Euclidean norm) of the difference between their values at two states w and v is at most a constant multiple of the ‘size’ of the state difference $w-v$. For example, let $g_1\left(t\right)={(0.3sin\left(x_1\right),0.4tanh\left(x_2\right))}^T$, we can choose ${\delta }_1=0.23$.

2.3. A Dynamic Event-Triggered Transmission Mechanism

To solve the above cluster synchronization problem, the widely-adopted synchronization controller takes the following form of

$$u_i\left(t\right)=K_i{e}_i\left(t\right)=K_i(x_i\left(t\right)-s_k\left(t\right)),\forall i\in {\mathcal{P}}_k,k\in \mathcal{M},$$

(4)

where $K_i>0$ is the controller gain to be designed and $e_i\left(t\right)$ represents the cluster synchronization error.

It is clear that the error signal $e_i\left(t\right)$ in (4) on node $i\in {\mathcal{P}}_k$ has to be transmitted to the controller at every continuous time instant t. This may cause excessive usage of the limited computation and communication resources of each node and the network medium. In the following section, a dynamic event-triggered mechanism is considered under which the cluster synchronization controller in (4) can be updated in an intermittent manner.

For any $i\in {\mathcal{P}}_k$, let the triggering time sequence be denoted by ${\left\{t_q^i\right\}}_{q=1}^{+\infty }$ with $0=t_1^i<t_2^i<\cdots <t_q^i<\cdots$. Then, the following triggering mechanism specifies how the triggering times can be recursively determined

$$\begin{array}{cc}\hfill t_{q+1}^i=& inf\{t>t_q^i|{\pi }_i{\eta }_i\left(t\right)+{\theta }_i[{\zeta }_i{e}_i^T\left(t\right){\mathsf{\Psi }}_i{e}_i\left(t\right)\hfill \\ \hfill & -{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right))]>0\},\hfill \end{array}$$

(5)

where ${\mathsf{\Psi }}_i$ is positive define matrix, ${\pi }_i>0$, ${\theta }_i>0$, ${\zeta }_i\in (0,1)$, $i\in {\mathcal{P}}_k$, and ${\eta }_i\left(t\right)$ is an auxiliary dynamic variable satisfying

$$\begin{array}{cc}\hfill {\dot{\eta }}_i\left(t\right)=& -{\varrho }_i{\eta }_i\left(t\right)+{\zeta }_i{e}_i^T\left(t\right){\mathsf{\Psi }}_i{e}_i\left(t\right)-{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right)),\hfill \end{array}$$

(6)

where ${\eta }_i\left(0\right)={\eta }_{i0}>0$ and ${\varrho }_i>0$, $i\in {\mathcal{P}}_k$.

Remark 3. 

The triggered condition ${\pi }_i{\eta }_i\left(t\right)+{\theta }_i[{\zeta }_i{e}_i^T\left(t\right){\mathsf{\Psi }}_i{e}_i\left(t\right)-{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right))]>0$ in (5) means that only when the current data (error) $e_i\left(t\right)$ satisfying the inequality will be triggered and released. From the sensor’s perspective, this basically means that the continuous data $e_i\left(t\right)$ has no need to be persistently transmitted to the controller. Meanwhile, at the controller side, during $[t_q^i,t_{q+1}^i)$, the controller will not be updated with any new data but instead using the previously triggered data $e_i\left(t_q^i\right)$, namely, $u_i\left(t\right)=K_i{e}_i\left(t\right)$ for any $t\in [t_q^i,t_{q+1}^i)$. As a result, compared with the continuous-time cluster synchronization controller (4), the consumption of computation and communication resources of the sensor and controller can be significantly reduced under the above event-triggered cluster synchronization controller. On the other hand, the auxiliary dynamic variable ${\eta }_i\left(t\right)$ possesses an important non-negative feature which plays an important role in reducing the frequency of data transmissions. Specifically, it is easy to get that ${\zeta }_i{e}_i^T\left(t\right){\mathsf{\Psi }}_i{e}_i\left(t\right)-{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right))>-{\displaystyle \frac{{\pi }_i{\eta }_i\left(t\right)}{{\theta }_i}}$ during $[t_q^i,t_{q+1}^i)$. Then, it follows from (6) that ${\dot{\eta }}_i\left(t\right)>-{\varrho }_i{\eta }_i\left(t\right)-{\displaystyle \frac{{\pi }_i{\eta }_i\left(t\right)}{{\theta }_i}}$, which leads to ${\eta }_i\left(t\right)\ge 0$ for $t\in [0,+\infty )$ based on the comparison principle.

Remark 4. 

${\pi }_i$ and ${\varrho }_i$ primarily suppress unnecessary triggers by adjusting the auxiliary variable’s influence, while ${\theta }_i$ and ${\zeta }_i$ directly tune the sensitivity of the error-based triggering condition—properly selecting them balances communication resource savings and synchronization performance. The

Table 2. Parameter → Effect on Triggering Frequency.

Parameter	Core Effect on Triggering Frequency	Simple Selection Guidelines
${\pi }_i$	Larger ${\pi }_i$ → Lower frequency	Choose a moderate value (e.g., 0.1–0.5) based on resource constraints.
${\theta }_i$	Larger ${\theta }_i$ →Higher frequency	Set to a value that avoids excessive triggers (e.g., 1–5).
${\zeta }_i$	Larger ${\zeta }_i$ (within $(0,1)$) →Higher frequency	Select between 0.2–0.8.
${\varrho }_i$	Larger ${\varrho }_i$ →Lower frequency	Choose a value matching the system’s time scale (e.g., 0.5–2).

shows the selection guidelines of parameters.

2.4. Modeling of Random Deception Attacks

Once the data packet $(t_q^i,e_i\left(t_q^i\right))$ with its time stamp $t_q^i$ is triggered, it will be released over certain communication network or channel. Such a released data packet is considered to be important for achieving the desired cluster synchronization objective. However, most realistic communication networks suffer from inherent security vulnerabilities due to their openness or insufficient protection against malicious cyber attacks. To make the desired cluster synchronization controller resilient and secure to malicious cyber attacks, it is thus imperative to incorporate cyber attacks into the controller design. In doing so, we first present the following random deception attack model

$${\overline{e}}_i\left(t\right)=\alpha \left(t\right)h\left(e_i\left(t_q^i\right)\right)+(1-\alpha \left(t\right))e_i\left(t_q^i\right),t\in [t_q^i,t_{q+1}^i)$$

(7)

for any $\forall i\in {\mathcal{P}}_k$, $k\in \mathcal{M}$, where ${\overline{e}}_i\left(t\right)$ represents the actually received data at the controller side, $h\left(e_i\left(t_q^i\right)\right)$ denotes the deception data or signal injected by attackers over the network or during network transmission. For simplicity and without loss of generality, it is assumed that $h\left(v\right)={(h_1\left(v\right),\cdots ,h_n\left(v\right))}^T$, $h_i\left(v\right)$, $i=1,\cdots ,n$, is a continuous function, and for $\forall v_1,v_2\in R^n$, $h(·)$ satisfies ${\left(h\left(v_1\right)-h\left(v_2\right)\right)}^T$$\left(h\left(v_1\right)-h\left(v_2\right)\right)\le {(v_1-v_2)}^{T}H(v_1-v_2)$, $h\left(0\right)=0$, where $H\in R^{n\times n}$ is a known positive definite matrix. The function $h(·)$ represents the adversary’s falsification strategy, for example, scaling, offsetting, or distorting the original error signal $e_i\left(t_q^i\right)$ to produce the attacked signal $h\left(e_i\left(t_q^i\right)\right)$. The matrix H serves as a bound on the attack’s maximum allowable distortion. Such a bounding assumption on the deception signal is reasonable since (1) realistic adversaries are often energy-limited and may not be able to inject arbitrarily large data packets, and (2) arbitrarily large injection signalS may be easily detected by the existing anomaly detector via checking the data residue.

Furthermore, $\alpha \left(t\right)$ in (7) is a Bernoulli distribution variable satisfying $\mathrm{Pr}(\mathrm{ff}\left(\mathrm{t}\right)=1)=\overline{\mathrm{ff}}$ and $\mathrm{Pr}(\mathrm{ff}\left(\mathrm{t}\right)=0)=1-\overline{\mathrm{ff}}$, where $\overline{\alpha }\in (0,1)$ is known constant. Such a stochastic variable is introduced to model the random characteristics of real-world deception attacks. Since our focus is placed on the deception attacks occurring within the network channels or during networked data transmission, it is mild to assume a homogeneous stochastic variable $\alpha \left(t\right)$ for all the network channels. The Bernoulli-distributed attack model adopted in this paper is a simplified yet practical choice, and its rationale lies in two key aspects aligned with real-world scenarios: First, it effectively captures the binary ’hit-or-miss’ nature of deception attacks—in actual communication channels, an attacker either injects falsified data (attack occurs) or does not interfere (no attack), and the Bernoulli variable directly maps this discrete stochasticity. Second, the model’s statistical property ($\mathbb{E}\left[\alpha \left(t\right)\right]=\overline{\alpha }$) enables tractable mean-square stability analysis, which is critical for deriving explicit linear matrix inequality (LMI) conditions and feasible controller gains—an essential step for validating the proposed secure synchronization framework through both theoretical proofs and numerical simulations.

Remark 5. 

While recent work on deception attacks focuses on output feedback PID control or switched system resilience, our study uniquely integrates dynamic event-triggered mechanisms with cluster synchronization, addressing the under-explored challenge of secure grouping in complex networks rather than full-network consensus. Unlike the static event-triggered designs, our auxiliary variable-based triggering rule (6) adaptively adjusts to random deception attacks. Compared to works handling asynchronous DoS attacks via linear auxiliary trajectories [19], we explicitly model deception attack dynamics with a Bernoulli variable and bounded disturbance matrix H, providing verifiable guidelines for H estimation that are absent in prior LMI-based resilient control frameworks.

2.5. The Problem to Be Addressed

Based on the dynamic event-triggered mechanism (5) and attack model (7), we are interested in constructing and design the following cluster synchronization controller

$$u_i\left(t\right)=K_i{\overline{e}}_i\left(t\right),t\in [t_q^i,t_{q+1}^i).$$

(8)

From (5)–(8), for $t\in [t_q^i,t_{q+1}^i)$, the synchronization error dynamics can be written as

$$\begin{array}{cc}\hfill {\dot{e}}_i\left(t\right)=& W_{1k}{\overline{f}}_k\left(e_i\left(t\right)\right)+W_{2k}{\overline{f}}_k\left(e_i(t-{\tau }_1\left(t\right))\right)+\sum _{j=1}^N{a}_{ij}{\mathsf{\Lambda }}_1{\overline{g}}_1\left(e_j\left(t\right)\right)+\sum _{j=1}^N{b}_{ij}{\mathsf{\Lambda }}_2{\overline{g}}_2\left(e_j(t-{\tau }_2\left(t\right))\right)\hfill \\ \hfill & +\alpha \left(t\right)K_{i}h\left(e_i\left(t_q^i\right)\right)+(1-\alpha \left(t\right))K_i{e}_i\left(t_q^i\right),\hfill \end{array}$$

(9)

where ${\overline{f}}_k\left(e_i\left(t\right)\right)=f_k\left(x_i\left(t\right)\right)-f_k\left(s_k\left(t\right)\right)$, ${\overline{f}}_k\left(e_i(t-{\tau }_1\left(t\right))\right)=f_k\left(x_i(t-\tau \left(t\right))\right)-f_k\left(s_k(t-{\tau }_1\left(t\right))\right)$, ${\overline{g}}_1\left(e_i\left(t\right)\right)=g_1\left(x_i\left(t\right)\right)-g_1\left(s_k\left(t\right)\right)$, ${\overline{g}}_2\left(e_i(t-{\tau }_2\left(t\right))\right)=g_2\left(x_i(t-{\tau }_2\left(t\right))\right)-g_2\left(s_k(t-{\tau }_2\left(t\right))\right)$, $i\in {\mathcal{P}}_k$, $k\in \mathcal{M}$,  $i\in \mathcal{V}$.

Furthermore, let ${ϵ}_i\left(t\right)=e_i\left(t\right)-e_i\left(t_q^i\right)$, $t\in [t_q^i,t_{q+1}^i)$, ${\tilde{e}}_k\left(t\right)={(e_{l_{k-1}+1}^T\left(t\right),\cdots ,e_{l_k}^T\left(t\right))}^T$, $k\in \mathcal{M}$. The error system can be rewritten as, for $k\in \mathcal{M}$,

$$\begin{array}{cc}\hfill {\dot{\tilde{e}}}_k\left(t\right)=& {\overline{W}}_{1k}{\overline{F}}_k\left({\tilde{e}}_k\left(t\right)\right)+{\overline{W}}_{2k}{\overline{F}}_k\left({\tilde{e}}_k(t-{\tau }_1\left(t\right))\right)+\sum _{j=1}^{\overline{m}}{\tilde{A}}_{kj}\otimes {\mathsf{\Lambda }}_1{\overline{G}}_1\left({\tilde{e}}_j\left(t\right)\right)\hfill \\ \hfill & +\sum _{j=1}^{\overline{m}}{\tilde{B}}_{kj}\otimes {\mathsf{\Lambda }}_2{\overline{G}}_2\left({\tilde{e}}_j(t-{\tau }_2\left(t\right))\right)+(\alpha \left(t\right)-\overline{\alpha }){\tilde{K}}_k{\overline{H}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))\hfill \\ \hfill & +\overline{\alpha }{\tilde{K}}_k{\overline{H}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))+(1-\overline{\alpha }){\tilde{K}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))-(\alpha \left(t\right)-\overline{\alpha }){\tilde{K}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right)),\hfill \end{array}$$

where

$${\overline{W}}_1=\mathrm{diag}\stackrel{n_k}{\overbrace{\{W_{1k},\cdots ,W_{1k}\}}},{\overline{W}}_2=\mathrm{diag}\stackrel{n_k}{\overbrace{\{W_{2k},\cdots ,W_{2k}\}}},$$

$${\overline{F}}_k\left({\tilde{e}}_k\left(t\right)\right)=({\overline{f}}_k^T\left(e_{l_{k-1}+1}\left(t\right)\right),\cdots ,{\overline{f}}_k^T{\left(e_{l_k}\left(t\right)\right)}^T,$$

$${\overline{F}}_k\left({\tilde{e}}_k(t-{\tau }_1\left(t\right))\right)={({\overline{f}}_k^T\left(e_{l_{k-1}+1}(t-{\tau }_1\left(t\right))\right),\cdots ,{\overline{f}}_k^T\left(e_{l_k}(t-{\tau }_1\left(t\right))\right))}^T,$$

$${\tilde{A}}_{kj}=\left(\begin{array}{ccc}{a}_{l_{k-1}+1,l_{j-1}+1}& \cdots & a_{l_{k-1}+1,l_j}\\ ⋮& & ⋮\\ a_{l_k,l_{j-1}+1}& \cdots & a_{l_k,l_j}\end{array}\right)\in R^{n_k\times n_j},$$

$${\overline{G}}_1\left({\tilde{e}}_j\left(t\right)\right)={({\overline{g}}_1^T\left(e_{l_{j-1}+1}\left(t\right)\right),\cdots ,{\overline{g}}_1^T\left(e_{l_j}\left(t\right)\right))}^T,$$

$${\tilde{B}}_{kj}=\left(\begin{array}{ccc}{b}_{l_{k-1}+1,l_{j-1}+1}& \cdots & b_{l_{k-1}+1,l_j}\\ ⋮& & ⋮\\ b_{l_k,l_{j-1}+1}& \cdots & b_{l_k,l_j}\end{array}\right)\in R^{n_k\times n_j},$$

$${\overline{G}}_2\left({\tilde{e}}_j(t-{\tau }_2\left(t\right))\right)={({\overline{g}}_2^T\left(e_{l_{j-1}+1}(t-{\tau }_2\left(t\right))\right),\cdots ,{\overline{g}}_2^T\left(e_{l_j}(t-{\tau }_2\left(t\right))\right))}^T,$$

$${\tilde{K}}_k=\mathrm{diag}\stackrel{n_k}{\overbrace{\{K_{l_{k-1}+1},\cdots ,K_{l_{k-1}+n_k}\}}},$$

$${\widetilde{ϵ}}_k\left(t\right)={({ϵ}_{l_{k-1}+1}^T\left(t\right),\cdots ,{ϵ}_{l_k}^T\left(t\right))}^T,$$

$${\overline{H}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))={(h^T(e_{l_{k-1}+1}\left(t\right)-{ϵ}_{l_{k-1}+1}\left(t\right)),\cdots ,h^T(e_{l_k}\left(t\right)-{ϵ}_{l_k}\left(t\right)))}^T.$$

The main problem to be addressed in this paper can now be stated as follows.

Problem 1. 

For the CDNs in (1), we aim to design a secure dynamic event-triggered cluster synchronization controller in the form of (8) such that the desired secure cluster synchronization objective is achieved regardless of the simultaneous effects of intermittent data transmission under (5) and random deception attacks under (7), i.e., $E\{{\displaystyle \sum _{i=l_{k-1}+1}^{l_k}}\parallel e_i\left(t\right)\parallel \}=0$ as $t\to +\infty$ for any $k\in \mathcal{M}$ and initial condition.

Before ending this section, some definitions, assumption, lemmas are recalled.

Definition 1 

([15]). Consider $D=\left(d_{ij}\right)\in R^{N\times N}$. If

(1) $d_{ij}\ge 0$, for $i\ne j$, and $d_{ii}=-{\displaystyle \sum _{j=1,j\ne i}^N}{d}_{ij}$=$-{\displaystyle \sum _{j=1,j\ne i}^N}{d}_{ji}$, $i=1,2,\cdots ,N$.

(2) D is irreducible.

Then we say $D\in {\mathcal{D}}_1$.

Definition 2 

([15]). For an $N\times N$ matrix

$$D=\left(\begin{array}{cccc}{D}_{11}\hfill & D_{12}\hfill & \cdots \hfill & D_{1m}\hfill \\ D_{21}\hfill & D_{22}\hfill & \cdots \hfill & D_{2m}\hfill \\ & & \cdots \hfill \\ D_{m1}\hfill & D_{m2}\hfill & \cdots \hfill & D_{mm}\hfill \end{array}\right),$$

with $D_{ii}\in R^{(l_i-l_{i-1})\times (l_i-l_{i-1})}$, $D_{ij}\in R^{(l_i-l_{i-1})\times (l_j-l_{j-1})}$, i, $j=1,2,\cdots ,m$, if each block $D_{ij}$ is a zero-row-sum matrix, then we say $D\in {\mathcal{D}}_1\left(m\right)$. Furthermore, if $D_{ii}\in {\mathcal{D}}_1$, $i=1,2,\cdots ,d$, then we say $D\in {\mathcal{D}}_2\left(m\right)$.

Assumption 3. 

The coupling matrix A in (1) satisfies $A\in {\mathcal{D}}_2\left(\overline{m}\right)$, $B\in {\mathcal{D}}_2\left(\overline{m}\right)$.

Remark 6. 

The non-delay coupling matrix A and delayed coupling matrix B must have two properties. (1) For each cluster, the sum of coupling weights from any node in the cluster to all other nodes in the same cluster is zero which ensures internal cluster balance. (2) Each submatrix of A and B corresponding to a single cluster is ’irreducible’, in other words, no isolated nodes in the cluster. For example, consider a CDN with 2 clusters: $P_1=\{1,2\}$, $P_2=\{3,4\}$. We can choose the non-delayed coupling matrix:

$$\left[\begin{array}{cccc}-1& 1& 0& 0\\ 1& -1& 0& 0\\ 0& 0& -2& 2\\ 0& 0& 2& -2\end{array}\right].$$

Lemma 1 

([41]). For any constant positive matrix $M\in R^{m\times m}$, scalar $\widehat{\tau }\le \tau \left(t\right)<\overline{\tau }$ and vector function $\dot{e}\left(t\right):[-\overline{\tau },\widehat{\tau }]\to R^m$ such that the following integration is well defined, then it holds that

$$\begin{array}{cc}\hfill & -(\overline{\tau }-\widehat{\tau }){\int }_{t-\overline{\tau }}^{t-\widehat{\tau }}{\left(\dot{e}\left(\vartheta \right)\right)}^{T}M\dot{e}\left(\vartheta \right)\mathrm{d}\vartheta \hfill \\ \hfill \le & {\left[\begin{array}{c}e(t-\overline{\tau })\\ e(t-\tau (t\left)\right)\\ e(t-\widehat{\tau })\end{array}\right]}^T\left[\begin{array}{ccc}-M& M& 0\\ \ast & -2M& M\\ \ast & \ast & M\end{array}\right]\left[\begin{array}{c}e(t-\overline{\tau })\\ e(t-\tau (t\left)\right)\\ e(t-\widehat{\tau })\end{array}\right].\hfill \end{array}$$

(10)

Lemma 2. 

(Schur Complement) Given matrices $U_1$, $U_2$, $U_3$, where $U_1^T=U_1$, $U_3^T=U_3>0$, then $U_1+U_2{U}_3^{-1}{U}_2^T<0$ if and only if

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{U}_1& U_2\\ U_2^T& -U_3\end{array}\right]<0,\left[\begin{array}{cc}-U_3& U_2^T\\ U_2& U_1\end{array}\right]<0.\end{array}$$

(11)

Lemma 3. 

For any matrices $\mathcal{R}>0$, $\mathcal{Q}$ and scalar ι, the following inequality holds

$$\begin{array}{c}\hfill -\mathcal{Q}{\mathcal{R}}^{-1}\mathcal{Q}\le {\iota }^2\mathcal{R}-2\iota \mathcal{Q}.\end{array}$$

(12)

For the sake of simplicity, some mathematical notations are introduced as follows.

$$e\left(t\right)={\left({\tilde{e}}_1^T\left(t\right),\cdots ,{\tilde{e}}_{\overline{m}}^T\left(t\right)\right)}^T,ϵ\left(t\right)={\left({\widetilde{ϵ}}_1^T\left(t\right),\cdots ,{\widetilde{ϵ}}_{\overline{m}}^T\left(t\right)\right)}^T,$$

$$\begin{array}{ccc}z\left(t\right)\hfill & =\hfill & (e^T\left(t\right),e^T(t-{\tau }_1\left(t\right)),e^T(t-{\tau }_1),e^T(t-{\tau }_2\left(t\right)),\hfill \\ & & e^T(t-{\tau }_2),{\overline{F}}^T\left(e\left(t\right)\right),{\overline{F}}^T\left(e(t-{\tau }_1\left(t\right))\right),{\overline{G}}_1^T\left(e\left(t\right)\right),\hfill \\ & & {\overline{G}}_2^T\left(e(t-{\tau }_2\left(t\right))\right),{\overline{H}}^T(e\left(t\right)-ϵ\left(t\right)),{ϵ}^T\left(t\right){)}^T,\hfill \end{array}$$

$$\mathsf{\Phi }=((1-\overline{\alpha })\tilde{K},0,0,0,0,{\tilde{W}}_1,{\tilde{W}}_2,\mathcal{A},\mathcal{B},\overline{\alpha }\tilde{K},-(1-\overline{\alpha })\tilde{K}),$$

$$\overline{F}\left(e\left(t\right)\right)=({\overline{F}}_1^T\left({\tilde{e}}_1\left(t\right)\right),\cdots ,{\overline{F}}_{\overline{m}}^T{\left({\tilde{e}}_{\overline{m}}\left(t\right)\right)}^T,$$

$$\overline{F}\left(e(t-{\tau }_1\left(t\right))\right)={({\overline{F}}_1^T\left({\tilde{e}}_1(t-{\tau }_1\left(t\right))\right),\cdots ,{\overline{F}}_{\overline{m}}^T\left({\tilde{e}}_{\overline{m}}(t-{\tau }_1\left(t\right))\right))}^T,$$

$${\overline{G}}_1\left(e\left(t\right)\right)={({\overline{G}}_1^T\left({\tilde{e}}_1\left(t\right)\right),\cdots ,{\overline{G}}_1^T\left({\tilde{e}}_{\overline{m}}\left(t\right)\right))}^T,$$

$${\overline{G}}_2\left(e(t-{\tau }_2\left(t\right))\right)={({\overline{G}}_2^T\left({\tilde{e}}_1(t-{\tau }_2\left(t\right))\right),\cdots ,{\overline{G}}_2^T\left({\tilde{e}}_{\overline{m}}(t-{\tau }_2\left(t\right))\right))}^T,$$

$${\tilde{W}}_1=\mathrm{diag}\{{\overline{W}}_{11},\cdots ,{\overline{W}}_{1\overline{m}}\},{\tilde{W}}_2=\mathrm{diag}\{{\overline{W}}_{21},\cdots ,{\overline{W}}_{2\overline{m}}\},$$

$$\mathcal{A}=\left(\begin{array}{ccc}{\tilde{A}}_{11}\otimes {\mathsf{\Lambda }}_1& \cdots & {\tilde{A}}_{1\overline{m}}\otimes {\mathsf{\Lambda }}_1\\ ⋮& & ⋮\\ {\tilde{A}}_{\overline{m}1}\otimes {\mathsf{\Lambda }}_1& \cdots & {\tilde{A}}_{\overline{m}\overline{m}}\otimes {\mathsf{\Lambda }}_1\end{array}\right),$$

$$\mathcal{B}=\left(\begin{array}{ccc}{\tilde{B}}_{11}\otimes {\mathsf{\Lambda }}_2& \cdots & {\tilde{B}}_{1\overline{m}}\otimes {\mathsf{\Lambda }}_2\\ ⋮& & ⋮\\ {\tilde{B}}_{\overline{m}1}\otimes {\mathsf{\Lambda }}_2& \cdots & {\tilde{B}}_{\overline{m}\overline{m}}\otimes {\mathsf{\Lambda }}_2\end{array}\right),$$

$$\overline{H}(e\left(t\right)-ϵ\left(t\right))={({\overline{H}}_1^T({\tilde{e}}_1\left(t\right)-{\widetilde{ϵ}}_1\left(t\right)),\cdots ,{\overline{H}}_{\overline{m}}^T({\tilde{e}}_{\overline{m}}\left(t\right)-{\widetilde{ϵ}}_{\overline{m}}\left(t\right)))}^T,$$

$$ϵ\left(t\right)={({\widetilde{ϵ}}_1\left(t\right),\cdots ,{\widetilde{ϵ}}_{\overline{m}}\left(t\right))}^T,\tilde{K}=\mathrm{diag}\{{\tilde{K}}_1,\cdots ,{\tilde{K}}_{\overline{m}}\},$$

$${\mathsf{\Theta }}_1=\mathrm{diag}\{{\theta }_1{\mathsf{\Psi }}_1,\cdots ,{\theta }_N{\mathsf{\Psi }}_N\},$$

$${\mathsf{\Theta }}_2=\mathrm{diag}\{{\theta }_1{\zeta }_1{\mathsf{\Psi }}_1,\cdots ,{\theta }_N{\zeta }_N{\mathsf{\Psi }}_N\},$$

$${\mathsf{\Theta }}_3=\mathrm{diag}\{{\zeta }_1{\mathsf{\Psi }}_1,\cdots ,{\zeta }_N{\mathsf{\Psi }}_N\},$$

$$\mathsf{\Psi }=\mathrm{diag}\{{\mathsf{\Psi }}_1,\cdots ,{\mathsf{\Psi }}_N\},$$

$$\mathcal{H}=I_N\otimes H=\mathrm{diag}\stackrel{N}{\overbrace{\{H,\cdots ,H\}}},$$

$${\tilde{\mathsf{\Gamma }}}_k=-{\displaystyle \frac{{\mathsf{\Gamma }}_{1k}^T+{\mathsf{\Gamma }}_{2k}^T}{2}},{\overline{\mathsf{\Gamma }}}_k={\displaystyle \frac{{\mathsf{\Gamma }}_{1k}^T{\mathsf{\Gamma }}_{2k}+{\mathsf{\Gamma }}_{2k}^T{\mathsf{\Gamma }}_{1k}}{2}},$$

$$\tilde{\mathsf{\Gamma }}=\mathrm{diag}\{{\tilde{\mathsf{\Gamma }}}_1,\cdots ,{\tilde{\mathsf{\Gamma }}}_1,\cdots ,{\tilde{\mathsf{\Gamma }}}_{\overline{m}},\cdots ,{\tilde{\mathsf{\Gamma }}}_{\overline{m}}\},$$

$$\overline{\mathsf{\Gamma }}=\mathrm{diag}\{{\overline{\mathsf{\Gamma }}}_1,\cdots ,{\overline{\mathsf{\Gamma }}}_1,\cdots ,{\overline{\mathsf{\Gamma }}}_{\overline{m}},\cdots ,{\overline{\mathsf{\Gamma }}}_{\overline{m}}\}.$$

3. Main Results

3.1. The Dynamic Event-Triggered Case

This subsection aims to deal with the secure cluster synchronization issue of CDNs (1) under dynamic event-triggered scheme and design suitable pinning controllers. Firstly, a theorem about secure cluster synchronization of CDNs under deception attacks is given.

Theorem 1. 

Consider the CDNs in (1), suppose that Assumptions 1–3 hold. For given parameters ${\tau }_M>0$, ${\overline{\tau }}_1,{\overline{\tau }}_2\in [0,1)$, ${\pi }_i>0$, ${\theta }_i>0$, ${\zeta }_i>0$, ${\eta }_i\left(0\right)>0$, ${\varrho }_i>0$, $i\in \mathcal{V}$; $\overline{\alpha }\in (0,1)$, ${\delta }_1>0$, ${\delta }_2>0$, ${\rho }_k>0$, ${\varpi }_k>0$, $n_k,p_k\in {\mathcal{N}}^{+}$, $k\in \mathcal{M}$, $\beta >0$, $\lambda \in (0,\beta )$, and matrices $H>0$ and $K_i$, $i\in \mathcal{V}$, if there exist scalars ${\iota }_q>0$, $q=1,\cdots ,6$, positive define matrices ${\tilde{Q}}_k$, ${\tilde{R}}_{1k}$, ${\tilde{R}}_{2k}$, ${\tilde{R}}_{3k}$, ${\tilde{R}}_{4k}$, ${\tilde{M}}_{1k}$, ${\tilde{M}}_{2k}$, $k\in \mathcal{M}$ such that

$$\begin{array}{c}\hfill \begin{array}{c}{\iota }_1{\pi }_i+\lambda -{\varrho }_i\le 0,i\in \mathcal{V},\hfill \end{array}\end{array}$$

(13)

$$\begin{array}{c}\hfill \tilde{\mathcal{D}}=\left[\begin{array}{ccc}\overline{\mathcal{D}}& {\tau }_1^2{\mathsf{\Phi }}^T& {\tau }_2^2{\mathsf{\Phi }}^T\\ \ast & -{\tau }_1^2{\tilde{M}}_1^{-1}& 0\\ \ast & \ast & -{\tau }_2^2{\tilde{M}}_2^{-1}\end{array}\right]<0\end{array}$$

(14)

hold, where

$$\begin{array}{cc}\hfill \overline{\mathcal{D}}=& \left[\begin{array}{ccccccccccc}{\mathcal{D}}_{11}+{\mathsf{\Theta }}_3& {\mathcal{D}}_{12}& 0& {\mathcal{D}}_{14}& 0& {\mathcal{D}}_{16}& {\mathcal{D}}_{17}& {\mathcal{D}}_{18}& {\mathcal{D}}_{19}& {\mathcal{D}}_{10}& {\mathcal{D}}_{111}\\ \ast & {\mathcal{D}}_{22}& {\mathcal{D}}_{23}& 0& 0& 0& {\mathcal{D}}_{27}& 0& 0& 0& 0\\ \ast & \ast & {\mathcal{D}}_{33}& 0& 0& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & {\mathcal{D}}_{44}& {\mathcal{D}}_{45}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & {\mathcal{D}}_{55}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{66}& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{77}& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{88}& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{99}& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{00}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\overline{\mathcal{D}}}_{1111}\end{array}\right],\hfill \\ \hfill {\mathcal{D}}_{11}=& (1-\overline{\alpha })(\tilde{Q}\tilde{K}+{\tilde{K}}^T\tilde{Q})+{\tilde{R}}_1+{\tilde{R}}_3+{\iota }_1{\mathsf{\Theta }}_2+{\iota }_4{\delta }_1{I}_{nN}-{\iota }_2\overline{\mathsf{\Gamma }}+{\iota }_6\mathcal{H}-{\tilde{M}}_1-{\tilde{M}}_2,\hfill \\ \hfill {\mathcal{D}}_{12}=& {\tilde{M}}_1,{\mathcal{D}}_{14}={\tilde{M}}_2,{\mathcal{D}}_{16}=\tilde{Q}{\tilde{W}}_1-{\iota }_2\tilde{\mathsf{\Gamma }},{\mathcal{D}}_{17}=\tilde{Q}{\tilde{W}}_2,{\mathcal{D}}_{18}=\tilde{Q}\mathcal{A},{\mathcal{D}}_{19}=\tilde{Q}\mathcal{B},\hfill \\ \hfill {\mathcal{D}}_{10}=& \overline{\alpha }\tilde{Q}\tilde{K},{\mathcal{D}}_{111}=-{\iota }_6\mathcal{H}-(1-\overline{\alpha })\tilde{Q}\tilde{K},{\mathcal{D}}_{22}=-(1-{\overline{\tau }}_1){\tilde{R}}_1+{\tilde{R}}_2-{\iota }_2\overline{\mathsf{\Gamma }}-2{\tilde{M}}_1,\hfill \\ \hfill {\mathcal{D}}_{23}=& {\tilde{M}}_1,{\mathcal{D}}_{27}=-{\iota }_3\tilde{\mathsf{\Gamma }},{\mathcal{D}}_{33}=-{\tilde{R}}_2-{\tilde{M}}_1,{\mathcal{D}}_{44}=-(1-{\overline{\tau }}_2){\tilde{R}}_3+{\tilde{R}}_4+{\iota }_5{\delta }_2{I}_{nN}-2{\tilde{M}}_2,\hfill \\ \hfill {\mathcal{D}}_{45}=& {\tilde{M}}_2,{\mathcal{D}}_{55}=-{\tilde{R}}_4-{\tilde{M}}_2,{\mathcal{D}}_{66}=-{\iota }_2{I}_{nN},{\mathcal{D}}_{77}=-{\iota }_3{I}_{nN},{\mathcal{D}}_{88}=-{\iota }_4{I}_{nN},\hfill \\ \hfill {\mathcal{D}}_{99}=& -{\iota }_5{I}_{nN},{\mathcal{D}}_{00}=-{\iota }_6{I}_{nN},{\overline{\mathcal{D}}}_{11,11}={\mathcal{D}}_{11,11}-\mathsf{\Psi },{\mathcal{D}}_{11,11}=-{\iota }_1{\mathsf{\Theta }}_1+{\iota }_6\mathcal{H},\hfill \\ \hfill \tilde{Q}=& \mathrm{diag}\{{\tilde{Q}}_1,\cdots ,{\tilde{Q}}_{\overline{m}}\},{\tilde{R}}_1=\mathrm{diag}\{{\tilde{R}}_{11},\cdots ,{\tilde{R}}_{1\overline{m}}\},{\tilde{R}}_2=\mathrm{diag}\{{\tilde{R}}_{21},\cdots ,{\tilde{R}}_{2\overline{m}}\},{\tilde{R}}_3=\mathrm{diag}\{{\tilde{R}}_{31},\cdots ,{\tilde{R}}_{3\overline{m}}\},\hfill \\ \hfill {\tilde{R}}_4=& \mathrm{diag}\{{\tilde{R}}_{41},\cdots ,{\tilde{R}}_{4\overline{m}}\},{\tilde{M}}_1=\mathrm{diag}\{{\tilde{M}}_{11},\cdots ,{\tilde{M}}_{1\overline{m}}\},{\tilde{M}}_2=\mathrm{diag}\{{\tilde{M}}_{21},\cdots ,{\tilde{M}}_{2\overline{m}}\},\hfill \end{array}$$

then the closed-loop networks (1) under dynamic event-triggered scheme (5) satisfying (6) is secure cluster synchronization for deception attacks satisfying (7).

Proof. 

Construct the following piecewise Lyapunov functional candidate

$$W\left(t\right)=\exp \{-\beta t\}V\left(t\right)+\sum _{i=1}^N{\eta }_i\left(t\right),$$

(15)

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right),$$

(16)

where $\beta >0$, and 

$$\begin{array}{cc}\hfill V_1\left(t\right)=& \sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T\left(t\right){\tilde{Q}}_k{\tilde{e}}_k\left(t\right),\hfill \\ \hfill V_2\left(t\right)=& \sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_1\left(t\right)}^t{\tilde{e}}_k^T\left(\nu \right){\tilde{R}}_{1k}{\tilde{e}}_k\left(\nu \right)\mathrm{d}\nu +\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_1}^{t-{\tau }_1\left(t\right)}{\tilde{e}}_k^T\left(\nu \right){\tilde{R}}_{2k}{\tilde{e}}_k\left(\nu \right)\mathrm{d}\nu \hfill \\ \hfill & +\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_2\left(t\right)}^t{\tilde{e}}_k^T\left(\nu \right){\tilde{R}}_{3k}{\tilde{e}}_k\left(\nu \right)\mathrm{d}\nu +\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_2}^{t-{\tau }_2\left(t\right)}{\tilde{e}}_k^T\left(\nu \right){\tilde{R}}_{4k}{\tilde{e}}_k\left(\nu \right)\mathrm{d}\nu ,\hfill \\ \hfill V_3\left(t\right)=& {\tau }_1\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_1}^0{\int }_{t+\vartheta }^t{\dot{\tilde{e}}}_k^T\left(\nu \right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k^T\left(\nu \right)\mathrm{d}\nu \mathrm{d}\vartheta +{\tau }_2\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_2}^0{\int }_{t+\vartheta }^t{\dot{\tilde{e}}}_k^T\left(\nu \right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k^T\left(\nu \right)\mathrm{d}\nu \mathrm{d}\vartheta \hfill \end{array}$$

where ${\tilde{Q}}_k=\mathrm{diag}\{Q_{l_{k-1}+1},\cdots ,Q_{l_k}\}$, ${\tilde{R}}_{ik}=\mathrm{diag}\{R_{i,l_{k-1}+1},\cdots ,R_{i,l_k}\}$, $i=1,2,3,4$, ${\tilde{M}}_{ik}=\mathrm{diag}\{M_{i,l_{k-1}+1},\cdots ,M_{i,l_k}\}$, $i=1,2$; $Q_l$, $R_{i,l}$, $M_{1l}$, $M_{2l}$, $i=1,2,3$, $l=1,\cdots ,N$, are symmetric positive define matrice with appropriate dimensions.

From Remark 3 and the definition of $V\left(t\right)$, we have $W\left(t\right)>0$. Then, we obtain

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_1\left(t\right)\right\}=E\left\{\sum _{k=1}^{\overline{m}}2{\tilde{e}}_k^T\left(t\right){\tilde{Q}}_k{\dot{\tilde{e}}}_k\left(t\right)\right\},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_2\left(t\right)\right\}=E\left\{\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T\left(t\right)({\tilde{R}}_{1k}+{\tilde{R}}_{3k}){\tilde{e}}_k\left(t\right)\right.-(1-{\dot{\tau }}_1\left(t\right))\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_1\left(t\right)){\tilde{R}}_{1k}{\tilde{e}}_k(t-{\tau }_1\left(t\right))\hfill \\ \hfill & -(1-{\dot{\tau }}_2\left(t\right))\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_2\left(t\right)){\tilde{R}}_{3k}{\tilde{e}}_k(t-{\tau }_2\left(t\right))\hfill \\ \hfill & +(1-{\dot{\tau }}_1\left(t\right))\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_1\left(t\right)){\tilde{R}}_{2k}{\tilde{e}}_k(t-{\tau }_1\left(t\right))-\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_1){\tilde{R}}_{2k}{\tilde{e}}_k(t-{\tau }_1)\hfill \\ \hfill & \left.+(1-{\dot{\tau }}_2\left(t\right))\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_2\left(t\right)){\tilde{R}}_{4k}{\tilde{e}}_k(t-{\tau }_2\left(t\right))-\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T(t-{\tau }_2){\tilde{R}}_{4k}{\tilde{e}}_k(t-{\tau }_2)\right\},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_3\left(t\right)\right\}=E\left\{{\tau }_1\left(\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_1}^0{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k\left(t\right)\mathrm{d}\vartheta \right.\right.\left.-\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_1}^0{\dot{\tilde{e}}}_k^T(t+\vartheta ){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k(t+\vartheta )\mathrm{d}\vartheta \right)\hfill \\ \hfill & +{\tau }_2\left(\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_2}^0{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k\left(t\right)\mathrm{d}\vartheta \right.\left.\left.-\sum _{k=1}^{\overline{m}}{\int }_{-{\tau }_2}^0{\dot{\tilde{e}}}_k^T(t+\vartheta ){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k(t+\vartheta )\mathrm{d}\vartheta \right)\right\}\hfill \\ \hfill & =E\left\{\sum _{k=1}^{\overline{m}}{\tau }_1^2{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k\left(t\right)\right.+\sum _{k=1}^{\overline{m}}{\tau }_2^2{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k\left(t\right)-{\tau }_1\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_1}^t{\dot{\tilde{e}}}_k^T\left(\vartheta \right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k\left(\vartheta \right)\mathrm{d}\vartheta \hfill \\ \hfill & \left.-{\tau }_2\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_2}^t{\dot{\tilde{e}}}_k^T\left(\vartheta \right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k\left(\vartheta \right)\mathrm{d}\vartheta \right\}.\hfill \end{array}$$

(19)

From (17)–(19) and Lemma 1, we have

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_1\left(t\right)\right\}\le E\left\{\sum _{k=1}^{\overline{m}}{\tilde{e}}_k^T\left(t\right){\tilde{Q}}_k\left[{\overline{W}}_1{\overline{F}}_k\left({\tilde{e}}_k\left(t\right)\right)\right.\right.+{\overline{W}}_2{\overline{F}}_k\left({\tilde{e}}_k(t-{\tau }_1\left(t\right))\right)+\sum _{j=1}^{\overline{m}}{\tilde{A}}_{kj}\otimes {\mathsf{\Lambda }}_1{\overline{G}}_1\left({\tilde{e}}_j\left(t\right)\right)\hfill \\ \hfill & +\sum _{j=1}^{\overline{m}}{\tilde{B}}_{kj}\otimes {\mathsf{\Lambda }}_2{\overline{G}}_2\left({\tilde{e}}_j(t-{\tau }_2\left(t\right))\right)+(\alpha \left(t\right)-\overline{\alpha }){\tilde{K}}_k{\overline{H}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))\hfill \\ \hfill & +\overline{\alpha }{\tilde{K}}_k{\overline{H}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))+(1-\overline{\alpha }){\tilde{K}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))\left.\left.-(\alpha \left(t\right)-\overline{\alpha }){\tilde{K}}_k({\tilde{e}}_k\left(t\right)-{\widetilde{ϵ}}_k\left(t\right))\right]\right\}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_2\left(t\right)\right\}\le E\left\{e^T\left(t\right)({\tilde{R}}_1+{\tilde{R}}_3)e\left(t\right)-e^T(t-{\tau }_1){\tilde{R}}_{2}e(t-{\tau }_1)\right.-e^T(t-{\tau }_2){\tilde{R}}_{4}e(t-{\tau }_2)\hfill \\ \hfill & \left.-e^T(t-{\tau }_1\left(t\right))((1-{\overline{\tau }}_1){\tilde{R}}_1-{\tilde{R}}_2)e(t-{\tau }_1\left(t\right))-e^T(t-{\tau }_2\left(t\right))((1-{\overline{\tau }}_2){\tilde{R}}_3-{\tilde{R}}_4)e(t-{\tau }_2\left(t\right))\right\},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & E\left\{{\dot{V}}_3\left(t\right)\right\}=E\left\{\sum _{k=1}^{\overline{m}}{\tau }_1^2{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k\left(t\right)+\sum _{k=1}^{\overline{m}}{\tau }_2^2{\dot{\tilde{e}}}_k^T\left(t\right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k\left(t\right)\right.\hfill \\ \hfill & -{\tau }_1\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_1}^t{\dot{\tilde{e}}}_k^T\left(\nu \right){\tilde{M}}_{1k}{\dot{\tilde{e}}}_k\left(\nu \right)\mathrm{d}\nu \left.-{\tau }_2\sum _{k=1}^{\overline{m}}{\int }_{t-{\tau }_2}^t{\dot{\tilde{e}}}_k^T\left(\nu \right){\tilde{M}}_{2k}{\dot{\tilde{e}}}_k\left(\nu \right)\mathrm{d}\nu \right\}\hfill \\ \hfill & \le E\left\{{\left[\begin{array}{c}e\left(t\right)\\ e(t-{\tau }_1\left(t\right))\\ e(t-{\tau }_1)\end{array}\right]}^T\left[\begin{array}{ccc}-{\tilde{M}}_1& {\tilde{M}}_1& 0\\ \ast & -2{\tilde{M}}_1& {\tilde{M}}_1\\ \ast & \ast & {\tilde{M}}_1\end{array}\right]\times \left[\begin{array}{c}e\left(t\right)\\ e(t-{\tau }_1\left(t\right))\\ e(t-{\tau }_1)\end{array}\right]+{\left[\begin{array}{c}e\left(t\right)\\ e(t-{\tau }_2\left(t\right))\\ e(t-{\tau }_2)\end{array}\right]}^T\right.\hfill \\ \hfill & \left.\times \left[\begin{array}{ccc}-{\tilde{M}}_2& {\tilde{M}}_2& 0\\ \ast & -2{\tilde{M}}_2& {\tilde{M}}_2\\ \ast & \ast & {\tilde{M}}_2\end{array}\right]\left[\begin{array}{c}e\left(t\right)\\ e(t-{\tau }_2\left(t\right))\\ e(t-{\tau }_2)\end{array}\right]+{\tau }_1^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_1\mathsf{\Phi }{z}^T\left(t\right)+{\tau }_2^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_2\mathsf{\Phi }{z}^T\left(t\right)\right\}\hfill \end{array}$$

(22)

From Assumptions 1 and 2, we can obtain

$$\begin{array}{cc}\hfill & {\left[\begin{array}{c}e\left(t\right)\\ \overline{F}\left(e\left(t\right)\right)\end{array}\right]}^T\left[\begin{array}{cc}\overline{\mathsf{\Gamma }}& \tilde{\mathsf{\Gamma }}\\ \ast & I_{nN}\end{array}\right]\left[\begin{array}{c}e\left(t\right)\\ \overline{F}\left(t\right)\end{array}\right]\le 0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {\left[\begin{array}{c}e(t-{\tau }_1\left(t\right))\\ \overline{F}\left(e(t-{\tau }_1\left(t\right))\right)\end{array}\right]}^T\left[\begin{array}{cc}\overline{\mathsf{\Gamma }}& \tilde{\mathsf{\Gamma }}\\ \ast & I_{nN}\end{array}\right]\left[\begin{array}{c}e(t-{\tau }_1\left(t\right))\\ \overline{F}\left(e(t-{\tau }_1\left(t\right))\right)\end{array}\right]\le 0,\hfill \end{array}$$

(24)

$$\begin{array}{c}\hfill {\overline{G}}_1^T\left(e\left(t\right)\right){\overline{G}}_1\left(e\left(t\right)\right)\le {\delta }_1{e}^T\left(t\right)e\left(t\right),\end{array}$$

(25)

$$\begin{array}{cc}\hfill & {\overline{G}}_2^T\left(e(t-{\tau }_2\left(t\right))\right){\overline{G}}_2\left(e(t-{\tau }_2\left(t\right))\right)\le {\delta }_2{e}^T(t-{\tau }_2\left(t\right))e(t-{\tau }_2\left(t\right)).\hfill \end{array}$$

(26)

The triggering condition in (5) can be rewritten as follows

$$\sum _{i=1}^N{\pi }_i{\eta }_i\left(t\right)-{ϵ}^T\left(t\right){\mathsf{\Theta }}_1ϵ\left(t\right)+e^T\left(t\right){\mathsf{\Theta }}_{2}e\left(t\right)>0.$$

(27)

From (20)–(27), we can further obtain

$$\begin{array}{cc}\hfill & E\left\{\dot{V}\left(t\right)\right\}\le E\left\{{\dot{V}}_1\left(t\right)+{\dot{V}}_2\left(t\right)+{\dot{V}}_3\left(t\right)\right\}+{\iota }_1(\sum _{i=1}^N{\pi }_i{\eta }_i\left(t\right)-{ϵ}^T\left(t\right){\mathsf{\Theta }}_1ϵ\left(t\right)+e^T\left(t\right){\mathsf{\Theta }}_{2}e\left(t\right))\hfill \\ \hfill & -{\iota }_2{\left[\begin{array}{c}e\left(t\right)\\ \overline{F}\left(e\left(t\right)\right)\end{array}\right]}^T\left[\begin{array}{cc}\overline{\mathsf{\Gamma }}& \tilde{\mathsf{\Gamma }}\\ \ast & I_{nN}\end{array}\right]\left[\begin{array}{c}e\left(t\right)\\ \overline{F}\left(t\right)\end{array}\right]-{\iota }_3{\left[\begin{array}{c}e(t-{\tau }_1\left(t\right))\\ \overline{F}\left(e(t-{\tau }_1\left(t\right))\right)\end{array}\right]}^T\left[\begin{array}{cc}\overline{\mathsf{\Gamma }}& \tilde{\mathsf{\Gamma }}\\ \ast & I_{nN}\end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{c}e(t-{\tau }_1\left(t\right))\\ \overline{F}\left(e(t-{\tau }_1\left(t\right))\right)\end{array}\right]-{\iota }_4({\overline{G}}_1^T\left(e\left(t\right)\right){\overline{G}}_1\left(e\left(t\right)\right)-{\delta }_1{e}^T\left(t\right)e\left(t\right))+{\iota }_5\left({\delta }_2{e}^T(t-{\tau }_2\left(t\right))e(t-{\tau }_2\left(t\right))\right)\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & -{\overline{G}}_2^T\left(e(t-{\tau }_2\left(t\right))\right){\overline{G}}_2\left(e(t-{\tau }_2\left(t\right))\right)-{\iota }_6({\overline{H}}^T(e\left(t\right)-ϵ\left(t\right))\overline{H}(e\left(t\right)-ϵ\left(t\right))\hfill \\ \hfill & -{(e\left(t\right)-ϵ\left(t\right))}^T\mathcal{H}(e\left(t\right)-ϵ\left(t\right)))\hfill \\ \hfill & \le E\left\{{\tau }_1^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_1\mathsf{\Phi }{z}^T\left(t\right)+{\tau }_2^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_2\mathsf{\Phi }{z}^T\left(t\right)\right.+\left.z^T\left(t\right)\mathcal{D}z\left(t\right)\right\}+{\iota }_1\sum _{i=1}^N{\pi }_i{\eta }_i\left(t\right),\hfill \end{array}$$

where $\mathcal{D}={\left(D_{ij}\right)}_{10\times 10}$, ${\iota }_i$, $i=1,\cdots ,5$ are some positive constants.

Introducing a positive scalar $\lambda \in (0,\beta )$, one has from (13) that

$$\begin{array}{cc}\hfill & E\{\dot{W}\left(t\right)+\lambda W\left(t\right)\}=E\left\{\exp \{-\beta t\}\dot{V}\left(t\right)\right\}+\sum _{i=1}^N{\dot{\eta }}_i\left(t\right)+\sum _{i=1}^N\lambda {\eta }_i\left(t\right)\hfill \\ \hfill & -(\beta -\lambda )E\left\{\exp \right\{-\beta t\left\}V\right(t\left)\right\}\hfill \\ \hfill & \le E\left\{{\tau }_1^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_1\mathsf{\Phi }{z}^T\left(t\right)+{\tau }_2^2{z}^T\left(t\right){\mathsf{\Phi }}^T{\tilde{M}}_2\mathsf{\Phi }{z}^T\left(t\right)\right.+\left.z^T\left(t\right)\mathcal{D}z\left(t\right)\right\}\hfill \\ \hfill & +{\iota }_1\sum _{i=1}^N{\pi }_i{\eta }_i\left(t\right)-{ϵ}^T\left(t\right)\mathsf{\Psi }ϵ\left(t\right)+e^T\left(t\right){\mathsf{\Theta }}_{3}e\left(t\right)+\sum _{i=1}^N\lambda {\eta }_i\left(t\right)-\sum _{i=1}^N{\varrho }_i{\eta }_i\left(t\right)\hfill \\ \hfill & \le E\left\{z^T\left(t\right)({\tau }_1^2{\mathsf{\Phi }}^T{\tilde{M}}_1\mathsf{\Phi }+{\tau }_2^2{\mathsf{\Phi }}^T{\tilde{M}}_2\mathsf{\Phi }+\overline{\mathcal{D}})z^T\left(t\right)\right\}.\hfill \end{array}$$

(29)

By applying Schur complement, one can obtain that (14) is equivalent to

$${\tau }_1^2{\mathsf{\Phi }}^T{\tilde{M}}_1\mathsf{\Phi }+{\tau }_2^2{\mathsf{\Phi }}^T{\tilde{M}}_2\mathsf{\Phi }+\overline{\mathcal{D}}<0.$$

(30)

Then, it follows from (29) and (30) that $E\left\{\dot{W}\left(t\right)\right\}<-\lambda W\left(t\right)$, which implies $\underset{t\to +\infty }{lim}$$E\{{\displaystyle \sum _{i=l_{k-1}+1}^{l_k}}\parallel e_i\left(t\right)\parallel \}=0$, $k\in \mathcal{M}$. Hence, the CDNs in (1) under the proposed controller (8) achieves secure cluster synchronization. This completes the proof.    □

Based on Theorem 1, the synchronization controller design in terms of the desired controller gain matrices $K_i$, $i\in \mathcal{V}$, can be performed. Firstly, pre- and post- multiplying the inequality (14) by $\mathrm{diag}\{I,\tilde{Q},\tilde{Q}\}$, which yields

$$\left[\begin{array}{ccc}\overline{\mathcal{D}}& {\tau }_1^2{\overline{\mathsf{\Phi }}}^T& {\tau }_2^2{\overline{\mathsf{\Phi }}}^T\\ \ast & -{\tau }_1^2\tilde{Q}{\tilde{M}}_1^{-1}\tilde{Q}& 0\\ \ast & \ast & -{\tau }_2^2\tilde{Q}{\tilde{M}}_2^{-1}\tilde{Q}\end{array}\right]<0,$$

(31)

where $\overline{\mathsf{\Phi }}=((1-\overline{\alpha })\tilde{Q}\tilde{K}$, 0, 0, 0, 0, $\tilde{Q}{\tilde{W}}_1$, $\tilde{Q}{\tilde{W}}_2$, $\tilde{Q}\mathcal{A}$, $\tilde{Q}\mathcal{B}$, $\overline{\alpha }\tilde{Q}\tilde{K}$, $-(1-\overline{\alpha })\tilde{Q}\tilde{K})$. Setting $\tilde{Q}\tilde{K}=\mathsf{\Xi }$, then (31) can be rewritten as

$$\left[\begin{array}{ccc}\widehat{\mathcal{D}}& {\tau }_1^2{\widehat{\mathsf{\Phi }}}^T& {\tau }_2^2{\widehat{\mathsf{\Phi }}}^T\\ \ast & -{\tau }_1^2\tilde{Q}{\tilde{M}}_1^{-1}\tilde{Q}& 0\\ \ast & \ast & -{\tau }_2^2\tilde{Q}{\tilde{M}}_2^{-1}\tilde{Q}\end{array}\right]<0,$$

(32)

where

$$\begin{array}{cc}\hfill {\widehat{\mathcal{D}}}_{11}=& (1-\overline{\alpha })(\mathsf{\Xi }+{\mathsf{\Xi }}^T)+{\tilde{R}}_1+{\tilde{R}}_3+{\iota }_1{\mathsf{\Theta }}_2+{\iota }_4{\delta }_1{I}_{nN}-{\iota }_1\overline{\mathsf{\Gamma }}+{\iota }_5\mathcal{H}-{\tilde{M}}_1-{\tilde{M}}_2+{\mathsf{\Theta }}_3,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\widehat{\mathcal{D}}}_{10}=& \overline{\alpha }\mathsf{\Xi },{\widehat{\mathcal{D}}}_{111}=-{\iota }_6\mathcal{H}-(1-\overline{\alpha })\mathsf{\Xi },\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathsf{\Phi }}=& {((1-\overline{\alpha })\mathsf{\Xi },0,0,0,0,\tilde{Q}{\tilde{W}}_1,\tilde{Q}{\tilde{W}}_2,\tilde{Q}\mathcal{A},\tilde{Q}\mathcal{B},\overline{\alpha }\mathsf{\Xi },-(1-\overline{\alpha })\mathsf{\Xi })}^T.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathcal{D}}=& \left[\begin{array}{ccccccccccc}{\widehat{\mathcal{D}}}_{11}& {\mathcal{D}}_{12}& 0& {\mathcal{D}}_{14}& 0& {\mathcal{D}}_{16}& {\mathcal{D}}_{17}& {\mathcal{D}}_{18}& {\mathcal{D}}_{19}& {\widehat{\mathcal{D}}}_{10}& {\widehat{\mathcal{D}}}_{111}\\ \ast & {\mathcal{D}}_{22}& {\mathcal{D}}_{23}& 0& 0& 0& {\mathcal{D}}_{27}& 0& 0& 0& 0\\ \ast & \ast & {\mathcal{D}}_{33}& 0& 0& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & {\mathcal{D}}_{44}& {\mathcal{D}}_{45}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & {\mathcal{D}}_{55}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{66}& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{77}& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{88}& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{99}& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{00}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\overline{\mathcal{D}}}_{11,11}\end{array}\right],\hfill \end{array}$$

In light of Lemma 3, one can get

$$\left[\begin{array}{ccc}\widehat{\mathcal{D}}& {\tau }_1^2{\widehat{\mathsf{\Phi }}}^T& {\tau }_2^2{\widehat{\mathsf{\Phi }}}^T\\ \ast & -2{\tau }_1^2\tilde{Q}+{\tau }_1^2{\tilde{M}}_1& 0\\ \ast & \ast & -2{\tau }_2^2\tilde{Q}+{\tau }_2^2{\tilde{M}}_2\end{array}\right]<0.$$

(33)

Based on the formulation above, the following theorem states a sufficient condition on the existence of the desired secure cluster dynamic event-triggered synchronization controller (8).

Theorem 2. 

Consider the CDNs in (1), suppose that Assumptions 1–3 hold. For given parameters ${\tau }_M>0$, ${\overline{\tau }}_1,{\overline{\tau }}_2\in [0,1)$, ${\pi }_i>0$, ${\mathsf{\theta }}_i>0$, ${\zeta }_i>0$, ${\eta }_i\left(0\right)>0$, ${\varrho }_i>0$, $i\in \mathcal{V}$; $\overline{\alpha }\in (0,1)$, ${\delta }_1>0$, ${\delta }_2>0$, ${\rho }_k>0$, ${\varpi }_k>0$, $n_k,p_k\in {\mathcal{N}}^{+}$, $k\in \mathcal{M}$, $\beta >0$, $\lambda \in (0,\beta )$, and matrix $H>0$, if there exist scalers ${\iota }_q>0$, $q=1,\cdots ,6$, some symmetric positive define matrices ${\tilde{Q}}_k$, ${\tilde{R}}_{1k}$, ${\tilde{R}}_{2k}$, ${\tilde{R}}_{3k}$, ${\tilde{M}}_k$, $k\in \mathcal{M}$, andΞ with appropriate dimensions, such that the inequalities (13) and (33) are satisfied, then the secure cluster synchronization problem is solved under the controller gain matrix given as

$$\tilde{K}={\tilde{Q}}^{-1}\mathsf{\Xi }.$$

(34)

Proof. 

By using Schur complement and $-\tilde{Q}{\tilde{M}}_1^{-1}\tilde{Q}\le -2\tilde{Q}+{\tilde{M}}_1$, $-\tilde{Q}{\tilde{M}}_2^{-1}\tilde{Q}\le -2\tilde{Q}+{\tilde{M}}_2$, The theorem can be conducted immediately from Theorem 1.    □

Remark 7. 

The LMIs (33) in Theorem 2 were solved using MATLAB R2023b with the Robust Control Toolbox (Version 6.15)—specifically, the lmilab environment and feasp function. This toolbox is widely adopted in control systems research for LMI-based design due to its compatibility with standard academic LMI formulations. Algorithm 1 is given to show how to solve LMI and compute controller gains.

3.2. The Static Event-Triggered Case

It is worth mentioning that the dynamic event-triggered mechanism in (5) includes the static one as a special case. In addition, the results for secure cluster synchronization of the CDNs in (1) under a static event-triggered mechanism can be developed straightforwardly from Theorem 1 by letting $\theta$ approach to $+\infty$. Such a static event-triggered mechanism can be described by

$$\begin{array}{cc}{t}_{q+1}^i=\hfill & inf\{t>t_q^i|{\zeta }_i{\left(e_i\left(t\right)\right)}^T{e}_i\left(t\right)-{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right))\le 0\},\hfill \end{array}$$

(35)

where ${\zeta }_i\in (0,1)$. Then the design criterion for secure cluster synchronization of the CDNs (1) under the above static event-triggered mechanism is stated as follows. The proof is omitted for concise.

Algorithm 1 LMI and Compute Controller Gains

Input: N, $\overline{m}$, $P=[P_1,P_2,\cdots ,P_{\overline{m}}]$, n, ${\tau }_1,{\tau }_2$, ${\tau }_M=max({\tau }_1,{\tau }_2)$, $W_{1k},W_{2k}$, ${\mathsf{\Gamma }}_{1k},{\mathsf{\Gamma }}_{2k}$, ${\delta }_1,{\delta }_2$, $A,B$, ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2$, $\overline{\alpha }\in (0,1)$, $H>0$, ${\pi }_i>0,{\theta }_i>0,{\zeta }_i\in (0,1),{\varrho }_i>0$, ${\eta }_0>0$), ${\iota }_q>0(q=1,\cdots ,6)$, $\beta >0,\lambda \in (0,\beta )$, $\mathrm{tol}={10}^{-8}$, $T_{\mathrm{sim}}$, $dt={10}^{-4}$.

Output: $K_i(i=1,\cdots ,N)$.  1: Step 1: Formulate LMI  2: 1.1 Define block-diagonal decision matrices: Q, $R_1$, $R_2$, $R_3$, $R_4$, $M_1$, $M_2$, $\mathsf{\Xi }$.  3: 1.2 Compute auxiliary matrices for triggering and attacks: ${\mathsf{\Theta }}_1$, ${\mathsf{\Theta }}_2$, ${\mathsf{\Theta }}_3$ with ${\mathsf{\Psi }}_i>0$ (predefined positive definite matrices, e.g., ${\mathsf{\Psi }}_i=I_n$).  4: 1.3 Construct core LMI block $\overline{\mathcal{D}}$: $${\mathcal{D}}_{11}=(1-\overline{\alpha })(\mathsf{\Xi }+{\mathsf{\Xi }}^T)+R_1+R_3+{\iota }_1{\mathsf{\Theta }}_2+{\iota }_4{\delta }_1{I}_{nN}-{\iota }_2\overline{\mathsf{\Gamma }}+{\iota }_6\mathcal{H}-M_1-M_2,$$ $${\mathcal{D}}_{12}=M_1,{\mathcal{D}}_{14}=M_2,{\mathcal{D}}_{16}=Q{\tilde{W}}_1-{\iota }_2\tilde{\mathsf{\Gamma }},{\mathcal{D}}_{10}=\overline{\alpha }\mathsf{\Xi },{\mathcal{D}}_{111}=-{\iota }_6\mathcal{H}-(1-\overline{\alpha })\mathsf{\Xi },$$ and fill remaining blocks (${\mathcal{D}}_{22},{\mathcal{D}}_{23},\cdots$).  5: 1.4 Form full LMI via Schur complement: $$\tilde{\mathcal{D}}=\left[\begin{array}{ccc}\overline{\mathcal{D}}& {\tau }_1^2{\mathsf{\Phi }}^T& {\tau }_2^2{\mathsf{\Phi }}^T\\ \ast & -{\tau }_1^2{M}_1^{-1}& 0\\ \ast & \ast & -{\tau }_2^2{M}_2^{-1}\end{array}\right]<0,$$ where $\mathsf{\Phi }={[(1-\overline{\alpha })\mathsf{\Xi },0,0,0,0,Q{\tilde{W}}_1,Q{\tilde{W}}_2,Q\mathcal{A},Q\mathcal{B},\overline{\alpha }\mathsf{\Xi },-(1-\overline{\alpha })\mathsf{\Xi }]}^T$.  6: 1.5 Add constraints: $$Q>0,R_1>0,R_2>0,R_3>0,R_4>0,M_1>0,M_2>0,{\iota }_1{\pi }_i+\lambda -{\varrho }_i\le 0(\forall i).$$   Step 2: Solve LMI and Controller Gains  7: 2.1 Call LMI solver (e.g., MATLAB feasp) to solve $\tilde{\mathcal{D}}<0$ with tolerance tol.  8: if no feasible solution exists then  9:    Print ’LMI infeasible: Relax $H,{\tau }_1,{\tau }_2,$ or ${\iota }_q$’ and terminate. 10: else 11:    Extract feasible matrices $Q_{\mathrm{feas}}$ and ${\mathsf{\Xi }}_{\mathrm{feas}}$. 12: end if 13: 2.2 Calculate controller gains: $K=Q_{\mathrm{feas}}^{-1}{\mathsf{\Xi }}_{\mathrm{feas}}$, and split K into per-node gains $K_i$ based on cluster partition P. 14: return $K_i$

Theorem 3. 

Consider the CDNs in (1), suppose that Assumptions 1–3 hold. For given parameters ${\tau }_M>0$, ${\overline{\tau }}_1,{\overline{\tau }}_2\in [0,1)$, ${\zeta }_i\in (0,1)$, $i\in \mathcal{V}$; $\overline{\alpha }\in (0,1)$, ${\delta }_1>0$, ${\delta }_2>0$, ${\rho }_k>0$, ${\varpi }_k>0$, $n_k,p_k\in {\mathcal{N}}^{+}$, $k\in \mathcal{M}$, and matrix $H>0$, if there exist scalers ${\iota }_q>0$, $q=1,\cdots ,6$, some symmetric positive define matrices ${\tilde{Q}}_k$, ${\tilde{R}}_{1k}$, ${\tilde{R}}_{2k}$, ${\tilde{R}}_{3k}$, ${\tilde{M}}_k$, $k\in \mathcal{M}$, and $\overline{\mathsf{\Xi }}$ with appropriate dimensions such that

$$\overline{\mathsf{\Pi }}=\left[\begin{array}{ccc}\breve{\mathsf{{\rm Y}}}& {\tau }_1^2{\breve{\mathsf{\Phi }}}^T& {\tau }_2^2{\breve{\mathsf{\Phi }}}^T\\ \ast & -2{\tau }_1^2\tilde{Q}+{\tau }_1^2{\tilde{M}}_1& 0\\ \ast & \ast & -{\tau }_2^2\tilde{Q}+{\tau }_2^2{\tilde{M}}_2\end{array}\right]<0,$$

(36)

where

$$\begin{array}{cc}\hfill {\mathsf{{\rm Y}}}_{11}=& (1-\overline{\alpha })(\overline{\mathsf{\Xi }}+{\overline{\mathsf{\Xi }}}^T)+{\tilde{R}}_1+{\tilde{R}}_3+{\iota }_1{\mathsf{\Theta }}_3+{\iota }_4{\delta }_1{I}_{nN}-{\iota }_2\overline{\mathsf{\Gamma }}+{\iota }_6\mathcal{H}-{\tilde{M}}_1-{\tilde{M}}_2,\hfill \\ \hfill {\mathsf{{\rm Y}}}_{10}=& \overline{\alpha }\overline{\mathsf{\Xi }},{\mathsf{{\rm Y}}}_{111}=-{\iota }_6\mathcal{H}-(1-\overline{\alpha })\overline{\mathsf{\Xi }},\hfill \\ \hfill \breve{\mathsf{\Phi }}=& ((1-\overline{\alpha })\overline{\mathsf{\Xi }},0,0,0,0,\tilde{Q}{\tilde{W}}_1,\tilde{Q}{\tilde{W}}_2,\tilde{Q}\mathcal{A},\tilde{Q}\mathcal{B},\overline{\alpha }\overline{\mathsf{\Xi }},-(1-\overline{\alpha })\overline{\mathsf{\Xi }}),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \breve{\mathsf{{\rm Y}}}=& \left[\begin{array}{ccccccccccc}{\mathsf{{\rm Y}}}_{11}& {\mathcal{D}}_{12}& 0& {\mathcal{D}}_{14}& 0& {\mathcal{D}}_{16}& {\mathcal{D}}_{17}& {\mathcal{D}}_{18}& {\mathcal{D}}_{19}& {\mathsf{{\rm Y}}}_{10}& {\mathsf{{\rm Y}}}_{111}\\ \ast & {\mathcal{D}}_{22}& {\mathcal{D}}_{23}& 0& 0& 0& {\mathcal{D}}_{27}& 0& 0& 0& 0\\ \ast & \ast & {\mathcal{D}}_{33}& 0& 0& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & {\mathcal{D}}_{44}& {\mathcal{D}}_{45}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & {\mathcal{D}}_{55}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{66}& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{77}& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{88}& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{99}& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathcal{D}}_{00}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\breve{\mathcal{D}}}_{11,11}\end{array}\right],\hfill \end{array}$$

then the CDNs in (1) under the static event-triggered mechanism (35) achieves secure cluster synchronization against deception attacks satisfying (7). Furthermore, the controller gain matrix is determined as $\tilde{K}={\tilde{Q}}^{-1}\overline{\mathsf{\Xi }}$.

Remark 8. 

The theoretical connection between the two mechanisms—where the static case (Theorem 3) emerges as a special case of the dynamic one when ${\theta }_i\to +\infty$—-stems from the gradual ’elimination’ of the auxiliary variable ${\eta }_i\left(t\right)$’s influence: as ${\theta }_i$ grows infinitely large, the dynamic triggering condition (5) simplifies to the static threshold rule (36), where only the error difference ${\zeta }_i{e}_i^T\left(t\right){\mathsf{\Psi }}_i{e}_i\left(t\right)-{(e_i\left(t\right)-e_i\left(t_q^i\right))}^T{\mathsf{\Psi }}_i(e_i\left(t\right)-e_i\left(t_q^i\right))\le 0$ determines triggering (the auxiliary ${\eta }_i\left(t\right)$ term becomes negligible).

4. An Illustrative Example

Consider a network of five nodes that are assigned into two clusters ${\mathcal{P}}_1=\{1,2\}$, ${\mathcal{P}}_2=\{3,4,5\}$. Moreover, the ith node described as (1) with ${\mathsf{\Lambda }}_1=\mathrm{diag}\{0.5,0.5\}$, ${\mathsf{\Lambda }}_2=\mathrm{diag}\{0.2,0.2\}$, $W_{11}=\mathrm{diag}\{1.2,0.8\}$, $W_{21}=\mathrm{diag}\{0.2,0.2\}$, $W_{12}=\mathrm{diag}\{0.8,0.9\}$, $W_{22}=\mathrm{diag}\{0.2,0.5\}$, $f_1\left(x_i\left(t\right)\right)=[0.6x_{i1}\left(t\right)-tanh\left(0.3x_{i1}\left(t\right)\right)+0.1x_{i2}\left(t\right)$, $0.8x_{i2}\left(t\right)-tanh\left(0.5x_{i2}\left(t\right)\right){]}^T$ with ${\mathsf{\Gamma }}_{11}=\left[\begin{array}{cc}0.6& 0.1\\ 0& 0.8\end{array}\right]$, ${\mathsf{\Gamma }}_{21}=\left[\begin{array}{cc}0.9& 0.1\\ 0& 1.3\end{array}\right]$, $f_2\left(x_i\left(t\right)\right)=[-0.3x_{i1}\left(t\right)-tanh\left(0.2x_{i1}\left(t\right)\right)+0.2x_{i2}\left(t\right)$, $0.4x_{i2}\left(t\right)-tanh\left(0.4x_{i2}\left(t\right)\right)]$ with ${\mathsf{\Gamma }}_{12}=\left[\begin{array}{cc}-0.3& 0.2\\ 0& 0.4\end{array}\right]$, ${\mathsf{\Gamma }}_{22}=\left[\begin{array}{cc}-0.1& 0.2\\ 0& 0.8\end{array}\right]$, $g_1\left(x_i\left(t\right)\right)=\left[\begin{array}{c}-0.8x_{i1}\left(t\right)\\ -0.8x_{i2}\left(t\right)\end{array}\right]$, $g_2\left(x_i\left(t\right)\right)=\left[\begin{array}{c}-0.1x_{i1}\left(t\right)\\ -0.1x_{i2}\left(t\right)\end{array}\right]$, ${\tau }_1\left(t\right)=0.1tanh\left(t\right)$, ${\tau }_2\left(t\right)=0.2tanh\left(t\right)$, and

$$\begin{array}{c}\hfill A=\left[\begin{array}{ccccc}-2& 2& 1& 0& -1\\ 2& -2& 0& 1& -1\\ 1& -1& -4& 2& 2\\ 1& -1& 1.5& -3& 1.5\\ 1& -1& 1& 1& -2\end{array}\right],B=\left[\begin{array}{ccccc}-3& 3& 0.1& 0.1& -0.2\\ 1& -1& 0.2& 0.2& -0.4\\ 1& -1& -3& 2& 1\\ 0.5& -0.5& 1& -2& 1\\ 0.1& -0.1& 1& 1& -2\end{array}\right].\end{array}$$

Choose ${\delta }_1=0.8$, ${\delta }_2=0.1$, ${\tau }_1=0.1$, ${\tau }_2=0.2$, ${\overline{\tau }}_1=0.1$, ${\overline{\tau }}_2\left(t\right)=0.1$, ${\pi }_1=0.2$, ${\pi }_2=0.1$, ${\pi }_3=0.1$, ${\pi }_4=0.2$, ${\pi }_5=0.2$, ${\theta }_i=1$, ${\zeta }_i=0.3$, ${\varrho }_i=1$, ${\eta }_i\left(0\right)=1$, $i=1,\cdots ,5$. Via solving LMI (33), the feasible controller gains are given as $K_1=\left[\begin{array}{cc}-28.8471& 0.0463\\ \ast & -28.2460\end{array}\right]$, $K_2=\left[\begin{array}{cc}-28.7249& 0.0463\\ \ast & -28.1023\end{array}\right]$, $K_3=\left[\begin{array}{cc}-29.7127& -0.0280\\ \ast & -29.9920\end{array}\right]$, $K_4=\left[\begin{array}{cc}-28.9436& -0.0745\\ \ast & -29.3441\end{array}\right]$, $K_5=\left[\begin{array}{cc}-28.6145& -0.0786\\ \ast & -29.1118\end{array}\right]$.

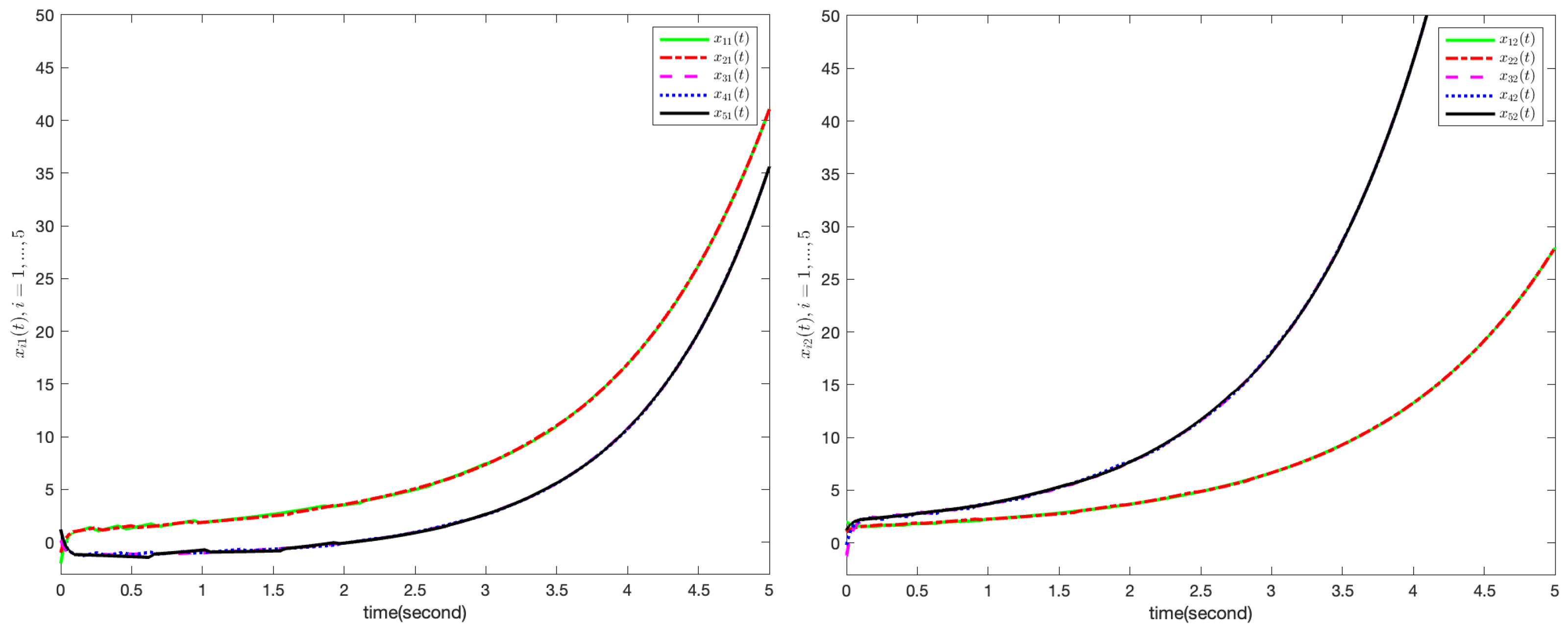
Applying the designed secure cluster synchronization controller, it is found that the CDNs can be synchronized into two clusters even in the presence of the simulated stochastic deception attacks. The related simulation results are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Specifically, from Figure 1, it can be concluded that the nodes are not synchronized without controllers. Under the controllers, nodes in the same cluster are synchronized and not synchronized in the different cluster from Figure 2. 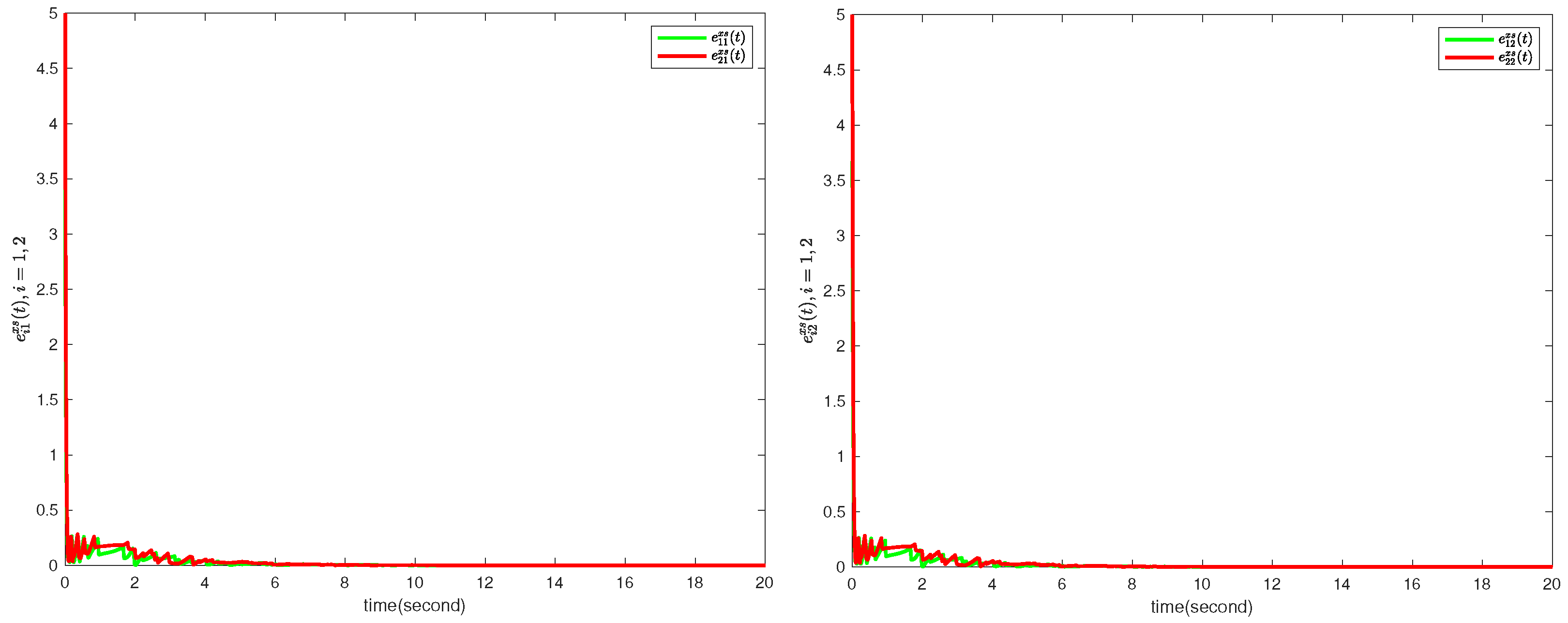Moreover, as shown in Figure 3, the trajectories of cluster errors $e_1^{xs}\left(t\right)={\sum }_{i=1}^2{\parallel x_i\left(t\right)-s_1\left(t\right)\parallel }^2$, $e_2^{xs}\left(t\right)={\sum }_{i=3}^5{\parallel x_i\left(t\right)-s_2\left(t\right)\parallel }^2$ are approaching zero, such findings illustrate that the theoretical results are effective. 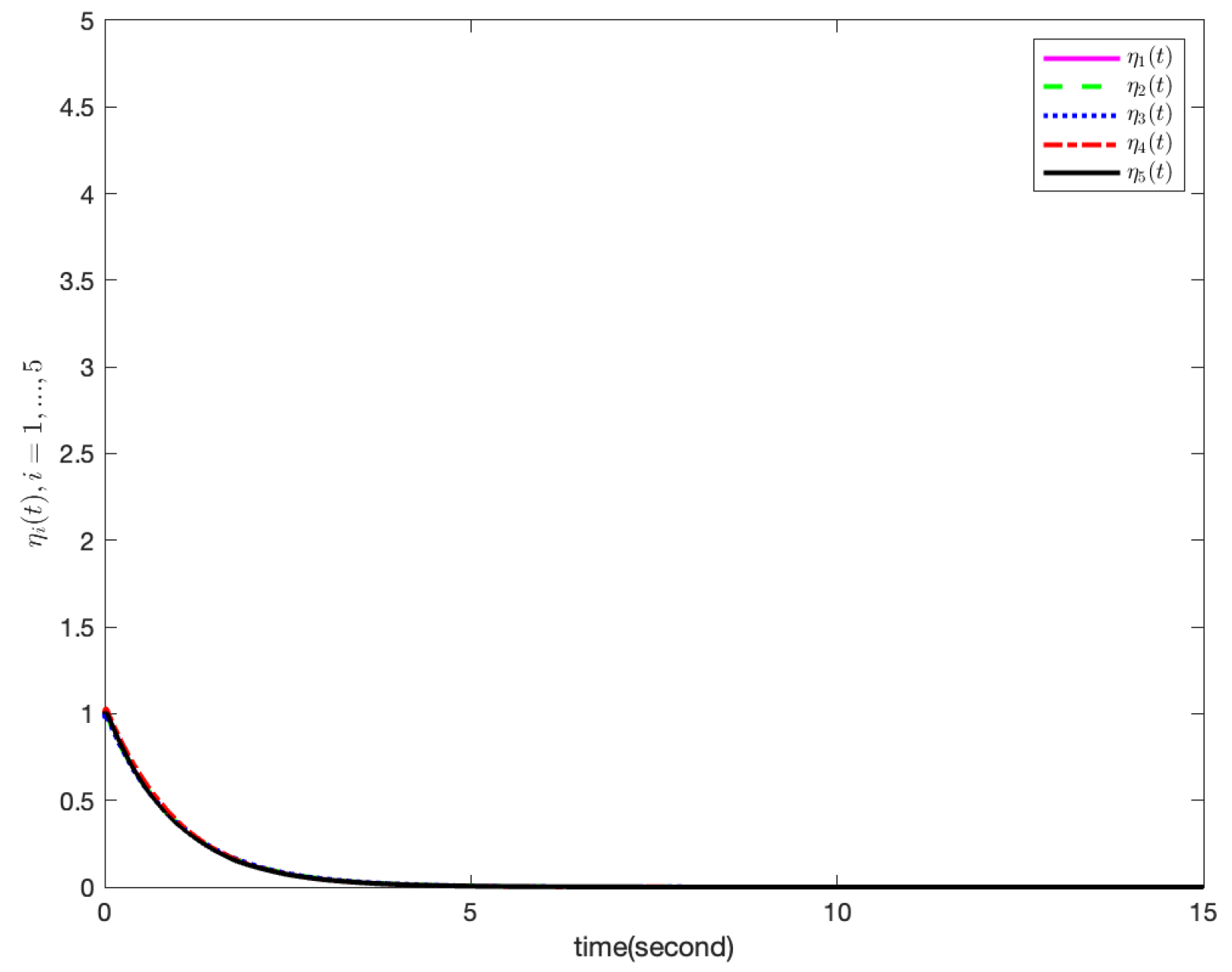In Figure 4, dynamic functions ${\eta }_i\left(t\right)$, $i=1,\cdots ,5$ are described and we can conclude that the trajectories of dynamic functions ${\eta }_i\left(t\right)$, $i=1,\cdots ,5$ are approaching zero while $t\to +\infty$. 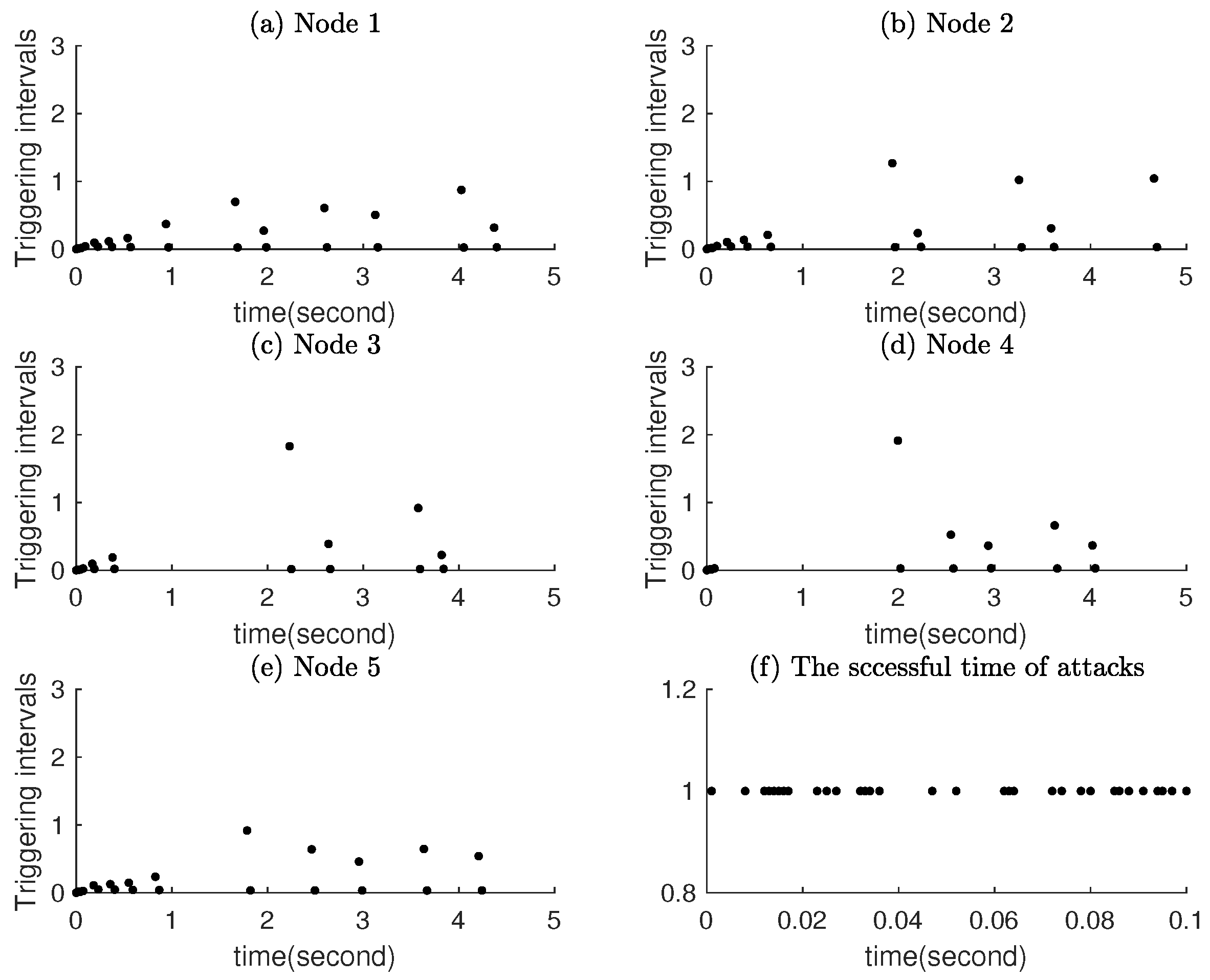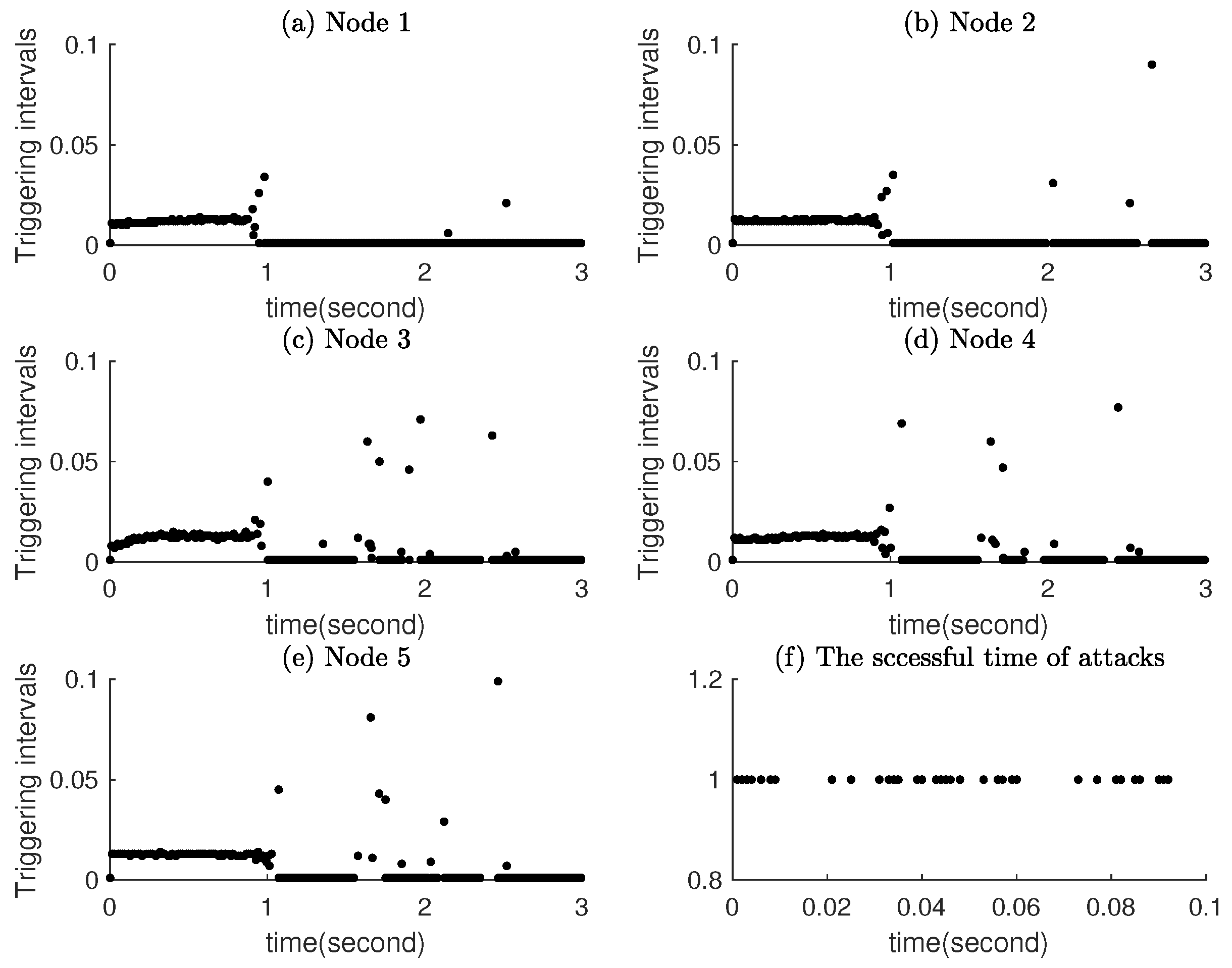Figure 5 show the dynamical event releasing instants and intervals of nodes in the CDNs as well as the occurring instants of the simulated stochastic deception attacks. Figure 6 show the static event releasing instants and intervals of nodes in the CDNs as well as the occurring instants of the simulated stochastic deception attacks. Figure 5 and Figure 6 intuitively illustrate two key improvements of the dynamic event-triggered mechanism: (1) it significantly reduces the number of triggering events; (2) it maintains more stable triggering intervals which avoided frequent unnecessary triggers caused by static threshold rigidness.

5. Conclusions

The secure cluster synchronization problem of CDNs under deception attacks has been investigated in this chapter. By taking into account both the effects of intermittent data transmissions under the distributed dynamic event-triggered mechanism and stochastic deception attacks, some sufficient conditions on the secure cluster synchronization performance analysis and controller design are established. Then, an illustrative example is given to show the effectiveness of the proposed theoretical methods and control schemes. In future work, we plan to explore two directions: (1) Markovian jump attack models: to capture time-varying attack probabilities (e.g., attackers may increase intensity during peak network traffic, leading to transition between ‘low-attack’ and ‘high-attack’ modes); and (2) Poisson-distributed attack models: to describe the random arrival of attack sequences. These extensions will allow us to address more complex attack behaviors while maintaining the core advantages of the dynamic event-triggered control framework proposed in this paper.