Research on the Condition Assessment Method for Marine Diesel Generators Considering the Effects of Fouling and Dust Deposition
Abstract
1. Introduction
1.1. Research Purpose and Significance
1.2. Related Works
1.3. Innovation and Contribution
- (1)
- A numerical analysis model was developed that comprehensively considers the dynamic evolution of fouling and its effect on convective heat transfer performance, revealing the quantitative relationship between stator winding fouling thickness, stator temperature, and convective heat transfer coefficient under different operating conditions.
- (2)
- Based on the analysis of the degradation process of generator convective heat transfer performance, a health state assessment model was established, using the convective heat transfer coefficient as the criterion for defining the health state space, thereby enabling accurate evaluation of the generator’s operational condition.
2. Numerical Analysis Model
2.1. Three-Dimensional Model
2.2. Numerical Simulation
2.2.1. Boundary Conditions
2.2.2. Mesh Generation and Sensitivity Analysis
2.2.3. Viscous Model and Accuracy Verification
2.3. Simulation Results
- (1)
- The stator coil temperature is primarily influenced by the environmental temperature and load power. The environmental temperature sets the baseline of the convective heat transfer, while an increase in load power strengthens the internal heat generation of the stator coil, thereby raising its maximum temperature.
- (2)
- Under the same environmental temperature and load conditions, an increase in fouling layer thickness significantly elevates the stator coil temperature, indicating that fouling amplifies the coupled effect of environmental temperature and load power on temperature rise.
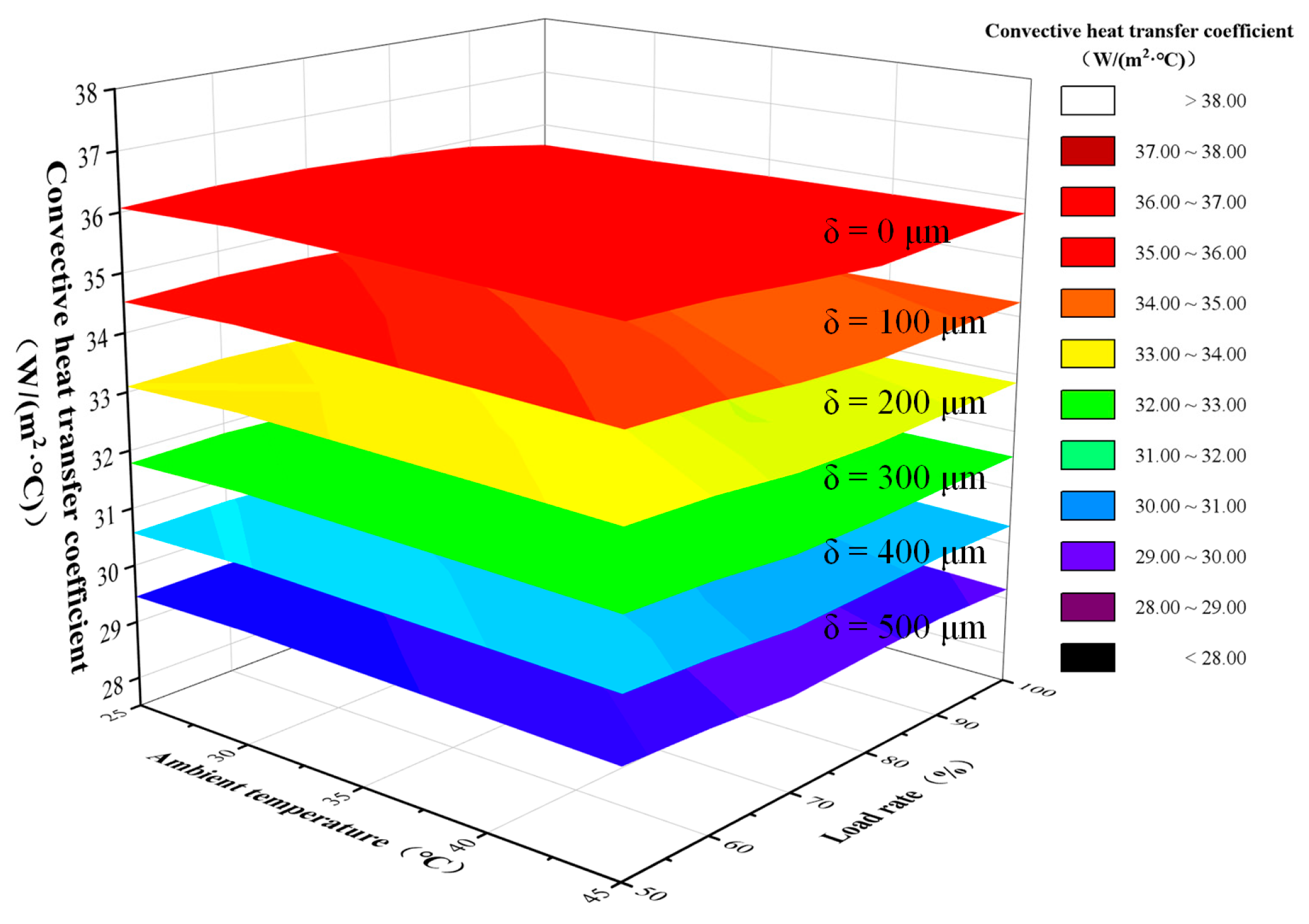
- (3)
- When the fouling layer thickness is fixed, the convective heat transfer coefficient varies only slightly with environmental temperature and load power but exhibits a clear stratification pattern, demonstrating its high sensitivity to fouling thickness.
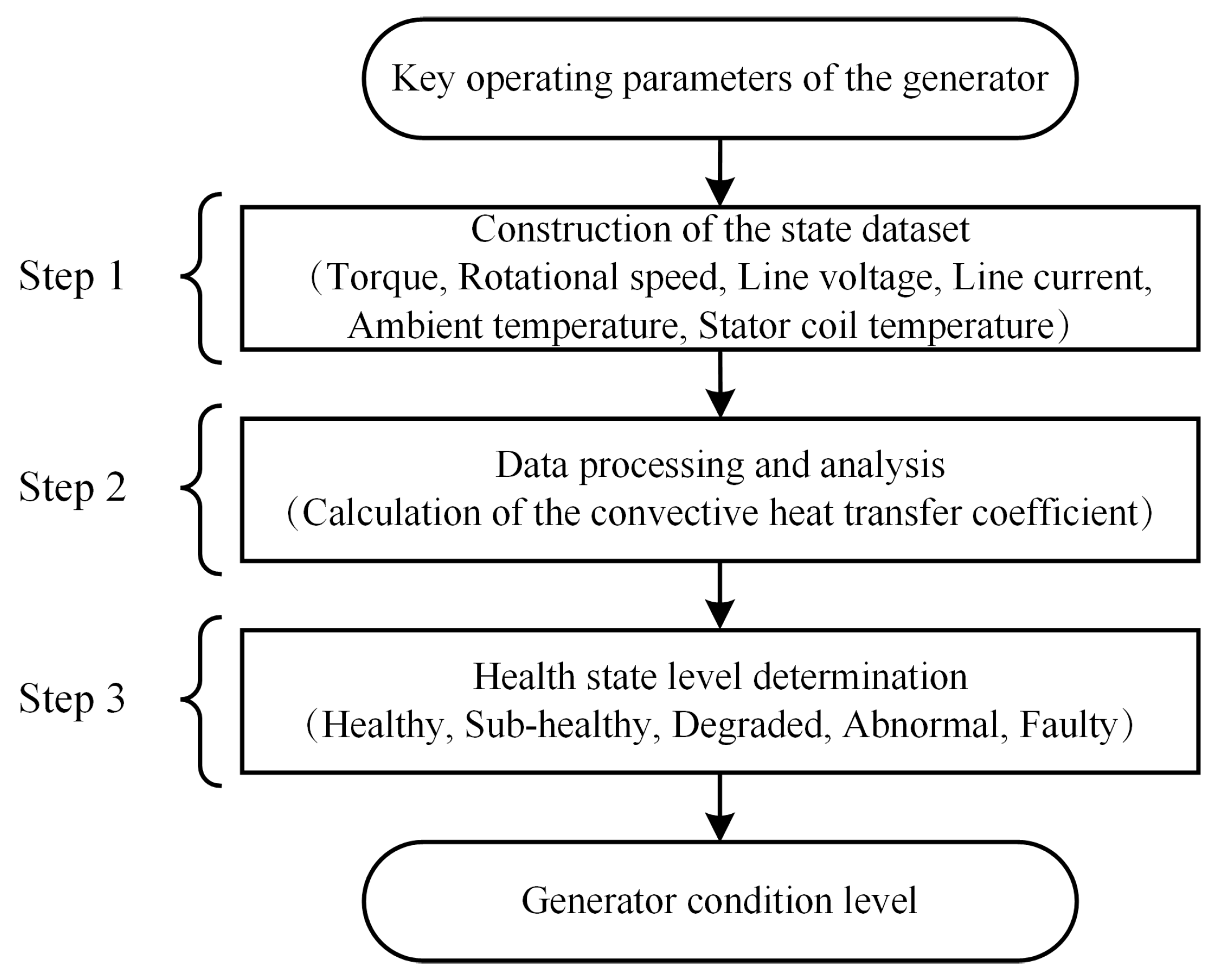
3. State Evaluation Model
3.1. Analysis of State Parameters
3.2. Division of Health State Ranges
3.3. State Assessment Workflow
4. Results and Discussion
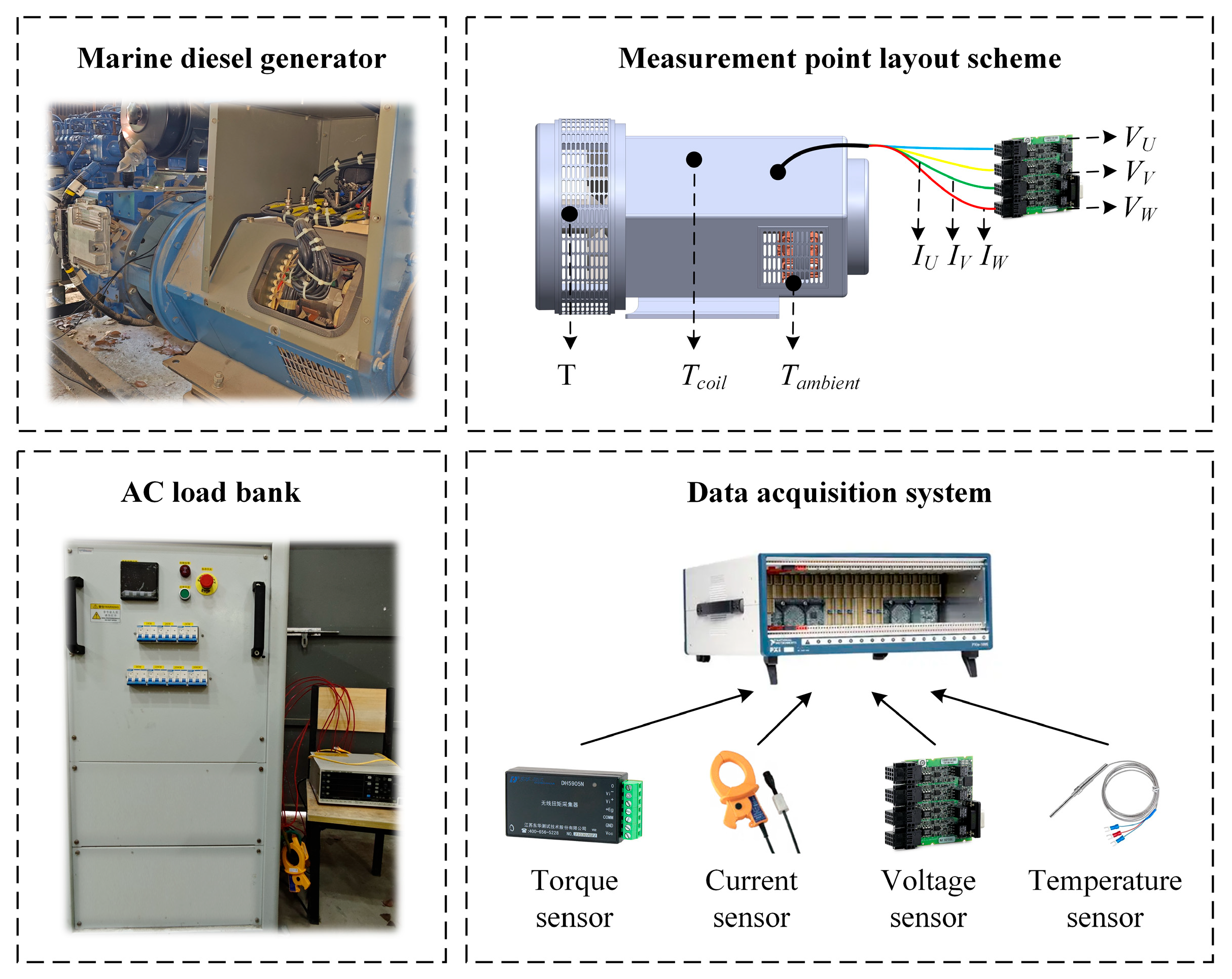
4.1. Experiments
4.2. Discussion
- (1)
- The average convective heat transfer coefficient is only minimally affected by variations in ambient temperature and load power; however, it exhibits a clear stratification pattern as the fouling-layer thickness increases, revealing its high sensitivity to dust and fouling accumulation.
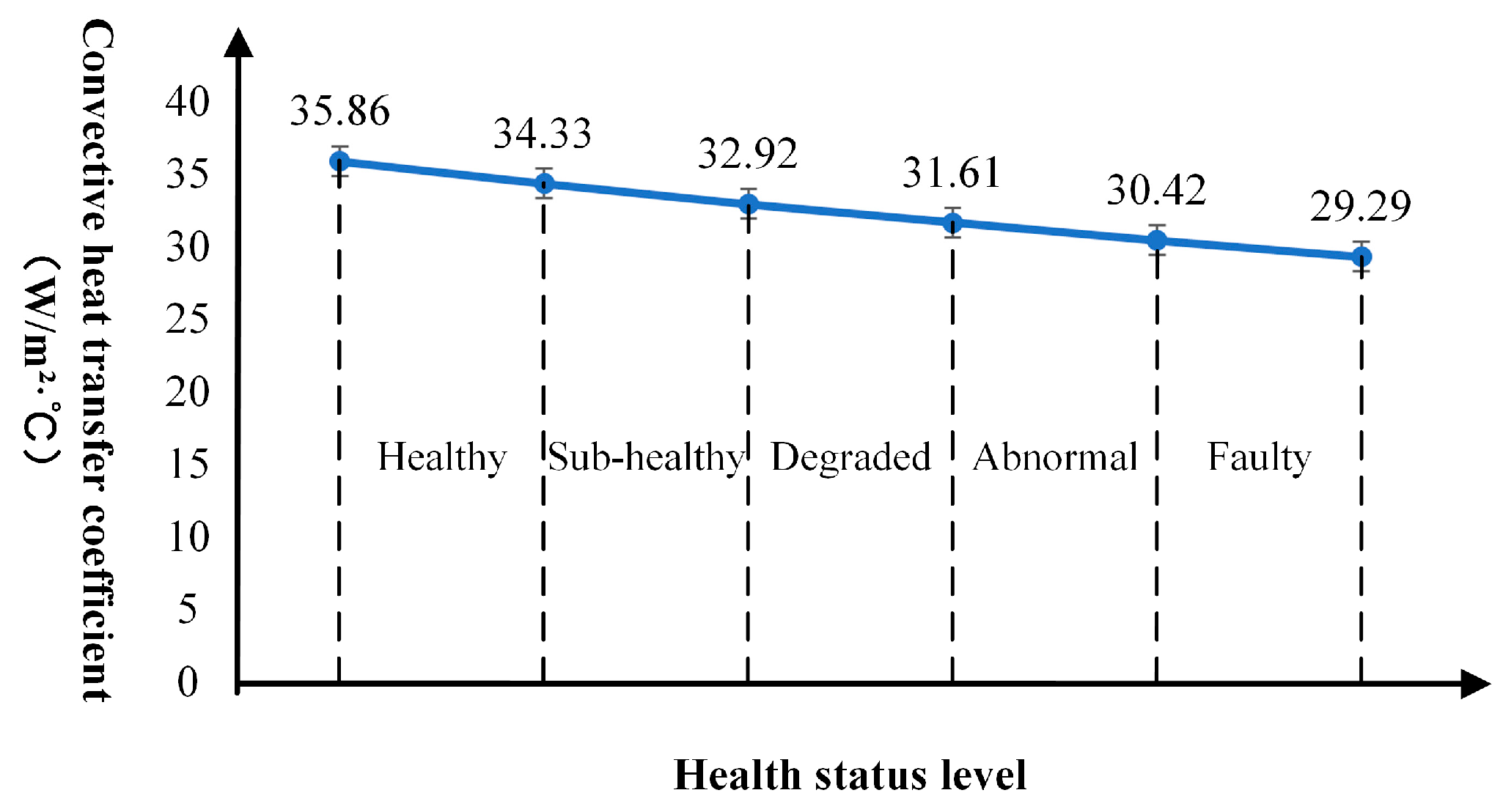
- (2)
- Based on the analysis of the convective heat transfer coefficient of the stator coil, the results for Groups 1~3 all fall within the range of . This indicates that during the first 150 h of the maintenance cycle, the generator remains in a “healthy” operating state. The results for Groups 4~5 fall within , showing that after approximately 300 h of continuous operation, the generator’s condition degrades to a “sub-healthy” state. The results for Groups 6~8 fall within , indicating that after 500 h of continuous operation, the generator further degrades to a “degraded” state. Finally, the results for Groups 9~10 fall within , suggesting that after 650 h of continuous operation, the generator enters an “abnormal” state.
- (3)
- The convective heat transfer coefficient of the generator stator coil decreases continuously with operating time, indicating that dust deposition increases thermal resistance and gradually degrades convective heat transfer performance. This demonstrates that the constructed health state assessment model can effectively visualize and quantify the degradation process under different operating conditions.
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The equivalent thermal resistance of the fouling layer | |
| The thermal conductivity of the fouling material | |
| The equivalent thickness of the fouling layer | |
| The Nusselt number | |
| The convective heat transfer coefficient | |
| The characteristic length | |
| The thermal conductivity of the fluid | |
| The copper loss power of the stator winding | |
| The heat transfer area | |
| The temperature difference between stator winding and ambient | |
| , | The time-dependent terms |
| , | The convective terms |
| The input power | |
| The torque | |
| The rotational speed | |
| The electromagnetic power on the stator side | |
| The output power | |
| The line voltage | |
| The line current | |
| The power factor | |
| The iron loss | |
| The rotor coil copper loss power | |
| The excitation power | |
| The mechanical loss power | |
| The health state parameter set at any given time |
References
- Luo, Y.; Kong, L.; Fang, S.; Shu, Y.; Niu, T.; Chen, G.; Liao, R. Reviews on the power management for shipboard energy storage systems. Sustain. Horiz. 2024, 9, 100094. [Google Scholar] [CrossRef]
- Tong, H.; Chen, S. A new pattern of green, intelligent and resilient international shipping: Conference report. Mar. Policy 2023, 152, 105587. [Google Scholar] [CrossRef]
- Hooshmand, H.; Nasiri, N.; Najafi Ravdanegh, S. Sustainable power management solutions for shipboard power systems: Incorporating CHP, hydrogen fuel cells, battery, and solar energy. J. Energy Storage 2025, 114, 115789. [Google Scholar] [CrossRef]
- Tao, J.; Li, W.; Guo, Y.; Zhang, H.; Dong, L.; Yang, Q. Investigation of electromechanical coupling torsional vibration in diesel generator sets. Mech. Syst. Signal Process. 2025, 230, 112622. [Google Scholar] [CrossRef]
- Li, B.; Ding, Y.; Ma, W.; Xiang, L.; Sui, C. A health condition assessment method for marine diesel engine turbochargers using zero-dimensional engine model and machine learning. Measurement 2025, 251, 117283. [Google Scholar] [CrossRef]
- Zhang, P.; Li, C.; Xu, H.; Zou, Y.; Wang, K.; Zhang, Y.; Sun, P. Bi-AAE: A binary adversarial autoencoder deep neural network model for anomaly detection in system-level marine diesel engines. Ocean Eng. 2024, 302, 117700. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Liu, R.W.; Liu, Y.; Yuan, Z. Data-driven methods for detection of abnormal ship behavior: Progress and trends. Ocean Eng. 2023, 271, 113673. [Google Scholar] [CrossRef]
- Berce, J.; Zupančič, M.; Može, M.; Golobič, I. A review of crystallization fouling in heat exchangers. Processes 2021, 9, 1356. [Google Scholar] [CrossRef]
- Zou, Z.; Liu, S.; Kang, J. Degradation mechanism and online electrical monitoring techniques of stator winding insulation in inverter-fed machines: A review. World Electr. Veh. J. 2024, 15, 444. [Google Scholar] [CrossRef]
- Abdulkarim, D.A.; Lazakis, I. Systems reliability and data-driven analysis for marine machinery maintenance planning and decision making. Machines 2024, 12, 294. [Google Scholar]
- Lim, S.; Oh, J.; Park, J. Maintenance time prediction for predictive maintenance of ship engines. Appl. Sci. 2025, 15, 4764. [Google Scholar] [CrossRef]
- Park, J.; Oh, J. Anomalistic symptom judgment algorithm for predictive maintenance of ship propulsion engine using machine learning. Appl. Sci. 2023, 13, 11818. [Google Scholar] [CrossRef]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.D.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Le, X.H.K.; Pop, I.; Sheremet, M.A. Thermogravitational convective flow and energy transport in an electronic cabinet with a heat-generating element and solid/porous finned heat sink. Mathematics 2021, 10, 34. [Google Scholar] [CrossRef]
- Xuan, H.K.L.; Pop, I.; Sheremet, M.A. Numerical simulation of solid and porous fins’ impact on heat transfer performance in a differentially heated chamber. Mathematics 2022, 10, 263. [Google Scholar] [CrossRef]
- Essarroukh, I.; López, J.M. Convective heat transfer in uniformly accelerated and decelerated turbulent pipe flows. Mathematics 2024, 12, 3560. [Google Scholar] [CrossRef]
- Moradnia, P.; Chernoray, V.; Nilsson, H. Experimental assessment of a fully predictive CFD approach for flow of cooling air in an electric generator. Appl. Energy 2014, 124, 223–230. [Google Scholar] [CrossRef]
- Bang, H.; Park, G.; Lee, S. Performance improvement of intercooler in biogas generators by using computational fluid dynamics. Appl. Therm. Eng. 2024, 243, 122541. [Google Scholar] [CrossRef]
- Bersch, K.; Connor, P.H.; Eastwick, C.N.; Galea, M.; Rolston, R. CFD optimisation of the thermal design for a vented electrical machine. In Proceedings of the IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Nottingham, UK, 20–21 April 2017; pp. 1–6. [Google Scholar]
- Han, Z.; Xu, Z.; Yu, X. CFD modeling for prediction of particulate fouling of heat transfer surface in turbulent flow. International J. Heat Mass Transf. 2019, 144, 118428. [Google Scholar] [CrossRef]
- Inamdar, H.V.; Groll, E.A.; Weibel, J.A.; Garimella, S.V. Air-side fouling of finned heat exchangers: Part 1, review and proposed test protocol. Int. J. Refrig. 2023, 151, 77–86. [Google Scholar] [CrossRef]
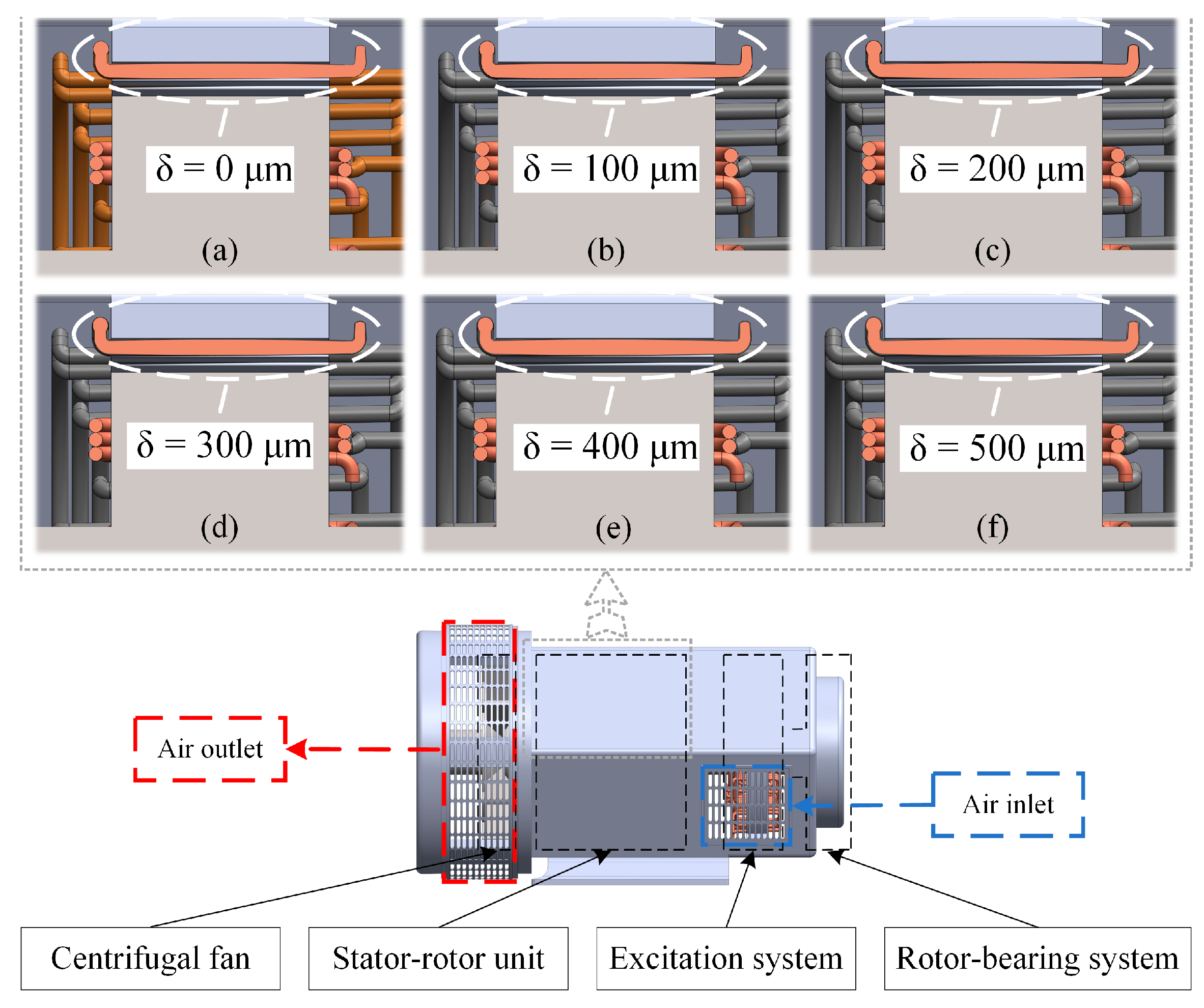

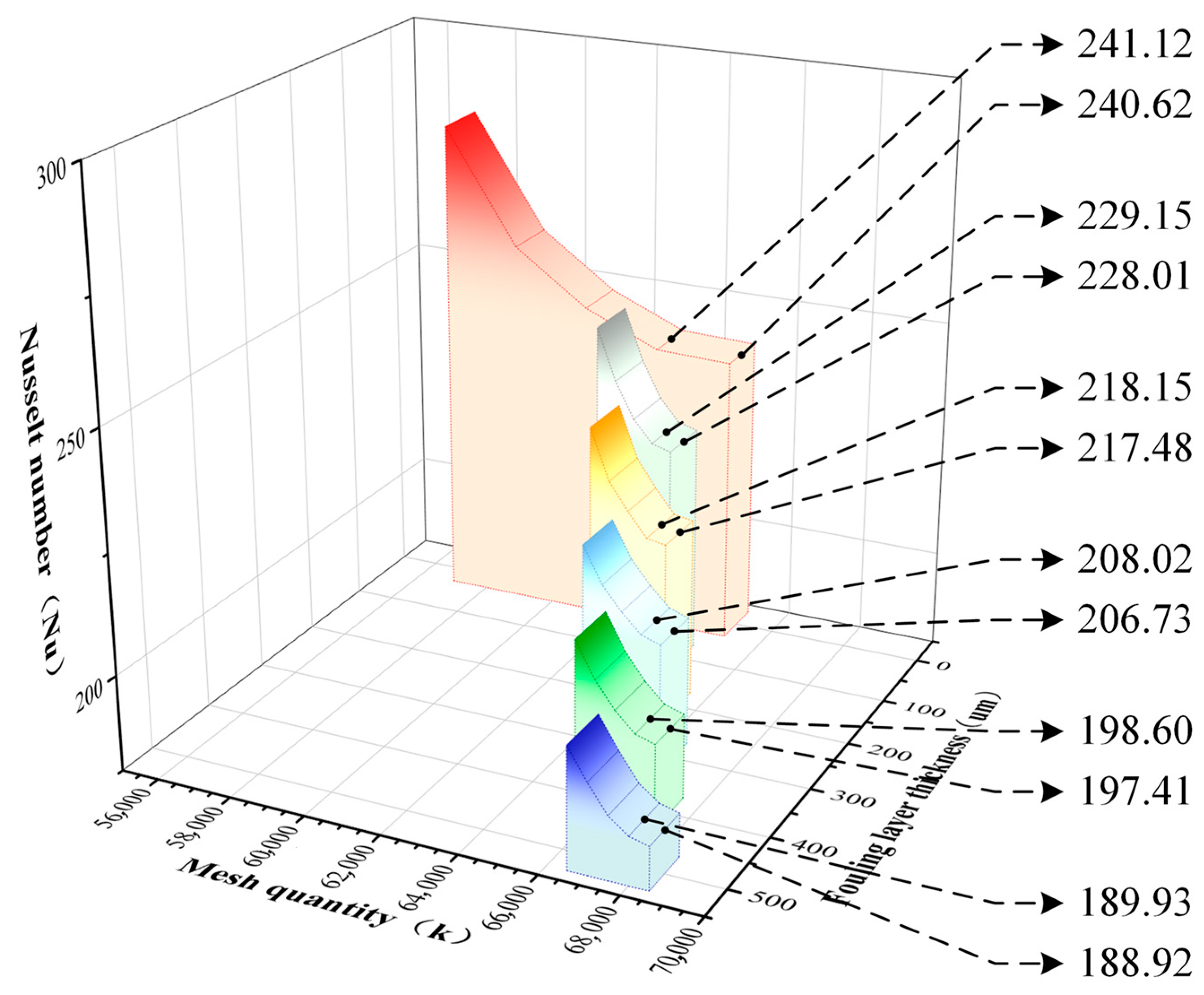
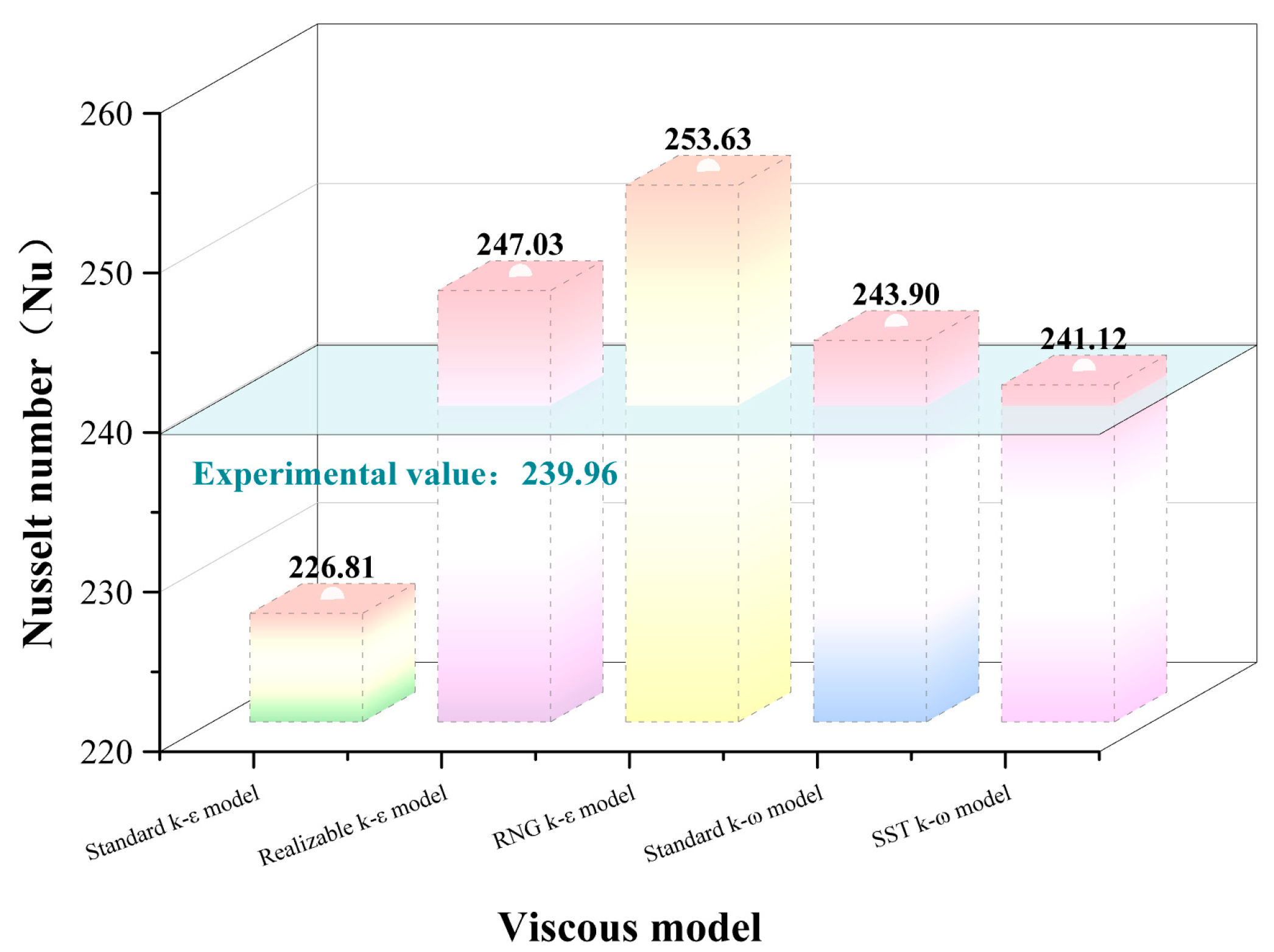
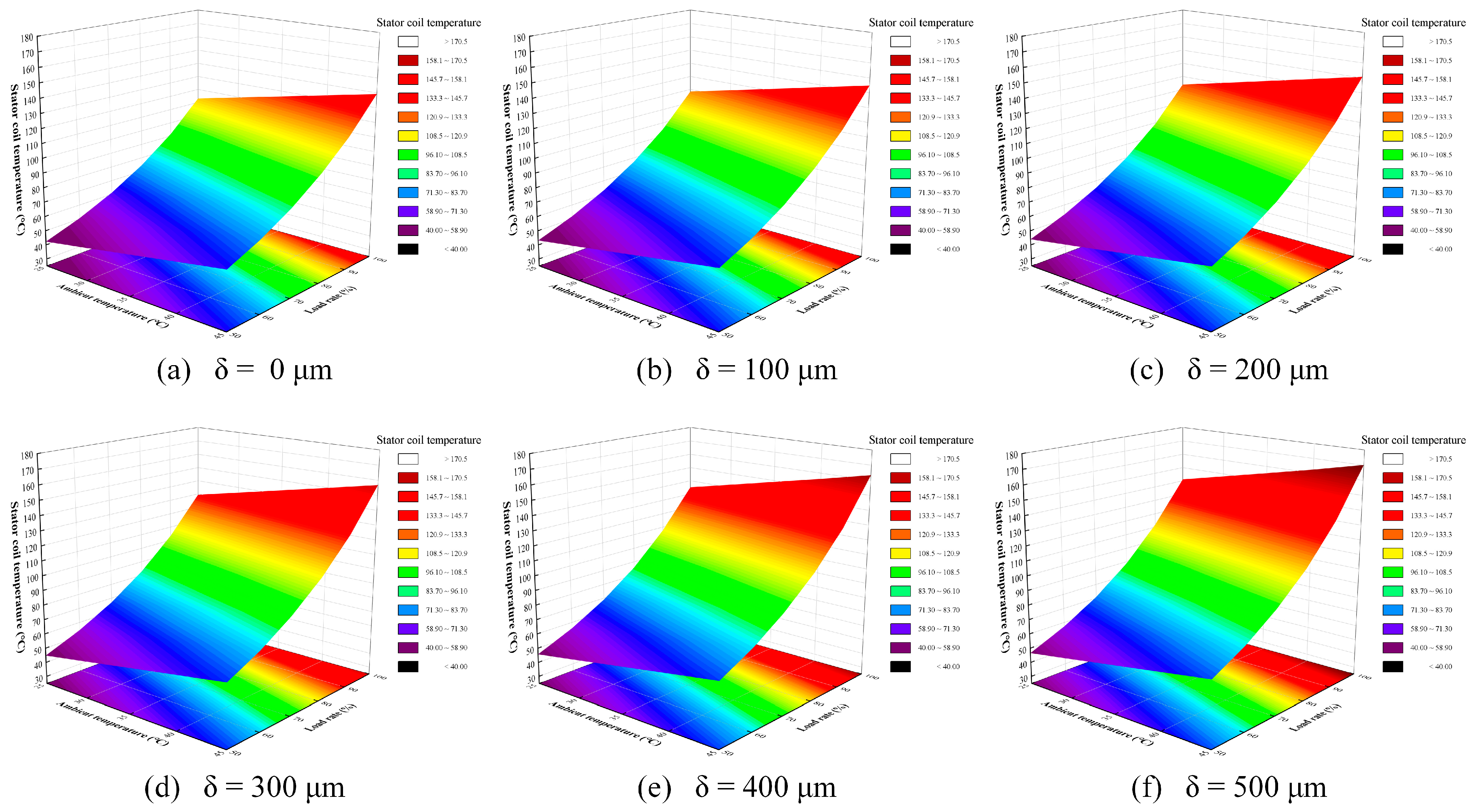
| 3D Model Number | Number of Cells (Thousand) | ||||
|---|---|---|---|---|---|
| Tiny | Coarse | Medium | Fine | Super Fine | |
| (a) 0 μm | 57,000 | 59,000 | 61,000 | 63,000 | 65,000 |
| (b) 100 μm | 62,500 | 63,000 | 63,500 | 64,000 | 64,500 |
| (c) 200 μm | 63,500 | 64,000 | 64,500 | 65,000 | 65,500 |
| (d) 300 μm | 64,500 | 65,000 | 65,500 | 66,000 | 66,500 |
| (e) 400 μm | 65,500 | 66,000 | 66,500 | 67,000 | 67,500 |
| (f) 500 μm | 66,500 | 67,000 | 67,500 | 68,000 | 68,500 |
| Parameter | Value/Units | Parameter | Value/Units |
|---|---|---|---|
| Rated voltage | Rated current | ||
| Rated power | Rated revolution | ||
| Standby power | Power factor | 0.8 | |
| Ingress Protection | IP23 | Insulation class | H |
| Test Group | ||||||
|---|---|---|---|---|---|---|
| 1 | 291.19 | 220.15 | 109.71 | 28.80 | 66.46 | 35.71 |
| 2 | 370.28 | 220.31 | 140.35 | 29.62 | 99.91 | 34.79 |
| 3 | 329.99 | 220.26 | 124.79 | 29.54 | 82.95 | 34.37 |
| 4 | 330.60 | 220.24 | 125.04 | 28.49 | 83.04 | 33.79 |
| 5 | 412.29 | 220.57 | 156.14 | 30.16 | 130.01 | 33.04 |
| 6 | 411.46 | 220.45 | 155.89 | 29.33 | 130.69 | 32.51 |
| 7 | 411.74 | 220.47 | 155.93 | 31.40 | 135.88 | 32.00 |
| 8 | 290.88 | 220.14 | 109.55 | 30.95 | 74.38 | 31.69 |
| 9 | 291.67 | 220.16 | 109.85 | 29.67 | 73.96 | 31.20 |
| 10 | 371.12 | 220.29 | 140.58 | 28.54 | 112.05 | 30.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Zhou, R.; Dai, J. Research on the Condition Assessment Method for Marine Diesel Generators Considering the Effects of Fouling and Dust Deposition. Mathematics 2025, 13, 3767. https://doi.org/10.3390/math13233767
Guo Y, Zhou R, Dai J. Research on the Condition Assessment Method for Marine Diesel Generators Considering the Effects of Fouling and Dust Deposition. Mathematics. 2025; 13(23):3767. https://doi.org/10.3390/math13233767
Chicago/Turabian StyleGuo, Yukuo, Ruiping Zhou, and Jiashun Dai. 2025. "Research on the Condition Assessment Method for Marine Diesel Generators Considering the Effects of Fouling and Dust Deposition" Mathematics 13, no. 23: 3767. https://doi.org/10.3390/math13233767
APA StyleGuo, Y., Zhou, R., & Dai, J. (2025). Research on the Condition Assessment Method for Marine Diesel Generators Considering the Effects of Fouling and Dust Deposition. Mathematics, 13(23), 3767. https://doi.org/10.3390/math13233767





