CQEformer: A Causal and Query-Enhanced Transformer Variant for Time-Series Forecasting
Abstract
1. Introduction
- Causal convolutional residual embedding in the input layer, emphasizing spatiotemporal locality and enforcing temporal causality. By focusing on residual features between consecutive time steps, the model improves sensitivity to sudden market shocks, structural breaks, and local anomalies, thereby enhancing short-term predictive accuracy and stability.
- Query-Enhanced multi-head self-attention mechanism, dynamically adjusting the Query matrix using higher-order statistical moments and entropy in time and frequency domains. This guides attention to regions exhibiting volatility clustering and sudden structural shifts, improving modeling of tail risks and nonlinear market behaviors.
2. Background
2.1. Problem Setup
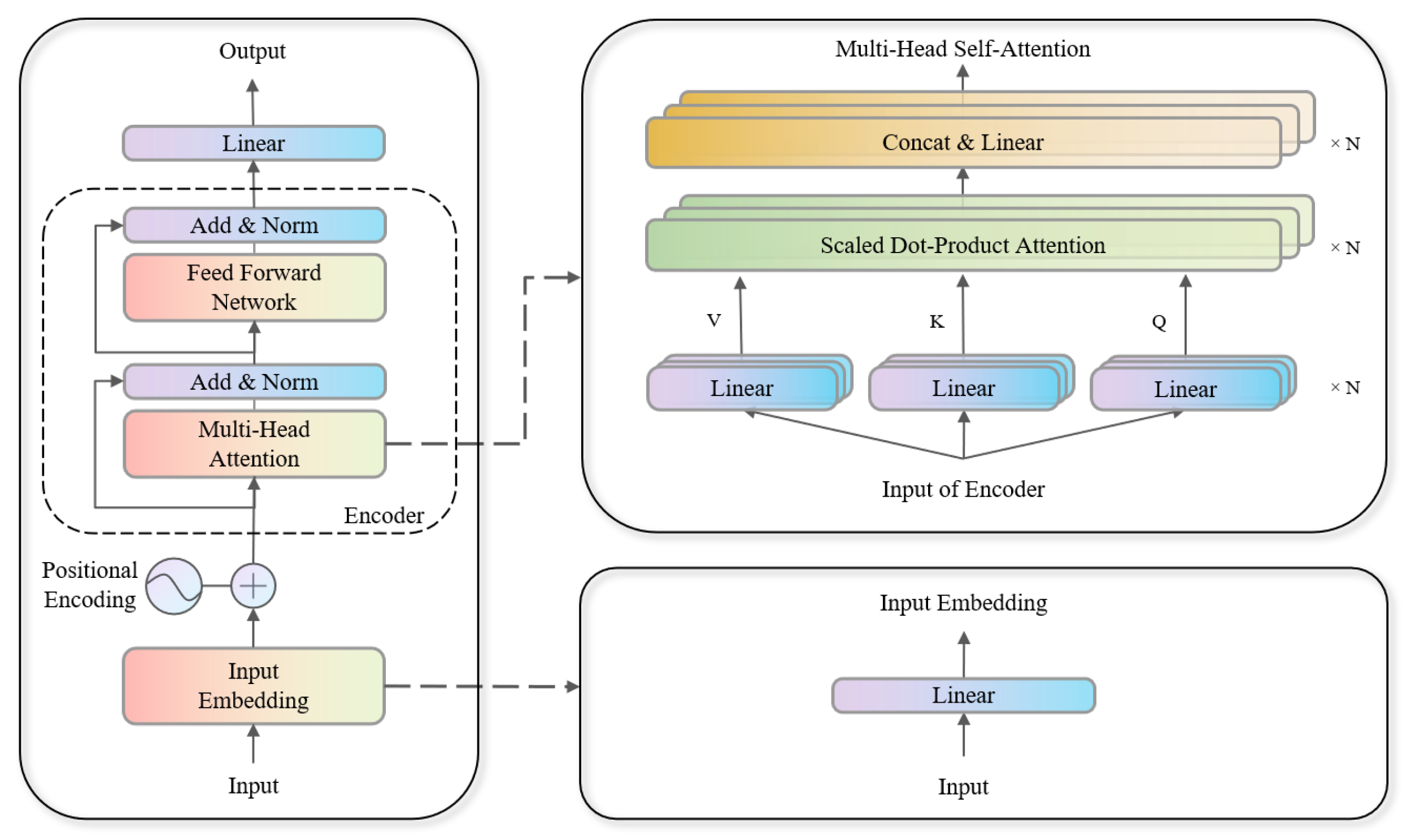
2.2. Encoder-Only Transformer
- Input Embedding and Positional Encoding
- Multi-Head Self-Attention
- First Res & LayerNorm
- Feed-Forward Network
- Second Res & LayerNorm
- Output Layer
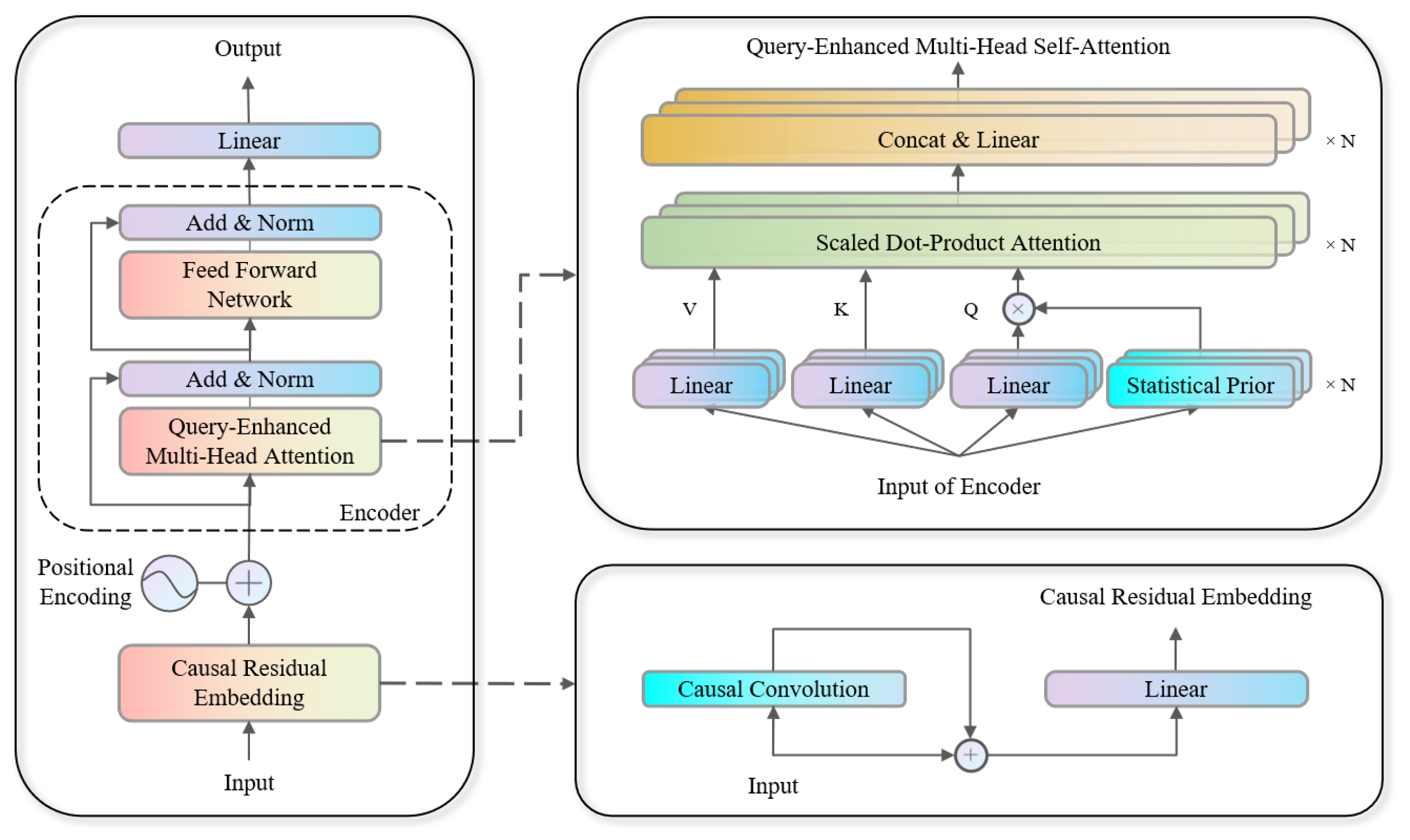
3. CQEformer (Causal Query-Enhanced Transformer)
3.1. Causal Residual Embedding
3.2. Query-Enhanced Multi-Head Self-Attention Mechanism
3.3. Forward Propagation Algorithm
3.4. Parameter Optimization
3.4.1. Gradient Derivation
| Algorithm 1 CQEformer Forecasting Procedure |
|
3.4.2. Parameter Update
4. Experiments
4.1. Data, Indicators and Standardization
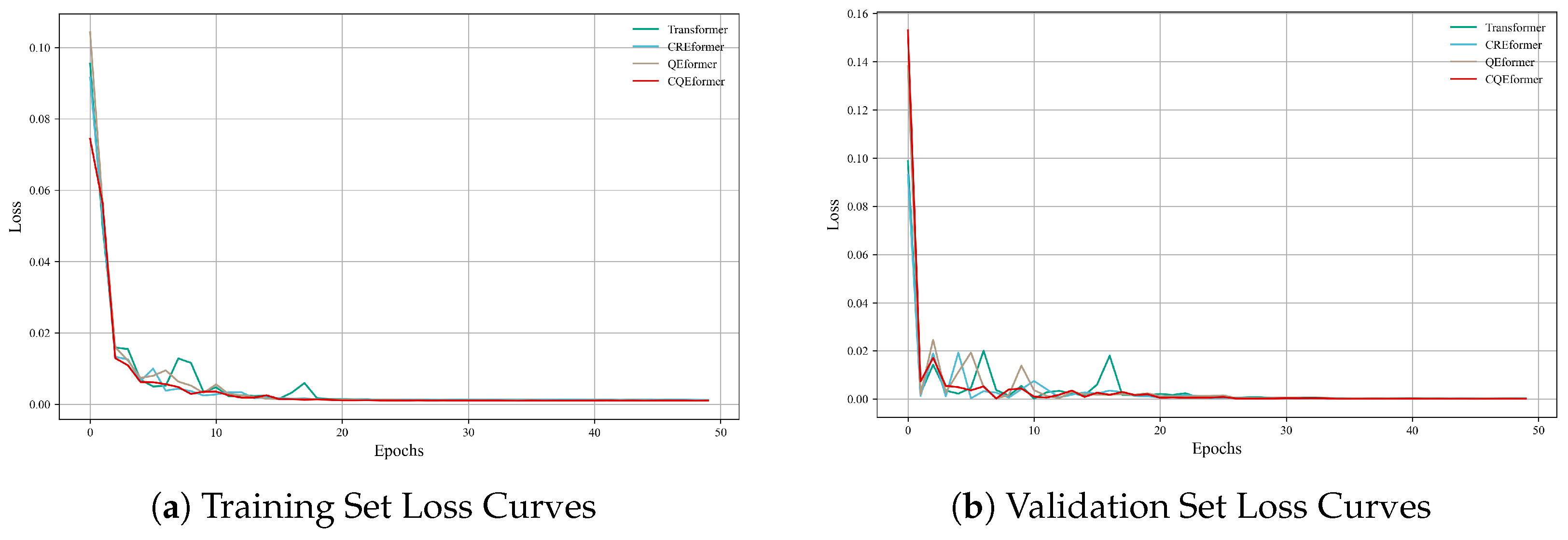
4.2. Experimental Setup
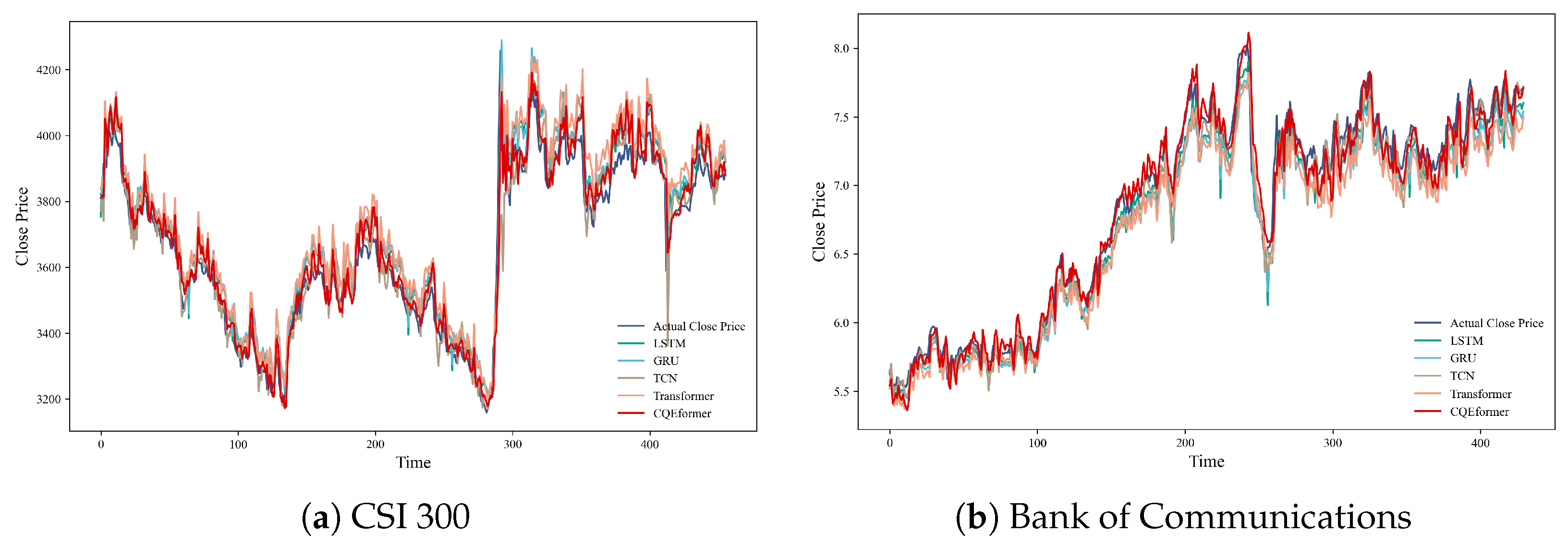
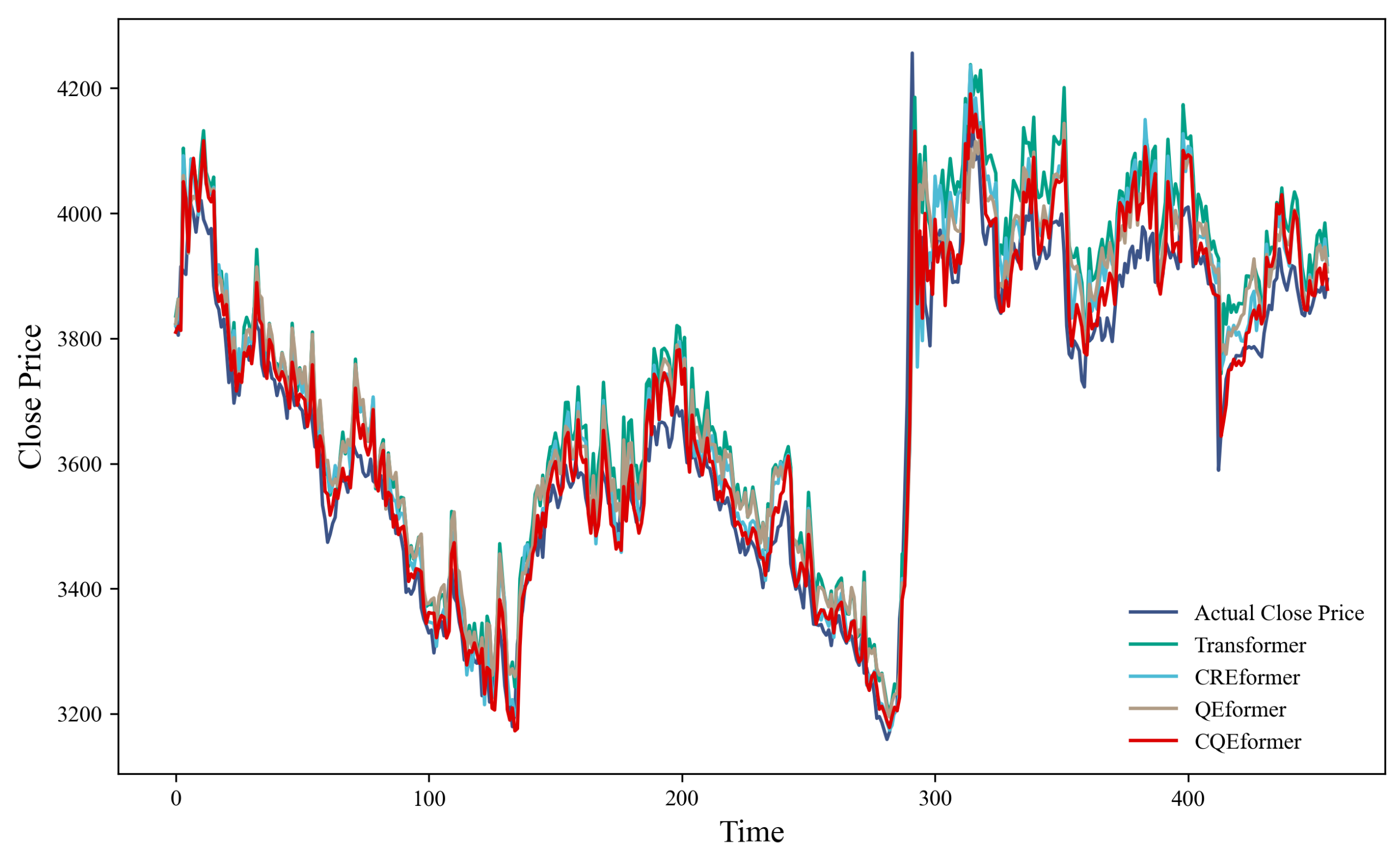
4.3. Multi-Model Comparison Experiment
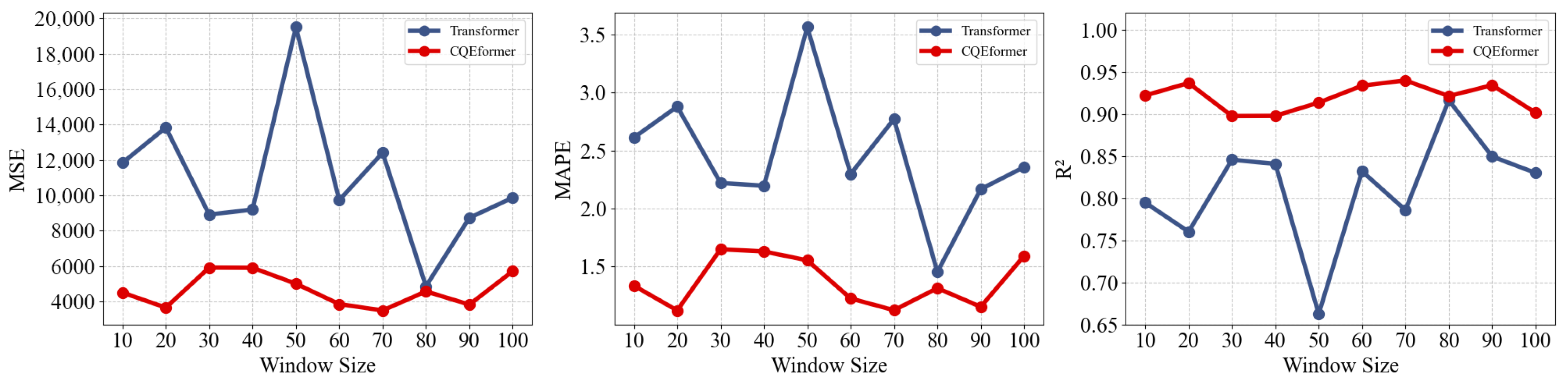
4.4. Time Window Sensitivity Experiment
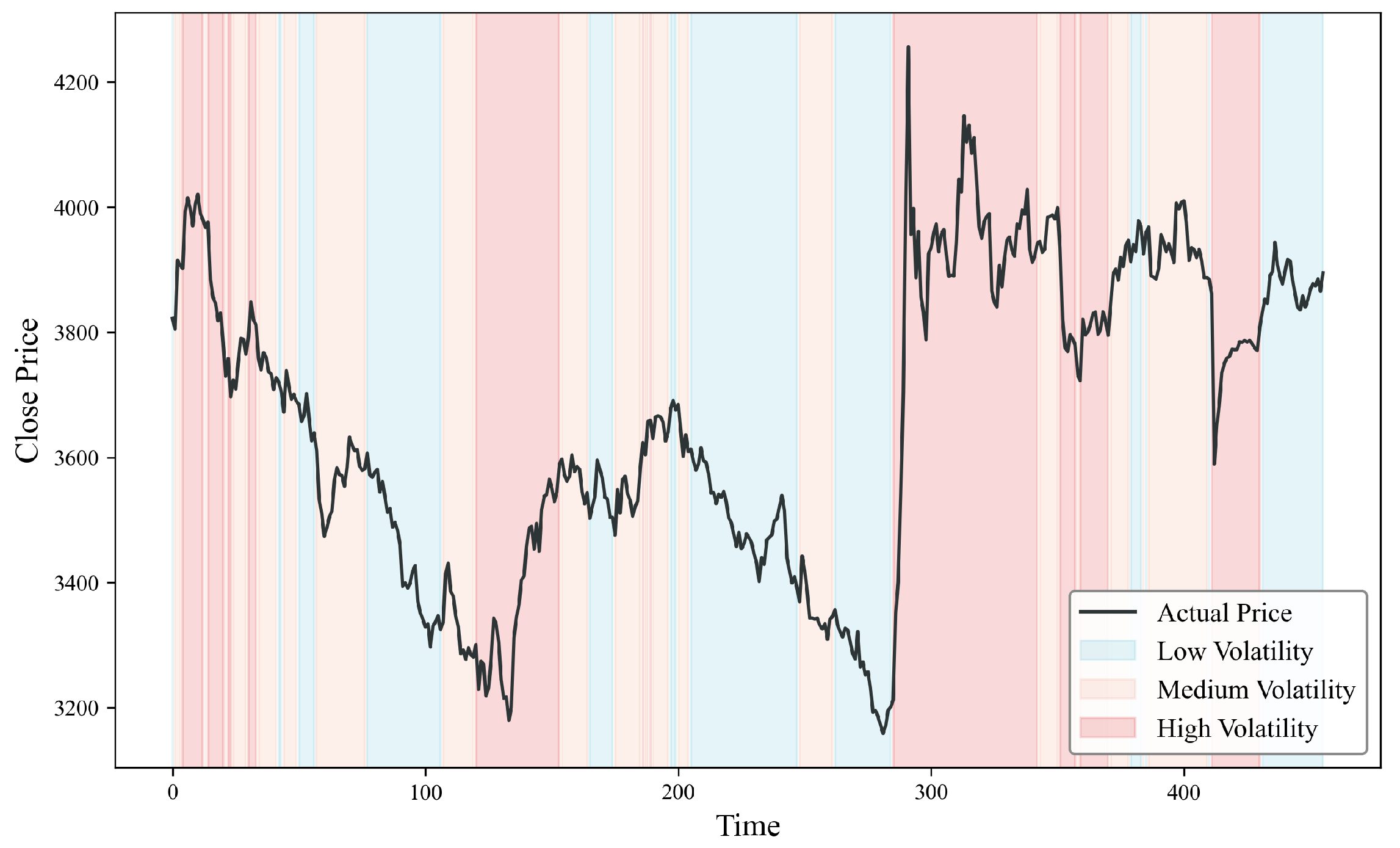
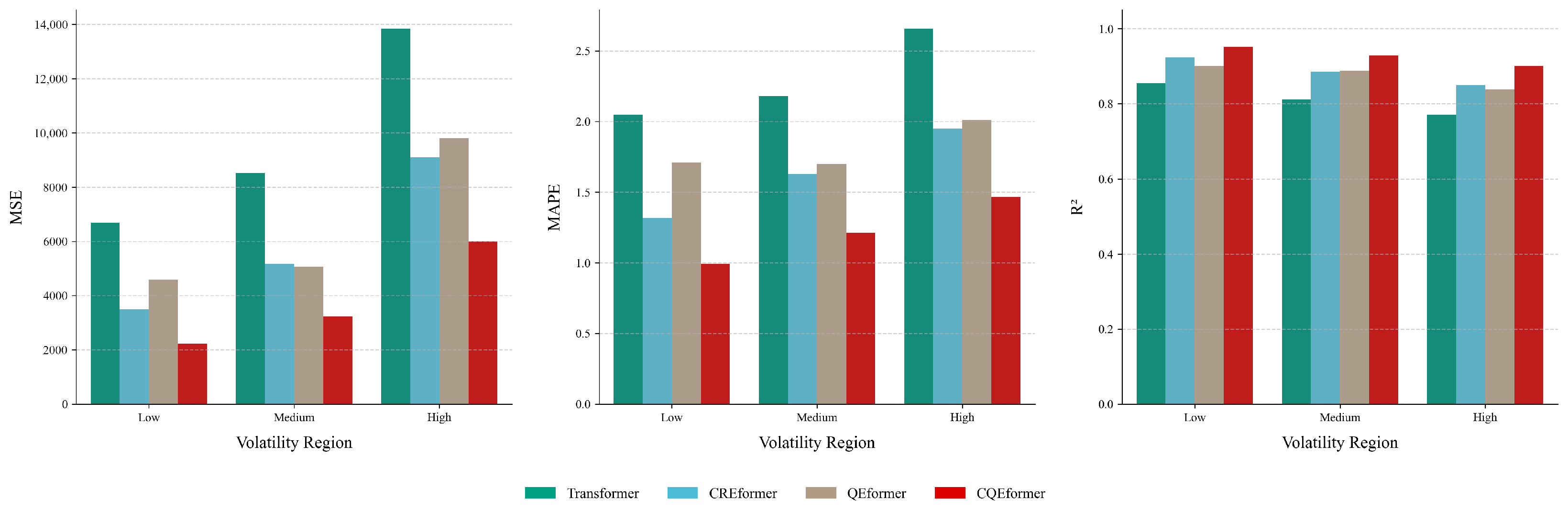
4.5. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Osborne, M.F.M. Periodic Structure in the Brownian Motion of Stock Prices. Oper. Res. 1962, 10, 345–379. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day Series in Time Series Analysis and Digital Processing; Holden-Day: Sydney, Australia, 1970. [Google Scholar]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Petrica, A.C.; Stancu, S.; Tindeche, A. Limitation of ARIMA Models in Financial and Monetary Economics. Theor. Appl. Econ. 2016, XXIII, 19–42. [Google Scholar]
- Wang, D.; Zheng, Y.; Lian, H.; Li, G. High-Dimensional Vector Autoregressive Time Series Modeling via Tensor Decomposition. J. Am. Stat. Assoc. 2022, 117, 1338–1356. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. Modeling and Forecasting Realized Volatility. Econometrica 2003, 71, 579–625. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.N.; Gunawan, D.; Kohn, R. A Statistical Recurrent Stochastic Volatility Model for Stock Markets. J. Bus. Econ. Stat. 2023, 41, 414–428. [Google Scholar] [CrossRef]
- Sang, S.; Li, L. A Novel Variant of LSTM Stock Prediction Method Incorporating Attention Mechanism. Mathematics 2024, 12, 945. [Google Scholar] [CrossRef]
- Lee, M.C. Research on the Feasibility of Applying GRU and Attention Mechanism Combined with Technical Indicators in Stock Trading Strategies. Appl. Sci. 2022, 12, 1007. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Chaudhuri, K., Jegelka, S., Song, L., Szepesvari, C., Niu, G., Sabato, S., Eds.; PMLR (Proceedings of Machine Learning Research): New York, NY, USA, 2022; Volume 162, pp. 27268–27286. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Chen, P.; Zhang, Y.; Cheng, Y.; Shu, Y.; Wang, Y.; Wen, Q.; Yang, B.; Guo, C. Pathformer: Multi-scale Transformers with Adaptive Pathways for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Zhou, Y.; Ye, Y.; Zhang, P.; Du, X.; Chen, M. TwinsFormer: Revisiting Inherent Dependencies via Two Interactive Components for Time Series Forecasting. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Liu, Y.; Qin, G.; Huang, X.; Wang, J.; Long, M. Timer-XL: Long-Context Transformers for Unified Time Series Forecasting. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Ding, Q.; Wu, S.; Sun, H.; Guo, J.; Guo, J. Hierarchical Multi-Scale Gaussian Transformer for Stock Movement Prediction. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, Yokohama, Japan, 11–17 July 2020; Special Track on AI in FinTech. Bessiere, C., Ed.; International Joint Conferences on Artificial Intelligence Organization: New York, NY, USA, 2020; pp. 4640–4646. [Google Scholar] [CrossRef]
- Zhang, Q.; Qin, C.; Zhang, Y.; Bao, F.; Zhang, C.; Liu, P. Transformer-based attention network for stock movement prediction. Expert Syst. Appl. 2022, 202, 117239. [Google Scholar] [CrossRef]
- Xu, H.; Xiang, L.; Ye, H.; Yao, D.; Chu, P.; Li, B. Permutation Equivariance of Transformers and its Applications. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 5987–5996. [Google Scholar] [CrossRef]
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- King, A. AKShare. GitHub. 2022. Available online: https://github.com/akfamily/akshare (accessed on 15 June 2025).
- California Department of Transportation. Traffic Dataset. In California Performance Measurement System (PeMS); California Department of Transportation: Sacramento, CA, USA, 2021. [Google Scholar]
| Indicator Name | Formula |
|---|---|
| Simple Moving Average | |
| Exponential Moving Average | |
| Double Exponential MA | |
| Triple Exponential MA | |
| Weighted Moving Average | |
| MACD | |
| MACD Signal Line | |
| MACD Histogram | |
| Relative Strength Index | |
| Rate of Change | |
| Momentum | |
| Commodity Channel Index | |
| Williams R | |
| Chande Momentum Oscillator | |
| Stochastic K | |
| Stochastic D |
| Data | Model | MSE | MAPE | Training Time | |
|---|---|---|---|---|---|
| CSI 300 | LSTM | 5979.9843 | 1.7470 | 0.8967 | 38.50 |
| GRU | 6791.7403 | 1.9428 | 0.8827 | 37.71 | |
| TCN | 5156.9241 | 1.3713 | 0.9109 | 42.26 | |
| Transformer | 9720.6929 | 2.2986 | 0.8320 | 68.85 | |
| CQEformer | 3839.0661 | 1.2252 | 0.9337 | 106.56 | |
| Bank of Communications | LSTM | 0.0219 | 1.6819 | 0.9582 | 40.46 |
| GRU | 0.0290 | 2.0708 | 0.9446 | 36.56 | |
| TCN | 0.0192 | 1.5426 | 0.9633 | 39.11 | |
| Transformer | 0.0430 | 2.5738 | 0.9179 | 64.35 | |
| CQEformer | 0.0163 | 1.3648 | 0.9688 | 102.27 |
| Model | MSE | MAPE | Training Time | |
|---|---|---|---|---|
| Transformer | 9720.6929 | 2.2986 | 0.8320 | 66.63 |
| CREformer | 5946.8689 | 1.6355 | 0.8972 | 73.53 |
| QEformer | 6516.6724 | 1.8091 | 0.8874 | 96.61 |
| CQEformer | 3839.0661 | 1.2252 | 0.9337 | 106.12 |
| Volatility (Average) | Model | MSE | MAPE | |
|---|---|---|---|---|
| Low (0.0064) | Transformer | 6680.7169 | 2.0489 | 0.8552 |
| CREformer | 3488.8279 | 1.3186 | 0.9244 | |
| QEformer | 4586.1880 | 1.7105 | 0.9006 | |
| CQEformer | 2228.9627 | 0.9931 | 0.9517 | |
| Medium (0.0088) | Transformer | 8523.8722 | 2.1798 | 0.8122 |
| CREformer | 5165.9218 | 1.6306 | 0.8862 | |
| QEformer | 5061.9404 | 1.6978 | 0.8885 | |
| CQEformer | 3233.8762 | 1.2110 | 0.9288 | |
| High (0.0155) | Transformer | 13840.4316 | 2.6567 | 0.7718 |
| CREformer | 9097.2318 | 1.9489 | 0.8500 | |
| QEformer | 9805.1429 | 2.0127 | 0.8383 | |
| CQEformer | 5993.2861 | 1.4650 | 0.9012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Li, L. CQEformer: A Causal and Query-Enhanced Transformer Variant for Time-Series Forecasting. Mathematics 2025, 13, 3750. https://doi.org/10.3390/math13233750
Tao Y, Li L. CQEformer: A Causal and Query-Enhanced Transformer Variant for Time-Series Forecasting. Mathematics. 2025; 13(23):3750. https://doi.org/10.3390/math13233750
Chicago/Turabian StyleTao, Yuze, and Lu Li. 2025. "CQEformer: A Causal and Query-Enhanced Transformer Variant for Time-Series Forecasting" Mathematics 13, no. 23: 3750. https://doi.org/10.3390/math13233750
APA StyleTao, Y., & Li, L. (2025). CQEformer: A Causal and Query-Enhanced Transformer Variant for Time-Series Forecasting. Mathematics, 13(23), 3750. https://doi.org/10.3390/math13233750






