Copula Dependent Censoring Models for Survival Prognosis: Application to Lactylation-Related Genes
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Copula Model for Dependent Censoring
2.3. Copula-Graphic Estimator
2.4. Testing Significance of Survival Difference
2.5. Hazard Ratio
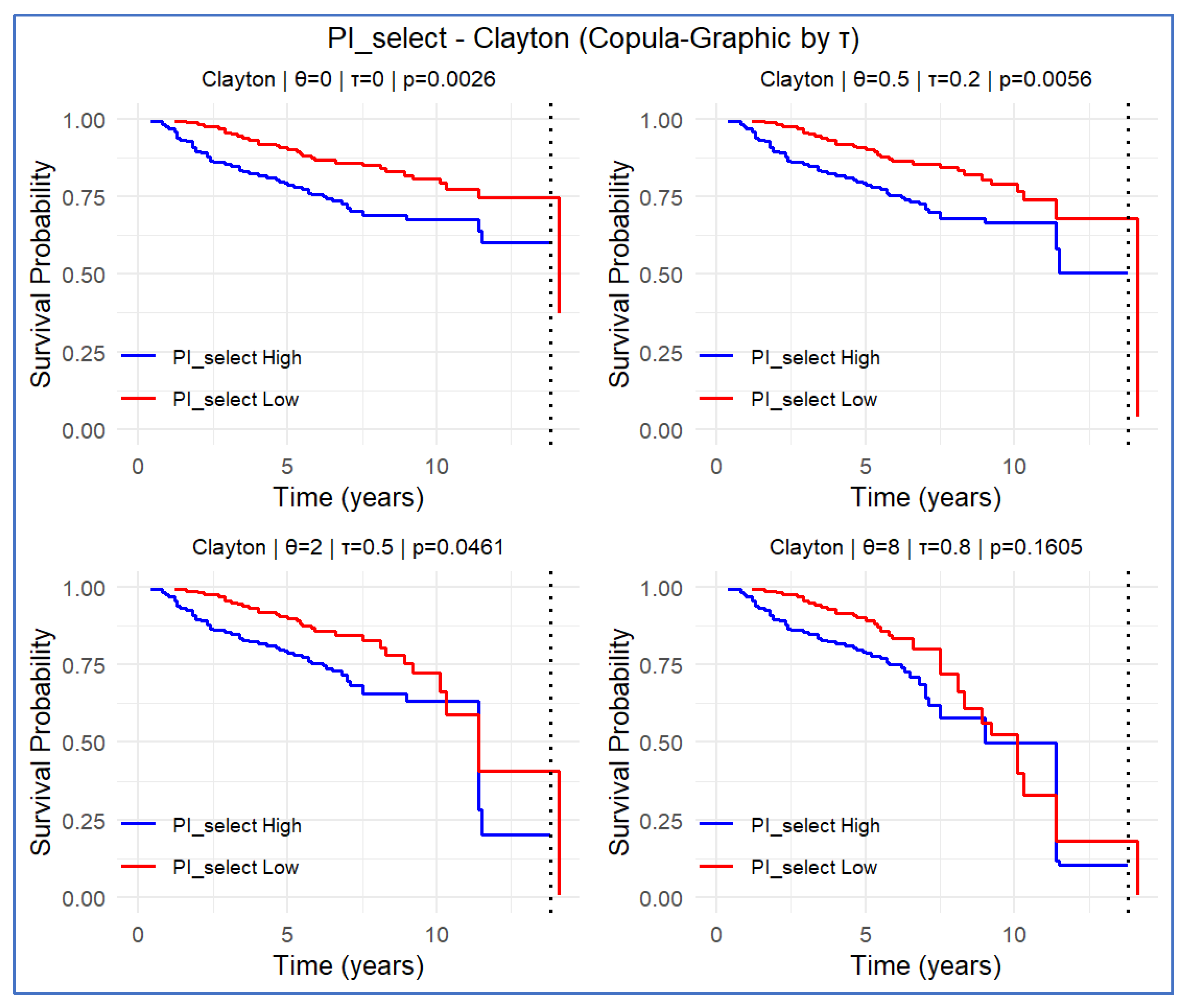
2.6. Prognostic Index
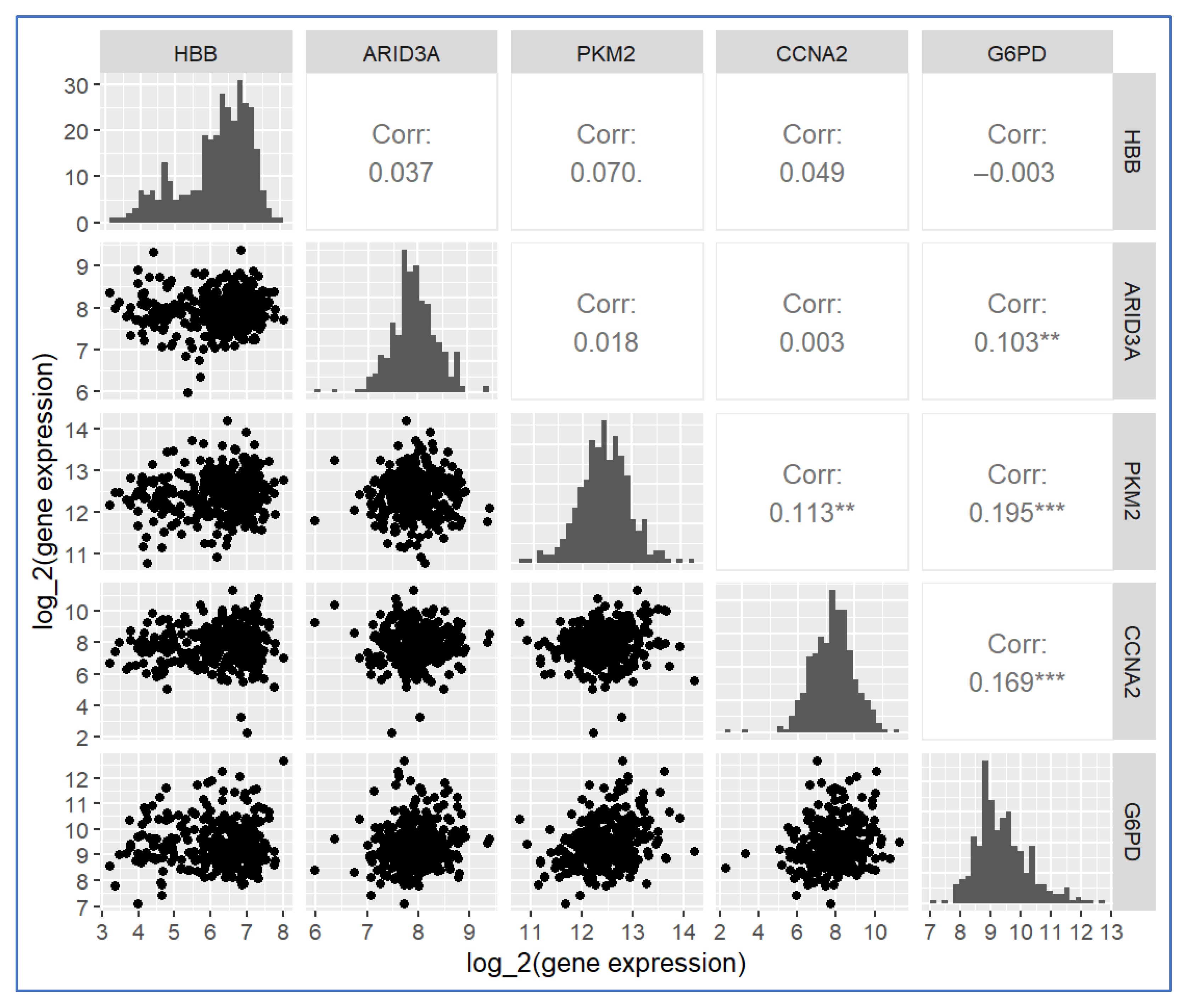
3. Results
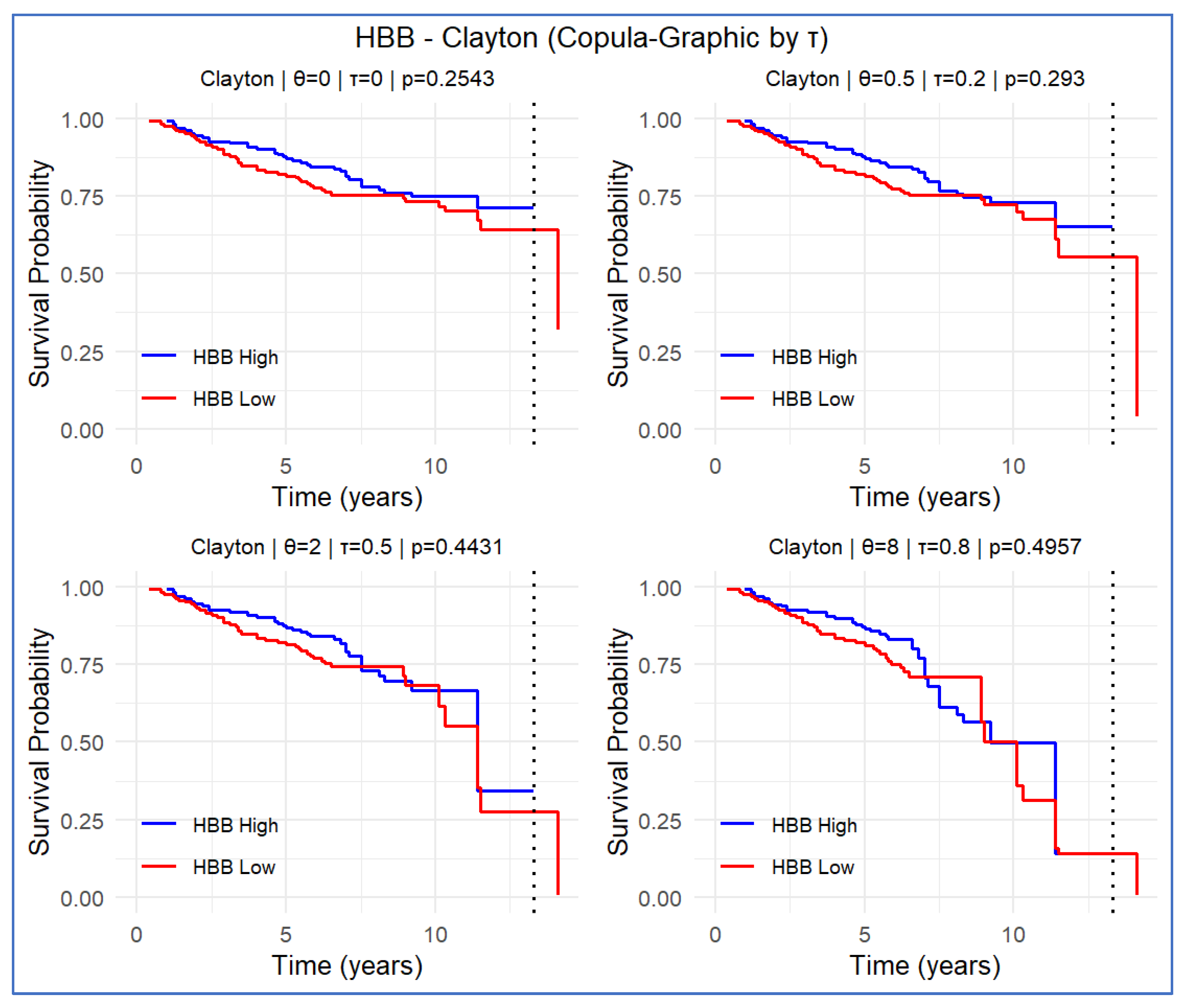
3.1. HBB Gene
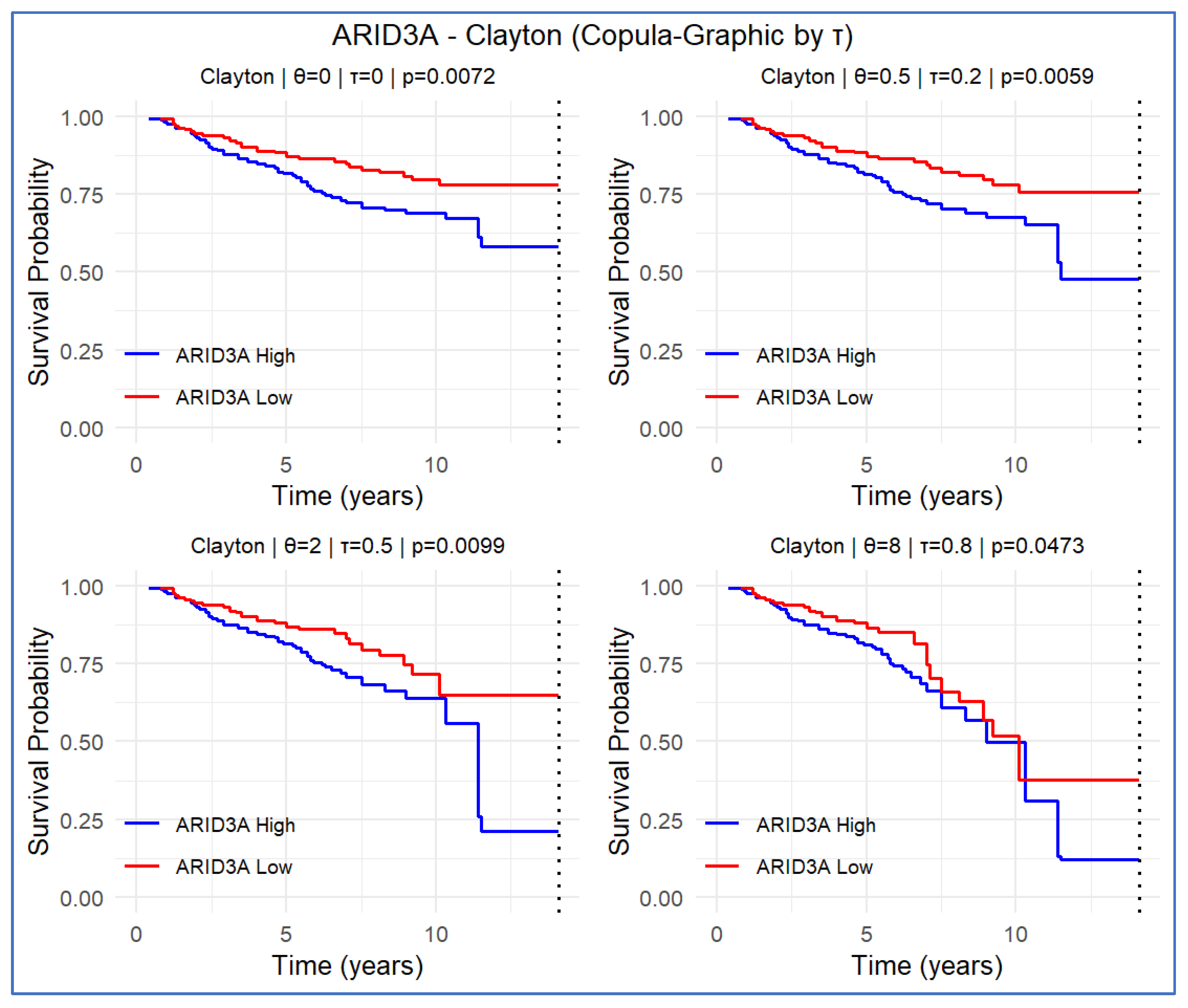
3.2. ARID3A Gene
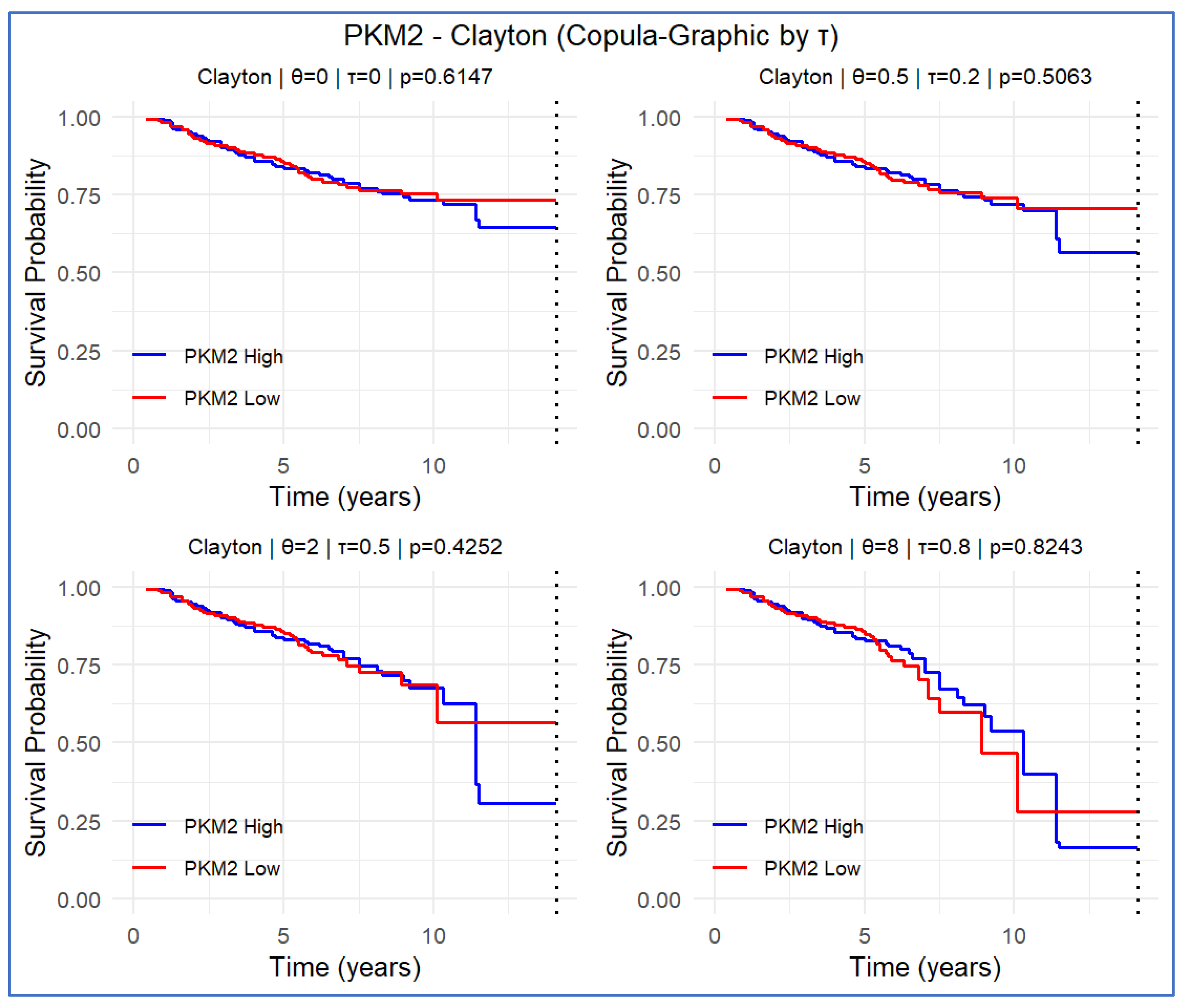
3.3. PKM2 Gene
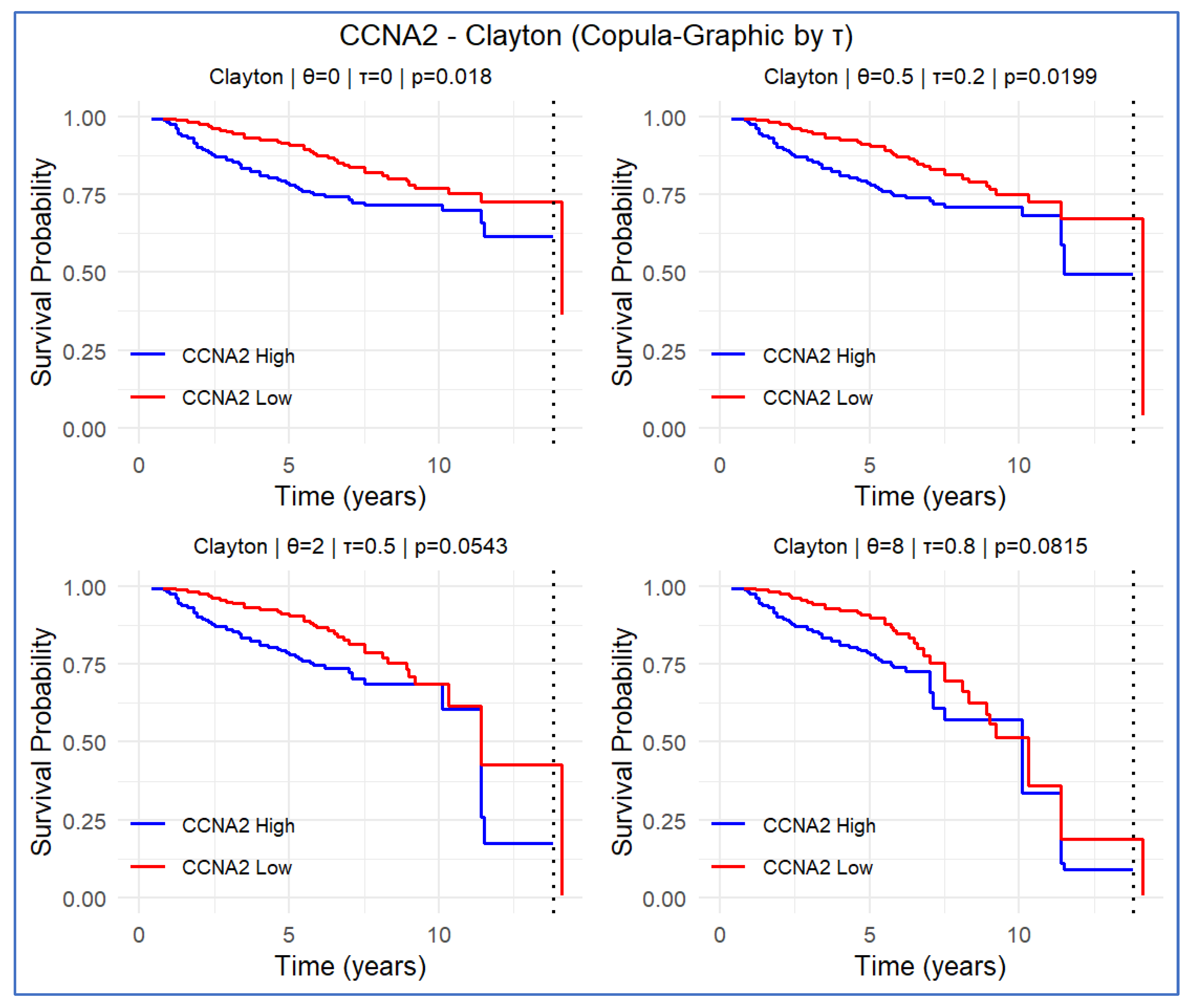
3.4. CCNA2 Gene
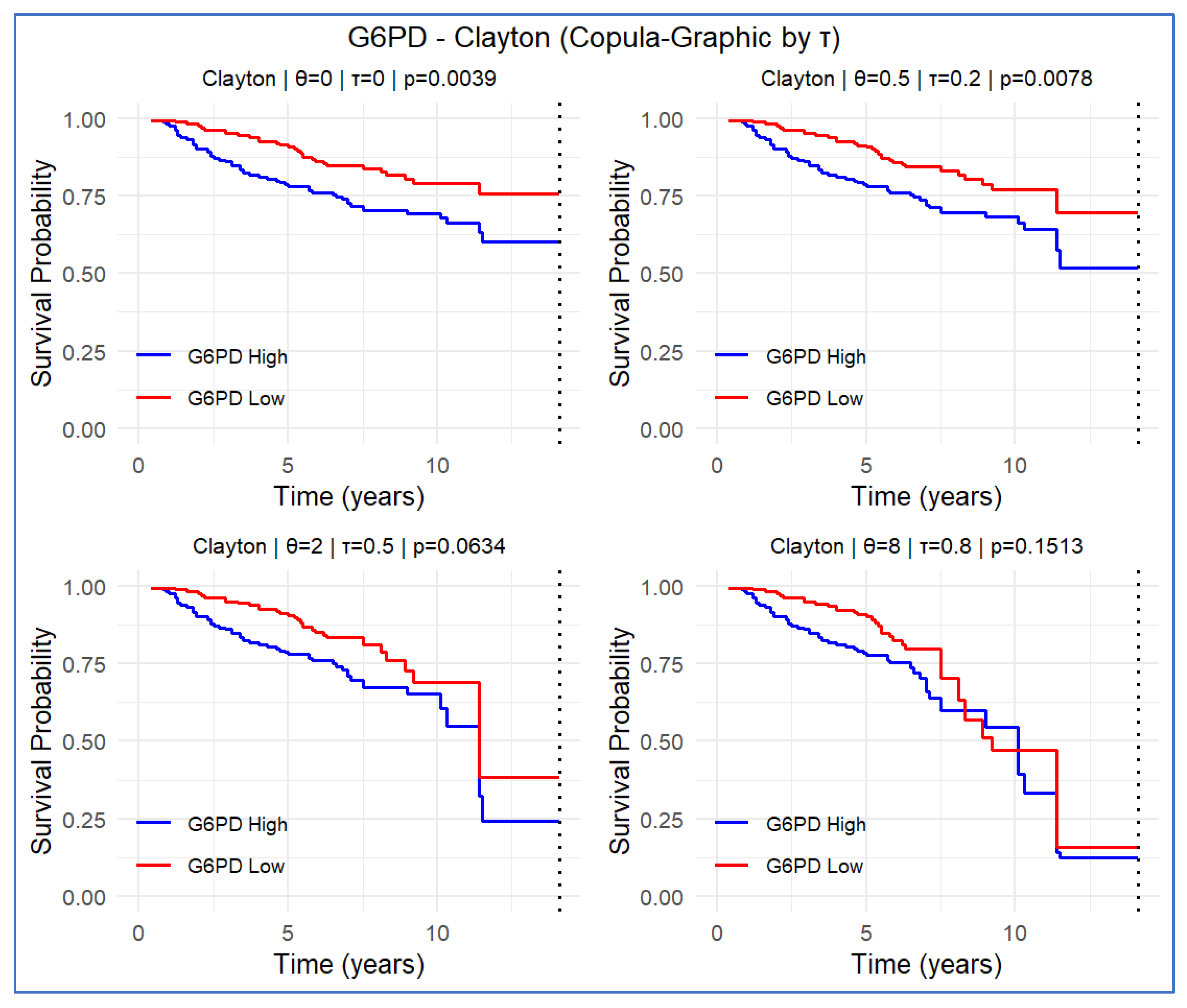
3.5. G6PD Gene
3.6. Combining Five Genes
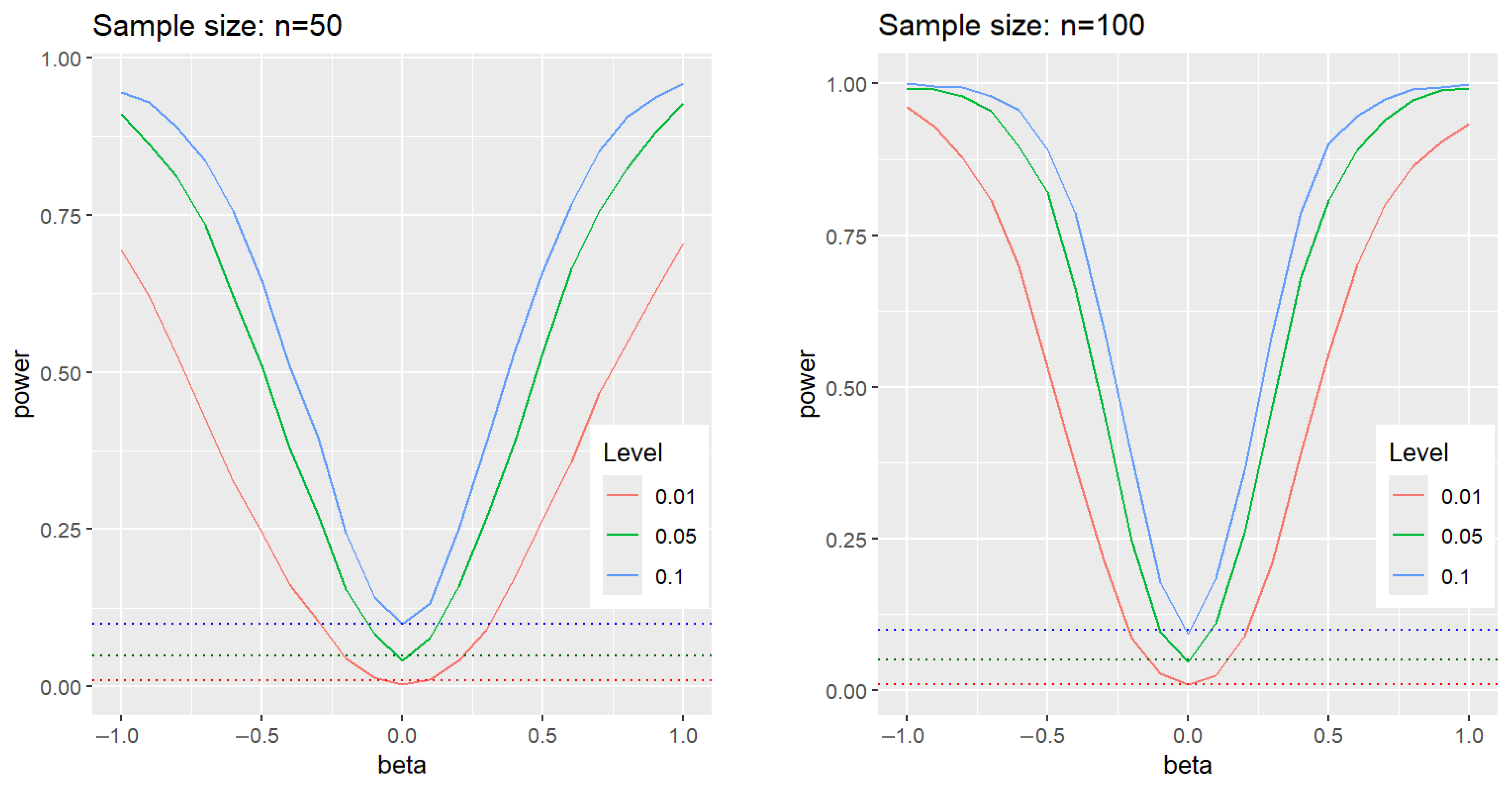
4. Simulation Study
5. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Examples of CG Estimators
References
- Witten, D.M.; Tibshirani, R. Survival analysis with high-dimensional covariates. Stat. Methods Med. Res. 2010, 19, 29–51. [Google Scholar] [CrossRef] [PubMed]
- Newcombe, P.J.; Ali, H.R.; Blows, F.M.; Provenzano, E.; Pharoah, P.; Caldas, C.; Richardson, S. Weibull regression with Bayesian variable selection to identify prognostic tumour markers of breast cancer survival. Stat. Methods Med. Res. 2017, 26, 414–436. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, J.; Liu, M.; Zhu, Q.; Li, Q.; Xie, C.; Han, C.; Wang, Y.; Gao, M.; Liu, J. Weighted correlation gene network analysis reveals a new stemness index-related survival model for prognostic prediction in hepatocellular carcinoma. Aging 2020, 12, 13502. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, A. Big Data Analytics in Oncology with R; CRC Press: New York, NY, USA, 2022. [Google Scholar]
- Chen, H.-Y.; Yu, S.-L.; Chen, C.-H.; Chang, G.-C.; Chen, C.-Y.; Yuan, A.; Cheng, C.-L.; Wang, C.-H.; Terng, H.-J.; Kao, S.-F.; et al. A five-gene signature and clinical outcome in non-small-cell lung cancer. N. Engl. J. Med. 2007, 356, 11–20. [Google Scholar]
- Beer, D.G.; Kardia, S.L.; Huang, C.-C.; Giordano, T.J.; Levin, A.M.; Misek, D.E.; Lin, L.; Chen, G.; Gharib, T.G.; Thomas, D.G.; et al. Gene-expression profiles predict survival of patients with lung adenocarcinoma. Nat. Med. 2002, 8, 816–824. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.-H.; Chen, H.-Y. Survival prediction based on compound covariate under Cox proportional hazard models. PLoS ONE 2012, 7, e47627. [Google Scholar] [CrossRef]
- Emura, T.; Matsui, S.; Chen, H.-Y. compound.Cox: Univariate feature selection and compound covariate for predicting survival. Comput. Methods Programs Biomed. 2019, 168, 21–37. [Google Scholar] [CrossRef]
- Jenssen, T.K.; Kuo, W.P.; Stokke, T.; Hovig, E. Association between gene expressions in breast cancer and patient survival. Hum. Genet. 2002, 111, 411–420. [Google Scholar] [CrossRef]
- Kao, K.J.; Chang, K.M.; Hsu, H.C.; Huang, A.T. Correlation of microarray-based breast cancer molecular subtypes and clinical outcomes: Implications for treatment optimization. BMC Cancer 2011, 11, 143. [Google Scholar] [CrossRef]
- Li, D.; Hu, X.J.; Wang, R. Evaluating Association between Two Event Times with Observations Subject to Informative Censoring. J. Am. Stat. Assoc. 2023, 118, 1282–1294. [Google Scholar] [CrossRef]
- Sotiriou, C.; Wirapati, P.; Loi, S.; Harris, A.; Fox, S.; Smeds, J.; Nordgren, H.; Farmer, P.; Praz, V.; Haibe-Kains, B.; et al. Gene expression profiling in breast cancer: Understanding the molecular basis of histologic grade to improve prognosis. J. Natl. Cancer Inst. 2006, 98, 262–272. [Google Scholar] [CrossRef]
- Haibe-Kains, B.; Desmedt, C.; Loi, S.; Culhane, A.; Bontempi, G.; Quackenbush, J.; Sotiriou, C. A Five-Gene Model to Robustly Identify Breast Cancer Molecular Subtypes. J. Natl. Cancer Inst. 2012, 104, 311–325. [Google Scholar] [CrossRef]
- Peng, M.; Xiang, L. Correlation-based joint feature screening for semi-competing risks outcomes with application to breast cancer data. Stat. Methods Med. Res. 2021, 30, 2428–2446. [Google Scholar] [CrossRef]
- Li, F.; Niu, Y.; Zhao, W.; Yan, C.; Qi, Y. Construction and validation of a prognostic model for lung adenocarcinoma based on endoplasmic reticulum stress-related genes. Sci. Rep. 2022, 12, 19857. [Google Scholar] [CrossRef]
- Ding, H.; Shi, L.; Chen, Z.; Lu, Y.; Tian, Z.; Xiao, H.; Deng, X.; Chen, P.; Zhang, Y. Construction and evaluation of a prognostic risk model of tumor metastasis-related genes in patients with non-small cell lung cancer. BMC Med. Genom. 2022, 15, 187. [Google Scholar] [CrossRef] [PubMed]
- Neto, C.; Brito, M.; Lopes, V.; Peixoto, H.; Abelha, A.; Machado, J. Application of Data Mining for the Prediction of Mortality and Occurrence of Complications for Gastric Cancer Patients. Entropy 2019, 21, 1163. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, Y.; Zhuang, M.; Zhu, L.; Dai, Y.; Lin, M. Screening and identification of CNIH4 gene associated with cell proliferation in gastric cancer based on a large-scale CRISPR-Cas9 screening database DepMap. Gene 2023, 850, 146961. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Y.; Wang, Y.X.; Shen, A.; Jian, R.; An, N.; Yuan, S.Q. Construction and validation of a prognostic prediction model for gastric cancer using a series of genes related to lactate metabolism. Heliyon 2023, 9, e16157. [Google Scholar] [CrossRef]
- Yoshihara, K.; Tajima, A.; Yahata, T.; Kodama, S.; Fujiwara, H.; Suzuki, M.; Onishi, Y.; Hatae, M.; Sueyoshi, K.; Fujiwara, H.; et al. Gene Expression Profile for Predicting Survival in Advanced-Stage Serous Ovarian Cancer across Two Independent Datasets. PLoS ONE 2010, 5, e9615. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Ni, D.; Cai, J.; Yang, J. Identification and validation of immunity-and disulfidptosis-related genes signature for predicting prognosis in ovarian cancer. Heliyon 2024, 10, e32273. [Google Scholar] [CrossRef]
- Emura, T.; Nakatochi, M.; Matsui, S.; Michimae, H.; Rondeau, V. Personalized dynamic prediction of death according to tumour progression and high-dimensional genetic factors: Meta-analysis with a joint model. Stat. Methods Med. Res. 2018, 27, 2842–2858. [Google Scholar] [CrossRef]
- Waldron, L.; Haibe-Kains, B.; Culhane, A.C.; Riester, M.; Ding, J.; Wang, X.V.; Ahmadifar, M.; Tyekucheva, S.; Bernau, C.; Risch, T.; et al. Comparative Meta-analysis of Prognostic Gene Signatures for Late-Stage Ovarian Cancer. J. Natl. Cancer Inst. 2014, 106, dju049. [Google Scholar] [CrossRef]
- Emura, T.; Nakatochi, M.; Murotani, K.; Rondeau, V. A joint frailty-copula model between tumour progression and death for meta-analysis. Stat. Methods Med. Res. 2017, 26, 2649–2666. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Jiang, W.; Yue, Q.; Ye, R.; Li, Y.; Hong, J.; Zhang, M. Radiomic model to predict the expression of PD-1 and overall survival of patients with ovarian cancer. Int. Immunopharmacol. 2022, 113, 109335. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Dong, C.; Shi, H.; Yan, Z.; Zhang, J.; Liu, J. Constructing and validating of m7G-related genes prognostic signature for hepatocellular carcinoma and immune infiltration: Potential biomarkers for predicting the overall survival. J. Gastrointest. Oncol. 2022, 13, 3169–3182. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Li, S.; Li, L.; Li, L.; Li, D.; Guo, H.; Gao, D.; Liu, S.; Ruan, C.; et al. Prognostic prediction and immune infiltration analysis based on ferroptosis and EMT state in hepatocellular carcinoma. Front. Immunol. 2022, 13, 1076045. [Google Scholar] [CrossRef]
- Xiang, X.; Guo, Y.; Chen, Z.; Zhang, F.; Huang, J.; Qin, Y. A prognostic risk prediction model based on ferroptosis-related long non-coding RNAs in bladder cancer: A bulk RNA-seq research and scRNA-seq validation. Medicine 2022, 101, e32558. [Google Scholar] [CrossRef]
- Zhou, L.; Cheng, Q.; Hu, Y.; Tan, H.; Li, X.; Wu, S.; Zhou, T.; Zhou, J. Cuproptosis-related LncRNAs are potential prognostic and immune response markers for patients with HNSCC via the integration of bioinformatics analysis and experimental validation. Front. Oncol. 2022, 12, 1030802. [Google Scholar] [CrossRef]
- Huang, J.; Xu, Z.; Yuan, Z.; Teh, B.M.; Zhou, C.; Shen, Y. Identification of a cuproptosis-related lncRNA signature to predict the prognosis and immune landscape of head and neck squamous cell carcinoma. Front. Oncol. 2022, 12, 983956. [Google Scholar] [CrossRef]
- Vannucchi, A.M.; Guglielmelli, P. Molecular prognostication in Ph-negative MPNs in 2022. Hematology 2022, 1, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Oh, I.; Seo, S.; Ahn, J. G2Vec: Distributed gene representations for identification of cancer prognostic genes. Sci. Rep. 2018, 8, 13729. [Google Scholar] [CrossRef]
- Kim, M.; Oh, I.; Ahn, J. An Improved Method for Prediction of Cancer Prognosis by Network Learning. Genes 2018, 9, 478. [Google Scholar] [CrossRef]
- He, Y.; Song, T.; Ning, J.; Wang, Z.; Yin, Z.; Jiang, P.; Yuan, Q.; Yu, W.; Cheng, F. Lactylation in cancer: Mechanisms in tumour biology and therapeutic potentials. Clin. Transl. Med. 2024, 14, e70070. [Google Scholar] [CrossRef]
- Sui, Y.; Shen, Z.; Wang, Z.; Feng, J.; Zhou, G. Lactylation in cancer: Metabolic mechanism and therapeutic strategies. Cell Death Discov. 2025, 11, 68. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, H.; Wang, Q.; Yu, X.; Ouyang, L. Lactate-induced protein lactylation in cancer: Functions, biomarkers and immunotherapy strategies. Front. Immunol. 2025, 15, 1513047. [Google Scholar] [CrossRef]
- Jiao, Y.; Ji, F.; Hou, L.; Lv, Y.; Zhang, J. Lactylation-related gene signature for prognostic prediction and immune infiltration analysis in breast cancer. Heliyon 2024, 10, e24777. [Google Scholar] [CrossRef]
- Staplin, N.D.; Kimber, A.C.; Collett, D.; Roderick, P.J. Dependent censoring in piecewise exponential survival models. Stat. Methods Med. Res. 2015, 24, 325–341. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.H. Analysis of Survival Data with Dependent Censoring: Copula-Based Approaches; Springer: Singapore, 2018. [Google Scholar]
- Schneider, S.; Demarqui, F.; Colosimo, E.A.; Mayrink, V.D. An approach to model clustered survival data with dependent censoring. Biom. J. 2020, 62, 157–174. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.; Demarqui, F.; de Freitas Costa, E. Free-ranging dogs’ lifetime estimated by an approach for long-term survival data with dependent censoring. Environ. Ecol. Stat. 2022, 29, 869–911. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Vishwakarma, G.K.; Banerjee, S.; Ong, S.H. A modified risk detection approach of biomarkers by frailty effect on multiple time to event data. J. Comput. Appl. Math. 2023, 419, 114681. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.-H. Gene selection for survival data under dependent censoring: A copula-based approach. Stat. Methods Med. Res. 2016, 25, 2840–2857. [Google Scholar] [CrossRef]
- Yeh, C.T.; Liao, G.Y.; Emura, T. Sensitivity analysis for survival prognostic prediction with gene selection: A copula method for dependent censoring. Biomedicines 2023, 11, 797. [Google Scholar] [CrossRef] [PubMed]
- Rivest, L.P.; Wells, M.T. A martingale approach to the copula-graphic estimator for the survival function under dependent censoring. J. Multivar. Anal. 2001, 79, 138–155. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2007. [Google Scholar]
- Braekers, R.; Veraverbeke, N. A copula-graphic estimator for the conditional survival function under dependent censoring. Can. J. Stat. 2005, 33, 429–447. [Google Scholar] [CrossRef]
- Emura, T.; Michimae, H. A copula-based inference to piecewise exponential models under dependent censoring, with application to time to metamorphosis of salamander larvae. Environ. Ecol. Stat. 2017, 24, 151–173. [Google Scholar] [CrossRef]
- Moradian, H.; Larocque, D.; Bellavance, F. Survival forests for data with dependent censoring. Stat. Methods Med. Res. 2019, 28, 445–461. [Google Scholar] [CrossRef] [PubMed]
- Lo, S.M.; Wilke, R.A. A copula model for dependent competing risks. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2010, 59, 359–376. [Google Scholar] [CrossRef]
- Zheng, M.; Klein, J.P. Estimates of marginal survival for dependent competing risks based on an assumed copula. Biometrika 1995, 82, 127–138. [Google Scholar] [CrossRef]
- de Uña-Álvarez, J.; Veraverbeke, N. Generalized copula-graphic estimator. Test 2013, 22, 343–360. [Google Scholar] [CrossRef]
- de Uña-Álvarez, J.; Veraverbeke, N. Copula-graphic estimation with left-truncated and right-censored data. Statistics 2013, 51, 387–403. [Google Scholar] [CrossRef]
- Emura, T.; Hsu, J.H. Estimation of the Mann–Whitney effect in the two-sample problem under dependent censoring. Comput. Stat. Data Anal. 2020, 150, 106990. [Google Scholar] [CrossRef]
- Emura, T.; Ditzhaus, M.; Dobler, D.; Murotani, K. Factorial survival analysis for treatment effects under dependent censoring. Stat. Methods Med. Res. 2023, 33, 61–79. [Google Scholar] [CrossRef]
- Lo, S.M.; Wilke, R.A. A regression model for the copula-graphic estimator. J. Econom. Methods 2014, 3, 21–46. [Google Scholar] [CrossRef]
- Kim, J.M.; Hwang, S.Y. The copula directional dependence by stochastic volatility models. Commun. Stat.-Simul. Comput. 2019, 48, 1153–1175. [Google Scholar] [CrossRef]
- Huang, X.W.; Wang, W.; Emura, T. A copula-based Markov chain model for serially dependent event times with a dependent terminal event. Jpn. J. Stat. Data Sci. 2021, 4, 917–951. [Google Scholar] [CrossRef]
- Das, S.; Bhattacharya, R.; Shome, M. A multi-treatment two stage allocation design for survival outcomes with nonrandom censoring: A copula-based approach. Seq. Anal. 2024, 43, 461–476. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Simon, R.M.; Korn, E.L.; McShane, L.M.; Radmacher, M.D.; Wright, G.W.; Zhao, Y. Design and Analysis of DNA Microarray Investigations; Springer: New York, NY, USA, 2003. [Google Scholar]
- Van Wieringen, W.N.; Kun, D.; Hampel, R.; Boulesteix, A.L. Survival prediction using gene expression data: A review and comparison. Comput. Stat. Data Anal. 2009, 53, 1590–1603. [Google Scholar] [CrossRef]
- Matsui, S. Predicting survival outcomes using subsets of significant genes in prognostic marker studies with microarrays. BMC Bioinform. 2006, 7, 156. [Google Scholar] [CrossRef]
- Lee, J.S.; Chu, I.S.; Heo, J.; Calvisi, D.F.; Sun, Z.; Roskams, T.; Durnez, A.; Demetris, A.J.; Thorgeirsson, S.S. Classification and prediction of survival in hepatocellular carcinoma by gene expression profiling. Hepatology 2004, 40, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Thorgeirsson, S.S. Genome-scale profiling of gene expression in hepatocellular carcinoma: Classification, survival prediction, and identification of therapeutic targets. Gastroenterology 2004, 127, S51–S55. [Google Scholar] [CrossRef] [PubMed]
- Marcucci, G.; Radmacher, M.D.; Maharry, K.; Mrózek, K.; Ruppert, A.S.; Paschka, P.; Vukosavljevic, T.; Whitman, S.P.; Baldus, C.D.; Langer, C.; et al. MicroRNA expression in cytogenetically normal acute myeloid leukemia. N. Engl. J. Med. 2008, 358, 1919–1928. [Google Scholar] [CrossRef] [PubMed]
- Matsui, S. Statistical issues in clinical development and validation of genomic signatures. In Design and Analysis of Clinical Trials for Predictive Medicine; CRC Press: Boca Raton, FL, USA, 2015; pp. 207–226. [Google Scholar]
| Model | Difference Metric D (p-Value) | ||||||
|---|---|---|---|---|---|---|---|
| HBB | ARID3A | PKM2 | CCNA2 | G6PD | PI | ||
| Clayton copula | (τ = 0.0) | 0.043 (0.254) | −0.097 (0.007) | −0.018 (0.615) | −0.087 (0.018) | −0.107 (0.004) | −0.111 (0.003) |
| (τ = 0.2) | 0.044 (0.293) | −0.111 (0.006) | −0.027 (0.506) | −0.095 (0.020) | −0.11 (0.008) | −0.113 (0.006) | |
| (τ = 0.5) | 0.040 (0.443) | −0.136 (0.010) | −0.041 (0.425) | −0.101 (0.054) | −0.097 (0.063) | −0.105 (0.046) | |
| .0 (τ = 0.8) | 0.028 (0.496) | −0.086 (0.047) | 0.009 (0.824) | −0.072 (0.082) | −0.058 (0.151) | −0.058 (0.160) | |
| Gumbel copula | .00 (τ = 0.0) | 0.043 (0.254) | −0.097 (0.007) | −0.018 (0.615) | −0.087 (0.018) | −0.107 (0.004) | −0.111 (0.003) |
| (τ = 0.2) | 0.039 (0.305) | −0.099 (0.008) | −0.022 (0.543) | −0.081 (0.031) | −0.101 (0.007) | −0.102 (0.006) | |
| (τ = 0.5) | 0.033 (0.422) | −0.098 (0.013) | −0.028 (0.475) | −0.073 (0.068) | −0.086 (0.029) | −0.085 (0.034) | |
| .00 (τ = 0.8) | 0.025 (0.514) | −0.083 (0.038) | −0.009 (0.821) | −0.07 (0.074) | −0.058 (0.128) | −0.059 (0.128) | |
| Frank copula | .00 (τ = 0.0) | 0.043 (0.254) | −0.097 (0.007) | −0.018 (0.615) | −0.087 (0.018) | −0.107 (0.004) | −0.111 (0.003) |
| (τ = 0.2) | 0.041 (0.298) | −0.101 (0.007) | −0.024 (0.534) | −0.084 (0.029) | −0.104 (0.007) | −0.105 (0.007) | |
| (τ = 0.5) | 0.035 (0.399) | −0.099 (0.016) | −0.027 (0.508) | −0.076 (0.065) | −0.088 (0.033) | −0.085 (0.041) | |
| (τ = 0.8) | 0.027 (0.465) | −0.077 (0.044) | 0.002 (0.968) | −0.07 (0.063) | −0.056 (0.123) | −0.057 (0.124) | |
| (τ = −0.2) | 0.043 (0.229) | −0.093 (0.009) | −0.015 (0.680) | −0.089 (0.013) | −0.107 (0.003) | −0.114 (0.001) | |
| (τ = −0.5) | 0.043 (0.217) | −0.088 (0.011) | −0.011 (0.747) | −0.089 (0.010) | −0.106 (0.003) | −0.114 (0.001) | |
| (τ = −0.8) | 0.043 (0.220) | −0.085 (0.013) | −0.010 (0.778) | −0.088 (0.011) | −0.105 (0.003) | −0.114 (0.000) | |
| Model | Hazard Ratio: exp(β) (p-Value) | ||||||
|---|---|---|---|---|---|---|---|
| HBB | ARID3A | PKM2 | CCNA2 | G6PD | PI | ||
| Univariate Cox | None | 0.964 (0.743) | 2.103 (0.002) | 1.229 (0.645) | 1.222 (0.042) | 1.611 (0.000) | 1.995 (0.000) |
| Clayton copula | (τ = 0.05) | 0.964 (0.736) | 2.118 (0.001) | 1.256 (0.288) | 1.222 (0.033) | 1.619 (0.007) | 1.987 (0.000) |
| (τ = 0.2) | 0.969 (0.781) | 2.095 (0.002) | 1.135 (0.616) | 1.222 (0.035) | 1.599 (0.001) | 1.959 (0.000) | |
| (τ = 0.5) | 0.991 (0.934) | 1.951 (0.002) | 1.049 (0.701) | 1.218 (0.030) | 1.327 (0.011) | 1.981 (n.a.) | |
| (τ = 0.8) | 1.022 (0.843) | 1.344 (0.468) | 1.056 (n.a.) | 1.216 (0.041) | 1.303 (0.014) | 1.122 (0.574) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahardinata, C.A.; Liao, G.-Y.; Emura, T. Copula Dependent Censoring Models for Survival Prognosis: Application to Lactylation-Related Genes. Mathematics 2025, 13, 3735. https://doi.org/10.3390/math13233735
Kahardinata CA, Liao G-Y, Emura T. Copula Dependent Censoring Models for Survival Prognosis: Application to Lactylation-Related Genes. Mathematics. 2025; 13(23):3735. https://doi.org/10.3390/math13233735
Chicago/Turabian StyleKahardinata, Clarissa Auryn, Gen-Yih Liao, and Takeshi Emura. 2025. "Copula Dependent Censoring Models for Survival Prognosis: Application to Lactylation-Related Genes" Mathematics 13, no. 23: 3735. https://doi.org/10.3390/math13233735
APA StyleKahardinata, C. A., Liao, G.-Y., & Emura, T. (2025). Copula Dependent Censoring Models for Survival Prognosis: Application to Lactylation-Related Genes. Mathematics, 13(23), 3735. https://doi.org/10.3390/math13233735







