Industry Index Volatility Spillovers and Forecasting from Crude Oil Prices Based on the MS-HAR-TVP Model
Abstract
1. Introduction
2. Literature Review
3. Notation
4. Model Summary
4.1. TVP-VAR Model
Bayesian Estimation of TVP-VAR Model
4.2. HAR Model
4.2.1. RV and HAR
4.2.2. Jump Volatility
4.2.3. Median Realized Volatility
4.2.4. Favorable and Unfavorable Volatility
4.3. MRS-HAR-RV-TVP Model
4.4. HAR-RV-TVP Model
- (1)
- HAR-RV-TVP-J model: in the framework of the original HAR-RV-J model, we add the jump part of parameter J (i.e., crude oil price) and the net pairwise spillover of daily volatility to parameter i, which causes volatility shocks; that is,
- (2)
- HAR-RV-TVP-TCJ model: in the framework of the original HAR-RV-TCJ model, we incorporate the net pairwise spillover constructed based on the median realized volatility and the median realized quartic variation into the volatility impact on parameter i; that is,
- (3)
- HAR-RV-TVP-RS model: based on the HAR-RV-RS model, we incorporate the net pairwise spillover constructed by the realized semivariances of the rise and fall between parameter i and j into the volatility impact on parameter i; that is,
- (4)
- HAR-RV-TVP-SJ model: based on the HAR-RV-SJ model, we construct the corresponding net pairwise spillover index by using the median realized volatility and the signed jump; that is,
4.5. Model Evaluation
5. Empirical Analysis and Result Testing
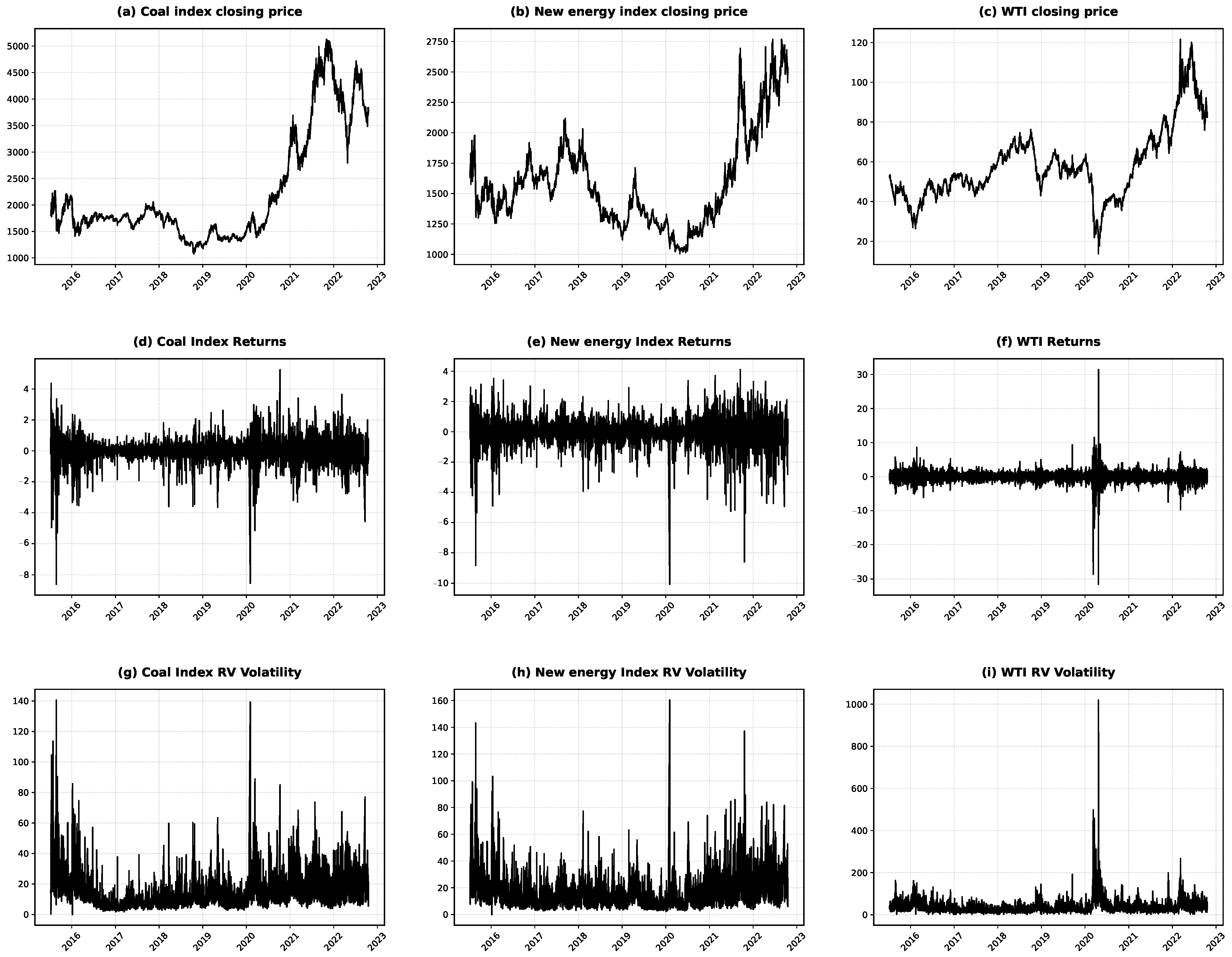
5.1. Sample Selection and Data Sources
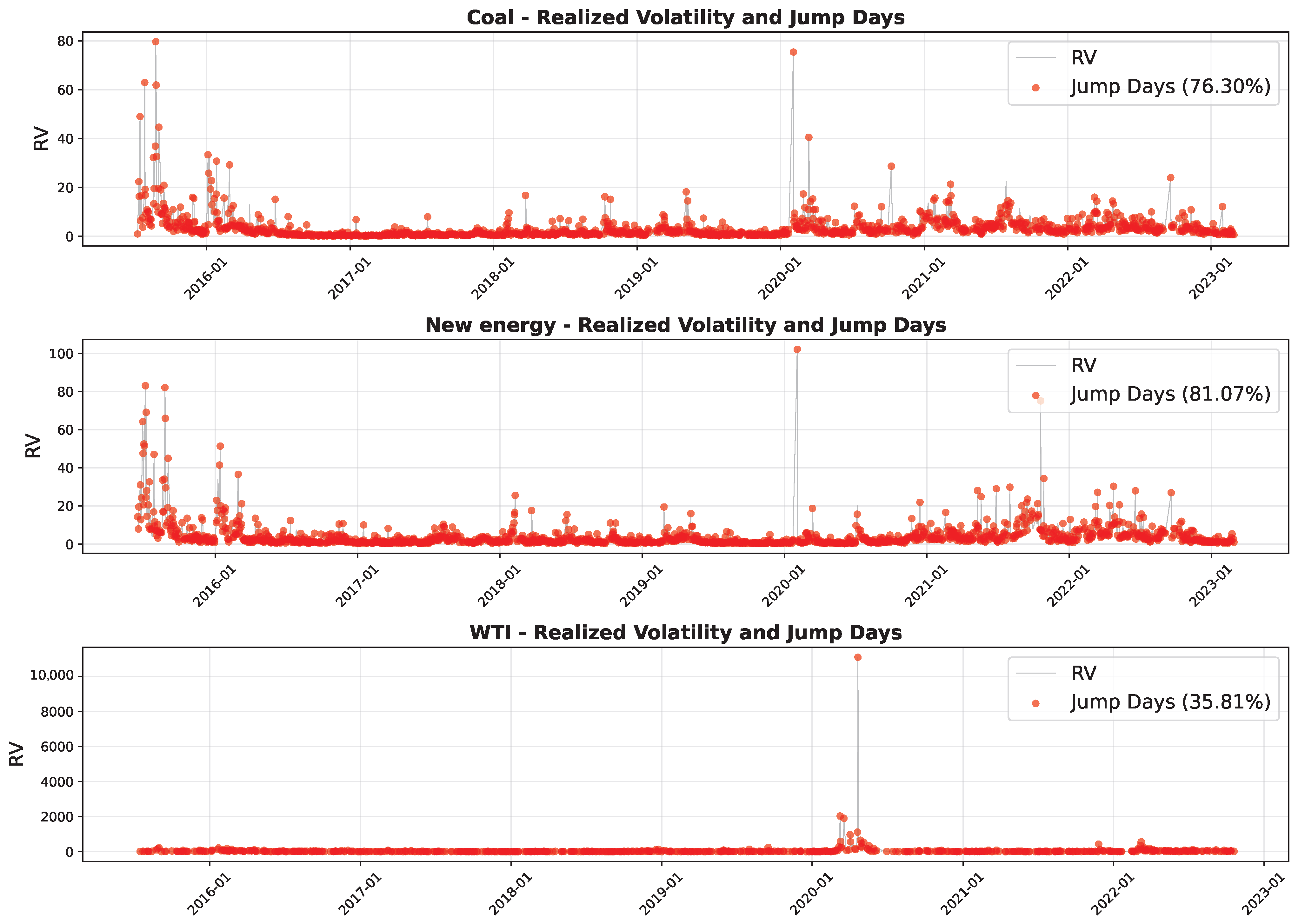
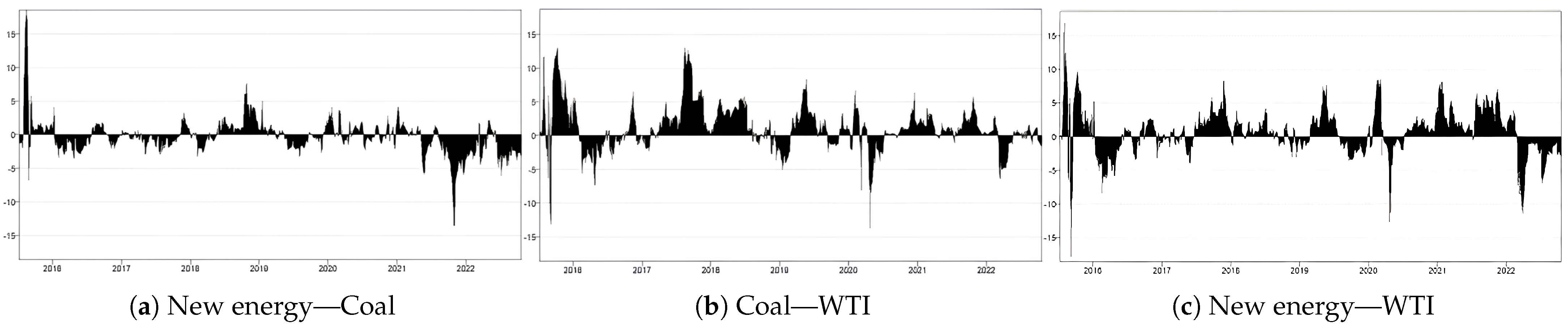
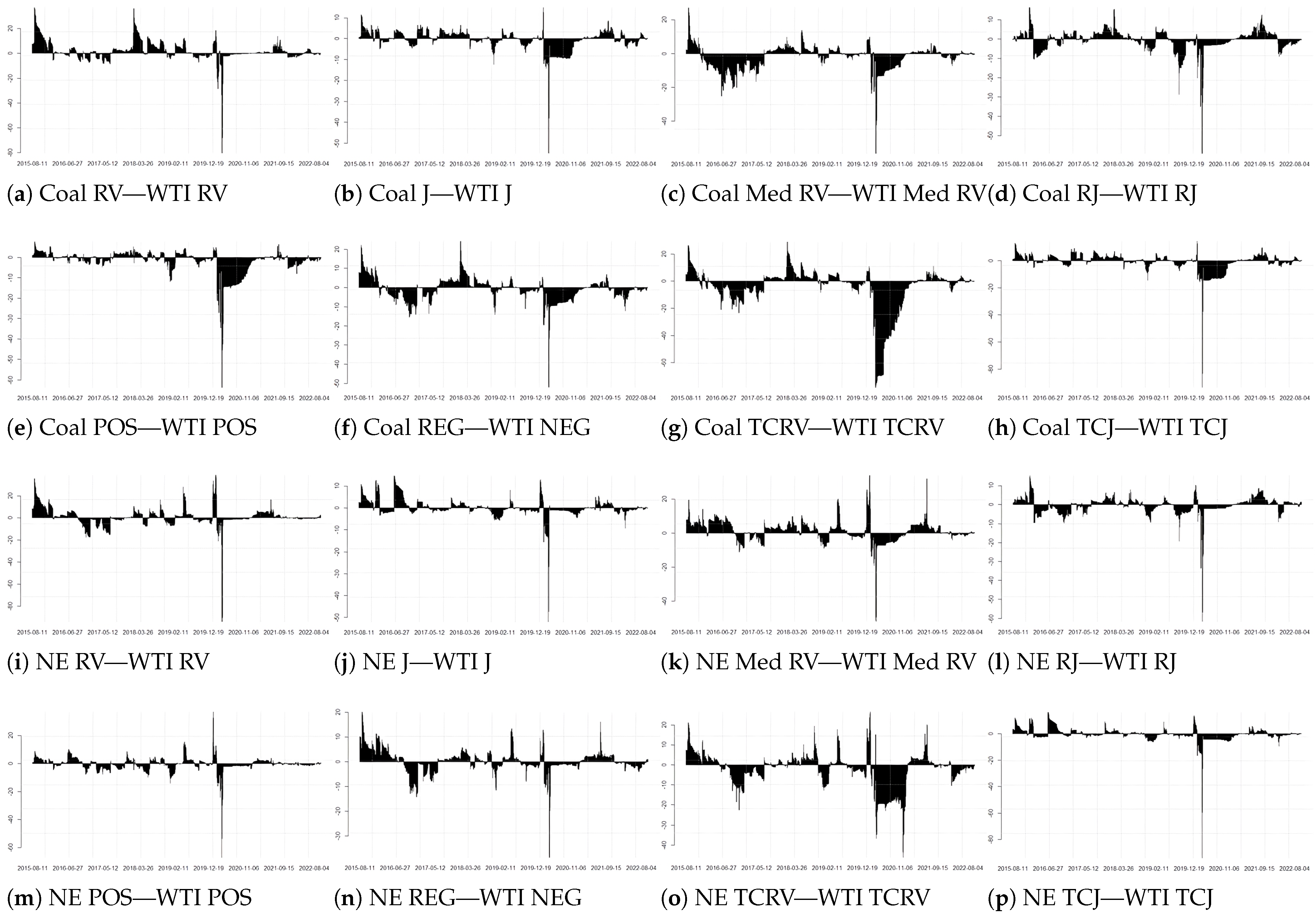
5.2. High-Frequency Return Volatility Spillover Effect
5.3. Parameter Estimation
5.3.1. HAR-RV Family Model Parameter Estimation
5.3.2. MS-HAR-RV Family Model Parameter Estimation
- New energy index jump dynamics: In the high-volatility state (), the short- and medium-term jump coefficient is statistically significant. In the low-volatility state (), the long-term jump coefficient is significant at the 1% level. This pattern suggests that jumps in low-volatility periods enhance long-memory properties, while high-volatility periods emphasize short- and medium-term dynamics.
- Coal index jump dynamics: In the high-volatility state, the jump coefficient exhibits weaker significance (10% level). In the low-volatility state, the medium-term jump coefficient becomes significant at the 1% level. However, the model’s in-sample fit shows no substantial difference between the two jump specifications. Unlike the new energy index, decomposing coal index volatility into high and low regimes does not yield additional explanatory power for jump dynamics.
- Good–bad volatility asymmetry (MS-HAR-RS): The MS-HAR-RS model reveals asymmetric volatility persistence across regimes. For both indices, the significance of positive volatility coefficients in the low-volatility state decreases substantially compared to the previous three models. Conversely, negative volatility coefficients exhibit increased significance relative to the HAR-RV benchmark. This finding indicates stronger volatility persistence during negative volatility episodes than during positive volatility periods.
- Signed jump model (MS-HAR-RV-SJ): The leverage jump model preserves the short- and medium-term memory properties observed in previous specifications during high-volatility states. In the low-volatility state, both index models show markedly higher significance levels compared to alternative models. Most in-sample coefficients satisfy the 1% significance level. However, the two indices diverge in their low-volatility fitting performance: the new energy index model achieves improved fit, while the coal index model experiences a significant deterioration in goodness-of-fit.
5.3.3. MS-HAR-TVP Family Model Parameter Estimation
5.4. Out-of-Sample Prediction and MCS Robustness Check
5.4.1. Out-of-Sample Forecasting
5.4.2. MCS Robustness Check
5.5. MCS Robustness Check and Diebold–Mariano Tests
6. Conclusions
- (1)
- Based on the high-frequency volatility decomposition of crude oil for coal and new energy indexes, we conduct the corresponding trend and jump volatility spillover test and find the volatility spillover aggregation effect and the asymmetry of positive and negative volatility spillover according to different statistics. Due to the many black swan events in the global energy market in the past five years, and in the post-pandemic era, the domestic economic recovery has significant differences in industry preference and policy orientation, which leads to the decay of the long memory of index volatility in different industries.
- (2)
- After adding the crude oil trend and jump factors, the in-sample fitting degree of the two types of index MS-HAR-TVP model families in the high volatility domain has significantly improved, while in the low volatility period, the crude oil price volatility cannot bring enough additional information to the model, and the index volatility rate will shrink before the crude oil volatility, which verifies the asymmetric impact of the crude oil volatility change on the domestic financial market again. The short-term trend of crude oil is opposite to that of the new energy index, but the same as that of the coal index, and the new energy index has the same influencing factors as crude oil, which leads to the higher significance of the jump spillover part than the coal index.
- (3)
- Combining the MCS test method, we find that both the trend and jump components of crude oil volatility can improve the accuracy and stability of the out-of-sample prediction of the domestic financial index. The discrete jump model (MS-HAR-TVP-J) and the significance jump model (MS-HAR-TVP-TCJ) based on the statistic perform well in different loss functions and different prediction time lengths, while the RS model family and the conditional jump model family based on the good and bad volatility perform worse than the other models in the two types of industry models. This indicates that due to the existence of a lot of endogenous jump volatility in the new energy and coal indexes, the trendiness decays with the prediction time length. Therefore, under some conditions, the MS-HAR-J also has a high out-of-sample prediction stability.
7. Limitations and Future Research Directions
Funding
Data Availability Statement
Conflicts of Interest
References
- Degiannakis, S.; Filis, G. Forecasting oil price realized volatility using information channels from other asset classes. J. Int. Money Financ. 2017, 76, 28–49. [Google Scholar] [CrossRef]
- Silvennoinen, A.; Thorp, S. Financialization, crisis and commodity correlation dynamics. J. Int. Financ. Mark. Inst. Money 2013, 24, 42–65. [Google Scholar] [CrossRef]
- Astudillo, K.; Flores, M.; Soliz, M.; Ferreira, G.; Varela-Aldás, J. A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series. Mathematics 2025, 13, 2300. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Econometric analysis of realized covariation: High frequency based covariance, regression, and correlation in financial economics. Econometrica 2004, 72, 885–925. [Google Scholar] [CrossRef]
- Lee, M.C. A Hybrid EGARCH–Informer Model with Consistent Risk Calibration for Volatility and CVaR Forecasting. Mathematics 2025, 13, 3108. [Google Scholar] [CrossRef]
- Patton, A.J.; Sheppard, K. Good volatility, bad volatility: Signed jumps and the persistence of volatility. Rev. Econ. Stat. 2015, 97, 683–697. [Google Scholar] [CrossRef]
- Antonakakis, N.; Chatziantoniou, I.; Gabauer, D. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Risk Financ. Manag. 2020, 13, 84. [Google Scholar] [CrossRef]
- Ma, F.; Wei, Y.; Huang, D.S. The Forecasting Performance of the High-frequency Volatility Models with the Markov-switching Regime and Jump. Syst. Eng. 2016, 34, 10–16. [Google Scholar]
- Cai, G.; Ying, X. The Forecasting Performance of the High-Frequency Volatility Models Based on Jumps, Good-Bad Volatility and Markov Regime-Switching. J. Sys. Sci. Math. Sci. 2020, 40, 521. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X. The Forecasting Performance of the High-Frequency Volatility Models Based on Errors and Markov Regime-Switching. J. Sys. Sci. Math. Sci. 2022, 42, 1200. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The model confidence set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Taylor, S.J. Modelling Financial Time Series; World Scientific: Singapore, 2008. [Google Scholar] [CrossRef]
- Corsi, F. A simple approximate long-memory model of realized volatility. J. Financ. Econom. 2009, 7, 174–196. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Kinnebrock, S.; Shephard, N. Measuring downside risk-realised semivariance. CREATES Res. Pap. 2008. [Google Scholar] [CrossRef]
- Huang, X.; Tauchen, G. The relative contribution of jumps to total price variance. J. Financ. Econom. 2005, 3, 456–499. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. Rev. Econ. Stat. 2007, 89, 701–720. [Google Scholar] [CrossRef]
- Granger, C.W.; Ding, Z. Varieties of long memory models. J. Econom. 1996, 73, 61–77. [Google Scholar] [CrossRef]
- Raggi, D.; Bordignon, S. Long memory and nonlinearities in realized volatility: A Markov switching approach. Comput. Stat. Data Anal. 2012, 56, 3730–3742. [Google Scholar] [CrossRef]
- Chen, S.; Guan, T.; Li, Y. Forecasting realized volatility of Chinese stock index futures based on jumps, good-bad volatility and Baidu index. Syst. Eng.-Theory Pract. 2018, 38, 299–316. [Google Scholar] [CrossRef]
- Hammoudeh, S.; Aleisa, E. Dynamic relationships among GCC stock markets and NYMEX oil futures. Contemp. Econ. Policy 2004, 22, 250–269. [Google Scholar] [CrossRef]
- Aloui, C.; Jammazi, R. The effects of crude oil shocks on stock market shifts behaviour: A regime switching approach. Energy Econ. 2009, 31, 789–799. [Google Scholar] [CrossRef]
- Soucek, M.; Todorova, N. Realized volatility transmission between crude oil and equity futures markets: A multivariate HAR approach. Energy Econ. 2013, 40, 586–597. [Google Scholar] [CrossRef]
- Narayan, P.K.; Gupta, R. Has oil price predicted stock returns for over a century? Energy Econ. 2015, 48, 18–23. [Google Scholar] [CrossRef]
- Salisu, A.A.; Raheem, I.D.; Ndako, U.B. A sectoral analysis of asymmetric nexus between oil price and stock returns. Int. Rev. Econ. Financ. 2019, 61, 241–259. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Gabauer, D. Volatility impulse response analysis for DCC-GARCH models: The role of volatility transmission mechanisms. J. Forecast. 2020, 39, 788–796. [Google Scholar] [CrossRef]
- Balcilar, M.; Gabauer, D.; Umar, Z. Crude Oil futures contracts and commodity markets: New evidence from a TVP-VAR extended joint connectedness approach. Resour. Policy 2021, 73, 102219. [Google Scholar] [CrossRef]
- Deng, C.; Zhao, K.; Wu, C. Does policy uncertainty increase economic and financial uncertainty in China? Syst. Eng.-Theory Pract. 2022, 42, 16. [Google Scholar]
- Wang, J.; Man, T.; Wang, L. Volatility Spillover Effects Between Carbon Futures and Stock Markets: A DGC-t-MSV-BN Model. Mathematics 2025, 13, 2412. [Google Scholar] [CrossRef]
- Zhu, F.; Fu, S.; Liu, X. A Quantile Spillover-Driven Markov Switching Model for Volatility Forecasting: Evidence from the Cryptocurrency Market. Mathematics 2025, 13, 2382. [Google Scholar] [CrossRef]
- Ari, Y.; Kurt, H.; Uçak, H. Volatility Spillovers Among EAGLE Economies: Insights from Frequency-Based TVP-VAR Connectedness. Mathematics 2025, 13, 1256. [Google Scholar] [CrossRef]
- Koop, G.; Korobilis, D. Large time-varying parameter VARs. J. Econom. 2013, 177, 185–198. [Google Scholar] [CrossRef]
- Muhly, P.S.; Solel, B. Tensor Algebras, Induced Representations, and the Wold Decomposition. Can. J. Math. 1999, 51, 850–880. [Google Scholar] [CrossRef]
- Koop, G.; Korobilis, D. Forecasting with High-Dimensional Panel VARs. Oxf. Bull. Econ. Stat. 2019, 81, 937–959. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y.; Smith, R.P. Pooled Mean Group Estimation of Dynamic Heterogeneous Panels. J. Am. Stat. Assoc. 1999, 94, 621–634. [Google Scholar] [CrossRef]
- Primiceri, G.E. Time varying structural vector autoregressions and monetary policy. Rev. Econ. Stud. 2005, 72, 821–852. [Google Scholar] [CrossRef]
- Koop, G.M. Forecasting with medium and large Bayesian VARs. J. Appl. Econom. 2013, 28, 177–203. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. Int. Econ. Rev. 1998, 39, 885–905. [Google Scholar] [CrossRef]
- Andersen, T.G.; Dobrev, D.; Schaumburg, E. Jump-robust volatility estimation using nearest neighbor truncation. J. Econom. 2012, 169, 75–93. [Google Scholar] [CrossRef]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econom. J. Econom. Soc. 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Kim, C.J. Dynamic linear models with Markov-switching. J. Econom. 1994, 60, 1–22. [Google Scholar] [CrossRef]
- Wu, L.; Xu, W.; Huang, D.; Li, P. Does the volatility spillover effect matter in oil price volatility predictability? Evidence from high-frequency data. Int. Rev. Econ. Financ. 2022, 82, 299–306. [Google Scholar] [CrossRef]
| Symbol | Description | Definition | Equation |
|---|---|---|---|
| Basic Variables | |||
| Realized Volatility | Sum of squared intraday returns on day t | (14) | |
| Log Return | (14) | ||
| Sampling Interval | Duration between each sampling, | (14) | |
| N | Sample Size | Number of intraday observations | (14) |
| HAR Model Components | |||
| Weekly RV | Average realized volatility over past 5 days | (15) | |
| Monthly RV | Average realized volatility over past 22 days | (15) | |
| HAR Coefficients | Daily, weekly, and monthly coefficients | (15) | |
| Jump Volatility Measures | |||
| Bipower Variation | Estimates quadratic variation | (17) | |
| Jump Component | (19) | ||
| Jump Test Statistic | Significant jump detection statistic | (21) | |
| Continuous Jump | Filtered jump variance using threshold | (22) | |
| Median RV | Median-based realized volatility (robust to jumps) | (23) | |
| Median RQ | Median-based realized quarticity | (24) | |
| Median Jump Stat | Jump test statistic based on | (25) | |
| Threshold CJ | Threshold continuous jump component | (26) | |
| Threshold CRV | Threshold continuous realized volatility | (27) | |
| Signed Volatility | |||
| Positive Semivariance | Sum of squared positive returns | (29) | |
| Negative Semivariance | Sum of squared negative returns | (29) | |
| Signed Jump | Difference: | After (30) | |
| TVP-VAR Model | |||
| Vector of Variables | dimensional vector | (1) | |
| Time-varying Coef. | coefficient matrix | (1) | |
| Covariance Matrix | Time-varying variance–covariance matrix | (1) | |
| Innovation Covariance | dimensional matrix | (2) | |
| VMA Coefficients | Wold decomposition coefficients | (3) | |
| Spillover Indices | |||
| GFEVD | Forecast error variance decomposition | (4) | |
| Spillover Element | Normalized spillover from j to i | (5) | |
| Directional Receive | Total spillover received by variable i | (6) | |
| Directional Transmit | Total spillover transmitted from variable i | (7) | |
| Net Pairwise Spillover | Net directional connectivity: | (8) | |
| Total Connectivity | Average total directional spillover (market risk) | (9) | |
| Indicator Function | (38) | ||
| Markov Switching | |||
| Regime State | : 1 = high vol, 2 = low vol | After (31) | |
| Transition Prob. | Probability of switching from state i to j | After (31) | |
| Regime-dependent Coef. | Coefficients conditional on regime | (32) | |
| Event | U.S. Eastern Time | Beijing Time |
|---|---|---|
| WTI trading day closes | Day , 4:00 p.m. | Day t, 4:00 a.m. |
| Time gap (information dissemination) | — | 5.5 h |
| CSI trading day t opens | Day t, 9:30 p.m. (previous night) | Day t, 9:30 a.m. |
| CSI trading day t closes | Day , 3:00 a.m. | Day t, 3:00 p.m. |
| Statistics | RV | MedRV | TCRV | J | TCJ | RS+ | RS− | SJ |
|---|---|---|---|---|---|---|---|---|
| Mean | 2.5072 | 2.3472 | 2.2296 | 0.2841 | 0.2872 | 1.3583 | 1.1488 | 0.2095 |
| Std | 3.6027 | 3.4548 | 3.2924 | 0.7957 | 0.6398 | 2.0271 | 1.8917 | 1.5479 |
| Skewness | 6.0086 | 5.4968 | 5.863 | 14.9856 | 5.111 | 5.5536 | 6.1873 | −0.5105 |
| Kurtosis | 70.3185 | 55.3743 | 64.2456 | 361.2518 | 37.5985 | 51.4381 | 69.9493 | 26.0639 |
| JB () | 35.22 *** | 22.02 *** | 29.52 *** | 909.42 *** | 10.51 *** | 19.17 *** | 34.93 *** | 4.71 *** |
| ADF | −6.69 *** | −6.72 *** | −6.75 *** | −8.40 *** | −8.08 *** | −6.90 *** | −6.76 *** | −11.90 *** |
| Q(10) | 3581 *** | 3474.6 *** | 3533.3 *** | 367.279 *** | 408.7 *** | 2572.6 *** | 2487.5 *** | 110.5 *** |
| Q(20) | 4735.5 *** | 4616.8 *** | 4685.0 *** | 497.24 *** | 558.49 *** | 3350.7 *** | 3382.1 *** | 160.37 *** |
| Statistics | RV | MedRV | TCRV | J | TCJ | RS+ | RS− | SJ |
|---|---|---|---|---|---|---|---|---|
| Mean | 2.3511 | 2.2864 | 2.1539 | 0.2377 | 0.2053 | 1.1649 | 1.1862 | −0.0214 |
| Std | 3.5271 | 3.4924 | 3.1941 | 0.7796 | 0.655 | 1.7545 | 2.0126 | 1.348 |
| Skewness | 6.2754 | 6.0799 | 5.6614 | 15.5546 | 11.0668 | 6.0235 | 6.4338 | −2.6243 |
| Kurtosis | 69.7195 | 60.9902 | 53.0168 | 359.814 | 184.0873 | 57.3449 | 69.5721 | 40.4899 |
| JB () | 34.73 *** | 26.77 *** | 20.34 *** | 902.72 *** | 237.93 *** | 23.77 *** | 34.65 *** | 11.54 *** |
| ADF | −6.00 *** | −6.111 *** | −5.957 *** | −7.912 *** | −8.908 *** | −5.548 *** | −6.619 *** | −12.13 *** |
| Q(10) | 3210 *** | 2920 *** | 3280 *** | 249 *** | 180.1 *** | 2840 *** | 2150 *** | 61.5 *** |
| Q(20) | 4900 *** | 4540 *** | 5100 *** | 473 *** | 349 *** | 4390 *** | 3300 *** | 105 *** |
| Statistics | RV | MedRV | TCRV | J | TCJ | RS+ | RS− | SJ |
|---|---|---|---|---|---|---|---|---|
| Mean | 10.8016 | 9.3647 | 9.3527 | 1.2596 | 1.5663 | 5.5456 | 5.2561 | 0.2895 |
| Std | 136.9467 | 138.1613 | 138.1603 | 20.2953 | 21.1453 | 63.6593 | 75.5081 | 27.4512 |
| Skewness | 37.2082 | 39.0282 | 39.0293 | 39.2769 | 38.043 | 32.4657 | 39.3031 | 8.5134 |
| Kurtosis | 1454.6906 | 1560.1182 | 1560.1759 | 1574.6315 | 1504.5284 | 1158.7191 | 1576.1005 | 748.2635 |
| JB () | 14,683 *** | 16,887 *** | 16,888 *** | 17,202 *** | 15,706 *** | 9321 *** | 17,234 *** | 3877 *** |
| ADF | −9.405 *** | −9.720 *** | −9.722 *** | −9.928 *** | −9.224 *** | −8.928 *** | −9.985 *** | −13.87 *** |
| Q(10) | 151 *** | 58.8 *** | 58.7 *** | 37 *** | 79.3 *** | 348 *** | 53.5 *** | 474 *** |
| Q(20) | 164 *** | 68.2 *** | 68.1 *** | 40.9 *** | 87.8 *** | 376 *** | 58.1 *** | 486 *** |
| Model | AIC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | 0.223 ** | 0.318 *** | 0.365 *** | 0.214 *** | 0.519 | 4429.3 | |||
| HAR-RV-J | 0.222 ** | 0.341 *** | 0.307 *** | 0.259 *** | −0.397 ** | −0.947 ** | −0.678 | 0.523 | 4423.4 |
| HAR-RV-TCJ | 0.223 ** | 0.341 *** | 0.304 *** | 0.256 *** | −0.05 | 1.268 *** | −0.431 | 0.523 | 4421.1 |
| HAR-RV-RS | 0.251 ** | 0.051 | 0.493 ** | 0.965 ** | 0.582 *** | 0.456 * | −0.531 | 0.452 | 5124.2 |
| HAR-RV-SJ | 0.297 ** | 0.274 *** | 0.340 *** | 0.238 *** | −0.232 *** | 0.182 | 0.458 | 0.512 | 4450.7 |
| Model | AIC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | 0.247 *** | 0.312 *** | 0.488 *** | 0.091 * | 0.567 | 4582.4 | |||
| HAR-RV-J | 0.318 *** | 0.351 *** | 0.513 *** | 0.093 | −0.327 ** | 0.523 | 0.874 | 0.574 | 4564.3 |
| HAR-RV-TCJ | 0.318 *** | 0.348 *** | 0.505 *** | 0.092 | 0.028 | −0.01 | 0.021 | 0.573 | 4565.6 |
| HAR-RV-RS | 0.292 ** | 0.519 *** | 0.23 | 0.552 * | 0.155 | 0.931 *** | −0.405 | 0.428 | 5608.5 |
| HAR-RV-SJ | 0.247 *** | 0.279 *** | 0.478 *** | 0.131 ** | 0.088 * | −0.007 | 0.312 | 0.574 | 4564.7 |
| New Energy | State 1 (s1) | State 2 (s2) | Coal | State 1 (s1) | State 2 (s2) |
|---|---|---|---|---|---|
| state1 (s1) | 0.837 | 0.125 | state1 (s1) | 0.859 | 0.143 |
| state2 (s2) | 0.163 | 0.875 | state2 (s2) | 0.141 | 0.857 |
| Model 1 | AIC | Loglike | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | 0.997 *** | 0.335 ** | 0.333 ** | 0.141 | 0.343 | 3214.8 | −1599.4 | |||
| 0.241 *** | −0.015 | 0.279 *** | 0.292 *** | 0.824 | ||||||
| HAR-RV-J | 1.016 *** | 0.316 *** | 0.215 * | 0.154 | −0.669 ** | 1.255 * | 1.368 | 0.333 | 3202.8 | −1587.4 |
| 0.268 *** | 0.118 *** | 0.243 *** | 0.333 *** | 0.068 | −0.057 | −1.571 *** | 0.839 | |||
| HAR-RV-TCJ | 1.010 *** | 0.317 *** | 0.216 * | 0.151 | −0.348 | 1.485 ** | 1.484 | 0.335 | 3201.8 | −1586.9 |
| 0.267 *** | 0.117 *** | 0.240 *** | 0.333 *** | 0.189 | 0.196 | −1.245 *** | 0.84 | |||
| HAR-RV-RS | 1.327 *** | 0.173 | 0.409 | 0.446 | 0.599 *** | 0.352 | −0.174 | 0.268 | 3925.3 | −1948.6 |
| 0.292 *** | −0.379 *** | 0.593 *** | 0.202 | 0.277 *** | 0.290 * | 0.215 | 0.734 | |||
| HAR-RV-SJ | 1.427 *** | 0.230 *** | 0.210 * | 0.248 * | −0.223 ** | 0.181 | 0.06 | 0.261 | 3209.2 | −1590.6 |
| 0.230 *** | 0.097 *** | 0.377 *** | 0.156 *** | −0.145 *** | 0.366 *** | 0.510 *** | 0.843 |
| Model 1 | AIC | Loglike | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | 1.078 *** | 0.228 *** | 0.494 *** | 0.056 | 0.414 | 3484.6 | −1734.3 | |||
| 0.219 *** | 0.155 *** | 0.192 *** | 0.155 *** | 0.776 | ||||||
| HAR-RV-J | 1.284 *** | 0.291 *** | 0.477 *** | 0.103 | −0.404 * | −0.584 | −0.747 | 0.434 | 3476.1 | −1724.0 |
| 0.230 *** | 0.143 *** | 0.212 *** | 0.175 *** | 0.016 | −0.055 | −0.314 | 0.786 | |||
| HAR-RV-TCJ | 1.294 *** | 0.287 *** | 0.473 *** | 0.102 | −0.11 | −0.078 | −0.652 | 0.433 | 3474.3 | −1723.1 |
| 0.230 *** | 0.143 *** | 0.212 *** | 0.174 *** | 0.159 * | 0.156 | −0.147 | 0.786 | |||
| HAR-RV-RS | 1.823 *** | 0.469 ** | −0.014 | 0.306 | −0.086 | 1.512 *** | −0.335 | 0.304 | 4384.9 | −2178.4 |
| 0.274 *** | 0.206 *** | −0.083 | 0.581 *** | 0.178 *** | 0.256 ** | −0.061 | 0.675 | |||
| HAR-RV-SJ | 1.144 *** | 0.225 *** | 0.505 *** | 0.053 | 0.11 | −0.048 | 0.017 | 0.45 | 3470.2 | −1721.1 |
| 0.250 *** | 0.122 *** | 0.112 *** | 0.197 *** | −0.054 * | 0.202 *** | 0.235 ** | 0.746 |
| New Energy | State 1 (s1) | State 2 (s2) | Coal | State 1 (s1) | State 2 (s2) |
|---|---|---|---|---|---|
| state1 (s1) | 0.836 | 0.125 | state1 (s1) | 0.857 | 0.140 |
| state2 (s2) | 0.163 | 0.875 | state2 (s2) | 0.143 | 0.860 |
| Model | State | AIC | Loglike | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | S1 | 1.088 *** | 0.256 *** | 0.383 *** | 0.172 | −0.007 | 0.326 | 3211.2 | −1595.6 | ||||
| S2 | 0.223 *** | 0.121 *** | 0.190 *** | 0.283 *** | 0.000 | 0.832 | |||||||
| HAR-RV-J | S1 | 0.934 *** | 0.375 *** | 0.278 ** | 0.098 | −0.545 ** | 0.984 | −0.741 | −0.014 ** | 0.096 ** | 0.369 | 3201.1 | −1580.9 |
| S2 | 0.254 *** | −0.023 | 0.282 *** | 0.356 *** | 0.221 | −0.15 | −0.959 ** | 0.000 | −0.001 | 0.839 | |||
| HAR-RV-TCJ | S1 | 0.990 *** | 0.335 *** | 0.211* | 0.128 | −0.336 | 1.699 ** | 1.69 | −0.016 ** | 0.083 * | 0.351 | 3210.5 | −1587.3 |
| S2 | 0.267 *** | 0.116 *** | 0.239 *** | 0.334 *** | 0.189 | 0.182 | −1.215 *** | 0.000 | 0.000 | 0.842 | |||
| HAR-RV-RS | S1 | 1.337 *** | 0.17 | 0.398 | 0.405 | 0.591 *** | 0.366 | −0.086 | −0.027 | 0.013 | 0.275 | 3201.1 | −1582.6 |
| S2 | 0.291 *** | −0.379 *** | 0.597 *** | 0.219 | 0.278 *** | 0.275 * | 0.212 | −0.001 | 0.001 | 0.737 | |||
| HAR-RV-SJ | S1 | 1.437 *** | 0.232 *** | 0.204 * | 0.263 ** | −0.223 ** | 0.188 | 0.034 | −0.006 | −0.01 | 0.268 | 3925.2 | −1944.6 |
| S2 | 0.230 *** | 0.094 *** | 0.377 *** | 0.157 *** | −0.150 *** | 0.384 *** | 0.512 *** | 0.000 | −0.001 | 0.845 |
| Model | State | AIC | Loglike | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HAR-RV | S1 | 1.087 *** | 0.231 *** | 0.492 *** | 0.055 | −0.003 | 0.414 | 3486.2 | −1733.1 | ||||
| S2 | 0.221 *** | 0.159 *** | 0.189 *** | 0.153 *** | 0.000 | 0.779 | |||||||
| HAR-RV-J | S1 | 1.322 *** | 0.254 *** | 0.530 *** | 0.106 | −0.302 | −0.767 | −0.663 | −0.003 | −0.007 | 0.441 | 3187.6 | −1575.8 |
| S2 | 0.229 *** | 0.232 *** | 0.118 * | 0.110 ** | −0.066 * | −0.003 | 0.388 | 0.000 | 0.000 | 0.767 | |||
| HAR-RV-TCJ | S1 | 1.313 *** | 0.282 *** | 0.462 *** | 0.133 | −0.136 | 0.051 | −1.154 | 0.033 * | −0.072 | 0.44 | 3180.4 | −1572.2 |
| S2 | 0.233 *** | 0.130 *** | 0.229 *** | 0.173 *** | 0.172 * | 0.104 | −0.152 | 0.000 | 0.000 | 0.787 | |||
| HAR-RV-RS | S1 | 1.785 *** | 0.459 ** | −0.062 | 0.412 | −0.094 | 1.541 *** | −0.402 | −0.178 * | 0.178 ** | 0.314 | 4383.4 | −2173.7 |
| S2 | 0.278 *** | 0.209 *** | −0.085 | 0.571 | 0.570 *** | 0.256 ** | −0.054 | −0.001 | 0.000 | 0.678 | |||
| HAR-RV-SJ | S1 | 1.170 *** | 0.228 *** | 0.503 *** | 0.05 | 0.11 | −0.052 | 0.018 | −0.005 | −0.004 | 0.45 | 3475.1 | −1719.5 |
| S2 | 0.254 *** | 0.124 *** | 0.111 *** | 0.195 *** | −0.055 * | 0.201 *** | 0.230 ** | 0.000 | 0.000 | 0.749 |
| Methods | H = 1 | H = 5 | ||||
|---|---|---|---|---|---|---|
| MAE | QLIKE | MAPE | MAE | QLIKE | MAPE | |
| HAR | 0.522 | 0.908 | 51.5 | 0.527 | 0.907 | 52.1 |
| MS-HAR | 0.512 | 0.902 | 48.3 | 0.523 | 0.897 | 49.7 |
| MS-HAR-TVP | 0.511 | 0.903 | 47.8 | 0.524 | 0.900 | 49.2 |
| HAR-RS | 1.000 | 1.000 | 98.6 | 0.995 | 1.000 | 97.8 |
| MS-HAR-RS | 0.997 | 0.985 | 95.2 | 0.996 | 0.976 | 94.6 |
| MS-HAR-TVP-RS | 0.999 | 0.989 | 96.1 | 1.000 | 0.980 | 95.8 |
| HAR-SJ | 0.545 | 0.919 | 53.8 | 0.549 | 0.920 | 54.2 |
| MS-HAR-SJ | 0.542 | 0.917 | 52.6 | 0.552 | 0.920 | 53.9 |
| MS-HAR-TVP-SJ | 0.533 | 0.918 | 51.4 | 0.546 | 0.919 | 52.7 |
| HAR-J | 0.524 | 0.909 | 50.8 | 0.529 | 0.909 | 51.6 |
| MS-HAR-J | 0.515 | 0.902 | 47.9 | 0.521 | 0.897 | 49.1 |
| MS-HAR-TVP-J | 0.517 | 0.901 | 45.2 | 0.526 | 0.896 | 48.3 |
| HAR-TCJ | 0.522 | 0.909 | 50.9 | 0.528 | 0.909 | 51.5 |
| MS-HAR-TCJ | 0.514 | 0.904 | 48.2 | 0.524 | 0.899 | 49.4 |
| MS-HAR-TVP-TCJ | 0.518 | 0.902 | 46.7 | 0.524 | 0.896 | 48.1 |
| Methods | H = 1 | H = 5 | ||||
|---|---|---|---|---|---|---|
| MAE | QLIKE | MAPE | MAE | QLIKE | MAPE | |
| HAR | 0.490 | 0.923 | 48.9 | 0.486 | 0.925 | 49.3 |
| MS-HAR | 0.497 | 0.905 | 46.8 | 0.495 | 0.909 | 47.5 |
| MS-HAR-TVP | 0.497 | 0.904 | 46.2 | 0.497 | 0.908 | 47.1 |
| HAR-RS | 0.999 | 1.000 | 97.3 | 0.998 | 1.000 | 96.8 |
| MS-HAR-RS | 1.000 | 0.975 | 94.5 | 1.000 | 0.983 | 93.9 |
| MS-HAR-TVP-RS | 0.992 | 0.977 | 95.1 | 0.999 | 0.984 | 94.7 |
| HAR-SJ | 0.498 | 0.934 | 51.2 | 0.491 | 0.934 | 50.8 |
| MS-HAR-SJ | 0.488 | 0.907 | 48.6 | 0.496 | 0.914 | 49.3 |
| MS-HAR-TVP-SJ | 0.489 | 0.906 | 47.9 | 0.497 | 0.912 | 48.7 |
| HAR-J | 0.489 | 0.926 | 49.7 | 0.485 | 0.925 | 49.5 |
| MS-HAR-J | 0.486 | 0.909 | 46.5 | 0.488 | 0.912 | 47.2 |
| MS-HAR-TVP-J | 0.483 | 0.910 | 44.8 | 0.487 | 0.913 | 46.6 |
| HAR-TCJ | 0.490 | 0.925 | 49.6 | 0.486 | 0.925 | 49.4 |
| MS-HAR-TCJ | 0.485 | 0.909 | 46.3 | 0.486 | 0.913 | 47.0 |
| MS-HAR-TVP-TCJ | 0.481 | 0.910 | 42.8 | 0.484 | 0.913 | 45.9 |
| Methods | H = 1 | H = 5 | ||||
|---|---|---|---|---|---|---|
| MAE () | QLIKE () | DM Test (p-Value) | MAE () | QLIKE () | DM Test (p-Value) | |
| HAR | 0.575 | 0.124 | – | 0.683 | 0.000 | – |
| MS-HAR | 0.973 | 0.841 | 0.156 | 0.757 | 0.647 | 0.234 |
| MS-HAR-TVP | 1.000 | 0.631 | 0.089 | 0.757 | 0.223 | 0.112 |
| HAR-RS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MS-HAR-RS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MS-HAR-TVP-RS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HAR-SJ | 0.041 | 0.000 | 0.428 | 0.076 | 0.000 | 0.385 |
| MS-HAR-SJ | 0.000 | 0.000 | 0.267 | 0.000 | 0.000 | 0.312 |
| MS-HAR-TVP-SJ | 0.271 | 0.000 | 0.189 | 0.094 | 0.000 | 0.245 |
| HAR-J | 0.502 | 0.016 | 0.523 | 0.623 | 0.000 | 0.467 |
| MS-HAR-J | 0.828 | 0.797 | 0.178 | 1.000 | 0.824 | 0.142 |
| MS-HAR-TVP-J | 0.766 | 1.000 | 0.032 ** | 0.733 | 1.000 | 0.018 ** |
| HAR-TCJ | 0.561 | 0.000 | 0.498 | 0.669 | 0.000 | 0.445 |
| MS-HAR-TCJ | 0.827 | 0.543 | 0.165 | 0.753 | 0.000 | 0.198 |
| MS-HAR-TVP-TCJ | 0.686 | 0.693 | 0.041 ** | 0.722 | 0.847 | 0.025 ** |
| Methods | H = 1 | H = 5 | ||||
|---|---|---|---|---|---|---|
| MAE () | QLIKE () | DM Test (p-Value) | MAE () | QLIKE () | DM Test (p-Value) | |
| HAR | 0.421 | 0.000 | – | 0.823 | 0.088 | – |
| MS-HAR | 0.018 | 0.890 | 0.245 | 0.273 | 0.942 | 0.198 |
| MS-HAR-TVP | 0.000 | 1.000 | 0.134 | 0.212 | 1.000 | 0.156 |
| HAR-RS | 0.386 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MS-HAR-RS | 0.386 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MS-HAR-TVP-RS | 0.386 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HAR-SJ | 0.101 | 0.000 | 0.512 | 0.557 | 0.000 | 0.478 |
| MS-HAR-SJ | 0.382 | 0.000 | 0.334 | 0.105 | 0.000 | 0.389 |
| MS-HAR-TVP-SJ | 0.324 | 0.721 | 0.267 | 0.000 | 0.635 | 0.312 |
| HAR-J | 0.499 | 0.000 | 0.489 | 0.795 | 0.000 | 0.523 |
| MS-HAR-J | 0.656 | 0.234 | 0.223 | 0.722 | 0.811 | 0.189 |
| MS-HAR-TVP-J | 0.862 | 0.090 | 0.048 ** | 0.925 | 0.767 | 0.067 * |
| HAR-TCJ | 0.426 | 0.000 | 0.467 | 0.886 | 0.014 | 0.501 |
| MS-HAR-TCJ | 0.757 | 0.207 | 0.198 | 0.827 | 0.782 | 0.176 |
| MS-HAR-TVP-TCJ | 1.000 | 0.000 | 0.028 ** | 1.000 | 0.705 | 0.035 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H. Industry Index Volatility Spillovers and Forecasting from Crude Oil Prices Based on the MS-HAR-TVP Model. Mathematics 2025, 13, 3723. https://doi.org/10.3390/math13223723
Yu H. Industry Index Volatility Spillovers and Forecasting from Crude Oil Prices Based on the MS-HAR-TVP Model. Mathematics. 2025; 13(22):3723. https://doi.org/10.3390/math13223723
Chicago/Turabian StyleYu, Haoqing. 2025. "Industry Index Volatility Spillovers and Forecasting from Crude Oil Prices Based on the MS-HAR-TVP Model" Mathematics 13, no. 22: 3723. https://doi.org/10.3390/math13223723
APA StyleYu, H. (2025). Industry Index Volatility Spillovers and Forecasting from Crude Oil Prices Based on the MS-HAR-TVP Model. Mathematics, 13(22), 3723. https://doi.org/10.3390/math13223723






