High-Resolution Numerical Scheme for Simulating Wildland Fire Spread

Abstract

Predicting wildland fire spread requires numerical schemes that can resolve sharp gradients at the fireline while remaining stable and efficient on practical grids. We develop a compact high-order finite-difference scheme for Hamilton–Jacobi level-set formulations of wildfire propagation, based on the anisotropic spread law of Mallet and co-authors. The spatial discretization employs a compact finite-difference derivative scheme to achieve spectral-like resolution with narrow stencils, improving accuracy and boundary robustness compared with wide-stencil ENO/WENO reconstructions. To control high-frequency artifacts intrinsic to non-dissipative compact schemes, an implicit high-order low-pass filter is incorporated and activated after each Runge–Kutta stage. Convergence is verified on the eikonal expanding-circle benchmark, where the method attains the expected high-order spatial accuracy as the grid is refined. The proposed scheme is then applied to wind-driven wildfire simulations governed by Mallet’s non-convex Hamiltonian, including a single ignition under moderate and strong wind. A complex topology test case is also considered, involving two ignitions that merge into a single front with the evolution of an internal unburnt island. The results demonstrate that the proposed method accurately reproduces fireline evolution even on coarse grids, achieving accuracy comparable to fifth-order WENO while maintaining superior fidelity in complex fireline topologies, where it better resolves multi-front interactions and topological changes in the fireline. This makes the method an efficient, accurate alternative for level-set wildfire modeling and readily integrable into existing frameworks.

1. Introduction

Wildland fires are among the most damaging natural hazards, producing significant ecological, economic, and social impacts worldwide [1,2,3]. Their dynamics result from complex multiscale interactions among vegetation, topography, and meteorological conditions [4]. Accurate simulation of wildfire propagation is therefore a problem of major scientific and societal importance, underpinning efforts in risk management, fire suppression, and climate impact assessment. Despite considerable progress, predicting the evolution of the fireline under realistic conditions remains challenging due to the strong nonlinearity, anisotropy, and multiscale coupling that characterize wildland fire behavior [5,6].

A range of modeling approaches have been proposed to predict wildfire spread. Empirical and semi-empirical models are widely used for operational purposes due to their simplicity, but they can lack robustness when applied outside their calibration range [7]. Physics-based approaches capture fundamental processes such as heat transfer and combustion but remain computationally prohibitive for large-scale applications [1]. Between these extremes, interface-tracking methods have emerged as a promising compromise, combining computational tractability with the ability to capture complex fireline geometries.

Among interface-tracking approaches, the level set method [8,9] provides a robust and versatile framework for modeling wildfire propagation. It represents the fire perimeter implicitly as the zero contour of a higher-dimensional scalar function, whose evolution is governed by a Hamilton–Jacobi (HJ) equation. The normal propagation speed in this equation is prescribed through a spread law that encodes the dependence of the fire-front velocity on wind and terrain conditions. In this context, the semi-empirical anisotropic model proposed by Mallet and co-authors [10] has attracted significant attention, as it captures the essential directional effects of wind-driven spread while remaining efficient for numerical implementation. However, the resulting Hamiltonians are generally non-convex, which complicates their numerical treatment and limits the applicability of fast-marching techniques [11], thereby motivating the use of time-dependent level set solvers [12].

Several modeling frameworks have successfully implemented the level set formulation to represent wildfire propagation within coupled atmosphere–fire simulations. The Weather Research and Forecasting model coupled with the SFIRE module (WRF–SFIRE) [13] is among the first operational frameworks to employ a level set formulation for wildfire propagation. It uses the semi-empirical spread law introduced by Mallet and co-authors [10]. In its original implementation, the fire spread equation was solved using a low-order Essentially Non-Oscillatory (ENO) scheme, which provided stability but introduced noticeable numerical diffusion that smoothed the advancing fireline. Subsequent developments have focused on improving numerical accuracy through higher-order reconstructions, leading to the adoption of Weighted ENO (WENO) schemes for the coupled atmosphere–fire system [14]. Muñoz-Esparza et al. [14] have performed a systematic comparison between first-order ENO (ENO1), third-order WENO (WENO3), and fifth-order WENO (WENO5) schemes, demonstrating that the fifth-order formulation achieves the most accurate front representation and improved consistency between the meteorological and fire fields.

Although higher-order ENO and WENO schemes have substantially improved the accuracy of level set solvers in wildfire models, they exhibit several drawbacks when applied to large-scale simulations. Their reliance on wide spatial stencils complicates boundary treatment, especially near complex topography or domain edges, and increases computational cost. In addition, their inherent numerical dissipation can attenuate fine-scale gradients of the fireline, reducing front sharpness in heterogeneous fuel or wind conditions. In comparison with traditional finite-difference methods, compact finite-difference schemes [15,16,17] provide spectral-like resolution with narrow stencils, enabling efficient implementation near boundaries. Compact schemes compute spatial derivatives implicitly and in a coupled manner along each coordinate line, achieving high overall accuracy without requiring operations that involve all grid points. This approach combines the robustness of local finite-difference discretizations with the accuracy of spectral methods, while the resulting tri-diagonal linear systems can be solved efficiently [18,19]. Beyond their computational efficiency, compact schemes also exhibit improved resolution in wave space [15,17,20]. This enables a more accurate representation of short spatial scales, an essential feature for wildfire fronts that evolve over a wide range of scales. Nevertheless, because compact schemes are inherently non-dissipative, they may develop oscillations in regions with steep gradients or near boundaries; thus, stabilization techniques such as high-order implicit filtering are required to ensure numerical robustness [20,21].

In this work, we address these limitations by introducing a high-order compact finite-difference scheme for Hamilton–Jacobi equations applied to wildfire modeling. A filtering procedure is enabled when oscillations occur, preserving high-order accuracy in smooth regions while ensuring stability. We validate the method through convergence studies on the eikonal equation and apply it to wildfire propagation scenarios driven by Mallet’s spread law, including single ignition, multiple ignitions, and island topologies. Systematic comparisons are performed with ENO1–3 and WENO5 schemes, implemented through the ToolboxLS package [22].

To this end, the principal contributions of this paper can be summarized as follows:

• Development of a compact high-order finite-difference scheme for Hamilton–Jacobi equations in wildfire applications with a dissipative boundary closure.
• Incorporation of a filtering mechanism to suppress spurious oscillations and stabilize the inherently non-dissipative scheme.
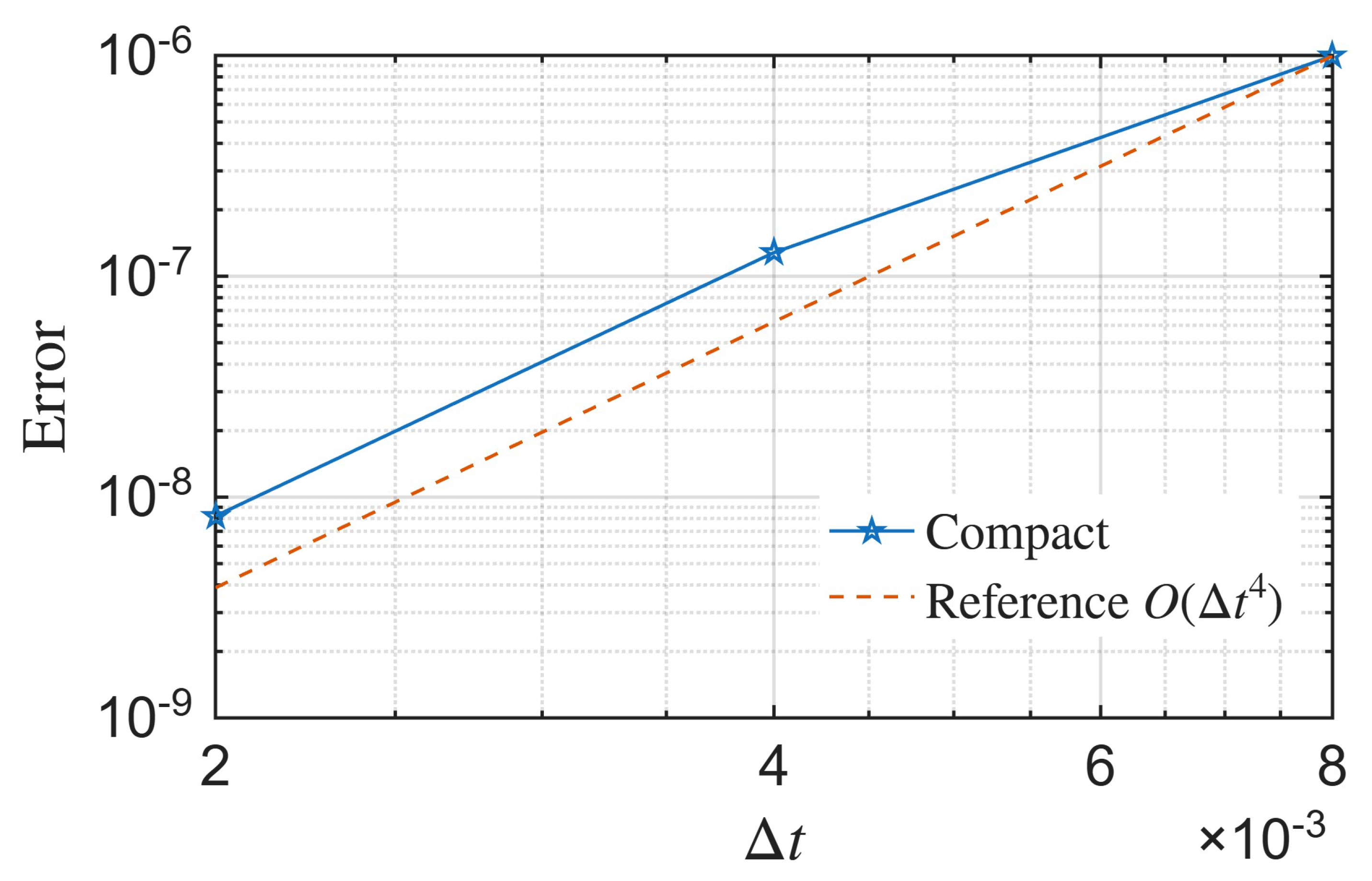
• Demonstration of convergence properties on a canonical benchmark problem.
• Simulation of realistic wildfire scenarios using Mallet’s anisotropic spread law.
• A comparative evaluation with ENO and WENO schemes is conducted, highlighting the proposed method’s accuracy and efficiency, particularly in complex topologies.

This paper is organized as follows: Section 2 introduces the wildfire spread model. Section 3 presents the numerical methodology, including compact discretization and filtering. Section 4 reports convergence studies and wildfire simulations. Finally, Section 5 summarizes the findings and outlines perspectives for future work.

2. Materials and Methods

2.1. Front Propagation Function for Wildland Fires

Even with complete and precise knowledge of topography, vegetation, and meteorological conditions, the physical mechanisms governing wildland fire spread are not yet fully understood. In particular, it remains difficult to derive from first principles accurate and generalizable expressions for the rate of spread based solely on environmental inputs. As a result, empirical and semi-empirical formulations remain essential for both operational and research applications.

A notable contribution in this direction is the model of Fendell and Wolff [23], which decomposes fire propagation into three distinct regions of the front—head, flanks, and rear—each governed by different dominant mechanisms, especially regarding the influence of wind. The spread velocity is then interpolated as a function of orientation relative to the wind direction, producing a strongly anisotropic fire-front shape (see Figure 1 in [10]).

For practical implementation within a level-set framework, a simplified version of the Fendell–Wolff model is advantageous. Mallet proposed such a reduction to preserve the asymmetric geometry of the propagating fire front while facilitating calibration and numerical treatment. Based on numerical experiments with the Multivac code [24], the following formulation is adopted:

$$\begin{array}{cc}F(U,\theta )={\epsilon }_0+a\sqrt{U{cos}^n\theta },\hfill & \mathrm{if}\left|\theta \right|\le {\displaystyle \frac{\pi }{2}},\hfill \\ F(U,\theta )={\epsilon }_0\left(\alpha +(1-\alpha )|sin\theta |\right),\hfill & \mathrm{if}\left|\theta \right|>{\displaystyle \frac{\pi }{2}},\hfill \end{array}$$

(1)

where the fire-front velocity $F(U,\theta )$ depends on the wind speed $U\ge 0$ and the orientation angle $\theta \in (-\pi ,\pi ]$ between the wind vector and the outward normal to the front.

ModelParameters

• ${\epsilon }_0>0$: Baseline spread velocity, corresponding to the flank rate of spread in the absence of wind.
• $a>0$: Scaling coefficient that modulates wind-driven acceleration at the head.
• $n\ge 1$: Exponent governing angular dependence at the head; higher values sharpen the transition between head and flank regimes. In this work, $n=3$ is adopted following the conclusion of Mallet et al. [10], wherein numerical experiments conducted with the level-set solver Multivac led to the selection of this value to reproduce the observed anisotropic wildfire perimeter.
• $\alpha \in [0,1]$: Ratio of rear-to-flank spread. The rear velocity is $\alpha {\epsilon }_0$, while the flank velocity remains ${\epsilon }_0$.

This reduction highlights the dominant influence of wind at the head of the fire front while keeping flank and rear velocities essentially wind-independent. Such an assumption reflects both experimental evidence of weak wind sensitivity in these regions and the limited reliability of available data. Despite its simplicity, the model captures the main asymmetries of fire spread and ensures continuity across the angular domain. Moreover, the reduced number of parameters facilitates calibration, either manually or through optimization methods. All simulations in the present study employ this simplified Mallet formulation.

2.2. Level Set Method

The level-set method, originally introduced by Osher and Sethian [8], is an Eulerian technique for tracking moving interfaces and propagating fronts. It has since become a standard tool in computational physics, with comprehensive treatments provided by Sethian [9]. In the context of wildfire modeling, level-set formulations have been successfully applied by Mallet and co-workers [10,24], where they proved particularly effective for handling the complex geometries and topological changes that arise in fire-front propagation.

Consider a fire perimeter that evolves from an initial curve ${\Gamma }_0$ at time $t=0$ to a final curve $\Gamma \left(T_f\right)$ at time $T_f$. At any intermediate time $t\in [0,T_f]$, the front is represented as the set of points $\Gamma \left(t\right)$ in ${\mathbb{R}}^N$. Each point $X\in \Gamma \left(t\right)$ moves in the normal direction with speed $F(X,\Gamma ,t)$, which may depend on position, time, and local front properties such as orientation relative to wind.

To represent this evolution, a level-set function $\phi :{\mathbb{R}}^N\times [0,T_f]\to \mathbb{R}$ is introduced, whose zero contour coincides with the moving front:

$$\Gamma \left(t\right)=\{x\in {\mathbb{R}}^N|\phi (x,t)=0\}.$$

(2)

The dynamics of $\phi$ are governed by a Hamilton–Jacobi equation of the form

$${\phi }_t(x,t)+F(x,\phi (x,t),t){\parallel \nabla \phi (x,t)\parallel }_2=0,x\in {\mathbb{R}}^N,t\in [0,T_f],$$

(3)

where the normal velocity F is extended from the fire perimeter to the entire computational domain through its dependence on $\phi$.

For numerical convenience, $\phi$ is often initialized as a signed-distance function, i.e., the Euclidean distance to the front $\Gamma \left(t\right)$, positive outside and negative inside:

$$\phi (x,t)=\left\{\begin{array}{cc}{d}_{\Gamma \left(t\right)}\left(x\right),\hfill & x\mathrm{outside}\Gamma \left(t\right),\hfill \\ -d_{\Gamma \left(t\right)}\left(x\right),\hfill & x\mathrm{inside}\Gamma \left(t\right),\hfill \end{array}\right.$$

(4)

with initial condition

$$\phi (x,0)=\left\{\begin{array}{cc}{d}_{{\Gamma }_0}\left(x\right),\hfill & x\mathrm{outside}{\Gamma }_0,\hfill \\ -d_{{\Gamma }_0}\left(x\right),\hfill & x\mathrm{inside}{\Gamma }_0.\hfill \end{array}\right.$$

(5)

Equations (3)–(5) define the initial-value problem for front evolution. Since Hamilton–Jacobi equations may admit multiple weak solutions, the physically relevant one is the viscosity solution, as defined by Crandall and Lions [25], which ensures uniqueness and stability under mild assumptions on the speed function F. In the pioneering work of Mallet et al. [10], the Hamilton–Jacobi equation governing the level-set formulation was discretized using a first-order Lax–Friedrichs scheme. This ensured stability for the non-convex Hamiltonian introduced by the anisotropic spread law but produced noticeably diffused fire perimeters. WENO schemes combine multiple local reconstructions through nonlinear weights that adapt to the local smoothness of the solution, achieving higher accuracy while avoiding spurious oscillations [26,27]. Later implementations, such as in WRF–SFIRE [14], adopted higher-order WENO schemes to improve accuracy. Among these, the fifth-order WENO formulation [14] provided the most accurate and stable fireline evolution under complex wind and terrain conditions. Although high-order WENO schemes have become the established standard for solving Hamilton–Jacobi equations in wildfire modeling, they present several limitations when applied to large-scale or high-resolution simulations. Their reliance on wide stencils complicates the treatment of boundary conditions, particularly in domains with complex topography, and increases communication overhead in parallel implementations. Moreover, the intrinsic numerical dissipation of these upwind-based reconstructions can blur fine-scale features of the fireline, which are critical for accurate prediction of spread dynamics in heterogeneous landscapes. An alternative approach is to employ high-order compact finite-difference schemes for the spatial discretization. The full discretization procedure is detailed in Section 3.

3. Numerical Methodology

In two dimensions, the governing Hamilton–Jacobi equation for wildfire propagation can be written as

$${\displaystyle \frac{\partial \phi }{\partial t}}+H\left(x,y,t,\nabla \phi \right)=0,(x,y)\in \Omega \subset {\mathbb{R}}^2,t\in (0,T],$$

(6)

with initial condition $\phi (x,y,0)={\phi }_0(x,y)$. The fire perimeter at time t is then defined as the zero level set $\Gamma \left(t\right)=\left\{\right(x,y)\in \Omega :\phi (x,y,t)=0\}$.

Let $\mathbf{U}(x,y,t)\in {\mathbb{R}}^2$ denote the local wind vector, with magnitude $U=\parallel \mathbf{U}\parallel$ and unit direction $\widehat{\mathbf{U}}=\mathbf{U}/U$. Where $\nabla \phi \ne 0$, the outward unit normal to the front is given by

$$\mathbf{n}(x,y,t)={\displaystyle \frac{\nabla \phi (x,y,t)}{\parallel \nabla \phi (x,y,t)\parallel }}.$$

(7)

Since the spread law depends on the orientation of the front with respect to the wind, the directional quantities $cos\theta$ and $|sin\theta |$ can be expressed directly as

$$cos\theta (x,y,t)=\mathbf{n}·\widehat{\mathbf{U}}={\displaystyle \frac{{\phi }_x{\widehat{U}}_x+{\phi }_y{\widehat{U}}_y}{\sqrt{{\phi }_x^2+{\phi }_y^2}}},|sin\theta |=\sqrt{1-{(\mathbf{n}·\widehat{\mathbf{U}})}^2}.$$

(8)

The rate of spread F is defined by the anisotropic propagation model of Section 2, depending on the wind magnitude U and the local orientation through $cos\theta$ and $|sin\theta |$. The Hamiltonian thus takes the form

$$H(x,y,t,p)=F\left(U(x,y,t),cos\theta (p,\widehat{\mathbf{U}}),|sin\theta (p,\widehat{\mathbf{U}})|\right)\parallel p\parallel ,p=\nabla \phi (x,y,t),$$

(9)

which leads to the explicit two-dimensional HJ equation

$${\phi }_t+F(U,cos\theta ,|sin\theta \left|\right)\sqrt{{\phi }_x^2+{\phi }_y^2}=0.$$

(10)

The initial condition is prescribed by an ignition set ${\Gamma }_0$, with $\phi (x,y,0)$ defined as the signed distance function to ${\Gamma }_0$. At the boundaries of the domain, homogeneous Neumann conditions are imposed to avoid spurious reflections:

$${\displaystyle \frac{\partial \phi }{\partial n}}=0\mathrm{on}\partial \Omega .$$

(11)

The numerical solution of Equation (10) is performed using a high-order compact finite-difference scheme for spatial derivatives and a fourth-order explicit Runge–Kutta scheme for time integration.

3.1. Higher-Order Spatial and Temporal Discretizations

Assuming a Cartesian discretization in each spatial direction, the computational domain $\Omega \equiv [0,L_x]\times [0,L_y]$ is partitioned into nodes with spacings

$$\Delta x={\displaystyle \frac{L_x}{N_x-1}},\Delta y={\displaystyle \frac{L_y}{N_y-1}},$$

where $N_x$ and $N_y$ are the number of points in x and y. Grid locations are $(x_i,y_j)$ with

$$x_i=(i-1)\Delta x,y_j=(j-1)\Delta y,1\le i\le N_x,1\le j\le N_y.$$

Boundary nodes $i\in \{1,N_x\}$ and $j\in \{1,N_y\}$ coincide with the physical boundary $\partial \Omega$. A collocated layout is used: $\phi$ and its discrete derivatives are stored at the same nodes.

High-order compact finite differences [15] are used to approximate the spatial derivatives of $\phi (x,y,t)$. These schemes compute derivatives implicitly and in a coupled manner along grid lines by solving tridiagonal systems.

We next summarize the compact formulas employed for the first derivatives in the HJ Equation (6).

On a uniform 1D grid, the interior centered compact relation for a smooth function $\varphi \left(x\right)$ reads

$$\beta {\varphi }_{i-2}^{\prime }+\alpha {\varphi }_{i-1}^{\prime }+{\varphi }_i^{\prime }+\alpha {\varphi }_{i+1}^{\prime }+\beta {\varphi }_{i+2}^{\prime }=c{\displaystyle \frac{{\varphi }_{i+3}-{\varphi }_{i-3}}{6h}}+b{\displaystyle \frac{{\varphi }_{i+2}-{\varphi }_{i-2}}{4h}}+a{\displaystyle \frac{{\varphi }_{i+1}-{\varphi }_{i-1}}{2h}},$$

(12)

with $h=\Delta x$. Fourth-order accuracy requires

$$a+b+c=1+2\alpha +2\beta ,a+2^{2}b+3^{2}c=2{\displaystyle \frac{3!}{2!}}(\alpha +2^2\beta ),$$

(13)

and the truncation error of the right-hand side of (12) is

$${\displaystyle \frac{4}{5!}}(-1+3\alpha -12\beta +10c)h^4{\varphi }^{\left(5\right)}.$$

Setting $\beta =0$ and $c=0$ yields a one-parameter fourth-order family (tridiagonal). With $\alpha =\frac{1}{3}$ the leading error coefficient vanishes and the scheme becomes formally sixth order.

To close the system of equations, suitable boundary closures are introduced which preserve the overall accuracy of the interior scheme. Thus, near boundaries, a two-point implicit closure preserves the tridiagonal structure:

$${\varphi }_1^{\prime }+\tilde{\alpha }{\varphi }_2^{\prime }={\displaystyle \frac{1}{h}}\left(\tilde{a}{\varphi }_1+\tilde{b}{\varphi }_2+\tilde{c}{\varphi }_3+\tilde{d}{\varphi }_4\right),$$

(14)

with third-order accuracy enforced by

$$\tilde{a}=-{\displaystyle \frac{11+2\tilde{\alpha }}{6}},\tilde{b}={\displaystyle \frac{6-\tilde{\alpha }}{2}},\tilde{c}={\displaystyle \frac{2\tilde{\alpha }-3}{2}},\tilde{d}={\displaystyle \frac{2-\tilde{\alpha }}{6}},$$

and truncation error $(2(\tilde{\alpha }-3)/4!)h^3{\varphi }_1^{\left(4\right)}$. Choosing $\tilde{\alpha }=3$ cancels the leading term (formally fourth order) but yields a dispersive leading error; $\tilde{\alpha }\ne 3$ produces a dissipative leading error, which can be advantageous near steep gradients. Guided by the dispersion and dissipation characteristics reported in [15] and by previous implementations in steep-gradient flow problems [21], a dissipative closure with $\tilde{\alpha }=2$ is adopted. Its effectiveness is confirmed herein through numerical comparisons with alternative closure formulations.

In two dimensions, the first derivative along x for a grid function $\varphi (x,y)$ are obtained by solving, for each fixed j,

$${\mathcal{P}}_x{\varphi }_{i,j}^{\prime }={\mathcal{Q}}_x{\varphi }_{i,j},j=1,\dots ,N_y,$$

(15)

where ${\mathcal{P}}_x$ and ${\mathcal{Q}}_x$ are compact finite-difference operators acting on grid functions, i.e.,

$${\mathcal{P}}_x,{\mathcal{Q}}_x:\mathcal{G}\left({\Omega }_h\right)\to \mathcal{G}\left({\Omega }_h\right),$$

with ${\Omega }_h=\Omega \cap {\mathbf{G}}_{\mathit{h}}$ and ${\mathbf{G}}_{\mathit{h}}=\{(x,y):x=(i-1)\Delta x,y=(j-1)\Delta y,i,j\in \mathbb{Z}\}$. The operators ${\mathcal{P}}_x$ and ${\mathcal{Q}}_x$ are defined as follows:

$$\begin{array}{c}\hfill {\mathcal{P}}_x{\varphi }_{i,j}^{\prime }=\left\{\begin{array}{cc}{\varphi }_{1,j}^{\prime }+\tilde{\alpha }{\varphi }_{2,j}^{\prime },\hfill & i=1;\hfill \\ {\varphi }_{1,j}^{\prime }+4{\varphi }_{2,j}^{\prime }+{\varphi }_{3,j}^{\prime }\hfill & i=2;\hfill & \hfill \\ {\varphi }_{i-1,j}^{\prime }+3{\varphi }_{i,j}^{\prime }+{\varphi }_{i+1,j}^{\prime },\hfill & i=3,\dots ,N_x-2;\hfill & \hfill \\ {\varphi }_{N_x-2,j}^{\prime }+4{\varphi }_{N_x-1,j}^{\prime }+{\varphi }_{N_x,j}^{\prime }\hfill & i=N_x-1;\hfill & \hfill \\ \tilde{\alpha }{\varphi }_{N_x-1,j}^{\prime }+{\varphi }_{N_x,j}^{\prime },\hfill & i=N_x,\hfill \end{array}\right.\end{array}$$

(16)

and

$$\begin{array}{c}\hfill {\mathcal{Q}}_x{\varphi }_{i,j}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2h}(\tilde{a}{\varphi }_{1,j}+\tilde{b}{\varphi }_{2,j}+\tilde{c}{\varphi }_{3,j}+\tilde{d}{\varphi }_{4,j}),}\hfill & i=1;\hfill \\ {\displaystyle \frac{3}{h}({\varphi }_{3,j}-{\varphi }_{1,j}),}\hfill & i=2;\hfill \\ {\displaystyle \frac{1}{12h}\left(28({\varphi }_{i+1,j}-{\varphi }_{i-1,j})+{\varphi }_{i+2,j}-{\varphi }_{i-2,j}\right),}\hfill & i=3,\dots ,N_x-2;\hfill \\ {\displaystyle \frac{3}{h}({\varphi }_{N_x,j}-{\varphi }_{N_x-2,j}),}\hfill & i=N_x-1;\hfill \\ {\displaystyle \frac{1}{2h}(\tilde{d}{\varphi }_{N_x-3,j}+\tilde{c}{\varphi }_{N_x-2,j}+\tilde{b}{\varphi }_{N_x-1,j}+\tilde{a}{\varphi }_{N_x,j}),}\hfill & i=N_x.\hfill \end{array}\right.\end{array}$$

(17)

Analogous operators ${\mathcal{P}}_y,{\mathcal{Q}}_y$ are defined along y by swapping indices. This yields a complete fourth-order approximation for first derivatives using compact formulas.

To this end, the HJ equation is written in semi-discrete form as

$${\displaystyle \frac{d{\phi }_{i,j}}{dt}}=R({\phi }_{i,j};t),$$

(18)

where the spatial operator is

$$R(\phi ;t)=-F_h\left(U,cos{\theta }_h,|sin{\theta }_h|\right)\sqrt{{\left({\mathcal{P}}_x^{-1}{\mathcal{Q}}_x\phi \right)}^2+{\left({\mathcal{P}}_y^{-1}{\mathcal{Q}}_y\phi \right)}^2}.$$

(19)

Here ${\mathcal{P}}_x^{-1}{\mathcal{Q}}_x$ and ${\mathcal{P}}_y^{-1}{\mathcal{Q}}_y$ denote the compact finite-difference approximations of the first derivatives in the x- and y-directions, respectively. The discrete orientation used in the spread law is computed from the gradient of $\phi$, discretized according to the above compact finite-difference formulas, together with the wind unit vector $\widehat{\mathbf{U}}=({\widehat{U}}_x,{\widehat{U}}_y)$ as

$$cos{\theta }_h={\displaystyle \frac{\left({\mathcal{P}}_x^{-1}{\mathcal{Q}}_x\phi \right){\widehat{U}}_x+\left({\mathcal{P}}_y^{-1}{\mathcal{Q}}_y\phi \right){\widehat{U}}_y}{\sqrt{{\left({\mathcal{P}}_x^{-1}{\mathcal{Q}}_x\phi \right)}^2+{\left({\mathcal{P}}_y^{-1}{\mathcal{Q}}_y\phi \right)}^2}}},|sin{\theta }_h|=\sqrt{1-{cos}^2{\theta }_h}.$$

(20)

The spread function is then evaluated pointwise from these discrete quantities:

$$F_h(U,cos{\theta }_h,|sin{\theta }_h\left|\right)=\left\{\begin{array}{cc}{\displaystyle {\epsilon }_0+a\sqrt{U{\left(max\{cos{\theta }_h,0\}\right)}^n},}\hfill & cos{\theta }_h\ge 0,\hfill \\ {\displaystyle {\epsilon }_0\left(\alpha +(1-\alpha )|sin{\theta }_h|\right),}\hfill & cos{\theta }_h<0.\hfill \end{array}\right.$$

(21)

Equations (19)–(21) provide the compact finite-difference spatial discretization of the level-set evolution equation.

3.2. Temporal Discretization

For the time integration of Equation (18), an explicit Runge–Kutta scheme with fourth-order accuracy (RK4) is employed,

$$\begin{array}{ccc}\hfill {\phi }^{n,1}& =& {\phi }^n,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\phi }^{n,2}& =& {\phi }^n+{\displaystyle \frac{\Delta t}{2}}{R}^{n,1},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\phi }^{n,3}& =& {\phi }^n+{\displaystyle \frac{\Delta t}{2}}{R}^{n,2},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\phi }^{n,4}& =& {\phi }^n+\Delta t{R}^{n,3},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\phi }^{n+1}& =& {\phi }^n+{\displaystyle \frac{\Delta t}{6}}\left(R^{n,1}+2R^{n,2}+2R^{n,3}+R^{n,4}\right),\hfill \end{array}$$

(26)

where $R^{n,\mathcal{l}}=R({\phi }^{n,\mathcal{l}};t^{n,\mathcal{l}})$ with $t^{n,1}=t^n$, $t^{n,2}=t^{n,3}=t^n+\Delta t/2$, and $t^{n,4}=t^n+\Delta t$.

For stability, the time step $\Delta t$ is constrained by the Courant–Friedrichs–Lewy (CFL) condition

$$\Delta t\le \mathrm{CFL}·{\displaystyle \frac{h_{min}}{max|H^{\prime }|}},h_{min}=min(\Delta x,\Delta y),$$

(27)

where $max|H^{\prime }|$ is the maximum spread rate in the domain [10]. In the numerical experiments presented below, the CFL number was set to $0.5$, unless otherwise stated. The stability and convergence of the present compact finite-difference scheme follow from the theoretical framework established by Lele [15]. As the Hamilton–Jacobi equation reduces locally to an advection-type form, the same stability criteria can be applied.

Despite the CFL restriction, for strongly nonlinear or non-convex Hamiltonians, the scheme employs a filtering stage applied at each time step. This prevents spurious oscillations while preserving high-order accuracy in smooth regions [16]. The next subsection gives the details of the filtering procedure.

3.3. Numerical Filtering

Compact-difference discretizations, like other centered schemes, are non-dissipative and thus susceptible to the growth of high-frequency numerical modes stemming from mesh non-uniformity, boundary closures, or strong nonlinearities. Since steep gradients naturally develop near the fireline (e.g, under strong winds), we incorporate an implicit high-order low-pass filter [16,20] to suppress spurious oscillations while preserving large-scale features.

Given a discrete field $\phi$, the filtered values ${\widehat{\phi }}_{i,j}$ in the x-direction are obtained by solving, for each fixed j,

$${\mathcal{P}}_f{\widehat{\phi }}_{i,j}={\mathcal{Q}}_f{\phi }_{i,j},j=1,\dots ,N_y,$$

(28)

with the compact operators ${\mathcal{P}}_f$ and ${\mathcal{Q}}_f$ defined by

$$\begin{array}{c}\hfill {\mathcal{P}}_f{\widehat{\phi }}_{i,j}=\left\{\begin{array}{cc}{\widehat{\phi }}_{1,j},\hfill & i=1;\hfill \\ {\alpha }_f{\widehat{\phi }}_{1,j}+{\widehat{\phi }}_{2,j}+{\alpha }_f{\widehat{\phi }}_{3,j},\hfill & i=2,\dots ,K;\hfill \\ {\alpha }_f{\widehat{\phi }}_{i-1,j}+{\widehat{\phi }}_{i,j}+{\alpha }_f{\widehat{\phi }}_{i+1,j},\hfill & i=K+1,\dots ,N_x-K;\hfill \\ {\alpha }_f{\widehat{\phi }}_{N_x-k,j}+{\widehat{\phi }}_{N_x-k+1,j}+{\alpha }_f{\widehat{\phi }}_{N_x-k+2,j},\hfill & i=N_x-K+1,\dots ,N_x-1;\hfill \\ {\widehat{\phi }}_{N_x,j},\hfill & i=N_x,\hfill \end{array}\right.\end{array}$$

(29)

and

$$\begin{array}{c}\hfill {\mathcal{Q}}_f{\phi }_{i,j}=\left\{\begin{array}{cc}{\phi }_{1,j},\hfill & i=1;\hfill \\ {\displaystyle \sum _{n=1}^{K+1}{a}_{n,i}{\phi }_{n,j},}\hfill & i=2,\dots ,K;\hfill \\ {\displaystyle \sum _{n=0}^K\frac{a_n}{2}\left({\phi }_{i+n,j}+{\phi }_{i-n,j}\right),}\hfill & i=K+1,\dots ,N_x-K;\hfill \\ {\displaystyle \sum _{n=1}^{K+1}{a}_{n,i-N_x+K+1}{\phi }_{N_x-n+1,j},}\hfill & i=N_x-K+1,\dots ,N_x-1;\hfill \\ {\phi }_{N_x,j},\hfill & i=N_x.\hfill \end{array}\right.\end{array}$$

(30)

System (28) yields a $2K$th-order accurate filter on a $(2K+1)$-point stencil. Following [20], the interior coefficients $a_0,\dots ,a_K$ and boundary coefficients $a_{n,i}$ are parameterized by ${\alpha }_f\in (-0.5,0.5]$, with larger ${\alpha }_f$ giving a less dissipative response. In practice, ${\alpha }_f\in [0.3,0.5)$ provides effective damping of spurious modes, and the filter order is chosen at least two orders higher than the underlying derivative approximation. A more detailed description of the filtering approach and the influence of the parameter ${\alpha }_f$ can be found in the studies of [16,20], who conducted an extended numerical investigation of compact filtering schemes for the Navier–Stokes equations. Their analysis provides valuable insight into the spectral response and dissipative characteristics.

It should be noted that the filtering process is not applied at the boundary nodes. In these regions, where the interior stencil cannot be used due to its extent, higher-order one-sided boundary filters are employed. The corresponding coefficients can be found in [21] (Tables 5–7 in Appendix A), while an extended compilation of boundary filter coefficients can be found in [28]. In the present implementation, the level-set function $\phi$ is filtered once after the final stage of the explicit Runge–Kutta time integration. Several filtering strategies were examined to identify the most effective configuration: (a) sequential application in both coordinate directions, (b) filtering in the x-direction only, and (c) filtering in the y-direction only. These variants can be combined with the core compact discretization scheme, resulting in a robust, high-order numerical solver. For brevity, filtering options are denoted as $F{(·)}^{{\alpha }_f}$, where · indicates the direction and ${\alpha }_f$ the filter parameter; for example, $F{\left(b\right)}^{0.49}$ denotes choice (a), filtering applied solely in the x-direction, with ${\alpha }_f=0.49$.

Remark 1.

After extensive testing of the available filtering strategies, it was found that the configuration denoted as $F{\left(a\right)}^{{\alpha }_f}$, with ${\alpha }_f\in [0.49,0.5)$, provides sufficient stabilization for all test cases presented in this work. Unless otherwise stated, all simulations employ an eighth-order filter applied sequentially in both coordinate directions, with ${\alpha }_f=0.49$. This choice offers an optimal balance between numerical accuracy and computational efficiency.

3.4. Extension to Three Dimensions and Computational Complexity

The proposed compact finite-difference formulation, due to its narrow stencil, can be readily extended to three-dimensional configurations. Each derivative is approximated by the same tridiagonal compact operator applied along the x, y, and z directions, ensuring both simplicity of implementation and retention of high-order accuracy and stability. The implicit nature of the scheme involves solving simple tridiagonal systems per direction, which can be efficiently implemented using parallel solvers [19]. The same holds for the filtering procedure, which can likewise be applied independently in each spatial direction using the one-dimensional formulas mentioned above while solving the corresponding tridiagonal systems. Thus, this structure makes the 3D extension straightforward and computationally efficient, in contrast to high-order WENO schemes that require wider stencils (two fictitious cells in each direction for the fifth-order scheme) and complex multi-dimensional reconstructions.

In addition, it is also important to discuss the relative computational complexity of the compact formulation compared with the high-order WENO scheme. In terms of algorithmic complexity, the WENO method [26] performs three candidate reconstructions at each grid point, each requiring nonlinear combinations of neighboring fluxes and the evaluation of smoothness indicators to determine local stencil weights. This nonlinear reconstruction process substantially increases the arithmetic intensity to preserve non-oscillatory behavior. By contrast, the compact formulation relies solely on linear operations through the solution of tridiagonal systems along each coordinate direction. The subsequent filtering stage is also linear and employs the same one-dimensional tridiagonal structure, maintaining algorithmic simplicity and low computational cost. Moreover, no additional ghost layers are required for the compact formulation, which reduces memory use and implementation effort, making the method especially suitable for three-dimensional Hamilton–Jacobi problems.

4. Results

In this section, we present a series of numerical experiments to assess the accuracy and robustness of the proposed compact finite-difference scheme for wildfire front propagation and to compare its performance with standard ENO and WENO discretizations. We perform comparisons using first-, second-, and third-order ENO schemes, as well as a fifth-order WENO scheme, implemented through the ToolboxLS package [22]. ToolboxLS is a MATLAB-based library designed for level-set computations on Cartesian grids in up to four spatial dimensions. It provides a flexible framework for implementing and testing numerical schemes for Hamilton–Jacobi equations. In this work, MATLAB R2023a and ToolboxLS version 1.1.1 is used. The ToolboxLS routines are modified to incorporate wildfire propagation governed by Mallet’s anisotropic spread model.

Two categories of numerical tests are presented: (i) convergence studies for the eikonal problem and (ii) wildfire simulations using Mallet’s anisotropic model.

4.1. Convergence Studies

We first consider the expansion of a circular front in the absence of wind, a standard benchmark for Hamilton–Jacobi solvers [8,9,22]. In this case, the exact solution is known: the fireline remains a circle of radius $r\left(t\right)=r_0+t$, where $r_0$ is the initial radius. The test is performed on successively refined Cartesian grids, and numerical errors are measured by comparing the computed fireline against the exact circle.

Table 1. Setup of the expanding circle test case used for convergence verification.

Data	Value	Comment
Domain	$\Omega =[0,3]\times [0,3]$
Initial front	Circle
Circle center	$\left(x_c,y_c\right)=(1.5,1.5)$	Domain center
Initial circle radius	$r_{\mathrm{initial}}=0.5$
Final circle radius	$r_{\mathrm{final}}=0.9$
Velocity	$F=1.0$	Constant
Duration	$T_f=0.4$
Time step	$\Delta t={10}^{-4}$

summarizes the setup: the fireline starts as a circle of radius $r_{\mathrm{initial}}=0.5$ centered in the domain $\Omega =[0, 3]\times [0, 3]$ and expands with constant velocity $F=1.0$. At final time $T_f=0.4$, the exact solution is a circle of radius $r_{\mathrm{final}}=0.9$, which is used to quantify numerical error and verify convergence of the proposed method. In the spatial convergence experiments, we choose the time step $\Delta t$ sufficiently small so that the temporal discretization error is negligible. As a result, the measured accuracy is dominated by the spatial error of the numerical scheme.

To this end, we define three error norms that compare the simulated fireline with the exact expanding circle solution. The first is

$$e_{\mathrm{spatial}}^1=\left|r_{\mathrm{simulated}}-r_{\mathrm{final}}\right|,$$

where $r_{\mathrm{simulated}}$ is the simulated radius, estimated as follows:

$$r_{\mathrm{simulated}}={\displaystyle \frac{1}{card\left({\Gamma }_d\right)}}\sum _{(x,y)\in {\Gamma }_d}\mathrm{d}\left((x,y),\left(x_c,y_c\right)\right),$$

where ${\Gamma }_d$ is the discretized front as returned by the simulation (at time $T_f$), card is the cardinal (number of points) and d is the Euclidian distance.

Additionally, if $T_{\mathrm{true}}(x,y)$ is the time at which the front is supposed to reach the point $(x,y)$:

$$e_{\mathrm{time}}^2=\sqrt{{\displaystyle \frac{1}{card\left({\Gamma }_d\right)}}\sum _{(x,y)\in {\Gamma }_d}{\left(T_f-T_{\mathrm{true}}(x,y)\right)}^2}$$

The last norm is an infinity norm:

$$e_{\mathrm{time}}^{\infty }=\underset{(x,y)\in {\Gamma }_d}{max}\left|T_f-T_{\mathrm{true}}(x,y)\right|.$$

Table 2. Errors versus spatial discretization and estimated convergence orders. Eikonal test.

$\mathbf{\Delta }\mathit{x}=\mathbf{\Delta }\mathit{y}$	${\mathit{N}}_{\mathit{x}}={\mathit{N}}_{\mathit{y}}$	${\mathit{e}}_{\mathbf{spatial}}^1$	Order	${\mathit{e}}_{\mathbf{time}}^2$	Order	${\mathit{e}}_{\mathbf{time}}^{\mathit{\infty }}$	Order
0.15	21	2.30 × ${10}^{-3}$	–	6.11 × ${10}^{-3}$	–	1.00 × ${10}^{-2}$	–
0.075	41	2.58 × ${10}^{-4}$	3.16	3.36 × ${10}^{-4}$	4.19	4.59 × ${10}^{-4}$	4.44
0.0375	81	3.64 × ${10}^{-6}$	6.15	6.85 × ${10}^{-6}$	5.62	1.82 × ${10}^{-5}$	4.65
0.01875	161	8.21 × ${10}^{-9}$	8.80	2.45 × ${10}^{-8}$	8.46	9.30 × ${10}^{-8}$	7.61
0.009375	321	4.98 × ${10}^{-14}$	13.7	4.02 × ${10}^{-13}$	15.6	1.05 × ${10}^{-12}$	16.4

reports the convergence results obtained with the proposed high-order compact scheme. In these simulations, the filtering procedure was activated, since the derivative of $\phi$ is not defined at the ignition point $(0,0)$ at all times. It should be emphasized that the convergence tests are carried out in smooth regions, far from the discontinuity in the derivative. These results confirm that the high-order compact scheme, combined with the eighth-order low-pass filter, achieves the expected convergence rate as we refine the grid. The variation observed in the convergence rate (Table 2) results from the combined influence of the leading truncation error, the interpolation formula used to locate the circular front, and the local discontinuity of the derivative at the domain center. For coarse and intermediate grids, the dominant truncation terms arise from the boundary closure relations, $-\frac{2}{4!}{h}^3{f}^{\left(4\right)}$ (first boundary equation) and $-\frac{4}{5!}{h}^4{f}^{\left(5\right)}$ (second boundary equation). For finer discretizations, these contributions decay and the next term, $\frac{3}{7!}{h}^6{f}^{\left(6\right)}$, becomes dominant, producing an apparent superconvergence with an order of accuracy beyond six. Furthermore, the perimeter of the circular front ($\phi =0$) is computed by interpolation from a band of three grid points on each side of the interface. For coarse grids, this interpolation is affected by the derivative singularity at $(x_0,y_0)=(1.5,1.5)$, whereas for the finest resolutions, the interpolation nodes lie very close to the perimeter and far from the singular region, resulting in an almost exact numerical representation of the analytical solution.

Further, we also assess the temporal accuracy of the proposed method by evaluating the error $e_{\mathrm{spatial}}^1$ for a series of time step refinements. As illustrated in Figure 1, the results demonstrate that the fourth-order temporal accuracy of the classical Runge–Kutta (RK4) method is achieved. The convergence study thus confirms that the proposed method attains high accuracy in both space and time for the eikonal test case.

Figure 2 illustrates the time evolution of the burned area, defined as the region where $\phi (x,y,t)\le 0$. The exact final circle of radius $r=0.9$ at $t=0.4$ is shown as a dashed blue line. The simulated burned region is displayed as shaded red areas at four intermediate times ($t=0.1,0.2,0.3,0.4$). The results demonstrate that the proposed method reproduces the burned area very accurately.

Figure 3 presents the $e_{\mathrm{spatial}}^1$ convergence results for the proposed compact scheme compared with ENO1–3 and WENO5. As expected, ENO1 and ENO2 exhibit first- and second-order behavior, while ENO3 and WENO5 achieve higher-order convergence. The proposed method (Compact) shows accuracy comparable to WENO5; for coarse grids its observed order is close to four due to the boundary closure formulas, but as the grid is refined the convergence rate increases beyond sixth order which is the order of the interior compact scheme.

4.2. Applying the Proposed Methodology to Fire Spread Applications

Next, we apply the proposed methodology to wildfire propagation using the anisotropic spread function introduced in Section 2. Representative test cases include a single ignition, two ignitions merging into a unified front, and the evolution of an unburnt island. These scenarios demonstrate the ability of the method to capture complex fireline geometries and topological changes with high accuracy and stability.

To ensure numerical stability, the Courant–Friedrichs–Lewy condition is evaluated at each iteration using an a priori estimate of $max|H^{\prime }|$ along the x- and y-directions, leading to

$$\Delta t\le {\displaystyle \frac{\Delta x}{a\left(\frac{n}{2}+1\right)\sqrt{U}}}.$$

4.2.1. Single Ignition

We consider a wind-driven fireline evolution initiated from a single circular ignition. The wind is imposed with constant magnitude, directed from left to right, and the spread velocity follows the anisotropic Mallet model with the same parameters used in the reference simulation of [10]. We evaluate the CFL number from the stability constraint given by Equation (18), using the prescribed model parameters. The complete simulation setup is summarized in

Table 3. Simulation parameters for the single-ignition test case.

Parameter	Value	Parameter	Value
n	3	Domain	$\Omega =[0,3]\times [0,3]$
U	100	Initial front	Circle
a	0.5	Circle center	$(1.5,1.0)$
${\epsilon }_0$	0.2	Initial radius	$r_{\mathrm{initial}}=0.5$
$\alpha$	0.5	Velocity definition	Equation (8)
$\Delta x$	0.025	Duration	$T_f=0.1$
$\Delta y$	0.025	Time step	$\Delta t=1.5\times {10}^{-3}$
CFL	0.06	Spatial resolution	$N_x=N_y=121$

.

For this configuration, the solution remains smooth throughout the simulation, and no filtering is required to maintain stability. The compact scheme preserves the integrity of the numerical solution without spurious oscillations or distortions, which confirms its inherent robustness under moderate wind conditions.

The results of this simulation are shown in Figure 4. The fireline, initially circular, progressively elongates in the wind direction. Consistent with [10], the burned area increases monotonically with time, since reignition is not permitted at the considered temporal scales. The proposed method accurately reproduces the characteristic structure of the propagating fireline: the downwind head region, the slower-moving rear, and the intermediate lateral flanks are all clearly resolved, in close agreement with the reference simulation of [10] (see their Figure 3).

4.2.2. Strong-Wind Simulation

We examine a strong-wind configuration by increasing the wind speed to $U=150$ and enlarging the domain to $\Omega =[0,4]\times [0,4]$ to accommodate the faster propagation. The fine reference solution was obtained on a $245\times 245$ grid with the proposed method, while comparative simulations were performed on a coarser $85\times 85$ grid. Notably, the filtering procedure is enabled, which effectively suppresses minor high-frequency oscillations arising in regions of steep fireline gradients under strong wind conditions.

Figure 5 (top) shows the evolution of the fireline up to $t=0.4$. The proposed compact scheme accurately captures the elongated front structure under strong anisotropy while maintaining numerical stability and sharp front representation. Up to $t=0.3$, we observe that the slope of the fireline remains smooth, and all schemes reproduce the overall shape consistently. At later times, however, the front steepens significantly. The lower panels of Figure 5 compare the fireline contours at $t=0.4$ obtained with all numerical schemes. At this stage, differences between methods become apparent: the low-order ENO schemes underestimate the burned area, while ENO3 exhibits spurious oscillations along the advancing front (bottom-left panel). In contrast, the proposed method yields the most accurate approximation, with fireline contours closely matching the fine-grid reference solution and outperforming both ENO and WENO approaches (bottom-right panel). Among the non-compact formulations, WENO5 provides the best overall performance.

4.2.3. Long-Time Simulation

We carry out a long-time simulation with model parameters

$$({\epsilon }_0,a,\alpha ,U)=(0.2,0.2,0.2,10),$$

on an enlarged computational domain $[0,10]\times [0,10]$ discretized with $201\times 201$ grid points in each direction. A CFL number of $0.2$ is used to maintain stability over the extended integration time. The initial ignition is prescribed as a circle of radius $0.5$ centered at $(1,5)$. Compared with the previous short-time tests, the scaling parameter a and the wind strength are now reduced in order to produce a more realistic fire shape after the long-time evolution. Since a is associated with the available fuel loading, its decrease corresponds to a lower effective fuel availability, while the smaller wind magnitude further limits the overall fire spread. As a result, the rate of spread decreases, and the fire front advances more slowly. We use this configuration to assess the long-term numerical stability of the proposed method up to $t_f=10$. As shown in Figure 6, snapshots at $t=\{0,0.1,0.5,1,2,5,10\}$ illustrate smooth, monotonic front propagation without spurious oscillations.

4.2.4. Two Ignitions with One Island

We examine the robustness of the method to topological changes using a two-ignition configuration with an internal unburnt island. Two initially independent ignitions are placed within the domain and evolve under wind forcing until they eventually merge into a single connected front. At the same time, an unburnt circular region (an “island”) is initialized inside one of the burning areas. The velocity parameters are kept at their default values, while the initialization of the simulation is summarized in

Table 4. Initialization parameters for the multiple-ignition and island test case.

Feature	Center $(\mathit{x},\mathit{y})$	Radius	Description
Circle A	$(0.9,1.5)$	$r_A=0.35$	Left ignition
Circle B	$(1.8,1.9)$	$r_B=0.25$	Right ignition
Island	$(1.0,1.4)$	$r_{\mathrm{Isl}}=0.20$	Unburnt region inside Circle A

.

The results are presented in Figure 7, which shows six snapshots of the fireline evolution obtained with the proposed methodology. The fine reference solution was computed on a $301\times 301$ grid, while comparison simulations were performed on a coarser $85\times 85$ grid. As the simulation progresses, the two ignitions expand and, driven by the wind, merge into a single front. Simultaneously, the unburnt island gradually shrinks as the surrounding fireline advances and is fully consumed by $t=0.1$. During fire-front merging, localized steep gradients may cause small deviations in the level-set function near the contact region. These numerical errors mainly originate from local non-smoothness of $\nabla \phi$. In this case, the filter $F{\left(a\right)}^{0.499}$ (close to no filtering) is enabled, which serves to stabilize the numerical solution during the merging phase. These results demonstrate that the compact finite-difference scheme naturally handles both the merging of independent fronts and the evolution of internal unburnt islands. This confirms its ability to capture realistic wildfire dynamics with complex fireline geometries and topological transformations.

Figure 8 compares the simulated fireline contours at $t=0.6$ for the multiple-ignition and island test case. Both panels focus on the region surrounding the unburnt island and the advancing fireline of Circle A, where the numerical solution is most affected by steep curvature and the close proximity of multiple fronts. Panel (a) presents an intermediate-scale view including the island and the neighboring portion of Circle A’s front, while Panel (b) provides a closer zoom highlighting the numerical behavior near the island boundary. Among the tested schemes, ENO1 produces the most inaccurate result, as the island boundary and the approaching fireline are numerically merged, leading to a loss of front distinction. ENO2 underestimates the extent of the fireline propagation from Circle A, primarily due to its excessive numerical diffusion near the ignition region. ENO3 and WENO5 improve the overall shape representation but still exhibit small phase errors of high curvature. In contrast, the proposed method reproduces the reference fireline with high fidelity, preserving the separation between the island and the advancing front, and maintaining a smooth, well-resolved interface throughout the domain.

5. Conclusions

This study introduced a high-order compact finite-difference scheme for simulating wildland fire propagation within a level-set, Hamilton–Jacobi framework. To ensure stability near steep gradients that naturally arise at the fireline, we incorporated an implicit high-order low-pass filter, effectively suppressing spurious high-frequency modes while preserving front sharpness and accuracy. Since the simulation time is relatively short, we employed a less dissipative compact filter with ${\alpha }_f=0.49$, which was sufficient to maintain numerical stability.

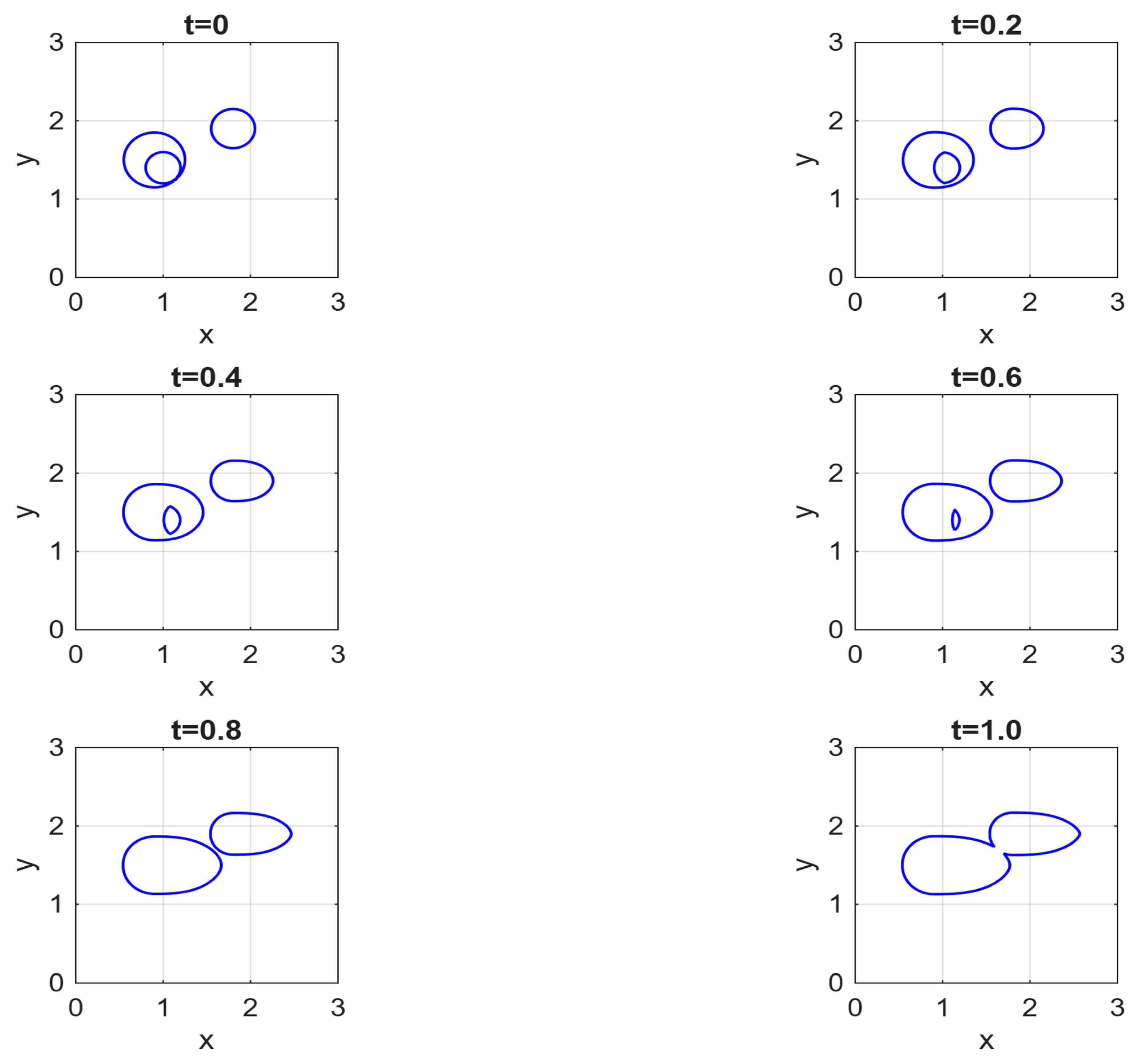
Convergence analysis based on the eikonal expanding-circle benchmark confirms that the scheme attains the expected high-order spatial accuracy. Applications to wind-driven wildfire scenarios governed by Mallet’s anisotropic spread law show that the method accurately reproduces the main features of fire dynamics, including the asymmetric head advance, merging fire fronts, and the extinction of unburnt islands. Across all test cases, the compact formulation achieves accuracy comparable to fifth-order WENO while retaining a narrow stencil, ensuring both efficiency and robustness near boundaries.

Overall, the proposed method provides an efficient and accurate alternative to the well-established ENO and WENO families of methods for level-set wildfire modeling. Its superior resolution in representing complex fireline geometries makes it a promising numerical foundation for future coupled atmosphere–fire simulations aimed at high-fidelity, predictive wildfire forecasting.