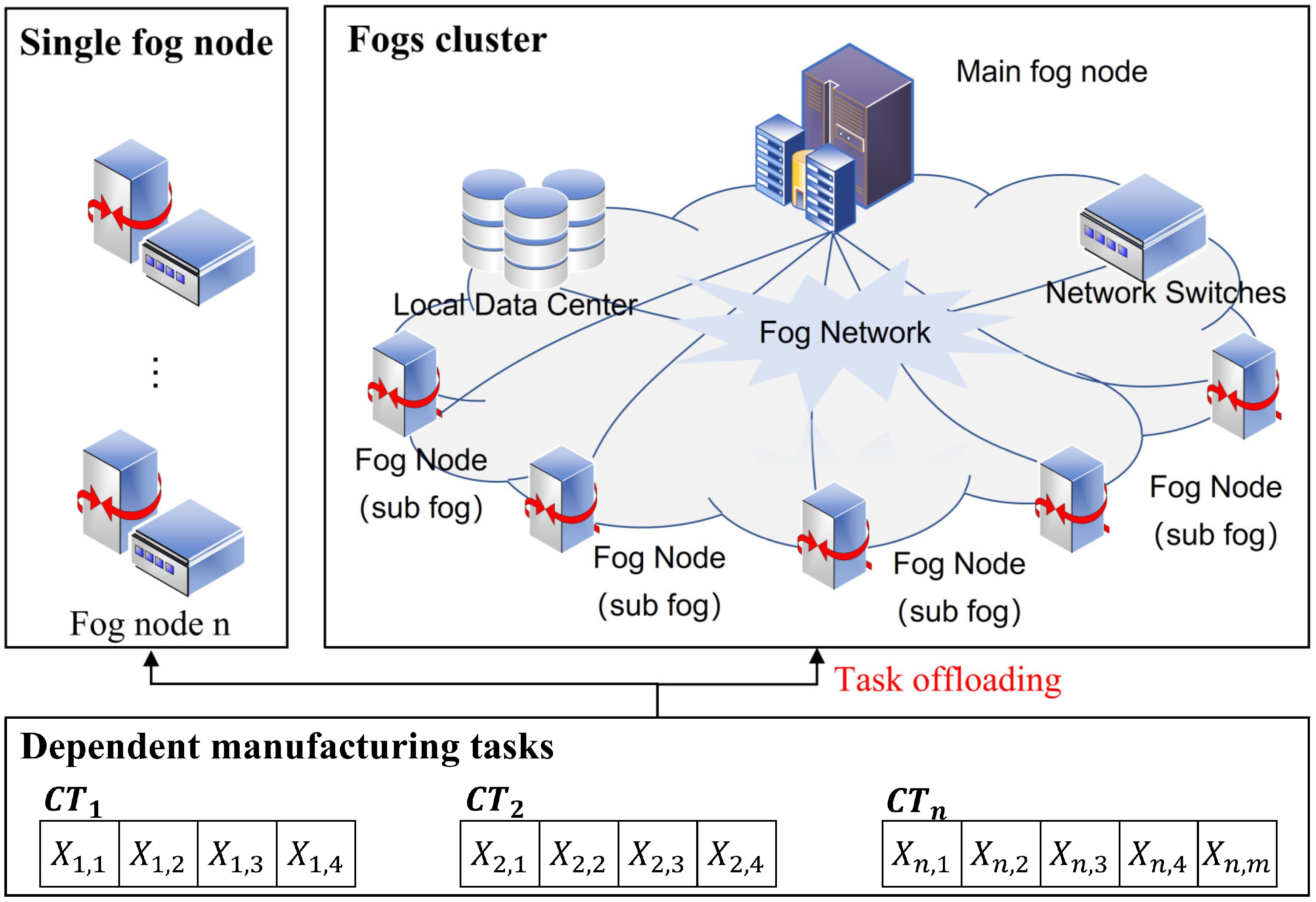
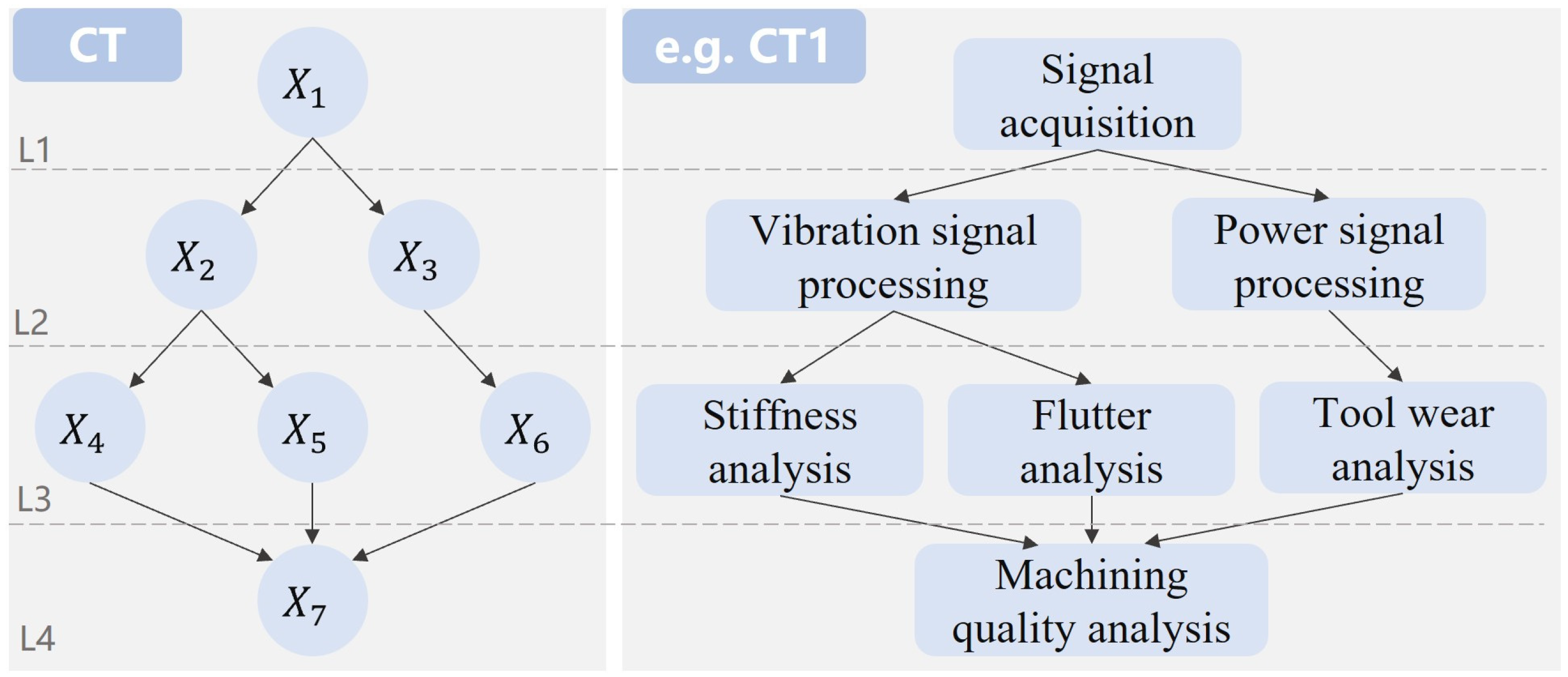
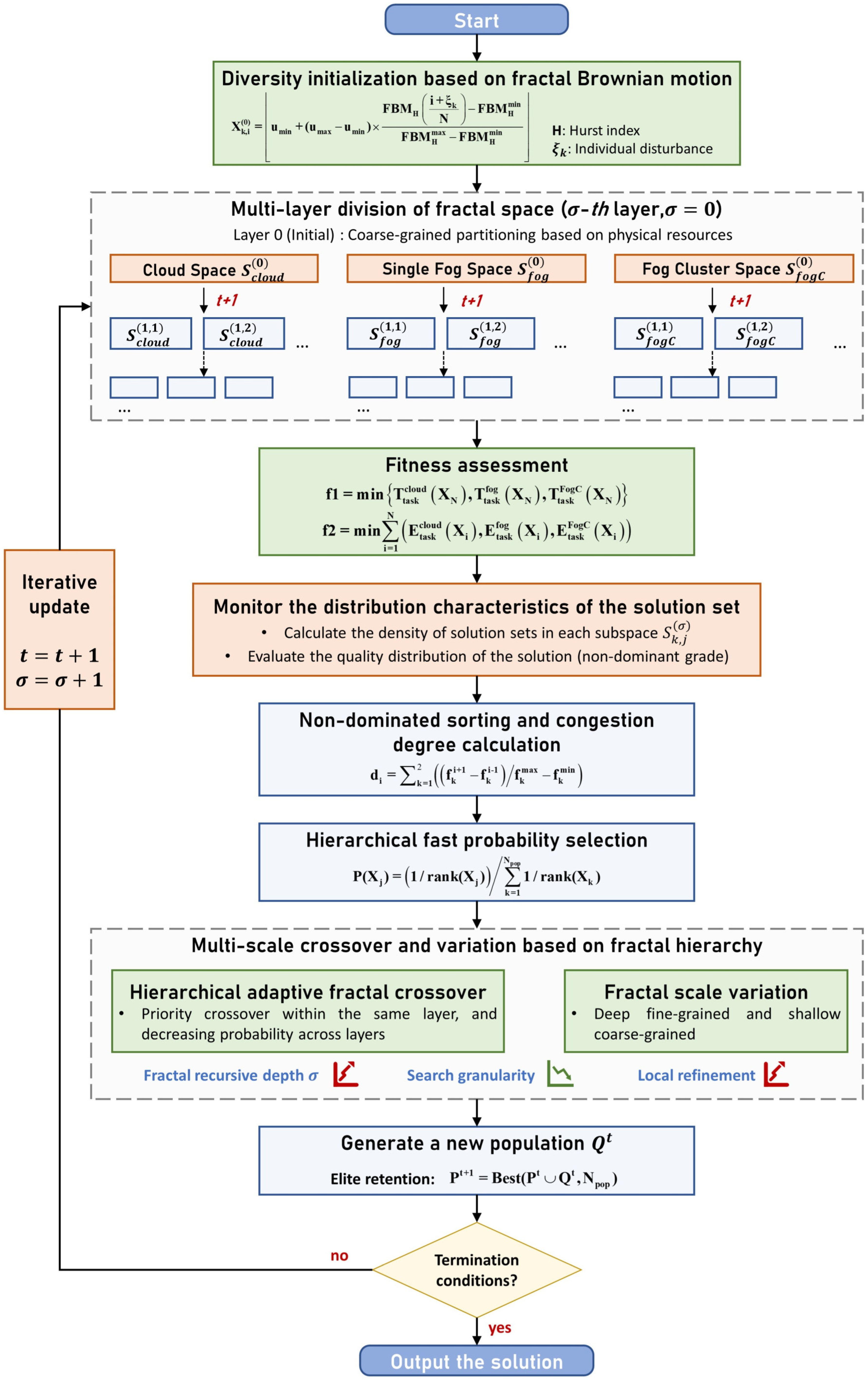
To comprehensively evaluate the effectiveness and applicability of the proposed approach, two types of experiments were conducted: simulation experiments and a practical case study. The simulation experiments were designed to benchmark the algorithm’s performance under various scenarios, and the case study was based on a digital twin-enabled smart manufacturing workshop, aiming to demonstrate the method’s practical value in real-world applications.
6.1. Simulation Experiment
The simulation experiments were carried out in a Python-based environment to assess the optimization performance of the proposed method under different configurations. The experiments were executed on a workstation equipped with an Intel Core i7-12700 CPU and 16 GB of RAM, running Windows 11 and Python 3.10. All algorithms and simulation models were implemented using standard Python libraries and customized modules. The customized modules included a task generator module that allowed users to configure task arrival patterns, dependency structures, and computational characteristics; a resource simulator module that modeled the computing capabilities and network conditions of cloud, fog nodes, and fog clusters; and an offloading decision executor module that implemented the proposed FS-NSGA-II algorithm and baseline methods. Users could modify module parameters through configuration files (in JSON format) to adapt the simulation to different manufacturing scenarios without altering the core code.
The simulation scene parameters were derived from the practical configurations of intelligent manufacturing environments, ensuring that the experimental setup closely reflected real-world industrial applications. In particular, the performance specifications of the computing nodes were aligned with those of commercially available products, providing a realistic basis for evaluating system behavior. The detailed parameter configuration for the cloud–fog hybrid computing scenario is summarized in
Table 4, including network topology, computational capabilities, task characteristics, and other essential features to guarantee the representativeness and validity of the simulation environment.
The key parameters of the FS-NSGA-II algorithm are summarized in
Table 5. The parameter configuration is grounded in evolutionary algorithm theory and established principles of fractal geometry. The evolutionary parameters (
,
) adhere to standard multi-objective optimization guidelines, which balance population diversity and computational efficiency. The fractal-specific parameters are initialized based on theoretical foundations:
provides optimal recursive partitioning depth for solution spaces with 3–8 decision variables;
follows the adaptive decomposition criterion that subspace variance should reduce to 10–20% before further subdivision; and the crossover/mutation probabilities implement the classical 70–30 exploitation–exploration balance with Gaussian perturbations constrained to ±0.6 standard deviations. These theoretically motivated initial values are subsequently validated and refined through the sensitivity analysis presented below.
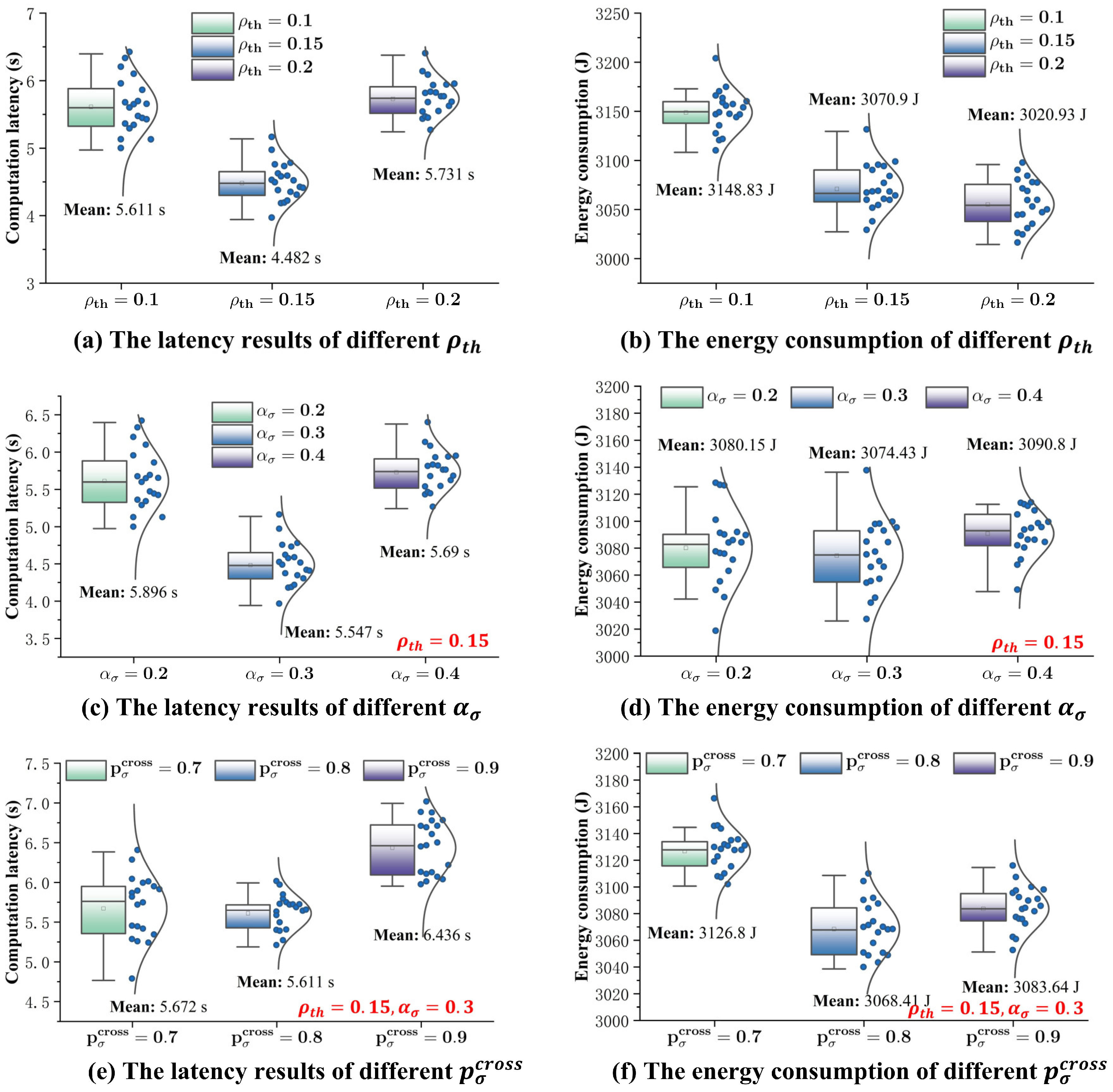
A sensitivity analysis was conducted to evaluate the effect that the core parameters of FS-NSGA-II have on optimization performance. The investigation focused on the fractal partition threshold (
), the Gaussian perturbation coefficient (
), and the fractal crossover probability (
), as these parameters fundamentally influence the algorithm’s search dynamics and solution diversity. The results of the sensitivity test are shown in
Figure 5.
(1) The fractal partition threshold () controls the granularity of recursive space division: a lower value enables finer partitioning, which enhances local exploitation but may incur higher computational costs, and a higher value favors broader exploration but can reduce solution precision. Experimental results show that setting to an intermediate value (0.15) achieves the best trade-off, yielding the lowest computation latency and energy consumption.
(2) The Gaussian perturbation coefficient () determines the intensity of random perturbations during the generation of solutions. Too small a value may limit the algorithm’s ability to escape local optima, while too large a value introduces excessive randomness that can slow down convergence. The results confirm that setting to 0.3 enhances both convergence speed and solution diversity.
(3) The fractal crossover probability () determines the likelihood of recombination within the fractal subspaces. Higher crossover probabilities promote genetic diversity but can disrupt the preservation of high-quality solutions, whereas lower probabilities may hinder exploration. The experiments indicate that achieves the best balance, leading to further improvements in both latency and energy metrics.
These observations highlight that the performance of FS-NSGA-II depends critically on the interplay between partition granularity, perturbation intensity, and genetic diversity mechanisms. Optimal parameter tuning, guided by their underlying roles, is thus essential for robust and efficient optimization. The recommended settings () were adopted in subsequent experiments.
To further assess the advanced nature and scalability of the proposed FS-NSGA-II, a comparative study was conducted against two representative baselines.
(1) NSGA-II [
38]: The classical non-dominated sorting genetic algorithm was adopted as the ablation reference for FS-NSGA-II. This comparison enabled a clear identification of the performance gains introduced by the fractal space partitioning mechanism.
(2) Differential Evolution (DE) [
45]: DE is a population-based evolutionary algorithm that demonstrates particular competitiveness in large-scale task offloading scenarios. Its robustness and simplicity in balancing exploration and exploitation make it a strong benchmark for multi-objective optimization in computation offloading problems.
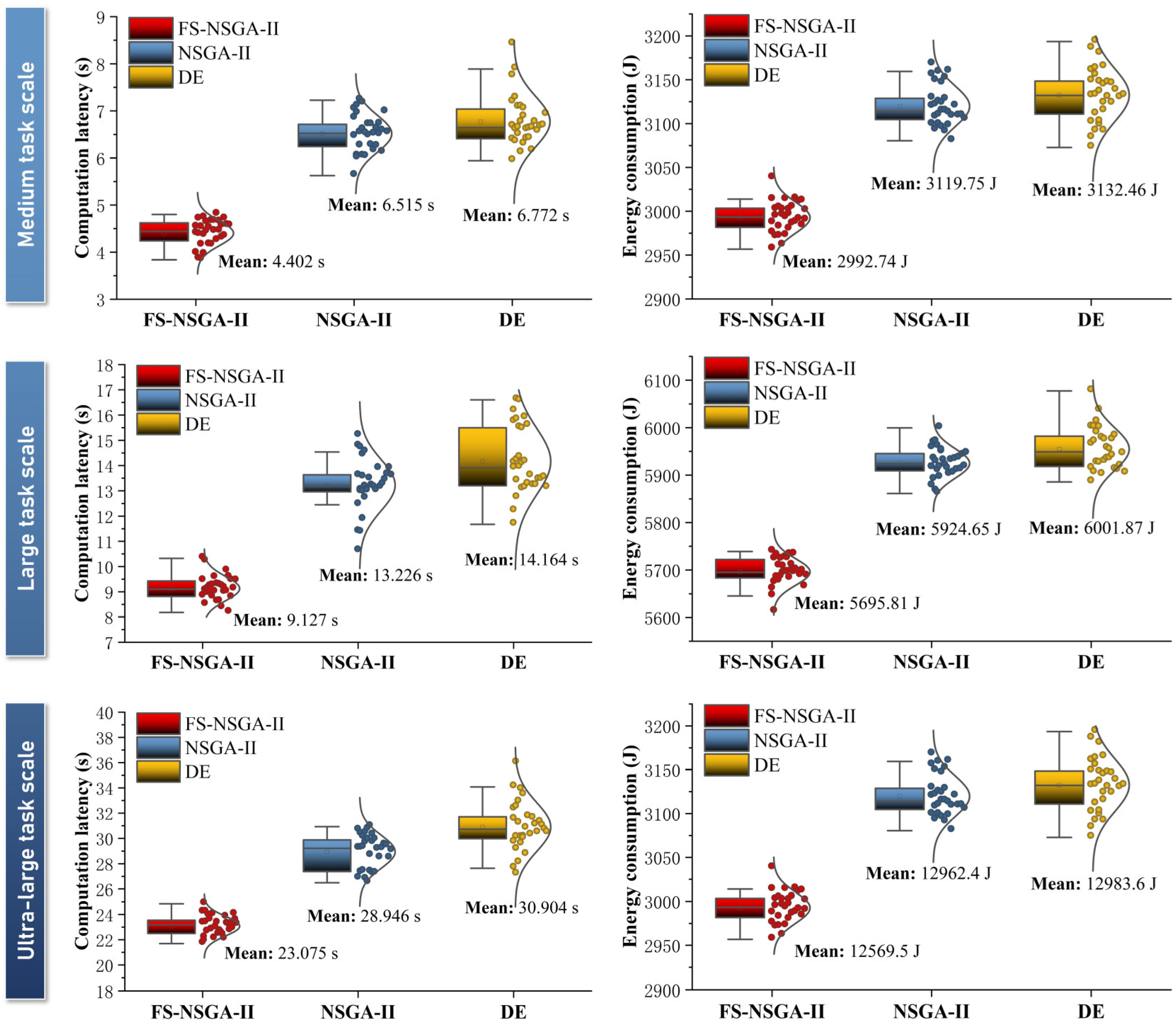
Experiments were performed using three different task scales, specifically medium, large, and ultra-large scenarios, to provide a comprehensive evaluation of the performance of algorithms under varying computational loads. For each scenario, all algorithms were independently applied for 30 runs to obtain statistically robust results. Key performance metrics included computation latency and energy consumption, as illustrated in
Figure 6.
The results demonstrate that FS-NSGA-II consistently outperforms both NSGA-II and DE across all task scales in terms of both computation latency and energy consumption. As the task scale increases, the superiority of FS-NSGA-II becomes increasingly pronounced. This can be attributed to the fractal space partitioning mechanism, which adaptively refines the granularity of the search space and maintains population diversity, thereby enabling the more effective exploration of the Pareto front in complex, large-scale environments. In the ultra-large task scenario, FS-NSGA-II achieved an average computation latency of 23.08 s, representing a 20.28% reduction compared to NSGA-II and 25.33% compared to DE. Similarly, the mean energy consumption decreased to 12,569.5 J, which is 3.03% and 3.19% lower than the respective baselines. In addition, as shown by the box plots and distribution curves, FS-NSGA-II not only achieved lower median values but also exhibited a tighter distribution with fewer outliers, indicating its greater robustness and solution consistency. The solution sets obtained by FS-NSGA-II displayed a more compact and symmetric distribution, highlighting its superior ability to maintain both convergence and diversity under varying problem scales.
To comprehensively evaluate the diversity of the obtained solution sets, the empirical cumulative distribution function (ECDF) and grouped histograms of crowding degrees are presented for each algorithm under different task scales in
Figure 7.
(1) The ECDF curves reveal that FS-NSGA-II exhibits a noticeable rightward shift compared to NSGA-II and DE. This phenomenon arises because fractal space partitioning recursively decomposes the objective space into hierarchical subspaces, constraining genetic operations within locally bounded regions. This structured decomposition prevents solution overcrowding in globally attractive areas and actively allocates search efforts to underexplored regions, thereby maintaining larger minimum distances between neighboring solutions. This indicates that a higher proportion of Pareto solutions in FS-NSGA-II possess larger crowding degrees, reflecting a more uniform and less clustered distribution of solutions. In the ultra-large task scenario, the 100th percentile crowding degree achieved by FS-NSGA-II reached 0.723. In contrast, NSGA-II and especially DE demonstrate rapid saturation in their ECDFs, implying that a large fraction of solutions are tightly packed, which may hinder the effective exploration of the Pareto front and limit the diversity of trade-offs available to the decision-maker.
(2) The grouped histograms further corroborate these findings. FS-NSGA-II achieves an even broader distribution of crowding degrees, with a substantial number of solutions in higher crowding degree intervals. This suggests that the algorithm not only generates a wider spread of solutions but also avoids premature convergence to high-density regions. By contrast, the histograms for NSGA-II and DE are skewed towards lower crowding degree intervals, indicating a tendency for these algorithms to produce more clustered populations and, thus, limited diversity.
Drawing on the superiority and preceding diversity analysis,
Table 6 provides a comprehensive quantitative comparison of all methods under different task scales. FS-NSGA-II consistently achieved the best performance, with the lowest mean maximum latency and energy consumption, as well as a higher number of Pareto solutions and greater mean crowding distance across all scales. Its improvements in IGD and HV further confirm their superior convergence and diversity. The standard deviations of key metrics remained low, reflecting the method’s robustness and stability. In addition, FS-NSGA-II maintained competitive runtime efficiency, with average computation times consistently lower than or comparable to the baselines as task size increased.
From a mechanism perspective, these improvements are primarily attributed to the synergy between fractal partitioning and evolutionary operators. The adaptive granularity of space partitioning enables the algorithm to allocate search efforts dynamically to underexplored regions; enhanced crossover and perturbation strategies further promote the dispersion and uniformity of solutions. As a result, FS-NSGA-II produces a well-distributed and robust Pareto front, which is particularly advantageous for real-world multi-objective decision-making scenarios.
6.2. Case Study
Further tests were conducted to evaluate the engineering applicability of the proposed CFHCC architecture. A digital twin manufacturing system for a specific type of cabin segment was selected as the testbed to investigate the practical benefits of the CFHCC architecture. As illustrated in
Figure 8, the physical and twin manufacturing spaces are interconnected through a hierarchical computing infrastructure. The system comprises one cloud server, two single-fog nodes, and four fog clusters, each containing four fog nodes. The cloud server is configured with 20 CPU cores, 128 GB of memory, and a 10 Gbps network interface. Each fog node is equipped with a 6-core processor and 8 GB of memory, and the fog clusters are connected via gigabit Ethernet.
Table 7 lists the computational tasks and parameters in the digital twin manufacturing system. Each task consists of several sub-tasks, with explicit data dependencies between them, some of which are designed to be processed in parallel. The data size and computational load of each sub-task are specified according to actual application requirements. These tasks are issued to the digital twin system concurrently at various time points to simulate the dynamic workload of the production environment in a realistic way.
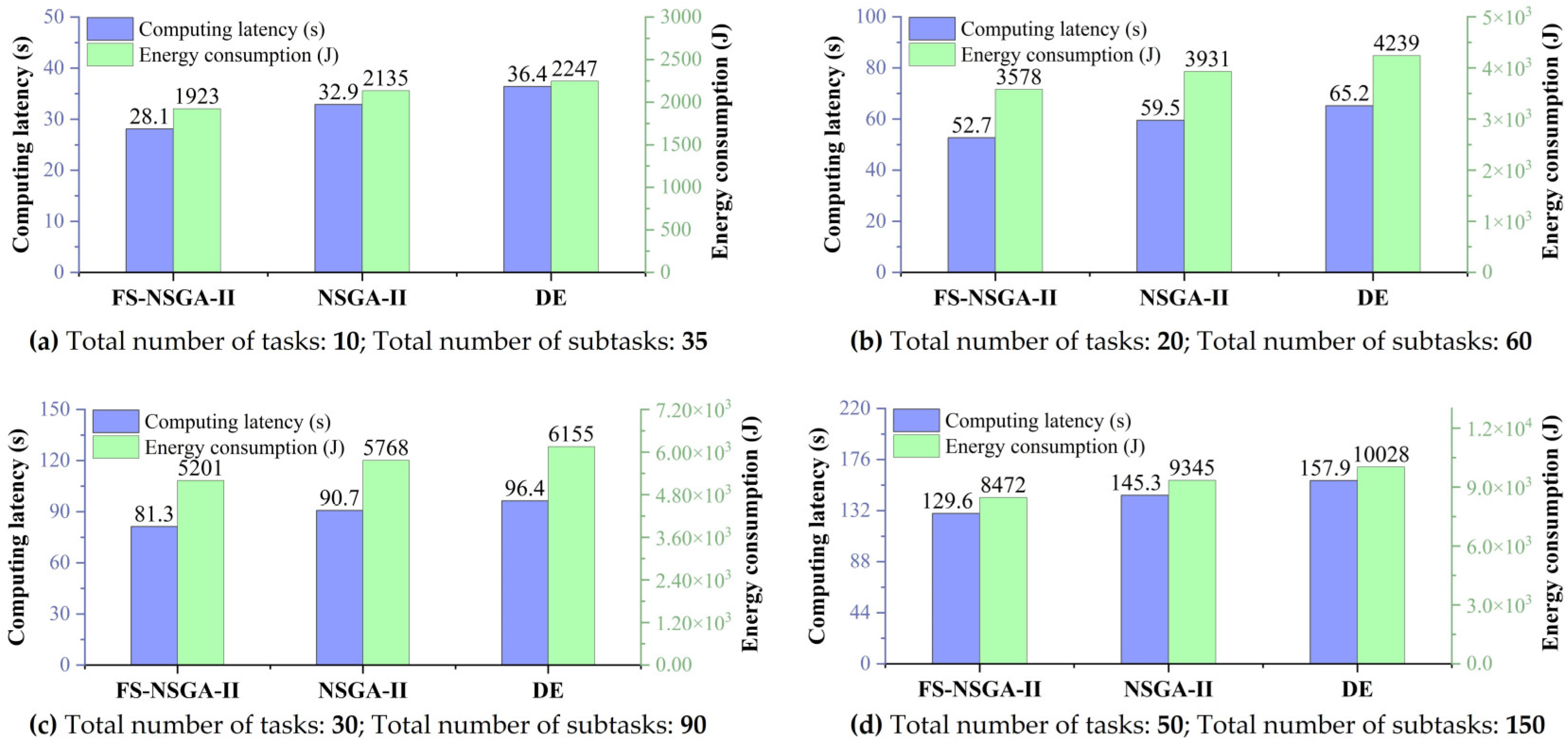
The experiment tested the actual performance of the FS-NSGA-II task offloading optimization method compared to other benchmarks under varying task quantities ranging from 10 to 50; the results are presented in
Figure 9. As the task scale expanded, FS-NSGA-II consistently maintained optimal performance with increasing advantages. In large-scale concurrent task offloading environments, the task offloading latency improved by 10.8% and 21.8% compared to NSGA-II and DE, respectively, while computational energy consumption increased by 9.34% and 15.52%, respectively. These results demonstrate that FS-NSGA-II possesses outstanding optimization capabilities in practical application environments.
To further evaluate the performance of collaborative offloading mechanisms, a series of comparative experiments was conducted. The test baselines are presented as follows:
(1) Cloud–Edge Collaborative Computing Framework (CECC) [
45]: Tasks can be offloaded either to the cloud or to a single-edge node, but no collaboration occurs among multiple fog nodes.
(2) Distributed Edge Framework (Edge) [
14]: Tasks are processed by independent edge nodes without the involvement of the cloud or any inter-fog coordination.
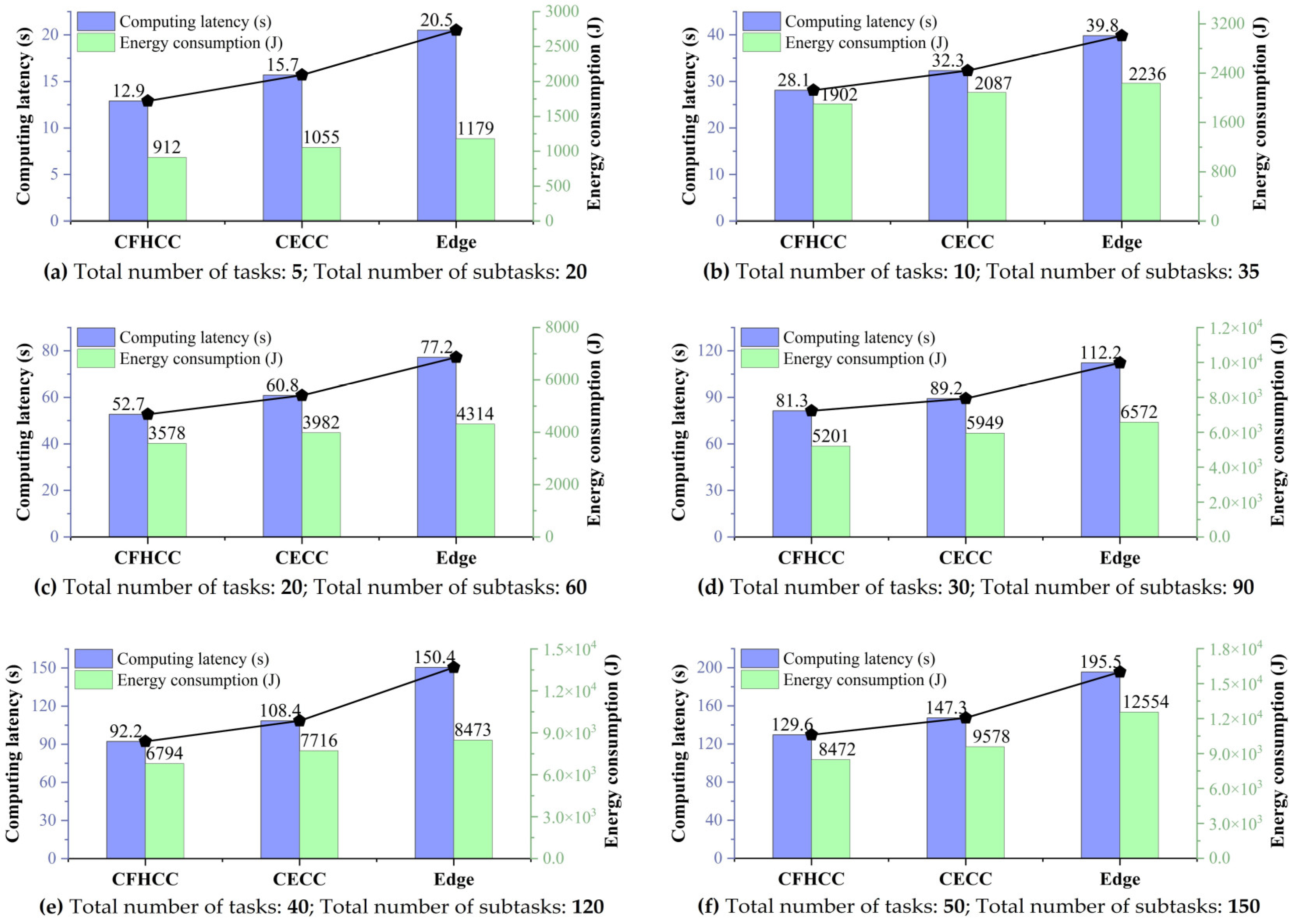
As illustrated in
Figure 10, the CFHCC framework demonstrates clear advantages over both CECC and edge frameworks under varying task scales. The CFHCC introduces a fog cluster mechanism that enables parallel processing and dynamic load balancing among multiple fog nodes. This collaborative capability results in reductions of 12.02% and 11.55% for maximum task delay and total energy consumption under large-scale tasks compared to the CECC framework. When compared with the edge framework, CFHCC achieves greater performance stability and efficiency. The absence of cloud participation in edge constrains the system’s capacity to handle computation-intensive or intensive task periods, leading to performance degradation and instability as the task scale grows.
Furthermore, the adoption of the CFHCC framework brings substantial practical benefits to the operation of digital twin systems. For monitoring-oriented tasks, collaborative fog clusters can process and analyze streaming sensor data in parallel, improving computational efficiency by 18.9% compared to the edge framework. For analysis-oriented tasks, the cloud’s abundant computational resources can be utilized for deep learning and large-scale data analysis, while the fog layer ensures timely preprocessing and feedback, improving computational efficiency by 28.3%.
These findings align with previous studies demonstrating the superiority of hierarchical fog–cloud architectures over purely cloud-centric or edge-only approaches [
9,
10,
21]. Although recent edge computing frameworks [
5,
14] typically employ independent edge nodes with limited local computing capacity, our collaborative fog cluster mechanism enables parallel task processing and dynamic load balancing among multiple fog nodes, resulting in 18.9% efficiency improvement over non-collaborative edge solutions.
While recent work has advocated for fully decentralized edge frameworks to address data privacy concerns, our case study demonstrates that completely eliminating cloud participation leads to significant performance degradation (up to 28.3% efficiency loss for analysis-intensive tasks) and instability under heavy workloads. This diverges from the common assumption in the literature [
46] that edge computing inherently trades computational capability for data locality. Our case study demonstrates that appropriately designed fog-level collaboration can simultaneously preserve data privacy at the edge while achieving computational performance comparable to cloud-centric approaches [
47], thereby addressing the critical gap between industrial data security requirements and computational efficiency demands.