Abstract
This paper investigates the asymptotic output tracking problem in probabilistic Boolean control networks by introducing the concept of the tracking region of attraction (TROA). For a constant reference signal, we provide a formal definition of the TROA, and establish the existence and uniqueness of the maximum TROA. The core contributions include a verifiable sufficient condition for TROA identification based on invariant set theory, a corresponding state feedback control design method, and a recursive algorithm for computing the maximum TROA. The proposed framework is validated through two simplified biological network case studies, including an apoptosis network and an Escherichia coli lactose operon network. Simulation results demonstrate that the designed controllers ensure asymptotic output tracking with probability one from any initial state within the maximum TROA.
Keywords:
Boolean control networks; probabilistic switching; output tracking control; tracking region of attraction; semi-tensor product (STP) MSC:
93C29; 93E99; 94C11
1. Introduction
In 1969, Kauffman introduced the Boolean network (BN) model to analyze genetic regulatory mechanisms, establishing a discrete dynamical framework for studying gene expression and interactions [1]. Differing from event-based discrete dynamical systems [2,3], in a BN, each gene is represented as a node whose state (active/inactive) is determined by logical rules depending on other genes. However, biological variability, experimental noise, and unobserved variables introduce significant uncertainty into gene expression data. To address this, Shmulevich et al. developed probabilistic Boolean networks (PBNs) in 2002, wherein each gene may have multiple predictors chosen probabilistically at each time step [4,5].
A major aim of Boolean modeling is to devise control strategies for biological systems. Datta et al. studied external control of specific nodes in a PBN, seeking control sequences that optimize a cost function over a finite horizon [6]. This led to the formulation of probabilistic Boolean control networks (PBCNs). Research on control-related issues in BNs and PBNs expanded considerably following Cheng et al.’s development of the semi-tensor product (STP) [7], which offers an algebraic framework for analyzing logical systems. Subsequent studies have explored various problems, including stability and stabilization [8,9,10,11,12,13,14,15], observability [16,17,18], state estimation [19,20,21,22,23], output tracking and regulation [24,25,26,27], fault detectability [28,29], and state compression [30]. The STP method has also been applied beyond biological modeling, including in nonlinear shift registers [31], evolutionary games [32], and fuzzy relational inequalities [33].
The output tracking control (OTC) problem aims to design controllers that enable a system’s output to closely follow a desired reference target. This is of significant practical value in areas such as robotic manipulation [34], flight control [35] and multiagent tracking control [36,37]. In biomedical applications, for instance, by viewing the organism as the output of a complex regulatory system, OTC principles can be applied to steer gene expression patterns toward a desirable state or a predefined healthy developmental trajectory. Within the framework of logical systems, OTC problems have been systematically investigated. Initial investigations by Li et al. established finite-time OTC designs for Boolean control networks, with [24] addressing a constant reference signal and [25] investigating output trajectories of a reference system. These results were subsequently extended to PBCNs, where finite-time tracking was studied in [38]. Furthermore, Chen et al. [39] introduced and investigated the problem of asymptotic output tracking for PBCNs.
Recent studies have further expanded the scope of output tracking in BNs, incorporating various practical considerations such as robustness against stochastic function perturbations [40], regulation under probabilistic outputs [41], and optimal control for Markov jump systems [42]. However, a common premise in these works is that output tracking can be guaranteed from any arbitrary initial state in the global state space. This assumption of global trackability is often too strong and may not hold in practical applications, where the system’s dynamics might only permit reliable tracking from a specific subset of states. This paper specifically addresses the asymptotic OTC problem for PBCNs by introducing the concept of the tracking region of attraction (TROA), which conceptually generalizes the existing tracking problem. If the maximum TROA is the entire state space, our framework seamlessly aligns with and confirms the global trackability assumption of existing methods [39,40,41,42]. If it is not, our approach is uniquely capable of determining the largest set of initial states from which tracking is achievable. In the latter scenario, which existing methods cannot handle, we further provide a verifiable condition for TROA identification and a corresponding controller design method. The core contributions are listed as follows:
- We formally define the concept of the TROA for PBCNs, which characterizes the set of initial states from which asymptotic output tracking of a constant reference signal can be achieved with probability one via state feedback control.
- A computationally verifiable sufficient condition for identifying whether a given set is a TROA is derived based on invariant set theory. Correspondingly, a constructive method for designing the required state feedback controller is provided.
- We establish the existence of the maximum TROA, and develop an effective recursive algorithm for its computation, offering a systematic solution to determine the largest set of initial states for which asymptotic tracking is feasible.
The rest of this paper is structured as follows. Section 2 covers the necessary preliminaries. Section 3 presents the main results, including the definition of the TROA, the sufficient condition for its identification, the control design method, and the algorithm for computing the maximum TROA. Section 4 provides illustrative examples to validate the theoretical findings. Finally, Section 5 concludes the paper.
2. Preliminaries
2.1. Notations
The basic symbols are given in Table 1.

Table 1.
Notations.
2.2. Model Introduction
Consider a PBCN model (with n internal nodes, m control input nodes, q output nodes and system modes) in algebraic form:
where is the internal state vector, is the control input vector, is the output state vector, is the switching signal variable, is the state transition matrix for the k-th mode, , and is the output structure matrix. Assume that the switching signals are independent and identically distributed with probability distribution . That is to say, for each , we have for all .
A state feedback control is given as follows:
where is called the feedback matrix, given by
Let and split this matrix into blocks of equal size by columns:
Moreover, define a matrix as follows:
Then based on the Proposition 2 of Reference [39], we can obtain the following results.
Proposition 1
([39]).
- (1)
- For any given , is the transition probability matrix (TPM) of the open-loop state sequence of PBCN (1) under the constant control , that is,
- (2)
3. Main Results
3.1. Problem Formulation
In control system design, a fundamental objective is to ensure the system’s output robustly follows a desired reference signal. However, a critical and often overlooked practical limitation is that this tracking capability may not be achievable from an arbitrary initial state. This motivates the concept of the tracking region of attraction (TROA). Intuitively, a TROA with respect to (w.r.t.) a given reference signal can be thought of as the system’s “safe operating envelope” of initial states. From any initial state within this set, there exists a control strategy that guarantees the output will converge to and remain at the desired target with probability one. Conversely, starting from outside this region, convergence cannot be assured. Identifying the TROA is therefore of paramount practical importance. It delineates the feasible starting conditions for a successful tracking operation, providing a clear operational boundary. In applications like steering a biological network to a healthy state, this means knowing which diseased or initial states are recoverable, thereby focusing control efforts where they are guaranteed to be effective and avoiding futile attempts from unrecoverable states.
This paper considers the case of a constant reference signal . This set-point regulation objective is not only central to many practical applications but also serves as a critical foundation for analyzing more complex tracking scenarios.
Definition 1.
A TROA of PBCN (1) w.r.t. the reference signal is said to be maximal if it is not a proper subset of any other TROA w.r.t. . The maximum TROA w.r.t. is the one that contains every other TROA w.r.t. . Due to the finiteness of states, the existence of maximal TROAs is straightforward. However, the existence of the maximum TROA is not immediate and requires proof. Moreover, the uniqueness of the maximal TROA is equivalent to the existence of the maximum TROA, as the presence of the maximum TROA implies it is the only maximal one, and conversely, if there is exactly one maximal TROA, it must be the maximum.
If the maximum TROA is the entire state space, the problem reduces to the output tracking problem studied in Reference [39]. However, if the maximum TROA is not the entire state space, the method in [39] cannot determine whether a given set is a TROA, nor can it find the maximum TROA. This is precisely the problem addressed in this paper.
We next focus on two fundamental problems:
- Problem 1: For a given set , how can we verify whether it is a TROA? If so, how to design the corresponding feedback controller?
- Problem 2: How to effectively compute the maximum TROA of PBCN (1) w.r.t. the reference signal ?
Define a subset of w.r.t. the reference signal as follows:
This subset contains all possible system states from the state space that produce the specific reference output signal when transformed by the output matrix H. In other words, is the collection of all internal states that result in the desired output . Therefore, is equivalent to .
Lemma 1.
For any given , Equation (3) holds iff
3.2. Invariant Sets and Control Invariant Sets
Definition 2.
A subset S is a control invariant set of the open-loop state sequence of PBCN (1) if, for every , there exists some such that
Definition 3.
A subset S is an invariant set of the closed-loop state sequence of PBCN (1) if, for all ,
The distinction between these two definitions centers on the role of the control. A set S is a control invariant set if for every state within it, one can find some immediate control action that will keep the next state in S with certainty. This defines a fundamental property of the system itself, confirming that confinement is possible. In contrast, a set S is an invariant set for a specific closed-loop control strategy if that pre-designed policy actively maintains the state within S from any starting point in the set. It follows that any invariant set must be control invariant. However, the reverse is not necessarily true. A control invariant set only confirms the existence of suitable control inputs for each state individually. A control law designed for the system, while it could potentially achieve this, is not automatically guaranteed to do so unless specifically intended.
For any given set , the maximum control invariant set of the open-loop state sequence contained in is denoted by , and the maximum invariant set of the closed-loop state sequence contained in is denoted by for a specific control law . Since any invariant set must be control invariant, it follows that . The following proposition gives a computation method for , as established in the Proposition 1 of Reference [43].
Proposition 2
([43]). Let be a subset of and . Then can be obtained by the following equations:
and
The following proposition is a reformulation of the Proposition 2 in [44].
Proposition 3
([44]). Let be a subset of . For any ,
iff and
- (1)
- there exists some such that ;
- (2)
- for all .
3.3. The TROA Identification Condition and Feedback Control Design Method
Using Lemma 1 and Proposition 3, we establish the following lemma.
Lemma 2.
For any given initial state , the output trajectory of PBCN (1) tracks the reference signal asymptotically in probability iff and the following two conditions hold:
- (1)
- there exists some such that the l-step transition probability from to is positive, i.e., ;
- (2)
- for all finite positive integers l, the transition probability from to is zero, i.e., .
Assume that . For a set containing , define a sequence of subsets of S recursively as follows:
where , regarded as a control constraint set for state , is defined as
Denote by the union over all non-negative integers l of the sets , that is, , which is also a subset of S.
Remark 1.
The core idea for TROA identification hinges on the dual role of the control constraint set . This set is pivotal because it ensures invariance by restricting controls that keep the state within S, while simultaneously enabling convergence by allowing controls that provide a positive probability of steering the state toward , as defined in (8). Consequently, a set S is a TROA if, under some control law , it is itself invariant and every state in S can reach the invariant set in finite time with positive probability. This dual guarantee ensures trajectories remain within the “safe” region S while converging to the target almost surely.
Lemma 3.
Let S be a subset of containing .
- (1)
- For all , it holds that .
- (2)
- There exists some such that .
Proof.
According to Definition 2, for every state , there exists some such that
Since , Equation (9) implies and further leads to . From the arbitrariness of , we have . Then applying the recurrence relation (8) preserves this inclusion, yielding . By mathematical induction, for all .
Since S is finite and the sequence is monotonic non-decreasing under set inclusion (by (1)), the number of distinct sets in the sequence does not exceed . Thus, there exists such that . Then, applying the recurrence relation (8) yields the equation for all . □
As established in Lemma 3, the sequence is monotonic non-decreasing and converges to in a finite number of steps, denoted by . Before convergence, this sequence is strictly increasing; each step incorporates new states that were not in but can reach it in one step with a positive probability under an allowable control. Therefore, the difference sets are guaranteed to be nonempty for . Moreover, the monotonic non-decreasing property of implies that . By recursively applying this decomposition to , we ultimately yield as a union of pairwise disjoint nonempty sets:
Then, for any , there exists a unique such that
The following theorem gives a sufficient condition for a set S to be a TROA of PBCN (1) w.r.t. the reference signal , and presents explicit conditions for the feedback control design to ensure that the PBCN’s output asymptotically tracks the reference signal from any initial state within S, thus providing a solution to Problem 1.
Theorem 1.
For a set containing , if , then S is a TROA of PBCN (1) w.r.t. the reference signal . In this case, the output trajectory of PBCN (1) will track the reference signal asymptotically in probability for any initial state under the state feedback control (2), provided that the feedback matrix K satisfies
Proof.
The definition of implies that conditions (12) are feasible for all . Moreover, since , for each , there exists a unique such that (11) holds. This implies that conditions (12) are feasible for all . Now we assume that conditions (12) hold.
By (12), for all , we have . This implies that is an invariant set of the closed-loop state sequence , and hence . Furthermore, note that for all . Thus, for all . This implies that S is also an invariant set of the closed-loop state sequence.
For any , by (12), there exists a and a sequence of states
such that for all , yielding that
That is, the condition (1) of Lemma 2 holds for all . This also implies that . Moreover, note that S is an invariant set. Hence, the condition (2) of Lemma 2 also holds for all . Therefore, by Lemma 2, the output trajectory of PBCN (1) will track asymptotically in probability for any initial state under the state feedback control (2). □
3.4. Computation of the Maximum TROA
Before presenting the method for computing the maximum TROA, we need to introduce a lemma. Since the existence of the maximum TROA has not been proven, we temporarily use maximal TROA instead.
Lemma 4.
Let be a set containing and let Ω be a maximal TROA of PBCN (1) w.r.t. the reference signal . If , then .
Remark 2.
Before proving Lemma 4, we provide an intuitive explanation of the proof strategy. The core idea is that the maximal TROA Ω is an invariant set under the feedback law that guarantees asymptotic tracking. For any state in Ω, the control ensures that the system remains within Ω and has a positive probability of moving closer to the target set in finite steps. When applying the mapping to a set S containing Ω, it recursively collects states that can reach the target set with positive probability under allowable controls (i.e., controls that keep the state within S with probability one). Since Ω is invariant and every state in it can eventually reach , the iterative process of naturally preserves the inclusion of Ω, ensuring .
Proof of Lemma 4.
Due to the maximality of and by Lemma 1, there exists a feedback control law of the form (2) such that
for all but for no .
For any , we have
If , it follows from (14) that
If , by (13), the right side of this inequality tends to 1 as , and hence
which also means . Therefore, for all , we have . That is, constitutes an invariant set of the closed-loop state sequence.
Assume that . For any , we have
which implies that . Moreover, for each , by (13) and Proposition 3, there exists some such that . We now prove by induction that holds for all . (1) For with ,
which, together with , implies that . (2) Assume that with implies . (3) For with ( is an invariant set),
and hence, there exists a such that and . The former implies , which together with and , further implies that . Thus by induction, we conclude that holds for all . Therefore, . □
The core idea for computing the maximum TROA is an iterative refinement process. Starting from the entire state space, each subsequent set is obtained by applying the mapping , which retains only those states from which a control exists that both keeps the system within the current candidate set with certainty and provides a positive probability of moving closer to the target set. States that cannot meet this condition are excluded in each iteration. The process repeats until the set converges, and this final set is the maximum TROA. The recursive process is formally defined as follows:
The intersection of these sets is defined as .
The following theorem establishes the convergence of the sequence of sets and shows that the limit set is exactly the maximum TROA of PBCN (1) w.r.t. the reference signal , thereby providing a solution to Problem 2.
Theorem 2.
There exists some such that . Furthermore, the maximum TROA of PBCN (1) w.r.t. exists and is equal to .
Proof.
This sequence of sets is monotonic non-increasing under set inclusion (i.e., ). Due to the finiteness of states, the sequence must stabilize in finitely many steps. That is, there exists some such that . This also implies that
Then it follows from Theorem 1 that is a TROA of PBCN (1) w.r.t. .
Consider any maximal TROA of PBCN (1) w.r.t. . Since , it follows from Lemma 4 that , and thus by induction, for all . The inclusion relation , with the maximality of , yields the equation . That is, any maximal TROA is equal to . Therefore, the maximum TROA of PBCN (1) w.r.t. exists and is equal to . □
The computational complexity per iteration of the recursive algorithm (15) based on Equations (8) is bounded by , and since the iteration converges in at most steps, the overall worst-case complexity of computing the maximum TROA is .
Theorem 2, together with Equation (16), implies that the maximum TROA satisfies . Letting , the set can be expressed as the union of pairwise disjoint subsets as in (10), and for any , there exists a unique such that (11) holds. Next, a corollary provides explicit design criteria for the feedback controller to ensure asymptotic tracking for any initial state within the maximum TROA .
Corollary 1.
Proof.
The proof is similar to that of Theorem 1. □
4. Illustrative Examples
4.1. Example 1
A reduced PBCN model of an apoptosis network is given as follows [45]:
where are the internal nodes, is the control input node, are the output nodes, is the switching signal variable, and the logical functions: , , , , , , , . Assume that .
Equate 1 and 0 to vectors and , respectively. Let and . Using the STP method in [7], PBCN can be converted into the algebraic form (1), where
Assume that the reference signal is (i.e., ). By (4), . Using Proposition 2 yields . By (15), we can obtain
It follows from Theorem 2 that the maximum TROA .
This result highlights a key advantage of our recursive algorithm. Applying just one iteration of the recursive process in (15), which corresponds to the approach in [39], would identify as the maximum TROA, since it includes all states from which there exists a control driving the system towards with a positive probability. However, our algorithm reveals that is not control invariant. Specifically, when , no control exists that simultaneously maintains the system within with probability one while ensuring eventual convergence to . The true maximum TROA is therefore the smaller set , which satisfies both invariance and convergence guarantees. This critical refinement demonstrates how our multi-step iteration approach overcomes the limitation of the existing methods, preventing the erroneous inclusion of the state where asymptotic tracking cannot be guaranteed.
By Corollary 1, a feedback matrix satisfies conditions (17) is obtained as follows:
Then under the feedback control (2) with the feedback matrix (19), the output trajectory of PBCN (18) can track asymptotically in probability for any initial state within the maximum TROA .
Define the index of the output as . Due to the finiteness of output states, we have the following equivalence:
By Proposition 1, , and hence , where .
Figure 1 shows the expected value of over time from every initial state. Crucially, the figure includes comparative cases: when the initial state lies inside , the expected value of asymptotically converges to the target value of 4; conversely, when the initial state is outside (e.g., or ), the expected value of fails to converge to 4. This figure confirms, from the perspective of statistical expectation, that the computed accurately delineates the set of initial states from which asymptotic output tracking can or cannot be achieved.
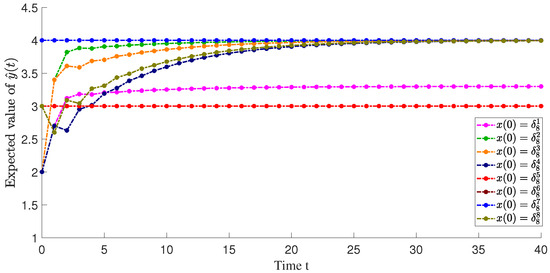
Figure 1.
The expected value of over time.
Figure 2 provides validation from the perspective of sample paths by explicitly comparing output trajectories from two specific initial states: (inside ) and (outside ). Subfigure (a) demonstrates that all sample paths of , under the initial condition , successfully converge to 4. In contrast, Subfigure (b) shows that, with the initial state , some paths of converge to 4 while others settle at 3. Together, these figures robustly support the effectiveness of the proposed method for computing the maximum TROA and the corresponding controller design strategy.
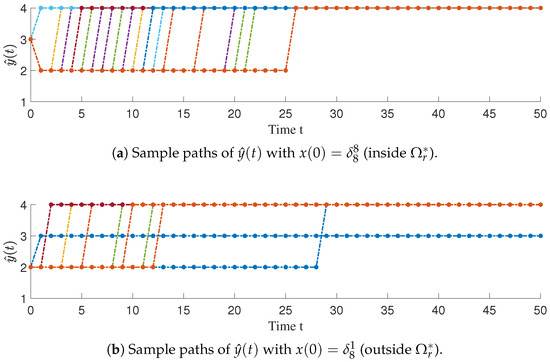
Figure 2.
Sample paths of for two different initial states. Each panel is generated from independent stochastic simulations. Note that many trajectories overlap, visually merging into a fewer number of lines.
4.2. Example 2
A PBCN model of an Escherichia coli lactose operon network is presented as follows [46]:
where are the internal nodes, are the control input nodes, are the output nodes, is the switching signal variable, and the logical functions are as follows:
Assume that . Let , and . Similarly, PBCN (20) can be converted into the algebraic form (1), where the state transition matrices and the output structure matrix are omitted.
Assume that the reference signal is (i.e., ). By (4), . Using Proposition 2, we obtain . By (15), we can successively calculate () and find that . By Theorem 2, the maximum TROA . Applying Corollary 1, a feedback control of the form (2) is constructed, where the feedback matrix is omitted. Under this control, the output trajectory of PBCN (20) can track asymptotically in probability for any initial state within the maximum TROA .
Let . Due to the finiteness of output states, we have the following equivalent relation:
Based on Proposition 1, , where .
Figure 3 depicts the evolution of the expected value of over time, illustrating its convergence behavior from different initial states. Subfigure (a) shows that when the initial state lies inside the maximum TROA , the expected value converges asymptotically to the target value of 3. In contrast, Subfigure (b) demonstrates that, for a representative set of initial states outside (i.e., ), the expectation fails to converge to 3, thereby validating the accuracy of the computed TROA in distinguishing initial states that permit asymptotic tracking.
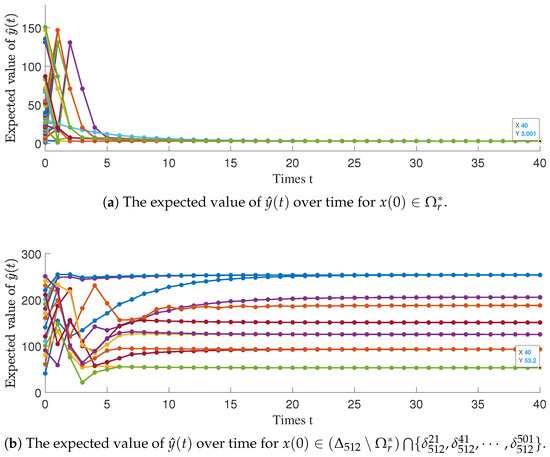
Figure 3.
The expected value of over time.
Figure 4 validates the TROA boundary through sample paths of under two distinct initial conditions. Subfigure (a) shows sample paths of originating from the initial state within , all of which converge to the target value of 3, confirming effective tracking. Subfigure (b) presents sample paths of from the initial state outside , where trajectories probabilistically diverge, with some reaching the target value of 3 and others converging to 254. This behavior confirms that asymptotic tracking cannot be guaranteed for initial states outside the maximum TROA.
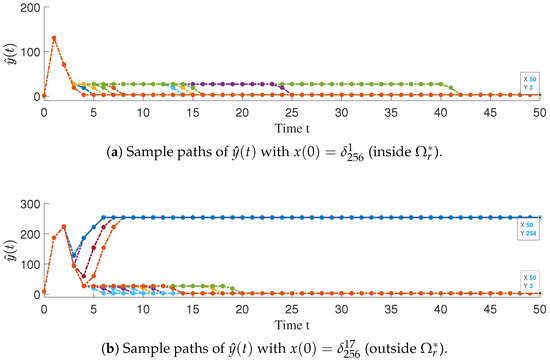
Figure 4.
Sample paths of for two different initial states. Each panel is generated from independent stochastic simulations.
In this example, the computed maximum TROA, , contains only 82 out of 512 states (∼16%), revealing a fundamental constraint on controlling this network. Biologically, this means that guaranteed asymptotic tracking to the desired output is possible only from a limited subset of initial genetic configurations. The network’s intrinsic dynamics, such as its attractor landscape, prevent reliable convergence from the vast majority (∼84%) of initial states. For synthetic biology, this implies that applying the classic inducer is guaranteed to switch the lac operon to the active state only if the pre-existing cellular state is within the TROA. This allows designers to distinguish between reliably inducible states and those where induction would be futile, thereby preventing wasted resources and failed experimental outcomes.
5. Conclusions
A systematic framework has been developed to address the asymptotic output tracking problem of PBCNs w.r.t. constant reference signals. The concept of the TROA was formally introduced, and the conditions under which a given set could be identified as a TROA were established. It was shown that the maximum TROA existed and could be effectively computed using a recursive method, and a state feedback controller was devised to achieve asymptotic tracking from any initial state within it. The entire methodology was ultimately validated through illustrative examples from biological network models, which confirmed the theoretical results and demonstrated the practical applicability of the proposed approach. Future research will extend this approach to other finite-field systems, such as multi-valued logical networks, and will further generalize it to systems with time-varying references and partial state observations.
It is important to note that the proposed method for computing the maximum TROA is exact but computationally intensive, with a worst-case complexity that grows exponentially with the number of nodes. This is consistent with the NP-hard nature of exact control synthesis in BNs. Therefore, the approach is best suited for small- to medium-sized networks. For large-scale systems, future work will focus on integrating model reduction, network decomposition, and approximation techniques to enable scalable TROA estimation.
Author Contributions
Writing—original draft preparation, B.C.; validation, B.C. and J.-J.M.; writing—review and editing, Y.X., M.L. and A.S.; funding acquisition, B.C., Y.X. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 62403253, 12401642 and 62503239), in part by the Natural Science Foundation of Jiangsu Province (Grant Nos. BK20240604 and BK20240606), and in part by the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (Grant Nos. NY223195, NY223198 and NY225004).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Li, B.; Lu, J.; Zhong, J.; Wang, Y. On the effect of dynamic event observations in distributed fault prognosis of discrete-event systems. IEEE Trans. Autom. Control 2025, 70, 2889–2901. [Google Scholar] [CrossRef]
- Li, B.; Wu, Y.; Lu, J.; Pan, Q.; Xu, W. Online information compression of finite-valued networks via finite automata approach and reinforcement learning. IEEE Trans. Inf. Theory 2025, 71, 8206–8216. [Google Scholar] [CrossRef]
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; Zhang, W. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002, 18, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Shmulevich, I.; Dougherty, E.R.; Zhang, W. From Boolean to probabilistic Boolean networks as models of genetic regulatory networks. Proc. IEEE 2002, 90, 1778–1792. [Google Scholar] [CrossRef]
- Datta, A.; Choudhary, A.; Bittner, M.L.; Dougherty, E.R. External control in Markovian genetic regulatory networks: The imperfect information case. Bioinformatics 2004, 20, 924–930. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H.; Li, Z. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach; Springer: London, UK, 2011. [Google Scholar]
- Wang, J.; Liu, W.; Fu, S.; Xia, J. On robust set stability and set stabilization of probabilistic Boolean control networks. Appl. Math. Comput. 2022, 422, 126992. [Google Scholar] [CrossRef]
- Wang, J.; De Leone, R.; Fu, S.; Xia, J.; Qiao, L. Stabilisation and set stabilisation of periodic switched Boolean control networks. Int. J. Control 2023, 96, 699–710. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, J.; Pan, Q.; Li, N. Minimal pinning control for set stability of Boolean networks. Appl. Math. Comput. 2024, 465, 128433. [Google Scholar] [CrossRef]
- Zhong, J.; Pan, Q.; Xu, W.; Chen, B. A framework of pinning control for non-periodical stable behaviors of large-scale asynchronous Boolean networks. IEEE Trans. Autom. Control 2024, 69, 5711–5726. [Google Scholar] [CrossRef]
- Feng, A.; Zhong, J.; Yerudkar, A.; Chen, H.; Wu, J. Event-triggered output feedback stabilization of Boolean control networks via Ledley solution. Commun. Nonlinear Sci. Numer. Simul. 2025, 145, 108710. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, A.; Wu, J.; Zhong, J.; Li, B. Robust set stabilization of Boolean control networks with edge removal perturbations. Commun. Nonlinear Sci. Numer. Simul. 2025, 140, 108355. [Google Scholar] [CrossRef]
- Chen, B.; Xue, Y.; Li, B.; Zhong, J. Local asymptotic set stabilization of probabilistic Boolean control networks via state feedback control. J. Frankl. Inst. 2025, 362, 107723. [Google Scholar] [CrossRef]
- Chen, B.; Li, B.; Wu, T.; Zheng, Y. Local stabilization of Boolean control networks via stochastic sampled-data control. Appl. Math. Comput. 2026, 511, 129746. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.G.; Huang, T.; Chakrabarti, P.; Che, W.W. Finite-time observability of Boolean networks with Markov jump parameters under mode-dependent pinning control. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 245–254. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.G.; Shen, Y.; Che, W.W. Pinning asymptotic observability of distributed Boolean networks. IEEE Trans. Cybern. 2024, 54, 5360–5368. [Google Scholar] [CrossRef]
- Sun, Y.; Fu, S.; Xia, L.; Xu, J. Minimal observability of switching Boolean networks. Math. Methods Appl. Sci. 2025, 48, 3291–3303. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Liang, J.; Li, M. State estimation for stochastic time-varying Boolean networks. IEEE Trans. Autom. Control 2020, 65, 5480–5487. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Shen, B.; Liang, J. Model evaluation of the stochastic Boolean control networks. IEEE Trans. Autom. Control 2022, 67, 4146–4153. [Google Scholar] [CrossRef]
- Li, B.; Pan, Q.; Zhong, J.; Xu, W. Long-run behavior estimation of temporal Boolean networks with multiple data losses. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 15004–15011. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.G. Shifting attack stabilization and estimation of hidden Markov Boolean networks. IEEE Trans. Cybern. 2025, 55, 1930–1940. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.G.; Shen, Y. Estimation of state and mode for Boolean networks with Markov jump parameters. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 4188–4197. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Xie, L. Output tracking control of Boolean control networks via state feedback: Constant reference signal case. Automatica 2015, 59, 54–59. [Google Scholar] [CrossRef]
- Li, H.; Xie, L.; Wang, Y. Output regulation of Boolean control networks. IEEE Trans. Autom. Control 2017, 62, 2993–2998. [Google Scholar] [CrossRef]
- Chen, B.; Xue, Y.; Shi, A. Optimal feedback policy for the tracking control of Markovian jump Boolean control networks over a finite horizon. Mathematics 2025, 13, 1332. [Google Scholar] [CrossRef]
- Fu, S.; Feng, J.E.; Zhao, Y.; Wang, J.; Pan, J. Dimensionality reduction method for the output regulation of Boolean control networks. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 5334–5347. [Google Scholar] [CrossRef]
- Tong, L.; Liang, J.; Hu, H.X. Fault detectability of asynchronous switched Boolean networks: A set reachability approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 3876–3888. [Google Scholar] [CrossRef]
- Tong, L.; Liang, J. Fault detectability of asynchronous delayed Boolean control networks with sampled-data control. IEEE Trans. Netw. Sci. Eng. 2024, 11, 724–735. [Google Scholar] [CrossRef]
- Li, B.; Lu, J.; Xu, W.; Zhong, J. Lossless state compression of Boolean control networks. IEEE Trans. Autom. Control 2024, 69, 4166–4173. [Google Scholar] [CrossRef]
- Gao, Z.; Feng, J.E. Research status of nonlinear feedback shift register based on semi-tensor product. Mathematics 2022, 10, 3538. [Google Scholar] [CrossRef]
- Fu, S.; Li, L.; Feng, J.E. Strategy optimization of controlled evolutionary games on a two-layer coupled network using Lebesgue sampling. Nonlinear Anal. Hybrid Syst. 2025, 56, 101570. [Google Scholar] [CrossRef]
- Wang, S.; Li, H. Resolution of fuzzy relational inequalities with Boolean semi-tensor product composition. Mathematics 2021, 9, 937. [Google Scholar] [CrossRef]
- Melhem, K.; Wang, W. Global output tracking control of flexible joint robots via factorization of the manipulator mass matrix. IEEE Trans. Robot. 2009, 25, 428–437. [Google Scholar] [CrossRef]
- Al-Hiddabi, S.A.; McClamroch, N.H. Tracking and maneuver regulation control for nonlinear nonminimum phase systems: Application to flight control. IEEE Trans. Control Syst. Technol. 2002, 10, 780–792. [Google Scholar] [CrossRef]
- Li, W.; Yan, S.; Shi, L.; Yue, J.; Shi, M.; Lin, B.; Qin, K. Multiagent consensus tracking control over asynchronous cooperation–competition networks. IEEE Trans. Cybern. 2025, 55, 4347–4360. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Yan, S.; Li, W. Consensus and products of substochastic matrices: Convergence rate with communication delays. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 4752–4761. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Guo, P. State feedback based output tracking control of probabilistic Boolean networks. Inf. Sci. 2016, 349–350, 1–11. [Google Scholar] [CrossRef]
- Chen, B.; Cao, J.; Luo, Y.; Rutkowski, L. Asymptotic output tracking of probabilistic Boolean control networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2780–2790. [Google Scholar] [CrossRef]
- Yang, X.; Li, H. Robust output tracking of Boolean control networks subject to stochastic function perturbations. IEEE Trans. Comput. Biol. Bioinform. 2025, 22, 382–389. [Google Scholar] [CrossRef]
- Zhong, J.; Pan, Q.; Xu, D.; Li, B.; Li, N. Output regulation of Boolean control networks under probabilistic outputs. IEEE Trans. Control Netw. Syst. 2025, 12, 28–37. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Xiao, G. Optimal control for reachability of Markov jump switching Boolean control networks subject to output trackability. Int. J. Control 2025, 98, 200–207. [Google Scholar] [CrossRef]
- Zhou, R.; Guo, Y.; Wu, Y.; Gui, W. Asymptotical feedback set stabilization of probabilistic Boolean control networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4524–4537. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Shen, Y.; Gui, W. Asymptotical stability of logic dynamical systems with random impulsive disturbances. IEEE Trans. Autom. Control 2021, 66, 513–525. [Google Scholar] [CrossRef]
- Kobayashi, K.; Hiraishi, K. An integer programming approach to optimal control problems in context-sensitive probabilistic Boolean networks. Automatica 2011, 47, 1260–1264. [Google Scholar] [CrossRef]
- Acernese, A.; Yerudkar, A.; Glielmo, L.; Del Vecchio, C. Reinforcement learning approach to feedback stabilization problem of probabilistic Boolean control networks. IEEE Control Syst. Lett. 2021, 5, 337–342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).