Fault-Tolerant Metric Dimension and Applications: Zero-Divisor Graph of Upper Triangular Matrices

Abstract

Graph invariants play a crucial role in understanding the structural and combinatorial characteristics of graphs. The fault-tolerant metric dimension, as a significant graph invariant, finds applications in diverse areas such as robust network optimization, autonomous robot navigation and intelligent sensor systems. In this paper, we investigate the fault-tolerant metric dimension and fault-tolerant edge metric dimension of zero-divisor graphs arising from upper triangular matrices over a finite commutative ring. The obtained results contribute to the understanding of metric-based fault tolerance in algebraically structured graphs.

1. Introduction

In recent years, the application of mathematics, especially in graph theory, has gained considerable importance. Distance-based measures in graphs have become a key focus of research with the metric dimensioonefivereceiving special attention due to its wide-ranging theoretical and practical applications.

The concept of metric dimension in graphs was first introduced by Slater [1], while the notion of resolving sets was independently defined by Harary and Melter [2]. Many investigations have been conducted into graph families with constant metric dimensions [3,4,5,6,7,8,9]. The fractional, strong, local and fault-tolerant variants of the core metric dimension have all been investigated [10,11,12,13,14,15,16,17,18,19,20,21,22]. Chartrand and colleagues [23,24] in 2000 found all connected graphs of order n with metric dimensions of $n-1$, $n-2$ or 1.

The interesting topic of the fault-tolerant metric dimension has been extensively studied by authors. Hernando et al. [25] put forward the new invariant fault-tolerant metric dimension (FTMD) in 2008 to determine the location of an intruder in a network in the event that one of the sensors fails, examining geometrically and combinatorially attractive graph families in terms of their fault-tolerant metric dimension. The FTMD of path graph and tree graphs were computed by Hernando et al. [25] after FTMD was introduced. A resolving set is said to be fault-tolerant if its vertices ensure that the structure of the graph may be accurately identified or connected even if any of them fail.

A graph G is considered cyclic when each edge forms a cycle of length n, where $n\ge 3$. It is represented as $C_n$. A graph G is bipartite if each edge joins a vertex in A and a vertex in B. This shows that there are two partite sets or subsets of the vertex sets A and B. In the event where every vertex in A is adjacent to every vertex in B, G is regarded as a complete bipartite graph where A and B are independent. When all $(n-1)$ vertices have degree one and one vertex has degree $(n-1)$, the complete bipartite graph is referred to as a star graph. It is denoted as $S_n$.

In a connected graph G, the metric representation of a vertex v with respect to an ordered subset $A=\{a_1,a_2,a_3,\dots ,a_n\}$ of vertices is the n-vector

$$r\left(v\right|A)=\left(d(v,a_1),d(v,a_2),\dots ,d(v,a_n)\right),$$

where $d(v,a_i)$ denotes the distance between v and $a_i$. For G, the metric dimension is the least cardinality resolving set that acts as a metric basis. The notation for it is $dim\left(G\right)$.

Numerous studies on zero-divisor graphs have been published recently. Beck was the first to suggest connecting a ring’s zero-divisors with a graph [26]. The vertices of G are assumed to be the elements of R, and two vertices, x and y, are considered neighboring if $x·y=0$. We refer to the graph G as R’s zero-divisor graph. The first people to simplify Beck’s zero-divisor graph were Anderson and Livingston [27]. Their objective was to provide an improved explanation of the ring’s zero-divisor structure. The zero-divisor graph Γ(R) is defined as follows: if and only if $ab=0$, two distinct vertices a and b are next to one another. This is referred to as the set of non-zero zero-divisors of R. Redmond [28] expanded the concept of a zero-divisor graph to include non-commutative rings. He demonstrated that given the non-commutative ring R, Γ(R) is connected if the set of left and right zero-divisors is equal. In 2002, DeMeyer et al. expanded the concept of zero-divisor graphs of rings to semi-groups [29]. Behboodi then provided the zero-divisor graphs for modules over commutative rings [30].

If $A\backslash \left\{p\right\}$ for every $p\in A$, where p is a vertex or edge, then A is a fault-tolerant and fault-tolerant edge resolving set to use as a resolving set for graph G. A fault-tolerant edge resolving set’s minimal cardinality is its fault-tolerant and fault-tolerant edge metric dimension. Its respective symbols are $f_{t}dim\left(G\right)$ and $f_{t}edim\left(G\right)$. With possible applications to filter networks, determining a graph’s fault-tolerant and fault-tolerant edge metric dimension is an intriguing yet challenging combinatorial problem. Only a small number of basic graph families have been studied thus far.

The analysis of the fault-tolerant metric dimension and fault-tolerant edge metric dimension of the commutative zero-divisor graph Γ(R), where R is the ring of all $3\times 3$ upper triangular matrices over the finite field ${\mathbb{Z}}_2$, has practical significance in the design of resilient, algebraically structured systems, particularly within the realm of cyber–physical networks. Many modern systems—such as modular robotics, power grid diagnostics, neural networks and distributed sensor arrays—operate under binary logic and exhibit structured inter-component dependencies. These dependencies can be effectively modeled using algebraic constructs such as rings over ${\mathbb{Z}}_2$. In this context:

• Each system component or module is represented by an element (matrix) of the ring,
• The zero-divisor graph captures incompatibilities or interference between modules (i.e., when the product of two elements is zero),
• Vertices in the graph represent vulnerable or fault-prone states,
• Edges represent interactions or fault-inducing dependencies.

In summary, studying the fault-tolerant (edge) metric dimension of algebraic graphs such as Γ(R) offers a theoretically grounded, practically applicable methodology for enhancing resilience in complex, modular systems. So, in this article we find the fault-tolerant metric dimension and fault-tolerant edge metric dimension of the commutative zero-divisor graph constructed from the ring of $3\times 3$ upper triangular matrices over ${\mathbb{Z}}_2$.

2. Preliminaries

The fault-tolerant metric dimension and fault-tolerant edge metric dimension of zero divisor graphs derived from upper triangular matrices are examined in this section along with other basic ideas.

Definition 1.

Assume that the graph G has a vertex set $P\left(G\right)$. For any pair of vertices $x,y\in P\left(G\right)$, there exists a vertex $z\in V$ such that the distance between y and z differs from the distance between x and z, even after some vertices in V are removed. This set is known as a fault-tolerant resolving set, denoted by FTRS and the fault-tolerant metric dimension is defined as the minimum cardinality of a FTRS.

Definition 2.

Assume that the graph G has an edge set $P\left(G\right)$. For any pair of edges $r,s\in P\left(G\right)$, there exists an edge $t\in E$ such that the length between s and t and the distance between r and t differ, even after some edges in E are deleted. This is known as a fault-tolerant edge resolving set and fault-tolerant edge metric dimension is defined as the minimum cardinality of a fault-tolerant edge resolving set.

Definition 3.

A zero-divisor graph is one in which the vertices represent the elements of the ring and pairs of zero-divisor elements are connected by edges. For example, $(V,E)$ is a zero-divisor graph, where V is the collection of non-zero zero-divisors of R and the vertices $x_1$ and $x_2$ are connected by an edge in V such that $x_1.x_2=0$. It is represented by $\Gamma \left(R\right)$.

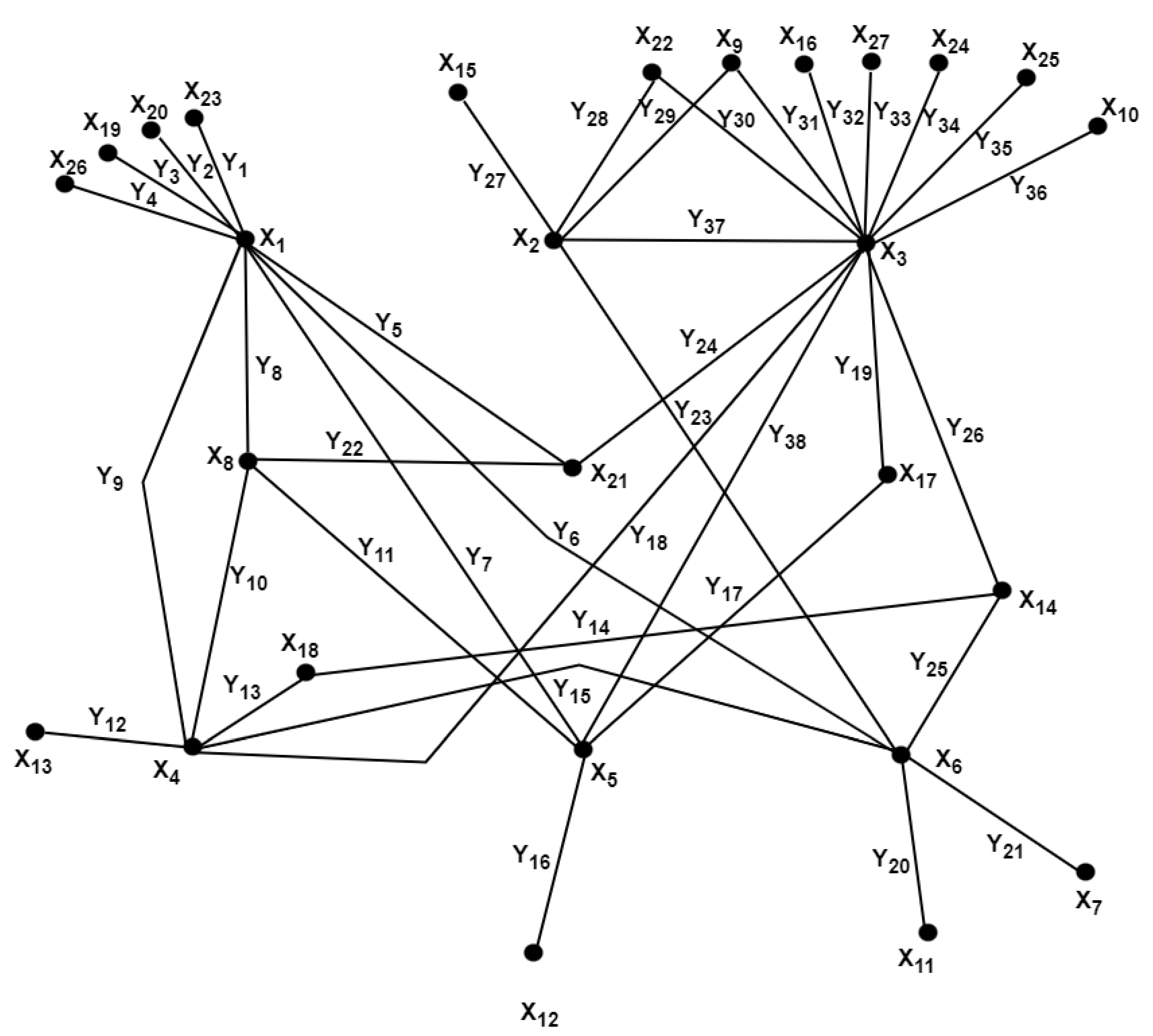
3. Zero-Divisor Graphs of the Upper Triangular Matrix ${\mathit{M}}_{\mathbf{3}}\mathbf{\left(}\mathit{R}\mathbf{\right)}$

We now examine the zero-divisor graph associated with the upper triangular matrix ring $M_3\left(R\right)$. A general element of $M_3\left(R\right)$ can be written as

$$A=\left(\begin{array}{ccc}p& q& r\\ 0& s& t\\ 0& 0& u\end{array}\right),$$

where $p,q,r,s,t,u\in R$ and R is a commutative ring (e.g., ${\mathbb{Z}}_n$, $\mathbb{R}$ or $\mathbb{C}$).

For the case $R={\mathbb{Z}}_2$, each entry can take values 0 or 1, leading to $2^6=64$ possible upper triangular matrices, including the zero matrix. Excluding the zero matrix, we obtain 63 nonzero elements in $M_3\left({\mathbb{Z}}_2\right)$. We denote these matrices by

$$X_1,X_2,\dots ,X_{27},$$

and analyze their products to determine adjacency in the corresponding zero-divisor graph $\Gamma \left(M_3\left({\mathbb{Z}}_2\right)\right)$.

Two matrices A and B are adjacent in $\Gamma \left(M_3\left({\mathbb{Z}}_2\right)\right)$ if and only if $AB=0$ or $BA=0$. Using this rule, we construct the vertex set $\{X_1,X_2,\dots ,X_{27}\}$ and identify all zero-divisor pairs to define the edge set of the graph. We’ll explore the graph which is derived from the vertices $X_1,X_2,X_3,\dots ,X_{26}$, $X_{27}$.

This Figure 1 ($Z_v$) shows that their vertices have a commutative relationship. In other words, if there is an edge between $X_1$ and $X_2$, then $X_1·X_2=0$ and $X_2·X_1=0$. Therefore, since the products of vertices connected by edges equal zero, they represent zero divisors. A zero divisor graph is created when these zero divisors are joined. As upper triangular matrix $X_{28},X_{29},X_{30},\dots ,X_{62},X_{63}$ doesn’t make any commutative zero-divisors, so we remove these vertices from the graph. Therefore zero-divisor graph of upper triangular matrix of $M_3\left({\mathbb{Z}}_2\right)$ given below in Figure 1 ($Z_v$).

3.1. Fault-Tolerant Metric Dimension of Zero-Divisor Graph Obtained from Upper Triangular Matrix of $M_3\left({\mathbb{Z}}_2\right)$

We calculate the fault-tolerant metric dimension of zero-divisor graph obtained from upper triangular matrix of $M_3\left({\mathbb{Z}}_2\right)$ in following theorem.

Theorem 1.

Let $Z_v$ be the zero-divisor graph obtained from upper triangular matrix ring $M_3\left({\mathbb{Z}}_2\right)$. Then, the fault-tolerant of the associated graph is i.e., $f_{t}dim\left(Z_v\right))\ge 15$.

Proof. 

The proof proceeds in two steps: first, we exhibit a resolving set of size 15 and show it is fault-tolerant by providing unique representations for all vertices and then, we prove by contradiction that no smaller set suffices. Now assume that $f_t\left(R\right)$ be a resolving set for the zero-divisor graph $Z_v$. Now, the given set

$$f_t\left(R\right)=\{x_9,x_{10},x_{11},x_{19},x_{20},x_{23},x_{24},x_{25},x_{27},x_{13},x_{26},x_{22},x_{16},x_7,x_{18}\}$$

is a fault-tolerant resolving set (FTRS). □

Distinct representations of vertices with respect to $f_t\left(R\right)$ (

Table 1. Distinct representations of vertices w.r.t to $f_t\left(R\right)$.

${\mathit{f}}_{\mathit{t}}\left(\mathit{R}\right)$	${\mathit{x}}_9$	${\mathit{x}}_{10}$	${\mathit{x}}_{11}$	${\mathit{x}}_{19}$	${\mathit{x}}_{20}$	${\mathit{x}}_{23}$	${\mathit{x}}_{24}$	${\mathit{x}}_{25}$	${\mathit{x}}_{27}$	${\mathit{x}}_{13}$	${\mathit{x}}_{26}$	${\mathit{x}}_{22}$	${\mathit{x}}_{16}$	${\mathit{x}}_7$	${\mathit{x}}_{18}$
$d\left(x_1\right|f_t\left(R\right))$	3	3	3	1	1	1	3	3	3	2	1	3	3	3	2
$d\left(x_2\right|f_t\left(R\right))$	1	2	2	3	3	3	2	2	2	3	3	1	2	2	3
$d\left(x_3\right|f_t\left(R\right))$	1	1	3	3	3	3	1	1	1	2	3	1	1	3	2
$d\left(x_4\right|f_t\left(R\right))$	2	2	2	2	2	2	2	2	2	1	2	2	2	2	1
$d\left(x_5\right|f_t\left(R\right))$	2	2	3	2	2	2	2	2	2	1	2	2	2	3	3
$d\left(x_6\right|f_t\left(R\right))$	2	3	1	2	2	2	3	3	3	2	2	2	3	1	2
$d\left(x_7\right|f_t\left(R\right))$	3	4	2	3	3	3	4	4	4	3	3	3	4	0	3
$d\left(x_8\right|f_t\left(R\right))$	3	3	3	2	2	2	3	3	3	2	3	3	3	3	2
$d\left(x_9\right|f_t\left(R\right))$	0	2	3	4	4	4	2	2	2	3	4	2	2	3	3
$d\left(x_{10}\right|f_t\left(R\right))$	2	0	4	4	4	4	2	2	2	3	4	2	2	4	3
$d\left(x_{11}\right|f_t\left(R\right))$	3	4	0	3	3	3	4	4	4	3	4	3	4	2	3
$d\left(x_{12}\right|f_t\left(R\right))$	3	3	4	3	3	3	3	3	3	4	3	3	3	4	4
$d\left(x_{13}\right|f_t\left(R\right))$	3	3	3	3	3	3	3	3	3	0	3	3	3	3	2
$d\left(x_{14}\right|f_t\left(R\right))$	2	2	2	3	3	3	2	2	2	3	3	2	2	2	1
$d\left(x_{15}\right|f_t\left(R\right))$	2	3	3	4	4	4	3	3	3	4	4	2	3	3	4
$d\left(x_{16}\right|f_t\left(R\right))$	2	2	4	4	4	4	2	2	2	3	4	2	0	4	3
$d\left(x_{17}\right|f_t\left(R\right))$	2	2	4	3	3	3	2	2	2	3	3	2	2	4	3
$d\left(x_{18}\right|f_t\left(R\right))$	3	3	3	3	3	3	3	3	3	2	3	3	3	3	0
$d\left(x_{19}\right|f_t\left(R\right))$	4	4	4	0	2	2	3	3	3	3	2	4	3	4	3
$d\left(x_{20}\right|f_t\left(R\right))$	4	4	4	2	0	2	3	3	3	3	2	4	3	4	3
$d\left(x_{21}\right|f_t\left(R\right))$	2	2	4	2	2	2	2	2	2	3	2	2	2	4	3
$d\left(x_{22}\right|f_t\left(R\right))$	2	2	3	4	4	4	2	2	2	3	4	0	2	3	3
$d\left(x_{23}\right|f_t\left(R\right))$	4	4	4	2	2	0	3	3	3	3	2	4	3	4	3
$d\left(x_{24}\right|f_t\left(R\right))$	2	2	4	4	4	2	0	2	2	3	4	2	2	4	3
$d\left(x_{25}\right|f_t\left(R\right))$	2	2	4	4	4	2	2	0	2	3	4	2	2	4	3
$d\left(x_{26}\right|f_t\left(R\right))$	4	4	4	2	2	2	4	4	4	3	2	4	4	4	3
$d\left(x_{27}\right|f_t\left(R\right))$	2	2	4	4	4	2	2	2	0	3	4	2	2	4	3

) are as follows:

Now, for each $a\in f_t\left(R\right)$, let $f_t^{\prime }\left(R\right)=f_t\left(R\right)-\left\{a\right\}$. It is necessary to demonstrate that $f_t^{\prime }\left(R\right)$ is also a resolving set. For example, if $a=x_9$, then

$$f_t^{\prime }\left(R\right)=(x_{10},x_{11},x_{19},x_{20},x_{23},x_{24},x_{25},x_{27},x_{13},x_{26},x_{22},x_{16},x_7,x_{18}).$$

It is now necessary to demonstrate that $f_t^{\prime }\left(R\right)$ is also a resolving set.

Distinct representations of vertices with respect to $f_t^{\prime }\left(R\right)$ (

Table 2. Distinct representations of vertices w.r.t to $f_t\left(R\right)$.

${\mathit{f}}_{\mathit{t}}\left(\mathit{R}\right)$	${\mathit{x}}_{10}$	${\mathit{x}}_{11}$	${\mathit{x}}_{19}$	${\mathit{x}}_{20}$	${\mathit{x}}_{23}$	${\mathit{x}}_{24}$	${\mathit{x}}_{25}$	${\mathit{x}}_{27}$	${\mathit{x}}_{13}$	${\mathit{x}}_{26}$	${\mathit{x}}_{22}$	${\mathit{x}}_{16}$	${\mathit{x}}_7$	${\mathit{x}}_{18}$
$d\left(x_1\right|f_t\left(R\right))$	3	3	1	1	1	3	3	3	2	1	3	3	3	2
$d\left(x_2\right|f_t\left(R\right))$	2	2	3	3	3	2	2	2	3	3	1	2	2	3
$d\left(x_3\right|f_t\left(R\right))$	1	3	3	3	3	1	1	1	2	3	1	1	3	2
$d\left(x_4\right|f_t\left(R\right))$	2	2	2	2	2	2	2	2	1	2	2	2	2	1
$d\left(x_5\right|f_t\left(R\right))$	2	3	2	2	2	2	2	2	1	2	2	2	3	3
$d\left(x_6\right|f_t\left(R\right))$	3	1	2	2	2	3	3	3	2	2	2	3	1	2
$d\left(x_7\right|f_t\left(R\right))$	4	2	3	3	3	4	4	4	3	3	3	4	0	3
$d\left(x_8\right|f_t\left(R\right))$	3	3	2	2	2	3	3	3	2	3	3	3	3	2
$d\left(x_9\right|f_t\left(R\right))$	2	3	4	4	4	2	2	2	3	4	2	2	3	3
$d\left(x_{10}\right|f_t\left(R\right))$	0	4	4	4	4	2	2	2	3	4	2	2	4	3
$d\left(x_{11}\right|f_t\left(R\right))$	4	0	3	3	3	4	4	4	3	4	3	4	2	3
$d\left(x_{12}\right|f_t\left(R\right))$	3	4	3	3	3	3	3	3	4	3	3	3	4	4
$d\left(x_{13}\right|f_t\left(R\right))$	3	3	3	3	3	3	3	3	0	3	3	3	3	2
$d\left(x_{14}\right|f_t\left(R\right))$	2	2	3	3	3	2	2	2	3	3	2	2	2	1
$d\left(x_{15}\right|f_t\left(R\right))$	3	3	4	4	4	3	3	3	4	4	2	3	3	4
$d\left(x_{16}\right|f_t\left(R\right))$	2	4	4	4	4	2	2	2	3	4	2	0	4	3
$d\left(x_{17}\right|f_t\left(R\right))$	2	4	3	3	3	2	2	2	3	3	2	2	4	3
$d\left(x_{18}\right|f_t\left(R\right))$	3	3	3	3	3	3	3	3	2	3	3	3	3	0
$d\left(x_{18}\right|f_t\left(R\right))$	3	3	3	3	3	3	3	3	2	3	3	3	3	0
$d\left(x_{19}\right|f_t\left(R\right))$	4	4	0	2	2	3	3	3	3	2	4	3	4	3
$d\left(x_{20}\right|f_t\left(R\right))$	4	4	2	0	2	3	3	3	3	2	4	3	4	3
$d\left(x_{21}\right|f_t\left(R\right))$	2	4	2	2	2	2	2	2	3	2	2	2	4	3
$d\left(x_{22}\right|f_t\left(R\right))$	2	3	4	4	4	2	2	2	3	4	0	2	3	3
$d\left(x_{23}\right|f_t\left(R\right))$	4	4	2	2	0	3	3	3	3	2	4	3	4	3
$d\left(x_{24}\right|f_t\left(R\right))$	2	4	4	4	2	0	2	2	3	4	2	2	4	3
$d\left(x_{25}\right|f_t\left(R\right))$	2	4	4	4	2	2	0	2	3	4	2	2	4	3
$d\left(x_{26}\right|f_t\left(R\right))$	4	4	2	2	2	4	4	4	3	2	4	4	4	3
$d\left(x_{27}\right|f_t\left(R\right))$	2	4	4	4	2	2	2	0	3	4	2	2	4	3

) are as follows:

Similar to this, we obtain distinct metric codes for every resolving set when we remove $(x_{11},x_{19},x_{20}$, $x_{23},x_{24},x_{25},x_{27},x_{13},x_{26},x_{22},x_{16},x_7,x_{18})$ from the FTRS $f_t\left(R\right)$.

As a result, we obtain distinct representations for every resolving set from FTRS. Thus, $f_{t}dim\left(Z_v\right))\ge 15$ is the fault-tolerant metric dimension of $Z_v$.

Secondly To confirm minimality, assume $f_{t}dim\left(Z_v\right)\le 14$. Assume that any resolving set for $Z_v$ is $f_t\left(R\right)$. It follows that $f_t\left(R\right)$= $(x_9,x_{10},x_{11},x_{19},x_{20},x_{23},x_{25},x_{27},x_{13},x_{26},x_{22},x_{16}$, $x_7,x_{18})$ is an FTRS. It is observed that the metric representations cease to be unique for the resolving sets when the vertex $x_{25}$ is removed. In this case, $f_t^{\prime }\left(R\right)=(x_9,x_{10},x_{11},x_{19},x_{20},x_{23}$; that is, $d(x_{24}\mid f_t^{\prime }\left(R\right))=d(x_{25}\mid f_t^{\prime }\left(R\right))$. Likewise, if we suppose $f_t\left(R\right)$= $(x_9,x_{10},x_{11},x_{20},x_{23},x_{24}{x}_{25}$, $x_{27},x_{13},x_{26},x_{22},x_{16},x_7,x_{18})$ is an FTRS and after we eliminate a vertex $x_{20}$, the metric representations for the resolving set are once again not unique. For example, for $f_t^{\prime }\left(R\right)$= $(x_9,x_{10},x_{11},x_{23},x_{24}{x}_{25}$,$x_{27},x_{13},x_{26},x_{22},x_{16},x_7,x_{18})$, then $d\left(x_{19}\right|f_t^{\prime }\left(R\right))=d\left(x_{20}\right|f_t^{\prime }\left(R\right))$ and so forth. Accordingly, $f_t\left(R\right)\nleqq 14$.

Therefore, graph $Z_v$ has a fault-tolerant metric dimension of 15, or $f_{t}dim\left(Z_v\right)=15$.

3.2. Fault-Tolerant Edge Metric Dimension of Zero-Divisor Graph Obtained from Upper Triangular Matrix of $M_3\left({\mathbb{Z}}_2\right)$

Figure 2$\left(Z_e\right)$ illustrates the structure of the zero-divisor graph in terms of its edges, where each edge represents a commutative zero-product relationship between two vertices. For clarity, we label each edge individually: for example, the edge between $X_1$ and $X_2$ is denoted as $Y_1$, the edge between $X_1$ and $X_{20}$ as $Y_2$, the edge between $X_1$ and $X_{19}$ as $Y_3$ and so on (as shown in Figure 2). In this context, an edge $Y_i=(X_j,X_k)$ indicates that the product of matrices $X_j$ and $X_k$ is zero in both directions: $X_j·X_k=0=X_k·X_j$. This mutual zero-product property confirms that $X_j$ and $X_k$ are commutative zero-divisors. As a result, the graph visually represents how these zero-divisors interact through commutative ring.

Using the following theorem, we compute the fault-tolerant edge metric dimension of the zero-divisor graph derived from the upper triangular matrix of $M_3\left({\mathbb{Z}}_2\right)$.

Theorem 2.

Let $Z_e$ be the zero-divisor graph (in terms of its edges) obtained from upper triangular matrix ring $M_3\left({\mathbb{Z}}_2\right)$. Then, the fault-tolerant of the associated graph is, i.e., $f_{t}edim\left(Z_e\right))\ge 19$.

Proof. 

The proof follows in two steps: In the first, we exhibit a resolving set of size 15 and show it is fault-tolerant by providing unique representations for all vertices and then, we prove by contradiction that no smaller set suffices.

Let $f_{t}e\left(R\right)$ be a resolving set for the zero-divisor graph $Z_e$ (

Table 3. Distinct representations of edges w.r.t to $f_{l}e\left(R\right)$.

${\mathit{f}}_{\mathit{l}}\mathit{e}\left(\mathit{R}\right)$	${\mathit{Y}}_1$	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	${\mathit{Y}}_{13}$	${\mathit{Y}}_{16}$	${\mathit{Y}}_{17}$	${\mathit{Y}}_{20}$	${\mathit{Y}}_{21}$	${\mathit{Y}}_{28}$	${\mathit{Y}}_{29}$	${\mathit{Y}}_{30}$	${\mathit{Y}}_{31}$	${\mathit{Y}}_{32}$	${\mathit{Y}}_{33}$	${\mathit{Y}}_{34}$	${\mathit{Y}}_{35}$	${\mathit{Y}}_{36}$	${\mathit{Y}}_{38}$
$d\left(Y_1\right|f_{l}e\left(R\right))$	0	1	1	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_2\right|f_{l}e\left(R\right))$	1	0	1	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_3\right|f_{l}e\left(R\right))$	1	1	0	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_4\right|f_{l}e\left(R\right))$	1	1	1	0	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_5\right|f_{l}e\left(R\right))$	1	1	1	1	2	2	2	3	3	3	3	2	2	2	2	2	2	2	2
$d\left(Y_6\right|f_{l}e\left(R\right))$	1	1	1	1	2	2	2	1	1	2	2	3	3	3	3	3	3	3	2
$d\left(Y_7\right|f_{l}e\left(R\right))$	1	1	1	1	2	1	1	2	2	3	3	2	2	2	2	2	2	2	1
$d\left(Y_8\right|f_{l}e\left(R\right))$	1	1	1	1	2	2	2	3	3	3	3	3	3	3	3	3	3	3	2
$d\left(Y_9\right|f_{l}e\left(R\right))$	1	1	1	1	1	2	2	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{10}\right|f_{l}e\left(R\right))$	2	2	2	2	1	2	2	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{11}\right|f_{l}e\left(R\right))$	2	2	2	2	2	1	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{12}\right|f_{l}e\left(R\right))$	2	2	2	2	1	3	3	2	2	3	3	2	2	2	2	2	2	2	3
$d\left(Y_{13}\right|f_{l}e\left(R\right))$	2	2	2	2	0	3	3	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{14}\right|f_{l}e\left(R\right))$	3	3	3	3	1	3	3	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{15}\right|f_{l}e\left(R\right))$	2	2	2	2	1	3	3	1	1	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{16}\right|f_{l}e\left(R\right))$	2	2	2	2	3	0	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{17}\right|f_{l}e\left(R\right))$	2	2	2	2	3	1	0	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{18}\right|f_{l}e\left(R\right))$	2	2	2	2	1	2	2	2	2	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{19}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	1	3	3	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{20}\right|f_{l}e\left(R\right))$	2	2	2	2	2	3	3	0	1	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{21}\right|f_{l}e\left(R\right))$	2	2	2	2	2	3	3	1	0	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{22}\right|f_{l}e\left(R\right))$	2	2	2	2	2	1	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{23}\right|f_{l}e\left(R\right))$	2	2	2	2	2	3	3	1	1	1	1	2	2	2	2	2	2	2	3
$d\left(Y_{24}\right|f_{l}e\left(R\right))$	2	2	2	2	2	2	2	3	3	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{25}\right|f_{l}e\left(R\right))$	2	2	2	2	2	3	3	1	1	2	2	2	2	2	2	2	2	2	2
$d\left(Y_{26}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	2	2	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{27}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	3	2	2	1	1	2	2	2	2	2	2	2	2
$d\left(Y_{28}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	3	2	2	0	1	1	2	2	2	2	2	2	2
$d\left(Y_{29}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	3	2	2	1	0	2	1	2	2	2	2	2	2
$d\left(Y_{30}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	1	2	0	1	1	1	1	1	1	1
$d\left(Y_{31}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	1	1	0	1	1	1	1	1	1
$d\left(Y_{32}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	2	1	1	0	1	1	1	1	1
$d\left(Y_{33}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	2	1	1	1	0	1	1	1	1
$d\left(Y_{34}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	2	1	1	1	1	0	1	1	1
$d\left(Y_{35}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	2	1	1	1	1	1	0	1	1
$d\left(Y_{36}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	2	2	1	1	1	1	1	1	0	1
$d\left(Y_{37}\right|f_{l}e\left(R\right))$	3	3	3	3	2	2	2	3	3	1	1	1	1	1	1	1	1	1	1
$d\left(Y_{38}\right|f_{l}e\left(R\right))$	2	2	2	2	2	1	1	3	3	2	2	1	1	1	1	1	1	1	0

). Now, the given set:

$$f_{te}\left(R\right)=\{Y_1,Y_2,Y_3,Y_4,Y_{13},Y_{16},Y_{17},Y_{20},Y_{21},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{38}\}$$

is fault-tolerant edge resolving set. □

Now suppose $a\in f_{t}e\left(R\right)$ and $f_t{e}^{\prime }\left(R\right)=f_{t}e\left(R\right)-\left\{a\right\}$. If $a=Y_1$, then $f_t{e}^{\prime }\left(R\right)=(Y_2,Y_3,Y_4,Y_{20},Y_{21},Y_{13},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{16},Y_{17},Y_{38})$ (The elements are now listed in sequential index order in the (

Table 4. Distinct representations of edges w.r.t to f_le′ (R).

fle′ (R)	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	${\mathit{Y}}_{13}$	${\mathit{Y}}_{16}$	${\mathit{Y}}_{17}$	${\mathit{Y}}_{20}$	${\mathit{Y}}_{21}$	${\mathit{Y}}_{28}$	${\mathit{Y}}_{29}$	${\mathit{Y}}_{30}$	${\mathit{Y}}_{31}$	${\mathit{Y}}_{32}$	${\mathit{Y}}_{33}$	${\mathit{Y}}_{34}$	${\mathit{Y}}_{35}$	${\mathit{Y}}_{36}$	${\mathit{Y}}_{38}$
$d\left(Y_1\right|f_{l}e\left(R\right))$	1	1	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_2\right|f_{l}e\left(R\right))$	0	1	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_3\right|f_{l}e\left(R\right))$	1	0	1	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_4\right|f_{l}e\left(R\right))$	1	1	0	2	2	2	4	4	3	3	3	3	3	3	3	3	3	2
$d\left(Y_5\right|f_{l}e\left(R\right))$	1	1	1	2	2	2	3	3	3	3	2	2	2	2	2	2	2	2
$d\left(Y_6\right|f_{l}e\left(R\right))$	1	1	1	2	2	2	1	1	2	2	3	3	3	3	3	3	3	2
$d\left(Y_7\right|f_{l}e\left(R\right))$	1	1	1	2	1	1	2	2	3	3	2	2	2	2	2	2	2	1
$d\left(Y_8\right|f_{l}e\left(R\right))$	1	1	1	2	2	2	3	3	3	3	3	3	3	3	3	3	3	2
$d\left(Y_9\right|f_{l}e\left(R\right))$	1	1	1	1	2	2	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{10}\right|f_{l}e\left(R\right))$	2	2	2	1	2	2	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{11}\right|f_{l}e\left(R\right))$	2	2	2	2	1	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{12}\right|f_{l}e\left(R\right))$	2	2	2	1	3	3	2	2	3	3	2	2	2	2	2	2	2	3
$d\left(Y_{13}\right|f_{l}e\left(R\right))$	2	2	2	0	3	3	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{14}\right|f_{l}e\left(R\right))$	3	3	3	1	3	3	2	2	3	3	2	2	2	2	2	2	2	2
$d\left(Y_{15}\right|f_{l}e\left(R\right))$	2	2	2	1	3	3	1	1	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{16}\right|f_{l}e\left(R\right))$	2	2	2	3	0	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{17}\right|f_{l}e\left(R\right))$	2	2	2	3	1	0	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{18}\right|f_{l}e\left(R\right))$	2	2	2	1	2	2	2	2	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{19}\right|f_{l}e\left(R\right))$	3	3	3	2	2	1	3	3	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{20}\right|f_{l}e\left(R\right))$	2	2	2	2	3	3	0	1	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{21}\right|f_{l}e\left(R\right))$	2	2	2	2	3	3	1	0	2	2	3	3	3	3	3	3	3	3
$d\left(Y_{22}\right|f_{l}e\left(R\right))$	2	2	2	2	1	1	3	3	3	3	2	2	2	2	2	2	2	1
$d\left(Y_{23}\right|f_{l}e\left(R\right))$	2	2	2	2	3	3	1	1	1	1	2	2	2	2	2	2	2	3
$d\left(Y_{24}\right|f_{l}e\left(R\right))$	2	2	2	2	2	2	3	3	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{25}\right|f_{l}e\left(R\right))$	2	2	2	2	3	3	1	1	2	2	2	2	2	2	2	2	2	2
$d\left(Y_{26}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	2	2	2	2	1	1	1	1	1	1	1	1
$d\left(Y_{27}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	2	2	1	1	2	2	2	2	2	2	2	2
$d\left(Y_{28}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	2	2	0	1	1	2	2	2	2	2	2	2
$d\left(Y_{29}\right|f_{l}e\left(R\right))$	3	3	3	3	3	3	2	2	1	0	2	1	2	2	2	2	2	2
$d\left(Y_{30}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	1	2	0	1	1	1	1	1	1	1
$d\left(Y_{31}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	1	1	0	1	1	1	1	1	1
$d\left(Y_{32}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	2	1	1	0	1	1	1	1	1
$d\left(Y_{33}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	2	1	1	1	0	1	1	1	1
$d\left(Y_{34}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	2	1	1	1	1	0	1	1	1
$d\left(Y_{35}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	2	1	1	1	1	1	0	1	1
$d\left(Y_{36}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	2	2	1	1	1	1	1	1	0	1
$d\left(Y_{37}\right|f_{l}e\left(R\right))$	3	3	3	2	2	2	3	3	1	1	1	1	1	1	1	1	1	1
$d\left(Y_{38}\right|f_{l}e\left(R\right))$	2	2	2	2	1	1	3	3	2	2	1	1	1	1	1	1	1	0

)).

Now we have to show that $f_t{e}^{\prime }\left(R\right)$ is also a resolving set.

Following are the Distinct representations of edges w.r.t to $f_t{e}^{\prime }\left(R\right)$ (Table 4):

Similarly, if we delete $\{Y_3,Y_4,Y_{20},Y_{21},Y_{13},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{16}$, $Y_{17},Y_{38}\}$ from the FTRS $f_{t}e\left(R\right)$ and the remaining edges of the graph are still able to uniquely identify each other edge.

As a result, we obtain distinct representations for every resolving set from FTRS. Thus, $f_{t}dim\left(Z_e\right))\ge 19$ is the fault-tolerant metric dimension of $Z_e$.

In the second step, to confirm minimality, assume $f_{t}dim\left(Z_e\right)\le 18$. Suppose there exists a smaller resolving set $f_t\left(R\right)$. Assume that any resolving set for $Z_e$ is $f_{t}e\left(R\right)$. Suppose $f_{t}e\left(R\right)$= $(Y_1,Y_2,Y_3,Y_4,Y_{20},Y_{21}$, $Y_{13},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{16},Y_{17})$ is a FTRS. Now, if we remove a edge $Y_{16}$, then the metric representations is not unique for resolving set $f_t{e}^{\prime }\left(R\right)$= $(Y_1,Y_2,Y_3,Y_4,Y_{20},Y_{21},Y_{13},Y_{28},Y_{29}$, $Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{17})$, i.e., $d\left(Y_{24}\right|f_t{e}^{\prime }\left(R\right))=d\left(Y_{38}\right|f_t{e}^{\prime }\left(R\right))$. Similarly when we assume $f_{t}e\left(R\right)$= $(Y_1,Y_2,Y_3,Y_4,Y_{20},Y_{21}$, $Y_{13},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{17},Y_{38})$ is a FTRS and when we remove a edge $Y_{17}$, again the metric representations is not unique for resolving set $f_t{e}^{\prime }\left(R\right)$ = $(Y_1$, $Y_2,Y_3,Y_4,Y_{20},Y_{21},Y_{13},Y_{28},Y_{29},Y_{30},Y_{31},Y_{32},Y_{33},Y_{34},Y_{35},Y_{36},Y_{38}$), i.e., $d\left(Y_{16}\right|f_t{e}^{\prime }\left(R\right))=d\left(Y_{17}\right|f_t{e}^{\prime }\left(R\right))$ and so on. Therefore $f_{t}e\left(R\right)\nleqq 18$.

Therefore, the fault-tolerant metric dimension of graph $Z_e$ is 19, or $f_{t}edim\left(Z_e\right)=19$.

4. Applications in Robotics of Fault-Tolerant and Fault-Tolerant Edge Metric Dimension of Zero-Divisors Graph Obtained for Upper Triangular Matrix in Robotics and Autonomous Navigation

4.1. Localization

Localization requires a robot to determine its unique position in a navigation graph. In $\Gamma \left(M_n\left(R\right)\right)$, vertices represent robot states (e.g., positions encoded by matrices in $M_n\left(R\right)$ and landmarks (elements of S are sensors or beacons (e.g., Wi-Fi access points). The FTMD ensures that each position has a unique distance vector, even if one landmark fails.

For a robot in a warehouse modeled by $\Gamma \left(T_2\left({\mathbb{Z}}_2\right)\right)$ with vertices as matrices $\left(\begin{array}{cc}0& a\\ 0& b\end{array}\right)$, $a,b\in \{0,1\}$, the position is computed via

$$r\left(v\right|S)\ne r(w\left|S\right)\forall v\ne w,$$

and for any $s_i\in S$,

$$r\left(v\right|S\backslash \left\{s_i\right\})\ne r\left(w\right|S\backslash \left\{s_i\right\}).$$

This allows the robot to localize using distances (e.g., signal strength or time-of-flight) to landmarks, ensuring reliability despite sensor failures. For example, a robot may use three landmarks to form a FTRS, ensuring unique identification even if one beacon malfunctions.

4.2. Path Planning

Path planning involves identifying specific paths (edges) between states. In $\Gamma \left(T_n\left(R\right)\right)$, edges represent feasible transitions (e.g., moving along a corridor). The FTEMD ensures that each edge has a unique distance vector to $W_E$, even after removing any $w_i\in W_E$:

$$r_E\left(e_1\right|W_E)\ne r_E\left(e_2\right|W_E),$$

and similarly for $W_E\backslash \left\{w_i\right\}$. For a drone navigating waypoints, where edges represent paths and zero-divisor constraints (e.g., $AB=0$ indicate blocked transitions, FTEMD ensures robust path selection. This is critical in dynamic environments with obstacles, ensuring the drone can distinguish between routes (e.g., different corridors) despite a sensor failure.

4.3. Practical Implementation

Computing FTMD and FTEMD involves solving combinatorial optimization problems. For FTMD, minimize $\left|S\right|$ subject to

$$\forall v\ne w,\exists s_i\in S\mathrm{such}\mathrm{that}d(v,s_i)\ne d(w,s_i),$$

and the same for $S\backslash \left\{s_i\right\}$. For FTEMD, minimize $|W_E|$ with analogous constraints for edges. These problems are often NP-hard, requiring heuristics or integer linear programming for practical computation.

Example 1.

Consider a robot in a warehouse modeled by $\Gamma \left(T_2\left({\mathbb{Z}}_2\right)\right)$. Vertices are matrices $\left(\begin{array}{cc}0& a\\ 0& b\end{array}\right)$, $a,b\in \{0,1\}$, representing positions. Edges exist if $AB=0$, indicating valid transitions. A FTRS S (e.g., two or three matrices) ensures localization with distances measured via sensors (e.g., LIDAR). The FTEMD supports path planning by ensuring unique identification of transitions, enabling the robot to navigate reliably even if one sensor fails.

In practice, robots use sensors (e.g., LIDAR, GPS) to measure distances to landmarks, mapping these to $\Gamma \left(T_n\left(R\right)\right)$. The robot compares its distance vector to precomputed resolving sets, stored in a lookup table or computed online. Fault tolerance is achieved by ensuring redundancy in landmark placementand maintaining system functionality despite single-point failures.

5. Discussion

The results show that the fault-tolerant edge metric dimension of $Z_e$ (19) is greater than the fault-tolerant metric dimension of $Z_v$ (15). This indicates that distinguishing edges is inherently more complex than distinguishing vertices in this algebraic structure. While FTMD focuses on vertex localization, FTEMD involves differentiating edge pairs, which requires more reference points due to additional relational dependencies. Hence, the higher FTEMD reflects the greater structural complexity and information redundancy needed for reliable edge identification in $Z_e$.

6. Conclusions

In this study, we determined the fault-tolerant metric dimension (FTMD) and the fault-tolerant edge metric dimension (FTEMD) of a zero-divisor graph, $Z_v$ and $Z_e$, respectively, obtaining $f_{t}dim\left(Z_v\right)=15$ and $f_{t}edim\left(Z_e\right)=19$. These values quantify the minimum number of vertices and edges required to ensure unique identification in the presence of faults.

The difference between FTMD and FTEMD has practical implications. A smaller FTMD (15) indicates that vertex-based localization systems, such as sensor networks for node identification, can operate efficiently with fewer reference points, whereas the higher FTEMD (19) reflects the greater complexity required when distinguishing edges, relevant for path planning and communication link reliability.

In multi-robot or network-centric systems, these metrics guide the placement of sensors or communication nodes to ensure robust coordination. The FTMD ensures reliable node localization even under sensor failure, while the FTEMD guarantees unique identification of paths or communication links, aiding fault-tolerant navigation and routing in networks with multiple robots.

Overall, these findings not only deepen the theoretical understanding of zero-divisor graphs but also provide actionable guidance for designing resilient sensor networks and path-planning systems that maintain reliability under faults.