A Three-Machine Flowshop Scheduling Problem with Linear Fatigue Effect
Abstract
1. Introduction
2. Literature Survey
3. Problem Description
3.1. MIP Model
| Set of machines | |
| Set of jobs | |
| Set of positions | |
| A very large positive constant | |
| Normal processing time of job j on machine i | |
| Processing time at position k on machine i | |
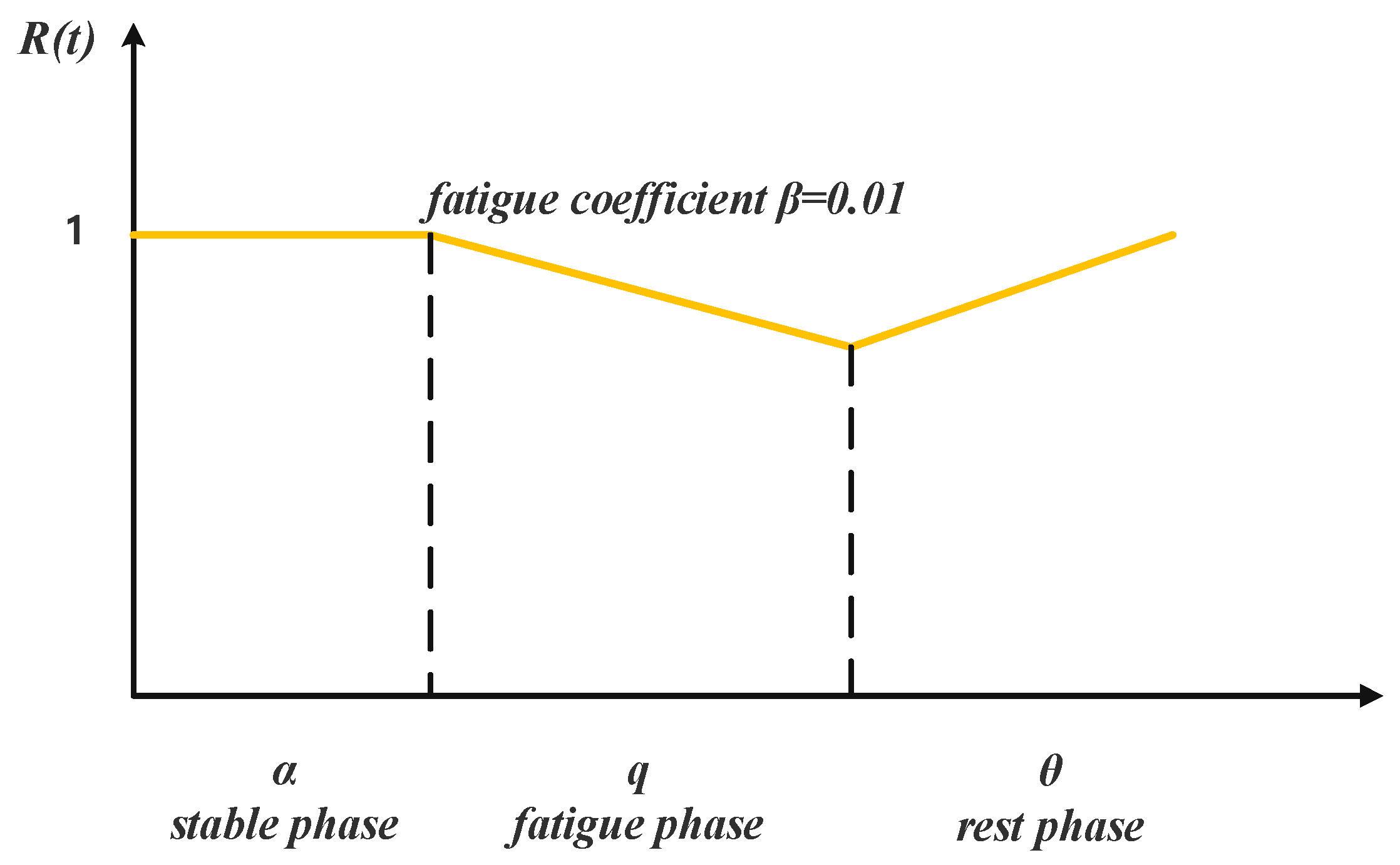
| Duration of the worker’s stable period | |
| Efficiency decay coefficient during the fatigue period | |
| Duration of the rest period | |
| Makespan (maximum completion time) | |
| Start time at position k on machine i | |
| Completion time at position k on machine i | |
| Stable period processing time for the j-th job in the second stage | |
| Fatigue period processing time for the j-th job in the second stage | |
| Accumulated working time before processing the j-th job in the second stage | |
| Accumulated working time after processing the j-th job in the second stage |
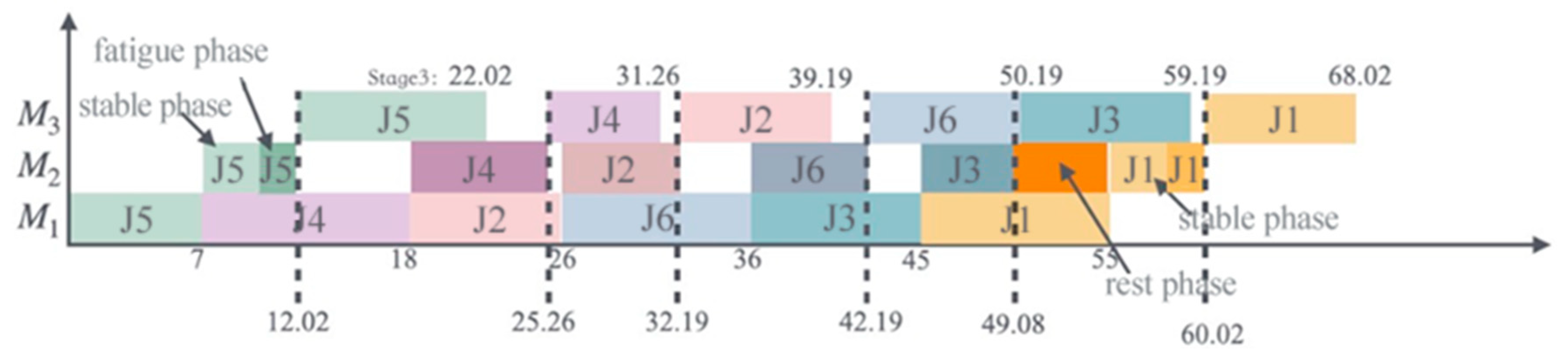
3.2. A Scheduling Instance
4. Iterated Tabu Search Algorithm
4.1. Encoding and Decoding
4.1.1. Encoding Method
- (1)
- Job Sequence Encoding:
- (2)
- Rest Point Encoding:
4.1.2. Decoding Method
- (1)
- Completion Time Calculation
| Pseudocode 1: Completion Time Calculation (Stage 1) | |
| 1 | Start |
| 2 | // Initialize start and completion time |
| 3 | |
| 4 | For k from 2 to n do |
| 5 | |
| 6 | |
| 7 | End |
| Pseudocode 2: Completion Time Calculation with Fatigue Effect (Stage 2) | |
| 1 | Start |
| 2 | Initialize cumulative working time to 0 |
| 3 | For k ← 1 to n do //Iterate through jobs starting from the first |
| 4 | // Step 1: Determine the start time of the current job |
| 5 | If then //If the current position is the planned rest point |
| 6 | //Start time must account for rest duration |
| 7 | Reset cumulative working time to zero after rest |
| 8 | Else |
| 9 | //Normal flow-shop rule |
| 10 | Cumulative working time ← Cumulative working time from the previous round |
| 11 | // Step 2: Calculate actual processing time based on fatigue effect |
| 12 | If job is processed entirely within the stable period α |
| 13 | |
| 14 | Else if job processing spans the stable and fatigue periods |
| 15 | |
| 16 | |
| 17 | calculate based on fatigue formula |
| 18 | |
| 19 | Else //Job is processed entirely within the fatigue period |
| 20 | calculate based on fatigue formula |
| 21 | End if |
| 23 | // Step 3: Update completion time and cumulative working time |
| 24 | |
| 25 | Cumulative working time |
| 26 | End for |
| 27 | End |
| Pseudocode 3: Completion Time Calculation | |
| 1 | Start |
| 2 | ←//Initialize start and completion time |
| 3 | ← |
| 4 | for k from 2 to n do |
| 5 | ← |
| 6 | ← |
| 7 | End |
- (2)
- Decision on Completion Time
4.2. Initial Population
| Pseudocode 4: Initial Population | |
| 1 | Start |
| 2 | For each job j∈{1, …, n} do |
| 3 | // Step 1: Calculate weighted priority index |
| 4 | wj ← w1·p1,j + w2·p2,j + w3·p3,j |
| 5 | End for |
| 6 | Sort jobs in descending order of wj |
| 7 | Construct greedy-based job sequence πg = (π1, π2, …, πn) |
| 8 | Add solution (πg, r) into initial population |
| 9 | // Step 2: Generate additional random sequences |
| 10 | For j = 1 to rand do |
| 11 | Generate random permutation πrand |
| 12 | Generate random rest point rrand∈{1, …, n} |
| 13 | Add solution (πrand, rrand) into initial population |
| 14 | End for |
| 15 | // Step 3: Combine greedy and random solutions |
| 16 | Return initial population {(π, r)} |
| 17 | End |
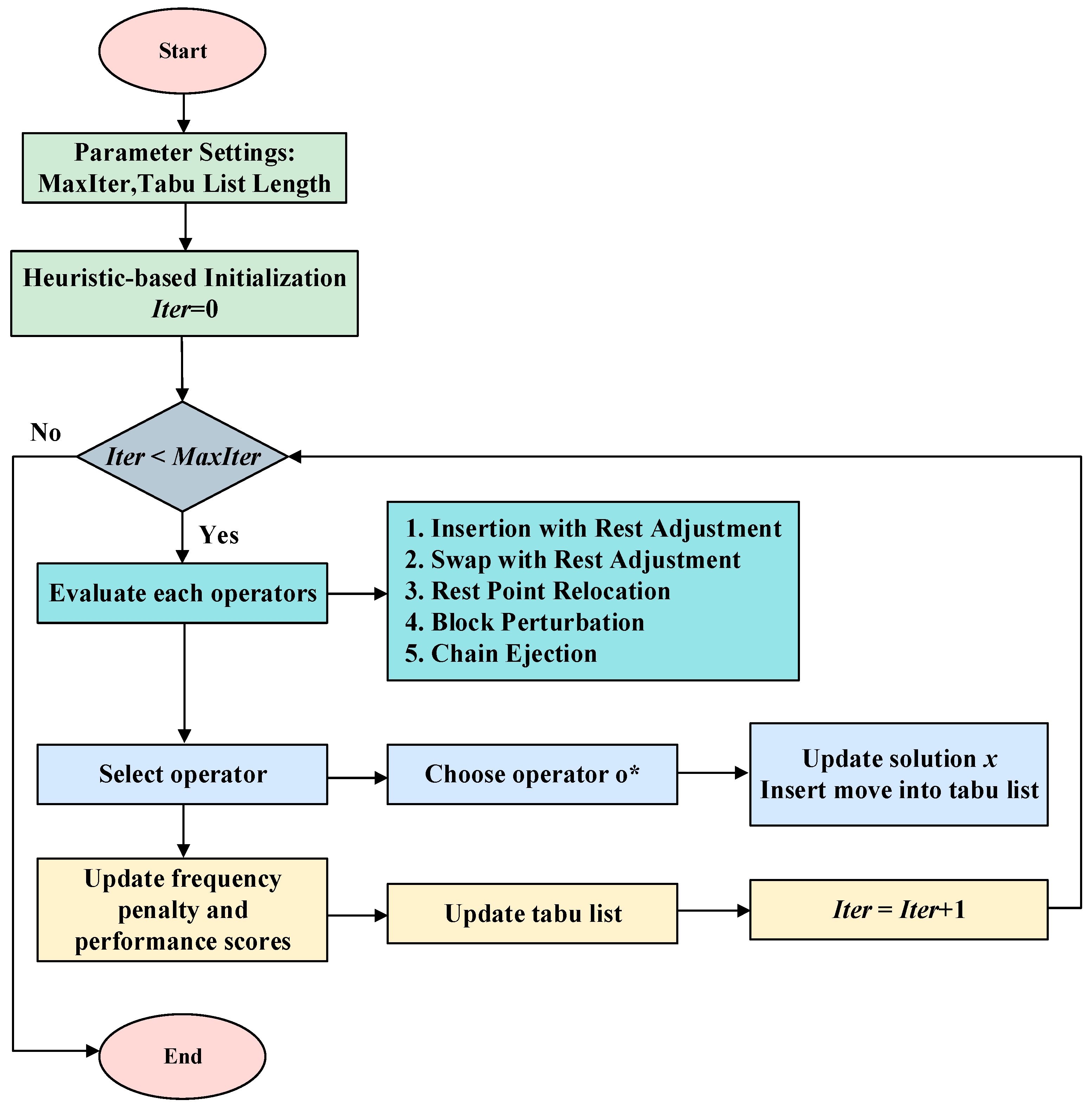
4.3. Tabu-Based Adaptive Search Mechanism
4.3.1. Problem-Specific Search Operators
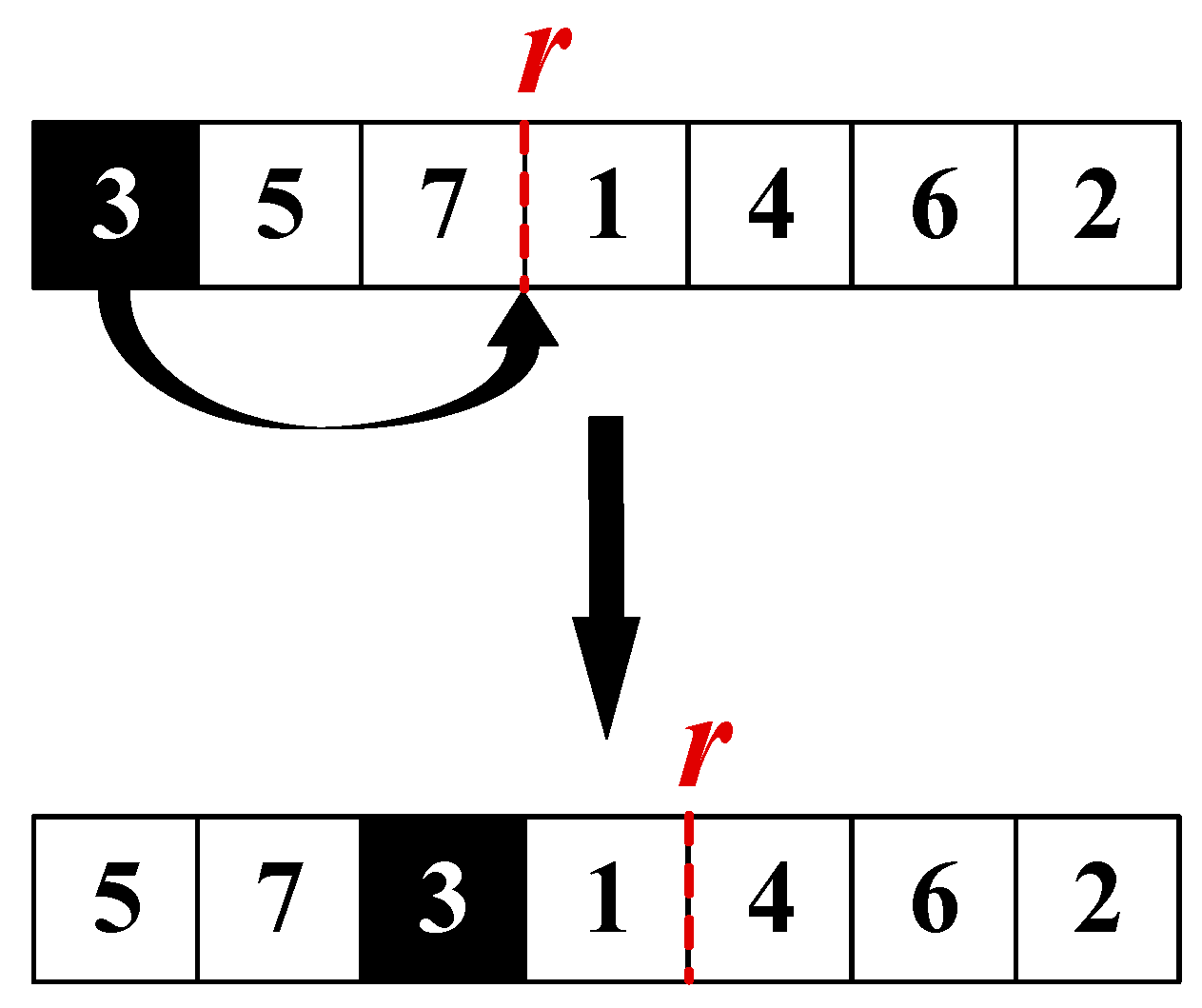
- (1)
- Insertion with Rest Adjustment
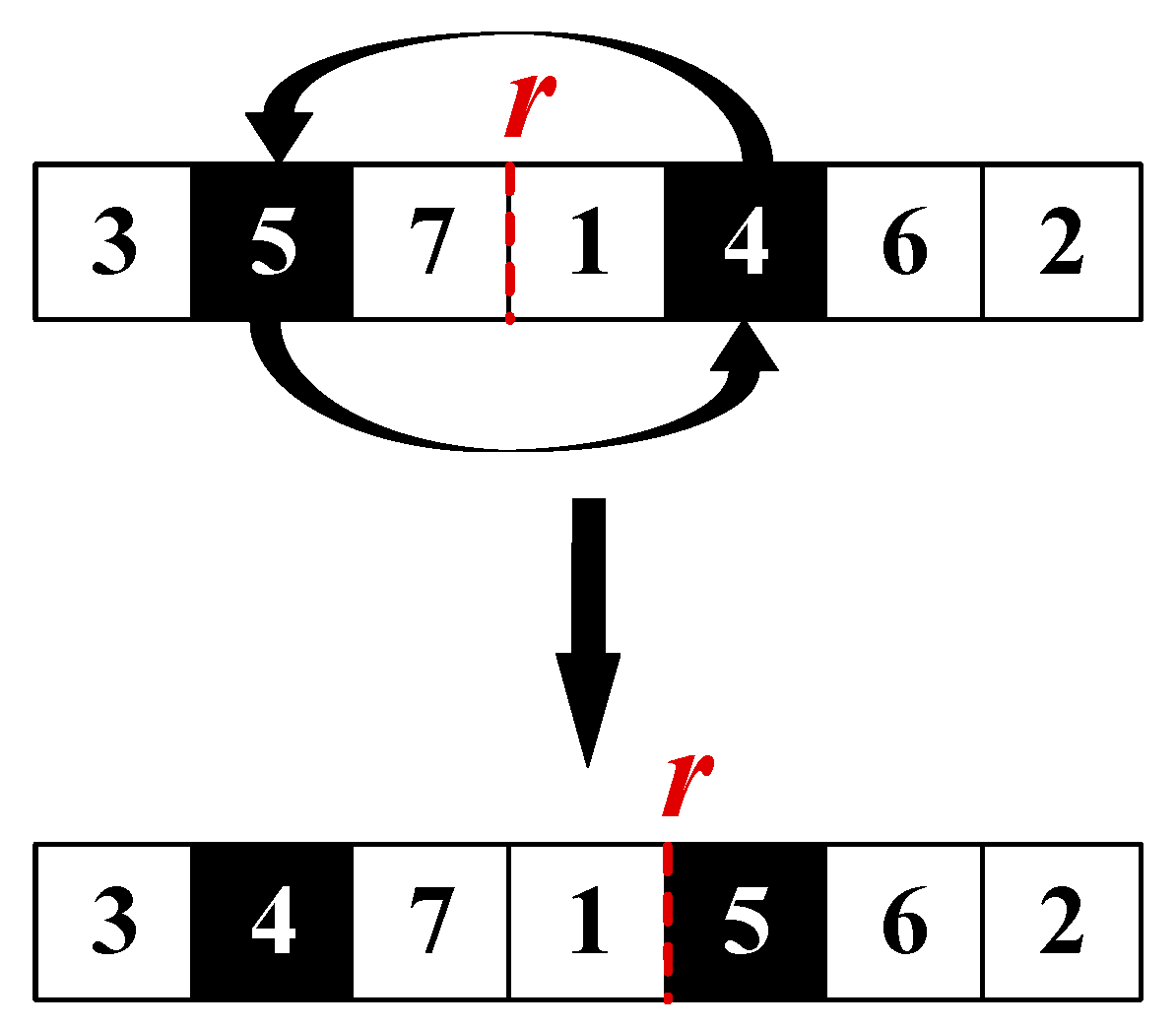
- (2)
- Swap with Rest Adjustment
- (3)
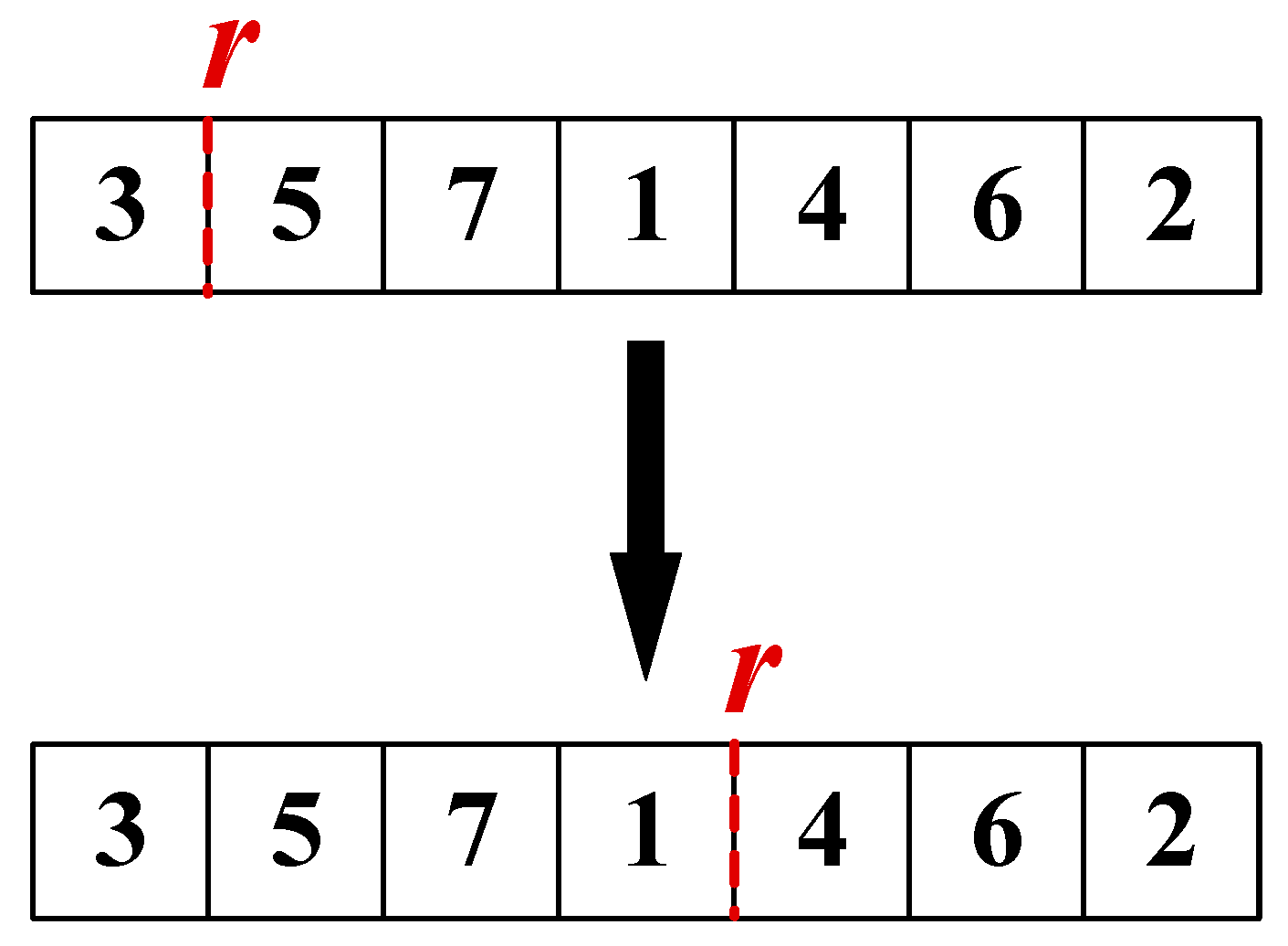
- Rest Point Relocation
- (4)
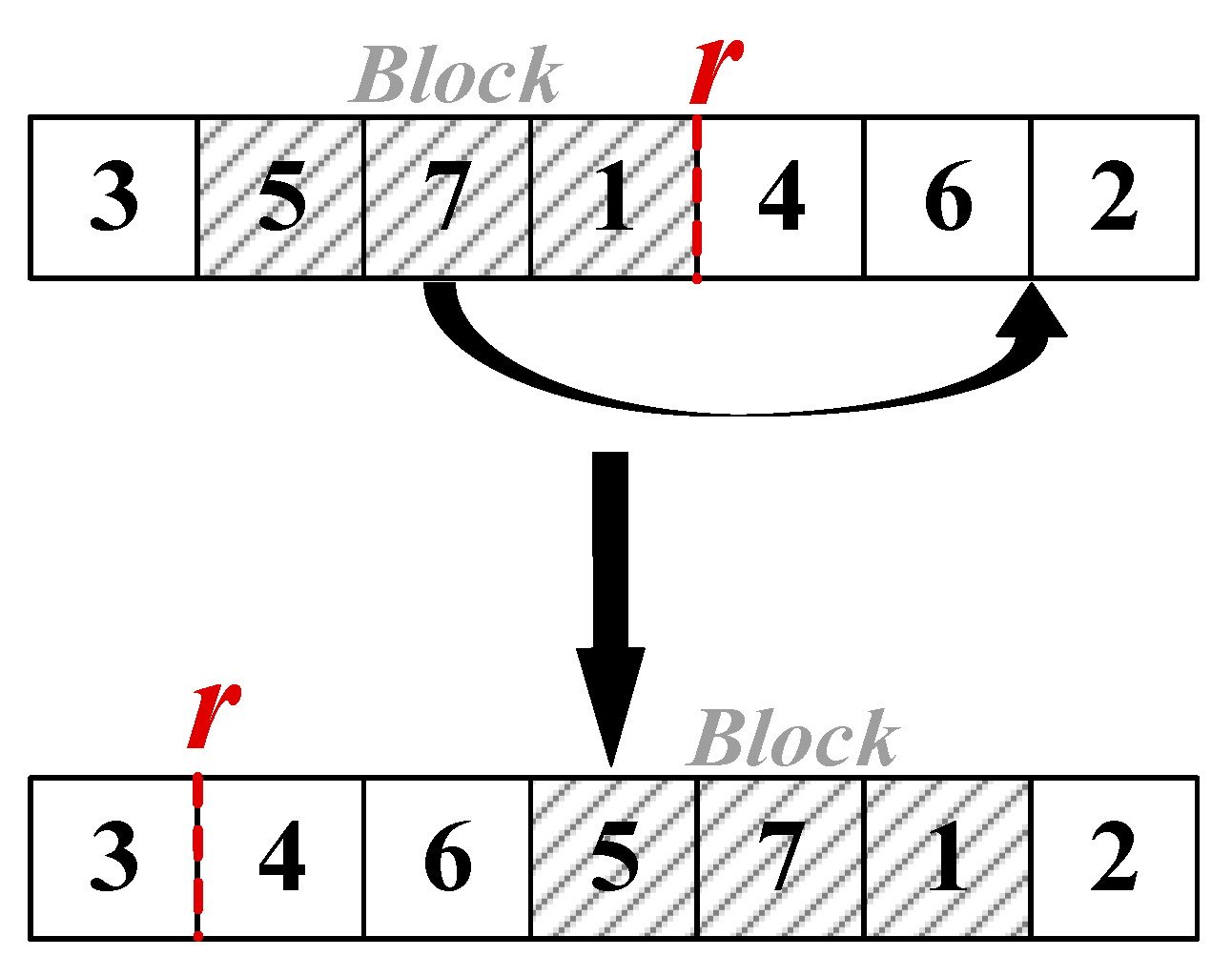
- Block Perturbation
| Pseudocode 5: Tabu-based Adaptive Search Mechanism | |
| 1 | Start |
| 2 | Initialize tabu list T = ∅ |
| 3 | For i from 1 to 30 do |
| 4 | // Step 1: Evaluate each operator |
| 5 | For each oi∈O do |
| 6 | Generate candidate moves from oi |
| 7 | For each move |
| 8 | If not tabu |
| 9 | Keep it |
| 10 | Else |
| 11 | Keep only if it improves the best global |
| 12 | End if |
| 13 | End for |
| 14 | Select the one with the best makespan |
| 15 | Record its improvement Δi |
| 16 | End for |
| 17 | // Step 2: Select operator |
| 18 | Choose operator o* that maximizes () |
| 19 | Update solution x, and insert move attributes into tabu list |
| 20 | // Step 3: Update scores and frequency |
| 21 | For each oi∈O do |
| 22 | Si ← (1 − λ) Si + λΔi |
| 23 | End for |
| 24 | Update frequency counters |
| 25 | // Step 4: Update tabu list |
| 26 | Decrease tenure of all tabu attributes and remove expired ones |
| 27 | End for |
| 28 | End |
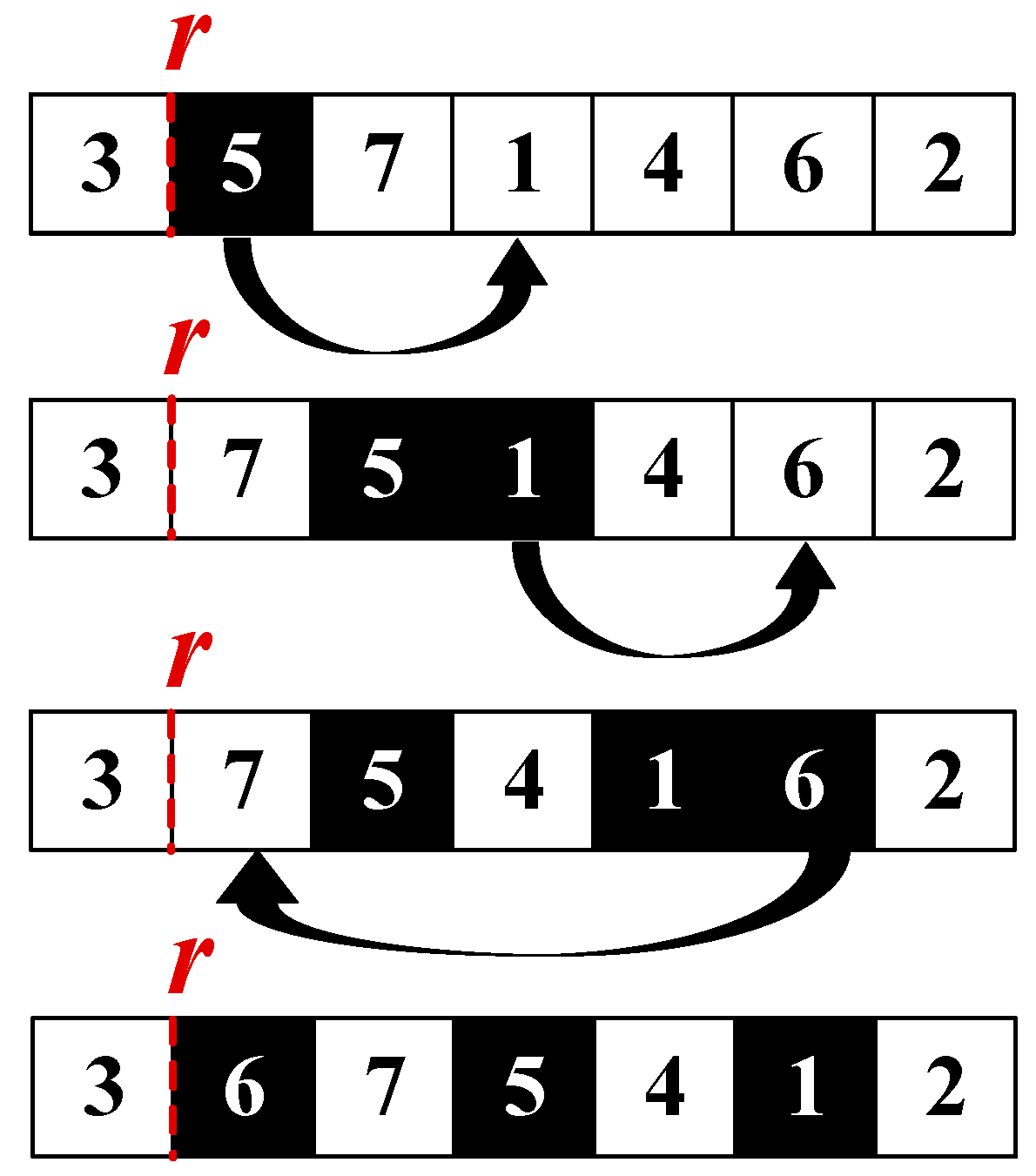
- (5)
- Chain Ejection
4.3.2. Tabu-Adaptive Strategy
4.4. Framework
5. Experimental Analysis
5.1. Experimental Conditions and Settings
- (1)
- Fatigue Effect Settings:
- (2)
- Test Scale
- (3)
- Processing Time Data
- (4)
- Experimental Environment
5.2. Orthogonal Experiment
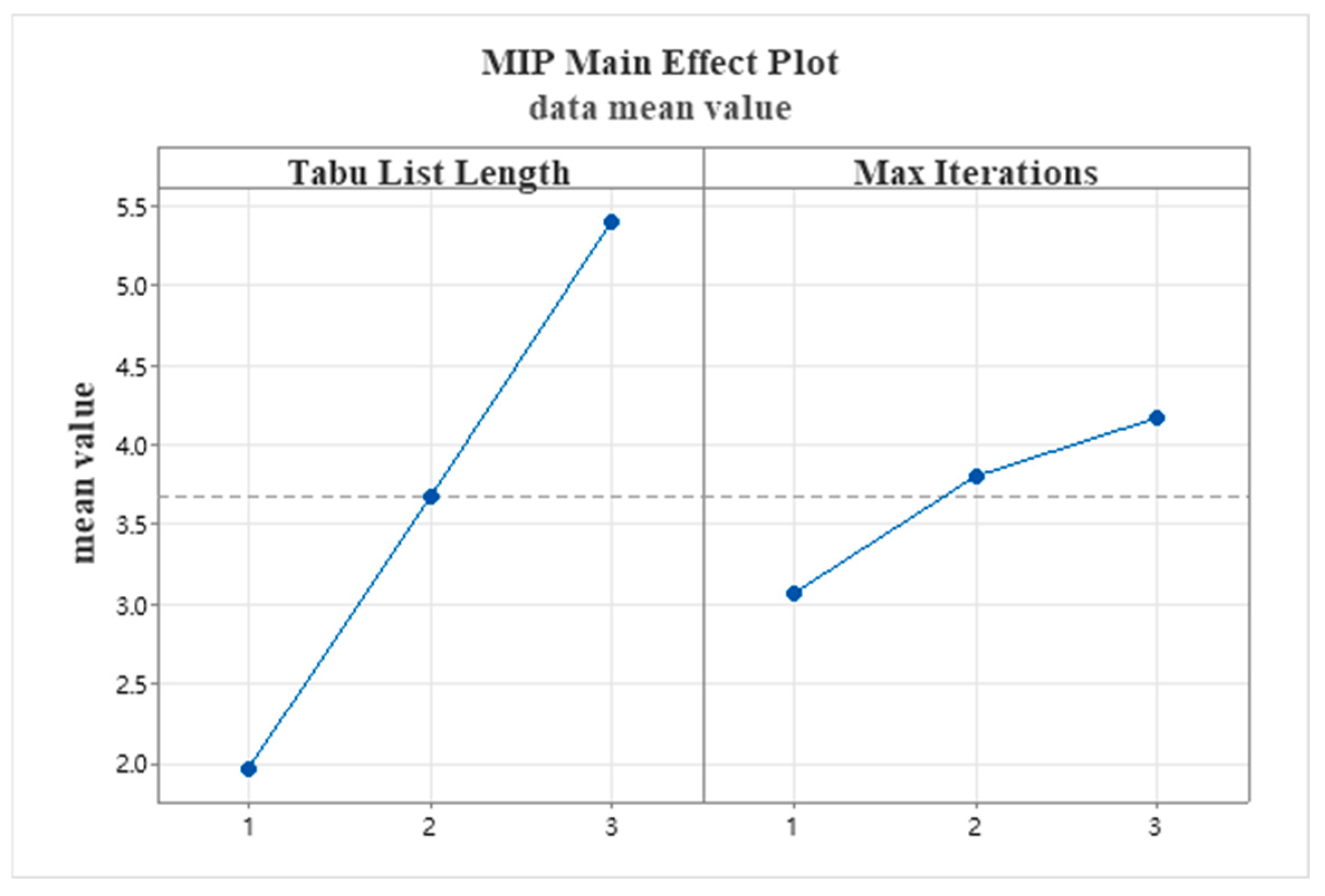
5.2.1. Improved Tabu Search Algorithm
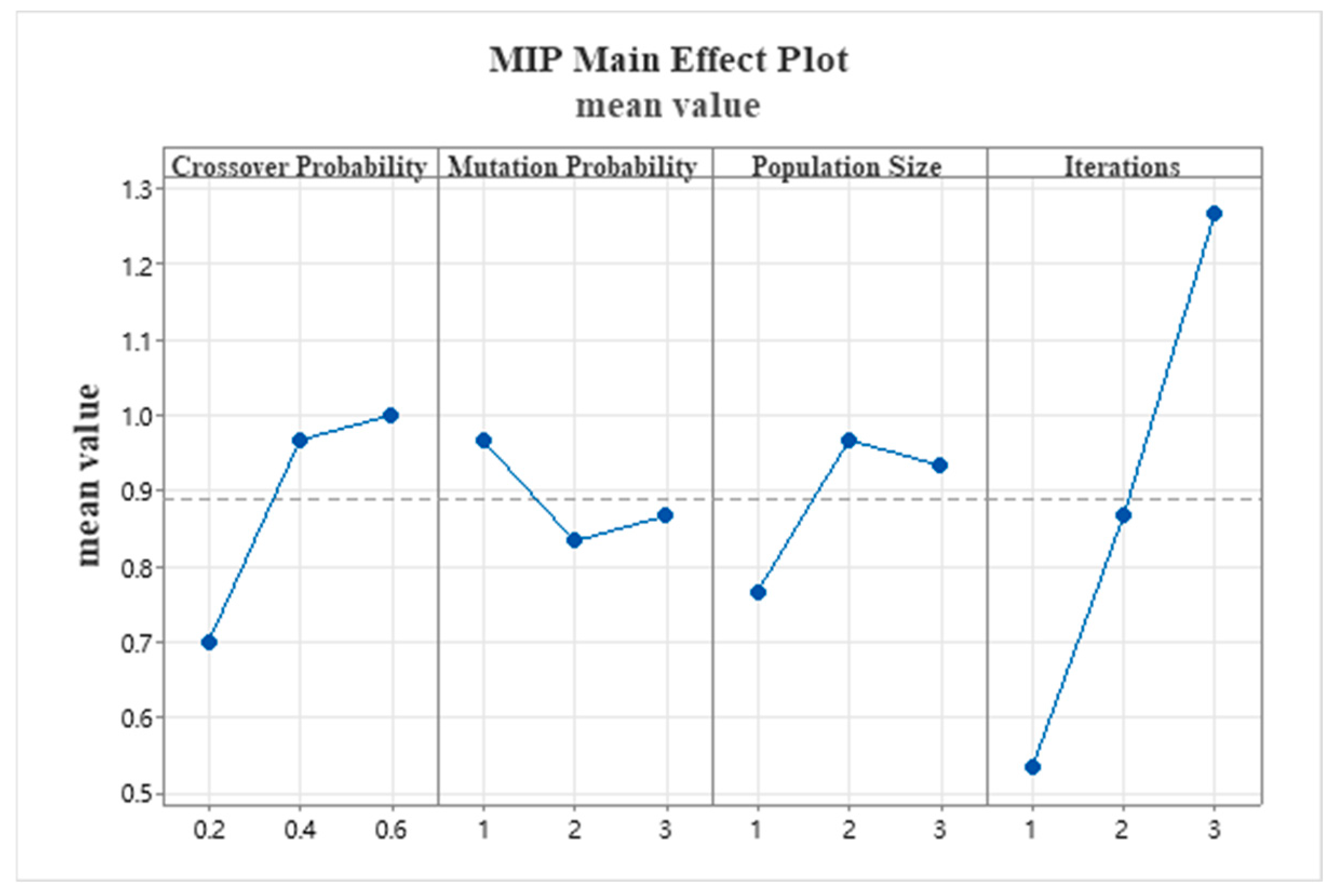
5.2.2. Differential Evolution
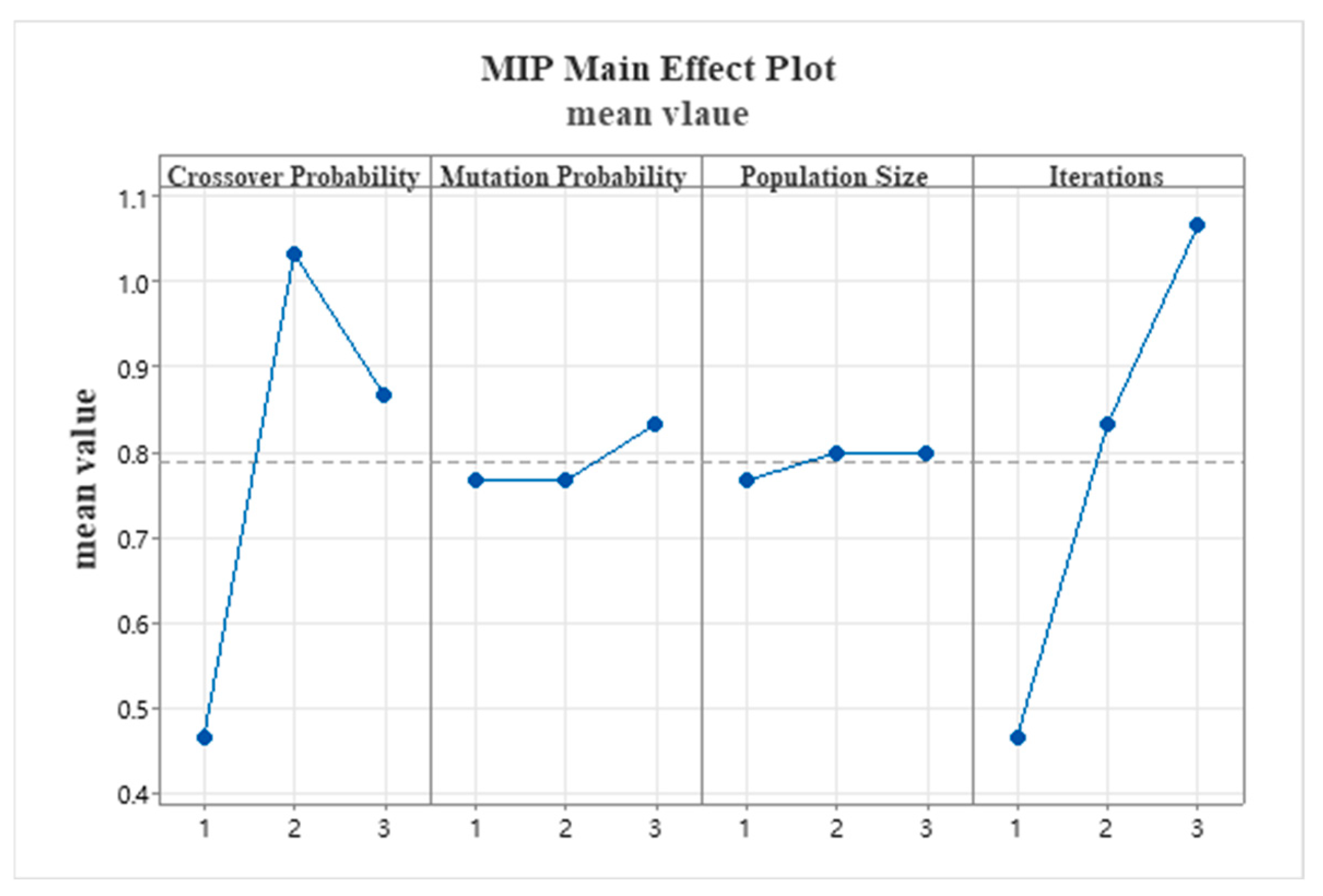
5.2.3. Genetic Algorithm
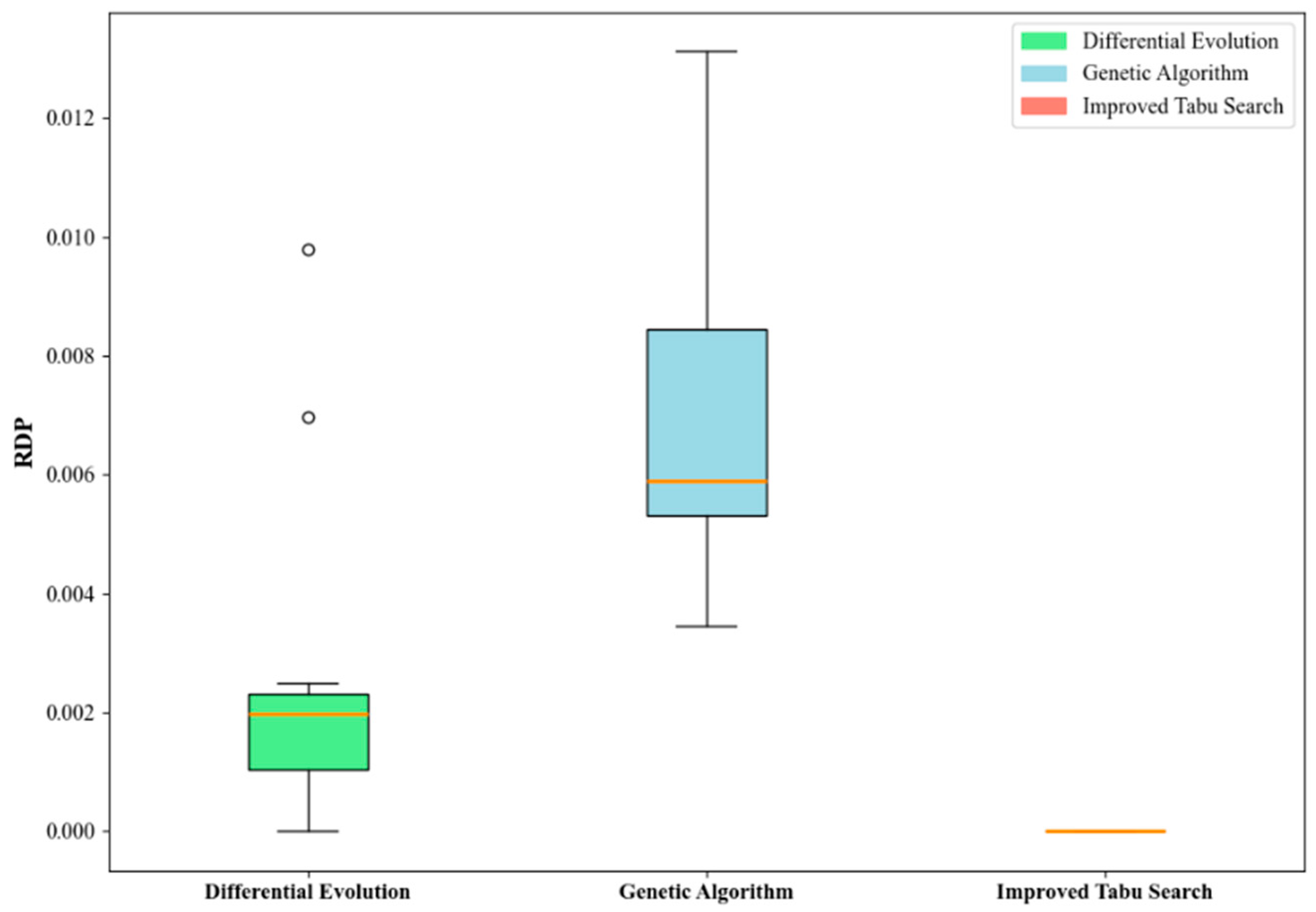
5.3. Comparative Experiment
5.4. Optimizer Comparison
5.5. Component Analysis Experiment
5.6. Fatigue Modeling Assessment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, C.; Zou, D.; Bai, D.; Wang, J.-B. Proportionate flowshop scheduling with position-dependent weights. Eng. Optim. 2020, 52, 37–52. [Google Scholar] [CrossRef]
- Bai, D.; Zheng, W.; Zang, C.; Yang, J.; Wu, C.-C.; Qin, H. Discrete optimization algorithms for distributed bi-agent flowshop scheduling with release dates. Swarm Evol. Comput. 2025, 98, 102101. [Google Scholar] [CrossRef]
- Li, K.; Xu, S.; Fu, H. Work-break scheduling with real-time fatigue effect and recovery. Int. J. Prod. Res. 2020, 58, 689–702. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Strong np-completeness results: Motivation, examples, and implications. JACM 1978, 25, 499–508. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; Sánchez, S.; Moreno-Camacho, C. A literature-based assessment of human factors in shop scheduling problems. IFAC-PapersOnLine 2019, 52, 49–54. [Google Scholar] [CrossRef]
- Lin, R.-C.; Sir, M.Y.; Sisikoglu, E.; Pasupathy, K.; Steege, L.M. Optimal nurse scheduling based on quantitative models of work-related fatigue. IIE Trans. Healthc. Syst. Eng. 2013, 3, 23–38. [Google Scholar] [CrossRef]
- McCormick, F.; Kadzielski, J.; Evans, B.T.; Landrigan, C.P.; Herndon, J.; Rubash, H. Fatigue optimization scheduling in graduate medical education: Reducing fatigue and improving patient safety. J. Grad. Med. Educ. 2013, 5, 107–111. [Google Scholar] [CrossRef]
- Bowden, Z.E.; Ragsdale, C.T. The truck driver scheduling problem with fatigue monitoring. Decis. Support Syst. 2018, 110, 20–31. [Google Scholar] [CrossRef]
- Nayeri, S.; Asadi-Gangraj, E.; Emami, S. Metaheuristic algorithms to allocate and schedule of the rescue units in the natural disaster with fatigue effect. Neural Comput. Appl. 2019, 31, 7517–7537. [Google Scholar] [CrossRef]
- Åkerstedt, T.; Klemets, T.; Karlsson, D.; Häbel, H.; Widman, L.; Sallinen, M. Acute and cumulative effects of scheduling on aircrew fatigue in ultra-short-haul operations. J. Sleep Res. 2021, 30, e13305. [Google Scholar] [CrossRef]
- Asadayoobi, N.; Taghipour, S.; Jaber, M. Optimising stochastic task allocation and scheduling plans for mission workers subject to learning-forgetting, fatigue-recovery, and stress-recovery effects. Expert Syst. Appl. 2023, 229, 120524. [Google Scholar] [CrossRef]
- Paredes-Astudillo, Y.A.; Botta-Genoulaz, V.; Montoya-Torres, J.R.; Caro, M.; Jimenez, J.-F. Incorporating learning and fatigue effects in flowshop scheduling: A case study. Int. J. Prod. Res. 2025, 63, 6364–6383. [Google Scholar] [CrossRef]
- Xu, S.; Hall, N.G. Fatigue, personnel scheduling and operations: Review and research opportunities. Eur. J. Oper. Res. 2021, 295, 807–822. [Google Scholar] [CrossRef]
- Berti, N.; Finco, S.; Battaïa, O.; Delorme, X. Ageing workforce effects in Dual-Resource Constrained job-shop scheduling. Int. J. Prod. Econ. 2021, 237, 108151. [Google Scholar] [CrossRef]
- Aribi, D.; Driss, O.B.; El-Haouzi, H.B. An Improved Decomposition-Based Multiobjective Evolutionary Algorithm for Human-Centric Flexible Job Shop Scheduling Problem. SN Comput. Sci. 2025, 6, 788. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Geetha, M.; Tosun, Ö. An improved particle swarm optimization algorithm to solve hybrid flowshop scheduling problems with the effect of human factors—A case study. Comput. Oper. Res. 2020, 114, 104812. [Google Scholar] [CrossRef]
- Paredes-Astudillo, Y.A.; Jimenez, J.-F.; Montoya-Torres, J.R.; Botta-Genoulaz, V. Fatigue Integration to the Flowshop Scheduling Problem. In Service Oriented, Holonic and Multi-Agent Manufacturing Systems for Industry of the Future; Springer: Cham, Switzerland, 2023; Volume 1136, pp. 135–147. [Google Scholar]
- Vermin, B.L.; Abbink, D.; Schulte, F. Bi-Objective Job-Shop Scheduling Considering Human Fatigue in Cobotic Order Picking Systems: A Case of an Online Grocer. Procedia Comput. Sci. 2024, 232, 635–644. [Google Scholar] [CrossRef]
- Usman, S.; Lu, C. Job-shop scheduling with limited flexible workers considering ergonomic factors using an improved multi-objective discrete Jaya algorithm. Comput. Oper. Res. 2024, 162, 106456. [Google Scholar] [CrossRef]
- Ostermeier, F.F. The impact of human consideration, schedule types and product mix on scheduling objectives for unpaced mixed-model assembly lines. Int. J. Prod. Res. 2020, 58, 4386–4405. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, A.; Ai, Y.; Tian, B.; Chen, L. Real-time scheduling of autonomous mining trucks via flow allocation-accelerated tabu search. IEEE Trans. Intell. Veh. 2022, 7, 466–479. [Google Scholar] [CrossRef]
- Xie, J.; Gao, L.; Li, X.; Gui, L. A hybrid genetic tabu search algorithm for distributed job-shop scheduling problems. Swarm Evol. Comput. 2024, 90, 101670. [Google Scholar] [CrossRef]
- Alhamad, K.; Alkhezi, Y. Hybrid genetic algorithm and tabu search for solving preventive maintenance scheduling problem for cogeneration plants. Mathematics 2024, 12, 1881. [Google Scholar] [CrossRef]
- Xing, L.; Liu, Y.; Li, H.; Wu, C.-C.; Lin, W.-C.; Chen, X. A novel tabu search algorithm for multi-AGV routing problem. Mathematics 2020, 8, 279. [Google Scholar] [CrossRef]
- Zhu, K.; Li, L.D.; Li, M. School Timetabling Optimisation using artificial bee colony algorithm based on a virtual searching space method. Mathematics 2021, 10, 73. [Google Scholar] [CrossRef]
- Wang, X.; Ren, T.; Bai, D.; Chu, F.; Lu, X.; Weng, Z.; Li, J.; Liang, J. Hybrid flow shop scheduling with learning effects and release dates to minimize the makespan. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 365–378. [Google Scholar] [CrossRef]
- Ren, T.; Wang, X.; Liu, T.; Wu, C.-C.; Bai, D.; Lin, L.; Guo, M. Exact and metaheuristic algorithms for flow-shop scheduling problems with release dates. Eng. Optim. 2022, 54, 1853–1869. [Google Scholar] [CrossRef]
- Andrade, C.E.; Silva, T.; Pessoa, L.S. Minimizing flowtime in a flowshop scheduling problem with a biased random-key genetic algorithm. Expert Syst. Appl. 2019, 128, 67–80. [Google Scholar] [CrossRef]
- Wang, X.; Chu, F.; Ren, T.; Bai, D. Bi-objective optimization of a flow shop scheduling problem under time-of-use tariffs. IEEE Trans. Autom. Sci. Eng. 2024, 22, 7679–7695. [Google Scholar] [CrossRef]
- Ma, L.B.; Li, N.; Guo, Y.N.; Huang, M.; Yang, S.X.; Wang, X.W.; Zhang, H. Learning to Optimize: Reference Vector Reinforcement Learning Adaption to Constrained Many-objective Optimization of Industrial Copper Burdening System. IEEE Trans. Cybern. 2022, 52, 12698–12711. [Google Scholar] [CrossRef]
- Wang, X.; Ren, T.; Bai, D.; Ezeh, C.; Zhang, H.; Dong, Z. Minimizing the sum of makespan on multi-agent single-machine scheduling with release dates. Swarm Evol. Comput. 2022, 69, 100996. [Google Scholar] [CrossRef]
| 10 | 8 | 9 | 11 | 7 | 10 | |
| 5 | 6 | 4 | 7 | 5 | 6 | |
| 8 | 7 | 9 | 6 | 10 | 8 |
| Level | Tabu List Length | Max Iterations |
|---|---|---|
| 1 | 3 | 100 |
| 2 | 5 | 200 |
| 3 | 7 | 300 |
| Tabu List Length | Max Iterations | MIR |
|---|---|---|
| 1 | 1 | 1.5 |
| 1 | 2 | 2.3 |
| 1 | 3 | 2.1 |
| 2 | 1 | 3.1 |
| 2 | 2 | 3.4 |
| 2 | 3 | 4.5 |
| 3 | 1 | 4.6 |
| 3 | 2 | 5.7 |
| 3 | 3 | 5.9 |
| Level | Crossover Probability | Mutation Probability | Population Size | Max Iterations |
|---|---|---|---|---|
| 1 | 0.2 | 0.2 | 50 | 100 |
| 2 | 0.4 | 0.4 | 100 | 200 |
| 3 | 0.6 | 0.6 | 150 | 300 |
| Crossover Probability | Mutation Probability | Population Size | Iterations | MIR |
|---|---|---|---|---|
| 0.2 | 1 | 1 | 1 | 0.3 |
| 0.2 | 2 | 2 | 2 | 0.7 |
| 0.2 | 3 | 3 | 3 | 1.1 |
| 0.4 | 1 | 2 | 3 | 1.5 |
| 0.4 | 2 | 3 | 1 | 0.6 |
| 0.4 | 3 | 1 | 2 | 0.8 |
| 0.6 | 1 | 3 | 2 | 1.1 |
| 0.6 | 2 | 1 | 3 | 1.2 |
| 0.6 | 3 | 2 | 1 | 0.7 |
| Crossover Probability | Mutation Probability | Population Size | Iterations | MIR |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0.1 |
| 1 | 2 | 2 | 2 | 0.5 |
| 1 | 3 | 3 | 3 | 0.8 |
| 2 | 1 | 2 | 3 | 1.3 |
| 2 | 2 | 3 | 1 | 0.7 |
| 2 | 3 | 1 | 2 | 1.1 |
| 3 | 1 | 3 | 2 | 0.9 |
| 3 | 2 | 1 | 3 | 1.1 |
| 3 | 3 | 2 | 1 | 0.6 |
| Number of Jobs | DE | GA | ITS |
|---|---|---|---|
| 50 | 0.697 | 0.658 | 0 |
| 0.111 | 1.312 | 0 | |
| 0.008 | 0.899 | 0 | |
| 100 | 0.979 | 0.409 | 0 |
| 0.086 | 0.631 | 0 | |
| 0.000 | 0.826 | 0 | |
| 150 | 0.203 | 0.550 | 0 |
| 0.225 | 0.545 | 0 | |
| 0.192 | 0.345 | 0 | |
| 200 | 0.226 | 0.523 | 0 |
| 0.249 | 0.534 | 0 | |
| 0.142 | 0.967 | 0 |
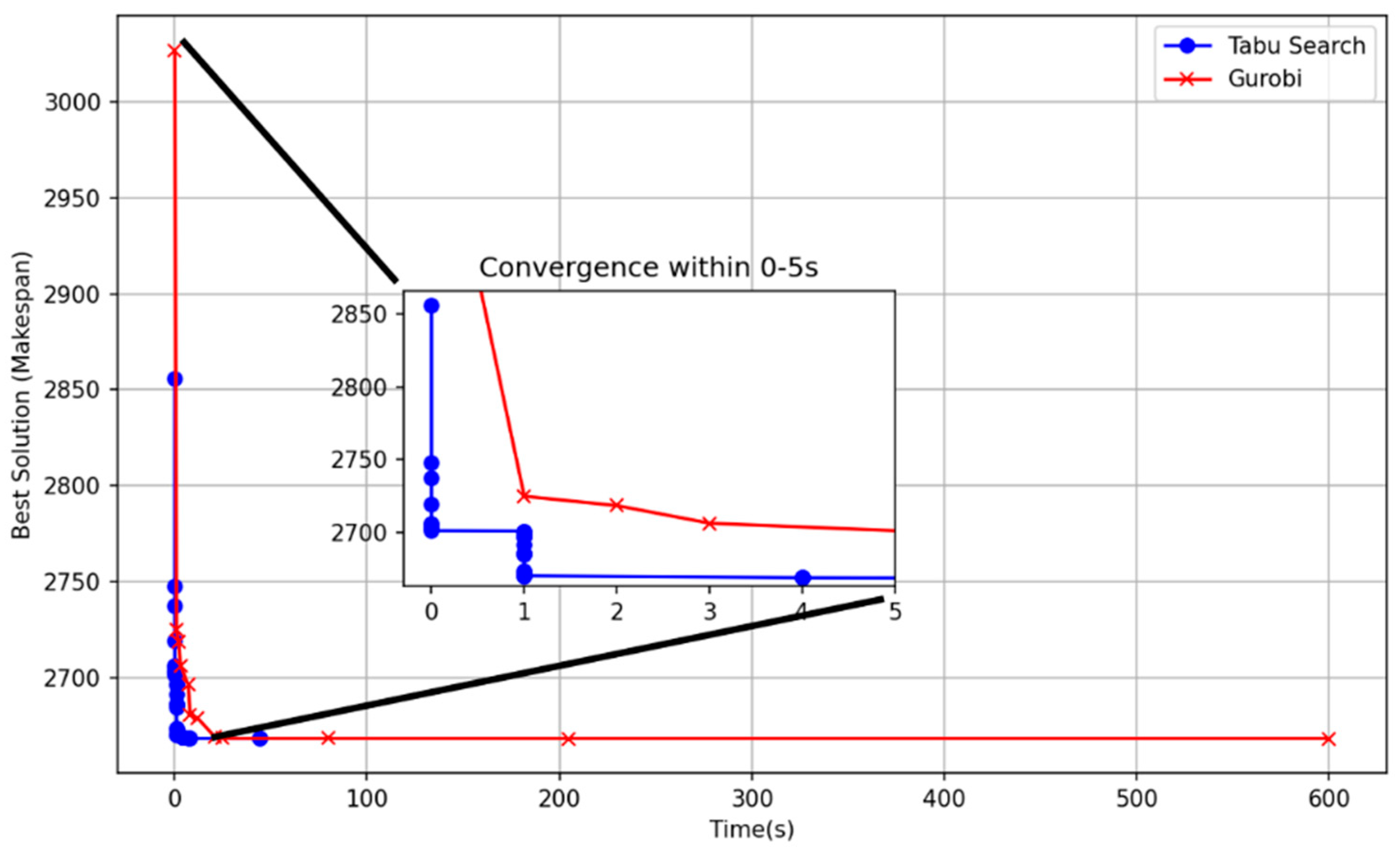
| Number of Jobs | ITS | Gurobi | RPD | ||
|---|---|---|---|---|---|
| Best Solution | Time (s) | Best Solution | Time (s) | ||
| 200 | 10,868.641 | 10 | 10,880.958 | 600 | 0.1133 |
| 300 | 16,178.460 | 42 | 16,186.516 | 600 | 0.0499 |
| 400 | 21,583.300 | 315 | 21,608.150 | 600 | 0.1153 |
| 500 | 27,360.297 | 126 | 27,407.431 | 600 | 0.1718 |
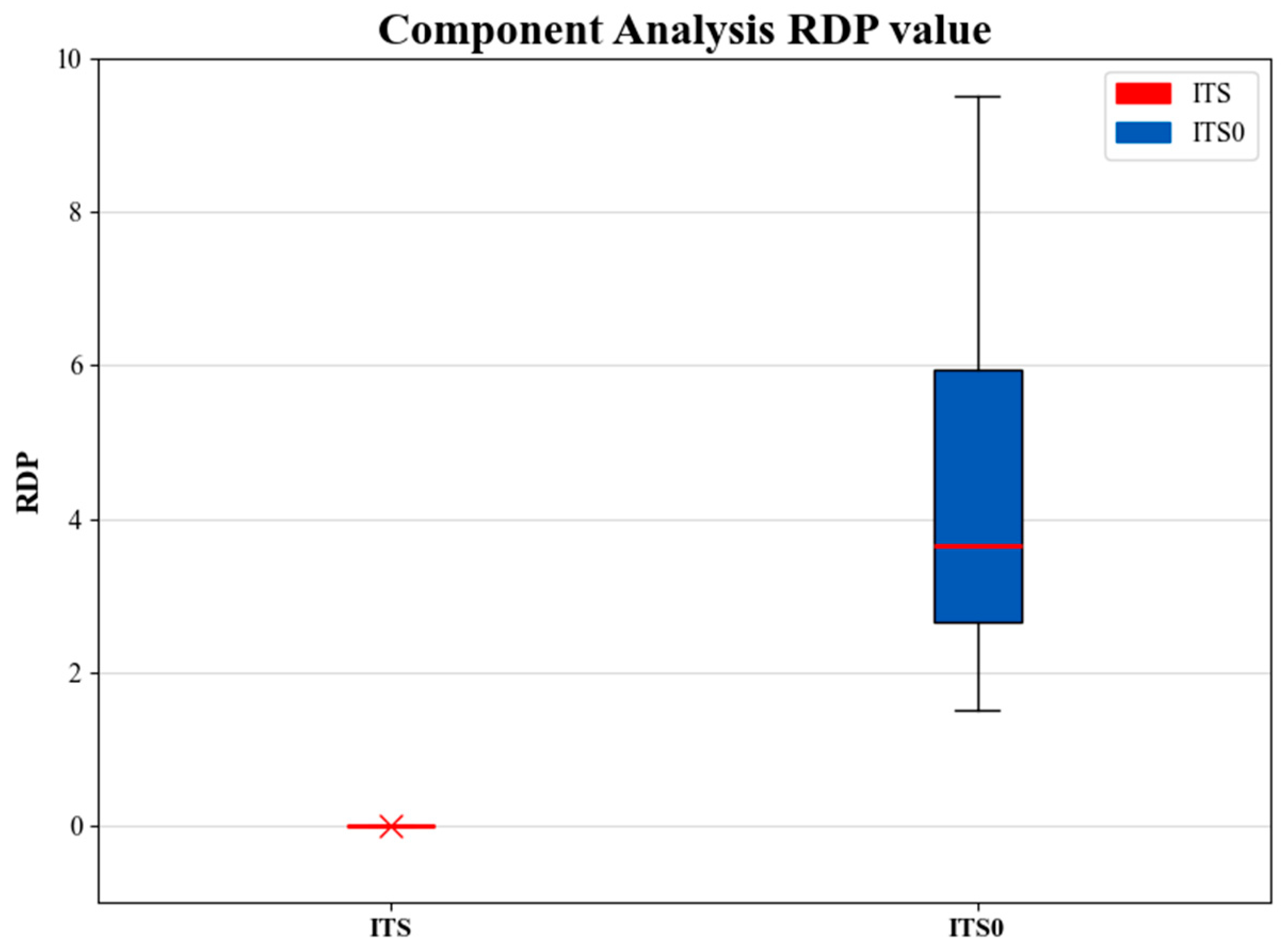
| Number of Jobs | ITS | ITS0 |
|---|---|---|
| 50 | 0 | 2.8 |
| 0 | 3.0 | |
| 0 | 1.5 | |
| 100 | 0 | 7 |
| 0 | 2.2 | |
| 0 | 5.1 | |
| 150 | 0 | 7.2 |
| 0 | 5.6 | |
| 0 | 3.5 | |
| 200 | 0 | 9.5 |
| 0 | 2.0 | |
| 0 | 3.8 |
| Job-machine | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
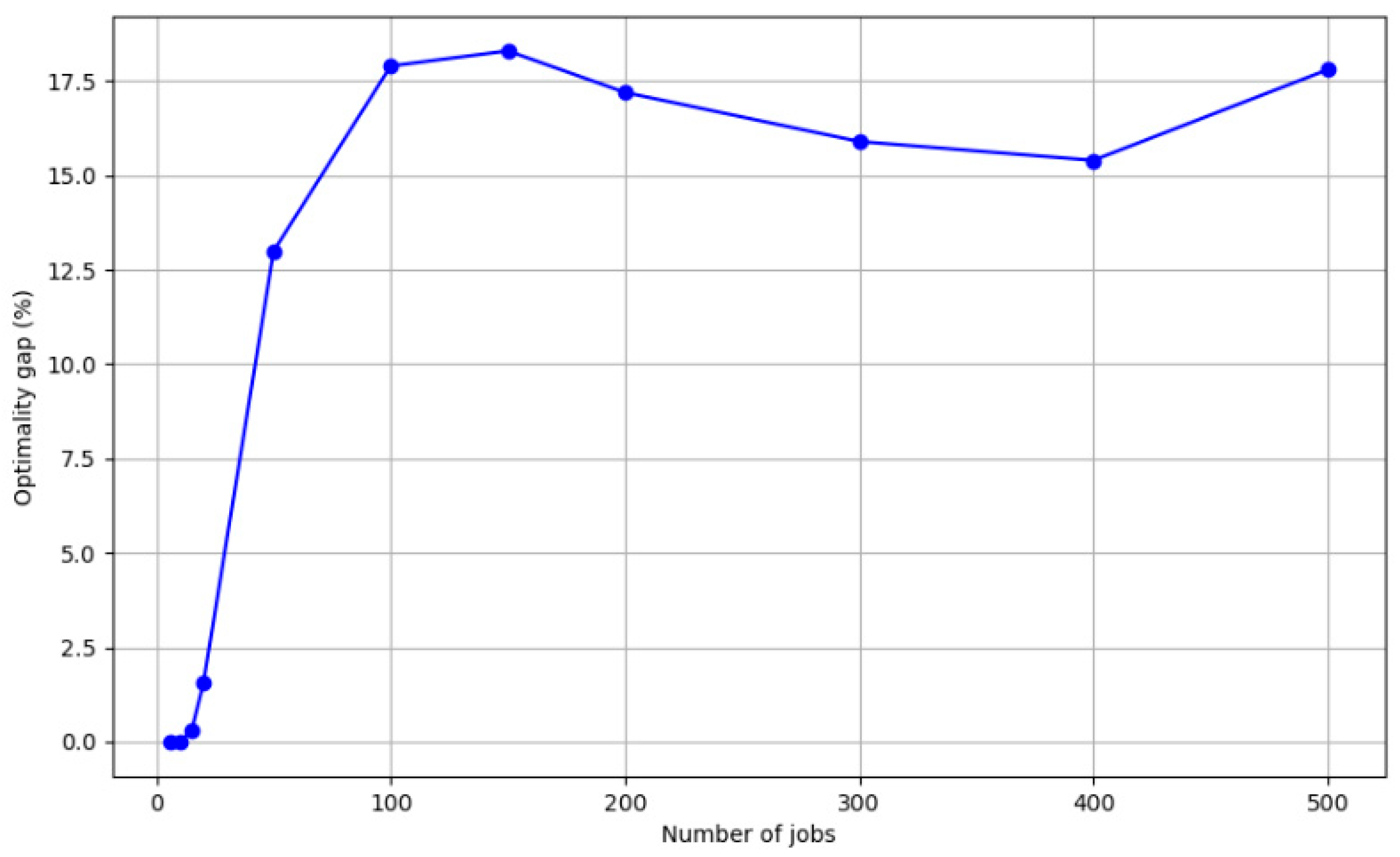
| Gap value (%) | −0.42 | 0.03 | 0.26 | 0.87 | 0.95 | 1.01 | 1.46 | 2.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Sun, Z.; Ai, X.; Zhao, B.; Lu, J.; Zhou, H.; Mao, X.; Wen, X.; Wu, C.-C.; Liu, S. A Three-Machine Flowshop Scheduling Problem with Linear Fatigue Effect. Mathematics 2025, 13, 3670. https://doi.org/10.3390/math13223670
Xu W, Sun Z, Ai X, Zhao B, Lu J, Zhou H, Mao X, Wen X, Wu C-C, Liu S. A Three-Machine Flowshop Scheduling Problem with Linear Fatigue Effect. Mathematics. 2025; 13(22):3670. https://doi.org/10.3390/math13223670
Chicago/Turabian StyleXu, Weiping, Zehou Sun, Xiaotian Ai, Baoyun Zhao, Jingyi Lu, Hanyu Zhou, Xinqi Mao, Xiaoling Wen, Chin-Chia Wu, and Shufeng Liu. 2025. "A Three-Machine Flowshop Scheduling Problem with Linear Fatigue Effect" Mathematics 13, no. 22: 3670. https://doi.org/10.3390/math13223670
APA StyleXu, W., Sun, Z., Ai, X., Zhao, B., Lu, J., Zhou, H., Mao, X., Wen, X., Wu, C.-C., & Liu, S. (2025). A Three-Machine Flowshop Scheduling Problem with Linear Fatigue Effect. Mathematics, 13(22), 3670. https://doi.org/10.3390/math13223670







