A New Memory-Processing Unit Model Based on Spiking Neural P Systems with Dendritic and Synaptic Behavior for Kronecker Matrix–Matrix Multiplication

Abstract

Currently, Kronecker Matrix–Matrix Multiplication play a crucial role in many advanced applications across science and engineering, such as Quantum Computing (Tensor Representation of Quantum States, Quantum Gate Construction), Machine Learning and Data Science (Kernel Methods, Tensor Decompositions), and Signal and Image Processing (Multi-dimensional Filtering, Compression Algorithms). However, the implementation of the Kronecker Matrix–Matrix Multiplication increasingly relies on systems with enhanced computational capabilities. Specifically, current implementations expend large amounts of external memory and requires a large number of processing units to perform this operation. As is commonly acknowledged, cutting-edge high-performance computing schemes still faces limitations in terms of energy and performance due to the bottleneck in data transfer between processing units and memory. To mitigate this limitation, memory processing units (MPUs) enable direct computation on in-memory data, reducing latency and eliminating the need for data transfer. On the other hand, spiking neural P systems, with their inherent parallelism and distributed processing capabilities, are therefore well-suited as foundational components for implementing such memory architectures efficiently. From the mathematical point of view, we present for the first time a neural, synaptic, and dendritic model to support the Kronecker Matrix–Matrix multiplication. To this end, the proposed spiking neural P system with their cutting-edge variants, such as anti-spikes, communication on request, synaptic weights, and dendritic–axonal delays, facilitates the creation of neural memory cells and spike-based routers. Hence, these elements potentially allow the design of novel processing memory architectures that markedly enhance data transfer efficiency between computational units and memory.

1. Introduction

In recent years, spiking neural P (SN P) systems have emerged as a novel class of parallel and distributed computational models [1]. These systems have garnered significant attention due to their proven effectiveness in tackling complex engineering challenges, including information security [2], signal processing [3], and arithmetic circuit design [3]. Despite notable achievements, ongoing efforts continue to enhance the computational power of standard SN P systems. A key limitation lies in their reliance on the soma of the neuron as the primary processing unit, which is governed by complex spiking rules. This dependence on sophisticated rule activation tends to constrain the overall computational efficiency of these systems [4]. To address this issue, researchers have investigated additional neuronal properties from both theoretical and biological perspectives. Drawing inspiration from neurobiological mechanisms, several advanced variants of SN P systems have been proposed [5]. These include features such as propagation delays [6], permeability [7], inhibitory synapses [8], structural plasticity [9], autapses [9], dendritic trunk/dendritic delays [10], myelin and dendritic spines [11], inhibitory rules [12], and microglia [13]. Beyond biologically inspired enhancements, other variants have been introduced based on abstract neural computing principles. These include stochastic rule application [14], extended channel rules [15], target indication mechanisms [8], multiple channels [16], colored spikes [17], scheduled synapses [18], request and antispike rules [19], weighted synapses [20], and communication-on-request protocols [21]. From a mathematical standpoint, incorporating these diverse features has markedly improved the computational capabilities of SN P systems. Recent developments have focused on designing compact arithmetic circuits, such as adders, subtractors, dividers, and multipliers, which outperform traditional binary circuits in terms of efficiency [22]. Consequently, the evolution of SN P system variants is paving the way for more powerful high-performance computing solutions, which are increasingly vital in real-world applications [3].

On the other hand, Duchen et al. [23] recently introduced a spike-based memory cell capable of executing basic arithmetic operations, where the results are stored directly within the same cell. This innovation leverages spiking neural P systems and their advanced variants, such as dendritic behavior and astrocyte-like control mechanisms. Although this represents a significant advancement, several challenges remain in the development of a fully memory processing unit (MPU) based on spiking neural P systems. Therefore, these emerging architectures hold promise for enabling matrix–matrix multiplication, which represents a core operation in computationally intensive domains, such as quantum computing, image processing, classification systems, Internet of Things (IoT), and data-intensive computing [24]. Moreover, this approach offers promising advancements in memory-intensive computing, rather than traditional computing-intensive paradigms. In such applications, transferring large datasets between processing cores and memory is both time and energy consuming, creating a significant performance bottleneck. To address this challenge, processing-in-memory (PIM) technology, also referred to as memory processing unit (MPU) architecture, has recently emerged [25]. This innovative solution enables computation to occur directly within the memory itself, effectively minimizing data movement and alleviating the bottleneck [26]. However, most existing approaches rely on near-memory architectures, where memory modules and processing units are positioned in close proximity but remain physically distinct. As a result, memory bandwidth remains constrained, limiting the overall system performance. In this work, we introduce a novel memory-processing unit (MPU) model based on Spiking Neural P systems along with their cutting-edge variants, in which neurons process and store computational results within the same unit. This architecture is specifically designed to perform Kronecker matrix–matrix multiplication, which is a fundamental operation widely used in advanced applications, such as quantum computing [27], image analysis [28], pattern classification [29], and information security [30].

2. The Proposed Memory-Processing Unit Model Based on Spiking Neural P Systems, ${\mathsf{\Pi }}_{\mathit{MEM}}$

Before presenting the proposed memory processing unit (${\mathsf{\Pi }}_{MEM}$), we provide some concepts and necessary notations related to the formal definition of the SN P systems and automata theory. In general terms, the SN P systems are mainly composed of neurons interconnected through synapses. Specifically, the behavior of the soma is regulated by rules (forgetting rule and firing rule) to process the information, which is encoded by means of spikes [1]. Recently, several variants of the SN P systems have been proposed to increase the computational capabilities of the soma and their synapses. In this work, we also describe the formal definition of these new variants of the SN P systems, such as anti-spikes [31,32], communication on request [32], synaptic weights [33] and dendritic–axonal delays [10]. In particular, the use of these variants has allowed us to build a memory-processing unit.

Definition 1.

We provide the formal definition of the SNP systems of degree $m\ge 1$ along with their variants, as follows:

$${\mathsf{\Pi }}_{SNP}=\{O,{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_m,syn,in,out\}$$

where

1.

$O=\{a_1,a_2,\dots ,a_k,{\overline{a}}_1,{\overline{a}}_2,\dots ,{\overline{a}}_l\}$ is the alphabet, where $a_i$ ($i\in \{1,2,\dots ,k\}$) represents a type of spikes, and ${\overline{a}}_j$ ($j\in \{1,2,\dots ,l\}$) represents a type of anti-spikes [31,32].

2.

${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_m$ denote neurons of the form ${\sigma }_i=(v_i,R_i)$, where

(a) 

$v_i$ is a multiset over alphabet O.

(b) 

$R_i$ denotes the finite set of spiking rules as follows:

i.

$E/a^c\to a^p;d$, where E is a regular expression over alphabet O, $c\ge 1$, $1\le p\le c$. d is the time units delay for this rule.

ii.

$a^s\to \lambda$, for $s\ge 1$ and $a^s\notin L\left(E\right)$.

iii.

$E/Q$, where Q is a finite set of queries of the forms $(a_k^p,{\sigma }_j)$ and $(a_k^{\infty },{\sigma }_j)$. The query $(a_k^p,{\sigma }_j)$ indicates that neuron (${\sigma }_i$) requests p copies of $a_k$ from neuron (${\sigma }_j$). On the other hand, the query $(a_k^{\infty },{\sigma }_j)$ indicates that all spikes ($a_k$) are requested from neuron (${\sigma }_j$) [32].

(c) 

$syn$ $\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}$ represents the synapses. Here, synapses have a specific synaptic weight (w), which indicates that $p·w$ spikes are received by some neuron (${\sigma }_i$) [33].

(d) 

$in,out$$\in \{1,2,\dots ,m\}$ denote the input and output neurons, respectively.

Once the formal definition of the SN P systems is provided, we present the proposed MPU based on SN P systems, ${\mathsf{\Pi }}_{MEM}$, which is configured to compute mathematical operations and store the results in the same unit. To achieve this, we proposed a basic spiking neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$ to perform arithmetic operations, such as addition, subtraction, and multiplication and two router neurons (${\sigma }_{r_t}$ and ${\sigma }_{r_p}$) to perform write/read operations between two integer numbers (u and v). The functionality of each element is described below.

• Basic spiking neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$.
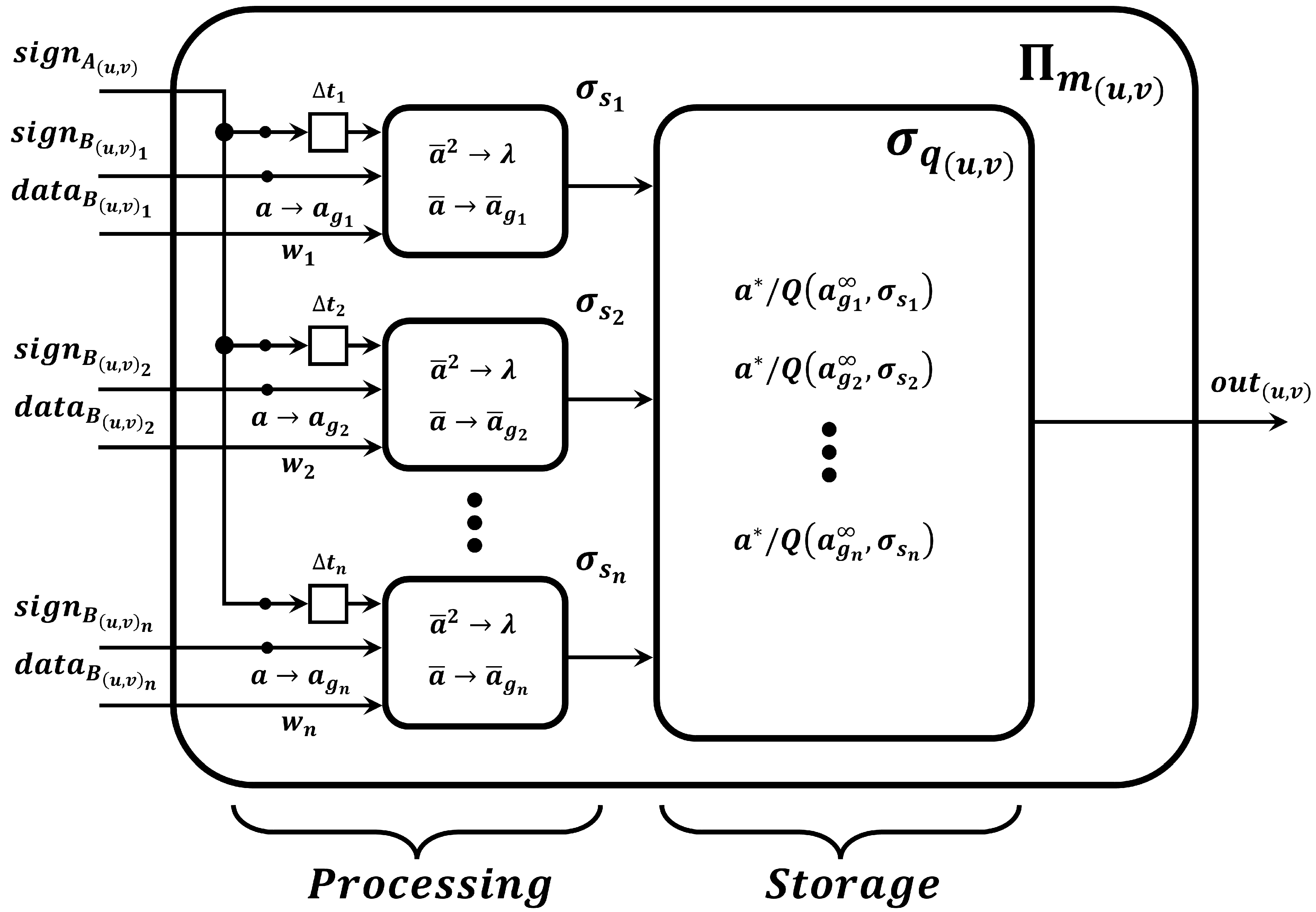
  The proposed neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$, is composed of a set of dendritic delays ($\Delta t_1,\Delta t_2,\dots ,\Delta t_n$), a set of neurons (${\sigma }_{s_1},{\sigma }_{s_2},\dots ,{\sigma }_{s_n}$), a set of synaptic weights ($w_1,w_2,\dots ,w_n$), and a neuron (${\sigma }_{q_{(u,v)}}$), as shown in Figure 1.

  Figure 1. Schematic of basic neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$.

  Figure 1. Schematic of basic neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$.
  The proposed spiking neural memory cell ${\mathsf{\Pi }}_{m_{(u,v)}}$ performs the dot product between two vectors ($A·B$) in parallel. To perform this operation, the vectors A and B must comply with the data format under the following criteria:

  -

  The components of vector A are represented with the synaptic weights ($w_1,w_2,\dots ,w_n$).

  -

  The components of vector B are decomposed into individual integer digits and encoded as spike trains.

  -

  The signs of the components of each vector (A and B) are represented with an anti-spike associated with each component.

  -

  The magnitude of the result of each component is represented by the number of spikes ($a_{g_1},a_{g_2},\dots ,a_{g_n}$) accumulated in a specific neuron (${\sigma }_{s_1},{\sigma }_{s_2},\dots ,{\sigma }_{s_n}$). If each magnitude of the result is negative, then there is an anti-spike (${\overline{a}}_{g_1},{\overline{a}}_{g_2},\dots ,{\overline{a}}_{g_n}$) associated with that magnitude.

  -

  All components of the resulting vector are stored in the same neuron (${\sigma }_{q_{(u,v)}}$), which can be read and write with their respective request rules.

  Specifically, the operation of the proposed neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$, is described as follows:

  1.

  At the initial simulation step ($t=0$), the magnitudes of the components of the vector A are assigned to each synaptic weight ($w_1,w_2,\dots ,w_n$), while the signs of each component are loaded as anti-spikes in the dendritic delays ($\Delta t_1,\Delta t_2,\dots ,\Delta t_n$).

  2.

  At simulation step $t=1$, each neuron (${\sigma }_{s_1},{\sigma }_{s_2},\dots ,{\sigma }_{s_n}$) receives anti-spikes, which represent the signs of vectors (A and B), from dendritic delays ($\Delta t_1,\Delta t_2,\dots ,\Delta t_n$) and inputs ($sig{n}_{B_{{(u,v)}_1}}$, $sig{n}_{B_{{(u,v)}_2}}$, …, $sig{n}_{B_{{(u,v)}_n}}$), respectively. At this time, each neuron (${\sigma }_{s_1},{\sigma }_{s_2},\dots ,{\sigma }_{s_n}$) activates some of its rules to determine the sign of each component of the resulting vector. Here, the forgetting rule (${\overline{a}}^2\to \lambda$) is activated when the result is positive and the firing rule ($\overline{a}\to {\overline{a}}_g$) is activated when the sign is negative. In general, when the sign of each component of the resulting vector is negative, it is sent to the neuron (${\sigma }_{q_{(u,v)}}$).

  3.

  From $t=2$ to $t=10$, each component of the vector B is fed to the neurons (${\sigma }_{s_1},{\sigma }_{s_2},\dots ,{\sigma }_{s_n}$) in the form of trains of colored spikes when the firing rules on synapses ($a\to a_{g_x}$, where $1\le x\le n$) are activated. In this time interval, the neuron (${\sigma }_{q_{(u,v)}}$) applies its request rules (($a^{*}/Q(a_{g_1}^{\infty },{\sigma }_{s_1})),(a^{*}/Q(a_{g_2}^{\infty },{\sigma }_{s_2})),\dots ,(a^{*}/Q(a_{g_n}^{\infty },{\sigma }_{s_n}$)).

  Therefore, the neuron (${\sigma }_{q_{(u,v)}}$) contains the results of the dot product ($A·B$), where each component of the result is expressed with a color of spikes with its respective anti-spike sign when the component is negative.

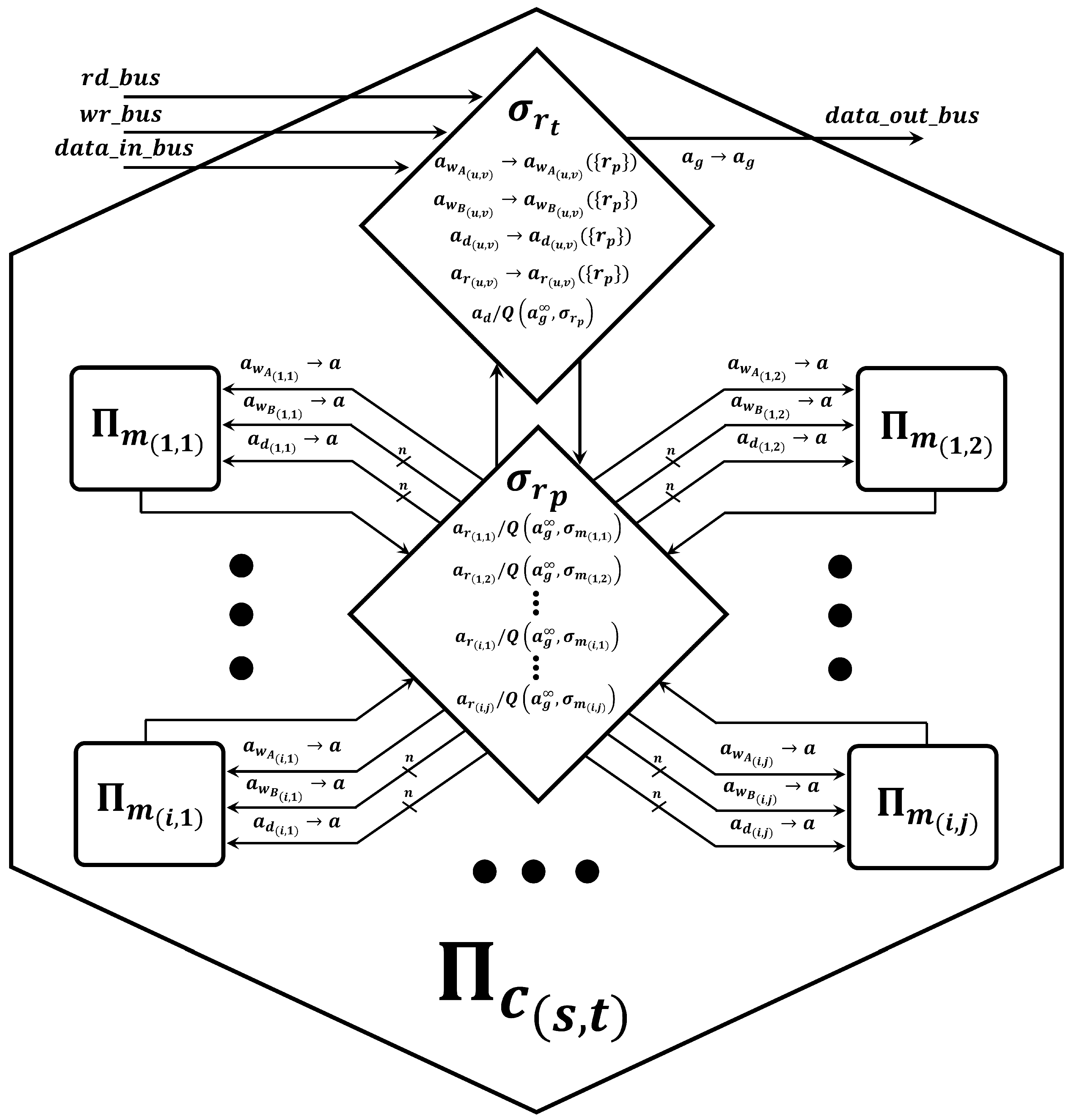
  Therefore, each basic spiking neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$, can perform parallel computation of vector arithmetic operations. In case of performing the computation of matrix operations, such as the inner product and the Kronecker product, these components need to be interconnected by router neurons (${\sigma }_{r_t}$ and ${\sigma }_{r_p}$), as shown in Figure 2. Under this configuration, we denominated this component as spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$.

  Figure 2. Schematic of spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$.

  Figure 2. Schematic of spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$.
• Spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$.
  Given the matrices A of size $i\times i$ and B of size $j\times j$, the spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$, performs the calculation of matrix multiplication ($C=A\times B$). Here, when both matrices A and B have the same dimensions (i.e., $i=j$), matrix multiplication is possible. In general, to calculate this operation, the spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$, performs the dot product between the rows of matrix A and the corresponding columns of matrix B through basic spiking neural memory cells (${\mathsf{\Pi }}_{m_{(1,1)}},{\mathsf{\Pi }}_{m_{(1,2)}},\dots ,{\mathsf{\Pi }}_{m_{(i,1)}},\dots ,{\mathsf{\Pi }}_{m_{(i,j)}}$). To obtain the corresponding element in the resulting matrix $C=A\times B$, the spiking neural memory core performs the dot product between the row i from A and column i from B.
  In general, the proposed spiking neural memory core, ${\mathsf{\Pi }}_{c_{(s,t)}}$, compute the matrix multiplication, as follows:

  -

  Writing stage. At this stage, the data is fed to each spiking neural memory cell. Specifically, the components of the matrices, A and B, are sent from the buses ($wr\_bus$ and $data\_in\_bus$) to the basic spiking neural memory cells (${\mathsf{\Pi }}_{m_{(1,1)}},{\mathsf{\Pi }}_{m_{(1,2)}},\dots ,{\mathsf{\Pi }}_{m_{(i,1)}},\dots ,{\mathsf{\Pi }}_{m_{(i,j)}}$). This is achieved by routing the spikes through router neurons (${\sigma }_{r_t}$ and ${\sigma }_{r_p}$) under the following considerations:

  1.

  Each component of matrices A and B are represented with the types of spikes $a_{w_{A_{(u,v)}}}$ and $a_{w_{B_{(u,v)}}}$, respectively. On the other hand, the signs of the components are represented with spikes of the type $a_{d_{(u,v)}}$. Here, u and v denote matrix indices; in this way, the spikes are identified between different neurons.

  2.

  The writing stage begins when the sign spikes of each component are sent via $wr\_bus$ to the router neuron ${\sigma }_{r_t}$. Here, the firing rule ($a_{d_{(u,v)}}\to a_{d_{(u,v)}}\left(\left\{r_p\right\}\right)$) is activated, and these sign spikes are sent to the router neuron ${\sigma }_{r_p}$. Therefore, the rules in synapses ($a_{d_{(i,j)}}\to a$) on systems ${\mathsf{\Pi }}_{m_{(i,j)}}$ are activated according its indices.

  3.

  Subsequently, the spikes of the matrix components ($a_{w_{A_{(u,v)}}}$ and $a_{w_{B_{(u,v)}}}$) enter to the router neuron (${\sigma }_{r_t}$) via input $data\_in\_bus$. As previous case, to transfer of the matrix components, the spikes are distributed from the router neuron (${\sigma }_{r_p}$) to the different basic spiking neural memory cells (${\mathsf{\Pi }}_{m_{(1,1)}},{\mathsf{\Pi }}_{m_{(1,2)}},\dots ,{\mathsf{\Pi }}_{m_{(i,1)}},\dots ,{\mathsf{\Pi }}_{m_{(i,j)}}$).

  -

  Processing stage. Once the matrix components are loaded into memory, the calculation of the product ($C=A\times B$) begins. Each basic neural memory cell, ${\mathsf{\Pi }}_{m_{(i,j)}}$, perform the dot product between the rows of A and the corresponding columns of B. The resulting matrix C is an $i\times i$ matrix, where the calculation of the components of C can be generalized as $c_{ij}=a_{1j}·b_{1i}+a_{2j}·b_{2i}+a_{3j}·b_{3i}+...+a_{ij}·b_{ij}$. This process is repeated for all elements of the resulting matrix C; thus, the resulting components are stored in the basic spiking neural memory cells (${\mathsf{\Pi }}_{m_{(1,1)}},{\mathsf{\Pi }}_{m_{(1,2)}},\dots ,{\mathsf{\Pi }}_{m_{(i,1)}},\dots ,{\mathsf{\Pi }}_{m_{(i,j)}}$).

  -

  Reading stage. At this stage, it is possible to read the results of matrix multiplication by following two steps:

  1.

  A spike of the type $a_{r_{(u,v)}}$ is sent to the router neuron (${\sigma }_{r_t}$) via $rd\_bus$, where $1\le u\le i$ and $1\le v\le j$. Here, u and v represent the indices of the component of the resulting matrix ($c_{ij}$) to be read. At this moment, a spike $a_{r_{(u,v)}}$ is sent to the router neuron (${\sigma }_{r_p}$) when the rule ($a_{r_{(u,v)}}\to a_{r_{(u,v)}}\left(\left\{r_p\right\}\right)$) is activated. Therefore, the router neuron (${\sigma }_{r_p}$) requests the component to any of the basic spiking neural memory cells (${\mathsf{\Pi }}_{m_{(1,1)}}$, ${\mathsf{\Pi }}_{m_{(1,2)}}$, …, ${\mathsf{\Pi }}_{m_{(i,1)}}$, …, ${\mathsf{\Pi }}_{m_{(i,j)}}$) by activating any of its request rules ($a_{r_{(1,1)}}/Q(a_g^{\infty },{\sigma }_{m_{(1,1)}})$, $a_{r_{(1,2)}}/Q(a_g^{\infty },{\sigma }_{m_{(1,2)}})$, …, $a_{r_{(i,1)}}/Q(a_g^{\infty },{\sigma }_{m_{(i,1)}})$, …, $a_{r_{(i,j)}}/Q(a_g^{\infty },{\sigma }_{m_{(i,j)}})$).

  2.

  In this step, if the requested result component ($c_{ij}$) is in the router neuron (${\sigma }_{r_p}$), it is necessary to send a spike $a_d$ into the router neuron (${\sigma }_{r_t}$) via $rd\_bus$. Here, the neuron (${\sigma }_{r_t}$) makes a request ($a_d/Q(a_g^{\infty },{\sigma }_{r_p}$) for the component of the neuron (${\sigma }_{r_p}$) and stores it in its soma. As a consequence of this, the requested result component is sent to the spiking neural memory core (${\mathsf{\Pi }}_{c_{(s,t)}}$) output via $data\_out\_bus$.

Once the explanation behavior of basic neural memory cell (${\mathsf{\Pi }}_{m_{(i,j)}}$) and spiking neural memory core (${\mathsf{\Pi }}_{c_{(s,t)}}$) is provided, it is possible to understand how the proposed memory-processing unit (${\mathsf{\Pi }}_{MEM}$) works. As can be seen from Figure 3, the proposed ${\mathsf{\Pi }}_{MEM}$ is composed of a set of neural memory cores ${\mathsf{\Pi }}_{c_{(s,t)}}$ and performs the computation of the Kronecker product between two matrices ($A\otimes B$). Here, the neural memory cores, ${\mathsf{\Pi }}_{c_{(s,t)}}$, are interconnected by four buses: $rd\_bus$, $wr\_bus$, $data\_in\_bus$, and $data\_out\_bus$. Through these buses, the memory-processing unit, ${\mathsf{\Pi }}_{MEM}$, enables the data transfer from external sources to the processing cores while storing the results in the same component.

To calculate the Kronecker product, the memory-processing unit, ${\mathsf{\Pi }}_{MEM}$, takes the input matrices (A and B) and divides them into smaller matrix fragments. These fragments are portions of the original matrices. In this manner, the data can be allocated more easily in each neural memory cores ${\mathsf{\Pi }}_{c_{(s,t)}}$. The Kronecker product involves a series of dot product operations between elements of the matrix fragments, where these operations are performed in parallel. In general, the segmentation of the input matrices (A and B) into smaller fragments and the distribution of them among neural memory cores (${\mathsf{\Pi }}_{c_{(s,t)}}$). This approach has enabled more efficient distribution of processing tasks, particularly during intensive computations involving large and complex matrices.

3. Discussion

Nowadays, modern applications are surpassing the computational capabilities of current computing systems. One critical aspect is linked to the memory since these applications are exceeding its bandwidth. This becomes more critical, especially when these applications require processing and storing large amounts of data. As a consequence, this produces a negative impact on these computing systems since this data transfer from/to memory highly demands time and energy. Until now, several authors have proposed several strategies to mitigate this negative aspect. These solutions are based on processing at the data array and processing in a unit near memory banks. Despite achieving significant improvements, there is an important issue to be solved. To achieve a true MPU, the memory cell must be equipped with computational capabilities and not just storage. Up till date, the existing MPU schemes systems still perform operations on distributed cores, and the result is stored on caches. Hence, the strategy of fetching and moving data from the memory to the computing unit is still inefficient. According to various authors, the MPUs need to be designed for a specific application field to achieve an optimal performance. Therefore, advanced applications, such as artificial intelligence, big data, cloud computing, image processing, and data encryption, among others, can achieve maximum efficiency by performing specific computations using a unique data-array structure. Specifically, these applications widely use matrix–matrix multiplication operations as basic mathematical operations. Recent studies in neuroscience have found that a neuron can intrinsically perform specific operations and retain the information in its memory [34,35,36,37]. Specifically, neuronal allocation refers to the process by which certain neurons within a network are selectively activated by specific stimuli to encode a particular memory while excluding others. Inspired by these neuronal biological behaviors, we have created a memory cell, in which neurons have been endowed with computing capabilities, and the result is stored on the same units to create distributed MPU devices. Obviously, the development of a general-purpose MPU opens new horizons in the improvement of advanced in-memory applications.

4. Conclusions

Inspired by diverse dendritic and axonal phenomena, we develop a new memory-processing unit, MPU. Specifically, this MPU was designed to fully exploit the structure and computational capabilities of the dendrites and axons. Based on this, our contributions are the following:

• We design a basic spiking neural memory cell, ${\mathsf{\Pi }}_{m_{(u,v)}}$, to perform arithmetic operations, such as addition, subtraction, and multiplication.
• We propose two router neurons (${\sigma }_{r_t}$ and ${\sigma }_{r_p}$) to efficiently write/read the spikes in each neural memory cell.

This significant achievement was possible thanks to the study of the structure of the dendrites and axon since these components are vital in the computation of the neuron and the storage of information in its soma. Future work will focus on designing specialized memory-processing-unit (MPU) architectures for implementation in memristor-based systems since these are particularly well-suited for neuromorphic computing due to their capacity to replicate the behavior of biological synapses and neurons, supporting the creation of highly integrated, energy-efficient, brain-inspired computing platforms.