Abstract
Recent studies in Visual Question Answering (VQA) have revealed that models often rely heavily on language priors rather than vision–language understanding, leading to poor generalization under distribution shifts. To address this challenge, we propose HQD-EM, a unified debiasing framework that combines the Hierarchical Question Decomposition (HQD) module with an Ensemble adaptive angular Margin (EM) loss. HQD systematically decomposes questions into multi-granular representations to capture layered language biases, while EM leverages bias confidence to modulate per-sample decision margins dynamically. Our method integrates an ensemble-based method with adaptive margin learning in an end-to-end trainable architecture. Experiments on VQA benchmarks demonstrate that HQD-EM significantly outperforms prior works on VQA-CP2 and VQA-CP1.
MSC:
68T07
1. Introduction
Visual Question Answering (VQA) [1,2] is a multimodal task that accepts natural language questions and images as inputs, integrating complementary information from both modalities to derive correct answers. This task requires models to deeply understand the intrinsic meanings embedded in both text and images, as well as to capture the complex relationships between them. VQA models have been actively researched since their inception and have consistently improved in performance [3,4,5,6,7,8]. However, VQA methods have been shown to rely heavily on language priors and learning shortcuts [9,10,11,12], leading to poor generalizability on the out-of-distribution (OOD) dataset and the development of robust or debiasing in VQA models.
Existing debiasing approaches for VQA fall into four main categories. Grounding-based methods [13,14] use additional attention maps or human annotations to align language with visual regions, but their reliance on external supervision limits scalability, and analyses show they often underutilize true visual content and default to learned language priors. Counterfactual-based techniques [15,16,17,18] augment data via synthetic perturbations, such as question rephrasing or image inpainting, to break spurious correlations; yet, these perturbations frequently violate the original dataset’s generation philosophy and incur heavy annotation or heuristic design costs. Adaptive margin loss-based methods (e.g., RMLVQA [19], AdaVQA [20]) dynamically adjust per-sample decision margins to improve feature separation, but they typically operate under single-modality assumptions and use only basic cross-entropy for bias learning. Ensemble-based models such as RUBi, LMH, GGE, and GenB [11,12,21,22] train auxiliary bias predictors to reweight or regularize the main model; yet, they lack systematic analysis and utilization of the complex, overlapping language biases inherent in natural questions.
Despite these advances, two key limitations remain. First, most methods address language bias at a single granularity, namely, whole questions or fixed heuristic splits, without multi-level, hierarchical analysis of nested syntactic and semantic bias patterns. Moreover, these approaches tend to suffer performance degradation as the number of tokens in the question increases. Second, ensemble- and margin-based techniques have been studied largely in isolation or connected sequentially, without an integrated framework that fuses ensemble-based methods and adaptive margin learning.
To overcome these issues, we propose HQD-EM (Hierarchical Question Decomposition with Ensemble adaptive angular Margin), as shown in Figure 1. This illustrates a concrete example of how a standard VQA model falls prey to language priors, where it memorizes the most common answer and outputs an erroneous response. Whereas we show an example where our HQD-EM framework is able to overcome that bias and infer the correct answer from the image.
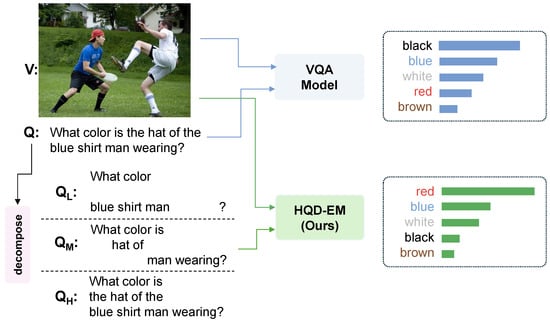
Figure 1.
An example of how traditional VQA models suffer from language biases. An example where our HQD-EM framework mitigates this issue.
In detail, we present HQD-EM, a unified debiasing framework that proposes two key components: (1) Hierarchical Question Decomposition (HQD), which decomposes each question into low-, middle-, and high-level variants and ensembles their predictions to learn language priors more reliably; and (2) the Ensemble adaptive angular Margin (EM) loss, where “ensemble” explicitly refers to using the ensemble of HQD outputs as the bias signal whose instance-level confidence dynamically modulates class-specific margins in a confidence-aware manner.
Our contributions are listed as follows:
- A novel architecture combining Hierarchical Question Decomposition Bias Module (HQD) and Ensemble adaptive angular Margin (EM) loss for unified debiasing.
- A multi-granular token-based decomposition that captures and mitigates complex, overlapping language biases.
- State-of-the-art results on VQA-CP2 and VQA-CP1, demonstrating superior generalization under challenging bias conditions while maintaining competitive performance on the standard VQA v2 dataset with minimal degradation in accuracy.
2. Related Work
Visual Question Answering (VQA) [1,2,23,24] has been an active field of research in recent years, with powerful models being developed on standard benchmarks [3,4,5,6,7,8,25]. However, researchers have shown that models can be reliant on dataset biases [9,26,27,28,29], particularly language priors, which can cause models to neglect visual information and rely on spurious correlations.
To address these challenges, diverse debiasing approaches for VQA can be broadly categorized into four families: grounding-based, counterfactual-based, adaptive margin loss-based, and ensemble-based methods. Grounding-based techniques seek to reinforce visual reasoning by leveraging additional attention maps or human annotations [13,14]; however, their reliance on external supervision limits scalability, and recent analyses have shown they often fail to truly leverage visual content, defaulting instead to regularization. Counterfactual-based methods augment training data with synthetic perturbations, such as question rephrasing or image inpainting, to reduce spurious correlations [16,17,18]; yet, they frequently diverge from the dataset’s original generation philosophy and require extensive annotation or heuristic design. Adaptive margin loss approaches (e.g., RMLVQA [19], AdaVQA [20]) assign per-sample margins based on answer frequency or difficulty, improving feature separation but typically operating within a single modality and under simplified bias assumptions. Ensemble-based models such as RUBi, LMH, GGE, and GenB [11,12,21,22] incorporate auxiliary bias predictors, typically question-only or image-only models, to reweight or regularize the main model. However, they fail to systematically analyze and address the complex, overlapping language biases embedded in natural questions. Another line of work explores adapter-based debiasing [30] to explore in- and out-of-distribution performance through adapters.
Despite these advances, two key limitations persist in prior works. First, most methods treat language bias at a single granularity, such as entire questions or fixed heuristic splits, without performing systematic, multi-level analysis of the rich, overlapping biases embedded in natural language. As a result, complex biases arising from nested syntactic or semantic patterns remain underexplored. Second, while ensemble and margin-based techniques both mitigate bias, they are typically studied in isolation or connected only sequentially, lacking an organic framework that fuses ensemble-based methods with adaptive margin learning in a unified manner.
To address these gaps, we propose HQD-EM (Hierarchical Question Decomposition with Ensemble adaptive angular Margin), the first framework to (i) hierarchically decompose each question into multi-granular variants for fine-grained bias detection and (ii) organically integrate an ensemble-based method with confidence-aware adaptive angular margin loss to achieve robust debiasing under challenging distribution shifts.
3. Proposed Method
Our HQD-EM framework is composed of two synergistic parts: the HQD module, which employs ensemble-based bias modeling to capture complex, layered language biases via hierarchical question decomposition, and the EM loss, which leverages these learned biases to adaptively adjust decision margins and perform effective debiasing (see Figure 2 for an overview). In Section 3.1, we first describe our VQA baseline. Section 3.2 presents the HQD question decomposition strategy. Section 3.3, illustrated in Figure 2a,b, details how the decomposed questions are used to train the bias model and how to apply debiasing, and finally, Section 3.4, depicted in Figure 2c, explains how the EM loss uses the trained bias models to modulate margins for robust generalization.
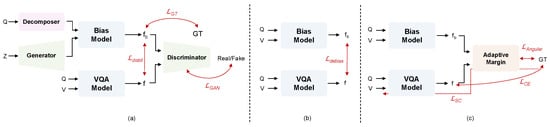
Figure 2.
Overview of HQD-EM. (a) Bias model training using hierarchical questions and pseudo-visual features. (b) Debiasing with pseudo-labels. (c) Ensemble-aware adaptive margin loss.
3.1. VQA Baseline
We adopt the Bottom-Up Top-Down (UpDn) architecture [31] as our VQA baseline. Given an input image v, a pre-trained Faster R-CNN [32] extracts n object-level feature vectors . Concurrently, the question q is encoded by GloVe [33] embeddings followed by a GRU [34] to produce . An attention-based fusion module , then computes weights over the visual features conditioned on the question embedding, yielding a joint multimodal representation of x where
This feature x is then passed through an MLP classifier to produce logits y where
which are transformed into answer probabilities . We denote this combined network of as for ease of notation, where necessary. We optimize this baseline using the standard cross-entropy loss against the one-hot ground-truth labels.
3.2. Hierarchical Question Decomposition Strategy
In this work, we refer to our multi-scale question decomposing strategy as Hierarchical Question Decomposition (HQD). HQD systematically splits each question into three levels—low, middle, and high—by first fixing the question token that encodes the question type and then randomly sampling the remaining tokens at different ratios. In low-level decomposition, we randomly select one-third of the question tokens (without replacement) and then form by keeping the selected tokens in their original left-to-right order (i.e., no reordering or shuffling). In middle-level decomposition, we similarly retain roughly half of the tokens in order. High-level decomposition makes no changes and retains the full token sequence. For example, the question “How many donuts have light purple sprinkles on them?” is transformed into a low-level variant “How many donuts purple?” (), a middle-level variant “How many have purple sprinkles on?” (), and a high-level variant “How many donuts have light purple sprinkles on them?” (). We choose the minimum ratio, one-third, for based on the token statistics of VQA-CP: the maximum question length used in the model is 14 tokens, with most questions being much shorter. Further decomposition could leave too few tokens. In addition, as we deterministically keep the question-type token, this could leave only one to two additional content tokens, creating a sentence that is too sparse to preserve meaningful context. We find that using a decomposition rate of one-third typically preserves 4–5 tokens while still enforcing substantial compression. We also present a variant that fixes both the question-type token and noun tokens (sampling over the remaining tokens to align with meaningful units), but empirically find that fixing only the question-type token yielded stronger performance and more robust debiasing; therefore, we adopt this setting (see Section 4.7). By exposing the model to these compressed and expanded variants, HQD enables learning of subtle distributed language biases at multiple granularities without sacrificing overall context.
3.3. Hierarchical Question Decomposition Training and Debiasing
As we also utilize an ensemble-based method, we create 2 models: a target model, which is the main model that is used for inference and testing, and a bias model, which is a similar model that we utilize to capture the biases and use for debiasing the target model. In our case, to capture both the dataset priors and the intrinsic biases of the target model, we adopt the same architectural structure as the target model. As previously mentioned, the target model produces logits: , where the bias model would produce the logits: , given a multimodal intermediary feature x. However, for the bias model, following GenB [12], we feed a Gaussian noise tensor z through a simple generator to create generated image features so the bias model learns bias representations that remain architecturally aligned with the backbone while stochastically capturing biases from the question.
z is then used to synthesize a pseudo-visual feature ,
where is a small generator network, and denote the number of region features and their dimensionality.
Our HQD bias model directly receives the decomposed questions , , and , along with the pseudo-visual feature .
Inside , each question variant is first encoded by its own subnetwork:
We empirically found that element-wise summation of the three subnetwork outputs yields the best performance, resulting in the fused question feature .
The fused question feature and the pseudo-visual feature are then passed through the attention-based fusion module and an MLP classifier to generate the final logits .
Binary Cross-Entropy Loss. This loss forces to overfit to dataset priors by matching its sigmoid outputs to the ground-truth answer distribution :
Adversarial Loss. A discriminator D [35] is trained to distinguish true VQA logits y, the output of the VQA model given image features v and question embedding q, from HQD bias logits , which capture spurious correlations learned by the bias model. Meanwhile, the bias model and generator G are optimized to fool D by producing logits that resemble the true VQA outputs. The resulting minimax game is:
This encourages to mimic the target model’s output distribution and capture its biases.
Knowledge Distillation Loss. To align more closely with the target VQA model, we minimize the Kullback–Leibler divergence [36] between the target logits and bias logits:
This distillation transfers fine-grained prediction patterns into the bias model.
Overall Loss of Training Bias. The overall objective for bias model training combines these terms:
where and are hyperparameters that balance each component’s contribution.
Debiasing the Target Model. After training , we generate bias logits by feeding the real image features v and each decomposed question into the bias model, following the design choices in GenB [12]. Let the target model’s logits be y and its predicted probabilities . We then construct pseudo-labels that reduce overly biased predictions while preserving bias intensity:
where is the one-hot ground truth and the i-th bias logit. Finally, the target model is optimized with a cross-entropy loss against these pseudo-labels:
This debiasing loss leverages the bias model’s confidence to steer the target model away from spurious correlations without discarding useful bias strength.
3.4. Ensemble Adaptive Angular Margin Loss
To further enhance robustness, inspired by previous work RMLVQA [19], we calibrate the loss using dataset-level statistics together with a bias signal learned via standard cross-entropy. In contrast, we tackle the limitation of such a CE (Cross Entropy) trained model, which is a largely static bias estimate by introducing an Ensemble adaptive angular Margin (EM) that dynamically modulates class-specific margins using both dataset priors and instance-level confidence of our HQD bias model, yielding a more effective debiasing model.
First, inspired by RMLVQA [19], for each question type , we compute frequency-based margins to penalize models less on common answers and more on rare ones:
where is the count of answer under and avoids division by zero. Here, reflects how frequent an answer is, and becomes a larger margin for rarer answers.
Next, we inject controlled randomness into these margins to prevent over-correction:
Sampling from a Gaussian centered on with standard deviation smooths margin extremes and improves generalization. In parallel, we derive an instance-level margin from the dedicated bias classifier’s output logits. We do this by training a separate classifier with standard cross-entropy loss to capture language biases. Then, we normalize the cross-entropy logits of the stand-alone bias model.
where is a temperature hyperparameter. Unlike previous works, here we then compute the per-instance margin as
Here, denotes the output of HQD, and is a hyperparameter. By injecting HQD’s output into the instance-specific margin , we organically couple HQD and EM. The well-trained HQD bias model provides instance-level confidence to modulate the base , complementing the standard CE-based bias estimation and capturing residual priors that the model might miss. We propose that this synergy yields a more context-aware margin and, ultimately, better debiasing.
We then merge the randomized and instance-level margins for the ground-truth class :
where is annealed from 1 to 0 over training, gradually shifting emphasis from global frequency priors to per-sample bias signals.
Finally, we impose these combined margins in an angular margin loss, which maximizes the angular distance between feature x and classifier weight :
where s scales features and is the angle to .
To train the bias-capturing classifier (which outputs logits ), we include its cross-entropy loss:
To further enhance feature discrimination of our model, we add an additional Supervised Contrastive (SC) loss, , as contrastive losses [37,38] have been shown to aid models in learning more representative features. Specifically, given a mini-batch of size B with feature vectors and corresponding labels , we define for each anchor j:
The SC loss [37] is then:
where we set the temperature for all experiments.
The full training objective is
This design leverages HQD’s bias signals to tailor margins at both global and instance levels, yielding fine-grained debiasing and robust generalization under distribution shifts.
4. Experiments
4.1. Setup
Datasets and evaluation protocol. We evaluate our method on two widely used benchmarks for assessing VQA model robustness to bias: VQA-CP2, VQA-CP1 [10]. VQA-CP2 and VQA-CP1 [10] are specifically designed to test overreliance on language priors by altering answer distributions between train and test splits. We additionally also show our experiments on VQA v2 [1] for reference. VQA v2 serves as an in-distribution benchmark to evaluate overall performance and performance degradation when debiasing is applied. We use the standard VQA accuracy metric for all evaluations.
Experimental Settings. All experiments were conducted on a single NVIDIA (NVIDIA, Santa Clara, USA) RTX 5000 Ada GPU. The end-to-end training time was approximately 10 h, and the peak GPU memory usage at roughly 8 GB. For reference, our baseline configuration was trained for about 8.5 h and with roughly 6 GB of memory usage. At inference time, as we only utilize the target model, evaluating 2048 samples took 0.98 s for the baseline and 1.07 s for our model. At training time, the parameter count for UpDn is 24.4 M, GenB is 55.5 M, and Ours is 67.0 M. At test time, the parameter count is for UpDn and GenB is 24.4 M, while Ours is 27.6 M. Thus, with only a modest overhead time, memory, and parameters relative to the baseline, our full model yields a notable improvement in accuracy.
4.2. Results on VQA-CP2 and VQA-CP1
As shown in Table 1, we evaluate HQD-EM by integrating it with the UpDn backbone. For fair comparison, all methods, excluding the base models, use UpDn as their backbone. When applied on VQA-CP2, HQD-EM establishes a new state-of-the-art in overall accuracy (62.53%) among all prior UpDn-based methods, including those employing data augmentation or balancing, and outperforms them by a notable margin. In particular, our model exhibits strong performance on both of the challenging tasks, Num (55.67%) and Other (50.44%), demonstrating its effectiveness.

Table 1.
Comparison of VQA-CP2 and VQA-CP1 performance across different debiasing methods. Our model, HQD-EM, achieves state-of-the-art overall accuracy on both VQA-CP2 and VQA-CP1. Bold and underline indicates best scores, bold indicates second best scores.
Compared to recent methods, BILI [50], DVM [51], FAN-VQA [29], and CVIV [52], HQD-EM consistently surpasses them in overall accuracy. Notably, on the Number (NUM) subset, which is considered a difficult subset, HQD-EM yields substantial margins of 13.91%, 4.62%, 10.55%, and 14.90% over BILI, DVM, FAN-VQA, and CVIV, respectively, while matching or exceeding performance across the remaining categories. On the VQA-CP1 benchmark, HQD-EM similarly achieves a 3.38% absolute improvement over the previous best, demonstrating its consistent efficacy across datasets.
4.3. Results on VQA v2
As shown in Table 2, prior methods that achieve high accuracy on VQA-CP2 experience substantial degradation when evaluated on the standard VQA v2 split. For example, AdaVQA [20] drops by 7.04% in overall accuracy, underscoring that strong VQA-CP2 performance often comes at the cost of poor in-distribution generalization. This makes VQA v2 performance essential as well. In contrast, our HQD-EM maintains excellent in-distribution performance, with only a 0.71% gap between VQA-CP2 and VQA v2 overall accuracy, demonstrating its robustness and stability across differing answer distributions.

Table 2.
Overall VQA v2 test accuracy and gap (VQA-CP2, VQA v2) for prior methods and HQD-EM (ours). Our HQD-EM achieves a minimal gap of 0.71%, indicating strong robustness across distribution shifts.
4.4. Effect of Losses
As shown in Table 3, we ablate individual components while keeping the others fixed. We do not remove independently, because it contains the pseudo labels predicted by the bias model trained with . Ablating it by removing it would eliminate the entire HQD bias-learning path. Also, ablating both and simultaneously would strip away core learning signals and make the comparison uninformative, so we do not ablate that configuration. Within , adding to the configuration without yields only a marginal improvement of . In contrast, utilizing both and leads to a substantial gain of , indicating that the adversarial signal and the distillation term complement each other and help the model more effectively learn the bias patterns captured by the HQD bias-learning path. On the side, enabling (with off) improves performance by , suggesting that the standard CE term remains beneficial when instance-wise margins are adjusted dynamically. Finally, activating further separates samples in the feature space and delivers the best overall score of 62.53%.

Table 3.
Ablation on loss components. ✓ indicates the loss is used; an empty cell indicates that the loss is removed. “Overall” reports the full method metric.
4.5. Effect on Instance Margin
As shown in Table 4, denotes the bias signal produced by a classifier trained with standard cross-entropy, whereas is the bias signal predicted by our HQD bias model. These signals are used by HQD-EM to adjust the margin dynamically on a per-sample basis. Using alone slightly outperforms using alone, suggesting that HQD captures bias more faithfully. More importantly, leveraging both signals yields the best result, 62.53%, indicating that they are complementary and that integrating HQD confidence into the margin leads to stronger, sample-aware regularization.

Table 4.
Ablation on the EM loss targets. We compare using the margin-conditioned signals and individually and jointly. ✓ indicates if the signal is used.
4.6. Effect of HQD Variants
As shown in Table 5, we examine the effect of each question decomposition level. Using all three levels together results in the highest accuracy, supporting our claim that captures global semantics and grammatical structure, provides partial yet salient information, and helps surface fine-grained biases. Using only , which corresponds to the original question without decomposition, achieves 62.01. Relying solely on or incurs small drops, likely because partial/masked variants miss global semantics. Among the two-level settings, configurations that include outperform the pair, suggesting provides a global anchor while and add complementary cues. Combining all three levels yields the best accuracy, 62.53%, indicating that HQD more fully exposes bias signals and enables stronger debiasing.

Table 5.
Ablation on hierarchical question decomposition variants. Each row denotes the use of one or more decomposition levels. Combining all three levels provides the best performance, indicating complementary semantic (high), partial (mid), and detailed (low) signals. ✓ indicates the which semantics are used.
4.7. Effect of Fixing Tokens in HQD
We ablate the tokens to fix when forming //. Motivated by the fact that the question-type token and head nouns often carry answer-relevant cues, we explicitly test which of these signals should be preserved during decomposition. We compare three variants: (i) fix no tokens; (ii) fix only the question-type token; (iii) fix the question-type token and nouns, then apply the prescribed retention ratios to the remaining tokens. As shown in Table 6, fixing only the question-type token gives the best overall accuracy (62.53%) versus fixing nothing (61.89%) or fixing type + nouns (62.08%). This indicates that preserving the type cue is sufficient while keeping beneficial randomness. Guided by this result, we intuitively adopt the type-only setting for all main experiments.

Table 6.
Effect of fixing tokens in HQD. All variants use identical retention ratios for (, , ), with fractional counts rounded to the nearest integer and original token order preserved. Fixing only the question-type token yields the best overall accuracy.
4.8. Effect of HQD-EM Across Token Lengths
As shown in Figure 3, both GenB and HQD-EM see their accuracy drop as questions grow longer, confirming that more tokens generally mean harder samples. Interestingly, HQD-EM outperforms the GenB baseline at every token-count bin, demonstrating that our hierarchical decomposition and ensemble margin loss together help the model maintain robust, bias-resilient reasoning even on complex, long-form questions. Moreover, this improvement is not confined to easier examples. HQD-EM exhibits consistent gains across all token lengths and difficulty levels, confirming that its superiority stems from genuinely better handling of harder queries rather than just boosting performance on simple cases.
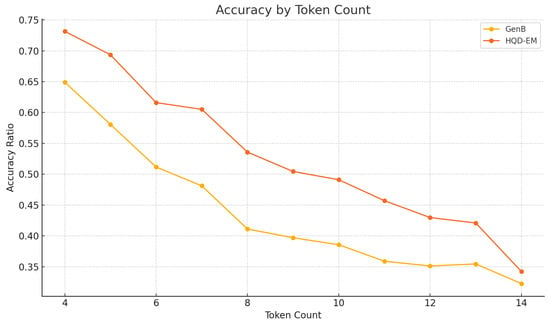
Figure 3.
Accuracy ratio across different token counts for GenB and HQD-EM. HQD-EM consistently outperforms GenB, especially on longer questions.
4.9. Design Choices in HQD Module
As shown in Table 7, we systematically evaluate three fusion operations—element-wise summation (“+”), element-wise product (“×”), and a small learned MLP—applied at both the attention and question levels within the HQD module. For the MLP variant, features are first concatenated and then passed through a lightweight multi-layer perceptron that projects the fused representation back to the original feature dimensionality. The configuration using summation for both attention- and question-level fusion achieves the highest overall accuracy of 62.53%, outperforming other fusion combinations involving the learned MLP. This result underscores that simple additive fusion is particularly effective for combining visual–attention and question features, suggesting that element-wise summation plays a critical role in uncovering the optimal HQD performance.

Table 7.
Impact of fusion strategies in the HQD module. +, ×, and MLP denote element-wise summation, product, and a small learned fusion network, respectively. When both attention and question level fusion use element-wise summation, the model achieves the best performance.
4.10. Effect of Different Backbones
Through our experiments in Table 8, we run an ablation on various popular VQA architectures to show that our method is model-agnostic. In particular, we apply our method to three diverse VQA architectures, SAN [39], BAN [4], and LXMERT [7]. We include additional information about the architectures in Appendix A. We compare our methods to previous methods, GenB, DQF, and BILI, where the scores are publicly available. In every case, the backbone with HQD-EM yields a substantial increase in overall VQA-CP2 accuracy. We find that, especially in the architectures of BAN and SAN, our method outperforms the previous methods by 2.12% in SAN and 5.76% in BAN. Although BAN is a more powerful baseline than UpDn, previous methods have been unable to surpass UpDn with debiasing methods, but our method shows an improvement over UpDn in VQA-CP2. In LXMERT, our method performs favorably, and we find that the only method that outperforms Ours is DQF. DQF is a counterfactual-based method that utilizes part-of-speech tagging to generate positive and negative counterfactuals. While on the UpDn backbone, our model outperforms DQF by 2.06%, we conjecture that, as LXMERT is a much larger pretrained model, DQF may perform slightly favorably with the large number of generated counterfactuals. However, we find that in some categories, namely Yes/No, our method outperforms by 1.91%. From the overall trend of how our method works across various baseline architectures, we find that HQD-EM is architecture-agnostic and believe that HQD-EM can be a potential solution for future debiasing methods in VQA.

Table 8.
Architecture ablation on the VQA-CP2 test. Gap denotes the increase in overall accuracy over the base architecture. HQD-EM achieves the largest performance gain across all three backbones. † indicates our reimplementation.
4.11. Qualitative Analysis
As shown in Figure 4, we compare the attention outputs and answer predictions of the GenB baseline against those of our HQD-EM. While GenB’s attention maps often scatter over irrelevant areas, leading to incorrect or unstable answers, HQD-EM repeatedly focuses on the truly informative regions of the image and arrives at the correct response. These examples highlight HQD-EM’s ability to overcome spurious language biases and deliver reliable visual grounding, making it significantly more robust for real-world deployment.

Figure 4.
Qualitative comparison between the baseline GenB and HQD-EM. HQD-EM locates the correct attention regions, enabling more precise inference and increased robustness against dataset biases. The boxes indicate attention from the model. Red boxes indicate erroneously attended regions, green boxes indicate correctly attended regions.
5. Conclusions
In this work, we introduced HQD-EM, a novel framework for robust VQA that combines Hierarchical Question Decomposition and adaptive angular Margin learning. By decomposing questions into high-, mid-, and low-level variants, our HQD module captures distributed and overlapping language biases with fine granularity. Complementarily, the EM loss utilizes frequency statistics and the bias model’s confidence in conjunction with the existing margin to apply dynamic, instance-specific margins, resulting in stronger generalization under biased conditions. Our extensive experiments on VQA-CP2 and VQA v2 confirm that HQD-EM not only surpasses existing methods in performance but also maintains strong accuracy in standard settings. We find that although decomposition itself can be helpful, keeping the question type is most helpful in allowing the bias model to understand biases. We also find that instead of decomposing sentences and using parts of the decomposed sentence, utilizing the high-level (the original sentence) is crucial for the bias model to capture biases. Our extensive ablation shows the importance of each component and how to utilize them best for their application while further revealing that individual question-level encoders and summation-based aggregation within HQD are crucial for maximizing bias mitigation. Overall, HQD-EM offers a unified and interpretable solution for mitigating complex multimodal biases, paving the way for more robust and trustworthy VQA systems. We believe that some limitations we have are that our method relies on sampling through rule-based means in order to make our method as light as possible. However, with existing powerful LLMs, a more dynamic method of generating and decomposing questions might be available, and we believe that may be a direction for future research.
Author Contributions
Conceptualization, J.W.C.; methodology, S.N.; software, S.N.; validation, J.W.C.; formal analysis, S.N.; investigation, S.N.; resources, J.W.C.; data curation, S.N.; writing—original draft preparation, S.N.; writing—review and editing, J.W.C.; visualization, S.N.; supervision, J.W.C.; project administration, J.W.C.; funding acquisition, J.W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT, RS-2025-02263977, Development of Communication Platform supporting User Anonymization and Finger Spelling-Based Input Interface for Protecting the Privacy of Deaf Individuals).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in VQA: Visual Question Answering at https://visualqa.org/index.html. Accessed 1 March 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VQA | Visual Question Answering |
| VQA-CP | Visual Question Answering with Changing Priors |
| HQD-EM | Heirachical Question Decomposition with an Ensemble adaptive angular Margin |
Appendix A
In this section, we include additional information about VQA architectures that we do not include in the main paper.
UpDn [31] (Bottom-Up and Top-Down Attention). UpDn combines object-level bottom-up visual features with top-down question-guided attention. A Faster R-CNN detector (pretrained on Visual Genome) proposes N regions; features are extracted via RoI pooling. The question is embedded and encoded by a GRU to produce a query vector q. A single question-guided soft top-down attention is then applied:
where denotes the gated-tanh nonlinearity used in the paper. VQA prediction is cast as multi-label classification over a fixed answer set (not a single-answer softmax):
and is trained with a sigmoid/BCE-style loss. This separates what to detect (detector) from where to look (question-conditioned attention), yielding interpretable region attention and strong VQA performance.
SAN [39] (Stacked Attention Networks). SAN performs iterative evidence localization with multi-step (stacked) attention. A CNN backbone provides a spatial grid of features ; an LSTM (the original paper also considers a CNN) encodes the question into . At stack k,
where is a fusion function (typically with a residual connection). After 2–3 stacks, an MLP over the fused representation outputs the answer. By repeatedly updating the query with attended visual evidence, SAN refines the focus from coarse to fine regions.
BAN [4] (Bilinear Attention Networks). BAN models fine-grained pairwise interactions between image regions and question tokens via low-rank bilinear pooling. Let region and token feature matrices be and , with shared low-rank projections and a glimpse-specific gating vector . The bilinear attention for glimpse g is:
where ∘ denotes the Hadamard product and is an all-ones vector. The joint feature can then be aggregated (in one convenient form) as:
with ⊙ being the element-wise product, the i-th column of X and the j-th column of Y. Outputs from several glimpses are aggregated (often with residual connections) and fed to a classifier. Compared to additive/multiplicative fusion, BAN’s bilinear attention captures richer token–region alignments while remaining trainable via low-rank factorization.
LXMERT [7] (Learning Cross-Modality Encoder Representations from Transformers). LXMERT adopts a transformer-based two-stream vision encoder and language encoder with a cross-modality encoder for interaction. Region features and box/positional embeddings from a detector (e.g., Faster R-CNN) are contextualized by a self-attentive vision transformer; question tokens are contextualized by a language transformer. A cross-modality transformer then performs bi-directional co-attention to align and fuse the streams into joint representations. Pretraining uses large-scale image–text corpora with the following tasks:
- Masked cross-modality language modeling
- Masked object prediction: RoI feature regression + detected-label (category/attributes) classification
- Cross-modality matching
- Image question answering
For VQA fine-tuning, the fused [CLS] (or pooled) representation is fed to an answer classifier, leveraging general-purpose pretrained multimodal representations for robust performance.
References
- Antol, S.; Agrawal, A.; Lu, J.; Mitchell, M.; Batra, D.; Lawrence Zitnick, C.; Parikh, D. Vqa: Visual question answering. In Proceedings of the ICCV, Santiago, Chile, 7–13 December 2015; pp. 4971–4980. [Google Scholar]
- Zhao, L.; Cai, D.; Zhang, J.; Sheng, L.; Xu, D.; Zheng, R.; Zhao, Y.; Wang, L.; Fan, X. Toward explainable 3d grounded visual question answering: A new benchmark and strong baseline. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 2935–2949. [Google Scholar] [CrossRef]
- Chen, Y.C.; Li, L.; Yu, L.; El Kholy, A.; Ahmed, F.; Gan, Z.; Cheng, Y.; Liu, J. UNITER: UNiversal Image-TExt Representation Learning. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 104–120. [Google Scholar]
- Kim, J.H.; Jun, J.; Zhang, B.T. Bilinear attention networks. In Proceedings of the NeurIPS, Montréal, QC, Canada, 3–8 December 2018; p. 1. [Google Scholar]
- Lu, J.; Batra, D.; Parikh, D.; Lee, S. ViLBERT: Pretraining Task-Agnostic Visiolinguistic Representations for Vision-and-Language Tasks. arXiv 2019, arXiv:1908.02265. [Google Scholar] [CrossRef]
- Su, W.; Zhu, X.; Cao, Y.; Li, B.; Lu, L.; Wei, F.; Dai, J. VL-BERT: Pre-training of Generic Visual-Linguistic Representations. arXiv 2020, arXiv:1908.08530. [Google Scholar] [CrossRef]
- Tan, H.; Bansal, M. LXMERT: Learning Cross-Modality Encoder Representations from Transformers. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 5100–5111. [Google Scholar] [CrossRef]
- Ma, J.; Wang, P.; Kong, D.; Wang, Z.; Liu, J.; Pei, H.; Zhao, J. Robust visual question answering: Datasets, methods, and future challenges. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5575–5594. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Batra, D.; Parikh, D. Analyzing the Behavior of Visual Question Answering Models. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–4 November 2016; Su, J., Duh, K., Carreras, X., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2016; pp. 1955–1960. [Google Scholar] [CrossRef]
- Agrawal, A.; Batra, D.; Parikh, D.; Kembhavi, A. Don’t Just Assume; Look and Answer: Overcoming Priors for Visual Question Answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4971–4980. [Google Scholar]
- Han, X.; Wang, S.; Su, C.; Huang, Q.; Tian, Q. Greedy Gradient Ensemble for Robust Visual Question Answering. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 1584–1593. [Google Scholar]
- Cho, J.W.; Kim, D.J.; Ryu, H.; Kweon, I.S. Generative Bias for Robust Visual Question Answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 11681–11690. [Google Scholar]
- Selvaraju, R.R.; Lee, S.; Shen, Y.; Jin, H.; Ghosh, S.; Heck, L.; Batra, D.; Parikh, D. Taking a hint: Leveraging explanations to make vision and language models more grounded. In Proceedings of the ICCV, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2591–2600. [Google Scholar]
- Wu, J.; Mooney, R.J. Self-critical reasoning for robust visual question answering. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; p. 1. [Google Scholar]
- Chen, L.; Yan, X.; Xiao, J.; Zhang, H.; Pu, S.; Zhuang, Y. Counterfactual samples synthesizing for robust visual question answering. In Proceedings of the CVPR, Seattle, WA, USA, 13–19 June 2020; pp. 10800–10809. [Google Scholar]
- Wen, Z.; Xu, G.; Tan, M.; Wu, Q.; Wu, Q. Debiased Visual Question Answering from Feature and Sample Perspectives. In Proceedings of the NeurIPS, Online, 6–14 December 2021; p. 1. [Google Scholar]
- Niu, Y.; Zhang, H. Introspective distillation for robust question answering. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2021; Volume 34, pp. 16292–16304. [Google Scholar]
- Cho, J.W.; Kim, D.J.; Jung, Y.; Kweon, I.S. Counterfactual Mix-Up for Visual Question Answering. IEEE Access 2023, 11, 95201–95212. [Google Scholar] [CrossRef]
- Basu, A.; Addepalli, S.; Babu, R.V. RMLVQA: A Margin Loss Approach for Visual Question Answering with Language Biases. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 11671–11680. [Google Scholar]
- Guo, Y.; Nie, L.; Cheng, Z.; Ji, F.; Zhang, J.; Bimbo, A.D. AdaVQA: Overcoming Language Priors with Adapted Margin Cosine Loss. arXiv 2021, arXiv:2105.01993. [Google Scholar] [CrossRef]
- Cadene, R.; Dancette, C.; Ben-younes, H.; Cord, M.; Parikh, D. RUBi: Reducing Unimodal Biases in Visual Question Answering. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; p. 1. [Google Scholar]
- Clark, C.; Yatskar, M.; Zettlemoyer, L. Don’t Take the Easy Way Out: Ensemble Based Methods for Avoiding Known Dataset Biases. In Proceedings of the EMNLP, Hong Kong, China, 3–7 November 2019; pp. 4069–4082. [Google Scholar]
- Johnson, J.; Hariharan, B.; Van Der Maaten, L.; Fei-Fei, L.; Lawrence Zitnick, C.; Girshick, R. Clevr: A diagnostic dataset for compositional language and elementary visual reasoning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2901–2910. [Google Scholar]
- Gurari, D.; Li, Q.; Stangl, A.J.; Guo, A.; Lin, C.; Grauman, K.; Luo, J.; Bigham, J.P. VizWiz Grand Challenge: Answering Visual Questions From Blind People. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3608–3617. [Google Scholar]
- Kim, B.S.; Kim, J.; Lee, D.; Jang, B. Visual Question Answering: A Survey of Methods, Datasets, Evaluation, and Challenges. ACM Comput. Surv. 2025, 57, 1–35. [Google Scholar] [CrossRef]
- Goyal, Y.; Khot, T.; Summers-Stay, D.; Batra, D.; Parikh, D. Making the v in VQA Matter: Elevating the Role of Image Understanding in Visual Question Answering. In Proceedings of the CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 6904–6913. [Google Scholar]
- Zhang, P.; Goyal, Y.; Summers-Stay, D.; Batra, D.; Parikh, D. Yin and Yang: Balancing and Answering Binary Visual Questions. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 5014–5022. [Google Scholar]
- Ouyang, N.; Huang, Q.; Li, P.; Cai, Y.; Liu, B.; Leung, H.f.; Li, Q. Suppressing Biased Samples for Robust VQA. IEEE Trans. Multimed. 2022, 24, 3405–3415. [Google Scholar] [CrossRef]
- Bi, Y.; Jiang, H.; Hu, Y.; Sun, Y.; Yin, B. Fair Attention Network for Robust Visual Question Answering. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 7870–7881. [Google Scholar] [CrossRef]
- Cho, J.W.; Argaw, D.M.; Oh, Y.; Kim, D.J.; Kweon, I.S. Empirical study on using adapters for debiased Visual Question Answering. Comput. Vis. Image Underst. 2023, 237, 103842. [Google Scholar] [CrossRef]
- Anderson, P.; He, X.; Buehler, C.; Teney, D.; Johnson, M.; Gould, S.; Zhang, L. Bottom-up and top-down attention for image captioning and visual question answering. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2018; pp. 6077–6086. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Advances in Neural Information Processing Systems; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C. GloVe: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; Moschitti, A., Pang, B., Daelemans, W., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2014; pp. 1532–1543. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised Contrastive Learning. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 18661–18673. [Google Scholar]
- Liang, Z.; Jiang, W.; Hu, H.; Zhu, J. Learning to Contrast the Counterfactual Samples for Robust Visual Question Answering. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020. [Google Scholar]
- Yang, Z.; He, X.; Gao, J.; Deng, L.; Smola, A. Stacked attention networks for image question answering. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 21–29. [Google Scholar]
- Jing, C.; Wu, Y.; Zhang, X.; Jia, Y.; Wu, Q. Overcoming Language Priors in VQA via Decomposed Linguistic Representations. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 11181–11188. [Google Scholar]
- Kv, G.; Mittal, A. Reducing language biases in visual question answering with visually-grounded question encoder. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XIII 16; Springer: Berlin/Heidelberg, Germany, 2020; pp. 18–34. [Google Scholar]
- Abbasnejad, E.; Teney, D.; Parvaneh, A.; Shi, J.; Hengel, A.v.d. Counterfactual Vision and Language Learning. In Proceedings of the CVPR, Seattle, WA, USA, 13–19 June 2020; pp. 10041–10051. [Google Scholar]
- Teney, D.; Kafle, K.; Shrestha, R.; Abbasnejad, E.; Kanan, C.; Hengel, A.v.d. On the Value of Out-of-Distribution Testing: An Example of Goodhart’s Law. arXiv 2020, arXiv:2005.09241. [Google Scholar]
- Gokhale, T.; Banerjee, P.; Baral, C.; Yang, Y. MUTANT: A Training Paradigm for Out-of-Distribution Generalization in Visual Question Answering. In Proceedings of the EMNLP, Online, 16–20 November 2020; pp. 878–892. [Google Scholar]
- Zhu, X.; Mao, Z.; Liu, C.; Zhang, P.; Wang, B.; Zhang, Y. Overcoming Language Priors with Self-supervised Learning for Visual Question Answering. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021. [Google Scholar]
- Chen, L.; Zheng, Y.; Xiao, J. Rethinking data augmentation for robust visual question answering. In Proceedings of the ECCV, Tel Aviv, Israel, 23–27 October 2022; pp. 95–112. [Google Scholar]
- Liu, J.; Wang, G.; Fan, C.; Zhou, F.; Xu, H. Question-conditioned debiasing with focal visual context fusion for visual question answering. Knowl.-Based Syst. 2023, 278, 110879. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Agrawal, A.; Lee, S. Overcoming language priors in visual question answering with adversarial regularization. In Proceedings of the NeurIPS, Montréal, QC, Canada, 3–8 December 2018; p. 1. [Google Scholar]
- Niu, Y.; Tang, K.; Zhang, H.; Lu, Z.; Hua, X.S.; Wen, J.R. Counterfactual VQA: A Cause-Effect Look at Language Bias. In Proceedings of the CVPR, Nashville, TN, USA, 20–25 June 2021; pp. 12700–12710. [Google Scholar]
- Zhao, L.; Li, K.; Qi, J.; Sun, Y.; Zhu, Z. Robust Visual Question Answering utilizing Bias Instances and Label Imbalance. Knowl.-Based Syst. 2024, 305, 112629. [Google Scholar] [CrossRef]
- Peng, D.; Li, Z. Robust visual question answering via polarity enhancement and contrast. Neural Netw. 2024, 179, 106560. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Liu, J.; Jin, L.; Li, Z. Unbiased Visual Question Answering by Leveraging Instrumental Variable. IEEE Trans. Multimed. 2024, 26, 6648–6662. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).