Asymptotic Distribution of the Functional Modal Regression Estimator
Abstract
1. Introduction
2. Functional Frame Work and Mathematical Support
3. Application to Confidence Interval Prediction
4. Empirical Analysis
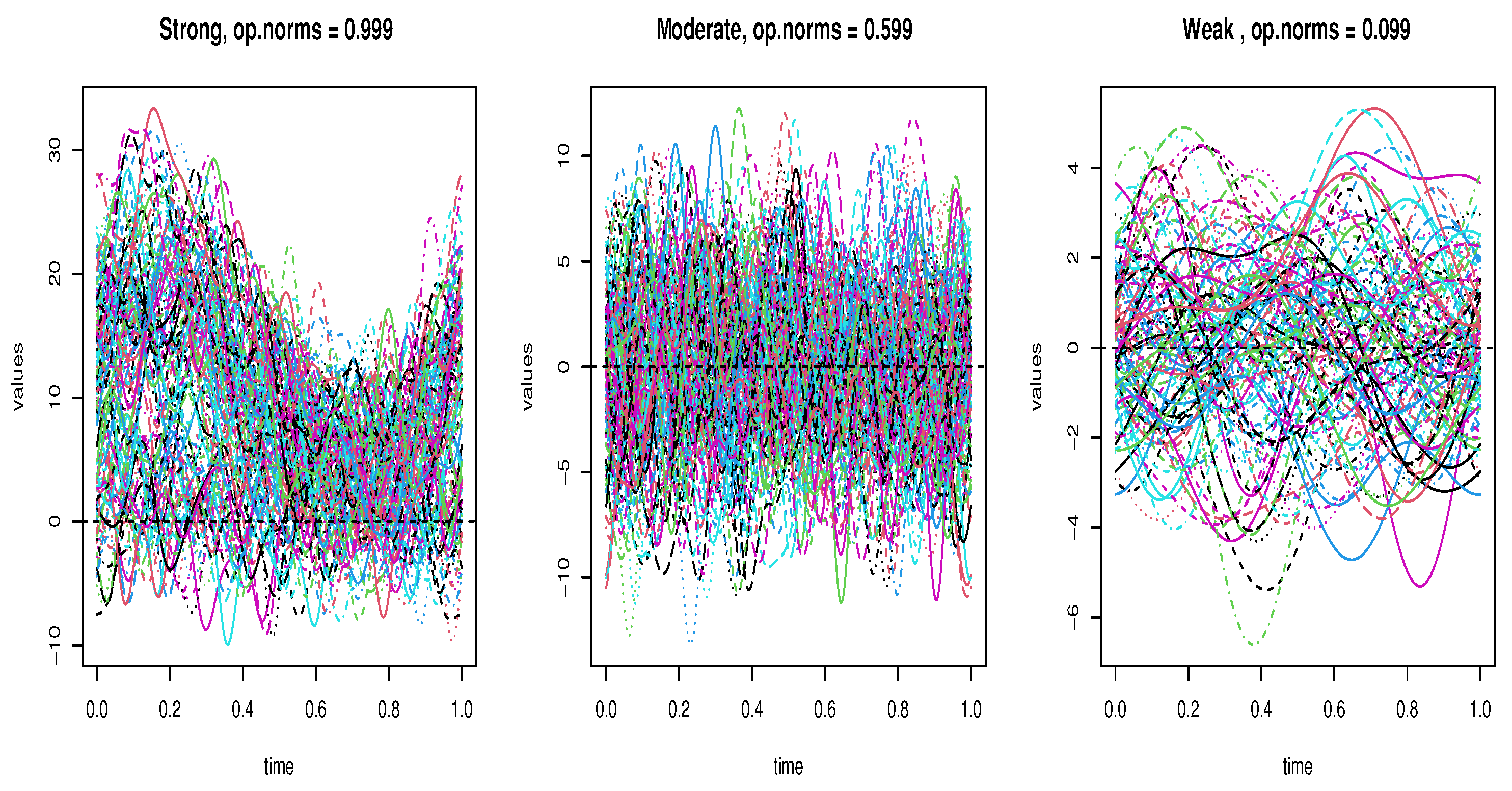
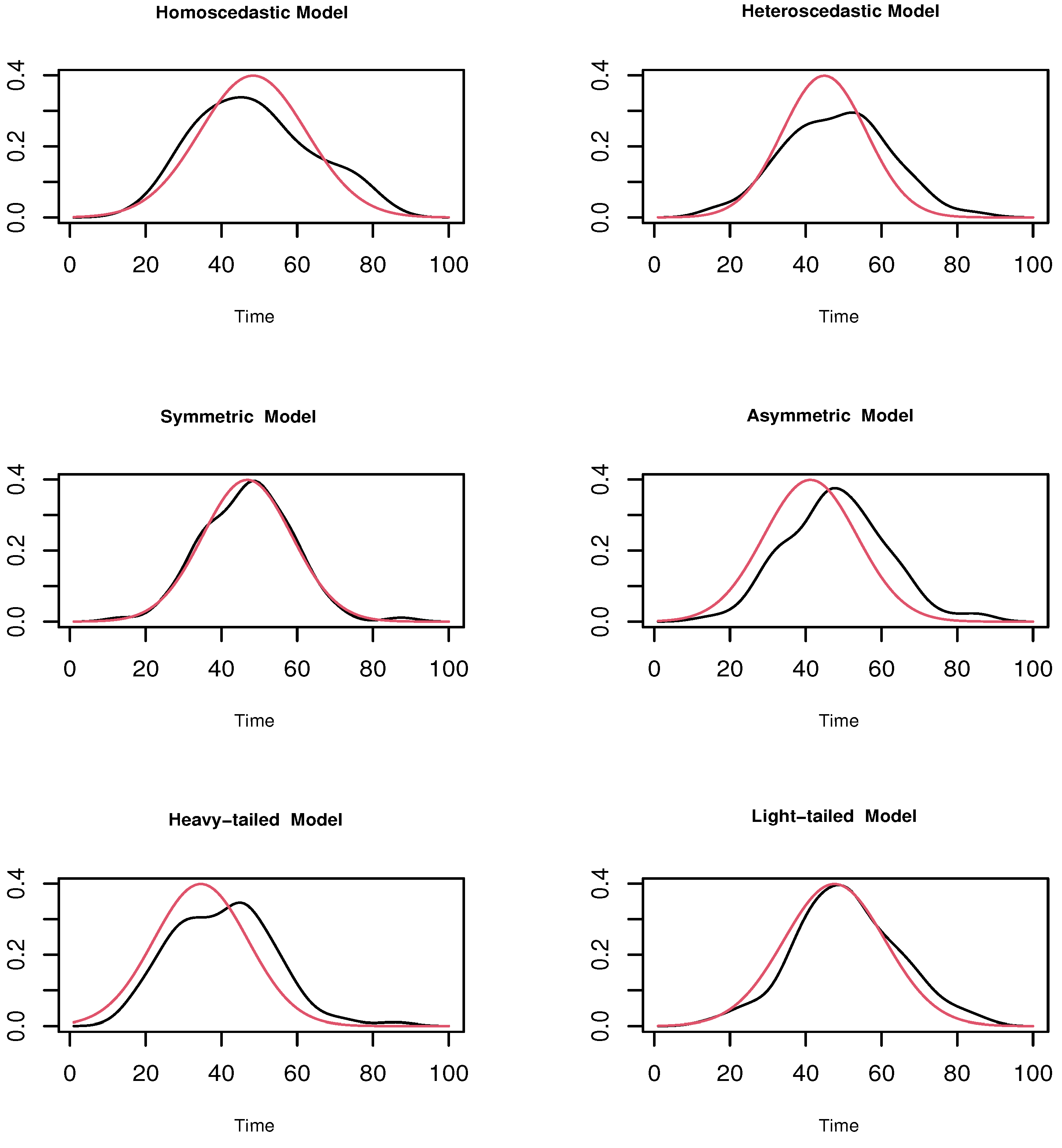
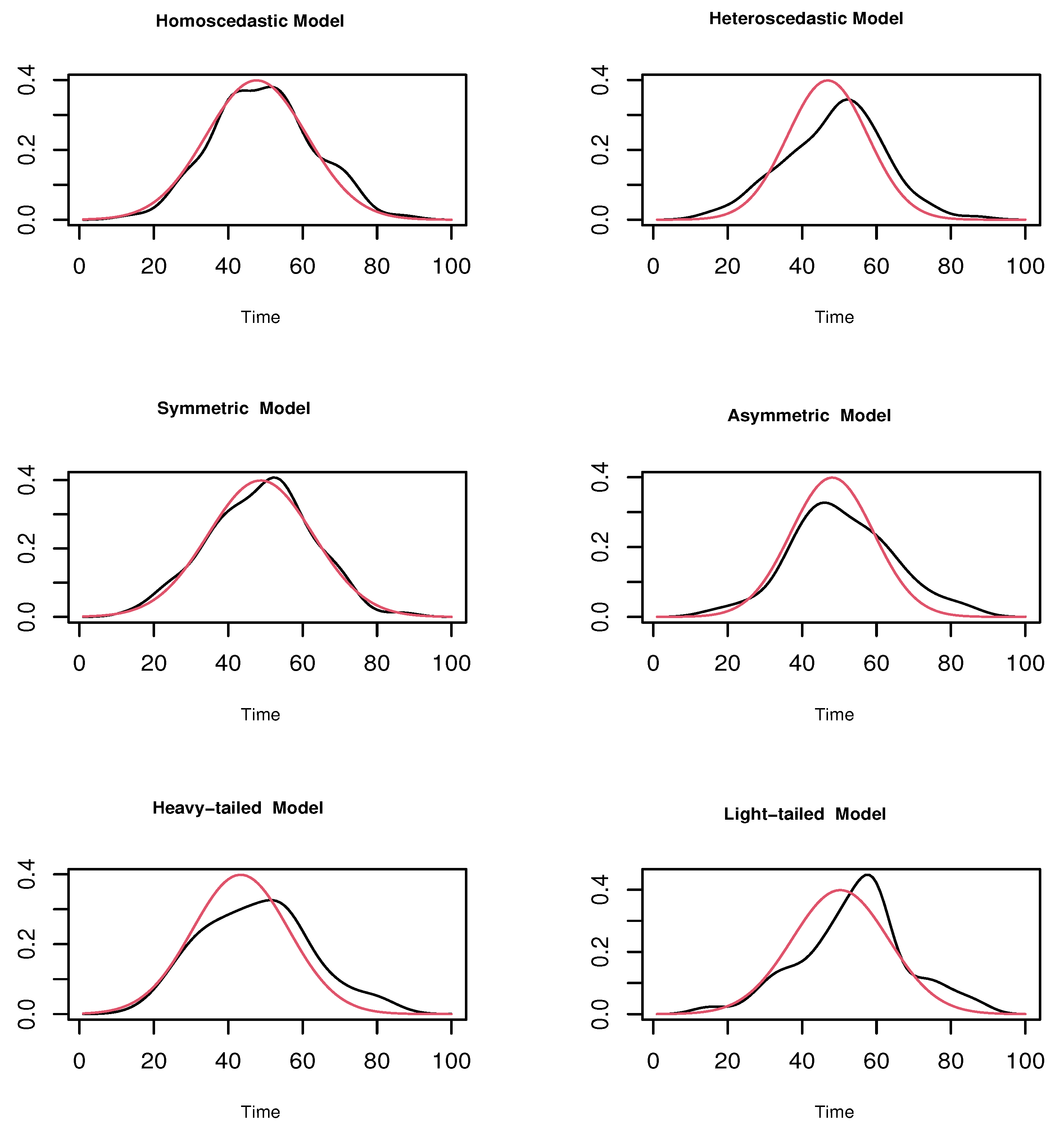
4.1. A Simulation Study
- Homoscedastic Model:
- Heteroscedastic Model:
- Symmetric Model:
- Asymmetric Model:
- Heavy-tailed Model:
- Light-tailed Model:
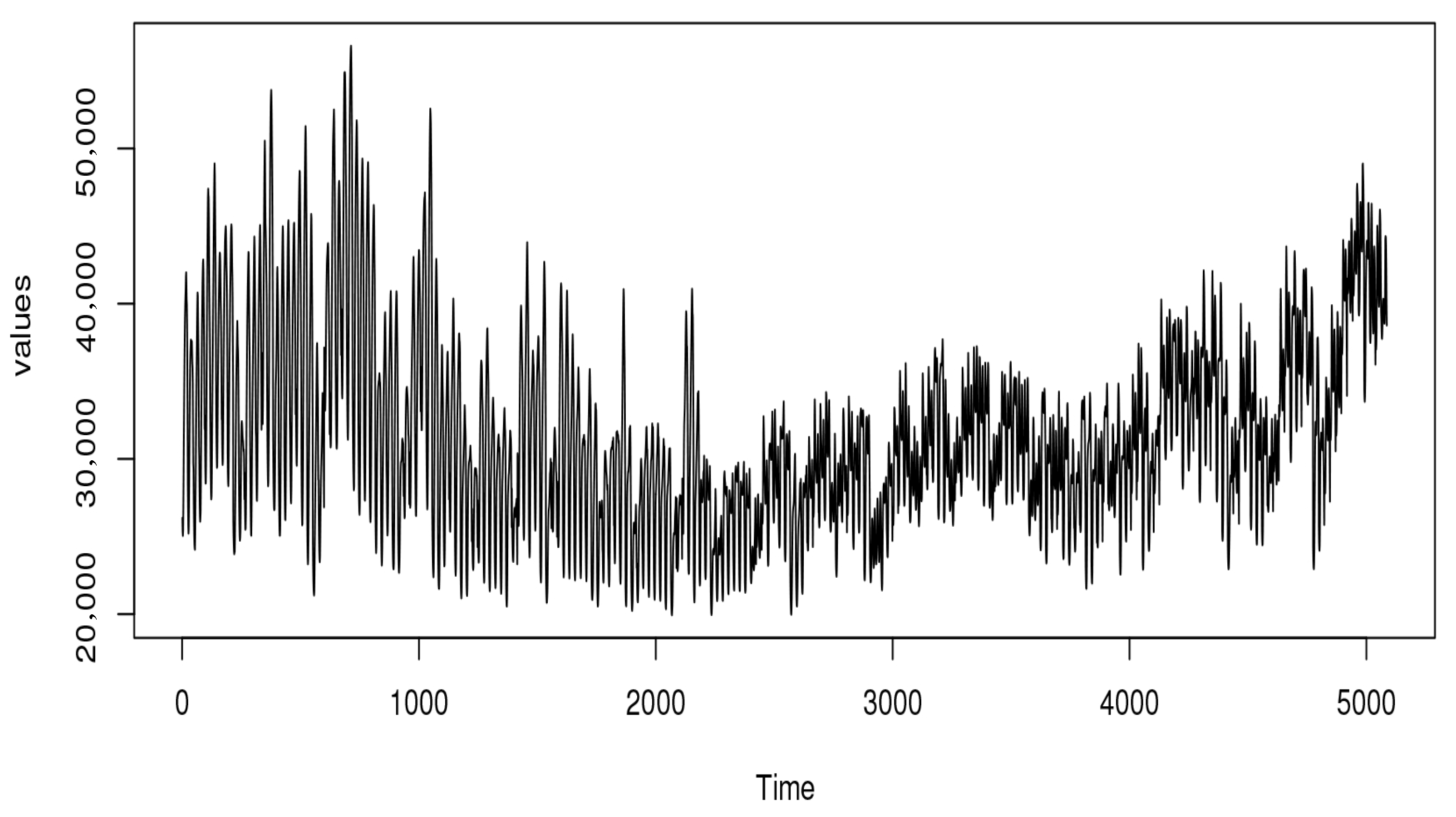
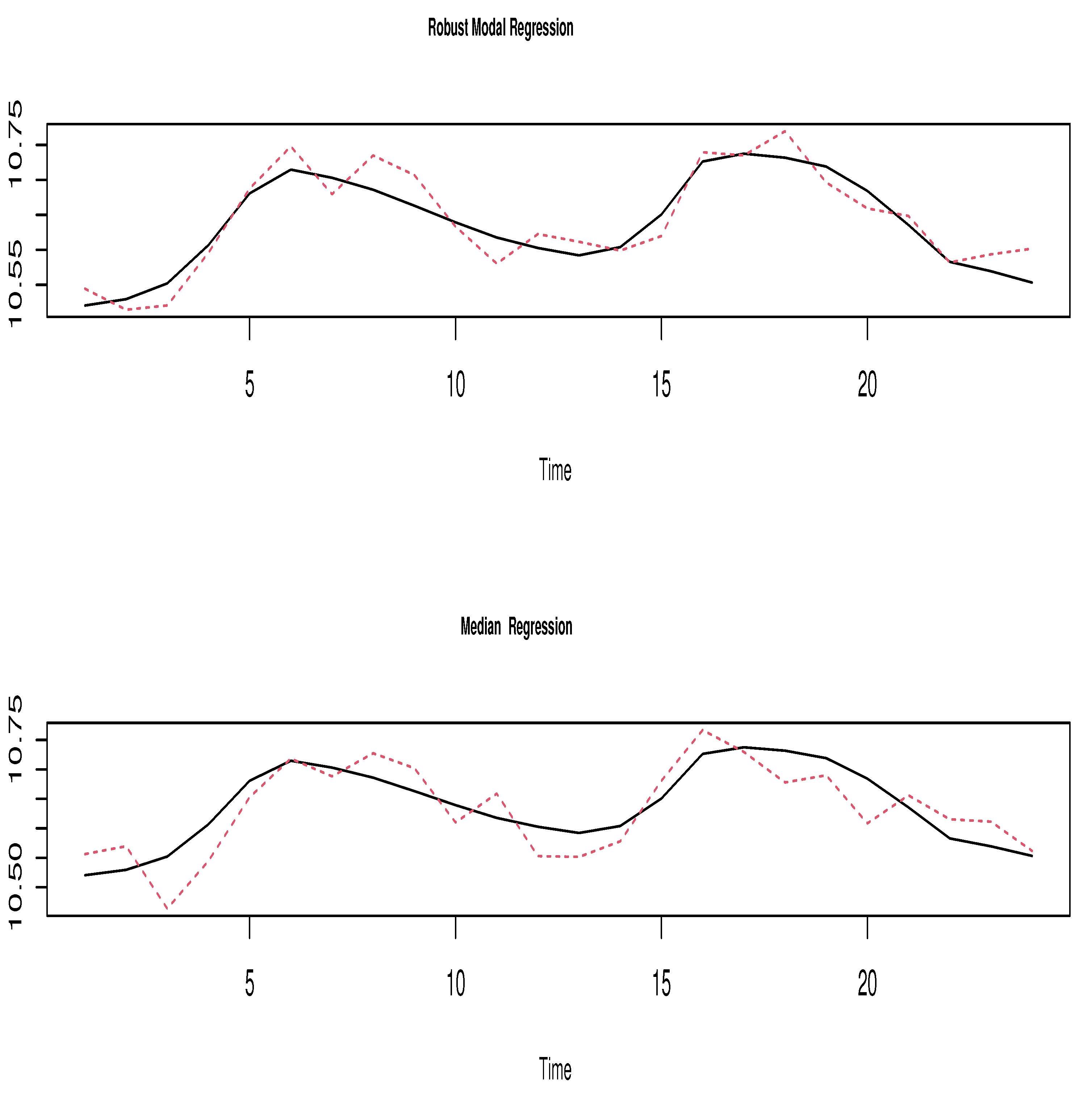
4.2. Real Data Example
5. Conclusions and Prospects
6. The Mathematical Development
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bosq, D. Linear Processes in Function Spaces; Lecture Notes in Statistics; Springer: New York, NY, USA, 2000; Volume 149. [Google Scholar]
- Ling, N.; Liu, Y.; Vieu, P. Conditional mode estimation for functional stationary ergodic data with responses missing at random. Statistics 2016, 50, 991–1013. [Google Scholar] [CrossRef]
- Bouzebda, S.; Laksaci, A.; Mohammedi, M. Single index regression model for functional quasi-associated time series data. REVSTAT 2022, 20, 605–631. [Google Scholar]
- Wang, L. Nearest neighbors estimation for long memory functional data. Stat. Methods Appl. 2020, 29, 709–725. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis. Theory and Practice; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Azzeddine, N.; Laksaci, A.; Ould-Saïd, E. On robust nonparametric regression estimation for a functional regressor. Stat. Probab. Lett. 2008, 78, 3216–3221. [Google Scholar] [CrossRef]
- Barrientos-Marin, J.; Ferraty, F.; Vieu, P. Locally modelled regression and functional data. J. Nonparametr. Stat. 2010, 22, 617–632. [Google Scholar] [CrossRef]
- Demongeot, J.; Hamie, A.; Laksaci, A.; Rachdi, M. Relative-error prediction in nonparametric functional statistics: Theory and practice. J. Multivar. Anal. 2016, 146, 261–268. [Google Scholar] [CrossRef]
- Ferraty, F.; Laksaci, A.; Vieu, P. Functional time series prediction via conditional mode estimation. C. R. Math. Acad. Sci. Paris 2005, 340, 389–392. [Google Scholar] [CrossRef]
- Ezzahrioui, M.H.; Ould-Saïd, E. Asymptotic normality of a nonparametric estimator of the conditional mode function for functional data. J. Nonparametr. Stat. 2008, 20, 3–18. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Kaid, Z.; Laksaci, A. Asymptotic properties of the kernel estimate of spatial conditional mode when the regressor is functional. AStA Adv. Stat. Anal. 2015, 99, 131–160. [Google Scholar] [CrossRef]
- Ling, N.; Vieu, P. Nonparametric modelling for functional data: Selected survey and tracks for future. Statistics 2018, 52, 934–949. [Google Scholar] [CrossRef]
- Bouanani, O.; Laksaci, A.; Rachdi, M.; Rahmani, S. Asymptotic normality of some conditional nonparametric functional parameters in high-dimensional statistics. Behaviormetrika 2019, 46, 199–233. [Google Scholar] [CrossRef]
- Cardot, H.; Crambes, C.; Sarda, P. Quantile regression when the covariates are functions. J. Nonparametr. Stat. 2005, 17, 841–856. [Google Scholar] [CrossRef]
- Wang, H.; Ma, Y. Optimal subsampling for quantile regression in big data. Biometrika 2021, 108, 99–112. [Google Scholar] [CrossRef]
- Jiang, Z.; Huang, Z. Single-index partially functional linear quantile regression. Commun. Stat. Theory Methods 2024, 53, 1838–1850. [Google Scholar] [CrossRef]
- Ferraty, F.; Laksaci, A.; Vieu, P. Estimating some characteristics of the conditional distribution in nonparametric functional models. Stat. Inference Stoch. Process. 2006, 9, 47–76. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Kaid, Z.; Laksaci, A. Spatial conditional quantile regression: Weak consistency of a kernel estimate. Rev. Roum. Math. Pures Appl. 2012, 57, 311–339. [Google Scholar]
- Chowdhury, J.; Chaudhuri, P. Nonparametric depth and quantile regression for functional data. Bernoulli 2019, 25, 395–423. [Google Scholar] [CrossRef]
- Mutis, M.; Beyaztas, U.; Karaman, F.; Shang, H.L. On function-on-function linear quantile regression. J. Appl. Stat. 2025, 52, 814–840. [Google Scholar] [CrossRef]
- Azzi, A.; Laksaci, A.; Ould-Saïd, E. On the robustification of the kernel estimator of the functional modal regression. Stat. Probab. Lett. 2021, 181, 109256. [Google Scholar] [CrossRef]
- Azzi, A.; Belguerna, A.; Laksaci, A.; Rachdi, M. The scalar-on-function modal regression for functional time series data. J. Nonparametr. Stat. 2024, 36, 503–526. [Google Scholar] [CrossRef]
- Alamari, M.B.; Almulhim, F.A.; Almanjahie, I.M.; Bouzebda, S.; Laksaci, A. Scalar-on-Function Mode Estimation Using Entropy and Ergodic Properties of Functional Time Series Data. Entropy 2025, 27, 552. [Google Scholar] [CrossRef]
- Almulhim, F.A.; Alamari, N.B.; Laksaci, A.; Kaid, Z. Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case. Axioms 2025, 14, 537. [Google Scholar] [CrossRef]
- Ferraty, F.; Mas, A.; Vieu, P. Nonparametric regression on functional data: Inference and practical aspects. Stat. Sin. 2007, 17, 113–136. [Google Scholar] [CrossRef]
- Jones, D.A. Nonlinear autoregressive processes. Proc. R. Soc. Lond. A 1978, 360, 71–95. [Google Scholar]
- Bradley, R.C. Introduction to Strong Mixing Conditions; Kendrick Press: Heber City, UT, USA, 2007; Volume I–III. [Google Scholar]
- Dedecker, J.; Doukhan, P.; Lang, G.; Leon, J.R.; Louhichi, S.; Prieur, C. Weak Dependence: With Examples and Applications; Lecture Notes in Statistics 190; Springer: New York, NY, USA, 2007. [Google Scholar]
- Ezzahrioui, M.; Ould-Saïd, E. Some asymptotic results of a non-parametric conditional mode estimator for functional time-series data. Stat. Neerl. 2010, 64, 171–201. [Google Scholar] [CrossRef]
- Liebscher, E. Central limit theorems for α-mixing triangular arrays with applications to nonparametric statistics. Math. Meth. Statist. 2001, 10, 194–214. [Google Scholar]
- Huber, P.J. Robust Statistics; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Hampel, F.R. A general qualitative definition of robustness. Ann. Math. Stat. 1971, 42, 1887–1896. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; Wiley: Chichester, UK, 2006. [Google Scholar]
- Laksaci, A.; Lemdani, M.; Ould Saïd, E. Asymptotic results for an L1-norm kernel estimator of the conditional quantile for functional dependent data with application to climatology. Sankhya A 2011, 73, 125–141. [Google Scholar] [CrossRef]




| Cases | Weak Correlation | Moderate Correlation | Strong Correlation |
|---|---|---|---|
| Homoscedastic Model | 1.07 | 1.15 | 1.26 |
| Heteroscedastic Model | 1.11 | 1.19 | 1.30 |
| Symmetric Model | 0.92 | 1.07 | 1.25 |
| Asymmetric Model | 0.86 | 1.17 | 1.28 |
| Heavy-tailed Model | 1.13 | 1.26 | 1.33 |
| Light-tailed Model | 1.14 | 1.29 | 1.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaid, Z.; Alamari, M.B. Asymptotic Distribution of the Functional Modal Regression Estimator. Mathematics 2025, 13, 3637. https://doi.org/10.3390/math13223637
Kaid Z, Alamari MB. Asymptotic Distribution of the Functional Modal Regression Estimator. Mathematics. 2025; 13(22):3637. https://doi.org/10.3390/math13223637
Chicago/Turabian StyleKaid, Zoulikha, and Mohammed B. Alamari. 2025. "Asymptotic Distribution of the Functional Modal Regression Estimator" Mathematics 13, no. 22: 3637. https://doi.org/10.3390/math13223637
APA StyleKaid, Z., & Alamari, M. B. (2025). Asymptotic Distribution of the Functional Modal Regression Estimator. Mathematics, 13(22), 3637. https://doi.org/10.3390/math13223637






