On the Extended Adjacency Eigenvalues of Graphs and Applications

Abstract

Let $A_{ex}\left(\mathcal{G}\right)$ be the extended adjacency matrix of G. The eigenvalues of $A_{ex}\left(\mathcal{G}\right)$ are called extended adjacency eigenvalues of $\mathcal{G}$. The sum of the absolute values of eigenvalues of the $A_{ex}$-matrix is called the extended adjacency energy ${\mathcal{E}}_{ex}\left(\mathcal{G}\right)$ of $\mathcal{G}$. In this paper, we obtain the $A_{ex}$-spectrum of the joined union of regular graphs in terms of their adjacency spectrum and the eigenvalues of an auxiliary matrix. Consequently, we derive the $A_{ex}$-spectrum of the join of two regular graphs, the lexicographic product of regular graphs, and the $A_{ex}$-spectrum of various families of graphs. Further, as applications of our results, we construct infinite classes of infinite families of extended adjacency equienergetic graphs. We show that the $A_{ex}$-energy of the join of two regular graphs is greater than or equal to their energy. We also determine the $A_{ex}$-eigenvalues of the power graph of finite abelian groups.

1. Introduction

Let $\mathcal{G}=\left(V\right(\mathcal{G}),E(\mathcal{G}\left)\right)$ be a graph, where $V\left(\mathcal{G}\right)=\{v_1,v_2,\dots ,v_n\}$ is the set of vertices and $E\left(\mathcal{G}\right)$ is the set of edges in $\mathcal{G}$. A graph $\mathcal{G}$ is called a simple graph if there are no loops or multiple edges. Two vertices u and v are said to be adjacent if there is an edge between them, and non-adjacent otherwise. A graph $\mathcal{G}$ is called connected if any two vertices $v_i,v_j\in V\left(\mathcal{G}\right)$ can be connected by paths from $v_i$ to $v_j$. Throughout this paper, we confine ourselves to connected simple graphs. For notions not defined explicitly in this paper, we refer the reader to the standard book [1].

The degree of the vertex $v_i\in V\left(\mathcal{G}\right)$ is the number of edges adjacent to $v_i$ and is denoted by $d_i=d\left(v_i\right)$. The adjacency matrix of a graph $\mathcal{G}$ is $A\left(\mathcal{G}\right)=\left(a_{ij}\right)$, where $a_{ij}=1$, if $v_i$ and $v_j$ are adjacent and $a_{ij}=0$, otherwise. The eigenvalues of $A\left(\mathcal{G}\right)$ are called the eigenvalues of $\mathcal{G}$, and the largest eigenvalue is the spectral radius of $\mathcal{G}$. The energy of $\mathcal{G}$, denoted by $\mathcal{E}\left(\mathcal{G}\right)$, is defined as the sum of the absolute values of the eigenvalues of $A\left(\mathcal{G}\right)$; that is,

$$\mathcal{E}\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^n}\left|{\lambda }_i\right|,$$

where ${\lambda }_i$, $1\le i\le n$ are the eigenvalues of $A\left(\mathcal{G}\right)$. The spectral properties, like the bounds for spectral radius and the energy of graphs, are well-studied, and many papers can be found in the literature with this theme. For some recent papers in this direction and related results, we refer the reader to [2,3,4].

Yang et al. [5] in 1994 considered an extended version of the adjacency matrix of a graph $\mathcal{G}$ by defining the extended adjacency matrix $A_{ex}\left(\mathcal{G}\right)$ as a square matrix of order n, whose $(i,j)$-entry is equal to ${\displaystyle \frac{1}{2}}\left({\displaystyle \frac{d_i}{d_j}}+{\displaystyle \frac{d_j}{d_i}}\right)$ if $v_i$ is adjacent to $v_j$, and zero otherwise. The eigenvalues of $A_{ex}\left(\mathcal{G}\right)$ are called the extended adjacency eigenvalues (shortly, $A_{ex}$-eigenvalues) of $\mathcal{G}$. The set of all $A_{ex}$-eigenvalues of $\mathcal{G}$, counted with their multiplicities, is called the extended adjacency spectrum (shortly, $A_{ex}$-spectrum). The largest eigenvalue of $A_{ex}\left(\mathcal{G}\right)$ is called the extended adjacency spectral radius (shortly, $A_{ex}$-spectral radius) of $\mathcal{G}$. The sum of the absolute values of the $A_{ex}$-eigenvalues is the extended adjacency energy ${\mathcal{E}}_{ex}\left(\mathcal{G}\right)$ (shortly, $A_{ex}$-energy) of $\mathcal{G}$. That is,

$${\mathcal{E}}_{ex}\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^n}\left|{\eta }_i\right|,$$

where ${\eta }_1,{\eta }_2,\dots ,{\eta }_n$ are the $A_{ex}$-eigenvalues of $\mathcal{G}$. Based on the $A_{ex}$-matrices of molecules, the influences of heteroatoms and multiple bonds were considered in [5]. The authors in [5] have shown that the $A_{ex}$-spectral radius and energy possess high discriminating power and correlate well with several physicochemical properties and biological activities of organic compounds. Recently, Gutman et al. [6] investigated the dependence of the $A_{ex}$-energy on molecular structure and established its basic characteristics. Furthermore, in the same paper, they established a relationship between the $A_{ex}$-energy and the geometric–arithmetic (GA) topological index, and their main finding was that the difference between the $A_{ex}$-energy and the total $\pi$-electron energy is linearly proportional to the difference between the number of edges and the GA index. The investigation of $A_{ex}$-spectral radius and energy was further extended, and several interesting results were obtained in [7,8,9,10,11,12,13,14].

In [7], the authors considered the problem of constructing graphs with the same $A_{ex}$-energy and different $A_{ex}$-spectrum. They showed the existence of graphs with this property. In the rest of this work, we focus on the study of $A_{ex}$-eigenvalues of the joined union of graphs. The motivation for this study is to devise a general method to generate graphs with the same $A_{ex}$-energy and different $A_{ex}$-spectrum. We also focus on the determination of the $A_{ex}$-eigenvalues of the power graph of finite abelian groups.

The rest of this paper is organized as follows. In Section 2, we obtain the $A_{ex}$-spectrum of the joined union of regular graphs in terms of the adjacency spectrum of the component graphs and the eigenvalues of an auxiliary matrix. As a consequence, we obtain the $A_{ex}$-spectrum of the join of two regular graphs and the lexicographic product of a graph with a regular graph. We derive the $A_{ex}$-spectrum of some well-known families of graphs. In Section 3, we utilize the results obtained in Section 2 to generate some infinite classes of infinite families of graphs with the same $A_{ex}$-energy and different $A_{ex}$-spectra. We show that the $A_{ex}$-energy of the join of two regular graphs is greater than or equal to their energy. In Section 4, we determine the $A_{ex}$-eigenvalues of the power graph of finite abelian groups.

2. Extended Adjacency Spectrum of Joined Union of Graphs

In this section, we obtain the $A_{ex}$-spectrum of the joined union of regular graphs. As a consequence, we obtain the $A_{ex}$-spectrum of the join of two regular graphs and the lexicographic product of a graph with a regular graph. We derive the $A_{ex}$-spectrum of some well-known families of graphs.

A block matrix is one that has entries as matrices. Consider the block matrix

$$M=\left(\begin{array}{cccc}{A}_{1,1}& A_{1,2}& \cdots & A_{1,s}\\ A_{2,1}& A_{2,2}& \cdots & A_{2,s}\\ ⋮& ⋮& \cdots & ⋮\\ A_{s,1}& A_{s,2}& \cdots & A_{s,s}\end{array}\right),$$

of order n whose rows and columns are partitioned according to a partition $P=\{P_1,P_2,\dots ,P_s\}$ of the set $X=\{1,2,\dots ,n\}.$ The quotient matrix $\mathcal{Q}$ (see [1,15]) of M is a matrix of order s whose entries are the average row sums of the blocks $A_{i,j}$ of M. The partition P is said to be equitable if each block $A_{i,j}$ of M has a constant row (column) sum, and in this case, $\mathcal{Q}$ is called the equitable quotient matrix. A vertex partition $\{V_1,V_2,\dots ,V_s\}$ of the vertex set $V\left(\mathcal{G}\right)$ of graph G is equitable if for each i and for all $u,v\in V_i$, we have $|N\left(u\right)\cap V_j|=|N\left(v\right)\cap V_j|$ for all $j.$ In general, the eigenvalues of $\mathcal{Q}$ interlace the eigenvalues of M. In case the partition is equitable, the following lemma was obtained in [15].

Lemma 1 

([15]). If the partition P of X of matrix M is equitable, then each eigenvalue of $\mathcal{Q}$ is an eigenvalue of $M.$

Let $\mathcal{G}=\mathcal{G}(V,E)$ be a graph of order n, and let ${\mathcal{G}}_i={\mathcal{G}}_i(V_i,E_i)$ be the graphs of order $n_i,$ for $i=1,\dots ,n$. The joined union $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ of graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n$ is the graph $H(W,F)$ with

$$\begin{array}{c}\hfill W=\bigcup _{i=1}^n{V}_i\mathrm{and}F=\bigcup _{i=1}^n{E}_i\cup \bigcup _{\{v_i,v_j\}\in E}{V}_i\times V_j.\end{array}$$

In other words, the joined union is the union of graphs ${\mathcal{G}}_1,\dots ,{\mathcal{G}}_n$ together with edges $v_{ik}{v}_{jl},$ where $v_{ik}\in {\mathcal{G}}_i$ and $v_{jl}\in {\mathcal{G}}_j$ whenever $v_i{v}_j$ is an edge in $\mathcal{G}$. Clearly, the usual join of two graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ is a special case of the joined union $K_2[{\mathcal{G}}_1,{\mathcal{G}}_2]={\mathcal{G}}_1\vee {\mathcal{G}}_2$, where $K_2$ is the complete graph of order 2.

In the following result, we obtain the $A_{ex}$-spectrum of the joined union of regular graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n$ in terms of the adjacency spectrum of the graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n$ and the eigenvalues of an auxiliary matrix.

Theorem 1. 

Let $\mathcal{G}$ be a graph of order $n\ge 3$ having m edges. Let ${\mathcal{G}}_i$ be a $r_i$-regular graph of order $n_i$ having adjacency eigenvalues ${\lambda }_{i1}=r_i\ge {\lambda }_{i2}\ge \dots \ge {\lambda }_{i{n}_i},$ where $i=1,2,\dots ,n$. The $A_{ex}$-spectrum of the joined union graph $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ of order $N={\displaystyle \sum _{i=1}^n}{n}_i$ consists of the eigenvalues ${\lambda }_{ik}\left({\mathcal{G}}_i\right)$ for $i=1,\dots ,n$ and $k=2,3,\dots ,n_i$. The remaining n eigenvalues are given by the matrix

$$M=\left(\begin{array}{cccc}{r}_1& {\tau }_{12}& \dots & {\tau }_{1n}\\ {\tau }_{21}& r_2& \dots & {\tau }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tau }_{n1}& {\tau }_{n2}& \dots & r_n\end{array}\right),$$

where for $i\ne j$, we have ${\tau }_{ij}={\displaystyle \frac{n_j}{2}}\left({\displaystyle \frac{r_i+c_i}{r_j+c_j}}+{\displaystyle \frac{r_j+c_j}{r_i+c_i}}\right)$, if $v_i\sim v_j$ and equal to 0 if $v_i\nsim v_j$. Note that $c_i={\displaystyle \sum _{v_j\in N_G\left(v_i\right)}}{n}_i$ is the sum of the cardinalities of the graphs ${\mathcal{G}}_j,j\ne i$ which corresponds to the neighbors of vertex $v_i\in \mathcal{G}$.

Proof. 

Let $V\left(\mathcal{G}\right)=\{v_1,\dots ,v_n\}$ be the vertex set of $\mathcal{G}$, and let $V\left({\mathcal{G}}_i\right)=\{v_{i1},\dots ,v_{i{n}_i}\}$ be the vertex set of ${\mathcal{G}}_i$ for $i=1,2,\dots ,n$. Let $H=\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ be the joined union of the graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n$. Clearly, the order of H is $N={\displaystyle \sum _{i=1}^n}{n}_i$. We first compute the degree of each vertex in $V\left(H\right)$. Evidently, the degree of each vertex $v_{ij}\in V\left(H\right)$ for $1\le i\le n$ and $1\le j\le n_i$ is the degree inside ${\mathcal{G}}_i$ plus the sum of cardinalities of the copies of ${\mathcal{G}}_j,j\ne i$, which corresponds to the neighbors of the vertex $v_i$ in $\mathcal{G}$. That is, for each $v_{ij}\in V\left({\mathcal{G}}_i\right)$, we have

$$d_H\left(v_{ij}\right)=r_i+{\displaystyle \sum _{v_j\in N_G\left(v_i\right)}}{n}_j=r_i+c_i,$$

(1)

where $c_i={\displaystyle \sum _{v_j\in N_G\left(v_i\right)}}{n}_j$. Obviously, $d_H\left(v_{ij}\right)$ is the same for each vertex in ${\mathcal{G}}_i$, $1\le j\le n_i$. We label the vertices in H from the vertices in ${\mathcal{G}}_1$ to the vertices in ${\mathcal{G}}_n$. With this labeling, the $A_{ex}$-matrix of H can be written as

$$A_{ex}\left(H\right)=\left(\begin{array}{cccc}A\left({\mathcal{G}}_1\right)& h(v_1,v_2)& \dots & h(v_1,v_n)\\ h(v_2,v_1)& A\left({\mathcal{G}}_2\right)& \dots & h(v_2,v_n)\\ ⋮& ⋮& \ddots & ⋮\\ h(v_n,v_1)& h(v_n,v_2)& \dots & A\left({\mathcal{G}}_n\right)\end{array}\right),$$

where $h(v_i,v_j)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{r_i+c_i}{r_j+c_j}}+{\displaystyle \frac{r_j+c_j}{r_i+c_i}}\right)J_{n_i\times n_j}$ if $v_i\sim v_j$ in $\mathcal{G}$ and equal to $0_{n_i\times n_j}$ otherwise. Note that when $A\left({\mathcal{G}}_i\right)$ is the adjacency matrix of ${\mathcal{G}}_i$, $J_{n_i\times n_j}$ is the all one-matrix and $0_{n_i\times n_j}$ is the zero matrix of order $n_i\times n_j$.

Since the graph ${\mathcal{G}}_i$ is a $r_i$-regular graph of order $n_i$, for all $i=1,2,\dots ,n$, the all one-vector $e_{n_i}={(1,1,\dots ,1)}^T$ is the eigenvector of the adjacency matrix $A\left({\mathcal{G}}_i\right)$ corresponding to the eigenvalue $r_i$, and all other eigenvectors are orthogonal to $e_{n_i}$ (as the matrix $A\left({\mathcal{G}}_i\right)$ being symmetric is orthogonally diagonalizable). Let ${\lambda }_{ik}$, where $2\le k\le n_i$, be any eigenvalue of $A\left({\mathcal{G}}_i\right)$ with the corresponding eigenvector $X={(x_{i1},x_{i2},\dots ,x_{i{n}_i})}^T$ satisfying $e_{n_i}^{T}X=0.$ Clearly, the column vector X can be regarded as a function defined on $V\left({\mathcal{G}}_i\right)$ assigning the vertex $v_{ij}$ to $x_{ij}$; that is, $X\left(v_{ij}\right)=x_{ij}$ for $i=1,2,\dots ,n$ and $j=1,2,\dots ,n_i$. Now, consider the vector $Z={(z_1,z_2,\dots ,z_N)}^T$, where

$$z_j=\left\{\begin{array}{cc}\hfill x_{ij}& \mathrm{if}{v}_{ij}\in V\left({\mathcal{G}}_i\right)\hfill \\ \hfill 0& \mathrm{otherwise}.\hfill \end{array}\right.$$

Since $e_{n_i}^{T}X=0$ and the coordinates of the vector Z corresponding to the vertices in ${\cup }_{j\ne i}{V}_j$ of H are zero, we have

$$\begin{array}{c}\hfill A_{ex}\left(H\right)Z=\left(\begin{array}{c}0\\ ⋮\\ 0\\ {\lambda }_{ik}X\\ 0\\ ⋮\\ 0\end{array}\right)={\lambda }_{ik}Z.\end{array}$$

This shows that Z is an eigenvector of $A_{ex}\left(H\right)$ corresponding to the eigenvalue ${\lambda }_{ik}$ for every eigenvalue ${\lambda }_{ik}$, where $2\le k\le n_i$, of $A\left({\mathcal{G}}_i\right)$. From this, it follows that for $1\le i\le n$ and $2\le k\le n_i$, ${\lambda }_{ik}$ is an eigenvalue of $A_{ex}\left(H\right)$. In this way, we obtain the ${\displaystyle \sum _{i=1}^n}{n}_i-n=N-n$ eigenvalues of $A_{ex}\left(H\right)$. The remaining n eigenvalues are the zeros of the characteristic polynomial of the following equitable quotient matrix:

$$M=\left(\begin{array}{cccc}{r}_1& {\tau }_{12}& \dots & {\tau }_{1n}\\ {\tau }_{21}& r_2& \dots & {\tau }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tau }_{n1}& {\tau }_{n2}& \dots & r_n\end{array}\right),$$

where for $i\ne j$, we have ${\tau }_{ij}={\displaystyle \frac{n_j}{2}}\left({\displaystyle \frac{r_i+c_i}{r_j+c_j}}+{\displaystyle \frac{r_j+c_j}{r_i+c_i}}\right)$ if $v_i\sim v_j$ and equal to 0 if $v_i\nsim v_j$. This completes the proof.    □

Example 1. 

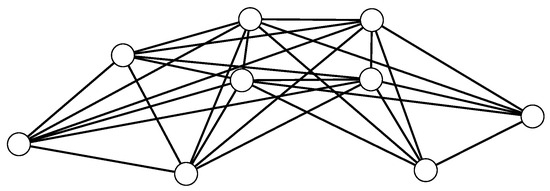
Consider the graph $H_1=P_3[K_3,C_4,P_2]$, as shown in Figure 1. For this graph, $n=3,n_1=3,n_2=4,n_3=2,\mathcal{G}=P_3,{\mathcal{G}}_1=K_3,{\mathcal{G}}_2=C_4,{\mathcal{G}}_3=P_2,r_1=2,r_2=2,r_3=1,N=9,c_1=4,c_2=5,c_3=4$. Also, the adjacency eigenvalues of $K_3$ are $r_1=2,{\lambda }_{12}=-1,{\lambda }_{13}=-1$; the adjacency eigenvalues of $C_4$ are $r_2=2,{\lambda }_{22}=0,{\lambda }_{23}=0,{\lambda }_{24}=-2$; and the adjacency eigenvalues of $P_2$ are $r_3=1,{\lambda }_{32}=-1$. Further, ${\tau }_{12}={\displaystyle \frac{n_2}{2}}\left({\displaystyle \frac{r_1+c_1}{r_2+c_2}}+{\displaystyle \frac{r_2+c_2}{r_1+c_1}}\right)={\displaystyle \frac{85}{21}},{\tau }_{21}={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_1+c_1}{r_2+c_2}}+{\displaystyle \frac{r_2+c_2}{r_1+c_1}}\right)={\displaystyle \frac{85}{28}},{\tau }_{13}=0={\tau }_{31},{\tau }_{23}={\displaystyle \frac{n_3}{2}}\left({\displaystyle \frac{r_2+c_2}{r_3+c_3}}+{\displaystyle \frac{r_3+c_3}{r_2+c_2}}\right)={\displaystyle \frac{74}{35}},{\tau }_{32}={\displaystyle \frac{n_2}{2}}\left({\displaystyle \frac{r_2+c_2}{r_3+c_3}}+{\displaystyle \frac{r_3+c_3}{r_2+c_2}}\right)={\displaystyle \frac{148}{35}}$. Therefore, based on Theorem 1, the $A_{ex}$-spectrum of $H_1=P_3[K_3,C_4,P_2]$ consists of the eigenvalues ${\lambda }_{12}=-1,{\lambda }_{13}=-1,{\lambda }_{22}=0,{\lambda }_{23}=0,{\lambda }_{24}=-2,{\lambda }_{32}=-1$. The remaining three $A_{ex}$-eigenvalues are the eigenvalues of the matrix $M=\left(\begin{array}{ccc}2& {\displaystyle \frac{85}{21}}& 0\\ {\displaystyle \frac{85}{28}}& 2& {\displaystyle \frac{74}{35}}\\ 0& {\displaystyle \frac{148}{35}}& 1\end{array}\right)$. Via direct calculation, it can be seen that the eigenvalues of M are $6.42490599,1.42776319$, and $-2.85266918$ (approximately).

Figure 1. The joined union $P_3[K_3,C_4,P_2]$ of the complete graph $K_3$, the cycle $C_4$, and the path $P_2$ with the parent graph path $P_3$.

The following consequence of Theorem 1 gives the $A_{ex}$-spectrum of the join of two regular graphs. Note that Corollary 1 was obtained in [7] as Theorem 3.7.

Corollary 1. 

Let ${\mathcal{G}}_i$ be an $r_i$-regular graph of order $n_i$ for $i=1,2$, and let ${\lambda }_{ik},$ where $2\le k\le n_i$ and $i=1,2$ be the adjacency eigenvalues of ${\mathcal{G}}_i$ other than $r_i$. Then, the $A_{ex}$-spectrum of $\mathcal{G}={\mathcal{G}}_1\vee {\mathcal{G}}_2$ consists of eigenvalues ${\lambda }_{1k}A\left({\mathcal{G}}_1\right)$, for $k=2,\dots ,n_1$ and eigenvalues ${\lambda }_{2k}A\left({\mathcal{G}}_1\right),$ for $k=2,\dots ,n_2$. The remaining two eigenvalues are given by the matrix

$$\left(\begin{array}{cc}{r}_1& {\displaystyle \frac{n_2}{2}}\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)\\ {\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)& r_2\end{array}\right),$$

which are ${\displaystyle \frac{1}{2}}\left(r_1+r_2\pm \sqrt{{(r_1-r_2)}^2+n_1{n}_2{\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)}^2}\right)$.

The following observation gives the $A_{ex}$-spectrum of the join of a regular graph with the union of two regular graphs of distinct degrees.

Corollary 2. 

Let ${\mathcal{G}}_i$ be a $r_i$-regular graph of orders $n_i$ that has adjacency eigenvalues $r_i={\lambda }_{i1}\ge {\lambda }_{i2}\ge \cdots \ge {\lambda }_{i{n}_i}$ for $i=1,2,3$. Then, the $A_{ex}$-spectrum of $\mathcal{G}={\mathcal{G}}_1\vee ({\mathcal{G}}_2\cup {\mathcal{G}}_3)$ consists of the eigenvalues ${\lambda }_{1k}\left(A\left({\mathcal{G}}_1\right)\right)$ for $k=2,\dots ,n_1$; the eigenvalues ${\lambda }_{2k}\left(A\left({\mathcal{G}}_2\right)\right)$ for $k=2,\dots ,n_2$; and the eigenvalues ${\lambda }_{3k}\left(A\left({\mathcal{G}}_3\right)\right)$ for $k=2,\dots ,n_3$. The remaining three eigenvalues are given by the following matrix:

$$\left(\begin{array}{ccc}{r}_2& {\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_2+n_1}{r_1+n_2+n_3}}+{\displaystyle \frac{r_1+n_2+n_3}{r_2+n_1}}\right)& 0\\ {\displaystyle \frac{n_2}{2}}\left({\displaystyle \frac{r_1+n_2+n_3}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2+n_3}}\right)& r_1& {\displaystyle \frac{n_3}{2}}\left({\displaystyle \frac{r_1+n_2+n_3}{r_3+n_1}}+{\displaystyle \frac{r_3+n_1}{r_1+n_2+n_3}}\right)\\ 0& {\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_3+n_1}{r_1+n_2+n_3}}+{\displaystyle \frac{r_1+n_2+n_3}{r_3+n_1}}\right)& r_3\end{array}\right).$$

Proof. 

Let $P_3$ be the path on 3 vertices, and let $\mathcal{G}={\mathcal{G}}_1\vee ({\mathcal{G}}_2\cup {\mathcal{G}}_3)$ be the join of the graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2\cup {\mathcal{G}}_3$. It is easy to see that $\mathcal{G}=P_3[{\mathcal{G}}_2,{\mathcal{G}}_1,{\mathcal{G}}_3]$; that is, $\mathcal{G}$ is the joined union of the graphs ${\mathcal{G}}_2,{\mathcal{G}}_1,{\mathcal{G}}_3$ when the parent graph is the path $P_3$. Now, using Theorem 1 and noting that $c_2=n_1$, $c_1=n_2+n_3$, and $c_3=n_1$, the result follows.    □

Example 2. 

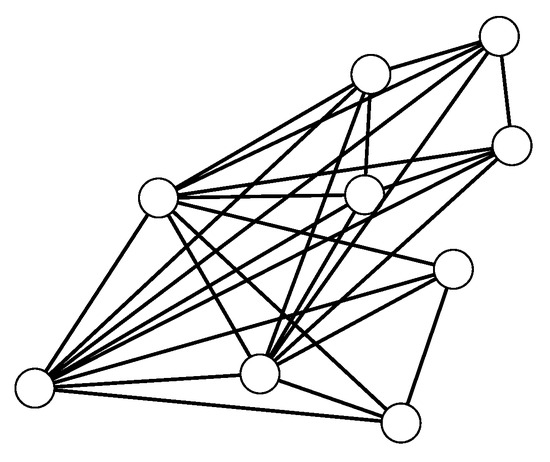
Consider the graph $H_2=K_3\vee (C_4\cup P_2)$ shown in Figure 2. For this graph, ${\mathcal{G}}_1=K_3,{\mathcal{G}}_2=C_4,{\mathcal{G}}_3=P_2,n_1=3,n_2=4,n_3=2,r_1=2,r_2=2,r_3=1$. Also, the adjacency eigenvalues of $K_3$ are $r_1=2,{\lambda }_{12}=-1,{\lambda }_{13}=-1$; the adjacency eigenvalues of $C_4$ are $r_2=2,{\lambda }_{22}=0,{\lambda }_{23}=0,{\lambda }_{24}=-2$; and the adjacency eigenvalues of $P_2$ are $r_3=1,{\lambda }_{32}=-1$. Therefore, based on Corollary 2, the $A_{ex}$-eigenvalues of $H_2=K_3\vee (C_4\cup P_2)$ consist of the eigenvalues ${\lambda }_{12}=-1,{\lambda }_{13}=-1,{\lambda }_{22}=0,{\lambda }_{23}=0,{\lambda }_{24}=-2,{\lambda }_{32}=-1$. The remaining three $A_{ex}$-eigenvalues of $H_2$ are the eigenvalues of the following matrix: $\left(\begin{array}{ccc}2& {\displaystyle \frac{111}{35}}& 0\\ {\displaystyle \frac{148}{35}}& 2& {\displaystyle \frac{5}{2}}\\ 0& {\displaystyle \frac{15}{4}}& 1\end{array}\right).$ Through direct calculation, it can be seen that the eigenvalues of this matrix are $6.59454826,1.41765991$, and $-3.01220817$ (approximately).

Figure 2. The graph $K_3\vee (C_4\cup P_2)=P_3[C_4,K_3,P_2]$.

The lexicographic product $\mathcal{G}\left[\mathcal{H}\right]$ of graphs $\mathcal{G}$ and $\mathcal{H}$ is the graph with vertex set $V\left(\mathcal{G}\right)\times V\left(\mathcal{H}\right)$ and edge $(a,x)(b,y)\in E\left(\mathcal{G}\left[\mathcal{H}\right]\right)$ whenever $ab\in E\left(\mathcal{G}\right),\mathrm{o}\mathrm{r} a=b \mathrm{a}\mathrm{n}\mathrm{d} xy \in E\left(\mathcal{H}\right)$. It is interesting to note that the lexicographic product $\mathcal{G}\left[\mathcal{H}\right]$ can be constructed by joined union $\mathcal{G}[{\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n]$ where ${\mathcal{G}}_i=\mathcal{H}$ for $1\le i\le n$. Note that in the case of ${\mathcal{G}}_i=K_1$, we get $\mathcal{G}[K_1,K_1,\dots ,K_1]=\mathcal{G}$, which means that every graph $\mathcal{G}$ is the joined union of some classes of graphs. Taking ${\mathcal{G}}_1={\mathcal{G}}_2=\cdots ={\mathcal{G}}_n$ in Theorem 1, we obtain the following result, which gives the $A_{ex}$-spectrum of the lexicographic product $\mathcal{G}\left[{\mathcal{G}}_1\right]$ of a graph $\mathcal{G}$ with a regular graph ${\mathcal{G}}_1$.

Theorem 2. 

Let $\mathcal{G}$ be a graph of order $n\ge 3$ having m edges. Let ${\mathcal{G}}_1$ be a $r_1$-regular graph of order $n_1$ having adjacency eigenvalues ${\lambda }_1=r_1\ge {\lambda }_2\ge \dots \ge {\lambda }_{n_1}$. The $A_{ex}$-spectrum of $\mathcal{G}\left[{\mathcal{G}}_1\right]$ consists of the eigenvalues ${\lambda }_k\left({\mathcal{G}}_1\right)$, where $k=2,3,\dots ,n_1$, each repeated n times. The remaining n eigenvalues are given by the matrix

$$M=\left(\begin{array}{cccc}{r}_1& {\tau }_{12}& \dots & {\tau }_{1n}\\ {\tau }_{21}& r_1& \dots & {\tau }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tau }_{n1}& {\tau }_{n2}& \dots & r_1\end{array}\right),$$

where for $i\ne j$, we have ${\tau }_{ij}={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_1+n_{1}d\left(v_i\right)}{r_1+n_{1}d\left(v_j\right)}}+{\displaystyle \frac{r_1+n_{1}d\left(v_j\right)}{r_1+n_{1}d\left(v_i\right)}}\right)$ if $v_i\sim v_j$, and equal to 0 if $v_i\nsim v_j$. Note that $d\left(v_i\right)$ is the degree of vertex $v_i$ in $\mathcal{G}$.

Proof. 

The proof follows directly from Theorem 1 by taking ${\mathcal{G}}_1={\mathcal{G}}_2=\cdots ={\mathcal{G}}_n;n_1=n_2=\cdots =n_n;r_1=r_2=\cdots =r_n$ and by using the fact that $c_i={\displaystyle \sum _{v_j\in N_{\mathcal{G}}\left(v_i\right)}}{n}_j=n_1{\displaystyle \sum _{v_j\in N_{\mathcal{G}}\left(v_i\right)}}1=n_{1}d\left(v_i\right)$ together with

$$\begin{array}{c}\hfill {\tau }_{ij}={\displaystyle \frac{n_j}{2}}\left({\displaystyle \frac{r_i+c_i}{r_j+c_j}}+{\displaystyle \frac{r_j+c_j}{r_i+c_i}}\right)={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_1+n_{1}d\left(v_i\right)}{r_1+n_{1}d\left(v_j\right)}}+{\displaystyle \frac{r_1+n_{1}d\left(v_j\right)}{r_1+n_{1}d\left(v_i\right)}}\right),\end{array}$$

if $v_i\sim v_j$.    □

Example 3. 

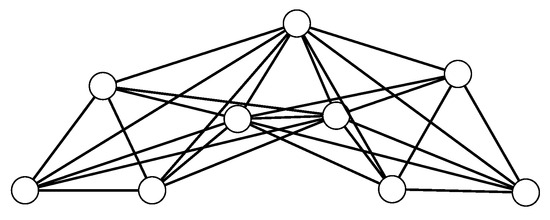
Consider the graph $H_3=P_3\left[K_3\right]=P_3[K_3,K_3,K_3]$, as shown in Figure 3. Let $v_1,v_2$ and $v_3$ be the vertices of $P_3$ with $d\left(v_1\right)=1,d\left(v_2\right)=2$ and $d\left(v_3\right)=1$. For the graph $H_3$, we have $\mathcal{G}=P_3,{\mathcal{G}}_1=K_3,n=3,n_1=3,r_1=2$. Also, the adjacency eigenvalues of $K_3$ are $r_1=2,-1,-1$. Further, ${\tau }_{12}={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{r_1+n_{1}d\left(v_1\right)}{r_1+n_{1}d\left(v_2\right)}}+{\displaystyle \frac{r_1+n_{1}d\left(v_2\right)}{r_1+n_{1}d\left(v_1\right)}}\right)={\displaystyle \frac{267}{80}}={\tau }_{21}={\tau }_{32}={\tau }_{23}$. Therefore, based on Theorem 2, the $A_{ex}$-eigenvalues of $H_3$ consist of the eigenvalue $-1$ repeated six times. The remaining three $A_{ex}$-eigenvalues are the eigenvalues of the following matrix: $\left(\begin{array}{ccc}2& {\displaystyle \frac{267}{80}}& 0\\ {\displaystyle \frac{267}{80}}& 2& {\displaystyle \frac{267}{80}}\\ 0& {\displaystyle \frac{267}{80}}& 2\end{array}\right)$. Through direct calculation, it can be seen that the eigenvalues of this matrix are $2+{\displaystyle \frac{267\sqrt{2}}{80}}\approx 6.7199377644,2-{\displaystyle \frac{267\sqrt{2}}{80}}\approx -2.71993776$, and 2.

Figure 3. The lexicographic product $P_3\left[K_3\right]=P_3[K_3,K_3,K_3]$ of the path $P_3$ with the regular graph $K_3$.

It is clear that the matrix M given in Theorem 2 is completely determined by the graph $\mathcal{G}$. In particular, taking ${\mathcal{G}}_1={\overline{K}}_{n_1}$, an empty graph on $n_1$ vertices in Theorem 2, we get the following consequence.

Corollary 3. 

Let $\mathcal{G}$ be a graph of order $n\ge 3$ having m edges. Let ${\overline{K}}_{n_1}$ be an empty graph on $n_1$ vertices. Then, the $A_{ex}$-spectrum of the $\mathcal{G}\left[{\overline{K}}_{n_1}\right]$ consists of the eigenvalues 0, with multiplicity $n(n_1-1)$ times and the n eigenvalues $n_1{\eta }_1,n_1{\eta }_2,\dots ,n_1{\eta }_n$, where ${\eta }_1\ge {\eta }_2\ge \cdots \ge {\eta }_n$ are the $A_{ex}$-eigenvalues of $\mathcal{G}$.

Proof. 

The proof follows directly from Theorem 2 by taking ${\mathcal{G}}_1={\overline{K}}_{n_1},r_1=0,{\lambda }_k\left({\mathcal{G}}_1\right)=0,$ for all k and using the fact that ${\tau }_{ij}={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{n_{1}d\left(v_i\right)}{n_{1}d\left(v_j\right)}}+{\displaystyle \frac{n_{1}d\left(v_j\right)}{n_{1}d\left(v_i\right)}}\right)={\displaystyle \frac{n_1}{2}}\left({\displaystyle \frac{d\left(v_i\right)}{d\left(v_j\right)}}+{\displaystyle \frac{d\left(v_j\right)}{d\left(v_i\right)}}\right)$ if $v_i\sim v_j$, and equal to 0 if $v_i\nsim v_j$.    □

In particular, by taking $\mathcal{G}=K_n$, the complete graph on n vertices, we obtain the following result as a direct consequence of Theorem 1.

Corollary 4. 

Let $K_n$ be the complete graph of order $n\ge 3$. Let ${\mathcal{G}}_i$ be a $r_i$-regular graph of order $n_i$ having adjacency eigenvalues ${\lambda }_{i1}=r_i\ge {\lambda }_{i2}\ge \dots \ge {\lambda }_{i{n}_i},$ where $i=1,2,\dots ,n$. The $A_{ex}$-spectrum of the joined union graph $K_n[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ of order $N={\displaystyle \sum _{i=1}^n}{n}_i$ consists of the eigenvalues ${\lambda }_{ik}\left({\mathcal{G}}_i\right)$ for $i=1,\dots ,n$ and $k=2,3,\dots ,n_i$. The remaining n eigenvalues are given by matrix M in Theorem 1 with ${\tau }_{ij}={\displaystyle \frac{n_j}{2}}\left({\displaystyle \frac{N+r_i-n_i}{N+r_j-n_j}}+{\displaystyle \frac{N+r_j-n_j}{N+r_i-n_i}}\right)$, if $v_i\sim v_j$, and equal to 0 if $v_i\nsim v_j$.

We observe that the complete p-partite graph $K_{n_1,n_2,\dots ,n_p}$ is the joined union of graphs ${\mathcal{G}}_i={\overline{K}}_{n_i}$, where the underlying graph is $K_p$. Therefore, $K_{n_1,n_2,\dots ,n_p}\cong K_p[{\overline{K}}_{n_1},{\overline{K}}_{n_2},\dots ,{\overline{K}}_{n_p}]$. Taking ${\mathcal{G}}_i={\overline{K}}_{n_i}$, in Corollary 4, we get the $A_{ex}$-spectrum of the complete p-partite graph $K_{n_1,n_2,\dots ,n_p}$, which consists of the eigenvalue 0 with multiplicity $N-n$, where $N={\displaystyle \sum _{k=1}^p}{n}_k$. The remaining p eigenvalues are given by matrix M in Theorem 1 with $r_i=0,{\tau }_{ij}={\displaystyle \frac{n_j}{2}}\left({\displaystyle \frac{N-n_i}{N-n_j}}+{\displaystyle \frac{N-n_j}{N-n_i}}\right)$, if $v_i\sim v_j$, and equal to 0 if $v_i\nsim v_j$.

Let $K_{a,b}$ be the complete bipartite graph with partite sets of cardinality a and $b,$ where $a+b=n$, clearly $K_{a,b}={\overline{K}}_a\vee {\overline{K}}_b$. A complete split graph, denoted by $C{S}_{\omega ,n-\omega }$, is a graph consisting of a clique on $\omega$ vertices and an independent set (a subset of vertices of a graph is said to be an independent set if the subgraph induced by them is an empty graph) on the remaining $n-\omega$ vertices such that each vertex of the clique is adjacent to every vertex of the independent set. We note that $C{S}_{\omega ,n-\omega }=K_{\omega }\vee {\overline{K}}_{n-\omega }$. Similarly, the cone graph is given by $C_{a,b}=C_a\vee {\overline{K}}_b$, and for $b=1$, we have wheel graph $W_{n+1}=C_n\vee K_1$ on $n+1$ vertices. As a special case of Corollary 1, we compute the $A_{ex}$-spectrum of the complete bipartite graph $K_{a,b}$, the complete split graph $C{S}_{\omega ,n-\omega },$ the cone graph $C_{a,b}$, and the wheel graph $W_{n+1}$ in the following result.

Corollary 5. 

(i) 

The $A_{ex}$-spectrum of $K_{a,b}$ consists of the eigenvalue 0 with multiplicity $a+b-2$ and the eigenvalues $\pm {\displaystyle \frac{a^2+b^2}{2\sqrt{ab}}}$.

(ii) 

The $A_{ex}$-spectrum of $C{S}_{\omega ,n-\omega }$ consists of the eigenvalue $-1$ with multiplicity $\omega -1$, the eigenvalue 0 with multiplicity $n-\omega -1$, and the eigenvalues

${\displaystyle \frac{1}{2}}\left(\omega -1\pm \sqrt{{(\omega -1)}^2+\omega (n-\omega ){\left({\displaystyle \frac{n-1}{\omega }}+{\displaystyle \frac{\omega }{n-1}}\right)}^2}\right)$.

(iii) 

The $A_{ex}$-spectrum of $C_{a,b}$ consists of the eigenvalues $2cos\left({\displaystyle \frac{2\pi k}{b}}\right)$, where $k=2,\dots ,a-1$, the eigenvalue 0 with multiplicity $b-1$, and the eigenvalues

${\displaystyle \frac{1}{2}}\left(2\pm \sqrt{4+ab{\left({\displaystyle \frac{b+2}{a}}+{\displaystyle \frac{a}{b+2}}\right)}^2}\right)$.

(iv) 

The $A_{ex}$-spectrum of $W_{n+1}$ consists of the eigenvalues $2cos\left({\displaystyle \frac{2\pi k}{n}}\right)$, where $k=2,\dots ,n-1$, and the eigenvalues

${\displaystyle \frac{1}{2}}\left(2\pm \sqrt{4+n{\left({\displaystyle \frac{3}{n}}+{\displaystyle \frac{n}{3}}\right)}^2}\right)$.

Proof. 

The proofs of (i)–(iv) follow directly from Corollary 1 using the fact that the adjacency spectrum of $K_{\omega }$ consists of eigenvalue $\omega -1$ and the eigenvalue $-1$ with multiplicity $\omega -1$; the adjacency spectrum of ${\overline{K}}_t$ consists of eigenvalue 0 with multiplicity t, and the adjacency spectrum (see [1]) of $C_n$ is $\left\{2cos\left({\displaystyle \frac{2\pi k}{n}}\right):k=1,2,\dots ,n\right\}$.    □

A friendship graph $F_n$ is a graph of order $2n+1$, obtained by joining $K_1$ with n copies of $K_2$; that is, $F_n=K_1\vee \left(n{K}_2\right)=K_{1,n}[K_1,\underset{n}{{\displaystyle \underbrace{K_2,K_2,\dots ,K_2}}}]$, where $K_1$ corresponds to the root vertex (vertex of degree greater than one) in $K_{1,n}$. In particular, by replacing some $K_2$s with $K_1$s in $F_n$, we get a firefly-type graph denoted by $F_{p,n-p}$, written as follows:

$$F_{p,n-p}=K_{1,n}[K_1,\underset{p}{\underbrace{K_1,K_1,\dots ,K_1}}\underset{n-p}{\underbrace{K_2,K_2,\dots ,K_2}}].$$

The $A_{ex}$-spectrum of the friendship graph $F_n$ and the firefly-type graph $F_{p,n-p}$ are given by the following result.

Corollary 6. 

(i) 

The $A_{ex}$-spectrum of $F_n$ consists of the eigenvalue $-1$ with multiplicity n, the eigenvalue 1 with multiplicity $n-1$, and the eigenvalues ${\displaystyle \frac{1}{2}}\left(1\pm \sqrt{1+{\displaystyle \frac{2{(n^2+1)}^2}{n}}}\right)$.

(ii) 

The $A_{ex}$-spectrum of $F_{p,n-p}$ consists of the eigenvalue 0 with multiplicity $p-1$, the eigenvalue $-1$ with multiplicity $n-p$, the eigenvalue 1 with multiplicity $n-p-1$, and the three eigenvalues of the matrix M given in Corollary 2 with $r_1=0,r_2=0,r_3=1,n_1=1,n_2=p$, and $n_3=2(n-p)$.

Proof. 

(i) follows from Corollary 1 by taking $r_1=0,r_2=1,n_1=1$, and $n_2=2n$. Similarly, (ii) follows from Corollary 2 by using the fact that $F_{p,n-p}=K_1\vee (p{K}_1\cup (n-p)K_2)$.    □

3. Extended Adjacency Energy

In this section, by using the results obtained in Section 2, we construct some new infinite families of non-cospectral extended adjacency equienergetic graphs.

Two graphs of the same order are said to be equienergetic if they are non-cospectral and have the same energy. The problem of constructing non-cospectral graphs that have the same energy is an active component of present research, and several papers have been published in this direction. For some recent works, we refer the reader to [16,17] and the references therein.

The authors in [7] have extended the concept of equienergetic graphs to the $A_{ex}$-matrix and defined the extended adjacency equienergetic graphs. Two graphs $\mathcal{G}$ and $\mathcal{H}$ of the same order are said to be extended adjacency equienergetic if they are non-cospectral and have the same $A_{ex}$-energy, that is, ${\mathcal{E}}_{ex}\left(\mathcal{G}\right)={\mathcal{E}}_{ex}\left(\mathcal{H}\right)$. It is clear that if two graphs are extended adjacency cospectral, they are extended adjacency equienergetic. Therefore, in what follows, we will be interested in finding extended adjacency equienergetic non-cospectral graphs. In fact, we will address the following problem for $A_{ex}$-eigenvalues.

Problem 1. 

How can families of non-isomorphic graphs be constructed such that they have equal $A_{ex}$-energy, but they do not have the same $A_{ex}$-spectrum?

It is clear that the $A_{ex}$-energy ${\mathcal{E}}_{ex}\left(\mathcal{G}\right)$ of a graph $\mathcal{G}$ represents the trace norm of the matrix $A_{ex}\left(\mathcal{G}\right)$. Note that the trace norm of a n-square matrix M is defined as ${\parallel M\parallel }_{*}={\displaystyle \sum _{i=1}^n}{\sigma }_i\left(M\right)$, where ${\sigma }_1\left(M\right)\ge {\sigma }_2\left(M\right)\ge \cdots \ge {\sigma }_n\left(M\right)$ are the singular values of M (i.e., the square roots of the eigenvalues of $M{M}^{*}$, where $M^{*}$ is the complex conjugate of M). Therefore, the study of this spectral graph invariant is not only interesting and important from a spectral graph theory point of view but is also important from a matrix theory point of view.

In the language of matrix theory, the above problem forms a part of the following interesting but hard problem.

Problem 2. 

How can matrices of order n with the same trace norm but a different spectrum be characterized?

For matrices associated with graphs, a large number of families of graphs are known with equal trace norm (energy) but different spectra, see [18]. In general, characterizing the square matrices of order n with equal trace norm is not easy. However, for matrices associated with graphs (called graph matrices), some sufficient conditions are known that guarantee their existence.

Problem 1 was addressed by Adiga et al. in [7], and some infinite families of non-isomorphic non-cospectral extended adjacency equienergetic graphs were constructed. The main tool used by the authors in [7] for the construction of such families was the following operations: join of graphs, double graph of a graph, and the duplication of a graph. In the rest of this section, we aim to construct new infinite families of non-cospectral extended adjacency equienergetic graphs. We will devise a general method to generate infinite classes of infinite families of non-cospectral extended adjacency equienergetic graphs.

The following result gives the $A_{ex}$-energy of the joined union $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ of regular graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n$.

Theorem 3. 

Let $\mathcal{G}$ be a graph of order $n\ge 2$ with m edges. Let ${\mathcal{G}}_i$ be a $r_i$-regular graph of order $n_i$ having energy $\mathcal{E}\left({\mathcal{G}}_i\right)$ for all $i=1,2,\dots ,n$. Then,

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}\left(\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]\right)={\displaystyle \sum _{i=1}^n}\mathcal{E}\left({\mathcal{G}}_i\right)-{\displaystyle \sum _{i=1}^n}{r}_i+{\displaystyle \sum _{i=1}^n}\left|x_i\right|,\end{array}$$

where $x_1,x_2,\dots ,x_n$ are the eigenvalues of the matrix M given in Theorem 1.

Proof. 

From Theorem 1, it is clear that if $r_i,{\lambda }_{ik}$, where $k=2,3,\dots ,n_i$ are the adjacency eigenvalues of ${\mathcal{G}}_i$, for $1\le i\le n$, then the $A_{ex}$-eigenvalues of graph $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ are ${\lambda }_{ik}$ for $k=2,3,\dots ,n_i$ and $i=1,2,\dots ,n$. The remaining n eigenvalues are the eigenvalues of the matrix M. Now, using the definition of $A_{ex}$-energy, the result follows.   □

Example 4. 

Consider the graph $H_1=P_3[K_3,C_4,P_2]$, as shown in Figure 1. In Example 1, we have found the $A_{ex}$-eigenvalues of the graph $H_1$, which are $-1$ repeated 3 times, 0 repeated 2 times, $-2$ repeated once, and the three eigenvalues $6.42490599,1.42776319$, and $-2.85266918$ of the matrix M. Therefore, based on the definition of $A_{ex}$-energy, we have

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_1\right)& ={\mathcal{E}}_{ex}\left(P_3[K_3,C_4,P_2]\right)\hfill \\ & =3|-1|+2\left|0\right|+|-2|+\left|6.42490599\right|+\left|1.42776319\right|+|-2.85266918|\hfill \\ & =15.70533836.\hfill \end{array}$$

Also, $K_3$ is a $r_1=2$ regular graph with adjacency eigenvalues $2,-1,-1$; $C_4$ is a $r_2=2$ regular graph with adjacency eigenvalues $2,0,0,-2$; and $P_2$ is a $r_3=1$ regular graph with adjacency eigenvalues $1,-1$. Therefore, $\mathcal{E}\left(K_3\right)=4,\mathcal{E}\left(C_4\right)=4,\mathcal{E}\left(P_2\right)=2$ and ${\displaystyle \sum _{i=1}^3}{r}_i=r_1+r_2+r_3=5$. Therefore, based on Theorem 3, we have

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_1\right)& ={\mathcal{E}}_{ex}\left(P_3[K_3,C_4,P_2]\right)=\mathcal{E}\left(K_3\right)+\mathcal{E}\left(C_4\right)+\mathcal{E}\left(P_2\right)-{\displaystyle \sum _{i=1}^3}{r}_i+{\displaystyle \sum _{i=1}^3}\left|x_i\right|\hfill \\ & =5+{\displaystyle \sum _{i=1}^3}\left|x_i\right|,\hfill \end{array}$$

where $x_1,x_2,x_3$ are the eigenvalues of matrix M. Inputting $x_1=6.42490599,x_2=1.42776319$, and $x_3=-2.85266918$, we see that Theorem 3 also gives ${\mathcal{E}}_{ex}\left(H_1\right)=15.70533836$.

Taking in particular $\mathcal{G}=K_2$ in Theorem 3 and using Theorem 1, we obtain the following result, which gives the $A_{ex}$-energy of the join of two regular graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$.

Corollary 7. 

For $i=1,2$, let ${\mathcal{G}}_i$ be a $r_i$-regular graph of order $n_i$. Then,

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}({\mathcal{G}}_1\vee {\mathcal{G}}_2)=\mathcal{E}\left({\mathcal{G}}_1\right)+\mathcal{E}\left({\mathcal{G}}_2\right)+\left(\right|x_1|+|x_2|-r_1-r_2),\end{array}$$

where $x_1,x_2$ are ${\displaystyle \frac{1}{2}}\left(r_1+r_2\pm \sqrt{{(r_1-r_2)}^2+n_1{n}_2{\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)}^2}\right)$.

Example 5. 

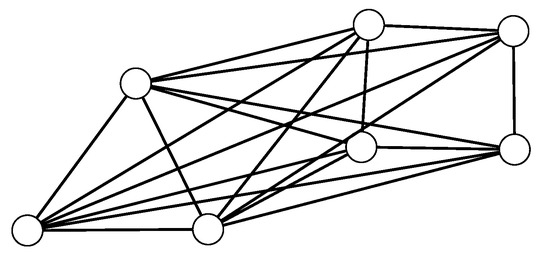
Consider the graph $H_4=K_3\vee C_4$, as shown in Figure 4. For this graph, we have $n_1=3,n_2=4,r_1=2,r_2=2$. Also, the adjacency eigenvalues of $K_3$ are $2,-1,-1$, and the adjacency eigenvalues of $C_4$ are $2,0,0,-2$. Using Corollary 1, it follows that the $A_{ex}$-eigenvalues of $H_4$ are $-1,-1,0,0,-2$. The remaining two $A_{ex}$-eigenvalues are the eigenvalues of the matrix $\left(\begin{array}{cc}2& {\displaystyle \frac{61}{15}}\\ {\displaystyle \frac{61}{20}}& 2\end{array}\right)$. Through direct calculation, it can be seen that the eigenvalues of this matrix are $2+{\displaystyle \frac{61\sqrt{3}}{30}}\approx 5.52183664$ and $2-{\displaystyle \frac{61\sqrt{3}}{30}}\approx -1.52183664$. Therefore, based on the definition of $A_{ex}$-energy, we have

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_4\right)& ={\mathcal{E}}_{ex}(K_3\vee C_4)\hfill \\ & =2|-1|+2\left|0\right|+|-2|+\left|5.52183664\right|+|-1.52183664|\hfill \\ & =11.04367328.\hfill \end{array}$$

Again, $\mathcal{E}\left(K_3\right)=4,\mathcal{E}\left(C_4\right)=4$, and $r_1=r_2=2$. It follows from Corollary 7 that

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_4\right)& ={\mathcal{E}}_{ex}(K_3\vee C_4)=\mathcal{E}\left(K_3\right)+\mathcal{E}\left(C_4\right)-(r_1+r_2)+|x_1|+|x_2|\hfill \\ & =4+4-4+\left|5.52183664\right|+|-1.52183664|=11.04367328.\hfill \end{array}$$

This shows that the value of $A_{ex}$-energy obtained through direct computation is in agreement with the value given by Corollary 7.

Figure 4. The join of graphs $K_3$ and $C_4$.

Taking in particular ${\mathcal{G}}_1={\mathcal{G}}_2=\dots ={\mathcal{G}}_n$ in Theorem 3, we obtain the following result, which gives the $A_{ex}$-energy of the lexicographic product $\mathcal{G}\left[{\mathcal{G}}_1\right]=\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_1]$ of $\mathcal{G}$ and ${\mathcal{G}}_1$, where ${\mathcal{G}}_1$ is a regular graph.

Corollary 8. 

Let $\mathcal{G}$ be a graph of order $n\ge 2$ with m edges. Let ${\mathcal{G}}_1$ be a $r_1$-regular graph with energy $\mathcal{E}\left({\mathcal{G}}_1\right)$. Then,

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}\left(\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_1]\right)=n\mathcal{E}\left({\mathcal{G}}_1\right)-n{r}_1+{\displaystyle \sum _{i=1}^n}\left|x_i\right|,\end{array}$$

where $x_1,x_2,\dots ,x_n$ are the eigenvalues of matrix M given in Theorem 2.

Example 6. 

Consider the graph $H_3=P_3\left[K_3\right]=P_3[K_3,K_3,K_3]$, as shown in Figure 3. In Example 3, we have shown that the $A_{ex}$-eigenvalues of $H_3$ consist of eigenvalue $-1$ repeated six times and the three eigenvalues $2+{\displaystyle \frac{267\sqrt{2}}{80}}\approx 6.71993776,2-{\displaystyle \frac{267\sqrt{2}}{80}}\approx -2.71993776$, and 2. Therefore, based on the definition of $A_{ex}$-energy, we have

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_3\right)& ={\mathcal{E}}_{ex}\left(P_3\left[K_3\right]\right)\hfill \\ & =6|-1|+\left|6.71993776\right|+|-2.71993776|+\left|2\right|\hfill \\ & =17.43987552.\hfill \end{array}$$

Again, the adjacency eigenvalues of $K_3$ are $2,-1,-1$ with degree of regularity $r_1=2$. It follows that $\mathcal{E}\left(K_3\right)=4$. Taking $n=3$ and ${\mathcal{G}}_1=K_3$ in Corollary 8, we get

$$\begin{array}{cc}\hfill {\mathcal{E}}_{ex}\left(H_3\right)& ={\mathcal{E}}_{ex}\left(P_3\left[K_3\right]\right)\hfill \\ & =3\mathcal{E}\left(K_3\right)-3r_1+{\displaystyle \sum _{i=1}^3}\left|x_i\right|\hfill \\ & =3\left(4\right)-3\left(2\right)+\left|6.71993776\right|+|-2.71993776|+\left|2\right|\hfill \\ & =17.43987552,\hfill \end{array}$$

as $x_1=6.71993776,x_2=-2.71993776$ and $x_3=2$. This shows that the value of $A_{ex}$-energy obtained via direct computation is in agreement with the value given by Corollary 8.

Matrix M is determined by the structure of $\mathcal{G}$, the orders $n_i$, and the degree of regularity $r_i$ of the graphs ${\mathcal{G}}_i$ for $i=1,2,\dots ,n$. We have the following observation from Theorem 3.

Corollary 9. 

Let $\mathcal{G}$ be a graph of order $n\ge 2$ with m edges. Let ${\mathcal{G}}_i$ and ${\mathcal{H}}_i$ be $r_i$-regular non-cospectral graphs of order $n_i$ with $\mathcal{E}\left({\mathcal{G}}_i\right)=\mathcal{E}\left({\mathcal{H}}_i\right)$ for all $i=1,2,\dots ,n$. Then, the graphs $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ and $\mathcal{G}[{\mathcal{H}}_1,\dots ,{\mathcal{H}}_n]$ are non-cospectral with

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}\left(\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]\right)={\mathcal{E}}_{ex}\left(\mathcal{G}[{\mathcal{H}}_1,\dots ,{\mathcal{H}}_n]\right).\end{array}$$

Proof. 

The proof follows from Theorem 3 based on the fact that matrix M is same for the graphs $\mathcal{G}[{\mathcal{G}}_1,\dots ,{\mathcal{G}}_n]$ and $\mathcal{G}[{\mathcal{H}}_1,\dots ,{\mathcal{H}}_n]$.    □

Example 7. 

Consider the graphs $H_5=P_3[K_3,C_4,2K_2]$ and $H_6=P_3[C_4,K_3,2K_2]$, shown in Figure 5. For graphs $H_5$ and $H_6$, we have $\mathcal{G}=P_3$, ${\mathcal{G}}_1=K_3,{\mathcal{G}}_2=C_4,{\mathcal{G}}_3=2K_2,{\mathcal{H}}_1=C_4,{\mathcal{H}}_2=K_3$, and ${\mathcal{H}}_3=2K_2$. Clearly, graphs ${\mathcal{G}}_1$ and ${\mathcal{H}}_1$ are regular of degree 2; graphs ${\mathcal{G}}_2$ and ${\mathcal{H}}_2$ are regular of degree 2; and graphs ${\mathcal{G}}_3$ and ${\mathcal{H}}_3$ are regular of degree 1. Also, the adjacency eigenvalues of $K_3$ are $2,-1,-1$, implying that $\mathcal{E}\left(K_3\right)=4$; the adjacency eigenvalues of $C_4$ are $2,0,0,-2$, implying that $\mathcal{E}\left(C_4\right)=4$; and the adjacency eigenvalues of $2K_2$ are $1,1,-1,-1$, implying that $\mathcal{E}\left(2K_2\right)=4$. Clearly, $\mathcal{E}\left({\mathcal{G}}_1\right)=\mathcal{E}\left({\mathcal{H}}_1\right)$, $\mathcal{E}\left({\mathcal{G}}_2\right)=\mathcal{E}\left({\mathcal{H}}_2\right)$, and $\mathcal{E}\left({\mathcal{G}}_3\right)=\mathcal{E}\left({\mathcal{H}}_3\right)$. Therefore, based on Corollary 9, we have

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}\left(P_3[K_3,C_4,2K_2]\right)={\mathcal{E}}_{ex}\left(P_3[C_4,K_3,2K_2]\right).\end{array}$$

Figure 5. The graphs $P_3[K_3,C_4,2K_2]$ and $P_3[C_4,K_3,2K_2]$.

A number of papers can be found in the literature regarding the construction of equienergetic regular graphs; see the book [18] and the references therein. Let $H_1$ and $H_2$ be the 4-regular graphs of order 9 shown in Figure 4.1 in [18] (see page number 26). Through direct calculation, we can see that graphs $H_1$ and $H_2$ are non-cospectral equienergetic graphs. The double graph $D\left(\mathcal{G}\right)$ of a graph $\mathcal{G}$ is the graph obtained by taking two copies of $\mathcal{G}$ and joining a vertex in the first copy to a vertex in the second copy whenever they are adjacent in $\mathcal{G}$. It is clear from the definition that if $\mathcal{G}$ is an r-regular graph, then its double graph $D\left(\mathcal{G}\right)$ is a $2r$-regular graph. Moreover, it is well-known that $\mathcal{E}\left(D\right(\mathcal{G}\left)\right)=2\mathcal{E}\left(\mathcal{G}\right)$, see [18]. Let $L\left(\mathcal{G}\right)=L^1\left(\mathcal{G}\right)$ be the line graph of $\mathcal{G}$, and let $L^k\left(\mathcal{G}\right)=L\left(L^{k-1}\left(\mathcal{G}\right)\right)$ for $k=2,3,\dots ,$ be the k-th iterated line graph of $\mathcal{G}$. Let ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ be two non-cospectral regular graphs of the same order and the same degree $r\ge 3$. Then, it is shown in Theorem 8.4 of [18] that for $k\ge 2$, the iterated line graphs $L^k\left({\mathcal{G}}_1\right)$ and $L^k\left({\mathcal{G}}_2\right)$ are non-cospectral equienergetic graphs of the same order and size. Since the graphs $H_1$ and $H_2$ are non-cospectral equienergetic 4-regular graphs, it follows from the above discussion that the double graphs $D\left(H_1\right)$ and $D\left(H_2\right)$ are non-cospectral equienergetic 8-regular graphs. Also, the iterated line graphs $L^k\left(H_1\right)$ and $L^k\left(H_2\right)$, where $k\ge 2$, are non-cospectral equienergetic regular graphs. Using graphs $H_1$ and $H_2$, we have the following observations from Corollary 9.

Corollary 10. 

Let $\mathcal{G}$ be a graph of order $n\ge 2$, and let $H_1,H_2,D\left(H_1\right),D\left(H_2\right),L^k\left(H_1\right)$, and $L^k\left(H_2\right)$ be the regular graphs defined above.

(i). 

The graphs

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{H_1,\dots ,H_1}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

and

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{H_2,\dots ,H_2}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

are non-cospectral extended adjacency equienergetic graphs.

(ii). 

The graphs

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{D\left(H_1\right),\dots ,D\left(H_1\right)}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

and

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{D\left(H_2\right),\dots ,D\left(H_2\right)}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

are non-cospectral extended adjacency equienergetic graphs.

(iii). 

The graphs

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{L^k\left(H_1\right),\dots ,L^k\left(H_1\right)}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

and

$$\begin{array}{c}\hfill \mathcal{G}[\underset{k_1}{\underbrace{L^k\left(H_2\right),\dots ,L^k\left(H_2\right)}},\underset{k_2}{\underbrace{{\overline{K}}_{n_1},\dots ,{\overline{K}}_{n_{k_2}}}},\underset{k_3}{\underbrace{K_{t_1},\dots ,K_{t_{k_3}}}},\underset{k_4}{\underbrace{K_{a_1,a_1},\dots ,K_{a_{k_4},a_{k_4}}}}]\end{array}$$

are non-cospectral extended adjacency equienergetic graphs, where $k_1,k_2,k_3$, and $k_4$ are whole numbers with $k_1\ge 2$ or $k_1,k_i\ge 1$, $i\ne 1$ and $k_1+k_2+k_3+k_4=n$.

Recently, it is shown that the $A_{ex}$-energy of a tree T is greater than the energy of T. Here, we show that the $A_{ex}$-energy of the join of two regular graphs is greater than their energy.

Theorem 4. 

Let ${\mathcal{G}}_i$ be a $r_i$-regular graph of order $n_i$ for $i=1,2$. Then,

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}({\mathcal{G}}_1\vee {\mathcal{G}}_2)\ge \mathcal{E}({\mathcal{G}}_1\vee {\mathcal{G}}_2),\end{array}$$

with equality if and only if $r_1-r_2=n_1-n_2$.

It is well-known (see [18]) that the energy of join ${\mathcal{G}}_1\vee {\mathcal{G}}_2$ of two regular graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ is given as follows:

$$\begin{array}{c}\hfill \mathcal{E}({\mathcal{G}}_1\vee {\mathcal{G}}_2)=\mathcal{E}\left({\mathcal{G}}_1\right)+\mathcal{E}\left({\mathcal{G}}_2\right)-(r_1+r_2)+\sqrt{{(r_1-r_2)}^2+4n_1{n}_2}.\end{array}$$

(2)

Also, based on Corollary 7, the $A_{ex}$-energy of join ${\mathcal{G}}_1\vee {\mathcal{G}}_2$ is given as follows:

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}({\mathcal{G}}_1\vee {\mathcal{G}}_2)=\mathcal{E}\left({\mathcal{G}}_1\right)+\mathcal{E}\left({\mathcal{G}}_2\right)-(r_1+r_2)+\sqrt{{(r_1-r_2)}^2+n_1{n}_2{\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)}^2}.\end{array}$$

(3)

From (2) and (3), we get

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}({\mathcal{G}}_1\vee {\mathcal{G}}_2)-\mathcal{E}({\mathcal{G}}_1\vee {\mathcal{G}}_2)=\sqrt{{(r_1-r_2)}^2+n_1{n}_2{\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)}^2}-\sqrt{{(r_1-r_2)}^2+4n_1{n}_2}.\end{array}$$

(4)

Now, $\sqrt{{(r_1-r_2)}^2+n_1{n}_2{\left({\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\right)}^2}\ge \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}$ gives that ${\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}\ge 2$, which is always true, as $r_1,r_2,n_1,n_2$ are positive integers. Using this together with Equation (4), the result follows. Equality occurs if and only if ${\displaystyle \frac{r_1+n_2}{r_2+n_1}}+{\displaystyle \frac{r_2+n_1}{r_1+n_2}}=2$, that is, if and only if ${(r_1+n_2)}^2+{(r_2+n_1)}^2=2(r_1+n_2)(r_2+n_1)$. This last equality gives ${\left((r_1+n_2)-(r_2+n_1)\right)}^2=0$, which is so if and only if $r_1-r_2=n_1-n_2$. This completes the proof.   □

Example 8. 

Consider the graph $H_4=K_3\vee C_4$ shown in Figure 2. For this graph, it is shown in Example 5 that the $A_{ex}$-eigenvalues of $H_4$ consist of the eigenvalue $-1$ repeated two times, the eigenvalue 0 repeated two times, the eigenvalue $-2$, and the two eigenvalues $5.52183664,-1.52183664$. Therefore, based on the definition of $A_{ex}$-energy, we get

$$\begin{array}{c}\hfill {\mathcal{E}}_{ex}(K_3\vee C_4)=11.04367328.\end{array}$$

Also, $K_3$ is a $r_1=2$ regular graph with $n_1=3$ and $\mathcal{E}\left(K_3\right)=4$, and $C_4$ is a $r_2=2$ regular graph with $n_2=4$ and $\mathcal{E}\left(C_4\right)=4$. Therefore, based on  Theorem 4, the adjacency energy of the graph $K_3\vee C_4$ is given as follows:

$$\begin{array}{cc}\hfill \mathcal{E}(K_3\vee C_4)& =\mathcal{E}\left(K_3\right)+\mathcal{E}\left(C_4\right)-(r_1+r_2)+\sqrt{{(2-2)}^2+4n_1{n}_2}\hfill \\ & =4+4-4+4\sqrt{3}=4+4\sqrt{3}\approx 10.9282032303.\hfill \end{array}$$

It is now clear that ${\mathcal{E}}_{ex}(K_3\vee C_4)>\mathcal{E}(K_3\vee C_4)$.

4. Applications to Algebraic Graphs

In this section, we consider the power graph of finite groups. As applications of Theorem 1 and its consequences obtained in Section 2, we determine their $A_{ex}$-eigenvalues.

If $\mathcal{G}$ is a finite group of order n with identity e, the power graph of $\mathcal{G}$, denoted by $\mathcal{P}\left(\mathcal{G}\right)$, is the simple graph with vertex set as the elements of group $\mathcal{G}$. Two distinct vertices $x,y\in \mathcal{P}\left(\mathcal{G}\right)$ are adjacent if and only if one is the positive power of the other, that is, $x^i=y$ or $y^j=x$, for positive integers $i,j$ with $2 \le i,j \le n$. Such graphs were introduced in [19], see also [20], and have valuable applications in both algebra and combinatorics.

The divisor d of the positive integer n (written as $d|n$) is a proper divisor of n if $1<d<n.$ Let ${\mathcal{D}}_n$ be a simple graph with the vertex set as the set of proper divisors $\{d_i:1,n\ne d_i|n,1\le i\le t\}$ of n and an edge set $\{d_i{d}_j:d_i|d_j,1\le i<j\le t\}$, for $1\le i<j\le t$. If the canonical decomposition of n is $n=p_1^{n_1}{p}_2^{n_2}\dots p_r^{n_r}$, where $r,n_1,n_2,\dots ,n_r$ are non-negative integers and $p_1,p_2,\dots ,p_r$ are distinct prime numbers, then the order of graph ${\mathcal{D}}_n$ is $|V\left({\mathcal{D}}_n\right)|={\displaystyle \prod _{i=1}^r}(n_i+1)-2.$ The structure of the power graph of ${\mathbb{Z}}_n$ can be written as a joined union of cliques, where cliques correspond to proper divisors of n and are given by the following result.

Theorem 5 

([21]). If ${\mathbb{Z}}_n$ is a finite cyclic group of order n, then the power graph $\mathcal{P}\left({\mathbb{Z}}_n\right)$ is given by

$$\mathcal{P}\left({\mathbb{Z}}_n\right)=K_{\varphi \left(n\right)+1}\vee {\mathcal{D}}_n[K_{\varphi \left(d_1\right)},K_{\varphi \left(d_2\right)},\dots ,K_{\varphi \left(d_t\right)}],$$

where $\varphi \left(n\right)$ is the Euler’s totient function.

The next result gives the $A_{ex}$-spectrum of $\mathcal{P}\left({\mathbb{Z}}_n\right)$.

Theorem 6. 

The $A_{ex}$-spectrum of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ consists of the eigenvalue $-1$ with multiplicity $\varphi \left(n\right)+{\displaystyle \sum _{i=1}^t}(\varphi \left(d_i\right)-1)=\varphi \left(n\right)+n-\varphi \left(n\right)-1-t=n-t-1$, as ${\displaystyle \sum _{i=1}^t}\varphi \left(d_i\right)={\displaystyle \sum _{d|n,d\ne 1,n}}\varphi \left(d_i\right)=n-\varphi \left(n\right)-1$. The remaining $t+1$ eigenvalues are the eigenvalues of matrix (5) given below

$$M=\left(\begin{array}{cccc}\varphi \left(n\right)& {\tau }_{12}& \dots & {\tau }_{1(t+1)}\\ {\tau }_{21}& \varphi \left(d_1\right)-1& \dots & {\tau }_{2(t+1)}\\ {\tau }_{31}& {\tau }_{32}& \dots & {\tau }_{3(t+1)}\\ ⋮& ⋮& \ddots & ⋮\\ {\tau }_{(t+1)1}& {\tau }_{(t+1)2}& \dots & \varphi \left(d_t\right)-1\end{array}\right),$$

(5)

where ${\tau }_{1j}={\displaystyle \frac{\varphi \left(d_{j-1}\right)}{2}}({\displaystyle \frac{n-1}{\varphi \left(d_{j-1}\right)+c_j-1}}+{\displaystyle \frac{\varphi \left(d_{j-1}\right)+c_j-1}{n-1}})$ and ${\tau }_{i1}={\displaystyle \frac{\varphi \left(n\right)+1}{2}}({\displaystyle \frac{\varphi \left(d_{i-1}\right)+c_i-1}{n-1}}+{\displaystyle \frac{n-1}{\varphi \left(d_{i-1}\right)+c_i-1}})$ for $2\le i,j\le t+1$. Also, ${\tau }_{ij}={\displaystyle \frac{\varphi \left(d_{j-1}\right)}{2}}\left({\displaystyle \frac{\varphi \left(d_{i-1}\right)-1+c_i}{\varphi \left(d_{j-1}\right)-1+c_j}}+{\displaystyle \frac{\varphi \left(d_{j-1}\right)-1+c_j}{\varphi \left(d_{i-1}\right)-1+c_i}}\right)$, if $v_i\sim v_j$, and equal to 0 if $v_i\nsim v_j$ for all $2\le i,j\le t+1$ and $c_i={\displaystyle \sum _{v_j\in N_{K_1\vee {\mathcal{D}}_n}\left(v_i\right)}}{n}_j$.

Proof. 

Let $\mathcal{P}\left({\mathbb{Z}}_n\right)$ be the power graph of ${\mathbb{Z}}_n$. Then, based on Theorem 5, we have

$$\mathcal{P}\left({\mathbb{Z}}_n\right)=\mathcal{H}[K_{\varphi \left(n\right)+1},K_{\varphi \left(d_1\right)},K_{\varphi \left(d_2\right)},\dots ,K_{\varphi \left(d_t\right)}],$$

where $\mathcal{H}=K_1\vee {\mathcal{D}}_n$ is the graph with the vertex set $\{v_1,\dots ,v_{t+1}\}$. Let us consider $G_1=K_{\varphi \left(n\right)+1},G_2=K_{\varphi \left(d_1\right)},\dots ,G_{t+1}=K_{\varphi \left(d_t\right)}$ in Theorem 1. Using the fact that graph $K_{\varphi \left(n\right)+1}$ is $\varphi \left(n\right)$ regular having adjacency eigenvalues $\varphi \left(n\right)$ with multiplicity 1 and $-1$ with multiplicity $\varphi \left(n\right)$, it follows from Theorem 1 that $-1$ is the extended adjacency eigenvalue of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ with multiplicity $\varphi \left(n\right)$. Also, the graph $K_{\varphi \left(d_i\right)}$ is ${\varphi }_i\left(d_i\right)-1$ regular, having adjacency eigenvalues $\varphi \left(d_i\right)-1$ with multiplicity 1 and $-1$ with multiplicity $\varphi \left(d_i\right)-1$ for $i=1,\dots ,t$. It follows from Theorem 1 that $-1$ is an extended adjacency eigenvalue of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ with multiplicity $\varphi \left(d_i\right)-1$, for all $t=1,2,\dots ,t$. The remaining $t+1$$A_{ex}$-eigenvalues of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ are the eigenvalues of matrix (5). This completes the proof.    □

Clearly, from Theorem 6, all the $A_{ex}$-eigenvalues of the power graph $\mathcal{P}\left({\mathbb{Z}}_n\right)$ are completely determined except for the $t+1$-eigenvalues, which are the eigenvalues of matrix M defined in Theorem 6. Further, it is also clear that matrix M depends upon the structure of graph ${\mathcal{D}}_n$, which is not known in general. However, if we give some particular values to n, then it may be possible to know the structure of the graph ${\mathcal{D}}_n$ and hence about the matrix M. This information can be helpful to determine the remaining $A_{ex}$-eigenvalues of the power graph $\mathcal{P}\left({\mathbb{Z}}_n\right)$.

If $n=p^s$, where p is a prime and s is a positive integer, then $\mathcal{P}\left({\mathbb{Z}}_n\right)$ is the complete graph $K_n$, and its $A_{ex}$-spectrum is $\left\{n-1,-1^{[n-1]}\right\}.$

Let $n=pq$, where p and q are primes with $p<q$. Then, the power graph $\mathcal{P}\left({\mathbb{Z}}_n\right)$ can be written as

$$P_3[K_{\varphi \left(pq\right)+1},K_{p-1},K_{q-1}].$$

Here, $\mathcal{H}=P_3,n_1=\varphi \left(pq\right)+1,n_2=p-1$ and $n_3=q-1$. Let $v_1,v_2,v_3$ be the vertices of $P_3$ with degree of vertex $v_1$ equal to two, then $c_2=\varphi \left(pq\right)+1=c_3$;

$$\begin{array}{cc}\hfill & {\tau }_{12}={\displaystyle \frac{\varphi \left(d_1\right)}{2}}\left({\displaystyle \frac{n-1}{\varphi \left(d_1\right)+c_2-1}}+{\displaystyle \frac{\varphi \left(d_1\right)+c_2-1}{n-1}}\right)={\displaystyle \frac{p-1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right),\hfill \\ & {\tau }_{13}={\displaystyle \frac{\varphi \left(d_2\right)}{2}}\left({\displaystyle \frac{n-1}{\varphi \left(d_2\right)+c_3-1}}+{\displaystyle \frac{\varphi \left(d_2\right)+c_3-1}{n-1}}\right)={\displaystyle \frac{q-1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right),\hfill \\ & {\tau }_{21}={\displaystyle \frac{\varphi \left(n\right)+1}{2}}\left({\displaystyle \frac{n-1}{\varphi \left(d_1\right)+c_2-1}}+{\displaystyle \frac{\varphi \left(d_1\right)+c_2-1}{n-1}}\right)={\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right),\hfill \\ & {\tau }_{31}={\displaystyle \frac{\varphi \left(n\right)+1}{2}}\left({\displaystyle \frac{n-1}{\varphi \left(d_2\right)+c_3-1}}+{\displaystyle \frac{\varphi \left(d_2\right)+c_3-1}{n-1}}\right)={\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right),\hfill \end{array}$$

and ${\tau }_{23}=0={\tau }_{32}$. Now, using Theorem 6, it follows that the $A_{ex}$-spectrum of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ consists of the eigenvalue $-1$ with multiplicity $n-3$. The other three $A_{ex}$-eigenvalues of $\mathcal{P}\left({\mathbb{Z}}_n\right)$ are the eigenvalues of the following matrix:

$$\left(\begin{array}{ccc}\varphi \left(pq\right)& {\displaystyle \frac{p-1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)& {\displaystyle \frac{q-1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)\\ {\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)& p-2& 0\\ {\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)& 0& q-2\end{array}\right).$$

From the above discussion, it is clear that if $n=pq$, where $p<q$ are primes, then we can completely determine all except three $A_{ex}$-eigenvalues of $\mathcal{P}\left({\mathbb{Z}}_n\right)$.

Example 9. 

Consider the finite abelian group ${\mathbb{Z}}_{15}$ shown in Figure 6. Here, $n=15,p=3,q=5$, and $\varphi \left(pq\right)=\varphi \left(15\right)=\varphi (3\times 5)=\varphi \left(3\right)\varphi \left(5\right)=8$. Also, ${\displaystyle \frac{p-1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{74}{35}},{\displaystyle \frac{q-1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{85}{21}},{\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{333}{35}}$ and ${\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{765}{84}}$. Therefore, the $A_{ex}$-spectrum of $\mathcal{P}\left({\mathbb{Z}}_{15}\right)$ consists of the eigenvalue $-1$ with multiplicity 12 and the 3 eigenvalues of the following matrix.

$$\left(\begin{array}{ccc}8& {\displaystyle \frac{74}{35}}& {\displaystyle \frac{85}{21}}\\ {\displaystyle \frac{333}{35}}& 1& 0\\ {\displaystyle \frac{765}{84}}& 0& 3\end{array}\right).$$

It is easy to see that the characteristic polynomial of this matrix is $-x^3+12x^2+{\displaystyle \frac{107693}{4900}}x-{\displaystyle \frac{7321}{100}}$, so the remaining three eigenvalues are approximately $13.2422117204,-3.0530403064$, and $1.8108285859$.

Figure 6. The graph $P_3[K_9,K_2,K_4]$, which is the power graph of ${\mathbb{Z}}_{15}$.

Example 10. 

Consider the finite abelian group ${\mathbb{Z}}_{35}$. Here, $n=35,p=5,q=7$ and $\varphi \left(pq\right)=\varphi \left(35\right)=\varphi (5\times 7)=\varphi \left(5\right)\varphi \left(7\right)=24$. Also, ${\displaystyle \frac{p-1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{485}{119}},{\displaystyle \frac{q-1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{514}{85}},{\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{p+\varphi \left(pq\right)-1}}+{\displaystyle \frac{p+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{12125}{476}}$ and ${\displaystyle \frac{\varphi \left(pq\right)+1}{2}}\left({\displaystyle \frac{n-1}{q+\varphi \left(pq\right)-1}}+{\displaystyle \frac{q+\varphi \left(pq\right)-1}{n-1}}\right)={\displaystyle \frac{1285}{51}}$. Therefore, the $A_{ex}$-spectrum of $\mathcal{P}\left({\mathbb{Z}}_{35}\right)$ consists of the eigenvalue $-1$ with multiplicity 32 and the 3 eigenvalues of the following matrix:

$$\left(\begin{array}{ccc}24& {\displaystyle \frac{485}{119}}& {\displaystyle \frac{514}{85}}\\ {\displaystyle \frac{12125}{476}}& 3& 0\\ {\displaystyle \frac{1285}{51}}& 0& 5\end{array}\right).$$

It is easy to see that the characteristic polynomial of this matrix is $-x^3+32x^2+{\displaystyle \frac{8357159}{169932}}x-{\displaystyle \frac{34902493}{56644}}$, so the remaining three eigenvalues are approximately $32.9252815124,-4.813308841$, and $3.88802732$.

If $n=pqr$, where $p,q,r$ are prime numbers with $p<q<r$, based on the definition of ${\mathcal{D}}_n$, the vertex set and edge set of ${\mathcal{D}}_n$ are $\{p,q,r,pq,pr,qr\}$ and $\left\{\right(p,pq),(p,pr),(q,pq),(q,qr),$$(r,pr),(r,qr)\}$, respectively. Let $\mathcal{H}=K_1\vee {\mathcal{D}}_n,$. Then, $\mathcal{P}\left({\mathbb{Z}}_n\right)=\mathcal{H}[K_{\varphi \left(n\right)+1},K_{\varphi \left(d_1\right)},\dots ,K_{\varphi \left(d_6\right)}]$, where $d_1=p,d_2=q,d_3=r,d_4=pq,d_5=pr$, and $d_6=qr$. Now, proceeding to the case $n=pq$, we can also determine the $A_{ex}$-eigenvalues of $\mathcal{P}\left({\mathbb{Z}}_n\right)$.

5. Conclusions

In this article, we have determined the $A_{ex}$-spectrum of the joined union of regular graphs in terms of their adjacency spectrum and the eigenvalues of an auxiliary matrix. As a consequence, we have determined the $A_{ex}$-eigenvalues of the join of two regular graphs, the lexicographic product of regular graphs, and the $A_{ex}$-eigenvalues of some well-known families of graphs. We have considered the problem of building graphs with different $A_{ex}$-eigenvalues but the same $A_{ex}$-energy. As applications of our results, we have constructed different classes of infinite families of extended adjacency equienergetic graphs. We also compared the energy and the $A_{ex}$-energy of the join of two regular graphs, and we showed that the $A_{ex}$-energy of the join of two regular graphs exceeds their energy. In addition, we discussed the $A_{ex}$-eigenvalues of the power graph of finite abelian groups. We showed that all except the $t+1$ $A_{ex}$-eigenvalues of the power graph of finite abelian groups are completely determined. We considered the cases when $n=p^z,pq$ and $pqr$, where $p,q,r$ are distinct primes, and we discussed the $A_{ex}$-eigenvalues of the power graph of ${\mathbb{Z}}_n$. The results presented in Section 4 concerning the power graph of ${\mathbb{Z}}_n$ have been rigorously verified using Python 3 and the NumPy library, as detailed in Appendix A. The following interesting problem can be considered for future research.

Problem 3. 

Discuss the $A_{ex}$-eigenvalues of the power graph of ${\mathbb{Z}}_n$ when $n=p^{t}q,p^t{q}^s,p^t{q}^s{r}^k$, where $p,q,r$ are distinct primes and $t,s,k$ are positive integers.