Observer-Based Local Stabilization of State-Delayed Quasi-One-Sided Lipschitz Systems with Actuator Saturation
Abstract
1. Introduction
- This is the first study to provide an estimate of the DOA for the OC problem associated with this class of systems. Furthermore, we employ an optimization procedure to maximize the estimated DOA.
- The design is achieved in only one step, which reduces implementation complexity.
- Using a suitable decoupling approach, the matrices are treated as decision variables, where and vary linearly with . This constitutes a significant advantage, since in [23], these matrices are constrained to act only as tuning variables.
2. Preliminaries
2.1. Notations
- ; ⊕ indicates the symmetric elements in the matrix expression; ; ; ; and (resp. ) denote the identity matrix (resp. the zero matrix).
- (resp. ) denotes the ℓ-th row of (resp. the ℓ-th component of ); (resp. ) indicates that is symmetric (resp. diagonal).
- For , (resp. ) signifies that is positive semi-definite (resp. negative definite); (resp. ) is the largest (resp. the smallest) eigenvalue of .
- (resp. ≥, <, ≤) means that (resp. ≥, <, ≤), ; (resp. ≥, <, ≤) means that (resp. ≥, <, ≤), .
- stands for the space of continuous functions from to .
- For , .
2.2. Problem Description
2.3. Essential Definitions and Lemmas
3. Main Results
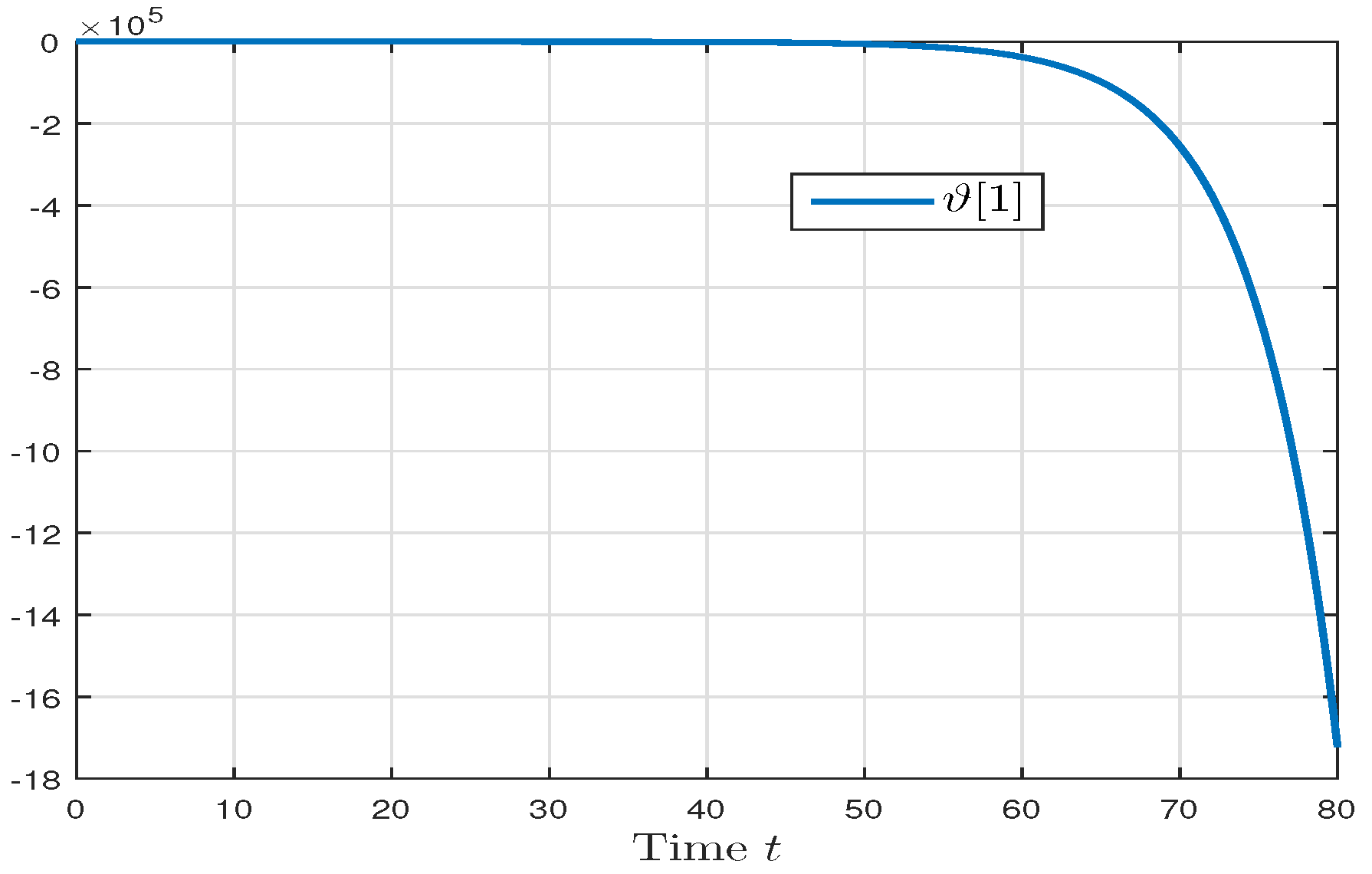
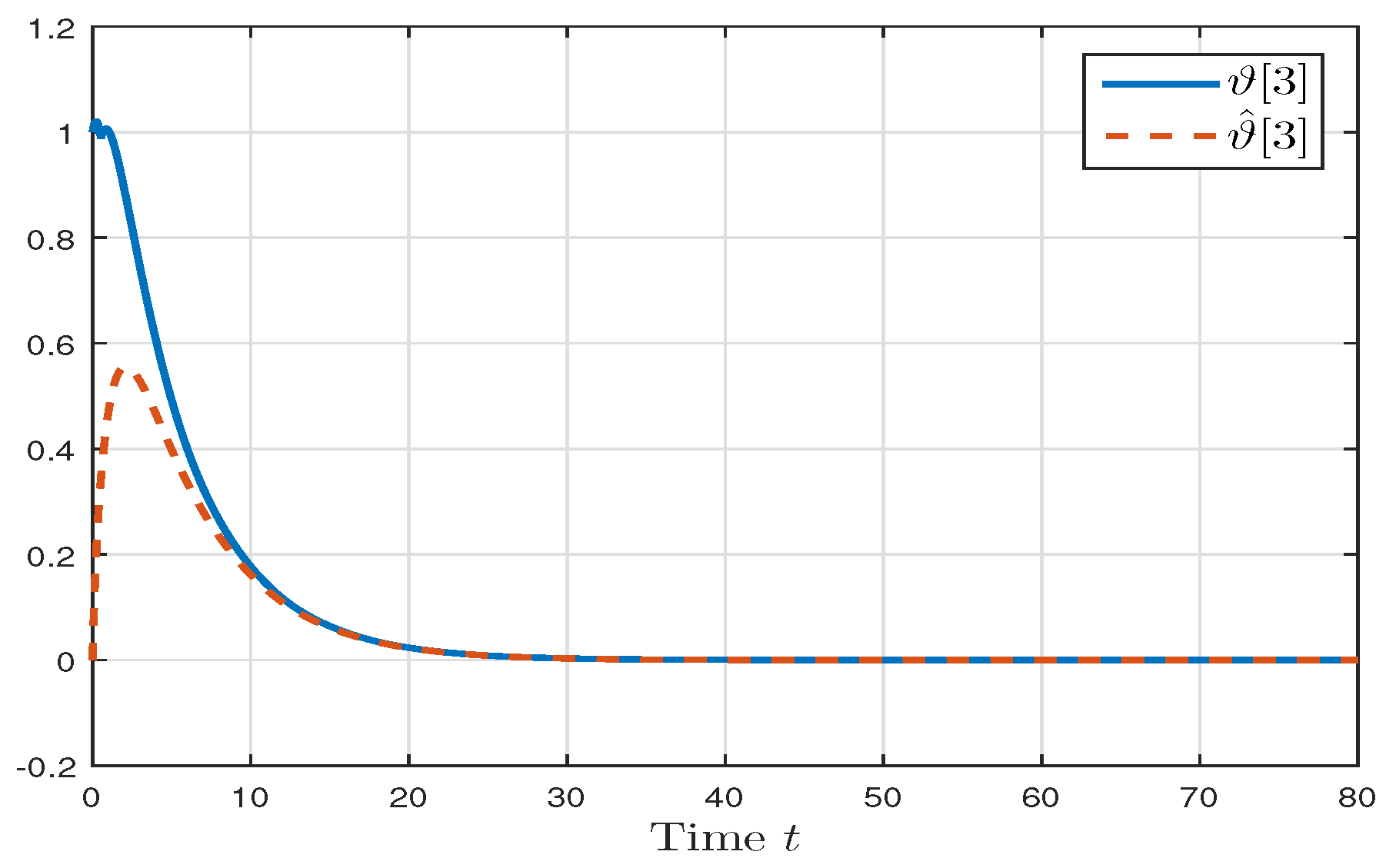
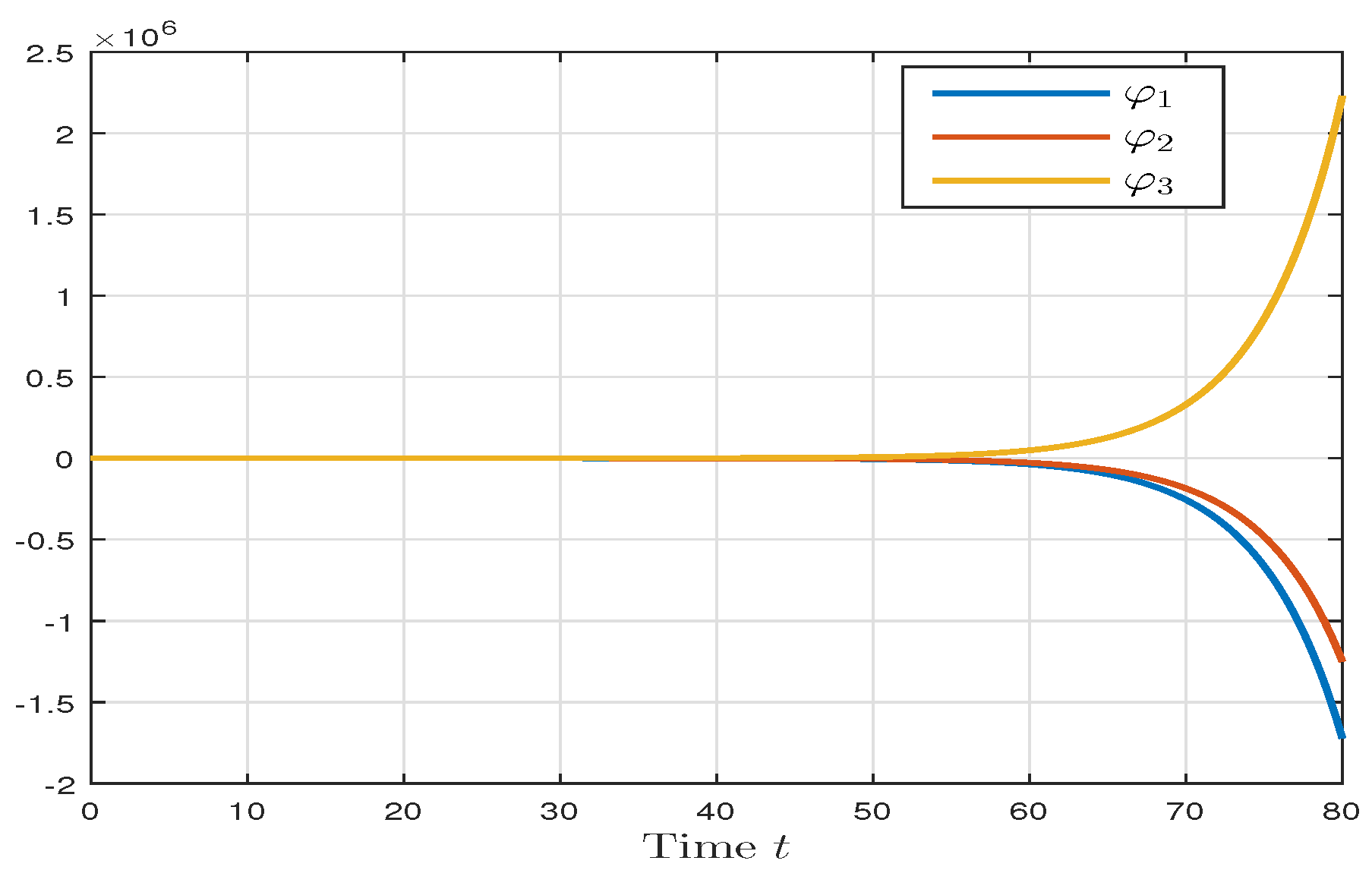
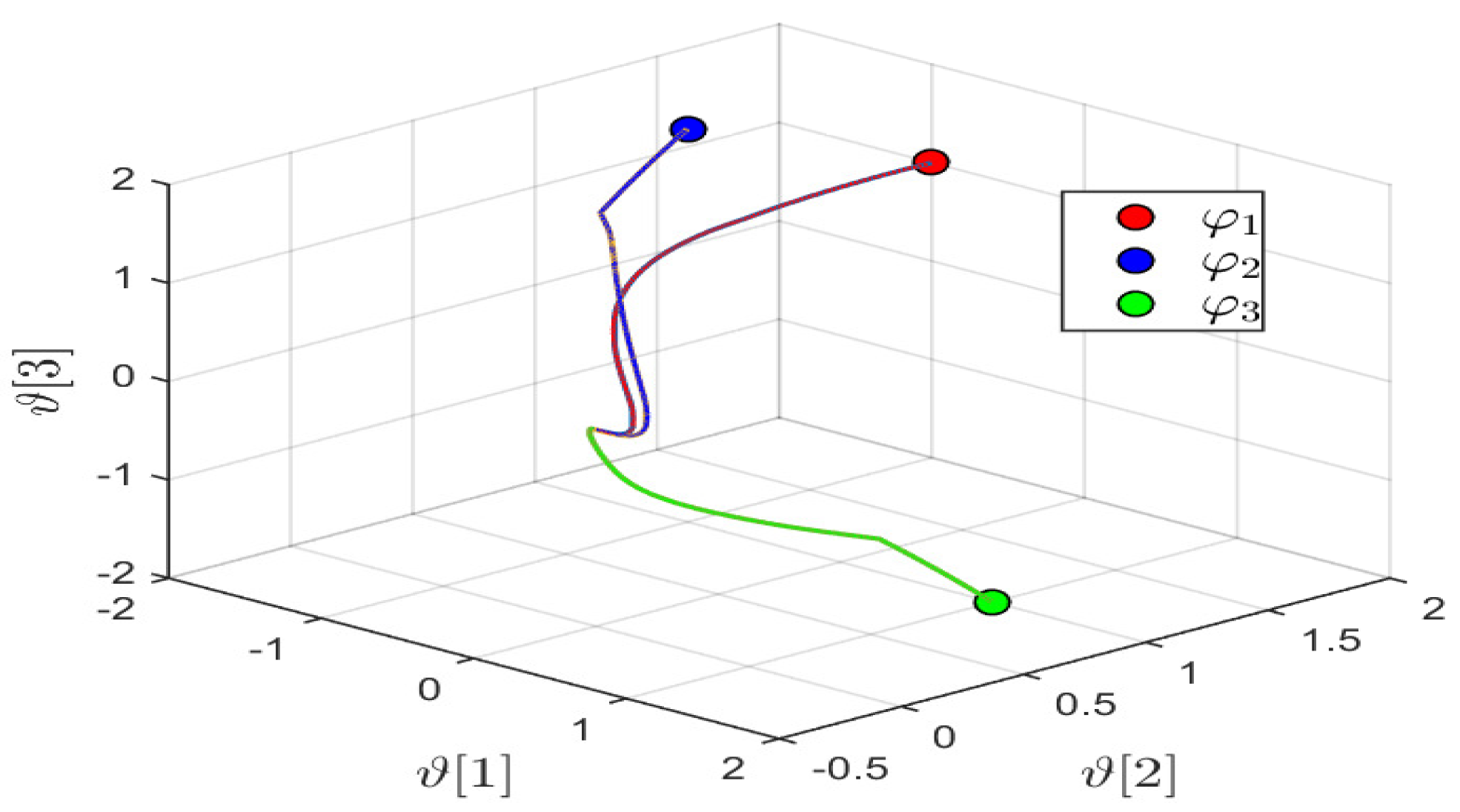
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gu, K.; Kharitonov, V.L.; Chen, J. Stability of Time-Delay Systems; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Hu, T.; Lin, Z. Control Systems with Actuator Saturation: Analysis and Design; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Tarbouriech, S.; Garcia, G.; Gomes da Silva, J.M., Jr.; Queinnec, I. Stability and Stabilization of Linear Systems with Saturating Actuators; Springer: London, UK, 2011. [Google Scholar]
- Dey, R.; Ghosh, S.; Ray, G.; Rakshit, A. Improved delay-dependent stabilization of time-delay systems with actuator saturation. Int. J. Robust Nonlinear Control 2014, 24, 902–917. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Fei, S.; Han, Q.L. Regional stabilization for discrete time-delay systems with actuator saturations via a delay-dependent polytopic approach. IEEE Trans. Autom. Control 2018, 64, 1257–1264. [Google Scholar] [CrossRef]
- Gomes da Silva, J.M., Jr.; Seuret, A.; Fridman, E.; Richard, J.P. Stabilization of neutral systems with saturating control inputs. Int. J. Syst. Sci. 2011, 42, 1093–1103. [Google Scholar] [CrossRef]
- Gassara, H.; Kchaou, M.; El Hajjaji, A.; Chaabane, M. Control of time delay fuzzy descriptor systems with actuator saturation. Circuits Syst. Signal Process. 2014, 33, 3739–3756. [Google Scholar] [CrossRef]
- Gassara, H.; El Hajjaji, A.; Chaabane, M. Control of time delay polynomial fuzzy model subject to actuator saturation. Int. J. Fuzzy Syst. 2016, 18, 763–772. [Google Scholar] [CrossRef]
- Li, T.; Wang, T.; Yu, Y.; Fei, S. Static anti-windup compensator for nonlinear systems with both state and input time-varying delays. J. Franklin Inst. 2020, 357, 863–886. [Google Scholar] [CrossRef]
- Jafari, E.; Binazadeh, T. A novel event-triggered nonlinear control approach for descriptor systems with time-varying delay and input saturation constraints. Eur. J. Control 2025, 86, 101384. [Google Scholar] [CrossRef]
- Rajamani, R. Observer for Lipschitz nonlinear systems. IEEE Trans. Autom. Control 1998, 43, 397–401. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, W.; Liang, S. Nonlinear observer design for one-sided Lipschitz systems with time-varying delay and uncertainties. Int. J. Robust Nonlinear Control 2017, 27, 1974–1998. [Google Scholar] [CrossRef]
- Zhu, F.L.; Han, Z.Z. A note on observer for Lipschitz nonlinear systems. IEEE Trans. Autom. Control 2002, 47, 1751–1754. [Google Scholar]
- Yang, Y.X.; Lin, C.; Chen, B.; Wang, Q.G. Reduced-order observer design for a class of generalized Lipschitz nonlinear systems with time-varying delay. Appl. Math. Comput. 2018, 337, 267–280. [Google Scholar] [CrossRef]
- Hu, G. Observers for one-sided Lipschitz nonlinear systems. IMA J. Math. Control Inf. 2006, 23, 395–401. [Google Scholar] [CrossRef]
- El Haiek, B.; El Aiss, H.; Hmamed, A.; El Hajjaji, A.; Tissir, E.H. New approach to robust observer-based control of one-sided Lipschitz non-linear systems. IET Control Theory Appl. 2019, 13, 333–342. [Google Scholar]
- Rehan, M.; Ahmad, S.; Hong, K.-S. Novel results on observer-based control of one-sided Lipschitz systems under input saturation. Eur. J. Control 2020, 53, 29–42. [Google Scholar] [CrossRef]
- Mirza, M.S.; Ahmad, S.; Masood, H.; Ali, M.U.; Zafar, A.; Kim, S.H. Robust Estimation-Based Control for Generalized One-Sided Lipschitz Nonlinear Systems in the Presence of Output Delays. IEEE Access 2023, 12, 1201–1216. [Google Scholar]
- Hu, G.D. A note on observer for one-sided Lipschitz non-linear systems. IMA J. Math. Control Inf. 2008, 25, 297–303. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, G.-D. Separation principle of quasi-one-sided Lipschitz non-linear systems. IET Control Theory Appl. 2020, 14, 2233–2241. [Google Scholar] [CrossRef]
- Hu, G.-D.; Dong, W.; Cong, Y. Separation principle for quasi-one-sided Lipschitz nonlinear systems with time delay. Int. J. Robust Nonlinear Control 2020, 30, 2430–2442. [Google Scholar] [CrossRef]
- Dong, W.; Zhao, Y.; Cong, Y. Reduced-order observer-based controller design for quasi-one-sided Lipschitz nonlinear systems with time delay. Int. J. Robust Nonlinear Control 2021, 31, 817–831. [Google Scholar] [CrossRef]
- Esmail, A.H.; Ghous, I.; Duan, Z.; Jaffery, M.H.; Li, S. Observer-based control for time-delayed quasi-one-sided Lipschitz nonlinear systems under input saturation. Fuzzy Sets Syst. 2024, 361, 107326. [Google Scholar]
- Tarbouriech, S.; Gomes Da Silva, J.M., Jr.; Garcia, G. Delay-dependent anti-windup strategy for linear systems with saturating inputs and delayed outputs. Int. J. Robust Nonlinear Control 2004, 14, 665–682. [Google Scholar] [CrossRef]
- Tarbouriech, S.; Prieur, C.; Gomes-da-Silva, J.M., Jr. Stability analysis and stabilization of systems presenting nested saturations. IEEE Trans. Autom. Control 2006, 51, 1364–1371. [Google Scholar]
- Chang, X.-H.; Zhang, L.; Park, J.H. Robust static output feedback H∞ control for uncertain fuzzy systems. Fuzzy Sets Syst. 2015, 273, 87–104. [Google Scholar] [CrossRef]
- Sato, M. Gain-scheduled output-feedback controllers depending solely on scheduling parameters via parameter-dependent Lyapunov functions. Automatica 2011, 47, 2786–2790. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aloui, A.; Kahouli, O.; Ayari, M.; Gassara, H.; Amraoui, L.E. Observer-Based Local Stabilization of State-Delayed Quasi-One-Sided Lipschitz Systems with Actuator Saturation. Mathematics 2025, 13, 3610. https://doi.org/10.3390/math13223610
Aloui A, Kahouli O, Ayari M, Gassara H, Amraoui LE. Observer-Based Local Stabilization of State-Delayed Quasi-One-Sided Lipschitz Systems with Actuator Saturation. Mathematics. 2025; 13(22):3610. https://doi.org/10.3390/math13223610
Chicago/Turabian StyleAloui, Ali, Omar Kahouli, Mohamed Ayari, Hamdi Gassara, and Lilia El Amraoui. 2025. "Observer-Based Local Stabilization of State-Delayed Quasi-One-Sided Lipschitz Systems with Actuator Saturation" Mathematics 13, no. 22: 3610. https://doi.org/10.3390/math13223610
APA StyleAloui, A., Kahouli, O., Ayari, M., Gassara, H., & Amraoui, L. E. (2025). Observer-Based Local Stabilization of State-Delayed Quasi-One-Sided Lipschitz Systems with Actuator Saturation. Mathematics, 13(22), 3610. https://doi.org/10.3390/math13223610




