Multiple Correspondence Analysis and Hierarchical Clustering of Occupational Exposure to COVID-19 Among Healthcare Workers in Castilla y León, Spain

Abstract

The COVID-19 pandemic represents a major challenge for healthcare systems, particularly affecting healthcare workers (HCW) due to their higher occupational risk. A retrospective observational study was conducted using data from 239,188 diagnostic tests performed on HCW from the Castilla y León (Spain) Health Service between March 2020 and March 2022. The objective was to explore associations between categorical variables, such as geographic areas, job categories, and infection status, through Multiple Correspondence Analysis and Hierarchical Clustering. The results revealed higher infection rates among HCW in regions near Madrid and in job categories with a greater care-related workload. These findings help identify risk factors and support the development of more effective occupational hazard prevention and health interventions to reduce infection risk and improve preventive measures.

1. Introduction

As is well known, on 11 March 2020, the World Health Organization (WHO) declared the emergency situation caused by the epidemic outbreak of COVID-19 [1]. This was an unprecedented health crisis of extraordinary magnitude and severity, with significant pressure placed on health services worldwide [2].

Although substantial efforts have been made to enhance occupational health and safety, workplace accidents remain a major cause of serious injuries and fatalities each year. This highlights the urgent need to further strengthen security measures to minimize both the occurrence and severity of such incidents. Risk assessment-based approaches have been widely used to detect potential hazards and predict injury severity, typically based on data from previous similar incidents. However, these severity metrics are often difficult to calculate when multiple variables such as key factors related to employees and the work environment that can substantially affect the severity of workplace accidents must be evaluated [3].

The Castilla y León Health Service (SACYL) is the public service that manages public healthcare services in that Spanish region. SACYL is part of the Spanish National Health System, established in 1986 and inherited from the National Health Institute.

In the field of occupational risk prevention and health, few studies during the COVID-19 pandemic have used Multiple Correspondence Analysis (MCA) as a methodological tool. One example is the study developed by Sakpere et al. [4], which applied MCA to analyze how factors such as boredom, remuneration, internet availability, and fear of COVID-19 affected the productivity of 466 workers in Nigeria. The results showed that internet access and satisfactory remuneration were positively associated with higher productivity, whereas boredom and exposure to negative news about the pandemic correlated with reduced productivity. Another relevant contribution explores the occupational safety and health of nurses during the COVID-19 pandemic through a qualitative approach, highlighting that this area has been a neglected part of quality care. Through semi-structured interviews with 14 nurses in hospitals in Iran, challenges such as the lack of adequate personal protective equipment, work overload, and significant emotional impact were identified. The results emphasize the importance of improving working conditions to ensure safe and quality care in health crisis contexts [5].

Another study analyzed the economic impact and spending patterns of Malaysian citizens during the COVID-19 pandemic collecting data from the first round of the ‘Effect of COVID-19 on Economy and Individuals’ survey, conducted by the Department of Statistics, in which MCA was applied to assess the differences before and during the pandemic [6].

In recent years, different dimensionality reduction techniques have been applied across different fields to simplify the analysis of high-dimensional data. Among these methods, the most used include the following:

• Principal Component Analysis (PCA): This technique is widely known for reducing dimensionality by transforming the original variables into a smaller set of uncorrelated variables, known as principal components [7].
• Biplot Methods: These are particularly useful for visualizing relationships between rows and columns of a data matrix. These techniques display data in a low-dimensional space, with the added benefit of showing direct relationships between variables [8,9].
• Classic Biplots: The GH-Biplot optimizes the representation of matrix columns in a scatter plot, while the JK Biplot offers optimal representation for rows [9,10].
• HJ-Biplot: This technique is known for its balanced representation of rows and columns in a low-dimensional space, making it particularly useful for high-dimensional data [11].
• Correspondence Analysis (CA): Although CA initially arose as a technique for contingency analysis, it can be applied in this field. Similarly to Biplot methods, it allows the rows and columns of any positive matrix to be represented in the same low-dimensional subspace [12,13].
• Multiple Correspondence Analysis: MCA is a powerful descriptive technique that, unlike Benzécri’s Correspondence Analysis, focuses on the relationships between several categorical variables and, more specifically, between their categories. This method is particularly suited for analyzing rectangular tables that contain individuals in rows (diagnostic tests in this study) and possible categories of the variables in columns [12,13,14].
• Optimal Scaling: This is a technique that transforms categorical variables into numerical values optimized to maximize an objective function (such as inertia) in multivariate analyses. In the context of MCA, this transformation is essential for representing relationships between categories in a low-dimensional Euclidean space [15,16,17].
• Ward’s method: To obtain the clusters, agglomerative hierarchical clustering was applied using Ward’s method on the factorial coordinates derived from the MCA. This method aims to minimize the increase in within-group variance at each merging step, ensuring maximum homogeneity within the groups [18,19].

García et al. applied MCA to identify groups of workers with similar psychosocial profiles in the greenhouse construction industry in Spain, thereby facilitating the design of more targeted and effective occupational health interventions. This approach demonstrates how MCA can optimize risk prevention by adapting to the real characteristics of workers and their working conditions [20].

In the context of the COVID-19 pandemic, MCA has proven to be a valuable tool for understanding the relationships between different variables, such as geographic location, HCW categories, and the results of diagnostic tests for SARS-CoV-2 [21,22]. By analyzing these variables over time, this study aims to provide insights into how the pandemic affected workers in the specialized care services of the SACYL, and to identify patterns that may be crucial for future occupational health strategies.

The central focus of this study is the identification of multivariate patterns of COVID-19 infection risk among HCW within the SACYL, simultaneously considering territorial and occupational variables. This approach has been scarcely explored using combined techniques such as MCA together with hierarchical cluster analysis (Ward + K-means), enabling the identification of complex occupational risk profiles in a large-scale categorical dataset—an approach not previously applied in regional healthcare settings. The novelty of this work lies in the integrated use of these methodologies applied to a large set of categorical data, which enables the detection of complex and specific risk profiles that would not be evident through univariate analyses or traditional spatial approaches. Furthermore, this approach allows for the simultaneous exploration of relationships among categorical territorial, professional, and infection-related variables, facilitating the detection of homogeneous groups with specific risk characteristics.

The use of this methodology on an extensive and categorical dataset represents a novel contribution that supports the development of more targeted and effective occupational health strategies in pandemic contexts.

The COVID-19 pandemic has had a significant impact on the health of HCW, with high and heterogeneous occupational exposure depending on geographic region and professional category. However, most available studies analyze these variables in isolation or using univariate approaches, which limits the understanding of complex risk patterns.

This paper is organized as follows: Section 2 presents the materials and methods used in this research, including a brief description of the statistical techniques; Section 3 details the main results achieved; Section 4 provides a discussion; and finally, the conclusions are stated in Section 5.

2. Materials and Methods

2.1. Multiple Correspondence Analysis

Within data analysis, multivariate methods allow researchers to analyze systematic patterns of variation in categorical data. MCA is a descriptive technique that, unlike PCA, studies the relationships among several categorical variables, and more precisely, among their categories [23]. Its domain of application, therefore, is rectangular tables that contain individuals in rows and the possible categories of the variables in columns [14,15,24]. Another aspect addressed by MCA is its ability to reduce the dimensionality of the data table—similar to PCA—but applied to categorical variables, where the table decomposition is performed through its factors [25].

Therefore, Multiple Correspondence Analysis is a multivariate statistical technique designed to analyze and visualize relationships among several categorical variables. It extends the principles of Correspondence Analysis to reduce and visualize data tables [26,27].

The MCA examines the relationships among any number of variables, each with multiple categories. These relationships are generally represented in a two-dimensional plot. This approach is designed to analyze complete disjunctive tables, which are contingency tables of qualitative variables. It must be considered that the categories of each variable are mutually exclusive, and each individual (in this case, a test) belongs to one and only one category.

Given a dataset with $n$ individuals and $Q$ categorical variables, where the $q$-th variable has $K_q$ categories, the total number of categories is

$$J=\sum _{q=1}^Q{K}_q.$$

(1)

Using Equation (1), the resulting matrix of individuals, variables, and categories is obtained, and serves as the basis for applying dimensionality reduction techniques in order to visualize the categories in a two-dimensional plane.

The data can be represented by a disjunctive matrix $Z$ of size $n\times J$, where each row corresponds to an individual and each column to a category, with entries $z_{ij}=1$ if individual $i$ possesses category $j$, and 0 otherwise, i.e., matrix $Z$ encodes the relationship between individuals and categories [26].

MCA can be performed either on a matrix containing the data encoded in binary form, the binary matrix, or on a matrix consisting of all possible cross-tabulations between the variables, the Burt matrix.

The Burt matrix, $B$, summarizes all pairwise category co-occurrences across individuals. It is then defined as: $B=Z^{t}Z$ where $B$ is a $J\times J$ symmetric matrix and $Z^t$ is the transposed matrix of $Z$. Each block $B_{qr}$ of size $K_q\times K_r$ within $B$ represents the contingency table of cross-tabulations between categories of variables $q$ and $r$. The diagonal blocks $B_{qq}$ are diagonal matrices containing the marginal frequencies of each category of variable $q$ [27,28].

Let $D$ be the diagonal matrix of column sums of $B$, and $N=B/n$ the matrix of relative frequencies. To perform an MCA, the Burt matrix must be normalized because categories may have very different marginal frequencies. Normalization ensures that each category contributes proportionally to the analysis, preventing high-frequency categories from dominating the results. The normalized Burt matrix for MCA is: $S=D^{-{\displaystyle \frac{1}{2}}}(N-r{c}^t)D^{-{\displaystyle \frac{1}{2}}}$, where $r$ and $c$ are the vectors of row and column marginal proportions, respectively. The eigen-decomposition of $S$ yields the principal axes and coordinates for graphical representation in the MCA space [29].

The total inertia of the system, which represents the global association among variables, is expressed as:

$$Inertia=\sum _{d=1}^D{\lambda }_d,$$

where ${\lambda }_d$ are the eigenvalues obtained from the decomposition of $S$, and $D$ is the number of retained dimensions. Each eigenvalue quantifies the proportion of total association captured by a corresponding principal axis [24,25,30].

This approach allows us to reduce the dimensionality of a high-cardinality categorical dataset while preserving the underlying structure of associations among categories. The resulting low-dimensional representation facilitates the detection of latent structures and proximity relationships between categories and individuals, enabling a robust multivariate exploration of complex categorical data.

2.2. Optimal Scaling and Dimensionality Reduction

The statistical technique of Optimal Scaling (OS) is a general strategy for nonlinear multivariate analysis. This approach is exemplified by methods such as MCA, which is applied specifically to categorical data. Thus, the objective of OS/MCA is to assign numerical values to categorical variables in such a way that the resulting dimensional representation maximizes the homogeneity among the variables, thereby explaining the greatest possible amount of variance (or inertia) in the dataset [30].

OS is formalized as an optimization problem solved via matrix decomposition. The process involves quantifying the categorical data and then searching for factorial axes that concentrate the maximum variance (inertia) in the fewest dimensions.

Each categorical variable $X_q$ is assigned a set of numerical quantifications $y_q=\{y_{q1},y_{q2},\dots ,y_{q{K}_q}\}$, corresponding to its $K_q$ categories. The transformed data matrix, $Y$, then consists of these quantified scores for all individuals.

The optimization problem is stated as follows:

$$\underset{\left\{y_{\mathit{qk}}\right\}}{\max }H=\sum _{q=1}^Q\sum _{r=1}^Q\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}{(y_q,y_r)}^2,$$

subject to the constraints imposed by the measurement level of each variable (nominal, ordinal, or interval) [15]. For nominal variables, no order constraint is applied, while for ordinal variables, transformations must be monotonic to preserve rank order [29,30].

The objective function, $H$, represents homogeneity, i.e., the degree of linear association among optimally transformed variables. Maximizing $H$ is equivalent to maximizing the total inertia of the transformed data, which measures the overall variance of the quantified variables relative to their centroid. The total inertia is given by:

$$I_T=\sum _{i=1}^n\sum _{q=1}^Q{w}_q(y_{iq}-{\bar{y}}_q{)}^2,$$

where $w_q$, $y_{iq}$, and ${\bar{y}}_q$ are the weight, the quantified score of individual $i$, and the weighted mean for variable $q$, respectively.

By maximizing $I_T$, the optimal quantifications $y_{qk}$ are those that maximize the projected inertia across the principal components obtained from $Y$. Thus, the category quantifications derived from optimal scaling correspond to those that explain the maximum amount of shared variance among variables under their respective scale-type constraints [16].

Conceptually, this transformation problem can be viewed as a constrained least-squares optimization, where nonlinear transformations are applied to categorical data to generalize the principles of PCA to nonmetric scales.

The optimization problem is typically solved using the Alternating Least Squares (ALS) algorithm, which alternates between updating the numerical quantifications for each category and the corresponding object (individual) scores until convergence is reached.

At each iteration, the algorithm minimizes the loss function:

$$L=\sum _{i=1}^n\sum _{q=1}^Q{w}_q(z_{iq}-{\widehat{z}}_{iq}{)}^2,$$

where $z_{iq}$ represents the observed categorical indicator, and ${\widehat{z}}_{iq}$ its reconstruction, based on the current quantifications. This approach ensures convergence toward the configuration that minimizes residual variance and maximizes the overall homogeneity among variables [29].

The ALS framework allows for the imposition of restrictions according to scale type, making it particularly well-suited for mixed data structures [12].

After optimal quantifications are obtained, PCA can be applied to the transformed dataset $Y$ to extract latent dimensions representing the dominant patterns of association. The eigen-decomposition problem can be expressed as:

$$Y^{T}Y{u}_d={\lambda }_d{u}_d,$$

(2)

with ${\lambda }_d$ as the eigenvalues representing the contribution of each principal component, and $u_d$ being the corresponding eigenvectors defining the principal axes.

The decomposition of optimally scaled data $Y$ using PCA (or SVD) is equivalent to performing an eigen-decomposition of the normalized Burt matrix used in MCA [24].

2.3. Clustering Models

After obtaining the transformed data matrix $Y$, where each categorical variable $X_q$ has been quantified into the optimal category scores $y_q$, the individuals are represented by coordinates ${\mathrm{y}}_i=(y_{i1},y_{i2},\dots ,y_{iQ})$ in a $Q$-dimensional Euclidean space. These coordinates, derived from the eigen-decomposition summarize the major associations among the categorical variables and can be used to identify homogeneous groups through clustering models.

Agglomerative Hierarchical Clustering (AHC) is a multivariate analysis technique used to identify and represent the similarity structure among objects or cases based on a set of variables [31]. This method belongs to the family of cluster analysis approaches, which aim to group elements based on internal similarity and external dissimilarity—that is, elements within the same group should be as similar as possible to each other, and as different as possible from those in other groups [30].

In the AHC approach, each individual initially forms its own cluster, and clusters are then successively merged according to a similarity (or dissimilarity) measure.

Let $d(i,i\prime )$ denote the Euclidean distance between individuals $i$ and $i\prime$ in the quantified space:

$$d(i,i\prime )=\parallel {\mathrm{y}}_i-{\mathrm{y}}_{i\prime }\parallel =\sqrt{\sum _{q=1}^Q(y_{iq}-y_{i\prime q}{)}^2}.$$

At iteration $t$, the partition of the data is represented as ${\mathcal{C}}^{\left(t\right)}=\{C_1^{\left(t\right)},C_2^{\left(t\right)},\dots ,C_{m_t}^{\left(t\right)}\}$, where $m_t$ is the number of clusters at step $t$ ($m_0=n$ and $m_T=1$). The algorithm merges, at each step, the two clusters that are most similar according to a defined linkage criterion [18].

Among linkage criteria, Ward’s method is used for data obtained from optimal scaling or MCA because it relies directly on inertia minimization, consistent with the same geometric concept used to derive $\mathrm{Y}$. Ward’s criterion minimizes the total within-cluster variance (inertia).

For any cluster $C_k$, its within-cluster inertia is defined as:

$$W(C_k)=\sum _{i\in C_k}\parallel {\mathrm{y}}_i-{\bar{\mathrm{y}}}_{C_k}{\parallel }^2,$$

where ${\bar{\mathrm{y}}}_{C_k}={\displaystyle \frac{1}{n_{C_k}}}{\sum }_{i\in C_k}{\mathrm{y}}_i$ is the centroid of cluster $C_k$, and $n_{C_k}$ is its size.

The total within-cluster inertia for a partition $\mathcal{C}$ containing $m$ clusters is:

$$W_T=\sum _{k=1}^{m}W\left(C_k\right).$$

At each step, Ward’s algorithm merges the pair of clusters $(C_a,C_b)$ whose union produces the smallest possible increase in total within-cluster inertia:

$$\Delta (C_a,C_b)={\displaystyle \frac{n_{C_a}{n}_{C_b}}{n_{C_a}+n_{C_b}}}\parallel {\bar{\mathrm{y}}}_{C_a}-{\bar{\mathrm{y}}}_{C_b}{\parallel }^2.$$

This expression quantifies the increase in total inertia that results from merging clusters $C_a$ and $C_b$. Then, the pair with the minimum $\Delta (C_a,C_b)$ is chosen for fusion, ensuring that at every step the resulting partition is as homogeneous as possible [32].

In summary, AHC using Ward’s method is a robust and widely accepted technique for exploring the underlying structure of data and classifying observations based on multivariate similarity [31].

2.4. Dataset

The SACYL is divided into 11 health areas (see Figure 1) that correspond to Ávila (AV), Bierzo (BI), Burgos (BU), East Valladolid (VE) and West Valladolid (VO), León (L), Palencia (P), Salamanca (SA), Segovia (SE), Soria (SO), and Zamora (Z).

For this study, data were collected from 239,188 diagnostic tests performed on healthcare workers across the 11 health areas of the SACYL, of which 35,286 corresponded to positive cases among specialized care workers. Serological tests were conducted on SACYL workers across the 11 health areas affected by COVID-19 between March 2020 and March 2022.

Upon completion of data collection, the data were processed and prepared for subsequent multivariate analysis. The data-cleaning phase included the removal of duplicate records, verification of inconsistencies in key fields, handling of missing data through exclusion or imputation depending on the relevance of the variable, and standardization of professional categories and healthcare units.

Duplicate records were removed using the SPSS duplicate detection function, which was used to identify and eliminate duplicated entries based on combinations of key variables (test ID, healthcare area (Area), professional category (Labor), test Result, and Date). This ensured that each test represented a unique case. The procedure was applied first to the 35,286 valid records of positive test results and then to the full dataset of 239,188 records (both positive and negative) without missing values. The analysis confirmed the absence of duplicates after cleaning, ensuring that each record corresponded to a unique test.

Additionally, it was verified that the main active variables (Area, Labor, Date, and Result) had no missing values (valid $n$ = 35,286; missing $n$ = 0), (valid $n$ = 239,188; missing $n$ = 0), which allowed the integrity of the full sample to be maintained in subsequent analysis.

After deleting duplicate records, categorical variable values were reviewed to detect coding errors, out-of-range values, or inconsistencies between related fields (e.g., area codes not matching the assigned professional category). These inconsistencies were corrected through recoding and validation against data provided by SACYL.

As no missing values were found in the active variables used for MCA, imputation techniques were not required.

Finally, during the data pre-processing phase, categorical variables were reviewed to ensure uniform coding. Equivalent categories were grouped under a single label (e.g., different labels referring to Medium and Senior Technician), and systematic recoding was applied to ensure consistency throughout the dataset.

The main variables considered were the following:

• Area: Healthcare area (11 categories: AV, L, BI, BU, VO, VE, SA, SE, Z, P, SO).
• Labor: Professional category (10 categories: ADM, ORD, NUR, MAN, SG, MP, SO, NCT, ST, MST).
• Date: Test period grouped by months (24 periods from March 2020 to March 2022, according to the codification used).
• Result: Test Result (P = positive, N = negative). This last variable was treated as supplementary in the MCA.

Consequently, the occupational health categories that were considered from the SACYL for this study are detailed in

Table 1. SACYL job codes.

Job Code	Description
ADM	Administrative
ORD	Orderly
NUR	Nursing
MAN	Management
SG	Specialized Graduate
MP	Maintenance Personnel
SO	Service Operator
NCT	Nursing Care Technician
ST	Specialist Technician
MST	Medium and Senior Technician

.

After an initial data-cleaning process, the dataset was categorized, and variables were labeled accordingly. An MCA was performed using SPSS v.28.0.1.1, applying dimension reduction analysis through optimal scaling. This approach assigns numerical values to categorical variables, ensuring proper classification after a discretization process. Thus, both positive and negative screening results are analyzed simultaneously.

In the MCA, the active variables used were the main professional categories, geographic areas, and the date of test administration. The test result (positive/negative) is a supplementary variable.

Optimal scaling in SPSS was used to assign numerical values to categorical variables, facilitating dimensionality reduction. The number of retained dimensions was based on inertia and the interpretability of the axes.

The main objective of optimal scaling is to find a numerical scale for the categories of each variable that maximizes an objective function, commonly multiple correlation or explained inertia in multivariate analysis [30].

This process enables the application of PCA, factor analysis, or MCA to originally categorical data [18].

During this research, the criteria for dimension selection were based on the following:

• Eigenvalues greater than 1.
• Minimum cumulative inertia of 60%.
• Average Cronbach’s alpha ≥ 0.30 (indicating low but acceptable internal consistency when the analysis is exploratory and involves categorical variables, as in Multiple Correspondence Analysis).

For the analysis including all tests (n = 239,188), the first two dimensions had eigenvalues of 1.325 and 1.269, explaining 33.13% and 31.72% of the variance, respectively, with a cumulative variance of 64.86%. For the analysis restricted to positive tests (n = 35,286), Dimension 1 explained 43.21% and Dimension 2 explained 41.03%, resulting in a cumulative variance of 84.24%. Based on these results, the first two dimensions were retained in both analyses.

As shown in

Table 2. Case Processing Summary.

Valid active cases	239,188
Active cases with missing values	0
Supplementary cases	0
Total	239,188
Cases used in the analysis	239,188

, the analysis indicates that there are 239,188 valid active cases, with no missing cases observed.

3. Results

The first step in the analysis was the descriptive analysis, which was performed for each variable considering the 239,188 test results.

Based on the descriptive statistics (

Table 3. Descriptive statistics using all the tests performed.

	n	Min	Max	Mean	SD
Area	239,188	1	11	5.44	2.824
Labor	239,188	1	10	4.87	2.462
Data	239,188	1	25	10.28	7.379
Result	239,188	1	2	1.85	0.355
Valid n (by list)	239,188

and

Table 4. Descriptive statistics using the tests with positive results.

	n	Min	Max	Mean	SD
Area	35,286	1	11	5.51	2.787
Labor	35,286	1	10	4.84	2.427
Data	35,286	1	25	12.37	8.204
Valid n (by list)	35,286

), the included variables exhibit a categorical structure with adequate dispersion among their modalities, which justifies the application of MCA as a technique for dimensionality reduction and exploration of associations between categories. The range of the variable Area (1–11) and the diversity of Labor (1–10) allow us to capture occupational variations within HCW, while Date (1–25) introduces a temporal dimension that provides context for exposure. In turn, Result (1–2) acts as an indicator variable for outcome (e.g., exposure or COVID-19 infection), facilitating the joint interpretation of association patterns between functions, areas, and outcomes. The high heterogeneity and considerable sample size (n = 239,188) strengthen the relevance of MCA, providing a solid basis for identifying latent relationships among categories and visually representing occupational profiles most associated with different levels of exposure.

When comparing the descriptive statistics for all tests performed (Table 3) with those for positive tests (Table 4), relevant differences are observed mainly in the temporal dimension. While the variables Area and Labor maintain very similar means and standard deviations, indicating a relatively homogeneous distribution of positive cases across different areas and professional categories, the variable Date shows an increase in its mean (from 10.28 to 12.37), suggesting a greater concentration of positive results in later periods of the record. This pattern may reflect the temporal evolution of the pandemic or changes in occupational exposure over time. Overall, the results indicate that the occupational structure remained stable, although incidence increased in later phases of the study.

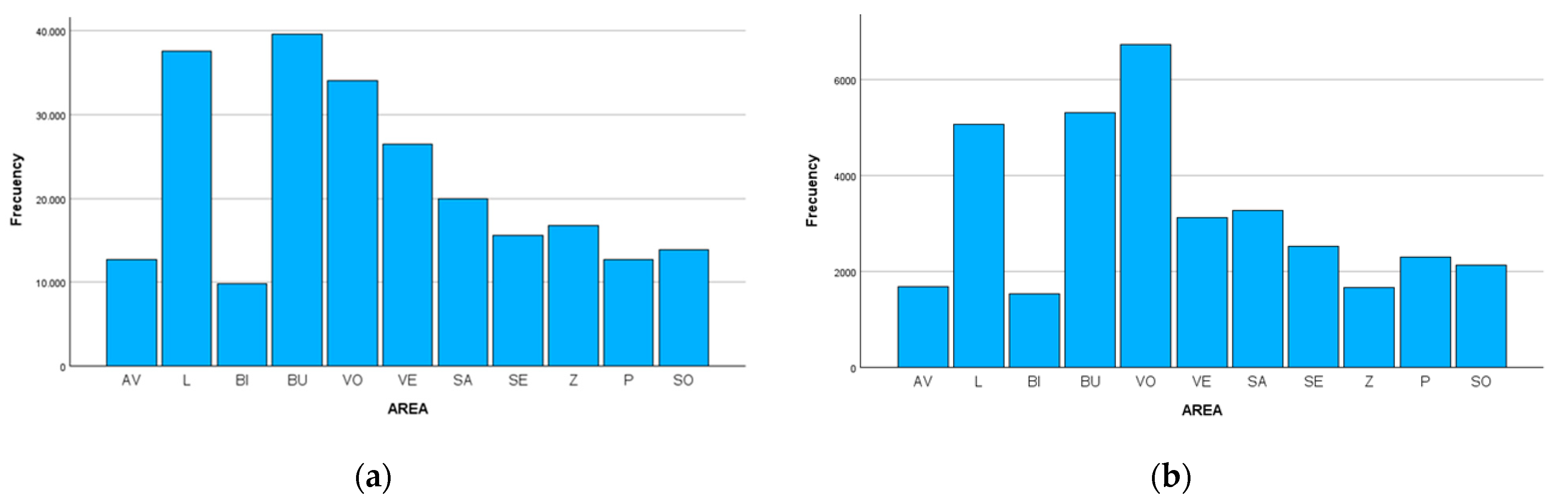
Figure 2a illustrates that Burgos was the Health Area where the highest number of diagnostic tests were conducted (including both positive and negative cases). In contrast, Figure 2b shows that Valladolid Oeste is the area with the highest number of positive diagnostic tests.

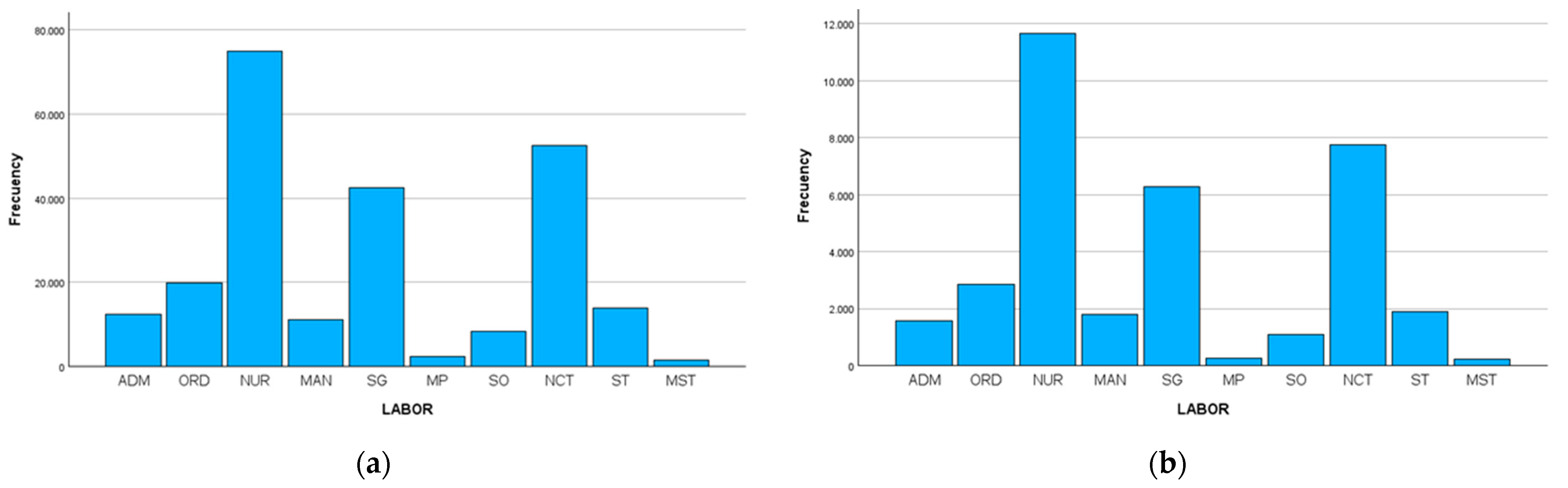
Figure 3 shows that the professional categories with the highest number of tests correspond to those involved in direct patient care, namely Specialist Physicians, Nurses, Nursing Care Technicians, and Orderlies.

By comparing Figure 4 with Figure 5, it can be observed that although May 2020 was the period when the highest number of tests were performed, January 2022 was the period with the greatest number of positive results.

Absolute and relative frequencies for the main variables (Area, Labor, Date, and Result) of the diagnostic tests performed, including both positive and negative outcomes, are included in

Table 5. Frequencies of the Area variable.

Area	Frequency	Percentage	Valid Percentage	Cumulative Percentage
AV	12,709	5.3	5.3	5.3
L	37,531	15.7	15.7	21.0
BI	9860	4.1	4.1	25.1
BU	39,661	16.6	16.6	41.7
VO	34,012	14.2	14.2	55.9
VE	26,496	11.1	11.1	67.0
SA	19,976	8.4	8.4	75.4
SE	15,577	6.5	6.5	81.9
Z	16,765	7.0	7.0	88.9
P	12,686	5.3	5.3	94.2
SO	13,915	5.8	5.8	100.0
Total	239,188	100.0	100.0

,

Table 6. Frequencies of the Labor variable.

Labor	Frequency	Percentage	Valid Percentage	Cumulative Percentage
ADM	12,284	5.1	5.1	5.1
ORD	19,912	8.3	8.3	13.5
NUR	74,938	31.3	31.3	44.8
MAN	11,079	4.6	4.6	49.4
SG	42,430	17.7	17.7	67.2
MP	2255	0.9	0.9	68.1
SO	8434	3.5	3.5	71.6
NCT	52,542	22.0	22.0	93.6
ST	13,868	5.8	5.8	99.4
MST	1446	0.6	0.6	100.0
Total	239,188	100.0	100.0

,

Table 7. Frequencies of the Date variable.

Date	Frequency	Percentage	Valid Percentage	Cumulative Percentage
mar-20	2923	1.2	1.2	1.2
apr-0	21,325	8.9	8.9	10.1
may-20	40,477	16.9	16.9	27.1
jun-20	17,902	7.5	7.5	34.5
jul-20	2258	0.9	0.9	35.5
aug-20	4814	2.0	2.0	37.5
sep-20	15,027	6.3	6.3	43.8
oct-20	14,757	6.2	6.2	50.0
nov-20	13,397	5.6	5.6	55.6
dec-20	9179	3.8	3.8	59.4
jun-21	15,932	6.7	6.7	66.1
feb-21	9110	3.8	3.8	69.9
mar-21	3409	1.4	1.4	71.3
apr-21	2827	1.2	1.2	72.5
may-21	2843	1.2	1.2	73.7
jun-21	2785	1.2	1.2	74.8
jul-21	8177	3.4	3.4	78.2
aug-21	4526	1.9	1.9	80.1
sep-21	2739	1.1	1.1	81.3
oct-21	2375	1.0	1.0	82.3
nov-21	3980	1.7	1.7	83.9
dec-21	13,843	5.8	5.8	89.7
jun-22	14,750	6.2	6.2	95.9
feb-22	5468	2.3	2.3	98.2
mar-22	4365	1.8	1.8	100.0
Total	239,188	100.0	100.0

and

Table 8. Frequencies of the Result variable.

Result	Frequency	Percentage	Valid Percentage	Cumulative Percentage
P	35,286	14.8	14.8	14.8
N	203,902	85.2	85.2	100.0
Total	239,188	100.0	100.0

.

The second step of the analysis corresponds to the representation of the results using MCA, specifically applying the optimal scaling method, whereby the total inertia and the proportion of variance explained by the first two principal dimensions obtained from the MCA indicate that these dimensions jointly capture 84% of the total inertia associated with the configuration of positive test results. This high cumulative inertia value confirms that the bidimensional solution provides an adequate and statistically robust representation of the underlying association structure.

• All tests (n = 239,188):

  ○

  Dimension 1: eigenvalue = 1.325 (33.13%);

  ○

  Dimension 2: eigenvalue = 1.269 (31.72%);

  ○

  Cumulative variance = 64.86%;

  ○

  Total eigenvalue (sum of active eigenvalues) = 2.594;

  ○

  Total inertia = 0.649 (see

  Table 9. Variance Accounted (all tests).

  Dimension	Cronbach’s Alpha	Variance Accounted for
  		Total (Eigenvalue)	Inertia	% of Variance
  1	0.327	1.325	0.331	33.133
  2	0.283	1.269	0.317	31.723
  Total		2.594	0.649
  Mean	0.305 1	1.297	0.324	32.428

  ¹ The mean Cronbach’s alpha is based on the mean eigenvalue.

  ).

• Positive tests (n = 35,286):

  ○

  Dimension 1: eigenvalue = 1.296 (43.21%);

  ○

  Dimension 2: eigenvalue = 1.231 (41.03%);

  ○

  Cumulative variance = 84.24%;

  ○

  Total eigenvalue = 2.527;

  ○

  Total inertia = 0.842 (see

  Table 10. Variance Accounted (positive tests).

  Dimension	Cronbach’s Alpha	Variance Accounted for
  		Total (Eigenvalue)	Inertia	% of Variance
  1	0.343	1.296	0.432	43.206
  2	0.281	1.231	0.410	41.029
  Total		2.527	0.842
  Mean	0.313 1	1.264	0.421	42.118

  ¹ The mean Cronbach’s alpha is based on the mean eigenvalue.

  ).

These indicators are presented alongside the factorial map and are discussed in terms of their suitability and interpretability, as shown in Table 9 and Table 10.

To identify homogeneous groups, a two-step procedure was followed: hierarchical analysis using Ward’s method on the object coordinates (scores) generated by the MCA, followed by K-means to refine the initial centroids obtained with Ward. Then, intra- and inter-group distances were evaluated, and a dendrogram was used to select the number of clusters. By doing this, five clusters were chosen based on interpretability and stability criteria.

The next step was to interpret these clusters in relation to the underlying MCA dimensions, with Dimension 1 representing the temporal evolution of the pandemic, from the initial outbreaks (March–April 2020) to the subsequent waves (2021–2022). However, Dimension 2 reflects territorial and professional differentiation, where positive values group areas with higher incidence (Valladolid Oeste, Burgos, León) and high-exposure categories (nursing, Specialized Graduate), while negative values group areas with lower impact or periods of low incidence.

When comparing Figure 6 and Figure 7, based on the coordinates resulting from the optimal scaling method (all tests), the areas of Burgos and León exhibit a similar pattern, as do Ávila, Valladolid Este, and Zamora. In contrast, Salamanca, Bierzo, Segovia, Soria, Valladolid Oeste, and Palencia show distinct trends. Moreover, in Figure 7, which displays the coordinates resulting from the positive tests, it can be observed that Salamanca and Valladolid Este share the same pattern, while León, Valladolid Oeste, and Burgos form a common cluster, and Ávila presents an isolated pattern.

Based on the distribution of positive results, Figure 7 identifies the following four distinct groups:

• Group 1: Salamanca, Valladolid Este, Palencia, and Bierzo.
• Group 2: León, Valladolid Oeste, and Burgos.
• Group 3: Segovia, Zamora, and Soria.
• Group 4: Ávila, which stands out from the other areas.

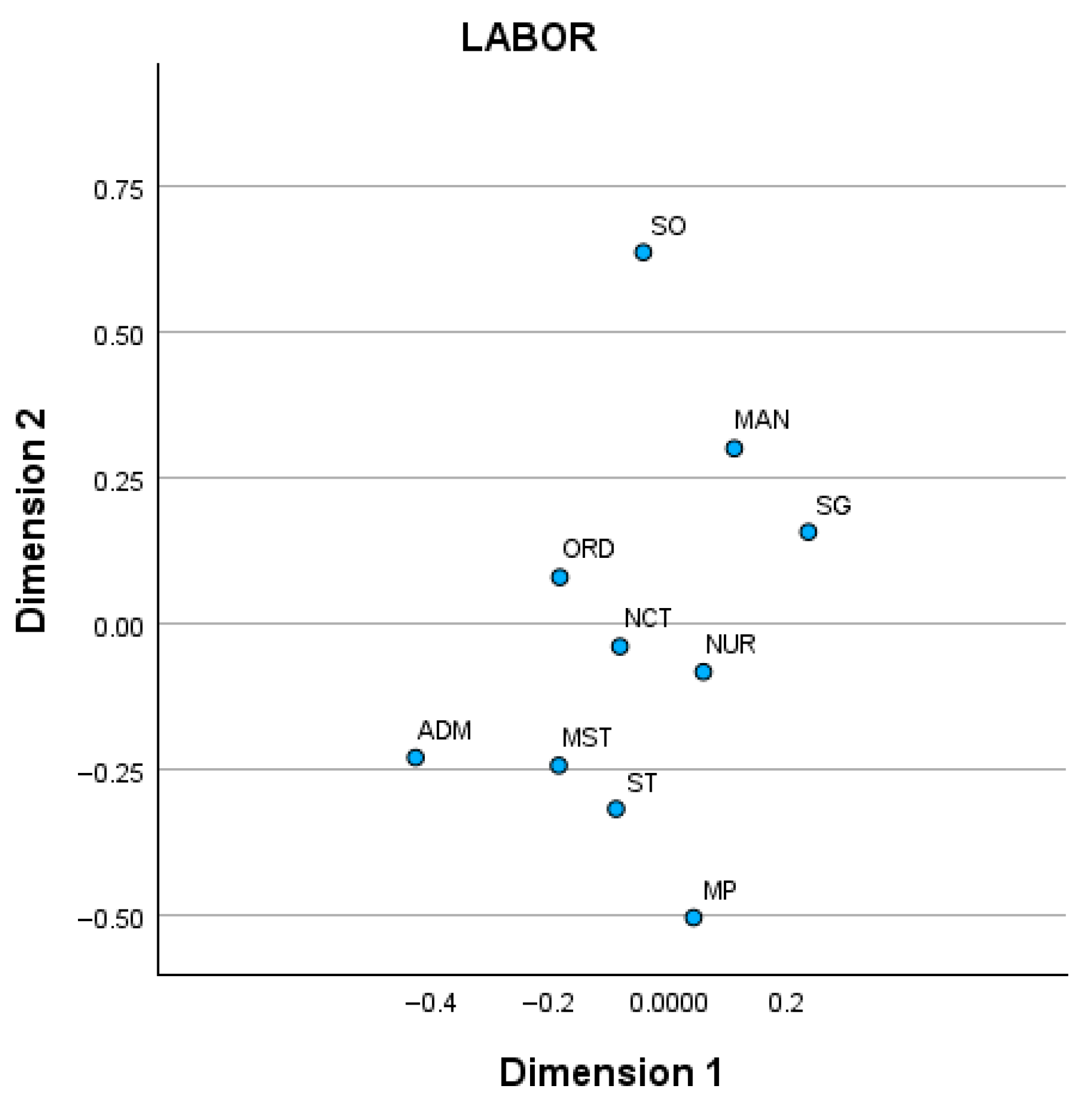
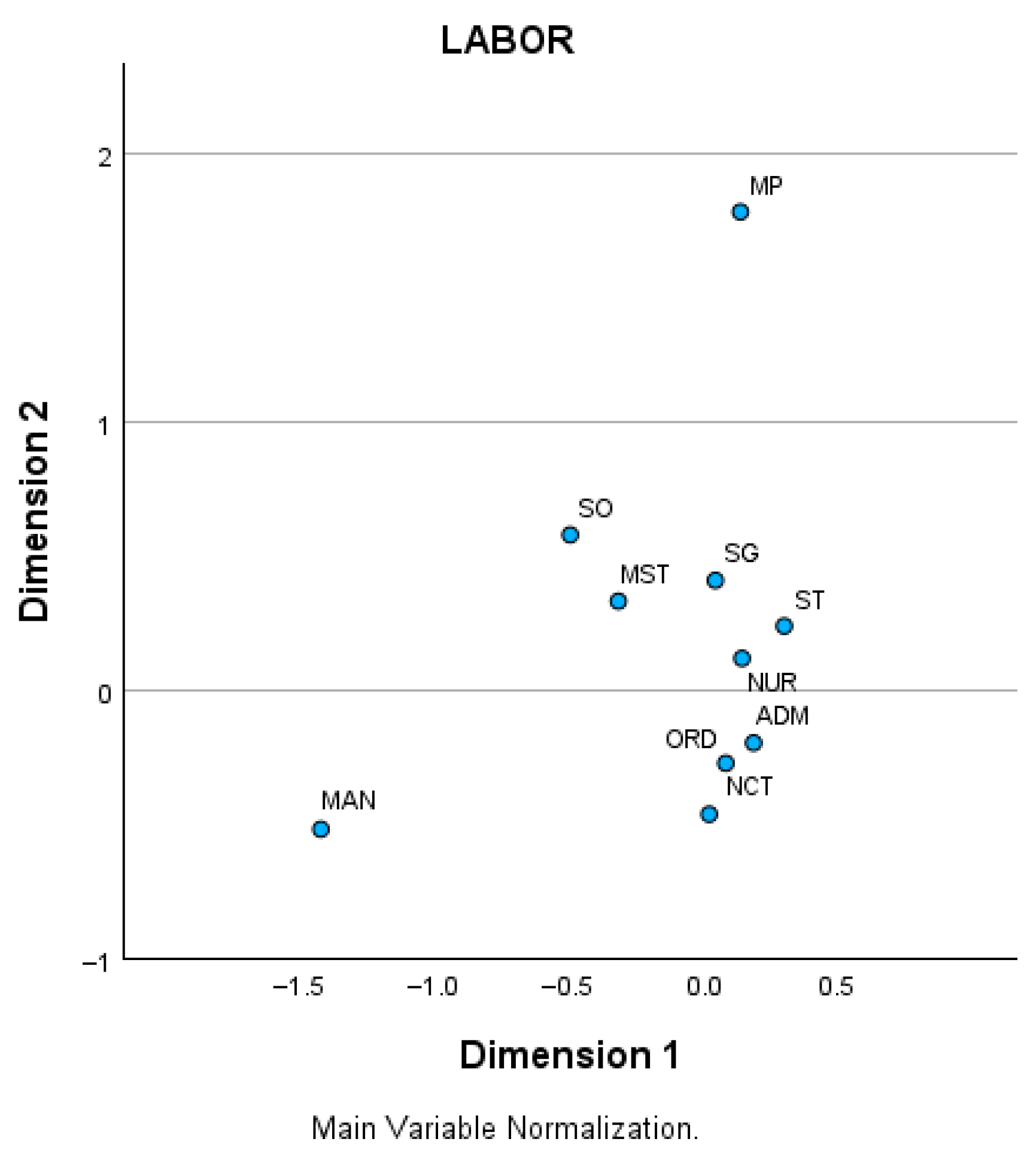
Regarding job categories across all tests, Figure 8 groups roles according to their behavior in the diagnostic tests. Management and Service Operator show similar trends, while care-related positions such as Specialist Graduate, Nursing, Nursing Care Technicians, and Orderlies form a distinct group. Another separate group includes Administrative, Medium and Senior Technicians, Specialist Technicians, and Maintenance Personnel.

Regarding job positions with positive results, Figure 9 highlights four main groups:

• Group 1: Care-related roles, including SG, NUR, ORD, NCT, ST, and ADM.
• Group 2: Service Operator and MST.
• Group 3: Only Maintenance staff.
• Group 4: Management as an independent category.

Figure 10 consolidates these findings through MCA. We then applied Ward’s method, which is more stable and accurate when working with scaling coordinates, as it minimizes within-group variance. Using the same coordinates and group assignments, we subsequently applied K-Means to refine the initial centroids obtained from Ward. The resulting coordinates are the category points or centroids, which represent the MCA projection. Categories located close together on the plane share similar profiles, while those positioned on opposite sides of axis 1 or 2 exhibit different behaviors.

Regarding tests with positive results, a comprehensive visualization is provided of the relationships between health areas, job categories, and test outcomes, considering monthly results from March 2020 to March 2022. Notably, Ávila stands out from other health areas, with its peak of infections occurring in March and April 2020. The most prevalent category was management staff, as most of them frequently travel to the capital. In contrast, Segovia, Zamora, and Soria experienced peaks in May 2020 and again in June 2021.

A third group includes Salamanca and Valladolid Este, which reached their peak at the end of 2021 and beginning of 2022, with SO and MST staff being the most affected. Finally, the most impacted areas—Valladolid Oeste, Burgos, and León—were characterized by a high prevalence of infections among healthcare personnel.

4. Discussion

The results obtained through Multiple Correspondence Analysis highlighted the effectiveness of this method in interpreting complex data; particularly categorical variables related to the evolution of the pandemic and occupational exposure. In the case of Castilla y León, MCA’s ability to synthesize multidimensional information into a single visual representation allowed for the identification of patterns that traditional methods might overlook [32].

The analysis incorporated several explanatory variables. Population density was included, hypothesized to correlate positively with transmission dynamics and thus explain regional variations in observed incidence rates. Heterogeneity in testing protocols, encompassing the implementation and accessibility of diagnostic assays across regions, was also considered as a variable potentially influencing case detection and reporting frequencies. Furthermore, differential availability and adherence to Personal Protective Equipment protocols across professional strata were hypothesized to modulate infection risk. Finally, parameters of labor mobility and social behaviors were included to model differential exposure patterns both within and external to occupational settings.

The analysis of 239,188 diagnostic tests conducted in Castilla y León offers insights into how COVID-19 affected different geographic areas and healthcare job categories. These patterns align with research that underscores disparities in infection risks based on job role, regional prevalence, and timing of pandemic waves.

Geographical heterogeneity was a key finding, with Burgos emerging as the health area with the highest number of diagnostic tests, possibly reflecting either higher local incidence or more aggressive testing protocols. The clustering analysis shows that areas like Ávila had unique infection trajectories, with peak infection rates at the onset of the pandemic (March–April 2020), unlike other regions peaking later.

This aligns with findings from Massachusetts and New York showing that healthcare worker infection rates often mirrored community infection trends more than internal hospital protocols [33,34]. In the case of Europe, spatially uneven risk distributions have been documented, in which health system capacity, commuting patterns, and socio-demographic conditions influence local outbreak dynamics [35,36].

Direct patient care roles, such as Specialized Graduates, Nurses, Nursing Care Technicians, and Orderlies, had significantly higher test volumes and formed a distinct cluster with the highest positive rates. This is consistent with several studies showing that frontline clinical workers had elevated COVID-19 risk due to higher exposure levels, especially early in the pandemic before universal masking and Personal Protective Equipment (PPE) availability improved [33,37,38]. This dynamic underscores the importance of adaptive preventive strategies that can evolve in response to changing risk profiles.

Interestingly, Maintenance Personnel also emerged as a group with high infection levels in late 2021 and early 2022. This aligns with findings that non-clinical HCWs such as environmental service workers also face high infection risk, potentially due to inadequate PPE or working in contaminated spaces [34,39].

The MCA findings illustrate the temporal dynamics of the pandemic’s spread, with different health areas and job roles peaking at various times. These trends are consistent with international observations that infection waves varied regionally, often influenced by local public health measures, hospital density, and community spread [40].

For example, early peaks in Ávila could be due to limited initial protective measures, while later peaks in areas like Salamanca and Bierzo could reflect subsequent waves or policy relaxation.

Findings that Specialized Graduates were most affected early in the pandemic and that Maintenance Personnel were hit later are supported by seroconversion studies, which show higher antibody rates in groups with sustained patient contact or exposure in high-risk hospital zones [39,40].

The dynamic highlighting of risk profiles through multivariate analysis facilitates the implementation of adaptive preventive strategies that can evolve as epidemiological and occupational conditions change. The ability to continuously update and monitor risk profiles allows preventive measures to be adjusted, focusing resources and efforts where they are most needed at any given time.

This adaptability is crucial in healthcare environments, where the dynamics of the pandemic, resource availability, and working conditions vary over time. Therefore, the methodological approach employed not only identifies risk patterns at a specific point in time but also provides a tool for continuous surveillance and informed decision-making in occupational health.

Although cluster analysis of healthcare areas based on positive COVID-19 tests has been previously explored [41,42], our study offers a novel perspective by integrating this analysis with MCA. This combined methodology not only identifies spatial groupings with high incidence but also characterizes multivariate risk profiles that simultaneously consider geographic, professional, and infection status variables.

The use of hierarchical clustering with Ward’s criterion applied to the factorial coordinates derived from MCA enables more precise segmentation based on complex latent patterns, surpassing traditional spatial or epidemiological aggregation. In this way, our approach provides a robust analytical tool for designing more targeted and effective occupational health interventions.

Thus, this discussion reinforces that occupational risk prevention during pandemics requires context-sensitive, adaptive, and evidence-based strategies. By integrating multivariate statistical approaches, risk management can be tailored to specific professional categories and local contexts, thereby safeguarding healthcare workers’ physical and mental health while strengthening the resilience of healthcare systems.

The main limitations inherent to this observational study based on secondary data are acknowledged. These include data quality and consistency, i.e., working with secondary records may involve issues related to the quality, accuracy, and homogeneity of the collected information, which may affect the validity of the results [43]; lack of control over confounding variables as it was not possible to adjust for or control potentially relevant variables such as age, sex, comorbidities, or workload, which limits the interpretation of observed associations; exploratory nature of MCA that was used with an exploratory approach to identify patterns and relationships among categorical variables, without inferential intent or the establishment of causal relationships [16]; and inability to establish causality because causal relationships between the analyzed variables cannot be inferred—only associations and patterns can be described due to the cross-sectional and observational design of the study.

5. Conclusions

Statistical methods, and particularly multivariate approaches, have proven to be indispensable tools in Occupational Risk Prevention, especially in the context of the COVID-19 pandemic. Multiple Correspondence Analysis enables the exploration of complex associations among categorical variables, allowing for the simultaneous representation of relationships between workers’ profiles, psychosocial factors, and health outcomes. This type of analysis facilitates the detection of patterns that would otherwise remain hidden, providing critical insights for preventive decision-making.

The joint analysis of positive and negative diagnostic test results revealed that a higher volume of testing in a given health area does not necessarily correspond to higher infection rates. This underscores the importance of interpreting epidemiological data cautiously and within its broader context. Furthermore, the evolution of the pandemic highlighted a shift in occupational vulnerability: initially, workers in management positions exhibited higher risk, but as the pandemic progressed, direct patient care categories such as nurses, nursing care technicians, specialized graduates, and orderlies were the most affected. This transition shows the dynamic nature of exposure risk and the necessity of adapting preventive strategies accordingly.

Geographically, the health areas of West Valladolid, Burgos, and León showed the highest concentration of risk, reinforcing the need for targeted surveillance and localized interventions. The case of Ávila further exemplifies how commuting patterns and structural characteristics can shape differential risk levels, highlighting the importance of contextualized analysis when designing preventive measures.

The dynamic profiling of risk through multivariate analysis facilitates the implementation of adaptive preventive strategies that can evolve as epidemiological and occupational conditions change. The ability to continuously update and monitor risk profiles allows for the adjustment of preventive measures, focusing resources and efforts where they are most needed at any given time.

This adaptability is crucial in healthcare settings, where the dynamics of the pandemic, resource availability, and working conditions vary over time. Therefore, the methodological approach employed not only identifies risk patterns at a specific moment but also provides a tool for continuous surveillance and informed decision-making in occupational health.