Certain Subclasses of Bi-Univalent Functions Involving Caputo Fractional Derivatives with Bounded Boundary Rotation

Abstract

In this paper, we introduce and investigate new subclasses of analytic bi-univalent functions defined via Caputo fractional derivatives with boundary rotation constraints. Utilizing the generalized operator ${\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }$, which encompasses and extends classical operators such as the Salagean differential operator and the Libera–Bernardi integral operator, we establish sharp coefficient estimates for the initial Taylor Maclaurin coefficients of functions within these subclasses. Furthermore, we derive Fekete–Szegö-type inequalities that provide bounds on the second and third coefficients and their linear combinations involving a real parameter. Our approach leverages subordination principles through analytic functions associated with the classes ${\mathcal{T}}_{\varsigma }\left(\xi \right)$ and ${\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$, allowing a unified treatment of fractional differential operators in geometric function theory. The results generalize several known cases and open avenues for further exploration in fractional calculus applied to analytic function theory.

1. Introduction

The investigation of bi-univalent functions, whose inverses are also analytic and univalent, remains a central topic in geometric function theory, particularly when it comes to bounding their coefficients. A promising approach in this direction is fractional calculus, with the Caputo fractional derivative offering a flexible tool to extend traditional operators and develop new subclasses of functions. In this work, we propose new families of bi-univalent functions involving Caputo-type fractional derivatives under certain boundary rotation conditions. We also derive sharp coefficient estimates and Fekete–Szegö-type inequalities that enhance and generalize previous results.

Let $\mathcal{A}$ represent the class of functions f that are analytic in the open unit disk $\Pi :=\{z\in \mathbb{C}:|z|<1\}$, and are of the form

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{k}_n{z}^n,$$

(1)

with the normalization condition $f^{\prime }\left(0\right)=1$. A well-known subclass of $\mathcal{A}$ is $\mathcal{S}$, which consists of all univalent functions in $\Pi$. Important subclasses of $\mathcal{S}$ include starlike, convex, and those functions whose derivatives have positive real parts.

For a fixed order $0\le ⋉<1$, the following are analytic characterizations of some well-known subclasses (see [1]):

$${\mathcal{S}}^{\ast }(⋉):=\left\{f\in \mathcal{S}:\Re \left({\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>⋉\right\},$$

$$\mathcal{C}(⋉):=\left\{f\in \mathcal{S}:\Re \left({\displaystyle \frac{{\left(z{f}^{\prime }\left(z\right)\right)}^{\prime }}{f^{\prime }\left(z\right)}}\right)>⋉\right\},$$

$$\mathcal{R}(⋉):=\left\{f\in \mathcal{S}:\Re \left(f^{\prime }\left(z\right)\right)>⋉\right\}.$$

A closely related topic is the class of functions with bounded boundary rotation. A function f is said to be in the class ${\mathcal{K}}_{\varsigma }$ if it is analytic in $\Pi$, has the form (1), and maps the unit disk conformally onto a region whose boundary rotation does not exceed $\varsigma \pi$. This class was first introduced by Pinchuk [2]. Functions in ${\mathcal{K}}_{\varsigma }$ satisfy the integral condition:

$${\int }_0^{2\pi }\Re \left({\displaystyle \frac{{\left(r{e}^{i\vartheta }{f}^{\prime }\left(r{e}^{i\vartheta }\right)\right)}^{\prime }}{f^{\prime }\left(r{e}^{i\vartheta }\right)}}\right)d\vartheta \le \varsigma \pi .$$

Another related concept is the class ${\mathcal{R}}_{\varsigma }$, which includes functions with bounded radius rotation. A function f belongs to ${\mathcal{R}}_{\varsigma }$ if it satisfies:

$${\int }_0^{2\pi }\Re \left({\displaystyle \frac{r{e}^{i\vartheta }{f}^{\prime }\left(r{e}^{i\vartheta }\right)}{f\left(r{e}^{i\vartheta }\right)}}\right)d\vartheta \le \varsigma \pi .$$

To analyze such functions, we consider the class ${\mathcal{T}}_{\varsigma }$, which consists of analytic functions W in $\Pi$ with $W\left(0\right)=1$, and which can be written as

$$W\left(z\right)={\int }_0^{2\pi }{\displaystyle \frac{1+z{e}^{-i\vartheta }}{1-z{e}^{-i\vartheta }}}dG\left(\vartheta \right),$$

where $G\left(\vartheta \right)$ is a function of bounded variation that satisfies:

$${\int }_0^{2\pi }dG\left(\vartheta \right)=2,{\int }_0^{2\pi }\left|dG\left(\vartheta \right)\right|\le \varsigma .$$

Noonan [3] was one of the early researchers to explore boundary and radius rotation using order-theoretic tools. This work was further developed by Padmanabhan and Parvatham [4], who provided a more detailed analysis of the class ${\mathcal{T}}_{\varsigma }$.

The class ${\mathcal{T}}_{\varsigma }\left(\xi \right)$, for $0\le \xi <1$, includes analytic functions $t\left(z\right)$ in $\Pi$ with $t\left(0\right)=1$, satisfying the condition:

$${\int }_0^{2\pi }{\displaystyle \frac{\Re \left(t\right(z\left)\right)-\xi }{1-\xi }}dz\le \varsigma \pi .$$

Lemma 1 

([5]). Let $t\left(z\right)=1+t_{1}z+t_2{z}^2+t_3{z}^3+\cdots \in {\mathcal{T}}_{\varsigma }\left(\xi \right)$, then for each $n\ge 1$,

$$|t_n| \le \varsigma (1-\xi ),$$

and this bound is sharp for some functions.

Example 1 

(Images of the Unit Circle under Analytic Functions: $coshz$ and $1+sinz$). Consider the analytic maps

$$f_1\left(z\right)=coshz,f_2\left(z\right)=1+sinz,$$

defined on the unit disk $\mathbb{U}$, and the unit circle

$$\mathbb{T}=\{z\in \mathbb{C}:|z|=1\}.$$

The corresponding images of $\mathbb{T}$ are

$$f_1\left(\mathbb{T}\right),f_2\left(\mathbb{T}\right),$$

which are plotted together with the bounded boundary rotation (BBR) region.

(1) 

Plots with BBR region

The BBR region is shown as a transparent disk of radius π, with arrows indicating the boundary directions (Figure 1 and Figure 2).

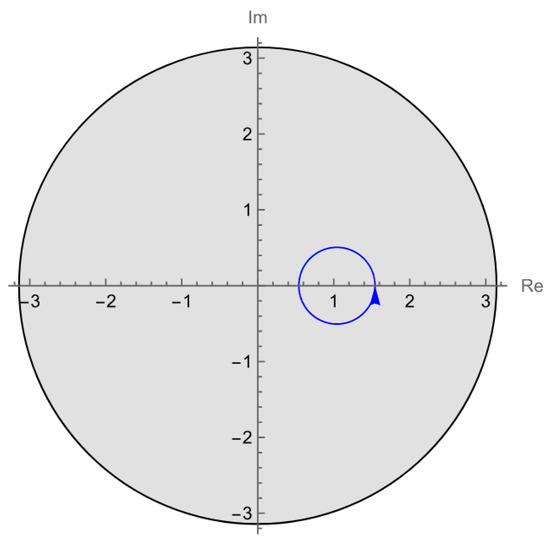
Figure 1. $f_1\left(z\right)=coshz$ with BBR region.

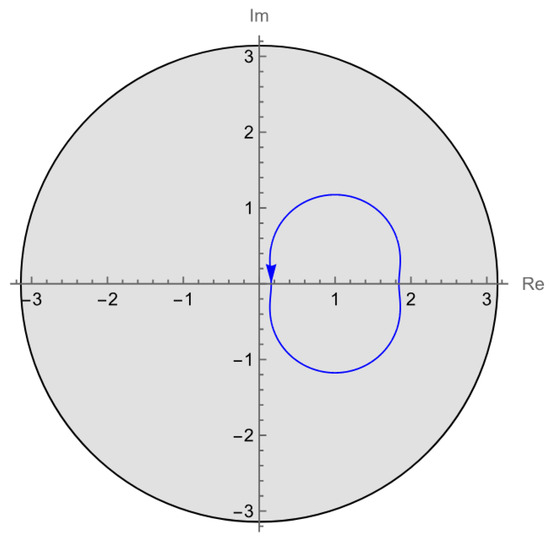
Figure 2. $f_2\left(z\right)=1+sinz$ with BBR region.

(2) 

Proof of Total Variation

Parametrize the circle by $z\left(t\right)=e^{it}$, $t\in [0,2\pi ]$, and let $\gamma \left(t\right)=f\left(z\right(t\left)\right)$. Then

$${\gamma }^{\prime }\left(t\right)=i{e}^{it}{f}^{\prime }\left(e^{it}\right).$$

• For $f_1\left(z\right)=coshz$:

  $$f_1^{\prime }\left(z\right)=sinhz\Rightarrow {\gamma }_1^{\prime }\left(t\right)=i{e}^{it}sinh\left(e^{it}\right).$$

  Numerical computation shows that

  $$\mathrm{TV}\left[\mathrm{Arg}\left({\gamma }_1^{\prime }\right)\right]\approx 12.5664,\mathit{winding}\approx 2,$$

  so the tangent vector of the image makes exactly two full turns.
• For $f_2\left(z\right)=1+sinz$:

  $$f_2^{\prime }\left(z\right)=cosz\Rightarrow {\gamma }_2^{\prime }\left(t\right)=i{e}^{it}cos\left(e^{it}\right).$$

  Numerical computation shows that

  $$\mathrm{TV}\left[\mathrm{Arg}\left({\gamma }_2^{\prime }\right)\right]\approx 6.99817,\mathit{winding}\approx 1,$$

  so the tangent vector of the image makes exactly one full turn.

These results are consistent with the numerical plots.

According to [6], any function $f\in \mathcal{S}$ has an inverse $f^{-1}$ that is analytic in a disk $\left|w\right|<r_0\left(f\right)$, where $r_0\left(f\right)\ge \frac{1}{4}$, and satisfies the identities

$$f^{-1}\left(f\left(z\right)\right)=z\mathrm{and}f\left(f^{-1}\left(w\right)\right)=w.$$

This inverse can be expressed by the following power series:

$$f^{-1}\left(w\right)=w-k_2{w}^2+(2k_2^2-k_3)w^3-(5k_2^3-5k_2{k}_3+k_4)w^4+\cdots .$$

(2)

A function $f\in \mathcal{A}$ is said to be bi-univalent if both f and its inverse $f^{-1}$ are univalent in the unit disk $\Pi$. The set of all such functions is denoted by $\Omega$. This class is nonempty. For instance, the functions

$$f_1\left(z\right)={\displaystyle \frac{z}{1-z}},f_2\left(z\right)={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+z}{1-z}}\right),f_3\left(z\right)=-log(1-z),$$

and their respective inverses

$$f_1^{-1}\left(w\right)={\displaystyle \frac{w}{1+w}},f_2^{-1}\left(w\right)={\displaystyle \frac{e^{2w}-1}{e^{2w}+1}},f_3^{-1}\left(w\right)={\displaystyle \frac{e^w-1}{e^w}},$$

are all members of $\Omega$. However, the Koebe function is not included in this class.

The Koebe function, defined by $\mathcal{K}\left(z\right)={\displaystyle \frac{z}{{(1-z)}^2}},$ is a fundamental example in the class of univalent functions $\mathcal{S}$. It maps the open unit disk $\mathbb{U}$ onto the entire complex plane except for the part of the negative real axis from $-\frac{1}{4}$ to $-\infty$. This mapping can also be written as

$$\mathcal{K}\left(z\right)={\displaystyle \frac{1}{4}}\left[{\left({\displaystyle \frac{1+z}{1-z}}\right)}^2-1\right],$$

which shows that the Koebe function is obtained through a composition of conformal mappings from the unit disk to the right half-plane and then onto the slit complex plane.

The concept of bi-univalent functions was introduced by Lewin [7], who showed that for any $f\in \Omega$, the second coefficient satisfies the bound $|k_2| <1.51$. Finding sharp bounds for the higher coefficients $|k_n|$ for $n\ge 3$ is still a widely open problem. Brannan and Clunie [8] proposed that $|k_2| \le \sqrt{2}$, while Netanyahu [9] later proved that the best possible bound for $|k_2|$ in $\Omega$ is exactly ${\displaystyle \frac{4}{3}}$.

Building on the contributions of Srivastava et al. [10], numerous researchers have explored new subclasses of $\Omega$ aiming to estimate the coefficients $|k_2|$ and $|k_3|$. In this direction, Brannan and Taha [11] proposed two well-known subclasses: the class of bi-starlike functions of order $\xi$, denoted by $S_{\Omega }^{\ast }\left(\xi \right)$, and the class of bi-convex functions of order $\xi$, denoted by $K_{\Omega }\left(\xi \right)$. Operators are essential tools in developing and analyzing subclasses of analytic functions. Differential and integral operators have been widely used in this context to define novel function classes in $\Omega$ and to derive coefficient estimates and related properties. Examples include the studies by Lupaş et al. [12], Jothibasu [13], Olatunji and Ajai [14], and Shaba [15,16], who investigated various linear and Salăgean-type operators to understand their effects on analytic and geometric features.

Definition 1 

([17]). Let f be analytic in a simply connected domain containing the origin. Then, the fractional integral of order $\delta >0$ is defined by

$${\mathbb{D}}_z^{-\delta }f\left(z\right)={\displaystyle \frac{1}{\Gamma \left(\delta \right)}}{\int }_0^z{\displaystyle \frac{f\left(t\right)}{{(z-t)}^{1-\delta }}}dt,$$

(3)

while the corresponding fractional derivative of order $0\le \delta <1$ is given by

$${\mathbb{D}}_z^{\delta }f\left(z\right)={\displaystyle \frac{1}{\Gamma (1-\delta )}}{\displaystyle \frac{d}{dz}}{\int }_0^z{\displaystyle \frac{f\left(t\right)}{{(z-t)}^{\delta }}}dt,$$

(4)

where the branch of the power function is chosen so that $log(z-t)$ is real whenever $z-t>0$.

Definition 2 

([18]). If $m\in \mathbb{N}$ and $0\le \delta <1$, the fractional derivative of order $m+\delta$ is defined as

$${\mathbb{D}}_z^{m+\delta }f\left(z\right)={\displaystyle \frac{d^m}{d{z}^m}}{\mathbb{D}}_z^{\delta }f\left(z\right).$$

(5)

Based on the groundwork laid by Srivastava and Owa [19], an important operator was introduced:

$${\mathcal{M}}_{\varrho }f\left(z\right):=\Gamma (2-\varrho )z^{\varrho }{\mathbb{D}}_z^{\varrho }f\left(z\right),$$

defined for functions $f\in \mathcal{A}$. This operator has the following series form:

$${\mathcal{M}}_{\varrho }f\left(z\right)=z+\sum _{n=2}^{\infty }\Phi (n,\varrho )k_n{z}^n,\mathrm{where}\Phi (n,\varrho )={\displaystyle \frac{\Gamma (n+1)\Gamma (2-\varrho )}{\Gamma (n+1-\varrho )}},$$

with $\varrho \in \mathbb{R}\setminus \{2,3,4,\dots \}$. Some notable instances of this operator are:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{0}f\left(z\right)& =f\left(z\right)=z+\sum _{n=2}^{\infty }{k}_n{z}^n,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\mathcal{M}}_{1}f\left(z\right)& =z{f}^{\prime }\left(z\right)=z+\sum _{n=2}^{\infty }n{k}_n{z}^n,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathcal{M}}_{j}f\left(z\right)& =\mathcal{M}\left({\mathcal{M}}_{j-1}f\left(z\right)\right)=z+\sum _{n=2}^{\infty }{n}^j{k}_n{z}^n,j=1,2,3,\dots \hfill \end{array}$$

(8)

This recursive Definition 2 is commonly referred to as the Salagean operator [20]. When $j=-k$ for positive integers k, the operator gives rise to classical operators such as the Libera–Bernardi integral operator [21].

Another notable fractional approach is due to Caputo [22], who proposed the operator:

$${\mathbb{D}}^{⋉}f\left(z\right)={\displaystyle \frac{1}{\Gamma (n-⋉)}}{\int }_a^n{\displaystyle \frac{f^{\left(n\right)}\left(t\right)}{{(n-t)}^{⋉+1-t}}}dt,$$

(9)

where $n\in \mathbb{N}$, $n-1<\Re (⋉)\le n$, and ⋉ may be a real or complex constant.

In a related development, Salah and Darus [23] introduced a generalization involving:

$${\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right):={\displaystyle \frac{\Gamma (2+\mathsf{ȷ}-\varrho )}{\Gamma (\mathsf{ȷ}-\varrho )}}{z}^{\varrho -\mathsf{ȷ}}{\int }_0^z{\displaystyle \frac{{\mathcal{M}}_{\mathsf{ȷ}}f\left(t\right)}{{(z-t)}^{\varrho +1-\mathsf{ȷ}}}}dt,$$

where $\mathsf{ȷ}-1<\varrho <\mathsf{ȷ}<2$. This operator has a power series representation given by (see [24]):

$${\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)=z+\sum _{n=2}^{\infty }{\mathcal{R}}_n^{\mathsf{ȷ},\varrho }{k}_n{z}^n,$$

where

$${\mathcal{R}}_n^{\mathsf{ȷ},\varrho }={\displaystyle \frac{\Gamma (2+\mathsf{ȷ}-\varrho )\Gamma (2-\mathsf{ȷ}){[\Gamma (n+1)]}^2}{\Gamma (n-\mathsf{ȷ}+1)\Gamma (n+\mathsf{ȷ}-\varrho +1)}}.$$

Special cases such as ${\mathcal{C}}_0^{0}f\left(z\right)=f\left(z\right)$ and ${\mathcal{C}}_1^{1}f\left(z\right)=z{f}^{\prime }\left(z\right)$ are easily recovered.

In reference [18], the authors introduced and investigated three subclasses of bi-univalent functions involving Caputo fractional derivatives with bounded boundary rotation. However, in the present paper, we focus on different subclasses and explore them through two distinct approaches. Although some of our results coincide with particular cases of those obtained in [18], our work extends the discussion to new subclasses with alternative structural properties.

Motivated by recent developments in the study of bi-univalent functions involving boundary rotation [25,26,27,28,29,30,31] and the application of Caputo-type operators [17,24,32,33], we propose and examine three new subclasses of bi-univalent functions in the unit disk. For these classes, we determine sharp coefficient bounds and derive Fekete–Szegö-type inequalities. Corollaries addressing special cases are also included.

2. Coefficient Bounds and Sharp Fekete–Szegö Results in the Function Class ${\mathcal{R}}_{\mathbf{\Omega }}^{\mathsf{ȷ},\mathbf{\varrho }}(\mathbf{\vartheta },\mathbf{\varsigma },\mathbf{\xi })$

In this section, we introduce and investigate a new subclass of analytic and bi-univalent functions defined through the generalized operator ${\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}$, without imposing any boundary rotation constraints. The characterization of this class is based solely on subordination to a normalized function ${\mathcal{T}}_{\varsigma }\left(\xi \right)$, allowing greater flexibility in geometric interpretations.

Definition 3.

Let f be a function given by the expansion in (1), and suppose that $f\in \mathcal{A}$. Then f is said to belong to the class ${\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$ if the following subordination conditions are satisfied:

$${\displaystyle \frac{z^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right]}^{1-\vartheta }}}\prec {\mathcal{T}}_{\varsigma }\left(\xi \right)\mathit{and}{\displaystyle \frac{w^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right]}^{1-\vartheta }}}\prec {\mathcal{T}}_{\varsigma }\left(\xi \right),$$

where the parameters satisfy $0\le \vartheta \le 1$, $2\le \varsigma \le 4$, $0\le \xi <1$, and $\mathsf{ȷ}-1<\varrho <\mathsf{ȷ}<2$. The function $g\left(w\right)$ is as defined in Equation (2).

Remark 1.

If we take $\vartheta =1$, then ${\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(1,\varsigma ,\xi )$ reduces to the class ${\mathcal{I}}_{\Omega }^{\mathsf{ȷ},\varrho }(\varsigma ,\xi )$. In this case, a function $f\in \mathcal{A}$, as defined in (1), belongs to ${\mathcal{I}}_{\Omega }^{\mathsf{ȷ},\varrho }(\varsigma ,\xi )$ if

$${\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}h\left(z\right)\right)}^{\prime }\prec {\mathcal{T}}_{\varsigma }\left(\xi \right)\mathit{and}{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right)}^{\prime }\prec {\mathcal{T}}_{\varsigma }\left(\xi \right),$$

with the same assumptions on ς, ξ, j, and ϱ.

Remark 2.

If we choose $\vartheta =0$ in Definition 3, the class ${\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(0,\varsigma ,\xi )$ becomes ${\mathcal{J}}_{\Omega }^{\mathsf{ȷ},\varrho }(\varsigma ,\xi )$. In this case, the function $f\in \mathcal{A}$ satisfies

$${\displaystyle \frac{z{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right)}^{\prime }}{{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)}}\prec {\mathcal{T}}_{\varsigma }\left(\xi \right)\mathit{and}{\displaystyle \frac{w{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right)}^{\prime }}{{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)}}\prec {\mathcal{T}}_{\varsigma }\left(\xi \right),$$

with the same conditions on ς, ξ, j, and ϱ. The function $g\left(w\right)$ is again the one defined in Equation (2).

Theorem 1.

Let the function f, defined as in (1), be a member of the class ${\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$. Then the coefficients $k_2$ and $k_3$ satisfy the bounds:

$$|k_2| \le \sqrt{{\displaystyle \frac{2\varsigma (1-\xi )}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}},$$

(10)

$$|k_3| \le {\displaystyle \frac{2\varsigma (1-\xi )}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.$$

(11)

Furthermore, for any real number $\aleph \in \mathbb{R}$, the following Fekete–Szegö-type estimate holds:

$$|k_3-\aleph k_2^2| \le \left\{\begin{array}{cc}{\displaystyle \frac{2\varsigma (1-\xi )(1-\aleph )}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)},}\hfill & \mathit{if}\aleph <\gimel ,\hfill \\ {\displaystyle \frac{\varsigma (1-\xi )}{{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)},}\hfill & \mathit{if}\gimel \le \aleph \le 2-\gimel ,\hfill \\ {\displaystyle \frac{2\varsigma (1-\xi )(\aleph -1)}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)},}\hfill & \mathit{if}\aleph >2-\gimel .\hfill \end{array}\right.$$

(12)

Here, the transition value ℷ is given by:

$$\gimel ={\displaystyle \frac{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)}}.$$

(13)

Throughout the paper, unless stated otherwise, we assume:

$$2\le \varsigma \le 4\mathit{and}0\le \xi <1.$$

The terms ${\mathcal{R}}_2^{\mathsf{ȷ},\varrho }$ and ${\mathcal{R}}_3^{\mathsf{ȷ},\varrho }$ are defined by:

$$\begin{array}{cc}\hfill {\mathcal{R}}_2^{\mathsf{ȷ},\varrho }& ={\displaystyle \frac{\Gamma (2+\mathsf{ȷ}-\varrho )\Gamma (2-\mathsf{ȷ}){[\Gamma \left(3\right)]}^2}{\Gamma (3-\mathsf{ȷ})\Gamma (3+\mathsf{ȷ}-\varrho )}},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathcal{R}}_3^{\mathsf{ȷ},\varrho }& ={\displaystyle \frac{\Gamma (2+\mathsf{ȷ}-\varrho )\Gamma (2-\mathsf{ȷ}){[\Gamma \left(4\right)]}^2}{\Gamma (4-\mathsf{ȷ})\Gamma (4+\mathsf{ȷ}-\varrho )}}.\hfill \end{array}$$

(15)

Proof. 

Since $f\in {\mathcal{R}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$, we have

$${\displaystyle \frac{z^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right]}^{1-\vartheta }}}=s\left(z\right),$$

(16)

and, correspondingly, for its inverse function g,

$${\displaystyle \frac{w^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right]}^{1-\vartheta }}}=t\left(w\right),$$

(17)

where s and t are analytic functions belonging to the subclass ${\mathcal{T}}_{\varsigma }\left(\xi \right)$, with power series expansions

$$\begin{array}{cc}\hfill s\left(z\right)& =1+s_{1}z+s_2{z}^2+s_3{z}^3+\cdots ,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill t\left(w\right)& =1+t_{1}w+t_2{w}^2+t_3{w}^3+\cdots .\hfill \end{array}$$

(19)

Expanding the expression in (16) using the operator ${\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{z^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}f\left(z\right)\right]}^{1-\vartheta }}}& =1+{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_{2}z\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)k_2^2+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)k_3\right)z^2+\cdots .\hfill \end{array}$$

(20)

Similarly, for the inverse function g we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{w^{1-\vartheta }{\left({\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right)}^{\prime }}{{\left[{\mathcal{C}}_{\varrho }^{\mathsf{ȷ}}g\left(w\right)\right]}^{1-\vartheta }}}& =1-{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_{2}w\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)k_2^2+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)(2k_2^2-k_3)\right)w^2+\cdots .\hfill \end{array}$$

(21)

By comparing coefficients from (20) and (21) with those from the respective expansions above, we obtain the following identities:

$$\begin{array}{cc}\hfill {\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_2& =s_1,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)k_2^2+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)k_3\right)& =s_2,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill -{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_2& =t_1,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)k_2^2+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)(2k_2^2-k_3)\right)& =t_2.\hfill \end{array}$$

(25)

Adding Equations (23) and (25), we eliminate $k_3$ and isolate $k_2^2$:

$$\begin{array}{cc}\hfill & \left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)k_2^2=s_2+t_2,\hfill \\ \hfill \Rightarrow & k_2^2={\displaystyle \frac{s_2+t_2}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.\hfill \end{array}$$

(26)

Now, by utilizing Lemma 1 in conjunction with Equation (26), we derive the following upper estimate for $|k_2|$:

$$|k_2{|}^2\le {\displaystyle \frac{2\varsigma (1-\xi )}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.$$

(27)

To obtain the bound for $|k_3|$, we subtract the respective expressions and find

$$k_3={\displaystyle \frac{s_2-t_2}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}+{\displaystyle \frac{s_2+t_2}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.$$

(28)

By rearranging and simplifying the right-hand side, we obtain a single rational expression:

$$k_3={\displaystyle \frac{s_2\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)-t_2\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)\right)}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)}}.$$

(29)

Once again, invoking Lemma 1 for Equation (23), we estimate the following upper bound for $|k_3|$:

$$|k_3| \le {\displaystyle \frac{2\varsigma (1-\xi )}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.$$

(30)

Let $\aleph \in \mathbb{R}$ be a fixed parameter. By combining Equations (23) and (26), the expression for $k_3-\aleph k_2^2$ becomes

$$k_3-\aleph k_2^2={\displaystyle \frac{s_2-t_2}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}+{\displaystyle \frac{(1-\aleph )(s_2+t_2)}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}}.$$

(31)

Rewriting with a common denominator, the expression simplifies to:

$$k_3-\aleph k_2^2={\displaystyle \frac{(s_2-t_2)\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)+(1-\aleph )(s_2+t_2)·2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)}}.$$

(32)

Finally, employing Lemma 1 on inequality (29), we establish the following upper estimate:

$$\begin{array}{c}\hfill |k_3-\aleph k_2^2| \le {\displaystyle \frac{\varsigma (1-\xi )\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)(2+\aleph )\right)+\varsigma (1-\xi )\left(2\aleph {\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)\right)}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\left({\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2({\vartheta }^2+\vartheta -2)+2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(\vartheta +2)\right)}}.\end{array}$$

(33)

□

Corollary 1 

(Particular Case $\vartheta =0$ [18]). Assuming the hypotheses of Theorem 1 are satisfied, then for the specific case $\vartheta =0$, the following estimates hold:

$$|k_2| \le \sqrt{{\displaystyle \frac{2\varsigma (1-\xi )}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }-2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2}}},$$

(34)

$$|k_3| \le {\displaystyle \frac{2\varsigma (1-\xi )}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }-2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2}},$$

(35)

and for any real constant $\aleph \in \mathbb{R}$, the following upper bound holds:

$$|k_3-\aleph k_2^2| \le \left\{\begin{array}{cc}{\displaystyle \frac{2\varsigma (1-\xi )(1-\aleph )}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }-2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2},}\hfill & \mathit{if}\aleph <{\gimel }_0,\hfill \\ {\displaystyle \frac{\varsigma (1-\xi )}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }},}\hfill & \mathit{if}{\gimel }_0\le \aleph \le 2-{\gimel }_0,\hfill \\ {\displaystyle \frac{2\varsigma (1-\xi )(1-\aleph )}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }-2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2},}\hfill & \mathit{if}\aleph >2-{\gimel }_0,\hfill \end{array}\right.$$

(36)

where

$${\gimel }_0={\displaystyle \frac{-2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }}{{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2}}.$$

Corollary 2 

(Particular Case $\vartheta =1$ [18]). Under the same conditions of Theorem 1, when $\vartheta =1$, the following bounds are valid:

$$|k_2| \le \sqrt{{\displaystyle \frac{\varsigma (1-\xi )}{3{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }}}},$$

(37)

$$|k_3| \le {\displaystyle \frac{\varsigma (1-\xi )}{3{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }}},$$

(38)

and for any $\aleph \in \mathbb{R}$,

$$|k_3-\aleph k_2^2| \le \left\{\begin{array}{cc}{\displaystyle \frac{\varsigma (1-\xi )(1-\aleph )}{6{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }},}\hfill & \mathit{if}\aleph <0,\hfill \\ {\displaystyle \frac{\varsigma (1-\xi )}{3{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }},}\hfill & \mathit{if}0\le \aleph \le 2,\hfill \\ {\displaystyle \frac{\varsigma (1-\xi )(1-\aleph )}{6{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }},}\hfill & \mathit{if}\aleph >2.\hfill \end{array}\right.$$

(39)

3. A Class of Analytic Functions Associated with the Caputo Fractional Derivative Operator

In this section, we introduce a new subclass of analytic bi-univalent functions based on the Caputo-type fractional operator ${\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)$. By selecting appropriate analytic functions h and p, we derive sharp bounds for the second and third Taylor coefficients, along with Fekete–Szegö-type inequalities associated with this new subclass.

Definition 4.

Let $h,p:U\to \mathbb{C}$ be two analytic functions satisfying

$$min\left\{Re\left(h\right(z\left)\right),Re\left(p\right(z\left)\right)\right\}>0,\mathit{for}\mathit{all}z\in \Pi ,$$

and normalized such that

$$h\left(0\right)=p\left(0\right)=1.$$

Assume that the function f, defined as in (1), belongs to the standard analytic function class $\mathcal{A}$. Then, f is said to be a member of the class ${\mathcal{B}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$ if the following conditions hold for all $z\in \Pi$ and $w\in \Pi$:

$$\begin{array}{cc}\hfill & f\in \Omega \mathit{and}(1-\vartheta ){\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)}}+\vartheta \left(1+{\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{″}}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}}\right)\in h\left(U\right),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & (1-\vartheta ){\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)}}+\vartheta \left(1+{\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{″}}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}}\right)\in p\left(U\right),\hfill \end{array}$$

(41)

where the function g is defined by (2).

Remark 3.

Various choices for the functions h and p lead to meaningful subclasses of the analytic function class $\mathcal{A}$. Notably, the following examples satisfy the assumptions of Definition 4:

• If

  $$h\left(z\right)=p\left(z\right)={\left({\displaystyle \frac{1+z}{1-z}}\right)}^{⋉},z\in \Pi ,0<⋉\le 1,$$

  (42)
• or if

  $$h\left(z\right)=p\left(z\right)={\displaystyle \frac{1+(1-2\xi )z}{1-z}},z\in \Pi ,0\le \xi <1,$$

then the functions h and p clearly satisfy the required conditions.

Theorem 2.

Suppose $f\in {\mathcal{B}}_{\Omega }^{\mathsf{ȷ},\varrho }(\vartheta ,\varsigma ,\xi )$, and let the functions s and t, given by (18) and (19), admit the expansions

$$s\left(z\right)=1+s_{1}z+s_2{z}^2+\cdots ,t\left(w\right)=1+t_{1}w+t_2{w}^2+\cdots ,$$

then the following coefficient bounds are valid:

1. 

The second coefficient $k_2$ satisfies

$$|k_2| \le min\left\{{\displaystyle \frac{1}{2\sqrt{2}}}\sqrt{{\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{\left|2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right|}}},\sqrt{{\displaystyle \frac{|s^{\prime }{\left(0\right)|}^2+{\left|t^{\prime }\left(0\right)\right|}^2}{2{\left|{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )\right|}^2}}}\right\}.$$

2. 

The third coefficient $k_3$ satisfies

$$\begin{array}{cc}\hfill |k_3| \le min& \{{\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{4\left|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )\right|}}+{\displaystyle \frac{|s^{\prime }{\left(0\right)|}^2+{\left|t^{\prime }\left(0\right)\right|}^2}{2{\left|{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )\right|}^2}},\hfill \\ \hfill & {\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{4\left|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )\right|}}+{\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{2\left|2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right|}}\}.\hfill \end{array}$$

(43)

3. 

Moreover, the Fekete–Szegö functional obeys the bound

$$\left|k_3-\eta k_2^2\right|\le {\displaystyle \frac{|t^{″}\left(0\right)|}{4\left|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )\right|}},$$

where

$$\eta ={\displaystyle \frac{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}.$$

Proof. 

To establish the theorem, we start by rewriting the identities (44) and (45) in their expanded forms:

$$(1-\vartheta ){\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)}}+\vartheta \left(1+{\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{″}}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}}\right)=s\left(z\right),$$

(44)

$$(1-\vartheta ){\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)}}+\vartheta \left(1+{\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime \prime }}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}}\right)=t\left(w\right).$$

(45)

Expanding the left sides of (44) and (45) in terms of the Taylor coefficients of f and g, respectively, yields

$$\begin{array}{cc}\hfill & (1-\vartheta ){\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)}}+\vartheta \left(1+{\displaystyle \frac{z{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{″}}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }f\left(z\right)\right)}^{\prime }}}\right)\hfill \\ \hfill & =1+{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_{2}z+\left[2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )k_3-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )k_2^2\right]z^2+\cdots ,\hfill \end{array}$$

(46)

and

$$\begin{array}{cc}\hfill & (1-\vartheta ){\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}{{\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)}}+\vartheta \left(1+{\displaystyle \frac{w{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{″}}{{\left({\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }g\left(w\right)\right)}^{\prime }}}\right)\hfill \\ \hfill & =1-{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_{2}w+[2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )(2k_2^2-k_3)\hfill \\ \hfill & -{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )k_2^2]w^2+\cdots .\hfill \end{array}$$

(47)

Matching coefficients for powers z and w in (46) and (47) leads to

$${\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_2=s_1,$$

(48)

$$2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )k_3-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )k_2^2=s_2,$$

(49)

$$-{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }(1+\vartheta )k_2=t_1,$$

(50)

$$2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )(2k_2^2-k_3)-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )k_2^2=t_2.$$

(51)

From the known relations (48) and (50), it follows immediately that

$$s_1=-t_1,$$

(52)

and consequently,

$$2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2{(1+\vartheta )}^2{k}_2^2=(s_1^2+t_1^2).$$

(53)

By combining Equations (49), (51), and (53), we deduce the relation

$$2\left[2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right]k_2^2=s_2+t_2,$$

(54)

which can be rearranged to explicitly solve for $k_2^2$ as

$$k_2^2={\displaystyle \frac{s_2+t_2}{2\left[2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right]}}.$$

(55)

From this, the upper bound for $|k_2|$ follows immediately:

$$|k_2| \le {\displaystyle \frac{1}{2\sqrt{2}}}\sqrt{{\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{\left|2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right|}}}.$$

(56)

Alternatively, employing Equation (55), another estimate for $|k_2|$ is given by

$$|k_2| \le \sqrt{{\displaystyle \frac{|s^{\prime }{\left(0\right)|}^2+{\left|t^{\prime }\left(0\right)\right|}^2}{2|{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }{(1+\vartheta )|}^2}}}.$$

(57)

To bound $|k_3|$, subtracting Equation (49) from (51) yields

$$4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )(k_3-k_2^2)=s_2-t_2.$$

(58)

Substituting (53) into (58) leads to the explicit formula

$$k_3={\displaystyle \frac{s_2-t_2}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}+k_2^2.$$

(59)

Substituting the value of $k_2^2$ obtained from Equations (55) and (53), we get two equivalent forms for $k_3$. The first is:

$$k_3={\displaystyle \frac{s_2-t_2}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}+{\displaystyle \frac{s_1^2+t_1^2}{2{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2{(1+\vartheta )}^2}}.$$

(60)

Alternatively, using a different expression for $k_2^2$, we have:

$$k_3={\displaystyle \frac{s_2-t_2}{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}+{\displaystyle \frac{s_2+t_2}{2\left[2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right]}}.$$

(61)

Hence, two upper bounds for $|k_3|$ follow. From (60), we get:

$$|k_3| \le {\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{4|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )|}}+{\displaystyle \frac{|s^{\prime }{\left(0\right)|}^2+{\left|t^{\prime }\left(0\right)\right|}^2}{2|{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }{(1+\vartheta )|}^2}},$$

(62)

while from (61), it follows that:

$$|k_3| \le {\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{4|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )|}}+{\displaystyle \frac{|s^{″}\left(0\right)|+|t^{″}\left(0\right)|}{2\left|2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )\right|}}.$$

(63)

Rearranging Equation (51) yields:

$$\left[{\displaystyle \frac{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}\right]k_2^2-k_3={\displaystyle \frac{t_2}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}.$$

(64)

Define

$$\eta ={\displaystyle \frac{4{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )-{\left[{\mathcal{R}}_2^{\mathsf{ȷ},\varrho }\right]}^2(1+3\vartheta )}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}.$$

Thus, the expression can be rewritten as

$$k_3-\eta k_2^2={\displaystyle \frac{-t_2}{2{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )}}.$$

(65)

Consequently, the following sharp upper bound for the Fekete–Szegö functional holds:

$$\left|k_3-\eta k_2^2\right|\le {\displaystyle \frac{|t^{″}\left(0\right)|}{4\left|{\mathcal{R}}_3^{\mathsf{ȷ},\varrho }(1+2\vartheta )\right|}}.$$

(66)

This completes the proof. □

4. Conclusions

This study presents an in-depth investigation of novel subclasses of bi-univalent functions, which are analytic and invertible in the unit disk and satisfy certain boundary rotation constraints. The main idea is to define these new subclasses using the Caputo fractional derivative, providing a powerful tool to extend classical results. By employing the generalized operator ${\mathcal{C}}_{\mathsf{ȷ}}^{\varrho }$, we derive new coefficient bounds, including sharp Fekete–Szegö-type inequalities, which are fundamental in geometric function theory. This approach offers significant flexibility for exploring functions with complex analytic and geometric properties. Furthermore, the study paves the way for future research, such as estimating higher-order coefficients $|k_n|,n\ge 4$, computing Hankel determinants or Krushkal-type inequalities, and applying modern fractional operators. Potential directions include the Riemann–Liouville operator and other recently introduced fractional operators, as well as investigating subordination principles and their applications to these newly defined subclasses.