A Bedbug Optimization-Based Machine Learning Framework for Software Fault Prediction

Abstract

Predicting software faults and identifying defective modules is a significant challenge in developing reliable software products. Machine Learning (ML) approaches on the historical fault datasets are utilized to classify faulty software modules. The presence of irrelevant features within the training datasets undermines the accuracy and precision of the software prediction models. Consequently, selecting the most effective features for module classification constitutes an NP-hard problem. This research introduces the Binary Bedbug Optimization Algorithm (BBOA) to extract the most effective features of training datasets. The primary contribution lies in the development of a binary variant of the Bedbug Optimization Algorithm (BOA) designed to effectively select effective features and build a classifier for identifying faulty software modules using ANN, SVM, DT, and NB algorithms. The model’s performance was evaluated using five standard real-world NASA datasets. The findings reveal that among the 21 features analyzed, features such as code complexity, lines of code, the total number of operands and operators, lines containing both code and comments, the total count of operators and operands, and the number of branch instructions play a critical role in predicting software faults. The proposed method achieved notable improvements, with increases of 5.97% in accuracy, 3.86% in precision, 2.37% in sensitivity (recall), and 3.06% in F1-score.

1. Introduction

Defects in software systems pose a significant threat to their reliability. As a result, software fault (defect) prediction is a critical area in software engineering. Predicting potential faults enables developers to identify and address defective modules early, which improves software quality before release [1]. This is especially important because a large portion of software defects typically originates from a small number of modules, in line with the Pareto principle [2,3]. Therefore, the ability to forecast and isolate faulty components early greatly improves software quality outcomes.

Software defect prediction (SDP) primarily focuses on identifying defect-prone modules in the software before the testing phase begins. This predictive capability is crucial, as complete testing of all software modules is an expensive task [4]. Various methods have been proposed for software defect prediction, including metaheuristic-based feature selection, ensemble learning, deep learning models, and hybrid approaches [5,6]. These techniques have shown improved prediction accuracy and efficiency on benchmark datasets. While these methods have demonstrated promising results across various benchmark datasets, some limitations persist: high computational complexity, limited feature reduction in some cases, sensitivity to training data size, and evaluation on a limited number of datasets and machine learning algorithms. Furthermore, several studies focus solely on improving classification metrics without considering the scalability or integration of their models with deep learning-based architectures.

In this study, a discretized Binary Bedbug Optimization Algorithm (BBOA) is introduced to enhance the feature selection process for software fault prediction. BBOA is a binary development of the Bedbug Optimization Algorithm (BOA), specifically designed to identify the most effective subset of features that significantly improve fault prediction accuracy. Inspired by the swarm behavior of bedbugs, the algorithm explores the feature space and identifies an optimal subset of features. The key contributions of this paper are as follows:

• Developing BBOA to construct an effective feature selector that identifies the most relevant features from historical software fault datasets.
• Evaluating the proposed feature selection technique using five widely recognized real-world datasets in the domain of software fault prediction.
• Enhancing the predictive performance of the SDP by eliminating about 57% of the ineffective features identified by the suggested feature selector. The proposed feature selection-based SDP provides 96.04% accuracy, 97.10% precision, 99.21% recall, and a 97.73% F1-score.
• Unlike the related SDP methods, which are sensitive to training data size and were developed using limited datasets, the proposed SDP is created using five standard and real-world datasets.
• Time complexity and sensitivity to the features of the training dataset are the drawbacks of the previous SDP methods, which are addressed in the suggested SDP.

The study aimed to address the following research questions (RQs):

• RQ1: Can BBOA efficiently identify and eliminate irrelevant or redundant features from training datasets?
• RQ2: Does the BBOA enhance the accuracy, recall, precision, and F1-score of ML approaches in SDP?
• RQ3: How does BBOA perform compared to other optimization algorithms in terms of convergence speed?

The remaining sections are arranged as follows: Section 2 reviews related work on software fault prediction and feature selection methods. Section 3 elaborates on the proposed BBOA and its application in feature selection for fault prediction. Section 4 discusses the experimental framework, results, and comparisons with other feature selection methods. Finally, Section 5 concludes the paper and highlights future research directions.

2. Related Works

Software fault prediction has been extensively studied, given its importance in maintaining and improving software quality. Some researchers have focused on enhancing fault prediction by optimizing feature selection, which is critical in software metrics datasets. In this context, Arasteh et al. [4] proposed a binary Gray Wolf Optimizer (bGWO) to effectively select the most influential features for defect classification. The approach utilizes the swarm intelligence of gray wolves in a binary search space to reduce redundant and irrelevant features. Experimental validation on five standard benchmark datasets demonstrated significant improvements in predictive performance when bGWO was combined with machine learning classifiers. The study identified key features such as basic complexity, lines of code, and operand-related metrics as the most impactful for defect prediction. By minimizing the feature space, the proposed method not only improved classifier performance but also reduced computational overhead. This contribution is particularly valuable for real-world applications where lightweight and interpretable fault prediction models are preferred.

Jiang et al. [5] proposed a novel ensemble learning (EL) framework, NRSEL, to enhance software fault prediction (SFP) by diverse and accurate learners. Their approach introduces neighborhood approximate reducts (NARs) as a new method for perturbing the attribute space. This dual-mode strategy creates a more effective ensemble. Empirical evaluation on 20 public datasets shows that SMOTE-NRSEL consistently outperforms existing EL methods and provides improvements in accuracy and F1-score on average. Statistical analysis using paired t-tests, Friedman tests, and Nemenyi tests confirms the significance of these gains. NAR offers three advantages over traditional attribute reduction techniques: it can process numerical attributes by avoiding information loss from discretization; it supports the generation of sufficient base learners; and it contributes to the diversity and performance of the ensemble.

Jingchi et al. in [6] extended traditional wavelet shrinkage estimation methods to address the challenge of long-term fault prediction during the software testing phase. While conventional wavelet methods have limitations in forecasting future fault behavior, this study introduced a long-term prediction techniques that integrate denoised fault count data with predicted values. A key contribution of the work is the development of W-SRAT2, an advanced software reliability assessment tool that extends its predecessor (W-SRAT) by incorporating these prediction algorithms. Through extensive empirical evaluation on six real-world software projects and testing over 2640 prediction configurations, the proposed methods consistently outperformed traditional Software Reliability Growth Models (SRGMs) based on maximum likelihood estimation. This research highlights the effectiveness of wavelet shrinkage for long-range reliability forecasting and offers a practical, automated solution for supporting decision-making in testing resource allocation and release planning.

To enhance the effectiveness of software fault prediction, some studies have revisited the foundations of metric-based prediction by refining the underlying quality indicators. A new suite of object-oriented code metrics was suggested in [7] to enhance the performance of the class-level fault proneness in comparison to traditional metric sets (such as those in the PROMISE repository). The authors introduced three new metrics targeting class complexity, coupling, and cohesion. The complexity metric incorporates weighted contributions of class fields, methods, and inheritance hierarchies; the coupling metric measures inter-class dependencies; and the cohesion metric assesses the internal connectivity of class members. These metrics aim to provide semantically fault-sensitive measurements rather than trivial code counts. Experimental validation demonstrated that the proposed metric suite achieves notable improvements in predictive performance, with increases of over 2% in AUC and precision, and approximately 1.5% in F1-score and recall. This work underscores the importance of domain-specific metrics in fault prediction models.

Gorkem et al. [8,9] have increasingly explored the application of deep learning (DL) to enhance automated software defect prediction (SDP) by overcoming limitations of traditional ML approaches. The study found that the majority of DL-based approaches remain supervised and rely heavily on manually extracted software metrics. Among DL models, the Convolutional Neural Network (CNN) emerged as the most commonly used model. Parameter tuning plays a pivotal role in enhancing the performance of ML-based software fault prediction (SFP) models. To fill this gap, Nikravesh et al. [9] proposed a Differential Evolution-based Parameter Tuners (DEPTs) for SDP using modern DE variants and a Swift-Finalize strategy. Traditional parameter tuning techniques, such as Grid Search and Random Search, are limited by high computational costs and an inability to utilize past optimization experiences. In contrast, the DEPTs aim to balance optimization effectiveness with runtime efficiency. The authors conducted an extensive empirical evaluation using 10 open-source projects. Results show that three out of five DEPTs improved prediction performance. This work reinforces the growing consensus that tuned ML models outperform their default-configured counterparts; furthermore, it highlights the need for intelligent tuning mechanisms.

Anbu et al. [10] proposed a Firefly Algorithm (FA)-based feature selection method for software defect prediction (SDP); the suggested feature selector was combined with different classifiers, such as SVM, Naïve Bayes, and KNN, on the KC1 dataset. The approach optimizes both classification accuracy and feature subset size. The results of experiments conducted indicate that SVM with a feature selector improved accuracy by up to 4.53% compared to its baseline. Precision, recall, and F-measure also improved, which demonstrates FA’s effectiveness in identifying relevant features. However, the study is limited by its evaluation on a single dataset and lacks comparison with other metaheuristic feature selectors like PSO or GA. Additionally, computational cost is not discussed, and the proposed multi-objective extension remains unexplored. Despite these limitations, the work highlights FA’s potential in enhancing SDP through efficient feature selection.

In [11], a machine-learning-based SDP using a feature selection method called SBEWOA was presented. This method combines Binary Whale Optimization with Grey Wolf and Harris Hawks strategies to improve the selection of relevant features. Applied to 16 PROMISE datasets, the framework includes preprocessing, resampling, and classifier comparison. Random Forest consistently outperformed other classifiers and state-of-the-art feature selection methods in terms of AUC and reduced feature count. The key strengths of the proposed approach include its high predictive accuracy, effective feature selection, and robustness across diverse datasets. However, it suffers from high computational complexity and only moderate feature reduction in some cases. Despite these limitations, SBEWOA presents a promising direction for improving fault prediction performance in software engineering tasks.

A recent study [12] proposed a hybrid approach for software fault prediction by combining an autoencoder with the K-means clustering algorithm. The autoencoder is employed for feature selection and dimensionality reduction, which leads to improved clustering accuracy and reduced training time. Experimental results on NASA PROMISE datasets demonstrated high performance, with 96% accuracy and 93% precision. Although the method utilizes the feature selector, the method’s effectiveness is sensitive to the size and characteristics of the training data. A further drawback is that the model has not been evaluated on modern software systems with evolving architecture. In [13], a Binary Chaos-based Olympiad Optimisation Algorithm (BCOOA) was suggested for feature selection in software defect prediction. By employing BCOOA, the study identified a minimal and highly effective subset of features (such as McCabe complexity, Halstead metrics, and code structure indicators) from the PROMISE repository. Experimental results indicate that the method provides 91.13% accuracy, 92.74% precision, and 97.61% recall. However, the method’s application was limited to a single dataset with homogeneous features, and its integration with deep learning models remains unexplored.

Table 1 compares the main merits and demerits of the related methods. This study addresses the challenges of the related methods by developing an efficient optimization algorithm to select highly effective features. The introduced feature selector eliminates ineffective and noisy features. The resulting effective and minimal dataset is then used to develop an accurate classifier using various ML approaches. The suggested method enhances both the generalizability and reliability of fault prediction models. Moreover, the study handles the imbalanced datasets effectively and provides robust performance across diverse software projects and datasets.

Table 1. The main characteristics of the related methods.

Ref	Method	Key Results	Contribution	Limitation
[4]	Binary Gray Wolf Optimizer (bGWO) + ML	Improved accuracy (95%), F1 (97%), and reduced feature size	Effective feature selection for fault classification using swarm intelligence	Limited to traditional ML; no deep learning exploration
[5]	Ensemble Learning (NRSEL) with NAR + SMOTE	Improved average AUC (90.70) and F1-score (90.51%); statistically significant	Robust ensemble via neighborhood attribute perturbation	The stability of the suggested method and the feature importance were not taken into consideration
[6]	Wavelet-based long-term fault trend estimation (W-SRAT2)	Outperformed traditional SRGMs	Extensive Evaluation of Wavelet-Based Methods and Broad Applicability	Limited to the specific dataset and a limited evaluation metric
[7]	New OO Metrics for class-level fault prediction	Improved accuracy (92%) and AUC (82.50%)	Domain-specific metrics capturing complexity, coupling, and cohesion	Insufficient AUC; no integration with advanced ML models
[8]	Deep Learning review (CNN focus)	DL models outperform ML when tuned	Comprehensive DL-based SDP analysis	DL models often rely on manually extracted metrics
[9]	Differential Evolution-based Parameter Tuning (DEPTs)	Improved accuracy in 70% benchmarks	Development of Differential Evolution (DE) as parameter tuners to improve software fault prediction	Focusing only on the parameters tuning and feature importance analysis was not considered.
[10]	Firefly Algorithm (FA) + SVM, NB, KNN	Improved accuracy (90%) and recall (91%)	FA-based efficient feature selector	Evaluated on limited datasets; lack of feature importance analysis
[11]	SBEWOA (Binary Whale + Grey Wolf + Harris Hawks)	High AUC, effective feature selection	Robust hybrid metaheuristic for feature selection	High computational complexity; limited feature reduction in some cases
[12]	Autoencoder + K-Means	Accuracy 96%, Precision 92%	Hybrid unsupervised model for dimensionality reduction	Sensitive to the performance of the autoencoder; Higher false negative rate
[13]	Binary Chaos-based Olympiad Optimization Algorithm (BCOOA)	Accuracy 91.13%, Recall 97.61%	Optimal feature selection for ML-based classifiers	Time complexity and sensitive to the training dataset

Table 1. The main characteristics of the related methods.

Ref	Method	Key Results	Contribution	Limitation
[4]	Binary Gray Wolf Optimizer (bGWO) + ML	Improved accuracy (95%), F1 (97%), and reduced feature size	Effective feature selection for fault classification using swarm intelligence	Limited to traditional ML; no deep learning exploration
[5]	Ensemble Learning (NRSEL) with NAR + SMOTE	Improved average AUC (90.70) and F1-score (90.51%); statistically significant	Robust ensemble via neighborhood attribute perturbation	The stability of the suggested method and the feature importance were not taken into consideration
[6]	Wavelet-based long-term fault trend estimation (W-SRAT2)	Outperformed traditional SRGMs	Extensive Evaluation of Wavelet-Based Methods and Broad Applicability	Limited to the specific dataset and a limited evaluation metric
[7]	New OO Metrics for class-level fault prediction	Improved accuracy (92%) and AUC (82.50%)	Domain-specific metrics capturing complexity, coupling, and cohesion	Insufficient AUC; no integration with advanced ML models
[8]	Deep Learning review (CNN focus)	DL models outperform ML when tuned	Comprehensive DL-based SDP analysis	DL models often rely on manually extracted metrics
[9]	Differential Evolution-based Parameter Tuning (DEPTs)	Improved accuracy in 70% benchmarks	Development of Differential Evolution (DE) as parameter tuners to improve software fault prediction	Focusing only on the parameters tuning and feature importance analysis was not considered.
[10]	Firefly Algorithm (FA) + SVM, NB, KNN	Improved accuracy (90%) and recall (91%)	FA-based efficient feature selector	Evaluated on limited datasets; lack of feature importance analysis
[11]	SBEWOA (Binary Whale + Grey Wolf + Harris Hawks)	High AUC, effective feature selection	Robust hybrid metaheuristic for feature selection	High computational complexity; limited feature reduction in some cases
[12]	Autoencoder + K-Means	Accuracy 96%, Precision 92%	Hybrid unsupervised model for dimensionality reduction	Sensitive to the performance of the autoencoder; Higher false negative rate
[13]	Binary Chaos-based Olympiad Optimization Algorithm (BCOOA)	Accuracy 91.13%, Recall 97.61%	Optimal feature selection for ML-based classifiers	Time complexity and sensitive to the training dataset

The previous studies have several gaps. Most were limited to traditional machine learning methods. They often ignored feature importance and model stability analysis. Many were tested on a few datasets and used limited evaluation metrics. Some showed low AUC values and were not combined with advanced ML models. Deep learning methods relied on manually extracted features. Several focused only on parameter tuning and missed feature importance analysis. Others had high computational costs, limited feature reduction, and were sensitive to training data or autoencoder performance, leading to higher false negatives.

3. Methods

3.1. Defect Prediction Process

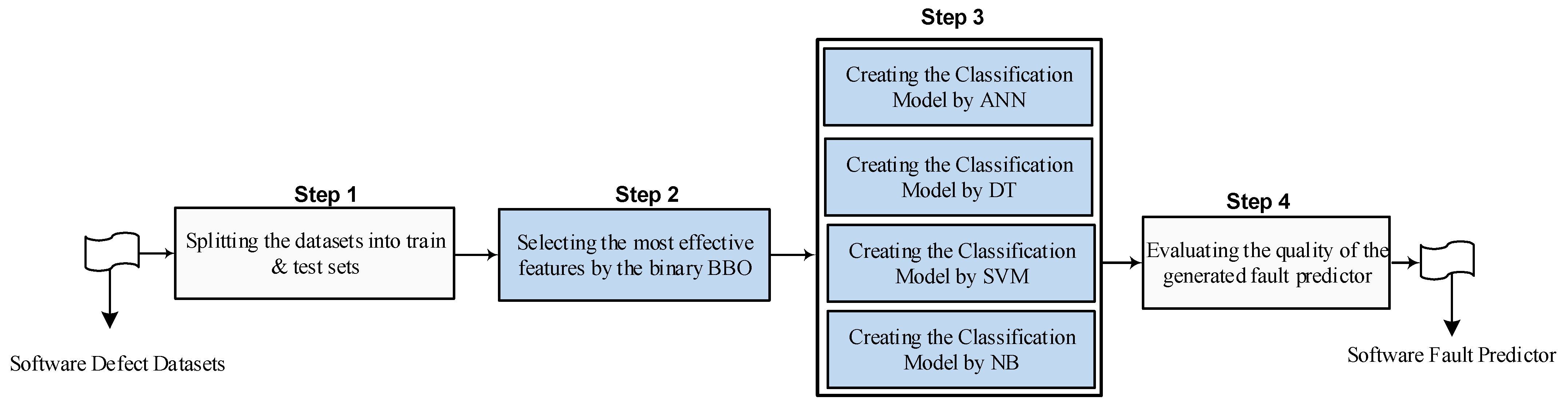
The present section describes a novel methodology for SDP that integrates the BBOA approach with various ML approaches. BBOA was utilized to identify the most influential features of datasets for use in ML models. The ML techniques applied in this study include k-nearest neighbors (KNN), artificial neural networks (ANN), DT, Naive Bayes (NB), and SVM. The suggested methodology’s workflow is illustrated in Figure 1. Standard datasets were employed to train the ML models and investigate the defect predictors’ performance [14]. BBOA is an important feature selector that identifies the most impactful features for defect prediction. This significantly boosts the accuracy and precision of classifiers, ensuring more reliable results.

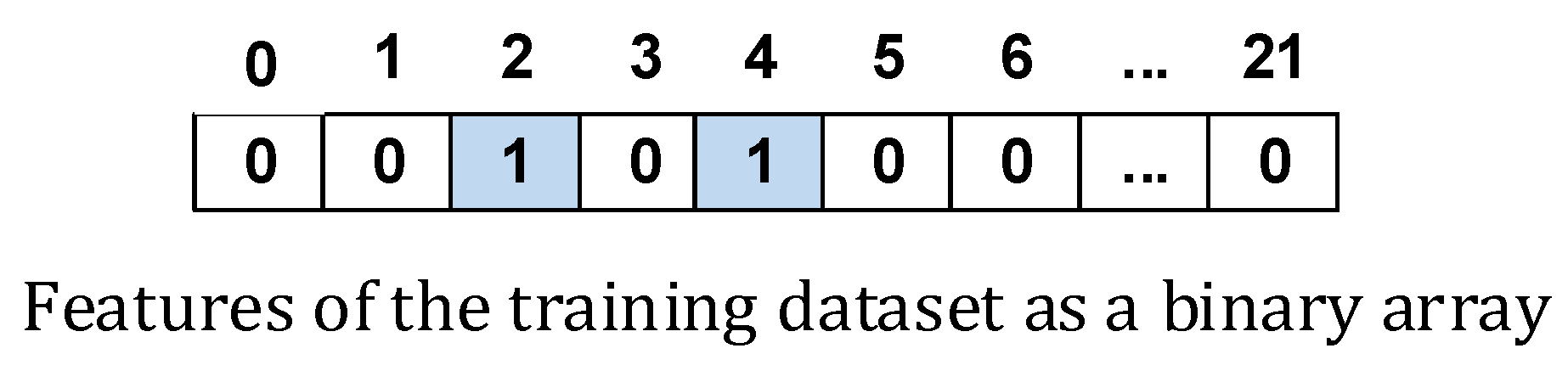
In the BBOA-based approach, each individual (bedbug) is modeled as a binary feature vector consisting of 21 elements. These elements correspond to the features labeled F1 to F21. Each bit in the binary array represents a specific feature, as depicted in Figure 2. A value of zero indicates that the feature is excluded, while a value of one indicates its inclusion in training. At the end of each BBOA iteration, the fitness value is calculated for every binary feature vector. This fitness value is derived from the training error and the number of chosen features, aiming to minimize both during each iteration. The algorithm iteratively refines the feature set to achieve the lowest possible training error.

3.2. Datasets Used for Training

The utilized datasets were sourced from the publicly available NASA resource [14]. These datasets encompass a variety of software metrics, including McCabe’s criterion, Halstead’s metrics, branch count, and five unique measures associated with lines of code. The datasets pertain to five projects: CM1, KC2, JM1, PC1, and KC1. The CM1 dataset, developed in C, includes 498 models (349 for training and 149 for testing) and represents an instrument for NASA spacecraft with a defective model percentage of 9.7%. The JM1 dataset, also in C, comprises 10,885 models (7619 for training and 3266 for testing) and is designed for predictive ground systems using real-time simulations, with a defective model percentage of 19%. The KC1 dataset, developed in C++, contains 2109 models (1476 for training and 633 for testing) and is used for data storage management in processing ground data, with a defective model percentage of 15.4%. The KC2 dataset, also in C++, includes 522 models (365 for training and 157 for testing) and supports scientific data processing, with a defective model percentage of 20%. Lastly, the PC1 dataset, created in C, consists of 1109 models (776 for training and 333 for testing) and is used for managing flight operations of Earth satellites, with a defective model percentage of 6.8%.

3.3. Feature Selection Method

After creating the dataset, the next phase involves deploying the BBOA for feature selection. This essential step isolates the most relevant features in the dataset, enhancing the performance of ML-based classification models. BBOA operates as a swarm-based optimization framework, integrating local and global search strategies through a heuristic, population-based, divide-and-conquer approach. Inspired by the Bedbug swarm, BBOA conceptualizes each population member as a bedbug striving to achieve optimal outcomes [15]. In BBOA, each bedbug is represented by a vector of 21 elements, corresponding to the total number of features. These randomly initialized populations include n rows (vectors) and 21 columns. The iterative process of BBOA ensures that the algorithm selects the most relevant features while minimizing redundancy.

The developed Binary Bedbug Optimization Algorithm (BBOA) is a modified version of the original BBOA, designed for binary feature selection tasks. It uses the sigmoid function to convert continuous values into binary, where the value 1 represents a selected feature and 0 represents an exclusion. Each bedbug represents a potential solution, and the population is iteratively updated by moving individuals toward the best current solution. Through this process, the algorithm transforms the continuous search space into a discrete binary form suitable for feature selection. BBOA is a swarm-based optimization framework that balances exploration and exploitation to identify the most relevant features while reducing redundancy. It can be independently applied with various machine learning and deep learning models, such as ANN, SVM, DT, and NB, by adjusting its fitness function based on their classification performance. This approach improves model accuracy and efficiency by selecting the most important features and minimizing irrelevant data.

The NASA datasets used in this study consist of 21 essentials for prediction and classification tasks, categorized into McCabe’s metrics, Halstead’s measures, and defect-related parameters. The features include code line count (LOC), cyclomatic complexity measure (v(g)), core complexity (eV(g)), structural complexity (iv(g)), total operators and operands (N), content volume (v), calculated program length (L), programming difficulty (D), cognitive intelligence (I), programming effort (B), bug predictions (E), programming time (T), total line count (LOCode), comment line count (LOComment), blank line count (LOBlank), mixed code and comment lines (LOCodeAndComment), distinct operators (uniq_Op), distinct operands (uniq_Opnd), total operators (total_Op), total operands (total_Opnd), and flow graph branch count (branchCount). Additionally, the defect count is included as a critical feature for defect prediction. BBOA ensures the selection of a robust subset of these features for optimized classification performance.

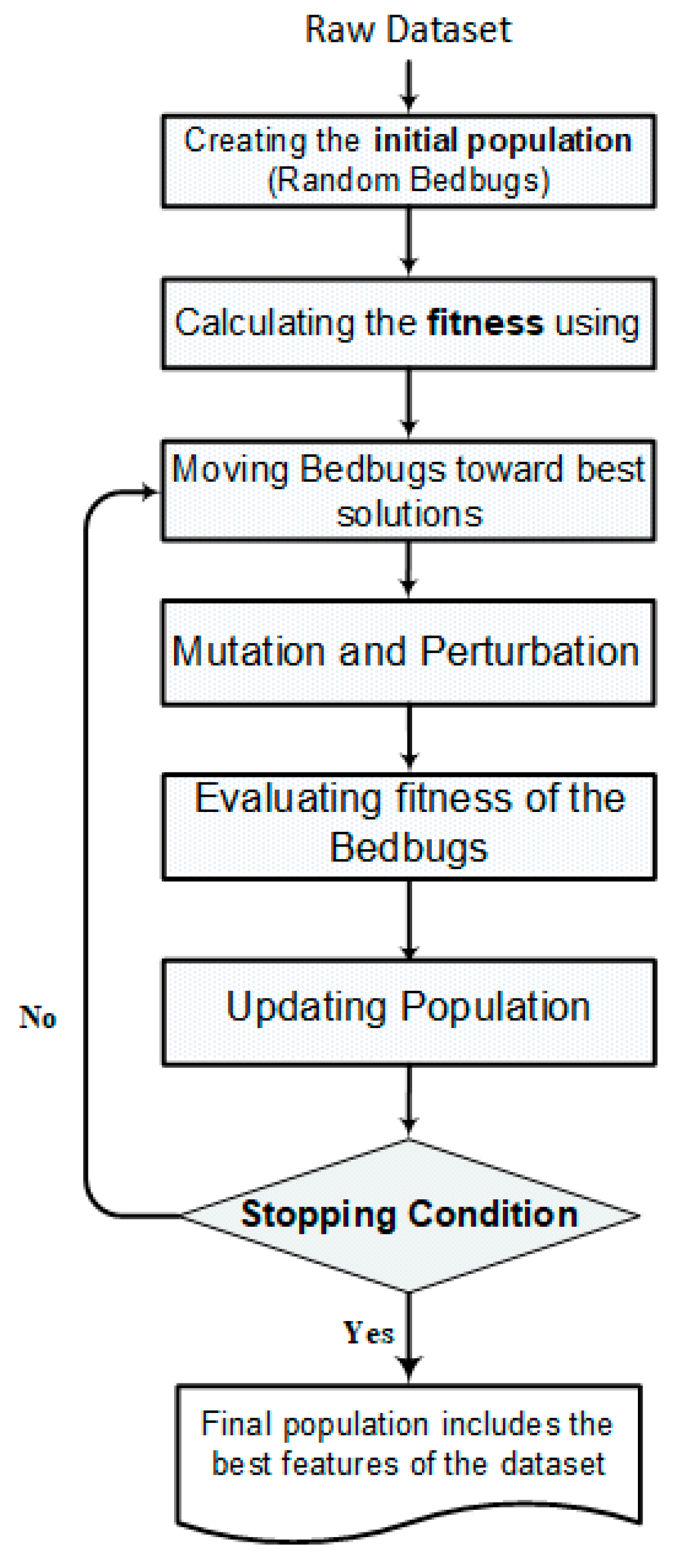
As illustrated in Figure 3, the BBOA workflow demonstrates its capability for addressing optimization challenges. It employs a population that represents bedbugs. Each bedbug explores distinct regions of the solution space. Within the BBOA framework, competitive exploration and exploitation have been applied. Each individual tracks their progress using a memory-based mechanism. The population is initially sorted, and a bedbug with the highest performance is designated as the global best, and the lowest as the global worst. A local search occurs to enhance the movement technique in the BBOA. Bedbugs in each population aim to imitate the highest-performing individual. In the BBOA, as shown in Figure 4, bed bugs move towards better solutions by two main behaviors (exploitation and exploration) inspired by real-world bed bug movement.

In the BBOA, the movement behavior of each bedbug is governed by a balance between exploration and exploitation strategies, inspired by the biological instincts of real bedbugs when searching for prey. Each bedbug adjusts its position in the search space based on three guiding components derived from both individual experience and collective intelligence. LBest (Local Best) refers to the best position an individual bedbug has found, which represents its personal success and guides its future movement. GBest (Global Best) is the best position discovered by any bedbug in the entire population, influenced by pheromone signals that promote cooperation and information sharing among bedbugs. SBest (Sensory Best) represents the bedbug’s attraction to heat emitted by the prey, helping it adapt to dynamic environments by using environmental cues during the search process.

As illustrated in Figure 4, the combined influence of LBest, GBest, and SBest governs the movement trajectory of each bedbug. After identifying these best values, the velocity and position of each bedbug are updated iteratively using Equations (3) and (4). These equations incorporate random factors and weighting coefficients to ensure a diverse search while gradually focusing on optimal regions. This movement mechanism allows BBOA to navigate complex optimization landscapes efficiently, avoid premature convergence, and increase the likelihood of finding global optima.

As illustrated in Equation (1), each bedbug adjusts its position and velocity based on the $LBest, GBest \mathrm{and} SBest$. Here, $V_i\left(t\right)$ shows the velocity of bedbug $i$ at iteration $t$, $X_i\left(t\right)$ displays the current position of bedbug i, and $r_1$, $r_2$, $r_3$ and $r$ represent the random numbers between 0 and 1. Furthermore, $\alpha ,\beta ,$ and $\gamma$ stand for the acceleration (learning) coefficients, and their values are selected randomly from the interval [0, 2]. Moreover, $\omega$ indicates the inertia weight, which is selected from [0.3, 0.9]. In the implemented BBOA, bedbugs tend to move towards the best solution in the population, and the best solution represents the most optimal feature subset.

$$\begin{gathered} V_i\left(t+1\right)=\mathrm{ }{\omega \times V}_i\left(t\right)+\alpha \times r_1\times \mathrm{ }\left({LBest}_i-X_i\left(t\right)\right)+\mathrm{ }\beta \times r_2\times \left(GBets-X_i\left(t\right)\right) \\ +\mathrm{ }\gamma \times r_3\times \mathrm{ }\left({SBest}_i-X_i\left(t\right)\right) \end{gathered}$$

(1)

$$X_i\left(t+1\right)=X_i\left(t\right)+V_i\left(t+1\right)$$

(2)

To evaluate the quality of selected feature vectors, fitness is calculated using Equations (3) and (4). Fitness serves as a minimization function that considers both the training error and the number of selected features. The training error is normalized between 0 and 1, computed as the difference between the model’s accuracy and 100, divided by 100. The second term in Equation (3), the number of features, also undergoes normalization within the range [0, 1] to ensure consistent scaling. The resulting fitness value represents the trade-off between reducing training error and feature count. The stopping criteria for the proposed BBOA-based feature selector are adapted to ensure both efficiency and solution quality. The algorithm stops when it reaches the maximum number of iterations, meaning the search process has run for the predefined number of cycles. Additionally, the algorithm stops if there is no improvement in the fitness value after a considerable number of consecutive iterations.

Fitness(i) = ErrorPercentage(i) + Used Features

(3)

$$ErrorPercentage\left(i\right)={\displaystyle \frac{100-Accuracy\left(i\right)}{100}}$$

(4)

3.4. Binary Strategy Using the Sigmoid Function in BBOA

The current section introduces a new binary strategy for the BBOA based on the Sigmoid function. Each solution (bedbug) in the population is assigned a unique serial number. As the objective is to select or exclude features, the binary solution is expressed using values of 0.0 and 1.0. A feature is selected if its binary value is one, while it is excluded if the value equals zero. The function utilized to map the continuous values in the BBOA’s individual array to binary values was the Sigmoid function [16]. As shown in Figure 1, the proposed BBOA is specifically employed to identify effective features. BBOA adjusts to problems requiring binary solutions by reconfiguring entities within the state space. This adaptation ensures its effectiveness in tackling binary optimization challenges. For feature selection tasks, this adaptation enables the solution to be constrained to binary values, creating a discrete variant suitable for BBOA.

The sigmoid function is suitable for binary transformer models in software fault prediction because it is smooth and differentiable, allowing efficient weight updates during training. It also keeps the output values stable, which is useful for imbalanced datasets that contain more non-faulty than faulty modules. Overall, it provides a simple and effective way to map learned features to binary outcomes in software fault prediction.

In BBOA, the exploration and exploitation update the bedbug population iteratively by attracting each individual toward the global best solution (best student). The position of the ith bedbug in the tth dimension is represented by the vector X_i (t). The Sigmoid equation is subsequently utilized in binary format to adjust the position of the solution within BBOA, as demonstrated in Equation (5). This function generates an output ranging from 0 to 1, representing the likelihood of a feature being selected. To convert this continuous value into a binary format, a threshold is introduced. Equation (6) incorporates a random threshold, rand, which follows a uniform distribution ranging from 0 to 1, to determine whether a feature is included (1) or excluded (0). Using Equations (5) and (6), the solutions in BBOA’s population are transformed into a discrete binary search space. This ensures the algorithm effectively navigates binary optimization problems.

$$SG\left(X_i\left(t\right)\right)={\displaystyle \frac{1}{1+{\mathrm{e}}^{-X_i\left(t\right)}}}$$

(5)

$$X_i\left(t+1\right)=\left\{\begin{array}{c}0, if rand<SG\left(X_i\left(t\right)\right),\\ 1, if rand\ge SG\left(X_i\left(t\right)\right).\end{array}\right.$$

(6)

This binary adaptation of BBOA enables an efficient search within the solution space, ensuring only the most related features are selected for ML model training. BBOA enhances the effectiveness of ML classifiers by reducing the feature set, while also lowering computational complexity. This makes it a reliable and efficient solution for high-dimensional feature selection challenges. Integrating Sigmoid-based binary mapping and fitness evaluation ensures that the algorithm effectively balances accuracy and simplicity in feature selection.

4. Results and Discussion

The experimental setup outlined in the current section establishes the foundation for evaluating the effectiveness of the proposed BBOA in SDP. The experimental design systematically evaluates BBOA’s performance by addressing key variables and comparing it to traditional feature selectors. The following subsections present a detailed analysis of the results, emphasizing BBOA’s impact on ML’s performance.

4.1. Datasets and the Experiments Platform

The effectiveness of the introduced approach in SDP is examined next. The ML approaches were selected based on the problem of predicting software faults and the characteristics of the datasets used. The size of datasets, noise of the dataset, quantity of features in the datasets, the datatype of the features, and distribution of the dataset values are the criteria for the ML selection. Software defect datasets often consist of features like code metrics, and the ML approaches must handle numerical data. The selected ML approaches were used to discover how specific software metrics contribute to defect prediction.

Most of the defect datasets are imbalanced, and the quantity of non-defective instances is greater than the quantity of defective instances. Most of the references cited in the manuscript, except ref. [5], which utilizes ensemble Learning (NRSEL) with NAR and SMOTE, do not apply any balancing techniques. Methods such as bGWO, W-SRAT2, DEPTs, FA, SBEWOA, and Autoencoder with K-Means mainly optimize the model performance without addressing data imbalance. They evaluate classifiers on unbalanced datasets, which can bias results toward the majority class. Incorporating balancing methods such as SMOTE or undersampling could improve fairness, accuracy, and the reliability of their findings.

SMOTE (Synthetic Minority Over-sampling Technique) is used to balance the dataset by creating synthetic samples of the minority class. In PROMISE datasets, the number of defective modules is much lower than that of non-defective modules, leading to class imbalance. SMOTE helps address this by generating new, synthetic defect samples from existing samples rather than simply duplicating them. This process ensures a better balance between the two classes and helps the model learn patterns from the minority class more effectively. SMOTE improves classifier performance, particularly in detecting defective modules, and reduces bias toward the majority class.

The proposed method combines the Binary Bedbug Optimization Algorithm (BBOA) with several ML models (ANN, DT, SVM, and NB) for feature selection and classification. BBOA identifies the most relevant features by minimizing error and reducing feature count. Each classifier then uses these selected features to build SDP models. In the method, the dataset is divided into training and testing sets, and BBOA runs for 100 iterations with 40 bedbugs to find the best feature subset. The ML is trained using the selected features, and performance is measured using accuracy, precision, recall, and F1-score. The process is repeated to improve reliability, and the results show that integrating BBOA improves feature selection, classification accuracy, and efficiency in software defect prediction. Algorithm 1 shows the integration of the suggested BBOA with DT.

Algorithm 1. The integration of the suggested BBOA with DT

Input: Dataset (e.g., CM1) Output: Classification performance metrics (Accuracy, Precision, Recall, F1) 1. Load dataset     - Separate inputs (features) and outputs (target labels) 2. Split data     - Divide the dataset into training and testing sets 3. Define parameters     - MaxIt = 30       // Maximum iterations for BBOA     - nBedbugs = 40    // Population size 4. For i = 1 to 3 do      Feature selection using BBOA      Identify selected features      Train Decision Tree using selected features      Test Decision Tree on test data      Evaluate model performance      Compute confusion matrix (TP, TN, FP, FN)      Accuracy = (TP + TN)/(TP + TN + FP + FN)      Precision = TP/(TP + FP)      Recall     = TP/(TP + FN)      F1 = 2 × (Precision × Recall)/(Precision + Recall)      Store performance results      Plot comparison between real and predicted outputs     End For 5. Display final results

The selected ML approach is suitable for handling this type of dataset. Some of the selected ML approaches, such as ANN, DT and SVM, provide strong performance on complex datasets. Finally, the selected algorithms are simple to implement and tune. To establish a baseline, results are first obtained using traditional ML approaches (i.e., ANN, SVM, DT, KNN, and NB) applied to datasets containing all features without any prior feature selection process. Subsequently, these results are compared with those obtained using the BBOA, designed explicitly for effective feature selection. This comparison highlights the effect of the proposed technique in enhancing ML approaches’ performance.

The experiments were performed using MATLAB 2022 on a Windows 10 machine with a Core i7 Intel processor and 4.0 GB of RAM.

Table 2. Parameter values for BBOA that are used in selecting significant features.

Parameter	Description	Recommended Value/Range
Population Size ($N$)	Number of bed bugs	40
Max Iterations	Total number of optimization cycles	100
$\beta$	Bed bug reproduction rate	0.5
$A$	Step Size	0.08

summarizes the calibration parameters employed for BBOA and ACO in the context of selecting significant features for predicting software defects. The evaluation framework compares ML approaches’ performance by running them with and without feature selection, focusing on main metrics such as accuracy, precision, and recall. The experiments use BBOA to showcase the benefits of a reduced feature set, improving both computational efficiency and classifier performance. Additionally, binary ACO is used as a benchmark to assess BBOA’s effectiveness in handling high-dimensional datasets. The BBOA parameters were initially selected based on values commonly used in prior studies on similar optimization problems; then, these values were adapted based on the obtained results during the experiments. The values indicated in Table 2, on average, are the best values.

For each dataset, 70% of the records were designated for training ML models, ANN, SVM, DT, KNN, NB, and SVM, while the remaining 30%, excluded from the training process, were set aside for testing and performance evaluation.

Table 3. Characteristics of the utilized datasets.

Dataset	No. of Records	No. of Test Records	No. of Train
CM1	496	149	347
KC2	522	157	365
PC1	1109	333	776
JM1	10,885	3266	7619
KC1	2109	633	1476

overviews the key characteristics of the training and testing datasets used in these experiments. CM1 is based on a software system created for one of NASA’s satellites using the C Language. According to the NASA Metrics Data Program (MDP), the software project at NASA, especially one utilizing a satellite sensor, is associated with the CM1 dataset. In contrast to the flight-related CM1 datasets, the KC1 offers information about ground-based software for a controller system, which is utilized for data processing and management, mission scenario simulation, and vital support for NASA’s operational systems. The software in KC1 deals with storage management tasks, such as allocating, organizing, and maintaining data in a storage system. PC1 is a component of the onboard flight software for the data processing of a spacecraft. The main functions of this mission-critical software are monitoring and controlling the telemetry information and managing communications between systems on the ground and spacecraft.

Similarly to the KC1 dataset, KC2 originates from a ground-based system. KC2 represents a different version and configuration of the software for managing data storage and related functionalities. This software is responsible for allocating, organizing, and maintaining data in storage systems and ensuring efficient and reliable data access. The NASA JM1 dataset is associated with a real-time ground-based software system developed in the C language. JM1 represents a real-time predictive system used for ground-based mission operations.

The software fault prediction datasets vary in size, from small ones like CM1 (496 records) to large ones like JM1 (10,885 records). Most of these datasets are imbalanced, with far fewer faulty modules than non-faulty ones. This can make models biased toward predicting non-faulty modules. Small datasets like CM1 and KC2 are more affected because faulty examples are very few. SMOTE (Synthetic Minority Over-sampling Technique) is commonly used to handle this problem. It creates synthetic examples of the minority class to balance the dataset. This helps models learn patterns of faulty modules better and improves prediction performance for the minority class.

The main functions of JM1 software are monitoring spacecraft and satellite performance, analyzing telemetry data, and managing mission-critical processes. A confusion matrix was used to assess model performance, providing the metrics needed to calculate sensitivity, specificity, and efficiency. This setup ensured that the evaluation criteria effectively captured the accuracy and robustness of the models under both standard and feature-selected conditions.

4.2. Evaluation Metrics

The current study uses accuracy, recall, precision, and F1-score as key evaluation metrics to effectively classify software functions (modules). The matrix of confusion is utilized as a vital analytical tool to evaluate the performance and accuracy of classification models. It categorizes predictions into four essential metrics:

• True-Positive (TP): Defective records (modules) classified correctly as defective.
• True-Negative (TN): Non-defective records classified correctly as non-defective.
• False-Negative (FN): Defective records classified incorrectly as non-defective.
• False-Positive (FP): Non-defective records classified incorrectly as defective

From the confusion matrix, critical performance measures such as accuracy, precision, recall, and F1-score are derived. These metrics are instrumental in evaluating the classification models’ effectiveness in predicting software module defects. A comprehensive experimental setup was designed using classifiers from multiple ML approaches (ANN, SVM, DT, and NB). This systematic evaluation approach provides an analysis of the methodology’s effectiveness in improving classification models for SDP, highlighting its potential advantages in feature selection and model performance enhancement.

4.3. Selected Features by BBOA (RQ1)

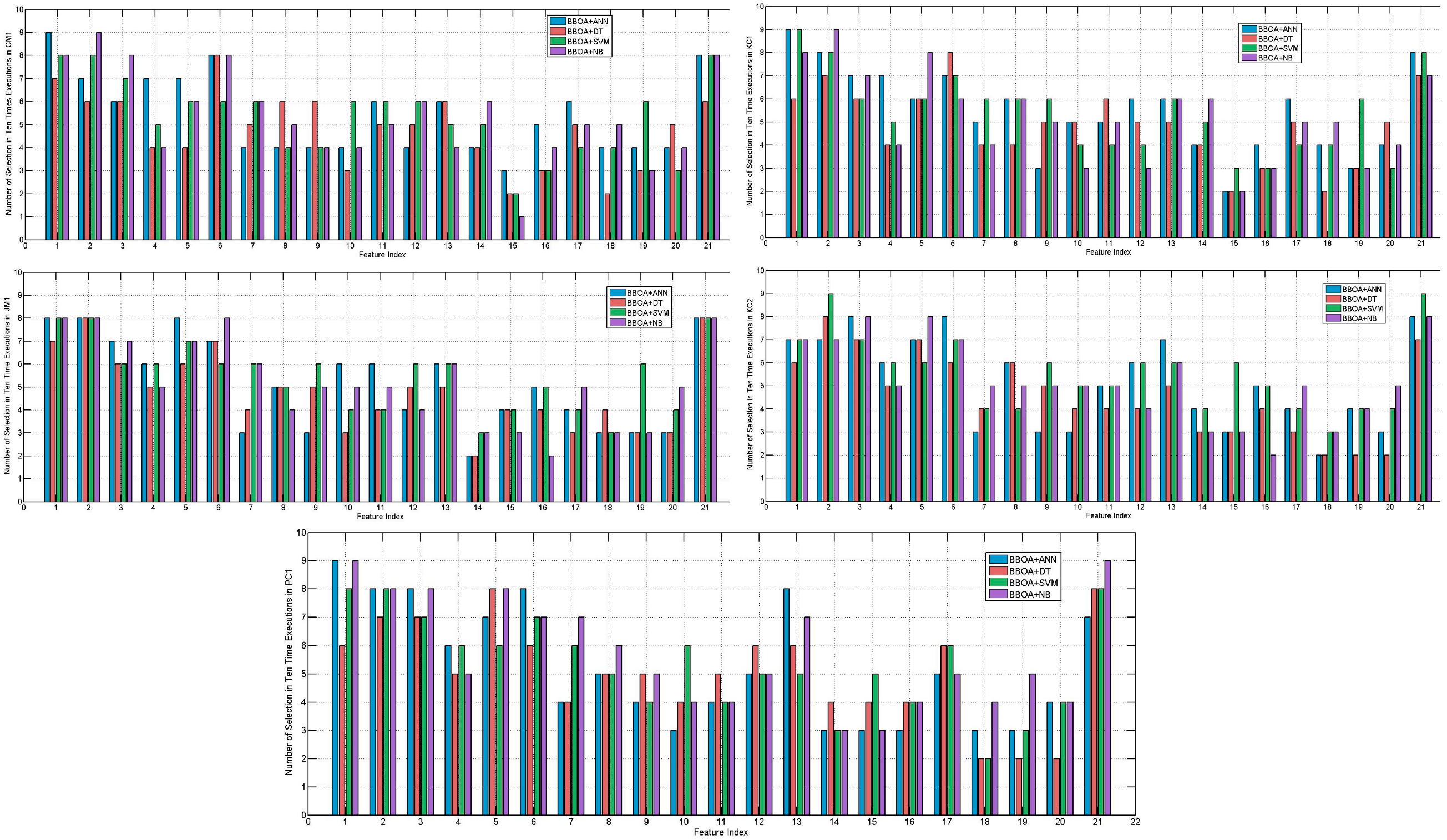
The first experiment employed the datasets to investigate the effectiveness of the suggested method in finding the most effective features of the dataset (RQ1). Feature selection plays a critical role in enhancing the performance of SDP methods by improving classification accuracy and eliminating redundant features. In this study, the performance of the BBOA in feature selection was evaluated and compared to the related methods. 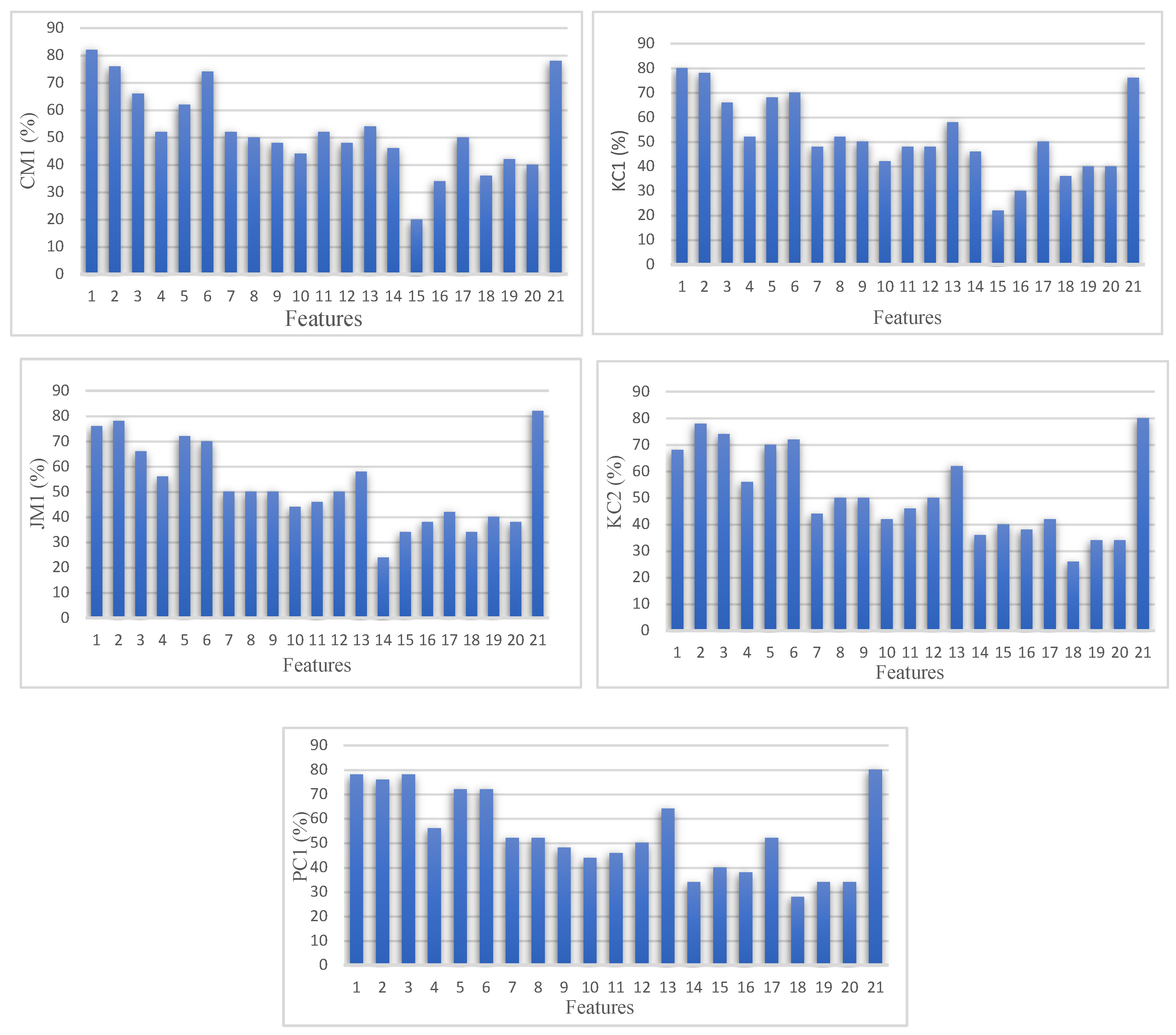The comparative analysis of results in the CM1 dataset, depicted in Figure 5, demonstrates the effectiveness of the BBOA in SDP feature selection. The BBOA was employed to select 21 features, and its performance was evaluated in combination with various ML algorithms. In all classifiers, the selected features consistently achieved relatively high importance scores, indicating their significant contribution for improving the SDP performance. Among the models, BBOA+ANN generally assigned higher scores across most features (especially features 1, 2, 5, 6, and 21). BBOA+KNN also demonstrated substantial utilization of features 1, 2, 5, and 21. Conversely, BBOA+DT and BBOA+NB showed greater variability, with lower scores for certain features (14–17), indicating a more selective or localized reliance on these features. Interestingly, features 1, 2, 6, and 21 consistently received high scores across all models, suggesting that these features are critical regardless of the classifier used. In contrast, features 14 and 15 often received lower importance scores, implying a weaker contribution to SDP decisions. Overall, these results show that BBOA effectively identifies a compact, informative feature subset of CM1.

The BBOA feature selector was evaluated on the KC1 dataset using five different classifiers: ANN, DT, SVM, KNN, and NB. Overall, BBOA demonstrated strong and consistent performance across all classifiers. BBOA combined with ANN and SVM maintained stable results, achieving higher defect prediction rates in most projects. BBOA+KNN also achieved competitive results, particularly excelling on features 1, 2, 5, and 21. Although minor variations were observed, especially with DT and NB in some classifiers, BBOA consistently selected effective feature subsets that enhanced the classification accuracy.

The BBOA feature selector was applied to the JM1 dataset in combination with different ML models. The selected feature subsets showed high consistency among classifiers. BBOA+ANN and BBOA+SVM achieved relatively stable and higher feature selection counts across most MLs. BBOA+KNN and BBOA+NB also demonstrated competitive selections but showed slightly more variation in features 14–19. In the PC1 dataset, BBOA combined with ANN and NB achieved higher feature selection counts in most ML algorithms. In contrast, BBOA+DT often selected fewer features, suggesting a tendency toward more minimal subsets with DT. BBOA+SVM and BBOA+KNN maintained a balanced selection strategy, selecting moderate numbers of features across different projects. Overall, BBOA succeeded in identifying compact feature subsets across different MLs, confirming its robustness for SDP on all datasets.

As shown in Figure 6, the feature selection rates achieved by the proposed BBOA on the CM1, KC1, JM1, KC2, and PC1 datasets show a varying degree of importance among the features. The selection rates ranged from a high of 82% to a low of 20%, indicating that some features were much more consistently selected across different runs. Features with selection rates above 70% can be considered highly effective for SDP. On the other hand, features with rates below 50% were selected less frequently, implying either lower relevance or potential redundancy. Notably, the lowest selection rate at 20% highlights features that may have minimal impact on prediction outcomes. Overall, BBOA effectively distinguished between more and less effective features, supporting its capability to enhance classification models by prioritizing key features.

Features such as Feature 1 (LOC) and Feature 21 (Branch count) consistently achieved the highest selection probabilities, with average rates of 76.8% and 79.2%, respectively, across all datasets. This highlights their dominant influence on model performance, suggesting they capture key characteristics relevant to defect prediction. Features 2 (Cyclomatic Complexity), 6 (volume of the code), and 5 (number of operators and operands in the code) also demonstrated strong selection rates, averaging 77.2%, 71.6%, and 68.8%, respectively, reinforcing their relevance. Conversely, some features, particularly Features 15 (count of blank lines), 16 (count of lines with comments), and 18, showed much lower average selection rates (31.2%, 35.6%, and 32%, respectively). Their lower probabilities indicate lesser importance or redundancy in the defect prediction model. These features were less consistently chosen across datasets and ML models, implying that their contribution to the SDP performance is relatively minor.

Additionally, the overall selection trends reveal that while a core set of features (e.g., 1, 2, 6, and 21) is vital across all datasets, the relevance of other features fluctuates depending on the dataset. This variability reflects the differences in project characteristics and data distributions. Ultimately, BBOA’s feature selection strategy successfully identified a compact and effective subset of features, improving the interpretability and efficiency of the defect prediction models. The method effectively discriminated between highly effective features and those with limited effectiveness.

Table 4. Ranking the features based on the selection rate.

Category	Features (Number and Name)	Average Selection Rate (%)
High Effective	1. LOC (Line count of code), 2. v(g) (Cyclomatic complexity), 3. eV(g) (Essential complexity), 6. v (Volume), 21. branchCount (Number of branches)	>70%
Medium Effective	4. iv(g) (Design complexity), 5. N (Operators and Operands), 8. D (Difficulty), 13. LOCode (Line count)	55–70%
Low Effective	7. L (Program length), 9. I (Intelligence), 10. B (Effort), 11. E (Number of Delivered Bugs), 12. T (Time to write program), 14. LOComment (Comments), 15. LOBlank (Blank lines), 16. LOCodeAndComment (Code and comment lines), 17. uniq_Op (Unique operators), 18. uniq_Opnd (Unique operands), 19. total_Op (Total operators), 20. total_Opnd (Total operands)	<55%

categorizes the software metrics based on their average selection rate across different datasets and ML models. Features such as LOC, Cyclomatic Complexity (v(g)), Essential Complexity (eV(g)), Volume (v), and Branch Count exhibited the highest selection rates. In contrast, features like Program Length (L), Intelligence (I), and other granular Halstead metrics demonstrated low effectiveness (<55%), suggesting they contribute less to SDP performance. Features with medium selection rates (55–70%), including Design Complexity (iv(g)) and Difficulty (D), moderately impact defect prediction, providing additional information.

After identifying the most influential features using the BBOA, the subsequent section evaluates the performance of various ML models trained on these optimized feature subsets to assess their effectiveness in the SDP. Some algorithms benefit more from BBOA-based feature selection because they are sensitive to irrelevant or redundant features. For example, SVM and ANN work better when the input features are informative and compact. BBOA removes unnecessary features, reducing noise and overfitting. Algorithms that handle many features well, like tree-based methods, gain less, while those affected by feature correlations or high dimensionality improve more with BBOA.

4.4. Predictive Performance of the Suggested SDP (RQ2)

The experiments on the CM1 dataset were conducted using the full features and selective features. The study focused on the classification performance metrics: accuracy, precision, sensitivity (recall), and F1-score. Each SDP was executed ten times. These metrics provided a baseline for comparing ML models both with and without feature selection. One major drawback of using all available features is the inclusion of irrelevant or redundant information, which can cause the overfitting problem. To address this problem, the BBOA was employed to select the most relevant feature subset. The created SDP models were compared using four performance metrics: Accuracy, Precision, F1-score, and Sensitivity.

The BBOA-optimized models consistently outperform their traditional method. BBOA+ANN achieves the highest accuracy (92.96%), compared to the base ANN (88.86%). BBOA+ML, BBOA+SVM, and BBOA+DT also exhibit improvements over their baselines by 6.07%, 8.85%, and 7.16%, respectively. This indicates that the BBOA significantly improves the classification ability across different algorithms by optimizing the feature selection. Precision is crucial in defect prediction to reduce false positives. The BBOA+DT (94.70%) and BBOA+SVM (93.82%) models provide the highest precision, surpassing even the ANN variants. Compared to traditional models, DT improves from 90.40% to 94.70%. NB shows an increase from 91.81% to 92.88%. This reflects the effectiveness of BBOA in targeting relevant features and reducing noisy attributes.

Sensitivity reflects the model’s ability to detect actual defective modules. In this metric, ANN (99.42%) and BBOA+ANN (99.42%) lead, suggesting that ANN-based models are highly capable of identifying defective modules. BBOA+NB (96.03%) and BBOA+SVM (95.51%) also show improvements compared to their baseline versions (92.49% and 88.22%). High sensitivity in BBOA-based models ensures fewer false negatives, which is vital in critical defect prediction. The F1-score balances precision and recall, making it an essential metric for imbalanced datasets like CM1. BBOA+SVM achieves the highest F1-score (95.31%), indicating an excellent balance. BBOA+ANN and BBOA+ML also perform well, with F1-scores of 94.82% and 94.05%, respectively.

Table 5. Average predictive performance of the suggested SDP in ten runs in the CM1 dataset.

Model	Accuracy (%)	Precision (%)	Sensitivity (%)	F1-Score (%)
ANN	88.86	89.34	99.42	94.09
BBOA+ANN	92.96	93.13	99.42	94.82
DT	83.36	90.40	91.19	90.78
BBOA+DT	90.51	94.70	92.43	93.27
NB	86.51	91.81	92.49	92.67
BBOA+NB	90.69	92.88	96.03	92.82
SVM	82.15	91.29	88.22	89.96
BBOA+SVM	91.00	93.82	95.51	95.31
ML	85.22	90.71	92.83	91.88
BBOA+ML	91.29	93.63	95.85	94.05

indicates the predictive performance of the suggested BBOA-based SDP in 10 runs.

To assess the effectiveness of the proposed BBOA+ML model on the KC1 dataset, we conducted ten runs and compared its performance with baseline classifiers and their BBOA-enhanced versions.

Table 6. Average predictive performance of the suggested SDP in ten runs in KC1 dataset.

Model	Accuracy (%)	Precision (%)	Sensitivity (%)	F1-Score (%)
ANN	88.96	69.82	96.04	91.87
BBOA+ANN	90.03	88.37	98.81	92.74
DT	81.04	87.69	90.00	88.83
BBOA+DT	85.27	88.52	92.20	90.59
NB	83.13	89.62	90.69	90.14
BBOA+NB	87.10	89.47	94.15	91.26
SVM	85.15	85.15	97.75	91.98
BBOA+SVM	87.23	87.74	98.66	92.40
ML	84.57	83.07	93.62	90.70
BBOA+ML	87.41	88.52	95.96	91.75

compares the predictive performance of the created SDPs in the KC1 dataset during ten runs with and without a feature selector. The BBOA+ML model achieved an average accuracy of 87.41%, outperforming its base ML SDP (84.57%). BBOA+ML still demonstrated solid performance, indicating that the BBOA optimization effectively improved the ML model’s classification capability. In terms of precision, BBOA+ML showed a notable improvement, recording 88.52%, compared to 83.07% for ML alone. This suggests that BBOA+ML is more reliable in minimizing false positives. While NB and BBOA+NB had slightly higher precision (89.62% and 89.47%, respectively), BBOA+ML still maintained competitive performance and far outperformed the standalone ANN (69.82%). BBOA+ML achieved a strong sensitivity of 95.96%, up from 93.62% for ML. This improvement confirms that BBOA+ML is highly effective in correctly identifying true positives. Regarding the F1-score (91.75%), BBOA+ML improved over the base ML model (90.70%), demonstrating its balance between precision and recall. The evaluation shows that BBOA+ML significantly enhances the classification performance of the original ML model in the KC1 dataset across all key metrics. These findings support the use of BBOA+ML as a reliable model for the SDP problem.

Based on the experimental results for the JM1 dataset, the performance of the BBOA+ML-based SDP demonstrates consistent superiority over other methods across all key performance metrics.

Table 7. Average predictive performance of the suggested SDP in ten runs in the JM1 dataset.

Model	Accuracy (%)	Precision (%)	Sensitivity (%)	F1-Score (%)
ANN	81.25	82.61	95.88	87.90
BBOA+ANN	89.49	88.77	97.79	91.32
DT	75.20	84.11	85.34	84.71
BBOA+DT	83.43	86.71	91.58	90.14
NB	80.46	83.43	94.77	88.67
BBOA+NB	85.98	85.76	96.39	91.12
SVM	77.75	83.62	92.93	86.17
BBOA+SVM	88.24	88.11	98.79	92.91
ML	78.67	83.44	92.23	86.86
BBOA+ML	86.78	87.34	96.14	91.37

compares the performance of different SDPs in JM1 dataset with and without feature selection. The BBOA+ML model achieves an average accuracy of 86.78%, which is higher than the base ML classifier (78.67%). This improvement shows that BBOA significantly enhances the classification capability of ML by optimally selecting features. BBOA+ML achieves an average precision of 87.34%, an improvement of nearly 4% over its base ML counterpart (83.44%). High precision is crucial in SDP, as it indicates fewer false positives, confirming that the model accurately identifies defective modules. With a sensitivity of 96.14%, BBOA+ML significantly outperforms the base ML (92.23%), indicating strong capability in identifying actual defective modules. It is especially important in defect prediction, as missing a defect can be more costly than a false alarm. The model reaches an F1-score of 91.37%, which is a balanced reflection of both precision and recall. This score is higher than the base ML (86.86%). The BBOA+ML model offers robust and balanced performance, demonstrating high accuracy, precision, sensitivity, and F1-score in the JM1 dataset. Although models like BBOA+ANN and BBOA+SVM show slightly better scores in some metrics, BBOA+ML consistently performs well across all metrics, making it a reliable and well-rounded choice for defect prediction.

As outlined in

Table 8. Average predictive performance of the suggested SDP in ten runs in the KC2 dataset.

Model	Accuracy (%)	Precision (%)	Sensitivity (%)	F1-Score (%)
ANN	83.81	85.17	94.71	90.26
BBOA+ANN	88.86	91.15	98.04	92.75
DT	81.40	87.22	89.76	88.43
BBOA+DT	82.43	90.19	87.87	88.92
NB	80.76	84.69	92.06	88.16
BBOA+NB	85.90	90.94	94.07	91.16
SVM	79.11	84.79	88.97	86.08
BBOA+SVM	86.10	92.34	97.55	89.31
ML	81.27	85.47	91.37	88.23
BBOA+ML	85.82	91.16	94.38	90.54

, the BBOA+ML model demonstrated improvements across the predictive metrics compared to the standalone ML in the KC2 dataset. BBOA+ML achieved an average accuracy of 85.82%, representing an improvement over the base ML model’s 81.27%. This suggests that BBOA effectively enhances the learning process of ML by optimizing features. The precision increased from 85.47% (ML) to 91.16% (BBOA+ML), highlighting a major reduction in false positives. This is crucial in defect prediction, where incorrectly identifying non-defective modules as defective can lead to unnecessary maintenance costs. The model also showed an improvement in sensitivity, rising from 91.37% (ML) to 94.38% (BBOA+ML). This indicates that the BBOA+ML model can more reliably identify actual defective modules, which is essential for minimizing the risk of overlooking faults in software systems. Finally, the F1-score improved from 88.23% to 90.54%, reflecting a well-balanced trade-off between precision and recall. The increase confirms that the BBOA+ML model maintains consistency in both identifying true positives and minimizing false detections. These results underscore the robustness of the BBOA+ML approach and its potential for practical SDP applications.

Regarding the results shown in

Table 9. Average predictive performance of the suggested SDP in ten runs in the PC1 dataset.

Classifier	Accuracy (%)	Precision (%)	Sensitivity (%)	F1-Score (%)
ANN	93.76	91.60	98.70	94.45
BBOA+ANN	95.66	94.95	99.30	96.41
DT	89.91	94.98	93.83	94.55
BBOA+DT	90.99	94.99	95.90	95.22
NB	87.87	94.50	92.29	93.37
BBOA+NB	90.57	94.90	94.59	95.14
SVM	84.32	95.40	87.52	91.26
BBOA+SVM	84.32	95.55	93.44	94.42
ML	88.96	94.12	93.09	93.41
BBOA+ML	90.39	95.09	95.81	95.29

, the BBOA+ML approach demonstrated superior performance compared to the ML models without a feature selector on the PC1 dataset over ten runs. This highlights the efficacy of integrating feature selectors (BBOA) with ensemble ML techniques. BBOA+ML achieved an average accuracy of 90.39%, outperforming the ML model (95.66%). In terms of precision, BBOA+ML scored 95.09%, an improvement over the ML (94.12%), indicating that the BBOA+ML approach is more effective at reducing false positives. BBOA+ML showed strong sensitivity at 95.81%, significantly higher than the baseline ML (93.08%). This makes the model especially valuable in safety-critical software projects. The F1-score of BBOA+ML was 95.29%, confirming balanced performance between precision and recall. It again outperformed the ML (93.41%), demonstrating the robustness of the feature selection mechanism in enhancing classification quality. The integration of BBOA with ML not only enhances predictive accuracy but also improves stability and reliability across all performance metrics. The feature optimization reduces redundancy, enabling better learning and generalization. BBOA+ML emerges as an effective approach for SDP in the PC1 dataset.

Table 10. Effect of the suggested feature selector on the performance of the SDC in different datasets.

Dataset	Model	Accuracy (%)	Precision (%)	F1-Score (%)	Sensitivity (%)
CM1	ML	85.22	90.71	91.88	92.83
	BBOA+ML	91.29	93.63	94.05	95.85
KC1	ML	84.57	83.07	93.62	90.70
	BBOA+ML	87.41	88.52	95.96	91.75
JM1	ML	78.67	83.44	92.23	86.86
	BBOA+ML	86.78	87.34	96.14	91.37
KC2	ML	81.27	85.47	91.37	88.23
	BBOA+ML	85.82	91.16	94.38	90.54
PC1	ML	88.96	94.12	93.09	93.41
	BBOA+ML	90.39	95.09	95.81	95.29

summarizes the comparative performance of the ML and the BBOA+ML hybrid model across five benchmark datasets (i.e., CM1, KC1, JM1, KC2, and PC1) using four evaluation metrics. The results clearly demonstrate that integrating the BBOA for feature selection significantly improves the ML model’s performance across all cases. BBOA+ML consistently achieves higher values across all metrics and datasets, with notable improvements in CM1 and JM1. These findings confirm the effectiveness of BBOA in improving SDP by optimizing the feature space.

The evaluation of different ML algorithms integrated with the BBOA for feature selection reveals clear trends in performance across five SDP datasets. Figure 7 illustrates the average accuracy and F1-score of the suggested SDP integrated with different ML algorithms. Among the tested models, BBOA+ANN consistently outperformed other combinations, achieving the highest average accuracy (91.4%) and F1-score (93.61%). This superior performance highlights the capability of ANN to effectively capture complex, non-linear patterns in the data, which is further enhanced by the BBOA-based feature selection. In contrast, BBOA+DT showed the weakest performance, with the lowest average accuracy (86.53%) and F1-score (91.63%) across all datasets. This suggests that DT, while interpretable and efficient, may not generalize as well in the presence of imbalanced data, even when feature selection is applied. BBOA+NB and BBOA+SVM (Support Vector Machine) showed moderate performance. These findings underscore the importance of selecting both an effective classification model and a robust feature selection method. The combination of BBOA with ANN and SVM appears to be powerful for improving the predictive performance of SDP models in software engineering applications.

Regarding the results, ANN usually performs better because it can learn complex, non-linear patterns. DT and NB are simpler and cannot capture these interactions. ANNs use layers of neurons with non-linear activation functions to find relationships between software metrics. BBOA feature selection improves ANN performance by choosing only the most important features. This reduces noise and helps the ANN focus on the patterns that matter, thereby improving fault prediction accuracy.

4.5. Convergence Speed and the Success Rate (RQ3)

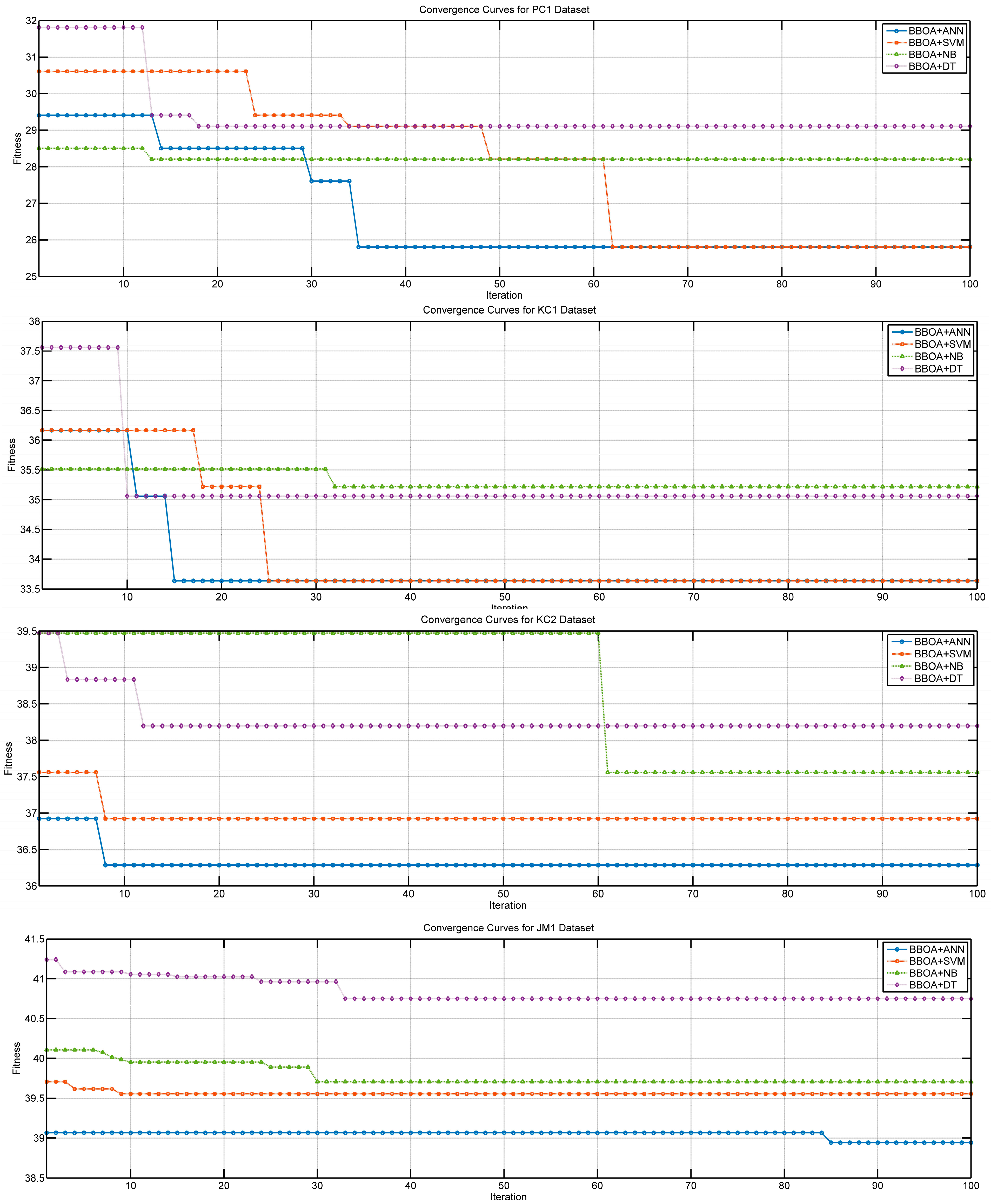
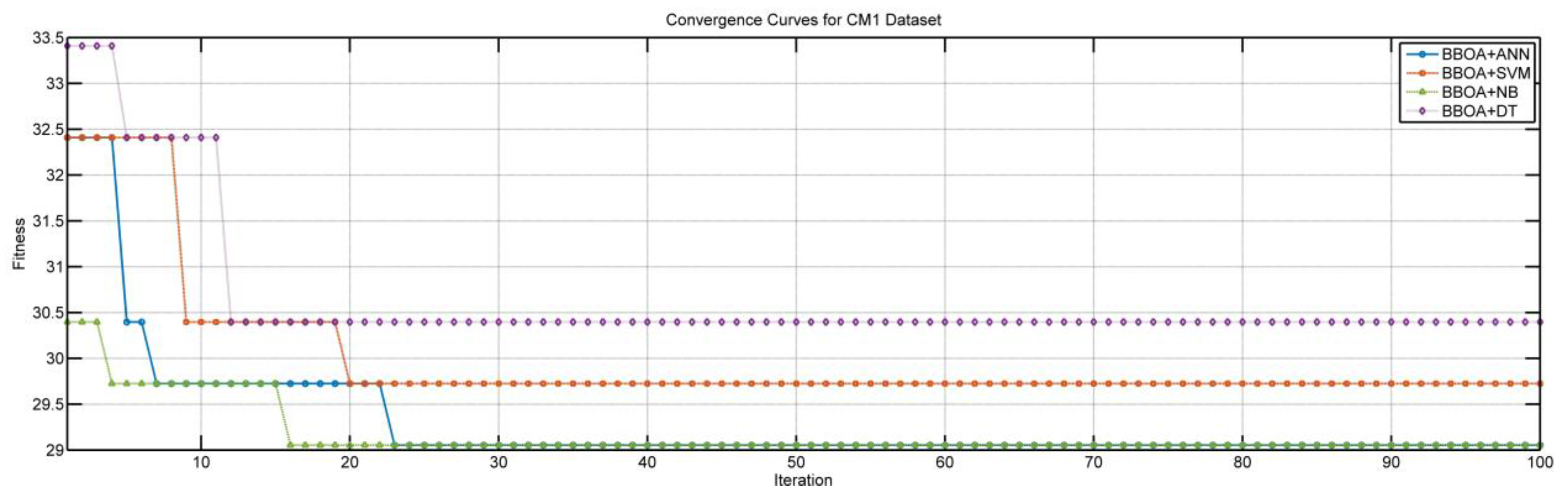
The convergence analysis reveals that BBOA is an effective metaheuristic for feature selection in SDP tasks. Figure 8 shows the convergence of the BBOA integrated with different CMl algorithms in different fault prediction datasets. The convergence plot of the BBOA over 100 iterations for the CM1 dataset indicates how effectively the algorithm selects relevant features. The fitness values represent the error rate and number of selected features. The BBOA+ANN shows gradual convergence, with a significant drop in fitness within the first 10 iterations. Despite slower convergence, the algorithm reaches the best final fitness (lowest fitness), indicating effective feature selection. BBOA+SVM provides faster convergence than ANN, with a sharp drop in fitness in the early iterations (about 8–12). The fast convergence indicates that BBOA, integrated with SVM, quickly identifies the most effective features; its final fitness is competitive and slightly higher than NB. The BBOA+NB quickly drops to a lower fitness value (around iteration 20). The final fitness for BBOA+NB is the lowest among all SVM and DT. In contrast, BBOA+DT shows slower convergence, and its fitness value is relatively higher (worse) than those of other algorithms. The lower convergence speed of BBOA+DT indicates that it requires more iterations to select the best features. In the CM1 dataset, BBOA+NB achieves the fastest convergence (about 20 iterations). BBOA+NB and BBOA+ANN provide the best fitness (lowest fitness). The lowest convergence and the highest (worth) fitness are associated with BBOA+DT.

As depicted in Figure 8, the convergence speed of BBOA on the JM1 dataset (a larger dataset) shows a stable, smooth optimization process across all integrated ML algorithms. BBOA+ANN achieved the lowest (best) fitness value, indicating the most effective feature selection among the classifiers of this dataset. BBOA+SVM and BBOA+NB showed similar convergence trends. BBOA+DT exhibited the highest (worst) fitness values, showing the least effective convergence. The convergence curves in Figure 8 for the PC1 dataset illustrate the optimization behavior of the proposed BBOA feature selector when integrated with different classifiers. The BBOA+SVM and BBOA+ANN demonstrate faster convergence (close to 65 iterations). BBOA+ANN converges in multiple stages with a sharp improvement in the 35th iteration. In contrast, BBOA+NB converges early but to a suboptimal fitness level. BBOA+DT exhibits the slowest convergence behavior. These results highlight BBOA’s potential for efficient feature selection in software fault prediction tasks. Totally, all SDPs benefit from the BBOA in identifying the faulty module. Simpler models like NB converge quickly, while more complex classifiers like ANN require more iterations.

In software fault prediction, features such as Lines of Code (LOC), Cyclomatic Complexity (CC), and Branch Count are often the most effective because they directly measure the structure and logic of the code. In the given classify() method in Figure 9, many nested conditions and branches create multiple execution paths, increasing the chance of logical errors or missed cases. CC and Branch Count describe the number of decisions in the code, while LOC reflects its size and effort required for maintenance. Although Halstead metrics measure cognitive effort, they do not fully capture the complexity of decisions in the code. Therefore, LOC, CC, and Branch Count remain more reliable for identifying fault-prone modules.

The ANOVA results shown in

Table 11. Anova statistical analysis of the results.

Metric	Source of Variation	Sum of Squares (SS)	df	Mean Square (MS)	F	p-Value	Significance
Accuracy	Between Groups	62.55	1	62.55	5.56	0.046	Significant
	Within Groups	89.94	8	11.24
	Total	152.49	9
F1-score	Between Groups	20.08	1	20.08	22.57	0.0013	Significant
	Within Groups	7.12	8	0.89
	Total	27.20	9

indicate that both accuracy and F1-score significantly increased when using BBOA+ML compared to the basic ML model. This suggests that the BBOA optimization effectively enhanced the model’s learning process, leading to more precise and balanced predictions. In other words, the optimized model not only made more correct classifications but also maintained better consistency between precision and recall.

The BBOA+ML method is suitable for predicting faults in software systems of different sizes. The datasets vary from small ones like CM1 (496 records) to large ones like JM1 (10,885 records). For small datasets, BBOA helps by selecting the most important features, reducing noise and improving learning efficiency. For large datasets, it reduces computational costs and focuses the ML model on the most informative metrics. This makes the method flexible and effective across a spectrum of software systems, from small to large projects. Table 12 compares the performance of the suggested method with some of the related works.

Table 12. The comparison of the suggested method with the previous SDP method.

Method	Predictive Performance	Feature Reduction	Feature Classification
[5]	AUC (90.70%), F1-score (90.51%)	Not evaluated	Non
[7]	Accuracy (92%), AUC (82.50%)	Not evaluated	Non
[9]	Accuracy (70%)	Not evaluated	Non
[10]	Accuracy (90%), recall (91%)	Not evaluated	Non
BBOA+ML	Accuracy (91.29%), sensitivity (95.85%)	57%	Features were prioritized

Table 12. The comparison of the suggested method with the previous SDP method.

Method	Predictive Performance	Feature Reduction	Feature Classification
[5]	AUC (90.70%), F1-score (90.51%)	Not evaluated	Non
[7]	Accuracy (92%), AUC (82.50%)	Not evaluated	Non
[9]	Accuracy (70%)	Not evaluated	Non
[10]	Accuracy (90%), recall (91%)	Not evaluated	Non
BBOA+ML	Accuracy (91.29%), sensitivity (95.85%)	57%	Features were prioritized

In a BBOA+ML fault predictor, there is often a tradeoff between precision and sensitivity. Precision shows how many predicted faults are correct, while sensitivity shows how many actual faults are detected. This tradeoff can be managed by adjusting the classification threshold, using weighted loss functions, or selecting features with BBOA that improve one metric without hurting the other too much. BBOA can also be used in multi-objective optimization to balance precision and sensitivity together, which is suggested as one of the future studies. The best balance depends on the application: safety-critical systems usually need higher sensitivity, while cost-sensitive testing may prefer higher precision.

This study has some limitations. It was conducted only on the PROMISE dataset, so the results may not generalize to other software projects. Only a modified binary version of BBOA was used, and other variants or metaheuristic algorithms might perform differently. Only ML models were tested, and other deep learning methods could give different results. The study did not analyze the scalability for very large web-based datasets. Finally, the method has not yet been validated in other domains, such as evolving software systems, which may limit its broader applicability.

5. Conclusions and Outlook

This study presented a modified binary version of the Bedbug Optimization Algorithm (BBOA) for feature selection in software defect prediction. The method selected a small but informative set of software metrics that improved the accuracy of ML models, as shown on the PROMISE dataset [14]. Important features chosen by BBOA included design complexity, program length, the number of operators and operands, program difficulty, and branch count. Using these features, the BBOA+ANN and BBOA+SVM frameworks achieved strong predictive results. Future work will apply this method to other software datasets, including architectural metrics. We also plan to combine software fault prediction with mutation testing [17,18,19] to increase the effectiveness of the mutation testing; indeed, the fault-prone modules which identified by the SDP techniques are considered as the target modules for mutation (fault injection). This technique enhances the mutation testing and reduces its computational cost. Additionally, BBOA-based feature selection could be developed for finding out the optimal features in the SQLi and XSS datasets [20]; hence, the predictive performance of the ML-based web security techniques can be enhanced thanks to the optimal features selected by the BBOA [20].