Numerical Modeling of a Gas–Particle Flow Induced by the Interaction of a Shock Wave with a Cloud of Particles
Abstract
1. Introduction
2. Mathematical Model
2.1. Discrete Model
2.2. Continuum Model
2.3. Model Closure
3. Two-Dimensional Model
3.1. Equations of Gas
3.2. Equations of Particles
4. Numerical Method
4.1. Numerical Schemes
4.2. Finite Volume Method
- —
- in x direction
- —
- in y directionThe integration step over time is selected based on the conditionwhere .
- —
- in x direction
- —
- in y direction
- —
- in x direction
- —
- in y direction
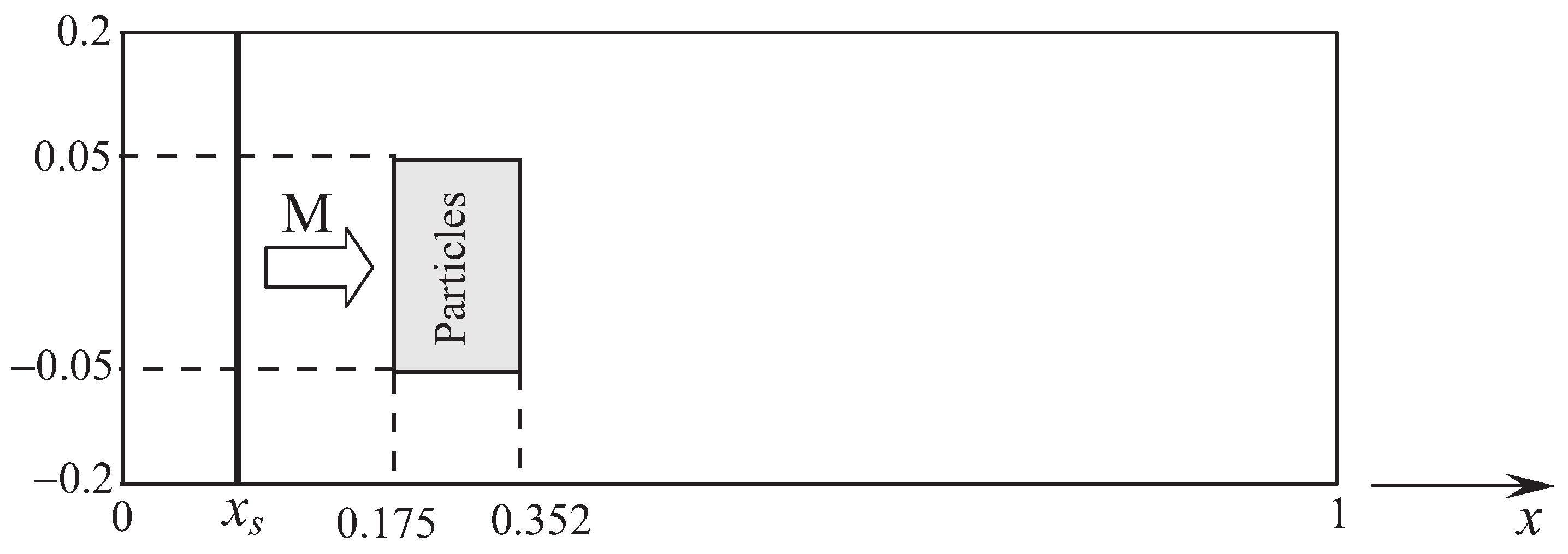
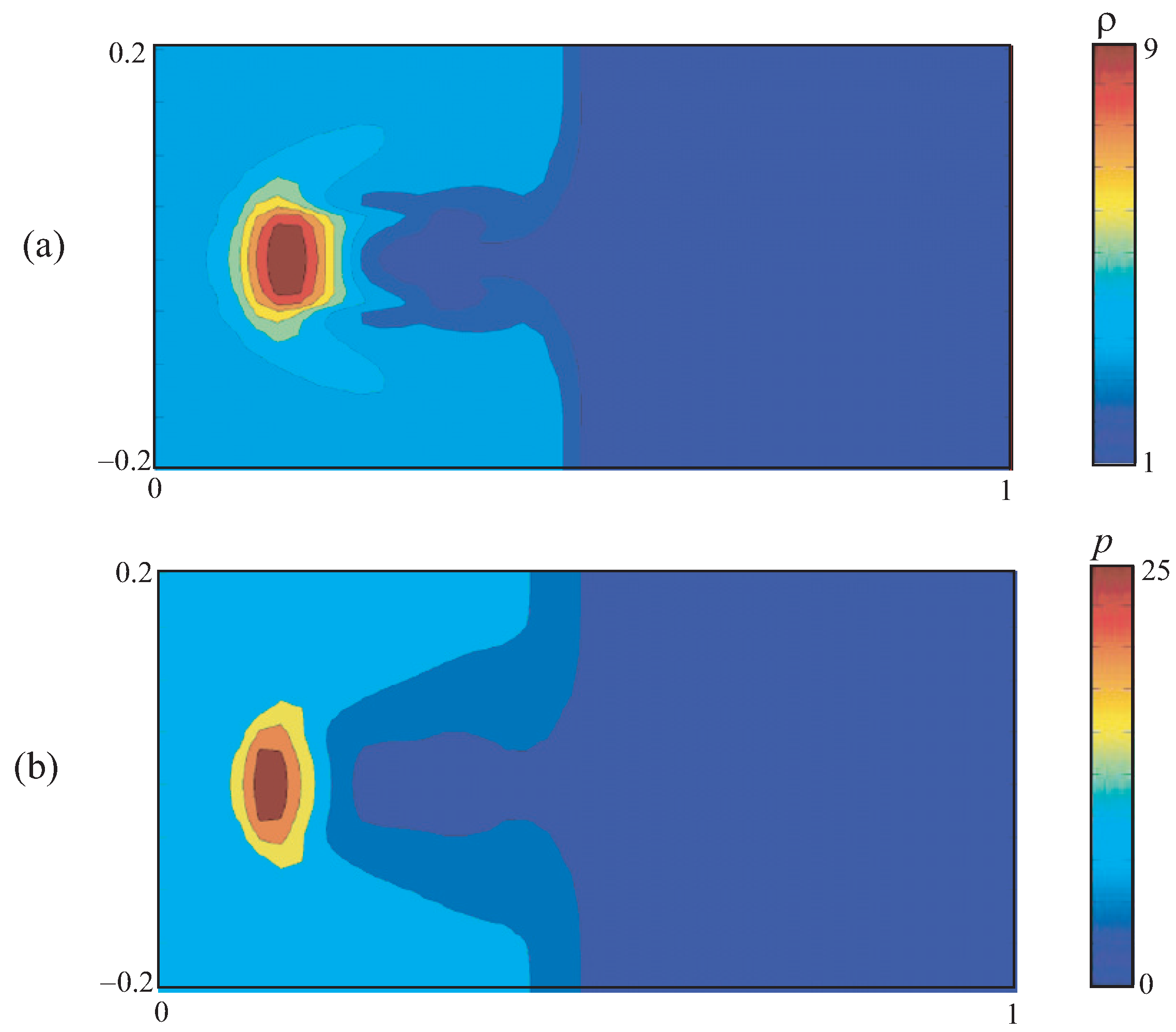
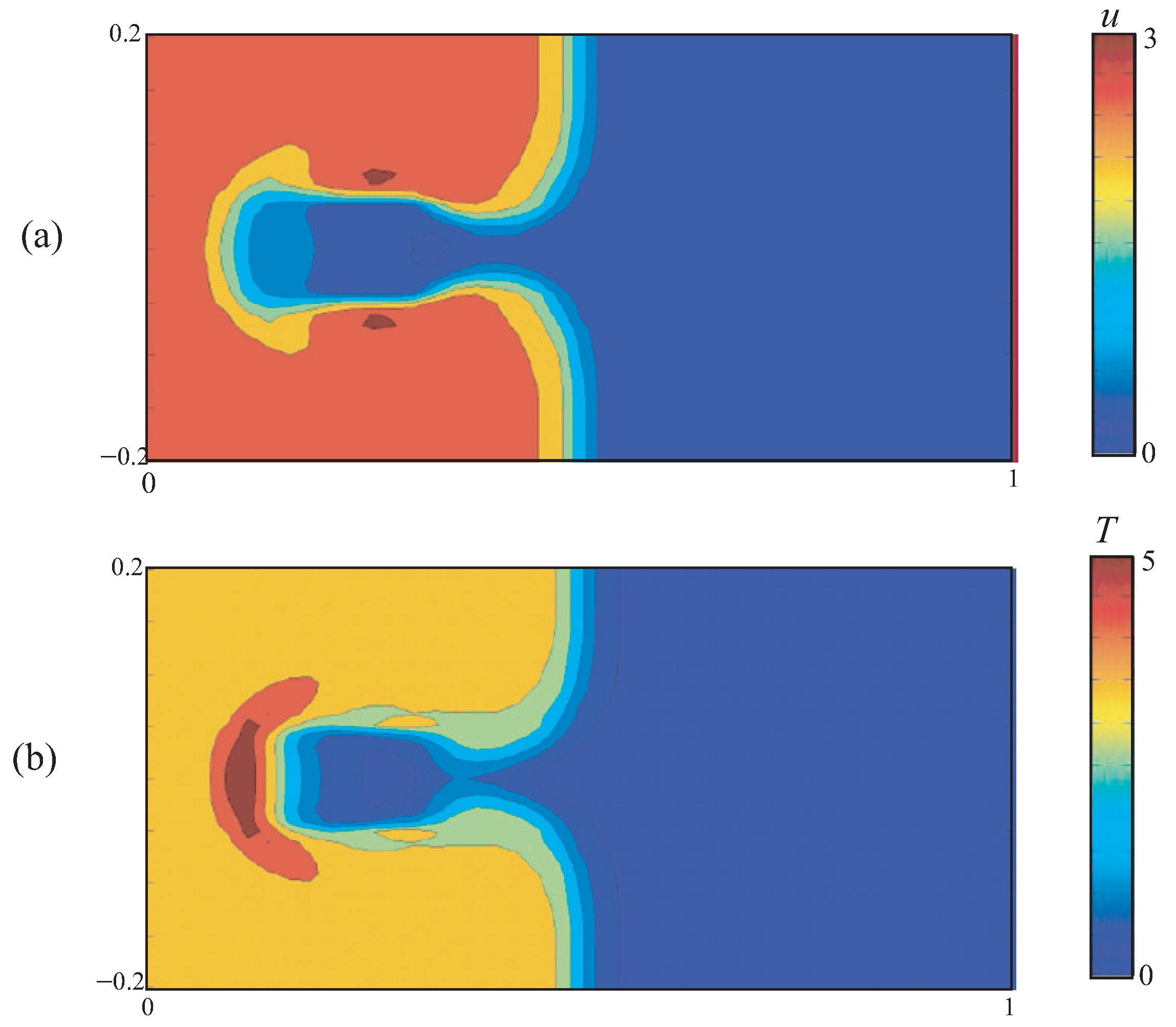
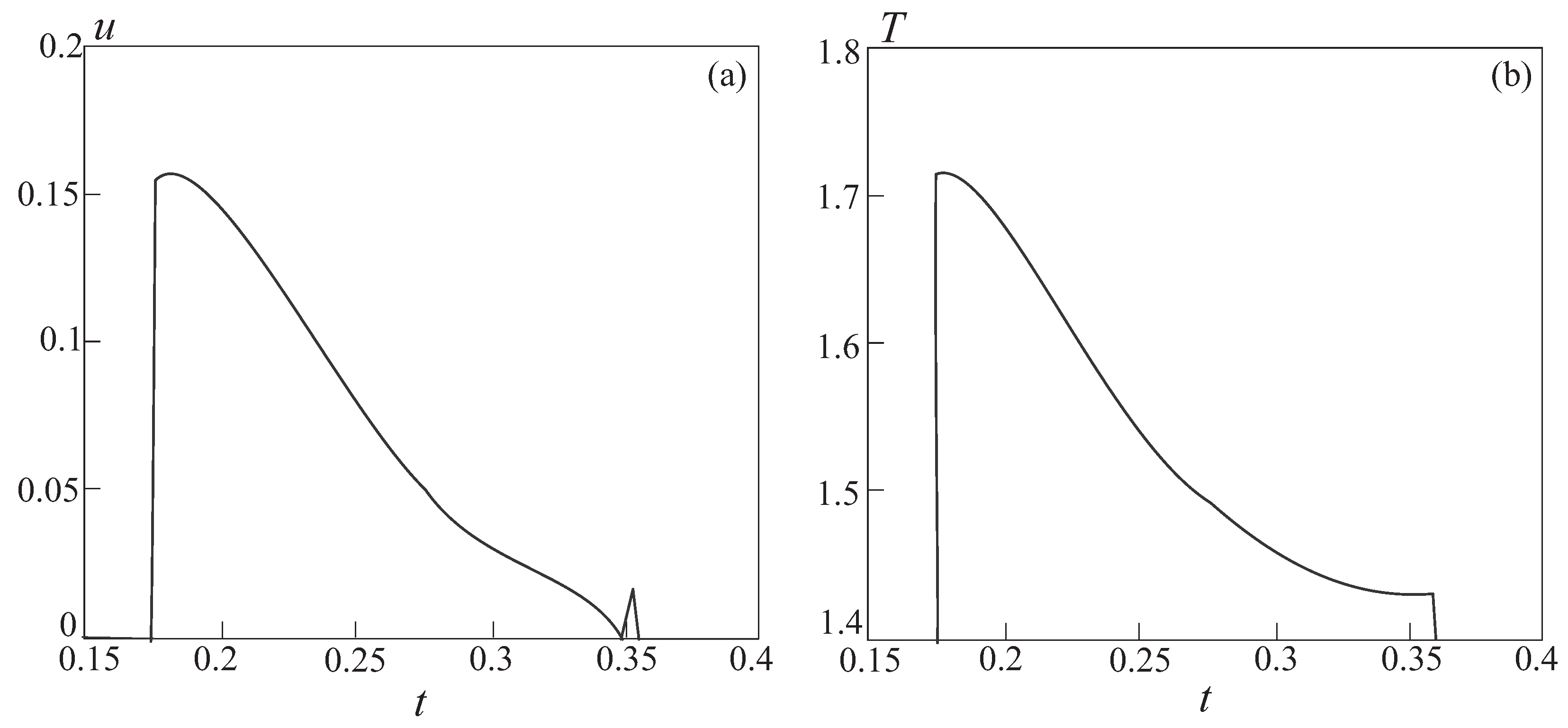
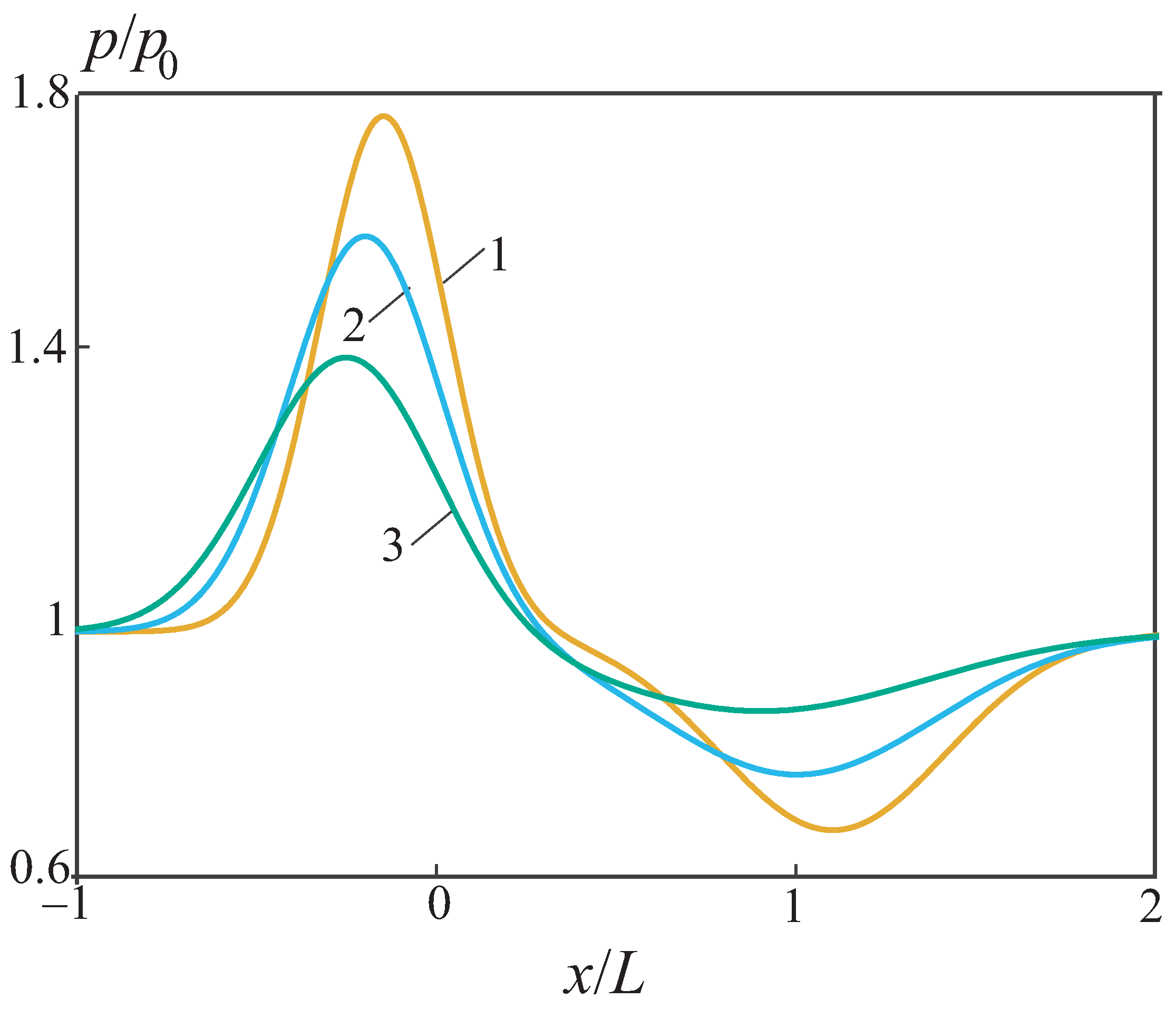
5. Results and Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eckhoff, R. Dust Explosions in the Process Industries; Gulf Professional Publishing: Houston, TX, USA, 2003; 720p. [Google Scholar]
- Brennen, C.E. Fundamentals of Multiphase Flows; Cambridge University Press: Cambridge, UK, 2005; 410p. [Google Scholar]
- Volkov, K.N.; Emelaynov, V.N. Gas-Particle Flows; Publishing House of Physical and Mathematical Literature: Moscow, Russia, 2008; 598p. [Google Scholar]
- Volkov, K.N.; Derugin, Y.N.; Emelaynov, V.N.; Kozelkov, A.S.; Teterina, I.V. Finite Difference Schemes in Gas Dynamics Problems on Unstructured Meshes; Publishing House of Physical and Mathematical Literature: Moscow, Russia, 2015; 416p. [Google Scholar]
- Ben-Dor, G. Dust entrainment by means of a planar shock induced vortex over loose dust layers. Shock Waves 1995, 4, 285–288. [Google Scholar] [CrossRef]
- Lhuillier, D.; Chang, C.-H.; Theofanous, T.G. On the quest for a hyperbolic effective-field model of disperse flows. J. Fluid Mech. 2013, 731, 184–194. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Mitkin, V.; Chang, C.H. The dynamics of dense particle clouds subjected to shock waves. Part 1. Experiments and scaling laws. J. Fluid Mech. 2016, 792, 658–681. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Chang, C.-H. The dynamics of dense particle clouds subjected to shock waves. Part 2. Modeling/numerical issues and the way forward. Int. J. Multiph. Flow 2017, 89, 177–206. [Google Scholar] [CrossRef]
- Regele, J.D.; Rabinovitch, J.; Colonius, T.; Blanquart, G. Numerical modeling and analysis of early shock wave interactions with a dense particle cloud. In Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, LA, USA, 25–28 June 2012. AIAA 2012-3161. [Google Scholar]
- Regele, J.D.; Rabinovitch, J.; Colonius, T.; Blanquart, G. Unsteady effects in dense, high speed, particle laden flows. Int. J. Multiph. Flow 2014, 61, 1–13. [Google Scholar] [CrossRef]
- Wagner, J.L.; Beresh, S.J.; Kearney, S.P. A multiphase shock tube for shock wave interactions with dense particle fields. Exp. Fluids 2012, 5, 1507–1517. [Google Scholar] [CrossRef]
- Clemins, A. Representation of two-phase flows by volume averaging. Int. J. Multiph. Flow 1988, 14, 81–90. [Google Scholar] [CrossRef]
- Jacobs, G.B.; Don, W.S.; Dittman, T. Computation of normal shocks running into a cloud of particles using a high-order particle-source-in-cell method. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA 2009-1310. [Google Scholar]
- Dittmann, T.B.; Jacobs, G.B.; Don, W.S. Dispersion of a cloud of particles by a moving shock: Effects of shape, angle of incidence and aspect ratio. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. AIAA 2011-441. [Google Scholar]
- Hosseinzadeh-Nik, Z.; Subramaniam, S.; Regele, J.D. Investigation and quantification of flow unsteadiness in shock-particle cloud interaction. Int. J. Multiph. Flow 2018, 101, 186–201. [Google Scholar] [CrossRef]
- Sen, O.; Gaul, N.J.; Davis, S.; Choi, K.K.; Jacobs, G.; Udaykumar, H.S. Role of pseudo-turbulent stresses in shocked particle clouds and construction of surrogate models for closure. Shock Waves 2018, 28, 579–597. [Google Scholar] [CrossRef]
- Mehta, Y.; Neal, C.; Salari, K.; Jackson, T.L.; Balachandar, S.; Thakur, S. Propagation of a strong shock over a random bed of spherical particles. J. Fluid Mech. 2018, 839, 157–197. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Mitkin, V.; Chang, C.-H. Shock dispersal of dilute particle clouds. J. Fluid Mech. 2018, 841, 732–745. [Google Scholar] [CrossRef]
- Osnes, A.N.; Vartdal, M.; Omang, M.G.; Pettersson Reif, B.A. Computational analysis of shock-induced flow through stationary particle clouds. Int. J. Multiph. Flow 2019, 114, 268–286. [Google Scholar] [CrossRef]
- Medvedev, S.P.; Frolov, S.M.; Gelfand, B.E. Attenuation of shock waves by granular material nozzles. J. Eng. Phys. Thermophys. 1990, 58, 924–928. [Google Scholar]
- Utkin, P.S. Mathematical modeling of the interaction of a shock wave with a dense particle bed within the framework of the two-fluid approach. Chem. Phys. 2017, 36, 61–71. [Google Scholar]
- Abe, A.; Takayama, K.; Itoh, K. Experimental and numerical study of shock wave propagation over cylinders and spheres. Trans. Model. Simul. 2001, 30, 209–218. [Google Scholar]
- Rogue, X.; Rodriguez, G.; Haas, J.F.; Saurel, R. Experimental and numerical investigation of the shock-induced fluidization of a particles bed. Shock Waves 1998, 8, 29–45. [Google Scholar] [CrossRef]
- Mehrabadi, M.; Tenneti, S.; Garg, R.; Subramaniam, S. Pseudo-turbulent gas-phase velocity fluctuations in homogeneous gas-solid flow: Fixed particle assemblies and freely evolving suspensions. J. Fluid Mech. 2015, 770, 210–246. [Google Scholar] [CrossRef]
- Sun, B.; Tenneti, S.; Subramaniam, S.; Koch, D.L. Pseudo-turbulent heat flux and average gas-phase conduction during gas-solid heat transfer: Flow past random fixed particle assemblies. J. Fluid Mech. 2016, 798, 299–349. [Google Scholar] [CrossRef]
- Shotorban, B.; Balachandar, S. Particle concentration in homogeneous shear turbulence simulated via lagrangian and equilibrium Eulerian approaches. Phys. Fluids 2006, 18, 065105. [Google Scholar] [CrossRef]
- Shotorban, B.; Balachandar, S. A Eulerian model for large-eddy simulation of concentration of particles with small stokes numbers. Phys. Fluids 2007, 19, 118107. [Google Scholar] [CrossRef]
- Shotorban, B.; Balachandar, S. Two-fluid approach for direct numerical simulation of particle-laden turbulent flows at small stokes numbers. Phys. Rev. E 2009, 79, 056703. [Google Scholar]
- Shotorban, B.; Jacobs, G.B.; Ortiz, O.; Truong, Q. An Eulerian model for particles nonisothermally carried by a compressible fluid. Int. J. Heat Mass. Transf. 2013, 65, 845–854. [Google Scholar] [CrossRef]
- Bulat, P.V.; Ilina, T.E.; Volkov, K.N.; Silnikov, M.V.; Chernyshov, M.V. Interaction of a shock wave with a cloud of particles and effect of particles on the shock wave weakening. Acta Astronaut. 2017, 135, 131–138. [Google Scholar] [CrossRef]
- Volkov, K. Interaction of a dense layer of solid particles with a shock wave propagating in a tube. Aerospace 2024, 11, 850. [Google Scholar] [CrossRef]
- Pandya, R.V.R.; Mashayek, F. Two-fluid large-eddy simulation approach for particle-laden turbulent flows. Int. J. Heat Mass Transf. 2002, 45, 4753–4759. [Google Scholar] [CrossRef]
- Mashayek, F.; Pandya, R.V.R. Analytical description of particle/droplet-laden turbulent flows. Prog. Energy Combust. Sci. 2003, 29, 329–378. [Google Scholar] [CrossRef]
- Verman, B.; Geurts, B.; Kuerten, H. Realizability conditions for the turbulent stress tensor in large-eddy simulation. J. Fluid Mech. 1994, 278, 351–362. [Google Scholar] [CrossRef]
- Gicquel, L.; Givi, P.; Jaberi, F.; Pope, S. Velocity filtered density function for large eddy simulation of turbulent flows. Phys. Fluids 2002, 14, 1196–1213. [Google Scholar] [CrossRef]
- Saito, T. Numerical analysis of dusty-gas flows. J. Comput. Phys. 2002, 176, 129–144. [Google Scholar] [CrossRef]
- Laurent, F.; Massot, M.; Villedieu, P. Eulerian multi-fluid modeling for the numerical simulation of coalescence in polydisperse dense liquid sprays. J. Comput. Phys. 2004, 194, 505–543. [Google Scholar] [CrossRef]
- Kah, D.; Laurent, F.; Massot, M.; Jay, S. A high order moment method simulating evaporation and advection of a polydisperse liquid spray. J. Comput. Phys. 2012, 231, 394–422. [Google Scholar] [CrossRef]
- Le Veque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: New York, NY, USA, 2002; 546p. [Google Scholar]
- Godunov, S.K. Difference method of numerical calculation of discontinuous solutions of hydrodynamic equations. Math. Collect. 1959, 47, 271–306. [Google Scholar]
- Khmel, T.A.; Fedorov, A.V. Numerical technologies for studying heterogeneous detonation of gas suspensions. Math. Model. 2006, 18, 49–63. [Google Scholar]
- Tunik, Y.V. Global modelling of heat release during initiation and propagation of detonation and deflagration waves in methane-air-particle systems. Shock Waves 1999, 9, 173–179. [Google Scholar] [CrossRef]
- Zhang, F.; Frost, D.L.; Thibault, P.A.; Murray, S.B. Explosive dispersal of solid particles. Shock Waves 2001, 10, 431–443. [Google Scholar] [CrossRef]
- Benkiewicz, K.; Hayashi, A.K. Two-dimensional numerical simulations of multi-headed detonations in oxygen-aluminum mixtures using an adaptive mesh refinement. Shock Waves 2003, 13, 385–402. [Google Scholar]
- Ludwig, T.; Roth, P. Modeling of laminar combustion wave propagation in reactive gas/particle mixtures. Int. J. Multiph. Flow 1997, 23, 93–111. [Google Scholar] [CrossRef]
- Murray, S.B.; Zhang, F.; Thibault, P.A. Transition from deflagration to detonation in an end multiphase slug. Combust. Flame 1998, 114, 13–25. [Google Scholar]
- Zhdan, S.A.; Prokhorov, E.S. Calculation of the cellular structure of spray detonation in the H2–O2 system. Combust. Explos. Shock Waves 2000, 36, 111–112. [Google Scholar]
- Papalexandris, M.V. Numerical simulation of detonations in mixtures of gases and solid particles. J. Fluid Mech. 2004, 507, 95–142. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Nikitin, V.F.; Legros, J.C. Ignition and combustion of turbulized dust-air mixtures. Combust. Flame 2000, 123, 46–67. [Google Scholar] [CrossRef]
- Tsuboi, N.; Hayashi, A.K.; Matsumoto, Y. Three-dimensional parallel simulation of cornstarch-oxygen two-phase detonation. Shock Waves 2000, 10, 277–285. [Google Scholar] [CrossRef]
- Kutyshev, A.G.; Rodionov, S.P. Plane detonation waves in gas suspensions of unitary fuel with spatially non-uniform distribution of particles. Combust. Explos. Shock Waves 1998, 34, 103–110. [Google Scholar]
- Loth, E.; Sivier, S.; Baum, J. Dusty detonation simulations with adaptive unstructured finite elements. AIAA J. 1997, 35, 1018–1024. [Google Scholar] [CrossRef]
- Veyssiere, B.; Bozier, O.; Khasainov, B.A. Effect of a suspension of magnesium particles on the detonation characteristics of methane-oxygen-nitrogen mixtures at elevated initial pressures. Shock Waves 2002, 12, 227–233. [Google Scholar] [CrossRef]
- Chang, E.J.; Kailasanath, K. Shock wave interactions with particles and liquid fuel droplets. Shock Waves 2003, 12, 333–341. [Google Scholar] [CrossRef]
- Khmel, T.A.; Fedorov, A.V. Interaction of a shock wave with a cloud of aluminum particles in a channel. Combust. Explos. Shock Waves 2002, 38, 89–98. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Khmel, T.A. Numerical modeling of formation of cellular heterogeneous detonation of aluminum particles in oxygen. Combust. Explos. Shock Waves 2005, 41, 84–98. [Google Scholar] [CrossRef]
- Gentry, R.A.; Martin, R.E.; Daly, B.J. An Eulerian differencing method for unsteady compressible flow problems. J. Comput. Phys. 1966, 1, 87–118. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Khmel, T.A. Mathematical modeling of detonation processes in a gas suspension of coal particles. Combust. Explos. Shock Waves 2002, 38, 103–112. [Google Scholar] [CrossRef]
- Schwendeman, D.W.; Wahle, C.W.; Kapila, A.K. The Riemann problem and a high-resolution Godunov method for a model of compressible two-phase flow. J. Comput. Phys. 2006, 212, 490–526. [Google Scholar] [CrossRef]
- Jacobs, G.B.; Don, W.S. A high-order weno-z finite difference based particle-source-in-cell method for computation of particle-laden flows with shocks. J. Comput. Phys. 2009, 228, 1365–1379. [Google Scholar] [CrossRef]
- Sengupta, K.; Shotorban, B.; Jacobs, G.B.; Mashayek, F. Spectral-based simulations of particle-laden turbulent flows. Int. J. Multiph. Flow 2009, 35, 811–826. [Google Scholar] [CrossRef]
- Fedorov, A.V. Structure of heterogeneous detonation of aluminum particles dispersed in oxygen. Combust. Explos. Shock Waves 1992, 28, 82–83. [Google Scholar] [CrossRef]
- Montagne, J.L.; Yee, H.C.; Vinokur, M. Comparative study of high-resolution shock-capturing schemes for a real gas. AIAA J. 1989, 27, 1332–1346. [Google Scholar] [CrossRef]
- Larrouturou, B. How to preserve the mass fraction positivity when computing compressible multi-component flows. J. Comput. Phys. 1991, 95, 59–84. [Google Scholar] [CrossRef]
- Abgrall, R. How to prevent pressure oscillations in multicomponent flow calculations: A quasi conservative approach. J. Comput. Phys. 1996, 125, 150–160. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkov, K. Numerical Modeling of a Gas–Particle Flow Induced by the Interaction of a Shock Wave with a Cloud of Particles. Mathematics 2025, 13, 3427. https://doi.org/10.3390/math13213427
Volkov K. Numerical Modeling of a Gas–Particle Flow Induced by the Interaction of a Shock Wave with a Cloud of Particles. Mathematics. 2025; 13(21):3427. https://doi.org/10.3390/math13213427
Chicago/Turabian StyleVolkov, Konstantin. 2025. "Numerical Modeling of a Gas–Particle Flow Induced by the Interaction of a Shock Wave with a Cloud of Particles" Mathematics 13, no. 21: 3427. https://doi.org/10.3390/math13213427
APA StyleVolkov, K. (2025). Numerical Modeling of a Gas–Particle Flow Induced by the Interaction of a Shock Wave with a Cloud of Particles. Mathematics, 13(21), 3427. https://doi.org/10.3390/math13213427




