Eliminating Packing-Aware Masking via LoRA-Based Supervised Fine-Tuning of Large Language Models

Abstract

Packing approaches enhance training efficiency by filling the padding space in each batch with shorter sequences, thereby reducing the total number of batches per epoch. This approach has proven effective in both pre-training and supervised fine-tuning of large language models (LLMs). However, most packing methods necessitate a packing-aware masking (PAM) mechanism to prevent cross-contamination between different text segments in the multi-head attention (MHA) layers. This masking ensures that the scaled dot-product attention operates only within segment boundaries. Despite its functional utility, PAM introduces significant implementation complexity and computational overhead during training. In this paper, we propose a novel method that eliminates the need for PAM during supervised fine-tuning with packing. Instead of masking, we introduce a learnable tensor derived from Low-Rank Adaptation (LoRA) with the query and value parameters of the attention mechanism. This tensor is trained to attenuate the subspace corresponding to cross-contamination, effectively replacing the function of PAM. Through component-wise decomposition of attention head outputs, we isolate the contamination component and demonstrate that it can be attenuated using the LoRA-derived tensor. Empirical evaluations on 7B-scale LLMs show that our method reduces training time and runtime overhead by completely removing the implementation associated with PAM. This enables more scalable and efficient supervised fine-tuning with packing, without compromising model integrity.

1. Introduction

Transformer-based architectures [1] have become the backbone of numerous pre-trained models and large language models (LLMs) [2,3,4,5,6], demonstrating state-of-the-art performance across a wide range of natural language processing tasks. These models are typically pre-trained on large-scale datasets and subsequently fine-tuned using supervised fine-tuning (SFT) for specific downstream applications. However, in practical scenarios, SFT is often constrained by limited computational resources, thereby motivating the need for more efficient training strategies.

One widely adopted approach to improve training efficiency is packing [7], which effectively utilizes the padding space within batches by replacing unused tokens with shortened sequences from the dataset. Packing has been successfully applied in both the pre-training [8,9,10] and SFT [11,12,13,14,15,16], significantly increasing GPU utilization and reducing the number of batches per epoch and training time. Existing packing strategies generally fall into two categories: offline [7,17] or online [18] packing. Offline approaches pre-pack sequences prior to training, while online approaches perform packing dynamically during training. Despite their efficiency gains, both approaches need packing-aware masking (PAM).

This PAM departs from traditional key-padding masks and causal (diagonal) masks in both structure and semantics. These traditional masks are often provided as two-dimensional tensors and are broadcast uniformly across all matrices in a three-dimensional attention tensor along a fixed axis. This operation minimizes both generation and transmission overhead. For example, in PyTorch-based training scenarios, the mask tensor’s data type (i.e., dtype) and device can be set once at the model level and then reused across attention layers; such reuse incurs minimal casting overhead because the casted mask is forwarded rather than recomputed. In contrast, PAM, whether in offline or online packing, requires distinct block-diagonal masks for each matrix within a batch tensor. Generating the mask tensor and applying it in scaled dot-product attention needs time and has implementation costs [7]. Since the mask tensor is inherently three-dimensional (${\mathbb{R}}^{B\times N\times N}$), constructing these masks on the CPU and stacking or transferring them to GPU devices at every training step introduces a significant runtime overhead. The cost further increases if the mask uses an integer dtype (e.g., long) instead of the supported boolean or floating-point formats, thereby triggering implicit casts. Additional overhead arises when unnecessary operations such as ‘clone()’ or ‘contiguous()’ are repeatedly applied.

Unlike two-dimensional masks that can often be precomputed and reused, PAM entails per-matrix mask construction, which raises casting and data-movement overheads. Moreover, PyTorch’s native scaled dot-product attention API automatically dispatches among FlashAttention-2, memory-efficient, and math backends based on the inputs; supplying an explicit three-dimensional attention mask generally precludes the fused Flash/memory-efficient paths unless masking is expressed via supported flags (e.g., causal), leading to fallback to a slower backend with reduced computational efficiency. These constraints also increase the implementation complexity of masking in training code. In sum, three-dimensional PAM entails more considerations than two-dimensional masking and can lead to training speed degradation, especially when per-matrix mask construction and backend fallback are involved.

To mitigate the overheads associated with PAM, several prior works have proposed alternatives, such as packing with applying Flash attention [18] and boundary-ware positional encoding [19]. While effective in controlled settings, these approaches are often non-trivial to integrate into standard SFT pipelines and frequently require custom implementations or backend overrides. Even when mask generation is optimized, runtime overheads may persist due to device-specific behaviors or library/package level leakage, depending on hardware and software configurations.

Meanwhile, LoRA (Low-Rank Adaptation) [20] has emerged as a widely adopted parameter-efficient fine-tuning method for large-scale pre-trained language models. Rather than updating all model parameters, LoRA introduces low-rank matrices into attention and feed-forward layers, significantly reducing both memory consumption and computational cost, while maintaining or even surpassing the performance of full fine-tuning. Variants such as Delta-LoRA [21], NoRA [22], and DoRA [23] further improve upon this framework by enhancing stability, inference efficiency, and parameter reduction. In practice, most SFT scenarios focus on adapting only the query and value projections, as this achieves strong performance with minimal adaptation overhead.

Recently, LoRA has been combined with sequence packing during SFT to further improve training efficiency. However, PAM remains a critical bottleneck in this setup due to its masking requirements. To address this, we propose a novel approach that eliminates the need for PAM during training, while maintaining the benefits of both packing and LoRA. Specifically, we begin by analyzing and formalizing the subspaces of tensors in the scaled dot-product attention mechanism under two conditions: when PAM is omitted, allowing potential cross-contamination between packed sequences, and when LoRA is applied to query and value projections (denoted as LoRA-Q and LoRA-V). Based on this analysis, we demonstrate that the learnable subspace induced by LoRA-Q and LoRA-V can naturally suppress or attenuate the contamination subspace that arises from removing PAM. This insight enables us to construct an efficient SFT framework that forgoes PAM entirely, thereby eliminating its implementation and runtime costs. The proposed approach erases both the implementation complexity and factors degrading training speed fundamentally. Furthermore, this combination guarantees not only simple and fast implementation but also decreases the packing and training time for SFT with packing and LoRA. We validate our method on multiple pre-trained models and SFT datasets available via Hugging Face, demonstrating its practical utility, scalability, and training-time improvements across diverse settings.

This paper is organized as follows: Section 2 reviews the scaled dot-product stage attention in Transformer with packing and LoRA. Section 3 outlines the possibility to replace cross-contamination to the LoRA space, without packing-aware masking. The pre-trained model and datasets for supervised fine-tuning, hyperparameters, and devices for the experiments are described in Section 4. The results and discussion for each experiment are presented with figures and tables. Finally, Section 5 summarizes the contributions of our approach.

2. Background and Related Work

2.1. Preliminaries

The operations in the scaled dot-product stage attention (SDPA) in traditional multi-head attention layer (MHA) in Transformer [1] are represented as follows:

$$\begin{array}{cc}\hfill q_i& =W_{Qi}^{T}x,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill k_i& =W_{Ki}^{T}x,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill v_i& =W_{Vi}^{T}x,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill S_{i0}& =q_i^T{k}_i/\sqrt{d_k},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\mathcal{A}}_{i0}& =\mathtt{softmax}\left(S_{i0}\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{i0}& ={\mathcal{A}}_{i0}{v}_i^T,\hfill \end{array}$$

(6)

where $x\in {\mathbb{R}}^{d\times N}$ and $W_{Qi},W_{Ki},W_{Vi}\in {\mathbb{R}}^{d\times d_k}$. They denote, respectively, the embedded input tensor and the learnable weights for i-th head in MHA. $d_k$ is equal to $d/h$. N, d, and h are the sequence length, model dimension, and the number of heads, respectively. ${\mathcal{H}}_{i0}$ in each head are concatenated and projected by a learnable output matrix. The result is added to the input x via a residual connection, followed by layer normalization.

2.2. SDPA with Packing

If packing is applied, a packing-aware mask is generated based on how the sequences are packed in the batch and added into the dot-product tensor [7] in the SDPA stage. The masking matrix consists of zero and negative infinite values with a block-diagonal pattern.   

$$\begin{array}{cc}\hfill & S_{i\mathcal{M}}=q_i^T{k}_i/\sqrt{d_k}+{\mathcal{M}}_i,\hfill \\ \hfill & where\mathcal{M}\in {\{0,-\infty \}}^{n\times n}\mathrm{with}\mathrm{a}\text{block-diagonal}\mathrm{structure}.\hfill \end{array}$$

(7)

Negative elements lead the attention scores between queries and keys from different sequences to approach zero after softmax, while ignoring cross-contamination values.

$${\displaystyle \frac{e^{-\infty }}{{\sum }_{m,n=1}^N{e}^{S_{i\mathcal{M}\{m,n\}}}}}\approx 0.$$

(8)

Therefore, the cross-contamination area cannot affect to head output.

In practice, masking is employed by adding large negative constants instead of $-\infty$ to designated positions, thereby forcing their probabilities to near zero and preventing numerical overflow or NaN values. This results in masked positions producing small but nonz-ero values after the softmax operation. However, these residual values contribute to the denominator in the normalization step, which increases the sensitivity of the probability distribution to differences among the scores of valid tokens [24]. Furthermore, as the size of the masked area grows and the number of valid tokens decreases, the same score differences yield proportionally larger changes in the resulting probability distribution, amplifying instability in attention weights [25].

2.3. SDPA with LoRA

The weights for query and key adaptation with LoRA are, respectively, added to the original weights (${W^{\prime }}_{Qi}=W_{Qi}+\Delta W_{Qi},{W^{\prime }}_{Ki}=W_{Ki}+\Delta W_{Ki}$). $\Delta W_{Qi}$ and $\Delta W_{Ki}$ are decomposed to learnable low-rank weights $B_{Qi,Ki}$ and $A_{Qi,Ki}$. Hence, $S_i$ is expressed as follows:

$$\begin{array}{}\mathrm{(9)}& S_i={\left({(W_{Qi}+\Delta W_{Qi})}^{T}x\right)}^T{(W_{Ki}+\Delta W_{Ki})}^{T}x/\sqrt{d_k}\mathrm{(10)}& \hspace{1em}=x^T{W}_{Qi}{W}_{Ki}^{T}x/\sqrt{d_k}+(x^T{W}_{Qi}\Delta W_{Ki}^{T}x+x^T\Delta W_{Qi}{W}_{Ki}^{T}x+x^T\Delta W_{Qi}\Delta W_{Ki}^{T}x)/\sqrt{d_k}\mathrm{(11)}& \hspace{1em}\equiv S_{io}+\Delta S_i,\end{array}$$

where $S_{io}$ and $\Delta S_i$ are equal to the first term of expansion of $S_i$ and the sum of the others, respectively. Therefore, ${\mathcal{H}}_i$ is described as follows:

$${\mathcal{H}}_i={\mathcal{A}}_i{v}_i^T=\mathtt{softmax}(S_{i0}+\Delta S_i)v_i^T\not\equiv {\mathcal{H}}_{i0}+\Delta {\mathcal{H}}_i.$$

(12)

Since softmax is not the linear function, ${\mathcal{H}}_i$ cannot be directly defined to ${\mathcal{H}}_{i0}+\Delta {\mathcal{H}}_i$.

In the case of only adding learnable parameters to value weight (${W^{\prime }}_{Vi}=W_{Vi}+\Delta W_{Vi}$), ${\mathcal{H}}_i$ can be decomposed to sum of head values and each term is defined as follows:

$${\mathcal{H}}_i={\mathcal{A}}_{i0}(x{W}_{Vi}^T+x\Delta W_{Vi}^T)\equiv {\mathcal{A}}_{i0}{v}_i^T+{\mathcal{A}}_{i0}\Delta v_i^T\equiv {\mathcal{H}}_{i0}+\Delta {\mathcal{H}}_i.$$

(13)

${\mathcal{H}}_{i0}$ is equal to the head output tensor from pre-trained parameters (Equation (6)) and constant term for trainable term $\Delta {\mathcal{H}}_i$. $\Delta {\mathcal{H}}_i$ directly influences attention-weighted output and shifts the output corresponding to the fine-tuning dataset.

In LoRA experiments, adapting the $\Delta W_{Qi}$ and $\Delta W_{Vi}$ (i.e., LoRA-Q and LoRA-V) achieves performance comparable to full fine-tuning [20,26,27]. Therefore, the terms with $\Delta W_{Ki}$ in $\Delta S_i$ in Equations (10) and (11) become zero. Consequently, ${\mathcal{H}}_i$ applied LoRA-Q and LoRA-V can be reformulated as follows:  

$$\begin{array}{}\mathrm{(14)}& {\mathcal{H}}_i=\mathtt{softmax}(S_{i0}+\Delta S_i)(v_{i0}+\Delta v_i)\mathrm{(15)}& \hspace{1em}=\mathtt{softmax}(S_{i0}+\Delta S_i)x{W}_{Vi}^T+\mathtt{softmax}(S_{i0}+\Delta S_i)x\Delta W_{Vi}^T,\mathrm{(16)}& \hspace{1em} where\Delta S_i=x^T\Delta W_{Qi}{W}_{Ki}^{T}x\equiv (\Delta q_i^T)k_i/\sqrt{d_k}.\end{array}$$

3. Methodology

3.1. Decomposing SDPA Output Without PAM

Regardless of whether the input x is packed, any element of ${\mathcal{H}}_i$ can be written as sum of products of attention tensor ${\mathcal{A}}_i$ and value entry $v_i$:

$${\mathcal{H}}_{i\{m,p\}}=\sum _{n=1}^N{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T,$$

(17)

where $m\in [1,N]$ and $p\in [1,d_k]$. If the input x is a packed sequence with two segments and boundary is t-th token of x, Equation (17) can be decomposed as follows:

$${\mathcal{H}}_{i\{m,p\}}=\sum _{n=1}^{t-1}{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T+\sum _{n=t}^N{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T.$$

(18)

For the elements of the first segment ${\mathcal{H}}_{i\{m<t,p\}}$, the first term in Equation (18) is the valid attention values and the second is the cross-contamination term. Conversely, the opposite holds for the elements of the second segment ${\mathcal{H}}_{i\{m\ge t,p\}}$. Without PAM (i.e., allowing cross-contamination), ${\mathcal{H}}_i$ with packing can be decomposed and defined as follows:

$${\mathcal{H}}_i\equiv {\mathcal{H}}_{i0}+{\mathcal{H}}_{iC},$$

(19)

where each term, respectively, corresponds to the valid attention and cross-contamination tensor.

3.2. Eliminating PAM via LoRA

Building on Equations (13) and (19), the PAM to avoid cross-contamination are not necessary if $\Delta {\mathcal{H}}_i$ can cover up ${\mathcal{H}}_{iC}$. Rather, the space of ${\mathcal{H}}_{iC}$ can be reused and updated as a space for SFT. In the case of adapting only LoRA-V for fine-tuning while allowing cross-contamination ($\Delta S_i=0,\Delta {\mathcal{H}}_i\ne 0$), ${\mathcal{H}}_i$ can be reformulated as follows:

$$\begin{array}{}\mathrm{(20)}& {\mathcal{H}}_{i\{m,p\}}={\displaystyle \sum _{n=1}^N}{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T+{\displaystyle \sum _{n=1}^N}{\mathcal{A}}_{i\{m,n\}}\Delta v_{i\{n,p\}}^T\mathrm{(21)}& \hspace{1em}\hspace{1em} ={\displaystyle \sum _{n=1}^{t-1}}{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T+{\displaystyle \sum _{n=t}^N}{\mathcal{A}}_{i\{m,n\}}{v}_{i\{n,p\}}^T+{\displaystyle \sum _{n=1}^N}{\mathcal{A}}_{i\{m,n\}}\Delta v_{i\{n,p\}}^T\mathrm{(22)}& \hspace{1em}\hspace{1em} \equiv {\mathcal{H}}_{i0\{m,p\}}+{\mathcal{H}}_{iC\{m,p\}}+\Delta {\mathcal{H}}_{i\{m,p\}}.\end{array}$$

Since ${\mathcal{H}}_{iC}$ is obtained from pre-trained parameters, it is a constant term for trainable $\Delta {\mathcal{H}}_i$. Therefore, $B_{Vi}$ and $A_{Vi}$ train to attenuate the cross-contamination while adapting to the SFT dataset. Namely, we can overlap ${\mathcal{H}}_{iC}$ while training LoRA-V and removing the PAM stage (Equation (7)) during fine-tuning with packing.

Similar to Equation (19), the locations of each valid attention and cross-contamination regions are unchanged by softmax, while only the values are rescaled. Therefore, the scaled dot-product before softmax with packing ($S_i$) can be decomposed by subspaces of valid attention and cross-contamination as follows:

$$S_i=S_{i0}+S_{iC},$$

(23)

where $S_{iC}$ is the cross-contamination term. As explained in Equation (12), $S_{iC}$ cannot be directly mapped to ${\mathcal{H}}_{iC}$. However, without PAM, LoRA-Q is also updated with perturbing cross-contamination before softmax.

$$S_i=S_{i0}+S_{iC}+\Delta S_i,$$

(24)

3.3. Perturbation Influence in LoRA Without PAM

With the first-order Taylor approximation for ${\mathcal{H}}_i$-applied LoRA-Q and LoRA-V, the perturbation of ${\mathcal{H}}_i$ under $\Delta S_i$ and $\Delta v_i$ can be expressed as follows:

$$\begin{array}{}\mathrm{(25)}& {\mathcal{H}}_i(\Delta S_i,\Delta v_i)\equiv {\mathcal{H}}_i(S_{i0}+\Delta S_i,v_{i0}+\Delta v_i)-{\mathcal{H}}_i(S_{i0},v_{i0})\mathrm{(26)}& \hspace{1em}\hspace{1em}\hspace{1em}\approx \left({\displaystyle \frac{\partial {\mathcal{H}}_i}{\partial S_i}}\right)[\Delta S_i]+\left({\displaystyle \frac{\partial {\mathcal{H}}_i}{\partial v_i}}\right)[\Delta v_i]=J_{\mathtt{softmax}}\left(S_{i0}\right)[\Delta S_i]v_{i0}+\mathtt{softmax}\left(S_{i0}\right)\Delta v_i,\end{array}$$

where $J_{\mathtt{softmax}}$ is softmax Jacobian. The detail deviation between Equations (25) and (26) is provided in Appendix A, including why higher-order terms can be safely ignored. $\Delta v_i$ is applied via direct multiplication, whereas $\Delta S_i$ first passes through the softmax Jacobian, which tends to suppress perturbations for $\Delta S_i$. Additionally, $\Delta S_i$ is generally a quadratic form involving LoRA-Q, making its contribution less significant relative to LoRA-V. In experiments, the gradient percentage of LoRA-V in the whole gradient per step is much greater than that of LoRA-Q during fine-tuning. This characteristic implies that the loss contribution associated with mitigating cross-contamination is concentrated after the softmax operation rather than before it.

Although the gradient percentage of LoRA-Q is much less than that of LoRA-V, LoRA-Q can be analyzed to train to attenuate the cross-contamination before softmax. As mentioned in Section 2.2, the masking with small but non-zero values and the masking area can affect to normalization of softmax and stability in attention weights. Since these sensitivities are increased when PAM is not applied, the additional learnable parameter LoRA-Q needs to be trained more than with PAM. While LoRA-Q is updated with the interaction of LoRA-V during training as expressed in Equation (26), the gradient contribution for LoRA-Q becomes larger, whereas that for LoRA-V becomes smaller compared to the case without PAM, particularly in highly packed steps. Estimating and comparing the gradient percentage of LoRA-Q and LoRA-V per step are described in Section 4.2.

3.4. Runtime Overheads of PAM

One of implementation complexities for packing is masking generation. For efficient execution during training, each mask is generated per training iteration and fed with inputs to the model. Algorithm 1 describes the packing-aware mask of the block-diagonal shape, which is imported in mask generation per training iteration. Let N be the sequence length. On the Flash attention [18] path, constructing a key-padding mask is $\mathcal{O}\left(N\right)$ in time and memory, whereas the causal mask is handled implicitly by the kernel (thus $\mathcal{O}\left(1\right)$). In contrast, the packing-aware (block-diagonal) attention mask, when materialized as an $N\times N$ keep-mask, requires $\mathcal{O}\left(N^2\right)$ time and memory; with batch size B, the cost grows linearly to $\mathcal{O}\left(B{N}^2\right)$. If cross-contamination is allowed, generating packing-aware mask with $\mathcal{O}\left(B{N}^2\right)$ is passed. The time difference with and without packing-aware mask generation is reported in

Table 1. Detailed timing results for batch generation, per-step, and per-epoch computations for ‘NousResearch/Llama-2-7b-hf’ model with ‘databricks/databricks-dolly-15k’ dataset. “Allow CC” denotes that cross-contamination is allowed (setting without PAM). All numbers except packing time are averages; units are seconds (s) or milliseconds (ms). The ‘Mask’ column is computed as ‘mask gen.’ + ‘mask h2d.’ per step.

Exp.	Allow CC	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
Base		$-$	0.8307	0.1000	0.1641	0.1641	0.8307	390.1433
Online (Fast)	×	60.0617	0.7493	1.8111	0.2653	2.0764	0.7472	166.1000
	✓	58.9256	0.7265	0.1027	0.1300	0.2326	0.7263	161.0433
	$\Delta$	−1.1361	−0.0228	−1.7085	−0.1353	−1.8438	−0.0210	−5.0567
	$\Delta (\%)$	−1.8916	−3.0428	−94.3294	−50.9989	−88.7979	−2.8045	−3.0444
Online (Delay)	×	60.4502	0.7509	2.3954	0.2660	2.6613	0.7482	166.4400
	✓	58.8972	0.7353	0.0600	0.1214	0.1814	0.7351	162.9933
	$\Delta$	−1.5530	−0.0155	−2.3354	−0.1446	−2.4800	−0.0130	−3.4467
	$\Delta (\%)$	−2.5691	−2.0775	−97.4952	−54.3609	−93.1838	−1.7535	−2.0708
Offline (Fast)	×	92.7946	0.7491	2.2307	0.2656	2.4963	0.7466	154.0567
	✓	91.4681	0.7406	0.0806	0.0610	0.1417	0.7405	152.3067
	$\Delta$	−1.3266	−0.0085	−2.1500	−0.2046	−2.3546	−0.0061	−1.7500
	$\Delta (\%)$	−1.4296	−1.1347	−96.3868	−77.0331	−94.3236	−0.8231	−1.1359
Offline (Delay)	×	95.0622	0.7413	2.3773	0.4832	2.8605	0.7384	152.4633
	✓	93.6683	0.7395	0.1182	0.0877	0.2059	0.7393	152.1033
	$\Delta$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
	$\Delta (\%)$	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361

.

Algorithm 1 Packing-aware mask generation
1: function MakeBlockDiagKeepMaskAndPos($\mathbb{B},N,\mathrm{pad}$)
2:     $Bnds\leftarrow \mathrm{sorted}\left(\right\{b\in \mathbb{Z}\mid 0\le b<N\}\cap \mathbb{B})$
3:     if $Bnds=⌀$ or $Bnds\left[0\right]\ne 0$ then
4:         $Bnds\leftarrow \left[0\right]\parallel Bnds$
5:     end if
6:     $Bnds\leftarrow Bnds\parallel \left[N\right]$	▷ append end sentinel
7:     $M\leftarrow {\mathbf{0}}^{N\times N}$; $p\leftarrow {\mathbf{0}}^N$	▷ keep-mask (1 = keep, 0 = mask)
8:     for $k=0$ to $\left|Bnds\right|-2$ do
9:         $s\leftarrow Bnds\left[k\right]$, $e\leftarrow Bnds[k+1]$	▷ segment $[s:e)$
10:         if $s<e$ then
11:            $M[s:e,s:e]\leftarrow 1$	▷ place a 1-block on the diagonal
12:         end if
13:     end for
14:     $P\leftarrow \mathrm{pad}·{\mathrm{pad}}^{\top }$	▷ outer product; zero padded rows/cols
15:     $M\leftarrow M\odot P$	▷M stays a keep-mask for Algorithm 2
16:     return $(M,p)$
17: end function

Algorithm 2 describes the collator that constructs attention masks and measures their generation time (’mask_gen_ms’). When cross-contamination is not allowed, the block-diagonal mask generation (Algorithm 1) is invoked at line 16, producing a full 3D attention mask. In contrast, when cross-contamination is allowed, a simple padding mask is generated. The variable ‘mask_gen_ms’ records the CPU-side wall-clock time required to generate the attention mask, enabling quantitative analysis of the masking overhead. The host-to-device (H2D) transfer time of the attention mask is measured separately by synchronizing CUDA streams before and after the data transfer. Specifically, we record the timestamps immediately before and after calling attention_mask.to(device) with torch.cuda.synchronize() on both sides, and compute the elapsed time in milliseconds as the H2D latency (’mask_h2d_ms’) for every training iteration. Both ‘mask_gen_ms’ and ‘mask_h2d_ms’ are represented in Section 4.2 as ‘mask gen.’ and ‘mask h2d’, respectively.

Algorithm 2 Collate with masking and timing

1: function collate(Examples)   2:     Examples = [ ${\left\{e{x}_i\right\}}_{i=1}^B$, pad_id, allow_contamination, build_position_ids, mask_dtype ]   3:     $t_0\leftarrow$ TimerNowMs()   4:     Stack input_ids and labels from $\left\{e{x}_i\right\}$ to tensors of shape $[B,N]$   5:     boundaries ← { $e{x}_i.\mathtt{boundaries}$ or ∅ }   6:     if allow_contamination then   7:         attention_mask ←$(\mathtt{input}\_\mathtt{ids}\ne \mathtt{pad}\_\mathtt{id})$ as long in $[B,N]$   8:         position_ids ← None   9:     else 10:         Initialize attention_mask $\in {\mathbb{R}}^{B\times N\times N}$ with zeros 11:         if build_position_ids then 12:            Initialize position_ids $\in {\mathbb{N}}^{B\times N}$ with zeros 13:         end if 14:         for $b\leftarrow 1$ to B do 15:            pad ←$(\mathtt{input}\_\mathtt{ids}[b]\ne \mathtt{pad}\_\mathtt{id})$ as long 16:            $(m,p)\leftarrow$MakeBlockDiagKeepMaskAndPos$\left(\mathtt{boundaries}\right[b],N,\mathtt{pad})$ 17:            attention_mask$\left[b\right]\leftarrow m$ 18:            if build_position_ids then 19:                position_ids$\left[b\right]\leftarrow p$ 20:            end if 21:         end for 22:     end if 23:     mask_gen_ms ←TimerNowMs() $-t_0$ 24:     return {input_ids, labels, attention_mask, boundaries, mask_gen_ms, position_ids} 25: end function

Furthermore, in practice, applying PAM introduces several training-time overheads. Each factor is detailed below, with references to the corresponding pseudocode lines in Algorithm 3.

• For a 3D block mask of size ${\mathbb{R}}^{B\times N\times N}$, converting the mask to float32 (line 10) and transforming the values in masking area to negative values (line 12), perform full-tensor reads/writes and arithmetic at $\mathcal{O}\left(B{N}^2\right)$, making the step bandwidth-bound and increasing kernel launches relative to simply forwarding the mask.
• Repeated preprocessing without semantic effect such as additional no-ops with ‘.contiguous()’ and ‘.clone()’ introduces extra kernels and full-tensor copies, as described in lines 13 to 15. When repeated rep times, they scale linearly with rep, further amplifying GPU memory traffic without changing computation semantics.
• Forcing the SDPA backend to math instead of Flash attention [18] (i.e., disabling flash/mem_efficient) removes the most optimized attention kernels as shown in line 23. Even with identical masks, the attention computation itself becomes slower, compounding the overheads introduced by 1 and 2 factors.
• Performing the above transformations inside each attention layer causes the same mask to be reprocessed L times per forward (for L layers). In contrast, a cached, additive mask prepared once at the model level would amortize this cost; thus, layer-local preprocessing multiplies both kernel count and memory traffic (lines 8 to 17).

If PAM is eliminated, training speed degradation and its contributing factors do not arise. Furthermore, the implementation for PAM stage including mask generation (Algorithm 1) and forwarding the mask to attention layer (Algorithm 3) are not required. The experiment setting with all of the above four factors is named ‘Delay’, which mimics worst-case masking slowdowns per Algorithm 3, while Fast skips them for optimization. We compare the training results without ‘Delay’, which is named ‘Fast’, as tabulated in Table 1 and 

Table 2. Average and standard deviation of loss and parameter-update percentage differences ($\Delta =✓-\times$) per step for the ‘NousResearch/Llama-2-7b-hf’ model on the ‘databricks/databricks-dolly-15k’ dataset. All parameter-update values are reported as percentages (%).

Exp.	$\mathbf{\Delta }$ Step Loss		$\mathbf{\Delta }$ Epoch Last Loss		$\mathbf{\Delta }$q_rel_mean		$\mathbf{\Delta }$q_p95		$\mathbf{\Delta }$q_max		$\mathbf{\Delta }$v_rel_mean		$\mathbf{\Delta }$v_p95		$\mathbf{\Delta }$v_max
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
Online(Fast)	0.036	0.576	−0.010	0.001	−0.805	0.197	−1.366	0.639	−3.400	1.178	0.465	0.352	0.470	0.357	0.295	0.216
Online(Delay)	0.044	0.597	0.001	0.014	−0.795	0.199	−1.260	0.596	−3.707	1.452	0.260	0.230	0.621	0.401	0.594	0.499
Offline(Fast)	−0.046	0.106	0.003	0.004	−1.306	0.373	−2.049	0.597	−5.717	2.077	0.206	0.262	0.008	0.285	0.470	1.252
Offline(Delay)	−0.044	0.101	−0.004	0.005	−1.351	0.385	−2.668	0.791	−5.935	2.225	0.260	0.269	0.327	0.304	0.654	1.295

.

Algorithm 3 Runtime overheads in attention layer with PAM
1: function ComplexCustomAttentionForward($H,M,\mathit{original}\_\mathit{forward},\mathit{config}$)
2:	▷$H\in {\mathbb{R}}^{B\times N\times d}$, M may be $\mathtt{None}$, $M\in \{B\times N,B\times N\times N\}$
3:    $M_{\mathrm{ext}}\leftarrow \mathtt{None}$
4:    $ms\leftarrow \mathit{config}.\mathtt{mask}\_\mathtt{stress}$
5:	▷ user options: enable, preprocess_in_forward, repeat_preproc, disable_sdp
6:    if $M\ne \mathtt{None}$ and$rank\left(M\right)=3$ then	▷ supports $B\times N\times N$
7:        $m\leftarrow M$
8:        if $ms.\mathtt{enable}$ and $ms.\mathtt{preprocess}\_\mathtt{in}\_\mathtt{forward}$ then
9:           if $dtype\left(m\right)\ne \mathtt{float}\mathtt{32}$ then
10:               $m\leftarrow \mathrm{A}\mathrm{STYPE}(m,\mathtt{float}\mathtt{32})$
11:           end if
12:           $m\leftarrow (1-m)·(-{10}^9)$	▷0/1 keep-mask → additive mask: keep$\to 0$, mask$\to -\infty$
13:           for $i\leftarrow 1$ to$max(0,ms.\mathtt{repeat}\_\mathtt{preproc})$ do
14:               $m\leftarrow m+0.0$;    $m\leftarrow$ Contiguous(m);    $m\leftarrow$ Clone(m)
15:	▷ intentional kernel/memory stress without changing values
16:           end for
17:        end if
18:        $M_{\mathrm{ext}}\leftarrow$ Unsqueeze(m, axis = 1)	▷$B\times 1\times N\times N$
19:    else if $M\ne \mathtt{None}$ then	▷$B\times N$ padding mask path
20:        $M_{\mathrm{ext}}\leftarrow M[:,\mathtt{None},\mathtt{None},:]$
21:    end if
22:    if $ms.\mathtt{enable}$ and $ms.\mathtt{disable}\_\mathtt{sdp}$ then
23:        return $\mathit{original}\_\mathit{forward}(\mathtt{self},H,\mathtt{attention}\_\mathtt{mask}=M_{\mathrm{ext}},\mathtt{sdpkernels}=$ MathOnly)
24:	▷ force math-only attention (disable Flash/SDPA)
25:    else
26:        return $\mathit{original}\_\mathit{forward}(\mathtt{self},H,\mathtt{attention}\_\mathtt{mask}=M_{\mathrm{ext}})$
27:    end if
28: end function

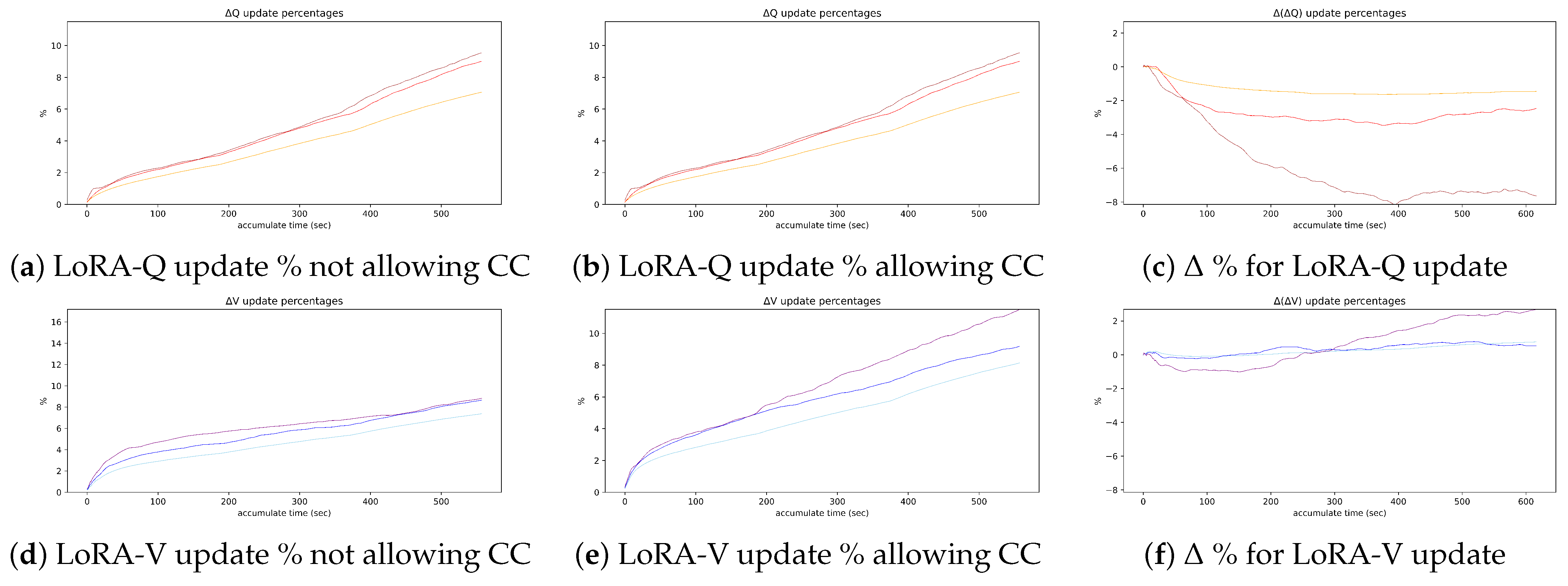
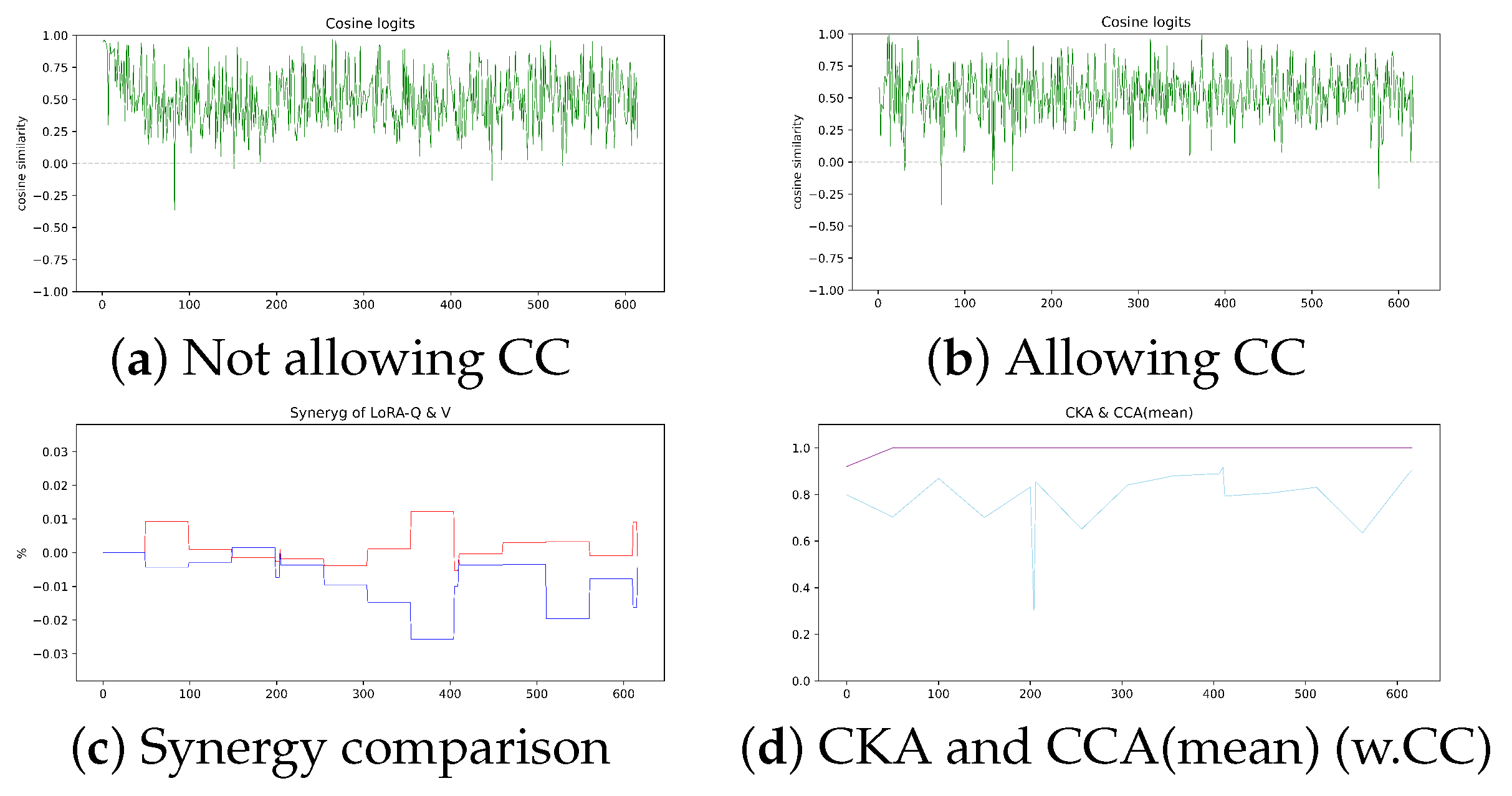
4. Results and Discussion

4.1. Experimental Setup

‘databricks/databricks-dolly-15k’ dataset [28] consists of 15,000 samples of instruction-response pairs. ‘tatsu-lab/alpaca’ and ‘yahma/alpaca_cleaned’ datasets [29] contain 52,000 samples. For supervised fine-tuning, we use the released version of the datasets from Hugging Face. Five parameter sets of pre-trained models are used to supervise fine-tuning, as shown in

Table 3. Comparison of four publicly available 7B-scale language models from Hugging Face.

Model Name	Base Architecture	# of Parameters
NousResearch/Llama-2-7b-hf 1 (NR)	Llama 2	7B
huggyllama/llama-7b 2 (HL)	LLaMA 1	6.74B
openlm-research/open_llama_7b [2] (OR)	OpenLLaMA	7B
mistralai/Mistral-7B-v0.1 [31] (MR)	Mistral 7B	7B
NousResearch/Llama-2-13b-hf 3 (NR(13B))	Llama 2	13B

¹ https://huggingface.co/NousResearch/Llama-2-7b-hf (1 September 2025) ² https://huggingface.co/huggyllama/llama-7b (1 September 2025) ³ https://huggingface.co/NousResearch/Llama-2-13b-hf (1 September 2025).

. All of the pre-trained models can be downloaded from Hugging Face Transformers [30]. Unless otherwise stated, we fine-tune all models with LoRA adapters on the query and value projections. For all 7B pre-trained models, we adopt $r=8$, following prior evidence that small ranks can be competitive with larger-rank configurations [20], and use $\alpha =32$, LoRA dropout of $0.1$, and a learning rate of $2\times {10}^{-4}$. The maximum sequence length per batch is set to 256 tokens with the batch size of 4 per device, except for ‘mistralai/Mistral-7B-v0.1’ model, which uses the batch size of 2 tokens per device.

All pre-trained models are fine-tuned for 3 epochs using distributed data parallelism (DDP) on 8 NVIDIA RTX A6000 GPUs and AMD EPYC 7513 32-Core Processor CPUs. Experiments are conducted on an NVIDIA server with driver 525.105.17 (CUDA 12.0) using PyTorch 2.1.2, Transformers 4.39.3, PEFT 0.10.0, Accelerate 0.27.2, and Datasets 2.19.1. We apply masking as an additive bias to $q_i{k}_i^T$. The final mask is $M=M_{pad}+M_{pack}+M_{causal}$, where $M_{pad}$ masks padding regions, $M_{pack}$ blocks cross-segment attention for packed inputs, and $M_{causal}$ is a strict upper-triangular bias implementing causality. Packing is applied at batch construction, and packing-aware attention masks are built on the fly per training step.

4.2. Reducing Training Time by Eliminating PAM

Table 1 and Table 2 describe the comparisons for PAM existence including online and offline packing, respectively marked as Online and Offline. The experiment setting with mimicked worst-case masking slowdowns per Algorithm 3 is named Delay, while Fast skips them for optimization. The training results without Delay are named Fast. The pre-trained model is ‘NousResearch/Llama-2-7b-hf’ and trained by ‘databricks/databricks-dolly-15k’ dataset. The title of column ‘Allow CC’ denotes that cross-contamination is allowed, where ‘×’ is applied PAM and ✓ is not.

As shown in Table 1, the reported packing time incudes batch generation under packing and the accumulated mask-generation time across training steps. Step time denotes the per-step runtime, including both the forward and backward passes. Values in the ‘Epoch time’ column are computed as the sum of step times over each epoch. Values in $\Delta$ rows are computed by subtracted values from allowing cross contamination to without allowing. Average and standard deviation values in the $\Delta$ rows for each experiment in Table 1 are derived from differences ($✓-\times$) in the packing time, per step and per epoch. $\Delta (\%)$ denotes the decreasing percentage ($(✓-\times )/\times$). Therefore, the smaller the $\Delta$ value (or $\Delta (\%)$) is (i.e., the more negative), the faster the training.

The values in Table 2 are also derived from differences ($\Delta$) for per-step loss, last loss per epoch, and update percentage for adaptive parameters (LoRA-Q and LoRA-V) per step. For each q or v projection l-th layer, the relative update magnitude is defined as

$$re{l}_l={\displaystyle \frac{\parallel \Delta W_l{\parallel }_F}{\parallel W_l{\parallel }_F+ϵ}}\times 100,(\%)$$

(27)

where $\Delta W_l=\left(B_l{A}_l\right)·scaling$ is the effective LoRA-Q increment and $W_l$ is the pre-trained base weight. ${\parallel ·\parallel }_F$ denotes Frobenius norm. We aggregate $re{l}_l$ across all query layers to report three summary statistics: ‘q_rel_mean’ (arithmetic mean), ‘q_rel_p95’ (95th percentile) and ‘q_rel_max’ (maximum). All values are dimensionless and reported in percentage. For the LoRA-V, we aggregate $re{l}_l$ across all value layers and respectively summarize them: ‘v_rel_mean’, ‘v_rel_p95’ (95th percentile), and ‘v_rel_max’ (maximum). Unless otherwise noted, the statistics are computed after each optimizer step (post-update) with the baseline $W_l$ taken at the start of training; $ϵ={10}^{-12}$ prevents division by zero. Frobenius norms are used throughout.

As shown in $\Delta$ rows for each experiment in Table 1, the packing time, step time, and epoch time are decreased when PAM is not applied by erasing the PAM stages. Since the packing-aware mask generation stage is passed, the values for packing time in $\Delta$ row are less than zero. Average values per step time for all $\Delta$ rows also decrease by eliminating the stage to forward packing-aware mask into the attention layer. For the packing time and average time values when both allowing or not allowing cross-contamination with Online, Fast is lower than Delay. Comparing Online and Offline experiments, Online packing is faster than Offline but the average time values is much faster in Offline since each batch is more compactly packed. Base is supervised fine-tuning with LoRA-Q and LoRA-V adaptive parameters to compare the value of packing itself. Both experiments shows shorter training time than Base for all time columns. The packing time for Base is not necessary to estimate.

Table 1 also reports the per-step masking overhead. Except the ‘packing time’ column, all values i the table are averages. ‘mask gen.’ and ‘mask h2d’ denote the average per-step times for mask generation and host-to-device transfer, respectively. ‘Mask’ is their per-step sum (Mask = mask gen. + mask h2d). All three columns are reported in milliseconds. ‘step time - Mask’ equals the step time minus ‘Mask’ in step level. The reductions reported in the $\Delta$ rows for ‘mask gen.’, ‘mask h2d’, and ‘Mask’ arise because the packing-aware mask generation (Algorithm 1) is entirely bypassed when cross-contamination is allowed. Generating PAM requires materializing an $N\times N$ keep-mask per sequence, leading to $\mathcal{O}\left(B{N}^2\right)$ time and memory, which is substantially higher than the costs for a key-padding mask $\mathcal{O}\left(BN\right)$ and the (flag-based) causal constraint $\mathcal{O}\left(B\right)$ on the Flash attention path. Consequently, ‘mask gen.’ under ‘Allow CC’ decreases by more than 20 times compared to not allowing cross-contamination. ‘mask h2d’ under ‘Allow CC’ is roughly halved, since a one-dimensional padding vector is transferred instead of an $N\times N$ mask. A small non-zero masking time remains due to computing the padding vector and enforcing the causal constraint inside the attention kernel. Therefore, the time for ‘mask gen.’ and ‘mask h2d.’ when allowing cross-contamination (not PAM) show similar values to those for Base.

We evaluate on an 8-subject subset of MMLU [32] in the K-shot (default $K=5$) multiple-choice setting.

Table 4. Evaluation results for eight subjects in MMLU benchmark with fine-tuned ‘NousResearch/Llama-2-7b-hf’ model with ‘databricks/databricks-dolly-15k’ dataset. “Allow CC” denotes that cross-contamination is allowed (setting without PAM). B denotes Base setting.

Exp.	Allow CC	Abstract Algebra	Computer Security	Econometrics	College Biology	Astronomy	High School	Clinical Knowledge	Professional Law
Base		0.300	0.510	0.289	0.347	0.303	0.252	0.370	0.330
Online (Fast)	×	0.280	0.470	0.325	0.465	0.355	0.258	0.375	0.365
	✓	0.330	0.480	0.316	0.382	0.316	0.232	0.385	0.360
	✓ $- \times$	0.050	0.010	−0.009	−0.083	−0.039	−0.026	0.010	−0.005
	✓ $- \mathbf{B}$	0.030	−0.030	0.027	0.035	0.013	−0.020	0.015	0.030
Online (Delay)	×	0.320	0.520	0.307	0.479	0.309	0.219	0.430	0.350
	✓	0.310	0.480	0.342	0.403	0.336	0.219	0.400	0.350
	✓ $- \times$	−0.010	−0.040	0.035	−0.076	0.026	0.000	−0.030	0.000
	✓ $- \mathbf{B}$	0.010	−0.030	0.053	0.056	0.033	−0.033	0.030	0.020
Offline (Fast)	×	0.340	0.530	0.325	0.472	0.342	0.298	0.475	0.355
	✓	0.340	0.500	0.298	0.410	0.362	0.252	0.405	0.325
	✓ $- \times$	0.000	−0.030	−0.026	−0.062	0.020	−0.046	−0.070	−0.030
	✓ $- \mathbf{B}$	0.040	−0.010	0.009	0.063	0.059	0.000	0.035	−0.005
Offline (Delay)	×	0.340	0.580	0.333	0.479	0.355	0.272	0.490	0.340
	✓	0.350	0.460	0.289	0.410	0.342	0.252	0.425	0.280
	✓ $- \times$	0.010	−0.120	−0.044	−0.069	−0.013	−0.020	−0.065	−0.060
	✓ $- \mathbf{B}$	0.050	−0.050	0.063	0.039	0.039	0.000	0.055	−0.050

reports per-subject accuracies only. For each subject, we concatenate K in-context examples and the test question with four options (A–D), followed by “Answer:”. The model selects the option whose answer letter attains the highest conditional log-likelihood (no sampling). The rows labeled $✓-\mathbf{B}$ represent the absolute difference between allowing contamination for each experiment and Base. The rows labeled $✓-\times$ reports the absolute difference between the two experiments following the definitions $\Delta$ used in Table 1. The results show performance comparable to the baseline, indicating that our approach shows similar performances for downstream tasks. The scores on all subjects for Online experiments vary only within $-0.08$ to $+0.05$, confirming that the proposed method maintains task-level performance while reducing overhead. The scores across all subjects in the Offline experiments vary only within a range of $-0.12$ to $+0.02$, which is slightly lower than those of the Online experiments. This is mainly because offline packing involves a more complex segment composition and is inherently more difficult to mitigate cross-contamination. However, performance comparison between allowing cross-contamination and Base shows similar or higher scores, varying within a range of $-0.05$ to $+0.06$ as shown in $✓-\mathbf{B}$ rows.

Although the unnecessary attention of cross-contamination is expected to make fine-tuning the models difficult, the loss difference between the training with and without PAM is not remarkable, as described in ‘$\Delta$ step loss’ and ‘$\Delta$ epoch last loss’ columns in Table 2. To compare the detail trajectory of loss, the figures in Figure 1 show the difference between two losses in Offline(Delay) experiment. Although cross-contamination is expected to require much more training cost, except at the beginning of training, the loss without PAM converges quickly to the loss with PAM. Rather, the training loss when allowing cross-contamination is lower than when not allowing. This lower loss distribution is also represented as negative average values for $\Delta$ step loss and $\Delta$ epoch loss columns in Table 2. In the remaining experiments, the average values for $\Delta$ loss are <±0.05, indicating that the models trained without PAM rapidly approach the performance of their with-PAM counterparts.

As mentioned in Equation (27), we measure the update percentages for LoRA-Q and LoRA-V per step and summarize to three statistics as shown in Table 2 and Figure 2. When cross-contamination is not allowed, all update percentages for LoRA-Q (Figure 2a) steadily increase more rapidly than percentages for LoRA-V (Figure 2d) during training, except the early part of the training. However, for the training when allowing cross-contamination as shown in Figure 2b,e, the percentages for LoRA-V increase much higher than percentages for LoRA-V, whereas they comparable to percentages for LoRA-V with not allowing. This means a higher perturbation of the step-wise gradient budget is allocated to value parameters, as explained in Section 3.3. These percentage differences between the two experiments are shown in Figure 2c,f. These results are represented as the negative average values for the columns (named with ‘$\Delta$q_’) in Table 2, while the average values with columns (named with ‘$\Delta$v_’) are positive.

In the above experiment, we apply $r=8$ as the default LoRA rank, following the original LoRA [20], which demonstrated it as a broadly effective setting. To further address other ranks, we additionally conduct experiments with $r=4$ and $r=16$ for Offline(Delay) setting in

Table A6. Detailed timing results for batch generation, per-step, and per-epoch computations for training r-rank parameters.

r	Allow CC	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
8	×	95.0622	0.7413	2.3773	0.4832	2.8605	0.7384	152.4633
	✓	93.6683	0.7395	0.1182	0.0877	0.2059	0.7393	152.1033
	$\Delta$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
	$\Delta (\%)$	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361
4	✓	93.6475	0.7240	0.0845	0.0778	0.1623	0.7238	148.9000
	$\Delta$	−1.4147	−0.0173	−2.2928	−0.4054	−2.6982	−0.0146	−3.5633
	$\Delta (\%)$	−1.4881	−2.3337	−96.4455	−83.8990	−94.3262	−1.9774	−2.3372
16	✓	93.6269	0.7251	0.0510	0.1238	0.1748	0.7249	149.1200
	$\Delta$	−1.4353	−0.0163	−2.3263	−0.3594	−2.6857	−0.0135	−3.3433
	$\Delta (\%)$	−1.5099	−2.1854	−97.8547	−74.3791	−93.8892	−1.8301	−2.1929

and

Table A7. Average and standard deviation of loss and parameter-update percentage differences ($\Delta =✓-\times$) per step for different r-rank. All parameter-update values are reported as percentages (%).

r	$\mathbf{\Delta }$ Step Loss		$\mathbf{\Delta }$ Epoch Last Loss		$\mathbf{\Delta }$q_rel_mean		$\mathbf{\Delta }$q_p95		$\mathbf{\Delta }$q_max		$\mathbf{\Delta }$v_rel_mean		$\mathbf{\Delta }$v_p95		$\mathbf{\Delta }$v_max
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
8	−0.045	0.101	−0.004	0.005	−1.351	0.385	−2.668	0.791	−5.935	2.225	0.260	0.269	0.327	0.304	0.654	1.295
4	−0.041	0.099	−0.002	0.004	−0.518	0.255	−1.525	0.692	−4.897	1.877	1.182	0.511	1.333	0.567	1.045	1.056
16	−0.047	0.100	−0.003	0.005	−1.910	0.574	−3.131	0.875	−6.418	2.363	−0.333	0.147	−0.233	0.179	−0.602	0.469

. The results confirm that the performance trends—such as mask generation and transmission time as well as step loss reduction—are consistent with those observed at $r=8$.

Table 5. Detailed timing results for batch generation, per-step, and per-epoch computations for pre-trained models with three datasets and Offline(Delay) setting. $\Delta$, $\Delta (\%)$ and units (s, ms) follow the same definition as in Table 1. All numbers except packing time are averages. The detailed values are represented in tables in Appendix B.

Datasets	Models	$\mathbf{\Delta }$	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
databricks databricks -dolly-15k	NR	✓ $- \times$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
		$\Delta (\%)$	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361
	HL	✓$- \times$	−1.1749	0.0024	−1.9042	−0.2856	−2.1899	0.0046	0.4933
		$\Delta (\%)$	−1.0437	0.3325	−94.0534	−62.9352	−88.3559	0.6382	0.3323
	OR	✓$- \times$	−1.2786	−0.0172	−2.2353	−0.3215	−2.5568	−0.0146	−3.2800
		$\Delta (\%)$	−1.7260	−2.3354	−95.5256	−80.4555	−93.3272	−1.9957	−2.3356
	MR	✓$- \times$	−1.1817	−0.0086	−0.9880	−0.1656	−1.1536	−0.0074	−3.4267
		$\Delta (\%)$	−1.5654	−0.9808	−90.1469	−62.0315	−84.6430	−0.8506	−0.9803
tatsu-lab /alpaca	NR	✓$- \times$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
		%	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361
	HL	✓$- \times$	−1.1749	0.0024	−1.9042	−0.2856	−2.1899	0.0046	0.4933
		%	−1.0437	0.3325	−94.0534	−62.9352	−88.3559	0.6382	0.3323
	OR	✓$- \times$	−1.2786	−0.0172	−2.2353	−0.3215	−2.5568	−0.0146	−3.2800
		%	−1.7260	−2.3354	−95.5256	−80.4555	−93.3272	−1.9957	−2.3356
	MR	✓$- \times$	−1.1817	−0.0086	−0.9880	−0.1656	−1.1536	−0.0074	−3.4267
		%	−1.5654	−0.9808	−90.1469	−62.0315	−84.6430	−0.8506	−0.9803
yahma/ alpaca _cleaned	NR	✓$- \times$	−6.9868	−0.0038	−2.0580	−0.2902	−2.3482	−0.0015	−4.2733
		$\Delta (\%)$	−0.6457	−0.5112	−94.2607	−78.4171	−91.9637	−0.1960	−0.5080
	HL	✓$- \times$	−7.3857	−0.0246	−2.1755	−0.2896	−2.4651	−0.0221	−27.8633
		$\Delta (\%)$	−0.7290	−3.2178	−96.2100	−75.6333	−93.2264	−2.9054	−3.2207
	OR	✓$- \times$	−6.2812	−0.0079	−1.9985	−0.2809	−2.2794	−0.0057	−8.3233
		$\Delta (\%)$	−0.6913	−1.0725	−95.7411	−68.6461	−91.3002	−0.7695	−1.0651
	MR	✓$- \times$	−6.8929	−0.0057	−1.0580	−0.1658	−1.2238	−0.0045	−12.3400
		$\Delta (\%)$	−0.7307	−0.6639	−90.7220	−61.3620	−85.2001	−0.5222	−0.6618

and

Table 6. Average and standard deviation of loss and parameter-update percentage differences ($\Delta =✓- \times$) per step for pre-trained models with three datasets and Offline(Delay) setting. All parameter-update values are reported as percentages (%).

Datasets	Models	$\mathbf{\Delta }$ Step Loss		$\mathbf{\Delta }$ Epoch Last Loss		$\mathbf{\Delta }$q_rel_mean		$\mathbf{\Delta }$q_p95		$\mathbf{\Delta }$q_max		$\mathbf{\Delta }$v_rel_mean		$\mathbf{\Delta }$v_p95		$\mathbf{\Delta }$v_max
		Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
databricks/ databricks -dolly-15k	NR	−0.045	0.101	−0.004	0.005	−1.351	0.385	−2.668	0.791	−5.935	2.225	0.260	0.269	0.327	0.304	0.654	1.295
	HL	−0.039	0.133	−0.017	0.009	−1.355	0.344	−1.880	0.814	−0.898	1.567	−0.017	0.257	−0.751	0.161	−2.196	0.786
	OR	−0.074	0.125	−0.042	0.027	−1.197	0.356	−1.994	0.993	−5.736	3.386	0.074	0.322	−0.897	0.393	−0.800	0.453
	MR	−0.032	0.071	−0.016	0.035	−2.907	0.879	−3.332	1.321	−10.206	4.398	−0.726	0.475	−0.808	0.426	−1.942	1.329
tatsu-lab/ alpaca	NR	−0.028	0.112	−0.012	0.012	−1.829	0.383	−4.924	1.530	−9.461	2.933	0.156	0.378	0.362	0.499	1.221	1.427
	HL	−0.038	0.115	−0.015	0.011	−1.453	0.273	−2.099	0.620	0.084	0.636	−0.094	0.281	−1.779	0.420	−2.295	0.661
	OR	−0.047	0.104	−0.022	0.005	−1.286	0.252	−1.863	0.530	−8.959	3.848	0.255	0.469	−0.718	0.327	−0.469	0.275
	MR	−0.019	0.057	−0.022	0.026	−3.473	0.776	−6.520	1.989	−14.982	5.375	−0.307	0.912	−0.305	0.601	0.315	1.537
yahma/ alpaca _cleaned	NR	−0.011	0.028	0.001	0.004	−1.273	0.197	−3.821	0.985	−5.540	1.662	0.696	0.401	1.619	0.701	3.503	2.006
	HL	−0.012	0.048	−0.014	0.009	−1.031	0.276	−0.869	0.367	1.186	0.808	0.275	0.266	−0.061	0.491	0.624	1.419
	OR	−0.020	0.037	−0.009	0.007	−1.384	0.273	−1.779	0.514	−15.632	7.442	0.717	0.450	0.003	0.234	−0.164	0.430
	MR	−0.009	0.025	0.002	0.021	−4.016	0.851	−13.299	4.164	−40.767	19.104	0.148	0.592	0.436	0.564	−1.673	1.078

report the differences of SFT results for four pre-trained models under the Offline(Delay) setting on each dataset to assess the generality of our approach. The original training result values for each dataset in Table 5 are represented separately for each dataset in Appendix B. In the rows labeled ‘databricks/databricks-dolly-15k’ in Table 5, almost-average values are negative ($✓<\times$), consistent with the previous experiment. In particular, values for mask generation and transmission stage are highly decreased by more than 90% and 60%, respectively. These decreases affect the decrease in time for packing, per step, and epoch. Table 6 shows the decreases for the average losses and update percentages, as similar to Table 2. The detailed timing results are tabulated in

Table A1. Detailed timing results for batch generation, per-step, and per-epoch computations for pre-trained models with ‘databricks/databricks-dolly-15k’ dataset and Offline(Delay) setting.

Models	Allow CC	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
NR	×	95.0622	0.7413	2.3773	0.4832	2.8605	0.7384	152.4633
	✓	93.6683	0.7395	0.1182	0.0877	0.2059	0.7393	152.1033
	$\Delta$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
	$\Delta (\%)$	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361
HL	×	112.5778	0.7217	2.0247	0.4538	2.4785	0.7192	148.4300
	✓	111.4029	0.7241	0.1204	0.1682	0.2886	0.7238	148.9233
	$\Delta$	−1.1749	0.0024	−1.9042	−0.2856	−2.1899	0.0046	0.4933
	$\Delta (\%)$	−1.0437	0.3325	−94.0534	−62.9352	−88.3559	0.6382	0.3323
OR	×	74.0801	0.7365	2.3400	0.3996	2.7395	0.7338	140.4333
	✓	72.8015	0.7193	0.1047	0.0781	0.1828	0.7191	137.1533
	$\Delta$	−1.2786	−0.0172	−2.2353	−0.3215	−2.5568	−0.0146	−3.2800
	$\Delta (\%)$	−1.7260	−2.3354	−95.5256	−80.4555	−93.3272	−1.9957	−2.3356
MR	×	75.4886	0.8768	1.0961	0.2668	1.3629	0.8754	349.5333
	✓	74.3069	0.8682	0.1080	0.1013	0.2093	0.8680	346.1067
	$\Delta$	−1.1817	−0.0086	−0.9880	−0.1656	−1.1536	−0.0074	−3.4267
	$\Delta (\%)$	−1.5654	−0.9808	−90.1469	−62.0315	−84.6430	−0.8506	−0.9803

. The averages for LoRA-V update percentage columns (named with ‘$\Delta$v_’) are also negative, but the averages for LoRA-Q (named with ‘$\Delta$q_’) are much less. Thus, the relative update percentage in LoRA-Q decreases more rapidly than in LoRA-V, with LoRA-V exhibiting larger perturbations to attenuate cross-contamination.

‘tatsu-lab/alpaca’ rows in Table 5 and Table 6 report SFT results for four pre-trained models on the ‘tatsu-lab/alpaca’ dataset. In Table 5, all time entries in the $\Delta$ rows are negative, consistent with the previous experiment tables. The detailed timing results are tabulated in

Table A2. Detailed timing results for batch generation, per-step, and per-epoch computations for pre-trained models with ‘tatsu-lab/alpaca’ dataset and Offline(Delay) experiment setting.

Models	Allow CC	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
NR	×	427.7267	0.7496	2.3093	0.3778	2.6870	0.7469	381.2733
	✓	424.4628	0.7346	0.1704	0.1522	0.3227	0.7343	373.6800
	$\Delta$	−3.2639	−0.0149	−2.1388	−0.2255	−2.3644	−0.0126	−7.5933
	$\Delta (\%)$	−0.7631	−2.0011	−92.6211	−59.7141	−87.9903	−1.6917	−1.9916
HL	×	374.9585	0.7537	2.5680	0.3756	2.9436	0.7508	383.3700
	✓	371.2932	0.7457	0.1661	0.1158	0.2819	0.7454	379.3267
	$\Delta$	−3.6653	−0.0079	−2.4019	−0.2598	−2.6617	−0.0053	−4.0433
	$\Delta (\%)$	−0.9775	−1.0614	−93.5319	−69.1693	−90.4233	−0.7111	−1.0547
OR	×	357.2428	0.7430	2.2023	0.4577	2.6599	0.7403	349.6967
	✓	354.3143	0.7334	0.1282	0.1501	0.2784	0.7331	345.2100
	$\Delta$	−2.9285	−0.0095	−2.0740	−0.3075	−2.3816	−0.0072	−4.4867
	$\Delta (\%)$	−0.8198	−1.2921	−94.1788	−67.2056	−89.5334	−0.9750	−1.2830
MR	×	377.5409	0.8698	1.2790	0.2471	1.5260	0.8683	849.5233
	✓	374.1231	0.8696	0.1125	0.1227	0.2352	0.8694	849.3233
	$\Delta$	−3.4178	−0.0002	−1.1665	−0.1243	−1.2908	0.0011	−0.2000
	$\Delta (\%)$	−0.9053	−0.0230	−91.2041	−50.3440	−84.5872	0.1256	−0.0235

. Table 6 shows the decreases for the average losses and update percentages, as similar to Table 6. The averages for each LoRA-V update percentage columns are also negative, but the corresponding averages for LoRA-Q is much less. Therefore, LoRA-V exhibits larger perturbations to attenuate cross-contamination.

The rows named with ‘yahma/alpaca_cleaned’ in Table 5 and Table 6 show SFT results for four pre-trained models on ‘yahma/alpaca_cleaned’ dataset, which contains many more samples than the previous two datasets. In the rows named with ‘yahma/alpaca_cleaned’ in Table 5, nearly all time entries in the $\Delta$ rows are negative and are smaller (i.e., more negative) than the values in the corresponding cells of other dataset rows. The detailed timing results are tabulated in

Table A3. Detailed timing results for batch generation, per-step and per-epoch computations for pre-trained models with ‘yahma/alpaca_cleaned’ dataset and Offline(Delay) experiment setting.

Models	Allow CC	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
NR	×	1081.9873	0.7433	2.1832	0.3702	2.5534	0.7407	841.1333
	✓	1075.0005	0.7395	0.1253	0.0799	0.2052	0.7393	836.8600
	$\Delta$	−6.9868	−0.0038	−2.0580	−0.2902	−2.3482	−0.0015	−4.2733
	$\Delta (\%)$	−0.6457	−0.5112	−94.2607	−78.4171	−91.9637	−0.1960	−0.5080
HL	×	1013.1999	0.7645	2.2612	0.3829	2.6441	0.7619	865.1433
	✓	1005.8142	0.7399	0.0857	0.0933	0.1791	0.7397	837.2800
	$\Delta$	−7.3857	−0.0246	−2.1755	−0.2896	−2.4651	−0.0221	−27.8633
	$\Delta (\%)$	−0.7290	−3.2178	−96.2100	−75.6333	−93.2264	−2.9054	−3.2207
OR	×	908.6478	0.7459	2.0874	0.4092	2.4966	0.7434	781.4233
	✓	902.3665	0.7379	0.0889	0.1283	0.2172	0.7377	773.1000
	$\Delta$	−6.2812	−0.0079	−1.9985	−0.2809	−2.2794	−0.0057	−8.3233
	$\Delta (\%)$	−0.6913	−1.0725	−95.7411	−68.6461	−91.3002	−0.7695	−1.0651
MR	×	943.3118	0.8586	1.1662	0.2702	1.4365	0.8572	1864.6200
	✓	936.4189	0.8529	0.1082	0.1044	0.2126	0.8527	1852.2800
	$\Delta$	−6.8929	−0.0057	−1.0580	−0.1658	−1.2238	−0.0045	−12.3400
	$\Delta (\%)$	−0.7307	−0.6639	−90.7220	−61.3620	−85.2001	−0.5222	−0.6618

. Table 6 shows the decreases for the average losses and update percentages, as similar to Table 6. The averages in ‘Δv_rel_mean’ is positive while the averages in ‘Δq_rel_mean’ is near zero or negative. That is, LoRA-V exhibits larger perturbations than LoRA-Q to mitigate cross-contamination.

To check that our approach is available to other LLM, we fine-tune a 13-billion pre-trained model(NousResearch/Llama-2-13b-hf).

Table 7. Detailed timing results for batch generation, per-step, and per-epoch computations for a 13B pre-trained model (‘NousResearch/Llama-2-13b-hf’) with ‘databricks/databricks-dolly-15k’ dataset and Offline(Delay) setting. $\Delta$, $\Delta (\%)$, and units (s, ms) follow the same definition as in Table 1. All numbers except packing time are averages. The detailed results are reported in Table A4.

Exp.	$\mathbf{\Delta }$	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
Online (Fast)	$✓-\times$	−2.6398	−0.0007	−0.9947	−0.0927	−1.0874	0.0005	−0.5833
	$\Delta (\%)$	−4.2218	−0.0725	−89.3139	−31.7140	−77.3384	0.0590	−0.0796
Offline (Fast)	$✓-\times$	−2.3581	−0.0003	−0.9566	0.0100	−0.9467	0.0006	−0.2733
	$\Delta (\%)$	−2.5067	−0.0361	−84.2240	4.2319	−68.9914	0.0780	−0.0400

and

Table 8. Average and standard deviation of loss and parameter-update percentage differences ($\Delta =✓- \times$) per step a 13B pre-trained model (‘NousResearch/Llama-2-13b-hf’) with ‘databricks/databricks-dolly-15k’ dataset. All parameter-update values are reported as percentages (%).

Exp.	$\mathbf{\Delta }$ Step Loss		$\mathbf{\Delta }$ Epoch Last Loss		$\mathbf{\Delta }$q_rel_mean		$\mathbf{\Delta }$q_p95		$\mathbf{\Delta }$q_max		$\mathbf{\Delta }$v_rel_mean		$\mathbf{\Delta }$v_p95		$\mathbf{\Delta }$v_max
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
Online(Fast)	1.267	2.814	0.000	0.000	0.483	0.360	2.382	2.437	7.378	3.454	8.883	5.252	20.151	12.563	43.604	17.801
Offline(Fast)	−0.053	0.679	0.000	0.000	1.484	0.788	6.269	3.070	9.388	3.967	3.839	2.572	6.666	4.406	−3.644	−3.644

show SFT results for pre-trained model with ‘databricks/databricks-dolly-15k’ datasets. Due to limitations in the experimental setup (devices capacity), we perform experiments with a small batch size (with 1), and thus did not show the same reduction in time as the previous 7B models. In Table 7, nearly all time entries in the $\Delta$ and $\Delta (\%)$ rows are negative, especially in mask generation and transmission time. Table 8 shows the decreases of the average losses and differences of update percentages. The averages of update percentage for LoRA-V are remarkably increased while the averages for LoRA-Q are not. Therefore, LoRA-V exhibits larger perturbations than LoRA-Q to mitigate cross-contamination.

LoRA introduces an additional $r(d_{in}+d_{out})$ parameters and a proportional amount of computation per projection matrix. This increase is linear in the low-rank dimension r, compared to the base model parameters $O(d_{in}\times d_{out})$, and thus the relative overhead (%) decreases as the model size grows. In this study, the LoRA adaptation is limited to the Q and V projections, resulting in minimal computational and memory increments, which remain negligible even for large-scale models (e.g., 34B, 70B). In contrast, the PAM mechanism scales with $\mathcal{O}\left(B{L}^2\right)$ in both mask construction and transfer buffer size, where B and L denote batch size and sequence length, respectively. As the context length increases (e.g., 8k–16k), PAM can become a dominant source of overhead due to mask generation and host-to-device (H2D) transfer latency. The proposed method removes the PAM pathway entirely, eliminating the $\mathcal{O}\left(B{L}^2\right)$ masking cost. Although the attention operation itself remains $\mathcal{O}\left(L^2\right)$, the reduction in PAM-induced overhead leads to a larger absolute performance gain for longer sequences. By discarding the $B\times L\times L$-scale mask buffer, the method also recovers GPU memory capacity, allowing longer sequence lengths or slightly larger micro-batches on the same hardware. This can mitigate the frequent batch-size-one bottleneck observed in large models and improve the effective training throughput. The complementary behavior of LoRA applied to Q/V remains valid as model capacity increases (see Section 3.4). However, quantitative verification on 34B/70B models with extended contexts (8k–16k) is left as future work due to resource constraints.

4.3. Complementary Training Between LoRA-V and LoRA-Q

As analyzed and expected in Section 3.1 and Section 3.2, all the training results show that pre-trained models with packing can be fine-tuned well without packing-aware masking by covering the tensor subspace from LoRA-V and LoRA-Q parameters. The time for batch generation, per step, and epoch are decreased since additional PAM stages are ignored. The loss differences between SFT with and without PAM are closed to zero for all experiments. Furthermore, the time overhead factors by applying PAM, as explained in Section 3.4, increase the average values per time column in tables. Reductions for each time seem too small to highlight the benefit of eliminating PAM. However, the implementation for PAM stage such as Algorithms 1 and 3 is not required and the implementation cost for PAM is erased. As expected in Section 3.3, the interactive training movements between LoRA-V and LoRA-Q are shown in the tables and figures for gradient percentages in the experiments (Section 4.2).

However, it is unclear whether LoRA-V and LoRA-Q actually interact during training. We thus examine whether adapting only one of them can attain comparable performance. Under the Offline(Delay) setting for ‘NousResearch/Llama-2-7b-hf’ model and ‘databricks/databricks-dolly-15k’ dataset,

Table 9. Detailed timing results for batch generation, per-step, and per-epoch computations for training LoRA-Q only or LoRA-V only with Offline(Delay) setting. $\Delta$, $\Delta (\%)$, and units (s, ms) follow the same definition as in Table 1. All numbers except packing time are averages. The detailed values are represented in Table A5.

Trained Param.	$\mathbf{\Delta }$	Packing Time (s)	Step Time (s)	Mask gen. (ms)	Mask h2d. (ms)	Mask (ms)	Step Time -Mask (s)	Epoch Time (s)
LoRA-Q & LoRA-V	$✓-\times$	−1.3939	−0.0018	−2.2591	−0.3955	−2.6546	0.0009	−0.3600
	$\Delta (\%)$	−1.4663	−0.2428	−95.0280	−81.8502	−92.8020	0.1157	−0.2361
LoRA-V -only	$✓-\times$	−1.3796	−0.1056	−2.2360	−0.4049	−2.6409	−0.1030	−21.7233
	$\Delta (\%)$	−1.4512	−14.2452	−94.0521	−83.7955	−92.3230	−13.9428	−14.2482
LoRA-Q -only	$✓-\times$	−1.3674	−0.1024	−2.2163	−0.3516	−2.5678	−0.0998	−21.0633
	$\Delta (\%)$	−1.4385	−13.8136	−93.2234	−72.7649	−89.7675	−13.5193	−13.8153

and Figure 3 compare training that adapts both LoRA-V and LoRA-Q against training that adapts only one of them. For the LoRA-V-only and LoRA-Q-only experiments, the rank is set to $r=64$ to attain performance comparable to the original LoRA setup [20]. In Table 9, the $\Delta$ rows for the V-only and Q-only settings for same pre-trained model and dataset in Table 9 report differences relative to the traditional “LoRA-V & LoRA-Q” configuration shown in the first row. The experiment setting that mimics worst-case masking slowdowns per Algorithm 3 is named Delay, while Fast skips them for optimization.

Across average time values in Table 9, both single-parameter experiments (LoRA-V-only or LoRA-Q-only) run faster than training both parameters without PAM, while the averages for masking generation and transmission time are similarly decreased. However, for the decreases in loss per step as shown in

Table 10. Average and standard deviation of loss and parameter-update percentage differences ($\Delta =✓-\times$) per step for training LoRA-Q only or LoRA-V only with Offline(Delay) setting. All parameter-update values are reported as percentages (%).

Trained Parameters	$\mathbf{\Delta }$ Step Loss		$\mathbf{\Delta }$ Epoch Last Loss		$\mathbf{\Delta }$q_rel_mean		$\mathbf{\Delta }$q_p95		$\mathbf{\Delta }$q_max		$\mathbf{\Delta }$v_rel_mean		$\mathbf{\Delta }$v_p95		$\mathbf{\Delta }$v_max
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
LoRA-Q & LoRA-V	−0.045	0.101	−0.004	0.005	−1.351	0.385	−2.668	0.791	−5.935	2.225	0.260	0.269	0.327	0.304	0.654	1.295
LoRA-V-only	−0.031	0.100	0.010	0.008	−5.052	2.161	−7.324	2.850	−10.831	4.522	−0.457	0.186	−0.435	0.247	−0.804	0.417
LoRA-Q-only	0.032	0.080	0.031	0.014	0.597	0.348	−0.371	0.218	−3.561	2.052	−4.540	1.693	−5.501	1.872	−6.092	1.662

, training both parameters shows greater decrease than training only one of them. Furthermore, for the averages of update percentages columns, training two-parameters notably shows positive averages in Δv_rel columns with negative averages in Δq_rel columns, while each training single-parameter shows much less update percentages for the corresponding training parameter comparing to training two parameters. These observations suggest that adapting both parameters yields complementary, interactive training effects, as explained in Section 3.3.

To verify that the two parameters learn complementarily not only through simple update percentage trends but also over the entire step, we measured the following three methods. First, at step t, we measure the alignment of the functional effects induced by the query-side and value-side adapters to check the complementary training for both adaptive parameters. Let $y\left(\theta \right)$ denote the model outputs (logits) for a fixed mini-batch. We form two infinitesimal “what-if” updates along the current gradients, restricted to each group:

$$\Delta {\theta }_Q=ϵ{\displaystyle \frac{g_Q}{\parallel g_Q{\parallel }_2}},\Delta {\theta }_V=ϵ{\displaystyle \frac{g_V}{\parallel g_V{\parallel }_2}},$$

(28)

and compute the resulting output changes:

$$\Delta y_Q=y(\theta +\Delta {\theta }_Q)-y\left(\theta \right),\Delta y_V=y(\theta +\Delta {\theta }_V)-y\left(\theta \right).$$

(29)

The cosine similarity is

$$\cos \_\mathrm{logit}={\displaystyle \frac{\langle \Delta y_Q,\Delta y_V\rangle }{\parallel \Delta y_Q{\parallel }_2{\parallel \Delta y_V\parallel }_2}}\in [-1,1],$$

(30)

where $\langle ,\rangle$ denotes dot-product. We evaluate in inference mode during all training steps, using FP32 for the dot-product and norms, and skipping steps where either norm $<{10}^{-8}$. We optionally report the same metric on the last hidden states instead of logits to reduce memory. If $\cos \_\mathrm{logit}\approx 0$, complementary effects acting along largely independent directions. As shown in Figure 3a,b, both experiments show similar cosine similarity distribution (near $0.5$) for all steps. This means that two-parameter groups are partial alignment and the cosine similarity is not enough to evaluate interaction.

Second, we quantify the interaction between the query-side and value-side LoRA adapters with a super-additivity score

$$S_{loss}=L_{Q+V}-L_Q-L_V+L_{base},$$

(31)

where $L_{base}$ is the loss with both adapters disabled, $L_Q$ and $L_V$ enable only the query or value adapter, and $L_{Q+V}$ enables both. By construction, $S_{loss}<0$ indicates synergy (the joint improvement exceeds the sum of individual improvements), while $S_{loss}>0$ suggests redundancy or antagonism. As shown in Figure 3c, across each 50 steps in the Offline(Delay) training in first experiment, the baseline condition (not allowing cross-contamination, red line) yields a slightly positive $S_{loss}$ (near-additive with mild redundancy), whereas the proposed approach (allowing cross-contamination, blue line) shifts $S_{loss}$ to a slightly negative value, indicating weak but consistent synergy. This trend persists when summarized over the final training phase ($S_{loss}$).

Lastly, to quantify the representational relationship between the query-side and value-side LoRA adapters, we employ Centered Kernel Alignment (CKA) and Canonical Correlation Analysis (CCA), two widely used measures for comparing neural representations. CKA [33] measures the alignment of representational subspaces independent of scaling, whereas CCA [34,35] quantifies linear correlation between feature activations. A high CKA or CCA score (closer to $1.0$) indicates strong representational alignment, while lower values suggest decorrelation or complementary subspace usage. As shown in Figure 3d, the higher values of both metrics (closer to $1.0$) indicate stronger alignment. The resulting mean ± std scores, CKA $=0.7828\pm 0.1434$ and CCA (mean) $=0.9955\pm 0.0183$, suggest that LoRA-Q and LoRA-V share an almost identical global subspace (high CCA) but maintain moderate local diversity (moderate CKA). This pattern implies that the two LoRA components learn complementary roles within a shared representational space, effectively attenuating cross-contamination without redundant updates.

Consequently, across training, the cosine similarity between Q- and V-induced updates concentrates around $0.5$, indicating partial alignment rather than strict complementarity. Nevertheless, the synergy score $S_{loss}$ when allowing cross-contamination is slightly negative, evidencing weak super-additivity. Furthermore, CKA and CCA scores while allowing cross-contamination indicate complementary attenuation between two adaptive parameters, enabling both adapters yields improvements beyond the sum of their individual effects.

5. Conclusions and Future Work

In this paper, we analyze scaled dot-product attention by decomposing the tensors derived from LoRA parameters and from packing that allows cross-contamination. We show that, in the absence of PAM, the cross-contamination subspace can be attenuated by the learnable subspace from LoRA-Q and LoRA-V parameters, and we then fine-tune the pre-trained models with both online and offline packing. Across experiments, training without PAM achieves losses comparable to those with PAM while reducing overall training time, especially mask generation and transmission stage. Ablations further show that LoRA-Q and LoRA-V learn jointly in a complementary and interactive manner during SFT. Therefore, eliminating PAM removes both implementation complexity and the factors of training-time overhead. Our scaling analysis suggests that the relative efficiency gain of removing PAM increases with longer context lengths L, whereas LoRA’s percentage overhead decreases as the model size grows. Comprehensive quantitative evaluations on larger models (34B and 70B) and extended contexts (8k–16k tokens) remain promising directions for future work.