Optimal Feedback Rate Analysis in Downlink Multi-User Multi-Antenna Systems with One-Bit ADC Receivers over Randomly Modeled Dense Cellular Networks

Abstract

Stochastic geometry provides a powerful analytical framework for evaluating interference-limited cellular networks with randomly deployed base stations (BSs). While prior studies have examined limited channel state information at the transmitter (CSIT) and low-resolution analog-to-digital converters (ADCs) separately, their joint impact in multi-user multiple-input multiple-output (MIMO) systems remains largely unexplored. This paper investigates a downlink cellular network in which BSs are distributed according to a homogeneous Poisson point process (PPP), employing zero-forcing beamforming (ZFBF) with limited feedback, and receivers are equipped with one-bit ADCs. We derive a tractable approximation for the achievable spectral efficiency that explicitly accounts for both the quantization error from limited feedback and the receiver distortion caused by coarse ADCs. Based on this approximation, we determine the optimal feedback rate that maximizes the net spectral efficiency. Our analysis reveals that the optimal number of feedback bits scales logarithmically with the channel coherence time but its absolute value decreases due to coarse quantization. Simulation results validate the accuracy of the proposed approximation and confirm the predicted scaling behavior, demonstrating its effectiveness for interference-limited multi-user MIMO networks.

1. Introduction

Stochastic geometry has become an indispensable tool for the modeling and performance analysis of modern wireless networks, as it enables a tractable yet accurate characterization of interference-limited systems with random spatial deployments. A growing body of work has applied stochastic geometry to study cellular networks under various scenarios and technologies [1,2,3,4,5,6,7]. For instance, ref. [1] developed a mathematical framework for computing the error probability in downlink multiple-input multiple-output (MIMO) systems using stochastic geometry, and ref. [2] introduced an equivalent-in-distribution approach to evaluate the performance of MIMO systems in stochastic cellular networks. The work in [3] modeled multi-user MIMO (MU-MIMO) heterogeneous networks to assess the success probability and area spectral efficiency, while ref. [4] examined the spectral and energy efficiency of intelligent reflecting surface (IRS)-assisted cellular networks. In addition, ref. [5] analyzed the spectral efficiency of multi-cell massive MIMO networks with spatial antenna correlation, ref. [6] focused on outage-based secrecy rates in scalable cell-free massive MIMO systems, and ref. [7] investigated the performance of non-orthogonal multiple access (NOMA) systems aided by reconfigurable intelligent surfaces (RISs).

A common element in these works is the use of a Poisson point process (PPP) to model base station (BS) locations and evaluate inter-cell interference, which is a dominant performance-limiting factor in dense cellular deployments. PPP-based approaches have also been extended to account for partial channel state information at the transmitter (CSIT) in MIMO systems, where accurate CSIT acquisition is constrained by feedback overhead. For example, ref. [8] considered a homogeneous PPP model in which each user feeds back quantized CSIT to the transmitter, enabling multi-antenna transmission in interference-limited environments. They analyzed the optimal feedback rate in terms of the net spectral efficiency, assuming maximum ratio transmission (MRT) for single-user cases and zero-forcing beamforming (ZFBF) for spatial division multiple access. Follow-up works expanded this framework toward different objectives, such as net secrecy rate optimization [9], and to configurations with multiple receive antennas [10]. Among these, ref. [10] addressed the single-user case, whereas ref. [8] focused on the multi-user scenario.

Most of the aforementioned studies, however, adopt the conventional assumption of infinite-resolution analog-to-digital converters (ADCs). In practice, high-resolution ADCs are both power-hungry and costly, particularly in systems operating over wide millimeter-wave bandwidths. This has motivated research into low-resolution ADCs—especially one-bit ADCs—as a power-efficient and cost-effective alternative [11]. The performance of communication systems employing one-bit ADCs has been extensively studied [11,12,13,14,15,16,17]. For example, ref. [12] investigated the capacity of a one-bit quantized single-input single-output Gaussian channel, while ref. [13] analyzed the achievable rates of MIMO systems with one-bit ADCs. Specifically, the authors in [13] derived an exact capacity expression for multiple-input single-output (MISO) channels and provided upper bounds for the capacities of single-input multiple-output (SIMO) and MIMO channels under the perfect CSIT assumption. Hybrid architectures with few-bit ADC receivers were also considered in [14], and the effect of partial CSIT via limited feedback was investigated in [15] for systems employing finite-bit ADCs at the receivers.

Despite this progress, the joint impact of multi-user interference, partial CSIT, and coarse quantization remains underexplored. While prior studies have examined one-bit ADC systems or limited feedback in isolation, few have considered multi-user MIMO transmission in dense cellular networks that jointly capture the effects of one-bit ADC receivers and partial CSIT based on limited feedback within a stochastic geometry framework. In our previous work [17], we analyzed the performance of multi-cell systems with limited feedback and low-resolution ADCs, derived the optimal feedback rate, and proposed an accurate approximation method for its determination. While those results provided valuable insights, they were obtained under the simplifying assumption of a single-user scenario, limiting both the practicality and generality of the conclusions. In this study, we address these limitations by extending the analysis to a multi-user setting, where simultaneous transmissions to multiple users introduce additional layers of interference and complexity. Compared to the single-user case, the multi-user setting poses the following additional challenges:

• Inter-user interference becomes a critical factor, requiring advanced precoding schemes such as ZFBF for effective mitigation.
• The benefit of feedback bits must be balanced not only against inter-cell interference but also against the need to accurately separate multiple users within the same cell.
• The joint statistical characterization of the signal-to-interference ratio (SIR) in a PPP network with both quantization error (from limited feedback) and receiver distortion (from one-bit ADCs) is analytically more involved.

To address these challenges, this paper investigates the optimal feedback rate in a multi-user MIMO cellular network with one-bit ADC receivers, where BSs are deployed according to a homogeneous PPP and operate under ZFBF precoding with limited feedback. The main contributions of this study are summarized as follows:

• We develop an analytically tractable approximation for the achievable spectral efficiency in a multi-user MIMO setting with one-bit ADC receivers and limited feedback. This approximation allows closed-form differentiation with respect to the number of feedback bits.
• Based on this approximation, we derive the optimal number of feedback bits that maximizes the net spectral efficiency. Our results show that the optimal feedback rate scales logarithmically with the channel coherence time. However, the use of one-bit ADCs reduces the absolute number of optimal feedback bits due to coarse quantization.
• Simulation results validate the proposed approximation and confirm the predicted scaling behavior, demonstrating its applicability to realistic multi-user, interference-limited cellular networks.

The remainder of this paper is organized as follows. Section 2 describes the system and channel models, beamforming strategy, and performance metrics. Section 3 presents the derivation of the optimal feedback rate. Section 4 provides simulation results, and Section 5 concludes the paper.

2. System Model

In this paper, we consider a cellular network, which is modeled as a two-dimensional plane where the base stations (BS) are deployed according to a homogeneous Poisson point process (PPP) with intensity $\lambda$. The distance from the origin to the nearest BS i is denoted by ${\mathbf{d}}_i$. Each BS has N antennas for transmission, while each user has a single antenna. Users are independently distributed according to another homogeneous PPP, independent of the BS process. It is assumed that the user density is sufficiently larger than $\lambda$, ensuring that each BS serves almost surely at least N user within its Voronoi cell.

We assume that the density of users are much higher than that of the BSs, such that each BS can randomly select sufficient number of users from its Voronoi cell for downlink transmission. Because of the stationarity of the homogeneous PPP, the ergodic spectral efficiency is identical across users, provided that all BSs adopt a common transmission strategy. Consequently, any user on the network can be chosen as a representative for performance evaluation. Thus, without loss of generality, any scheduled user can be considered as a target user for performance evaluation. Moreover, The stationarity of homogeneous PPP also implies that the target user for performance evaluation can be assumed to be located at the origin by means of a suitable parallel translation.

2.1. Channel Model

Each BS serves K single-antenna users, and we assume that each BS exploits the full diversity, which means $K=N$ for this study. We denote the target user located at the origin as user k. User k is served by the nearest BS to the origin, which is denoted as BS $b_k$. Then, the received signal of user k is modeled as

$$\begin{array}{c}\hfill y_k=\parallel {\mathbf{d}}_{b_k}{\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_k^H{\mathbf{v}}_k{s}_k+\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\parallel {\mathbf{d}}_{b_k}{\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_k^H{\mathbf{v}}_{k^{\prime }}{s}_{k^{\prime }}+\sum _{i=1,i\ne b_k}^{\infty }{\parallel {\mathbf{d}}_i\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i{\mathbf{t}}_i+z_k,\end{array}$$

(1)

where the channel between BS $b_k$ and user k is modeled as ${\mathbf{h}}_k\in {\mathbb{C}}^{N\times 1}$. The entries of ${\mathbf{h}}_k$ are independently and identically distributed (i.i.d.) circularly symmetric complex Gaussian random variables with unit variance (Rayleigh fading). The beamforming vector associated with the user k is denoted as ${\mathbf{v}}_k$, while $s_k$ denotes the information symbol for user k. The additive noise $z_k$ is also modeled as a circularly symmetric complex Gaussian random variable with unit variance. The path loss exponent $\alpha \in \mathbb{R}$ is assumed to satisfy $\alpha >2$, and P denotes the total transmit power, implying that $\mathbb{E}\left[\right|s_k{|}^2]=P$. In addition, we assume an ideal channel estimation such that each user has perfect knowledge of its downlink channel vector. As the system is assumed to employ one-bit ADCs at the receiver, the real and imaginary components of $y_k$ are quantized separately using two independent ADCs. Consequently, the one-bit quantized received signal is given as follows:

$$\begin{array}{c}\hfill r_k=\mathrm{sign}\left(Re\left[y_k\right]\right)+\mathrm{sign}\left(Im\left[y_k\right]\right)\mathbf{j}\end{array}$$

(2)

where $\mathbf{j}$ represents the imaginary unit and sign is the sign function.

Note that our study is mainly conducted under the assumption of Rayleigh fading for small-scale fading, and it is therefore applicable primarily to wireless channels with rich scattering environments.

For notational simplicity, we use the following simplified notation regarding the distance between the target user (i.e., user k) and its serving BS (i.e., BS $b_k$):

$$\begin{array}{c}\hfill \mathbf{d}={\mathbf{d}}_{b_k}.\end{array}$$

(3)

At last, we summarize multi-cell parameters ${\mathbf{h}}_{k,i}$, ${\mathbf{t}}_i$, and ${\mathbf{G}}_i$ as follows:

• ${\mathbf{h}}_{k,i}$: Channel vector from BS i to the target user.
• ${\mathbf{t}}_i$: Information symbol vector of BS i prepared for its associated users.
• ${\mathbf{G}}_i$: Beamforming matrix of BS i contructed for spatial division multiplexing to its associated users.

2.2. Limited Feedback Model

This study assumes communication systems based on frequency division duplex (FDD), where the BS cannot directly estimate its downlink channel. Thus, the receiver is needed to provide some information about the downlink channel to its associated BS. A well-known approach in this context is the limited feedback technique, in which each user is equipped with a predefined codebook and quantizes the channel direction vector to the closest one within the codebook. The target user’s channel direction vector is defined as

$$\begin{array}{c}\hfill {\tilde{\mathbf{h}}}_k\triangleq {\displaystyle \frac{{\mathbf{h}}_k}{\parallel {\mathbf{h}}_k\parallel }}.\end{array}$$

(4)

Although an explicit codebook-based approach can be used, this study instead adopts the well-known approximation model called the spherical-cap approximation of vector quantization (SCVQ). The SCVQ model provides an upper bound approximation of performance in the context of codebook-based limited feedback. Moreover, for a sufficiently large B, this bound becomes tight, which explains why SCVQ is widely used to analyze MIMO systems with limited feedback. Let vector ${\widehat{\mathbf{h}}}_k$ denote the result of the quantization, which is called quantized vector in this study. This quantized vector can generally be expressed as

$$\begin{array}{c}\hfill {\widehat{\mathbf{h}}}_k=(cos{\theta }_k){\tilde{\mathbf{h}}}_k+(sin{\theta }_k){\mathbf{f}}_k,\end{array}$$

(5)

where ${\mathbf{f}}_k$ represents an istropically distributed vector within the left null space of ${\tilde{\mathbf{h}}}_k$ and the square of $sin{\theta }_k$ is defined as the quantization error. Using the SCVQ model [18], the cumulative distribution function (CDF) of the quantization error is approximated as follows:

$$\begin{array}{c}\hfill F_{{sin}^2{\theta }_k}\left(x\right)=\left\{\begin{array}{cc}{2}^B{x}^{N-1},\hfill & 0\le x\le \delta ,\hfill \\ 1,\hfill & x\ge \delta ,\hfill \end{array}\right.\end{array}$$

(6)

where $\delta =2^{-{\displaystyle \frac{B}{N-1}}}$ and B is the number of feedback bits per user. This CDF implies that

$$\begin{array}{c}\hfill {sin}^2{\theta }_k\stackrel{d}{=}\delta ·{\beta }_{N-1,1},\end{array}$$

(7)

where ${\beta }_{\alpha ,\beta }$ denotes a random variable following the beta distribution with parameters $\alpha$ and $\beta$.

2.3. Zero-Forcing Beamforming

For spatial division multiplexing, we use limited-feedback-based zero-forcing beamforming (ZFBF) at transmitter [19,20]. That is, ${\mathbf{v}}_i$ in (1) is given by the i-th normalized column of ${\widehat{\mathbf{H}}}_{\mathbf{inv}}$, where ${\widehat{\mathbf{H}}}_{\mathbf{inv}}$ is calculated as the pseudo-inverse matrix of quantized CDIs, as follows:

$$\begin{array}{c}\hfill \widehat{\mathbf{H}}=[{\widehat{\mathbf{h}}}_1,\dots ,{\widehat{\mathbf{h}}}_K],{\widehat{\mathbf{H}}}_{\mathbf{inv}}=\widehat{\mathbf{H}}{\left({\widehat{\mathbf{H}}}^H\widehat{\mathbf{H}}\right)}^{-1}.\end{array}$$

(8)

For each i, each BS located at ${\mathbf{d}}_i$ constructs its own ZFBF precoding matrix ${\mathbf{V}}_i$ using the quantized CDIs provided by its associated users.

2.4. Performance Metric

According to information theory, the instantaneous rate is upper-bounded by the mutual information between the received signal and the transtmitted signal. In this context, as noted above, the mutual information between the quantized received signal r and the original transmitted signal s serves as an upper-bound on the instantaneous rate achieved by the target user, which is defined as

$$\begin{array}{c}\hfill R(\mathcal{H},\mathcal{D})\triangleq \underset{F_s}{\max }I(r;s),\end{array}$$

(9)

for given channel realization $\mathcal{H}$ and BS locations $\mathcal{D}$, where maximization is taken over all possible input distributions of s.

2.5. Main Scope of This Study

The application considered in this paper, together with the experimental tools used for its implementation, can be summarized as follows, with details provided in this section as follows:

• Cellular mobile networks are modeled using PPP.
• Rayleigh fading is adopted as the small-scale fading model assuming rich-scattering environments.
• ZFBF is employed as a distributed spatial division multiple access scheme with multiple transmit antennas.
• Frequency division duplex is adopted as the duplexing scheme, enabling CSI feedback to improve the performance of ZFBF.
• The CSI feedback scheme is approximated using the SCVQ model.

Feedback-based precoding is one of the most widely used schemes in mobile communication standards, and the contribution of this work lies in providing analytical results that can be directly applied to the implementation of feedback-based precoding in such practical cellular networks.

3. Analysis of Optimal Feedback Rate

3.1. Spectral Efficiency for Channel Model

From Section II, we use index $b_k$ to denote the target BS for performance evaluation, which simultaneously serves K users indexed by $1,\dots ,K$ via ZFBF. Among these users, the target user of interest is denoted as user k. From (1), the received signal of user k is expressed as

$$\begin{array}{c}\hfill y_k={\parallel \mathbf{d}\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_k^H{\mathbf{v}}_k{s}_k+\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\parallel \mathbf{d}\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_k^H{\mathbf{v}}_{k^{\prime }}{s}_{k^{\prime }}+\sum _{i=1,i\ne b_k}^{\infty }{\parallel {\mathbf{d}}_i\parallel }^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i{\mathbf{t}}_i+z_k.\end{array}$$

(10)

On the right-hand side, the first term represents the desired signal of the target user (i.e., user k). The second term represents the interference caused by the signals intended for the other $K-1$ users served by $b_k$, which we refer to as intra-cell multi-user interference. Finally, the third term represents the interference generated by signals transmitted from other BSs in the network, referred to as multi-cell interference.

In general, the spectral efficiency of a communication system depends on the SINR of the received signal, which is defined as

$$\begin{array}{cc}\hfill {\mathrm{SIN}\mathrm{R}}_k(B,K)& ={\displaystyle \frac{{\displaystyle \frac{P}{K}{\parallel \mathbf{d}\parallel }^{-\alpha }{\left|{\mathbf{h}}_k^H{\mathbf{v}}_k\right|}^2}}{{\displaystyle \frac{P}{K}{\parallel \mathbf{d}\parallel }^{-\alpha }\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\left|{\mathbf{h}}_k^H{\mathbf{v}}_{k^{\prime }}\right|}^2+\frac{P}{K}{\parallel {\mathbf{d}}_i\parallel }^{-\alpha }\sum _{i=1,i\ne b_k}^{\infty }{∥{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i∥}^2+{\sigma }_Z^2}}},\hfill \end{array}$$

(11)

where ${\sigma }_Z^2$ denotes the variance of the thermal noise. By normalizing with respect to the transmit power, this can be reformulated as

$$\begin{array}{cc}\hfill {\mathrm{SIN}\mathrm{R}}_k(B,K)& ={\displaystyle \frac{{\displaystyle {\parallel \mathbf{d}\parallel }^{-\alpha }{\left|{\mathbf{h}}_k^H{\mathbf{v}}_k\right|}^2}}{{\displaystyle {\parallel \mathbf{d}\parallel }^{-\alpha }\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\left|{\mathbf{h}}_k^H{\mathbf{v}}_{k^{\prime }}\right|}^2+{\parallel {\mathbf{d}}_i\parallel }^{-\alpha }\sum _{i=1,i\ne b_k}^{\infty }{∥{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i∥}^2+\frac{K{\sigma }_Z^2}{P}}}}.\hfill \end{array}$$

(12)

In the denominator, the term ${\displaystyle \frac{K{\sigma }_Z^2}{P}}$ vanishes as the transmit power P becomes sufficiently large. Thus, in this high-power regime, the denominator is dominated by intra- and inter-cell interference so that the SINR can be approximated as

$$\begin{array}{cc}\hfill {\mathrm{SIN}\mathrm{R}}_k(B,K)& \approx {\displaystyle \frac{{\displaystyle {\parallel \mathbf{d}\parallel }^{-\alpha }{\left|{\mathbf{h}}_k^H{\mathbf{v}}_k\right|}^2}}{{\displaystyle {\parallel \mathbf{d}\parallel }^{-\alpha }\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\left|{\mathbf{h}}_k^H{\mathbf{v}}_{k^{\prime }}\right|}^2+{\parallel {\mathbf{d}}_i\parallel }^{-\alpha }\sum _{i=1,i\ne b_k}^{\infty }{∥{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i∥}^2}}}\triangleq {\mathrm{SIR}}_k(B,K),\hfill \end{array}$$

(13)

where we call ${\mathrm{SIR}}_k(B,K)$ at the right-hand side the signal-to-interference ratio (SIR). We employ this SIR as the primary performance metric in this study, which can be reformulated as follows:

$$\begin{array}{cc}\hfill {\mathrm{SIR}}_k(B,K)& ={\displaystyle \frac{{\displaystyle {\left|{\mathbf{h}}_k^H{\mathbf{v}}_k\right|}^2}}{{\displaystyle \underset{\Phi }{\underbrace{{\parallel {\mathbf{h}}_k\parallel }^2{\sum }_{k^{\prime }\ne k}^K{\left|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_{k^{\prime }}\right|}^2}}+\underset{\Psi }{\underbrace{{\sum }_{i=1,i\ne b_k}^{\infty }{∥\frac{{\mathbf{d}}_i}{\mathbf{d}}∥}^{-\alpha }{∥{\mathbf{h}}_{k,i}^H{\mathbf{G}}_i∥}^2}}}}}={\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2{|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k|}^2}{\Phi +\Psi }}.\hfill \end{array}$$

(14)

In (14), $\Phi$ and $\Psi$ are induced by the intra-cell multi-user interference and multi-cell interference described in (10), respectively.

Furthermore, the target user’s downlink channel can be modeled as a one-bit quantized complex Gaussian channel, which is notified in [12]. In [12], the maximum mutual information of a one-bit quantized complex Gaussian channel is derived as

$$\begin{array}{c}\hfill 2(1-{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{\mathrm{SIN}\mathrm{R}}\right)\right)),\end{array}$$

(15)

and the maximum is achieved when the real and imaginary part of the signal are composed of two independent antipodal components, which is called quadrature phase shift keying (QPSK). In (15), ${\mathit{H}}_b(·)$ represents the binary entropy function,

$$\begin{array}{c}\hfill {\mathit{H}}_b\left(p\right)=-p·logp-(1-p)·log(1-p),\end{array}$$

(16)

where $\mathit{Q}(·)$ denotes the Gaussian Q-function, which corresponds to the complementary cumulative distribution function of the standard normal distribution, and is defined as

$$\begin{array}{c}\hfill \mathit{Q}\left(x\right)={\int }_x^{\infty }{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{t^2}{2}}}dt.\end{array}$$

(17)

As we discussed above, the effect of thermal noise is negligible in the system model considered in this paper. Therefore, we use SIR instead of SINR, which leads to the following:

$$\begin{array}{cc}\hfill R(\mathcal{H},\mathcal{D})& =2\left(1-{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{{\mathrm{SIR}}_k}\right)\right)\right)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & =2\left(1-{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{{\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2{|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k|}^2}{\Phi +\Psi }}}\right)\right)\right),\hfill \end{array}$$

(19)

and the ergodic spectral efficiency achieved by the target user is expressed as

$$\begin{array}{cc}\hfill R_e& =\mathbb{E}\left[2\left(1-{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{{\mathrm{SIR}}_k}\right)\right)\right)\right]\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & =\mathbb{E}\left[2\left(1-{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{{\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2{|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k|}^2}{\Phi +\Psi }}}\right)\right)\right)\right].\hfill \end{array}$$

(21)

We consider the following ergodic net spectral efficiency as the main performance metric:

$$\begin{array}{cc}\hfill R_{Net}& \triangleq R_e-{\displaystyle \frac{B}{T_c}}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & =2-2·\mathbb{E}\left[{\mathit{H}}_b\left(\mathit{Q}\left(\sqrt{{\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2{|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k|}^2}{\Phi +\Psi }}}\right)\right)\right]-{\displaystyle \frac{B}{T_c}},\hfill \end{array}$$

(23)

where $T_c$ denotes the channel coherence time.

3.2. Approximation of the Spectral Efficiency

In order to simplify the performance analysis and to derive bounds on the system performance, we aim to obtain a mathematical approximation of the SIR defined in (14). Since ${\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k$ is the inner product of two i.i.d. N-dimensional unit vectors, ${|{\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k|}^2$ follows beta distribution with parameters 1 and $N-1$. Focusing on $\left(a\right)(\parallel {\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_{k^{\prime }}{\parallel }^2)$, ${\mathbf{v}}_{k^{\prime }}$ is a vector within the nullspace of ${\tilde{\mathbf{h}}}_k(k\ne k^{\prime })$, which are i.i.d. vectors. Given ${\tilde{\mathbf{h}}}_k$, the ZF beamformer ${\mathbf{v}}_{k^{\prime }}$ lies in the null space of ${\widehat{\mathbf{h}}}_k$, and it is uniformly distributed over that $(N-1)$-dimensional subspace. Due to SCVQ (or RVQ), the estimated channel vector can be represented as

$$\begin{array}{c}\hfill {\tilde{\mathbf{h}}}_k={\widehat{\mathbf{h}}}_k·cos{\theta }_k+{\mathbf{g}}_k·sin{\theta }_k,\end{array}$$

where vector ${\mathbf{g}}_k$ is within the nullspace of ${\widehat{\mathbf{h}}}_k$ and our discussion of ${\mathbf{v}}_{k^{\prime }}$ and ${\widehat{\mathbf{h}}}_k$ means that ${\widehat{\mathbf{h}}}_k{\mathbf{v}}_{k^{\prime }}=0$, which is derived as follows:

$$\begin{array}{cc}\hfill {\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_{k^{\prime }}& ={\overline{){\widehat{\mathbf{h}}}_k{\mathbf{v}}_{k^{\prime }}}}^0·cos{\theta }_k+{\mathbf{g}}_k·{\mathbf{v}}_{k^{\prime }}sin{\theta }_k,\hfill \\ \hfill \parallel {\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_{k^{\prime }}{\parallel }^2& ={sin}^2{\theta }_K·{\left|{\mathbf{g}}_k{\mathbf{v}}_{k^{\prime }}\right|}^2.\hfill \end{array}$$

(24)

Building on the distributional analysis of ${\tilde{\mathbf{h}}}_k^H{\mathbf{v}}_k$, the vectors ${\mathbf{g}}_k$ and ${\mathbf{v}}_{k^{\prime }}$ are assumed to be i.i.d. over the $N-1$ dimensional space. Consequently, the squared inner product of between them follows a Beta distribution with parameters $(1,N-2)$, i.e., ${\beta }_{1,N-2}$. Then, we can rewrite the SIR as approximated form with stochastic distributions as follows:

$$\begin{array}{c}\hfill {\mathrm{SIR}}_k(B,K)\approx {\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2\beta (1,N-1)}{{\parallel {\mathbf{h}}_k\parallel }^2{sin}^2{\theta }_k{\displaystyle \sum _{k^{\prime }=1,k^{\prime }\ne k}^K\beta (1,N-2)}+\Psi }}\triangleq {\mathrm{SIR}}_k^{approx}.\end{array}$$

(25)

Also for ease of analysis, we additionally consider the following approximated SINR, which is obtained by ignoring the intra-cell multi-user interference term, ${\parallel {\mathbf{h}}_k\parallel }^2{sin}^2{\theta }_k{\displaystyle \sum _{k^{\prime }=1,k^{\prime }\ne k}^K\beta (1,N-2)}$, in the denominator of ${\mathrm{SIR}}_k^{approx}$:

$$\begin{array}{c}\hfill {\mathrm{SIR}}_k^{-}\triangleq {\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2{\beta }_{1,N-1}}{\Psi }}.\end{array}$$

(26)

3.3. Derivation of Optimal Feedback Rate

As the instantaneous achievable rate, discussed in later sections, is expressed as a function of SIR and will be differentiated to identify its optimal point, we first derive the derivative of the SIR in this section as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dB}}{\mathrm{SIR}}_k^{approx}& =(-1)·{\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2\beta (1,N-1)}{{\left\{{\underbrace{{\parallel {\mathbf{h}}_k\parallel }^2·2^{-\frac{B}{N-1}}{\beta }_{N-1,1}·{\displaystyle \sum _{k^{\prime }=1,k^{\prime }\ne k}^K\beta (1,N-2)}}}_{I_U}+\Psi \right\}}^2}}\times \hfill \end{array}$$

$$\begin{array}{cc}& {\parallel {\mathbf{h}}_k\parallel }^{2}ln2·\left(-{\displaystyle \frac{1}{N-1}}\right)·\underset{I_U/{\parallel {\mathbf{h}}_k\parallel }^2}{\underbrace{2^{-{\displaystyle \frac{B}{N-1}}}{\beta }_{N-1,1}·{\displaystyle \sum _{k^{\prime }=1,k^{\prime }\ne k}^K\beta (1,N-2)}}}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{1}{N-1}}ln2·{\displaystyle \frac{{\parallel {\mathbf{h}}_k\parallel }^2\beta (1,N-1)}{{\{I_U+\Psi \}}^2}}·I_U\hfill \end{array}$$

(28)

Utilizing the properties we derived above, we have the following approximations:

$$\begin{array}{cc}\hfill R_{Net}& =R_e-{\displaystyle \frac{B}{T_c}}\approx \mathbb{E}\left[2(1-H_b\left(Q\left(\sqrt{{\mathrm{SIR}}_k^{approx}}\right)\right))\right]-{\displaystyle \frac{B}{T_c}}\triangleq R_{Net}^{approx}\hfill \end{array}$$

(29)

Note that the true optimal point that maximizes $R_{Net}$ can be analyzed by investigating the critical points of its derivative, i.e.,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dB}}{R}_{Net}=0,\end{array}$$

(30)

and the corresponding optimal value of B that corresponds to the zero-crossing point of (30) is denoted by $B^{*}$. However, obtaining an explicit value of $B^{*}$ is extremely difficult, although it can be numerically calculated based on an exhaustive simulation. Thus, instead of directly investigating the zero-crossing points of (30), we consider the derivative of the approximated net rate, which is given by

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dB}}{R}_{Net}^{approx}\hfill \\ \hfill & =\mathbb{E}\left[{\displaystyle \frac{1}{N-1}}ln2·{\parallel {\mathbf{h}}_k\parallel }^2·2^{-{\displaystyle \frac{B}{N-1}}}{\beta }_{N-1,1}·\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\beta }_{1,N-2}·{\displaystyle \frac{{\mathrm{SIR}}_k^{approx}}{\{I_U+\Psi \}}}·G^{\prime }\left({\mathrm{SIR}}_k^{approx}\right)\right]-{\displaystyle \frac{1}{T_c}}.\hfill \end{array}$$

(31)

The zero-crossing point of (31) approximates the true optimal value $B^{*}$, and we denote this approximation as ${\widehat{B}}_1^{*}$ for simplicity in comparison. Based on previous results, we know that the optimal value of $B^{*}$ is typically large and increases as $T_c$ increases. Thus, assuming that $B^{*}$ is sufficiently large, we may consider further approximation, described as follows:

$$\begin{array}{c}\hfill \Psi \approx I_U+\Psi .\end{array}$$

(32)

The rationale behind this approximation is that, for a sufficiently large B, the level of multi-user interference becomes dominated by the level of multi-cell interference, since the former decreases as B increases, whereas the latter remains independent of B. Applying this approximation, the derivative of $R_{Net}^{approx}$ can be approximated as

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dB}}{R}_{Net}^{approx}& \approx 2^{-{\displaystyle \frac{B}{N-1}}}·{\displaystyle \frac{ln2}{N-1}}\mathbb{E}\left[{\parallel {\mathbf{h}}_k\parallel }^2{\beta }_{N-1,1}·\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\beta }_{1,N-2}·{\displaystyle \frac{1}{\psi }}·{\mathrm{SIR}}_k^{-}·G^{\prime }\left({\mathrm{SIR}}_k^{-}\right)\right]-{\displaystyle \frac{1}{T_c}}.\hfill \end{array}$$

(33)

Denoting the zero-crossing point as ${\widehat{B}}_2^{*}$, we obtain the second approximation of $B^{*}$ as follows:

$$\begin{array}{cc}\hfill {\widehat{B}}_2^{*}& =(N-1){log}_2\left(T_c·\underset{E_0}{\underbrace{{\displaystyle \frac{ln2}{N-1}}·\mathbb{E}\left[{\parallel {\mathbf{h}}_k\parallel }^2{\beta }_{N-1,1}·\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\beta }_{1,N-2}·{\displaystyle \frac{1}{\psi }}·{\mathrm{SIR}}_k^{-}·G^{\prime }\left({\mathrm{SIR}}_k^{-}\right)\right]}}\right)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & =(N-1){log}_2{T}_c+(N-1){log}_2{E}_0\hfill \end{array}$$

(35)

Although it is difficult to obtain an exact deterministic expression for $E_0$, Equation (34) remains meaningful because it reveals the scaling behavior of the optimal B as a function of $T_c$. This scaling property has been a key performance metric in studies investigating the optimal feedback rate. In short, provided that $E_0$ converges to a finite value, this equation indicates that the optimal number of feedback bits (in approximation) grows logarithmically with $T_c$.

A key differentiating result is that, while in the single-user setting of [17] the scaling rate of the optimal B coincides with that under infinite-resolution ADCs (IR-ADC), in the multi-user case considered in this paper, the slope is different from the IR-ADC case derived in [8]. Specifically, the scaling rate of the optimal number of feedback bits is not dependent on the path loss exponent, if the target user employs one-bit ADCs. As a consequences, the absolute value of $B^{*}$ can be significantly reduced when one-bit ADCs are used, as we further discuss in the following section. The following

Table 1. Comparison of optimal feedback rates found in the literature with our results.

Transmit Scheme	ADC Type	Optimal Feedback Rate
MRT for single user [8]	Infinite-resolution ADCs	(N − 1) log2 Tc
ZFBF for multiple users [8]	Infinite-resolution ADCs	$\frac{\alpha (N-1)}{2}$ log2 Tc
MRT for single user [17]	One-bit ADCs	(N − 1) log2 Tc
ZFBF for multiple users (this study)	One-bit ADCs	(N − 1) log2 Tc

summarizes the scaling rates derived in previous studies along with that derived in this study.

4. Simulation Results

In this section, we provide simulation results to substantiate the analytical results discussed in Section 3, thereby confirming their validity and reliability under the specified conditions. To ensure clarity in the comparison, we summarize some important parameters which were defined in the previous section as follows:

• B indicates the number of feedback bits, while $B^{*}$ denotes the true optimal value of B that maximizes $R_{Net}$.
• ${\widehat{B}}_1^{*}$ and ${\widehat{B}}_2^{*}$ are approximated values of $B^{*}$.

In this section, ergodic net spectral efficiency $R_{Net}$ and its approximation $R_{Net}^{approx}$ are obtained through simulation experiments performed using the Monte Carlo method, in accordance with the established guidelines presented as follows:

• Initialization: Set the system parameters as N, K, B, $\alpha$, and $\lambda$. The network radius is fixed to a sufficiently large value. In our situations, we adopt a radius of 5 km for the entire network, while $\alpha =4$ and $\lambda ={10}^{-5}/\pi$ are used as constant values.
• BS locations: At each transmission frame, the number of BSs is drawn from a Poisson distribution with parameter $\lambda$. Given this realization, the BS locations are then generated according to a homogeneous Poisson point process over a two-dimensional plane. This procedure ensures that the spatial distribution of BSs follows the statistical characteristics induced by the density parameter $\lambda$.
• User and channel setup: In this step, the target user, denoted by user k, is assumed to be located at the origin of the two-dimensional plane. Based on the BS locations determined in step 2, the Euclidean distances ${\mathbf{d}}_i$ between the origin and each BS are computed. The BS with the minimum distance to the origin is designated as BS $b_k$, which serves the target user. The small-scale fading channel between BSs and the target user is denoted by ${\mathbf{h}}_k$. Each element of ${\mathbf{h}}_k$ is independently drawn from a circularly symmetric complex Gaussian distribution as defined in Section 2.
• Channel quantization and precoding: Each user quantizes its channel direction vector, and the result of quantization is denoted as ${\widehat{\mathbf{h}}}_k$. This quantized vector is obtained by following the SCVQ model described in Section 2.2. Then, the precoding vectors ${\mathbf{v}}_k,k=1,\dots ,K$ are obtained by computing the pseudo-inverse of $\widehat{\mathbf{H}}$, as described in Section 2.3.
• Net spectral efficiency: At each frame, evaluate the instantaneous net spectral efficiency $R_{Net}$ and its approximation $R_{Net}^{approx}$ can be obtained by calculating their corresponding expressions defined in the previous section.
• Monte Carlo simulation: Iterate the procedure described in steps 1 through 5 over numerous channel realizations, and compute the ergodic averages to obtain the overall net spectral efficiency and its approximation.

All simulations were carried out in MATLAB (ver. R2024b) on a high-performance CPU (Intel Core i9 processor) without employing GPU acceleration. For each scenario, more than 300,000 frames were generated to ensure the reliable estimation of $R_{Net}$.

In Figure 1, we verify the accuracy of the SCVQ model used for performance analysis. In general, the SCVQ model is considered a valid approximation when B is sufficiently large. In our study, the optimal value of B derived falls in a relatively large range (e.g., $B^{*}\ge 15$ if $T_c\ge$ and $N\ge 4$), and thus we assumed that the SCVQ model holds well. As can be seen in Figure 1, when $B=9$, there still exists a noticeable gap compared to the RVQ (used as a lower bound). However, this gap diminishes as B increases, and at $B=15$, the results converge within a negligible margin of error.

Figure 2 and Figure 3 illustrate the comparison of the rate, its derivative (differential rate), and their corresponding approximations for cases $N=4$ and $N=8$, respectively. The vertical lines represent the optimal point of each ergodic achievable rate, which corresponds to the zero-crossing point of the derivatives on the B-axis. We can find that the two vertical lines representing the zero-crossing points are located at the same B or in a small gap (under 1 bit), which means that our approximation fits well with the theoretically derived results.

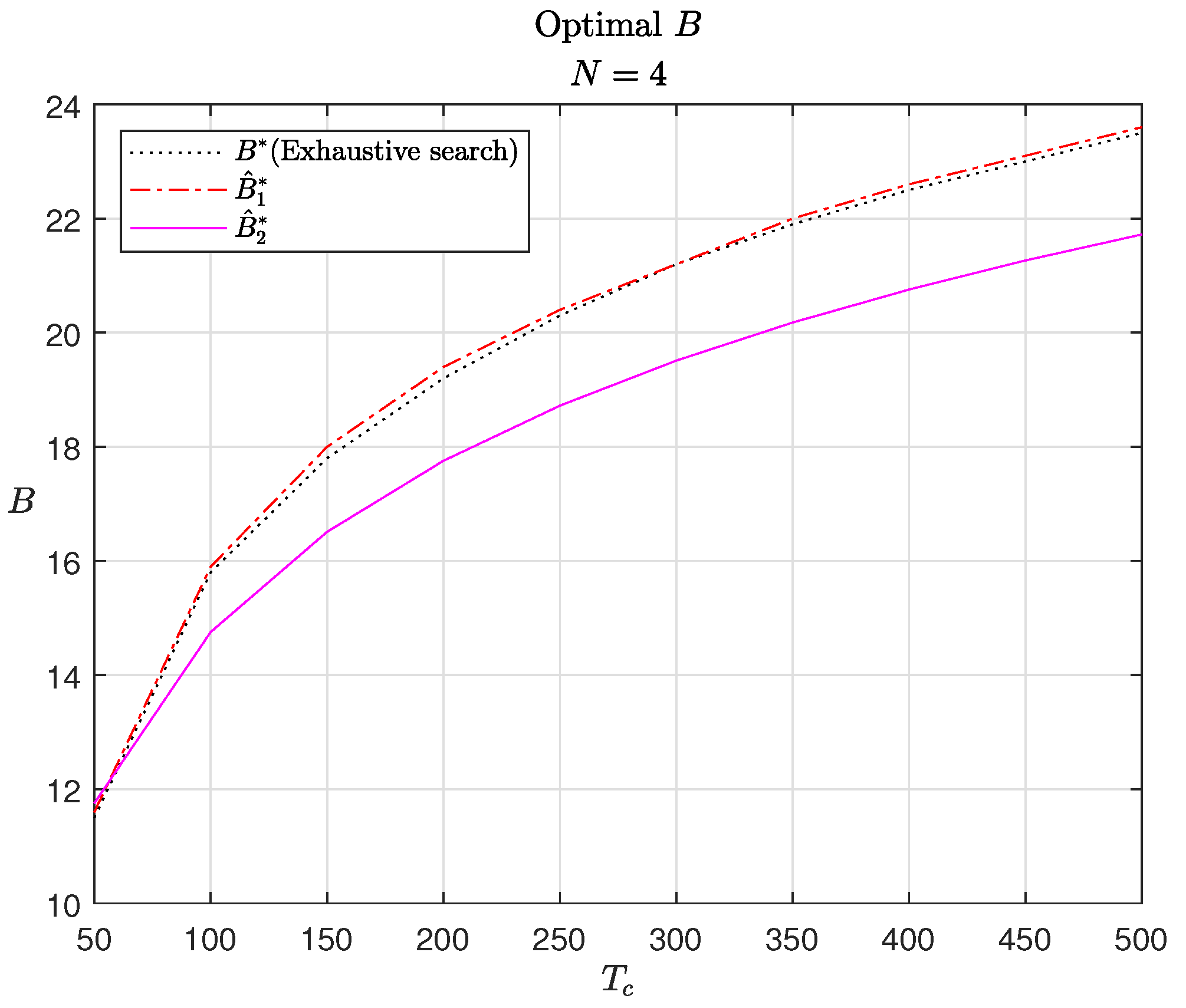
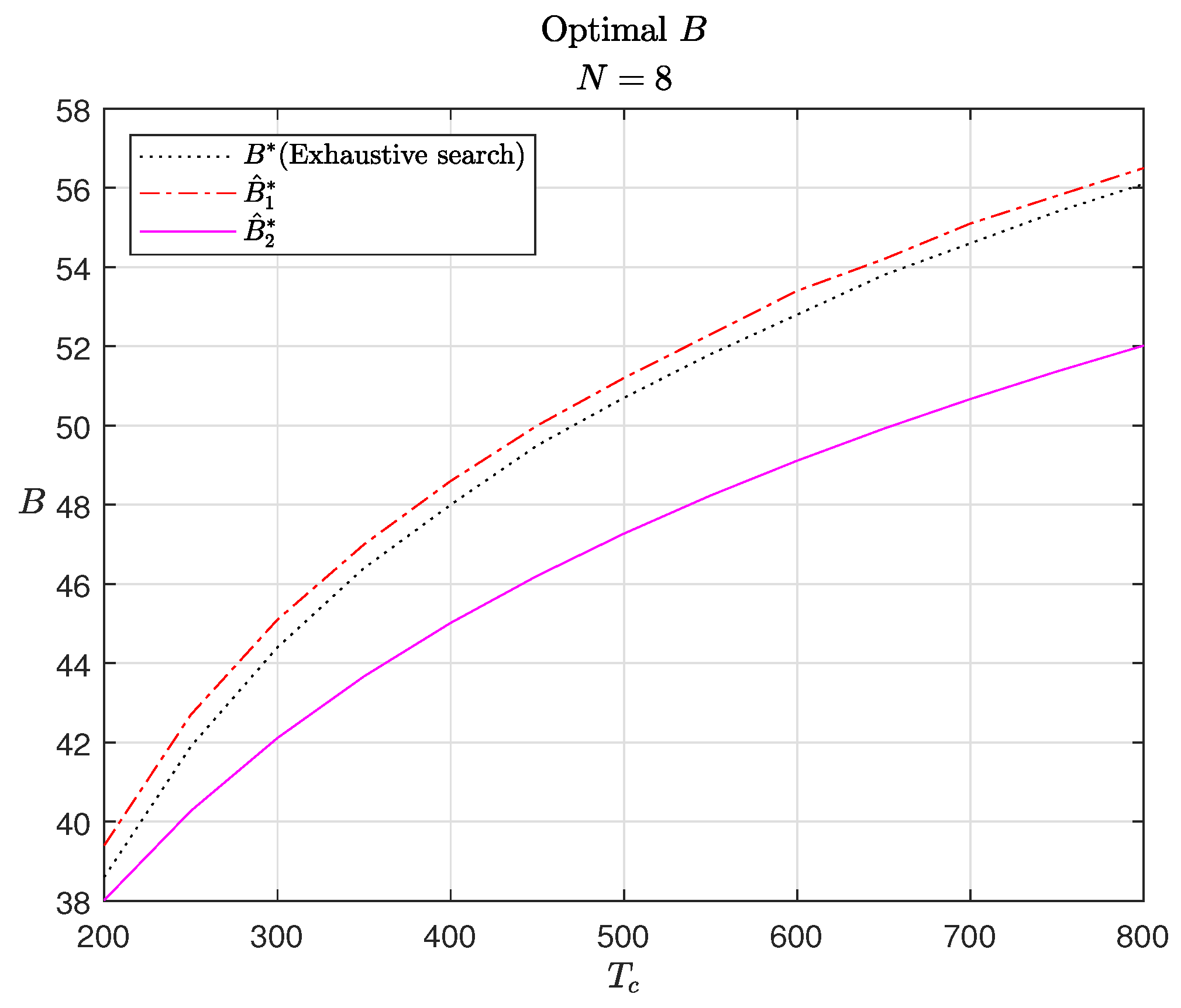
In Figure 4 and Figure 5, the optimal number of feedback bits is presented as a function of $T_c$, along with their analytical approximations. The vertical lines in Figure 2 and Figure 3 indicate the optimal values of B corresponding to specific values of $T_c$ shown in Figure 4 and Figure 5, thereby illustrating how the optimal B varies with $T_c$. In addition, we plot ${\widehat{B}}_1^{*}$ and ${\widehat{B}}_2^{*}$, which approximate the true optimum $B^{*}$. While ${\widehat{B}}_1^{*}$ provides an accurate approximation of $B^{*}$, the gap between ${\widehat{B}}_2^{*}$ and $B^{*}$ is larger due to the additional simplifications adopted for analytical tractability. Nevertheless, the primary goal of this simplification is to characterize the scaling behavior of the optimal feedback rate, and in this regard, ${\widehat{B}}_2^{*}$ successfully fulfills its purpose, as it exhibits the same scaling rate as $B^{*}$. Moreover, because $R_{Net}$ varies slowly with respect to B, the resulting $R_{Net}$ values corresponding to ${\widehat{B}}_2^{*}$ and $B^{*}$ are very close, as demonstrated in Figure 4 and Figure 5. This observation indirectly confirms that both approximations, $\widehat{B}{1}^{*}$ and ${\widehat{B}}_2^{*}$, are sufficiently accurate for maximizing the net spectral efficiency $R_{Net}$.

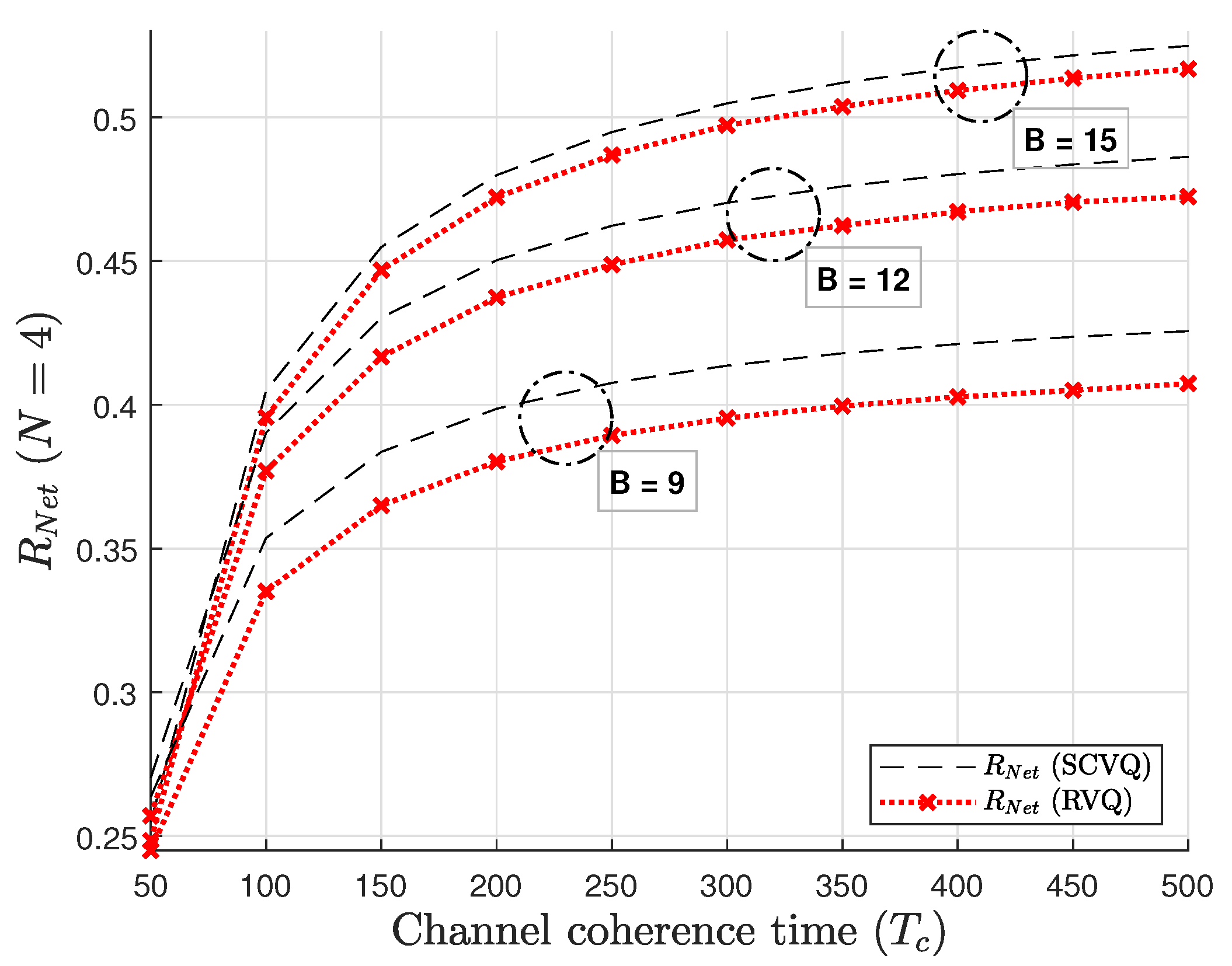
Figure 6 and Figure 7 compare the net spectral efficiency achieved using the optimal values of B, which vary as a function of $T_c$, as identified in the previous results. The spectral efficiency is plotted as a function of $T_c$, along with that obtained using a fixed B for reference. As expected, employing the optimal B consistently outperforms the fixed-B cases. It is also observed that, depending on the range of $T_c$, the fixed-B curve intermittently intersects the curve corresponding to the optimal B. Figure 6 and Figure 7 further compare the resulting spectral efficiencies for $B=B^{*}$, $B={\widehat{B}}_1^{*}$, and $B={\widehat{B}}_2^{*}$, to validate the accuracy of our analysis in the previous section. The case $B=B^{*}$ is obtained via exhaustive search and serves as a performance benchmark (red curve). The results for both approximations (blue star and blue cross markers) closely follow the benchmark, with only minor deviations. This confirms the earlier observation of a “small gap” in the predicted optimal B; the slight discrepancy in B leads to a practically negligible difference in the net spectral efficiency.

5. Conclusions

This paper analyzed the optimal feedback rate in a multi-user MIMO cellular network employing one-bit ADC receivers within a stochastic geometry framework. By developing an analytically tractable approximation for the achievable spectral efficiency, we derived closed-form insights into how limited feedback and coarse quantization jointly influence system performance. Our results show that the optimal feedback rate maintains a logarithmic dependence on channel coherence time but the presence of one-bit quantization reduces the absolute number of feedback bits required. Simulation results validate both the accuracy of the proposed approximation and the predicted scaling law, providing practical design guidelines for feedback resource allocation in power- and cost-constrained MIMO systems with low-resolution ADCs.

Looking ahead, future research may extend this analysis to architectures employing few-bit or mixed-resolution ADCs, while incorporating spatial correlation, user mobility, or millimeter-wave propagation effects into the channel model. Another promising direction is to develop adaptive transmission strategies that jointly optimize power control, beamforming, and feedback allocation. Moreover, evaluating alternative performance metrics such as energy efficiency, latency, or secrecy rate would offer a broader understanding of the inherent trade-offs. These research directions build upon the analytical framework presented in this work and can further guide the design of practical, high-performance wireless networks operating under stringent hardware and feedback constraints.