Abstract
Deep coal rocks exhibit strong time-dependent behavior, including significant plastic deformation and large tunnel displacements, which complicate tunnel support in deep underground engineering. A fractional creep model considering strong time-dependence was developed based on the classical Nishihara framework to capture this behavior. Additional time-dependent strains induced by stress-state variations were considered, with long-term rock strength adopted as the damage stress threshold. The stress difference between nominal and post-damage stress, , defined as the stress gradient, was applied to a viscoelastic–plastic body containing a fractional Abel dashpot, producing conventional creep strain and strong time-dependent strain. The model was extended from one-dimensional to three-dimensional under triaxial stress conditions. The validity of the model was verified using triaxial creep test data for argillaceous sandstone and coal in deep roadways, and the model parameters were determined. The results demonstrate that the model accurately reproduces the full creep process, particularly the nonlinear accelerated stage influenced by strong time-dependence. Through stress-gradient-induced variations in strong time-dependent strain, the proposed creep model elucidates the progression of deformation in the strong time-dependent stage, offering a theoretical framework for the quantitative assessment of deep rock’s strong time-dependence. Sensitivity analysis identified the stress level, fractional order, and strong time-dependence coefficient as key factors affecting strong time-dependent creep behavior. These findings indicate that tunnel support structures in deep environments are prone to instability, underscoring the necessity of accounting for strong time-dependence to ensure long-term stability.
Keywords:
strong time-dependent behavior; fractional derivative; creep model; stress gradient; deep coal rock MSC:
26A33; 35R11; 44A10; 47A62; 74S40
1. Introduction
As shallow geological resources become depleted, the exploitation and utilization of deep resources have become routine. Ensuring the long-term stability of deep underground engineering is therefore essential for their safe and efficient extraction. Deep rock masses exhibit inherent attributes determined by their geological environment, including environments characterized by high stress, high temperature, and high pore pressure, as well as additional properties induced by resource extraction, such as pronounced disturbance and strong time-dependent behavior [1]. Creep, as a key manifestation of the time-dependent nature of rocks, is a critical factor governing the long-term stability of deep rock engineering. Owing to the complexity of rock creep, classical element-based creep models, such as the Burgers, Nishihara, and Maxwell models, fail to fully capture all three stages of creep, particularly the nonlinear accelerated-creep stage occurring when stress exceeds the long-term rock strength [2]. Hence, it is crucial to develop a creep model with fewer parameters, robust fitting capability, and the ability to represent the time-dependent characteristics of deep rock.
Rock is a heterogeneous geological material containing numerous micro-defects whose evolution is strongly time-dependent. The authors of studies on rock time-dependence have conducted creep deformation experiments on various rock types [3], employing different equipment [4] and loading paths [5,6]. To capture the full creep process, some researchers have incorporated damage effects into creep models, allowing parameters such as the elastic modulus to degrade over time, thereby constructing creep models that account for time-dependent damage [7,8,9]. However, most creep models introduce additional parameters to describe the accelerated-creep stage, which makes their element composition overly complex. To simplify creep modeling while capturing nonlinear features, fractional calculus has been applied to develop elements such as the Abel dashpot [10], variable-coefficient Abel dashpot [11,12,13,14], and super-Abel dashpot [15]. On this basis, improved versions of classical models, such as the Nishihara model [16], have been proposed to capture the complete creep process. To further reduce model parameters and improve simplicity, creep models based on variable-order fractional derivatives have been proposed, demonstrating strong a capability to characterize the time-dependent mechanical behavior of rock creep [17,18]. Overall, well-established constitutive models have been developed to describe the general creep behavior of rocks.
In deep underground engineering, particularly in deep rocks surrounding roadways, rocks subjected to long-term high geostress commonly exhibit strong time-dependent behavior [19]. This behavior is typically manifested as large plastic deformation and prolonged creep, which have significant implications for roadway support and long-term stability [20]. Previous studies have shown that the “three-high” environment of deep mining (i.e., high stress, high temperature, and high pore pressure) promotes rheological deformation. Mining disturbances can induce a transition from elastic to plastic responses, leading to sustained stress redistribution and large-scale deformation [21]. Laboratory experiments and field monitoring further confirm that rock failure under high confining pressure is often accompanied by substantial plastic deformation and creep [22]. Some deep roadways even experience continuous deformation at rates of several hundred millimeters per month [23]. Recent investigations indicate that the spatio-temporal evolution of pores and microfractures plays an important role in driving this strong time-dependent deformation [24,25]. To capture these complex behaviors, various constitutive approaches, such as fractional viscoplastic and modified creep models, have been developed and applied to describe the full creep process of deep rocks [26]. These efforts provide valuable theoretical foundations and practical insights for understanding and modeling the strong time-dependent behavior of deep surrounding rock.
To better characterize the strong time-dependent behavior of deep rock, this study interprets the unique mechanical responses of deep rock, links time-dependent features with creep properties, and incorporates the memory effect of fractional operators. Based on an improved fractional Nishihara model and considering stress state variations in deep rock, a fractional creep model accounting for strong time-dependence is proposed. This model not only effectively captures the strong time-dependent behavior of deep rock but also provides a theoretical basis for predicting long-term deformation. In addition to its theoretical significance, the proposed fractional creep model also has important engineering implications. Predicting the time-dependent deformation of deep rock masses is crucial for maintaining roadway stability, and the model provides a means to evaluate long-term creep behavior under complex stress conditions. Such insights can guide practical tunnel support design, including the optimization of support timing, the selection of appropriate stiffness and reinforcement strategies, and the establishment of safety margins against delayed instability. Therefore, the present study not only contributes to advancing the theoretical framework of fractional creep modeling but also provides a valuable reference for the rational design of support systems in deep coal mining.
2. Fractional Derivative Analysis of Strong Time-Dependent Rock Behavior
2.1. Characterization of Strong Time-Dependent Behavior in Deep Rock
As mining depth increases, deep mining has become routine. Xie et al. [27] defined “deep” as a stress state related to geostress levels and the properties of surrounding rock, with strong time-dependence being a distinct mechanical response to this state. Conventional time-dependence generally refers to the temporal evolution of the physical and mechanical properties and deformation behavior of rock [28]. In general, rock time-dependence encompasses three aspects: (1) the degradation of physical and mechanical properties; (2) the brittle–ductile transition; and (3) the three stages of rheology.
According to the definition of strong time-dependence in deep rocks proposed by Xie et al. [28], and considering creep evolution, time-dependence can be represented by the three creep stages: primary, steady-state, and accelerated creep. In deep rocks, due to the high-stress environment, strong time-dependence is characterized specifically by the accelerated-creep stage. Thus, the onset of strong time-dependence corresponds to the initiation of accelerated creep, and the accelerated-creep stage itself defines the period of strong time-dependence. Therefore, the accelerated-creep stage can be regarded as the hallmark of strong time-dependence in deep rocks, as illustrated in Figure 1 and Figure 2.
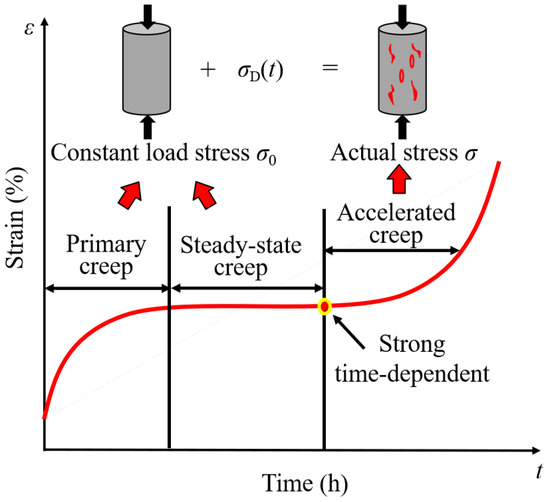
Figure 1.
Three-stage creep curves of deep rocks.
In creep modeling, damage evolution under external load has been shown to cause strength reduction and mechanical degradation of rock [29,30,31], manifesting as increased effective stress and reduced elastic modulus. These effects correspond to two approaches: geometric changes in the active area and energy-based changes in Young’s modulus. Using the standard area-based expression of damage variables [32], and drawing from Weibull-based meso-element evolution [33] and ultrasonic evidence [16,34] during creep, evolution of the active area of deep rock under strong time-dependence is assumed to follow a negative exponential law. Accordingly, the proposed damage variable for deep rock with strong time-dependence is formulated as
where denotes the damaged cross-sectional area; A the intact area; the time of damage onset; and a coefficient related to the strong time-dependence of deep rock, which acts as a material parameter that reflects the unique characteristics of coal rock, such as lithology and the prevailing stress environment. Specifically, in the context of deep coal rock, is used to account for the strong time-dependent effects that influence damage evolution under high-stress conditions. This parameter is not simply a fitting parameter but is tied to the specific stress states and damage processes in deep geological environments. Therefore, we define as the strong time-effect coefficient, which governs the rate of damage evolution under the extreme conditions typically found in deep coal deposits. By incorporating , we are able to better capture the influence of these time-dependent effects on the damage characteristics of coal rock.
Research has demonstrated that rock creep involves a damage stress threshold, equal to the long-term strength at which micro-cracks begin to form. Hence, long-term strength is adopted here as the damage threshold [35]. The following strong time-dependent behavior of deep rock emerges when stress reaches this level: micro-defects develop rapidly, micropores and fractures coalesce and propagate, damage accumulates, and the rock’s resistance to deformation weakens until micro-cracks connect to form macroscopic fractures, resulting in failure [36]. At this point, the long-term strength, the onset of damage, and the initiation of strong time-dependence coincide. Therefore, the creep model proposed herein incorporates a stress gradient to account for the altered stress state after damage, and the additional strain induced is used to quantify the strong time-dependent characteristics of deep rock.
The accumulation of damage in the time-dependent stage results in a gradual reduction in the rock’s effective load-bearing area. Based on Lemaitre’s strain equivalence principle [37] and the damage formulation of Cao et al. [29], and accounting for the relationship between nominal and actual stresses, a damage-inclusive stress expression is presented [38].
where denotes the long-term strength; represents the nominal stress, i.e., the stress applied during the creep experiment; and is the actual stress, i.e., the stress acting on the specimen after damage occurs, as illustrated in Figure 1.
The mechanical properties of deep rocks, particularly those surrounding deep roadways, differ substantially from those of shallow rocks. Under the “three-high” deep environment, rocks exhibit a brittle-to-ductile transition, and failure is associated with considerable plastic deformation [20]. Nonlinear large deformations are pronounced, and in deep rock surrounding roadways, extensive creep coupled with strong time-dependent effects commonly occurs, complicating support and leading to severe deformation [22]. Consequently, from an engineering perspective, the strong time-dependent behavior of deep rocks is characterized by evident time-dependent effects under deep environmental conditions and by significant high-magnitude deformations, which are frequently observed in the large deformations of deep rock surrounding roadways [19].
Based on the creep deformation of surrounding rock in deep underground engineering, triaxial creep test data from different deep rocks were used to further assess their strong time-dependent characteristics. Long-term triaxial creep tests on mudstone–sandstone at varying depths were conducted by Zheng et al. [39] (Figure 2a), and on sandy mudstone from Pingmei No. 1 Mine by Chen et al. [40] (Figure 2b). The results demonstrate that deep rocks under high confining pressures exhibit pronounced strong time-dependent behavior compared to shallow rocks under lower pressures. For instance, mudstone–sandstone failed at 209 h under 18 MPa, much later than 174 h under 9 MPa, while sandy mudstone failed at 73 h under 20 MPa, exceeding 60 and 42 h at 15 and 10 MPa, respectively. Failure strains similarly increased with confining pressure: 25.63‰versus 19.66‰ for mudstone–sandstone, and 5.33%, 4.86%, and 4.30% for sandy mudstone. These findings confirm that the maximum creep deformation rises with confining pressure and reaches its peak during the strong time-dependent stage, illustrating the large-deformation effect inherent in deep rocks.
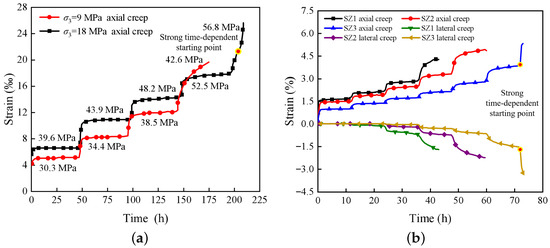
Figure 2.
Creep curves of deep rocks under different confining pressures: (a) Creep curves of argillaceous sandstones at 9 MPa and 18 MPa confining pressures [39]. (b) Creep curves of sandy mudstone at 10 MPa (SZ1), 15 MPa (SZ2), and 20 MPa (SZ3) confining pressures [40].
The results of the analysis of the creep curves for different deep rocks in Figure 2 indicate that strong time-dependent behavior only manifests under high confining pressures, regardless of whether the rock is mudstone–sandstone or sandy mudstone. Consequently, only deep rocks exhibit pronounced strong time-dependent characteristics. Furthermore, under high-confining-stress conditions in deep environments, higher deviatoric stress during the creep process leads to increased creep strain rates, facilitating the transition of rocks into the strong time-dependent stage.
2.2. Fractional Mechanical Element Considering Strong Time-Dependent Characteristics
Fractional calculus allows for a more precise description of certain nonlinear characteristics through the adjustment of its order. The study of fractional calculus theory has gradually expanded across multiple disciplines and has been applied in a wide range of fields.
Fractional calculus has multiple definitions, with the Riemann–Liouville (R-L), Grünwald–Letnikov, and Caputo forms being the most widely used. R-L fractional calculus has attracted widespread attention due to its concise formulation and reliable performance. For a function of order , the R-L fractional integral is defined as follows: if we assume that f is piecewise continuous on and integrable over any finite subinterval for and , then
where denotes the Gamma function.
The R-L fractional derivative of order for a function is defined as follows: if we assume that , and let m denote the smallest integer exceeding and , then
where denotes the differential operator.
The Abel dashpot is a typical application of fractional calculus, with its fractional order ranging between 0 and 1. It can be used to describe the viscoelastic and viscoplastic behavior of materials. Its constitutive relation is given as follows [16]:
where and represent the stress and strain of the material, respectively; is the viscosity coefficient; is the fractional order with ; and t is the time.
In typical creep conditions, the stress is maintained at (i.e., in Equation (5)). By integrating Equation (5) with the R-L fractional operator, the creep behavior of the Abel dashpot is obtained as follows:
When strong time-dependent properties are taken into account, internal damage occurs within the rock, and an Abel dashpot considering strong time-dependence is introduced. As a result of the damage, the stress applied to the Abel dashpot, , is no longer constant but a time-varying quantity denoted by . Accordingly, Equation (5) is modified to reflect the strong time-dependent behavior:
By rearranging Equation (7) and applying the R-L fractional operator, the creep equation expression of the Abel dashpot considering strong time-dependence is obtained as follows:
To clearly compare the mechanical behavior of the two dashpots, the parameters of , , and were substituted into Equations (6) and (8), respectively. The resulting creep curves under identical stress conditions are shown in Figure 3. It can be observed that the strain variation in the Abel dashpot is relatively small and only captures the first two stages of creep, whereas the Abel dashpot considering strong time-dependent behavior exhibits larger strain increments and faster creep rates, effectively describing the nonlinear strong time-dependent stage of creep.
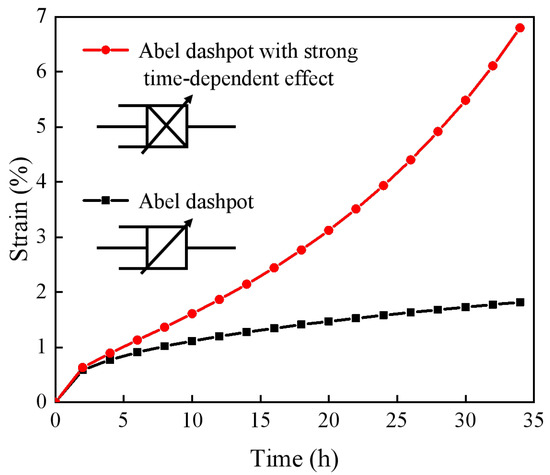
Figure 3.
Creep curves of two kinds of Abel dashpot.
Further analysis was conducted on the Abel dashpot considering strong time-dependent behavior. By substituting , and into Equation (8), a set of creep curves illustrating strain variation with respect to the derivative order under creep conditions was obtained (Figure 4a). Keeping all other parameters unchanged and varying only the strong time-dependent coefficient while setting in Equation (8), another set of creep curves showing strain variation with was obtained (Figure 4b). These results indicate that the Abel dashpot considering strong time-dependent effects can accurately capture the entire creep process and effectively represent the strong time-dependent behavior of deep rock masses.
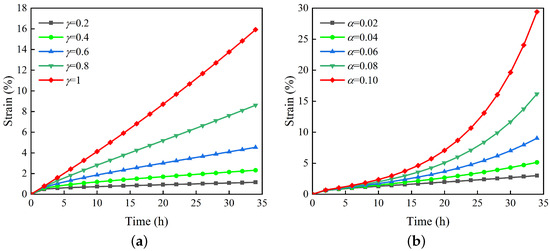
Figure 4.
Unsteady creep described by the Abel dashpot considering the influence of strong time-dependence behavior: (a) Creep curves under different orders . (b) Creep curves under different strong time-dependent coefficients .
3. Establishment of Fractional Creep Model Considering Strong Time-Dependent Behavior
3.1. Characterization of Strong Time-Dependent Behavior in Creep Model
The creep behavior of rock is generally classified as stable or unstable depending on whether the applied external load exceeds the long-term strength . In deep rocks, especially surrounding deep roadways, the prevailing high-stress conditions () give rise to strong time-dependent characteristics. Consequently, the creep process can be distinguished into three stages: primary, steady-state, and accelerated creep (i.e., the strong time-dependent stage), as shown in Figure 1.
At the onset of the strong time-dependent stage of rock creep, internal damage develops, characterized by the initiation, propagation, and eventual coalescence of micro-cracks, culminating in failure. Cao et al. [29] proposed that the creep damage variable D can be identified either by examining changes in Young’s modulus from an energy perspective or by analyzing variations in the effective active region from a geometrical perspective. Wu et al. [38] emphasized that during the accelerated-creep stage, damage accumulation progressively reduces the effective load-bearing area, which in turn increases the effective stress acting on the specimen. Consequently, a stress increment is introduced between the actual stress and the nominal stress, herein defined as the stress gradient, as illustrated in Figure 1. Lemaitre’s strain equivalence principle [37] further states that the strain of a damaged body subjected to stress is equivalent to that of an undamaged body subjected to effective stress .
Drawing on the work of Cao et al. [29] and Lemaitre’s strain equivalence principle, the damage variable was introduced into the stress gradient. For cases where the nominal stress exceeds the long-term strength , the combined effects of nominal stress and stress gradient were applied to the viscoplastic element in Zhou’s creep model [2] to characterize the strong time-dependent response of deep rock. Once the accelerated-creep stage is reached, the viscoplastic strain is decomposed into two components: the conventional viscoplastic strain and the strong time-dependent strain. Accordingly, in model construction, the viscoplastic Abel dashpot is replaced by a strong time-dependent Abel dashpot to better capture these effects (Figure 5). This replacement enhances the model’s capacity to simulate nonlinear time-dependent creep in deep rock masses.
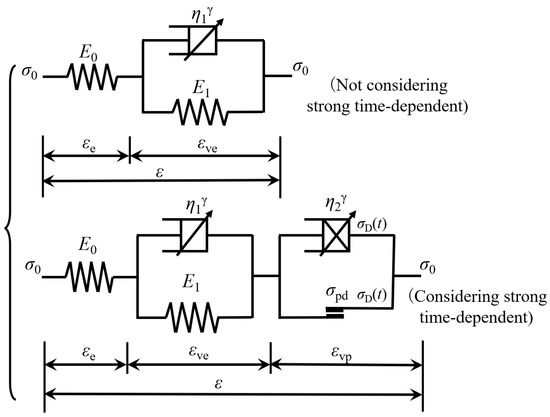
Figure 5.
Schematic view of creep constitutive model.
3.2. Establishment of a One-Dimensional Strong Time-Dependent Creep Model
For , the rock undergoes stable creep. Following the method proposed by Zhou et al. [2] (Figure 5), the creep equation for this condition, where strong time-dependent effects are not considered, can be derived as
where and denote the elastic moduli of Hooke’s body in the elastic and viscoelastic components, respectively; represents the viscosity coefficient of the Abel dashpot; denotes the one-parameter Mittag–Leffler function; and is the fractional-order parameter.
For , the viscoplastic element in the creep model is activated, with given by
where is the yield stress, and represents the stress of the friction element.
Based on the parallel arrangement of the components, the total stress of the viscoplastic element considering strong time-dependent behavior can be expressed as
where denotes the stress of the Abel dashpot considering strong time-dependent effects.
For , the viscoplastic strain arises from the combined action of two stress components: the nominal stress and the stress gradient .
where denotes the conventional viscoplastic strain, and represents the strong time-dependent strain.
The strain under the action of nominal stress is first analyzed. Considering Equation (11), the corresponding constitutive relationship can be expressed as
where denotes the order of the derivative, and is the viscosity coefficient of the strong time-dependent Abel dashpot in the viscoplastic element.
By reorganizing Equation (14), the following expression is obtained:
By applying the Laplace transform and its inverse to Equation (15), and considering the initial condition at , the analytical solution can be obtained as follows:
For the strong time-dependent strain under , combined with Equation (11), the constitutive relation is given by
By reorganizing Equation (17), the following expression is obtained
By performing Laplace and inverse Laplace transforms on Equation (18) and applying the initial condition at , the analytical solution is given by
where the two-parameter Mittag–Leffler function is defined by
Based on Figure 5 and the Boltzmann superposition principle, the constitutive equation of the fractional creep model with strong time-dependent characteristics is
Namely,
In summary, the complete expression of the fractional creep model considering strong time-dependent effects is
When , the first term in the above expression represents the elastic strain; the second term corresponds to the viscoelastic strain; the third term denotes the conventional viscoplastic strain; and the fourth and fifth terms account for the strong time-dependent strains.
3.3. Establishment of a Three-Dimensional Strong Time-Dependent Creep Model
Rocks in deep underground engineering are generally under triaxial stress conditions. To more accurately represent engineering reality, the model’s constitutive equations are formulated in three-dimensional stress terms. In this context, the stress tensor is decomposed into the spherical stress component and the deviatoric stress component , such that , with denoting the Kronecker delta. Likewise, the strain tensor can be decomposed into the spherical strain component and the deviatoric strain component , i.e., .
In the creep model, the strain of the elastic element can be represented according to the generalized Hooke’s law as
where and K are the shear modulus and bulk modulus of the elastic element, respectively.
Under the assumptions that deep rocks behave isotropically, volumetric creep is negligible, and Poisson’s ratio remains constant throughout the creep process, the 3D constitutive relation for the viscoelastic element can be formulated as
where is the shear modulus of the viscoelastic element.
For the viscoplastic component, the Perzyna model [41] and the associated flow rule are adopted. Considering the initial condition at , the expressions for the two types of creep strains in the viscoplastic element can be obtained. For the conventional viscoplastic strain , the 3D strain expression is
where
where F stands for the rock yield function, stands for the reference initial yield, and is a first-order power function.
Following the 3D derivation of conventional viscoplastic strain, the 1D strong time-dependent strain is transformed to give the 3D creep strain expression for
Considering that the deviatoric stress tensor plays the primary role during the creep process, the following yield function can be adopted:
where is the second invariant of the deviatoric stress tensor, defined as
For a conventional triaxial compression test, where and , the 3D creep equation of the viscoplastic body in the axial direction can be expressed as
4. Model Validation and Characterization of Strong Time-Dependent Creep Behavior
4.1. Determination of Creep Model Parameters
The effectiveness and applicability of the fractional creep model incorporating strong time-dependent effects are primarily determined by its capacity to reproduce experimental results. To gain further insight into the triaxial creep behavior of deep coal roadways and to predict their long-term deformation, Xu et al. [41] performed triaxial creep tests on coal specimens extracted from the Xing’an Coal Mine under varying axial deviatoric stresses. In the present work, these experimental data were utilized to validate and calibrate the proposed model. The coal specimens were sampled from a roadway at an approximate burial depth of 700 m. After sealed transportation to the laboratory, intact coal blocks were cut and polished in the same orientation into standard cylindrical specimens with dimensions of 50 mm× H100 mm, in accordance with the standards of the ISRM. Triaxial compression and creep tests were subsequently conducted using a servo-controlled triaxial rheometer under identical laboratory temperature and humidity conditions.
To simulate stress under deep conditions, a confining pressure of 30 MPa was imposed. A triaxial compression test was initially performed at this confining pressure, and the triaxial compressive strength was determined to be 112.43 MPa. Using this strength as a reference, graded-loading creep tests were subsequently conducted under the same confining pressure, with each creep stage maintained for 72 h. At the final stress level of 75 MPa, creep failure occurred after 0.98 h. The detailed experimental results are presented in Figure 6. The data reveal that under high confining pressure, coal undergoes prolonged creep before experiencing catastrophic failure with significant deformation, which is characteristic of strong time-dependent behavior in deep rocks. Accordingly, the experimental data corresponding to the final creep stage were adopted for fitting and validation of the proposed creep model.
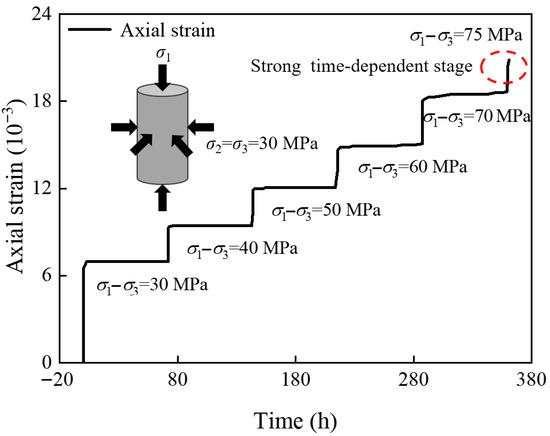
Figure 6.
Experimental creep data for deep coal under graded loading [42].
Based on the triaxial creep test data for coal from deep roadways, the strong time-dependent fractional creep model expressed in Equation (32) was fitted using the nonlinear least-squares method. To validate the general applicability of the model, the creep test data for deep mudstone–sandstone under high confining pressure reported by Zheng et al. [39] in Section 2.1 were also employed for model fitting. The fitted parameters are summarized in Table 1, and the corresponding model results are shown in Figure 7.

Table 1.
Parameter fitting results for different experimental creep data and different creep models.
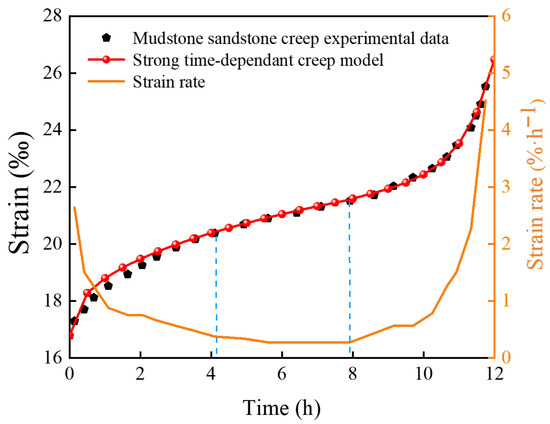
Figure 7.
Schematic diagram of the results of fitting the strong time-dependent creep model to the experimental creep data for argillaceous sandstone.
The Nishihara model, owing to its flexibility in describing diverse creep behaviors, has been extensively adopted in engineering practice [33]. The strong time-dependent creep model developed herein was established on the basis of this classical framework. Moreover, an improved Nishihara model incorporating fractional derivatives was introduced by Yan et al. [10], which exhibits similarities to the present formulation. Comparative analysis against this model enables a clearer demonstration of the superiority of the proposed strong time-dependent creep model. Accordingly, the Nishihara model and Yan’s improved variant were both employed to fit the coal creep data, and their performance was evaluated in parallel with the proposed model. The experimental data and fitting curves are compared in Figure 8.
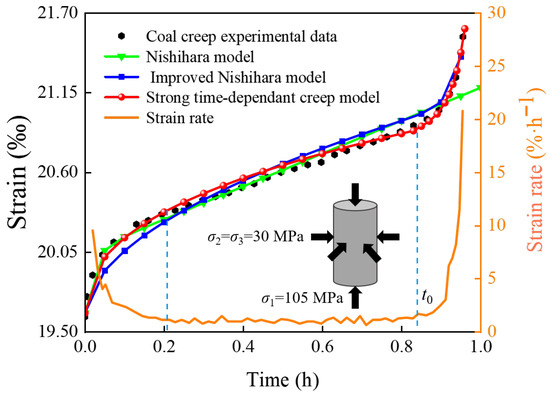
Figure 8.
Schematic diagram of the results of fitting different creep models to the experimental creep data for coal.
4.2. Validation of the Creep Model and Analysis of Strong Time-Dependent Behavior
The reliability of the strong time-dependent creep model was validated by analyzing the three stages of creep. The separation times of these stages were identified from the evolution of the strain rate in Figure 8. During the primary creep stage, the coal strain rate decreased progressively and stabilized at approximately by 0.21 h. Within 0–0.21 h, the Nishihara and modified Nishihara models predicted strain rates lower than the experimental observations, whereas the strong time-dependent creep model exhibited closer agreement, accurately reproducing the gradual attenuation process. Between 0.21 and 0.83 h, the strain rate remained nearly constant, corresponding to the steady-state creep stage. In this phase, the Nishihara and modified models slightly overpredicted the strain rate, while the strong time-dependent creep model showed almost complete overlap with the experimental curve, demonstrating superior accuracy.
At a creep duration of 0.83 h, the strain rate of deep coal exhibited rapid escalation, rising from to within a brief interval, signaling entry into the strong time-dependent stage and a concomitant rapid increase in creep deformation until failure. Figure 8 illustrates that, during this stage, the Nishihara model maintained a relatively low strain rate, with its creep curve approaching linearity and deviating substantially from the observed data. The modified Nishihara model partially captured the accelerated creep in the strong time-dependent stage; however, its strain rate increased more slowly than the experimental measurements, and the predicted onset of the strong time-dependent stage was delayed, limiting its ability to accurately represent the behavior of deep coal. Conversely, the strong time-dependent creep model demonstrated excellent agreement with experimental observations, with strain rates rising in synchrony, thereby effectively representing the nonlinear acceleration characteristic of deep coal creep.
The fitting accuracy of the creep models was evaluated by comparing the predicted responses with experimental data. To quantify the goodness of fit and associated uncertainty, correlation coefficients () and residual sums of squares () were calculated under the 95% confidence interval, as presented in Table 2. It is evident that the strong time-dependent creep model exhibits an approaching unity and a minimal , indicating superior agreement with experimental observations. The Nishihara model performed the worst, failing to reproduce the accelerated-creep stage. Although the modified Nishihara model of Yan et al. [10] captured the acceleration trend, its fitting precision was limited, the predicted strain rates were lower than observed, and the predicted onset of accelerated creep was delayed. In comparison, the proposed strong time-dependent creep model, with a reduced number of parameters, achieved the highest fitting accuracy and accurately reflected the pronounced time-dependent characteristics of deep coal.

Table 2.
Fitting results of creep models to experimental data.
From the standpoint of model formulation, the modified Nishihara model proposed by Yan et al. [10] fits the rapid accumulation of strain in the accelerated-creep stage solely by increasing the exponent of the time term. By contrast, the strong time-dependent creep model accounts for the internal damage accumulation in deep coal, where modifications in the stress state and the progressive evolution of micropores and fractures induce strong time-dependent strains, thereby characterizing the strain variation in the accelerated-creep stage. Consequently, the strong time-dependent creep model offers a more rigorous theoretical approach to investigating the interplay between internal damage and mechanical response, providing a comprehensive representation of deep coal rock creep behavior.
In conclusion, the strong time-dependent fractional creep model proposed herein successfully describes the entire creep process of deep rock, with particular emphasis on the nonlinear strong time-dependent phase. While prior studies [28,43] have only offered qualitative accounts of this behavior, the current model incorporates the strong time-dependent strain arising from stress gradients during creep, allowing the evolution of strain in the strong time-dependent stage to be quantified. This provides a theoretical framework for the quantitative characterization of deep rock’s strong time-dependent properties. Model analysis further reveals that significant deformations can occur in deep tunnels, potentially leading to instability of support structures. Hence, consideration of strong time-dependent behavior is essential for optimizing support strategies and ensuring the long-term stability of deep underground engineering.
4.3. Parametric Sensitivity Analysis of the Creep Model
To elucidate the impacts of key factors on the strong time-dependent behavior of deep coal rock, a sensitivity analysis was carried out on the stress level (), the fractional orders (), and the strong time-dependent coefficient (), which critically influence the evolution of the strong time-dependent stage.
For the sensitivity analysis, all model parameters except the stress level were fixed based on the fitted results of the mudstone–sandstone creep experiments in Table 1. Creep responses under varying stress levels were evaluated for both stable creep and accelerated creep considering strong time-dependent effects, as illustrated in Figure 9. The results indicate that creep strain increases with rising stress level. During stable creep, the steady-state stage slightly shortens, while in the accelerated-creep stage, the time to onset of accelerated deformation decreases. Notably, even when the stress is reduced by an order of magnitude, stress level changes still markedly influence the accelerated-creep stage, demonstrating the critical role of stress in controlling the strong time-dependent behavior of deep rock. Higher stress levels result in more pronounced strong time-dependent characteristics.
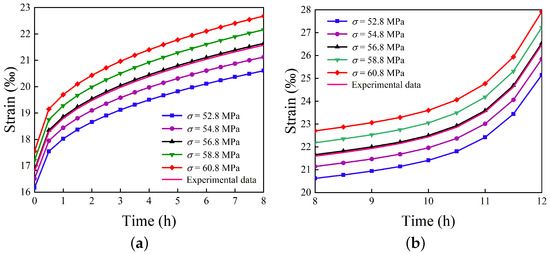
Figure 9.
Creep curves under different stress levels: (a) Stable creep. (b) Accelerated creep considering strong time-dependence.
The fractional-order parameter is a critical factor influencing the strong time-dependent behavior of deep coal rocks. By varying while keeping other parameters constant, the evolution of creep curves with respect to can be obtained, as shown in Figure 10. The results indicate that a higher leads to a shorter time for coal rocks to enter the accelerated-creep stage, larger corresponding strong time-dependent strains, and higher creep rates during the accelerated stage. Consequently, the strong time-dependent characteristics of deep rock masses become more pronounced, and rock failure becomes more likely.
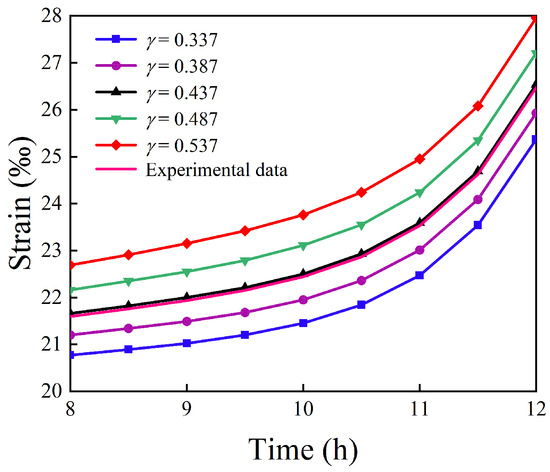
Figure 10.
Creep curves under different fractional orders .
From Section 2, it is evident that the strong time-dependent coefficient alters the actual stress, which can be quantified through creep deformation to assess deep coal rock’s strong time-dependent behavior. By varying while keeping all other parameters constant, the evolution of creep curves with respect to was examined (Figure 11). The results indicate that during the accelerated-creep stage, higher values, corresponding to larger stress gradients, produce more severe damage, greater strong time-dependent strains, higher creep rates, and earlier onset of acceleration. Consequently, the strong time-dependent behavior of deep coal rock becomes more pronounced, increasing the likelihood of failure. These findings suggest that the stress gradient enhances both creep strain and creep rate, giving rise to the nonlinear acceleration characteristic of the strong time-dependent stage.
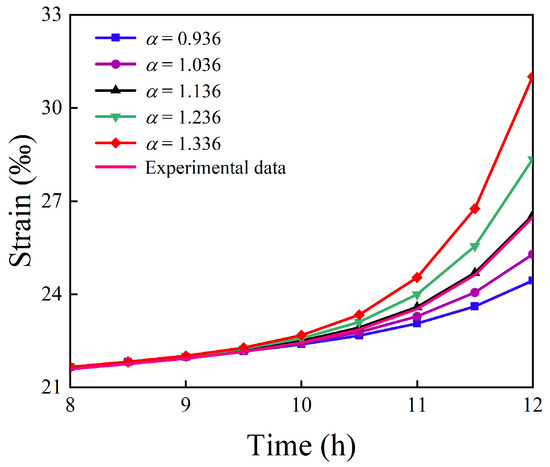
Figure 11.
Creep curves under different strong time-dependent coefficients .
5. Conclusions
To characterize the strong time-dependent behavior of deep coal rock, a fractional creep model considering strong time-dependent effects is proposed. This model is based on the Nishihara model and integrates fractional derivative theory, continuum damage mechanics, and the strain equivalence principle, accounting for the strong time-dependent strain induced by stress gradients during creep. The main conclusions are as follows.
- (1)
- Based on field measurements of deep rock surrounding roadways and triaxial creep tests under high confining pressures, deep rock exhibits pronounced plastic deformation and strong time-dependent behavior, which can result in large roadway deformations that are difficult to support. These observations reveal the evolutionary patterns of strong time-dependent characteristics in deep rock from a deep engineering perspective.
- (2)
- Considering strong time-dependent effects, deep coal rock creep deviates from conventional behavior, with the actual stress evolving slowly. The stress increment , treated as a stress gradient, was incorporated into a strong time-dependent Abel dashpot element, forming a three-dimensional creep model that effectively represents the strong time-dependent properties of deep coal rock.
- (3)
- The proposed fractional strong time-dependent creep model outperforms the Nishihara and modified Nishihara models in fitting deep coal rock creep data, especially during the nonlinear accelerated-creep stage. By incorporating stress-gradient-induced strain, the model provides a quantitative measure of deep rock’s strong time-dependent behavior. Sensitivity analysis indicates that increasing stress levels, fractional orders, and the strong time-dependent coefficient enhances ultimate creep strain, shortens the steady-state stage, and accelerates the onset of nonlinear creep, reinforcing the strong time-dependent characteristics of deep coal rock.
Author Contributions
Conceptualization, S.Y. and W.J.; methodology, W.J.; software, S.X.; validation, S.X. and W.J.; formal analysis, S.Y.; investigation, H.W. and L.A.; data curation, W.J.; writing—original draft preparation, W.J. and S.Y.; writing—review and editing, S.Y.; visualization, W.J., H.W.; supervision, S.Y. and S.X.; funding acquisition, W.J., S.Y. and S.X. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the S&T Innovation and Development Project of Information the Institution of the Ministry of Emergency Management (Project No. 2025506), the National Natural Science Foundation of China (52204110, 52574121, 52504102), the Deep Earth Probe and Mineral Resources Exploration—National Science and Technology Major Project (2024ZD1003902), the Intergovernmental International Science and Technology Innovation Cooperation Key Special Project (2025YFE0109800), and the European Commission Horizon Europe Marie Skłodowska-Curie Actions Staff Exchanges Project—LOC3G (101129729).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors thank the editors and anonymous reviewers for their valuable and constructive suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xie, H.P. Research framework and anticipated results of deep rock mechanics and mining theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Qiao, L.P.; Wang, Z.C.; Liu, J.; Li, W. Internal state variable creep constitutive model for the rock creep behavior. Bull. Eng. Geol. Environ. 2022, 81, 456. [Google Scholar] [CrossRef]
- Lyu, C.; Xu, D.; Liu, J.F.; Ren, Y.; Liang, C.; Zhao, C.X. Investigation on very long-term brittle creep test and creep-damage constitutive model for granite. Acta Geotech. 2023, 18, 3947–3954. [Google Scholar] [CrossRef]
- Hu, S.C.; Zhang, C.X.; Ru, W.K.; Han, J.M.; Guo, S.H.; Zhou, X.D.; Yang, L. Creep properties and energy evolution characteristics of weakly cemented rock under step loading. Int. J. Rock Mech. Min. Sci. 2023, 170, 105428. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tang, J.Z.; Wang, S.S.; Yang, D.S.; Zheng, W.T. An experimental and modeling investigation on creep mechanical behavior of granite under triaxial cyclic loading and unloading. Rock Mech. Rock Eng. 2022, 55, 5577–5597. [Google Scholar] [CrossRef]
- Liu, Y.D.; Zhang, H.J.; Qin, Z.; Chen, X.X.; Liu, W.L. Energy evolution and deformation features of re-loading creep failure in yellow sandstone after cyclic water intrusion. Int. J. Rock Mech. Min. Sci. 2025, 186, 106019. [Google Scholar] [CrossRef]
- Zheng, Z.M.; Yu, Y.; Cheng, P. A modified creep model for rock considering hardening and damage. Mech. Time-Depend. Mater. 2023, 28, 289–301. [Google Scholar] [CrossRef]
- Reyes de Luna, E.; Kryvko, A.; Pascual-Francisco, J.B.; Hernández, I.; Samayoa, D. Generalized Kelvin–Voigt creep model in fractal space-time. Mathematics 2024, 12, 3099. [Google Scholar] [CrossRef]
- Yan, B.Q.; Guo, Q.F.; Ren, F.H.; Cai, M.F. Modified Nishihara model and experimental verification of deep rock mass under the water-rock interaction. Int. J. Rock Mech. Min. Sci. 2020, 128, 104250. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.W.; Wang, X.Y.; Wang, L.; Su, T.; Wei, Q.; Deng, T.F. A triaxial creep model for deep coal considering temperature effect based on fractional derivative. Acta Geotech. 2022, 17, 1739–1751. [Google Scholar] [CrossRef]
- Yang, S.; Song, H.C.; Zhou, H.W.; Xie, S.L.; Zhang, L.; Zhou, W.T. A fractional derivative insight into full-stage creep behavior in deep coal. Fractal Fract. 2025, 9, 473. [Google Scholar] [CrossRef]
- Wu, J.P.; Hu, B.; Li, J.; Zhang, X.Y.; Dai, X.; Cui, K. Fractional-order constitutive modeling of shear creep damage in carbonaceous mud shale: Experimental verification of acoustic emission ringing count rate analysis. Fractal Fract. 2025, 9, 610. [Google Scholar] [CrossRef]
- Yang, S.; Zhou, W.T.; Xie, S.L.; Lei, B.; Song, H.C. Fractional order analysis of creep characteristics of sandstone with multiscale damage. Mathematics 2025, 13, 2551. [Google Scholar] [CrossRef]
- Chen, J.; Lu, D.; Wu, F.; Fan, J.Y.; Liu, W. A non-linear creep constitutive model for salt rock based on fractional derivatives. Therm. Sci. 2019, 23, 773–779. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L.; Duan, Z.Q.; Ding, J.Y. A fractional derivative approach to full creep regions in salt rock. Mech. Time-Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]
- Gao, Y.F.; Yin, D.S. A full-stage creep model for rocks based on the variable-order fractional calculus. Appl. Math. Model. 2021, 95, 435–446. [Google Scholar] [CrossRef]
- Wu, F.; Liu, J.; Zou, Q.L.; Li, C.B.; Chen, J.; Gao, R.B. A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2021, 25, 101–118. [Google Scholar] [CrossRef]
- Zuo, J.P.; Wang, J.T.; Jiang, Y. Macro/meso failure behavior of surrounding rock in deep roadway and its control technology. Int. J. Coal Sci. Technol. 2019, 6, 301–319. [Google Scholar] [CrossRef]
- Yan, L.H.; Chang, J.C.; Shi, W.B.; Wang, T.; Qiao, L.Q.; Guo, Y.J.; Wang, H.D. Creep deformation characteristics and control technology in deep mine soft rock roadway. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 144. [Google Scholar] [CrossRef]
- Gao, H.; Xie, H.P.; Zhang, Z.T.; Lu, J.; Zhang, D.M.; Zhang, R.; Wu, M.Y. True triaxial energy evolution characteristics and failure mechanism of deep rock subjected to mining-induced stress. Int. J. Rock Mech. Min. Sci. 2024, 176, 105724. [Google Scholar] [CrossRef]
- Yang, Z.L.; Zhang, C.; Yang, D.H. Investigation of the time-dependent stability of a coal roadway under the deep high-stress condition based on the cvisc creep model. Sustainability 2023, 15, 12673. [Google Scholar] [CrossRef]
- Yang, K.Y.; Chen, C.X.; Sun, Y.L.; Xia, K.Z.; Wang, T.L. Mining-induced deformation for a haulage drift of the hanging wall at Jinshandian iron mine in China. Front. Earth Sci. 2023, 10, 998759. [Google Scholar] [CrossRef]
- Xie, S.L.; Zhou, H.W.; Jia, W.H.; Cao, Y.P.; Hu, X.F.; Yue, H.N.; Zhang, L. Effects of creep deformation on the spatial evolution of pore and fracture structures in coal under unloading confining pressure. Int. J. Rock Mech. Min. Sci. 2024, 174, 105658. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.M.; Gao, M.Z.; Jia, W.H.; Xie, S.L.; Hou, W.; Wang, X.Y.; Zhang, H. Spatio-temporal evolution of pore and fracture structures in coal induced by initial damage and creep behavior: A real-time NMR-based approach. Int. J. Min. Sci. Technol. 2024, 34, 1409–1425. [Google Scholar] [CrossRef]
- Li, X.F.; Wu, D.; Wu, M.X. Creep characteristics and fractional rheological model of granite under temperature and disturbance load coupling. Mech. Time-Depend. Mater. 2023, 28, 81–98. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, M.Z.; Zhang, R.; Peng, G.Y.; Wang, W.Y.; Li, A.Q. Study on the mechanical properties and mechanical response of coal mining at 1000 m or deeper. Rock Mech. Rock Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. J. China Coal Soc. 2019, 44, 1283–1305. [Google Scholar] [CrossRef]
- Ping, C.; Wen, Y.D.; Wang, Y.X.; Yuan, H.P.; Yuan, B.X. Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 2016, 75, 900. [Google Scholar] [CrossRef]
- Shan, R.L.; Bai, Y.; Ju, Y.; Han, T.Y.; Dou, H.Y.; Li, Z.L. Study on the triaxial unloading creep mechanical properties and damage constitutive model of red sandstone containing a single ice-filled flaw. Rock Mech. Rock Eng. 2021, 54, 833–855. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, H.; Zou, Q.L.; Li, C.B.; Chen, J.; Gao, R.B. Viscoelastic-plastic damage creep model for salt rock based on fractional derivative theory. Mech. Mater. 2020, 150, 103600. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.G.; Su, Y.H. A statistical damage constitutive model for softening behavior of rocks. Eng. Geol. 2012, 143–144, 1–17. [Google Scholar] [CrossRef]
- Zhou, H.W.; Jia, W.H.; Xie, S.L.; Su, T.; Zhang, L.; Ma, B.W.; Hou, W. A statistical damage-based fractional creep model for Beishan granite. Mech. Time-Depend. Mater. 2023, 27, 163–183. [Google Scholar] [CrossRef]
- Ran, H.; Guo, Y.; Feng, G.; Qi, T.; Du, X. Creep properties and resistivity-ultrasonic-AE responses of cemented gangue backfill column under high-stress area. Int. J. Min. Sci. Technol. 2021, 31, 401–412. [Google Scholar] [CrossRef]
- Ru, W.; Hu, S.; Zhou, A.; Luo, P.; Gong, H.; Zhang, C.; Zhou, X. Study on creep characteristics and nonlinear fractional-order damage constitutive model of weakly cemented soft rock. Rock Mech. Rock Eng. 2023, 56, 8061–8082. [Google Scholar] [CrossRef]
- Jia, W.H.; Zhou, H.W.; Xie, S.L.; Wang, Y.M.; Hu, X.F.; Zhang, L. Pore-pressure and stress-coupled creep behavior in deep coal: Insights from real-time NMR analysis. Int. J. Min. Sci. Technol. 2024, 34, 77–90. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Zou, Q.; Chen, J.; Liu, W.; Peng, K. Long-term strength determination and nonlinear creep damage constitutive model of salt rock based on multistage creep test: Implications for underground natural gas storage in salt cavern. Energy Sci. Eng. 2020, 8, 1592–1603. [Google Scholar] [CrossRef]
- Zheng, H.; Cai, Q.; Zhou, W.; Lu, X.; Li, M.; Qi, C.; Jiskani, I.M.; Zhang, Y. Creep behaviours of argillaceous sandstone: An experimental and modelling study. Appl. Sci. 2020, 10, 7602. [Google Scholar] [CrossRef]
- Chen, X.Y.; Wang, X.F.; Zhang, D.S.; Qin, D.D.; Wang, Y.; Wang, J.Y.; Chang, Z.C. Creep and control of the deep soft rock roadway (DSRR): Insights from laboratory testing and practice in Pingdingshan mining area. Rock Mech. Rock Eng. 2022, 55, 363–378. [Google Scholar] [CrossRef]
- Heeres, O.M.; Suiker, A.S.J.; de Borst, R. A comparison between the Perzyna viscoplastic model and the consistency viscoplastic model. Eur. J. Mech. A Solids 2002, 21, 1–12. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Ranjith, P.G. Damage model of coal under creep and triaxial compression. Int. J. Rock Mech. Min. Sci. 2015, 80, 337–345. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhou, H.W.; Cao, Z.G.; Rong, T.L.; Zhang, Y. Strong timeliness characteristics of coal and rock based on nonlinear rheological theory. J. China Coal Soc. 2021, 46, 713–720. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).