Analysis and Control of Rumor Propagation Model Considering Multiple Waiting Phases

Abstract

Rumors pose serious harm to society and exhibit a certain degree of repetitiveness. Existing rumor propagation models often have simple rules and neglect the repetitiveness of rumors. Therefore, we propose a new SCWIR rumor propagation model (susceptible, commented, waited, infected, recovered) by introducing the user’s repeated waiting behavior to simulate the potential for rumors to lie dormant and spread opportunistically. First, we present the dynamic equations of the model, then introduce three influencing factors to improve the model. Next, by solving for the equilibrium points and the basic reproduction number, we discuss the local and global stability of the rumor-free/rumor equilibrium points. Finally, we perform numerical simulations to analyze the effects of different factors on rumor propagation. The results show that the introduction of the multiple waiting mechanism helps simulate the repetitiveness of rumor propagation. Among the rumor suppression strategies, the effectiveness, from highest to lowest, is as follows: government intervention, information dissemination and popularization, and accelerated rumor value decay, with government intervention playing a decisive role. Information dissemination can reduce the intensity of rumors at the source.

1. Introduction

Rumors refer to statements deliberately fabricated by individuals that do not align with objective facts, and their propagation usually leads to certain negative impacts. The rapid development of the internet has not only made it easier for people to access information but has also intensified the spread of rumors. Rumor propagation tends to have a certain repetitiveness, with some individuals who spread rumors temporarily retreating and then becoming active again. Additionally, individuals who are easily swayed may enter a short-term observation and waiting phase when the public opinion environment improves. Existing research on rumor propagation has overlooked this aspect. Therefore, we will conduct an in-depth study on rumor propagation. In recent years, many scholars have proposed various effective methods for researching rumor propagation models [1,2]. At present, theoretical studies based on infectious disease models [3] and simulation studies based on complex networks [4] are common approaches for examining information diffusion mechanisms in the networks.

In the early stages of rumor dissemination research, it was observed that the spread of infectious diseases and rumors share similarities, as both involve propagation through individual interactions within a network. Scholars were inspired by infectious disease models and further applied them to rumor propagation, leading to models such as SI [5], SIS [6], and SIR [7]. Wang et al. [8] developed the SEIR rumor propagation model, introducing an exposed (E) state to represent individuals who are aware of the information but have not yet disseminated it. Wang et al. [9] developed the SEIRD model, categorizing individuals who believe rumors into different levels to simulate the dynamics of rumor spread. With the growth of internet users, the diversity of user relationships has become more apparent, and the role of group interactions in information dissemination is increasingly significant [10,11,12]. Wang et al. [13] introduced the PN-UHTR dynamic evolution model, integrating individual behavior with the information spread layer to examine the effects of various strategies on information spread within a hypernetwork. Zhang et al. [14] examined strategies for controlling information, including perceived value and timeliness, constructing the SE2IR information propagation model. Markovich et al. [15] used closeness centrality to evaluate node leadership. Nie et al. [16] examined user contact capacity, finding that higher contact capacity leads to greater information popularity. Gong et al. [17] combined the hypernetwork model to establish the UHIR model, exploring the effects of factors such as user trust and information characteristics on rumor propagation. Dong et al. [18] studied the impact of various communication channels and time delays on rumor spread.

In social networks, information browsing behavior is shaped by multiple factors, including public opinion, psychological influences, and personality traits [19], posing significant challenges to rumor control. During sudden events, not everyone makes immediate decisions; some individuals remain neutral, waiting for developments before taking action. Existing rumor propagation models insufficiently account for these factors, neglecting the presence of neutral individuals and their impact on rumor dissemination. To fill these gaps, we develop the SCWIR model, offering the following contributions:

(1)

Establish the initial model by introducing class C members (commenters), representing individuals who engage in commenting on the rumor event, and class W members (waiters), representing neutral waiting individuals who, after being exposed to the event, choose to observe the development of the situation.

(2)

Consider the nature of secondary infection, where neutral wait-and-see individuals may include those who temporarily awakened but later returned to believing the rumor. At the same time, the model also considers the varying rumor propagation abilities corresponding to different levels of belief in the rumor.

(3)

Introduce government intervention to guide the population in resisting rumors; incorporate information popularization rate and information timeliness to study their impacts on rumor propagation. Propose a debunking coefficient and an information timeliness coefficient to improve the SCWIR model.

(4)

Accelerate the decay of information value, strengthen government debunking efforts, and implement earlier interventions to ensure the basic reproduction number $R_0<1$, thereby suppressing rumors.

2. Preparation Work

2.1. SEIR Rumor Propagation Model

In rumor propagation, some users who know the information do not immediately spread it but still retain the ability to do so. To account for this, the SEIR model introduces exposed individuals (E). As shown in Figure 1, susceptible individuals become exposed with a probability $\alpha$ upon encountering the rumor. Exposed individuals transition to infected with a probability $\beta$, while infected individuals recover and become immune with a probability $\gamma$. The SEIR model initially considers the scenario where users adopt a neutral, wait-and-see attitude upon their first encounter with a rumor but overlooks the possibility of repeated waiting instances. Building on the SEIR model, this paper fully accounts for multiple waiting scenarios and introduces three influencing factors to analyze and control rumor propagation.

2.2. Comparative Analysis

In existing models, changes in rumor propagation are often unidirectional and irreversible, with insufficient consideration of user stance changes during rumor spread and overlooking the possibility of repeated waiting scenarios. To address these limitations, the SCWIR model offers the following advantages:

(1)

It accounts for the various possibilities of user stance transitions during rumor events. These transitions are reversible and multidirectional, comprehensively considering users shifting between commenting, believing, remaining neutral, or being indifferent upon encountering rumors. It also considers the situation where users wait multiple times for the development of the situation.

(2)

It examines the effect of factors such as information popularization rate and information timeliness on different user groups during rumor propagation. Additionally, it explores the role of government intervention in guiding user behavior.

(3)

It considers the different roles that neutral waiting, commenting, and forwarding groups of believers play in rumor propagation.

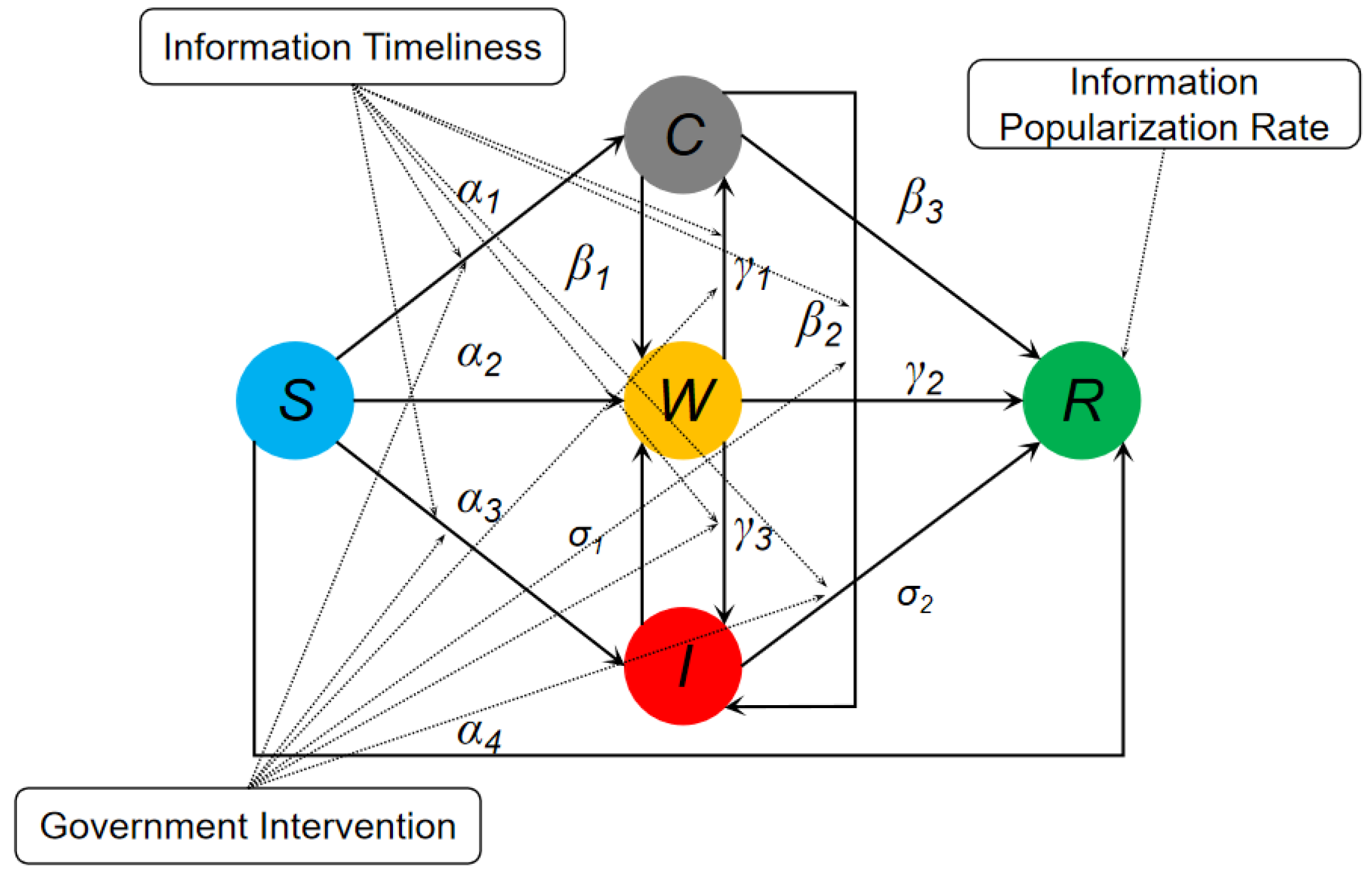
3. SCWIR Rumor Propagation Model

3.1. Model Description

This paper presents a rumor propagation model, SCWIR, which considers multiple waiting situations. It introduces Commented (C) individuals, who comment on the rumor, and Waited (W) individuals, who remain neutral and wait for the event to develop, including those who initially believed the rumor but later woke up and returned to a neutral waiting state. Furthermore, the model considers the varying propagation capabilities of commenters and spreaders based on their belief level in the rumor. The model classifies network users into five distinct states: susceptible (S), commenters (C), wait-and-see individuals (W), infected or spreaders (I), and recovered or immune (R).

To facilitate the establishment, analysis, and study of the model, the following assumptions are made:

(1)

Assume the total population is N, where the initial spreaders (I) account for one-thousandth of the population, and the remaining individuals are susceptible (S). During the propagation process, no new nodes are added or removed, and the total population N remains constant.

(2)

Wait-and-see individuals (W) include those who adopt a neutral, wait-and-see stance after first encountering the rumor, as well as those who, after initially believing the rumor, awaken and revert to waiting again. This means that wait-and-see individuals have the potential to believe the rumor a second time.

(3)

Commenters (C) and spreaders (I) occasionally spread rumors, causing the susceptible individuals they interact with to transition into commenters (C), wait-and-see individuals (W), spreaders (I), or immune individuals (R) with probabilities ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, and ${\alpha }_4$, respectively. Similarly, wait-and-see individuals (W) interacting with commenters (C) or spreaders (I) transition to commenters (C), immune individuals (R), or spreaders (I) with probabilities ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$, respectively.

(4)

Commenters (C) have a weaker spreading ability compared to spreaders (I), with the model assuming C’s ability is half that of I.

(5)

Commenters (C) who come into contact with spreaders (I) may transition into new spreaders with a probability ${\beta }_2$. Additionally, commenters may awaken and adopt a wait-and-see stance with a probability of ${\beta }_1$ or become immune to the rumor with a probability of ${\beta }_3$.

(6)

Spreaders (I) have the potential to awaken, transitioning to wait-and-see individuals (W) with a probability ${\sigma }_1$ or to immune individuals (R) with a probability ${\sigma }_2$.

(7)

Once individuals transition to immune (R), they no longer respond to the rumor event in any way. Building on these, the SCWIR model is developed, as shown in Figure 2. The parameters definitions are provided in

Table 1. Parameters definitions of the SCWIR model.

Parameter	Definition
${\alpha }_1$	Probability of susceptible users engaging in comments.
${\alpha }_2$	Probability of susceptible users adopting a wait-and-see approach.
${\alpha }_3$	Probability of susceptibles spreading
${\alpha }_4$	Probability of susceptibles being immune to the rumor.
${\beta }_1$	Probability of commenters adopting a wait-and-see approach.
${\beta }_3$	Probability of commenters spreading the rumor.
${\beta }_4$	Probability of commenters becoming immune.
${\gamma }_1$	Probability of waiting individuals engaging in comments.
${\gamma }_2$	Probability of waiting individuals recovering or becoming immune.
${\gamma }_3$	Probability of waiting individuals spreading the rumor.
${\sigma }_1$	Probability of spreaders adopting a wait-and-see approach.
${\sigma }_2$	Probability of spreaders recovering or becoming immune.

.

3.2. Propagation Dynamics Equation

In this subsection, building on the assumptions outlined in Section 3.1, the dynamic equations for the SCWIR model are formulated. S(t), C(t), W(t), I(t), and R(t) represent the proportions of susceptibles, commenters, wait-and-see individuals, spreaders, and immune individuals, respectively, at time t.

$${\displaystyle \frac{dS\left(t\right)}{dt}}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}S\left(t\right)C\left(t\right)-{\alpha }_{2}S\left(t\right)-\left({\alpha }_1+{\alpha }_3\right)S\left(t\right)I\left(t\right)-{\alpha }_{4}S\left(t\right)$$

(1)

$${\displaystyle \frac{dC\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_1}{2}}S\left(t\right)C\left(t\right)+{\alpha }_{1}S\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_1}{2}}W\left(t\right)C\left(t\right)+{\gamma }_{1}W\left(t\right)I\left(t\right)-{\beta }_{1}C\left(t\right)-{\beta }_{2}C\left(t\right)I\left(t\right)-{\beta }_{3}C\left(t\right)$$

(2)

$${\displaystyle \frac{dW\left(t\right)}{dt}}={\alpha }_{2}S\left(t\right)+{\beta }_{1}C\left(t\right)+{\sigma }_{1}I\left(t\right)-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}W\left(t\right)C\left(t\right)-{\gamma }_{2}W\left(t\right)-\left({\gamma }_1+{\gamma }_3\right)W\left(t\right)I\left(t\right)$$

(3)

$${\displaystyle \frac{dI\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_3}{2}}S\left(t\right)C\left(t\right)+{\alpha }_{3}S\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_3}{2}}W\left(t\right)C\left(t\right)+{\gamma }_{3}W\left(t\right)I\left(t\right)+{\beta }_{2}C\left(t\right)I\left(t\right)-{\sigma }_{1}I\left(t\right)-{\sigma }_{2}I\left(t\right)$$

(4)

$${\displaystyle \frac{dR\left(t\right)}{dt}}={\alpha }_{4}S\left(t\right)+{\gamma }_{2}W\left(t\right)+{\sigma }_{2}I\left(t\right)+{\beta }_{3}C\left(t\right)$$

(5)

$$\left\{\begin{array}{c}{\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4=1\hfill \\ {\beta }_1+{\beta }_2+{\beta }_3=1\hfill \\ {\gamma }_1+{\gamma }_2+{\gamma }_3=1\hfill \\ {\sigma }_1+{\sigma }_2=1\hfill \\ S\left(t\right)+C\left(t\right)+W\left(t\right)+I\left(t\right)+R\left(t\right)=1\hfill \\ {\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }_1,{\gamma }_2,{\gamma }_3,{\sigma }_1,{\sigma }_2>0\hfill \end{array}\right.$$

(6)

Equations (1)–(5) represent the changes in susceptible persons, commentators, observers, disseminators, and immune persons in rumor propagation. Equation (6) defines the constraints that the model must adhere to.

3.3. Quantitative Analysis of Influencing Factors

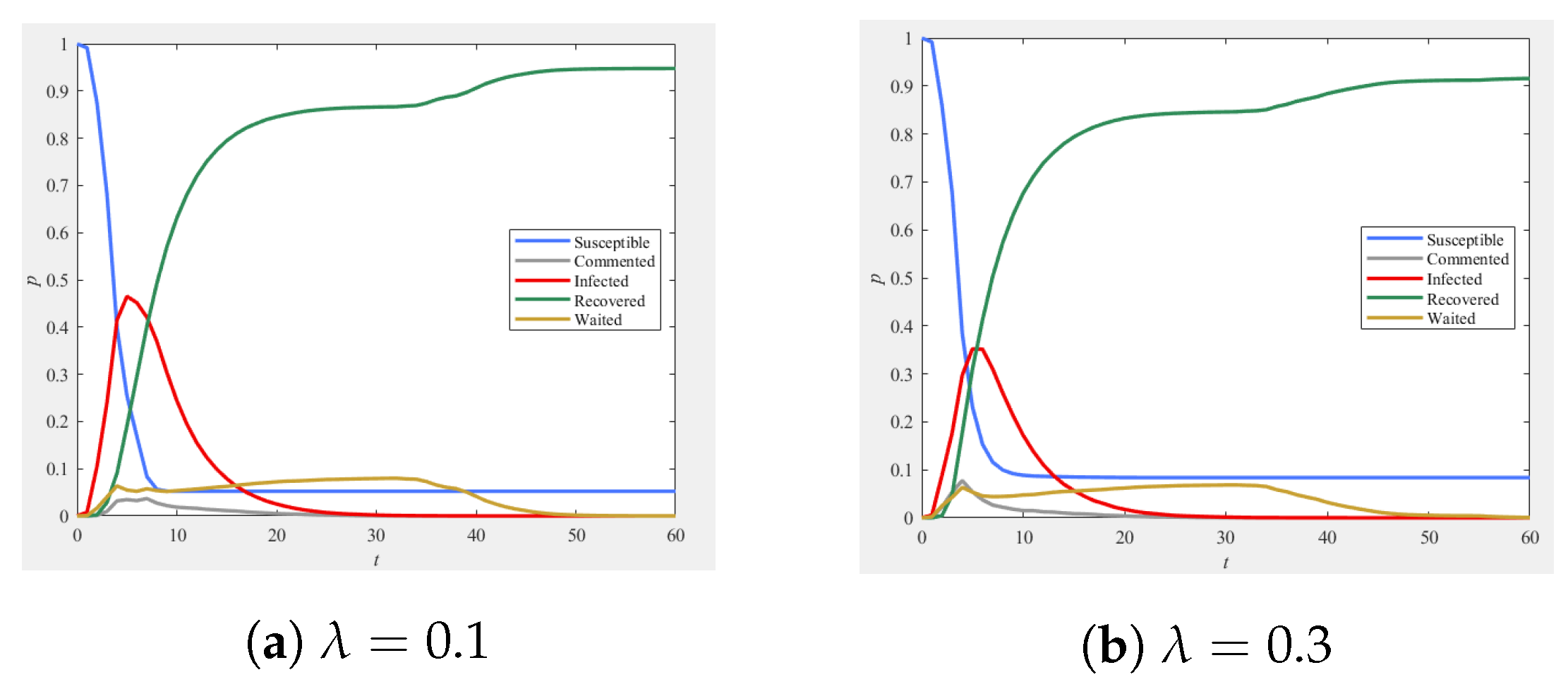
3.3.1. Information Timeliness

Different rumors demonstrate varying degrees of information timeliness. For example, COVID-19 rumors receive more attention than general flu rumors, and COVID-19 rumors tend to have a longer lifespan, with a slower decay in information value. The value of a rumor decreases over time, leading to a decline in its attention. There is a type of neuron model called LIF (Leaky Integrate-and-Fire) [20], where the membrane potential decreases over time. This characteristic is similar to the concept of information timeliness. The membrane potential’s time-dependent change can be expressed as

$$\tau {\displaystyle \frac{du}{dt}}=-u\left(t\right)$$

(7)

Here, $u\left(t\right)$ is the neuron’s membrane potential. Solving the differential equation yields

$$u\left(t\right)=c_0{e}^{-{\displaystyle \frac{1}{\tau }}t}$$

(8)

The decay of rumor information is analogized to the decay of a neuron’s membrane potential. When a rumor (similar to a stimulus) is initially spread, its “information potential” is high, attracting a lot of attention. Over time, its influence gradually weakens, much like how a neuron’s membrane potential naturally decays. This paper uses this analogy to simulate the impact of information timeliness decay on rumor propagation, defining the formula for measuring rumor information timeliness as follows:

$$l=l_0{e}^{-\lambda t}$$

(9)

Here, l is the information timeliness coefficient, representing the impact of information timeliness on rumor propagation. $l_0$ is the information’s initial value, t represents time, and $\lambda$ is the information decay coefficient, with $0<\lambda <1$. A larger $\lambda$ corresponds to a quicker decay in the value of information.

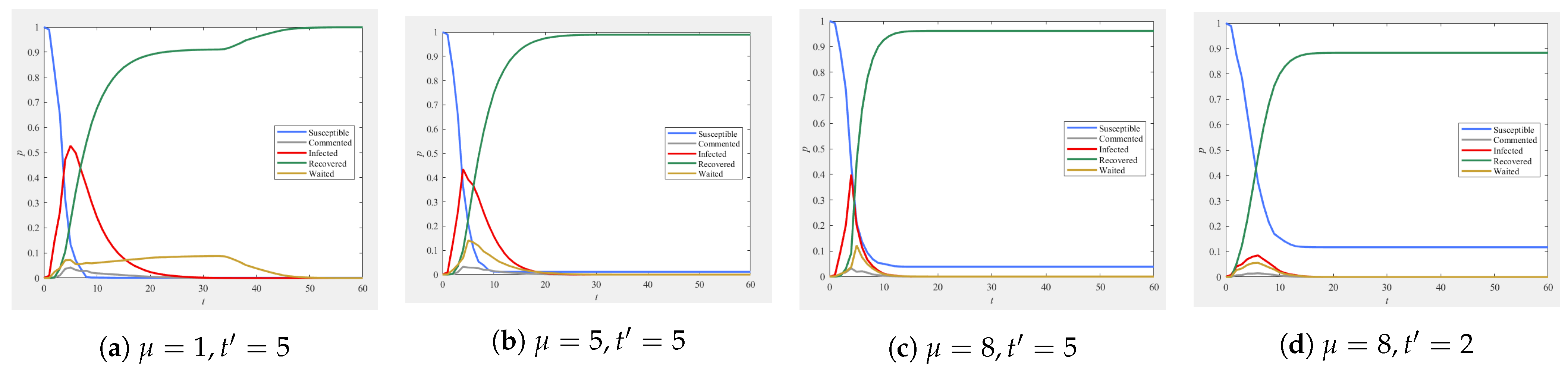
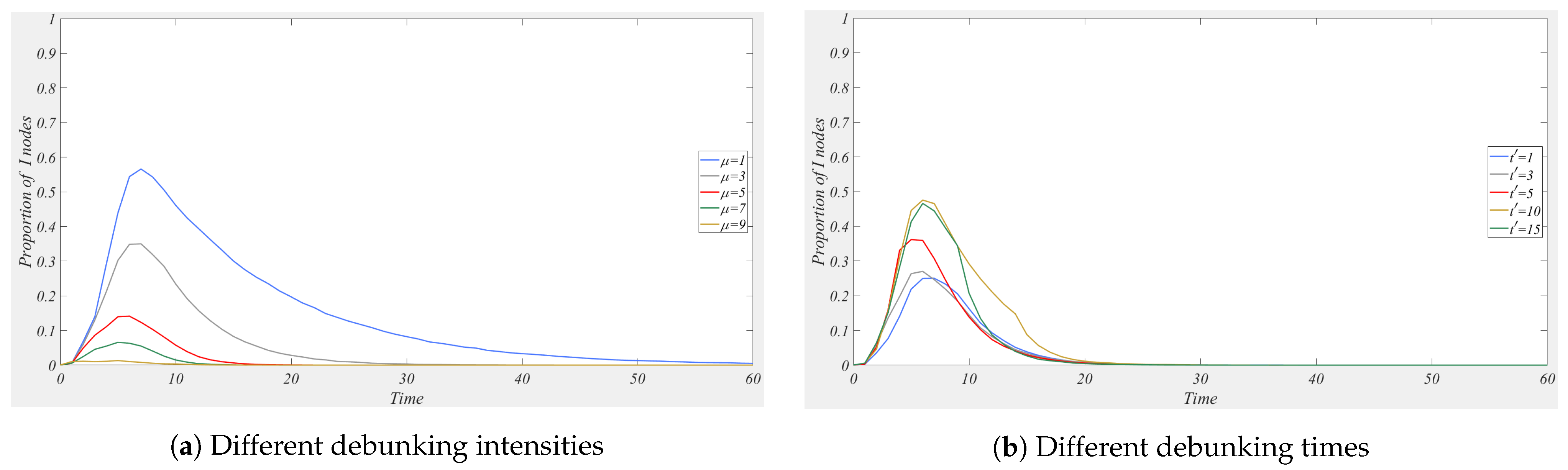
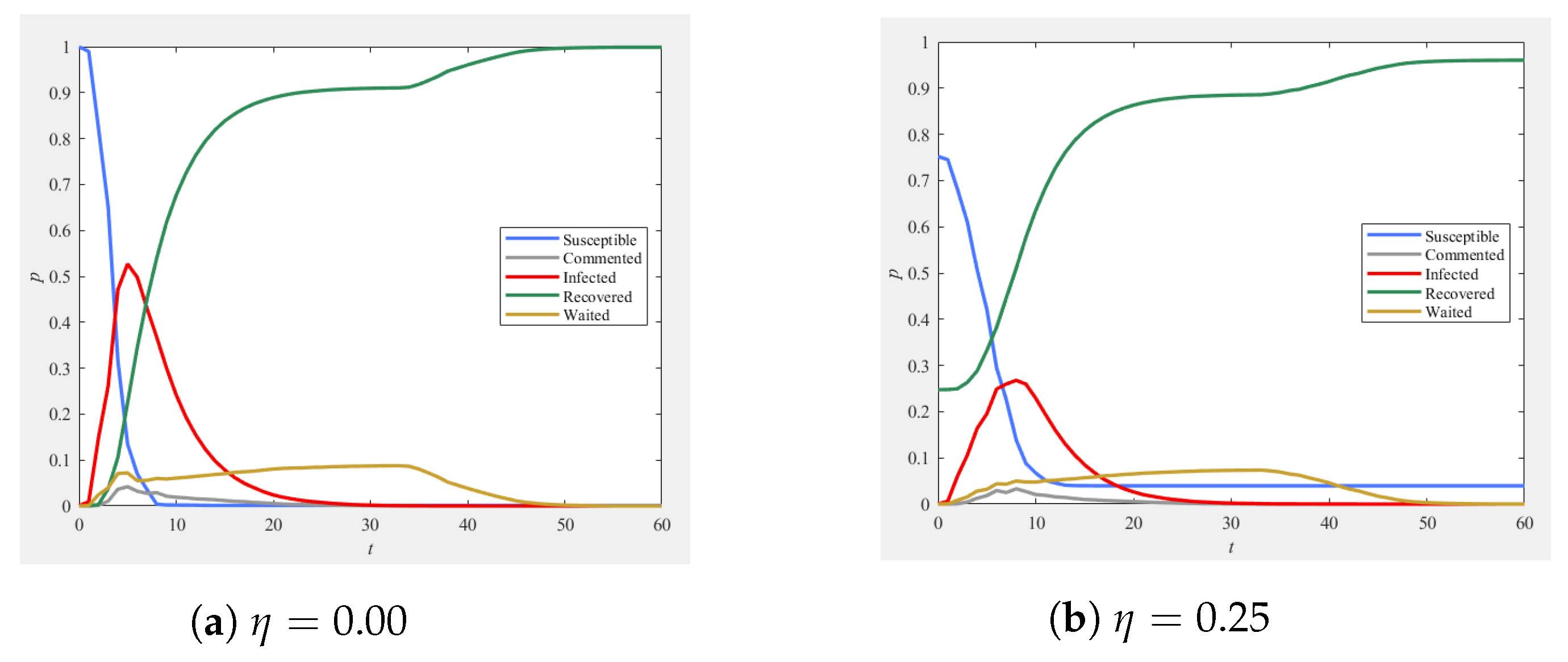
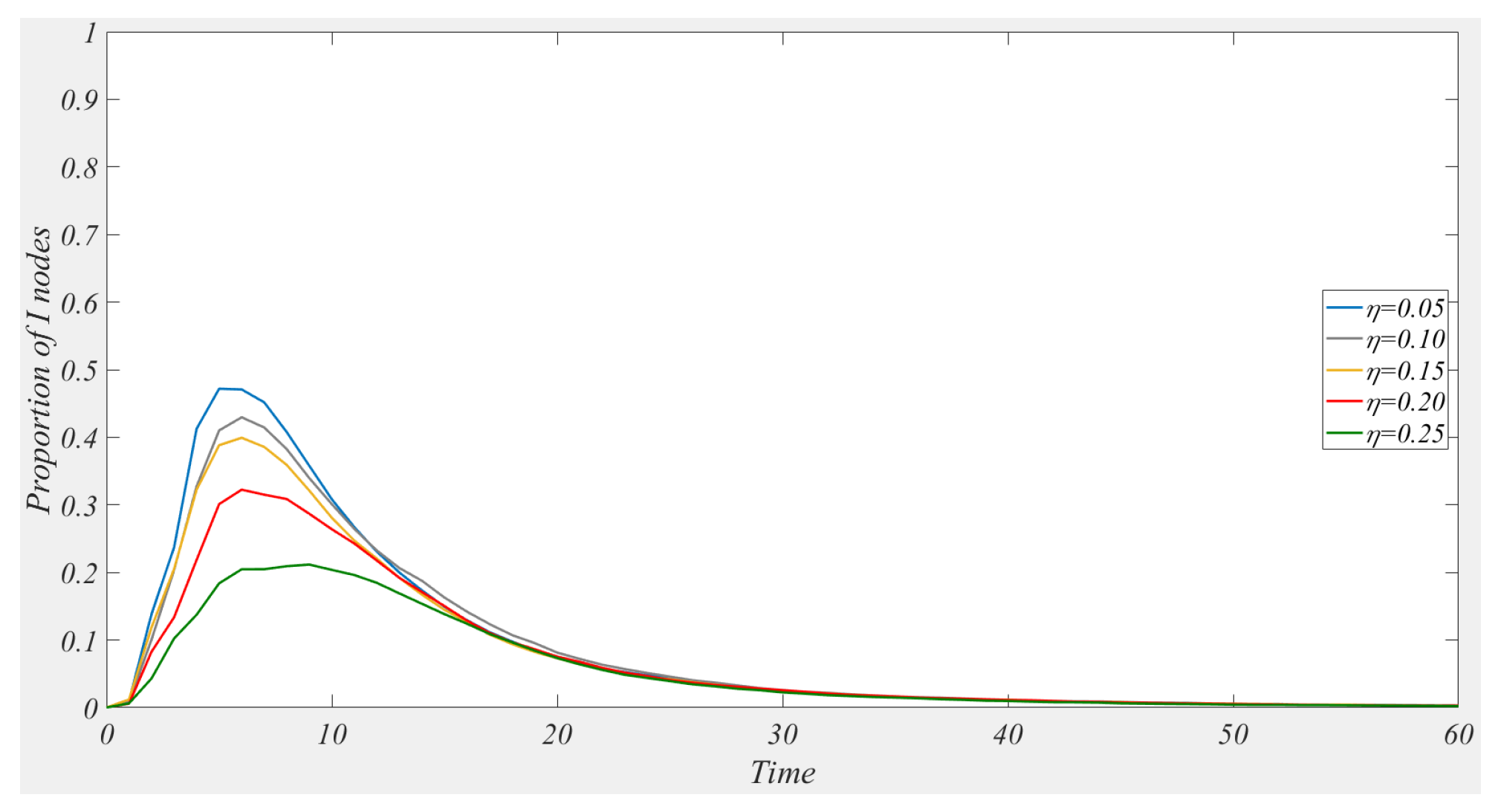
3.3.2. Government Intervention

Government debunking can significantly reduce rumor spread and aid in restoring the online public opinion landscape. Due to the limited number of network nodes, the impact of government intervention will also experience some decay. We adjust Equation (8) to simulate government debunking in order to suppress rumors. When the government begins to debunk rumors, a large number of users receive the debunking information, and the probability of rumor propagation decreases rapidly. However, some nodes with smaller degrees may still have difficulty accessing debunking messages, causing the decline in propagation probability to slow down. The formula for measuring government debunking is defined as follows:

$$g={\displaystyle \frac{1}{\mu }}{e}^{-{\displaystyle \frac{t}{t^{\prime }}}}$$

(10)

where g is the information diffusion coefficient after government intervention, t represents the current time, and $t^{\prime }$ represents the time when debunking begins. The earlier the debunking starts, the smaller the probability of rumor propagation. $\mu$ represents the strength of debunking, with $1\le \mu \le 10$. The greater the debunking strength, the smaller the likelihood of rumor propagation.

3.3.3. Information Popularization Rate

Actively popularizing positive and accurate information about rumors can raise the number of initially immune users, providing a certain level of prevention against rumor propagation. In this study, the information popularization rate is introduced, with the parameter $\eta$ representing the information popularization coefficient, indicating the scope of information popularization. At $t=0$, set

$$R\left(0\right)=\eta ,I\left(0\right)=⌊N/1000⌋,S\left(0\right)=1-R\left(0\right)-I\left(0\right),C\left(0\right)=0,W\left(0\right)=0$$

(11)

Here, $0\le \eta \le 1$, $R\left(0\right),I\left(0\right),S\left(0\right),C\left(0\right),$ and $W\left(0\right)$ represent the ratios of recovered, infected, susceptible, commented, and waited individuals in the social network at time $t=0$, respectively.

3.4. The Improved SCWIR Model

Considering the interventions from Section 3.3, the improved SCWIR model is shown in Figure 3. All references to the SCWIR model thereafter refer to the improved model. The propagation dynamics equations are updated as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)-{\alpha }_{2}S\left(t\right)-\left({\alpha }_1+{\alpha }_3\right)glS\left(t\right)I\left(t\right)-{\alpha }_{4}S\left(t\right)\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_1}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{1}glS\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_1}{2}}glW\left(t\right)C\left(t\right)+{\gamma }_{1}glW\left(t\right)I\left(t\right)-{\beta }_{1}C\left(t\right)-{\beta }_{2}glC\left(t\right)I\left(t\right)-{\beta }_{3}C\left(t\right)\hfill \\ {\displaystyle \frac{dW\left(t\right)}{dt}}={\alpha }_{2}S\left(t\right)+{\beta }_{1}C\left(t\right)+{\sigma }_{1}I\left(t\right)-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)-{\gamma }_{2}W\left(t\right)-\left({\gamma }_1+{\gamma }_3\right)glW\left(t\right)I\left(t\right)\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{3}glS\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)+{\gamma }_{3}glW\left(t\right)I\left(t\right)+{\beta }_{2}glC\left(t\right)I\left(t\right)-{\sigma }_{1}I\left(t\right)-{\sigma }_{2}I\left(t\right)\hfill \\ {\displaystyle \frac{dR\left(t\right)}{dt}}={\alpha }_{4}S\left(t\right)+{\gamma }_{2}W\left(t\right)+{\sigma }_{2}I\left(t\right)+{\beta }_{3}C\left(t\right)\hfill \end{array}\right.$$

(12)

4. Stability Analysis

In this chapter, we apply the next-generation matrix method to calculate the basic reproduction number and use Lyapunov theory to analyze the stability of the system (12) at the rumor-free/rumor equilibrium points. Since immune individuals no longer respond to the rumor, they do not disrupt the system’s equilibrium. At the same time, when the number of immune individuals increases, it indicates that there are still individuals in the system who believe the rumor. We simplify Equation (12) to

$$\left\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)-{\alpha }_{2}S\left(t\right)-\left({\alpha }_1+{\alpha }_3\right)glS\left(t\right)I\left(t\right)-{\alpha }_{4}S\left(t\right)\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_1}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{1}glS\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_1}{2}}glW\left(t\right)C\left(t\right)+{\gamma }_{1}glW\left(t\right)I\left(t\right)-{\beta }_{1}C\left(t\right)-{\beta }_{2}glC\left(t\right)I\left(t\right)-{\beta }_{3}C\left(t\right)\hfill \\ {\displaystyle \frac{dW\left(t\right)}{dt}}={\alpha }_{2}S\left(t\right)+{\beta }_{1}C\left(t\right)+{\sigma }_{1}I\left(t\right)-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)-{\gamma }_{2}W\left(t\right)-\left({\gamma }_1+{\gamma }_3\right)glW\left(t\right)I\left(t\right)\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}}={\displaystyle \frac{{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{3}glS\left(t\right)I\left(t\right)+{\displaystyle \frac{{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)+{\gamma }_{3}glW\left(t\right)I\left(t\right)+{\beta }_{2}glC\left(t\right)I\left(t\right)-{\sigma }_{1}I\left(t\right)-{\sigma }_{2}I\left(t\right)\hfill \end{array}\right.$$

(13)

4.1. Stability Analysis of the Rumor-Free Equilibrium Point

First, it is necessary to determine the situation of the model at the rumor-free equilibrium point, where the rate of change in the state densities is zero. It is easy to see that the rumor-free equilibrium point of Equation (13) is $E_0(\varpi ,0,0,0)$, where it represents the density of susceptibles in the absence of commenters, waiters, and spreaders.

The basic reproduction number is a threshold that determines whether information can propagate within a system. Driessche developed a method for determining the basic reproduction number [21]. The system is divided into n compartments, with the compartments of infected individuals grouped and the compartments of uninfected individuals in another group. Let $x_i\left(t\right)$ represent the compartment containing infected individuals, then

$$x_i\left(t\right)=f_i\left(t\right)-v_i\left(t\right)$$

(14)

In the equation, $f_i\left(t\right)$ represents the count of newly infected individuals, and $v_i\left(t\right)=v_i^{-}\left(t\right)-v_i^{+}\left(t\right)$, where $v_i^{+}\left(t\right)$ represents the count of individuals moving into compartment i from other compartments, and $v_i^{-}\left(t\right)$ represents the number of individuals moving out of compartment i. Driessche proved that if F and V denote the Jacobian matrices of f and v at the equilibrium point without disease $E_0$, and $F^{\prime }$ and $V^{\prime }$ are the matrix forms of $f_i\left(t\right)$ and $v_i\left(t\right)$, then the fundamental reproduction number $R_0$ of the system can be written as

$$R_0=\rho \left(F{V}^{-1}\right)$$

(15)

In the equation, $F{V}^{-1}$ is the next generation matrix, and $\rho$ represents the spectral radius.

In the SCWIR model, moving from the S state to the C, W, or I state represents individuals who have all been exposed to the rumor and are considered infected individuals. If they transition to the R state, they are considered immune to the rumor, thus belonging to the immune group. Therefore, in this system, the infected compartments are the Commented state (C), Waited state (W), and Infected state (I). Based on the concepts of the next-generation matrix, we can derive

$$F^{\prime }=\left[\begin{array}{c}{\displaystyle \frac{{\alpha }_1}{2}}glS\left(t\right)C\left(t\right)\\ {\alpha }_{2}S\left(t\right)\\ {\displaystyle \frac{{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{3}glS\left(t\right)I\left(t\right)\end{array}\right]$$

(16)

$$V^{\prime }=\left[\begin{array}{c}-{\displaystyle \frac{{\gamma }_1}{2}}glW\left(t\right)C\left(t\right)-{\gamma }_{1}glW\left(t\right)I\left(t\right)+{\beta }_{2}glC\left(t\right)I\left(t\right)+{\beta }_{3}C\left(t\right)\\ {\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)+{\gamma }_{2}W\left(t\right)+({\gamma }_1+{\gamma }_3)glW\left(t\right)I\left(t\right)\\ -{\displaystyle \frac{{\gamma }_3}{2}}glW\left(t\right)C\left(t\right)-{\gamma }_{3}glW\left(t\right)I\left(t\right)-{\beta }_{2}glC\left(t\right)I\left(t\right)+{\sigma }_{2}I\left(t\right)\end{array}\right]$$

(17)

Calculate its Jacobian matrix, and obtain

$$F=\left[\begin{array}{ccc}{\displaystyle \frac{{\alpha }_1}{2}}glS\left(t\right)& 0& 0\\ 0& 0& 0\\ {\displaystyle \frac{{\alpha }_3}{2}}glS\left(t\right)& 0& {\alpha }_{3}glS\left(t\right)\end{array}\right]$$

(18)

$$V=\left[\begin{array}{ccc}-{\displaystyle \frac{{\gamma }_1}{2}}glW\left(t\right)+{\beta }_{2}glI\left(t\right)+{\beta }_3& -{\displaystyle \frac{{\gamma }_1}{2}}glC\left(t\right)-{\gamma }_{1}glI\left(t\right)& -{\gamma }_{1}glW\left(t\right)+{\beta }_{2}glC\left(t\right)\\ {\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glW\left(t\right)& {\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glC\left(t\right)+{\gamma }_2+({\gamma }_1+{\gamma }_3)glI\left(t\right)& ({\gamma }_1+{\gamma }_3)glW\left(t\right)\\ -{\displaystyle \frac{{\gamma }_3}{2}}glW\left(t\right)-{\beta }_{2}glI\left(t\right)& -{\displaystyle \frac{{\gamma }_3}{2}}glC\left(t\right)-{\gamma }_{3}glI\left(t\right)& -{\gamma }_{1}glW\left(t\right)-{\beta }_{2}glC\left(t\right)+{\sigma }_2\end{array}\right]$$

(19)

Substitute the equilibrium point $E_0$ into the equation.

$$F=\left[\begin{array}{ccc}{\displaystyle \frac{{\alpha }_1}{2}}gl\varpi & 0& 0\\ 0& 0& 0\\ {\displaystyle \frac{{\alpha }_3}{2}}gl\varpi & 0& {\alpha }_{3}gl\varpi \end{array}\right]$$

(20)

$$V=\left[\begin{array}{ccc}{\beta }_3& 0& 0\\ 0& {\gamma }_2& 0\\ 0& 0& {\sigma }_2\end{array}\right]$$

(21)

The next generation matrix is

$$F{V}^{-1}=\left[\begin{array}{ccc}{\displaystyle \frac{{\alpha }_{1}gl\varpi }{2{\beta }_3}}& 0& 0\\ 0& 0& 0\\ {\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\beta }_3}}& 0& {\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\sigma }_2}}\end{array}\right]$$

(22)

Calculate its eigenvalues:

$${\lambda }_1={\displaystyle \frac{{\alpha }_{1}gl\varpi }{2{\beta }_3}},{\lambda }_2={\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\sigma }_2}},{\lambda }_3=0$$

(23)

According to the constraint conditions (6) and the parameter definitions, it is known that users who only comment have a higher probability of recovery, ${\beta }_3>{\sigma }_2$ and ${\displaystyle \frac{{\alpha }_1}{2}}<{\alpha }_3$, thus ${\lambda }_1<{\lambda }_2$. The fundamental reproduction number is given by

$$R_0=max({\lambda }_1,{\lambda }_2,{\lambda }_3)={\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\sigma }_2}}={\displaystyle \frac{l_0{\alpha }_3\varpi }{\mu \left({\sigma }_2\right)e^{\frac{1+\lambda t^{\prime }}{t^{\prime }}t}}}$$

(24)

4.1.1. Local Stability Analysis of the Rumor-Free Equilibrium Point

Theorem 1.

For the dynamical system (13), when $R_0<1$, the system is locally asymptotically stable at the rumor-free equilibrium point $E_0$. When $R_0>1$, the system is unstable at the rumor-free equilibrium point $E_0$.

Proof of Theorem 1.

We analyze the local stability of the model by calculating the Jacobian matrix of the system at the rumor-free equilibrium point $E_0$. Let

$${\Theta }^S\left(t\right)={\displaystyle \frac{dS\left(t\right)}{dt}},{\Theta }^C\left(t\right)={\displaystyle \frac{dC\left(t\right)}{dt}},{\Theta }^W\left(t\right)={\displaystyle \frac{dW\left(t\right)}{dt}},{\Theta }^I\left(t\right)={\displaystyle \frac{dI\left(t\right)}{dt}}$$

(25)

$$J={\displaystyle \frac{\partial ({\Theta }^S\left(t\right),{\Theta }^C\left(t\right),{\Theta }^W\left(t\right),{\Theta }^I\left(t\right))}{\partial \left(S\right(t),C(t),W(t),I(t)}}$$

(26)

The calculation yields

$$J=\left[\begin{array}{cccc}{a}_{11}& a_{12}& 0& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& 0\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]$$

(27)

where

$$\begin{array}{cc}\hfill & a_{11}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}glC\left(t\right)-{\alpha }_2-({\alpha }_1+{\alpha }_3)glI\left(t\right)-{\alpha }_4\hfill \\ \hfill & a_{12}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}glS\left(t\right)\hfill \\ \hfill & a_{14}=-({\alpha }_1+{\alpha }_3)glS\left(t\right)\hfill \\ \hfill & a_{21}={\displaystyle \frac{{\alpha }_1}{2}}glC\left(t\right)+{\alpha }_{1}glI\left(t\right)\hfill \\ \hfill & a_{22}={\displaystyle \frac{{\alpha }_1}{2}}glS\left(t\right)+{\displaystyle \frac{{\gamma }_1}{2}}glW\left(t\right)-{\beta }_1-{\beta }_{2}glI\left(t\right)-{\beta }_3\hfill \\ \hfill & a_{23}={\displaystyle \frac{{\gamma }_1}{2}}glC\left(t\right)+{\gamma }_{1}glI\left(t\right)\hfill \\ \hfill & a_{24}={\alpha }_{1}glS\left(t\right)+{\gamma }_{1}glW\left(t\right)-{\beta }_{2}glC\left(t\right)\hfill \\ \hfill & a_{31}={\alpha }_2\hfill \\ \hfill & a_{32}={\beta }_1-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glW\left(t\right)\hfill \\ \hfill & a_{33}=-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}glC\left(t\right)-{\gamma }_2-({\gamma }_1+{\gamma }_3)glI\left(t\right)\hfill \\ \hfill & a_{41}={\displaystyle \frac{{\alpha }_3}{2}}glC\left(t\right)+{\alpha }_{3}glI\left(t\right)\hfill \\ \hfill & a_{42}={\displaystyle \frac{{\alpha }_3}{2}}glS\left(t\right)+{\displaystyle \frac{{\gamma }_3}{2}}glW\left(t\right)+{\beta }_{2}glI\left(t\right)\hfill \\ \hfill & a_{43}={\displaystyle \frac{{\gamma }_3}{2}}glC\left(t\right)+{\gamma }_{3}glI\left(t\right)\hfill \\ \hfill & a_{44}={\alpha }_{3}glS\left(t\right)+{\gamma }_{3}glW\left(t\right)+{\beta }_{2}glC\left(t\right)-{\sigma }_2\hfill \end{array}$$

(28)

Substitute $E_0$ and solve for its characteristic equation.

$$|J\left(E_0\right)-\lambda E|=\left|\begin{array}{cccc}-{\alpha }_2-{\alpha }_4-\lambda & -{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}gl\varpi & -({\alpha }_1+{\alpha }_3)gl\varpi & 0\\ 0& {\displaystyle \frac{{\alpha }_1}{2}}gl\varpi -{\beta }_3-\lambda & 0& {\alpha }_{1}gl\varpi \\ 0& 0& -{\gamma }_2-\lambda & 0\\ 0& 0& 0& {\alpha }_{3}gl\varpi -{\sigma }_2-\lambda \end{array}\right|=0$$

(29)

The eigenvalues of the Jacobian matrix $J\left(E_0\right)$ are obtained as follows:

$${\lambda }_1=-{\alpha }_2-{\alpha }_4,{\lambda }_2={\displaystyle \frac{{\alpha }_1}{2}}gl\varpi -{\beta }_3,{\lambda }_3=-{\gamma }_2,{\lambda }_4={\alpha }_{3}gl\varpi -{\sigma }_2$$

(30)

Clearly, ${\lambda }_1<0$ and ${\lambda }_3<0$, so it is only necessary to determine the sign of ${\lambda }_2$ and ${\lambda }_4$. According to the parameter definitions and concepts, it is known that ${\displaystyle \frac{{\alpha }_1}{2}}<{\alpha }_3$, and under normal conditions, the probability of recovery for commenters is greater than that for spreaders, i.e., ${\beta }_3>{\sigma }_2$, so ${\lambda }_2<{\lambda }_4$.

$${\lambda }_4={\alpha }_{3}gl\varpi -{\sigma }_2={\sigma }_2({\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\sigma }_2}}-1)={\sigma }_2(R_0-1)$$

(31)

Since ${\sigma }_2>0$, when $R_0<1$, ${\lambda }_2<0$ and ${\lambda }_4<0$ hold, and all eigenvalues of Equation (29) are negative. Therefore, the system (13) is locally stable at the rumor-free equilibrium point $E_0$. Additionally, when $R_0>1$, the eigenvalue ${\lambda }_4$ becomes positive, and the system is unstable at the rumor-free equilibrium point $E_0$. □

4.1.2. Global Stability Analysis of the Rumor-Free Equilibrium Point

Theorem 2.

For the dynamical system (13), when the fundamental reproduction number $R_0<1$, the system is globally stable at the rumor-free equilibrium point: $E_0$.

Proof of Theorem 2.

Define the Lyapunov function of the system (13) as shown in Equation (32).

$$V\left(t\right)=C\left(t\right)+W\left(t\right)+I\left(t\right),V\left(t\right)\ge 0$$

(32)

Take the derivative of both sides.

$$\begin{array}{cc}\hfill {\displaystyle \frac{dV\left(t\right)}{dt}}& ={\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}glS\left(t\right)C\left(t\right)+{\alpha }_{3}glS\left(t\right)I\left(t\right)+{\alpha }_{2}S\left(t\right)-{\sigma }_{2}I\left(t\right)-{\beta }_{3}C\left(t\right)-{\gamma }_{2}W\left(t\right)\hfill \\ \hfill & \le 3{\alpha }_{3}glS\left(t\right)I\left(t\right)-{\sigma }_{2}I\left(t\right)-{\beta }_{3}C\left(t\right)-{\gamma }_{2}W\left(t\right)\hfill \\ \hfill & \le 3{\alpha }_{3}gl\varpi I\left(t\right)-3{\sigma }_{2}I\left(t\right)\hfill \\ \hfill & =3{\sigma }_2({\displaystyle \frac{{\alpha }_{3}gl\varpi }{{\sigma }_2}}-1)I\left(t\right)\hfill \\ \hfill & =3{\sigma }_2(R_0-1)I\left(t\right)\hfill \end{array}$$

(33)

When $R_0<1$, ${\displaystyle \frac{dV\left(t\right)}{dt}}<0$ holds. ${\displaystyle \frac{dV\left(t\right)}{dt}}=0$ holds only at the rumor-free equilibrium point $E_0(\varpi ,0,0,0)$. According to the Lyapunov theorem, it can be inferred that when $R_0<1$, the system is globally asymptotically stable at the rumor-free equilibrium point $E_0$. □

4.2. Stability Analysis of the Rumor Equilibrium Point

In this subsection, we primarily analyze the stability of the system at the rumor equilibrium point. We first assume that there exists a rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$, and the dynamical system (13) satisfies the following equation

$$\left\{\begin{array}{c}1-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}gl{S}^{*}{C}^{*}-{\alpha }_2{S}^{*}-({\alpha }_1+{\alpha }_3)gl{S}^{*}{I}^{*}-{\alpha }_4{S}^{*}=0\hfill \\ {\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}{C}^{*}+{\alpha }_{1}gl{S}^{*}{I}^{*}+{\displaystyle \frac{{\gamma }_1}{2}}gl{W}^{*}{C}^{*}+{\gamma }_{1}gl{W}^{*}{I}^{*}-{\beta }_1{C}^{*}-{\beta }_{2}gl{C}^{*}{I}^{*}-{\beta }_3{C}^{*}=0\hfill \\ {\alpha }_2{S}^{*}+{\beta }_1{C}^{*}-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}{C}^{*}-{\gamma }_2{W}^{*}-({\gamma }_1+{\gamma }_3)gl{W}^{*}{I}^{*}=0\hfill \\ {\displaystyle \frac{{\alpha }_3}{2}}gl{S}^{*}{C}^{*}+{\alpha }_{3}gl{S}^{*}{I}^{*}+{\displaystyle \frac{{\gamma }_3}{2}}gl{W}^{*}{C}^{*}+{\gamma }_{3}gl{W}^{*}{I}^{*}+{\beta }_{2}gl{C}^{*}{I}^{*}-{\sigma }_1{I}^{*}-{\sigma }_2{I}^{*}=0\hfill \end{array}\right.$$

(34)

Thus, we obtain

$$\begin{array}{c}{I}^{*}={\displaystyle \frac{{\alpha }_3{\gamma }_3{\beta }_{2}gl}{(\frac{3{\alpha }_3}{2}+\frac{3{\gamma }_3}{2}+{\beta }_2)gl+{\sigma }_1+{\sigma }_2}}\hfill \\ S^{*}={\displaystyle \frac{1}{{\alpha }_2+\frac{3({\alpha }_1+{\alpha }_3)}{2}gl{I}^{*}+{\alpha }_4}}\hfill \\ C^{*}={\displaystyle \frac{{\alpha }_1{\gamma }_1{\beta }_{2}gl{I}^{*}+{\alpha }_1}{(\frac{3({\alpha }_1+{\gamma }_1)}{2}-{\beta }_2)gl{I}^{*}+{\beta }_1+{\beta }_3}}\hfill \\ W^{*}={\displaystyle \frac{{\alpha }_2{\beta }_1{\sigma }_{1}gl{I}^{*}+{\alpha }_2{\beta }_1+{\beta }_1{\sigma }_1}{{\gamma }_2+\frac{3({\gamma }_1+{\gamma }_3)}{2}gl{I}^{*}}}\hfill \end{array}$$

(35)

Based on the above equation, we can calculate the expression for $R^{*}$. Therefore, there exists a rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$.

4.2.1. Local Stability Analysis of the Rumor Equilibrium Point

Theorem 3.

If $H\left(I^{*}\right)>0,G\left(I^{*}\right)>0,K\left(I^{*}\right)>0$ and $H\left(I^{*}\right)G\left(I^{*}\right)>K\left(I^{*}\right)$, then the system (13) is locally stable at the rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$.

Proof of Theorem 3.

Obtain the Jacobian matrix of the system at the rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$.

$$J\left(E_1^{*}\right)=\left[\begin{array}{cccc}{a}_{11}& a_{12}& 0& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& 0\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]$$

(36)

where

$$\begin{array}{cc}\hfill & a_{11}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}gl{C}^{*}-{\alpha }_2-({\alpha }_1+{\alpha }_3)gl{I}^{*}-{\alpha }_4\hfill \\ \hfill & a_{12}=-{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}gl{S}^{*}\hfill \\ \hfill & a_{14}=-({\alpha }_1+{\alpha }_3)gl{S}^{*}\hfill \\ \hfill & a_{21}={\displaystyle \frac{{\alpha }_1}{2}}gl{C}^{*}+{\alpha }_{1}gl{I}^{*}\hfill \\ \hfill & a_{22}={\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}+{\displaystyle \frac{{\gamma }_1}{2}}gl{W}^{*}-{\beta }_1-{\beta }_{2}gl{I}^{*}-{\beta }_3\hfill \\ \hfill & a_{23}={\displaystyle \frac{{\gamma }_1}{2}}gl{C}^{*}+{\gamma }_{1}gl{I}^{*}\hfill \\ \hfill & a_{24}={\alpha }_{1}gl{S}^{*}+{\gamma }_{1}gl{W}^{*}-{\beta }_{2}gl{C}^{*}\hfill \\ \hfill & a_{31}={\alpha }_2\hfill \\ \hfill & a_{32}={\beta }_1-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}\hfill \\ \hfill & a_{33}=-{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{C}^{*}-{\gamma }_2-({\gamma }_1+{\gamma }_3)gl{I}^{*}\hfill \\ \hfill & a_{41}={\displaystyle \frac{{\alpha }_3}{2}}gl{C}^{*}+{\alpha }_{3}gl{I}^{*}\hfill \\ \hfill & a_{42}={\displaystyle \frac{{\alpha }_3}{2}}gl{S}^{*}+{\displaystyle \frac{{\gamma }_3}{2}}gl{W}^{*}+{\beta }_{2}gl{I}^{*}\hfill \\ \hfill & a_{43}={\displaystyle \frac{{\gamma }_3}{2}}gl{C}^{*}+{\gamma }_{3}gl{I}^{*}\hfill \\ \hfill & a_{44}={\alpha }_{3}gl{S}^{*}+{\gamma }_{3}gl{W}^{*}+{\beta }_{2}gl{C}^{*}-{\sigma }_2\hfill \end{array}$$

(37)

Its characteristic equation is

$$(\lambda +d)({\lambda }^3+H\left(I^{*}\right){\lambda }^2+G\left(I^{*}\right)\lambda +K\left(I^{*}\right))=0$$

(38)

$$\begin{array}{cc}\hfill & H\left(I^{*}\right)=a+b+c\hfill \\ \hfill & G\left(I^{*}\right)=ab+d+e\hfill \\ \hfill & K\left(I^{*}\right)=a+ab+de+c\hfill \end{array}$$

(39)

where

$$\begin{array}{cc}\hfill & a=({\alpha }_1+{\gamma }_1-{\beta }_2)gl{I}^{*},b={\displaystyle \frac{({\gamma }_1+{\gamma }_3)gl{I}^{*}+{\gamma }_2}{{\gamma }_{1}gl{I}^{*}+{\beta }_1}},c={\displaystyle \frac{-({\alpha }_3+{\gamma }_3+{\beta }_2)gl{I}^{*}-{\sigma }_2}{{\gamma }_{3}gl-{\sigma }_1}}\hfill \\ \hfill & d={\displaystyle \frac{({\alpha }_1+{\gamma }_1-{\sigma }_1)gl{I}^{*}+{\beta }_1}{2{\alpha }_{3}gl{I}^{*}+{\gamma }_3}},e={\displaystyle \frac{{\alpha }_{2}gl{I}^{*}-{\alpha }_4}{({\beta }_3+{\gamma }_3)gl{I}^{*}}}\hfill \end{array}$$

(40)

Thus, we obtain ${\lambda }_1=-d<0$, and

$${\lambda }^3+H\left(I^{*}\right){\lambda }^2+G\left(I^{*}\right)\lambda +K\left(I^{*}\right)=0$$

(41)

According to the Routh–Hurwitz criterion, if $H\left(I^{*}\right)>0,G\left(I^{*}\right)>0,K\left(I^{*}\right)>0$ and $H\left(I^{*}\right)G\left(I^{*}\right)>K\left(I^{*}\right)$, then ${\lambda }^2,{\lambda }^3$, and ${\lambda }^4$ have negative real parts. Therefore, the system (13) is locally stable at the rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$. □

4.2.2. Global Stability Analysis of the Rumor Equilibrium Point

Theorem 4.

For the dynamical system (13), if there exists a Lyapunov function $V\left(t\right)>0$ $(t\ne 0),V\left(0\right)=0$, and ${\displaystyle \frac{dV\left(t\right)}{dt}}<0$, then the system is globally stable at the rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$.

Proof of Theorem 4.

Let $g\left(a\right)=a-1-lna$, where a > 0 and $g\left(a\right)\ge 0$. We construct the Lyapunov function as follows:

$$V\left(t\right)=a{S}^{*}g\left({\displaystyle \frac{S\left(t\right)}{S^{*}}}\right)+b{C}^{*}g\left({\displaystyle \frac{C\left(t\right)}{C^{*}}}\right)+c{W}^{*}g\left({\displaystyle \frac{W\left(t\right)}{W^{*}}}\right)+d{I}^{*}g\left({\displaystyle \frac{I\left(t\right)}{I^{*}}}\right)$$

(42)

Let $x={\displaystyle \frac{S\left(t\right)}{S^{*}}},y={\displaystyle \frac{C\left(t\right)}{C^{*}}},z={\displaystyle \frac{W\left(t\right)}{W^{*}}},h={\displaystyle \frac{I\left(t\right)}{I^{*}}}$, a, b, c, and d be positive constants. Taking the derivative, we obtain

$${\displaystyle \frac{dV\left(t\right)}{dt}}=a(1-{\displaystyle \frac{1}{x}}){\displaystyle \frac{dS\left(t\right)}{dt}}+b(1-{\displaystyle \frac{1}{y}}){\displaystyle \frac{dC\left(t\right)}{dt}}+c(1-{\displaystyle \frac{1}{z}}){\displaystyle \frac{dW\left(t\right)}{dt}}+d(1-{\displaystyle \frac{1}{h}}){\displaystyle \frac{dI\left(t\right)}{dt}}$$

(43)

Substituting, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{dV\left(t\right)}{dt}}& =-(b{\displaystyle \frac{{\alpha }_1+{\alpha }_3}{2}}gl{S}^{*}{C}^{*}+d({\alpha }_1+{\alpha }_3)gl{S}^{*}{I}^{*})g\left(x\right)-(c{\alpha }_2+a{\alpha }_4)g\left({\displaystyle \frac{1}{x}}\right)\hfill \\ \hfill & +(d{\beta }_{2}gl{C}^{*}{I}^{*}+c{\beta }_1{C}^{*}-a{\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}{C}^{*}-c{\displaystyle \frac{{\gamma }_1}{2}}gl{W}^{*}{C}^{*})g\left(y\right)-(c{\beta }_1+d{\beta }_{2}gl+{\beta }_3)g\left({\displaystyle \frac{1}{y}}\right)\hfill \\ \hfill & +(b{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}{C}^{*}+d({\gamma }_1+{\gamma }_3)gl{W}^{*}{I}^{*}-a{\alpha }_2{S}^{*}-b{\beta }_1{C}^{*}-d{\sigma }_1{I}^{*})g\left(z\right)\hfill \\ \hfill & -(({\displaystyle \frac{b}{2}}+d)({\gamma }_1+{\gamma }_3)gl+{\gamma }_2)g\left({\displaystyle \frac{1}{z}}\right)+(d{\sigma }_1{I}^{*}-a{\alpha }_{3}gl{S}^{*}{C}^{*}-c{\gamma }_{3}gl{W}^{*}{C}^{*}-b{\beta }_{2}gl{C}^{*}{I}^{*})g\left(h\right)\hfill \\ \hfill & -(c{\sigma }_1+{\sigma }_2)g\left({\displaystyle \frac{1}{h}}\right)+(a{\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}{C}^{*}-b({\beta }_1{C}^{*}+{\beta }_{2}gl{C}^{*}{I}^{*}+{\beta }_3{C}^{*}))g\left(xy\right)\hfill \\ \hfill & +(b{\beta }_1{C}^{*}-b{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}{C}^{*}-d({\gamma }_1+{\gamma }_3)gl{W}^{*}{I}^{*})g\left(yz\right)\hfill \\ \hfill & +(a{\alpha }_{3}gl{S}^{*}{I}^{*}+c{\gamma }_{3}gl{W}^{*}{I}^{*}-d{\sigma }_1{I}^{*}-d{\sigma }_2{I}^{*})g\left(zh\right)\hfill \end{array}$$

(44)

It is possible to find suitable constants a, b, c and d, such that the following equation holds

$$\begin{array}{cc}\hfill & d{\beta }_{2}gl{C}^{*}{I}^{*}+c{\beta }_1{C}^{*}-a{\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}{C}^{*}-c{\displaystyle \frac{{\gamma }_1}{2}}gl{W}^{*}{C}^{*}\le 0\hfill \\ \hfill & b{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}{C}^{*}+d({\gamma }_1+{\gamma }_3)gl{W}^{*}{I}^{*}-a{\alpha }_2{S}^{*}-b{\beta }_1{C}^{*}-d{\sigma }_1{I}^{*}\le 0\hfill \\ \hfill & d{\sigma }_1{I}^{*}-a{\alpha }_{3}gl{S}^{*}{C}^{*}-c{\gamma }_{3}gl{W}^{*}{C}^{*}-b{\beta }_{2}gl{C}^{*}{I}^{*}\le 0\hfill \\ \hfill & a{\displaystyle \frac{{\alpha }_1}{2}}gl{S}^{*}{C}^{*}-b({\beta }_1{C}^{*}+{\beta }_{2}gl{C}^{*}{I}^{*}+{\beta }_3{C}^{*})\le 0\hfill \\ \hfill & b{\beta }_1{C}^{*}-b{\displaystyle \frac{{\gamma }_1+{\gamma }_3}{2}}gl{W}^{*}{C}^{*}-d({\gamma }_1+{\gamma }_3)gl{W}^{*}{I}^{*}\le 0\hfill \\ \hfill & a{\alpha }_{3}gl{S}^{*}{I}^{*}+c{\gamma }_{3}gl{W}^{*}{I}^{*}-d{\sigma }_1{I}^{*}-d{\sigma }_2{I}^{*}\le 0\hfill \end{array}$$

(45)

Therefore, ${\displaystyle \frac{dV\left(t\right)}{dt}}\le 0$ holds, and ${\displaystyle \frac{dV\left(t\right)}{dt}}=0$ holds only at the rumor equilibrium point $E_1^{*}=(S^{*},C^{*},W^{*},I^{*})$. Thus, the dynamical system (13) is globally asymptotically stable at the rumor equilibrium point $E_1^{*}$. □

5. Experiment and Result Analysis

5.1. Related Networks

In this section, simulation experiments will be conducted on the baseline model and the SCWIR model based on the NW small-world network, BA scale-free network, hypernetwork, and Facebook network. The first three networks are constructed through algorithms, while the Facebook network is from a public dataset (Stanford large network dataset collection ego-Facebook [EB/OL]. http://snap.stanford.edu/data/ego-Facebook.html (accessed on 1 December 2023)). The parameters for each network are provided in

Table 2. Network parameters.

Networks	NW	BA	Hypernetwork	Facebook
Nodes	1000	1000	1000	4039
Edges	4473	8550	10,313	88,234
Average degree	8.9460	17.1000	20.6180	43.6910
Clustering factor	0.5278	0.5560	0.8252	0.6055

.

The NW small-world network consists of 1000 nodes, having an average degree of 8.9460 and a rewiring probability of 0.3. The network’s degree distribution follows a Poisson distribution. The BA scale-free network is initially set up with 500 nodes. Following the preferential attachment rule, new nodes are continuously added, increasing the total to 1000 nodes, having an average degree of 17.1000, and its degree distribution follows a power-law distribution. The hypernetwork, which accounts for group relationships, includes 1000 nodes, having an average degree of 20.6180, and its degree distribution follows a power law. The degree distribution of the Facebook network follows a power law, showing characteristics of small-world networks, scale-free networks, and hypernetworks.

5.2. Experimental Design

This paper uses the Monte Carlo (MC) method to compare information propagation across different networks. The basic settings are as follows:

(1)

The data for nodes and edges in each network are shown in Table 2.

(2)

Each network undergoes 1000 independent experiments, and the final results are taken as the average of the experimental outcomes.

(3)

N represents the total number of network nodes, and the initial number of information sources is set as $0.1\%$ of the total nodes, rounded up if not divisible.

(4)

Model parameter settings. The infection and recovery probabilities in the SIS model are 0.7 and 0.3, respectively. The infection and recovery probabilities in the SIR model are 0.7 and 0.3, respectively. The latency, infection, and recovery probabilities in the SEIR model are 0.3, 0.7, and 0.3, respectively. The experimental parameters for the SCWIR model are as follows: ${\alpha }_1=0.2,{\alpha }_2=0.2,{\alpha }_3=0.5,{\alpha }_4=0.1,{\beta }_1=0.3,{\beta }_2=0.6,{\beta }_3=0.1,{\gamma }_1=0.4,{\gamma }_2=0.2,{\gamma }_3=0.4,{\sigma }_1=0.7,{\sigma }_2=0.3,l_0=1.0$.

(5)

All experiments in this paper were conducted using the MATLAB programming tool, version MATLAB R2018a.

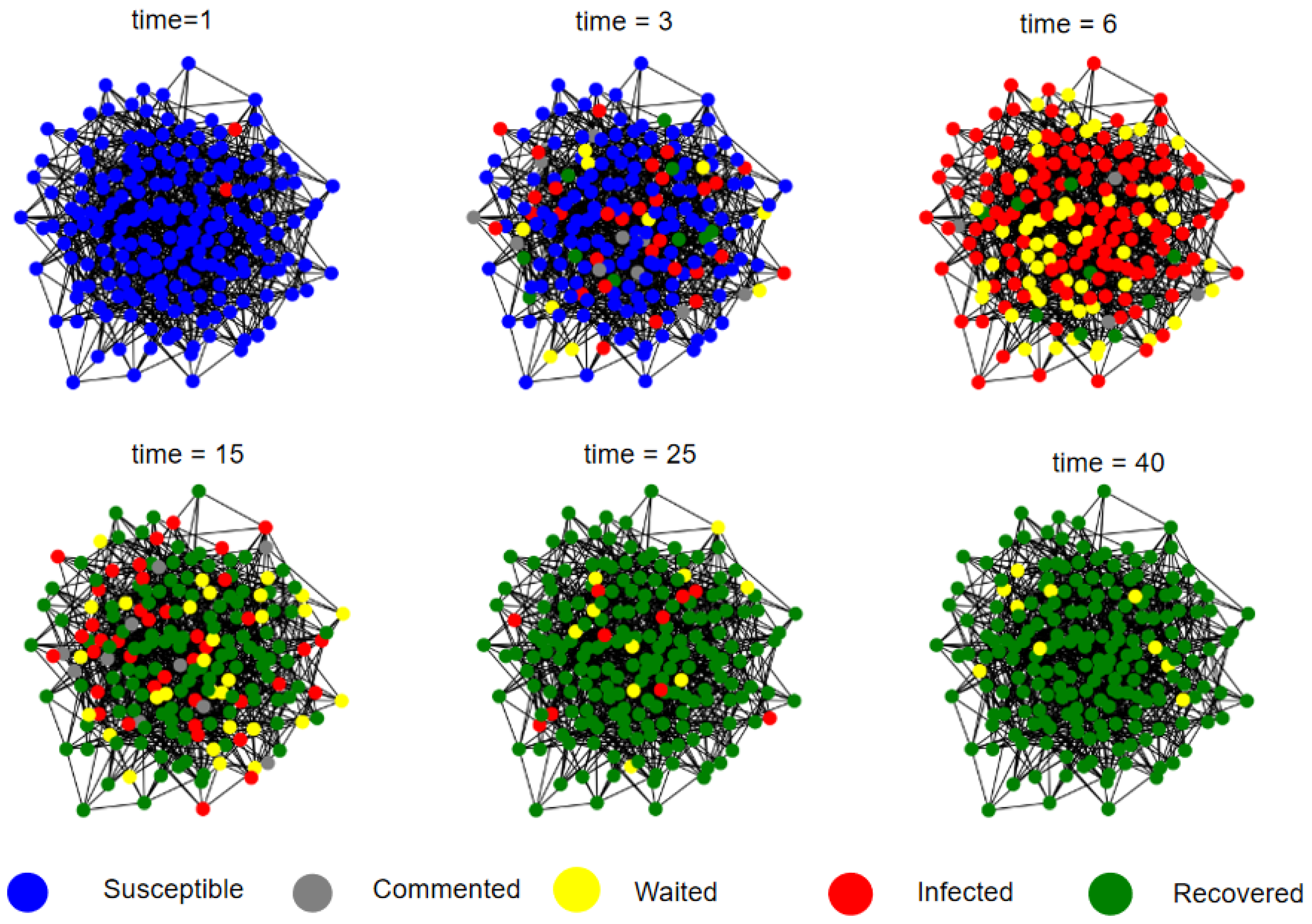
5.3. Visualization of the Propagation Process

This section visualizes the simulation process of the SCWIR model and analyzes its propagation dynamics.

As shown in Figure 4, at the initial stage, the network contains a small number of rumor sources. These source nodes propagate the rumor, influencing their adjacent nodes and indirectly affecting other nodes. At $t=6$, a large number of spreading nodes and neutral waiting nodes appear in the network, indicating that the rumor has gained significant attention. During this stage, commenters further propagate the rumor and may transition into spreaders. At $t=15$, the intensity of the rumor decreases due to the decay in information value. Some users become immune to the rumor, while others, after gaining awareness, return to a neutral state to observe the situation. In the later stages, public opinion stabilizes, and most users lose interest in the rumor. From the figure, we can see that the stage from $t=6$ to $t=15$ is the phase of rapid rumor decay. During this period, rumors are suppressed due to debunking by authoritative organizations, and the decay of the rumor’s informational value also causes it to lose its ability to spread. In the experiment, we will analyze the factors contributing to the rapid decay of rumors and seek optimal control strategies.

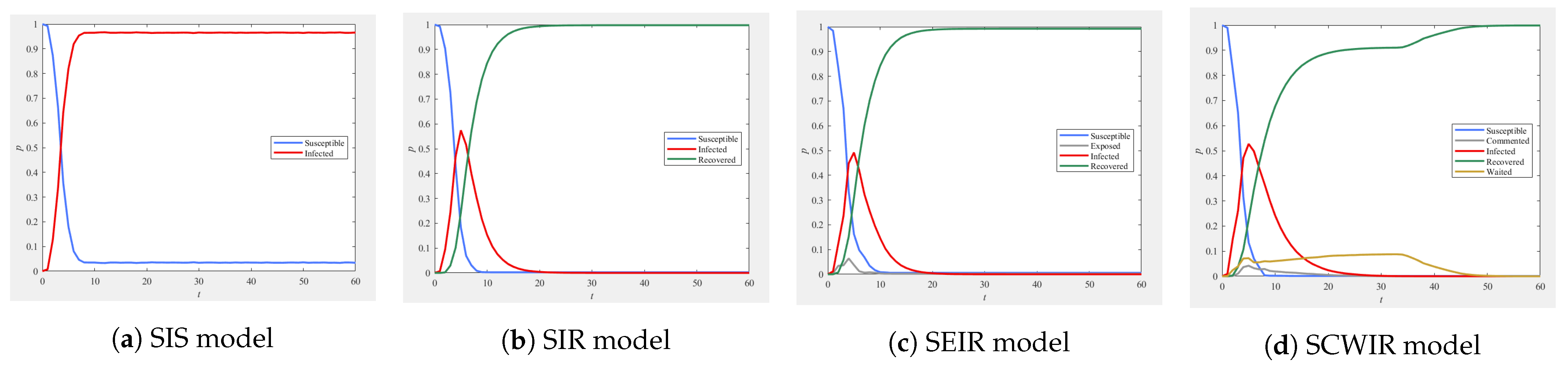
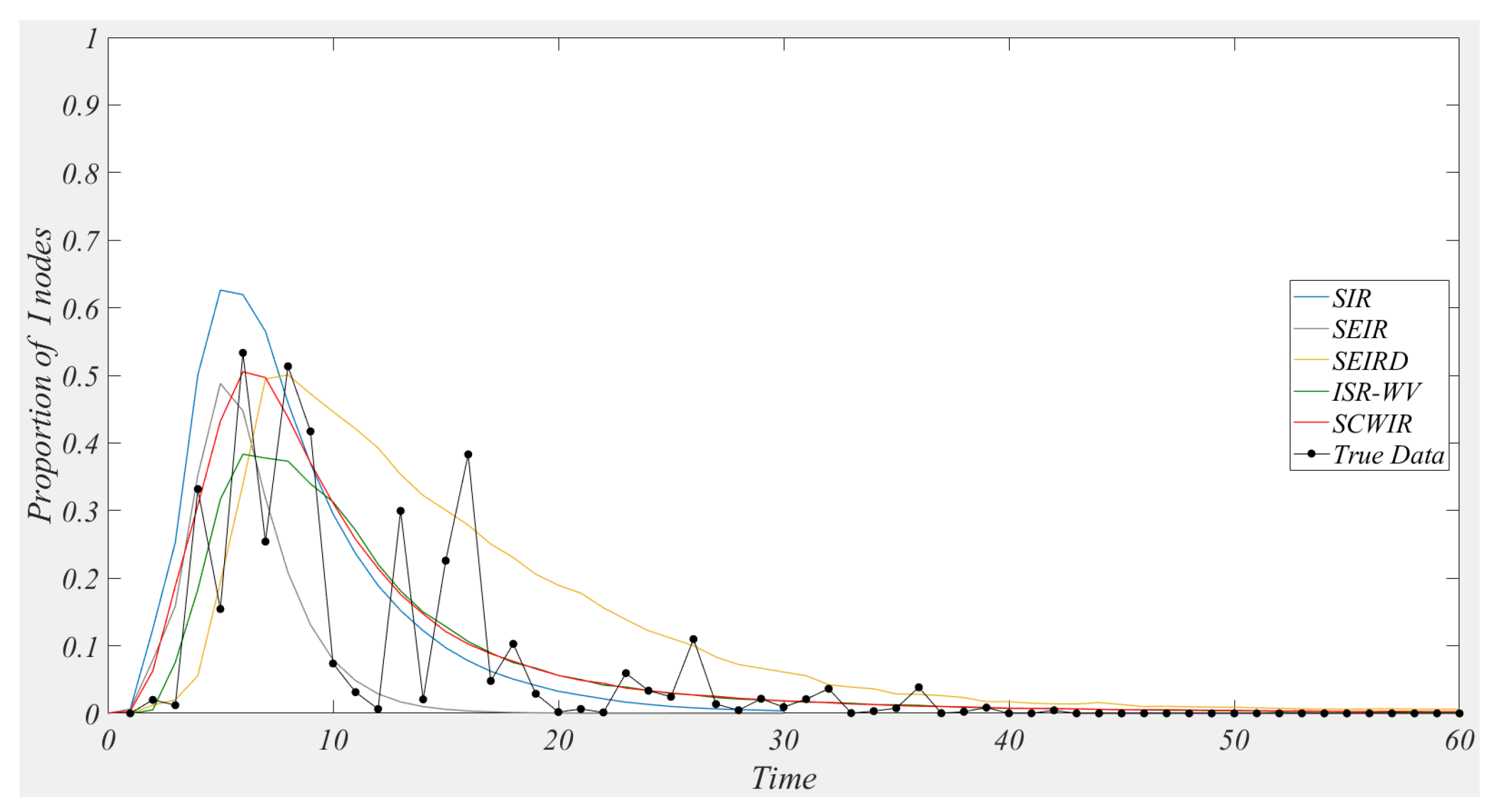
5.4. Comparison of Models

In this subsection, we simulate 60 h of rumor propagation for each model on the Facebook network and provide a comparative analysis.

The experiment randomly selects $0.1\%$ of the nodes as the initial spreaders, with all other nodes remaining in the susceptible (S) state. As shown in Figure 5, the SIS model classifies participants in rumor propagation into simple categories, with only susceptibles and spreaders. In this model, over $90\%$ of users spread rumors, which does not align with reality.The SIR model considers users’ permanent immunity to rumors but ignores the possibility of short-term immunity. Once users gain awareness, they immediately exit rumor propagation. The SEIR model includes a hidden state where users receive but do not spread information, more accurately representing the neutral waiting state of users. However, it inadequately considers transitional phases in state changes and still assumes that users exit rumor propagation permanently upon gaining awareness, neglecting the possibility of re-belief in the rumor. The SCWIR model thoroughly accounts for multiple waiting states where users observe the development of events after being exposed to rumors. It also includes short-term immunity behaviors, where users gain awareness after initially believing the rumor and temporarily adopt a neutral waiting stance.

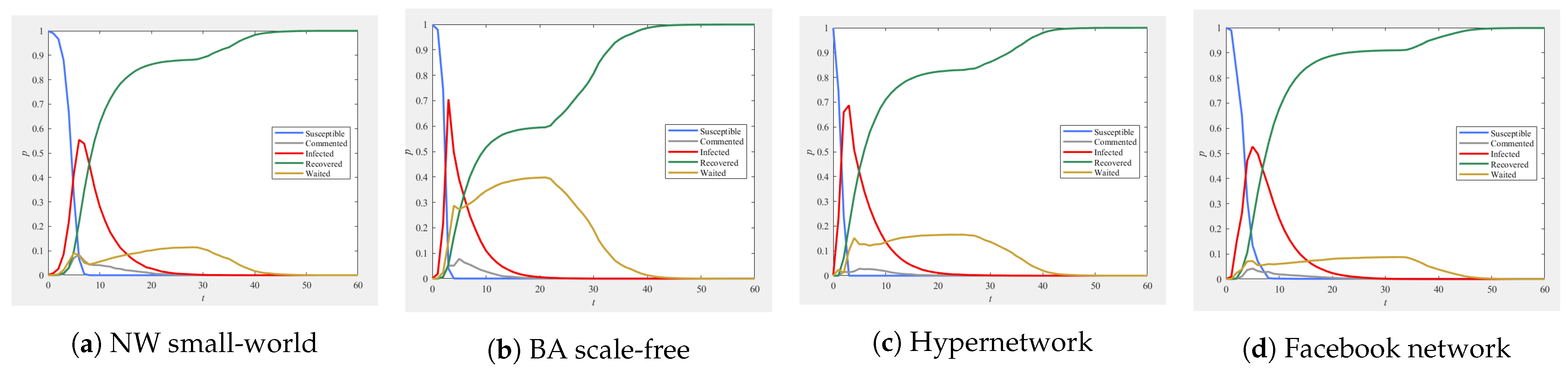
5.5. Impact of Different Network Structures

Rumor propagation effects vary across different network structures. In this subsection, we compare the experimental results of the SCWIR model across different network structures. As shown in Figure 6, in the NW network, users influence only their neighboring nodes, leading to slower rumor diffusion and a later peak in the number of spreaders. After initially encountering the rumor, some users choose to wait and observe; as the number of commenters and spreaders steadily declines, some easily swayed users choose to wait again, increasing the number of observers. In the BA network, there are ’hub’ nodes, and changes in their state significantly impact user stances. When a ’hub’ node spreads a rumor, its supporters rapidly disseminate it, leading to a sharp increase in the number of spreaders and an earlier peak. When a ’hub’ node awakens and switches to the immune state, its followers become observers. In the super network, the group relationships facilitate faster rumor propagation, leading to a higher peak in the number of spreaders, with the peak occurring earlier. The Facebook network, which combines characteristics of small-world, scale-free, and super networks, produces smoother experimental results and more reasonable predictions for the spreaders.

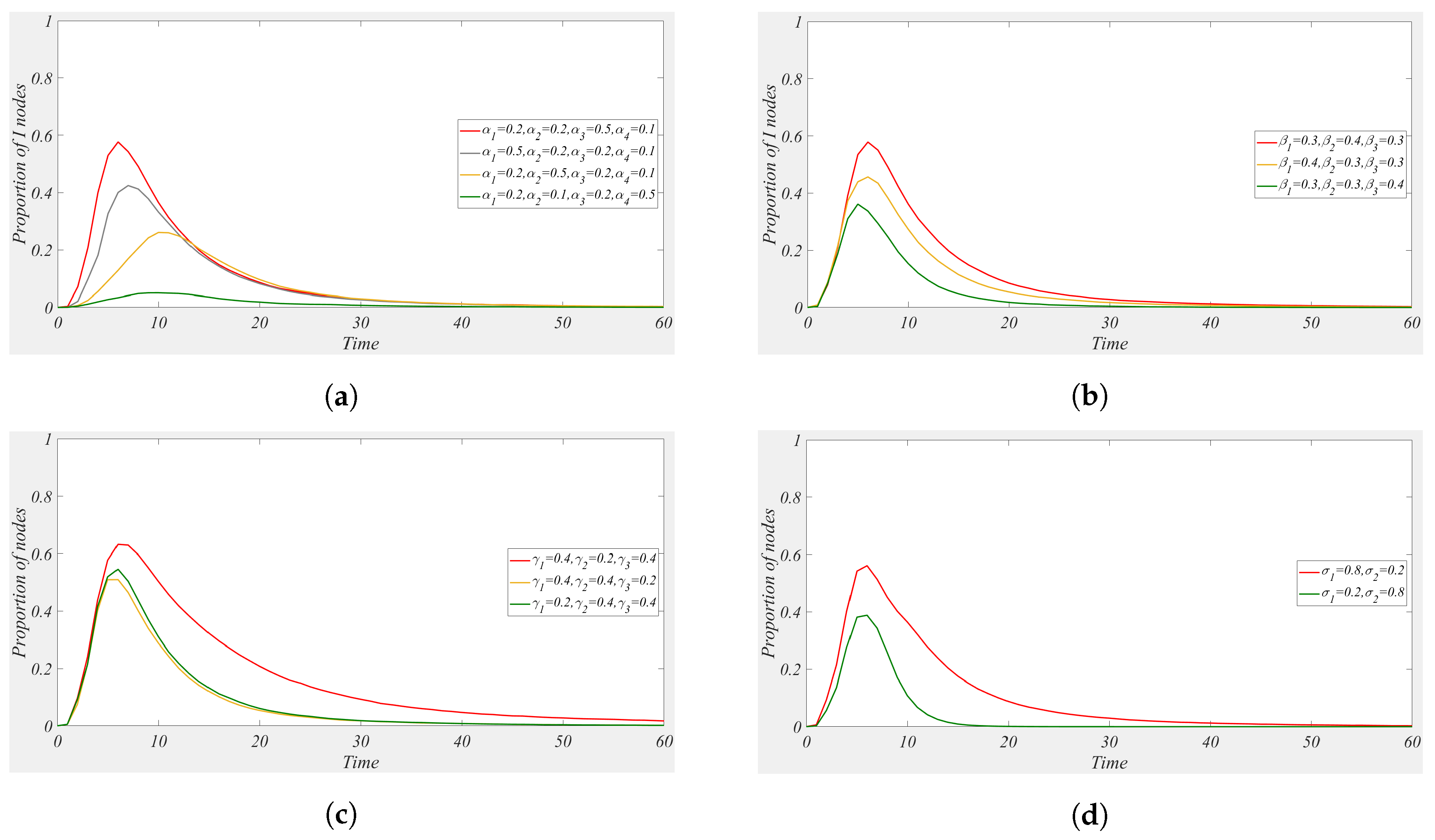
5.6. Parameter Sensitivity Analysis

In this subsection, we conduct a sensitivity analysis of the model parameters. Except for the parameters shown in the figure, the remaining parameters are set according to the experimental design section. The experimental results are shown in Figure 7. In Figure 7a, when the probability ${\alpha }_3$ is relatively large, the peak of rumor propagation is higher. When the probability ${\alpha }_4$ is large, the rumor propagation intensity is very low. This indicates that to suppress rumors, we need to reduce the probability of users spreading and commenting on rumors and increase the probability of users’ immunity to rumors, with particular focus on controlling the propagation probability ${\alpha }_3$. In Figure 7b, it shows that the probability ${\beta }_2$ of users who participate in commenting on the rumor further spreading the rumor is a key factor contributing to the increase in the peak of rumor propagation. From Figure 7c, we observe that when the probability ${\gamma }_2$ of bystanders becoming immune to rumors is low, rumor propagation becomes more severe. Therefore, to reduce the impact, we need to decrease the probability of bystanders re-engaging in the rumor event, thus increasing ${\gamma }_2$. In Figure 7d, ${\sigma }_2$ represents the probability that propagating users lose interest in the rumor. When ${\sigma }_2$ is large, the scope of rumor propagation is smaller. In conclusion, to effectively control rumors, strategies should be implemented to reduce the propagation probabilities ${\alpha }_3$ and ${\beta }_2$ and the bystander probability ${\sigma }_1$ while increasing the immunity probabilities ${\alpha }_4$ and ${\sigma }_2$. The sensitivity analysis of the parameters related to influencing factors will be provided later in the text.

5.7. The Influence of Various Factors

5.7.1. Information Timeliness

The decay in rumor value diminishes the focus given to it. As shown in Figure 8, when the information decay coefficient $\lambda =0.1$, the peak number of spreaders is higher, while at $\lambda =0.3$, the peak number of spreaders is lower, indicating that the quicker the decay of rumor value, the less popular the rumor becomes. At $\lambda =0.3$, the number of commenters slightly increases, suggesting that when the rumor’s information value decays quickly, people are more inclined to comment on the rumor. At $\lambda =0.3$, the number of observers is lower, indicating that fewer users choose to wait for the situation to develop when the rumor’s popularity is low. Additionally, the number of susceptibles not exposed to rumor is higher at $\lambda =0.3$, as users quickly lose interest in the rumor when its information value decays rapidly, leading to fewer users spreading the rumor. Some susceptible individuals remain unaffected by the rumor, and its spread is limited. As shown in Figure 9, the greater the information decay coefficient, the faster the information value decays, the lower the peak number of spreaders, and the slower the increase in the number of spreaders.

5.7.2. Government Intervention

Government debunking can guide users to resist rumors, curb rumor spread, and restore the public opinion environment more quickly. As shown in Figure 10b, when intervention occurs at $t^{\prime }=5$ with a debunking intensity $\mu =5$, it can be observed that, at the beginning of the intervention, the number of spreaders declines sharply. After debunking, the wait-and-see group spreads the debunking information to their adjacent nodes, and the believing group quickly becomes active, leading to a swift decline in the number of spreaders and commenters. Some hesitant users turn into wait-and-see individuals, increasing the number of observers. The recovery time for the public opinion environment is advanced. When the debunking intensity is increased to $\mu =8$ and debunking starts at $t^{\prime }=5$, the number of believers decreases faster, and the public opinion environment recovers more quickly. Timely debunking by the government prevents the believing group from spreading rumors, controlling the spread range, and preventing some susceptible individuals from being exposed to the rumors. In Figure 10d, when the debunking time $t^{\prime }=2$ and the debunking intensity $\mu =8$, only a small number of users are exposed to the rumors, and most users are directly immune to the rumors. Moreover, more susceptible individuals are not exposed to the rumors. As shown in Figure 11, when the debunking time is set at $t^{\prime }=5$, a higher debunking intensity leads to a lower peak number of spreaders. When the debunking intensity $\mu =3$, the earlier the debunking time, the lower the peak number of spreaders.

5.7.3. Information Popularization Rate

Positive information related to rumor debunking can help users develop immunity, providing a certain level of prevention against rumor spread. As shown in Figure 12, when the information education rate reaches $25\%$, $25\%$ of users become immune to rumors, reducing the susceptible user count to $75\%$, thereby minimizing the rumor’s impact. The number of propagators, commenters, and observers decreases, effectively controlling the rumor spread. Some susceptibles do not come into contact with the rumor. As shown in Figure 13, the larger the scope of information popularization, the smaller the number of rumor spreaders.

5.7.4. Influence of Multiple Factors

By adopting multiple suppression strategies, the spread of rumors can be more effectively controlled. As shown in Figure 14a, introducing government debunking with a debunking strength of $\mu =5$ and a debunking time of $t^{\prime }=5$, while accelerating the information value decay with a decay coefficient $\lambda =0.3$, allows the rumor-believing population to wake up in time, and the number of immune individuals increases rapidly, accompanied by a rise in the number of observers. In Figure 14b, combining government debunking with information education, with an initial immune population ratio of $R\left(0\right)=\eta =0.25$, the rumor’s impact scope is reduced, leading to an increase in the number of susceptible individuals not exposed to the rumor, while the number of propagators decreases. Figure 14c shows that when educational information is provided and the decay of information value is accelerated, the population changes remain relatively stable and there is a certain level of suppression. However, compared to the government’s forced intervention, the rumor’s spread cycle is longer, and the spread is wider, with a less ideal suppression effect, highlighting the decisive role of government intervention. In Figure 14d, when all three factors are introduced, only $10.73\%$ of individuals are affected by the rumor, $32.42\%$ of susceptible individuals remain unexposed to the rumor, and the number of immune individuals increases rapidly, showing significant suppression of the rumor.

5.8. Data Comparison

To validate the model’s effectiveness, we compare the simulation results with real data. A public dataset [18] containing 68,625 reposts was selected as the rumor case data. We compare the simulation results of the SIR [7], SEIR [8], SEIRD [9], ISR-WV [18], and SCWIR models with the forwarding data for analysis.

As shown in Figure 15, the SIR model has a simple user classification, but it overlooks the middle stages of rumor propagation, making its prediction of the rumor’s intensity too high. The SEIR model predicts the rumor dissipates too early, presenting an overly idealized view of its spread. The SEIRD model, which takes into account the heavy believers and the lag in rumor propagation, introduces the characteristic of delay in rumor dissipation, but it overlooks the fact that rumors disappear quickly once they lose attention, leading to a slower dissipation prediction. The ISR-WV model, considering multi-channel communication, allows more opportunities for users to spread and debunk rumors, offering a better simulation of rumor transmission, although it tends to be conservative in predicting peak propagation. The SCWIR model proposed in this paper, by considering users’ multiple waiting phases and information timeliness, successfully models the delayed dissipation of rumors. The multiple waiting mechanism captures the herd mentality of users, better fitting the rumor propagation data. Ultimately, due to the effect of information timeliness, the model avoids the issue of prolonged rumor persistence. To quantitatively analyze the model’s fitting performance, we computed the Root Mean Square Error (RMSE), Pearson correlation coefficient, and cosine similarity between the predicted forwarding results of each model and the actual forwarding data. As shown in

Table 3. Forward prediction experiment comparison results.

Model∖Index	RMSE	Pearson Correlation Coefficient	Cosine Similarity
SIR	0.0763	0.8501	0.8065
SEIR	0.0754	0.8593	0.8172
SEIRD	0.0744	0.8637	0.8321
ISR-WV	0.0731	0.8711	0.8695
SCWIR	0.0688	0.8997	0.8812

, the introduction of multiple waiting mechanisms and information timeliness allows for a better simulation of users’ waiting and observing behaviors in rumor propagation. It also avoids the issue of overly prolonged rumor persistence in the simulation. Therefore, the mechanisms proposed in our model are both effective and reasonable.

6. Conclusions

This paper aims to study rumor propagation. Addressing the issues of missing intermediate transition phases and neglecting the repetitiveness of rumors in existing rumor propagation models, it proposes a new SCWIR rumor propagation model. By considering users’ repeated waiting behaviors, the model simulates the potential dormancy and subsequent resurgence of rumors. It accounts for the possibility of individuals who spread rumors becoming temporarily dormant and then active again, as well as the short-term observation and waiting phase that easily swayed individuals might enter. This paper presents the dynamic equations of the model and, by solving the model’s equilibrium points and basic reproduction number, discusses the local and global stability of the rumor-free and rumor equilibrium points. Finally, numerical simulations analyze the impact of different factors on rumor propagation. The results show that the introduction of a repeated waiting mechanism helps simulate the repetitiveness of rumor propagation. Among rumor suppression strategies, the suppression effects rank from highest to lowest as government intervention, science popularization, and accelerating the decay of rumor value, with government intervention playing a decisive role. Science popularization can reduce the initial heat of rumors at the source. In future work, we will explore the content of rumors, analyze user sentiment, and investigate more effective rumor control strategies.