Abstract
In recommendation tasks, most existing models that learn users’ preferences from user–item interactions ignore the relationships between items. Additionally, ensuring that the crossed features capture both global graph structures and local context is non-trivial, requiring innovative techniques for multi-scale representation learning. To overcome these difficulties, we develop a novel neural network, CoGraph, which uses a graph to build the relations between items. The item co-occurrence pattern assumes that certain items consistently appear in pairs in users’ viewing or consumption logs. First, to learn relationships between items, a graph whose distance is measured by Normalised Point-Wise Mutual Information (NPMI) is applied to link items for the co-occurrence pattern. Then, to learn as many useful features as possible for higher recommendation quality, a Convolutional Neural Network (CNN) and the Transformer model are used to parallelly learn local and global feature interactions. Finally, a series of comprehensive experiments were conducted on several public data sets to show the performance of our model. It provides valuable insights into the capability of our model in recommendation tasks and offers a viable pathway for the public data operation.
Keywords:
recommender systems; convolutional neural network; graph neural network; co-occurrence pattern; transformer model MSC:
68T09
1. Introduction
In our daily activities, such as online shopping [1,2], entertainment consumption [3,4], and social networks [5,6], the constant introduction of new items poses a challenge for users to make informed decisions [7,8]. The abundance of choices can lead to fatigue and confusion in decisions, making it challenging for users to choose the most suitable options according to their needs, prompting users to seek assistance from recommender systems to streamline their selection process and alleviate decision-making burdens.
Recent progress in deep learning has shown promising results for recommendation systems, with advances in this field playing an essential role in enhancing the capabilities of recommendation algorithms [9,10]. Graph Neural Networks (GNNs) are designed to operate directly on graph structures. The core features of GNNs include realizing feature learning by aggregating node neighbor information, capturing complex non-Euclidean relationships in graphs, and flexibly adapting heterogeneous graphs and dynamic graphs [11]. Prominent GNN types include Graph Convolutional Networks (GCNs) [12], Graph Attention Networks (GATs) [13], Graph Autoencoders [14], and Adversarially Regularized Graph Autoencoders [15], each tailored for tasks such as representation learning and unsupervised feature extraction [16]. In addition to recommendation tasks, GNNs have been successfully employed to improve the reliability and efficiency of power systems, especially under high uncertainty from renewable energy sources [16]. In addition, a multi-fidelity GNN framework has demonstrated the potential to combine high-precision and low-precision data, thereby reducing computational demands and enhancing model robustness across diverse scenarios in power systems [17]. Despite these advancements, many existing recommendation systems focus primarily on user–item interactions, overlooking the intricate relationships that exist between different items within the system [4,18,19]. An item co-occurrence pattern is proposed to discover such relationships that assumes that some items always occur in pairs in users’ favorite lists. Figure 1 demonstrates a toy example of a movie co-occurrence pattern. In users’ viewing logs, it is always easy to view Harry Potter movies sequentially.
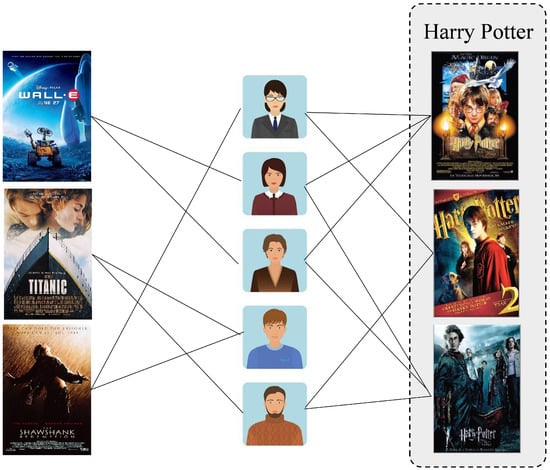
Figure 1.
Toy example of co-occurrence patterns in movies.
Recently, co-occurrence patterns have been explored to improve recommendation quality. For example, to improve Matrix Factorization (MF) performance, Liang et al. [18] first proposed an item co-occurrence pattern and combined it with MF, providing a new perspective to exhibit a connection between two items. Wu et al. [20] added item co-occurrence information to metric learning to provide a more detailed representation of the relationships between items. To achieve a higher recommendation quality, Chen et al. [21] proposed CoCNN to learn accurate features by directly applying a Convolutional Neural Network (CNN) to an item co-occurrence pattern. These models fully use the potential information of the user–item interactions. However, they are still confronted with key challenges; e.g., it is extremely stiff when it comes to capturing both global graph structures and local context from the user–item interactions.
To tackle the above difficulties, we designed a co-occurrence graph neural network (CoGraph), which utilizes a graph to link all items. Through powerful representation learning capabilities, graph methods have a strong ability to learn accurate features by message functions and a neighborhood aggregation strategy [22,23,24]. Next, to achieve better performance, Normalised Point-Wise Mutual Information (NPMI) [25] is applied to evaluate the strength of the item connection. According to NPMI, we built an undirected graph based on historical data and applied a Graph Neural Network (GNN) to model item relationships and generate precise embeddings.
Recent studies [26,27,28,29] show that feature crossing improves the performance of deep models. CNNs are powerful in acquiring local features from inputs [30,31], and Transformer networks demonstrate a strong capacity to learn the dependencies between elements of input features [32,33,34]. Thus, in this paper, to fully and deeply explore the relationships between features, CNNs and Transformer networks, which complement each other, are applied to parallelly capture local and global feature information, respectively.
Our main contributions are as follows:
- To enhance recommendation systems, we developed a novel framework to consider both user–item and item–item correlations simultaneously.
- To learn accurate features of items, co-occurrence relationships are built by a graph, in which NPMI is used to measure the distance.
- To capture the interactions across features, CNNs and Transformer networks are used to parallelly learn both local and global levels of user intentions.
- Detailed experiments on four public data sets demonstrate that our CoGraph model outperforms some competitive baseline methods.
2. Related Work
2.1. Feature Crossing-Based Recommendation
To learn information from user–item interactions, the following two methods are commonly used: feature crossing in neural networks and attention mechanisms.
Feature crossing in neural networks. Wang et al. [35] designed a cross-network to apply explicit feature crossings efficiently. To model feature interactions between items, Wang et al. [36] conserved collaborative signals with messages passing by element-wise products between two connected nodes. To capture fine-grained interactions between individual behaviors, Xie et al. [37] learned user unbiased preferences from different types of positive/negative and explicit/implicit feedback.
Attention mechanism. An attention mechanism is effective in learning a deeper representation of each item by analyzing its relationships with other items [38]. For example, the self-attention of Transformer models the relationships between items and, by memorizing dependencies, concentrates on important parts of inputs [2,39]. To capture high-order dynamic information in a sequence, self-attention learns the representation by modeling the long-range dependencies between collaborative items [40,41]. Rather than treating preferences uniformly, as most existing models do, attention-based models distinguish users’ preferences over items by automatically assigning weights to different items [4,42].
Both solutions completely use implicit knowledge of user–item interactions and show that the item relationships effectively improve recommendation quality. In this paper, we use CNNs and Transformer to parallelly learn both local and global levels of feature interactions.
2.2. Graph-Based Recommendation
In graph-based recommendation [43], the user and item are represented as nodes, and the users’ behaviors are considered as edges. Hence, the potential relations between the user and the item can be obtained by executing path exploration, and further realizing the recommendation. Compared with traditional recommendation approaches, graph-based recommendation facilitates the representation of interactions among users and items.
To handle the problem of high-order connectivity modeling, Wang et al. [44] proposed a Neural Graph Collaborative Filtering (NGCF) method based on a Graph Convolutional Network (GCN) to explicitly encode the high-order interconnections in the interaction graph to capture richer collaborative filtering signals. Based on this, Ye et al. [45] presented an improved NGCF by denoising the structure of the user–item graph and adding random noise into embeddings to enhance the robustness of NGCF. Because of the different weights and semantics of multiple types of user behavior, Jin et al. [46] introduced an approach to construct a heterogeneous graph network based on a GCN to improve performance. Meanwhile, He et al. [47] proposed a minimized GCN that only retains the neighborhood aggregation to lighten the model structure. Zhang et al. [19] designed a graph-based regularization method to enhance the quality of representations in the embedding layers, enabling a more effective capture of relationships between users and items.
With the exception of only considering the user–item graph as a reference, Fan et al. [5] designed a GraphRec model based on a GNN that aggregates user–item graphs and user–user social graphs to enhance the modeling performance of users. To address the issue of cold start, Cai et al. [48] introduced an approach based on a heterogeneous GNN, which applies a hierarchical attention aggregation to utilize the sparse attribute of new users and the heterogeneous relationship between existing users and items, thereby generating high-quality user representation. In terms of capturing high-order proximity, [49] proposed a method to boost the accuracy of implicit recommendation, through random-walk on user–item graphs to capture high-order proximity information. In addressing the problem of processing large-scale edges and nodes, Ying et al. [50] presented a GCN-based approach combined with random-walk to obtain essential proximity information from large-scale graphs.
Recent studies further showcase the evolution of graph-based recommendation methods. For instance, Bansal et al. [51] proposed a multilingual personalized hashtag recommendation system utilizing GNNs to improve hashtag relevance in low-resource Indic languages, addressing linguistic diversity challenges. Further, Chen et al. [52] introduced the CT-GNN model, integrating temporal information into GNNs for recommendations, enhancing accuracy and diversity by capturing temporal associations. The authors of Sedhain et al. [53] developed a knowledge graph-based recommendation system enriched by neural collaborative filtering, which leverages multi-hop neighborhood information to resolve cold-start and redundancy issues. Finally, Wu [54] presented KGAT-AX, which integrates auxiliary information into knowledge graph embeddings via an attention mechanism, achieving superior performance in personalized recommendations.
3. Proposed Model
3.1. Preliminary
Consider two sets: U, consisting of m users, and I, containing n items. Their interaction forms a matrix, , whose element is defined as follows:
Next, we establish a co-occurrence matrix, , whose element is the distance between i and j. To retrieve valuable insights from a co-occurrence pattern, the relationship between items is modeled as a weighted bipartite graph, . In graph G, S also means the adjacent matrix. A graph embedding function maps the nodes of a graph into a lower-dimensional space [55].
3.2. Architecture
To learn accurate embeddings from user–item interactions, a graph-based approach is used to capture co-occurrence relationships effectively. Moreover, we enrich the model’s representation capabilities by incorporating feature cross-interactions at both local and global levels. Thus, CoGraph, with a co-occurrence pattern, has three key designs: (1) a weighted bipartite graph describing the relationships between items; (2) a CNN learning local feature crossings; and (3) Transformer learning global feature crossings. Figure 2 shows the framework of CoGraph.
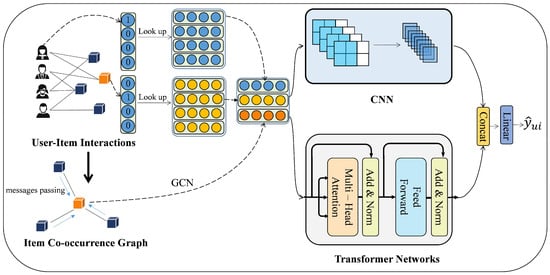
Figure 2.
Framework of CoGraph.
3.2.1. Co-Occurrence Graph
We use a graph to learn embeddings from a co-occurrence pattern. A pattern is represented as a graph, where each edge is labeled with a weight to indicate the distance between items. Given two items, i and j, NPMI [25] measures the distance, defined as follows:
where , and is the number of items. denotes the number of items i and j co-occurring in the data; and denote the numbers of the items i and j, respectively.
Compared to other metrics like PMI, which can produce unbounded values and may be difficult to interpret, NPMI provides a standardized measure. Additionally, while correlation coefficients can indicate linear relationships, they may not adequately capture the nuances of probabilistic relationships, especially in the case of categorical data. NPMI’s probabilistic foundation allows it to reveal associations that may not be linear, making it particularly suited for our analysis. Recent studies [56,57] have successfully employed NPMI to analyze relationships in similar contexts, illustrating its effectiveness as a metric for understanding associations in complex datasets.
Some co-occurrence links may be redundant or irrelevant. Thus, considering all co-occurrence links may degrade learning performance. Only important and useful links should be generated. To obtain accurate embeddings, it is necessary to prune the graph. Thus, we use the threshold, k, to filter noisy edges. Finally, the distance of node, , is used to measure graph connectivity and create an edge list. The operation is defined as follows:
In the construction of the graph, (1) a user–item interaction matrix is used to calculate co-occurrence matrices for both users and items, which quantify how often users interact with the same items and how often items are rated by the same users; (2) after calculating PMI scores, which reflect the strength of association between users and items based on their co-interaction patterns, we obtain NPMI scores to facilitate comparisons across different user–item pairs; and (3) we create an edge list that captures the connections between nodes () based on their interactions, resulting in a graph representation.
GCNs, one of the most popular and promising methods for graphs, are used to generate embeddings of items. In the co-occurrence graph, G, to obtain the embedding of an item i, , we first randomly sample neighbors from its neighbor set, , and then perform the graph convolution as follows:
where denotes the sigmoid function.
3.2.2. CNN Learning
By using the power of the receptive field, Convolutional Neural Networks (CNNs) effectively retrieve meaningful and abstract features from input data [21,58,59]. Our model introduces two innovative approaches to thoroughly investigate and understand the relationships between user–item interactions and item–item connections: (1) learning local feature interaction by a CNN and (2) global feature interaction by a Transformer network.
To construct a connection matrix that effectively links user and item representations, we define their input, , as follows:
where and denote the embedding of the user and item, respectively; is a contextual feature from an item graph; d denotes the dimensionality of each embedding.
Then, we apply a series of convolutional filters to the connection matrix in order to extract meaningful features. The filtering operation is defined as follows:
where W represents a filter with a size of ; ⊗ is a convolution operation; b denotes the bias; and denotes an activation function.
We design CNN learning for processing input data through a series of convolutional layers, incorporating both 2D and 1D convolutions. The network takes input data, reshapes them to fit the 2D convolutional layer, applies the convolution and activation, then reshapes the output for a subsequent 1D convolutional layer, which further processes the data before producing a final output through another ReLU activation. The output size is determined based on the transformations applied during the convolutions, ultimately yielding a flattened output vector suitable for the further task.
3.2.3. Transformer Learning
In CNNs, the receptive field, with a limited ability to obtain the interaction of global features, relies on the size of the convolutional kernel and the depth of the layers. To further investigate the intricate connections among elements within the features, a Transformer encoder network has been carefully constructed to capture a wide global receptive field. Transformer aims to capture the global interactions among features by effectively constructing comprehensive relationships between users and their associated items. The architecture of the Transformer has N identical sublayers, with each sublayer consisting of two critical modules: multi-head self-attention and feed-forward mechanisms [33,60,61].
Multi-head self-attention is a crucial element of the Transformer architecture; it enables the model to simultaneously attend to various parts of the input sequence. This module determines the significance of each element within the sequence, facilitating the capture of long-range dependencies and relationships. A multi-head self-attention mechanism, characterized by h heads, initially learns representations simultaneously across multiple heads before concatenating all the acquired representations into a single output. This process can be mathematically expressed as follows:
where represents a set of trainable weights that facilitate the final transformation of the concatenated representations.
Given an input , the attention scores for each pair of features are computed using the self-attention mechanism. Each individual attention head, indexed by (where ), is defined as follows:
where Q, K, and V represent the query, key, and value matrices, respectively; denotes the dimension of the key vectors. The softmax function is used to normalize the attention scores, assigning suitable weights to various features in the input.
The feed-forward mechanism, on the other hand, includes two linear transformations separated by a ReLU activation function. This module helps the model learn complex non-linear relationships within the data. The feed-forward mechanism in each sublayer is defined as follows.
where , , , and are learnable parameters and ReLU denotes the rectified linear unit activation function. This module applies two linear transformations with a non-linear activation function in between, enabling the model to learn complex patterns in related data.
Together, these two modules work in harmony within each sublayer of the Transformer architecture to process and transform the input data. By stacking sublayers sequentially, the Transformer learns complex patterns and relationships within the data, making it a potent tool for a variety of tasks.
3.2.4. Prediction
Once CNN co-occurrence feature and Transformer feature have been extracted, they are merged to create a unified representation that captures feature interactions at both local and global levels within the data. To construct the preference representation , we concatenate the CNN and Transformer features as follows:
Subsequently, the merged representation is fed into a Multi-Layer Perceptron (MLP) to learn complex non-linear mappings from input data to output predictions. The final prediction, denoted as , is generated by applying the MLP to the concatenated representation:
3.3. Optimization
In recommendation scenarios, the binary cross-entropy optimization criterion is widely utilized to assess loss during training. Let O and represent a set of observed and unobserved interactions, respectively, the loss function can be defined by
where is the ground truth label for the user–item pair , which takes a value of 1 if the interaction is observed (i.e., ) and 0 if it is unobserved (i.e., ); represents the predicted probability that the user u will interact with item i, as output by the model.
By minimizing this loss function, the model is optimized to produce high probabilities for observed interactions and low probabilities for unobserved ones, thus improving its predictive accuracy. The binary cross-entropy loss is particularly effective because it provides a smooth gradient that facilitates the training of neural networks, allowing for efficient convergence towards optimal parameters.
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets
We evaluated our model’s performance using four datasets: Lastfm, MovieLens100K, MovieLens1M, and BookCross, all of which are accessible online through the GroupLens platform (https://grouplens.org/datasets (accessed on 1 May 2024)). Lastfm is a music recommendation dataset suitable for evaluating the model’s ability to handle sparse data with its sparsity. MovieLens100K and MovieLens1M are benchmark datasets in movie recommendation that are suitable for testing the performance of models at different data sizes. BookCross provides a book recommendation scenario which tests the model’s generalizability across domains. Important statistics such as the number of users, items, and interactions for each dataset are summarized in Table 1. Consistent with established evaluation procedures found in prior studies like [62,63,64], we applied a leave-one-out evaluation technique to evaluate the performance of the proposed model.

Table 1.
Statistics for all data sets.
4.1.2. Metrics
The performance of our model is assessed using two primary evaluation metrics: Normalized Discounted Cumulative Gain (NDCG) and Hit Ratio (HR). NDCG, a ranking metric, assigns greater significance to correct recommendations positioned at the higher ranks of the recommendation list [65]. Specifically, NDCG@K is computed as follows:
where denotes the relevance score of the item at rank i, and is the ideal DCG@K, computed based on the relevance scores of items in the optimal ranking order.
On the other hand, HR@K, a common metric for evaluating recommendation quality, emphasizes the accuracy of the recommendations delivered:
where refers to the number of users for whom at least one relevant item appears within the top K recommendations.
4.1.3. Baseline Methods
To verify the effectiveness of CoGraph, we compared our model against the following methods:
BPR [63], which assigns a higher score to an observed interaction than its unobserved counterparts.
NeuMF [64], which combines MLP with MF to capture high-rank and low-rank features, respectively.
CoFactor [18], which uses the shifted positive PMI to measure the distance between items. Then, co-occurrence item embedding regularizes the objective function of MF for better recommendations.
GCN [44], which first builds a graph by user–item interactions and then uses a GCN to learn the representations.
DeepLight [29], which models feature interactions in the shallow component.
CoCNN [21], which designs a framework to build the link between item–item and user–item and directly applies a CNN to an item co-occurrence pattern.
4.1.4. Parameter Settings
In our experiment, Python is used as the primary programming language for model development and data processing. Specifically, we employed PyTorch, a widely-used deep learning framework, for implementing our model architecture and training processes. PyTorch was chosen for its flexibility and ease of use, particularly for building complex neural networks and conducting experiments efficiently.
All methods have three key hyper-parameters: regularization coefficient (), learning rate (), and feature size (d). We chose from , from , , and d from . Other hyper-parameters are determined by the default settings. To effectively tune hyperparameters, grid search was used to help us find the optimal set of hyperparameters. Finally, the average results of five random iterations were reported.
Our model is configured with multiple components: embeddings for users and items; a graph convolution layer for item relationships; CNNs for learning local features; a Transformer encoder for learning global features; and MLP for nonlinear mapping. We initialize the weights of the user and item embeddings using a normal distribution with a mean of 0 and a standard deviation of 0.1.
4.2. Results and Analysis
4.2.1. Overall Performance Comparison
Initially, a set of experiments was conducted to evaluate the performance of all methods on different datasets. The NDCG@10 and HR@10 scores on all datasets are summarized in Table 2. From the results in Table 2, the following conclusions are drawn:

Table 2.
HR@10 and NDCG@10 scores of all methods.
First, it is evident that CoGraph consistently achieves the best results for both metrics in most cases. The consistent outperformance of GCN by CoGraph across all datasets highlights the fact that GCN is primarily designed to model user–item relationships and may lack the capability to capture feature interactions effectively. The possible reason might be that, in GCN, the propagation of item embeddings through neighboring users instead of items directly during graph embedding updates may limit the exploration of item relationships.
Second, in most cases, CoGraph demonstrates superior performance over CoCNN, suggesting that a basic feature concatenation strategy may not be sufficient in capturing the complex relationships between items. Using a co-occurrence graph in recommendation tasks is crucial for acquiring precise embeddings. Further analysis reveals that the limitations of CoCNN mainly lie in the following aspects: (1) CoCNN performs feature learning from the co-occurrence matrix primarily relying on CNNs, which makes it difficult to capture complex relationships between items. (2) CoCNN focuses more on local feature learning while failing to exploit the global graph structure. In contrast, CoGraph captures complex relationships between items through GNNs and employs parallel CNN and Transformer structures to explore feature interactions at local and global levels. However, in terms of HR, CoGraph exhibits inferior performance on the dense MovieLens100K dataset, with three potential explanations: (1) noisy item co-occurrence contexts in the dataset, leading to imprecise representations learned by CoGraph; (2) the uniform treatment of item relationships neglecting varying distances; and (3) the failure to model feature interactions, resulting in limited performance.
Finally, CoGraph outperforms the MF-based model, CoFactor, due to two critical advantages: the neural network foundation of CoGraph enables it to identify deep and non-linear features through its hidden layers, and its strategic use of an item graph ensures a more precise understanding of item relationships than can be achieved with co-occurrence regularization. High-quality recommendation systems necessitate a broader perspective that encompasses not only user–item but also item–item relationships, offering a richer and more accurate compilation of features.
4.2.2. Performance of Co-Occurrence Graph
Next, to investigate the effect of the co-occurrence graph within CoGraph, we introduce a simplified model of CoGraph, CoGraph-x, which lacks the co-occurrence graph. We then conduct a comparative analysis of the performances of CoGraph-x and CoGraph across several datasets, with the results shown in Figure 3.
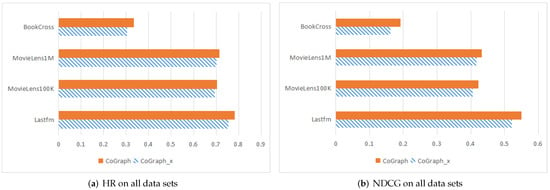
Figure 3.
Effect of co-occurrence graph.
From Figure 3, we can see that CoGraph achieves significantly better performance with larger HR and NDCG values than CoGraph-x on all datasets. The possible reason is that the features learned from the graph contain historical information about items; thus, the features represent items directly, whereas the features (embeddings) of CoGraph-x start with random initialization, leading to features without any useful information. Therefore, the co-occurrence pattern is effective in enriching user–item interactions, and the representations learned by the graph improve feature accuracy.
Moreover, we investigated the performance of graph depth in recommendation systems by adjusting the number of layers to one, two, three, and four. Our experiments were conducted on two datasets: the largest one, Movielens1M, and the smallest one, Lastfm, with the results illustrated in Figure 4. Our findings reveal that the recommendation performance reaches its peak when the graph consists of two layers. Conversely, increasing the number of layers beyond this optimal point diminishes the effectiveness of the graph, suggesting that a more complex structure may not always yield better results.
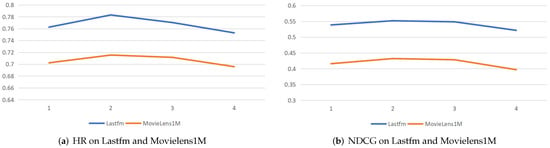
Figure 4.
Performance trends of CoGraph by adjusting graph depth.
4.2.3. Parameter Sensitivity Study
There are two important hyper-parameters in the CoGraph model, i.e., the feature size d and the noisy edge k. In this subsection, we study the impacts of these parameters on CoGraph.
We empirically set the feature size d to 16, 32, 64, 128, and 256, respectively. As shown in Figure 5a, we can see that the performance of CoGraph is progressively higher in terms of HR on both Lastfm and Movielens1M, when the feature size increases. This indicates that CoGraph learns more useful information when the feature size is larger. Figure 5b illustrates that CoGraph performs relatively better with increasing feature sizes, in terms of NDCG on both Lastfm and Movielens1M. This result again verifies that CoGraph shows stronger representation ability when it has a larger feature size.
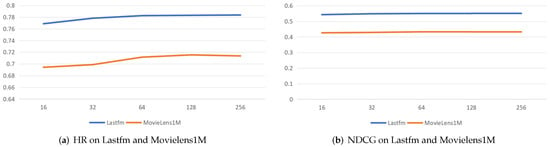
Figure 5.
The performance trends of CoGraph by adjusting feature size d in the graph.
Subsequently, we explored the impact of the parameter k on the effectiveness of filtering out noisy edges in the graph. We selected values from the set for our analysis. Our experiments were carried out on two datasets: Lastfm and Movielens1M. The results are presented in Figure 6.
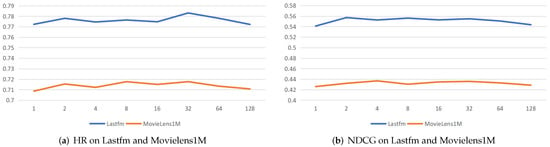
Figure 6.
The performance trends of CoGraph by filtering out different noisy edges k in the graph.
From Figure 6, these observations revealed that when k is greater than 0, the performance shows a slight improvement compared to when k is set to 0. This enhancement may be attributed to the effective filtering of certain noisy connections, allowing the graph neural network to learn more accurate features. However, as k increases significantly, we notice a decline in model performance. This suggests that overly aggressive filtering can lead to the loss of valuable information, ultimately resulting in a less effective model. Thus, while some degree of noise reduction is beneficial, excessive filtering may hinder the model’s ability to generalize and perform well.
4.2.4. Ablation Study
Finally, to evaluate the specific contributions of the CNN and Transformer components to the overall performance of the recommendation, we introduce two specific variants of CoGraph: CoGraph-CNN and CoGraph-Transformer. These variants were designed by omitting the CNN and Transformer segments from the original CoGraph model, respectively. All other conditions, including hyper-parameters like the regularization coefficient and learning rate, remained constant across these variants, matching those of the optimal configuration of CoGraph. To thoroughly examine their impact, we systematically tested feature sizes (d) from the set for CoGraph and its variants. The comparative results are shown in Figure 7.
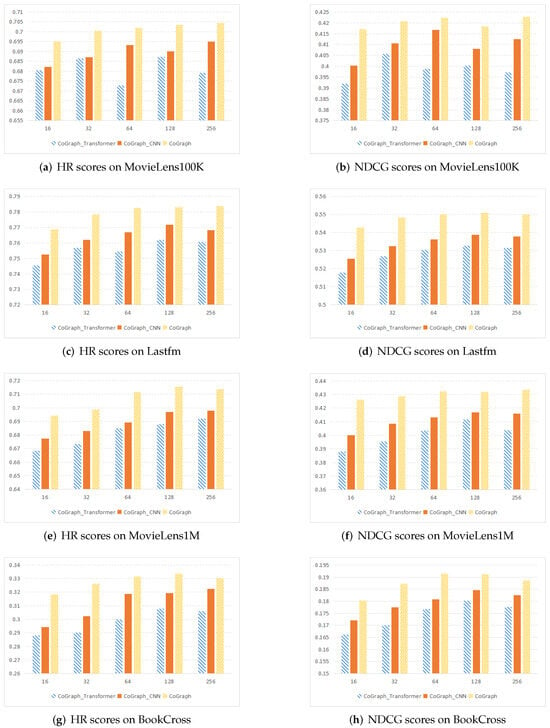
Figure 7.
Effect of feature crossing.
Observed from the results in Figure 7, we conclude the following: CoGraph outperforms its simplified models across all datasets in evaluation metrics, highlighting the effectiveness of its feature crossing methods in autonomously learning feature interactions and thereby improving recommendation accuracy. In most scenarios, CoGraph-CNN presents the weakest performance, likely because it primarily learns localized feature interactions through the kernel and struggles with deep feature learning. Additionally, CoGraph demonstrates greater stability as the feature size (d) increases; stability is also enhanced by the additional fitting parameters of the Transformer component, which aids in achieving more accurate vectors and steadying the performance. Therefore, the CNN and Transformer components serve an indispensable role in the feature crossing process of CoGraph.
5. Conclusions
The potential of deep learning in recommendations is often hampered by an inadequate representation of item relationships. Thus, we propose a novel graph-based framework, namely, CoGraph, which fuses the capabilities of CNNs with Transformer to optimize recommendation performance. Our approach initiates with the creation of a graph that links items based on co-occurrence, enhancing representation depth. In addition, we adopt NPMI to assess item correlations and deploy a GNN to extract useful features from the graph. Finally, we integrate a CNN with a Transformer model to capture both local and global feature interactions, thereby enriching the feature discovery process. Experimental results show the success of CoGraph in extracting valuable features from co-occurrence data, underscoring its effectiveness for a range of recommendation tasks.
Nonetheless, the proposed method comes with some limitations and challenges when applied in practical settings. Firstly, it requires comprehensive data that capture the complex relationships between users, items, and context. Small or sparse datasets may not be sufficient for the model to learn meaningful patterns. In addition, CNNs and Transformers are often regarded as "black-box" models, which means it can be difficult to interpret or explain why a particular recommendation was made. In future work, we aim to explore several promising directions to extend the impact of our model. An area is the application of CoGraph in public large data operations, where the integration of publicly available data enables more robust cross-domain management and system improvement. Further work will also explore improving the interpretability of the crossed features generated by CoGraph, helping users better understand and trust the recommendation process.
Author Contributions
Conceptualization, C.C. and X.Z.; methodology, X.Z.; software, X.Z.; validation, Y.L. (Yunxuan Liu) and Y.L. (Yuanguo Lin); formal analysis, Y.L. (Yunxuan Liu); investigation, D.C.; resources, D.C.; data curation, H.C.; writing—original draft preparation, C.C. and X.Z.; writing—review and editing, Y.L. (Yuanguo Lin) and H.C.; visualization, H.C.; supervision, X.Z.; project administration, Y.L. (Yuanguo Lin); funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Social Science Foundation of China [No. 24BZZ060], and in part by the Fujian Province Key Project of Basic Theoretical Research in Philosophy and Social Sciences [No. FJ2023MGCA034].
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors would like to thank Michael McAllister for proofreading this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, J.; Huang, P.; Zhao, H.; Zhang, Z.; Zhao, B.; Lee, D.L. Billion-scale commodity embedding for e-commerce recommendation in alibaba. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 839–848. [Google Scholar]
- Chen, Q.; Zhao, H.; Li, W.; Huang, P.; Ou, W. Behavior Sequence Transformer for E-commerce Recommendation in Alibaba. In Proceedings of the 1st International Workshop on Deep Learning Practice for High-Dimensional Sparse Data, Anchorage, AK, USA, 5 August 2019; pp. 1–4. [Google Scholar]
- Chen, M.; Zhou, X. DeepRank: Learning to Rank with Neural Networks for Recommendation. Knowl.-Based Syst. 2020, 209, 106478. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Zhou, X. CoNet: Co-occurrence neural networks for recommendation. Future Gener. Comput. Syst. 2021, 124, 308–314. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph Neural Networks for Social Recommendation. In Proceedings of the 28th International Conference on World Wide Web, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Ma, H.; Yang, H.; Lyu, M.R.; King, I. Sorec: Social Recommendation Using Probabilistic Matrix Factorization. In Proceedings of the 17th ACM Conference on Information and Knowledge Management, Napa Valley, CA, USA, 26–30 October 2008; pp. 931–940. [Google Scholar]
- Lee, D.; Kang, S.; Ju, H.; Park, C.; Yu, H. Bootstrapping user and item representations for one-class collaborative filtering. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, (SIGIR-21), New York, NY, USA, 11–15 July 2021; pp. 317–326. [Google Scholar]
- Chen, L.; Wu, L.; Zhang, K.; Hong, R.; Wang, M. Set2setrank: Collaborative set to set ranking for implicit feedback based recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 11–15 July 2021; pp. 585–594. [Google Scholar]
- Li, K.; Zhou, X.; Lin, F.; Zeng, W.; Alterovitz, G. Deep probabilistic matrix factorization framework for online collaborative filtering. IEEE Access 2019, 7, 56117–56128. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, W.; Lin, F.; Zeng, W.; Zhou, X.; Wu, P. Knowledge-aware reasoning with self-supervised reinforcement learning for explainable recommendation in MOOCs. Neural Comput. Appl. 2024, 36, 4115–4132. [Google Scholar] [CrossRef]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph neural networks in recommender systems: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hasanzadeh, A.; Hajiramezanali, E.; Narayanan, K.; Duffield, N.; Zhou, M.; Qian, X. Semi-implicit graph variational auto-encoders. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. arXiv 2018, arXiv:1802.04407. [Google Scholar]
- Taghizadeh, M.; Khayambashi, K.; Hasnat, M.A.; Alemazkoor, N. Multi-fidelity graph neural networks for efficient power flow analysis under high-dimensional demand and renewable generation uncertainty. Electr. Power Syst. Res. 2024, 237, 111014. [Google Scholar] [CrossRef]
- Morgoyeva, A.D.; Morgoyev, I.D.; Klyuyev, R.V.; Kochkovskaya, S.S. Forecasting hourly electricity generation by a solar power plant using machine learning algorithms. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2023, 334, 7–19. [Google Scholar] [CrossRef]
- Liang, D.; Altosaar, J.; Charlin, L.; Blei, D.M. Factorization Meets the Item Embedding: Regularizing Matrix Factorization with Item Co-occurrence. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; pp. 59–66. [Google Scholar]
- Zhang, W.; Lin, Y.; Liu, Y.; You, H.; Wu, P.; Lin, F.; Zhou, X. Self-Supervised Reinforcement Learning with dual-reward for knowledge-aware recommendation. Appl. Soft Comput. 2022, 131, 109745. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Q.; Nie, R.; Cao, J. Effective Metric Learning with Co-occurrence Embedding for Collaborative Recommendations. Neural Netw. 2020, 124, 308–318. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Ma, T.; Zhou, X. CoCNN: Co-occurrence CNN for recommendation. Expert Syst. Appl. 2022, 195, 116595. [Google Scholar] [CrossRef]
- Fu, D.; He, J. SDG: A Simplified and Dynamic Graph Neural Network. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 11–15 July 2021; pp. 2273–2277. [Google Scholar]
- Wu, J.; Wang, X.; Feng, F.; He, X.; Chen, L.; Lian, J.; Xie, X. Self-supervised Graph Learning for Recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 11–15 July 2021; pp. 726–735. [Google Scholar]
- Feng, F.; He, X.; Tang, J.; Chua, T.S. Graph Adversarial Training: Dynamically Regularizing based on Graph Structure. IEEE Trans. Knowl. Data Eng. 2019, 33, 2493–2504. [Google Scholar] [CrossRef]
- Bouma, G. Normalized (pointwise) mutual information in collocation extraction. Proc. GSCL 2009, 30, 31–40. [Google Scholar]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, VIC, Australia, 19–25 August 2017. [Google Scholar]
- Liu, B.; Tang, R.; Chen, Y.; Yu, J.; Guo, H.; Zhang, Y. Feature generation by convolutional neural network for click-through rate prediction. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 1119–1129. [Google Scholar]
- Deng, W.; Pan, J.; Zhou, T.; Kong, D.; Flores, A.; Lin, G. DeepLight: Deep lightweight feature interactions for accelerating CTR predictions in ad serving. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Online, 8–12 March 2021; pp. 922–930. [Google Scholar]
- Yue-Hei Ng, J.; Yang, F.; Davis, L.S. Exploiting local features from deep networks for image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 8–10 June 2015; pp. 53–61. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable cnn for joint description and detection of local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 8092–8101. [Google Scholar]
- Ding, Y.; Jia, S.; Ma, T.; Mao, B.; Zhou, X.; Li, L.; Han, D. Integrating stock features and global information via large language models for enhanced stock return prediction. arXiv 2023, arXiv:2310.05627. [Google Scholar]
- Chen, D.; Hong, W.; Zhou, X. Transformer Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
- Yun, S.; Jeong, M.; Kim, R.; Kang, J.; Kim, H.J. Graph transformer networks. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Wang, R.; Fu, B.; Fu, G.; Wang, M. Deep & cross Network for Ad Click Predictions. In Proceedings of the 23th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1–7. [Google Scholar]
- Wang, H.; Zhang, F.; Zhao, M.; Li, W.; Xie, X.; Guo, M. Multi-task Feature Learning for Knowledge Graph Enhanced Recommendation. In Proceedings of the 28th International Conference on World Wide Web, San Francisco, CA, USA, 13–17 May 2019; pp. 2000–2010. [Google Scholar]
- Xie, R.; Ling, C.; Wang, Y.; Wang, R.; Xia, F.; Lin, L. Deep Feedback Network for Recommendation. In Proceedings of the 29th International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 2519–2525. [Google Scholar]
- Chen, D.; Zhou, X. AttMoE: Attention with Mixture of Experts for remaining useful life prediction of lithium-ion batteries. J. Energy Storage 2024, 84, 110780. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, Y.; Zhang, Y.; Sun, F.; Lin, X.; Sun, H.; Wu, J.; Jiang, P.; Ge, J.; Ou, W.; et al. Personalized Re-ranking for Recommendation. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 3–11. [Google Scholar]
- Luo, A.; Zhao, P.; Liu, Y.; Zhuang, F.; Wang, D.; Xu, J.; Fang, J.; Sheng, V.S. Collaborative Self-Attention Network for Session-based Recommendation. In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI-20), Yokohama, Japan, 7–15 January 2021; pp. 2591–2597. [Google Scholar]
- Kang, W.C.; McAuley, J. Self-Attentive Sequential Recommendation. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 197–206. [Google Scholar]
- He, X.; He, Z.; Song, J.; Liu, Z.; Jiang, Y.G.; Chua, T.S. Nais: Neural Attentive Item Similarity Model for Recommendation. IEEE Trans. Knowl. Data Eng. 2018, 30, 2354–2366. [Google Scholar] [CrossRef]
- Wang, B.; Chen, J.; Li, C.; Zhou, S.; Shi, Q.; Gao, Y.; Feng, Y.; Chen, C.; Wang, C. Distributionally Robust Graph-based Recommendation System. In Proceedings of the ACM on Web Conference 2024, Singapore, 13–17 May 2024; pp. 3777–3788. [Google Scholar]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.S. Neural graph collaborative filtering. In Proceedings of the 42nd international ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar]
- Ye, H.; Li, X.; Yao, Y.; Tong, H. Towards robust neural graph collaborative filtering via structure denoising and embedding perturbation. ACM Trans. Inf. Syst. 2023, 41, 1–28. [Google Scholar] [CrossRef]
- Jin, B.; Gao, C.; He, X.; Jin, D.; Li, Y. Multi-behavior recommendation with graph convolutional networks. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 659–668. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Cai, D.; Qian, S.; Fang, Q.; Hu, J.; Xu, C. User cold-start recommendation via inductive heterogeneous graph neural network. ACM Trans. Inf. Syst. 2023, 41, 64. [Google Scholar] [CrossRef]
- Yang, J.H.; Chen, C.M.; Wang, C.J.; Tsai, M.F. HOP-rec: High-order proximity for implicit recommendation. In Proceedings of the 12th ACM Conference on Recommender Systems, Vancouver, BC, Canada, 31 August 2018; pp. 140–144. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Bansal, S.; Gowda, K.; Kumar, N. Multilingual personalized hashtag recommendation for low resource Indic languages using graph-based deep neural network. Expert Syst. Appl. 2024, 236, 121188. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, F.; Guo, X.; Chen, J.; Sha, K.; Wang, Y. Combine temporal information in session-based recommendation with graph neural networks. Expert Syst. Appl. 2024, 238, 121969. [Google Scholar] [CrossRef]
- Sedhain, S.; Menon, A.K.; Sanner, S.; Xie, L. Autorec: Autoencoders meet collaborative filtering. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18 May 2015; pp. 111–112. [Google Scholar]
- Wu, Z. An efficient recommendation model based on knowledge graph attention-assisted network (kgatax). arXiv 2024, arXiv:2409.15315. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Tiady, S.; Jain, A.; Sanny, D.R.; Gupta, K.; Virinchi, S.; Gupta, S.; Saladi, A.; Gupta, D. MERLIN: Multimodal & Multilingual Embedding for Recommendations at Large-scale via Item Associations. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, Boise, ID, USA, 21–25 October 2024; pp. 4914–4921. [Google Scholar]
- Patel, M.; Deepak, G. SCRF: Strategic Course Recommendation Framework. In International Conference on Intelligent Systems Design and Applications; Springer: Cham, Switzerland, 2023; pp. 380–389. [Google Scholar]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN variants for computer vision: History, architecture, application, challenges and future scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Strub, F.; Mary, J. Collaborative Filtering with Stacked Denoising Autoencoders and Sparse Inputs. In Proceedings of the 29th NIPS Workshop on Machine Learning for eCommerce, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidtthieme, L. BPR: Bayesian Personalized Ranking from Implicit Feedback. In Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T. Neural Collaborative Filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- Yun, H.; Raman, P.; Vishwanathan, S. Ranking via robust binary classification. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).