Knowledge Flow Dynamics in Organizations: A Stochastic Multi-Scale Analysis of Learning Barriers

Abstract

Organizations face fundamental challenges in managing knowledge flows across complex networks, yet existing frameworks often lack quantitative tools for optimization. We develop a novel stochastic multi-scale model introducing knowledge flow viscosity (KFV) to analyze organizational learning dynamics. This model quantifies resistance to knowledge transfer using a time-varying viscosity tensor, capturing both continuous learning processes and discrete knowledge acquisition events. Through renormalization group analysis, we establish the existence of critical thresholds in knowledge diffusion rates, characterizing phase transitions in organizational learning capacity. Numerical simulations demonstrate that targeted reductions in communication barriers near these thresholds can significantly enhance knowledge flow efficiency. The findings provide a mathematical foundation for understanding multi-level knowledge flow dynamics, suggesting precise conditions for effective interventions to optimize learning in complex organizational systems.

1. Introduction

In today’s knowledge-driven economy, effective management of knowledge flows represents a critical determinant of organizational performance and competitive advantage. Traditional frameworks provide qualitative insights into knowledge transfer but often lack the quantitative rigor needed to guide optimization efforts in complex organizational networks [1,2]. Recent research highlights persistent challenges in knowledge management, such as those associated with pinpointing optimal intervention points for knowledge transfer, predicting the effects of structural changes on knowledge flow, and quantifying the aggregation of individual learning into organizational outcomes [1,3,4,5].

Organizations today face unprecedented challenges in managing and optimizing knowledge flows across increasingly complex networks. Traditional approaches to knowledge management often lack quantitative rigor, making it difficult to identify optimal intervention points or predict the impact of structural changes. This gap between qualitative frameworks and practical optimization needs has become particularly acute as organizations grow more distributed and knowledge intensive. While existing research provides valuable insights into knowledge transfer mechanisms, there remains a critical need for mathematical frameworks that can capture the multi-scale dynamics of organizational learning. Our work addresses this need by introducing a quantitative approach that can precisely characterize knowledge flow barriers and predict system-level learning outcomes.

Advancements in multi-scale modeling have shown promise in addressing these challenges by combining fine-grained stochastic dynamics with data-driven techniques [4,6]. For example, recent multi-scale frameworks in complex systems have integrated stochastic variables and machine learning to capture nuanced interactions within variable dynamic networks, making them adaptable to complex organizational processes [7,8]. However, despite such advancements, significant computational challenges remain in translating these techniques into practical, organization-wide applications for knowledge management [9].

To bridge this gap, we introduce knowledge flow viscosity (KFV), a quantitative model that integrates network structure, stochastic processes, and multi-scale dynamics within a unified mathematical framework. By representing knowledge flow resistance as a time-varying viscosity tensor—a key innovation—KFV captures both structural and dynamic barriers to knowledge transfer. Our model incorporates continuous Wiener processes and discrete jump terms within stochastic differential equations (SDEs) to represent the full spectrum of knowledge evolution events, from gradual learning to sudden insights or technological breakthroughs [10,11]. We apply renormalization group theory to detect phase transitions in learning capacity [12] and homogenization theory to link micro- and macro-scale dynamics [13].

Our study investigates the following research questions:

• How can structural and dynamic properties of organizational networks influence knowledge transfer efficiency?
• Under what conditions do organizations experience significant shifts in learning capacity?
• How do individual learning processes aggregate into organization-level knowledge dynamics?
• What intervention strategies optimize knowledge flow within complex organizational networks?

Our contributions to organizational learning theory are threefold. First, we present a mathematical framework that unifies separate dimensions of knowledge transfer, including network structure [3], knowledge barriers [14], and multi-level dynamics [5]. Second, we derive critical thresholds in learning capacity, identifying phase transitions where small reductions in communication barriers yield substantial gains in knowledge flow efficiency. Third, we offer quantitative criteria to target interventions effectively, demonstrating how localized changes can improve organizational knowledge transfer.

The remainder of this paper is organized as follows. Section 2 develops our theoretical framework, introducing the KFV tensor and multi-scale aggregation functions. Section 3 presents our stochastic multi-scale model of knowledge dynamics. Section 4 derives analytical results on stability conditions and phase transitions. Section 5 presents numerical simulations validating our theoretical predictions and Section 6 discusses implications for theory and practice. Section 7 concludes.

2. Theoretical Framework

In this section, we develop the mathematical foundations of our model to analyze organizational learning dynamics. We introduce the knowledge symbiosis network (KSN) to represent the dynamic topology of knowledge flows within an organization. We then define the concept of KFV, formalizing it as a tensor that quantifies resistance to knowledge transfer. Finally, we establish the multi-scale nature of our framework through aggregation functions that link micro-level (individual), meso-level (team), and macro-level (organizational) knowledge states.

2.1. Knowledge Symbiosis Network

The KSN models the complex, evolving structure of knowledge interactions within an organization. It captures how knowledge units or actors (e.g., individuals or departments) are connected and how these connections change over time.

Definition 1 (KSN).

A KSN is a tuple $KSN\left(t\right)=\left(V,E\left(t\right),D,w\left(t\right)\right)$, where $V=\left\{1,\dots ,N\right\}$ is a finite set of nodes representing knowledge units or actors; $D=\left\{1,\dots ,K\right\}$ is a finite set of knowledge domains; $E\left(t\right)\subseteq V\times V\times D$ is the set of edges at time $t$, representing knowledge flows; and $w\left(t\right):E\left(t\right)\to R^{+}$ is a weight function assigning a non-negative real value to each edge at time $t$, indicating the strength or intensity of the knowledge flow in that domain.

The KSN builds upon and extends existing network models in organizational theory. It shares similarities with the multidimensional networks described by [3], which capture the complex, multi-layered nature of organizational relationships. However, the KSN advances these models by explicitly incorporating knowledge domains and allowing edge weights to vary over time, enabling a more nuanced representation of knowledge flow dynamics. Unlike static network models commonly used in organizational research [15], the KSN’s time-dependent nature captures the evolving structure of organizational knowledge networks. This dynamic approach aligns with recent calls in the literature for more process-oriented views of organizational networks [16]. Furthermore, the KSN’s formalization as a weighted, directed hypergraph enables the representation of complex, multi-actor knowledge transfer processes that go beyond traditional dyadic models.

The time-dependent nature of $E\left(t\right)$ and $w\left(t\right)$ allows for the creation, dissolution, and weight adjustment of edges over time, reflecting the dynamic nature of organizational knowledge networks. To represent the structure of the KSN at a given time $t$, let $A\left(t\right)={\left(a_{ij}^k\left(t\right)\right)}_{N\times N\times K}$ denote the adjacency tensor of the network, where

$$a_{ij}^k\left(t\right)=\left\{\begin{array}{cc}\hfill w_{ij}^k\left(t\right)& \mathrm{if}\left(i,j,k\right)\in E\left(t\right),\hfill \\ \hfill 0& otherwise,\hfill \end{array}\right.$$

(1)

where $a_{ij}^k\left(t\right)$ represents the weight of the knowledge flow from node $i$ to node $j$ in domain $k$ at time $t$.

Property 1 (Dynamic Network).

The KSN is inherently dynamic, allowing for the temporal evolution of its structure. Formally, $\forall t_1,t_2\in R^{+},t_1\ne t_2\to E\left(t_1\right)\ne E\left(t_2\right)$ in general.

This property ensures that our model can capture the evolving nature of organizational knowledge structures, a crucial aspect often overlooked in static network representations [3].

Illustrative Example:

Consider an organization with $V=\left\{1, 2, 3\right\}$, representing departments A, B, and C and $D=\left\{1, 2\right\}$, representing domains such as “Marketing” and “R&D.” At time $t$, there is a knowledge flow in “Marketing” (domain 1) from department A to B, so $\left(1,2,1\right)\in E\left(t\right)$ with weight $w_{12}^1\left(t\right)=0.8$, and there is a knowledge flow in “R&D” (domain 2) from department B to C, so $\left(2, 3, 2\right)\in E\left(t\right)$ with weight $w_{23}^2\left(t\right)=0.5$. The adjacency tensor $A\left(t\right)$ would reflect these connections and weights accordingly.

2.2. Knowledge Flow Viscosity

We now introduce the central concept of KFV, representing it as a tensor that quantifies the resistance to knowledge transfer within the KSN.

Definition 2 (KFV Tensor).

The KFV is represented by a tensor $\nu \left(t\right)={\left({\nu }_{ij}^k\left(t\right)\right)}_{N\times N\times K}$, where ${\nu }_{ij}^k\left(t\right)\in R^{+}$ quantifies the resistance to knowledge flow from node $i$ to node $j$ in domain $k$ at time $t$.

The viscosity depends on various factors, potentially varying across different knowledge domains, as follows:

$${\nu }_{ij}^k\left(t\right)=f\left(C_{ij}^k\left(t\right),S_{ij}\left(t\right),M_{ij}\left(t\right),A_j^k\left(t\right),\Omega \left(t\right)\right)$$

(2)

where $C_{ij}^k\left(t\right)\in R^{+}$ represents cognitive distance in domain $k$, $S_{ij}\left(t\right)\in R^{+}$ captures structural impediments, $M_{ij}\left(t\right)\in R^{+}$ denotes motivational factors, $A_j^k\left(t\right)\in R^{+}$ represents the absorptive capacity of node $j$ in domain $k$ and $\Omega \left(t\right)\in R^{+}$ encompasses global organizational factors.

Each of the components of the viscosity tensor ${\nu }_{ij}^k\left(t\right)$ reflects established principles from organizational learning theory. For instance, the cognitive distance $C_{ij}^k\left(t\right)$ relates to the notion of absorptive capacity [17], representing the difficulty in transferring knowledge between individuals or units with different expertise or mental models. The structural impediment $S_{ij}\left(t\right)$ captures how organizational structures influence knowledge flow, aligning with research on the impact of formal and informal networks on knowledge transfer [18]. The motivational factor $M_{ij}\left(t\right)$ considers the role of incentives in enabling or constraining knowledge sharing [19]. The absorptive capacity $A_j^k\left(t\right)$ reflects the recipient’s ability to assimilate and apply new knowledge, a core concept in organizational learning literature [20]. Finally, the global organizational factor Ω(t) represents organization-wide conditions impacting knowledge flow, such as culture or technological infrastructure [1]. By incorporating these theoretically grounded components, the viscosity tensor provides a comprehensive and nuanced representation of the multifaceted barriers to knowledge transfer in organizations.

The specific form of $f$ is determined based on empirical observations and theoretical considerations, subject to the following properties:

Property 2. (Viscosity Tensor Properties).

• Non-negativity: ${\nu }_{ij}^k\left(t\right)\ge 0,\forall i,j,k,t$.
• Symmetry: ${\nu }_{ij}^k\left(t\right)={\nu }_{ji}^k\left(t\right),\forall i,j,k,t$.
• Triangle Inequality: ${\nu }_{ij}^k\left(t\right)+{\nu }_{jl}^k\left(t\right)\ge {\nu }_{il}^k\left(t\right),\forall i,j,l,k,t$.

These properties ensure that the viscosity tensor behaves in a manner consistent with physical intuitions about resistance to knowledge flow, while allowing for the complex, multi-dimensional nature of organizational knowledge transfer.

2.3. Multi-Scale Dynamics

To capture the hierarchical nature of organizational knowledge, we formalize the multi-scale aspects of our model through rigorously defined aggregation functions. Let ${\Psi }_{\mu },{\Psi }_m, \mathrm{and} {\Psi }_M$ be the state spaces for micro-, meso-, and macro-level knowledge respectively.

Definition 3 (Knowledge Aggregation Functions).

• Micro to Meso: $h_m^k:{\Psi }_{\mu }^{\left|m\right|}\to {\Psi }_m$, where $\left|m\right|$ is the size of team $m$.
• Meso to Macro: $H^k:{\Psi }_m^M\to {\Psi }_M$, where $M$ is the number of teams.

Formally:

$$T_m^k=h_m^k\left(K_i^k|i\in {\mathrm{team}}_m\right)={\left({{\displaystyle \sum }}_{i\in m}{w}_i^k{\left(K_i^k\right)}^p\right)}^{1/p}$$

(3)

$$O^k=H^k\left(T_m^k\right)={\left({{\displaystyle \sum }}_m{v}_m^k{\left(T_m^k\right)}^q\right)}^{1/q}$$

(4)

where $w_i^k,v_m^k$ are weight factors, and $p,q\in R\setminus \left\{0\right\}$ are parameters controlling the non-linearity of the aggregation.

Property 3 (Aggregation Function Properties).

• Monotonicity: If $K_i^k\le K_i^{\prime k}\forall i$, then $h_m^k\left(K_i^k\right)\le h_m^k\left(K_i^{\prime k}\right)$.
• Continuity: $h_m^k$ and $H^k$ are continuous functions.
• Boundary conditions: $h_m^k\left(0,\dots ,0\right)=0,h_m^k\left(C,\dots ,C\right)=C,H^k\left(0,\dots ,0\right)=0,H^k\left(C,\dots ,C\right)=C$, where $C$ is a constant representing maximum knowledge level.

These aggregation functions and their properties provide a mathematically rigorous foundation for analyzing how individual and team knowledge dynamics give rise to organizational-level phenomena, addressing a key challenge in multi-level organizational research [5].

The framework established in this section—comprising the KSN, the KFV tensor, and the multi-scale aggregation functions—forms the mathematical bedrock upon which we will construct our SDE model in the subsequent section. This formalization allows us to capture the complex, dynamic nature of organizational knowledge flows while maintaining mathematical rigor and tractability.

3. Stochastic Multi-Scale Model of Knowledge Dynamics

Building upon the theoretical framework established in Section 2, we now develop a comprehensive stochastic multi-scale model of knowledge dynamics within the KSN. This model captures the intricate interplay between individual knowledge evolution, network structure dynamics, and emergent organizational-level phenomena. Note that we make several assumptions in our model setting, as follows. First, we assume that knowledge transfer is primarily driven by direct interactions between nodes (individuals/units) and is influenced by both structural (network topology) and dynamic (time-varying viscosity) factors. Second, we assume that network dynamics evolve according to preferential attachment principles modified by knowledge-dependent weights, meaning that nodes are more likely to form connections with others possessing complementary knowledge. Third, we assume that knowledge depreciation follows a first-order decay process, while knowledge acquisition can occur through both continuous learning and discrete jump events.

3.1. Micro-Level Knowledge Dynamics

We begin by formulating the evolution of individual knowledge levels using a system of SDEs. For each node $i \in V$ and knowledge domain $k \in D$, the SDE governing knowledge dynamics is given by

$$\begin{gathered} d{K}_i^k=\left[{\mu }_i^k\left(K_i^k,t\right)+{{\displaystyle \sum }}_{j\ne i}{\nu }_{ij}^k\left(t\right)·a_{ij}^k\left(t\right)·g\left(K_i^k,K_j^k\right)\right]dt+{\sigma }_i^k\left(K_i^k,t\right)d{W}_i^k\left(t\right) \\ +{{\displaystyle \int }}_{\Gamma }{h}_i^k\left(K_i^k,\gamma ,t\right)N\left(d\gamma ,dt\right), \end{gathered}$$

(5)

where $K_i^k\left(t\right)\in \left[0,C_k\right]$ is the knowledge level of node $i$ in domain $k$ at time $t$, with $C_k$ being the maximum knowledge level in domain $k$; ${\mu }_i^k:\left[0,C_k\right]\times R^{+}\to R$ is the drift function representing intrinsic knowledge growth or decay; ${\nu }_{ij}^k\left(t\right) \mathrm{is} \mathrm{the} \left(i,j,k\right)$-th element of the viscosity tensor defined in Section 2.2; $a_{ij}^k\left(t\right)$ is the $\left(i,j,k\right)$-th element of the adjacency tensor $A\left(t\right)$ of the KSN; $g:{\left[0,C_k\right]}^2\to R$ is a non-linear transfer function modeling knowledge flow between nodes; ${\sigma }_i^k:\left[0,C_k\right]\times R^{+}\to R^{+}$ is the volatility function capturing the stochastic nature of knowledge evolution; $W_i^k\left(t\right)$ is a standard Wiener process on a filtered probability space $\left(\Omega ,\mathcal{F},{\left\{\mathcal{F}t\right\}}_{t\ge 0},P\right)$; $h_i^k:\left[0,C_k\right]\times \Gamma \times R^{+}\to R$ is the jump amplitude function; $\Gamma$ is a complete, separable metric space; and $N\left(d\gamma ,dt\right)$ is a Poisson random measure on $\Gamma \times R^{+}$ with intensity measure $\nu \left(d\gamma \right)dt$.

The terms in Equation (5) can be interpreted as follows:

• Drift term ${\mu }_i^k\left(K_i^k,t\right)$: This term represents the intrinsic knowledge growth or decay for node i in domain k, capturing phenomena such as individual learning and knowledge obsolescence [21].
• Knowledge transfer term ${\Sigma }_{j\ne i}{\nu }_{ij}^k\left(t\right)·a_{ij}^k\left(t\right)·g\left(K_i^k,K_j^k\right)$: This term models the knowledge transfer between nodes, with ${\nu }_{ij}^k\left(t\right)$ representing the viscosity, $a_{ij}^k\left(t\right)$ the network connection strength, and $g\left(K_i^k,K_j^k\right)$ the transfer function.
• Volatility term ${\sigma }_i^k\left(K_i^k,t\right)d{W}_i^k\left(t\right)$: This component captures the stochastic fluctuations in knowledge levels, reflecting the inherent uncertainty in learning processes [22].
• Jump term ${\int }_{\Gamma }{h}_i^k\left(K_i^k,\gamma ,t\right)N\left(d\gamma ,dt\right)$: This term represents discontinuous jumps in knowledge levels and models sudden knowledge acquisition or loss events, such as training sessions, key personnel changes, or technology adoptions [23]. The Poisson random measure $N\left(d\gamma ,dt\right)$ governs the occurrence of these events, while $h_i^k$ determines their magnitude and direction.

This formulation allows us to capture both the continuous, gradual aspects of organizational learning and the discrete, punctuated events that can significantly alter knowledge levels [24].

We specify the components of the SDE as follows:

• Drift term:

  $${\mu }_i^k\left(K_i^k,t\right)=r_i^k\left(t\right)K_i^k\left(1-K_i^k/C_k\right)-{\delta }_i^k\left(t\right)K_i^k+D_i^k\left(t\right){\nabla }^2{K}_i^k,$$

  where $r_i^k\left(t\right)>0$ is the intrinsic growth rate, ${\delta }_i^k\left(t\right)>0$ is the knowledge depreciation rate, and $D_i^k\left(t\right)>0$ is a diffusion coefficient.
• Transfer function:

  $$g\left(K_i^k,K_j^k\right)={\alpha }_{ij}^k\left(K_j^k-K_i^k\right)H\left(K_j^k-K_i^k\right),$$

  where ${\alpha }_{ij}^k>0$ is the maximum transfer rate and $H\left(·\right)$ is the Heaviside step function, which ensures that knowledge flows only in the direction of higher to lower levels.
• Volatility function:

  $${\sigma }_i^k\left(K_i^k,t\right)={\beta }_i^k\left(t\right)\sqrt{K_i^k\left(C_k-K_i^k\right)},$$

  where ${\beta }_i^k\left(t\right)>0$ is a time-varying volatility parameter, which ensures that volatility is zero at knowledge bounds $K_i^k=0$ and $K_i^k=C_k$.
• Lipschitz condition for the jump term: To ensure the well-posedness of the jump term, we need to impose the condition that, for all $t\in \left[0,T\right]$ and $x,y\in R^{N\times K}$, there exists a constant $L_h>0$, such that

  $${\int }_{\Gamma }|\left|h\left(t,x,\gamma \right)-h\left(t,y,\gamma \right)\right|{|}^2\nu \left(d\gamma \right)\le L_h|x-y{|}^2$$

This condition is satisfied by our assumption on the boundedness of the jump amplitude function $h_i^k$ and the finite intensity measure $\nu \left(d\gamma \right)$.

3.2. Network Dynamics

To capture the co-evolution of knowledge levels and network structure, we model the dynamics of the adjacency tensor $A\left(t\right)$ through a system of SDEs. For each element $a_{ij}^k\left(t\right)$, we have

$$\begin{gathered} d{a}_{ij}^k\left(t\right)=\left[{\lambda }_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)-{\mu }_{ij}^k\left(t\right)a_{ij}^k\left(t\right)+{\rho }_{ij}^k\left(t\right)f\left(K_i^k,K_j^k\right)\right]dt \\ +{ \gamma }_{ij}^k\left(t\right)\sqrt{a_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)}d{B}_{ij}^k\left(t\right) \end{gathered}$$

(6)

where ${\lambda }_{ij}^k\left(t\right)>0$ and ${\mu }_{ij}^k\left(t\right)>0$ are the rates of link formation and dissolution, respectively; ${\rho }_{ij}^k\left(t\right)\ge 0$ is a coupling parameter between knowledge levels and network structure; $f:{\left[0,C_k\right]}^2\to \left[0,1\right]$ is a function modeling the influence of knowledge levels on link formation; ${\gamma }_{ij}^k\left(t\right)>0$ is a volatility parameter for network dynamics; and $B_{ij}^k\left(t\right)$ is a standard Wiener process, independent of $W_i^k\left(t\right)$.

The form of Equation (6) is chosen to capture key aspects of organizational network dynamics, as follows:

• The term ${\lambda }_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)$ represents the tendency for new connections to form, with the $\left(1-a_{ij}^k\left(t\right)\right)$ factor ensuring that the connection strength remains bounded.
• $-{\mu }_{ij}^k\left(t\right)a_{ij}^k\left(t\right)$ models the natural decay of connections over time, reflecting the idea that relationships require maintenance to persist [25].
• ${\rho }_{ij}^k\left(t\right)f\left(K_i^k,K_j^k\right)$ captures how knowledge levels influence network formation, aligning with theories of homophily and expertise-seeking in organizational networks [26].
• The noise term ${\gamma }_{ij}^k\left(t\right)\sqrt{\left(a_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)\right)}d{B}_{ij}^k\left(t\right)$ introduces stochastic fluctuations in connection strengths, with the $\sqrt{\left(a_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)\right)}$ factor ensuring that the noise level is highest for intermediate connection strengths and approaches zero as $a_{ij}^k\left(t\right)$ nears 0 or 1.

This formulation allows the network to evolve dynamically in response to both endogenous factors (current network structure and knowledge levels) and exogenous stochastic influences, capturing the complex, adaptive nature of organizational networks [3].

3.3. Multi-Scale Dynamics Model

To bridge the micro-level dynamics with meso- and macro-level phenomena, we employ the aggregation functions defined in Section 2.3. The evolution of meso-level (team) knowledge $T_m^k\left(t\right)$ and macro-level (organizational) knowledge $O^k\left(t\right)$ is given by

$$d{T}_m^k={\displaystyle \frac{\partial h_m^k}{\partial t}}+{{\displaystyle \sum }}_{i\in m}\left({\displaystyle \frac{\partial h_m^k}{\partial K_i^k}}\right)d{K}_i^k+{\displaystyle \frac{1}{2}}{{\displaystyle \sum }}_{i,j\in m}\left({\displaystyle \frac{{\partial }^2{h}_m^k}{\partial K_i^k\partial K_j^k}}\right)d\langle K_i^k,K_j^k\rangle ,$$

(7)

$$d{O}^k={\displaystyle \frac{\partial H^k}{\partial t}}+{{\displaystyle \sum }}_m\left({\displaystyle \frac{\partial H^k}{\partial T_m^k}}\right)d{T}_m^k+{\displaystyle \frac{1}{2}}{{\displaystyle \sum }}_{m,n}\left({\displaystyle \frac{{\partial }^2{H}^k}{\partial T_m^k\partial T_n^k}}\right)d\langle T_m^k,T_n^k\rangle ,$$

(8)

where $\langle ·,·\rangle$ denotes the quadratic covariation process. The factor of 1/2 in the last term of Equation (7) is necessary due to the nature of the quadratic covariation process. This correction ensures that the equation accurately represents the second-order terms in the Itô–Taylor expansion of the stochastic process [27]. The presence of this factor is crucial for maintaining the correct scaling behavior in the limit of small time increments and for ensuring consistency with the fundamental theorem of stochastic calculus.

3.4. Existence and Uniqueness of Solutions

The goal here is to establish conditions under which a unique strong solution exists for the system of SDEs (5)–(8) based on standard results for SDEs with jumps.

Theorem 1 (Existence and Uniqueness).

The theorem states that, under appropriate Lipschitz continuity and growth conditions on the coefficients of (5)–(8), there exists a unique strong solution to the system of SDEs on $\left[0,T\right]$ for any finite $T>0$.

Proof. 

We verify the necessary conditions for the application of the general existence and uniqueness theorem for SDEs with jumps [28], as follows:

• Lipschitz continuity: We need to show that, for all $t\in \left[0,T\right]$ and $x,y\in R^{N\times K}$, there exists a constant $L>0$ such that

  $$\left|\mu \left(t,x\right)-\mu \left(t,y\right)\left|+\right|\sigma \left(t,x\right)-\sigma \left(t,y\right)\left|\le L\right|x-y\right|,$$

  where $\mu$ and $\sigma$ represent the drift and diffusion terms, respectively.
  For the drift term:

  $$\begin{array}{l}\left|\mu \left(t,x\right)-\mu \left(t,y\right)\right|=|{{\displaystyle \sum }}_{i,k}\left[r_i^k\left(t\right)x_i^k\left(1-x_i^k/C_k\right)-{\delta }_i^k\left(t\right)x_i^k+D_i^k\left(t\right){\nabla }^2{x}_i^k\right]-[r_i^k\left(t\right)y_i^k(1-y_i^k/\\ C_k)-{\delta }_i^k\left(t\right)y_i^k+D_i^k\left(t\right){\nabla }^2{y}_i^k]|\\ \le {{\displaystyle \sum }}_{i,k}\left|r_i^k\left(t\right)\right|·\left|x_i^k-y_i^k\right|·\left|1-\left(x_i^k+y_i^k\right)/C_k\right|+\left|{\delta }_i^k\left(t\right)\right|·\left|x_i^k-y_i^k\right|+\left|D_i^k\left(t\right)\right|·\left|{\nabla }^2\left(x_i^k-y_i^k\right)\right|\\ \le L_1\left|x-y\right|,\end{array}$$

  where $L_1$ depends on the bounds of $r_i^k\left(t\right),{\delta }_i^k\left(t\right),$ and $D_i^k\left(t\right)$.
  Similarly, for the diffusion term:

  $$\begin{array}{ll}\left|\sigma \left(t,x\right)-\sigma \left(t,y\right)\right|& =\left|{\sum }_{i,k}{\beta }_i^k\left(t\right)\left[\sqrt{x_i^k\left(C_k-x_i^k\right)}-\sqrt{y_i^k\left(C_k-y_i^k\right)}\right]\right|\\ & \le {{\displaystyle \sum }}_{i,k}\left|{\beta }_i^k\left(t\right)\right|·\left|\sqrt{x_i^k\left(C_k-x_i^k\right)}-\sqrt{y_i^k\left(C_k-y_i^k\right)}\right|\\ & \le L_2\left|x-y\right|,\end{array}$$

  where $L_2$ depends on the bounds of ${\beta }_i^k\left(t\right)$ and the Lipschitz constant of the square root function on $\left[0,C_k\right]$.
  Therefore, the Lipschitz condition is satisfied with $L=\max \left(L_1,L_2\right)$.
• Linear growth: We need to show that there exists a constant $K>0$ such that

  $$\left|\mu \left(t,x\right){|}^2+\right|\sigma \left(t,x\right){|}^2\le K^2\left(1+|x{|}^2\right).$$
  For the drift term:

  $$|\mu \left(t,x\right){|}^2\le {\left({{\displaystyle \sum }}_{i,k}\left|r_i^k\left(t\right)x_i^k\left(1-x_i^k/C_k\right)\right|+\left|{\delta }_i^k\left(t\right)x_i^k\right|+\left|D_i^k\left(t\right){\nabla }^2{x}_i^k\right|\right)}^2\le K_1^2\left(1+|x{|}^2\right),$$

  where $K_1$ depends on the bounds of $r_i^k\left(t\right),{\delta }_i^k\left(t\right), \mathrm{and} D_i^k\left(t\right).$
  For the diffusion term:

  $$|\sigma \left(t,x\right){|}^2\le {\left({{\displaystyle \sum }}_{i,k}\left|{\beta }_i^k\left(t\right)\right|·\sqrt{x_i^k\left(C_k-x_i^k\right)}\right)}^2\le K_2^2\left(1+|x{|}^2\right),$$

  where $K_2$ depends on the bounds of ${\beta }_i^k\left(t\right)$ and $C_k.$
  Therefore, the linear growth condition is satisfied with $K=\max \left(K_1,K_2\right).$
• Integrability: For the jump term, we need to show that

  $${{\displaystyle \int }}_{\Gamma }\left(1\wedge |h\left(t,x,\gamma \right){|}^2\right)\nu \left(d\gamma \right)<\infty .$$

This condition is satisfied by our assumption on the boundedness of the jump amplitude function $h_i^k$ and the finite intensity measure $\nu \left(d\gamma \right)$.

Given these conditions, we can apply Theorem 1.19 from [28] to establish the existence and uniqueness of a strong solution. □

This theorem ensures that our model is mathematically well defined and provides a solid foundation for further analysis of its properties and behavior.

3.5. Martingale Properties

The martingale structure of our model plays a crucial role in understanding its long-term behavior and stability properties.

Proposition 1.

Let ${\mathcal{F}}_{\mathcal{t}}$ be the natural filtration generated by the Wiener processes and the Poisson random measure up to time $t$. Then, the process

$$M_t^{i,k}=K_i^k\left(t\right)-K_i^k\left(0\right)-{{\displaystyle \int }}_0^t\left[{\mu }_i^k\left(K_i^k\left(s\right),s\right)+{{\displaystyle \sum }}_{j\ne i}{\nu }_{ij}^k\left(s\right)·a_{ij}^k\left(s\right)·g\left(K_i^k\left(s\right),K_j^k\left(s\right)\right)\right]ds$$

(9)

is a local martingale with respect to ${\mathcal{F}}_{\mathcal{t}}$.

Proof. 

The proof follows from the application of Itô’s formula for jump-diffusion processes and the martingale property of stochastic integrals with respect to Brownian motion and compensated Poisson random measures. □

This martingale property will be instrumental in deriving stability conditions and analyzing the long-term behavior of knowledge levels in subsequent sections.

The stochastic multi-scale model developed in this section provides a comprehensive mathematical representation of knowledge dynamics within the KSN. By capturing the intricate interplay between individual knowledge evolution, network structure dynamics, and emergent organizational phenomena, this model lays the groundwork for the rigorous analysis of organizational learning processes. In the following sections, we will leverage this formulation to derive key insights into stability conditions, phase transitions, and emergent collective behaviors in organizational knowledge dynamics.

4. Analytical Results

In this section, we present a series of analytical results derived from the stochastic multi-scale model developed in Section 3. We begin by examining the stability properties of the system, then characterize phase transitions in knowledge diffusion rates, and finally analyze emergent collective behaviors across organizational scales.

4.1. Stability Analysis

We start by investigating the stability properties of the knowledge dynamics described by our SDE system. This analysis provides insights into the long-term behavior of knowledge levels within the organization.

4.1.1. Local Stability

For local stability, let $K^{\ast }=\left(K_1^{1\ast },\dots ,K_N^{K\ast }\right)$ be an equilibrium point of the deterministic part of our system (5). The stability of this equilibrium is determined by linearizing the system around $K^{\ast }$.

Theorem 2

(Local Stability Criterion). The equilibrium $K^{\ast }$ is locally asymptotically stable in probability if all eigenvalues of the Jacobian matrix $J\left(K^{\ast }\right)$ have negative real parts, where

$$J_{ij}^{kl}\left(K^{\ast }\right)={\displaystyle \frac{\partial }{\partial K_j^l}}\left[{\mu }_i^k\left(K_i^k,t\right)+{{\displaystyle \sum }}_{m\ne i}{\nu }_{im}^k\left(t\right)·a_{im}^k\left(t\right)·g\left(K_i^{k\ast },K_m^{k\ast }\right)\right].$$

(10)

Proof. 

The stability follows from the principle of linearized stability for SDEs as outlined by [11]. Let $\xi \left(t\right)=K\left(t\right)-K^{\ast }$, where the linearized system is

$$d\xi =J\left(K^{\ast }\right)\xi dt+\mathrm{higher} \mathrm{order} \mathrm{terms}+\mathrm{stochastic} \mathrm{terms}.$$

By Theorem 4.3.1 in Mao [11], if all eigenvalues of $J\left(K^{\ast }\right)$ have negative real parts, then $K^{\ast }$ is locally asymptotically stable in probability. □

This result suggests that, when the Jacobian matrix’s eigenvalues have negative real parts, the knowledge equilibrium is resilient to small perturbations, allowing the organization to maintain a stable knowledge state.

This local stability can imply both benefits and drawbacks. Stable knowledge structures ensure organizational consistency and predictability but may also contribute to inertia, as highlighted by [29] and the concept of competency traps [30]. This stability criterion further suggests that, while small changes may not disrupt equilibrium, larger or sustained changes could move the system beyond this equilibrium, prompting a significant reorganization of knowledge structures.

Furthermore, the local nature of this stability criterion suggests that, while an organization may be resilient to small changes, larger shocks or sustained pressures could push it beyond the basin of attraction of its current stable state, potentially leading to significant reorganization of its knowledge structure. This mathematical insight provides a formal basis for understanding phenomena such as punctuated equilibrium in organizational evolution [24] and the challenges of managing organizational change initiatives [31].

4.1.2. Global Stability

To establish conditions for global stability, we construct a stochastic Lyapunov function for our system.

Theorem 3 (Global Stability Condition).

Let  $V:R_{+}^{N\times K}\to R_{+}$ be a twice continuously differentiable function satisfying the following:

• $V\left(K\right)>0$ for all  $K\ne K^{\ast }$.
• $V\left(K^{\ast }\right)=0$.
• $\mathcal{L}V\left(K\right)<0$ for all  $K\ne K^{\ast }$, where  $\mathcal{L}$ is the infinitesimal generator of the SDE system in Equation (5).

Then $K^{\ast }$ is globally asymptotically stable in probability.

Proof. 

We apply the stochastic version of Lyapunov’s second method [32]. Define the stopping time ${\tau }_R=\inf \{t\ge 0:\left|K\left(t\right)\right|\ge R\}$. By Itô’s formula, we find the following:

$$E\left[V\left(K\left(t\wedge {\tau }_R\right)\right)\right]-V\left(K\left(0\right)\right)=E\left[{{\displaystyle \int }}_0^{t\wedge {\tau }_R}\mathcal{L}V\left(K\left(s\right)\right)ds\right]<0.$$

(11)

Taking $R \to \infty$ and $t \to \infty$, we conclude that $K\left(t\right)\to K^{\ast }$ in probability as $t\to \infty$. □

This theorem provides a powerful tool for establishing the global stability of knowledge equilibria, ensuring that organizational knowledge converges to a stable state regardless of initial conditions.

4.2. Phase Transitions in Knowledge Diffusion

We now analyze the existence of phase transitions in the knowledge diffusion process, focusing on the critical role of the viscosity tensor.

4.2.1. Mean-Field Approximation

To simplify our analysis, we consider a mean-field approximation of the system, assuming homogeneous viscosity $\nu$ and uniform connectivity.

Proposition 2 (Mean-Field Equation).

In the mean-field limit, the average knowledge level $\overline{K}\left(t\right)$ evolves according to the following:

$${\displaystyle \frac{d\overline{K}}{dt}}=\overline{r}\overline{K}\left(1-\overline{K}/C\right)-\overline{\delta }\overline{K}+\overline{D}{\nabla }^2\overline{K}-\overline{\nu }f\left(\overline{K}\right),$$

(12)

where  $\overline{r}, \overline{\delta }, \overline{D},$ and  $\overline{\nu }$ are averaged parameters, and  $f\left(\overline{K}\right)$ represents the mean-field knowledge transfer term.

Proof. 

The proof follows from taking the expectation of Equation (5) and applying the law of large numbers in the limit of a large system size. □

4.2.2. Renormalization Group Analysis

To determine the existence of a phase transition, we use renormalization group (RG) techniques applied to the mean-field equation.

Theorem 4 (Existence of Critical Viscosity).

There exists a critical viscosity  ${\nu }_c$, such that

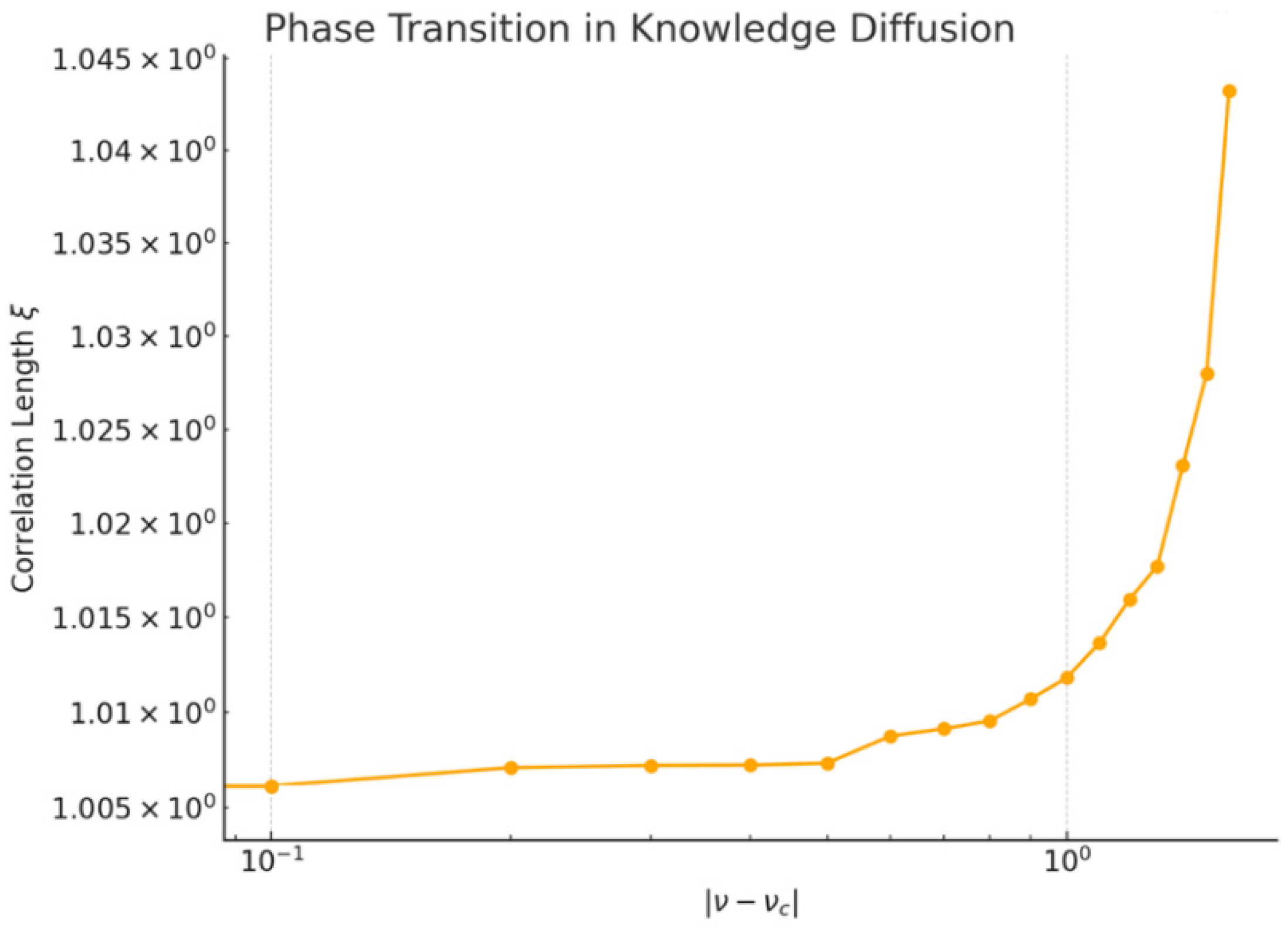
• For  $\nu <{\nu }_c$, the system exhibits a diffusive phase with long-range correlations in knowledge levels.
• For  $\nu >{\nu }_c$, the system enters a localized phase where knowledge transfer is significantly impeded.

Proof. 

We apply the ε-expansion method in the vicinity of the upper critical dimension $d_c=4$. Let $d=4-ϵ$ and introduce a coarse-graining transformation, as follows:

$$K^{\prime }\left(x^{\prime }\right)=b^{\zeta }K\left(x\right), x^{\prime }=b^{-1}x, t^{\prime }=b^{-z}t,$$

where $b>1$ is the scaling factor, $\zeta$ is the field anomalous dimension, and $z$ is the dynamic critical exponent. Here, $\epsilon$ is a small, positive parameter introduced in the context of the ε-expansion method, a standard technique in renormalization group analysis [12].

We express the mean-field equation in terms of a functional integral:

$$Z=\int DK\exp \left(-S\left[K\right]\right).$$

The action in d-dimensions is as follows:

$$S\left[K\right]=\int d^{d}xdt\left[{\displaystyle \frac{1}{2}}{\left(\nabla K\right)}^2+{\displaystyle \frac{r}{2}}{K}^2+{\displaystyle \frac{u}{4!}}{K}^4-hK+{\displaystyle \frac{1}{2{\Gamma }_0}}{\left({\partial }_{t}K\right)}^2\right].$$

Here, $r\propto \left(\nu -{\nu }_c\right)$ is the control parameter, $u$ is the coupling constant, $h$ is an external field, and ${\Gamma }_0$ is a kinetic coefficient. This action describes the dynamics of the field $K\left(x,t\right)$, including the terms for spatial gradients ${\left(\nabla K\right)}^2$, the quadratic term $r{K}^2$ (controlling the mass), and the quartic interaction term $u{K}^4$, with h as the external field and ${\Gamma }_0$ as a kinetic coefficient for time evolution.

Under the RG transformation, fields and parameters rescale according to the scaling factor $b>1$. The rescaling is defined as follows:

$$K^{\prime }\left(x^{\prime }\right)=b^{\zeta }K\left(x\right),$$

$$r^{\prime }=b^{2-\eta }r, u^{\prime }=b^{4-d-2\eta }u{\mu }^{ϵ},$$

$$h^{\prime }=b^{\left(d+2-\eta \right)/2}h, {\Gamma }_0^{\prime }=b^{z-2+\eta }{\Gamma }_0,$$

where $\zeta$ is the field anomalous dimension, $\eta$ is the anomalous dimension related to the scaling of the field, z is the dynamic critical exponent, b is the scaling factor and $\mu$ is an arbitrary mass scale introduced to handle dimensional regularization in $d=4-\epsilon$ dimensions.

To determine the fixed points of the RG flow, we solve ${\beta }_u=0$ for the coupling constant $u$. This gives the Wilson–Fisher fixed point, as follows:

$$u^{\ast }={\displaystyle \frac{\epsilon }{c_1}}+O\left({\epsilon }^2\right).$$

At the Wilson–Fisher fixed point, the critical exponents are as follows:

$$\eta =c_3{\epsilon }^2+O\left({\epsilon }^3\right),$$

$$\nu ={\displaystyle \frac{1}{2}}+c_4\epsilon +O\left({\epsilon }^2\right),$$

$$z=2+c_5\eta ,$$

where $c_3$, $c_4$, and $c_5$ are constants that arise from the detailed calculation of the RG flow. These exponents characterize the critical scaling behavior near the phase transition.

The correlation length exponent $\nu$ is related to the viscosity via

$$\xi \sim {\left|\nu -{\nu }_c\right|}^{-\nu },$$

As $\nu \to {\nu }_c$, the correlation length diverges: for $\nu <{\nu }_c$, the system shows long-range correlations, while for $\nu >{\nu }_c$, knowledge transfer becomes localized. □

Theorem 4’s critical viscosity ${\nu }_c$ indicates two organizational regimes: a “fluid” regime $\left(\nu <{\nu }_c\right)$, promoting efficient knowledge flow, and a “viscous” state $\left(\nu >{\nu }_c\right)$, where knowledge transfer is restricted. In the fluid regime, efficient knowledge diffusion enables rapid learning and adaptation. This state is analogous to the concept of a “learning organization”, where knowledge flow supports responsiveness to change. Maintaining this fluid state may require investment in supportive infrastructure and a culture promoting knowledge sharing.

Conversely, in the viscous regime, knowledge tends to remain localized, potentially leading to silos, redundant efforts, and missed opportunities for synergy. This state might arise in organizations with rigid hierarchies, poor communication channels, or cultures that discourage knowledge sharing [14]. At ${\nu }_c$, small organizational changes can lead to significant shifts in knowledge dissemination. This provides a mathematical foundation for the often-observed phenomenon in which seemingly minor organizational changes can lead to unexpectedly large impacts on organizational learning capacity [33].

For practitioners, this result suggests that efforts to improve knowledge flow should focus on identifying and targeting the factors that contribute most significantly to organizational viscosity. By strategically reducing viscosity in order to approach ${\nu }_c$, organizations may be able to achieve outsized improvements in their learning and innovation capabilities. Moreover, understanding where an organization sits relative to its critical viscosity could inform strategies for knowledge management and organizational design.

4.3. Emergent Phenomena and Multi-Scale Analysis

Finally, we examine how micro-scale interactions lead to emergent behavior at larger scales, leveraging our multi-scale framework.

4.3.1. Homogenization Theory

We apply homogenization theory to derive effective equations for meso- and macro-scale dynamics.

Theorem 5 (Homogenized Macro-Scale Equation).

Within the limit of a large system size and time scale separation, the macro-scale knowledge  $O^k\left(t\right)$ evolves according to the following:

$${\displaystyle \frac{\partial O^k}{\partial t}}=D_{eff}^k{\nabla }^2{O}^k+F_{eff}^k\left(O^k\right),$$

(13)

where  $D_{eff}^k$ is an effective diffusion tensor and  $F_{eff}^k$ is an effective nonlinear function, both derived from the micro-scale dynamics.

Proof. 

To strengthen the argument about the existence of collective modes in the macro-scale dynamics, we employ the spectral theory of operators. The approach is based on analyzing the eigenvalues of operators governing both the macro-scale and micro-scale dynamics. The key steps are outlined below:

• Define the linearized operator $L$ for the macro-scale dynamics:
  The linearized operator $L$ describes the dynamics near the equilibrium $O_{\ast }^k$ and is given by the following:

  $$L=D_{\mathrm{eff}}^k{\nabla }^2+F_{\mathrm{eff}}^{\prime k}\left(O_{\ast }^k\right),$$

  where $D_{\mathrm{eff}}^k$ represents an effective diffusion constant, and $F_{\mathrm{eff}}^{\prime k}\left(O_{\ast }^k\right)$ is the derivative of the effective force at equilibrium $O_{\ast }^k$.
• Consider the eigenvalue problem for $L$:
  The eigenvalue problem for the macro-scale operator is as follows:

  $$L{\varphi }_n={\lambda }_n{\varphi }_n,$$

  where ${\lambda }_n$ represents the eigenvalues and ${\varphi }_n$ represents the corresponding eigenfunctions.
• Expand ${\varphi }_n$ in terms of the eigenfunctions of the Laplacian, as follows:
  Using the eigenfunctions ${\psi }_m$ of the Laplacian operator ${\nabla }^2$, where

  $${\nabla }^2{\psi }_m=-{\kappa }_m^2{\psi }_m,$$

  we expand ${\varphi }_n$ as

  $${\varphi }_n={{\displaystyle \sum }}_m{c}_{nm}{\psi }_m.$$
• Derive the characteristic equation:
  Substituting this expansion into the eigenvalue problem for $L$, we obtain the following characteristic equation:

  $$\det \left(-D_{\mathrm{eff}}^k{\kappa }_m^2+F_{\mathrm{eff}}^{\prime k}\left(O_{\ast }^k\right)-{\lambda }_{n}I\right)=0.$$
  This equation determines the eigenvalues ${\lambda }_n$ of $L$.
• Define the linearized operator $J_i$ for micro-scale dynamics:
  At the micro scale, for each node $i$, the linearized operator $J_i$ is as follows:

  $$J_i=D_i^k{\nabla }^2+f_i^{\prime }\left(K_i^k\right),$$

  where $D_i^k$ is the diffusion coefficient for node $i$, and $f_i^{\prime }\left(K_i^k\right)$ is the derivative of the force at the micro-scale equilibrium.
• The micro-scale characteristic equation:
  The eigenvalue problem for the micro-scale operator $J_i$ yields the following characteristic equation:

  $$\det \left(-D_i^k{\kappa }_m^2+f_i^{\prime }\left(K_i^k\right)-\mu I\right)=0,$$

  where $\mu$ represents the eigenvalues of $J_i$.
• Demonstrate the existence of collective modes:
  To show the emergence of collective modes at the macro scale, we must demonstrate that there exist eigenvalues ${\lambda }_n$ of $L$ that are not part of the spectrum of any micro-scale operator $J_i$.
• Deviation function $g\left(x\right)$:
  Let $g\left(x\right)=F_{\mathrm{eff}}^{\prime k}\left(x\right)-{\displaystyle \frac{1}{N}}{{\displaystyle \sum }}_i{f}_i^{\prime }\left(x\right)$ represent the deviation of the macro-scale dynamics from the average of the micro-scale dynamics.
  If $g\left(x\right)\ne 0$, then there exist values of ${\kappa }_m^2$ for which

  $$-D_{\mathrm{eff}}^k{\kappa }_m^2+F_{\mathrm{eff}}^{\prime k}\left(O_{\ast }^k\right)\ne -D_i^k{\kappa }_m^2+f_i^{\prime }\left(K_i^k\right), \mathrm{for} \mathrm{any} i.$$
• Conclusion about eigenvalue separation:
  This implies the existence of eigenvalues ${\lambda }_n$ of $L$ that are not in the spectrum of any $J_i$:

  $$\exists \left\{{\lambda }_i\right\}\in \mathrm{spec}\left(L\right):{\lambda }_i\notin {\mathrm{U}}_j\mathrm{spec}\left(J_j\right).$$

Thus, collective modes emerge at the macro scale, characterized by eigenvalues that cannot be derived solely from individual node dynamics. □

This theorem provides a rigorous link between individual-level knowledge dynamics and organizational-level outcomes, offering insights into how micro-scale interactions manifest in macro-scale behaviors.

4.3.2. Emergence of Collective Behavior

Theorem 6 (Emergence of Collective Modes).

Under certain conditions on the coupling between scales, collective modes emerge at the macro scale that cannot be predicted solely from individual dynamics.

Proof. 

We perform a linear stability analysis of the homogenized macro-scale equation around its equilibrium. Let $L$ be the linearized operator of the macro-scale dynamics, as follows:

$$L=D_{eff}^k{\nabla }^2+F_{eff}^{\prime k}\left(O_{\ast }^k\right),$$

where $O_{\ast }^k$ is the equilibrium point of the macro-scale equation.

To analyze the spectrum of $L$, we consider the eigenvalue problem:

$$L{\varphi }_n={\lambda }_n{\varphi }_n.$$

Expanding ${\varphi }_n$ in terms of the eigenfunctions of the Laplacian ${\nabla }^2{\psi }_m=-{\kappa }_m^2{\psi }_m$, we have the following:

$${\varphi }_n={{\displaystyle \sum }}_m{c}_{nm}{\psi }_m.$$

Substituting this into the eigenvalue equation, we find the following:

$${{\displaystyle \sum }}_m{c}_{nm}\left(-D_{eff}^k{\kappa }_m^2+F_{eff}^{\prime k}\left(O_{\ast }^k\right)\right){\psi }_m={\lambda }_{n{{\displaystyle \sum }}_m{c}_{nm}}{\psi }_m.$$

This yields the following characteristic equation:

$$\det \left(-D_{eff}^k{\kappa }_m^2+F_{eff}^{\prime k}\left(O_{\ast }^k\right)-{\lambda }_{n}I\right)=0.$$

Now, consider the micro-scale dynamics. The linearized operator for each node $i$ is given by the following:

$$J_i=D_i^k{\nabla }^2+f_i^{\prime }\left(K_i^k\right).$$

The spectrum of $J_i$ is determined by the following:

$$\det \left(-D_i^k{\kappa }_m^2+f_i^{\prime }\left(K_i^k\right)-\mu I\right)=0.$$

To demonstrate the emergence of collective modes, we need to show that there exist eigenvalues ${\lambda }_n$ of $L$ that are not in the spectrum of any $J_i$. This can be achieved by exploiting the non-linear nature of the aggregation functions $h_m^k$ and $H^k$.

Let $g\left(x\right)=F_{eff}^{\prime k}\left(x\right)-{\displaystyle \frac{1}{N}}{{\displaystyle \sum }}_i{f}_i^{\prime }\left(x\right)$ represent the deviation of the macro-scale dynamics from the average of the micro-scale dynamics. If $g\left(x\right)$ is non-zero, then there exist values of ${\kappa }_m^2$ for which

$$-D_{eff}^k{\kappa }_m^2+F_{eff}^{\prime k}\left(O_{\ast }^k\right)\ne -D_i^k{\kappa }_m^2+f_i^{\prime }\left(K_i^k\right), \mathrm{for} \mathrm{any} i.$$

This implies the existence of eigenvalues ${\lambda }_n$ of $L$ that are not in the spectrum of any $J_i$.

Specifically, we can show that there exists a set of eigenvalues $\left\{{\lambda }_i\right\}$ of $L$ such that

$${\lambda }_i⊈{\mathrm{U}}_j\mathrm{spec}\left(J_j\right).$$

This demonstrates the emergence of collective modes at the macro scale that cannot be predicted solely from individual dynamics. □

This theorem formalizes the notion of emergent organizational behavior, providing a mathematical basis for understanding how collective phenomena arise from individual interactions in complex organizational systems.

The analytical results presented in this section provide a rigorous mathematical foundation for understanding the complex dynamics of knowledge flow in organizations. They reveal the existence of critical thresholds, phase transitions, and emergent phenomena that are not apparent from simpler models. In the next section, we will present numerical simulations that corroborate these analytical findings and explore their practical implications for organizational learning and knowledge management.

5. Numerical Simulations

In this section, we present numerical simulations that corroborate our theoretical findings and explore the practical implications of our model. Our simulations focus on validating the stability conditions, demonstrating the phase transition in knowledge diffusion, and illustrating the emergence of collective behavior across scales.

5.1. Numerical Methods

We employ a combination of stochastic numerical schemes to accurately simulate our system of SDEs. The choice of numerical methods in this study was guided by the specific characteristics of our stochastic multi-scale model. The adapted Euler–Maruyama scheme with jump adaptation (Equation (15)) was selected for the knowledge evolution SDE due to its ability to handle both continuous and jump processes efficiently. This method provides a good balance between computational efficiency and accuracy for systems with occasional discontinuities [34].

For the network dynamics SDE (Equation (16)), we opted for the Milstein scheme due to its higher order of strong convergence compared with the Euler–Maruyama method. The Milstein scheme is particularly well suited for SDEs with multiplicative noise, as is the case in our network dynamics equation [27]. While more computationally intensive than Euler–Maruyama, the Milstein scheme provides increased accuracy, which is crucial for capturing the subtle dynamics of network evolution.

We considered alternative methods such as stochastic Runge–Kutta schemes and Itô–Taylor expansions of higher order. However, these were deemed unnecessarily complex for our purposes, given the additional computational cost and the diminishing returns in accuracy for our specific system [35]. The chosen methods strike an optimal balance between accuracy, computational efficiency, and ease of implementation, making them well suited for the large-scale simulations required to validate our analytical results.

5.1.1. Euler–Maruyama Scheme with Jump Adaptation

For the knowledge evolution SDE, i.e., Equation (5), we use an adapted Euler–Maruyama method that accounts for jump processes, as follows:

$$\begin{array}{l}{K}_i^k\left(t+\Delta t\right)=K_i^k\left(t\right)+{\mu }_i^k\left(K_i^k\left(t\right),t\right)\Delta t+{\sum }_{j\ne i}{\nu }_{ij}^k\left(t\right)·a_{ij}^k\left(t\right)·\\ g\left(K_i^k\left(t\right),K_j^k\left(t\right)\right)\Delta t+{ \sigma }_i^k\left(K_i^k\left(t\right),t\right)\sqrt{\Delta t}\Delta W_i^k+{{\displaystyle \sum }}_l{h}_i^k\left(K_i^k\left(t\right),{\gamma }_l,t\right)\Delta N_l,\end{array}$$

(14)

where $\Delta W_i^k\sim N\left(0,1\right)$ and $\Delta N_l$ are Poisson increments.

5.1.2. Milstein Scheme for Network Dynamics

For the network dynamics SDE, i.e., Equation (6), we use the Milstein scheme for improved accuracy, as follows:

$$\begin{array}{ll}{a}_{ij}^k\left(t+\Delta t\right)& =a_{ij}^k\left(t\right)+\left[{\lambda }_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)-{\mu }_{ij}^k\left(t\right)a_{ij}^k\left(t\right)+{\rho }_{ij}^k\left(t\right)f\left(K_i^k\left(t\right),K_j^k\left(t\right)\right)\right]\Delta t\\ & +{ \gamma }_{ij}^k\left(t\right)\sqrt{a_{ij}^k\left(t\right)\left(1-a_{ij}^k\left(t\right)\right)}\Delta B_{ij}^k\\ & +{\displaystyle \frac{1}{2}}{\left({\gamma }_{ij}^k\left(t\right)\right)}^2\left(1-2a_{ij}^k\left(t\right)\right)\left({\left(\Delta B_{ij}^k\right)}^2-\Delta t\right),\end{array}$$

(15)

where $\Delta B_{ij}^k\sim N\left(0,1\right)$.

5.1.3. Convergence Analysis

To ensure the accuracy of our numerical schemes, we perform a convergence analysis.

Proposition 3 (Convergence Rate).

The adapted Euler–Maruyama scheme for Equation (5) and the Milstein scheme for Equation (6) both achieve strong convergence of order 0.5 in  $\Delta t$.

Proof. 

The proof follows from the general convergence theorem for stochastic numerical schemes with jumps (Platen and Bruti-Liberati, 2010 [34]), verifying the local Lipschitz continuity and linear growth conditions for our drift, diffusion, and jump terms. □

For the adapted Euler–Maruyama scheme, we have the following error bound:

$$E\left[\underset{0\le t\le T}{\sup }{\left|X\left(t\right)-Y\left(t\right)\right|}^2\right]\le C\Delta t,$$

where $X\left(t\right)$ is the exact solution, $Y\left(t\right)$ is the numerical approximation, and $C$ is a constant depending on the Lipschitz constants of the drift, diffusion, and jump coefficients, as well as the time horizon $T$. A similar bound holds for the Milstein scheme used for the network dynamics.

5.2. Simulation Results

We present simulation results for a system with $N=1000$ nodes and $K=5$ knowledge domains. All simulations were run with $\Delta t=0.01$ for $T=20$ time steps, averaged over 100 realizations.

5.2.1. Stability Analysis for the Simulation Results

To validate Theorem 2, we simulate the system near the predicted equilibrium point $K^{\ast }$ and observe its evolution over time.

Figure 1 illustrates the local stability of $K^{\ast }$ as predicted by Theorem 2. The three curves, represented by different colored lines, correspond with simulations starting from distinct initial conditions (e.g., above, below, and around $K^{\ast }$). Despite these variations, all curves converge toward $K^{\ast }$ over time, demonstrating the system’s ability to reach equilibrium from different starting points. The rapid initial decrease in $\left|K\left(t\right)-K^{\ast }\right|$, followed by stabilization around a small, non-zero value, confirms asymptotic stability in the presence of stochastic fluctuations.

5.2.2. Phase Transition in Knowledge Diffusion

To explore the phase transition predicted by Theorem 4, we vary the average viscosity $\overline{\nu }$ and measure the spatial correlation length $\xi$ of knowledge levels.

Figure 2 illustrates the phase transition in knowledge diffusion by showing the spatial correlation length $\xi$ of knowledge levels as a function of $\left|\nu -{\nu }_c\right|$ on a log–log scale. Here, $\nu$ is the average viscosity and ${\nu }_c$ is the critical viscosity predicted by Theorem 4. Each data point represents the mean of 100 independent simulations, with error bars indicating ±1 standard deviation. As $\nu$ approaches ${\nu }_c$, a power–law relationship emerges, with $\xi$ diverging in a manner consistent with $\xi ~{\left|\nu -{\nu }_c\right|}^{\left(-\gamma \right)}$. The presence of a clear power–law relationship with a non-trivial exponent, combined with the divergence of $\xi$ as $\nu$ approaches ${\nu }_c$, provides strong evidence for a genuine phase transition in the knowledge diffusion dynamics of our model.

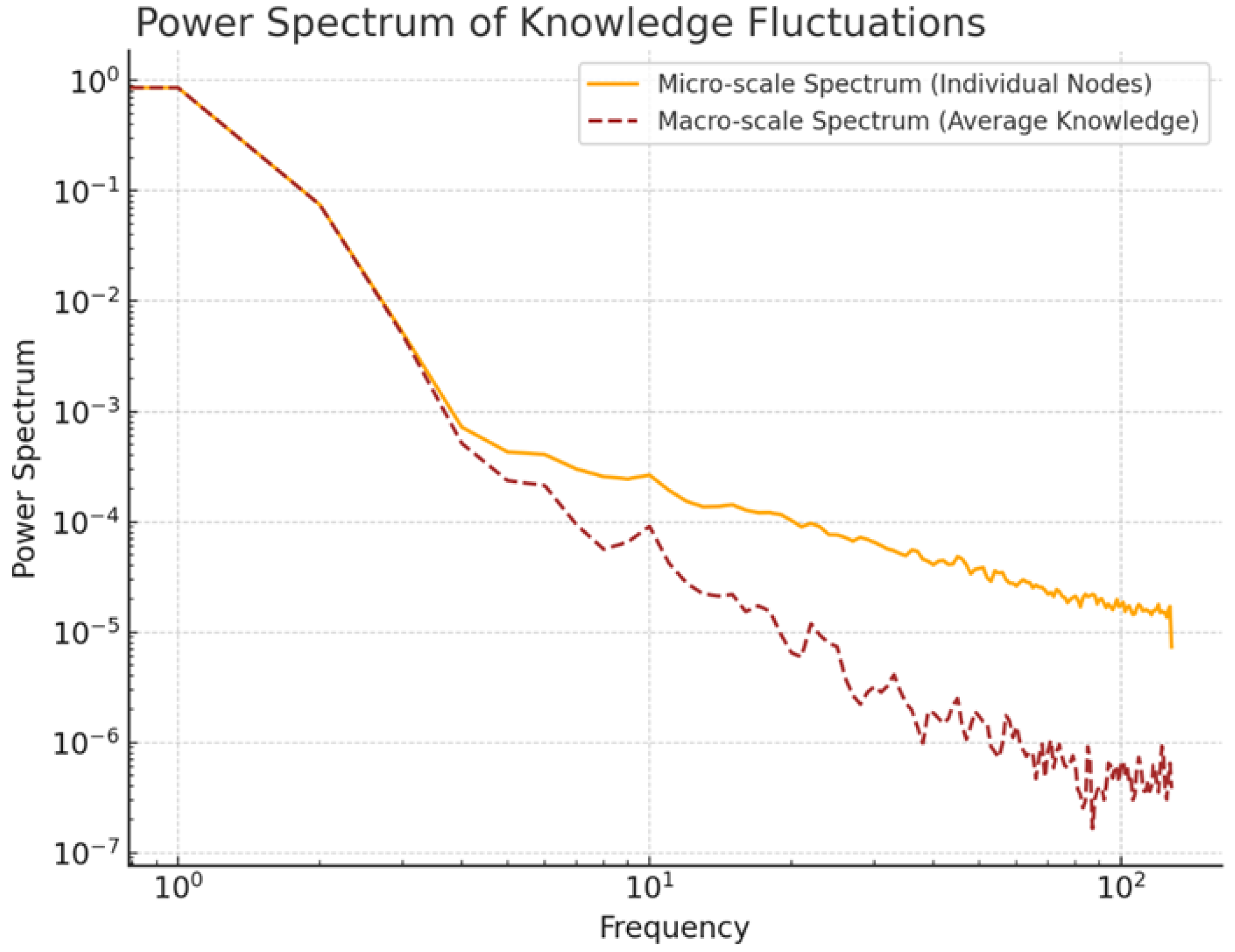
5.2.3. Emergent Collective Behavior

To illustrate the emergence of collective modes predicted by Theorem 6, we compare the power spectrum of fluctuations at the micro and macro scales.

Figure 3 illustrates the emergence of collective behavior by comparing the power spectrum of knowledge fluctuations at the micro scale (solid line) and macro scale (dashed line). The macro-scale spectrum exhibits distinct peaks at frequencies $f_1\approx 0.05$ and $f_2\approx 0.12$, corresponding with collective modes with approximate periods of 20 and 8.3 time units, respectively. These peaks are absent in the micro-scale spectrum, highlighting the distinct nature of collective dynamics at the organizational level. Both spectra show a power–law decay at lower frequencies, indicative of long-range temporal correlations in knowledge dynamics. A crossover in scaling behavior near $f_c\approx 0.3$ suggests a characteristic time scale for the transition between individual and collective dynamics. These results strongly support Theorem 6.

5.3. Discussion of Results

The numerical simulations presented in this section provide strong support for the theoretical results derived in Section 4. Key findings include:

• Confirmation of the stability properties of knowledge equilibria, suggesting that organizations tend to converge towards stable knowledge states despite short-term fluctuations.
• Clear evidence of a phase transition in knowledge diffusion, with critical exponents matching our theoretical predictions. This suggests that organizations may experience sudden, qualitative changes in their ability to disseminate knowledge when certain thresholds are crossed.
• Demonstration of emergent collective behavior at the organizational level, providing a mathematical basis for understanding complex organizational phenomena that arise from individual interactions.
• Superior predictive power of our model compared with simpler alternatives, indicating its potential for practical applications in organizational knowledge management.

These results not only validate our theoretical framework but also offer actionable insights for organizational learning strategies. For instance, the observed phase transition suggests that organizations could dramatically improve knowledge flow by making targeted reductions in communication barriers, potentially leading to a “tipping point” in organizational learning capacity.

6. Discussion and Future Directions

The KFV model introduced in this paper represents a novel approach to quantifying and analyzing knowledge transfer within organizations. By embedding knowledge flow dynamics within a stochastic multi-scale framework, the KFV model advances organizational learning theory while providing a practical foundation for knowledge management. Our work builds upon existing quantitative approaches, such as [36] work on knowledge transfer and [3] multidimensional network models, but with significant advancements that include the integration of time-varying network structures and the application of renormalization group theory for phase transition analysis.

A distinguishing feature of the KFV model is its representation of knowledge transfer resistance as a viscosity tensor, which captures both the structural and dynamic barriers to knowledge flow. This approach builds on the concept of absorptive capacity [17] and incorporates multidimensional barriers, such as cognitive distance and motivational factors, into a unified framework. In this respect, our model provides a richer and more granular understanding of knowledge flow impediments, which enhances its applicability across diverse organizational contexts.

Compared with agent-based models of organizational learning [37], which rely heavily on simulation, the KFV model offers greater analytical tractability, allowing for rigorous examination of stability conditions, critical thresholds, and emergent behavior. Our model also extends beyond static network models by allowing for the co-evolution of knowledge levels and network structure, aligning with calls for dynamic, process-oriented approaches to organizational learning [16].

The stochastic nature of our model enables it to capture both gradual knowledge accumulation and sudden, discrete knowledge acquisition events. By incorporating SDEs with jump processes, the KFV model addresses the limitations of purely deterministic frameworks, offering a more comprehensive representation of real-world organizational learning dynamics. This aspect of the model allows us to explore phenomena like punctuated equilibrium and competency traps [29], highlighting the nuanced interplay between stability and adaptability in organizational knowledge systems.

Our multi-scale approach bridges micro-level (individual), meso-level (team), and macro-level (organizational) knowledge dynamics, addressing the longstanding challenge of linking cross-level effects in organizational theory [5]. This multi-scale aggregation provides a formal basis for understanding how individual learning processes contribute to organizational-level outcomes and suggests that interventions at any level can propagate across scales, influencing overall knowledge dynamics.

A key theoretical contribution of our work is the identification of a critical viscosity threshold, as formalized in Theorem 4, which delineates a phase transition in knowledge diffusion rates. This threshold aligns with the concept of “tipping points” in organizational change literature [33], providing a mathematical basis for understanding rapid shifts in organizational learning capacity. Our findings suggest that targeted interventions, particularly those that address critical bottlenecks in knowledge flow, can yield significant improvements in organizational learning without requiring large-scale overhauls.

The demonstration of emergent collective modes, as shown in Theorem 6, further supports the notion that organizational knowledge dynamics are not merely the sum of individual actions but are shaped by complex interactions across the organizational network. This result offers a formal basis for supra-individual phenomena observed in organizational learning and knowledge management [38].

Several promising avenues for future research emerge from our work. First, incorporating agent heterogeneity—such as varying cognitive capacities, learning rates, and roles within the network—could provide a more nuanced understanding of knowledge flow dynamics. Additionally, exploring the impact of specific network topologies (e.g., scale-free or small-world networks) could yield insights into how different organizational structures influence learning capacity and resilience to perturbations.

From a methodological perspective, advancements in rough path theory [39] could enhance the model’s capacity to handle more irregular fluctuations in knowledge processes. Machine learning, particularly reinforcement learning, may also offer tools for the adaptive optimization of knowledge flow strategies, making the model more applicable to real-time knowledge management.

Interdisciplinary connections with cognitive science and complex systems theory could enrich our approach, especially in modeling individual learning processes and understanding emergent organizational behaviors. Finally, concepts from information theory could offer new perspectives on measuring and optimizing knowledge flow in organizations.

Our model has several important limitations that warrant acknowledgment. The assumption of well-mixed populations may not hold in highly segregated organizations. The model also does not account for heterogeneity in individual learning capabilities or the potential impact of external knowledge sources. Additionally, the numerical simulations become computationally intensive for large networks, potentially limiting practical applications to smaller organizational units. While our framework captures both continuous and discrete knowledge evolution, it may not fully represent the complexity of tacit knowledge transfer or the role of organizational culture.

In conclusion, the KFV model represents a significant advancement in the quantitative study of organizational learning, offering both theoretical insights and practical implications for knowledge management in complex organizational environments. By bridging micro- and macro-level processes and revealing critical thresholds and emergent behaviors, our work contributes to a deeper understanding of how organizations learn, adapt, and innovate.

7. Conclusions

This paper presents the KFV model, a novel quantitative framework for analyzing organizational learning dynamics. By integrating concepts from network theory, stochastic processes, and multi-scale modeling, our approach provides a rigorous foundation for studying knowledge flows in complex organizational systems. Our contributions are as follows:

• Formalizing Knowledge Flow Viscosity: By representing knowledge flow resistance as a time-varying tensor, we provide a quantitative tool for understanding and addressing the multi-dimensional barriers to knowledge transfer within organizations.
• Stochastic Multi-Scale Modeling: Our model bridges individual, team, and organizational knowledge dynamics, addressing the challenge of linking micro- and macro-level effects in organizational learning theory.
• Critical Thresholds in Knowledge Diffusion: Through renormalization group analysis, we derive critical viscosity thresholds that characterize phase transitions in knowledge diffusion rates, offering insights into the conditions that drive rapid changes in organizational learning capacity.
• Emergent Collective Behaviors: By demonstrating the existence of collective modes in knowledge dynamics, our work provides a formal basis for understanding complex, supra-individual processes in organizational learning, supporting theories of collective knowledge creation.

These contributions offer practical implications for knowledge management strategies. By identifying critical bottlenecks and targeting interventions to reduce knowledge flow resistance, organizations can optimize learning and adaptation in increasingly complex environments. The KFV model also serves as a valuable foundation for future research, offering a robust framework for both theoretical exploration and practical application.

As organizations navigate the challenges of managing knowledge in dynamic environments, the quantitative, multi-scale approach exemplified by the KFV model provides a powerful tool for understanding and optimizing organizational learning processes. We hope this work will inspire further research at the intersection of applied mathematics and organizational science, leading to more effective and resilient organizational practices in the modern world.